I frequently receive the question – how do we ascertain the distances to faraway stars? Take, for instance, a star situated 100 light years away, how can we be certain of its distance? In this article, I will elucidate a time-honored technique for determining the distance to stars. This technique is known as the one-year stellar parallax method..
History
Parallax is the phenomenon where the position of a stationary object appears to change depending on the observer’s location. The ancient Greek scientist Aristarchus of Samos first suggested using parallax to measure the distance to stars. However, with the methods available at the time, he was unable to detect any visible parallax in the stars he observed. He correctly concluded that the stars were too far away for their parallax to be observed.
The concept that parallax could serve this purpose emerged as a result of the belief that the Sun orbited around the Earth. Regrettably, Europe entered a period of intellectual decline known as the Dark Ages, during which the geocentric model of the universe reigned for nearly two millennia. The absence of parallax was considered as evidence against the Earth’s rotation around the Sun.
In the 17th century, certain astronomers asserted that they had detected the parallax of certain stars. However, it is likely that these claims were the result of errors and imprecise measurements. The techniques available to them were too imprecise for determining parallax accurately.
In 1837, the Russian astronomer Vasily Yakovlevich Struve became the first person to accurately determine the parallax of stars. Shortly after, his achievement was replicated by the German astronomer Friedrich Bessel and the Englishman Thomas Henderson. However, during this time, measurements were still prone to significant inaccuracies, with variations of up to 20-30 percent in parallax measurements of the same star. The introduction of photography revolutionized the field, as astronomers were no longer reliant on sketching their observations through telescopes, which often led to errors and inaccuracies. Today, ultra-long-range radio interferometry is utilized to achieve incredibly precise measurements for parallax determination.
Using parallax to calculate the distance to stars
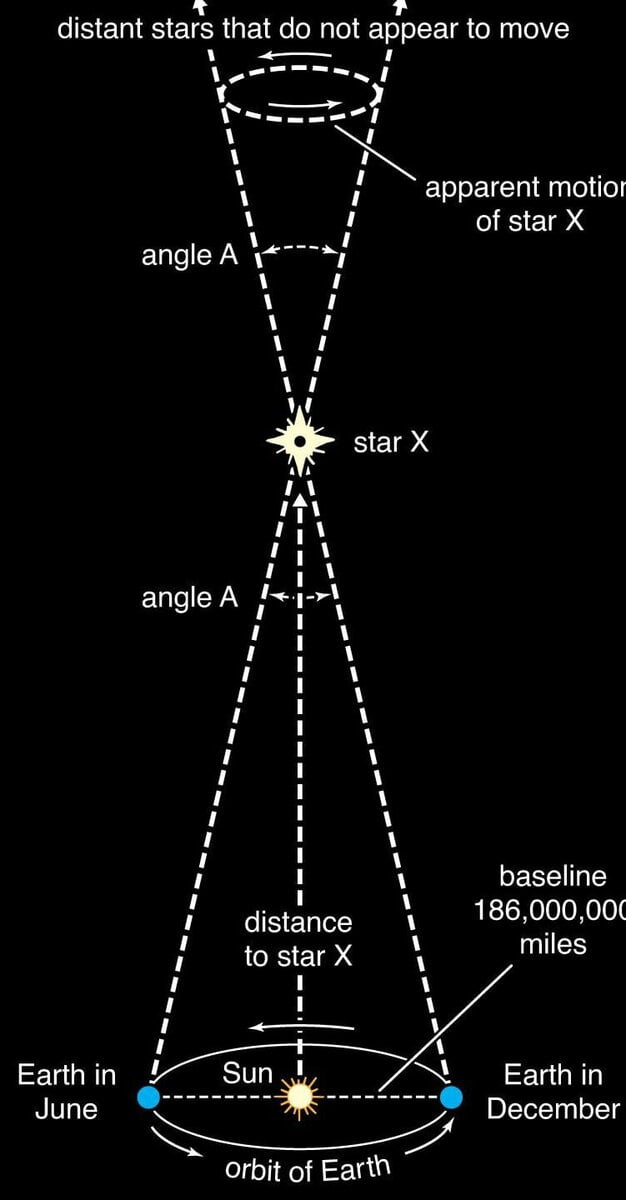
By knowing the distance between the observation points and the angle of parallax, it becomes quite simple to determine the distance to an object.
With the use of basic geometry principles, this distance can be calculated by dividing the distance between the observation points (L) by twice the sine of half the parallax angle (α).
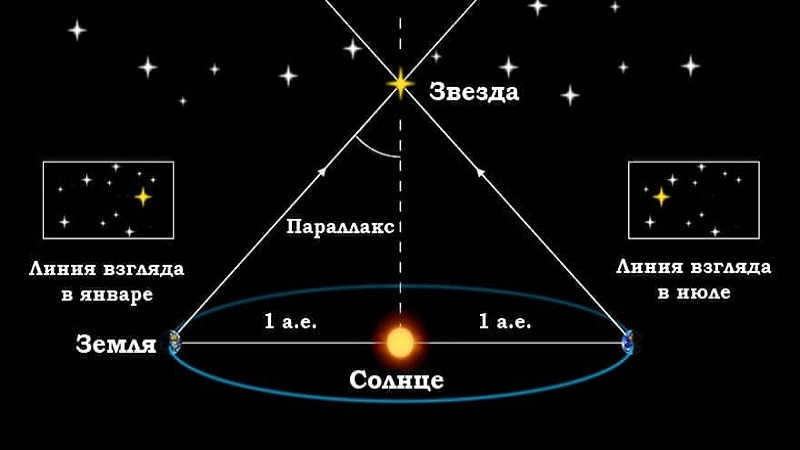
The points opposite each other on Earth’s orbit are typically selected as the measurement points for parallax.
As we can observe, the Earth’s positions on different sides of the Sun, along with the star being studied, form various triangles. The median of this triangle (which is the line connecting the star under investigation and the Sun) represents the desired distance.
Thanks to the technique of parallax, we have a unique unit of measurement for astronomical distances called the parsec (abbreviated as par alx-sec nda ). The parsec is defined as the distance to a star with a parallax angle of 1 arc second and is approximately equal to 3.26 light-years.
P.S. Although there are other methods available to measure distances to stars and galaxies, such as spectral analysis (known as spectral parallax), Tully-Fisher and Faber-Jackson sequences, in this article I am specifically focusing on the most fundamental and easily understandable method.
Make sure to subscribe to my channel and also to my Telegram channel . There, you can find a wealth of interesting material and get the opportunity to ask your own questions.

The measurement of distances to faraway celestial objects, like stars, is not directly possible. Instead, scientists rely on measurable characteristics of these objects, such as their brightness or the periodic variations in their coordinates, to calculate their distances. Various methods have been devised to determine stellar distances, each with its own limitations. Now, let’s examine in detail the process of how scientists ascertain the distance to stars.
Utilizing parallax
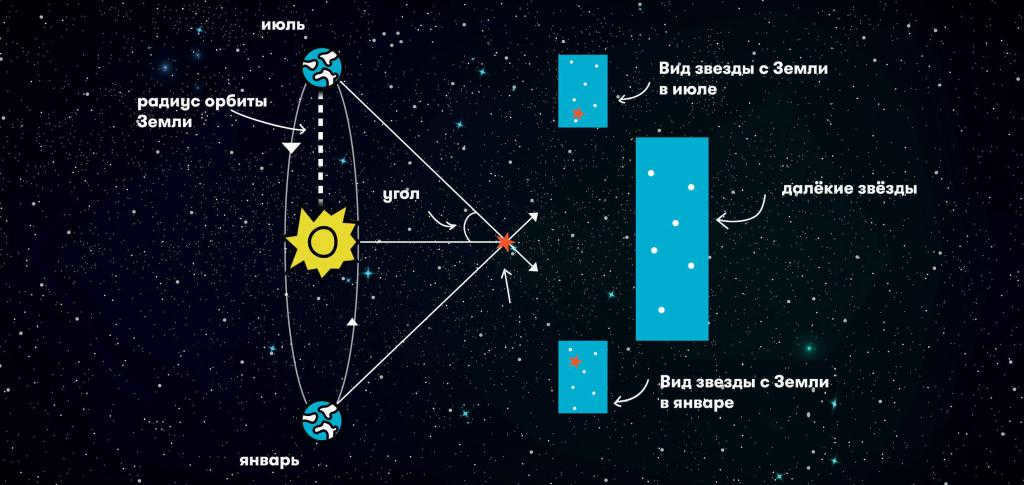
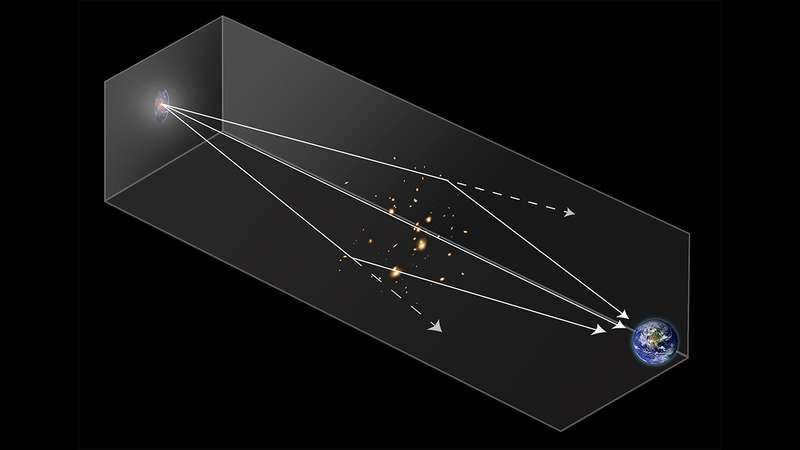
Parallax refers to the shift in position of an observed object in relation to a distant background when the observer’s viewpoint changes. By knowing the distance between the observation points (known as the parallax baseline) and the angular displacement of the object, it becomes straightforward to calculate its distance. The smaller the displacement, the greater the distance of the object. Interstellar distances are vast, so to maximize the angle, the largest possible baseline is utilized – the position of the star is measured at opposite points of the Earth’s orbit. This technique is known as stellar annual parallax.
Understanding how the distance to stars is measured using the stellar annual parallax method has become simpler. The measurement is derived from one side of a triangle formed by the observer, the Sun, and the distant star. The formula to calculate the distance is r = a/sin p, where: r represents the distance to the star, a is the distance from the Earth to the Sun, and p is the annual parallax of the star. Given that the parallax of all stars is less than 1 arc second (1”), the sine of the small angle can be approximated by the angle itself in radian measure: sin p ≈ p”/206265. Consequently, the formula becomes: r = a∙206265/p”, or, in astronomical units, r = 206265/p”.
Units of interstellar distances
Interstellar distances are often measured in various units. One commonly used unit is the parsec, which is equal to 206,265 astronomical units or approximately 30.8 trillion kilometers. Another commonly used unit is the light-year, which represents the distance that electromagnetic waves travel in a vacuum over the course of a year without being influenced by gravitational fields. One light-year is equal to about 9.5 trillion kilometers or approximately 0.3 parsecs. Therefore, one parsec is roughly equivalent to 3.26 light-years.
Accuracy of the parallactic approach
The precision of measuring parallax under terrestrial circumstances presently enables the calculation of star distances up to 200 parsecs. Subsequent enhancements in precision are attained through observations conducted with space telescopes.

Despite this limitation, the trigonometric parallax method is utilized as a reference point for calibrating other techniques for calculating distances to stars.
Astronomical Photometry. Understanding Stellar Magnitude
Astronomical photometry involves the measurement of the intensity of electromagnetic radiation emitted by celestial objects, including those in the optical range. Various methods, based on photometric parameters, are employed to determine the distance to stars as well as other remote entities, such as galaxies. One of the fundamental concepts utilized in photometric techniques is stellar magnitude, also known as luminosity (represented by the symbol m ).
The measurement of visible stellar magnitude is based on the brightness of the star and is represented on a scale where an increase in magnitude signifies a decrease in brightness (as established historically). For instance, the Sun has an apparent stellar magnitude of -26.7 m, Sirius has a magnitude of -1.46 m, and Proxima Centauri, the closest star to the Sun, has a magnitude of +11.05 m.

The absolute stellar magnitude is a calculated value that represents the apparent magnitude of a star if it were located at a distance of 10 pc. This parameter is used to compare the brightness of different stars based on their distance. For example, the Sun has an absolute magnitude of +4.8 m, Sirius has an absolute magnitude of +1.4 m, and Proxima has an absolute magnitude of +15.5 m. These stars are located at distances of 0.000005, 2.64, and 1.30 parsecs, respectively. The differences in their absolute magnitudes reflect variations in their luminosity, which is a crucial astrophysical property.
Spectra and brightness of celestial bodies
Scientists refer to the overall energy emitted by a star (or any other object) per unit of time as its luminosity, denoted as L. Luminosity can be determined using the absolute magnitude of a star, but unlike this magnitude, it is not affected by the distance between the star and the observer.
This Hertzsprung-Russell diagram provides a means of approximating the absolute luminosities of stars based on their spectral classes. By establishing a simple relationship between absolute magnitude, apparent magnitude, and distance, we can effectively determine the distances to these celestial bodies. The formula for this process is as follows: lg r = 0.2(m – M)+1. In this equation, r represents the distance, m signifies the apparent magnitude of the star, and M represents the absolute magnitude. Although the accuracy of this method may not be perfect, it does allow us to make a rough estimation of the distance.
There are certain stars whose luminosity can be uniquely determined based on a specific physical parameter. As a result, astronomers are able to accurately calculate the distance to these stars by analyzing the decrease in light intensity according to the inverse square law. The smaller the apparent brightness of the star, the greater its distance from us. Some examples of such stars include Cepheids and Type Ia supernovae.
Cepheids are a type of variable star whose luminosity is directly related to their pulsation period. By measuring the luminosity and period of a Cepheid, it is possible to easily determine its distance. Cepheids tend to be extremely bright, and with the help of modern telescopes, astronomers can observe Cepheids in other galaxies and use them to calculate the distance to those galaxies.

Supernovae of Type Ia are explosions that occur in binary star systems when a star reaches a critical mass value. These explosions always have the same luminosity and luminosity decay pattern, which enables us to calculate the distance. The brightness of supernovae can be equivalent to the brightness of an entire galaxy, allowing astronomers to estimate distances on a cosmological scale of billions of parsecs.
The most distant
A large number of individuals are familiar with the nearest star to our planet – Proxima Centauri. However, among the stars currently identified, which one is situated at the greatest distance?

So, what is the farthest star that we know of in the entire Universe? Its name is MACS J1149+2223 Lensed Star-1, or simply LS1, and it is located a staggering 9 billion light-years away. The discovery of this star is truly remarkable, as it was only made possible through a fortunate gravitational microlensing event in a distant galaxy that was itself lensed by a closer cluster of galaxies. To calculate the distance to LS1, astronomers utilized a different technique known as cosmological redshift. This method is employed to determine the distances to the most remote objects in the Universe, which cannot be observed as individual stars. LS1 serves as an extraordinary and captivating example of how scientists are able to gauge the distances to stars.
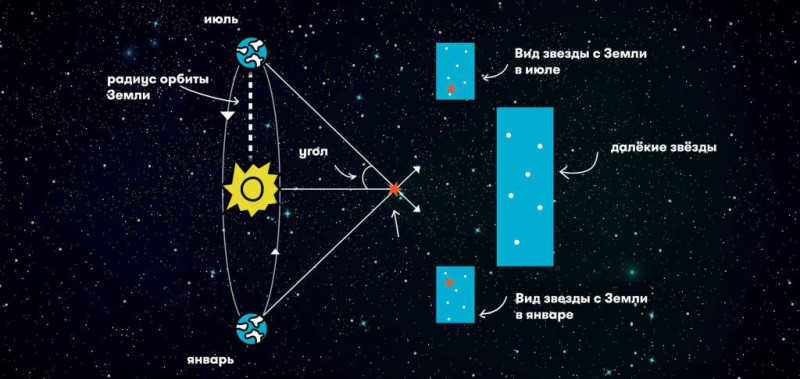
Distances to nearby stars are determined by scientists through the measurement of parallax. This involves observing how a nearby star appears to shift in relation to the background stars as the Earth orbits the Sun. It’s similar to how a finger appears to shift when you look at it with your left and right eyes through a window. The distance from the Earth to the Sun is already accurately measured, so it simplifies the process into a geometric problem of finding the dimensions of a triangle based on a known side and two angles.
In 1837, the Russian scientist Vasily Yakovlevich Struve (originally Friedrich Georg Wilhelm Struve) used this method at the Pulkovo Observatory to determine the distance to Vega, a bright bluish star that is particularly visible during the summer and fall.
Since 1989, the HIPPARCOS satellite has been using the same method to determine and refine distances to a million stars.
Approximate distances to distant stars are determined using statistical methods and recognized patterns. For instance, a specific class of variable stars known as Cepheids exhibit a noticeable correlation between the period of change in luminosity and their maximum brightness. Alternatively, the brightest stars within an object are sometimes utilized, as there exists a relatively clear upper limit to star brightness.
When gazing at the glittering night sky, the stars may not appear to be very far away. They seem like tiny specks in the vast universe. However, this is merely an illusion.
In reality, the stars are not minuscule, and the distance between them and us is akin to an enormous chasm. Furthermore, the gap between the stars themselves is also immense. Certainly, this may be difficult for us to comprehend, but it is not a challenge for the expanse of outer space.
Long ago, there was a belief that all celestial bodies were equidistant from each other. However, as the study of space progressed, perspectives began to shift.

How do scientists measure the distance to stars?
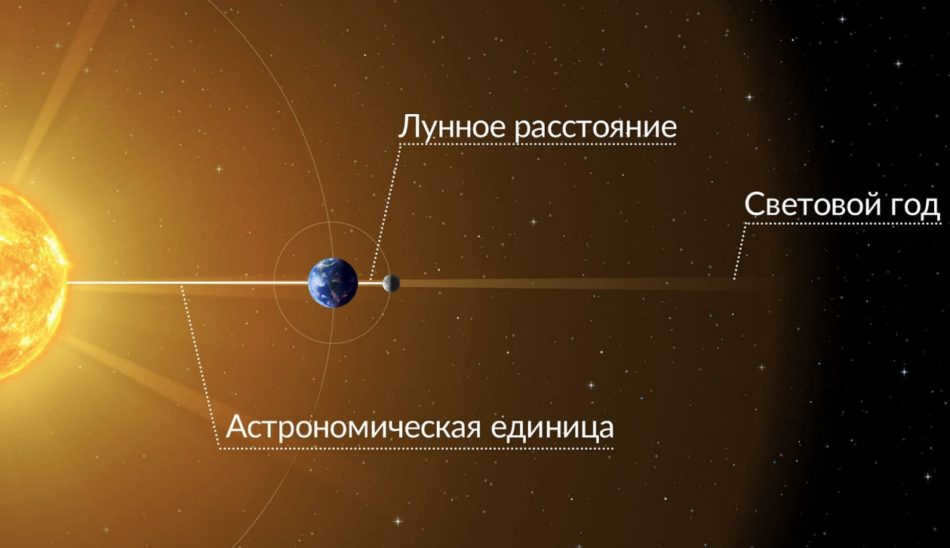
I am curious about the units that astronomers use to measure the distance to stars. Instead of using regular kilometers, astronomers use light-years or parsecs to measure the distance to stars and other celestial bodies.
A light-year is the distance that a light ray travels in one year, assuming its speed is equal to 300,000 kilometers per second. It’s mind-boggling to think that one light-year is equivalent to 9.5 trillion kilometers.
Using meters and kilometers to determine the distances between stars and from Earth to them is extremely challenging and problematic.
Furthermore, the megaparsec, which happens to be a million times larger than the standard one (equivalent to 3,260,000 light-years), can serve as a viable unit for quantification.

Techniques and Approaches for Measuring Stellar Distances
Human beings always seek to understand the properties, characteristics, and unique qualities of everything around us. In the present day, we have the ability to calculate any distance using practical and theoretical methods.
However, determining the distance to stars presents a unique challenge. The most commonly used method for this purpose is known as parallax.
Parallax refers to the apparent shift in the position of an object relative to a distant background, which is directly influenced by the observer’s perspective.
When it comes to calculating the distance to stars, scientists conduct observations from opposite sides of the Sun, with a 6-month interval between them. This allows them to measure the apparent shift in the position of the star and estimate its distance.
If a star were located 1 parsec or 3.26 light-years away from Earth, its parallax would be 1 second of arc. Fortunately, it is unlikely that there are any other stars situated so close to us.
Different methods for calculating the distance to stars
There are various techniques available for determining the distance to stars. One such method is the photometric approach, which involves measuring the illumination produced by sources of equal strength and power. The resulting illumination value is inversely proportional to the square of the distance between the bodies.
Another way to determine distances to stars is by analyzing their spectrum. This involves studying the chemical composition, physical characteristics, and spectra of the stars.
As it is common knowledge, the Sun is our nearest star. Hence, the distance to it is often measured in kilometers (149.6 million kilometers), which translates to 8.3 light minutes.
The vastness of the distances between stars and planets in our solar system is truly impressive. For instance, the distance between Earth and the planet Pluto is approximately 5 light hours, and the nearest star to us (Proxima Centauri) is located 4.2 light years away.
Just think about how much we already know and have access to, and how much more there is to discover about our Universe!


Proxima Centauri (a star that is considered to be one of the smallest in the universe).

Currently, there are additional cumulative discounts (ranging from 2% to 25%) available for 58,741 educational establishments. To determine the discount applicable to all staff members of your educational institution, please access your personal Infoworks account.


Enrich your professional skills with our specialized training program
Specialist in Occupational Safety and Health
In addition to this special offer, you may also be eligible for an educational institution discount (which depends on the number of your colleagues who have enrolled in Infoworks courses)
Currently, we provide additional discounts (ranging from 2% to 25%) to 58,741 educational institutions. To discover the discount available for all members of your educational institution, simply log in to your personal Infoworks account.


Professional retraining course
Organization of librarian activity in professional education
In addition to this discount, you can also take advantage of the discount offered by your educational institution, which is based on the number of colleagues who have already completed the Infowork course.
Currently, 58,741 educational institutions are eligible for additional discounts ranging from 2% to 25%. To determine the specific discount available to all employees of your educational institution, please log into your personal Infoworks account.


Clustering of Requests
Explanation of the presentation slide by slide:

2 slide The parallax method is used to determine distances to stars. This method has been known for over 2,000 years and was first applied to stars 160 years ago.
It involves measuring the small angular displacements of stars when observed from different positions along the Earth’s orbit, which occur at different times of the year.


On slide 3, scientists use the average radius of the Earth’s orbit, which is 1 astronomical unit (a.u.), as a reference point. This is because the distances to the stars are much greater than the distances to the bodies of the solar system.
They measure the annual parallax (π) to determine the distance to a star. The annual parallax is the angle at which the average radius of Earth’s orbit would be seen from the star, perpendicular to the direction to the star.

One parsec is equal to 3.26 light-years, which is equivalent to 206,265 astronomical units or 3.08∙1013 kilometers. The parallax of even the closest stars is smaller than 1 arcsecond. The concept of parallax is closely connected with the parsec, which is one of the fundamental units of distance measurement in astronomy. A parsec is defined as the distance to a star whose annual parallax is 1 arcsecond. There are also other units used in astronomy, such as the kiloparsec (1 kpc = 103 pc) and the megaparsec (1 Mpc = 106 pc). In addition to the parsec, another commonly used unit of distance is the light-year, which is the distance that light travels in one year (1 sv. yr. = 9.46∙1012 km). Therefore, in astronomy, the units of distance measurement include kilometers, astronomical units, gigaparsecs, and parsecs.


Slide 5: The parallax method is currently the most accurate way of determining distances to stars, but it is not applicable to stars that are more than 300 pc away from us. It requires measuring extremely small shifts in the position of stars – less than one hundredth of a second of arc!
The Hipparchus satellite accurately determined the distances to stars.


During ancient times, the brightest stars were referred to as stars of the first stellar magnitude. In the 2nd century BC, the Greek astronomer Hipparchus compiled a catalog of stars that were visible to the naked eye. He proposed a classification system that divided all visible stars into six classes. Hipparchus labeled the brightest stars as stars of the first magnitude. Additionally, the faintest stars were known as stars of the sixth magnitude, 6m. When telescopes are utilized, fractional, zero, and even negative apparent stellar magnitudes are employed. For instance, the Sun has an apparent magnitude of 26.8m. Hipparchus was instrumental in these early classifications.

When looking up at the sky without any telescopes, only a small number of stars, less than 6,000, can be seen. These stars are usually up to the sixth stellar magnitude. However, when using telescopes, the number of observable stars increases to billions upon billions. In the field of astronomy, scientists use the concept of luminosity I instead of the phrase “luminosity from a star.” The Milky Way can be seen near the Southern Cross.


In the 8th slide, it is stated that the difference in brightness between two stars at a distance of 5m is 100 times, which means that x5 = 100. Let’s convert this equation into logarithmic form:
So, for two stars with luminosities I1 and I2 and stellar magnitudes m1 and m2, there is a relationship:

Slide 9 The visible magnitudes of stars, denoted by m, do not provide any information about their luminosities, denoted by L, due to the variations in distances to the stars.
Absolute stellar magnitude, denoted by M, represents the apparent magnitude a star would have if it were located at the standard distance of 10 parsecs (r0 = 10 pc).
The relationship between absolute stellar magnitude M, apparent stellar magnitude m, and distance to the star r in parsecs can be expressed as follows:
By utilizing this equation, we can determine the distance to the star r in parsecs:


Slide 10: Let’s solve the problem.
Given that the equatorial coordinates of a bright star are α = 18h37m, δ = +38°47′, we need to determine what kind of star it is and calculate its distance in parsecs. We know that the apparent magnitude is 0.1m and the absolute magnitude is 0.5m.
Using the Windows Calculator or Excel spreadsheets, we can calculate the distance to be approximately 1092 parsecs, which is equivalent to about 8.3 parsecs or 27 light-years.
By consulting a star chart, we can identify this star as α Lyrae, also known as Vega. To verify the result, we can refer to the reference table in the textbook X “Basic information about bright stars visible in Russia,” which confirms the coincidence of our result.
Worksheets and resources for educators and teachers
Over 10,000 educational materials for learning at school and at home

The measurement of distances to faraway celestial objects, such as stars, is not directly attainable. Instead, scientists rely on various measurable characteristics of these objects, such as their luminosity or the periodic shifts in their positions, to calculate their distances. Multiple techniques have been developed to calculate stellar distances, each with its own specific range of applicability. Let us delve deeper into the process of how scientists determine the distances to stars.
Parallax refers to the shift in the apparent position of an object against a distant background when the observer’s viewpoint changes. By measuring the angular displacement of the object and knowing the distance between the observation points (known as the parallax baseline), it becomes possible to calculate the object’s actual distance. Generally, objects that have a smaller offset value are located further away. When it comes to interstellar distances, they are vast, so astronomers use the largest possible baseline which involves measuring the position of a star at opposite points of Earth’s orbit. This approach is known as stellar annual parallax.
Now, we can easily comprehend the methodology behind determining the distance to stars using the stellar annual parallax technique. This method involves calculating the distance as one side of a triangle formed by the observer, the Sun, and the distant star. To be precise, the distance (r) is equal to a divided by the sine of the annual parallax (p): r = a/sin p. Here, a represents the distance from the Earth to the Sun, while p denotes the annual parallax of the star. Since the parallaxes of all stars are smaller than 1 arc second (1″), we can approximate the sine of this small angle by the angle itself in radian measure: sin p ≈ p”/206265. Consequently, we obtain the following expression: r = a∙206265/p”, or, in terms of astronomical units, r = 206265/p”.
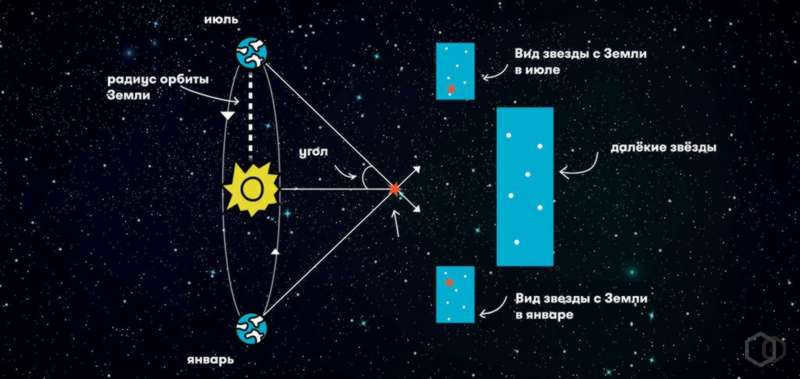
Measuring Distances Between Stars
It’s obvious that the resulting equation is not practical, especially when dealing with such enormous distances in kilometers or astronomical units. That’s why astronomers use the parsec (abbreviated as pc) as a standard unit for measuring interstellar distances. A parsec is defined as the distance to a star with an annual parallax of 1 second. With this unit, the equation becomes much simpler and more convenient: r = 1/p pc.
A parsec is equivalent to 206,265 astronomical units or roughly 30.8 trillion kilometers. Commonly used in popular literature and articles, the light-year is a unit of distance representing the travel of electromagnetic waves in a vacuum over the course of one year, unaffected by gravitational fields. Approximately 9.5 trillion kilometers or 0.3 parsecs, a light-year is equivalent to one parsec approximately 3.26 times.
The current ground-based conditions only permit the measurement of parallax to determine distances to stars up to 200 parsecs. To achieve even greater accuracy, observations must be conducted using space telescopes.


Therefore, the launch of the European satellite known as “Hipparchus” (HIPPARCOS) in 1989 resulted in two significant advancements. Firstly, it allowed for an increase in the distance measurement capability up to 1000 parsecs. Secondly, it significantly enhanced the accuracy of the previously known stellar distances. Another European satellite called Gaia, which was launched in 2013, further improved measurement precision by two orders of magnitude. Gaia provides astronomers with the ability to determine the distance to stars within a radius of 40 kiloparsecs and holds the potential for discovering new exoplanets. The Hubble Space Telescope also achieves a similar level of accuracy as Gaia, making it a valuable tool for optical measurements, potentially nearing the limits of its capabilities.
Despite its limitations, the trigonometric annual parallax serves as a reference point for calibrating other techniques for measuring distances to stars.
Photometry: Understanding Stellar Magnitude
Photometry in astronomy involves measuring the intensity of electromagnetic radiation emitted by celestial objects, particularly in the optical range. Various techniques rely on photometric parameters to determine distances to stars and other objects like galaxies. One important concept in photometry is stellar magnitude, also known as luminosity (represented by the symbol m).

Absolute stellar magnitude is a derived value that represents the apparent magnitude a star would have if it were located at a distance of 10 parsecs. This value is used to compare the brightness of different objects based on their distance. For example, the Sun has an absolute magnitude of +4.8, Sirius has an absolute magnitude of +1.4, and Proxima has an absolute magnitude of +15.5. These values reflect the different luminosities of these stars, which are located at distances of 0.000005, 2.64, and 1.30 parsecs, respectively.
Spectra and brightness of stars
The total energy emitted by a star (or any other object) per unit time, known as luminosity L, is a term used by astronomers. Luminosity can be calculated using the absolute stellar magnitude, but unlike magnitude, it does not rely on distance.
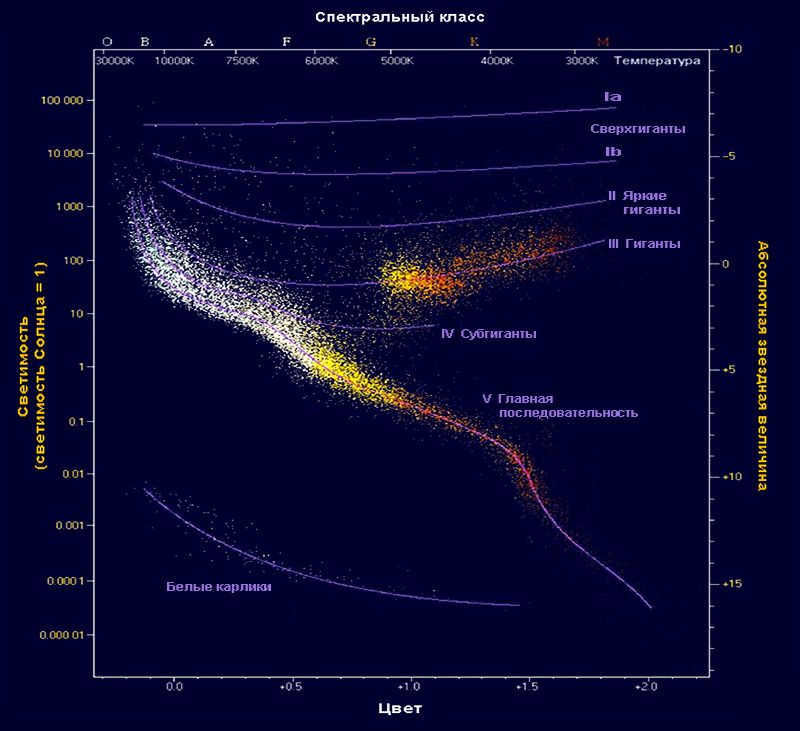
Stars are classified into different spectral classes based on their emission spectrum, which primarily indicates their temperature (which in turn determines their color). Generally, stars of the same spectral class have similar luminosity (although there are exceptions, which can be identified by analyzing the spectrum). The relationship between “spectrum – luminosity” (or “color – stellar magnitude”) is illustrated on the Hertzsprung-Russell diagram.
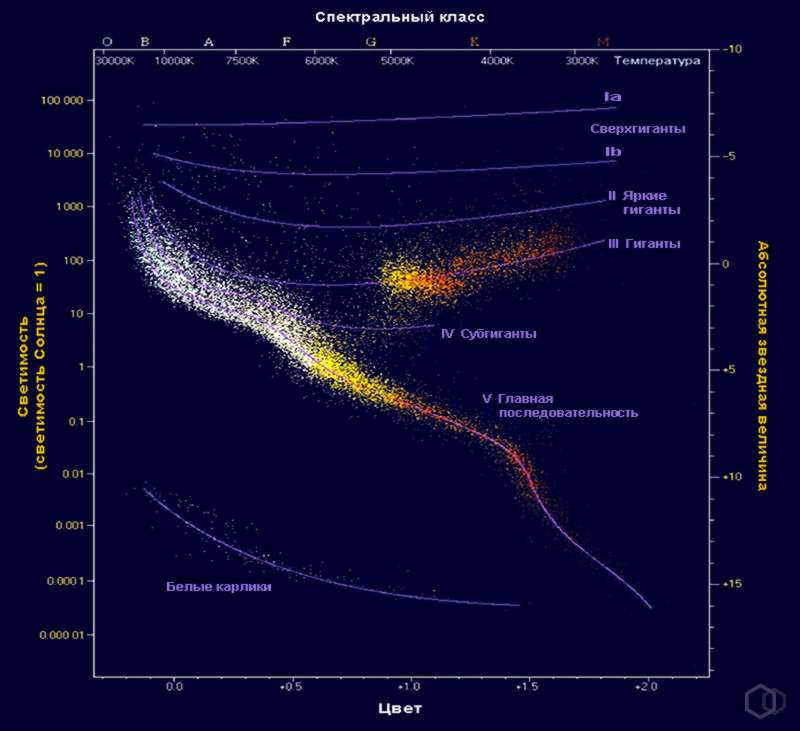
This diagram enables scientists to determine the absolute magnitudes of stars based on their spectral classes. By establishing a simple relationship between absolute magnitude, visible magnitude, and distance, it becomes clear how to calculate the distance to stars. The formula is as follows: lg r = 0.2(m – M)+1. In this equation, r represents the distance, m represents the apparent stellar magnitude, and M represents the absolute magnitude. While this method is not highly accurate, it does provide a rough estimate of the distance.
Standard candles in astronomy
In the field of astronomy, there exist certain stars that possess a unique characteristic – their luminosity can be directly correlated to a specific physical parameter. This correlation allows astronomers to accurately determine the distance to these stars by studying the drop in luminosity according to the inverse square law. The smaller the apparent magnitude of a star, the greater its distance from us. Prominent examples of such stars include Cepheids and Type Ia supernovae.
Cepheids are a type of variable star, meaning their luminosity fluctuates over time. However, the period of their pulsations is directly proportional to their luminosity. By measuring both the period and luminosity of a Cepheid, one can easily calculate its distance from our vantage point. Cepheids are known for their exceptional brightness, making them visible even in other galaxies. This allows astronomers to accurately gauge the distance to these galaxies using Cepheids as reference points.

Type Ia supernovae are explosions that occur when a specific type of star in binary systems reaches a critical mass. These explosions always have the same luminosity and light decay, which enables astronomers to calculate the distance. The brightness of these supernovae can be as intense as that of an entire galaxy, allowing astronomers to estimate distances on cosmological scales ranging in the billions of parsecs.
The Most Distant Star
Most individuals are familiar with Proxima Centauri, which is the nearest star to us. However, have you ever wondered about the farthest known star?
Recently, scientists have discovered the most distant star within our Galaxy. It is situated outside the spiral disk of the Milky Way, precisely on the outer rim of the galactic halo, approximately 122,700 pc or 400,000 light years away, in the constellation Libra. This particular star is a red giant with a magnitude of 18. While there are certainly more distant stars, it remains challenging to accurately determine their location within our Galaxy.

So, which star holds the title for being the farthest known in the Universe? Its name is MACS J1149+2223 Lensed Star-1, or LS1 for short, and it can be found a staggering 9 billion light-years away. The discovery of this star is a splendid stroke of astronomical fortune, as the chance to observe a star at such an immense distance was made possible by a gravitational microlensing event occurring within a distant galaxy that was itself lensed by a closer cluster of galaxies. Astronomers employed a different method to determine the star’s distance, using cosmological redshift calculations. This technique is utilized to ascertain the distances of the most remote objects in the Universe, objects that are too far away to be individually resolved into distinct stars. LS1 serves as a remarkable and captivating example of how astronomers are able to gauge the distances to these distant celestial bodies.

Urban residents have become accustomed to finding their whereabouts using the typical postal address: city, street, house, apartment. However, adventurous individuals such as hikers, mushroom pickers, anglers, hunters, and backpackers are now relying more on GPS coordinates. In this modern age, many people are embracing technology to navigate their way through remote areas and unfamiliar terrains.
Triangle is a minor constellation situated in the Northern Hemisphere of the celestial sphere. It encompasses a sum of 25 stars that are visible to the unaided eye, occupying a modest expanse of approximately 131.8 square degrees.

When you gaze up at the dark expanse above, a multitude of gleaming stars become visible to your naked eye. Without the aid of specialized instruments, these stars seem nearly identical in magnitude. Some emit a slightly stronger radiance, while others appear more subdued. And what .

A telescope. Such intrigue and fascination surround this word. What exactly is this instrument? What purpose does it serve?
Every celestial body in the solar system possesses its own distinct characteristics, including mass, diameter, trajectory, and various other parameters. Among these metrics, orbital velocity stands out as a particularly significant factor, indicating the speed at which a planet traverses its designated orbit.
It is not uncommon for us to come across individuals being referred to as “TV stars!” But who exactly are these people? How did they manage to attain fame? What factors aided or obstructed their journey? And is it conceivable for others to replicate their path to stardom? Let us delve into these queries and attempt to gain a better understanding.

The extent of modern telescopes’ capabilities, particularly with the assistance of natural elements, is a fascinating topic. The recent and remarkable finding of Icarus, the farthest star currently discovered in the Universe, showcases the potential for observing incredibly distant cosmic phenomena.
Throughout countless centuries, humans have gazed skyward, fixating on the brilliant celestial bodies known as stars. Initially, stars were classified based on their luminosity and placement within constellations. However, as technology advanced and the field of astronomy flourished, scientists devised even more intricate systems of categorization. Nevertheless, there are still enigmatic aspects of the cosmos that continue to elude our understanding.
Polaris is likely one of the most frequently referenced stars. It is mentioned in works of fiction, in the logs of sailors, and scientific studies. The reason for Polaris’s fame, and even popularity, is mainly due to its role as a guiding star.


Jupiter is the fifth planet in our Solar System and is classified as a gas giant. Its name is derived from the Roman god Jupiter, who is the equivalent of Zeus in Greek mythology. This article provides details about the solar system’s parameters, Jupiter’s orbital period around the Sun, and other characteristics of this massive planet.
A parsec is a unit of measurement for distance, equivalent to roughly 20 trillion miles (or 31 trillion kilometers) or 206,264 times the distance from the Earth to the Sun.
Additionally, a parsec is equal to 3.26 light-years, which is the distance one would travel in 3 years and 3 months at the speed of light.

What is the meaning of the term “parsec”?
The term “parsec” is derived from the combination of the words “parallax” and “second”. In this context, a second does not refer to a unit of time, but rather a unit of measurement for plane angles, specifically an angular (or arc) second.
Parallax serves as a meter to determine the change in position of a celestial object in relation to an observer. In the field of astronomy, diurnal, annual, and centennial parallax are distinguished.
Daily parallax is a method that measures the difference in the direction to a celestial body from a specific point on Earth and from the center of the Earth. On the other hand, annual parallax takes into consideration the Earth’s rotation around the Sun when calculating the same parameters. Lastly, century parallax allows us to determine the difference relative to the observer, taking into account the movements of the observed object in the galaxy.
F. W. Bessel, a German astronomer, initiated the examination of the distances separating celestial bodies in 1838.

After an extensive research effort, he successfully calculated the yearly parallax of the celestial body known as 61 Cygni.

Scientists used a widely known and traditional astronomical technique in their calculations, which allows them to determine the distance to a star based on the difference in angles.
In order to accomplish this, it is necessary to conduct 2 studies and perform measurements.
Initially, the measurements were taken while the Earth was oriented towards the Sun from one side.
Subsequently, the next set of measurements were taken after a period of 6 months when the planet was facing the Sun from the opposite side.
The term “parsec” was coined in the early 20th century by G. H. Turner, an astronomer from Great Britain.
Who is credited with inventing the parsec?
The credit for inventing the parsec goes to Friedrich Wilhelm Bessel, a German astronomer, who made the first successful measurements of distances to space objects in 1838. Bessel’s groundbreaking work allowed him to accurately calculate the annual parallax for the star 61 Swan, marking a significant milestone in the history of astronomy.
In his research, Bessel employed a venerable astronomical method that involved recording the difference in angles between two measurements to determine the distance to the star. This method, which has been used for centuries, proved crucial in Bessel’s groundbreaking calculations.
The term “parsec” itself was actually coined much later, in 1913, by the British astronomer Herbert Hall Turner.
Regrettably, numerous individuals possess a very limited understanding of astronomy and physics. However, this does not in any way diminish their worth. It would simply be splendid if every individual on Earth possessed the ability to sing, paint, and calculate logarithms. Now, let’s get back to the topic at hand… Ah yes, here we go. Some individuals mistakenly believe that a “light-year” and a “parsec” are units of time. However, this is completely untrue.
A parsec is equivalent to a distance of approximately 3.26 light-years, or roughly 31 trillion kilometers. So, why was the parsec created if light-years already measure cosmic distances, which is the distance light travels in one year? Well, there is a fascinating secret behind this (of course not). In reality, the parsec was introduced due to the utilization of one of the earliest methods for determining the distance to the stars.


By utilizing the principle of parallax, scientists are able to determine the distances to nearby stars. A slight shift in their position is measured, allowing for the calculation of their distance. This is achieved by recording their location in the sky during different seasons, such as spring and fall, when the Earth is at opposite points in its orbit around the Sun. By analyzing the detected displacement, the distance to these stars can be determined. This method is based on basic principles of geometry, making it quite straightforward. However, it is important to note that this approach is only effective for stars that are relatively close.
A parsec is defined as the distance that an object must be moved in order for its annual trigonometric parallax to measure one arc second. Proxima Centauri, the star closest to our solar system, is approximately 1.3 parsecs away from the Sun. Additionally, our Milky Way galaxy spans over 31,000 parsecs.
Moreover, it should be noted that a parsec is not a commonly used unit of measurement in astronomy. Typically, astronomers rely on astronomical units to measure cosmic distances…
Illustrations of astronomical distances
Ever since the introduction of parsecs, scientists have had the capability to determine the distances to numerous celestial entities, not only within the confines of our own Milky Way galaxy, but also throughout the vast expanse of the entire universe.
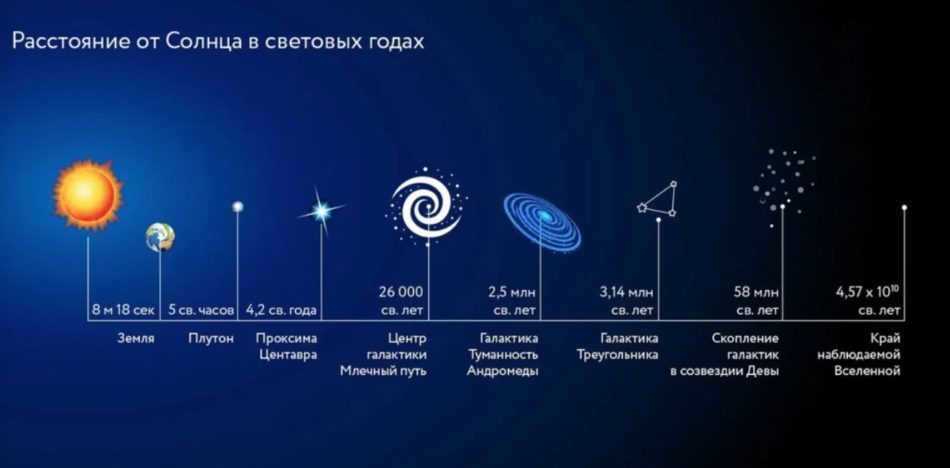
It is common knowledge that Proxima Centauri is the nearest star to Earth. It is situated at a distance of 1.3 parsecs from the Sun. Additionally, it is 8 kiloparsecs away from the galactic center.
The gap between Proxima Centauri and the Andromeda Nebula measures 0.77 megaparsecs.
The total size of the Milky Way is approximately 30 kiloparsecs. The distance between Earth and the observable edge of the Universe in the night sky is estimated to be around 4 gigaparsecs.
As can be observed, the parsec serves as a highly convenient unit of measurement. It is valuable to understand the equivalent values of a parsec in kilometers and light years.
Consequently, the process of determining distances between any celestial bodies within the cosmos is made easier.
It is commonly employed when calculating the distances between objects within the Milky Way.
With the continuous advancement of technology, researchers will soon have the capability to examine and compute the vast distances separating various galaxies.
An issue with the parsec is that it necessitates the expertise of skilled astronomers. Performing calculations using this unit can be challenging for the average individual.
Ways to Study Distances in the Universe
Direct Methods:
- Using standard candles
- Using measuring rods
- Applying Hubble’s Law
- And many other techniques…
Understanding Parallax
Parallax in astronomy refers to the phenomenon where an object appears to change its position on the celestial sphere in relation to other objects due to the observer’s change in observation location.
Parallax occurs when an object’s position seems to shift due to the observer’s movement or change in position.
The concept of parallax is applicable in various systems:
- Diurnal parallax (geocentric equatorial parallax) – related to Earth’s rotation
- The meridional geocentric parallax is associated with the variation in the observer’s latitude.
- The annual parallax (heliocentric parallax) is connected to the Earth’s orbit around the Sun.
Explanation of parsec
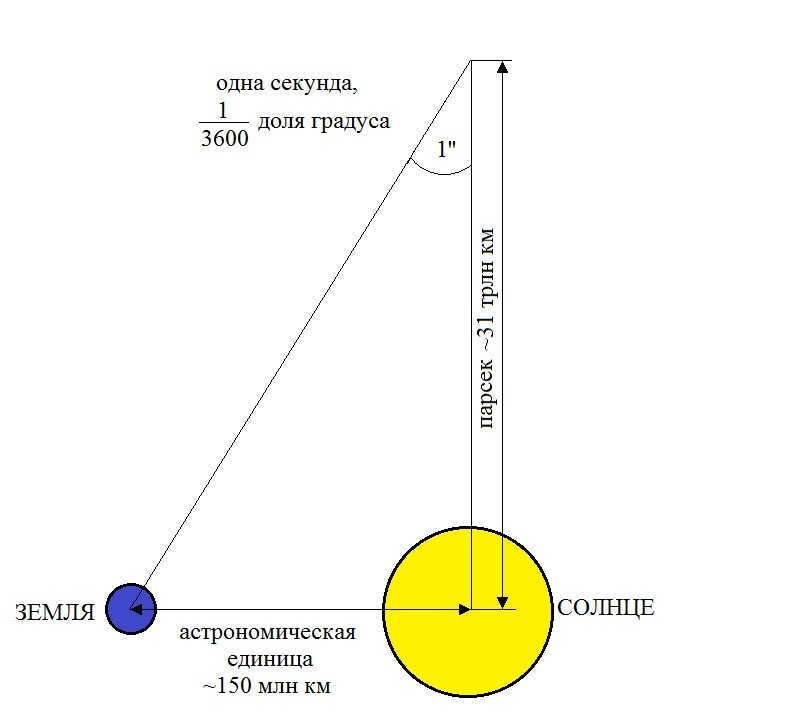
If the parallax angle remains constant, trigonometry can be used to determine the distances to stars (since we know the distance from the Earth to the Sun). Turner introduced the parsec as the unit of measurement in 1913, defining it as the distance from the Sun to a star with a parallax angle of 1 arc second.
This term was formed by combining the words parallax and second. The idea of parallax is connected to the Earth’s rotation (diurnal parallax), the change in latitude of the observer (geocentric meridian parallax), or the Earth’s orbit around the Sun (annual parallax). The definition states that 1 parsec (pc) is the distance from which half of the major axis of the Earth’s orbit is visible as an arc 1 second long. This distance is the reciprocal of the heliocentric body parallax. Parsec is now abbreviated as pc, previously as ps. The abbreviation ps is not specified nowadays because it is the same as the abbreviation picosecond.
Light Year (LY)
Light has a finite speed of 299,792,458 m/s, allowing it to cover a distance of approximately 300,000 km per second. By multiplying this distance by the 365 days in a year, we determine that light travels a staggering 946,800,000,000,000,000 km in the span of a single year. Scientists have designated this immense distance as 1 light year.
Conversion table for Astronomical units to Parsecs.
Astronomical unit Parsec
| 1,000,000 | 5,000,000 | 10,000,000 | 2.5 * 10^7 | 5 * 10^7 | 10 * 10^7 | 2.5 * 10^8 | 5 * 10^8 |
| 4.848 | 24.242 | 48.485 | 121.212 | 242.423 | 484.847 | 1,212.117 | 2,424.234 |
Conversion table from Astronomical units to Parsecs
Astronomical unit Parsec
Subscribe to the Telegram Channel of UFO World
Receive instant notifications about new Articles on your phone
V. Sun and stars
§ 22. Distances to stars. Radiation characteristics of stars
Additional resources for the lesson
Our Sun is commonly referred to as a typical star, but within the vast array of stars in the universe, there are many that differ significantly in their physical characteristics. Therefore, a more comprehensive understanding of stars can be provided by the following definition: a star is a celestial object that is spatially isolated, gravitationally bound, and opaque to radiation. It undergoes thermonuclear reactions that transform hydrogen into helium, either in the past, present, or future, on a significant scale.
The Sun has been in existence for billions of years and has undergone minimal changes during that time. This is because thermonuclear reactions continue to occur in its core, where four protons (hydrogen nuclei) combine to form an alpha particle, which is a helium nucleus made up of two protons and two neutrons. However, more massive stars deplete their hydrogen reserves much more quickly, typically within tens of millions of years. Once the hydrogen supply is exhausted, reactions between helium nuclei begin to produce carbon-12, a stable isotope, as well as other reactions that yield oxygen and heavy elements such as sodium, sulfur, and magnesium. As a result, the nuclei of numerous chemical elements, including iron, are formed deep within stars.
In the case of the most massive stars, the cessation of all thermonuclear reactions leads to a dramatic explosion known as a supernova. These explosions are incredibly powerful and can be observed as supernova outbursts.
All the components that compose our planet and all life on it were created through the process of thermonuclear reactions happening in stars. Thus, stars are not only the most prevalent objects in the Universe, but they are also crucial for comprehending the phenomena and processes taking place within it.
Thermonuclear reactions are the distinguishing characteristic that sets stars apart from planets. Consequently, the contemporary definition of a planet is formulated as follows: a planet is a celestial body that orbits a star or a remnant of a star, possessing enough mass to assume a spherical shape due to its own gravitational force. Additionally, planets have the capability to clear out small objects from their vicinity, but they do not undergo fusion reactions within their interior, neither in the present nor in the past.
1. Annual parallax and distances to stars
The concept that stars are distant suns has been known since ancient times. However, determining their exact distance from Earth has long been a challenge. Aristotle recognized that by observing the position of a star from two diametrically opposite points in the Earth’s orbit, one could detect a change in the direction to the star (Fig. 5.12).
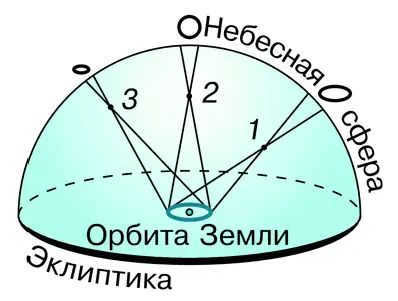
This apparent (parallactic) shift of the star will be used to determine its distance: the larger the shift, the closer the star is to us. However, not only Aristotle himself, but even much later Copernicus failed to observe this shift. It was only in the late 19th century, when telescopes were equipped with instruments for precise angular measurements, that it became possible to measure this shift in the closest stars.
The annual parallax of a star p is the angle at which the major semi-axis of Earth’s orbit (equal to 1 a. e.), perpendicular to the direction to the star, could be observed from the star (Fig. 5.13).
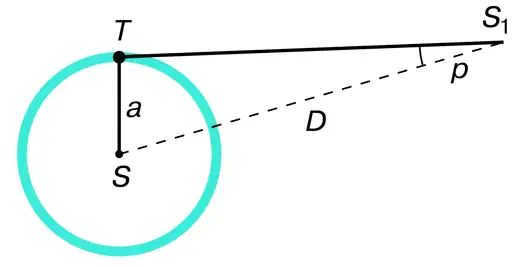
The distance to the star in astronomical units can be calculated using the formula D = a / Sin p, where a represents the major semi-axis of the Earth’s orbit.
If we replace the sine of the minor angle with the magnitude of the angle itself, expressed in radian measure, and take a = 1 a.e., the formula becomes:
D = 206 265" / p.
The year 1837 marked an important milestone in the field of astronomy, as it was the first time that accurate measurements of the annual parallax were successfully obtained. Vasily Yakovlevich Struve, a Russian astronomer, played a crucial role in this achievement by determining the annual parallax of Vega (α Lyra), the brightest star in the Northern Hemisphere. Simultaneously, astronomers in other countries also measured the parallaxes of two other stars, one of which was α Centauri. Interestingly, α Centauri turned out to be the closest star to us, despite being invisible from Russia. Its annual parallax was a mere 0.75″, a tiny angle that can be compared to the visibility of a 1-mm-thick wire from a distance of 280 meters. Given the minuscule nature of these angular displacements, it is understandable why it took so long for scientists to detect and measure them.
A parsec is a unit of distance that is defined as the distance at which the parallax of the stars equals 1". This unit gets its name from the words “parallax” and “second”. The distance in parsecs can be calculated by taking the inverse of the annual parallax. For instance, if the parallax of a Centauri is 0.75", then its distance is 1.3 parsecs.
A light-year is a unit of distance that represents the distance traveled by light in one year, with light traveling at a speed of 300,000 km/s. It takes more than four years for light from the nearest star to reach Earth, while it takes about eight minutes for light from the Sun to reach us, and a little over one second for light from the Moon to reach us.
1 parsec is equivalent to 3.26 light-years, 206,265 astronomical units, or 3 ∙ 10^13 kilometers.
To this day, the Hipparcos satellite has accurately measured the annual parallaxes of over 118,000 stars, with an accuracy of 0.001".
Therefore, through the utilization of the annual parallax measurement, we are now capable of precisely ascertaining the distances to stars that are situated 1000 parsecs, or 3000 light-years away from our position. Distances to stars that are located even further away are determined through alternative methodologies.
2. Apparent and absolute magnitudes of stars.
Stellar luminosity
Once astronomers managed to establish the distances to stars, it became evident that stars at the same distance might exhibit varying levels of apparent brightness (i.e., luminosity). It became apparent that stars possess differing levels of luminosity. The Sun appears to be the most radiant entity in the sky merely due to its much closer proximity compared to all other stars.
Luminosity denotes the overall energy emitted by a star within a given timeframe.
This is expressed in absolute units (watts) or in units relative to the Sun’s luminosity.
When studying celestial bodies, it is a common practice to compare stars based on their luminosity, which is calculated as their stellar magnitude at a standardized distance of 10 pc.
The absolute stellar magnitude, denoted by M, refers to the apparent stellar magnitude that a star would have if it were located at a distance D0 = 10 pc.
To determine the absolute stellar magnitude M, we can use the distance to the star D (or its parallax – p) and its apparent stellar magnitude t. It is important to note that the luminosity of two sources with a difference of one in their stellar magnitudes differs by a factor of 2.512. In other words, for stars with stellar magnitudes t1 and t2, the ratio of their luminosities I1 and I2 can be expressed as:
For the same star, the ratio of the luminosities for its apparent and absolute stellar magnitudes will be:
I : I0 = 2.512 M-m,
where I0 represents the luminosity of the star if it were located at a distance D0 = 10 pc.
It is known that the luminosity of a star is inversely proportional to the square of the distance to it. Therefore,
I : I0 = D02 : D2.
2.512 M-m = D02 : D2.
Taking the logarithm of this expression, we can derive
0.4(M-m) = lg 10 2 – lg D2,
M = m + 5 – 5lgD,
M = m + 5 + Ig p.
The absolute magnitude of the Sun, M⊙, is equal to 5m. In other words, if the Sun were located at a distance of 10 pc, it would appear as a star with a magnitude of five.
Once you have the absolute stellar magnitude of star M, it becomes a simple task to calculate its luminosity L. By taking the Sun’s luminosity L⊙ = 1 as a reference point, we can determine that:
lg L = 0.4(5 – M).
When it comes to luminosity (radiation power), stars exhibit significant variations: some emit energy hundreds of thousands of times greater than the Sun, while others emit energy tens of thousands of times weaker. The absolute stellar magnitudes of the most luminous stars (giants and supergiants) can reach M = -9 m, while dwarf stars with the lowest luminosity have an absolute stellar magnitude of M = + 17 m.
3. Spectra, Color, and Temperature of Stars
The study of star radiation is essential to gather information about stars. When observing stars, one can easily notice their diverse range of colors. It is widely understood that the color of a star, like any heated body, is dependent on its temperature. A more comprehensive understanding of this correlation can be achieved through the examination of stellar spectra. For most stars, these spectra consist of absorption lines against a continuous background spectrum.
The temperature of the star’s outer layers, where the radiation originates from, is determined by both the energy distribution in the continuous spectrum (Figure 5.14) and the intensity of various spectral lines.
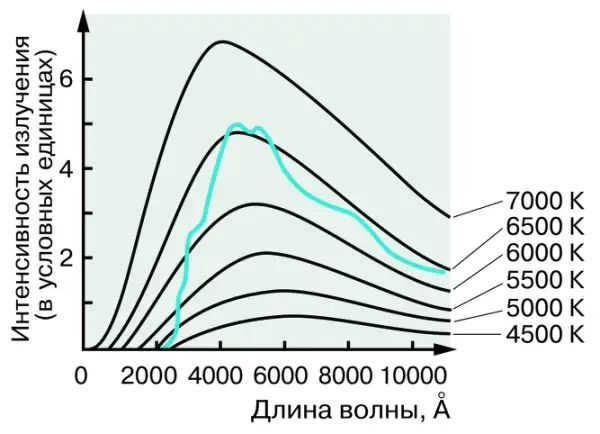
Fig. 5.14. Energy distribution in the continuous spectrum of the Sun and a black body at varying temperatures
The temperature of the emitting object determines the wavelength at which the maximum emission occurs. As the temperature increases, the position of the maximum shifts from the red end to the violet end of the spectrum. Mathematically, this relationship is described by Wien’s law:
λmax = 0.29 / T,
where λmax represents the wavelength (in cm) at which the maximum emission occurs, and T is the absolute temperature.
It has been discovered that the temperature range for different types of stars is between 2500 and 50,000 K. Alterations in temperature impact the state of atoms and molecules in stars’ atmospheres, resulting in changes in their spectra. Based on distinct spectral characteristics, stars are classified into spectral classes, denoted by Latin letters, arranged in descending order of temperature: O, B, A, F, G, K, M.
The coolest (red) stars in class M exhibit absorption lines of certain two-atomic molecules (such as oxides of titanium, zirconium, and carbon) in their spectra. Notable examples of stars with temperatures around 3000 K include Antares and Betelgeuse.
Yellow stars of class G with temperatures around 6000 K, such as the Sun, exhibit a predominance of metal lines, including iron, sodium, and calcium, in their spectra. The star Capella shares similarities with the Sun in terms of temperature, spectrum, and color.
White stars of class А with a temperature of approximately 10,000 K (such as Vega, Deneb, and Sirius) are characterized by hydrogen lines and numerous faint lines of ionized metals in their spectra. The spectra of the hottest stars also feature both neutral and ionized helium lines.
The variation in stellar spectra is accounted for by the disparity in temperature and other physical circumstances in star atmospheres, rather than the array of their chemical composition. The analysis of spectra reveals that hydrogen and helium prevail in the composition of star atmospheres (and stars as a whole). All other chemical elements make up only a small fraction, not exceeding a few percent.
The equation λ – λ0 / λ0 = υ / c represents the relationship between the wavelength λ0 of a spectral line for a stationary source and the wavelength λ in the spectrum of a moving source.
The Doppler effect can be observed in various regions of the spectrum, including the optical range, and is extensively employed in the field of astronomy.
4. Diagram of spectrum and luminosity
In the early twentieth century, two astronomers, Einar Hertzsprung from Holland and Henry Russell from the USA, compared and presented data on the luminosity and spectra of stars in the form of a diagram. This diagram became known as the “Hertzsprung-Russell diagram”. By plotting the spectral classes (temperatures) of stars on the horizontal axis and their luminosities (absolute stellar magnitudes) on the vertical axis, each star can be represented by a specific point on this diagram (Figure 5.15).
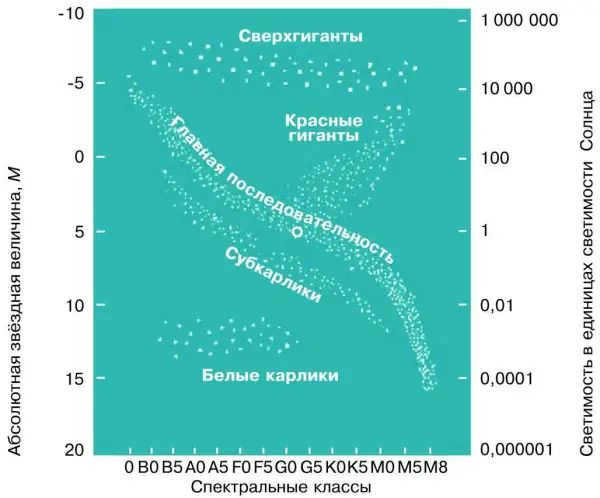
It was not until the late 20th century that there was a significant increase in knowledge about the physical processes taking place in stars and a clear understanding of their evolution. This allowed for a theoretical explanation of the empirical regularities that represent the “spectrum – luminosity” diagram.