Equatorial coordinates refer to the specific set of coordinates used in astronomy to describe the position of luminaries in the sky or points on the celestial sphere. These coordinates are defined by two angular quantities, which uniquely determine the location of objects in the celestial sphere. Unlike other coordinate systems, the equatorial coordinate system is a spherical coordinate system that does not consider the distance of objects.
Celestial coordinate systems vary based on their principal plane and origin. Depending on the specific task, astronomers may choose to use different coordinate systems. The most commonly utilized systems include the horizontal and equatorial coordinate systems, although there are also less frequently used systems such as the ecliptic, galactic, and others.
The Coordinate System in the Horizontal Plane
Within this particular system, the primary plane is the mathematical horizon. One of the coordinates is the luminosity’s altitude (h) or its zenith distance (z). The other coordinate is the azimuth (A).
The luminary’s height (h) refers to the arc of the vertical circle that extends from the mathematical horizon to the luminary, or the angle between the plane of the mathematical horizon and the direction towards the luminary. Altitudes are measured from 0° to +90° towards the zenith and from 0° to -90° towards the nadir.
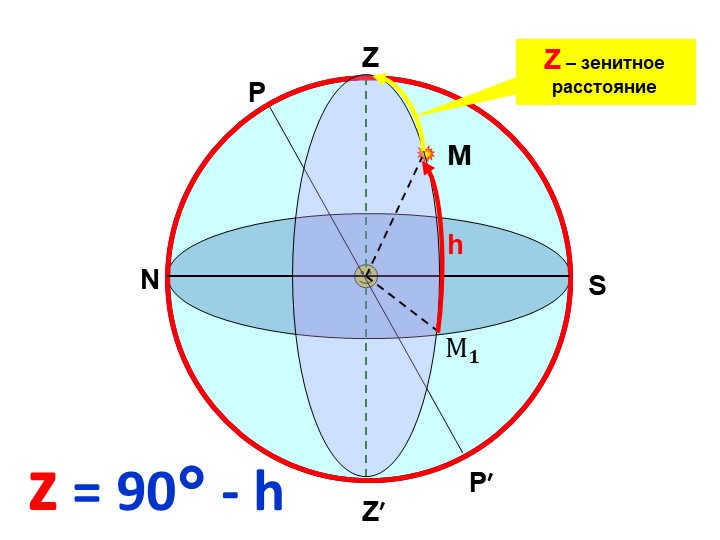
The zenith distance (z) of a luminary is the arc of the vertical circle that extends from the zenith to the luminary, or the angle between the plumb line and the direction towards the luminary. Zenith distances are measured from 0° to 180°, starting from the zenith and reaching the nadir.
Azimuth A refers to the angle between the south point and the vertical circle of a celestial body, or the angle formed by the noon line and the intersection of the mathematical horizon with the vertical circle of the celestial body. Azimuths are measured in the direction of the daily rotation of the celestial sphere, ranging from 0° to 360° west of the south point. In some cases, azimuths are measured from 0° to +180° west and from 0° to -180° east. (In geodesy, azimuths are measured from a point north.)
The plane of the celestial equator serves as the primary plane in this system. One of the coordinates in this system is the declination δ (sometimes referred to as the polar distance p). Another coordinate is the hour angle t.
The declination δ of a celestial body represents the arc from the celestial equator to the body, or the angle between the plane of the celestial equator and the direction to the body. Declinations are measured from 0° to +90° towards the north pole of the world and from 0° to -90° towards the south pole of the world.
The angle of time t of the celestial object is the distance along the celestial equator from the highest point of the celestial equator (which is where the celestial equator intersects with the celestial meridian) to the declination circle of the celestial object, or the angle between the planes of the celestial meridian and the declination circle of the celestial object. Time angles are measured in the direction of the daily rotation of the celestial sphere, specifically to the west of the highest point of the celestial equator, ranging from 0° to 360° (in degrees) or from 0 h to 24 h (in hours). Occasionally, time angles are measured from 0° to +180° (0 h to +12 h) to the west and from 0° to -180° (0 h to -12 h) to the east.
The alternate equatorial coordinate system
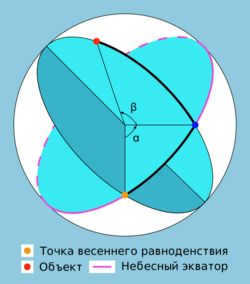
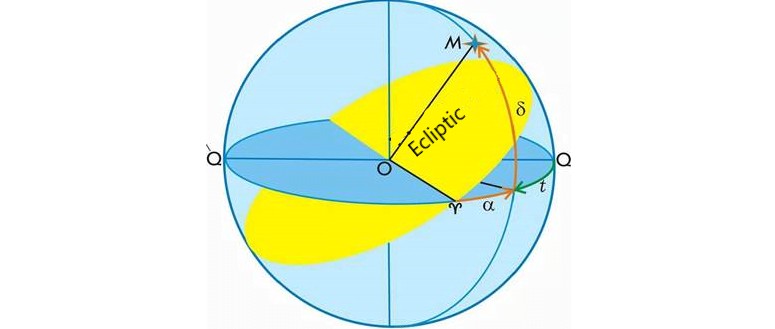
In this particular system, just like in the initial equatorial system, the primary plane happens to be the plane of the celestial equator, and one of the coordinates is identified as the declination β (less commonly known as the polar distance p). The other coordinate is referred to as the direct ascent α.
Direct ascent (RA,α) of a luminary is the arc of the celestial equator that extends from the vernal equinox to the luminary’s declination circle, or it can also be described as the angle between the direction towards the vernal equinox and the plane of the luminary’s declination circle. Direct ascensions are calculated in the opposite direction to the daily rotation of the celestial sphere, ranging from 0° to 360° (in degrees) or from 0 h to 24 h (in hours).
RA is similar to Earth’s longitude in the field of astronomy. Both RA and longitude measure the east-west angle along the equator, and both have a starting point at zero on the equator. Longitude has the prime meridian as its zero point, while RA has the point in the sky where the Sun crosses the celestial equator at the vernal equinox as its zero point.
Declination (δ) in astronomy is one of the coordinates in the equatorial coordinate system. It represents the angular distance on the celestial sphere from the plane of the celestial equator to the celestial body, and is usually measured in degrees, minutes, and seconds of arc. Declination is positive when north of the celestial equator and negative when south.
- An object located on the celestial equator has a declination of 0°
- The declination of the north pole of the celestial sphere is +90°
- The sign of the declination is always present, regardless of whether it is positive or negative.
- When a celestial object passes through the zenith, its declination is equal to the observer’s latitude. In the northern hemisphere, a positive sign is used for northern latitudes and a negative sign for southern latitudes.
- In the northern hemisphere, celestial objects with a declination greater than 90° – φ do not go below the horizon and are referred to as non-sunsetting.
- If the declination of an object is less than -90° + φ, it is called a non-descending and cannot be observed at latitude φ. [1]
Ecliptic coordinate system
In this system, the primary plane is known as the ecliptic plane. One of the coordinates in this system is referred to as the ecliptic latitude (β), while the other is called the ecliptic longitude (λ).
The ecliptic latitude (β) of a celestial body is the measurement of the arc between the ecliptic and the body, or the angle formed by the ecliptic plane and the direction towards the body. Ecliptic latitudes are measured from 0° to +90° for the north pole of the ecliptic, and from 0° to -90° for the south pole of the ecliptic.
The position of a celestial object λ on the ecliptic can be measured by its ecliptic longitude. This is the distance along the ecliptic from the vernal equinox point to the object’s circle of latitude, or the angle between the direction to the vernal equinox point and the plane of the object’s circle of latitude. Ecliptic longitudes are measured in the direction of the Sun’s annual motion along the ecliptic, which is from west to east within a range of 0° to 360°.
Galactic coordinate system
In this system, the primary plane is the plane of our Galaxy. There are two coordinates in this system: galactic latitude b and galactic longitude l.
The galactic latitude b of a celestial object is the arc of the circle of galactic latitude from the ecliptic to the celestial object, or the angle between the plane of the galactic equator and the direction towards the celestial object.
Galactic latitudes are measured from 0° to +90° towards the north galactic pole and from 0° to -90° towards the south galactic pole.
The position C is near to the direction of the Milky Way center, but not exactly the same, as the latter is slightly below the galactic equator due to the solar system’s elevation above the galactic disk. The chosen origin point C is such that the intersection of the galactic and celestial equators at a right ascension of 280° corresponds to a galactic longitude of 32.93192° (at epoch 2000).
The equatorial coordinates of the origin point C at epoch 2000 are:
Changes in celestial coordinates as the celestial sphere rotates
Elevation e, zenith distance z, azimuth A, and hour angle t of celestial objects are constantly changing due to the rotation of the celestial sphere, as they are measured from points not connected with this rotation. The declination δ, polar distance p, and right ascension α of celestial objects do not change with the rotation of the celestial sphere, but they can change due to the movements of celestial objects not related to the daily rotation.
Origin and Usage
The utilization of celestial coordinates dates back to ancient civilizations. The ancient Greek mathematician Euclid, around 300 B.C., documented several systems in his writings. Ptolemy’s Almagest includes Hipparchus’ star catalog, which features the locations of 1022 stars in the celestial coordinate system known as the ecliptic.
The study of changes in celestial coordinates has led to significant discoveries in the field of astronomy, providing crucial insights into the nature of the universe. These discoveries encompass various phenomena, such as precession, nutation, aberration, parallax, and the proper motions of stars. The utilization of celestial coordinates enables us to tackle the challenges of time measurement and determine the geographic coordinates of different locations on Earth’s surface. Moreover, celestial coordinates play a vital role in the creation of star catalogs, the analysis of the true movements of celestial bodies (both natural and artificial) in celestial mechanics and astrodynamics, as well as the examination of the spatial distribution of stars in stellar astronomy problems.
The horizontal coordinate system is employed for determining the direction to the celestial body by means of angular instruments and when observing through a telescope installed on an azimuthal rig.
The initial equatorial coordinate system is utilized for establishing the precise time and for observations through a telescope mounted on an equatorial mount.
The secondary equatorial coordinate system represents a prevalent coordinate system in astrometry. This system is employed for creating star maps and describing the positions of celestial bodies in catalogs.
The ecliptic coordinate system is utilized in theoretical astronomy for determining the orbits of celestial bodies.
Notes
- ↑Siegel F. Yu. The Starry Sky Treasury – A Guide to Constellations and the Moon / Edited by G. S. Kulikov. – 5th Edition. – Moscow: Nauka, 1986. – Pp. 57-58. – 296 pages. – 200,000 copies.
Lesson Objective: The objective of this lesson is to review the concepts of the celestial sphere, altitude, azimuth of the luminary. To develop an understanding of the celestial meridian, celestial equator, declination, and direct ascent. To cultivate the ability to determine the equatorial coordinates of the luminary and apply the acquired knowledge to solve qualitative problems.
Get the File:
Preview:
Download the astronomy lesson on the “Equatorial Coordinate System”
Grade: 11th
Location: Saransk, MOU “Lukhovsky Lyceum”
Lesson Type: New Material Learning Lesson
Lesson Objective: To review the concepts of the celestial sphere, altitude, and azimuth of celestial bodies. To understand the concepts of the celestial meridian, celestial equator, declination, and right ascension. To develop the ability to determine the equatorial coordinates of celestial bodies and apply this knowledge to solve qualitative problems.
Educational Connection: To review concepts from the geography course, such as geographical coordinates (using examples on a globe), the Earth’s rotation axis, the Earth’s north and south poles, and the Earth’s equator.
Developing: The objective is to establish a correlation between the components of the Earth globe (Earth equator, meridians, and parallels) and the celestial sphere, fostering attention and speech development, as well as enhancing independent work skills. The aim is to instill the ability to apply equatorial coordinates of celestial bodies in order to solve qualitative problems.
The goal is to form a comprehensive understanding of the world (including nature, society, and oneself) and to emphasize the role and significance of astronomy within the field of sciences.
Equipment required for this lesson includes a model of the celestial sphere, a starry sky map (to be displayed on the board), movable starry sky maps (to be distributed as handouts), the teacher’s computer, a multimedia projector, and the “Astronomy” disk.
Progress of the lesson
1. Organizational aspect
2. Captivating students’ attention
Today’s topic: “Equatorial coordinate system”.
During this class, we will review the process of determining geographical coordinates and establish a comparison with the equatorial coordinates of celestial bodies.
We will review the fundamental components of the celestial sphere and illustrate them using a physical model
3. The true horizon plane
7. North point (N) and South point (S)
9. Elevation of the celestial body above the horizon
Exploration of novel content
The positions of stars in the horizontal coordinate system vary as a result of the Earth’s daily rotation. This is because the reference point in this system is tied to the rotating Earth (the south point S and point Q lie on the celestial meridian). In order to prevent the coordinates of the stars from changing due to the daily rotation, a reference point that remains stationary relative to the stars and also participates in the daily rotation must be chosen. The point of the vernal equinox has been selected as this reference point, and the coordinate system in which the stars do not undergo changes in their coordinates due to daily rotation is known as the equatorial coordinate system, which we will now examine.
Demonstration. Model of the celestial sphere, Earth’s globe.
The first equatorial coordinate system.
The initial equatorial coordinate system
The declination of the celestial body is the angular distance from the celestial equator to the celestial body, measured along the declination circle. Declination ranges from -90o to 90o, with celestial bodies having a declination of 0o being located north of the equator, and those with a declination of 0o being located south of it. Alternatively, the polar distance, p, represents the angular distance from the celestial body to the pole instead of the declination.
The hour angle, t, is the arc of the celestial equator between the celestial meridian and the declination circle of the celestial body. It is measured from the Q point in a clockwise direction. Hour angle varies from 0o to 360o in degree measurement or from 0h to 24h in hour measurement (360o corresponds to 24h, 1h equals 15o, 1m equals 15′, 1s equals 15″).
The position of stars in the horizontal and first equatorial coordinate systems varies as a result of the Earth’s daily rotation. This is because these systems are tied to the rotating Earth, with the south point S and point Q being located on the celestial meridian. To ensure that the coordinates of the stars remain constant despite the Earth’s rotation, a fixed reference point that also moves with the Earth’s rotation must be chosen. The vernal equinox point serves as this reference point, and the coordinate system in which the stars do not change their coordinates due to daily rotation is known as the second equatorial coordinate system.
Second equatorial coordinate system
The path followed by the Sun as it appears to move across the sky throughout the year, due to the Earth’s orbit around the Sun, is known as the ecliptic. The ecliptic is tilted at an angle in relation to the equator. The points where the ecliptic and equator intersect are referred to as the equinoxes. The point where the Sun crosses from the southern hemisphere of the celestial sphere to the northern hemisphere is called the vernal equinox, while the opposite point is known as the autumnal equinox.
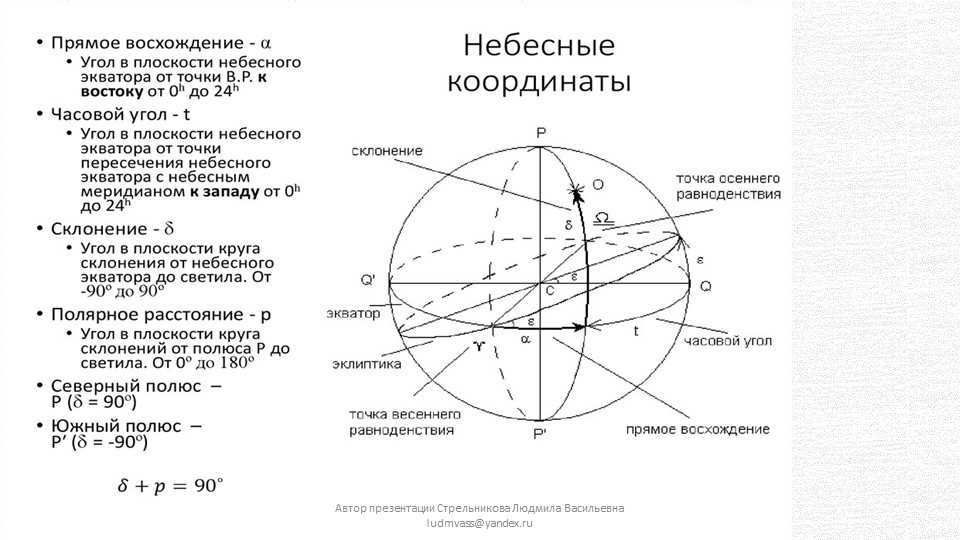
In the second equatorial coordinate system, the primary plane, similar to the first one, is the plane of the celestial equator, and the origin is the point of the vernal equinox (Fig. 7). The initial coordinate is also known as the declination. The second coordinate, referred to as the right ascension, is the distance along the celestial equator from the vernal equinox to the luminary’s declination circle, measured counterclockwise. Similar to the hour angle, the right ascension is measured in hours.
The second equatorial coordinate system
Establishment. Resolving qualitative problems
1. Determine the equatorial coordinates of stars using a PCZN (mobile star map)
2. A star remains above the horizon for half of the day. What is its declination?
Answer: For all latitudes, it is a star with a declination of 0. At the equator, any star will be above the horizon for half of the day.
3. Is it possible for a celestial body to pass through the points of east, zenith, west, and nadir within a single day?
Response: This phenomenon can occur at the Earth’s equator with stars located on the celestial equator.
4. If two stars have the same right ascension, at what latitude on Earth would both stars rise and set simultaneously?
Take-home assignment. Lesson outline, p. 4 of the textbook “Astronomy” (Vorontsov-Veliaminov).

11th Grade Astronomy Lesson Plan: “Exploring the Solar System’s Major Planets”
This lesson will focus on the fascinating topic of the major planets in our solar system, providing students with a comprehensive understanding of their characteristics and classifications.

Prospectus for an astronomy lesson: “The Celestial Sphere and the Starry Sky”
This lesson plan for astronomy includes a presentation, handouts, and the lesson outline itself.

11th Grade Astronomy Lesson Plan: Model of the “Hot Universe”
This lesson plan was created based on the astronomy textbook by V.M. Churgin.

Lesson plan for 11th grade astronomy class
Exploring the planets in the Earth group and beyond

Prospectus for an Astronomy Lesson on the “Earth-Moon System”.
The goals of this lesson are to explore the physical conditions, relief, rocks, and internal structure of the Moon. Additionally, students will learn about the significance of Moon studies, the structure and phases of the Moon, and develop concepts related to the topic.

Lesson Plan for Astronomy: The Horizontal Coordinate System. Luminary’s Altitude and Azimuth
Objective of the Lesson: To develop an understanding of the celestial sphere, as well as the altitude and azimuth of a luminary. To cultivate the ability to apply acquired knowledge in solving qualitative problems. Tasks of the Lesson: Educational: to review key concepts.
Outline of a lesson on astronomy titled “Small celestial bodies in our solar system”.
An outline for an interactive astronomy class for 11th graders.

At the moment, 58,752 educational institutions have the opportunity to benefit from extra cumulative discounts ranging from 2% to 25%. To determine the specific discount applicable to all staff members at your educational institution, please sign in to your personal Infoworks account.


Enroll in our professional retraining course
Become a teacher of secondary vocational education. Learn the theory and practice of implementing FSES of the new generation.
You can also receive an additional discount based on the number of colleagues from your educational institution who have already taken Infowork courses.
Currently, there are accumulative discounts available for 58,752 educational institutions, ranging from 2% to 25%. To find out what discount is applicable to all employees of your educational institution, simply log in to your personal Infoworks account.


Enroll in our professional retraining course
Learn about state and municipal management in educational organizations.
We can offer you an additional discount based on the number of colleagues from your educational institution who have already taken Infowrok courses.
Currently, there are 58,752 educational institutions that receive discounts ranging from 2% to 25%. To find out what discount is available for all employees of your educational institution, simply log in to your personal Infoworks account.


Getting ready for the literature USE. Exploring the mesmerizing poetry of F.I. Tyutchev
Breakdown of the presentation by individual slides:

Slide number 1: Equatorial coordinates
The presenter of this presentation is Ludmila Strelnikova. She can be contacted at [email protected]
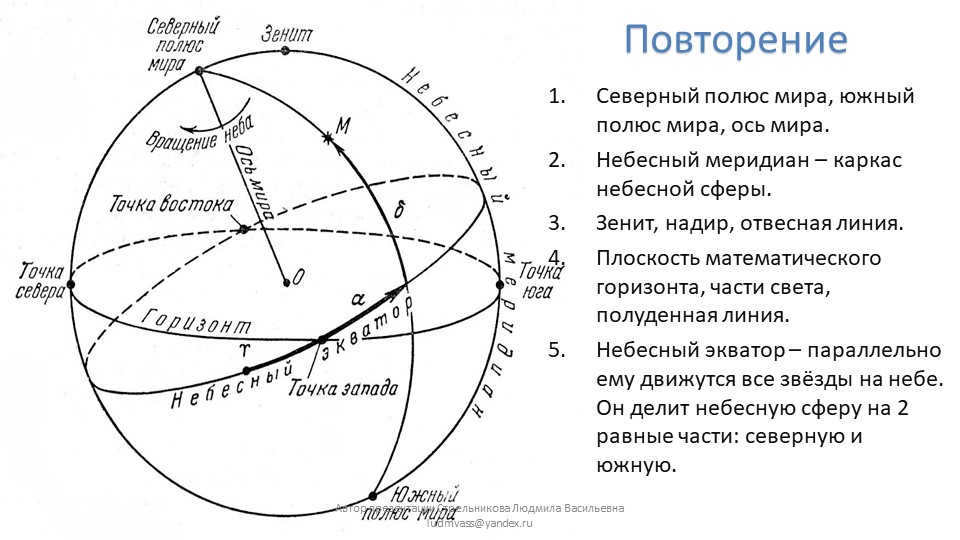
2nd Slide Repetition
The northernmost point of the world, the southernmost point of the world, and the axis of the world.
The celestial meridian is the reference line of the celestial sphere.
Zenith, nadir, and plumb line are important terms.
The plane of the mathematical horizon, the regions of the world, and the noon line are also significant.
The celestial equator is the line along which all the stars in the sky move parallelly. It divides the celestial sphere into two equal parts: the north and the south.
The author of the presentation is Lyudmila Strelnikova. Contact her at [email protected].


Lesson Plan for Slide 3
Topic: Celestial coordinates
In this lesson, we will explore celestial coordinates and learn how to find stellar coordinates. We will also have some independent work to practice what we have learned.
Presenter: Lyudmila Strelnikova
Contact: [email protected]
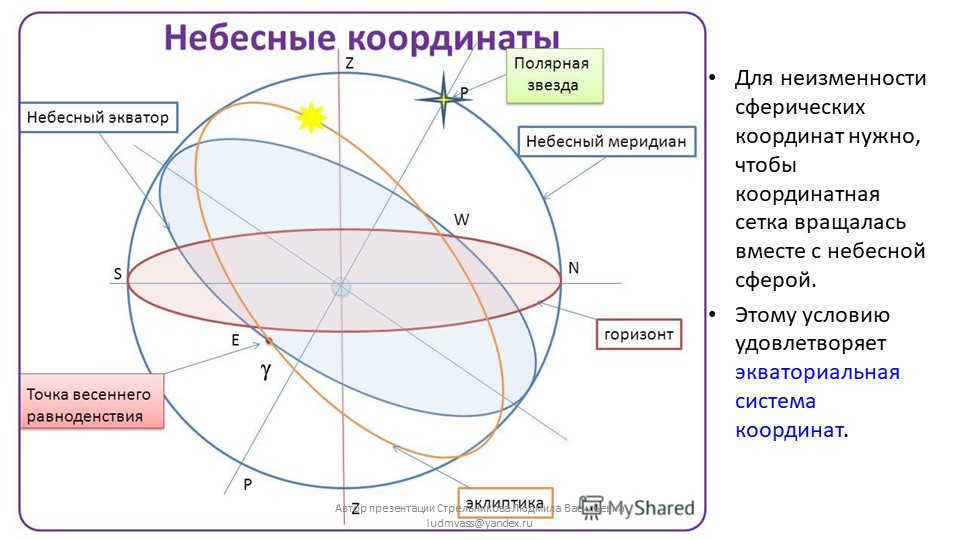
Slide 4: In order for spherical coordinates to remain invariant, it is essential that the coordinate grid rotates along with the celestial sphere.
This requirement is fulfilled by the equatorial coordinate system.
Author of the presentation: Ludmila Strelnikova ([email protected])
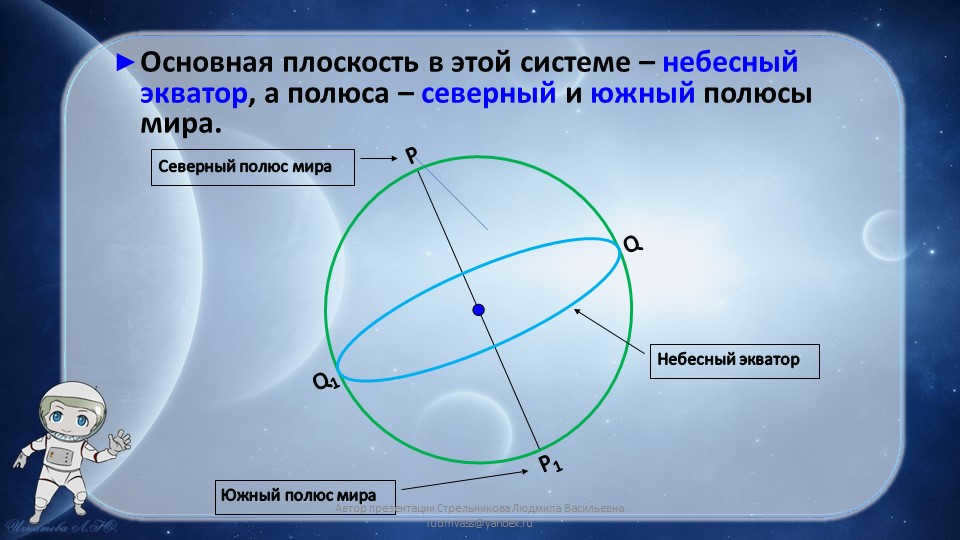

Slide 5: In this coordinate system, the celestial equator is the primary plane, and the north and south poles of the world mark its extremities.
Q
Q1
P
P1
The celestial equator
The North Pole of the World
The South Pole of the World
Presented by Ludmila Strelnikova at [email protected]
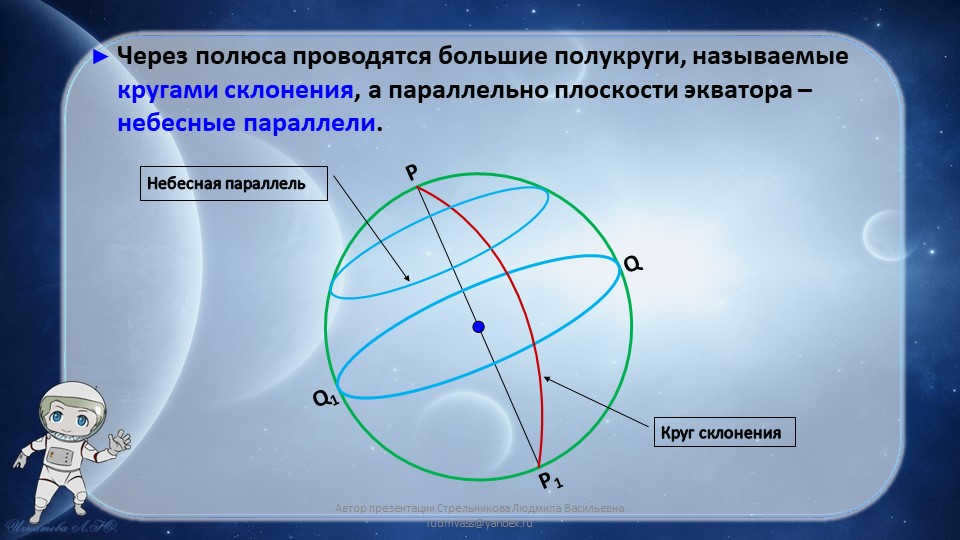
On the 6th slide, there are large semicircles known as declination circles that are depicted passing through the poles. Additionally, the celestial parallels are illustrated as being parallel to the equator’s plane.
Q
Q1
P
P1
Declination circle
Celestial parallel
The author of the presentation is Ludmila Strelnikova, and she can be contacted at [email protected]
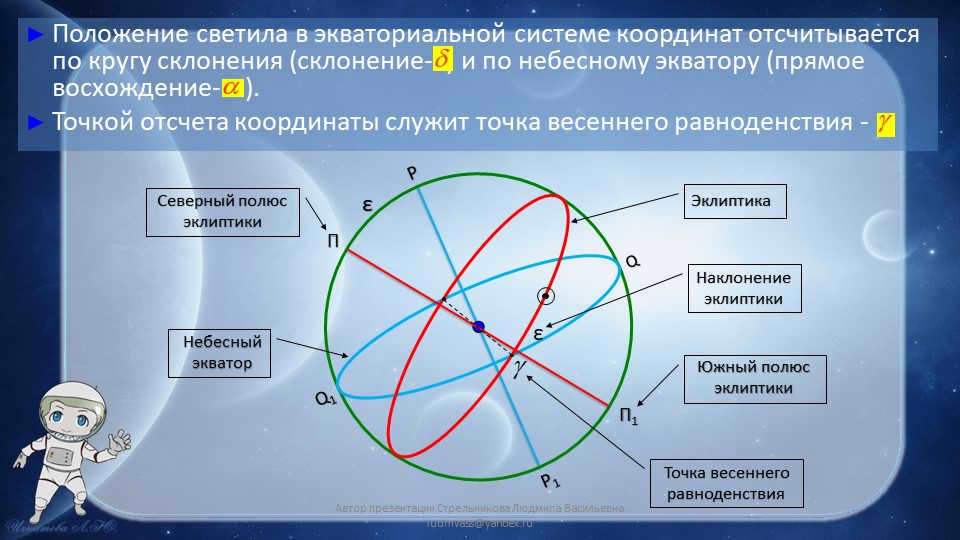

Slide 7: The position of the luminary in the equatorial coordinate system is determined by measuring along the circle of declination (declination) and along the celestial equator (right ascension). The starting point of the coordinates is the vernal equinox point – Q, Q1, P, P1, Π, Π1, North Pole, ecliptic, South Pole, ecliptic, ε, Ecliptic, celestial equator, ε, inclination, ecliptic, Vernal point, equinox. Presentation by author Ludmila Strelnikova ([email protected]).
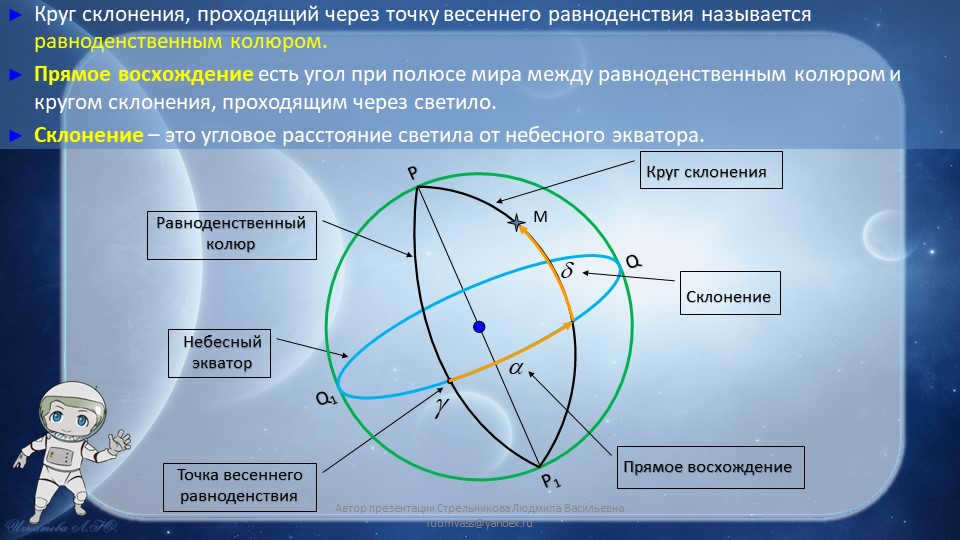
Slide 8: The equinox colure is defined as the circle of declination that passes through the point of the vernal equinox.
Direct ascension refers to the angle at the celestial pole between the equinox colure and the circle of declination that passes through the luminary.
Declination represents the angular distance of the luminary from the celestial equator.
The celestial equator is a reference line in the celestial sphere.
The point of the vernal equinoxes is a significant point in the celestial sphere.
Q and Q1 are specific points in the celestial sphere.
P and P1 are also specific points in the celestial sphere.
The declination circle is a circular path in the celestial sphere.
The equinox colure is an important line in the celestial sphere.
M is an unspecified point in the celestial sphere.
Direct Ascension is a term used in celestial navigation.
Declination is a fundamental concept in celestial coordinates.
This presentation was authored by Ludmila Strelnikova ([email protected]).


Slide number 9 focuses on the practical applications of equatorial coordinates of stars. These coordinates are widely used in various fields such as creating star maps and catalogs, determining geographic coordinates on Earth’s surface, aiding in space orientation, timekeeping, and studying the Earth’s rotation. The author of this presentation is Ludmila Strelnikova ([email protected]).


Slide 10 on Coordinates:
δ represents the declination or the latitude of a place, which is measured in degrees ranging from 0 to 90°. It indicates whether the location is in the northern hemisphere (+) or the southern hemisphere (-).
On the other hand, α refers to the direct ascent or the longitude, which is measured in hours and minutes. The presentation was created by Ludmila Strelnikova, and for any inquiries, you can reach her at [email protected].
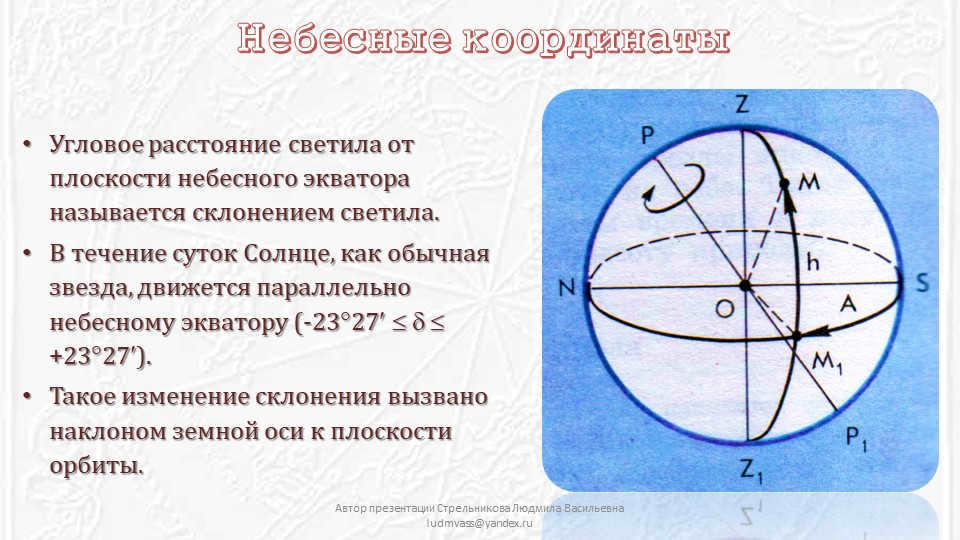
Slide 11 Celestial coordinates
The declination of a celestial body refers to its angular distance from the celestial equator.
Throughout the day, the Sun, like any other star, moves in parallel to the celestial equator (-2327 +2327).
This change in declination is caused by the Earth’s axis being tilted with respect to the orbital plane.
Author of the presentation: Lyudmila Vasilyevna Strelnikova, contact: [email protected]

On slide 13, we have the Ecliptic and the Celestial Equator. Additionally, we can see the point of the vernal equinox. This presentation was authored by Lyudmila Strelnikova, who can be reached at [email protected].

Here are 15 examples of slides:
α – Sirius, the big dog
δ = -16º 41'
α = 6h 44 min
α – Procyon, the small dog
δ = +5º 17'
α = 7h 38min
α – Betelgeuse, part of the Orion constellation
δ = +7º 24'
α = 5h 53min
Example 1
Example 2
The author of the presentation is Lyudmila Strelnikova. You can contact her at [email protected].

Slide number 16: Discover the coordinates of these celestial bodies
First option
α – Volopassus
β – Small Dog
τ – Cetus
Second option
α – Eagle
α of Lyra
α – Virgo
This presentation was created by Ludmila Strelnikova. For any inquiries, please contact her at [email protected]

Currently, there are 58,752 educational establishments that provide additional cumulative discounts ranging from 2% to 25%. To determine the discount available for all staff members of your educational institution, please sign in to your personal Infoworks account.


A course for professional retraining is available.
Teacher of secondary vocational education. Implementation of the new generation Federal State Educational Standard (FSES) – theory and practice.
We can offer you an additional discount for your educational institution. The amount of the discount depends on the number of your colleagues who have already completed Infowork courses.
Currently, there are additional cumulative discounts available for 58,752 educational institutions, ranging from 2% to 25%. To find out the specific discount that applies to all employees of your educational institution, please log in to your personal Infoworks account.


Professional course for retraining
State and local government management in educational institutions.
We can apply the discount of your educational institution to this discount (it depends on how many of your colleagues have taken Infowork courses).
Currently, 58,752 educational institutions are receiving additional discounts (ranging from 2% to 25%). To determine the discount available to all employees of your educational institution, please log in to your personal Infoworks account.


Getting ready for the literature section of the Unified State Exam. Exploring the fascinating realm of poetry by F.I. Tyutchev
Overview of the presentation through separate slides:


On the picture, you can see that every star has left its trace in the shape of a circular arc.
The central point of all these arcs is located close to Polaris.
The location that the Earth’s axis of rotation points towards is known as the North Pole of the Earth.
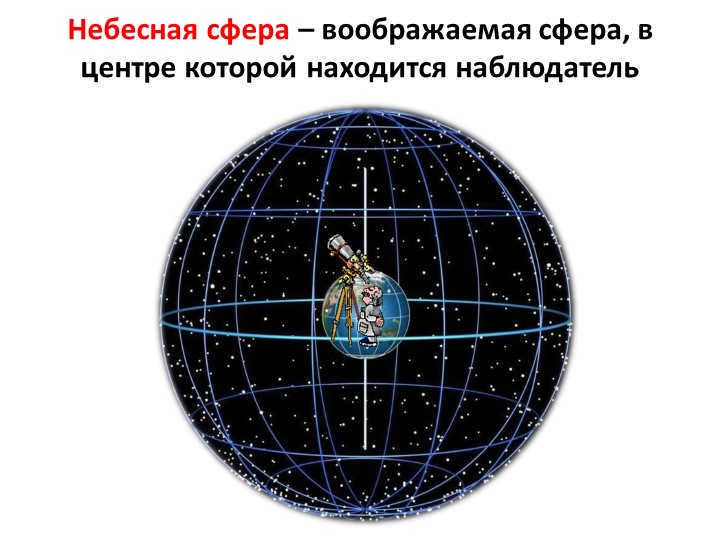

Slide 4: The celestial sphere can be described as a hypothetical sphere that is conceptualized to have an observer positioned at its center.
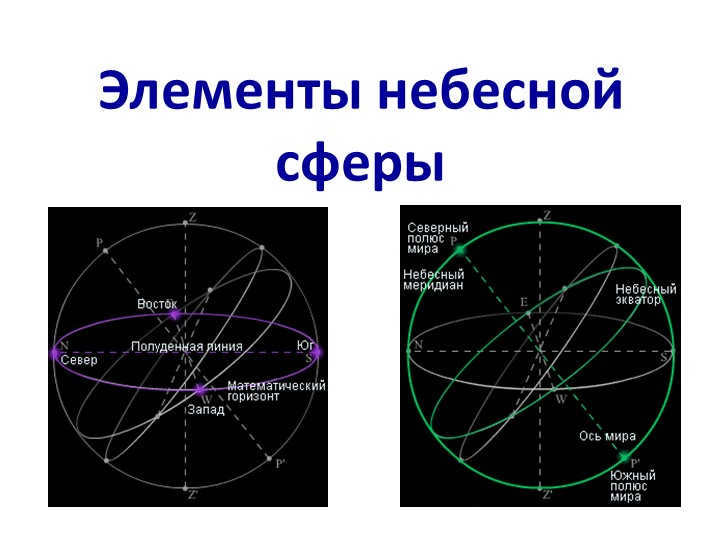
There are 5 different elements that make up the celestial sphere.
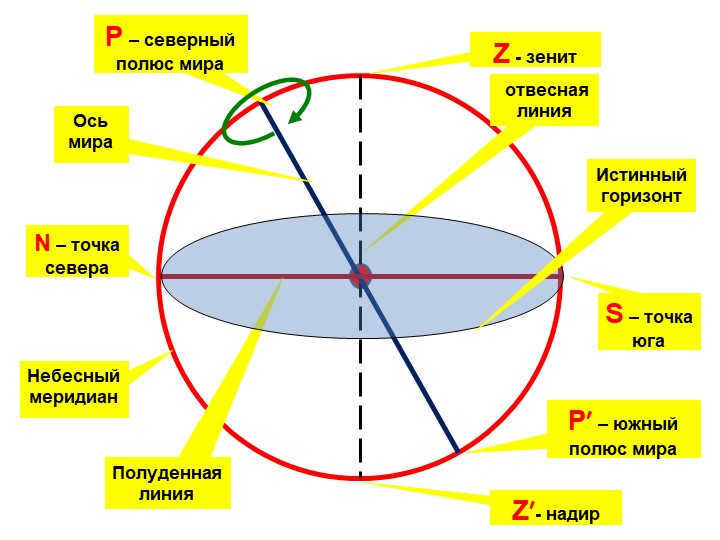
Slide number 6 Celestial meridian
plumb line
Z – the point directly above an observer
Z′ – the point directly below an observer
World axis
P – the point in the northern hemisphere where the celestial meridian intersects the horizon
P′ – the point in the southern hemisphere where the celestial meridian intersects the horizon
Noon line
True horizon
N – the point in the northern direction
S – the point in the southern direction

Slide number 7 explains that the celestial meridian refers to the great circle of the celestial sphere. This circle’s plane intersects with the plumb line and the axis of the world.
Slide 1: Horizontal coordinates
An object’s position is determined in relation to the horizon and the south direction.
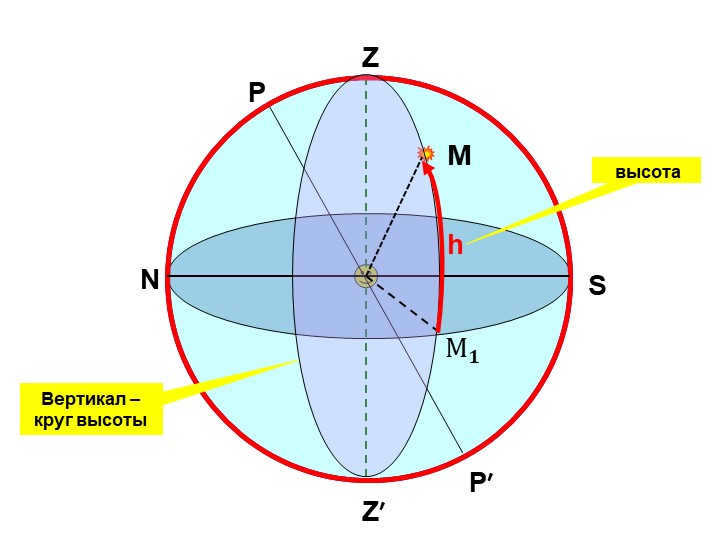

Horizontal coordinates of a star in 11 slides:
The angular distance from the horizon along the great circle, known as the vertical height h, can be used to determine the position of a star.
The altitude of the star can vary from 0° to +90° above the horizon and from 0° to -90° below the horizon.
Slide 13 Z
Z′
N
S
P
P′
M
Vertical – circle of height
A
The angular distance azimuth A is measured to the west from the south point to the vertical.
h
The azimuth varies between:
0° to 360°
M 𝟏
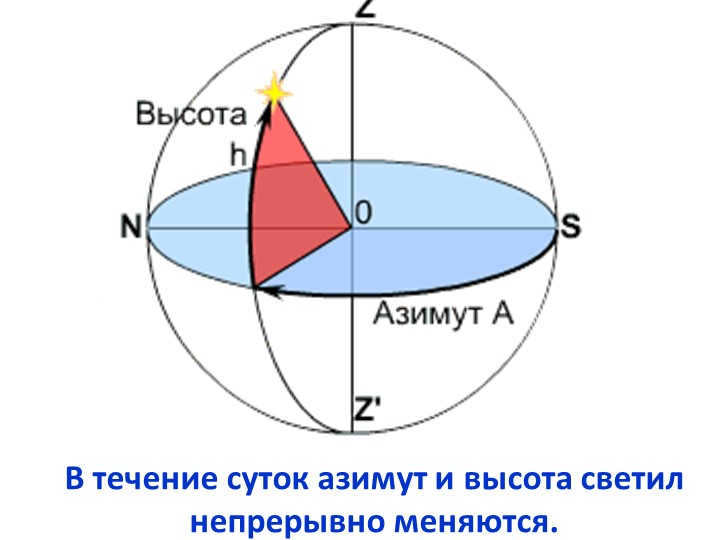
Slide 15 Celestial Body Culminations
Culmination refers to the moment when a celestial body crosses the celestial meridian.
As the luminaries orbit the Earth’s axis, they create diurnal parallels.
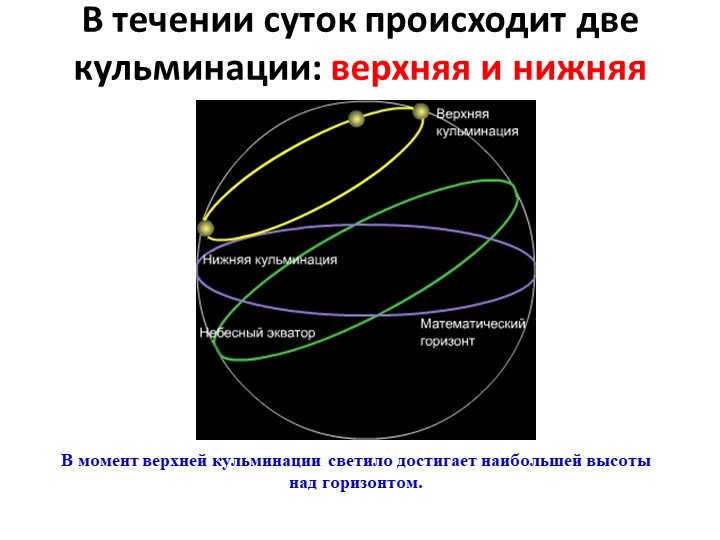
Throughout the day, there are two high points: the upper climax and the lower climax.
During the upper culmination, the luminary reaches its highest point above the horizon.
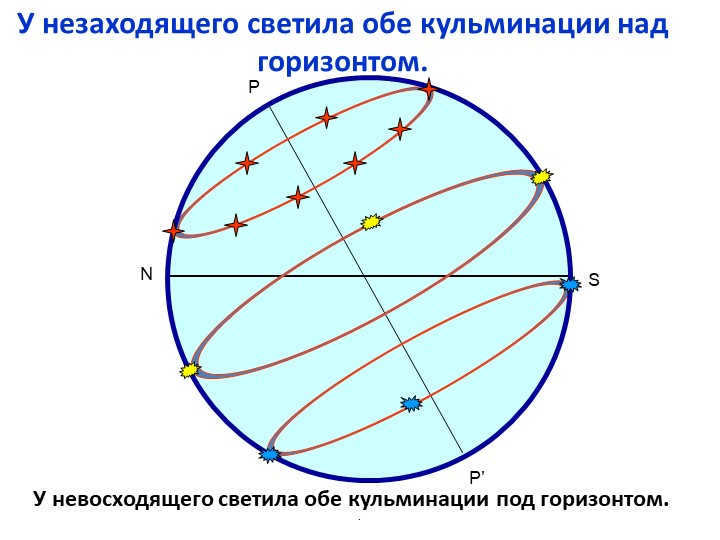

Slide 17: A luminary that does not set has both of its climaxes above the horizon.
.
N
S
P
P'
A luminary that does not ascend has both of its culminations below the horizon.

Slide 18. Equatorial Coordinates
Equatorial coordinates refer to a coordinate system that remains unaffected by the observer’s position and the time of day. These coordinates are solely determined by the proper motions of celestial bodies.
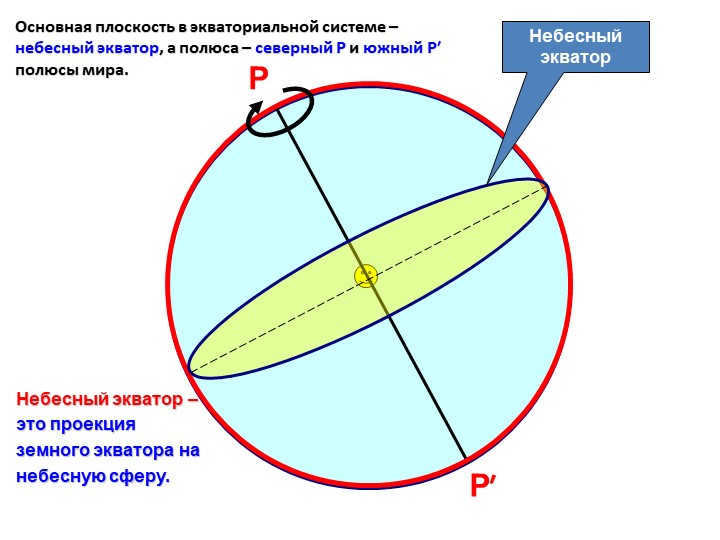
Slide 19
Point P
The celestial equator
The celestial equator
represents the earth’s equator projected onto
the celestial sphere.
The primary plane in the equatorial system is the celestial equator, with the northern P and southern P′ poles of the globe serving as the poles.
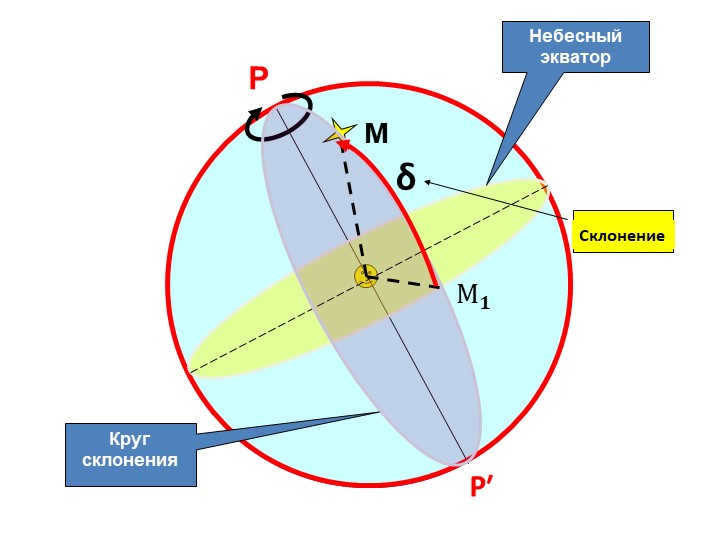
In the 20th slide, there are points labeled P and R’, the Celestial equator, and the Circle of declination. The Circle of declination is denoted by δC, and M represents the declination M.

21 Slide δ (delta) – The declination of a luminary refers to the angular separation of the luminary from the celestial equator, as measured along the circle of declination either to the north or south of the celestial equator. The unit of measurement for declination is degrees.

22 slide Solution:
Problem #1
What is the declination of Sirius (α of the Big Dog) in relation to Polaris if the angular distance between them is 106°?
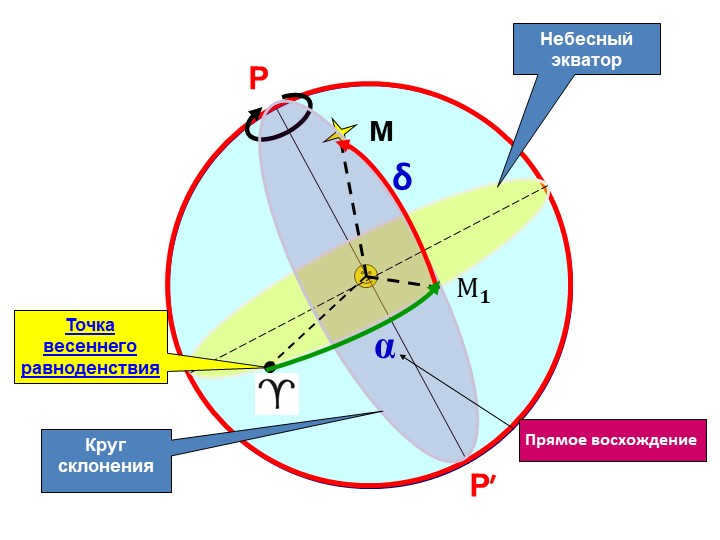
There are 23 slides P and P′ on the celestial equator and the circle of declination.
At the vernal equinox point, there is α, δ, Direct Ascension, and the symbols М 𝟏 and М.


Slide 24 – The direct ascension (α) represents the length of the arc on the celestial equator from the point of the vernal equinox to the declination circle of the luminary.
It is measured in hours, ranging from 0h to 24h.
1 hour is equivalent to 60 minutes or 15°.
Similarly, 1° is equal to 4 minutes.

On slide 25, we need to solve the following problems:
Problem number 2
Express the angles 90° and 103° in hour measure.
Problem number 3
Express the direct ascent angles of 5h24min and 18h36min in angular measure.

Slide number 26, question number 4.
During the vernal equinox, the sun is positioned exactly on the celestial equator. What are the values of its declination and right ascension?

Recap of Slide 27:
What are the equatorial coordinates of a luminary called?
Do the equatorial coordinates of a star change throughout the day?
What characteristics of the daily movement of luminaries allow for the use of the equatorial coordinate system?
4. What is a culmination?
5. During which culmination does a luminary have the lowest altitude above the horizon?
6. What is the celestial sphere?
7. What coordinates are known as geographic coordinates?
8. What coordinates are equatorial coordinates?
There are 6,331,114 materials available in the database.
Additional materials
- Textbook: “Astronomy (basic level)”, by Vorontsov-Vel’yaminov B.A., Straut E.K.
- Subject: Section 13. Determining distances and sizes of objects in the Solar System
- Textbook: “Astronomy (basic level)”, by Vorontsov-Vel’yaminov B.A., Straut E.K.
- Subject: Section 4. Celestial coordinates and star charts
- Textbook: “Astronomy (basic level)”, by Vorontsov-Veliaminov B.A., Straut E.K.
- Subject: Section 18. Planets of the Earth group
You may find these courses interesting:
- Professional development course “Organizing student research in accordance with FSES requirements”
- Professional retraining course “Clinical Psychology: Organizing Rehabilitation Work in the Social Sphere”
- Advanced training course “Enterprise Economics: Evaluating Activity Efficiency”
- Advanced training course “Financial Management: Preventing Bankruptcy”
- Advanced training course “Business Communication Ethics”
- Advanced training course “Teaching Astronomy in Secondary School: Specifics”
- Professional retraining course “Marketing Organization in Tourism”
- Course on professional development: “Introduction to Tourism Management”
- Course on professional retraining: “Teaching Astronomy: Theory and Methodology in Educational Institutions”
- Course on professional retraining: “Managing Information Technology Resources”
- Course on professional retraining: “Assistant-Referent Activities with Foreign Language Knowledge”
- Course on professional retraining: “Teaching Criminal Law: Theory and Methodology in Educational Institutions”
- Course on professional retraining: “Standardization and Metrology”
Leave your feedback
If you think that the content violates any copyright laws or should be removed from the website for any other reason, you can submit a complaint about it. Remove content
Author information
- On the website for: 5 years and 9 months
- Subscribers: 0
- Total views: 63214
- Total content: 55 pieces
25 minutes ago
21 minutes ago
Video lecture on Modern Education: Developing Artistic and Creative Abilities of Preschool Children
37 minutes ago
Video lecture on the Study of Classical Russian Literature in a Modern Context in Lessons with Consideration of FSES SOOO
Gift certificates
The responsibility for resolving any disputes regarding the materials themselves and their content rests with the users who posted the material on the site. However, the site administration is prepared to provide assistance in resolving any issues related to the site’s operation and content. If you notice any unauthorized use of materials on this site, please notify the site administration through the feedback form.