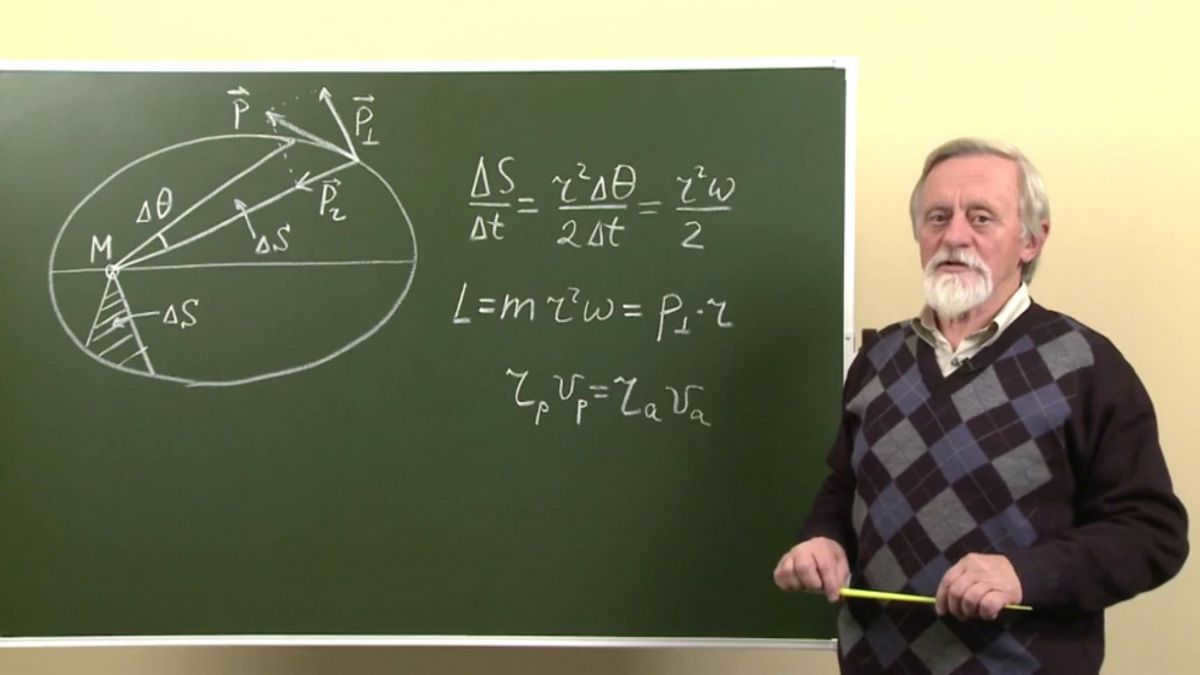During this lesson, we will revisit the formulation of the universal law of gravitation. We will explore the reasons why the movement of planets deviates from Kepler’s laws. Additionally, we will discuss the impact of tides on celestial bodies and delve into the methods of determining their masses.
Currently, you do not have the ability to view or share the instructional video with your students
In order to access this and other video lessons within the curriculum, you will need to add it to your personal account.
Unlock amazing possibilities

Outline for the lesson on “The Movement of Celestial Bodies in the Presence of Gravitational Forces”
By the 17th century, the initial phase of studying the movement of celestial bodies had been completed, and their kinematics, or the understanding of how they move, had been uncovered. However, the dynamics of planetary motion remained a puzzle. This led to the emergence of new inquiries. Firstly, what is the reason behind the planets’ motion and their orbiting around the Sun? Secondly, what is the explanation for the stability of our planetary system?
To find answers to these inquiries, let us recollect that any material object, if it lacks support, descends towards its surface. And while our planet was once perceived as the central body of the cosmos, the phenomenon of gravity was only deemed as an earthly occurrence. However, the discoveries made by Copernicus and his followers revealed that Earth is just an ordinary planet that orbits the Sun similar to other planets. As a result, certain scientists hypothesized that gravity is not exclusive to Earth but also exists in other celestial bodies.
Following the emergence of the heliocentric system of the universe and the laws of Kepler and Galileo’s law of inertia, scientists presented a significant mechanical challenge of constructing the trajectory of a planet.
Robert Hooke was the first person to make an attempt at solving the problem. His approach was founded on three key assumptions. Firstly, he believed that the gravitational force exerted by celestial bodies is always directed towards their center. This means that not only will parts of the celestial body be attracted to each other, but also any other celestial bodies within the range of this force.
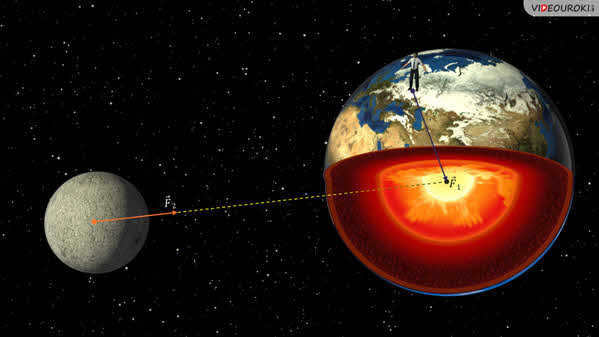
According to Galileo’s law of inertia, any object in linear motion will continue moving in a straight line until it is redirected by another external force and forced to follow a circular, elliptical, or other complex trajectory.
Furthermore, Hooke proposed that gravitational forces become stronger as the distance between the object and the center of gravity decreases.
Ten years later, the English astronomer Edmund Halley demonstrated that the force of attraction decreases in proportion to the square of the distance:
Everything appeared to be predestined. However, the issue with the mechanical malfunction remained unresolved due to the scientists’ lack of understanding of mass and the laws of dynamics, despite these concepts having already been formulated by Newton. Newton’s exceptional ability to discern the physical foundation within the intricacy of phenomena, along with his mathematical brilliance, enabled him to fully resolve this problem.
The tale of Newton, the apple, and the moon is widely known. Yet, at its core lies Newton’s brilliance. His thought process was something along the lines of this: given that the gravitational force diminishes in proportion to the square of the distance, the Moon, positioned at a distance approximately 60 times its radius from Earth, should experience an acceleration that is 3600 times smaller than the acceleration of free fall near the Earth’s surface.
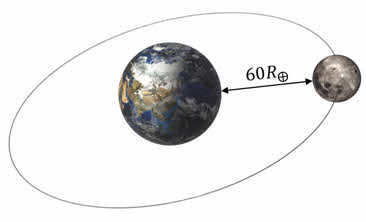
If we assume the acceleration due to gravity on Earth to be 9.8 m/s2, then the acceleration imparted by Earth to the Moon is approximately 0.0027 m/s2.
Alternatively, the Moon, being a body moving in a circular path, experiences an acceleration given by a = ω2r.
If we consider the period of the Moon’s orbit around Earth to be 27.32 days and the radius of Earth to be 6400 km = 3.84 ∙ 108 m, then the orbital acceleration of the Moon is also approximately 0.0027 m/s2.
What does this equality signify? It tells us that the force responsible for keeping the Moon in its orbit is the gravitational force exerted by Earth, but weakened by a factor of 3600 compared to the force experienced on Earth’s surface.
In 1687, Newton finally published the law of universal gravitation. Remember that this law states that any two objects exert a force on each other that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them:
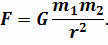
The gravitational constant, denoted by the coefficient of proportionality G, is essential in understanding the law of universal gravitation. This constant was introduced by Isaac Newton, who made a groundbreaking discovery that not only allowed for the mathematical proof of Kepler’s laws, but also their extension. Newton demonstrated that the movement of a celestial body within the gravitational field of another celestial body can be described by one of the conic sections: circle, ellipse, parabola, or hyperbola.
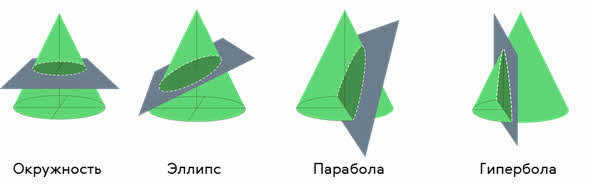
This principle was known as Kepler’s initial general law.
It is worth mentioning that Kepler’s principles are strictly observed only when considering the movement of two separate bodies, such as the Sun and a planet, influenced by their mutual attraction. This type of movement in astronomy is referred to as undisturbed motion.
However, it is important to note that our solar system consists of not only 8 large planets, but also dwarf planets, numerous smaller planets, asteroids, and comets. All of these celestial bodies interact not only with the Sun, but also with each other through the force of gravity. As a result, the actual movement of celestial bodies does not adhere to Kepler’s laws.
Deviations in the movement of objects from Kepler’s laws are referred to as perturbations. The actual movement of the objects is known as perturbed motion or pre-turbations.
However, these perturbations are relatively small due to the significant mass of the Sun compared to the combined mass of all the bodies in the solar system. The largest perturbations in the movement of celestial bodies are caused by Jupiter, which is over 300 times more massive than Earth. The deviations become particularly noticeable when asteroids and comets pass close to a specific planet.

While the perturbations may not be significant for sizable celestial bodies, studying them enables us to accurately determine the mass and location of the perturbing object. A remarkable illustration of this phenomenon in the field of astronomy arose with the detection of Neptune, accomplished through the examination of perturbations observed in the orbit of Uranus.
William Herschel discovered Uranus in 1781. However, after fifty years of studying its movement, scientists noticed that Uranus’s motion did not align with the predicted motion, even when accounting for the gravitational influences of all known planets at the time. This led to the hypothesis that there must be another massive planet located beyond Uranus’s orbit. Based on this theory, researchers calculated the hypothetical planet’s orbit and pinpointed its position in the night sky. On September 23, 1846, Johann Galle confirmed the existence of the eighth planet in our solar system, located approximately where the calculations had indicated.

As per the famous saying by Dominic Arago, Neptune is often referred to as “a celestial body discovered with the stroke of a pen”.
Another illustration of an unsettling force is the phenomenon of tides. These tidal movements, known to humanity since ancient times, have only been comprehensively explained through the principles of universal gravitation. In order to comprehend the occurrence of tides, let us consider a simple scenario: the Earth, the Moon, and three specific points – two located on the Earth’s surface and one at its center. The Moon, influenced by its own gravitational force, will induce acceleration in these points. However, since they are positioned at varying distances from the Moon, the accelerations they experience will differ.
The difference between the acceleration caused by the gravitational pull of another body at a given point and at the center of the planet is known as tidal acceleration.
At points A and B, tidal accelerations are oriented away from the Earth’s center. This causes the Earth’s shells, particularly the water shell, to be pulled in both directions along the line connecting the Moon and Earth’s centers. Essentially, the planet experiences tides at these points. Additionally, along the circle whose plane is perpendicular to this line, low tide occurs on the Earth.
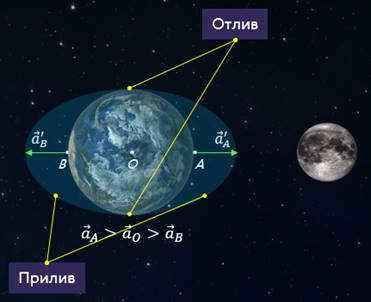
Due to the Earth’s daily rotation and the gravitational attraction of the Moon, tidal friction occurs between the vast bodies of water involved in tidal events and the ocean floor. This phenomenon results in a deceleration of the Earth’s rotation, causing the length of a day to increase by 0.0014 seconds every 100 years. The same mechanism also slows down the Moon’s rotation, resulting in its permanent facing towards us.
Mass is one of the fundamental characteristics of any celestial body. The law of universal gravitation enables us to determine the mass of celestial bodies, including the Earth’s mass. As you may recall from physics, gravity exerts its force on an object near the Earth’s surface.
.
If an object is in motion solely due to the force of gravity, it is possible to derive a formula for calculating the mass of our planet by using the known value of the acceleration due to gravity and applying the law of universal gravitation.
By substituting the known values into this formula and performing basic calculations, we can determine that the mass of the Earth is approximately 6 x 10^24 kilograms.
Therefore, by knowing the radius of a celestial body and the acceleration due to gravity on it, it is possible to determine its mass.
Nevertheless, it is widely recognized that calculating the acceleration of free fall near the surface of any planet can be an arduous and sometimes insurmountable task. However, there exists an alternative approach. Let us examine it. Suppose we have two entities, which exert gravitational forces upon each other, and they revolve around a shared center of mass at established distances with a period denoted as T.
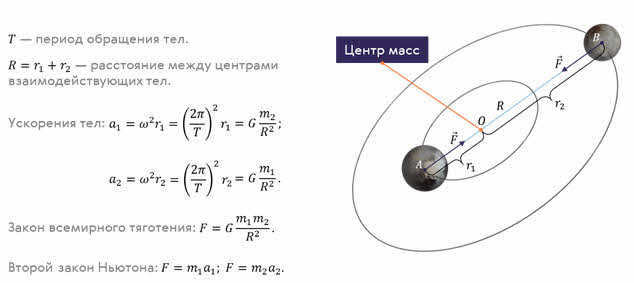
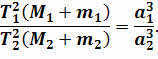
The equation we have recorded is known as Kepler’s third generalized law: the squares of the sideric periods of the moons multiplied by the sum of the masses of the main celestial body and the moon are equal to the cubes of the major semi-axes of the moon’s orbits.
For instance, if we have knowledge of the average distance from the Earth to the Sun and from the Earth to the Moon, as well as the periods of the Earth’s orbit around the Sun and the Moon’s orbit around the Earth, we can calculate the mass of our star (in Earth masses).

Every celestial body in the Universe is originated from vast clouds of gas and dust, which can be significantly larger than the Sun, sometimes even hundreds or millions of times larger. However, these primary formations are widely dispersed and scattered across hundreds or even thousands of light years. If they possess any rotation, it is typically imperceptible due to the fact that it takes billions of years for them to complete a single revolution. Meanwhile, all other forms of matter and energy revolve around them, inevitably influenced by the force of gravity.


When two objects are in motion relative to each other, their gravitational force generates a rotational force.
Tidal acceleration
This phenomenon is referred to as tidal acceleration by astrophysicists. Every celestial body in the Universe possesses angular momentum. Stars and systems are formed from clouds of gas and dust. This is how our solar system came into existence.
What Causes Planets to Rotate in Reverse?
It is fascinating to note that the rotational direction of a planet can undergo significant changes. This phenomenon can be attributed to the gravitational effects exerted by the planet’s parent star or other celestial bodies. A notable example of planets with retrograde rotation are Venus and Uranus. These planets exhibit an east-west movement, which is opposite to the rotational direction of other planets in our solar system. It is believed that the angular momentum of these planets has been altered as a result of encountering a highly massive body during their evolutionary history.
Matter is in constant motion
It may seem peculiar, as both we and our homes remain in the same location today as we were a week ago. However, even a week from now, and today, and a hundred years from now, everything on our planet will continue to be carried along at the same speed as the Earth’s rotation around the Sun. That speed is 108,000 kilometers per hour. Our planet travels a great distance, 940 million kilometers in one cycle. And all life on Earth is partaking in this motion without even realizing it.
And what about the motion of galaxies
Galaxies are constantly in motion within outer space. This perpetual movement is primarily driven by the force of gravity, which acts as the binding force that prevents galaxies from dispersing across the expansive universe. Consequently, it is predicted that our galaxy will eventually collide with the Andromeda galaxy in a few billion years. The precise details of this collision and its ultimate outcome remain unknown. However, it is anticipated that the larger of the two galaxies will consume its smaller counterpart, resulting in the formation of a new and distinct galaxy.

An illustration showcasing the phenomenon of galaxy merging, captured by the Gemini spectrograph.
The denizens of the Solar System may remain unaware of this celestial occurrence. In general, sentient beings inhabiting the planet Earth during this juncture will likely be preoccupied with the imminent transition of the Sun into its next evolutionary phase – transforming into a red giant.
Does the universe have rotational motion?
It is highly unlikely. In order to investigate this, researchers have been analyzing cosmic microwave radiation maps, which contain the oldest light in the universe. These maps were generated from data collected by a satellite over a span of five years. The extensive analysis revealed that the universe does not possess a discernible direction of rotation.
Join the UFO World telegram channel for updates
Receive immediate notifications of new Articles on your phone
Planetary movementThroughout the ages, the movements of planets have captivated the human gaze, prompting observation and investigation of celestial entities. As a result, various theories have emerged over the centuries, aiming to elucidate the motion of these celestial bodies. Among the scholars who made such observations was Ptolemy of Alexandria, who formulated a model where the Earth was positioned at the center of the universe.
Currently, our understanding is that the movement of celestial bodies is consistent, everlasting, and follows a circular path, or a combination of various cycles. Conversely, it is evident that the Sun is at the heart of the solar system, as the stars are remote objects that remain fixed in place. While they may appear to be in motion from our vantage point on Earth, in reality, they are much farther away than we perceive and do not orbit around the Sun.
Earth’s Movements
It is worth noting that Copernicus’ theory was supported by Galileo, who provided experimental evidence to substantiate it. The discovery that Jupiter’s satellites, referred to as the “planet’s medicine man,” orbit around Jupiter suggests that the Earth is not the center of everything. Through observations made with a telescope, it has been determined that stars do not appear magnified and are located at a significant distance from us, making parallax impossible to observe.
Make sure to also check out: Characteristics of the Solar System’s Three Largest Gas Planets
The imprudent behavior of Galileo when it came to defending Copernicus’ heliocentric theory led him into grave trouble: he found himself condemned by the Inquisition and arrested in his residence on the outskirts of Florence, where only one of his students, such as Torricelli, came to visit him.
Therefore, prior to discussing the movements of all the planets, it is important to acknowledge that planet Earth itself has three movements: diurnal rotation, annual rotation, and annual tilt of its axis. The backward movement of the planets is a result of Earth’s motion. The distance from Earth to the Sun is minuscule compared to the distance to the stars.
The motion of the planets and the principles governing them.
The human intellect is truly remarkable as it possesses the ability to comprehend the behavior of the natural world through diligent study. It is through this same mode of reasoning, mixed with a sense of wonder for the natural world, that we have arrived at such a comprehensive and elegantly simple principle, known as the law of gravity. This law states that every object in the universe exerts an attractive force on every other object.
The force of attraction between two objects, caused by gravity, is incredibly strong and is directly proportional to the mass of each object while inversely proportional to the square of the distance between them. Furthermore, the object responds to this force by accelerating in the direction of the force, with the amount of acceleration inversely proportional to the mass of the object.
It is this data that is essential for an adequately skilled mathematician to deduce all the implications of these two principles. However, it is crucial to provide a more detailed account of the implications of these principles and the behavior of the planets. The latter is currently being investigated by the German astronomer Johannes Kepler, who has conducted various studies on celestial bodies situated in the vastness of space.
As a result, Kepler was regarded as a man with an abundance of groundbreaking ideas in the 17th century. Nevertheless, there is no question that the most significant accomplishment of this distinguished scientist was the formulation of the law of planetary motion.
Thanks to Kepler’s advancements, it became feasible to determine accurate principles that served as the foundation of celestial mechanics. A comprehensive method of comprehending the motions of the planets is precisely what the field of forecasting entails – the orbits of not only the planets, but also the stars and all other celestial entities.
Kepler’s 3 laws
When it comes to the movement of the celestial bodies, there exist three fundamental laws that govern the motion of planets. In the pursuit of understanding the intricate patterns of the heavens, the renowned astronomer Tycho Brahe enlisted the help of Kepler to validate his observations regarding the orbit of Mars. Kepler, utilizing the invaluable data obtained from these investigations, was able to formulate his initial and subsequent laws of planetary motion a mere four years following Brahe’s untimely demise in 1605. Eventually, in the year 1619, Kepler unveiled his third and final law, solidifying his contributions to the field of astronomy.
Kepler’s primary principle
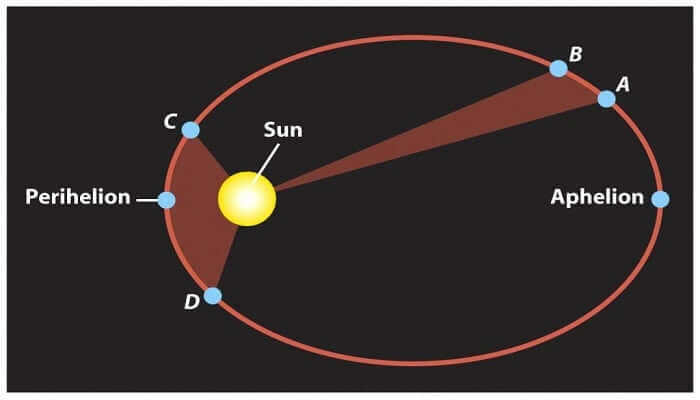

The initial law demonstrates that the planets travel in flat orbits around the Sun that are both closed and elliptical in form, with the Sun positioned at one of the foci. This principle, known as the heliocentric theory, established that all planets orbit the Sun in elliptical paths with the Sun being located at one of the foci within each ellipse.
Kepler’s second law
Kepler’s second law, also known as the law of equal areas, states that a line that connects a planet to the sun will sweep out equal areas in equal time intervals. This means that as a planet moves closer to the sun in its elliptical orbit, it will move faster, and as it moves farther away, it will move slower. This law helps to explain the varying speeds of planets in their orbits.


The law of areas is illustrated by a line connecting the Sun and a planet that covers equal areas in equal amounts of time. This law defines the areolar velocity as the area swept by the position vector of a planet with the Sun as its origin. According to this law, “The areolar velocity of a planet remains constant throughout its trajectory.”
It is important to emphasize that this second law states that the radius vector, which connects any planet with the Sun, sweeps equal areas in equal amounts of time.
Kepler’s third law
Kepler’s third law states that the ratio of the square of a planet’s period to the cube of the major semi-axis of its elliptical orbit is constant for all planets. In other words, the square of a planet’s sidereal period is directly proportional to the cube of its mean distance from the Sun. It is important to note that the sidereal period refers to the time it takes for a planet to complete one full revolution.
While it may appear challenging to comprehend, it remains an exceptionally sophisticated method for computing the positions of planets. The most remarkable aspect of Kepler’s revelation is that he formulated his initial two principles prior to the invention and utilization of refractor telescopes by groundbreaking astronomers like Galileo Galilei. This suggests that his research was grounded in direct and meticulous observations of the celestial sphere.
Kepler: Fascinating Insights
Despite Kepler’s limited comprehension of the validity of his laws, the introduction of Isaac Newton’s revolutionary theory of gravity provided a comprehensive understanding of planetary motion. While Kepler’s laws were initially derived from observations of planetary orbits, the incorporation of Newton’s gravitational principles extended their applicability to any lighter object orbiting a more massive one.
However, nowadays it is not considered a significant issue to possess knowledge about the positions and orbits of the planets within our solar system. This is due to the fact that planetary movements play a crucial role in predicting the trajectories of satellites like Voyager and Cassini. These spacecraft utilized the gravitational force of the planets to slingshot themselves across vast distances. Without the contributions of Brahe, Kepler, and Newton and their laws, programming the extensive paths of these satellites would have been impossible.
The information provided in this article adheres to our principles of editorial integrity. To report any inaccuracies, please click here.
Full article link: postpost “Planets” 3 laws governing planetary motion in space

During the 1600s, Johannes Kepler, a renowned mathematician and astronomer from Germany, formulated three fundamental laws that describe the motion of planets within the solar system. These laws were established based on meticulous observations of celestial objects conducted by Tycho Brahe and other intrepid space pioneers of that era.

First Law of Kepler
Kepler observed that Brahe’s observations deviated from the concept of planets moving in circular orbits around the Sun. This was particularly evident in the case of Mars, where Brahe’s observations indicated a non-circular trajectory. Brahe’s calculations were highly accurate, leaving no doubt about their accuracy among his followers.

Afterward, the German mathematician proceeded to consider the paths of celestial bodies as ellipses, each of which possesses two focal points. These focal points are arbitrary points selected in such a way that the sum of the distances from any point on the ellipse to these focal points remains constant. In the case of an elliptical orbit, one of the focal points is occupied by the Sun.
The shape of the ellipse can be determined by calculating the ratio between the focal distance and the major semi-axis of the orbit. This value is known as the eccentricity of the orbit. When the eccentricity is equal to zero, the orbit transforms into a perfect circle. If the eccentricity ranges from zero to one, the ellipse takes on varying degrees of elongation. When the eccentricity exceeds one, the orbit becomes a parabola.
Kepler’s Second Law
When a celestial body moves along an elliptical orbit, it undergoes acceleration and deceleration at different segments of the orbital path.

A German scientist discovered that if any two segments of a planet’s orbital path, which it passes through in equal time intervals, are taken, and radius vectors are drawn from their endpoints to the central star, the resulting areas will be equal. This is a simplified statement of the second law.
In order for the constancy of areas to be maintained, the body must move at different speeds at different points along its orbit. For example, the Earth moves faster when it is closest to the Sun compared to when it is at its farthest distance from it.
Kepler’s Third Law
The third principle relating to the movement of celestial objects within the solar system pertains specifically to the notions of perihelion and aphelion. When a line is drawn between these two points, it represents the major axis of the planet’s orbit. Consequently, half of this line is known as the major semi-axis.

Kepler inferred from his observations that the squared ratio of complete revolutions around the central star for any two planets in the system is always equal to the squared ratio of the major semiaxes of their orbital paths to the cube.
The challenge in proving and accepting Kepler’s three laws was that he derived them through empirical means. However, in the late 17th century, Newton discovered the classical theory of gravitation. He helped establish the validity of the German astronomer’s conclusions and described the planets’ motion as an elliptical orbit around the Sun. Newton determined that, apart from an object’s mass and distance from the star, no other properties influence gravitational attraction.
Newton also modified Kepler’s third postulate by recognizing that the mass of a celestial object must be taken into consideration in order to satisfy the relation. This interpretation of the third law assists in determining the mass of a planet or satellite, given the magnitude of its orbit and orbital period.
Johannes Kepler’s laws aided in determining the shape of the planetary trajectory, calculating the period of planetary orbit, their velocity, and the changes in velocity as they approach and move away from the Sun. The scientist inferred that the Earth is not a special astronomical object within the system and established that it adheres to all three laws, just like any other planet in our solar system.
Calculation of celestial body positions in the sky. Part 1
Recently, there has been a lot of discussion about Mars. During this time, I had a question that I couldn’t shake off due to my naive curiosity: “Where is Mars right now, and in which direction?” This led me to wonder: “How do we determine the positions of other planets?” It’s clear that the trajectories of planets in relation to Earth can be quite complex. While planetariums like this one can help, they are not the answer we’re looking for.
In this series of articles, my aim is to present the information in the most straightforward manner possible. Consequently, we will create a basic program that provides the user with the specific locations to observe the planets in our solar system from any given point on Earth at any given time. The objective is to convey the fundamental principles that underpin the Kepler orbit model, without relying on common knowledge, except for Newton’s laws and the law of universal gravitation.
For those inquisitive minds, kindly proceed beneath the feline.
It should be acknowledged that the subsequent content presupposes a certain degree of familiarity with Newton’s laws, fundamental principles of geometry, vector algebra, and differential calculus.
What is the mechanism behind the movement of planets?
When considering the interactions between planets, the shifting of the solar system’s center of gravity relative to the sun’s center of gravity, and other factors, the movement of planets becomes incredibly intricate and cannot be precisely defined analytically. It’s important to note that even the problem of three-body motion cannot be solved analytically. Therefore, let’s establish which models we will be working within. We will be utilizing the Kepler orbit model. While there are numerous other models available, they are all semi-analytical and ultimately reduce to determining the parameters of the Keplerian orbit at a specific moment in time. In essence, a Keplerian orbit serves as an approximation for the complex movement of a planet at a given point in time. The Keplerian parameters for planetary orbits can be found at nssdc.gsfc.nasa.gov/planetary/factsheet, where the epoch (or specific moment in time) is specified when these Keplerian orbit parameters accurately indicate the position of the celestial body. Typically, this initial moment is the epoch J2000.0, which occurred at noon on January 1, 2000. The Kepler model is quite accurate when calculating the motion of bodies over a short period of time. The accuracy is sufficient to not perceive any visual errors or discrepancies through a small telescope. Of course, more precise models are required when calculating the trajectory of a spacecraft traveling to another planet.
Orbit of Kepler
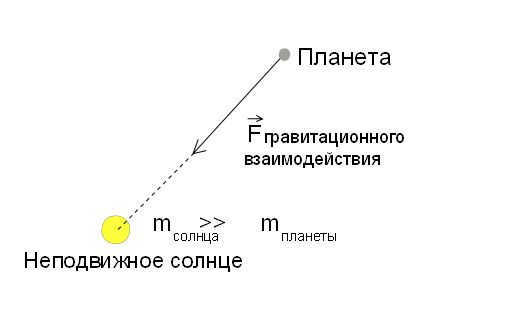
Now, let’s begin with the fundamental assumptions of this model. The first assumption is that the Sun’s mass is significantly greater than the combined mass of all the planets. This implies that the interactions between planets can be disregarded when compared to the interactions between the Sun and each planet individually. Hence, we can simplify the problem to a two-body interaction (meaning we can focus on the Sun’s interaction with each planet separately). Additionally, considering that the planet’s mass is much smaller than the Sun’s mass, the interaction becomes one-sided, meaning the planet’s motion does not affect the Sun’s motion in any way. Consequently, we can treat the planet as a point-like object moving within a stationary gravitational field. This can be summarized as follows:
Interaction of Gravitation
What exactly is gravitational interaction? It serves as a fundamental interaction that affects all material bodies universally. Although there is much to discuss about gravitation, let’s focus on the key point. According to Newton’s classical theory of gravitation, the gravitational attraction force between two material points with masses m1 and m2 that are separated by a distance R, is directly proportional to their masses and inversely proportional to the square of the distance between them – as represented by the formula:
Here, G represents the gravitational constant (a coefficient of proportionality). It’s important to highlight that the gravitational force always acts from the center of gravity of one body to the center of gravity of the other, and its magnitude is inversely proportional to the square of the distance between them (known as the law of inverse squares).
It’s worth noting that in the context of our discussion, a material point on a spherical planet in a vacuum is solely subjected to the gravitational force from the Sun. In this scenario, the gravitational force field can be described as a central force field. In a central field of forces, the force acting on a body at any given point within the field always passes through the center of the field (in our case, the center of gravity of the Sun), and the magnitude of this force is solely determined by the distance to that center.
Newton’s second law
In inertial reference systems, the acceleration experienced by an object is directly proportional to the force applied to it, has the same direction as the force, and is inversely proportional to the object’s mass.
The change in momentum is proportional to the applied force and occurs in the direction of the force.
This version, while less precise (we must make reservations about reporting systems, but that is not our concern at the moment), is much more clear. The amount of motion in this case is referred to as the momentum of the object, which is calculated by multiplying the object’s mass by its velocity:
Therefore, let’s express the verbal formulation in symbolic form:
Or if we express the momentum of an object and treat mass as a constant (mass is not always constant, but in this case it is), we obtain the following well-known formula:
Where vector represents the acceleration of the object. We must remember that acceleration, momentum, velocity, and force are all vector quantities. Let’s agree that if a vector quantity has a vector symbol, it is a vector, otherwise it is its magnitude.
Kepler’s Second Law
Every planet orbits in a plane that passes through the center of the Sun. In equal intervals of time, the radius vector connecting the Sun and the planet sweeps out equal areas.
I understand that “got the law” doesn’t sound very professional, but unfortunately, that’s what it’s called. This name comes from the fact that Kepler didn’t deduce it, but rather intuitively discovered it based on his observations. In other words, he empirically obtained it, which qualifies it as a law.
Below, you can see an illustration of this law (the figure is taken from a wikipedia article).
Differential equation for the orbit
Let’s examine the cross product of the position vector and velocity vector more closely. The position vector can be expressed as the product of the magnitude of the position vector (the distance from the origin to a point) and a unit vector in the direction of the position vector:
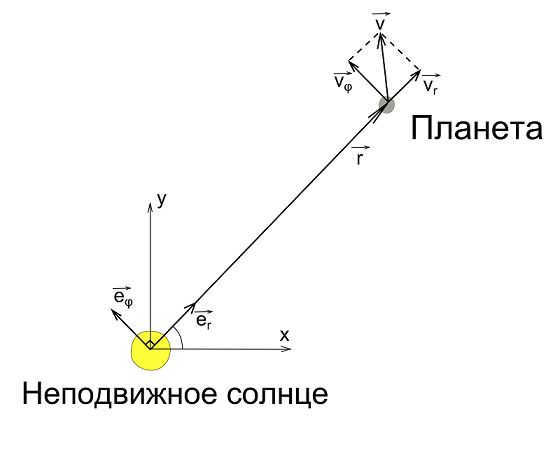
Then, the velocity vector can be written as:
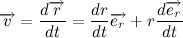
And the cross product of the position vector and velocity vector can be expressed as:
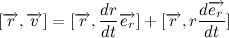
Considering the fact that the vectors and have the same direction, we can conclude that . Therefore:
Let’s now explore the time derivative of a unit vector:
The diagram illustrates that over time, the vector undergoes rotation by the angle . The difference between vectors and is equivalent to vector . For small angles, the following equation holds true:
As approaches zero, the directions of vectors and become aligned, while the direction of vector becomes perpendicular to them. Let’s introduce a unit vector , which is perpendicular to and coincides with the direction of motion of its endpoint. Therefore:
By taking the limit, we have:
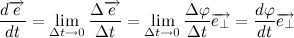
Here, represents the angular velocity of vector . Let’s denote
Now, let’s revisit the product of the vector’s radius and velocity, considering:
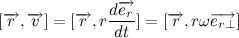
It is evident that vectors and are mutually perpendicular. Let’s introduce another unit vector , which is perpendicular to vectors and . Hence, the vectors , and form an orthonormalized basis. By definition of the vector product, we obtain:
Consequently, . Let’s introduce the notation, . It’s worth noting that:
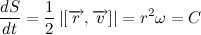
Returning to Newton’s second law, the force vector acting on the body, can be written as the magnitude of the gravitational force multiplied by the orth :
Where m1 and m2 represent the masses of the planet and the sun, respectively. Let’s consider the case where the mass of the planet is reduced to unity, and henceforth we will not mention the mass of the planet, as it does not affect the motion trajectory. Let’s introduce the notation, , then:
Now, let’s describe the acceleration vector as follows:
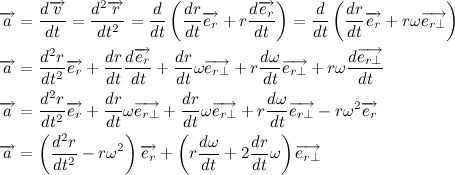
Let’s examine the contents of the second bracket:
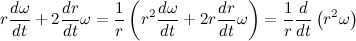
However, we already know that , hence it follows that , thus:
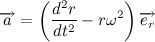
Let’s introduce the notation . Recall that we previously introduced the notation , and it’s evident that .
Now, let’s express the derivative of the radius vector’s modulus in terms of C:
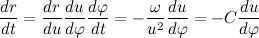
Now, let’s express the second derivative of the radius vector’s modulus in terms of C:
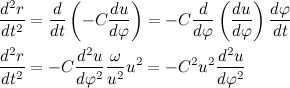
Given the obtained result, let’s rewrite the expression for the acceleration vector:
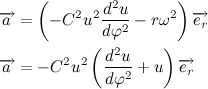
Then, Newton’s second law can be expressed as:
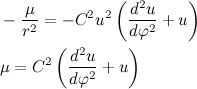
Let’s rewrite the resulting differential equation in a more familiar form:
I believe many of you have already guessed what the obtained differential equation is, but I will conclude the first part here to avoid overwhelming the reader and myself.
We have derived a differential equation that describes the path followed by a material point in a gravitational field. This equation is highly useful for describing the trajectories of planets and other celestial bodies.
Remaining Tasks
The derived differential equation does not include a time parameter, so we lack information about the motion’s nature. Therefore, we need to introduce a time component to our equation. Additionally, we will explore different coordinate systems and their transformations to determine the positions of the planets in relation to the observer’s frame of reference.
Kepler’s Laws
This lesson can be accessed with a subscription
Already subscribed? Log in