In the realm of atoms and subatomic particles, gravitational forces are significantly smaller in comparison to other forms of force interactions between particles. Observing the gravitational interaction between various bodies around us, despite their massive weights, is a challenging task. However, gravity plays a crucial role in determining the behavior of celestial objects such as planets, comets, and stars, as well as keeping us firmly grounded on Earth.
The motion of planets in the solar system is governed by gravity. Without it, the planets that comprise the solar system would disperse in different directions and become lost in the vast expanse of outer space.
The laws of planetary motion have always fascinated people, sparking their curiosity about the movement of planets and the structure of the Solar System. This exploration eventually led to the development of the theory of gravitation and the discovery of the universal law of gravity.
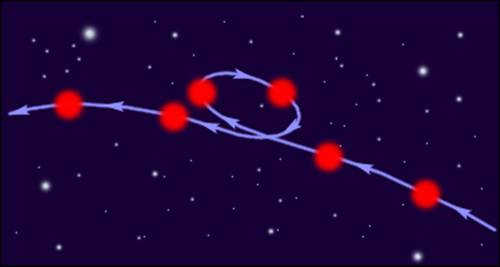
When observed from Earth, the paths of planets appear to follow intricate trajectories (Fig. 1.24.1). The first attempt to construct a model of the Universe was made by Ptolemy (~140 AD). According to Ptolemy’s model, Earth was positioned at the center of the universe, with planets and stars moving in both large and small circles, like a grand celestial dance.
 |
| Figure 1.24.1: A symbolic representation of the observed motion of Mars against a background of fixed stars. |
The geocentric system lasted for over 14 centuries and was only replaced in the mid-16th century by the heliocentric Copernican system. The Copernican system simplified the trajectories of the planets. In the early 17th century, the German astronomer Johannes Kepler formulated three empirical laws of motion for the planets in the solar system, based on the Copernican system. Kepler’s laws were derived from observations made by the Danish astronomer Tycho Brahe.
Kepler’s First Law (1609):
All planets follow a path that can be described as an elliptical orbit, with the Sun located at one of the focal points.
Figure 1.24.2 illustrates the elliptical orbit of a planet with a significantly smaller mass compared to that of the Sun. The Sun occupies one of the foci of the ellipse. The point on the trajectory closest to the Sun is referred to as the perihelion, while the point farthest from the Sun is known as the aphelion. The distance between the aphelion and the perihelion represents the major axis of the ellipse.
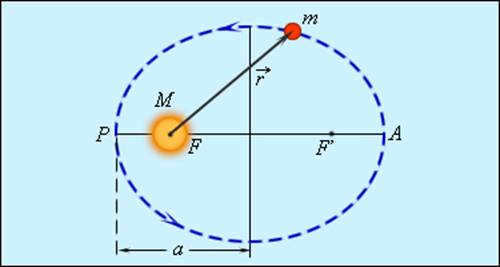 |
| Figure 1.24.2. The orbit of a planet with mass m M is elliptical. The length of the major semi-major axis is denoted by a, while F and F' represent the orbital focal points. |
With the exception of Pluto, most planets in the solar system have orbits that are nearly circular.
Kepler’s Second Law (1609):
The planet’s trajectory covers equal areas in equal time intervals.
Figure 1.24.3 demonstrates Kepler’s second law.
Kepler’s second law is essentially the conservation of momentum. In Figure 1.24.3, the momentum vector of the celestial body and its components are shown, as well as the area covered by the planet’s trajectory for a small time interval Δt which is approximately equal to the area of a triangle with base rΔθ and height r:
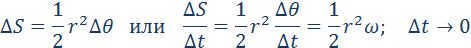
Here is the angular speed.
The magnitude of momentum L is equivalent to the product of the magnitudes of the vectors and :
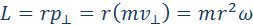
The first law of Kepler states that:
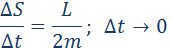
Hence, in accordance with Kepler’s second law, the angular momentum L remains constant throughout the motion.
Specifically, given that the velocities of the planet at perihelion and aphelion are perpendicular to the radius vectors, it follows from the law of conservation of momentum:
The relationship between the squares of the orbital periods of the planets and the cubes of the major semi-axes of their orbits is described by Kepler’s Third Law.
All the planets in the solar system fulfill Kepler’s Third Law with an accuracy of better than 1%.
In Figure 1.24.4, two orbits are shown: one is a circular orbit with a radius of R, and the other is an elliptical orbit with a major semi-axis of a. According to the third law, if R = a, then the orbital periods of both orbits are equal.
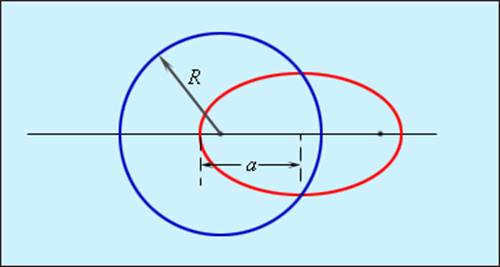 |
| Figure 1.24.4 Circular and elliptical orbits. The orbital periods of the bodies on these orbits are the same when R = a. |
Although Kepler’s laws were a significant advancement in understanding planetary motion, they were ultimately derived from empirical observations. Kepler’s laws lacked a theoretical foundation, which was addressed by Isaac Newton in 1682 when he discovered the law of universal gravitation:
where M and m represent the masses of the Sun and the planet, R is the distance between them, and G = 6.67-10 -11 N-m 2 /kg 2 is the gravitational constant. Newton proposed that gravitational forces not only govern the motion of planets in the solar system but also act between any objects in the Universe. This includes the gravitational force experienced by objects near the Earth’s surface.
When a planet moves in a circular orbit, it automatically satisfies Kepler’s first and second laws. According to the third law, the period of revolution, T, is related to the radius of the orbit, R, by the equation T^2 ~ R^3. This relationship allows us to determine the dependence of the gravitational force on the distance. The gravitational force acting on the planet is due to the interaction between the planet and the Sun:
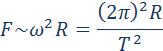
The conservation property of gravitational forces allows us to introduce the concept of potential energy. In the case of universal gravitation, it is convenient to measure the potential energy relative to an infinitely distant point.
The potential energy of a mass m located at a distance r from a stationary mass M is equal to the work done by gravitational forces in moving the mass m from this point to infinity.
The mathematical process for calculating the potential energy of a body in a gravitational field involves summing up the work done over small displacements (Fig. 1.24.5).
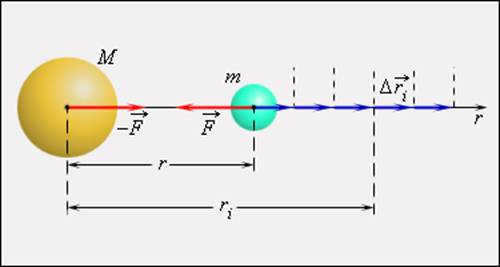 |
| Figure 1.24.5. Calculation of the potential energy of a body in a gravitational field |
The law of gravitation that governs the interaction between objects not only applies to individual masses, but also extends to objects with spherical symmetry. The gravitational force can be calculated as the work done at a small displacement:
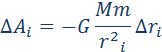
In order to determine the total work required to move a mass m from its initial position to infinity, we must calculate the sum of the work ΔAi for each small displacement:
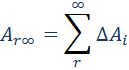
As Δri approaches zero, the sum transforms into an integral. By performing calculations for the potential energy, we derive the following expression.
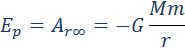
The presence of the negative sign signifies that the gravitational forces operate as a form of attraction.
When an object exists within the gravitational field, situated at a distance r from the gravitational center, and possesses a certain velocity υ, its overall mechanical energy can be quantified as follows:
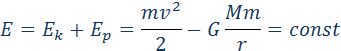
As per the principle of energy conservation, the overall energy of an object within a gravitational field remains constant.
The total energy may be positive, negative, or zero. The sign of the total energy determines the type of motion of a celestial body (Fig. 1.24.6).
When E = E1 < 0, the object cannot move away from the center of gravity beyond a distance of r > rmax. In such cases, the celestial body moves in an elliptical orbit (such as planets in the solar system and comets).
When E = E2 = 0, the body has the ability to move infinitely. The velocity of the body at infinity will be zero. The body follows a parabolic path.
When E = E3 > 0, the motion follows a hyperbolic trajectory. The body moves away towards infinity, while still retaining some kinetic energy.
Kepler’s laws are applicable not only to the movement of planets and celestial bodies within the solar system, but also to the motion of artificial satellites and spacecraft. In this scenario, the Earth is the center of gravity.
The initial orbital velocity represents the velocity at which a satellite moves in a circular orbit close to the Earth’s surface.
In order to place a body, such as a satellite, into orbit around the Earth, it is necessary to achieve this velocity and overcome the force of gravity.
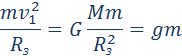
The velocity required for a spacecraft to overcome the Earth’s gravitational pull and become a man-made satellite of the Sun (artificial planet) is known as the second space velocity. When achieving this velocity, the spacecraft will follow a parabolic path away from the Earth.
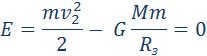
Figure 1.24.7 shows the space velocities. Suppose the velocity of the spacecraft is υ1 = 7.9-10 3 m/s and is parallel to the Earth’s surface. In this case, the spacecraft will orbit the Earth in a circular path at a low altitude. If the initial velocity is higher than υ1 but lower than υ2 = 11.2-10 3 m/s, the spacecraft’s orbit will be elliptical. When the initial velocity is υ2, the spacecraft will follow a parabolic path, and with even higher initial velocity, it will follow a hyperbolic trajectory.
Additional articles within this category:

During the early 17th century, the German mathematician and astronomer Johannes Kepler formulated the first law of planetary motion, which brought about a revolutionary change in our comprehension of how celestial bodies, particularly planets, move around the Sun. These laws established a strong basis for Isaac Newton’s subsequent research on universal gravitation and laid the groundwork for contemporary celestial mechanics. Kepler’s breakthroughs constituted a significant advancement in the field of astronomy and had a profound impact on our understanding of the structure and behavior of the solar system.
Introduction
Johannes Kepler (1571-1630) played a crucial role during the scientific revolution by connecting the contributions of Copernicus and Galileo and setting the stage for Newton’s revolutionary laws of motion. Kepler, who was born in Weil der Stadt, Germany, initially pursued studies in theology but later became fascinated by astronomy. He joined forces with the renowned Danish astronomer Tycho Brahe and utilized Brahe’s vast collection of observational data to formulate his own principles governing the movement of planets.
Kepler’s Initial Principle: The Principle of Ellipses
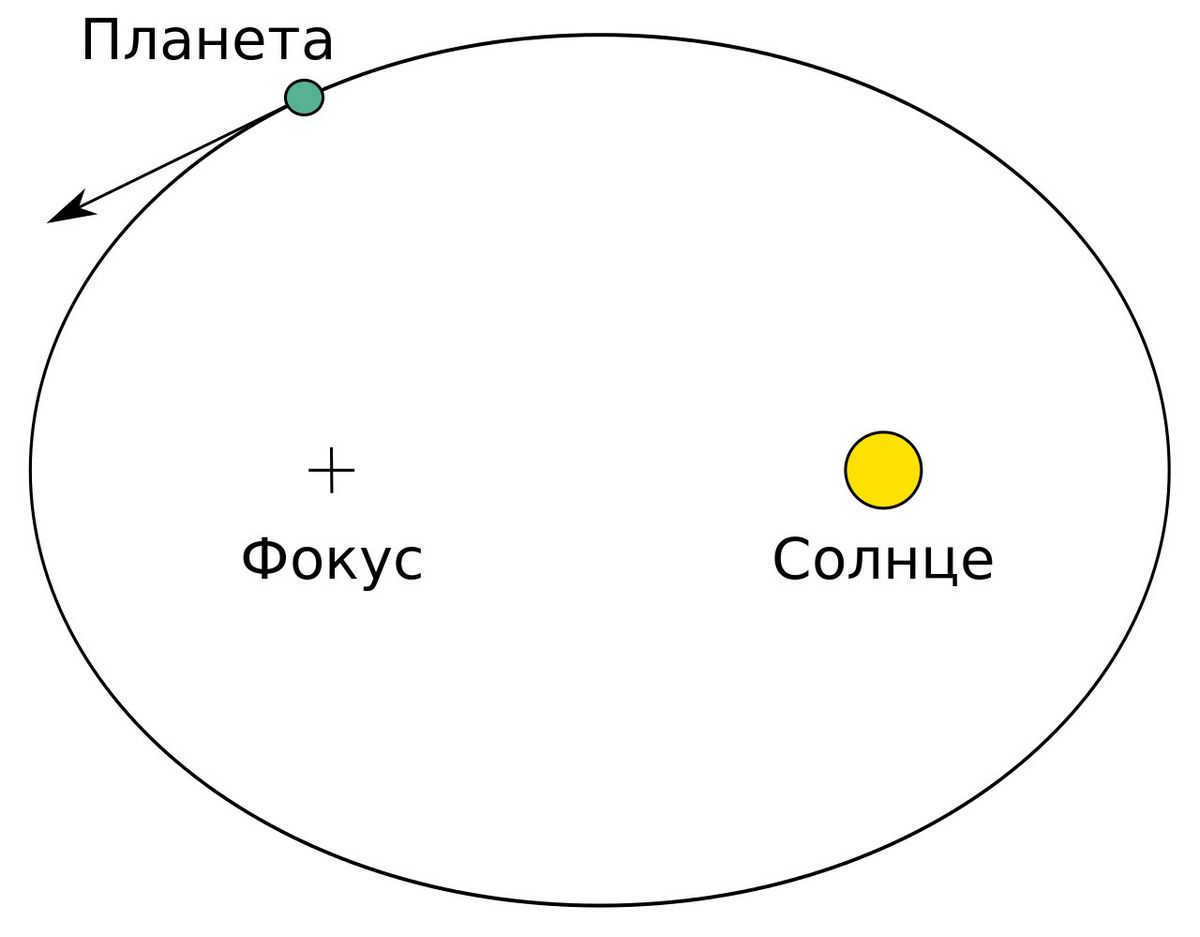
Kepler’s initial law, known as the law of ellipses, declares that the path of every planet encircling the Sun is an ellipse with the Sun situated at one of the two foci. An ellipse is a geometric shape that resembles a stretched-out circle and possesses two focal points. The Sun occupies one of these focal points, while the planet follows an elliptical trajectory with the Sun at its center of mass. This principle negated the previous notion that planets move in flawless circles around the Earth.
The shape of an ellipse is determined by its eccentricity, ranging from a perfectly circular orbit (eccentricity of 0) to a highly elongated orbit (eccentricity close to 1). According to Kepler’s first law, the eccentricity of a planet’s orbit is connected to its distance from the Sun. Planets like Earth, with low eccentricity, have orbits that are almost circular, whereas planets like comets, with higher eccentricity, have more elongated orbits.
Kepler’s Second Law: The Law of Areas
Kepler’s Second Law is also known as the Law of Areas. This law states that a line drawn from a planet to the sun sweeps out equal areas in equal time intervals. In other words, as a planet moves in its elliptical orbit around the sun, it moves faster when it is nearer to the sun and slower when it is farther away. This law helps explain why planets do not move at a constant speed in their orbits. Instead, they speed up and slow down as they move closer to and farther away from the sun. This law is one of the three laws of planetary motion formulated by the German astronomer Johannes Kepler in the early 17th century. It was a significant breakthrough in understanding the motion of celestial bodies and played a crucial role in the development of modern astronomy.
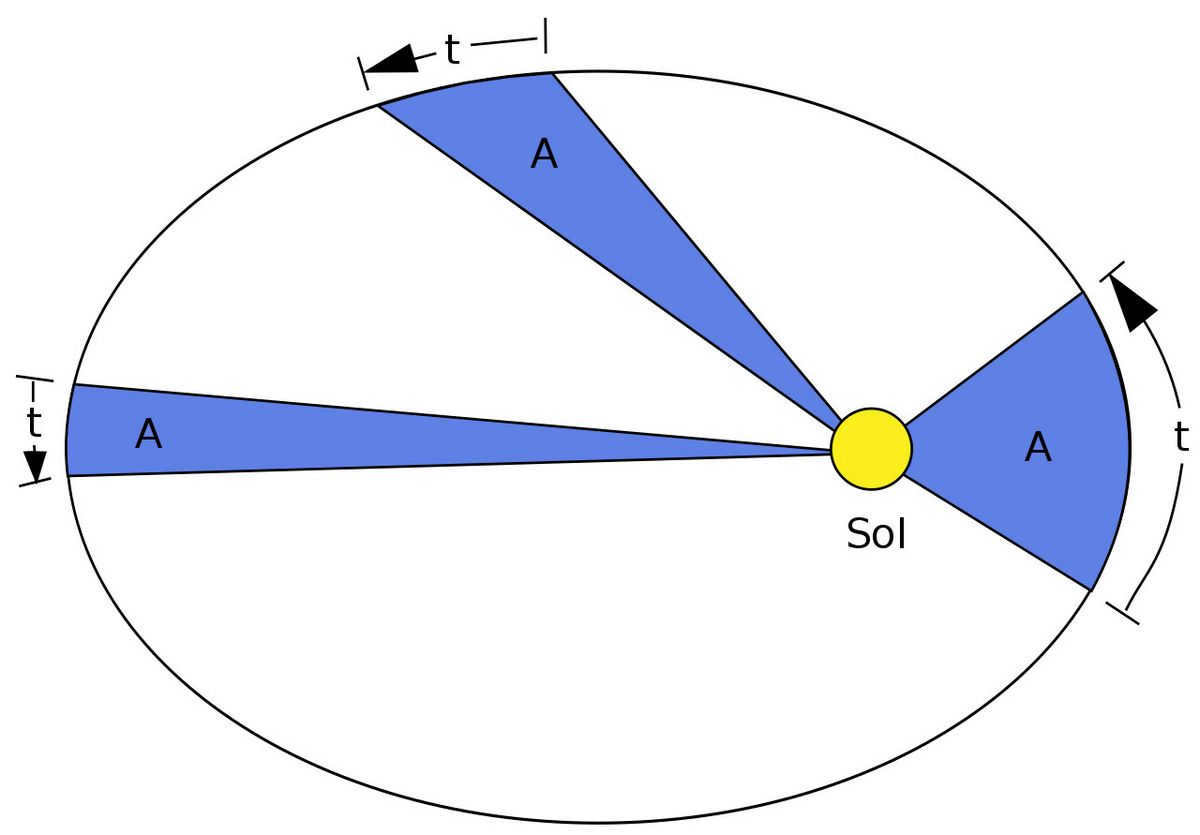
Kepler’s second law, also known as the law of areas, explains the velocity of a planet as it orbits. It states that the line connecting the planet to the Sun will cover equal areas in equal amounts of time. In simpler terms, when a planet is closer to the Sun (at perihelion), it moves faster, and when it is farther away (at aphelion), it moves slower.
This law has significant implications for our understanding of angular momentum conservation. As a planet moves closer to the Sun, its velocity increases in order to maintain angular momentum, and as it moves away, its velocity decreases. As a result, the planet spends more time in the outer regions of its orbit, leading to equal areas being covered in equal time intervals.
Kepler’s Third Law: The Law of Harmonic Motion
The first law of Kepler states that there is a mathematical correlation between the time it takes for a planet to orbit around the Sun and its average distance from the Sun. This law, also known as the harmonic law, states that the square of the planet’s orbital period is directly proportional to the cube of its average distance from the Sun. To express this mathematically:
- T represents the orbital period of the planet in years,
- R represents the average distance from the planet to the Sun in astronomical units, and
- k is a constant of proportionality that depends on the masses of the objects involved.
This legislation enables astronomers to determine the orbital period of a planet by utilizing its mean distance from the Sun, as well as the inverse calculation. Furthermore, it served as a significant milestone in Newton’s subsequent investigations into universal gravitation and the recognition that the force governing planetary motion is dependent on their masses and their distance from the Sun.
Heritage and Impact
Kepler’s discoveries on the planetary movement have left a lasting impact on scientific discourse, paving the way for future breakthroughs in astronomy and physics. By demonstrating that the motion of planets can be described mathematically, Kepler’s laws revolutionized our understanding of celestial bodies and revealed new insights into the underlying principles governing their movement.
Building upon Kepler’s laws, Isaac Newton incorporated them into his own laws of motion and universal gravitation. Newton’s groundbreaking work, published in his monumental Philosophiæ Naturalis Principia Mathematica in 1687, provided a comprehensive explanation of celestial bodies’ motion and established a unified framework for comprehending the physical laws that govern the universe.
Today, Kepler’s laws continue to be fundamental principles in the fields of astronomy and celestial mechanics. They are taught in educational institutions worldwide and serve as the foundation for accurately predicting planetary positions, investigating exoplanets, and exploring our solar system.
Kepler’s laws of planetary motion mark a pivotal moment in the history of science, shedding light on the nature of our solar system and enhancing humanity’s comprehension of the universe. They exemplify the significance of observation, mathematical deduction, and the unwavering quest for knowledge that propels scientific advancement.
“I am seated, maintaining a distance from others, tackling tasks from the USE exam, and in the process, encountering the astronomical 24th law of Kepler. While not entirely comprehensible, it is undeniably fascinating,” – such is the sentiment shared by numerous eleventh-grade physics students. We shall now elucidate how to comprehend these laws and effectively apply them when tackling problem-solving exercises.

The Earth’s Shape
It is difficult for us to imagine now, but there was a time when people believed that the Earth was flat. The ancient Greeks, for example, thought that the Earth was a plane floating in the air and surrounded by glaciers. Similarly, in India, it was believed that the Earth rested on the backs of three elephants standing on a tortoise. Surprisingly, there are still some people who hold these beliefs. However, there is plenty of evidence to prove that our planet is not actually flat. Here are a few pieces of evidence to spark some interesting conversations.
The alteration of day and night
According to adherents of the flat Earth theory, the transition between day and night occurs because the Moon and Sun revolve above the Earth – thus, that is their explanation:
However, this particular model poses a number of inquiries:
- Why do the duration of daytime and nighttime fluctuate throughout the year?
- What accounts for the varying hues observed during sunrise and sunset?
- How is it possible to occasionally witness the Moon and the Sun simultaneously?
- Why do the Moon and Sun not emerge from the same location every time?
- If there is no gravitational force, what causes them to rotate at all?
Lunar eclipses
In the event that the Earth is in fact a flat surface, the occurrence of lunar eclipses poses a perplexing question. In order for an eclipse to transpire, the Sun must be positioned on one side of the Earth’s disk, while the Moon rests on the opposite side. Consequently, the traditional notion of day and night, as previously elucidated, becomes obsolete, as day and night would simultaneously envelop the entire Earth.
Assuming the Earth is a flat surface, the sunlight would behave similarly to the light emitted from a flashlight. In other words, when the Sun sets, tall objects located in the opposite direction of the Sun would continue to cast shadows.
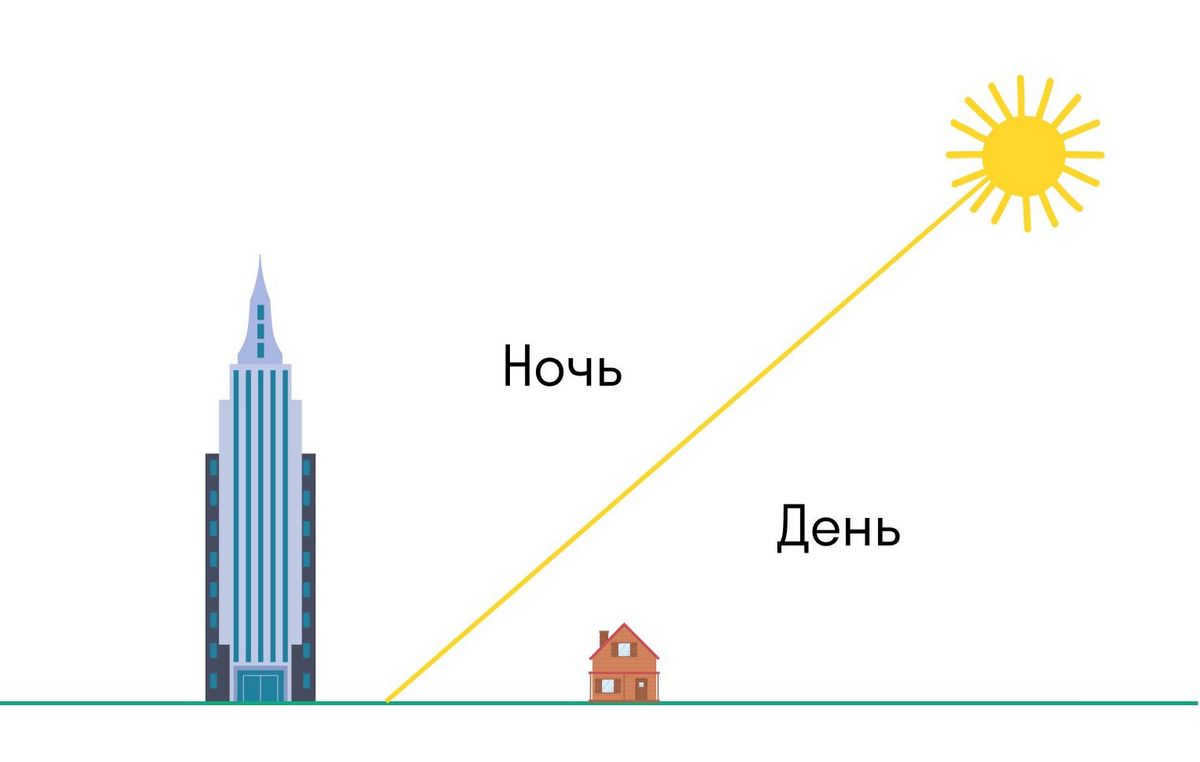
Furthermore, in the case of a spherical Earth, buildings or mountains would still receive sunlight even after the Sun has set or before it has risen.
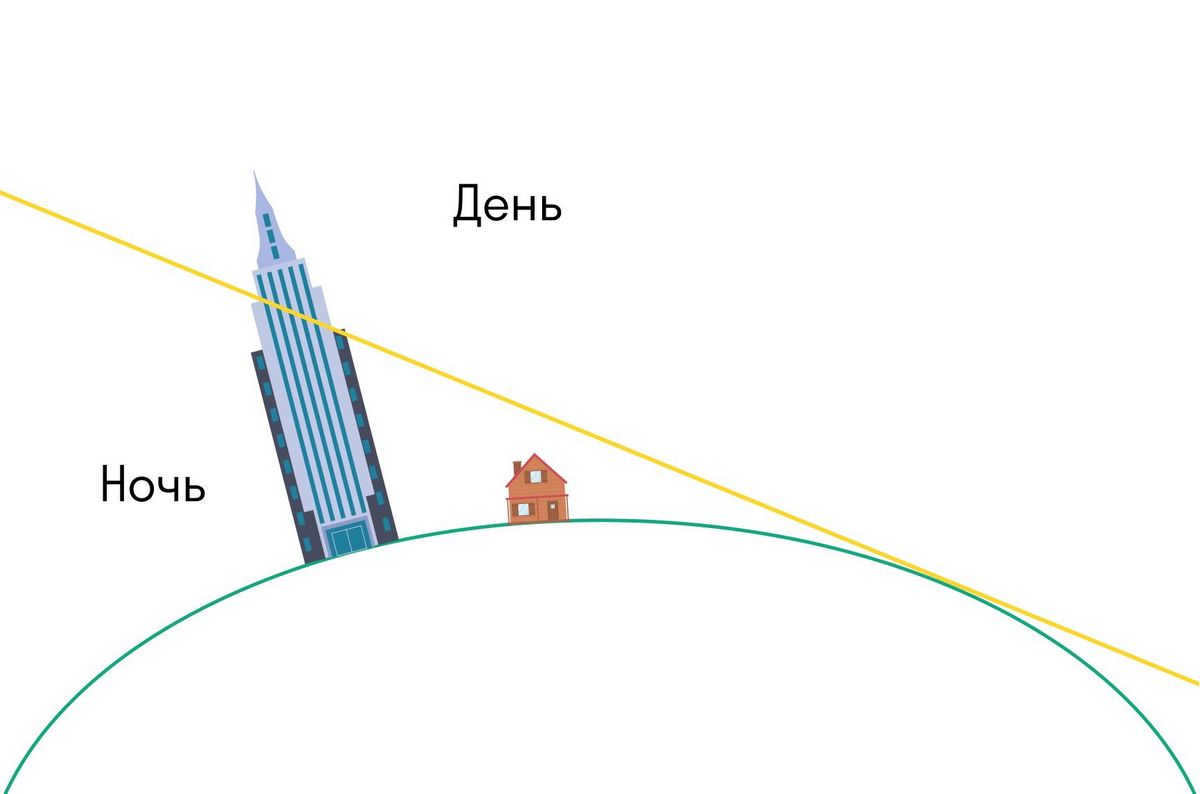
If you observe the sunrise or sunset in the mountains – or view images – you will witness this phenomenon.
Indeed, the Earth is not flat – that fact has been established. However, it cannot be described as a perfect sphere either; the Earth is actually in the shape of an ellipsoid.
An ellipsoid is a flattened sphere with an elliptical cross-section. It is along the path of this ellipse that all satellites orbit.
Flexible schedules, a variety of classes to choose from, no stress about homework, and no tedious parent-teacher conferences.

Ellipse.
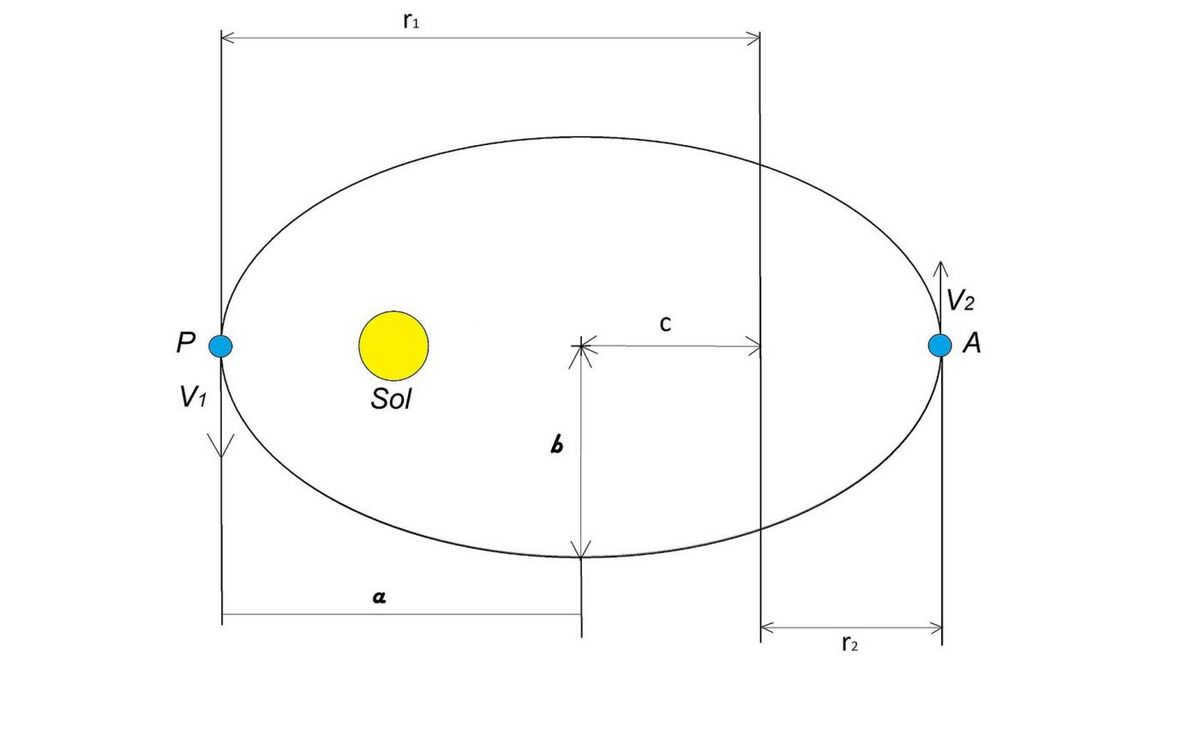
An ellipse is a closed curve in the plane, a particular instance of an oval. It possesses two axes of symmetry, both horizontal and vertical, which are formed by two semi-axes.
Additionally, an ellipse possesses two focal points, which are points where the sum of distances from any point P(x,y) remains constant.
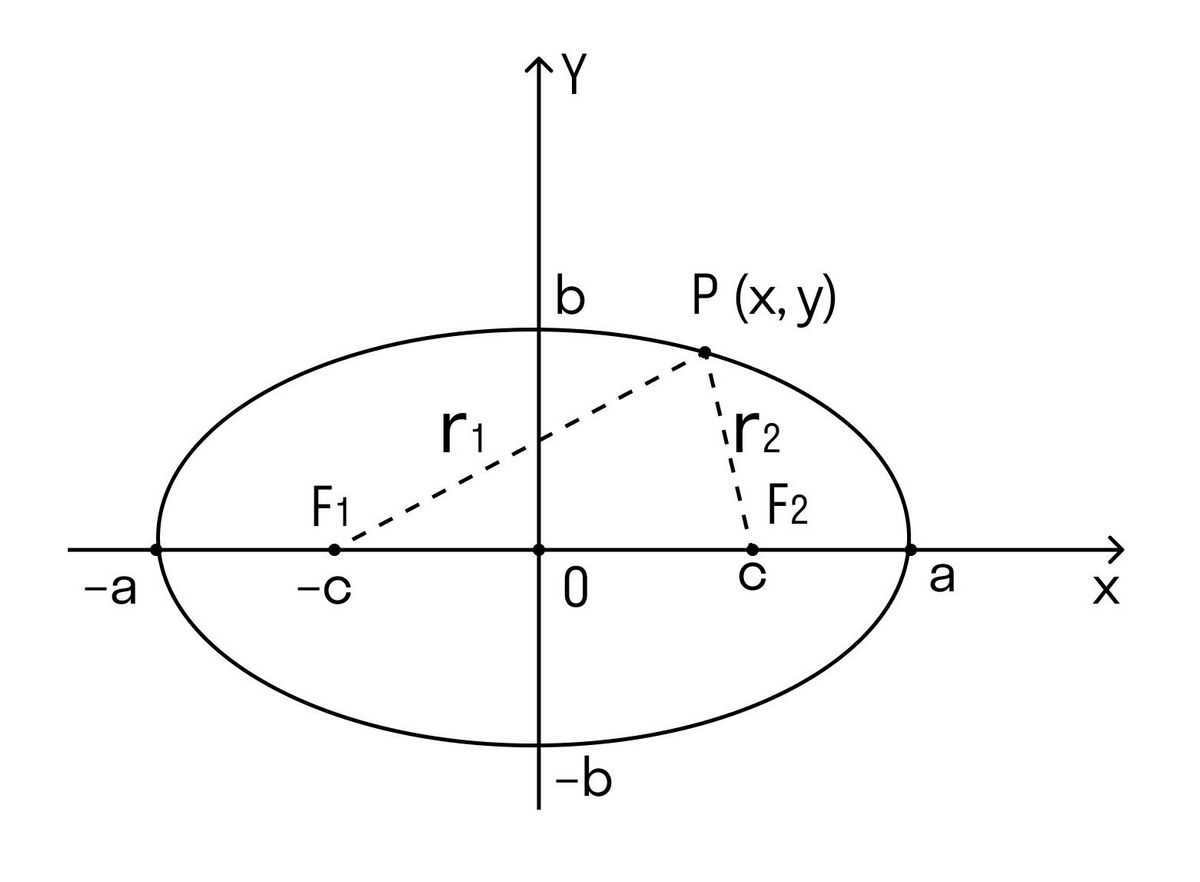
F1 and F2 are the focal points
c is equal to half the distance between F1 and F2
a is the major semi-axis
b is the minor semi-major axis
r1 and r2 are the focal radii
Now we have all the necessary concepts to understand Kepler’s laws.
Experience the USE physics preparation courses with a skilled teacher at Skysmart online school!

Kepler’s First Law
Every planet in the solar system orbits the Sun in an elliptical path, with the Sun located at one of the foci.
The Sun is positioned at one of the foci of the ellipse. The point on the trajectory that is closest to the Sun is referred to as the perihelion, while the point A, which is farthest from the Sun, is known as the aphelion.
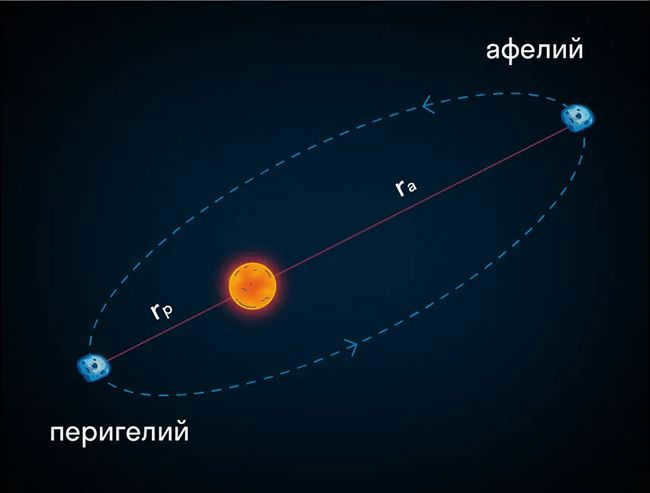

The first law of Kepler is quite straightforward, yet significant as it significantly advanced the field of astronomy during its time. Prior to this discovery, astronomers held the belief that planets moved exclusively in circular orbits. If observations contradicted this belief, scientists would supplement the primary circular motion with small circles that the planets described around the points of the main circular orbit. Kepler had the advantage of accessing Tycho Brahe’s extensive database of observations and, through studying them, he transcended the old concepts.
Kepler’s second principle (the law of equal areas)
The orbit of a planet around the Sun can be divided into equal segments, and the radius vector connecting the planet to the Sun will sweep out equal areas in equal amounts of time.
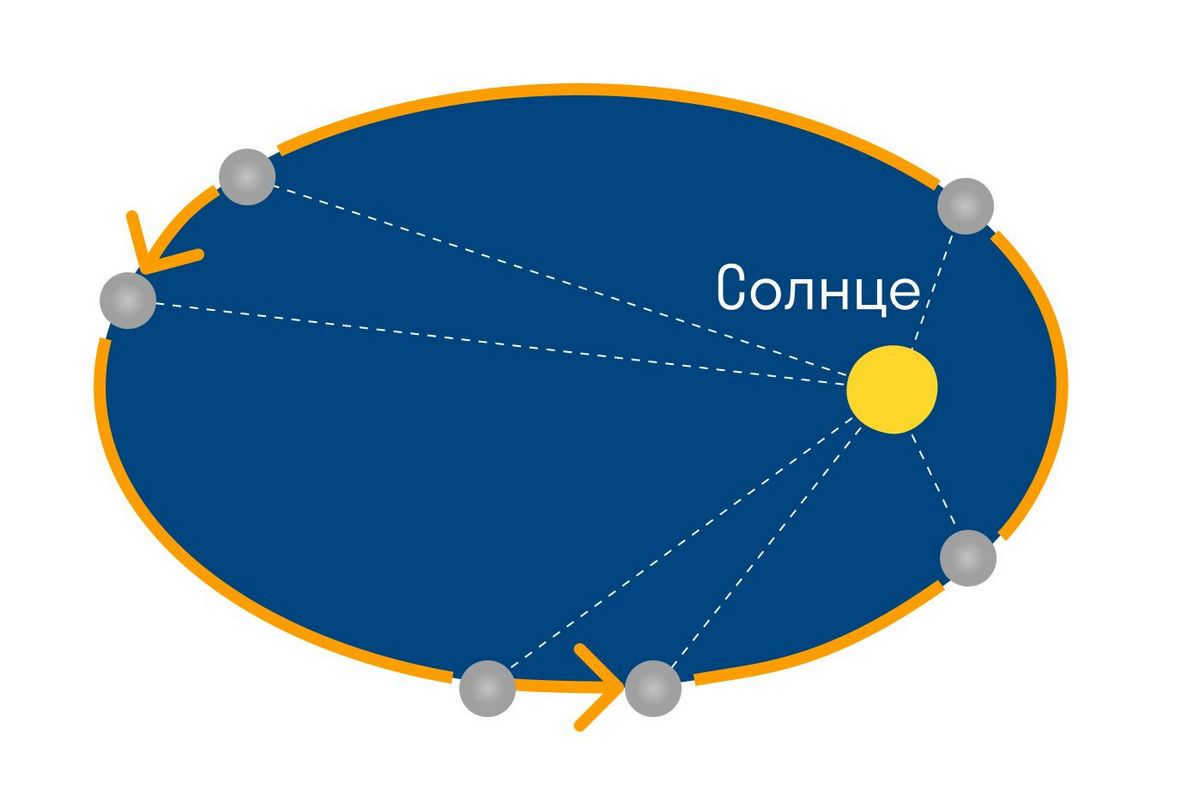
According to Kepler’s Second Law, each planet orbits the Sun in a plane that passes through the Sun’s center. Furthermore, the radius-vector connecting the Sun and the planet sweeps out equal areas in equal intervals of time. As a result, the planets move at varying speeds around the Sun. They reach their maximum speed at perihelion and their minimum speed at aphelion.
Kepler’s Third Law
The periods of the planets’ orbits are related to the major semi-axes of their orbits by the equation: the square of the orbital period is proportional to the cube of the major semi-axis.
Kepler’s third law establishes a connection between the revolution period of planets around the Sun and the major semi-axes of their orbits. This law holds true for both planets and satellites, with an error margin of less than 1%.
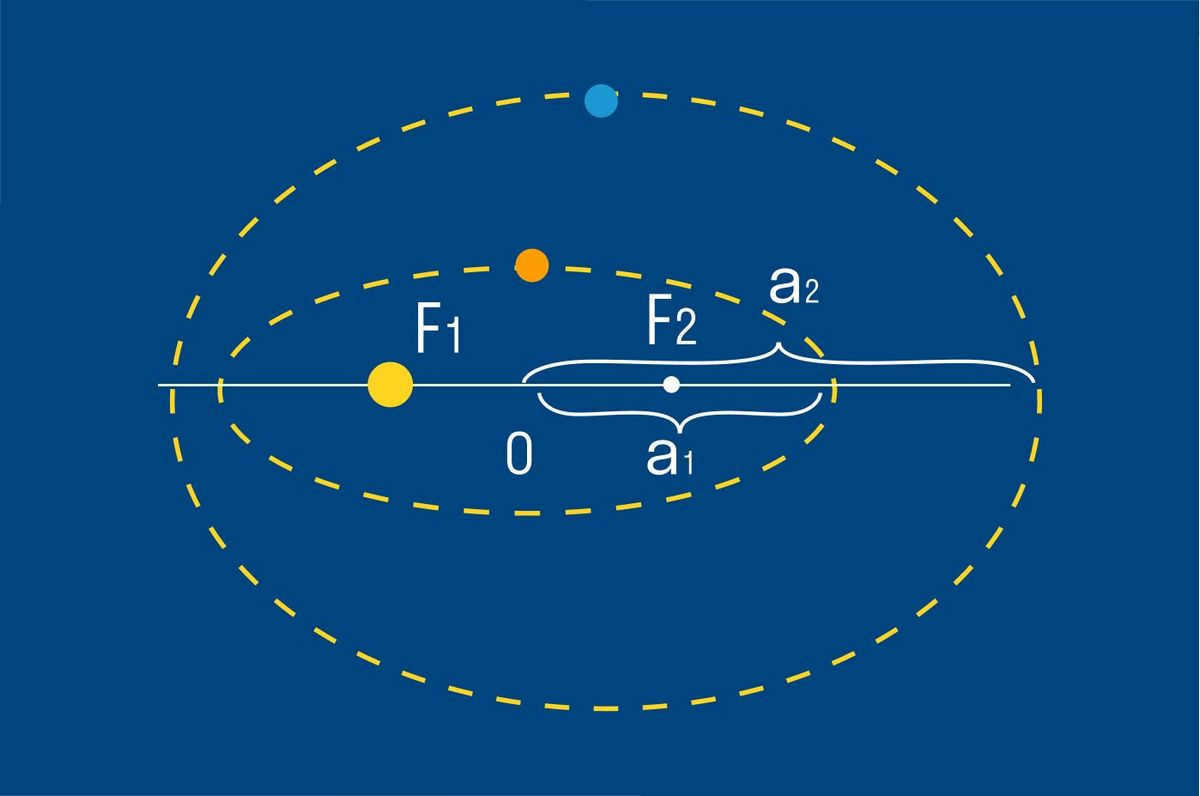

Kepler’s third law
T1 and T2 represent the orbital periods of two planets [c]
a1 and a2 represent the major semi-axes of planetary orbits [m]
By utilizing this principle, it is possible to calculate the length of a year (the time for a complete revolution around the Sun) for any given planet, provided its distance from the Sun at aphelion is known.
Conversely, it is also possible to calculate the orbit by knowing the orbital period.
Law of Universal Gravitation
The laws formulated by Kepler were based on observations and generalizations. These laws served as the foundation for the law of universal gravitation, which states that all objects are attracted to each other. The force of universal gravitation is directly proportional to the product of the masses of the objects and inversely proportional to the square of the distance between them.
The equation for the force of gravitation, according to this law, is as follows:
Law of Universal Gravitation
F – gravitational force [N]
M – mass of the first object (often a planet) [kg]
m – mass of the second object [kg]
R – distance between the objects [m]
G – gravitational constant
G = 6.67 x 10-11 m3 kg-1 s-2
Newton was the first scientist to propose that gravitational forces exist between all objects in space and that these forces dictate the motion of these objects.
The initial and secondary cosmic speeds
Kepler’s laws apply not only to the movement of planets and other celestial bodies within the solar system, but also to the motion of man-made satellites and spacecraft. In this case, the Earth serves as the center of gravity.
In Douglas Adams’ series of books, The Hitchhiker’s Guide to the Galaxy, it is stated that flying is simply a matter of missing the Earth. To orbit the Earth as an artificial satellite, one must attain the first cosmic velocity of 7.9 km/s. Here’s how it works:
An artificial satellite is a spacecraft that revolves around the Earth in a geocentric orbit. To achieve this, the vehicle must possess an initial velocity that is equal to or greater than the first space velocity.
First space velocity
v1 – first space velocity [m/s]
g – acceleration due to gravity on a given planet [m/s2]
R – radius of the planet [m]
On planet Earth, g ≈ 10 m/s2.
There are also second and third space velocities. The second space velocity is the speed required for a spacecraft to become an artificial satellite of the sun, and the third space velocity is the speed needed to travel outside the solar system.
Second space velocity
v2 – second space velocity [m/s]
g – represents the gravitational acceleration on a specific celestial body [m/s2]
R – denotes the radius of the celestial body [m]
On Earth, the acceleration due to gravity is approximately 10 m/s2.
Enroll in the complimentary course offered by child psychologist Ekaterina Murashova for contemporary parents and be automatically eligible for a chance to win 8 lessons.

During his era, Kepler extracted three principles by analyzing the observations made by other scientists, namely Tycho Brahe and Copernicus. These principles offer an explanation of the planetary orbit around the sun. The foundation for his connections stemmed from practical knowledge and scientific trials. Kepler’s principles serve as a valuable resource in the advancement of the field of astronomy.

Some believe that Kepler’s laws have an error margin of no more than 1%. However, it is worth noting that Kepler himself did not have scientific evidence to support his conclusions, rather he proposed them intuitively.
Later on, these assumptions were theoretically proven by Isaac Newton and were further justified by classical mechanics.
Undoubtedly, the works of Kepler greatly contributed to our understanding of the internal system of motion of celestial bodies.
To understand means to compare external perceptions with internal ideas and assess the degree of their correspondence.
Johannes Kepler
Kepler’s first law
This law describes the shape of planetary orbits in our solar system. According to Kepler’s first law, the planets follow elliptical paths around the Sun. The Sun is located at one of the two points within the ellipse called the foci. The shape of the ellipse is determined by its eccentricity, which measures the degree of deviation from a perfect circle. The eccentricity is calculated by dividing the distance from the center of the ellipse to the focus by the length of the major semi-axis. If this distance is zero, the ellipse becomes a circle.


The confirmation of Kepler’s first law lies in the discovery and utilization of the law of universal gravitation in the field of astronomy.
The law of universal gravitation was formulated by Isaac Newton, who demonstrated that every celestial object exerts an attractive force on another object along an imaginary line connecting their centers of mass. This force is directly proportional to the mass of each object and inversely proportional to the square of the distance between them.
Kepler’s first law is connected to Newton’s laws.
Newton’s second law states that the acceleration of an object is directly proportional to the inverse of the total forces acting on it. Furthermore, the acceleration is inversely proportional to the mass of the object.
The Law of Areas: Kepler’s Second Law
Also known as the second Keplerian law, the law of areas states that every planet follows a specific orbital plane that passes through the center of the Sun. Furthermore, the line connecting the planet to the Sun sweeps equal areas in equal amounts of time.

In our solar system, the planets exhibit a rather erratic pattern of movement as they revolve around the Sun. An interesting observation is that the speed of a planet is greater when it is closest to the Sun compared to when it is farthest away.
This phenomenon is particularly noticeable at the beginning of the year, where we can observe the Sun’s visible motion being faster than at other times. This is because at this time, our planet Earth is situated at its closest point to the Sun in its orbit, which is known as perihelion. On the opposite end of the spectrum, we have aphelion, which refers to the Earth being at its farthest point from the Sun.
Kepler’s Third Law
Often referred to as the harmonic law, Kepler’s Third Law states that the square of a planet’s rotation period around the Sun is proportional to the cube of the major semi-axis of the planet’s orbit.
However, Kepler’s law is not entirely accurate according to the rules of gravitational force, as it does not account for factors such as the mass of the planet.
The harmonic law, when combined with the law of gravitation, is applicable for measuring the mass of a celestial object, but only if their orbits have been established.


Kepler’s third law states that there is a direct correlation between the distance of a planet from its star and the time it takes for the planet to complete one orbit. In other words, the closer a planet is to its star, the shorter its orbital period.
Application of Kepler’s Laws
Kepler’s laws play a crucial role in understanding the motion of planets in astronomy. These laws provide explanations and definitions for the non-uniform movement of celestial bodies. Additionally, they enable the determination of object positions and facilitate calculations of body mass.
An interesting fact is that the majority of planets in the solar system have orbits that closely resemble circles. However, Mars and Pluto exhibit a unique convexity in their orbits.
Clearly, the planetary laws of motion are equivalent to the laws of motion that govern satellites, including artificial ones. In other words, anything we launch into space moves according to these very principles.
From this, we can deduce that our knowledge of these laws allowed us to successfully launch space rockets, which in turn propelled us forward in our exploration of the universe.
There is no doubt that Kepler made an immense contribution to the field of astronomy. He can be considered an extraordinary individual in every sense of the word. During his time, nobody had the same vision of the universe as he did. In fact, he himself wrote: “This man has been appointed to spend his time solving difficult problems that discourage others.”
And indeed, it was through his work that the field of planetary astronomy was established. It opened a window to the Universe, allowing us to observe and measure what we see.
However, at first, only a pair of regulations were released. Subsequently, a decade later, Kepler’s third law became accessible to the general populace.

Naturally, not all the hypotheses put forward by scientific intellectuals prove to be accurate. However, their input is undoubtedly invaluable. Previously, we have discussed numerous significant findings that have emerged from the field of astronomy. Today, I believe we have revisited this topic and reaffirmed its importance.
Throughout his lifetime, I. Kepler dedicated his efforts to substantiating the notion that our solar system possessed a mystical essence. In the beginning, his pursuits revolved around establishing parallels between the system’s configuration and the regular polyhedra found in ancient Greek geometry. During Kepler’s era, the presence of six planets was acknowledged, with the prevailing belief that they resided within crystal spheres. The renowned scientist hypothesized that these spheres were arranged in a manner that allowed for the precise fitting of polyhedrons of the correct shape between neighboring spheres. For instance, a cube inscribed within an external environment, which in turn housed a sphere, fit perfectly between Jupiter and Saturn. Similarly, a tetrahedron occupied the space between Mars and Jupiter. However, after numerous years of observing celestial bodies, Kepler formulated his laws, which ultimately discredited his polyhedra theory.

Laws
The heliocentric system, developed by Copernicus, replaced the geocentric Ptolemaic system of the world. Subsequently, Kepler discovered the laws governing the motion of planets around the sun.
After extensive observation of the planets, Kepler formulated three fundamental laws. In this article, we will examine these laws in detail.
The initial statement
As per Kepler’s initial principle, every planet within our system follows a closed curve known as an ellipse. Our star is situated at one of the foci of the ellipse. There are only two foci: these represent two points positioned inside the curve, with the sum of the distances from either focus to any point on the ellipse remaining constant. Following extensive observations, the scientist was able to determine that the orbits of all the planets within our system are nearly situated within the same plane. Some celestial entities follow elliptical orbits that closely resemble a circle. Only Pluto and Mars follow more elongated orbits. Based on these findings, Kepler’s initial principle is referred to as the elliptical law.


The Law of Orbits
By studying the movement of celestial bodies, scientists have discovered that a planet’s speed varies depending on its distance from the Sun. When a planet is closer to the Sun, it moves faster, and when it is farther away, it moves slower. These points of closest approach and greatest distance are known as perihelion and aphelion, respectively.
Kepler’s second law, also known as the Law of Areas, states that each planet moves in a plane that passes through the center of our Sun. Additionally, the line connecting the Sun and the planet sweeps out equal areas in equal times, meaning that the planet covers more area in a shorter amount of time when it is closer to the Sun.
Therefore, it is evident that celestial bodies orbit the yellow dwarf in an irregular manner, with the highest velocity occurring at perihelion and the lowest velocity at aphelion. This phenomenon can be observed through the movement of our own planet, Earth. Each year, in the beginning of January, Earth accelerates as it reaches perihelion, resulting in the Sun moving at a faster pace along the ecliptic compared to other times of the year. Conversely, in early July, Earth reaches aphelion, causing the Sun to slow down its movement along the ecliptic.
The Law of Planetary Rotation
Kepler’s third law establishes a correlation between the orbital period of planets around a star and their average distance from it. This fundamental principle was applied by the scientist to all the celestial bodies in our solar system.
Understanding the principles
Kepler’s laws became comprehensible only after Newton’s breakthrough in discovering the law of gravitation. Newton proposed that physical entities engage in gravitational attraction, which applies universally to all material objects and physical fields. Newton’s assertion states that two stationary bodies mutually exert a force on each other that is directly proportional to the multiplication of their masses and inversely proportional to the square of the distance between them.
Perturbed Motion
The movement of celestial bodies within our solar system is dictated by the gravitational force exerted by the yellow dwarf star. If these bodies were solely influenced by the Sun’s gravitational force, their movements would adhere strictly to Kepler’s laws of motion. This type of movement is known as unperturbed or Keplerian motion.
In reality, however, all objects within our system are influenced not only by our star, but also by each other. As a result, no body can move along a perfect ellipse, hyperbola, or circle. When a celestial body deviates from Kepler’s laws during its movement, it is referred to as a perturbation, and the overall motion is known as perturbed motion. This is the motion that is considered to be real.
The orbits of celestial bodies are not fixed ellipses. Instead, they undergo changes in their elliptical paths due to the gravitational attraction exerted by other bodies within the system.

The Impact of I. Newton
Isaac Newton derived the law of universal gravitation from Kepler’s laws of planetary motion. It was the concept of universal gravitation that Newton utilized to address problems in celestial mechanics.
Following Isaac, advancements in celestial mechanics involved the development of mathematical science to solve equations that expressed Newton’s laws. Newton established that a planet’s gravitational force is determined by its distance and mass, with factors like temperature and composition having no effect.
Newton’s scientific research demonstrated that the third Keplerian law was not entirely precise. He revealed the significance of taking into account the planet’s mass in calculations, as the motion and weight of the planets are interconnected. This harmonious fusion unveils the correlation between the Keplerian laws and Newton’s law of gravitation.
The application of Newton’s and Kepler’s laws has formed the foundation for the development of astrodynamics. This field of study falls within the realm of celestial mechanics and focuses on analyzing the movement of artificially created celestial bodies, such as satellites, interplanetary stations, and various spacecraft.
Astrodynamics is responsible for calculating the spacecraft’s orbits, determining the necessary launch parameters, selecting the appropriate orbit, planning necessary maneuvers, and considering the gravitational impact on the spacecraft. These practical tasks are just a few examples of the challenges astrodynamics tackles. The knowledge and results obtained from astrodynamics are essential for a wide range of space missions.
Celestial mechanics, closely linked to astrodynamics, explores the motion of natural celestial bodies under the influence of gravitational forces.

Pathways
A pathway is defined as the path taken by a point within a designated area. Within the realm of celestial mechanics, it is postulated that the path of a celestial body within the gravitational field of another body with significantly greater mass can be represented by a conic section in a rectangular coordinate system. This conic section may take the form of a parabola, ellipse, circle, or hyperbola. In all cases, the focal point of the conic section will align with the center of the system.
For a significant period of time, there was a prevailing belief that orbits should be perfectly circular. Scientists dedicated considerable efforts towards identifying the exact circular trajectory of celestial bodies, but their endeavors proved unsuccessful. It was only Kepler who managed to elucidate that planets do not follow circular orbits, but rather elongated ones. This groundbreaking realization enabled him to formulate three laws that could accurately describe the motion of celestial bodies in orbit. Kepler’s discoveries encompassed the following elements of an orbit: its shape, inclination, position within the spatial plane, size, and temporal reference. Irrespective of its shape, all of these elements collectively determine the nature of an orbit. In calculations, the primary coordinate plane can be defined as the plane of the ecliptic, galaxy, planetary equator, and so on.
There have been many studies indicating that orbits can vary in their geometric shape, ranging from elliptical to rounded. These shapes can be further classified into closed and unclosed orbits. Additionally, orbits can also be categorized based on their angle of inclination to the Earth’s equator, with options including polar, inclined, and equatorial orbits.