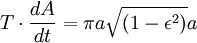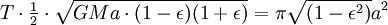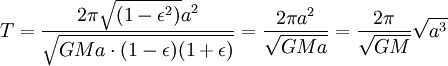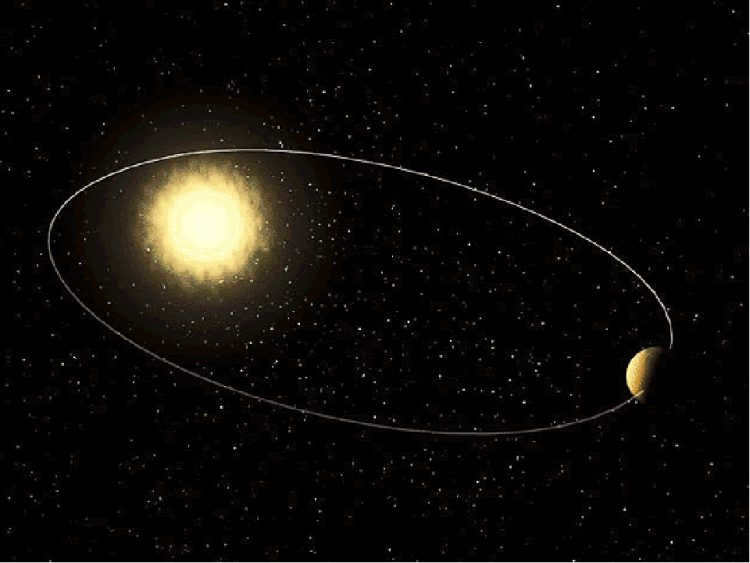
- History of Astronomy
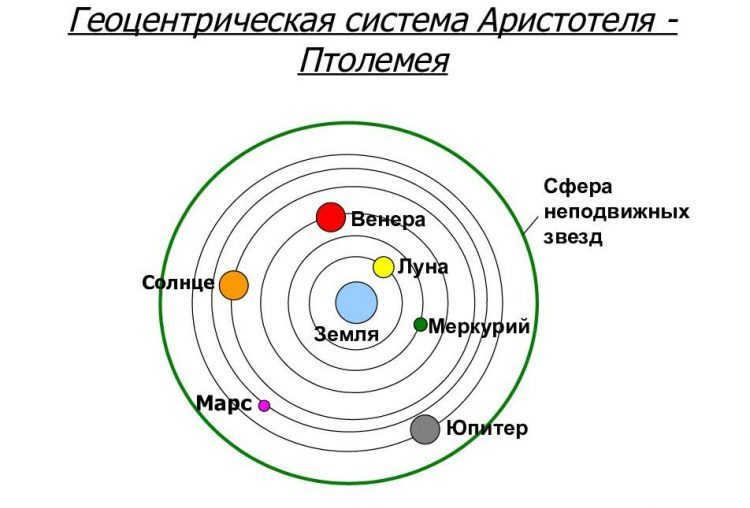
In the late 16th century, there was a significant development in the field of astronomy. It involved a clash between two different models of our solar system: the geocentric system proposed by Ptolemy, where the Earth is considered the center of rotation for all celestial bodies, and the heliocentric system introduced by Copernicus, which suggests that the Sun is the central body.
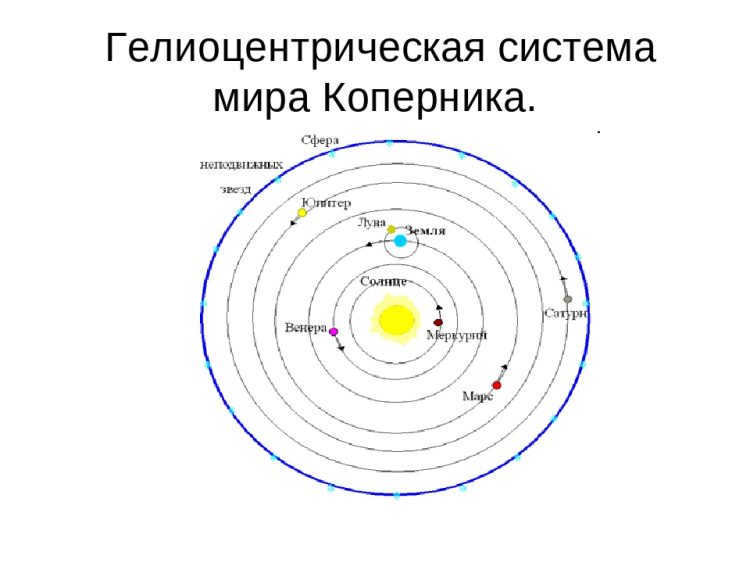
While Copernicus was closer to understanding the true nature of the solar system, his work was not without its flaws. One of the main flaws was his assertion that the planets orbit the Sun in circular paths. This meant that Copernicus’ model was still inconsistent with the observations, much like Ptolemy’s system. To address this discrepancy, the Polish astronomer introduced an additional motion called the epicycle, where the planet moved in a circular path while its center also moved around the Sun. However, this adjustment did not completely resolve the divergence in most parts of the model.
In the early 17th century, the German astronomer Johannes Kepler analyzed the results of astronomical observations by the Dane Tycho Brahe and studied the system of Nicolaus Copernicus. As a result, he derived the fundamental principles governing the motion of planets, known as Kepler’s Three Laws.
Tycho Brahe, known for his exceptional observational skills, dedicated many years to compiling a comprehensive work on planetary observations and hundreds of stars. The accuracy of his measurements surpassed that of all his predecessors.
Kepler’s primary principle about ellipses.
The planets in the solar system travel along paths that are shaped like elongated circles, with the Sun positioned at one of the focal points.
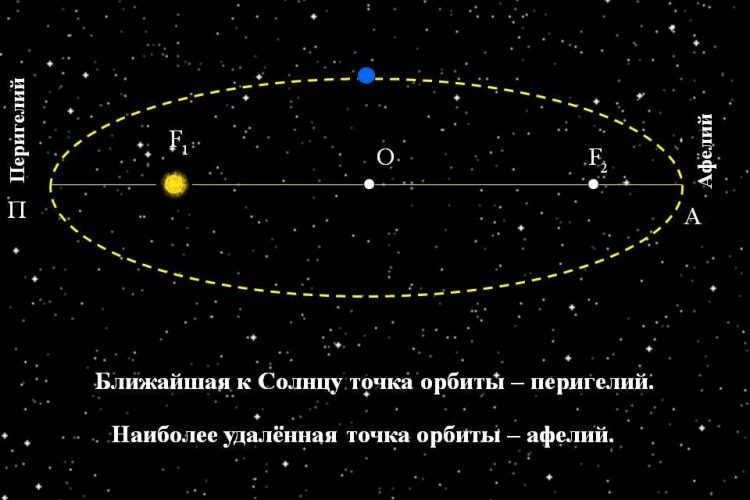
As per Kepler’s first law, all the planets in our system traverse a closed curve known as an ellipse. Our star is situated at one of the foci of the ellipse. There are two foci: these represent two points within the curve where the sum of the distances to any point on the ellipse remains constant.
After extensive observations, scientists have discovered that the orbits of all the planets in our system lie nearly in the same plane. Some celestial bodies follow elliptical orbits that are close to being circular. Only Pluto and Mars have more elongated orbits. Hence, Kepler’s first law has been referred to as the law of ellipses.
Kepler’s second law (also known as the law of areas).
The planet’s radius-vector traces out equal areas in equal time intervals.
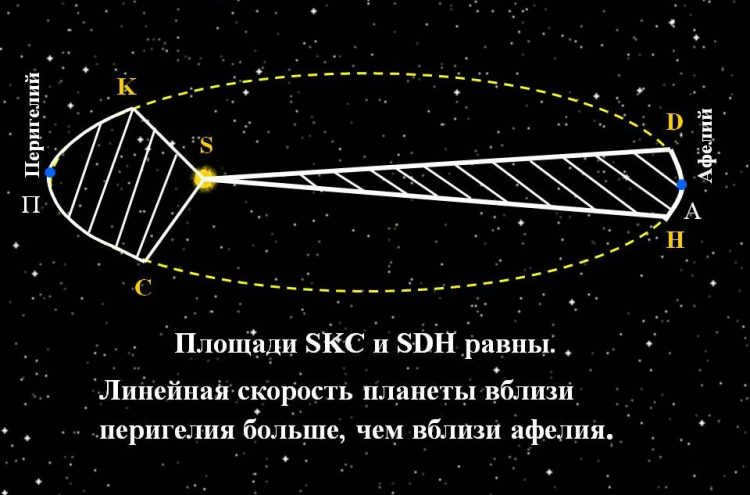
According to Kepler’s second law, each planet orbits in a plane that goes through the center of the Sun. Additionally, the radius-vector connecting the Sun and the planet traces out equal areas as the planet moves. This means that the celestial bodies do not move in a uniform manner around the Sun. They reach their highest velocity when they are closest to the Sun (perihelion) and their lowest velocity when they are farthest from the Sun (aphelion).
This phenomenon can be observed in the movement of the Earth. Every year in early January, the Earth moves faster as it passes through perihelion. As a result, the Sun moves more quickly along the path of the ecliptic compared to other times of the year. In early July, the Earth reaches aphelion, causing the Sun to move at a slower pace along the ecliptic.
The relationship between the squares of the orbital periods of the planets and the cubes of the major semi-axes of their orbits is a fundamental astronomical principle.
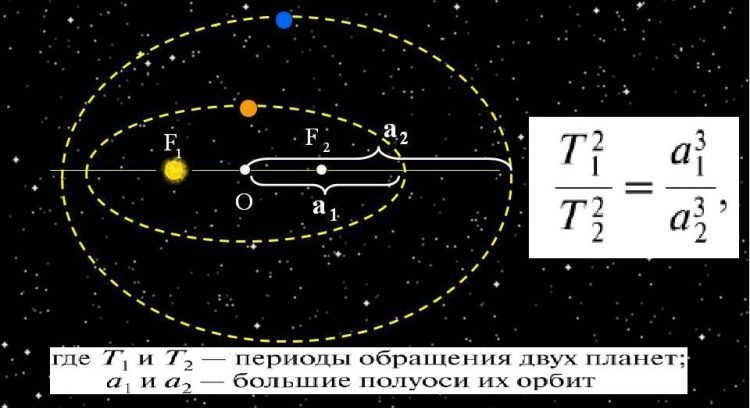
According to Kepler’s third law, there is a correlation between the orbital period of celestial bodies around a central object and their average distance from it. This law is applicable to both planets and satellites, with an accuracy of up to 1%.
Based on this law, it is possible to calculate the length of a year (the time it takes for a complete revolution around the Sun) for any planet, given its distance from the Sun. Conversely, the same law can be used to determine the orbit by knowing the period of revolution.
Continued Progress
While Kepler’s laws had a relatively small margin of error, they were derived through observation rather than theoretical reasoning. However, this issue was eventually resolved by Isaac Newton, who in 1682 established the principle of universal gravitation..
Kepler’s laws represented a significant breakthrough in comprehending and elucidating the movements of celestial bodies.
Video
can be rephrased as
Visual Content
.
The fundamental principles utilized in the field of astronomy include the subsequent laws:
- The laws established by Kepler;
- Newton’s law or the principle of universal gravitation;
- Hubble’s Law (pertaining to the dispersion of galaxies).
Kepler’s Laws
In 1619, Johannes Kepler, a German astronomer, mechanic, and mathematician (1571-1630), published his work entitled The Harmony of the World, wherein he derived a series of astronomical principles concerning the movement of planets.
Kepler postulated that planetary orbits possess an elliptical shape, with the Sun positioned as one of the focal points. The area vectors connecting the Sun to the planet remain constant over equal time intervals. The squares of the orbital periods of the planets revolving around the Sun are related to each other in the same proportion as their average distances from the Sun, raised to the power of three.
Kepler’s First Law
Planetary orbits can be described as closed curves in the shape of ellipses, with two focal points located within the orbit at fixed distances. Kepler’s discovery revealed that all planetary orbits lie in a single plane. While Mars and Pluto have highly elongated orbits, the other planets have orbits that closely resemble circles. As a result, Kepler’s First Law is commonly referred to as the law of ellipses.
Are you having difficulty figuring it out by yourself?
Consider seeking assistance from your instructors
Kepler’s Second Law
The velocities of planets are at their highest when they are closest to the Sun, and conversely, they are at their lowest when they are farthest from the Sun. According to Kepler’s Second Law, all planets revolve in a plane that passes through the center of the Sun. The radius-vector connecting the Sun to the planet traces out equal areas in equal time intervals.
Kepler’s Third Law
The periods of complete revolution of the planets have a relationship where the squares of the periods are proportional to the cubes of the greatest semi-major axes of the orbits.
This law demonstrates the connection between the period of orbital revolution and the distance between the planet and the Sun.
Kepler’s laws are highly accurate (with an error of around 1%), although they are primarily based on practical observations and inferences. It was only in 1682 that they could be theoretically justified, following Newton’s discovery of the law of universal gravitation.
Figure 1: Kepler’s Laws (a – first, b – second, c – third).
Law of Universal Gravitation
Isaac Newton (1643-1727), the English physicist and mathematician, developed the law of universal gravitation, which asserts that all objects impact each other through mutual attraction. These forces are referred to as gravitational or universal gravitational forces and are evident on all entities in the cosmos.
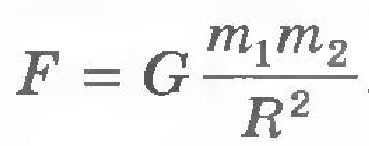
Figure 2: The Law of Universal Gravitation
Newton proposed the formula for the law of universal gravitation, which states that:
- \(G\) is the gravitational constant,
- \(m_1\) and \(m_2\) are the masses of the interacting bodies,
- \(r\) is the distance between them,
- \(F\) is the force of attraction
The law of universal gravitation states that any material bodies attract each other with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. This force acts along the line connecting the bodies.
Attempt to seek assistance from your educators
The physical significance of the gravitational constant arises from the law of universal gravitation. If the masses are both 1 kg and the distance between them is 1 m, then the gravitational constant \(G\) is equivalent to the gravitational force \(F\), meaning that the gravitational force and the gravitational constant are identical.
The gravitational constant \(G\) is equal to \(67-10-11 N m to g N-m^2/kg^2.\).
Gravitational forces occur between any objects made of matter, but they are only noticeable when one object has a significantly larger mass than the other. For example, the force of attraction between the Earth or any other planet and an object is known as gravity. This force of gravity causes an object to accelerate during free fall.
The force of gravity always points towards the center of the Earth or planet. When an object is undergoing acceleration, its weight is determined by the equation: \(P = M – (g + a)\), where \(a\) is the acceleration of the object moving upwards or downwards. Therefore, when an object is in space or in free fall, it experiences weightlessness because its mass is equal to zero.
Figure 3: The Law of Universal Gravitation
Hubble’s Law
Edwin Hubble, an American astronomer born in 1889 and died in 1953, made a groundbreaking discovery that demonstrates the constant expansion of the universe. He also revealed that this expansion is uniform and isotropic, meaning that the universe is expanding in all directions at the same rate.
In addition to confirming the theory of the universe’s expansion, Hubble’s law also provides evidence for the Big Bang theory, which explains the origin of the universe. The most widely accepted formulation of Hubble’s Law is as follows:
- \(V\) represents the velocity of galaxies,
- \(h_0\) is the constant of proportionality that relates the distance between the Earth and an object in space to its recessional velocity (known as the Hubble Constant),
- \(R\) represents the distance to the galactic structure.
There is an alternative representation of Hubble’s law: \(\Delta v = H_0 \cdot R\) , where:
- The velocity of light (\(C\)) is the speed at which light travels.
- The red spectral shift (\(Z\)) refers to the displacement of the lines in the spectrum of chemical elements towards the red end of the electromagnetic spectrum when they are moving away from an observer.
Hubble’s law holds a significant position in astronomy due to its wide application in confirming scientific hypotheses and observing space and celestial objects. However, its main importance lies in the postulate of the universe’s constant expansion, which also serves as evidence for the Big Bang theory.
The observation of cosmic bodies’ motion has been a topic of interest for humans since ancient times. In ancient Greece, complex models were developed to explain the motion of planets within the solar system. These models involved intricate lines known as epicycles to describe the planets’ apparent motion across the sky. The first known attempt to describe the universe was made by Ptolemy in the second century AD (Fig. 1).
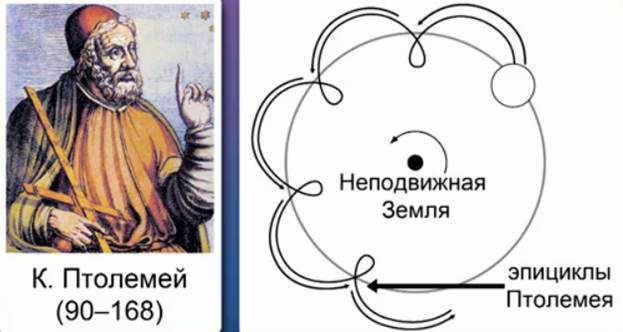
Fig. 1. C. Ptolemy’s geocentric model
He suggested placing the Earth at the center of the universe, with the movements of the planets explained by Ptolemy’s epicycles, which consisted of large and small circles.
In the 16th century, Copernicus proposed a heliocentric model of the world as a replacement for Ptolemy’s geocentric model. This meant placing the Sun at the center of the Universe and suggesting that all the planets, including the Earth, revolve around the Sun (Fig. 2).
Figure 2. The model by N. Copernicus that places the Sun at the center of the Solar System
In the early 17th century, German astronomer Johannes Kepler analyzed a vast amount of astronomical data collected by Danish astronomer Tycho Brahe. As a result, Kepler formulated his empirical laws, which have been named after him – Kepler’s laws.
Kepler’s First Law
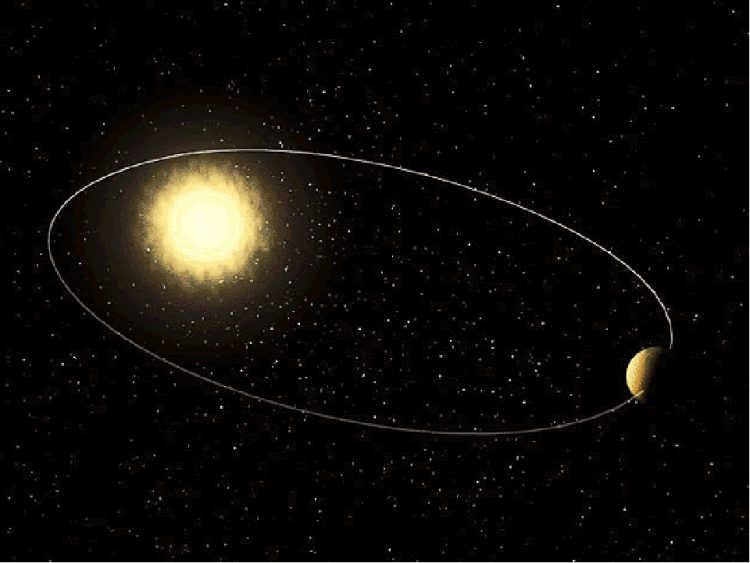
The planets in our Solar System all follow an elliptical path. An ellipse is a basic mathematical curve known as a second-order curve. During the Middle Ages, these curves were referred to as conic intersections – when a cone or cylinder is intersected by a plane, the resulting curve represents the path along which the planets in our Solar System move.
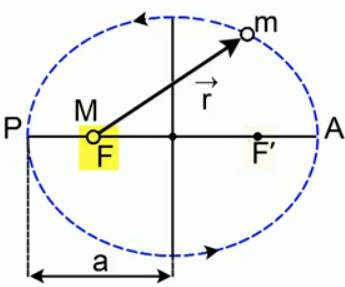
Figure 3. Curve of planetary motion
The curve shown in Figure 3 exhibits two designated points known as foci. The sum of the distances from any point on the ellipse to these foci remains constant. One of these foci corresponds to the center of the Sun (F), while the point on the curve nearest to the Sun (P) is referred to as the perihelion, and the farthest point (A) is known as the aphelion. The distance from the perihelion to the center of the ellipse is referred to as the major semi-axis, while the vertical distance from the center of the ellipse to the ellipse itself represents the minor semi-axis of the ellipse.
When a planet travels along an elliptical path, the area described by the vector connecting the Sun’s center to the planet changes. For instance, as the planet moves from one point to another within a time interval ∆t, the radius vector describes a different area ∆S.
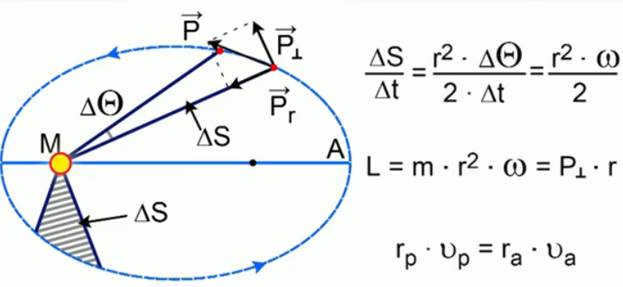
Figure 4. Kepler’s Second Law
According to Kepler’s second law, the planets’ radius vectors describe equal areas for equal time intervals.
Figure 4 illustrates the angle ∆Θ, which represents the rotation angle of the radius vector during a specific time interval ∆t. Additionally, it depicts the planet’s momentum (), which is tangentially directed to its trajectory. The momentum is divided into two components: the component along the radius vector () and the component perpendicular to the radius vector (⊥).
Let’s calculate the values related to Kepler’s second law. According to Kepler, when equal intervals of time pass, the same amount of area is covered. This means that the ratio of these areas remains constant. This ratio is often referred to as the sector velocity, which represents the speed at which the radius vector changes. So, what is the area (∆S) covered by the radius vector in a time interval (∆t)? It can be approximated as the area of a triangle with a height approximately equal to the radius vector and a base approximately equal to r ∆ω. Using this information, we can express ∆S as half of the height multiplied by the base and divided by ∆t:
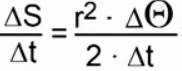
The concept of angular velocity refers to the rate at which the angle changes.
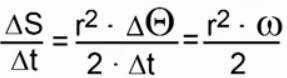
According to Kepler’s third law, the product of the square of the distance to the center of the Sun and the angular velocity at a specific time remains constant.
However, when we multiply the expression r^2ω by the mass of the object m, we get a quantity that can be represented as the product of the length of the radius vector and the momentum in the direction perpendicular to the radius vector:
This physical property, known as the “momentum of the quantity of motion,” is calculated by multiplying the radius vector by the perpendicular component of momentum.
Kepler’s Second Law states that in a gravitational field, the momentum of the quantity of motion remains constant. This leads to a straightforward yet crucial observation: at aphelion and perihelion, the points where the distance to the center of the Sun is the smallest and greatest respectively, the velocity is perpendicular to the radius vector. As a result, the product of the radius vector and the velocity at one point is equal to the product at another point.
The Third Law of Kepler
The Third Law of Kepler states that the proportion between the square of a planet’s revolution period around the Sun and the cube of its major semi-axis is constant for all planets in the solar system.
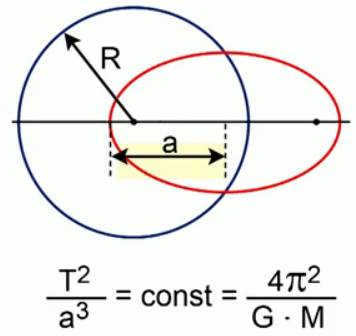
Figure 5 depicts two arbitrary paths taken by the planets. One of these paths takes the form of an ellipse with a semi-axis of length (a), while the other path takes the shape of a circle with a radius of (R). The time it takes for a planet to complete one revolution along either of these paths, known as the orbital period, is directly related to the length of the semi-axis or the radius. When an ellipse transforms into a circle, the major semi-axis simply becomes the radius of that circle. Kepler’s Third Law asserts that when the length of the major semi-axis is equal to the radius of the circle, the orbital periods of the planets around the Sun will be identical.
When it comes to the circle, we can determine this ratio by applying Newton’s second law and the law of motion for an object on a circle. This constant is 4π^2 divided by the gravitational constant (G) and the mass of the Sun (M).
Summary
During the latter half of the 20th century, scientists observed that certain stars located far away from the center of our Galaxy were not conforming to Kepler’s law. This discovery suggests that our understanding of gravity at the scale of our Galaxy is incomplete. One possible explanation for the discrepancy in the speed of distant stars is the presence of unobservable mass within our Galaxy. This mass, known as dark matter or hidden mass, does not interact with light or electromagnetic forces but only with gravity. The existence of dark matter poses a significant challenge for physicists in the 21st century.
Kepler’s Laws – a set of physical laws discovered by Johannes Kepler that explain the movement of planets around the Sun.
Kepler’s First Law (Law of Ellipses)
Each planet in the solar system orbits in an elliptical path, with the Sun located at one of the foci.
Here, c represents the distance from the center of the ellipse to its focus (half of the interfocal distance), while a represents the major semi-axis. The value e is known as the eccentricity of the ellipse. When c = 0 and e = 0, the ellipse transforms into a circle.
According to Newton’s Law of Universal Gravitation, there is a mutual attraction between every object in the universe. This attraction occurs along a line that connects the centers of mass of the objects and is directly proportional to the mass of each object. Additionally, the attraction is inversely proportional to the square of the distance between the objects. This law implies that the acceleration, denoted as a, can be expressed in the following form:
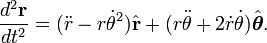
The motion of each planet can be described by the equation
By substituting the value of “and” into the second equation, we can derive
After performing integration, we can express this as
Let’s consider a constant, denoted as , which represents the specific angular momentum ().
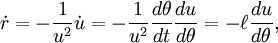
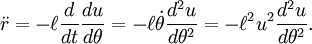
become equal to
We can derive the equation of the conic section by considering the eccentricity e and placing the origin of the coordinate system at one of the foci. This directly leads to the conclusion of Kepler’s first law, which is derived from Newton’s law of universal gravitation and Newton’s second law.
Kepler’s Second Law (Law of Squares)
Each planet moves in a plane that passes through the center of the Sun, and for equal periods of time, the radius vector connecting the Sun and the planet sweeps out equal areas.
When we apply this law to our solar system, two important concepts emerge: the perihelion, which is the point on the orbit closest to the Sun, and the aphelion, which is the point furthest from the Sun. Therefore, according to Kepler’s second law, a planet moves around the Sun at different speeds, with a higher linear velocity at perihelion than at aphelion.
Every year in early January, the Earth accelerates as it passes through perihelion, causing the apparent movement of the Sun along the ecliptic to also speed up compared to the average for the year. Conversely, in early July, when the Earth passes through aphelion, it decelerates, resulting in a slower movement of the Sun along the ecliptic. This phenomenon can be explained by the law of areas, which states that the force governing the orbital motion of the planets is directed towards the Sun.
The angular momentum of a point particle with mass m and velocity can be defined as:
,
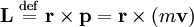where \mathbf{r} is the radius vector of the particle and \mathbf{p} is the momentum of the particle.
.
Let’s take the derivative of both sides of the equation with respect to time.
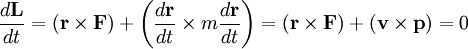where M – represents the mass of the Sun, and m1 and m2 – represent the masses of the planets.
Given that motion and mass are interconnected, this combination of Kepler’s harmonic law and Newton’s law of gravitation is utilized to calculate the masses of planets and satellites if their orbital periods and orbits are known.
According to Kepler’s second law, the orbital body’s radius-vector traces out the same area within the same time intervals. To illustrate, if we divide time into infinitesimally small intervals when the planet is at points A and B (perihelion and aphelion), we can estimate the area by using triangles. These triangles have heights that are equal to the distance from the planet to the Sun and bases that are equal to the product of the planet’s velocity and time.
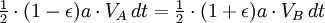
Applying the principle of energy conservation to the overall energy of the planet at points A and B, we can express it as follows:
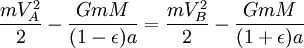
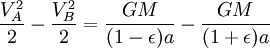
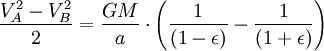
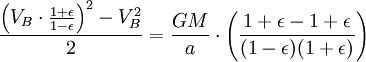
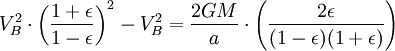
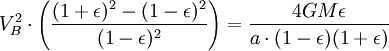
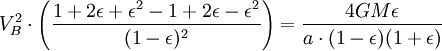
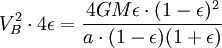
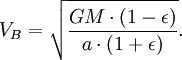
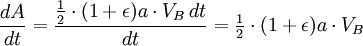
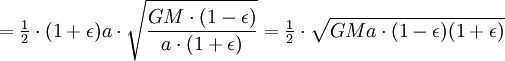
Nevertheless, the combined size of the ellipse is (equivalent to πab since ). Consequently, the complete revolution duration is equivalent to
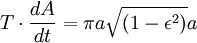
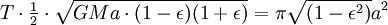
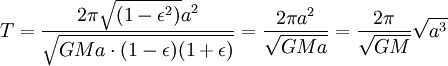
Please take note that if the mass m is not insignificantly small in comparison with M, then the planet will revolve around the Sun at the same velocity and in the same trajectory as a material point revolving around the mass of M + m (refer to reduced mass). Consequently, the mass M in the last equation should be substituted by M + m:
Wikimedia Foundation . 2010 .
Kepler’s laws – a set of scientific principles discovered by Johannes Kepler that explain the movement of the planets around the Sun.
Kepler’s First Law (Law of Ellipses)
The Sun is located at one of the foci of each planet’s elliptical orbit in the solar system.
In the equation, c represents the distance from the center of the ellipse to its focus (half of the interfocal distance), and a represents the major semi-axis. The value e is known as the eccentricity of the ellipse. When c = 0 and e = 0, the ellipse transforms into a circle.
According to Newton’s Law of Universal Gravitation, “every object in the universe exerts a gravitational force on every other object along a line connecting their centers of mass, with the magnitude of the force being directly proportional to the mass of each object and inversely proportional to the square of the distance between them.” This means that the acceleration a takes the following form.
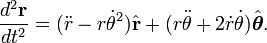
Expressed in terms of coordinates, the equation is written as follows:
After replacing a with b in the second equation, we get
Integrating, we can express this as
Assume that there exists a constant, denoted as , which represents the particular angular momentum (). Let’s consider the case where
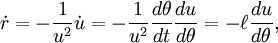
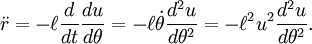
become equal to
We have derived the equation for the conic section, which has a eccentricity e and the origin of the coordinate system located at one of the foci. Consequently, Newton’s law of universal gravitation and Newton’s second law directly lead to Kepler’s first law.
Kepler’s Second Law (Law of Squares)
Every planet moves in a plane that passes through the center of the Sun, and during equal intervals of time, the radius vector connecting the Sun and the planet sweeps out equal areas.
When applied to our solar system, this law gives rise to two important concepts: perihelion, which is the point in the orbit closest to the Sun, and aphelion, which is the farthest point in the orbit. As a result of Kepler’s second law, it is evident that the planet’s motion around the Sun is not uniform, with a greater linear velocity at perihelion compared to aphelion.
Every year in early January, the Earth moves faster as it passes through perihelion. This causes the apparent movement of the Sun along the ecliptic to the east to be faster than the average for the year. In early July, as the Earth passes through aphelion, its movement slows down, resulting in a slower movement of the Sun along the ecliptic. The law of areas states that the force governing the orbital motion of the planets is directed towards the Sun.
The angular momentum of a point particle with mass m and velocity is defined as:
.
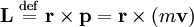Here, the radius-vector of the particle is denoted by a and the momentum of the particle is denoted by p.
.
Let’s differentiate both parts of the equation with respect to time
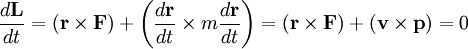
Given the relationship between motion and mass, the combination of Kepler’s harmonic law and Newton’s law of gravitation is employed to calculate the masses of planets and satellites, provided their orbits and orbital periods are known.
According to Kepler’s second law, the radius-vector of a celestial body in orbit covers equal areas in equal time intervals. By considering very small time intervals when the planet is at points A and B (perihelion and aphelion), we can approximate the area as triangles with heights equivalent to the distance between the planet and the Sun, and a base equal to the product of the planet’s velocity and time.
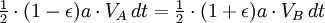
By applying the principle of energy conservation to the total energy of the planet at points A and B, we can express it as
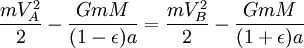
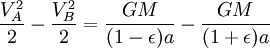
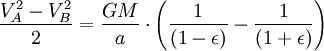
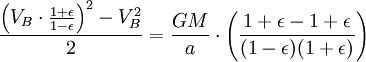
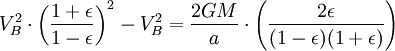
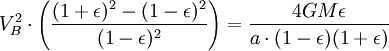
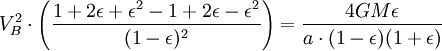
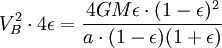
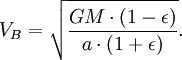
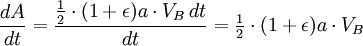
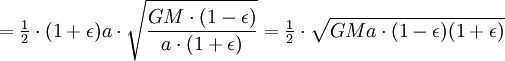
Nonetheless, the aggregate area of the ellipse is (which is equivalent to πab since ). Hence, the complete period of revolution is equivalent to
