Our understanding of the cosmos is closely tied to humanity’s ability to measure distances in space. For centuries, astronomers have grappled with the question “how far?” in their quest to unravel the mysteries of the universe. However, this thirst for knowledge could not be quenched until the advent of highly sensitive and advanced instruments. Despite the continuous evolution of our understanding of the physical world, the true extent of the vastness of space remained obscured. Philosophers and astronomers throughout history pondered cosmic distances and tirelessly sought methods to quantify them, but their efforts were in vain due to the lack of necessary tools. It was only when telescopes had been utilized by astronomers for a considerable period of time and brilliant minds had dedicated themselves to studying the vast wealth of information they provided, that a breakthrough occurred. The marriage of precise mechanics and flawless optics finally gave birth to an instrument capable of tackling the problem of distances. Barriers were shattered, and a collective effort of astronomers with their knowledge, skills, and intuition commenced, all with the goal of determining the immense gaps that separate us from the celestial realms.
In 1838, three astronomers (located in different parts of the world) successfully calculated the distances to specific stars. Friedrich Wilhelm Bessel, hailing from Germany, determined the distance to the star Swan 61. Vasily Struve, an exceptional Russian astronomer, calculated the distance to the star Vega. Meanwhile, at the Cape of Good Hope in South Africa, Thomas Henderson measured the distance to Alpha Centauri, the star closest to the Sun. In each of these instances, astronomers measured incredibly minute angular distances in order to ascertain what is known as parallax. Their accomplishments can be attributed to the fact that the stars they measured were relatively nearby to Earth.
In astronomy, there is no universal method for determining distances. As we move from nearby celestial bodies to more distant ones, different methods are used to estimate distances, with each method building upon the previous one. The accuracy of these distance estimations is limited by either the accuracy of the simplest methods or the accuracy of the astronomical unit of length (a.e.), which is determined through radar measurements with a mean-square error of 0.9 km. The current value of the astronomical unit is known to be 149597867.9 ± 0.9 km. Considering various adjustments, the International Astronomical Union adopted a revised value of 1 a.e. = 149597870 ± 2 km in 1976.
Determining the Distances to the Planets
The average distance r of a planet from the Sun, expressed in fractions of an astronomical unit (a.e.), can be determined by its orbital period T:
r = T/Earth years
This formula is derived from Kepler’s third law, which states that the squares of the orbital periods of the planets around the Sun are related as the cubes of their average distances from the Sun.
When calculating the average distance, the mass of the planet m can be neglected compared to the mass of the Sun mc.
The distances to the Moon and other planets can also be accurately determined using radiolocation methods.
The Parallax Technique.
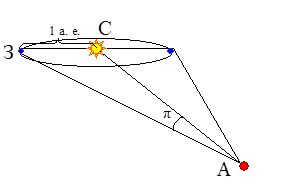
Because of the Earth’s yearly movement around the sun, stars that are nearby appear to move slightly compared to more distant “fixed” stars. Over the course of a year, one of these stars will trace out a small ellipse on the sky, with the size of the ellipse becoming smaller as the star gets farther away. In terms of angles, the major semi-axis of this ellipse is roughly equal to the maximum angle at which the star can be seen from a distance of 1 astronomical unit (the major semi-axis of the Earth’s orbit) perpendicular to the line connecting the observer and the star. This angle, known as the annual or trigonometric parallax (p), is half of the star’s apparent displacement each year and is used to determine its distance based on trigonometric calculations involving the sides and angles of the WSA triangle, where the angle p and the base (the major semi-axis of the Earth’s orbit) are known (see Figure 1).
The distance r to the star, calculated using the trigonometric parallax value p, can be determined using the formula:
r = 206265''/p (a. e.),
where the parallax p is measured in angular seconds.
For the purpose of determining distances to stars using parallaxes, astronomy employs a unique unit of measurement called a parsec (ps). A star located at a distance of 1 ps possesses a parallax equal to 1”. By applying the aforementioned formula, 1 ps is equivalent to 206265 astronomical units (a.e.) or 3.086-10 18 cm.
In addition to the parsec, astronomers also utilize another specialized unit of measurement known as the light year, which denotes the distance that light travels in the span of 1 year. This unit is equal to 0.307 ps or 9.46-10 17 cm.
The nearest star to our Solar System, Proxima Centauri, is a red dwarf with a magnitude of 12. It possesses a parallax of 0.762, indicating that its distance is 1.31 ps (equivalent to 4.3 light-years).
Table 1. The twenty closest stars.
Our understanding of the universe is closely tied to humanity’s capacity to measure distances in space. For countless years, the question “how far?” has been of utmost importance to astronomers seeking to comprehend the universe’s properties. However, this pursuit of knowledge could not be fulfilled until highly sensitive and flawless instruments became available. As a result, while our understanding of the physical world has evolved over time, the mysteries surrounding the vastness of space have remained. Throughout history, philosophers and astronomers have contemplated cosmic distances and diligently searched for ways to measure them. Unfortunately, their efforts were in vain due to the lack of necessary instruments. Eventually, after astronomers had used telescopes for many years and the first brilliant minds had focused their talents on studying the wonders revealed by these telescopes, the combination of precise mechanics and impeccable optics led to the creation of an instrument capable of solving the distance problem. Barriers were overcome, and numerous astronomers pooled their knowledge, expertise, and intuition to determine the immense distances that separate us from the stellar realms.
Back in 1838, three astronomers from different corners of the globe managed to successfully calculate the distances to specific stars. Friedrich Wilhelm Bessel, located in Germany, was able to determine the distance to the star Swan 61. Vasily Struve, a highly regarded astronomer hailing from Russia, calculated the distance to the star Vega. Meanwhile, at the Cape of Good Hope in South Africa, Thomas Henderson tackled the task of measuring the distance to the star closest to the Sun, Alpha Centauri. In each of these instances, the astronomers utilized the incredibly minute angular distance in order to determine the parallax. The reason behind their triumphant achievements lies in the fact that the stars they measured were relatively close to our planet Earth.
There is no single universal method for determining distances in the field of astronomy. As we transition from nearby celestial bodies to those that are further away, different methods of distance determination are employed, with each method building upon the previous one. The accuracy of distance estimates is ultimately limited by the precision of the least accurate method used or by the precision of the astronomical unit of length (a.e.), which is determined through radar measurements and has an average error of 0.9 km. The current value of the astronomical unit is 149597867.9 ± 0.9 km. Taking into consideration various adjustments, the International Astronomical Union established in 1976 that 1 a.e. is equal to 149597870 ± 2 km.
Determination of distances to the planets.
The average distance r of a planet from the Sun (in astronomical units) can be calculated using the period of its revolution T:
where r is expressed in astronomical units, and T is measured in Earth years. The mass of the planet m compared to the mass of the sun mc can be disregarded. This formula is derived from Kepler’s third law, which states that the squares of the orbital periods of the planets around the Sun are proportional to the cubes of their average distances from the Sun.
The distances to the Moon and planets can also be accurately determined using radiolocation methods.
The Parallax Technique.
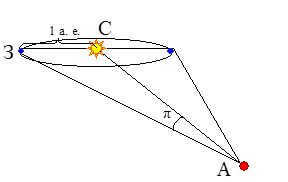
Because of the Earth’s yearly movement around the sun, stars that are close to us appear to move slightly compared to distant stars that are considered “fixed”. Over the course of a year, a star traces out a small elliptical path on the celestial sphere. The size of this ellipse is smaller the farther away the star is. In terms of angular measurement, the major semi-axis of this ellipse is approximately equal to the maximum angle at which the star can be seen from a distance of 1 astronomical unit (the major semi-axis of the Earth’s orbit) perpendicular to the star’s direction. This angle, known as the annual or trigonometric parallax (p), represents half of the star’s apparent displacement per year. It is used to determine the star’s distance by employing trigonometric relationships between the sides and angles of the WSA triangle. In this triangle, the angle p and the base (the major semi-axis of the Earth’s orbit) are known (see Figure 1).
The distance r to the star can be calculated based on its trigonometric parallax p using the following formula:
r = 206265''/p (a. e.),
where the parallax p is given in angular seconds.
When determining distances to stars using parallaxes, astronomy employs a unique unit of length known as the parsec (ps). A star situated at a distance of 1 ps has a parallax equivalent to 1”. Based on the aforementioned formula, 1 ps is equivalent to 206265 astronomical units (a.e.) or 3.086-10 18 cm.
Additionally, alongside the parsec, another specialized unit of measurement for distances is utilized – the light year (which represents the distance light travels in 1 year). It is equal to 0.307 ps or 9.46-10 17 cm.
The closest star to our Solar System, the 12th magnitude red dwarf Proxima Centauri, possesses a parallax of 0.762, signifying that its distance is 1.31 ps (4.3 light-years).
Table 1. The twenty closest stars.
Our understanding of the universe is closely tied to mankind’s capacity to measure distances in space. For centuries, astronomers have grappled with the question “how far?” in their quest to comprehend the nature of the cosmos. However, this thirst for knowledge could only be quenched once sophisticated and highly accurate instruments became available. Despite the continuous evolution of our understanding of the physical world over the years, the mysteries surrounding the vastness of space have remained intact. Philosophers and astronomers throughout history have pondered the vast cosmic distances and tirelessly sought ways to measure them. Unfortunately, their efforts were in vain due to the lack of suitable instruments. It wasn’t until the advent of telescopes and the brilliance of early astronomers that a breakthrough occurred. The combination of precise mechanics and advanced optics finally yielded an instrument capable of solving the problem of measuring distances. Barriers were overcome, and astronomers from various backgrounds pooled their knowledge, expertise, and intuition to determine the immense distances that separate us from the stars.
In 1838, the distances to certain stars were successfully measured by three astronomers located in different parts of the world. Friedrich Wilhelm Bessel, a German astronomer, determined the distance to the star Swan 61. Vasily Struve, an exceptional Russian astronomer, calculated the distance to the star Vega. Meanwhile, Thomas Henderson, conducting his research at the Cape of Good Hope in South Africa, measured the distance to Alpha Centauri, the closest star to the Sun. In each of these cases, the astronomers used the parallax method, which involves measuring an incredibly small angular distance. The key to their success was the relatively close proximity of the stars they were measuring.
There are various methods used in astronomy to determine distances, with each method building upon the previous one as we study celestial bodies that are progressively farther away. The accuracy of these distance estimates is limited by either the accuracy of the simplest methods or by the accuracy of the astronomical unit of length (a.e.). The value of the astronomical unit of length is known from radar measurements with a mean square error of 0.9 km and is equal to 149597867.9 ± 0.9 km. Taking into consideration changes in the astronomical unit of length, the International Astronomical Union adopted a value of 1 a.e. = 149597870 ± 2 km in 1976.
Expressed in a. e., r represents the value of r in astronomical units, while T is measured in Earth years. The mass of the planet m can be disregarded when compared to the mass of the sun, mc. This formula is derived from Kepler’s third law, which states that the squares of the orbital periods of planets around the Sun are proportional to the cubes of their average distances from the Sun.
The precise distances to the Moon and other planets are determined using radiolocation methods.
Determination of distances to the closest stars.
The technique of parallax.
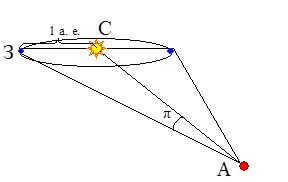
Because of the Earth’s yearly orbit, nearby stars appear to move slightly in comparison to distant “fixed” stars. Over the course of a year, such a star traces a small ellipse on the celestial sphere. The size of this ellipse decreases as the star gets farther away. In terms of angular measurement, the major semi-major axis of this ellipse is approximately equal to the maximum angle at which the star is seen, 1 a.e. (the major semi-major axis of the Earth’s orbit), perpendicular to the direction of the star. This angle (p), known as the star’s annual or trigonometric parallax, is equal to half of its apparent displacement per year. It is used to calculate the distance to the star based on trigonometric relationships between the sides and angles of the WSA triangle. In this triangle, the angle p and the base (the major semi-axis of the Earth’s orbit) are known (see Figure 1).
The distance r to the star, determined by the value of its trigonometric parallax p, can be calculated as:
r = 206265''/p (a. e.),
where the parallax p is expressed in angular seconds.
Figure 1: Determining the distance to a star using the parallax method (A – star, Z – Earth, S – Sun).
In astronomy, a special unit of length called the parsec (pc) is used for convenience in determining distances to stars using parallaxes. A star at a distance of 1 pc has a parallax of 1''. According to the formula above, 1 pc = 206265 a. e. = 3.086 × 1018 cm.
Another special distance unit used is the light-year, which is the distance that light travels in 1 year. It is equal to 0.307 pc, or 9.46 × 1017 cm.
The minimum measurable trigonometric parallax is approximately 0.01”, making it suitable for measuring distances up to 100 parsecs with a relative error of 50%. (For distances up to 20 parsecs, the relative error is less than 10%.) So far, this method has been used to determine distances to around 6000 stars. However, for stars that are further away, the photometric method is primarily used in astronomy.
Below is Table 1, which lists the twenty closest stars.


When observing the night sky, a multitude of stars come into view. The majority of these stars are part of our own galaxy, known as the Milky Way. However, an intriguing question arises: can we perceive stars from other galaxies? This inquiry is not straightforward and necessitates an understanding of stars, galaxies, and the mechanisms by which we observe celestial objects at vast distances.
The arrangement of celestial bodies
Celestial bodies are immense spheres of incandescent gas that emit radiant energy and warmth as a consequence of the fusion reactions happening within their cores. A nuclear reaction denotes a course of action wherein alterations transpire within the nuclei of atoms, leading to the discharge or assimilation of extensive quantities of energy. Such nuclear reactions within celestial bodies serve as the wellspring of the energy that upholds thermonuclear incineration and empowers the celestial body to persist and radiate light and warmth for countless millions and billions of years.
Characteristics of stars
Stars possess a variety of physical properties, including variations in size, mass, and temperature. These unique attributes play a crucial role in determining the color, brightness, and stage of development of each star. Take, for instance, our Sun, a yellow star of moderate size, currently situated at the midpoint of its lifespan.
Luminosity and observability of stars
The brightness of a star is determined by two primary elements: its absolute brightness (or magnitude) and its distance from the observer. Absolute magnitude represents the apparent stellar magnitude that a star would exhibit if it were positioned at a set distance of 10 parsecs or 32.6 light years, accurately depicting the true brightness of the star. Conversely, apparent magnitude measures the brightness of a celestial body (specifically, the luminosity it emits) as observed from the vantage point of an observer on Earth. Stars that are in closer proximity to Earth appear brighter to us.
Determining the distance to a star can be a challenging task due to its immense remoteness. Nonetheless, astronomers have devised multiple techniques to accurately measure these vast distances. Among the most frequently employed methods is the parallax method, which capitalizes on the star’s shifting position in relation to more distant objects when observed from various points within Earth’s orbit.
What exactly is a galaxy?
A galaxy is an enormous system composed of billions of stars, gas, dust, and mysterious dark matter. In the vast expanse of the universe, our own galaxy, known as the Milky Way, is just one out of countless billions of galaxies.
The makeup of galaxies
Most galaxies exhibit either a spiral, elliptical, or irregular shape. Spiral galaxies, like our very own Milky Way, feature rotating “arms” that extend from a central bar or beam. The particular arm that houses our solar system is known as the Orion Arm.
Calculating the distance to galaxies
Estimating the distance to galaxies presents a formidable challenge. Scientists employ various techniques, such as studying fluctuating stars called Cepheids and the explosive events of supernovae, in order to gauge the distances to galaxies.
Estimating the distance to galaxies
Observing cepheids is a primary technique for measuring the distance to galaxies. Cepheids are stars that vary in brightness on a regular basis. The fluctuations in brightness of cepheids are connected to their absolute brightness, which enables astronomers to utilize them as “standard candles”. The standard candle approach relies on astronomical objects that possess a well-established correlation between their luminosity and other characteristics, such as periods of brightness variation. By gauging the luminosity of these objects and contrasting it with their observed brightness, astronomers are able to ascertain their distances.

Now that we have determined what stars and galaxies are and how we calculate their distance, let’s address the initial query: is it possible to observe stars in other galaxies?
Unfortunately, the answer is mostly negative. The majority of stars visible to the naked eye reside within our own galaxy, the Milky Way. Due to the immense distance, it is impossible to discern individual stars within other galaxies, even with the aid of advanced telescopes.
The visibility of a star is influenced by various factors. These factors encompass the star’s absolute brightness, its distance from Earth, the presence of dust and gas in the space between the star and us, and the lighting conditions on our planet.
Obstacles in the natural environment
The presence of dust and gas in interstellar space can pose challenges in observing remote celestial objects such as stars and galaxies. This phenomenon is referred to as interstellar dimming.
Limitations in Technology
Our ability to observe distant stars is restricted by the technological capabilities of telescopes and other astronomical instruments. The larger and more precise the telescope, the greater the distance we can see. The primary mirror or lens diameter of a telescope plays a crucial role in its strength, as it determines the amount of light the telescope can gather.
- Telescopes with low power: These telescopes typically have a lens or primary mirror diameter of less than 10 cm. They are suitable for beginner astronomers or hobbyists who wish to study the moon, planets, and some bright deep space objects.
Summary
When observing the night sky, we typically only see the stars within our own galaxy, the Milky Way. This is due to the vast distance between us and other galaxies, as well as limitations imposed by natural phenomena and our observational technology.
A galaxy is a vast system composed of stars, gas, dust, and dark matter. The Milky Way, our own galaxy, is approximately 13.6 billion years old, making it roughly the same age as the universe itself. It is estimated to contain anywhere from 100 to 400 billion stars.
2. Is it possible to see stars from other galaxies?
In most cases, the answer is no. The stars within other galaxies are typically too far away for us to distinguish them individually.
3. How do we measure the brightness of a star?