Determining latitude using star observations. How can we calculate geographical coordinates using stars?
Assuming you are familiar with geographical coordinates and that the altitude of the North Star above the horizon is roughly equal to the latitude of the observation location. To be precise, the North Star is not exactly at the North Pole, but rather about a degree away from it. Therefore, measuring the height of the North Star is sufficient to determine latitude. Let’s revisit a passage from the book “Mysterious Island”.
Cyrez Smith went back to the Pipes. By the light of the fireplace, he shaped two small, polished planks and connected them at the ends, creating a circular device with movable legs. He used a thick acacia thorn he found in the bushes to secure them together.
In the southern part of the sky, the horizon line was clearly visible, illuminated from beneath by the moon’s first rays. It could be accurately determined. At that moment, the southern cross constellation appeared to be upside down to the observer, with the alpha star located closer to the south pole at the base of the constellation.
This constellation is not as close to the Antarctic pole as the polar star is to the Arctic pole. The star alpha is approximately twenty-seven degrees away. Cyrus Smith was aware of this and had to consider this distance in his calculations. Additionally, the engineer had observed this star as it crossed the lower meridian, which made the calculations much simpler.
Cyrus Smith aligned one leg of his compass with the sea horizon and the other with the star alpha, using the distance between them to determine the angular distance of alpha from the horizon. To ensure the accuracy of the angle, he secured both legs of the instrument to a third cross-board using acacia thorns, firmly fixing the distance between them.
There is an error in the author’s description. In April, during this time of year, the southern cross is actually in the upper culmination around midnight, not in the lower position. This means that it crosses the meridian above the pole, and the height of alpha is actually over 60°. However, this is not the main issue. To use an “Angle Measuring Instrument” like the one described, one would likely need to be a chameleon, as it would be impossible to visualize such a large angle with just your hands. The device would need to be mounted on a tripod at the very least. By the way, it would be much simpler and more accurate to measure the zenith distance of a star (the vertical direction does not need to be visualized and can be easily obtained with a plumb bob) rather than its height above the horizon.
Moreover, being a resident of the northern hemisphere (similar to the characters in Jules Verne’s novels), I would never be able to recall the declination of the alpha of the southern cross. Would you?
Perchance, we should consider an alternative approach – and this particular method has been well-known since ancient times. It involves determining latitude by means of a gnomon and the position of the sun.
Similar to our previous endeavor, let us ascertain the altitude of the sun – albeit this time at midday, when the gnomon’s shadow aligns with the noon line (by the way, do note down the precise time of noon – it will prove useful to us in the future).
Currently, the primary issue when determining latitude is the task of finding the sun’s declination at the time of observation, preferably without the aid of a computer (since we are stranded on a desert island). Even the exceptional memory of Cyrese Smith will not be of assistance here, as this value will need to be calculated without the use of calculations!
We are aware that the sun’s declination ranges from -23.5° to 23.5° (which represents the tilt of the Earth’s axis to the ecliptic and the latitude of the tropic lines). Hopefully, we can remember these values even while stranded on a desert island. To simplify the problem, we will assume that the sun moves uniformly along the ecliptic. In this case, the sun’s declination can be roughly determined using the following formula.
D represents the number of days that have elapsed since the vernal equinox.
Visually, this can be accomplished in the following way:
Let’s create a circular shape with a radius of 23.5 units (the exact unit of measurement doesn’t matter, it can be a matchstick, for example, if we are drawing on sand). Divide the circle into 12 equal parts, just like in the previous task. However, this time, each division represents a month, or more precisely, an interval of 30.5 days. Now we need to mark the dates of our observations on the circle, taking into account the horizontal axis – the line of equinoxes (March 21 and September 22), and the vertical axis – the solstices (June 22 and December 22). To minimize errors, it’s best to mark the date closest to these points. The point where the date intersects the vertical axis will give us the value of the sun’s declination. All that’s left is to measure it accurately using our “Length Standard” – a matchstick. This simple construction ensures that we can determine the declination with an accuracy of no worse than half a degree.
Now, by examining the diagram, we have the ability to determine the latitude of the observation point.
The declination of the sun, denoted as O, along with the height of the sun above the horizon, denoted as h, can be used in this calculation.
Now let’s address the matter of longitude. In this case, it is essential to have knowledge of time. Fortunately, in contrast to the 19th century, accurate clocks are now readily available. Therefore, we can assume that we know the time with an error margin of no more than half a minute. Our task seems relatively straightforward this time, as longitude (measured in hours) is simply the difference between local time and Greenwich Mean Time (GMT). The only remaining challenge is to determine GMT. However, we must ensure that GMT corresponds to true solar time, as we determine the moment of noon based on the position of the sun. Our clocks display mean solar time, which is slightly different from true solar time. This discrepancy arises because the sun moves unevenly along the ecliptic, leading to slight variations in the duration of the day throughout the year. To overcome this inconvenience, a standardized system called “Uniform” average solar time was adopted. This system is based on an imaginary point that moves perfectly uniformly along the celestial equator. The difference between mean solar time and true solar time can be as much as 16 minutes, which is known as the equation of time. We will delve into this topic further in the next chapter. For now, let’s assume that we either have knowledge of this correction or we are observing one of the four days in a year when mean solar time coincides with true solar time – April 16, June 14, September 1, and December 25.
TGR – True Greenwich Mean Solar Time.
TM – True local time.
Tn – Mean Apparent Time of the n – one time zone.
A is at the time of local noon.
(Longitude is considered to be positive east of Greenwich).
The number of time zone in this formula is an integer, showing how many hours the time differs from Greenwich time. Thus, Moscow is in the second time zone, but in the 30s of the XX century was introduced the “Decree” time, one hour ahead of the zone time, in addition, in summer the hands of the clock are moved forward by one hour, therefore, the difference between Moscow and Greenwich time is 3 hours in winter and 4 – in summer.
We can now determine Greenwich true solar time, and therefore the geographic longitude of the place of observation.
And now let’s reconsider the actions of Jules Verne’s characters:
– Is it not April 15th today?
– Yes, Mr. Sayres,” answered the young man.
– If I am not mistaken, tomorrow will be one of the four days in the year when true time and mean time align. This means that tomorrow, my dear, the sun will pass the meridian a few seconds before noon. If the weather is good, I might be able to calculate the longitude of our island within a few degrees.
Cyres Smith discovered an immaculate spot on the shoreline that had been leveled by the tide. The fine layer of sand was incredibly smooth, with each grain perfectly aligned as if it had been meticulously arranged. Although it may not have been completely level, the six-foot pole that was inserted into the sand was intentionally tilted slightly to the south. This adjustment was made because the inhabitants of Lincoln Island were located in the southern hemisphere and experienced daylight from the northern horizon, rather than the southern horizon where the sun would typically be.
Then Harbert realized the method the engineer would use to determine the exact moment the sun reached its highest point in the sky or passed through the meridian, which is essentially noon for the area. This method relied on the shadow cast by a stick in the sand. Using this technique, Cyrese Smith could obtain highly accurate results without the need for any instruments.
When the shadow was at its shortest, it would be precisely twelve o’clock in the afternoon. The observer simply had to monitor the end of the shadow to see when it started to lengthen again. By angling the pole towards the south, Smith made the shadow larger, making it easier to observe any changes. After all, the larger the hand on a clock, the more noticeable its movement. Therefore, the shadow of the pole on the sand acted as the equivalent of a hand on a clock’s dial.
The journalist had his chronometer in his possession, ready to record its reading at the exact moment when the shadow would be at its shortest. This calculation was done on April 16, a day when mean time aligns with true time. As a result, Gideon Spelet’s watch had to display the accurate Washington time, which made the calculations much simpler.
In the meantime, the sun continued its slow journey across the sky. The shadow of the wand gradually decreased in length. However, the engineer noticed that it appeared to be lengthening once again and asked:
“What is the time now? Five hours and one minute?” Spilett promptly replied.
Now the only thing left to do was to perform the calculation. It was a fairly straightforward process. The time difference between Washington and Lincoln’s Island was approximately five hours. In other words, when it was noon on Lincoln’s Island, it was five o’clock in the evening in Washington. According to astronomical observations, the sun moves across the sky at a rate of one degree every four minutes, or fifteen degrees per hour. Multiplying fifteen degrees by five gives us a total of seventy-five degrees.
Therefore, if Washington is located at a longitude of 77°3’11”, or approximately seventy-seventh degree west of the Greenwich meridian, which is considered zero by both Americans and the English, it can be concluded that Lincoln’s Island is situated at a longitude of 77° 75° west of Greenwich, equivalent to 152° west longitude.
Cyrese Smith shared this information with his friends. After taking into account the errors in observation, he determined that Lincoln’s Island is located between the thirty-fifth and fortieth parallels, and between the one hundred and fiftieth and one hundred and fifty-fifth meridians to the west of Greenwich.
M – Yes. The logic and calculations are impeccable, but in terms of practical observations, it is not ideal. The length of the shadow around noon changes gradually, making it difficult to accurately determine the moment when it will be the shortest. The margin of error is likely to be around 10-15 minutes. Additionally, the angle of the gnomon “on the Eye” and any potential unevenness in the site’s horizontality will introduce further inaccuracies in the measurements. What’s particularly frustrating is that the engineer had already determined the direction of the meridian, but inexplicably did not utilize it to determine the exact moment of noon.
What is the level of accuracy of our obtained result? Let’s attempt to approximate it. Let’s assume that the error in measuring the gnomon shadow in terms of angle does not exceed 1/2° and is due to the indistinctness of the shadow. Approximately the same magnitude of error can also occur in the placement of the gnomon, such as its deviation from the vertical and its distance from the horizontal surface. Additionally, our geometric calculations in determining the sun’s declination and height can introduce another error of 1/2°. Therefore, the total error, which has a tendency to accumulate, can reach 1.5 degrees. When determining longitude, errors are only caused by observations with the gnomon and the error of our clock. Therefore, if we know the time to the nearest half minute, which is equivalent to 1/8° in angular units, the total error could be approximately 1° 8′ of arc. To estimate these values in terms of distance, we must consider that 1 nautical mile (1852 m) is equal to the average length of the meridian arc of 1 arc minute. Therefore, the deviation of our calculated coordinates from the true coordinates will not exceed 90 miles in latitude and 68 miles in longitude. It is important to note that since we are not on the equator, the length of 1′ parallel decreases with increasing latitude, so the error in longitude could be noticeably smaller.
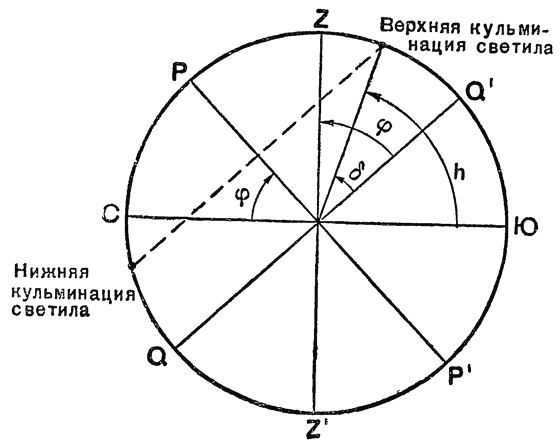
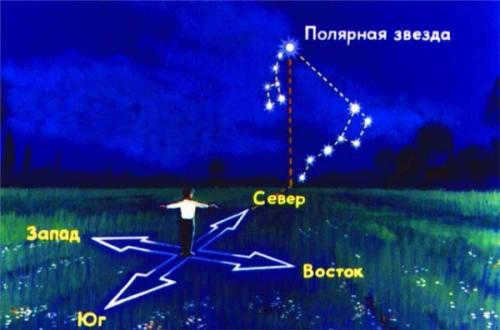
You can calculate the geographic latitude by observing Polaris. If we consider Polaris as the North Pole of the world, then the height of Polaris above the horizon gives us an approximate value for the geographic latitude of the observation location. By measuring the height of Polaris during its upper and lower culminations, we can obtain a more precise latitude value for the observation location: \
We derive this equality from the equations \(h_ = δ – (90° – φ)\) and \(h_ = 90° + φ – δ\). The formula \(φ = \frac + h_>\) is applicable to all non-ascending stars whose upper and lower culminations occur on the same side of the zenith.
How to Calculate Geographic Latitude Using Polaris. Using Clock, Sun, and Stars for Orientation, and Determining Geographic Longitude and Latitude in the Field.
Determining the compass direction and finding the cardinal points is a relatively easy task. However, in the absence of a compass, there are alternative methods that can be used, such as relying on the position of the sun, stars, or plants. In the northern hemisphere, one can determine the direction of north by standing facing south at noon. The shadow cast by the body will point towards the north, acting as an arrow.
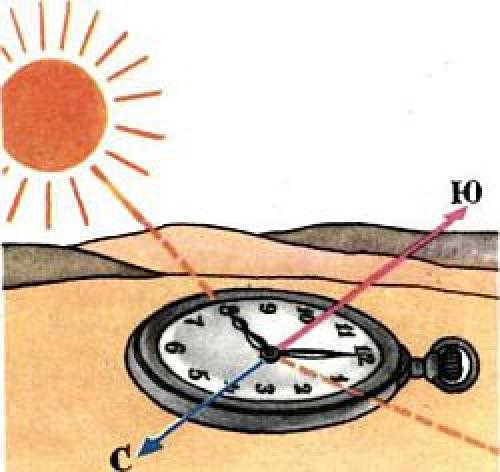

In this situation, the left side will indicate the west, while the right side will indicate the east. In the southern hemisphere, the opposite is true. The shadow will be cast to the south, and the west and east will be on the left and right sides respectively. If you place a watch on a flat surface and rotate it until the hour hand is pointing directly at the sun, then mentally draw a straight line from the center of the dial to the number 1 (13 hours), the angle formed by this line and the hour hand will be bisected by a line that runs from north to south (see illustration). In this scenario, before 12 noon, the south will be to the right of the sun, and after twelve o’clock – to the left.
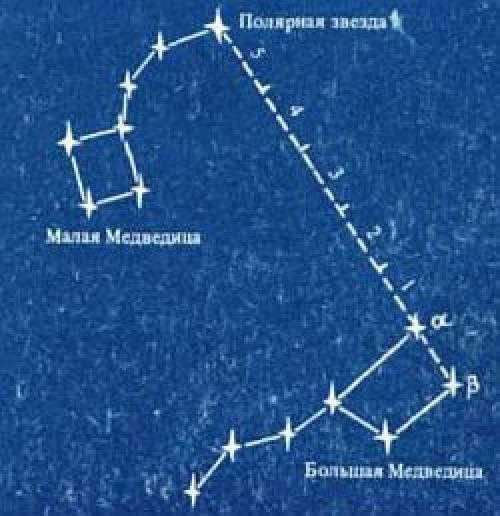
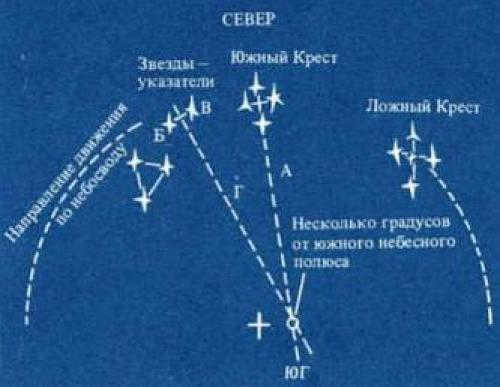
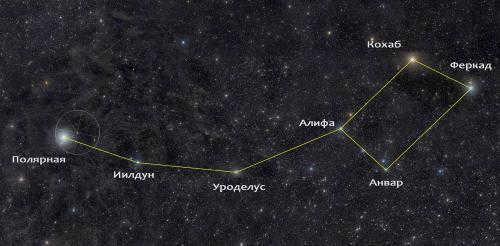
When navigating at night in the northern hemisphere, the easiest way to find your bearings is by locating Polaris, which is situated above the North Pole. The constellation Big Dipper can help you locate Polaris in the night sky, as it has a distinct shape resembling a large bucket with a handle. To locate Polaris, you can draw an imaginary straight line through the two outermost stars of the Big Dipper’s ladle. If you measure the distance between these stars and extend it five times along the line, you will eventually reach a bright star – this is Polaris (see diagram). In the southern hemisphere, navigation is typically done using the constellation Southern Cross, which consists of four bright stars arranged in the shape of a cross.
The direction and orientation to the south can be determined by line A, which is mentally drawn through the long axis of the Cross. In order to obtain a more precise determination of the celestial South Pole, two pointer stars that are located to the left of the Southern Cross can be utilized. By connecting these stars with an imaginary line B-B through the middle of the Cross and then drawing a perpendicular line D, one can extend it until it intersects with line A. The point of intersection is located close to the South Pole (refer to the figure). It is important to note that the true Southern Cross is sometimes mistaken for the false cross. The stars of the false cross are not as bright and are positioned further apart.
Identify the sides of the horizon using the sun and stars. Discovering the Directions of the Skyline
In various challenging situations, it is crucial for an individual to have the ability to navigate the terrain and have a basic understanding of where to go. In order to do this, one must first accurately determine the cardinal directions, especially finding the north. There are multiple methods for determining the directions, with the most well-known being the use of a compass.
However, it is important to note that not everyone may have access to a compass at all times. As a result, it is essential to be familiar with alternative techniques for determining the directions without a compass, such as using the sun, clocks, stars, the moon, and natural markers for orientation.
Method No. 1: Finding north using the North Star.
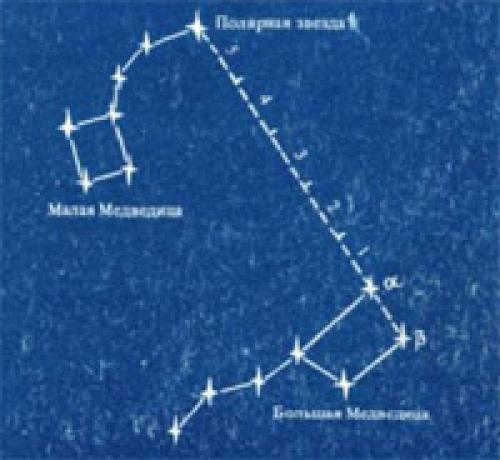
1). Locate the Big Dipper constellation in the night sky.
2). Extend the distance between the two outermost stars in a straight line towards the Little Dipper constellation. Extend it five times to reach the last star in the Little Dipper’s tail. This star is known as Polaris, which can be used as a reference point to determine the direction of north by mentally drawing a plumb line to the Earth.
Discovering the directions of the horizon using the sun and stars.
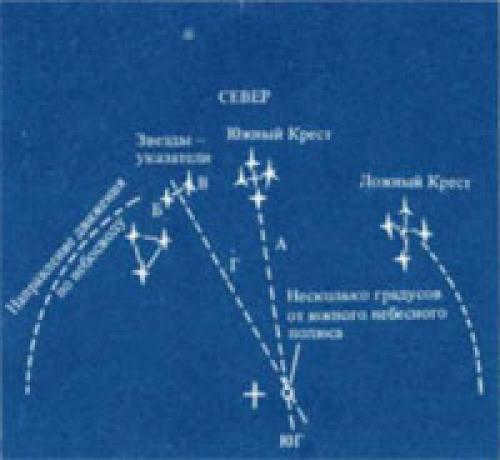
Method No. 2: Finding the sides of the world by observing the constellation of the Southern Cross.
This technique is applicable for determining directions in the southern hemisphere. The Southern Cross constellation is made up of four bright stars arranged in the shape of a cross. To accurately determine the South direction, draw a straight line through the two stars on the left side of the Southern Cross. The point where this line intersects with a line drawn back from the Southern Cross will indicate the direction South.
Determining the directions of the world using the Southern Cross constellation
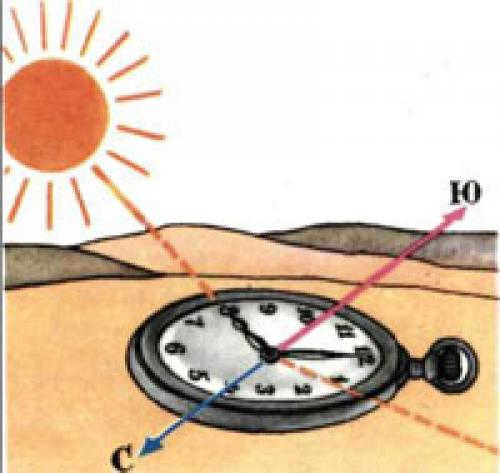
Method #3. Determining the directions of the world using the Sun and a clock.
In sunny weather, it is possible to determine the sides of the world with the help of a clock. To do this, position the clock so that the hour hand points towards the Sun. Divide the angle between the hour hand and 12 o’clock in half, and the line that divides this angle will point towards the South. Before 12 o’clock, the South will be on the right side of the Sun, and after 12 o’clock, it will be on the left. This method is suitable for determining direction during the day, specifically from 6 am to 6 pm.
During the summer months, several regions in the country adjust their clocks by one hour, causing noon to occur at 13:00. This means that the angle between the hour hand and the number 1 is measured to determine the time. In the USSR and later in Russia, a decree was implemented to advance the time by one hour, resulting in noon occurring at 14:00 during the summer. Consequently, the angle pointing to the South is now measured between the hour hand and the number 2.

Determining the sides of the world by using the position of the Sun and stars.
If you want to learn more, you can find additional information here.
Method #4. Determining the sides of the world by using the position of the Moon and clock.
The directions of the sides of the world by using the position of the Moon can be determined in the same way as with the Sun. However, it is necessary to first determine the time when the Sun will be in the same direction as the Moon. To determine the sides of the world, follow these steps:
1). Divide the radius of the Moon’s disk into six equal parts and determine how many of these parts are visible.
3). It is necessary to mark the obtained number on the dial and align it with the direction towards the Moon. The line that divides the angle between number 1 (in winter) or number 2 (in summer) and the direction to the Moon will indicate the South direction.
How to find the geographic latitude of any place? How to determine the latitude of any object?
You can determine the latitude and longitude on a map by looking at the parallel on which the object is marked. If it is not indicated, you can calculate the distance between the neighboring lines and find the degree of the parallel you are looking for.
At the equator, the geographic latitude is 0°. Points that lie on the same parallel will possess identical latitude. When observing a map, this is evident by the lines that run horizontally across the frame. On a globe, the parallels intersect with the 0° and 180° meridians. It’s important to note that geographic latitudes range from 0° up to 90° at the poles.
Ways to Determine Latitude and Longitude. Finding the Precise Geographic Coordinate Values
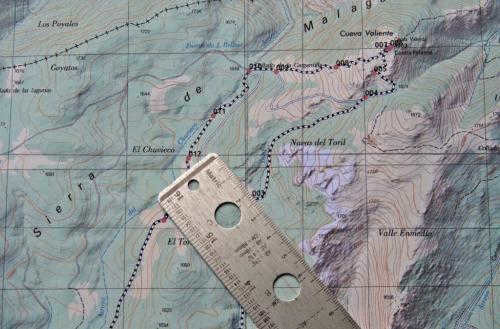

If you want to determine the precise latitude and longitude of a point with an accuracy greater than 0.5 degrees, there are a few steps you can take. First, you’ll need to determine the scale of the map you’re using. Most maps have a scale bar in one of the corners, which indicates the relationship between distances on the map and distances in geographic coordinates and kilometers on the ground.
Once you’ve located the scale bar, you can use a simple ruler with millimeter divisions to measure the distance on the scale bar. For example, let’s say that 50 mm corresponds to 1 degree of latitude and 40 mm corresponds to 1 degree of longitude.
Longitude can be determined by following similar steps. To start, place a ruler parallel to the latitude lines and measure the distance from the chosen point on the map to the nearest meridian. Let’s assume this distance is 10 mm to the meridian of 67° west longitude. Using the rules of proportion, we can calculate that the longitude of the object is -67.25° (the negative sign indicates west longitude).
Discovering the latitude of a location. Tip 5: Unveiling the geographic latitude
Having knowledge of the geographic latitude of your residence can prove to be extremely beneficial. Even though modern navigation devices can effortlessly pinpoint your exact coordinates, mastering traditional navigation methods remains significant and captivating.
- Basic knowledge of astronomy, plus:
- – two wooden rails,
- – a screw and nut,
- – a protractor.
In order to calculate the geographic latitude of a location, you will need to create a simple protractor.
Take two rectangular wooden rails that are one and a half to two meters long and attach their ends together using a hinge mechanism. Insert one end of the hinge into the ground and ensure it is vertically aligned using a plumb line. The second rail should move smoothly on the hinge, which can be created using a screw and nut.
This initial setup should be done during the daytime, before it gets dark. Of course, the weather should be clear enough to allow for observation of the night sky.
As the evening approaches, step outside and locate Polaris in the night sky.
To find this star, first locate the constellation known as Ursa Major, or the Great Bear. To do this, face north and look for the seven stars that form the shape of a large dipper. This constellation is usually fairly easy to spot.
Now, visualize a line extending through the two outermost stars of the dipper, pointing towards the socket. Then, mentally measure five equal segments along this line, using the distance between the two stars as a guide.
You will come across a bright star that serves as Polaris. Just make sure you are not mistaken: the star you find should mark the end of the smaller dipper, which is part of the constellation Ursa Minor, or the Little Bear.
Do the equatorial coordinates of the star change throughout the day? Determining geographical coordinates using stars.
I’m sure you’re familiar with geographical coordinates and how the height of the North Star above the horizon is approximately equal to the latitude of the observation point. More precisely, it is the height of the celestial pole, as the North Star is not exactly at the North Pole, but rather about a degree away from it. Therefore, measuring the height of the celestial pole is sufficient for determining latitude. Let’s take another look at a passage from the book “Mysterious Island”.
Cyrez Smith came back to the Pipes. Using the light from the hearth, he shaped two small polished planks and connected them at the ends to create a circular object with movable legs. He used a thick acacia thorn he found in the brushwood to secure them together.
In the southern part of the sky, the horizon line was clearly visible, illuminated from beneath by the moon’s first rays. It could be accurately determined. At this moment, the southern cross constellation appeared to be upside down to the observer, with the alpha star located at the base of the constellation, closer to the south pole.
This particular constellation is not in as close proximity to the Antarctic pole as Polaris is to the Arctic pole. The primary star, alpha, is approximately twenty-seven degrees away from it. Cyrus Smith was aware of this fact and had to factor in this distance when making his calculations. Additionally, the engineer observed this star as it crossed the lower meridian, which greatly aided in the calculations.
To determine the angular distance of alpha from the horizon, Cyrus Smith aligned one leg of his circular instrument with the sea horizon and the other with the star alpha. He then measured the distance between them to fix the angle. To ensure accuracy, he secured both legs of the instrument to a third cross-board using acacia thorns, firmly anchoring the distance between them.
After completing this task, the only thing left to do was to calculate the aforementioned angle, while also considering the altitude adjustment and the change in the horizon’s position. In order to accomplish this, it was essential to ascertain the elevation of the plateau. The resulting angle will provide the height of star Alpha, and thus, the position of the pole above the horizon – which represents the latitude of the island, as the latitude of any location on the globe is always equivalent to the height of the pole above the horizon at that particular point.
Here, the author has also made an error – during this time of the year (the events described occur in April), the Southern Cross is actually in its upper culmination around midnight, not in its lower culmination. This means that it crosses the meridian above the pole, and the altitude of the alpha star exceeds 60°. However, the main issue here is that using an “Angle Measuring Instrument” like this would require one to be a chameleon, since such a large angle cannot be accurately visualized by hand. The device would need to be mounted on a tripod at the very least. By the way, it would be much simpler and more precise to measure the zenith distance of the star (the vertical direction does not need to be visualized and can be easily obtained with a plumb bob) rather than its height above the horizon.
As in the previous study, let’s calculate the altitude of the sun – this time at midday, when the shadow of the gnomon aligns with the midday line (by the way, make a note of the exact time of midday – it will come in handy later.
Now the primary challenge in determining latitude is obtaining the sun’s declination at the time of observation, preferably without the use of a computer (considering we are on a deserted island). I believe even the extraordinary memory of Sayres Smith won’t be of assistance here; we’ll have to calculate this value, but – without any calculations!
We are aware that the angle of the sun’s position changes from -23.5° to 23.5°. This variation is due to the Earth’s axial tilt and the latitude of the tropics. These values are important to remember, even if we find ourselves on a deserted island. To simplify the problem, let’s assume that the sun moves uniformly along the ecliptic. In this case, we can approximate the sun’s angle using the following formula.
D represents the number of days that have passed since the vernal equinox.
We can also represent this graphically:
Create a circle with a radius of 23.5 units (the specific unit of measurement doesn’t matter – it could be a matchstick, for example, if we were drawing on sand). Divide the circle into 12 equal parts to represent the months, with each part representing an interval of 30.5 days. Now, mark the date of our observations on the circle, taking into account the horizontal axis as the line of equinoxes (March 21 and September 22), and the vertical axis as the solstices (June 22 and December 22). It’s best to mark the date closest to these points to minimize errors. The projection of the marked point on the vertical axis will give us the value of the sun’s declination. To measure it accurately, we can use our “Length Standard” – a matchstick. This simple construction ensures that we can determine the declination with an accuracy of no worse than 1/2 degree.
The determination of latitude using the sun is a common method.
By analyzing the figure, we can easily calculate the latitude of the observation point.
The declination of the sun (O) and the height of the sun above the horizon (h) are the key factors in this calculation.
Now let’s focus on the topic of longitude. In order to do so, we must consider the element of time. Fortunately, in contrast to the Julvern XIX century, accurate clocks are now quite common. Therefore, we can assume that we have access to the current time with an error margin of no more than thirty seconds. Our task at hand appears to be relatively straightforward – longitude, when measured in hours, is simply the difference between the local time and Greenwich time. The only remaining challenge is to determine the exact Greenwich time. However, since we determine the moment of noon based on the position of the sun (also known as true solar time), it is imperative that our Greenwich time also aligns with true solar time. It is worth noting that our clocks display mean solar time, which slightly differs from true solar time due to the sun’s uneven movement along the ecliptic and the slight variation in day length throughout the year. This inconsistency can be quite inconvenient for timekeeping purposes. To address this issue, a concept known as “Uniform” mean solar time has been adopted. This system is based on an imaginary point that moves perfectly uniformly along the celestial equator. The difference between mean solar time and true solar time can reach up to sixteen minutes and is referred to as the equation of time. In the next chapter, we will delve further into this topic. For now, let us assume that we are aware of this correction or that we are observing one of the four days where mean solar time coincides with true solar time – April 16th, June 14th, September 1st, and December 25th.
tm – The actual local time.
Tn – The average apparent time of the specific time zone.
A refers to the time of local noon.
(Longitude is considered positive when east of Greenwich).
In this formula, the time zone number is an integer that represents the number of hours the zone time differs from Greenwich time. For example, Moscow is in the second time zone, but in the 1930s, the “Decree” time was introduced, which is one hour ahead of the zone time. Additionally, during the summer, the clock is moved forward by one hour. As a result, the difference between Moscow and Greenwich time is 3 hours in winter and 4 hours in summer.
Now we can calculate the Greenwich true solar time and determine the geographical longitude of the observation location.
Now let’s reconsider how the characters in Jules Verne’s story acted:
– Is today April 15th, right?
– Yes, Mr. Sayres," answered the young man.
– If I’m not mistaken, tomorrow will be one of the four days in the year when true time coincides with mean time. In other words, my child, tomorrow the sun will pass the meridian a few seconds before noon. If the weather is good, I might be able to calculate the longitude of our island within a few degrees.
Cyrus Smith discovered a pristine, level patch of shore that had been carefully smoothed by the ebb and flow of the tide. The surface of the sand was so polished, it resembled a mirror, and each individual grain lay precisely next to one another, as if purposefully aligned. While it may not have been completely flat, the six-foot pole inserted into the sand was deliberately tilted slightly towards the south, opposite to the direction of the sun. This adjustment was necessary due to the fact that the inhabitants of Lincoln Island resided in the southern hemisphere, where daylight appeared above the northern horizon, rather than the southern.
Then Harbert realized how the engineer planned to determine the exact moment when the sun reached its highest point in the sky or passed through the imaginary line known as the meridian, which in other words, indicated the time of noon for that particular area. This method involved using the shadow cast by a stick on the sand. By carefully observing this shadow, Cyrese Smith could accurately determine the time without the need for any sophisticated instruments.
Indeed, as soon as the shadow reached its shortest length, it would be precisely twelve o’clock in the afternoon. All Smith had to do was monitor the shadow’s end and take note of when it started to lengthen again. By angling the pole towards the south, Smith could make the shadow larger and thus easier to track its changes. After all, the bigger the hand on a clock, the more noticeable its movement. In essence, the shadow of the pole on the sand served as the equivalent of a hand on a clock.
When the opportune moment arrived, Cyrese Smith knelt down and commenced marking the gradual decline of the shadow by inserting small twigs into the earth. The engineer’s comrades, bending low, observed this procedure with immense interest.
The journalist held his chronometer in his hand, ready to record its reading at the exact minute when the shadow would be at its shortest. The calculation was done on April 16, the day when the mean time coincides with the true time. Therefore, Gedeon Spelet’s watch readings had to correspond to the accurate Washington time, which greatly simplified the calculations.
In the meantime, the sun was slowly traversing the sky. The shadow of the stick was becoming shorter and shorter. However, it appeared to the engineer that it was starting to lengthen again, and he inquired:
– ‘Five hours and one minute,’ Spilett replied immediately.
Now the only thing left to do was to make the calculation. It was quite simple. The time difference between Washington and Lincoln’s Island was, approximately, five hours – in other words, when it was noon on Lincoln’s Island, it was already five o’clock in the evening in Washington. The sun, in its apparent motion around the earth, moves one degree in four minutes, or fifteen degrees in an hour. Fifteen degrees multiplied by five is seventy-five degrees.
Therefore, if Washington is located at 77°3’11”, or approximately seventy-seven degrees from the Greenwich meridian, which is considered zero by both Americans and English, it can be concluded that Lincoln’s Island is 77°75° West of Greenwich, which is equivalent to 152° West longitude.
M – Yes. While all the reasoning and calculations are impeccable, the practical observations in this case are rather unsatisfactory. The rate at which the length of the shadow changes around noon is quite slow, making it difficult to accurately determine the moment when it becomes the shortest. There is a likelihood of an error margin of about 10-15 minutes. Additionally, the inclination of the gnomon “on the Eye” and the possibility of the site not being perfectly horizontal will introduce further inaccuracies in the measurements. What is even more frustrating is that the engineer had previously established the direction of the meridian, but for some inexplicable reason, did not utilize it in determining the exact moment of noon.
Let’s attempt to approximate the accuracy of the result we obtained. We can assume that the error in observing the gnomon shadow in terms of angular measurement is no more than 1/2°. This error is due to the indistinctness of the shadow and is approximately equivalent to the errors in gnomon installation (deviation from vertical and site from horizontal surface), as well as errors in our geometric constructions for determining the sun’s declination and height, which add another 1/2°. Therefore, the total error, which has the unfortunate property of accumulating, can reach one and a half degrees. When determining longitude, errors are only caused by observations with the gnomon and the error in our clock. If we know the time to the nearest half minute, which is equivalent to 1/8° in angular units, the total error can be about 1° 8′ of arc. To estimate these values in terms of distance, we must remember that 1 nautical mile (1852 m) is equal to the average length of the meridian arc of 1 arc minute. This means that the deviation of the coordinates we determined from the true coordinates will not exceed 90 miles in latitude and 68 miles in longitude. Additionally, considering that we are not on the equator (the arc length in 1′ parallel decreases with increasing latitude), the longitude error can be noticeably less.
Stars’ Coordinates. Horizontal Coordinate System
Displays the positions of stars and other celestial objects in the “here and now” mode relative to the horizon. The first coordinate represents the elevation of the object above the horizon. It is measured in degrees. The maximum value is +90° (zenith). Celestial bodies located on the horizon have a coordinate value of zero. On the other hand, objects located at the nadir point or directly below the observer have a minimum elevation of -90° – which is the zenith.
The second parameter is the azimuth, which represents the angle between the horizontal lines pointing to the object and the north. This coordinate system is also known as topocentric due to its association with a specific location on the earth’s surface.
However, this system is not without its limitations. Both coordinates for each star in this system change every second, making it less suitable for accurately describing the positions of stars within constellations.
What is the declination of stars? Positive or negative declination (astronomy)
The declination (δ) in astronomy is one of the two coordinates used in the equatorial coordinate system. It represents the angular distance on the celestial sphere from the plane of the celestial equator to the star and is typically measured in degrees, minutes, and seconds of arc. The declination is considered positive when it is located north of the celestial equator and negative when it is located south of it.
- An object located on the celestial equator has a declination of 0°
- The declination of the north pole of the celestial sphere is +90°
- The declination of the south pole is -90°
Declination always carries a sign, even if it is positive.
In the northern hemisphere of the Earth, celestial objects with a declination δ greater than 90° – φ do not go below the horizon, thus they are referred to as non-setting. In the southern hemisphere of the Earth, celestial objects with a declination δ greater than 90° + φ (where φ is taken with a minus sign) are also non-setting.
Table of Star Coordinates. Sun Coordinates
The daily change in the Sun’s declination d® is 0.4° during the month before and after the vernal and autumnal equinoxes, and 0.1° during the month before and after the summer and winter solstices. During the second month after the dates of 21.03, 22.06, 23.09, and 22.12, the change is -0.3°. The daily variation in the direct sunrise a® is 1° throughout the year. The precise coordinates can be obtained from the Nautical Astronomical Yearbook (MAE). These data can be used to approximate the meridional height H® of the Sun on a given date and latitude. To calculate this, we first determine d® for the given date and then find
For instance, let’s take December 25 as an example, where d® = 23.2° S in terms of latitude (f = 45.5° N; Z® = 45.5° – (- 23.2°) = 68.7°; H ® = 21.3°. It is a simple task to determine the dates when the polar day and night begin and end. In approximate terms, the beginning and end of the polar day can be determined by the condition d® = 90° – (f + 1°) when d® is the same as f, while the beginning and end of the polar night can be determined by the condition f® = 90° – (f-1°) when f® is different from f. By changing f by 1°, we can estimate the half-diameter of the Sun and the astronomical refraction. For example, at a latitude of 75°N, the polar day will begin and end at d® = 14° N, which means that it will start on May 1 and end on August 13. On the other hand, the polar night will last from November 7 to February 5.
What does Polaris mean? Overview


Polaris and its companions can be observed in this image taken by the Hubble Space Telescope.
Polaris, the most brilliant and nearest pulsating variable star of the Cepheus delta classification, has a period of 3.97 days. However, Polaris is an exceptionally atypical Cepheid: its pulsations diminish over a span of roughly several decades: in 1900, the fluctuation in brightness was approximately ±8%, whereas in 2005 it was around 2%. Furthermore, over this time period, the star has experienced an average increase in luminosity of 15%.
Polaris is actually a trinary star system. At the heart of the system lies the massive Polaris A (α UMi A), a supergiant star that shines 2000 times brighter than our Sun and boasts a mass 4.5 times greater than our Sun. Polaris B (α UMi B), with a mass of 1.39 solar masses, is situated at a considerable distance from Polaris A, making it easily observable even from Earth’s surface using telescopes. In 1929, an analysis of Polaris’s spectrum revealed that Alpha Ursae Minoris is in fact a binary star, confirming earlier observations made in 1924 (Moore, J. H and Kholodovsky, E. A.). Polaris A’s companion is located at a distance of 18.5 astronomical units. Meanwhile, Polaris P (α UMi P or α UMi a or α UMi Ab), with a mass of 1.26 solar masses, is positioned so close to the supergiant star that it could only be captured on camera by the Hubble Space Telescope after the equipment was reconfigured. The approximate orbital period of Polaris P around α UMi A is about 30 years. Polaris B, on the other hand, completes its orbit around the α UMi A/P binary system in approximately 100,000 years. Additionally, there are two other distant components designated α UMi C and α UMi D, but these stars are much older and are not physically connected to Polaris.
The variation of Polaris from the north point. Characteristics of Polaris and important legends
Prior to searching for Polaris, it is important to familiarize oneself with its key characteristics. This will not only aid in locating it more quickly in the night sky, where there are no labels indicating star names or constellation boundaries, but also prevent common errors. Additionally, there are several misconceptions surrounding Polaris. Therefore, people tend to be mistaken about the following:
Polaris is positioned directly above the Earth’s North Pole on the celestial sphere, hence its name “Polaris”. However, it is not directly overhead, as it would not be able to indicate north from that position. Interestingly, Polaris can only be seen in the middle of the sky when observed from the North Pole. As one moves farther away from the pole, the star gradually descends towards the horizon until it becomes completely hidden from view at the equator. This means that Polaris cannot be used as a reference point in the southern half of the planet, where the direction is determined by the Southern Cross constellation.
How to locate equatorial coordinates. Equatorial coordinates
The equatorial coordinate system is a well-known method for locating celestial objects. In this system, the primary plane is the celestial equator. One of the key coordinates used in this system is known as declination δ (sometimes referred to as polar distance p).
Another important coordinate that can be used is:
- hour angle t (in the first equatorial coordinate system)
- right ascension (in the second equatorial coordinate system).
- The angle between the plane of the celestial equator and the direction to the luminary is known as the declination δ of a luminary. It can also be defined as the arc of the celestial meridian from the celestial equator to the luminary.
Declination is measured between 0 ° and 90 ° on both sides.
- The angle between the north pole of the world and the direction to the luminary is known as the polar distance p of a luminary. It can also be defined as the arc of the declination circle from the north pole of the world to the luminary.
Polar distances are measured between 0 ° and 180 ° in the direction from the north pole of the world to the south pole.
- The hour angle t of a luminary is the distance along the celestial equator from the point where it intersects with the celestial meridian to the circle of declination of the luminary.
Hour angles are measured in the direction of the daily rotation of the celestial sphere, which is westward from the point where the celestial equator intersects with the celestial meridian. The range of hour angles is from 0° to 360° (in degrees) or from 0h to 24h (in hours). Sometimes, hour angles are measured from 0° to 180° (0h to 12h) to the west and from 0° to -180° (0h to -12h) to the east.
Another equatorial coordinate system
In this alternative system, similar to the previous equatorial system, the primary plane remains the celestial equator, and one of the coordinates is represented by (δ) (less commonly, the polar distance p). However, the second coordinate -(α)- is now defined as the arc along the celestial equator from the point of vernal equinox to the declination circle of the celestial body, or the angle formed between the direction towards the point of vernal equinox and the plane of the declination circle of the celestial body. Thus, the reference point is set at the location where the Sun intersects the vernal equator (known as the point of the vernal equinox). This angle is measured in the eastern direction relative to the apparent position of the Sun’s center, which is opposite to the rotation of the celestial sphere, along the celestial equator, and ranges from 0 ° to 360 ° (in degrees) or from 0h to 24h (in hours).
Characteristics of celestial declination
- Celestial declination is measured in degrees. A positive declination indicates a position north of the celestial equator, while a negative declination indicates a position south of the celestial equator.
- An object located on the celestial equator has a declination of 0°.
- The declination of the north pole of the celestial sphere is +90°.
- The declination of the south pole is -90°.
- The declination of a celestial object that passes through a specific point is equal to the angular distance from the celestial equator to that point.
In the Northern Hemisphere of the Earth, for a given latitude φ:
As the position of the celestial equator gradually changes, the equatorial coordinate system is always referenced to the principal plane and the direction to the vernal equinox.
Table of Equatorial Coordinates of Stars. Equatorial Coordinates and Star Chart
In order to locate stars in the night sky, create star charts, and determine time and geographic coordinates, it is essential to have knowledge of the coordinates of the stars.
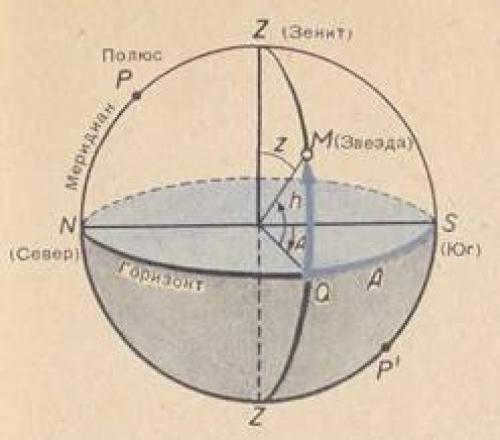
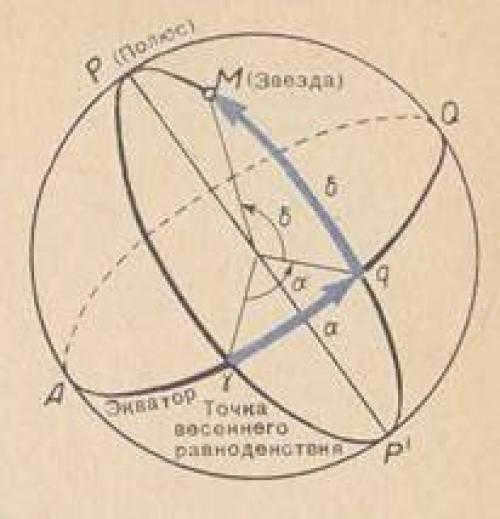
Figure 38 – Coordinate Systems. On the left – with respect to the horizon; altitude h and azimuth A; on the right – with respect to the celestial equator: right ascension Alpha and declination Delta.
The second geographical coordinate on Earth is known as longitude, which represents the angle between the plane of the initial meridian and the meridian plane of a specific location. In the celestial sphere, the second coordinate is referred to as right ascension, which measures the angle between the plane of a semicircle drawn from the world’s pole through a celestial body (known as the circle of declination), and the plane of a semicircle drawn from the world’s pole through the vernal equinox point on the equator (known as the initial circle of declination). This point is called the vernal equinox because it is the location on the celestial sphere where the Sun is positioned on March 21, when the length of the day equals the length of the night. The right ascension, denoted as Alpha, is measured counterclockwise from the vernal equinox, following the diurnal rotation of the sky. Both geographical longitude and right ascension are commonly expressed in units of time, rather than degrees, taking advantage of the fact that the Earth and the sky appear to make one complete revolution around their axis in 24 hours. This allows for the following ratio to be derived:

As an illustration, the geographical longitude, or right ascension, of 3 h 10 min 20 sec can be computed as 47°35'00". It is quite simple to comprehend that stars reach their highest point successively in the order of increasing right ascension.
Equatorial coordinates, also known as declination and right ascension (Alpha and Delta), remain constant for stars unless high accuracy is needed, as they change slowly over time. The vernal equinox point also shifts as the starry sky rotates on a daily basis. Consequently, the positions of stars in relation to the equator and the vernal equinox are independent of the observer’s location or the time of day. Appendix IV provides a compilation of the Alpha and Delta coordinates of several prominent stars. This same coordinate grid is displayed on the interactive star map. Unlike stars, the Sun, Moon, and planets are constantly in motion relative to the background of stars. As a result, their positions are not included on the map, but their coordinates for each day of the year can be found in specialized astronomical calendars.
1. Find out the star coordinates:
2. Identify the stars based on the approximate coordinates:
3. Determine the equatorial coordinates and the constellations they belong to:
| 1) Fall equinox point | A) α = 6h, δ = 23°, Gemini |
| 2) Winter solstice point | B) α = 18h, δ = 23°, Sagittarius |
| C) α = 12h, δ = 0°, Virgo | |
| D) α = 24h, δ = 0°, Pisces |
1. Find out the star coordinates:
2. Identify the stars based on the approximate coordinates:
3. Find the equatorial coordinates and identify the constellations in which they are situated
Related
Add a comment Cancel reply

- RECENT ARTICLES
- All school graduates on May 21, 2023
- Space gate of our planet on May 21, 2023
- Physics. 8th grade. Section – mechanics. Game “find a pair” on May 15, 2023
- Funny pictures for kids (13)
- Video for kids (8)
- UPR (5)
- Dates and Events in Astronomy (12)
- For students (384)
- Tickets (6)
- Distance Learning (159)
- 10th grade (65)
- 11th grade (56)
- 8th grade (16)
- 9th grade (22)
- Didactic materials (60)
- Tests (31)
- Astronomy (49)
- Biology (1)
- Geography (1)
- Environment (15)
- Technology (1)
- Physics (180)
- Pedagogical projects (2)
- Social Projects (3)
- Management projects (1)
- Educational projects (59)
- If the luminary’s declination is less than the geographic latitude, it reaches its highest point to the south of the zenith, at z = φ – δ or at an altitude of h = 90 – φ + δ
- If the luminary’s declination is equal to the geographic latitude, it reaches its highest point directly at the zenith, with z = 0 and h = +90
- If the luminary’s declination is greater than the geographic latitude, it reaches its highest point to the north of the zenith, at z = s – φ or at an altitude of h = 90 + φ – s
METHODIST.SITE © 2023
All rights reserved. Reproduction of materials is only permitted with the mandatory indication of a direct, active, and open-to-indexing hyperlink to metodist.site.
Privacy Policy.
Scientists, who are actively involved in the study of space and the sky, have come to the conclusion that everything in our surroundings is constantly moving. The fascinating history of the development of coordinates and their systems dates back to ancient times. It is clear that the establishment of coordinate systems was driven by the necessity to navigate through unknown terrains and comprehend the intricate structure of the celestial surface.

Sky above the clouds
To determine the position and motion of celestial objects, humanity has developed various methods and techniques. Additionally, unique numerical and symbolic notations have been created. In reality, there are multiple systems that establish the coordinates of objects. The primary differences lie in the selection of the primary plane and the reference point. Since we perceive the sky as a sphere when observing from Earth, astronomical coordinates are also spherical. Furthermore, they represent specific arcs of circles on the sphere. It is important to note that these coordinates are calculated in degrees, and sometimes in hours.
System of Horizontal Coordinates
The primary plane in this system is represented by the mathematical horizon, while the zenith and nadir are the points at the poles. The horizontal coordinate system finds its application in terrestrial observations, whether they are conducted with the naked eye or through the lens of a telescope. Its purpose lies in observing celestial bodies, including stars, and tracking their motion across the sky. Naturally, this system is employed within the confines of the solar system.

The horizontal coordinate system is a method used for observing and measuring the motion of celestial bodies, which is constantly changing.
Definitions in the coordinate system
A plumb line refers to a straight line that passes through the center of the sky and corresponds to the direction of the plumb line relative to the observer’s position. This line intersects vertically with the center of the planet and the observer’s location.
Zenith and nadir are two opposite points in the coordinate system. The zenith is the point where the plumb line intersects with the sky directly above the observer’s head. On the other hand, the nadir is the point diametrically opposite to the zenith.
The mathematical boundary of the sky is the celestial equator, which is a circle on the celestial sphere. It is perpendicular to the vertical line and cuts the entire sky into two equal parts: the visible and the invisible. The visible part of the sky, with its highest point at the zenith, is the portion that can be seen by an observer. On the other hand, the invisible part, with its lowest point at the nadir, is the portion that cannot be seen.
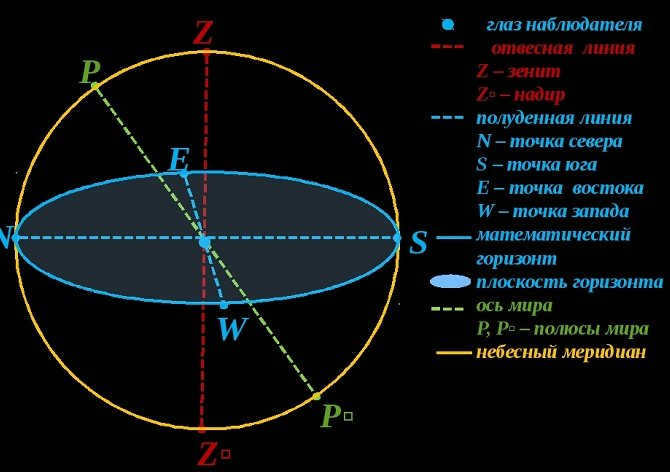
Calculating the coordinates of stars
Simultaneously, the mathematical horizon does not align with the observable horizon. This is due to two reasons. Firstly, the Earth’s surface is uneven, resulting in varying observation points. Secondly, the curvature of light rays in our planet’s atmosphere.
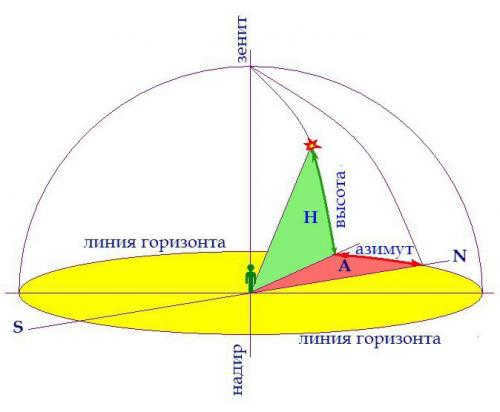
When it comes to astronomy, there are three main horizontal coordinates to consider: altitude, zenith distance, and azimuth. The altitude of a luminary refers to the angle between its position in the sky and the mathematical horizon. This measurement ranges from 0° to +90° when measured from the horizon to the zenith, and from 0° to -90° when measured from the horizon to the nadir. Another important coordinate is the zenith distance, which is the angle between the zenith and the luminary. This measurement ranges from 0° to 180°. Finally, azimuth is the angle between the southern point of the horizon and the vertical line passing through the luminary. This measurement is counted in the direction of the daily rotation of the celestial sphere, ranging from 0° to 360°, with the western direction being the reference point.
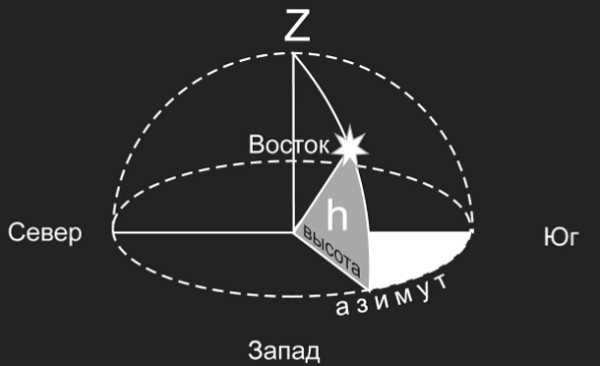
Azimuth
Independent work on Astronomy “Celestial coordinates and star maps”
Independent work №2 “Celestial coordinates and star maps”
Variant1
.
What is a constellation?
A
.. A group of stars that are physically related to each other, such as having the
the same origin. Б
. A group of bright stars located close together in space
. A constellation refers to a region of the sky within some defined boundaries.
Decode the entry Regulus (α of Leo)
Find on a star chart and name the object with coordinates: α = 15h 12m, δ = – 90.
Determine which constellations are fully visible at midnight on January 1.
midnight on January 1. Which constellations are rising, setting constellations at this time.
Independent work “Celestial coordinates and star maps”
Option2
.
The brightest stars were referred to as first magnitude stars, while the dimmest stars were referred to as sixth magnitude stars.
By how many times are the 1st magnitude stars brighter than the 6th magnitude stars? Select the correct option:
A. 100 times.
B
B. By a factor of 50.
B
C. By a factor of 25.
Decipher the notation Deneb (α Swan).
Locate on the star map and name the object with coordinates: α =3h 40m, δ = +480.
Determine which constellations are fully visible at midnight on February 1.
Which constellations are rising and setting constellations at this time?
Independent work “Celestial coordinates and star maps”
Option3
.
What is the celestial sphere?
A
. The earth’s surface bounded by the horizon line.
. An imaginary spherical surface of arbitrary radius used to study the positions and motions of the celestial luminaries. B
. An imaginary line that touches the surface of the globe at the observer’s location.
Decipher the entry Algol (β Perseus)
Find on a star chart and name the object that has coordinates: α=10h 08m , δ=+11°57′.
Identify the constellations that are fully visible at midnight on March 1.
At midnight on March 1, we can observe which constellations are rising and setting at this time.
For my independent work, I have chosen the topic of “Celestial coordinates and star maps.”
Option 4
Let’s start by understanding what is meant by declination. Please select the correct statement from the following options:
A. Declination refers to the angular distance of a luminary from the celestial equator.
B. Declination refers to the angle between the horizon line and the luminary.
Now, let’s decode the entry for Polaris (α the Little Bear).
We also need to determine the equatorial coordinates of the star β Lyrae on a star chart.
To find out which constellations are fully visible at midnight on April 1, we can refer to a moving star map (MSCM).
At midnight on April 1, we can observe which constellations are rising and setting at this time.
Independent work “Celestial coordinates and star maps”
Option5.
1.
What is the definition of right ascension?
A
. The angle between the plane of the celestial meridian and the celestial equator.
What is the definition of declination?
. The angle between the noon line and the axis of apparent rotation of the celestial sphere.
What is the definition of celestial longitude?
. The angle between the planes of the great circles, one passing through the poles of the world and a given luminary, and the other through the poles of the world and the vernal equinox, lying on the equator.
What is the definition of celestial latitude?
. The angle between the plane of the celestial equator and the plane of the ecliptic, measured along the ecliptic.
Decipher the entry Mizar (ε the Big Dipper)
Determine from a star chart the equatorial coordinates of the star: α of the Big Dipper.
Determine from a moving star chart (MSCM) which constellations are fully visible at midnight on May 1.
midnight on May 1. Which constellations are appearing, disappearing constellations at this time.
Task: Celestial coordinates and star maps
Variant: 6.
Question: 1.
Where does the celestial equator cross the horizon line?
A
.At the points in the north and
.At the points east and west;
B
.At the points of zenith and nadir.
Decipher the entry Aldebaran (α of Taurus)
Find out from a star chart the equatorial coordinates of the following star: γ Orion
Find out from a moving star chart (MSCM) which constellations are fully visible at
midnight on June 1. What constellations are appearing, disappearing constellations at this time.
Independent work “Celestial coordinates and star maps”
Option7
.
Stellar magnitude is a characteristic that indicates:
A
.The size of a star
B
. The distance to a star
C
. The temperature of the star
D
. The brilliance of the star
Interpret the entry for Regulus (α of Leo)
In which constellation is the Moon located if its coordinates are: α =20h 30m , δ = -200
Determine which constellations are fully visible at midnight on July 1.
At midnight on July 1, which constellations are rising and which are setting at this time.
Independent work “Celestial coordinates and star maps”
Variant8
.
The best stars to see in the sky are of what magnitude: A. +6
B
. +1
C
. 0
D
. –1
E
.–6
Decipher the information about Sirius (α of the Big Dog)
Using a star chart, find out the equatorial coordinates of the star α Perseus.
Find out which constellations are fully visible at midnight on August 1 using a moving star chart (MSCM). Also, determine which constellations are rising and which are setting at this time.
Individual task “Celestial coordinates and star maps”
Variant9.
1.
How many stars in total can be observed in the sky during the day?
A
.About 2500.
B
.About 5000.
C
.About 10000.
Decipher the information about Arcturus (α of Volopassus)
Determine the constellations that are visible at midnight on September 1 using a mobile star chart (MSCM). Also, identify the constellations that are rising or setting at this time.
Independent project: Celestial coordinates and star maps
Option: 10
How many constellations are there in the sky?
A – 108
B – 68
C – 88
Find the meaning of the term Akrab (β Scorpius).
In which constellation can the galaxy M 31 be found, given its coordinates: α = 0h 40m, δ = + 410.
Determine the constellations that are fully visible at midnight on October 1 using the mobile star map (MSM).
What constellations are rising or setting at this time?
Individual assignment “Celestial coordinates and star maps”
Option11
.
The celestial coordinates of a star in the night sky are determined by:
A
.α – right ascension; δ – declination;
. α – longitude; δ – latitude; B .α – declinarity; δ – right ascension;
Г
.α – latitude; δ – longitude.
Decode the entry for Procyon (α of the Lesser Dog)
Determine on a star chart the equatorial coordinates of the following star: α Orion
Determine from a mobile star chart (MSCM) which constellations are fully visible at midnight on November 1.
Which constellations are rising and setting at this time.
Individual assignment “Celestial coordinates and star maps”
Option12.
1.
Who is credited with introducing the classification of stars based on their brightness and the concept of apparent stellar magnitude?
A. Aristotle;
B.
. Hipparchus;
C.
. Ptolemy
D.
. Bayer
Decipher the designation Mirach (β of Andromeda)
Determine the equatorial coordinates of the following star on a star chart: β Orion
Determine which constellations are fully visible at midnight on December 1.
Which constellations are rising or setting at midnight on December 1?
Independent work “Celestial coordinates and star maps”
Option13
.
Which astronomer first used Greek letters in descending order of brightness to label the prominent stars in each constellation? A.
Tycho Brahe;
B
. N. Copernicus;
V
. G.Galileo;
Decrypt the information about Hamal (α of Aries) on a star chart.
Find the equatorial coordinates of the star: α of the Lesser Dog.
Identify the constellations that are fully visible at 12 hours on January 1 using a moving star map (MSCM). Also, determine which constellations are rising and setting at this time.
Independent project “Celestial coordinates and star maps”
Option14.
1.
From any location on Earth’s surface, the naked eye can observe approximately:
A. 10,000 stars;
B
A. 3,000 stars;
V
A. 7,000 stars.
Decrypt the information about Spica (α of Virgo).
Determine the celestial coordinates of Arcturus (α Volopassus).
Determine what constellations are completely visible at 12:00 on February 1st.
At 12:00 on February 1st, which constellations are rising and setting at this time.
Independent task “Celestial coordinates and star maps”
Option15.
1.
The angle that is measured from a point south of S along the horizon towards the vertical.
. Azimuth
Б
. Elevation
В
. Hour angle
Г
. Declination
Decipher the entry for Rigel (β of Orion).
Determine the equatorial coordinates of the following star on a star chart: α Leo.
Determine which constellations are fully visible at 12:00 p.m. on March 1st using a moving star chart (MSCM).
At 12:00 p.m. on March 1st, which constellations are rising and setting at this time.
Independent work “Celestial coordinates and star maps”
Option16.
1.
The current position of the north pole of the Earth can be identified by several key factors:
A
It coincides with the position of the star Polaris.
B
It is located 1.5 degrees away from the star in the constellation of the Little Bear.
C
It is located near the brightest star in the entire sky, known as Sirius.
D
It is located in an area where there are no visible stars, making it detectable only with instruments.
Decode the entry for the star Altair, also known as Alpha of the Eagle.
Find the equatorial coordinates of the star Alpha Leo on a star chart.
Using a moving star chart (MSC), determine which constellations are fully visible at 12:00 p.m. on April 1.
At 12 hours on April 1, observe which constellations are rising and setting at this time.
Independent work “Celestial coordinates and star maps”
Option17
A certain area of the starry sky with clearly delineated limits, encompassing all the luminaries belonging to it and having its own is called ….
А
. Celestial sphere
. Galaxy
В
. Constellation
Г
. Group of stars
Decipher the entry Capella (α of Ascendant)
Determine on a star chart the equatorial coordinates of the following star: α Scorpius
Determine from the moving star map (MSK) which constellations are fully visible at
12 hours on May 1. Which constellations are rising, setting constellations at this time.
Independent work “Celestial coordinates and star maps”
Option18.
1.
Equatorial coordinates:
A
.Declination and right ascension;
B
.Latitude and longitude;
. Elevation and azimuth;
C
.Azimuth and right ascension;
D
.Latitude and declination.
Decode the entry for Castor (α Gemini)
Find the equatorial coordinates of the following star on a star chart: α of Eagle
Determine from a moving star map (MSCM) which constellations are fully visible at 12:00 p.m. on June 1.
At 12 hours on June 1, which constellations are rising and setting at this time.
Independent work “Celestial coordinates and star maps”
Option19
.
What is the definition of a constellation?
A
A constellation is a specific section of the celestial sphere that has well-defined boundaries.
B
A constellation is an arrangement of stars on the celestial sphere.
В
Constellations consist of bright stars.
Г
A constellation is a cluster of stars located in the northern hemisphere.
Д
A constellation is a cluster of stars that can be found at the equator.
Can you decipher the entry for Pollux (β Gemini)?
Using the map, determine which celestial body has coordinates α = 19h 29m, δ = +280.
Consult a moving star chart (MSCC) to find out which constellations are fully visible at 12h on July 1. Also, identify the constellations that are rising and setting at this time.
Assignment: “Celestial coordinates and star maps”
Option20.
1.
What term is used to describe the brightness of stars? 1. Visible stellar magnitude
2. The emission that can be seen with the naked eye. 3. The brightness or radiance of an object.
2;
A
. 1 and 2;
B
. Only 3;
C
. 2 and 3;
D
. Only 1
Decipher the information about Fomalhaut (the alpha star of the South Pisces).
Find out which star has the coordinates: alpha = 4h 31m, delta = +160 30′
Find out which constellations are fully visible at 12:00 on August 1 using a star chart.
At 12:00 on August 1, which constellations are rising and which constellations are setting?
Independent assignment “Celestial coordinates and star charts” Option 21.
To determine the view of the night sky on any chosen day and time for a specific location
.Atlas of the celestial sphere;
A
.An astronomical calendar;
B
.Telescope;
A portable representation of the celestial sky;
Д
A record of celestial bodies.
Decode the information for Bellatrix (γ of Orion)
Locate the star with the following coordinates on the star map: α =22h55m δ= -30°
Determine which constellations are fully visible at 12:00 p.m. on September 1.
At 12 hours on September 1, identify the constellations that are rising and setting at this time.
Individual assignment “Celestial coordinates and star maps” Variant
22.
1.
Stellar brightness
Vega
is equivalent to
0.03
and the stellar brightness of
Deneb
is
1.25
. Which of these
Decode the information for Mizar (ζ of the B. Bear )
Locate the star with the following coordinates on a star map: α =1h06m δ =+35°.
Determine which constellations are fully visible at 12:00 p.m. on October 1 according to the moving star chart (MSC). Also, identify which constellations are rising or setting at this specific time.
Independent Assignment: “Celestial Coordinates and Star Maps” Option
23.
1.
Which stars in the constellations are labeled with the letter α?
А
.The hottest;
Б
.The largest;
Decode the designation for Alderamin (α Cepheus).
Using a star chart, locate the star at the coordinates: α = 4h35m δ = +16°
Determine which constellations are fully visible at 12:00 p.m. on November 1 by referring to the moving star chart (MSC).
12 hours on November 1. Which constellations are rising or setting at this time.
Independent work “Celestial coordinates and star maps” Variant
24.
1.
What is the name of the brightest star in the sky?
A
. Altair;
B
. Polar;
C
. Sirius.
Decrypt the entry Benetnash (η of the Big Dipper)
Using a star map, locate the star with the given coordinates: α =14h50m δ =-16°-
Identify from the moving star map (MSK) the constellations that are fully visible at
12 hours on December 1. Which constellations are rising, and which are setting at this time.
The initial equatorial coordinate system
This system takes the surface of the celestial equator as a flat plane, and the reference point is denoted as Q. Moreover, the coordinates represent declination and hour angle. If you are curious about declination, you can learn more about it here. Hour angle refers to the arc between the celestial meridian and the declination circle, with measurements ranging from 0° to 360°. It is worth mentioning that the first equatorial coordinate system is utilized due to the continuous movement of our planet throughout the day. Therefore, the vernal equinox point serves as the starting point, as it remains fixed relative to the stars.
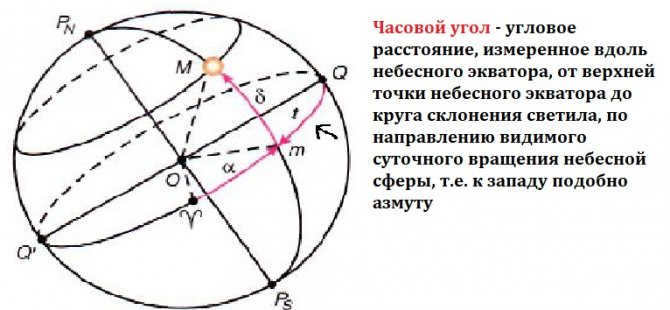
Hour angle
The second equatorial coordinate system
Interestingly, the primary plane and reference point of this system are similar to the previous one. However, the coordinates in this system are declination and right ascension. Specifically, right ascension represents the arc along the celestial equator, from the vernal equinox point to the celestial circle. Moreover, the measurement is done in hours. Nevertheless, it is counted in the opposite direction, clockwise. On the other hand, this second system of coordinates is characterized by constant star coordinates. Unlike the first system, their positions are not affected by the Earth’s movement during the day. This system is employed to determine the motion of celestial bodies over the course of a year.
It is crucial to understand that the coordinates can vary in every situation. As a result, numerous challenges arise. However, these challenges can be resolved by utilizing an appropriate system tailored to the specific circumstances. In general, different systems are frequently employed to tackle problems and establish coordinates. The introduction of coordinate systems enabled scientists to chart the vast expanse of the night sky and delineate the structure of the celestial realm. This breakthrough has significantly advanced the fields of astronomy and astrology. Furthermore, equatorial coordinate systems find application across various scientific disciplines.

The celestial canopy
Undoubtedly, the advancement and execution of specific systems establish the foundation of astral exploration. We strive to approach its comprehension as closely as conceivable. Naturally, the numerous techniques, computations, and methodologies presently in employment aid in the expansion of our perspectives.
1 Fundamental locations of the celestial sphere
In astronomy, the concept of the celestial sphere is introduced to determine the apparent position and motion of celestial bodies. This sphere has arbitrary dimensions and an arbitrary center. An observer is situated at the center point O, and the sphere rotates in sync with the celestial vault. A plumb line ZOZ’ is used to indicate the observer’s direction, regardless of their location. The point directly above the observer’s head, Z, is known as the Zenith, while its opposite point, Z’, is called the Nadir. The great circle SWNE, perpendicular to the plumb line, is referred to as the true or mathematical horizon. This horizon divides the sphere into two halves: one visible and one invisible to the observer. The line PP’ is the world axis, around which the celestial sphere rotates. The plane EQWQ’, perpendicular to the world axis, is the celestial equator. It divides the celestial sphere into the northern and southern hemispheres. The great circle PZQSP’Z’Q’N is known as the celestial meridian, which divides the celestial sphere into the Eastern and Western hemispheres. The NOS line is called the noon line.
The relative positions of the main components of the celestial sphere are influenced by the geographic latitude of the observer’s position. The world axis PP’ is inclined to the plane of the mathematical horizon. The positions of the celestial bodies in the sky are measured using celestial coordinates, which are two values (central angles or arcs of great circles) that quantify their positions in relation to the main planes, lines, and points of the celestial sphere.
2 The Horizontal Coordinate System
The primary plane of the horizontal coordinate system is the mathematical horizon NWSE, and counting is done from the Z zenith and from one of the points of the mathematical horizon. One coordinate is the zenith distance z (Zenith distance to the south zv = φ – δ; to the north zn = 180 – φ – δ) or the luminary’s height above the horizon h. The luminary’s altitude h is the height of the vertical circle mM from the mathematical horizon to the luminary, or the central angle mOM between the plane of the mathematical horizon and the direction to the luminary M. Altitudes are counted from 0 to 90 towards the zenith and from 0 to -90 towards the nadir. The zenith distance of a luminary is the arc of the vertical circle ZM from the luminary to the zenith. z + h = 90 (1). The position of the vertical circle is determined by the arc of the coordinate – azimuth A. Azimuth A is the arc of the mathematical horizon Sm from the south point S to the vertical circle passing through the luminary. Azimuths are counted in the direction of rotation of the celestial sphere, i.e. to the west of the southern point, in the range from 0 to 360. The coordinate system is used for direct determinations of the apparent positions of the luminaries using angular measuring instruments.
The starting point is known as the celestial equator Q. One of the coordinates is called declination. Declination refers to the arc mM that stretches from the celestial equator to the luminary along the hour circle PMmP′. It is measured from 0 to +90 towards the north pole and from 0 to -90 towards the south pole. p += 90. The position of the hour circle is determined by the hour angle t. The hour angle of the luminary M is the arc Qm that goes from the upper point Q of the celestial equator to the hour circle PMmP′, which passes through the luminary. Hour angles are measured in the direction of the diurnal rotation of the celestial sphere, west of Q within the range of 0 to 360 or 0 to 24 hours. This coordinate system is commonly used in practical astronomy to accurately determine the time and diurnal rotation of the sky. It is essential in calculating the daily movement of the Sun, Moon, and other celestial bodies.
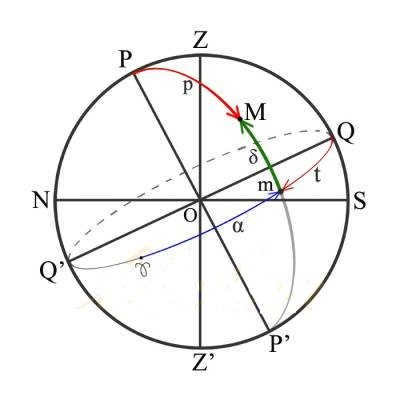
4 The second equatorial coordinate system
There are two coordinates in this system: declination and the right ascension α. The right ascension α of the star M is referred to as the arc of the celestial equator ♈m from the vernal equinox point ♈ to the hour circle passing through the star. It is measured in the opposite direction of the daily rotation within a range of 0 to 360 or 0 to 24 hours. This system is used to calculate star coordinates and create catalogs. It also determines the annual motion of the Sun and other stars.
5 Height of the celestial pole above the horizon, and the height of the star in the meridian
The height of the celestial pole above the horizon is always equal to the astronomical latitude of the observer’s location: