The Earth has an average weight of approximately 5.976 sextillion tons, a staggering number with 21 decimal places. Just visualizing such a figure can be overwhelming due to the multitude of zeros involved! However, determining the mass of our planet is far from a simple task, unlike weighing a watermelon. We cannot simply place the entire Earth on a scale! As a result, it took scientists many centuries to unravel the mystery and provide an answer to this perplexing question.
Exploring the Earth’s Parameters: A Brief History
In the early days of human civilization, various theories existed regarding the size, shape, and mass of the Earth. Ancient cultures conceived of the Earth as a hemisphere or a “flat plate” supported by three whales or a colossal turtle, forming the foundation of the universe’s pyramid. Alternatively, some believed that elephants upheld the Earth. Regardless, a prevailing belief in ancient times was that the Earth was flat and possessed an outer edge.
During the Middle Ages, there were significant advancements in understanding the shape and weight of the Earth. Giordano Bruno, who was ultimately executed by the Inquisition, was the first to discover that the Earth is spherical. Another important figure in Earth science was Magellan, who circumnavigated the globe and provided practical evidence supporting the theory of a round Earth.
Unveiling the Secrets of Earth’s Weight – Ancient Revelations
The Earth, being a tangible entity, possesses a multitude of distinctive characteristics, with weight being the foremost among them. This profound realization made by scholars from the medieval era has paved the way for a myriad of scientific breakthroughs and explorations. Hence, the question arises: how heavy is our planet? As per the principles of physics, weight represents the force exerted by a body upon a support. Nevertheless, the Earth lacks any physical form of support. Consequently, it can be inferred that the Earth does not possess weight. Nevertheless, it possesses an awe-inspiring attribute – mass!
What is the weight of the Earth in kilograms?
In an attempt to determine the Earth’s size, the Greek scientist Erastostosthenes conducted an innovative experiment. He measured the shadow of various cities in Greece using a stick and compared the results, which allowed him to derive a formula for calculating the Earth’s volume.
These pages provide information on:
The weight of a cloud
The weight of a tank
The weight of a brain
The weight of an egg
A Weight Calculator
Now it’s time to apply the formulas and compute the weight of our planet. The initial estimation of Earth’s mass was conducted by Dr. N. Makelin from Scotland in 1774. The outcome of his calculations suggested that the Earth weighed around 5.879 sextillion tons. However, this value has slightly increased to 5.976 sextillion tons.
The weight of the Earth is approximately 5.976 sextillion tons.
Nevertheless, these discrepancies do not imply any inaccuracies in the medieval scientist’s calculations. On the contrary, these measurements are remarkably precise, and the difference can be attributed to the continuous accumulation of cosmic dust, which contributes to the gradual increase in Earth’s mass. Each year, our planet becomes approximately 30,000 tons heavier!
By the way, you can easily calculate the weight of the Earth using the principle of gravity. All you need to do is hang a small weight on a thread and measure its precise position. Then, place a ton of lead next to it. The gravitational attraction between the two objects will cause the small weight to shift slightly to the side, by less than 0.00002 mm. Although this value is incredibly small, it can still be utilized to determine the mass of the Earth. All you have to do is measure the gravitational force exerted by the Earth on the weight, as well as the attractive force between the weight and the lead. By comparing the relative difference between these forces, it is possible to calculate the mass of the Earth.
Distribution of Earth’s Mass
It is common knowledge that the composition of our planet is diverse. Hence, presented below is an approximate breakdown of Earth’s total mass in descending order:
- The mantle, which consists of iron, calcium, and magnesium silicates, weighs approximately 4.043 x 10^24 kg.
- The core, made up of iron and nickel, has a mass of about 1.93 x 10^24 kg.
- The Earth’s crust, which serves as the habitat for humanity, accounts for 0.026 x 10^24 kg.
- The hydrosphere, encompassing the planet’s water bodies, contributes approximately 0.0014 x 10^24 kg.
- The atmosphere, weighing approximately 0.0000051 x 10^24 kg.
What is the weight of the Earth in comparison to other planets?
The Earth is the largest planet in the group of Earth-like planets. For instance, Mars weighs about 0.108 times the weight of the Earth, Venus weighs 0.815 times, and Mercury weighs 0.055 times.
However, the gas giant planets are much larger and have a similar weight to Earth. If we take Jupiter as a comparison, our planet is 317.8 times lighter, but it is still much heavier than any other planet in the solar system. To put it in perspective, Saturn is 95.1 times heavier than Earth, Neptune is 17.2 times heavier, and Uranus is 14.5 times heavier.
Now we have an understanding of the Earth’s weight and how it compares to the weight of other planets in the solar system.
What is the method for determining the weight of the Sun?
In our daily lives, the force of gravity between objects (aside from gravity itself) is intangible. Gravity, or gravitation, is overshadowed by other forces and is relatively insignificant. The perception of gravity’s strength is largely a result of the immense masses of celestial bodies like the Earth and other cosmic entities. However, it is only through delicate experiments that we can truly measure the attraction between smaller bodies.
The formula above can determine the value of the gravitational constant, denoted as G, where m1 and m2 are the masses of the small balls and r is the distance between them and the large balls.
By knowing the gravitational constant G and applying the law of gravitation, it is possible to calculate the mass of not only the Earth but also other celestial bodies. For instance, let’s assume that the mass of the Earth is represented by the variable M. Consequently, any object with a mass of t will experience an attractive force from the Earth, given by the expression:
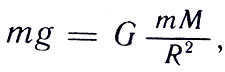
The mass of the Earth can be calculated by using the radius, denoted as R. Therefore, the equation for the mass of the Earth is
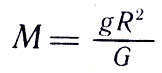
By substituting the given values of the variables into the equation, we can calculate
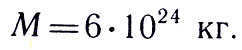
The Earth and the Moon rotate around a shared center of gravity C, situated within the Earth, in accordance with the law of gravitation. We can represent the distance from the Earth’s center to this point as x. By applying the principles of mechanics, we can derive the following relationship:
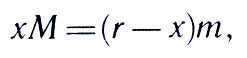
The mass of the Earth, denoted by M, can be calculated using the formula mentioned above. It takes into account the mass of the Moon (m) and the distance between the Earth and the Moon (r). The motion of the Earth around point C causes a change in the astronomical longitude of the Sun. Precise astronomical observations have determined that the value of x is equal to 4635 km. Therefore, the mass of the Earth can be accurately determined using this information.
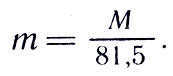
Once we have determined the mass of the Moon, we can move on to determining the mass of the Sun. Assume that there is a planet with a mass of t that has a satellite with a mass of m 1 . Let M represent the mass of the Sun, T represent the period of revolution of the planet around the Sun, and T 1 represent the period of revolution of the satellite around the planet. According to Kepler’s refined third law, we can conclude:
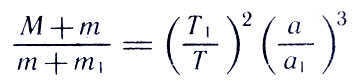
The equation can be rewritten as follows: a and a 1 represent the semi-major axes of the planet’s and the satellite’s orbits, respectively. Given that the mass of the Sun is significantly larger than that of the planet, and the mass of the satellite is even smaller than that of the planet, we can assume that the two masses are approximately equal.
Earth is an extraordinary planet in our solar system. It is not the tiniest, but it is also not the largest: it holds the fifth spot in terms of size. Among the planets in the Earth group, it takes the top spot in terms of mass, diameter, and density. Our planet resides in the vastness of outer space, and determining its weight is no easy task. We cannot simply place it on a scale and measure its weight, so we calculate it by adding up the mass of all the materials that compose it. This calculation roughly amounts to 5.9 sextillion tons. To grasp the magnitude of this figure, we can write it out mathematically: 5 900 000 000 000 000 000 000. The sheer number of zeros in this figure is mind-boggling.
The quest for determining the magnitude of our planet throughout history
Throughout the ages and across various civilizations, scientists and scholars have continuously sought to unravel the mystery of Earth’s weight. In ancient times, it was widely believed that our planet rested upon the backs of colossal marine creatures such as whales or even elephants, while others imagined it as a flat entity with distinct boundaries.
As time progressed, the Middle Ages saw a shift in perceptions regarding the shape and weight of our planet. Among those who dared to challenge convention was G. Bruno, who proposed the concept of Earth as a spherical object. Tragically, his audacious ideas led to his untimely demise at the hands of the Inquisition. Another pivotal figure in the exploration of Earth’s dimensions was the intrepid adventurer Magellan, who boldly proclaimed the planet’s roundness, shedding light on its radius and mass.
The planet Earth is a physical entity with distinct characteristics, one of which is its weight. This groundbreaking revelation has sparked a multitude of scientific investigations. According to the principles of physics, weight is the force exerted by an object on its support. Since the Earth lacks any form of support, we can infer that it does not possess weight. However, it does possess an immense mass.
The Mass of the Earth
Eratosthenes, an ancient Greek scientist, made an initial attempt to determine the magnitude of the planet. In various cities of Greece, he conducted measurements of shadows and then compared the collected data in order to estimate the Earth’s volume. Following his footsteps, the Italian scientist G. Galileo made further calculations, ultimately discovering the law of free gravity. The torch of determining the Earth’s mass was subsequently passed to I. Newton, who, through his measurement attempts, unveiled the law of gravity.

The Scottish scientist N. Makelin was the first to successfully calculate the weight of the Earth. According to his findings, the planet’s mass is equivalent to 5.9 sextillion tons. Presently, this figure has experienced an increase, primarily due to the accumulation of cosmic dust on the Earth’s surface. Approximately thirty tons of dust settle on the planet annually, contributing to its overall weight.
Mass of the Earth
In order to determine the exact weight of the Earth, it is necessary to have knowledge of the composition and weight of the various substances that make up the planet.
- Mantle. The weight of this layer is approximately 4.05 X 10 24 kilograms.
- Core. The weight of this layer is less than that of the mantle, only 1.94 X 10 24 kilograms.
- Crust of the Earth. This portion is very thin and weighs only 0.027 X 10 24 kilograms.
- The hydrosphere and atmosphere. These layers weigh 0.0015 X 10 24 and 0.0000051 X 10 24 kilograms, respectively.
By adding up these values, we can determine the overall weight of the Earth. However, different sources may provide different measurements for the mass of the planet. So, how much does the Earth weigh in tons, and what about the weights of other planets? The weight of the Earth is approximately 5.972 X 10 21 tons. The radius of the Earth is 6,370 kilometers.

By utilizing the force of gravity, one can easily determine the Earth’s mass. To accomplish this, a thread is employed and a small weight is suspended from it. The precise location of the weight is established. A ton of lead is placed nearby. There is an attractive force between the two objects, causing the weight to be displaced slightly to the side. Even a minuscule displacement of 0.00003 mm enables the calculation of the planet’s mass. Measuring the attractive force between the weight and the Earth, as well as the attractive force between the small weight and the large one, provides the necessary data for determining the Earth’s mass.
The mass of Earth and other planets
Earth is the largest planet in the group of terrestrial planets. In comparison to Earth, Mars has a mass that is approximately 0.1 times that of Earth, while Venus has a mass that is about 0.8 times that of Earth. Gas giants, on the other hand, are significantly larger than Earth. For instance, Jupiter is 317 times larger than Earth, Saturn is 95 times heavier, and Uranus is 14 times heavier. There are even planets that weigh over 500 times more than Earth, such as the massive gas bodies found outside of our solar system.
Planet Earth is the third largest planet in the solar system. It is also the largest in terms of mass, diameter, and density among the terrestrial planets, which include Venus, Mercury, Earth, and Mars. However, Earth is only 14 times less massive than Uranus, which is a gas planet.
Our article will provide a detailed explanation of the Earth’s mass and the methods used to calculate it.
The Relationship Between Gravity, Mass, and Weight
Gravity, mass, and weight are fundamental physical quantities, but many people often confuse their meanings. It is important to clarify the definition of each concept.
- Gravity is the force that acts on any object near the Earth’s surface or in relation to another object. In simpler terms, gravity is the force that attracts objects to the Earth’s surface.
- Weight is the physical force or magnitude with which an object interacts with a support. For example, if an object is at rest on the Earth’s surface, its weight is the force with which it interacts with the surface. The standard unit of measurement is newtons.
- The mass of an object is a measurement of its gravitational interaction, which can be measured in grams, kilograms, centners, tons. This interaction is based on the universal law of gravitation, discovered by Isaac Newton.
- Earth’s mass has been a subject of study for centuries, with many great scientists dedicating their efforts to measuring it. The dimensions of our planet were first calculated by Eratosthenes around 240 BC.
For numerous centuries, the field of physics and astronomy was under the influence of Ptolemy’s geocentric system, which proposed that the Earth occupied the central position in the solar system. It was only after the groundbreaking findings of individuals such as N. Copernicus, I. Kepler, G. Galileo, and others that a thorough examination of the Earth’s characteristics commenced. This period saw the unveiling of the fundamental principles of dynamics, namely the laws formulated by I. Newton, which in turn paved the way for the determination of the Earth’s mass.
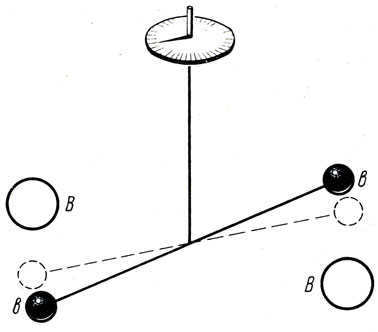
The measurement of the Earth’s mass was initially conducted in the 18th century by a British chemist named G. Cavendish. To carry out his experiment, Cavendish utilized a torsion scale equipped with lead balls attached to the ends. By introducing two large lead balls to these smaller ones in alternating fashion, the scientist was able to determine the ratio between the gravitational attraction of the small ball to the large one and the gravitational attraction of the Earth. The calculated mass of the Earth turned out to be approximately 6-10^21 kilograms, a value very close to the modern-day accepted mass of the Earth, which is approximately 5.98-10^24 kilograms.
The formula for calculating the mass of the Earth based on the fundamental laws of dynamics is as follows:
Discover the precise measurement of the Earth’s mass – the third planet in our solar system. Detailed explanation of the calculation formula, equation with its components, and the ultimate result of the planet’s mass.
It amounts to an astonishing 5.9736 x 10 24 kg. Remarkable!
How can we determine the mass of the Earth?
However, it is even more intriguing to uncover the method employed to establish the Earth’s mass in the first place. It all revolves around the gravitational pull exerted by our planet on nearby objects.
According to the principles of physics, any object with mass is subject to attraction. If you place two billiard balls side by side, they will gravitate towards one another. This force is imperceptible to the naked eye, but it is detected by sensitive instruments. This calculation helps deduce the mass of both objects.
Newton postulated that the mass of spherical objects is concentrated at their centers. Thus, we can utilize the equation:
- F represents the force of gravity between them.
- G, which is a constant, equals 6.67259 × 10 -11 m 3 /kg s 2 .
- -M1 and M2 denote the attracting masses.
- R signifies the distance between them.
Let’s consider that one of the masses is the Earth, and the other is a kilogram sphere. The force between them measures 9.8 kg * m/s 2 . The Earth’s radius is 6,400,000 meters. By incorporating these values into the formula, the result is 6 x 10 24 kg.
It should be noted that when asking about the concept, it is correct to use the term “mass” instead of “weight”, as the latter refers to the force required to calculate the gravitational field. You can take a ball and measure its weight on both Earth and the Moon, and the readings will differ. However, mass is a constant value, and Earth’s mass remains the same.
Although it may seem significant, it’s important to remember that there are larger objects in our solar system. For instance, our star surpasses Earth’s mass by 330,000 times, and Jupiter by 318 times. There are also smaller objects, such as Mars, whose mass is only 11% of Earth’s mass.
We are fortunate to have the highest planetary density in the solar system, which is 5.52 g/cm3. This density is due to the presence of a metallic core surrounded by a rocky mantle. In contrast, less dense planets like Jupiter consist mainly of hydrogen and other gases. Now you have an understanding of Earth’s mass.
The mass of Earth (M or M⊕, with ⊕ being the astronomical symbol for planet Earth) is a measurement of mass that is equal to the mass of Earth itself. The most accurate estimate of Earth’s mass is currently M⊕ = 5.9722 × 10 kg with a standard uncertainty of 6 × 10 kg (a relative error of 10). The recommended value in 1976 was (5.9742 ± 0.0036) × 10 kg. This is equivalent to an average density of 5515 kg⋅m.
Earth mass is the standard unit of mass in astronomy and is utilized to describe the masses of other celestial bodies, including terrestrial planets similar to Earth and exoplanets. One solar mass is approximately equivalent to 333,000 Earth masses. The mass of the Earth does not incorporate the mass of the Moon. The Moon’s mass is roughly 1.2% of the Earth’s mass, so the combined mass of the Earth and Moon system is roughly 6.0456 × 10 kg.
The majority of the mass is made up of iron and oxygen (around 32% each), magnesium and silicon (around 15% each), and calcium, aluminum, and nickel (around 1.5% each).
The unit of mass in astronomy
The estimation of Earth’s mass is as follows:
M ⊕ = (5.9722 ± 0.0006) × 10 24 kg = (5.9722 \; \ pm \; 0.0006) \ times 10 ^ \; \ mathrm > ,
which can be represented in terms of solar mass as:
M ⊕ = 1 332 946.0487 ± 0.0007 M ⊙ ≈ 3.003 × 10-6 M ⊙ = < \ frac > \; \ mathrm > \ approximately 3.003 \ times 10 ^ \; \ mathrm >> .
The precise measurement of the ratio between Earth’s mass and lu mass is:
M ⊕ / ML = 81.3005678 ± 0.0000027 / M_ = 81.3005678 \; \ pm \; 0.0000027> .
| Earth’s Moon | 0.0123000371 (4) | |
| The Sun | 332946.0487 ± 0.0007 | |
| Mercury | 0.0553 | |
| Venus | 0.815 | |
| Earth | 1 | By definition |
| Mars | 0.107 | |
| Jupiter | 317.8 | |
| Saturn | 95.2 | |
| Uranus | 14.5 | |
| Neptune | 17.1 | |
| Pluto | 0.0025 | |
| Eris | 0.0027 | |
| Gliese 667 Cc | 3.8 | |
| Kepler-442b | 1.0 – 8.2 |
The geocentric gravitational constant, also known as the product of G M ⊕ for Earth, is defined as (398600441.8 ± 0.8) × 10 m s. It is determined by collecting laser location data from satellites like LAGEOS-1 that orbit around our planet. Another way to calculate G M ⊕ is by studying the movement of the Moon or the time it takes for a pendulum to swing at various heights. However, these alternative methods are not as precise as studying the motion of artificial satellites.
The uncertainty of the geocentric gravitational constant is extremely low, being 2 × 10, which is 50000 times smaller than the uncertainty for M ⊕ itself. M ⊕ can only be determined by dividing the product G of M ⊕ by G, and G is known with a relative uncertainty of 4.6 × 10 (according to the 2014 NIST recommended value). As a result, M ⊕ will have a similar level of uncertainty. Due to this and other factors, astronomers prefer to use the unreduced product of G M ⊕ or mass ratios (masses expressed in units of Earth mass or solar mass) instead of mass in kilograms when referencing and comparing planetary objects.
Composition
The Earth’s composition is characterized by significant variations in density. The upper crust has a density of less than 2700 kg/m³, while the inner core has a density of 13000 kg/m³. The Earth’s core, although only accounting for 15% of its volume, makes up more than 30% of its mass. On the other hand, the mantle constitutes 84% of the Earth’s volume and approximately 70% of its mass. The crust, in contrast, represents less than 1% of the total mass.
The majority of the Earth’s mass, around 90%, is composed of an iron-nickel alloy (with 95% iron) in the core, while the mantle and crust consist of silicon dioxides (approximately 33%) and magnesium oxide (around 27%). Other minor components include iron (II) oxide (5%), aluminum oxide (3%), and calcium oxide (2%), as well as various trace elements. In terms of elemental composition, iron and oxygen account for approximately 32% each, while magnesium and silicon make up about 15% each. Calcium, aluminum, and nickel each contribute around 1.5%. Carbon comprises 0.03% of the Earth’s composition, water accounts for 0.02%, and the atmosphere represents approximately one part per million.
A Brief History of Measurement

The Mendenhall gravimeter apparatus, showcased in the 1897 Scientific Journal, utilized pendulums. This groundbreaking portable gravimeter, invented by Thomas C. Mendenhall in 1890, provided the most precise relative measurements of the local gravitational field of the Earth.
The Earth’s mass is determined indirectly by measuring other quantities, such as the density of the Earth, its gravity, or the gravitational constant. The initial measurement in the Schiehallion experiment during the 1770s resulted in an underestimation of approximately 20%. However, the Cavendish experiment conducted in 1798 achieved a more accurate value with an error margin of just 1%. Over time, the level of uncertainty decreased significantly to about 0.2% in the 1890s and further to 0.1% by 1930.
Estimates made in the early days
Prior to the direct measurement of the gravitational constant, scientists had to rely on estimates to determine the mass of the Earth. These estimates were based on observations of the Earth’s crust and calculations of its average density, as well as estimations of its volume. In the 17th century, estimates of the Earth’s volume were made by measuring a circumference of 60 miles (97 km) per degree of latitude, which corresponded to a radius of 5,500 km (86% of the Earth’s actual radius of about 6,371 km). However, this resulted in an estimated volume that was about one-third smaller than the actual value.
The precise measurement of the Earth’s average density had long been a challenge. Early theories proposed that the Earth was predominantly composed of either water (Neptunism) or volcanic rock (Plutonism), both of which suggested a lower than actual average density, estimating a total mass of around 10 kg. Remarkably, Isaac Newton, working without reliable data, made an estimate that the Earth’s density would be five or six times that of water, which is remarkably close to the modern value of 5.515. Newton did, however, underestimate the Earth’s volume by approximately 30%, resulting in his estimate being equivalent to (4.2 ± 0.5) × 10 kg.
During the 18th century, scientists were able to estimate the average density of the Earth indirectly by utilizing Newton’s law of universal gravitation and what is now known as the gravitational constant. One of the early methods used to estimate the Earth’s average density was through the observation of a slight deflection of a pendulum near a mountain, as demonstrated in Schiehallion’s experiment. Newton himself reviewed this experiment in his work Principia, but he pessimistically concluded that the effect would be too minuscule to be measured.
In an effort to ascertain the density of the Earth, Pierre Bouguer and Charles Marie de la Condamine embarked on an expedition from 1737 to 1740. Their approach involved measuring the period of a pendulum at various altitudes, which provided insight into the force of gravity. The team conducted experiments in Ecuador and Peru, specifically at the Pichincha volcano and Mount Chimborazo. Bouguer documented their findings in a 1749 paper, noting that they were able to detect a deviation of 8 angular seconds. While this level of accuracy fell short of accurately estimating the Earth’s average density, Bouguer asserted that it was sufficient evidence to disprove the theory of a hollow Earth.
In 1772, Nevil Maskelyne, the Royal Astronomer, proposed that the Royal Society should conduct a new experiment. He believed that this experiment would bring honor to the nation where it was performed. Maskelyne suggested two potential locations for the experiment: Whernside in Yorkshire and the Blencathra – Skiddaw Array in Cumberland. To further investigate this proposal, the Royal Society established an Attention Committee, consisting of Maskelyne, Joseph Banks, and Benjamin Franklin. The committee assigned astronomer and surveyor Charles Mason the task of finding an appropriate mountain for the experiment.
After an extensive search during the summer of 1773, Mason announced that the most suitable option was Schiehallion, a mountain located in the central Scottish Highlands. This peak was isolated from neighboring hills, which would minimize their gravitational influence, and its symmetrical ridge running from east to west would simplify the calculations. The steep slopes on the north and south sides would position the experiment near the mountain’s center of mass, maximizing the deflection effect. The experiment was carried out by Nevil Maskelyne, Charles Hutton, and Reuben Burrow, and it was completed by 1776. In his report in 1778, Hutton stated that the Earth’s average density was estimated to be 9 5 >> Mt. Schiehallion. This corresponds to an average density approximately 4 ⁄ 2 times higher than that of water (i.e., about 4.5 g/cm³), which is about 20% lower than the modern value. However, it still indicates a significantly higher average density than that of typical rock, suggesting for the first time that the Earth’s interior might largely consist of metal. Hutton estimated that this metallic portion occupies approximately ⁄ 31 (or 65%) of the Earth’s diameter (the modern value is 55%). With the average density of the Earth determined, Hutton was able to input specific values into Jerome Lalande’s planetary tables, which previously could only express the densities of major objects in the solar system in relative terms.
The Cavendish experiment
In 1798, Henry Cavendish became the first scientist to conduct a laboratory experiment aimed at directly measuring the gravitational attraction between two objects. By combining Newton’s Second Law and Newton’s Law of Universal Gravitation, Cavendish was able to calculate the mass of the Earth.
In modern terms, the mass of the Earth is determined using the gravitational constant and the average radius of the Earth.
Cavendish’s experiment yielded an average density of 5.45 g/cm³, which was approximately 1% lower than the value accepted in modern times.
The 19th century
was a time of significant historical and cultural change.

The experimental setup created by Francis Bailey and Henry Foster was used to determine the density of the Earth through the Cavendish method.
Although the mass of the Earth can be inferred by specifying its radius and density, it was not common practice to explicitly state the absolute mass until the late 19th century when scientific notations using powers of 10 were introduced. This was because using absolute numbers would have been impractical. In Ritchie’s (1850) work, the mass of the Earth’s atmosphere is given as “11,456,688,186,392,473,000 lbs.” (equivalent to 1.1 × 10 pounds = 5.0 × 10 kg, with the modern value being 5.15 × 10 kg). Ritchie also mentions that in comparison to the weight of the Earth, this enormous sum becomes insignificant.
In the first half of the nineteenth century, scientists conducted further investigations with pendulums. However, as the century progressed, these experiments gradually became less efficient compared to the repeated Cavendish experiment. In fact, the modern value of G, which determines the mass of the Earth, is still obtained through precise repetitions of the Cavendish experiment.
In 1821, Francesco Carlini made measurements in the Milan area using pendulums and determined the density value ρ to be 4.39 g/cm. Edward Sabin refined this value in 1827 to 4.77 g/cm, and Carlo Ignazio Giulio further refined it in 1841 to 4.95 g/cm. Meanwhile, George Biddell Airy attempted to determine ρ by measuring the difference in pendulum period between the surface and the bottom of a mine. The initial tests took place in Cornwall from 1826 to 1828, but they were unsuccessful due to fire and flooding. Finally, in 1854, Airy obtained a value of 6.6 g/cm by conducting measurements in a coal mine in Harton, Sunderland. Airy’s method assumed that the Earth had a spherical stratification. Later, experiments carried out by Robert von Sterneck (1839-1910) in mines in Saxony and Bohemia in 1883 provided average density values ρ ranging from 5.0 to 6.3 g/cm. This led to the development of the concept of isostasy, which limits the accuracy of measuring ρ using plumb bob deviation or pendulums. Despite the low probability of accurately estimating the Earth’s average density through this method, Thomas Corwin Mendenhall conducted a gravimetric experiment in Tokyo and on the summit of Mount Fuji in 1880, resulting in a value of ρ = 5.77 g/cm.
Contemporary significance
The uncertainty surrounding the present-day estimation of Earth’s mass can be attributed solely to the uncertainty in the gravitational constant G since at least the 1960s. Measuring G has proven to be extremely challenging, and several highly accurate measurements taken between the 1980s and 2010s have yielded conflicting results. Zagitov (1969) provided a value of M ⊕= 5.973 (3) × 10 kg (with a relative error of 5 × 10) based on the G measurement conducted by Heil and Chrzanowski (1942).
Since that time, there has been only a slight improvement in accuracy. Most modern measurements are essentially repetitions of the Cavendish experiment, yielding results (within the standard uncertainty) that range from 6.672 to 6.676 × 10 m kg (with a relative error of 3 × 10) in publications since the 1980s. However, the NIST recommended value in 2014 is close to 6.674 × 10 m kg, with a relative error below 10. According to the Astronomical Almanach Online as of 2016, the recommended standard error for the mass of the Earth, M ⊕5.9722 (6) × 10 kg, is 1 × 10.
Variation
The Earth’s mass is not constant and can change over time. It can increase due to the accumulation of various materials, such as micrometeorites and cosmic dust. On the other hand, it can also decrease due to the loss of hydrogen and helium gas. When these factors are combined, the net loss of material is estimated to be around 5.5 × 10 kg (or 5.4 × 10 long tons) per year. This amount accounts for approximately 10% of the Earth’s total mass.
The annual net loss of 5.5 × 10 kg is primarily caused by atmospheric leakage, which results in the loss of approximately 100,000 tons. Additionally, an average of 45,000 tons is lost due to falling dust and meteorites. However, it’s important to note that the margin of error for this mass loss is only 0.01% (or 6 × 10 kg), which means that it does not significantly affect the calculated value of the Earth’s mass.
There are additional variations in mass that occur as a result of the principle of mass-energy equivalence, although these variations are relatively insignificant. It is estimated that there is a loss of mass, amounting to 16 tons per year, due to a combination of nuclear fission and natural radioactive decay.
Furthermore, there is an additional loss of mass, estimated to be 65 tons per year since the mid-20th century, as a result of spacecraft on escape trajectories. In the first 53 years of the space age, Earth lost approximately 3,473 tons of mass, but it is worth noting that this trend is now declining.
Related Content
Earth is a one-of-a-kind celestial body within our solar system. While it may not be the smallest planet, it also doesn’t hold the title for the largest; it falls in fifth place in terms of size. Among the Earth group of planets, it stands out as the largest when it comes to mass, diameter, and density. Positioned in the vastness of outer space, determining the weight of Earth proves to be quite a challenge. Since it’s impossible to physically place the planet on a scale, its weight is calculated by summing up the mass of all the materials that compose it. This calculation yields a staggering 5.9 sextillion tons. To put this astronomical figure into perspective, it can be written mathematically as 5 900 000 000 000 000 000 000. The sheer number of zeros in this figure is enough to make anyone’s eyes water.
The quest to determine the magnitude of our planet throughout history
Diverse scholars spanning centuries and cultures have embarked on a journey to ascertain the weight of our Earth. In antiquity, the prevailing belief held that our planet was akin to a level surface, supported by colossal whales or turtles. Various societies even substituted elephants for whales. Nevertheless, these diverse civilizations shared a common perception of a flat Earth, bound by a discernible perimeter.

In the Middle Ages, there were shifts in the understanding of shape and weight. G. Bruno was the first to discuss the spherical shape, but unfortunately, he was executed by the Inquisition due to his beliefs. Another important contribution to scientific knowledge about the Earth’s radius and mass was made by the explorer Magellan, who proposed the idea that the planet was round.
The initial findings
The planet Earth is a tangible entity with distinct characteristics, including its weight. This revelation paved the way for a multitude of investigations. In accordance with the principles of physics, weight is the force exerted by an object on a surface. Considering that the Earth lacks any surface to support it, we can deduce that it possesses no weight, although it does possess a substantial mass.
For the initial attempt at determining the magnitude of the planet, Eratosthenes, an ancient Greek scientist, took the initiative. In various cities within Greece, he measured the shadow and subsequently compared the collected data. This methodology allowed him to estimate the planet’s size. Following in his footsteps, G. Galileo, an Italian scientist, conducted his own calculations. It was through his efforts that the law of free gravity was discovered. I. Newton then took up the mantle of determining the weight of the Earth. Through his various measurement attempts, he ultimately uncovered the law of gravity.

In a groundbreaking discovery, Scottish scientist N. Makelin successfully determined the weight of the Earth for the very first time. According to Makelin’s calculations, the Earth’s mass is a staggering 5.9 sextillion tons. However, it is important to note that this figure has since increased. The discrepancy in weight can be attributed to the accumulation of space dust on the surface of the planet. Approximately thirty tons of dust settle on the Earth each year, causing its weight to gradually increase over time.
Mass of the Earth
In order to determine the exact weight of the Earth, it is necessary to have knowledge of the composition and weight of the various substances that make up the planet.
- Mantle. The weight of this layer is approximately 4.05 X 10 24 kg.
- Core. This layer is lighter than the mantle, weighing only 1.94 X 10 24 kg.
- Crust of the Earth. This part is very thin and has a weight of only 0.027 X 10 24 kg.
- The hydrosphere and atmosphere. These layers have weights of 0.0015 X 10 24 and 0.0000051 X 10 24 kg, respectively.
By adding up all of this data, we can determine the weight of the Earth. However, there are different sources that provide varying estimates for the planet’s mass. So, how much does planet Earth weigh in tons, and what are the weights of other planets? The weight of the planet is 5.972 X 10 21 tons. The radius is 6,370 kilometers.

By utilizing the concept of gravity, it is possible to easily ascertain the mass of the Earth. To achieve this, a string is utilized and a small object is suspended from it. The exact position of the object is determined. Then, a ton of lead is positioned nearby. There exists an attractive force between the two objects, which causes the suspended weight to deviate slightly to the side. Even a minuscule deflection of 0.00003 mm allows for the calculation of the planet’s mass. To accomplish this, it is sufficient to measure the attractive force in relation to the weight and the attractive force between the small weight and the large weight. The resulting data enables the calculation of the Earth’s mass.
Earth is the biggest planet in the group of planets that belong to the Earth. In comparison, Mars weighs approximately 0.1 times the weight of Earth, and Venus weighs 0.8 times. The weight of Mercury is about 0.05 times the weight of Earth. The gas giants are much larger than Earth. When comparing Jupiter and our planet, Jupiter is 317 times larger, while Saturn is 95 times heavier and Uranus is 14 times heavier. There are planets that weigh 500 times or more than Earth. These are enormous gas entities that can be found outside of our solar system.
How can I determine the mass of the Earth?
If we know the values of G, g, and R, we can calculate the mass of the Earth.
Is this something a 10th grade student can figure out?
The formula for calculating the mass of the Earth is M earth = (g * R earth square) / G, where R is the radius of the Earth, G is equal to 6.67 * 10 to the power of -11, and g is the acceleration due to gravity.
It seems like you recently learned about this topic and wanted to show off your knowledge.
ddinblue just wrote it down and didn’t ask for any additional details.
I’m sure you’ll forget all about it once you start playing DotC.
To determine the mass of the Earth, you divide the force of gravity acting on an object by the acceleration due to gravity.
This formula is derived from the gravitational force between two bodies, if I’m not mistaken.
Well, I’ll need to elucidate the resolution
Who is scrutinizing the subject (Users: 0, Guests: 1)
What methods have scientists utilized to determine the mass of the Earth and other celestial bodies?
When it comes to planets, they are too massive to be placed on a conventional scale. So how did scientists succeed in ascertaining the Earth’s mass? How is the mass of remote celestial objects quantified?
Interesting concepts of physics
There are two different approaches to determining the mass of the Earth: utilizing a barometer combined with mathematical calculations, or analyzing neutrino particles.
Barometer and Newton’s Laws
This method has been employed since the 18th century. It involves applying Newton’s second law (F=mg) and the law of universal gravitation (F=G*m*M/R^2) to make the calculations.
In this context, F represents the gravitational force of the Earth on the barometer, G is the gravitational constant, R stands for the radius of the planet, m represents the mass of the instrument, and M corresponds to the mass of the planet.
Alternatively, the mass of the Earth can be calculated separately using the formula: M = g*R^2/G, where g represents the acceleration due to gravity.
The measurement of the acceleration of free fall was conducted by dropping a barometer from a tall tower and recording the time it took to reach the ground. It was observed that the barometer traveled approximately 9.8 meters per second for each successive second. Thus, the acceleration due to gravity, denoted as g, is equal to 9.8 m/s².
The circumference of the Earth has been known since ancient times. This remarkable discovery was made by the Greek mathematician Eratosthenes in the 3rd century BC.
Eratosthenes carefully selected the day of the summer solstice for his experiment. During this time, the sun is at its highest point in the sky, and at precisely 12 o’clock noon, it casts the shortest shadow of the year.
The Earth is not a perfect sphere, and thus its radius was determined to be 6371 kilometers.
The most challenging task was to determine the value of the gravitational constant coefficient. In order to accomplish this, the researchers conducted an experiment involving a one-ton lead ball and measured the force with which it attracted the barometer.
By plugging all of these numbers into the equation, the scientists calculated that the weight of the Earth is six septillion kilograms or 6^24 kg.
These are the minuscule subatomic particles that are emitted by the sun and pass through the planet.
What is the process of measuring the mass of planets?
In the Middle Ages, during the time of Kepler and Galileo, scientists already had knowledge about the characteristics of the planets in our solar system. Even then, they were able to roughly determine the mass of the planets using simple methods and instruments. Nowadays, modern astronomy has developed various techniques for calculating the characteristics of planets, stars, clusters, and galaxies.
Facts about the planets in our solar system
Did you know that the Sun holds 99.9% of the total mass in our solar system? The combined mass of all the planets is only around 0.01%. Out of that 0.01%, the gas giants make up 99% of the mass, with Jupiter and Saturn alone contributing 90%.
Calculation of Earth and Moon Mass
To determine the mass of the planets within the solar system, it is most convenient to begin with Earth. As we recall, the force of gravity can be expressed by the equation F=mg, where m represents the mass of the object and F is the force exerted upon it.
Additionally, we can refer to Newton’s universal law of gravitation:
By comparing these two equations and utilizing the known gravitational constant of 6.67430(15)-10-11 m³/(kg-s²), we are able to calculate the mass of Earth. We possess knowledge of Earth’s gravitational acceleration, 9.8 m/s², as well as the planet’s radius. By substituting these values into the equation, we arrive at an approximate mass of 5.97 x 10²⁴ kg.
By knowing the Earth’s mass, we can easily calculate the parameters for other celestial bodies in the solar system, including the Moon, planets, and Sun. When it comes to the Moon, the calculation is relatively straightforward. We simply need to consider that the distances from the centers of the bodies to the center of mass are inversely proportional to their masses. By substituting the appropriate values for the Earth and the Moon, we can determine that the Moon has a mass of 7.36 × 10²²² kilograms.
Next, let’s discuss the methods used to measure the masses of the Earth’s group of planets, such as Mercury, Venus, and Mars. Following that, we will explore the gas giants, and finally, we will delve into the masses of exoplanets, stars, and galaxies.
Methods for Determining Planetary Masses
One common approach to determining the masses of planets is through the application of Kepler’s third law. According to this law, the square of a planet’s orbital period is proportional to the cube of the major semi-axis of its orbit. Newton expanded upon this law by incorporating the masses of celestial bodies into the equation. The resulting formula is:
When it comes to exoplanets and other stars (excluding single stars), the field of astronomy typically employs a technique known as analyzing apparent perturbations and oscillations. This approach is founded on the principle that all massive objects influence or “perturb” the orbits of one another.
By utilizing this method, astronomers were able to calculate and identify the presence of planets like Neptune and Pluto even before they were visually observed, popularly referred to as being “discovered at the tip of a pen.”
The masses of the planets in the solar system
After discussing the general methods for calculating the masses of various celestial bodies and obtaining the values for the Moon, Earth, and the Galaxy, it is now time to rank the planets in our system based on their mass.
At the top of the list, we have Jupiter, which has the largest mass among all the planets in the solar system. In fact, its mass is just one order of magnitude away from being double that of our entire system. If Jupiter were a bit more massive, we could have had two suns instead. The mass of this gas giant is approximately 1.9 × 10²⁷ kilograms.
Interestingly, Jupiter is the only planet in our system whose center of mass for rotation with the Sun is located outside the surface of the star. It is approximately 7% of the distance between them, measured from the surface of the Sun.
Saturn is the second most massive planet, weighing 5.7 × 10²⁶ kg. Following Saturn is Neptune, which weighs 1 × 10²⁶ kg. In fourth place is Uranus, a gas giant with a mass of 8.7 × 10²⁵ kg.
The next group of planets are terrestrial bodies, made of rock and unlike the gas giants, they have smaller radii and higher densities.
The heaviest planet in this group is Earth, whose mass we have already calculated. Venus comes next, with a mass of 4.9 × 10²⁴ kg. Mars is lighter, weighing only 6.4 × 10²³ kg, which is almost 10 times less than Venus. The planet with the smallest mass is Mercury, weighing 3.3 × 10²³ kg. Interestingly, Mercury is even lighter than two satellites in the solar system, Ganymede and Callisto.
Determining the masses of stars and galaxies
To ascertain the properties of individual star systems, the gravimetric method is utilized. Its essence lies in measuring the gravitational redshift of the star’s light. This is done using the formula ∆V=0.635 M/R, where M and R represent the star’s mass and radius, respectively.
The mass of a star can also be determined indirectly based on its visible spectrum and luminosity. Initially, the star’s luminosity class is identified from the Hertzsprung-Russell diagram, followed by calculating the mass/luminosity relationship. It is important to note that this approach is not applicable to white dwarfs and neutron stars.
The calculation of a galaxy’s mass primarily relies on the rotational velocity of its stars (or, in the case of a non-spiral galaxy, the relative velocity of the stars). According to Newton’s universal law of gravitation, the centrifugal force exerted by the stars in a galaxy can be represented by the following formula:
In this instance, we substitute the distance from the Sun to the center of our galaxy and its mass into the formula. This enables us to determine the mass of the Milky Way, which amounts to 2.2 × 10⁴⁴⁴g.
It is important to note that this value only accounts for the mass of the galaxy without factoring in the stars whose orbits lie beyond the Sun’s rotational orbit. Consequently, for more precise calculations, the outermost stars in the arms of spiral galaxies are taken into consideration.
If you enjoy this post, please share it with your friends!
The Earth’s mass ( M E or M ⊕where ⊕ is the standard astronomical symbol for the planet globe ) is defined as the mass of the Earth. The most accurate estimate of the Earth’s mass is M ⊕ = 5.9722 × 10 24 kg , with an uncertainty of 6 × 10 20 kg (relative uncertainty of 10 -4 ). [2] The recommended value in 1976 was (5.9742 ± 0.0036) × 10 24 kg . [3] This is equivalent to an average density of 5515 kg.m -3 .
Earth is the standard unit of mass in astronomy used to measure the mass of other planets, including rocky Earth-like planets and exoplanets. One Solar mass is approximately equal to 333,000 times the mass of the Earth. The mass of the Earth does not include the mass of the Moon. The Moon has a mass that is about 1.2% of the mass of the Earth, so the total mass of the Earth + Moon system is approximately 6.0456 × 10 24 kg.
The majority of the Earth’s mass is made up of iron and oxygen (approximately 32% each), followed by magnesium and silicon (approximately 15% each), and then calcium, aluminum, and nickel (approximately 1.5% each).
Measuring the mass of the Earth accurately is a challenging task as it involves determining the gravitational constant, which is a physical constant with the lowest level of precision due to the relatively weak gravitational force. The first relatively accurate measurement of the Earth’s mass was achieved in the Schiehallion experiment conducted in the 1770s, which provided a value within 20% of the actual mass. The Cavendish experiment of 1798 further improved the accuracy, bringing it within 1% of the modern value.
Unit of mass in astronomy
The estimated mass of the Earth is:
M ⊕ = (5.9722 ± 0.0006) × 10^24 kilograms = (5.9722 ± 0.0006) × 10^24 kg
This can also be expressed in terms of solar mass:
M ⊕ = (1,332,946.0487 ± 0.0007) M ⊙ ≈ 3.003 × 10^-6 M ⊙
The ratio of the mass of the Earth to the mass of the Moon has been measured accurately. The current best estimate is:
M ⊕ / M L = 81.3005678 ± 0.0000027
| moon | 0.012 300 0371 (4) | [4] |
| sun | 332 946 .0487 ± 0.0007 | [2] |
| Mercury | 0.0553 | [6] |
| Venus | 0.815 | [6] |
| globe | 1 | By definition |
| Mars | 0.107 | [6] |
| Jupiter | 317.8 | [6] |
| Saturn | 95.2 | [6] |
| Uranus | 14.5 | [6] |
| Neptune | 17.1 | [6] |
| Pluto | 0.0025 | [6] |
| Eris | 0.0027 | |
| Gliese 667 Cc | 3.8 | [7] |
| Kepler-442b | 1.0 – 8.2 | [8] |
The uncertainty of the geocentric gravitational constant is only 2 × 10 -9 , which is 50,000 times smaller than the uncertainty for M ⊕ itself. M ⊕ can only be determined by dividing the mass of Earth (in grams) by the mass of an object (also in grams), and the mass of Earth is known with a relative uncertainty of 4.6 × 10 -5 (based on the 2014 NIST recommended value). Therefore, M ⊕ will have the same uncertainty at best. Because of this and other factors, astronomers prefer to use the unabbreviated mass of Earth (in grams) or mass ratios (expressed in units of Earth mass or Solar mass) when comparing and contrasting planetary objects.
Essay
The Earth’s density exhibits significant variations, ranging from less than 2700 kg⋅m -3 in the upper crust to as high as 13,000 kg⋅m -3 in the Inner Core. [12] The Core accounts for 15% of the Earth’s volume but over 30% of its mass, while the Mantle comprises 84% of the volume and approximately 70% of the mass. The Crust, on the other hand, represents less than 1% of the mass. [12] Iron-nickel alloy, primarily composed of iron (95%), constitutes about 90% of the Earth’s mass in the Core (30%), while the Mantle and Crust consist mainly of silicon dioxide (approximately 33%) and magnesium oxide (around 27%). In addition, there are minor contributions from iron (II) oxide (5%), aluminum oxide (3%), and calcium oxide (2%) [13], as well as various trace elements, such as iron and oxygen (about 32% each), magnesium and silicon (approximately 15% each), and calcium, aluminum, and nickel (around 1.5% each). Carbon constitutes 0.03%, water accounts for 0.02%, and the atmosphere makes up about one part per million. [14]
The Evolution of Measurement Systems

The Mendenhall gravimeter apparatus, featured in the 1897 Scientific Journal, utilized pendulums to provide precise relative measurements of the local gravitational field of the Earth. Developed by Thomas S. Mendenhall in 1890, this portable gravimeter was renowned for its accuracy.
Indirect methods are employed to determine the mass of the Earth, such as measuring its density, gravity, or gravitational constant. The initial measurement conducted in the 1770s through the Schiehallion experiment resulted in an underestimation of approximately 20%. The subsequent Cavendish experiment in 1798 yielded the correct value with an accuracy of 1%. By the 1890s, the margin of uncertainty had decreased to around 0.2%, and further improved to 0.1% by 1930.
Since the 1960s (WGS66), scientists have had accurate measurements of the Earth’s figure, with a precision of four significant digits. This means that the uncertainty in the mass of the Earth has primarily been determined by the measurement of the gravitational constant. In the 1970s, the relative uncertainty was 0.06% [17], but by the 2000s, it had decreased to 0.01% (10^-4). Currently, the relative uncertainty is 10^-4, which is equivalent to 6 × 10^20 kg in absolute terms. To put this into perspective, it is roughly 70% of the mass of a minor planet, such as Ceres.
Initial approximations
Prior to conducting direct measurements of the gravitational constant, approximations of the Earth’s mass were constrained to estimations of the Earth’s average density derived from observations of the Earth’s crust, as well as estimations of the Earth’s volume. In the 17th century, estimations of the Earth’s volume were based on an estimated circumference of 60 miles (97 km) per degree of latitude, which corresponded to a radius of 5,500 km (86% of the actual value). The true radius of the Earth is approximately 6371 km), resulting in an estimated volume that was approximately one-third smaller than the accurate value. [18]
In the 18th century, the understanding of Newton’s Law of Universal Gravitation enabled scientists to indirectly estimate the average density of the Earth by calculating the gravitational constant. One of the early methods used to estimate the Earth’s average density was the observation of a pendulum’s slight deflection near a mountain, as demonstrated in the Schiehallion experiment. Although Newton mentioned this experiment in his Principia, he pessimistically believed that the effect would be too minuscule to be measured accurately.
In an expedition that took place from 1737 to 1740, Pierre Bouguer and Charles Marie de la Condamine set out to determine the Earth’s density by measuring the period of a pendulum, which would also indicate the force of gravity, at different altitudes. These experiments were conducted at Volcan Pichincha and Mount Chimborazo in Ecuador and Peru. According to a 1749 paper by Bouguer, they were able to detect a deviation of 8 seconds of arc, although this level of accuracy was not sufficient to definitively estimate the Earth’s average density. However, Bouguer did state that this finding was enough to prove that the Earth was not hollow.
Schiehallion experiment
There was a call for experts to conduct a new experiment proposed by Nevil Maskelyne, the Royal Astronomer, in 1772. He believed that this experiment would bring great honor to the country where it took place. Two potential locations for the experiment were suggested: Whernside in Yorkshire and the Blencathra-Skiddo Array in Cumberland. To further explore these options, the Royal Society established an Attention Committee comprised of Maskelyne, Joseph Banks, Benjamin Franklin, and others. The committee assigned the task of finding a suitable mountain to Charles Mason, an astronomer, and a surveyor.
After an extensive search, Mason announced in the summer of 1773 that Schiehallion, a mountain in the central Scottish Highlands, was the most suitable candidate. [22] Schiehallion was situated away from other nearby hills, minimizing their gravitational influence, and its symmetrical east-west ridge made calculations easier. The steep slopes on its north and south sides placed the experiment near its center of mass, maximizing the deflection effect. The experiment was carried out by Nevil Maskelyne, Charles Hutton, and Reuben Burrow, and was completed by 1776. Hutton (1778) reported that the average density of the Earth was estimated to be 9 5 >> that of Mount Schiehallion. [23] This corresponds to an average density about 4 1 ⁄2 times higher than that of water (i.e., about 4.5 g/cm3), which is approximately 20% lower than the modern value, but still significantly higher than the average density of typical rock. This discovery indicated for the first time that the Earth’s interior may be predominantly composed of metal. Hutton estimated that this metallic portion extends to about 20 ⁄31 (or 65%) of the Earth’s diameter (the modern value is 55%). [24] By using the value of the average density of the Earth, Hutton was able to establish some values for Jerome Lalande’s planetary tables, which previously could only express the densities of major objects in the solar system in relative units. [23]
Henry Cavendish made history in 1798 by being the first person to directly measure the gravitational attraction between two objects in a laboratory setting. By combining Newton’s Second Law and Newton’s Law of Universal Gravitation, he was able to determine the mass of the Earth.
In modern times, we can calculate the mass of the Earth using the gravitational constant and the average radius of the Earth.
Cavendish’s groundbreaking research also led to the discovery that the average density of the Earth is approximately 5.45 g/cm3, which is slightly lower than the current accepted value by about 1%.
During the 19th century

Francis Bailey and Henry Foster conducted an experiment using the Cavendish method to determine the density of the Earth.
Although the mass of the Earth can be deduced from its radius and density, it was not common practice to explicitly state the absolute mass until the late 19th century when scientific notation using powers of 10 was introduced. This was because expressing absolute numbers would be inconvenient. According to Ritchie (1850), the mass of the Earth’s atmosphere was “11,456,688,688,186,392,473,000 lbs.” (equivalent to 1.1 × 10^19 lb = 5.0 × 10^18 kg in modern units, with a more accurate value of 5.15 × 10^18 kg) and he states that “compared with the weight of the globe, this enormous sum becomes negligible.” [25]
Absolute measurements of Earth’s mass have only been recorded since the second half of the 19th century, primarily in popular literature rather than scientific publications. In the past, the mass of the Earth was referred to as “14 septillion pounds” (14 Quadrillionen Pfund) [6.5 × 10^24 kg] in Masius’ work in 1859 [26]. Beckett, in 1871, stated the “weight of the earth” as “5842 quintillion tons” [5.936 × 10^24 kg] [27]. The Encyclopedia Britannica’s New Volumes (Vol. 25, 1902) defines “Earth’s mass in gravitational measure” as “9.81996 × 6370980.2” with the logarithm of the Earth’s mass given as “14.600522” [3.98586 × 10^14]. However, it is important to note that this value is the gravitational parameter in m^3-C^-2 (modern value 3.98600 × 10^14), and not the absolute mass.
Experiments involving pendulums persisted well into the early 1800s. However, by the latter half of the century, these experiments were superseded by repeated trials of Cavendish’s experiment. To this day, the precise value of grams (and thus the Earth’s mass) is derived from meticulously accurate repetitions of Cavendish’s groundbreaking experiment.
Contemporary worth
The uncertainty surrounding the present-day estimation of the Earth’s mass is entirely attributable to the imprecision of the gravitational constant gram since at least the 1960s. [29] Measuring gram has long been recognized as a notoriously challenging task, and various high-precision measurements conducted from the 1980s to the 2010s have yielded conflicting outcomes. [30] Zagitov (1969) based his measurement of grams on the work of Heyl and Chrzanowski (1942), who determined that M ⊕ = 5.973(3) × 10 24 kg, with a relative uncertainty of 5 × 10 -4 .
Since that time, there has been only a slight improvement in accuracy. Most modern measurements are repetitions of the Cavendish experiment, yielding results (within the standard uncertainty) ranging from 6.672 to 6.676 × 10. -11 m 3 kg -1 s -2 (relative error 3 × 10 -4 ) in reports since the 1980s. However, the recommended value by NIST in 2014 is close to 6.674 × 10 -11 m 3 kg -1 s -2 with a relative error of less than 10 -4 . The Astronomical Almanac Online as of 2016 recommends a standard uncertainty of 1 × 10 -4 for the Earth’s mass, M ⊕ 5.9722(6) × 10 24 kg [2]
Fluctuation
The mass of the Earth is subject to variation, influenced by both gains and losses resulting from the accumulation of incoming materials, such as micrometeorites and cosmic dust, as well as the loss of hydrogen and helium. Overall, the net material loss is estimated to be around 5.5 × 10^7 kg (5.4 × 10^4 long tons) per year. This accounts for approximately 10-17% of the total land mass [31]. The annual net loss of 5.5 × 10^7 kg is primarily attributed to the loss of 100,000 tons through atmospheric escape, while an average of 45,000 tons is gained from falling dust and meteorites. The margin of error for this calculation is within 0.01% (6 × 10^20 kg), thus the calculated value of Earth’s mass remains unaffected by this factor.
The depletion of mass is a result of gases escaping from the atmosphere. Approximately 95,000 tons of hydrogen per year (3 kg/s) and 1,600 tons of helium per year are released into the atmosphere [32] [33]. On the other hand, the primary contributor to mass gain is the influx of various materials such as cosmic dust and meteors. These substances play a significant role in increasing the Earth’s mass. The estimated amount of material added annually ranges from 37,000 to 78,000 tons [34] [35], although this can vary significantly. For instance, the Chicxulub Impactor event, with an average mass estimate of 2.3 × 10^17 kg [36], added 900 million times the usual amount of dust to the Earth’s mass in a single occurrence.





