

- Residence
- Astral objects

Luminosity
Stars appear differently to observers on Earth, with some appearing brighter and others appearing dimmer.
However, the visual appearance does not accurately represent the true radiation power of the stars, as they are located at varying distances.
For instance, the blue star Rigel in the Orion constellation has an apparent magnitude of 0.11, while the nearby Sirius, the brightest star in the sky, has an apparent magnitude of minus 1.5.
However, Rigel actually emits visible light energy 2200 times more than Sirius, but it appears fainter because it is 90 times farther away from us compared to Sirius.
Therefore, the apparent magnitude alone cannot serve as a reliable characteristic of a star, as it is dependent on the star’s distance.
The true characteristic of a star’s radiative power is its luminosity, which refers to the total energy emitted by a star over a specific time period.
Luminosity in astronomy refers to the total energy emitted by any astronomical object, such as a planet, star, or galaxy, over a given unit of time. It is typically measured in absolute units, such as watts (W) in the International System of Units (SI) or erg/s in the GHS system (centimeter-gram-second). Another common unit of measurement is the Sun’s luminosity (Ls), which is equivalent to approximately 3.86-10 33 erg/s or 3.8-10 26 W.
Luminosity is not influenced by the distance to the object, only the apparent stellar magnitude is affected by it.
Luminosity is a crucial characteristic of stars as it enables us to compare different types of stars with each other in diagrams such as “spectrum – luminosity” and “mass – luminosity”.
The calculation of a star’s luminosity can be done using the following formula:
where R is the radius of the star, T is the temperature of its surface, and σ is the Stefan-Boltzmann constant.
It is worth noting that the luminosities of stars can vary greatly: there are stars whose luminosities are 500,000 times greater than that of the Sun, while there are dwarf stars whose luminosities are about the same number of times less.
While the luminosity of a star can be measured in physical units, such as watts, astronomers often prefer to express it in units relative to the Sun’s luminosity.
Another way to express the true luminosity of a star is through its absolute stellar magnitude.
Let’s imagine that we have placed all the stars side by side and view them from the same distance. In this case, the apparent stellar magnitude will no longer depend on the distance and will be solely determined by the luminosity.
The standard distance is defined as 10 parsecs, which is denoted as 10 ps.
The absolute stellar magnitude (M) refers to the apparent stellar magnitude (m) that a star would have at this standard distance.
In other words, the absolute stellar magnitude quantitatively represents the luminosity of an object, corresponding to the stellar magnitude it would have at a distance of 10 parsecs.
Due to the inverse square law, the luminosity of an object is inversely proportional to the square of the distance.
Let’s consider the illuminance, denoted as E, produced by a star located r parsecs away from the Earth. We can also define E0 as the illuminance from the same star at a standard distance r0 (10 pc).
By applying Pogson’s formula, we can calculate the difference in magnitudes, denoted as m – M, which is given by -2.5 times the logarithm of the ratio of E to E0. This can be further simplified as -2.5 times the logarithm of the ratio of r0 to r, which can be written as -5 times the logarithm of r0 plus 5 times the logarithm of r.
M = m + 5lgr0 – 5lgr .
M = m + 5 – 5lgr . (1)
If in (1) r = r0 = 10 pcthen M = m – according to the absolute stellar magnitude definition.
The distance modulus refers to the discrepancy between the apparent (m) and absolute (M) stellar magnitudes.
While the absolute stellar magnitude M is determined solely by the intrinsic brightness of the star, the apparent stellar magnitude m also depends on the distance r (in parsecs) to the star.
Let’s consider the calculation of the absolute stellar magnitude for a Centauri, one of the closest and brightest stars to us.
With an apparent stellar magnitude of -0.1 and a distance of 1.33 parsecs, substituting these values into formula (1) gives us: M = -0.1 + 5 – 5lg1.33 = 4.3.
This means that the absolute stellar magnitude of Centauri is similar to the absolute stellar magnitude of the Sun, which is 4.8.
We must also take into account the absorption of starlight by the interstellar medium, which diminishes the star’s brightness and increases the apparent stellar magnitude m.
In this case: m = M – 5 + 5lgr + A(r), where the term A(r) represents the contribution of interstellar absorption.
Apparent and absolute stellar magnitudes are topics discussed on the Wikipedia page about Luminosity.

The luminosity of a star refers to the immense amount of energy it releases into space, primarily in the form of various types of rays. It is a measure of the total radiant energy emitted by a star over a specific time period. Luminosity plays a crucial role in the study of stars as it is influenced by all the unique characteristics of a star.
When discussing the brightness of a star, it is important to clarify that it is often mistaken for other characteristics of the celestial body. However, the concept is actually quite simple – one just needs to understand the role of each attribute.
The brightness of a star (L) primarily represents the amount of energy it emits – and is therefore measured in watts, similar to other quantitative measures of energy. This value remains consistent regardless of the observer’s position. For instance, the Sun has a luminosity of 3.82 × 10 26 W. The luminosity of the Sun is frequently used as a reference point to compare the brightness of other stars, which is more convenient – in this case, it is denoted as L☉ (☉ being the symbol for the Sun).
- The brightness of an object is quantified by its visible stellar magnitude or brilliance (m), which is measured in conventional units. The lower the stellar magnitude, the brighter the object appears to the observer. For instance, when observed from Earth, the Sun has a stellar magnitude of -26.7, Arcturus has a magnitude of -0.05, and Spica has a magnitude of +1.04. In reality, Arcturus is 210 times brighter and 25 times larger than the Sun, while Spica is 8300 times brighter and 5 times larger. However, due to their distance from Earth, Arcturus and Spica do not appear as bright. The apparent stellar magnitude is employed in Earth-based observations to facilitate the classification and identification of stars in the night sky.
- When considering the aforementioned factors, luminosity stands out as the most insightful and versatile attribute. It provides us with knowledge about the dimensions, weight, and even the magnitude of nuclear reactions.
- More objective, but not synonymous with brightness, is the absolute magnitude (M) of a star. This is the magnitude of a star that can be seen from a distance of 10 parsecs. The most commonly used absolute magnitude is the bolometric absolute magnitude, which takes into account all the radiation spectra of the star, including X-ray and ultraviolet. For example, the Sun has a bolometric absolute magnitude of +4.7, while Arcturus has a bolometric absolute magnitude of -0.38. Astronomers use the absolute magnitude to calculate the luminosity of a star.
- Hypergiants (0);
- The brightest supergiants (Ia+);
- Bright supergiants (Ia);
- Normal supergiants (Ib);
- Bright giants (II);
- Normal giants (III);
- Subgiants (IV);
- Main-sequence dwarfs (V);
- Subdwarfs (VI);
- White dwarfs (VII);
- Luminosity, which refers to the total amount of energy emitted by a star per unit time (L),
- Surface temperature,
- Mass,
- Radius.
Luminosity is frequently mistaken for apparent stellar magnitude (m), which refers to the amount of energy visible to an observer – in simple terms, how brightly an object can be seen at a specific location in the Universe. (This characteristic is also referred to as luminosity). Stellar magnitude is unitless – it is measured in conventional units, and the lower the value, the brighter the object. Additionally, magnitude is subjective – the distance from the luminous object matters more than its actual luminosity.
Resources related to the subject

The photo of Star Arcturus taken by F. Espenak is displayed here.
One of the most informative and versatile characteristics of a star is its luminosity. Luminosity represents the intensity of a star’s radiation and provides a wealth of information about the star, including its size, mass, and the intensity of its nuclear reactions.
Discovering the origin of radiation in a star doesn’t take much time. All the energy that can exit the star is generated through thermonuclear fusion reactions in its core. Under gravitational pressure, hydrogen atoms fuse together to form helium, releasing a tremendous amount of energy. In more massive stars, not only hydrogen but also helium and occasionally heavier elements like iron undergo fusion. This leads to an even greater release of energy.
The amount of energy released during a nuclear reaction is directly influenced by the star’s mass. The larger the star, the more gravity compresses its core, resulting in a higher rate of hydrogen transforming into helium. However, the star’s luminosity is not solely determined by nuclear energy—it must also be radiated outward.
Resources related to the subject

And this is where the role of the radiation zone becomes important. Its impact in the process of energy transfer is significant, as can be observed in everyday situations. For instance, an incandescent bulb, with its filament heating up to 2800 °C, will not noticeably change the room temperature even after 8 hours of use – whereas a regular battery, with a temperature of 50-80 °C, will warm up the room to a noticeably uncomfortable level. The difference in efficiency can be attributed to the varying amounts of surface area that radiate energy.
It appears that when determining the luminosity of a star, the size of the star plays a more significant role than the temperature and energy of its core. This, however, is not entirely accurate. Blue giants, despite their high luminosity and temperature, have comparable luminosity to red supergiants, which are significantly larger in size. Furthermore, the star known as R136a1, which is both incredibly massive and one of the hottest stars, possesses the highest luminosity of any star currently known. Until a new star with even higher luminosity is discovered, this settles the debate regarding the most crucial parameter for determining luminosity.
Astronomy applications of luminosity
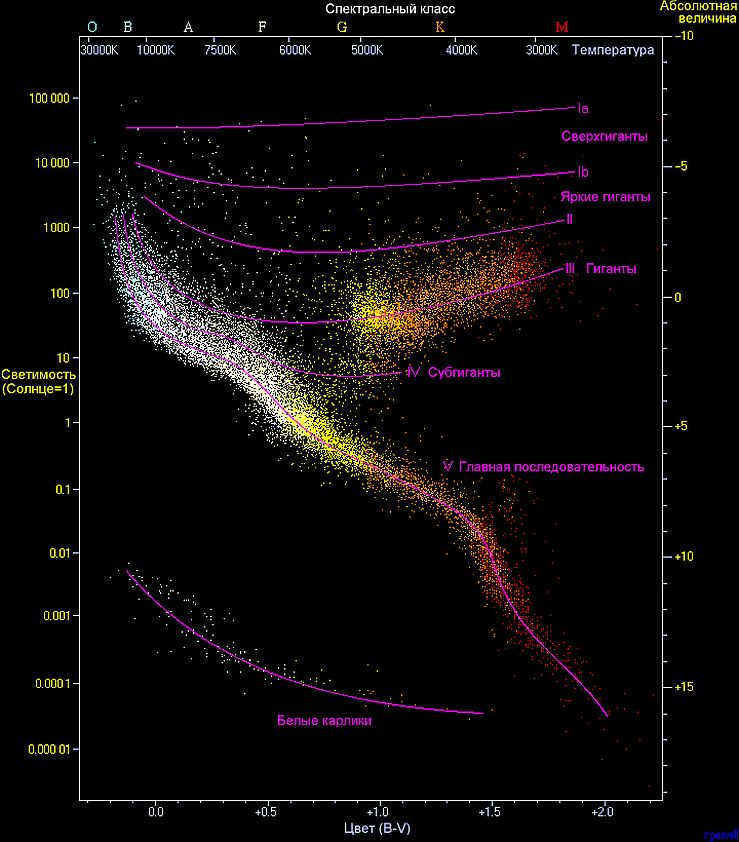
The Hertzsprung-Russell diagram.
Hence, luminosity serves as a relatively accurate representation of both a star’s energy and its surface area. This is the reason why astronomers utilize it in numerous classification diagrams for comparing stars. One such diagram is the Hertzsprung-Russell diagram, which reveals intriguing patterns in the distribution of stars throughout the universe. For instance, it enables the easy determination of a star’s age. The Yerkes spectral classification of stars also relies on luminosity, including the identification of “white dwarfs” and “supergiants”.
If you enjoy this post, why not share it with your friends?
Astrophysics includes the study of photometry in cosmic objects. However, stellar photometry, in particular, has a significant impact on stellar astronomy, so it is essential to become familiar with the fundamental principles of photometry.
Visible stellar magnitude m is a measure of the amount of light created by a source at the place of observation, considering the absorption of light by the Earth’s atmosphere. The relationship between stellar magnitude m and light intensity is determined by the Weber-Fechner law, which was discovered by English astronomer N. Pogson in the mid-19th century. Pogson found that there is a ratio of about 100 between the interval of 5 stellar magnitudes and the ratio of light fluxes or light intensity. He defined this ratio as exactly 100, which means that a decrease in luminosity by one stellar magnitude corresponds to a decrease in light intensity from the object by slightly more than a factor of 2.5. The value a represents the zero point of the stellar magnitude scale, which is determined by the choice of the photometric standard. Usually, a group of stars with accurately measured brightness is chosen as the standard. The luminosity of any star can be determined in relation to the standard star using the formula where the zero index represents the corresponding magnitude for the standard star.
To calculate the absolute stellar magnitude, which measures the luminosity of a star, one can use the known apparent stellar magnitude and the distance from the Sun. This absolute magnitude is defined as the apparent magnitude transferred to a standardized distance common to all stars. By knowing the apparent magnitude V and the distance to the star, the absolute magnitude MV can be easily determined. It is important to note that the change in distance to the star corresponds to a change in illuminance according to the ratio (r/r0)2. The absolute magnitude is determined by the formula: MV = V – 5 * log10(r/r0), where the distance r0 is taken as 10 parsecs. This expression is valid only if there is no scattering or absorbing matter between the observer and the star. If there is such matter, a part of the difference (V – MV) should be attributed to the scattering or absorption of light. However, absorption of light only affects the apparent magnitude V, not the absolute magnitude MV. The absorption of light decreases the star’s luminosity, increasing the apparent magnitude. If we do not take light absorption into account, V – MV is called the distance modulus, and if we do take it into account, it is called the true distance modulus denoted by (V0 – MV). It is important to obtain the true distance modulus from observational data to estimate the true distance to a cosmic object. The determination of absolute stellar magnitudes and distance moduli is a crucial task in stellar astronomy.
Please note that the index V is included in the absolute stellar magnitude designation to highlight that MV represents the energy emitted by a star within a specific spectral range, rather than across the entire spectrum.
To conclude, there is a clear relationship between the absolute stellar magnitude MV and the star’s luminosity L, similar to the connection between apparent stellar magnitude and luminosity, where the index s denotes the values for the Sun. Therefore, MVs = +4 m .83.
In reality, stellar magnitudes can vary as there are no identical celestial bodies in our Universe. While there may be similarities and parameters that allow us to categorize objects, there will always be at least slight differences between them.
The brightness of an object in astronomy is represented by the concept of stellar magnitude, which is a dimensionless numerical value. This value indicates the energy flux of all photons emitted by the celestial body per second per unit area.

What do stellar magnitudes mean?
There are two types of stellar magnitudes in the field of astronomy: apparent and absolute.
Apparent magnitude
The apparent magnitude is a measure of the visible brightness of stars and is used for visual observations in different wavelength ranges, such as ultraviolet and infrared.
It actually depends on the luminosity and the distance of the celestial body. In other words, the smaller the apparent magnitude of a star, the brighter it is in reality.

Sirius (the brightest star)
Absolute stellar magnitude.
The absolute stellar magnitude is utilized to precisely characterize an object, which is equivalent to the value at a distance of 10 parsecs from it. The absolute magnitude is employed to compare the luminosity of stars since it is not dependent on their distance from us.
Furthermore, the absolute value of the star’s brightness is necessary for calculating its luminosity.
How to Determine Stellar Magnitude
In the 2nd century BC, the Ancient Greek astronomer Hipparchus devised a system to classify stars based on their brightness. He categorized the brightest stars as first magnitude and the dimmest stars as sixth magnitude.
In simpler terms, a first magnitude star is the brightest star visible in the sky.
Hipparchus was the first to introduce this classification, but subsequent scientists have expanded on his work and added to our knowledge of celestial bodies.
In 1856, Norman Pogson proposed a different method for calculating the scale of stellar brightness, which has since become widely accepted.
The formula for calculating the difference between stellar magnitudes is given by m = -2.5log(L/L0), where m is the stellar magnitude of the body, and L is the luminosity from it.
It’s important to note that Pogson’s formula can only determine the difference between magnitudes, not the actual magnitudes themselves. This is because the calculation requires a zero point, which represents the luminosity corresponding to the zero measure of the star.
The zero point used to be defined as Vega’s luminosity, but it has been redefined over time. However, when visually observed, Vega is still considered as the zero measure.
Interestingly, the brightest objects in the sky have negative stellar magnitudes.
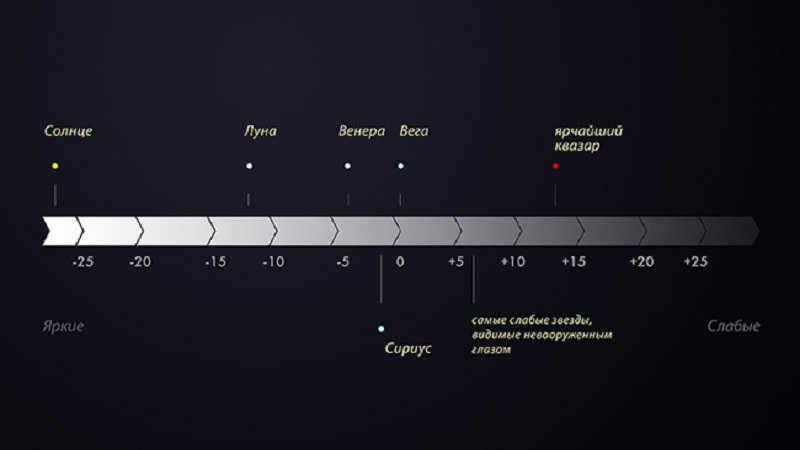
By the way, in contemporary astronomy, stellar magnitudes are utilized not just for stars, but also for planets and other celestial entities. However, when characterizing them, both the apparent and absolute values are taken into consideration.
Therefore, stellar brightness and stellar magnitude are significant indicators of an object. Naturally, they are influenced by other chemical and physical properties of the celestial body.
The luminaries’ light shines brightly in the night sky. Nevertheless, modern instruments and techniques enable astronomers to observe stars with high magnitudes. To put it simply, it has become feasible to perceive even the faintest of stars.
Exercises on a spheroidal mirror
The distinction between the brightness and luminosity of a star is important. When discussing stars, there are two key measurements that describe a star’s luminosity: absolute stellar magnitude, which represents the star’s apparent brilliance if it were 10 parsecs away, and luminosity, which quantifies the amount of energy emitted by the star in one second. Additionally, there is a measurement called apparent stellar magnitude, which indicates how well we can see the star.
For the purpose of this discussion, we will focus on the luminosity of stars.
The luminosity of a star represents the total amount of radiant energy emitted by the star over a specific time period. It is closely tied to many other characteristics of the star.
The quantity of energy released during a nuclear reaction is directly influenced by the mass of the star – the bigger it is, the greater the compression of the radiant core due to gravity, resulting in the simultaneous conversion of more hydrogen into helium. However, luminosity, which refers to the amount of energy radiated outward, is not solely determined by nuclear energy. So, what significance does luminosity hold in the field of astronomy?
The application of luminosity in astronomy.
The previous passage discussed the correlation between a star’s temperature and its luminosity. Astronomers utilize this relationship to determine the star’s parameters, particularly when the object’s color, which serves as an accurate indicator of its heating, is distorted by gravitational forces. Furthermore, the brightness of a star is indirectly connected to its composition. A luminous star with fewer elements heavier than helium and hydrogen in its matter has the potential to acquire more mass, which is a crucial factor in determining its brightness.
However, why is it that stars with equal luminosity do not appear equally bright when observed in the night sky?
If you found this article interesting, I hope you enjoyed reading it. Don’t forget to give it a thumbs up if you liked it, and feel free to check out my other articles as well.
As you may be aware, the luminosity of stars is a key characteristic that distinguishes them. It serves as the initial indicator by which we differentiate the celestial bodies in the night sky.
Nevertheless, stellar luminosity is not constant, as even with the naked eye, one can observe that some stars shine more brightly than others. In fact, in the field of astronomy, stellar luminosity does not measure how bright a star appears to an observer, but rather its radiation intensity.

How Stars Shine in the Sky and Emit Light
It’s quite simple – stars produce energy and emit light as a result of thermonuclear reactions happening inside them, which generate very high temperatures.
To explain further, when hydrogen is converted into helium, a tremendous amount of energy is released, causing the hydrogen to burn. In the case of massive stars, not only hydrogen burns, but also helium and sometimes even heavier elements. This leads to the production of even more energy.
The majority of this energy is in the form of various types of radiation, which collectively give stars their shining ability.
Therefore, the luminosity of a star represents the total amount of energy emitted as radiation over a specific period of time.

The luminosity of Betelgeuse is 80,000 times higher than that of the Sun, and its maximum luminosity is 105,000 times higher than that of the Sun.
Consequently, the amount of energy emitted by a star determines its luminosity, with the mass of the star playing a significant role.
Mass plays a crucial role in determining the level of luminosity in stars. However, it is not solely responsible for energy production; that energy must also be brought to the surface. Interestingly, the size of the radiating surface also impacts the brightness of a star. The larger the surface area, the more intense the emission.
Therefore, the luminosity of a star is not only influenced by the amount of energy it emits, but also by the size of its surface.
It is important to note that the temperature inside and on the surface of any celestial body affects many of its parameters and properties.
To start with, this characteristic enables you to compare various kinds of stars as it is influenced by nearly all stellar parameters.
The luminosity of stars can be determined by utilizing the following equation:
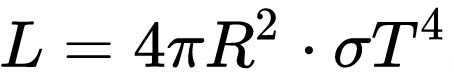
The equation to determine the luminosity of a star
In this equation, the variables are as follows: R represents the star’s radius, T represents the surface temperature, and σ represents the Stefan-Boltzmann constant.
From the equation, it is evident that the key factors affecting luminosity are mass, size, and temperature. By knowing the total amount of radiant energy emitted by a celestial body, we can derive other important information.
It is important, however, not to confuse the luminosity of stars with their brightness and brilliance. While brilliance refers to a visual indicator of an object’s brightness, we are discussing the quantity of radiated energy. To calculate luminosity, it is necessary to determine the absolute magnitude of the star (stellar magnitude at a distance of 10 parsecs from the body).


Spica can be identified as the brightest star in the constellation Virgo and holds the sixteenth position in terms of brightness in the night sky, exhibiting an apparent stellar magnitude of +1.04.
It is worth noting that the term “apparent stellar magnitude” is often misused to describe the luminosity of stars. However, it is important to understand that the concept of luminosity takes into account the distance of the object, making it a subjective measurement.
When studying celestial objects, the level of brightness is a crucial factor as it is influenced by the chemical and physical properties of the star. This means that by knowing this measurement, we can gather a wealth of information. For instance, we can determine the composition, color, size, mass, and even the intensity of thermonuclear reactions.
Interestingly, the familiar twinkling of stars in the night sky is caused by various factors. There are countless phenomena occurring around us that often go unnoticed or are not pondered upon.
To an observer on Earth, these luminous stars are undoubtedly captivating celestial entities. However, the mechanics behind their glow and the processes involved can be perplexing and unfathomable at times. Nevertheless, we can all appreciate the beauty of the Universe and its diverse creations.

Stars release an immense quantity of energy into the vast expanse of outer space, which is predominantly composed of various types of rays. The cumulative radiant energy emitted by a celestial body over a given duration is referred to as the star’s luminosity. Understanding the luminosity of a star is crucial in the exploration of celestial bodies as it encompasses all the fundamental attributes of the star.
The Basics of Stellar Brightness
When discussing the brightness of a star, it is important to understand that it can be easily mistaken for other characteristics of the celestial body. However, it is actually quite simple – each characteristic has its own distinct function.
The brightness of a star (L) primarily represents the amount of energy that the star emits, and is therefore measured in watts, similar to any other quantitative measure of energy. It is an objective value that remains constant regardless of the observer’s position. For example, the Sun has a brightness value of 3.82 × 10 26 W. This value is often used as a reference point to compare the brightness of other stars, and is denoted as L☉ (☉ being the graphical symbol for the Sun).
Luminosity is frequently mistaken for apparent stellar magnitude (m), which refers to the amount of energy visible to an observer – in other words, how brightly an object can be seen at a specific location in the Universe. This measurement is also known as luminosity. Stellar magnitude is unitless and is measured in conventional units, with smaller values indicating brighter objects. It is worth noting that magnitude is subjective, as the distance from the luminous object is more significant than its actual luminosity.
Resources about the subject


Star Arcturus as seen from Earth. The photo was taken by F. Espenak.
Undoubtedly, the most informative and versatile characteristic among the ones mentioned above is luminosity. Luminosity provides a detailed representation of a star’s radiation intensity and can be utilized to determine various characteristics of a star, including its size, mass, and the intensity of nuclear reactions.
Luminosity from A to Z
The magnitude of energy released during a nuclear reaction is directly dependent on the size of the star – the bigger it is, the stronger the gravity compresses the radiant core, and the more hydrogen is simultaneously transformed into helium. However, the luminosity of the star is not solely determined by nuclear energy – it also needs to be radiated outward.
Resources related to the subject

And this is where the radiation area comes into action. Its impact on the energy transfer process is substantial, which can be easily observed even in a household setting. For instance, an incandescent light bulb with a filament that reaches a temperature of 2800 °C will not cause a significant change in room temperature even after being operated for 8 hours. On the other hand, a typical battery with a temperature ranging from 50-80 °C will heat up the room to a noticeable level. The variation in efficiency can be attributed to the disparity in the surface area responsible for radiating energy.
The proportion of a star’s core area to its surface area is often comparable to the ratios of a light bulb filament and a battery. The core of a red supergiant can be as small as one ten-thousandth of the star’s total diameter. As a result, the luminosity of a star is greatly influenced by the size of its radiating surface, which is the star’s own surface. The temperature is not as significant in this regard. The surface heat of the star Aldebaran is 40% lower than the temperature of the Sun’s photosphere, but due to its large size, its luminosity is 150 times greater than that of the Sun.
Therefore, when determining the luminosity of a star, the significance of its size surpasses that of core temperature and energy. That being said, this does not mean that these factors are insignificant. For instance, blue giants exhibit both high luminosity and temperature, yet their luminosity is comparable to that of red supergiants, which are considerably larger in size. It is worth noting that the star R136a1, one of the most massive and hottest stars known, possesses the highest luminosity of any star discovered thus far. Until a new star with even higher luminosity is identified, this effectively settles the ongoing debate regarding the most dominant parameter for luminosity.

The Hertzsprung-Russell diagram
In the previous paragraph, we discussed how the temperature of a star can impact its brightness. Astronomers utilize this correlation to calculate the characteristics of a star, especially when the color, which is the most reliable indicator of an object’s temperature, is altered by gravitational forces. Moreover, the brightness of a star is indirectly linked to its composition. The fewer elements present in the star’s matter that are heavier than helium and hydrogen, the greater its mass can be, which is a crucial factor in determining the star’s brightness.
The luminosity of stars and the luminosity of the Sun
Stars generate and expel immense quantities of energy into the vast expanse of outer space. The collective energy emitted by a star is referred to as its luminosity. Luminosity denotes the total energy released by a star over a given period and is measured in absolute units (SI, W; GHS, erg/s) or in terms of the Sun’s luminosity (L⊙ = 3.827⋅10 33 erg/s = 3.827⋅10 26 W). Luminosity is contingent upon all the characteristics of a star and stands as one of the most vital parameters. Luminosity remains unaffected by the distance to the object, thereby enabling comparisons to be drawn between different types of stars. It is feasible to approximate the luminosity of stars by employing the following formula:
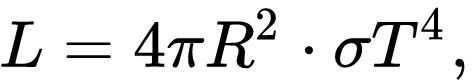
The luminosity of a star can be calculated using the formula:
L = 4πR^2σT^4
where L is the luminosity, R is the radius of the star, T is the temperature of its photosphere, and σ is the Stefan-Boltzmann constant. This formula shows that the luminosity depends on the size of the star and the temperature of its photosphere. By substituting the data of the Sun into this formula, we can calculate its luminosity.
In addition to calculating luminosity, we can also measure it by comparing the light intensity of other stars to the Sun’s light intensity. This method is more convenient and visually informative.

Due to its informative characteristics, luminosity is utilized in numerous classification charts and diagrams that astronomers employ to compare stars. It effectively and accurately represents the energy and surface area (size) of a star.
Stars release a vast quantity of energy into the outer space, predominantly consisting of various types of rays. The total radiant energy emitted by a star during a specific timeframe is referred to as the star’s luminosity. Luminosity plays a crucial role in the examination of celestial bodies as it is dependent on all the star’s characteristics.
Basic Aspects of Stellar Brightness
When discussing the brightness of a star, it is important to understand that it can easily be mistaken for other properties of a celestial object. However, in reality, it is quite straightforward – one just needs to comprehend the role of each characteristic.
The brightness of a star (L) primarily indicates the amount of energy it radiates – and is therefore measured in watts, similar to any other quantitative energy attribute. It is an objective value: it remains constant regardless of the observer’s position. For instance, the Sun has a luminosity of 3.82 × 1026 watts. The luminosity of our Sun is often utilized as a reference to gauge the brightness of other stars, which is much more convenient for comparison – in such cases, it is denoted as L☉, (☉ being the graphic symbol for the Sun).
Luminosity is frequently mistaken for apparent stellar magnitude (m), which refers to the amount of energy that is visible to an observer – in other words, how brightly an object can be seen at a specific location in the Universe. This measurement is also known as luminosity. Stellar magnitude is a dimensionless quantity that is measured in conventional units, with smaller values indicating greater brightness. It is also a subjective measurement, as the distance from a luminous object is more significant than its true luminosity.
Clearly, the most informative and versatile characteristic among the ones mentioned above is luminosity. Since luminosity represents the intensity of a star’s radiation in the most comprehensive way, it can provide information about various characteristics of the star, such as its size, mass, and the intensity of nuclear reactions.
Luminosity: An A-Z Guide
The luminosity of a star is directly influenced by its mass. In simple terms, the larger the star, the more gravity compresses its core, leading to a higher conversion of hydrogen into helium. However, nuclear energy is not the sole factor that determines a star’s luminosity, as it must also be radiated outward into space.
And that’s where the radiation zone comes in. Its impact on the process of energy transfer is significant, as can be easily observed in everyday life. For example, an incandescent bulb, with a filament that reaches a temperature of 2800 °C, will not have a significant effect on the room temperature after being used for 8 hours. On the other hand, a conventional heater with a temperature of 50-80 °C will noticeably warm up the room. This difference in efficiency is due to variations in the amount of surface area that radiates energy.
The proportion of the core area of a star to its surface is often comparable to the ratios of the filament in a light bulb and the battery – the cross-sectional area of a red supergiant’s core can be as small as one ten-thousandth of the star’s total diameter. Therefore, the brightness of a star is heavily influenced by the surface area that emits radiation, or the star’s own surface. In this case, temperature is not as significant. The surface temperature of the star Aldebaran is 40% lower than the temperature of the Sun’s photosphere – but due to its large size, its brightness surpasses that of the Sun by 150 times.
The application of luminosity in the field of astronomy
The previous passage has discussed the correlation between a star’s temperature and its luminosity. Scientists in the field of astronomy utilize this connection to determine various characteristics of a star, particularly when the color, which is the most precise indicator of an object’s heating, is influenced by the force of gravity. Furthermore, the luminosity of a star is indirectly linked to its composition. The smaller the amount of elements heavier than helium and hydrogen present in the star’s structure, the greater its capacity to accumulate mass – a crucial factor in determining the star’s brightness.
Describing celestial objects can be quite perplexing. Apparent magnitude, absolute magnitude, and luminosity are just a few of the parameters that only apply to stars. In this article, we will focus on understanding luminosity. What exactly is the luminosity of a star? And does it have any connection to its visibility in the night sky? Furthermore, we will explore the luminosity of our very own Sun.
The Characteristics of Stars
Stars are celestial bodies that emit light and are formed through the compression of gases and dust due to gravity. At the core of stars, nuclear reactions occur, which give them their luminosity. The spectrum, size, luminosity, and internal structure are the main defining features of stars, and these characteristics vary based on the star’s mass and chemical composition.

What is the luminosity of stars?
Stars emit energy through thermonuclear reactions. Luminosity is a physical measurement that quantifies the amount of energy a celestial body produces over a specific period of time.
It is often mistaken for other parameters, such as the brightness of stars in the night sky. However, brightness or apparent magnitude is an approximate characteristic that is not directly measured. It is mostly determined by the star’s distance from Earth and only indicates how well the star can be seen in the sky. The lower the value, the brighter the star appears.

Unlike the luminosity of stars, which is an objective parameter and independent of the observer’s location, the absolute stellar magnitude is a measure of the brightness of a star that can be seen by an observer at a distance of 10 parsecs or 32.62 light-years. Although approximate to luminosity, it is not identical and is commonly used in the calculation of a star’s luminosity. The luminosity of a star is a characteristic that determines its energy output and can vary during different stages of its evolution.
The measurement of energy emitted by a celestial object is defined in different units such as watts (W), joules per second (J/s), or ergs per second (erg/s). There are multiple methods available to calculate this parameter.
One way to calculate it is by using the formula L = 0.4(Ma – M) if the absolute magnitude of the desired star is known. Here, the letter L represents luminosity, M represents the absolute stellar magnitude, and Ma represents the absolute magnitude of the Sun (4.83 Ma).
Another method requires more information about the celestial body. If the radius (R) and the surface temperature (Tef) are known, the luminosity can be determined using the formula L = 4πR2sT4ef. Here, the letter s represents the Stefan-Boltzmann constant, which is a stable physical quantity.
The luminosity of our Sun is equivalent to 3.839 × 10^26 watts. To simplify matters and make them easier to understand, scientists often compare the luminosity of celestial bodies to this value. As a result, there are entities that are thousands or even millions of times dimmer or more intense than our Sun.

Classification of Star Luminosity
In order to compare stars, astronomers employ various classifications. These classifications are based on spectra, size, temperature, and other factors. However, to obtain a more comprehensive understanding, multiple characteristics are often considered simultaneously.
The central Harvard classification system is based on the spectral emissions of stars. It utilizes Latin letters, each corresponding to a specific color of radiation (O-blue, B-white-blue, A-white, etc.).

Stars that belong to the same spectrum can exhibit varying levels of luminosity. As a result, scientists have devised the Yerkes classification system, which takes this factor into consideration. It categorizes stars based on their luminosity, as determined by their absolute magnitude. Thus, each type of star is assigned not only a letter corresponding to its spectrum, but also a number that represents its luminosity. The categories are as follows:
The Hertzsprung-Russell diagram illustrates the correlation between absolute magnitude, temperature, spectrum, and luminosity of stars. Its inception dates back to 1910, when it merged the Harvard and Yerkes classifications, enabling a more comprehensive approach to the assessment and categorization of celestial bodies.
Variations in Brightness
There is a strong correlation between the different characteristics of stars. The luminosity of a star is influenced by both its temperature and mass, which in turn are dependent on the chemical composition of the star. In general, stars with a lower abundance of heavy elements tend to have a greater mass.
The largest and most powerful stars in the universe are hypergiants and supergiants, which have significant mass and luminosity. However, they are also extremely rare. On the other hand, the majority of stars are dwarfs, which have lower mass and luminosity compared to the giants. Dwarfs make up approximately 90% of all stars.
The blue hypergiant R136a1 is currently recognized as the largest star in existence, surpassing all others in mass. Its luminosity is an astonishing 8.7 million times greater than that of the Sun. In the constellation of Swan, there is a variable star known as R Swan that exceeds the Sun’s luminosity by an impressive 630,000 times. Additionally, the star S Goldfish surpasses this parameter by an impressive 500,000 times. On the other end of the size spectrum, the star 2MASS J0523-1403 is one of the smallest stars known, with a luminosity of just 0.00126 times that of the Sun.
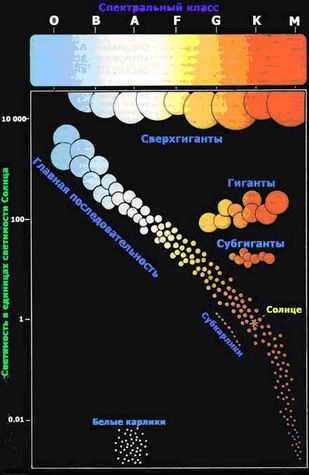
Thanks to the research conducted by astronomers from various countries, we have gained a wealth of knowledge regarding the development and evolution of stars in recent decades. These insights have been obtained through the careful observation of numerous stars at different stages of their life cycles.
The primary attributes of stars include:
All of these characteristics are interconnected, and this relationship is visually represented in the Hertzsprung-Russell diagram (the picture illustrates the correlation between Spectrum and Luminosity).
By examining this diagram, we can observe that the stars form a specific pattern. The band that extends from the top left corner to the bottom right corner is referred to as the “main sequence”. Situated in the upper right corner are the red giants, which are both cool and massive. In the lower left corner, we find the white dwarfs, which are extremely hot but also very compact. It is worth noting that the Sun belongs to the G2 spectral class.
Now, let’s delve deeper into the fundamental characteristics.

The measurement of star brightness (L) is typically given in terms of the Sun’s brightness (4x erg/s). The brightness of a star can be determined by measuring the amount of energy that reaches the Earth, assuming the distance to the star is known. The brightness of stars can vary greatly, with the majority of stars being classified as “dwarfs” and having a brightness that is often insignificant, especially when compared to the Sun.
The star’s absolute magnitude is a characteristic of its luminosity. Another concept is the apparent stellar magnitude, which is influenced by the star’s luminosity, color, and distance. The absolute magnitude is typically used to estimate the size of stars regardless of their distance. To determine the true magnitude, one can place the stars at a hypothetical distance, such as 10PK. Stars with high luminosity have negative values. For instance, the sun has an apparent magnitude of -26.8. At a distance of 10KPK, this value would be +5 (the faintest stars visible to the naked eye have a value of +6).
The temperature on the surface
By utilizing the established principles of thermodynamics, we are able to ascertain the temperature of an object by gauging the wavelength at which black color radiation reaches its maximum intensity.
As a result, if the surface temperature is within the range of 3-4 thousand K, it will emit a reddish hue, while a temperature of 6-7 thousand K will produce a yellow color. Furthermore, a surface temperature of 10-12 thousand K will manifest as a white or blue shade. The subsequent table details the specific wavelength intervals that correspond to the various colors observable within the optical spectrum.
The relationship between color and wavelength
The arrangement of star spectra acquired by the progressive alteration of their surface layers is indicated by the subsequent letters: O, B, A, F, G, K, M (in order of increasing temperature). Each of these classes is further divided into 10 additional subclasses (for instance, B1, B2, B3…). A comprehensive categorization of the spectral class of stars is depicted in the subsequent table.
Stars’ Spectral Classes
| Class designation of stars | Characteristics of spectral lines | Surface temperature, K |
| O | Presence of ionized helium | > 30,000 |
| B | Presence of neutral helium | 11,000 – 30,000 |
| A | Presence of hydrogen | 7,200 – 11,000 |
| F | Presence of ionized calcium | 6,000 – 7,200 |
| G | Presence of ionized calcium and neutral metals | 5,200 – 6,000 |
| K | Presence of neutral metals | 3,500 – 5,200 |
| M | Presence of neutral metals and absorption bands of molecules |
Author: Tatiana Sidorova, update date: 17.05.2018
Reprinting without an active link is prohibited!
As we are aware, the brightness of stars is a key characteristic of theirs. This is the initial way in which we differentiate the celestial bodies in the night sky.
However, the brightness of stars varies, as even with the naked eye, one can observe that some shine more brightly than others. In reality, in the field of astronomy, the brightness of stars does not indicate how bright they appear to an observer, but rather their radiation intensity.

Reasons why stars shine brightly and emit light
The process is quite straightforward – stars generate energy and release light as a result of incredibly high-temperature thermonuclear reactions occurring within them.
To be more precise, when hydrogen is converted into helium, an immense amount of energy is released, causing hydrogen to ignite. In massive stars, not only helium but also other heavier elements can ignite. In such cases, even more energy is produced.
This energy manifests in various forms of radiation, all of which contribute to the luminosity of stars.
Therefore, the luminosity of a star refers to the total amount of radiant energy emitted during a specific time period.


The luminosity of Betelgeuse is 80,000 times higher than that of the Sun, and its maximum luminosity is 105,000 times higher than that of the Sun
Therefore, the greater the energy generated by the celestial body, the greater its luminosity. It appears to be dependent on the object’s mass.
Mass plays a crucial role, not only determining the luminosity level of stars but also in the process of bringing energy from the inside to the surface. Additionally, the size of the radiating surface impacts the brightness of a stellar body, with larger surfaces producing stronger radiation.
Hence, the luminosity of stars is a reflection not only of the amount of energy emitted but also of the size of their surface.
Furthermore, it is important to acknowledge that the temperature inside and on the surface of any celestial object influences various indicators and properties.
Methods for determining the luminosity of stars
One of the primary purposes of determining the luminosity of stars is to compare and contrast different types of stars. This characteristic is influenced by nearly all stellar parameters, making it an essential factor in understanding the nature of stars.
The luminosity of stars can be calculated using the following formula:
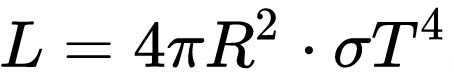
The equation for determining the luminosity of a star is as follows:
L = 4πR²σT⁴
where L represents the luminosity, R is the radius of the star, T is the surface temperature, and σ is the Stefan-Boltzmann constant.
From this formula, it is evident that the key factors in determining the luminosity are the mass, size, and temperature of the star. By knowing the total radiant energy emitted by a star, we can deduce other important properties.
However, it is crucial to differentiate between the luminosity and brightness of stars. While luminosity refers to the amount of radiated energy, brightness is a visual indicator of the object’s intensity. To calculate the luminosity, the absolute magnitude of the star (stellar magnitude at a distance of 10 parsecs) must be known.

Spica, located in the constellation of Virgo, is widely recognized as the most brilliant star in the sky, boasting an apparent stellar magnitude of +1.04.
It is worth noting that many people mistakenly use the term “apparent stellar magnitude” to refer to the luminosity of stars. However, this is a subjective measurement that heavily relies on the distance to the object in question.
The luminosity of celestial bodies plays a crucial role in the study of stars as it provides valuable insights into their chemical and physical properties. By understanding this indicator, we can glean information about the composition, color, size, mass, and even the intensity of thermonuclear reactions taking place within them.
Interestingly, the twinkling of stars that we observe in the night sky is influenced by a multitude of factors. There is a vast array of phenomena occurring around us that often go unnoticed or unconsidered.





