Definition of a parsec and a light year - Explore the Universe: Your Guide to Astronomy

When it comes to faraway celestial entities, those not well-versed in the field of astronomy often wonder: how do astronomers, astrophysicists, and cosmologists ascertain the distance to the object being studied and how do they go about determining it? In this article, I will delve into the methods employed by astronomers to measure distances to celestial objects and the measurement systems they rely on for their calculations.

Units of Measurement in Astronomy

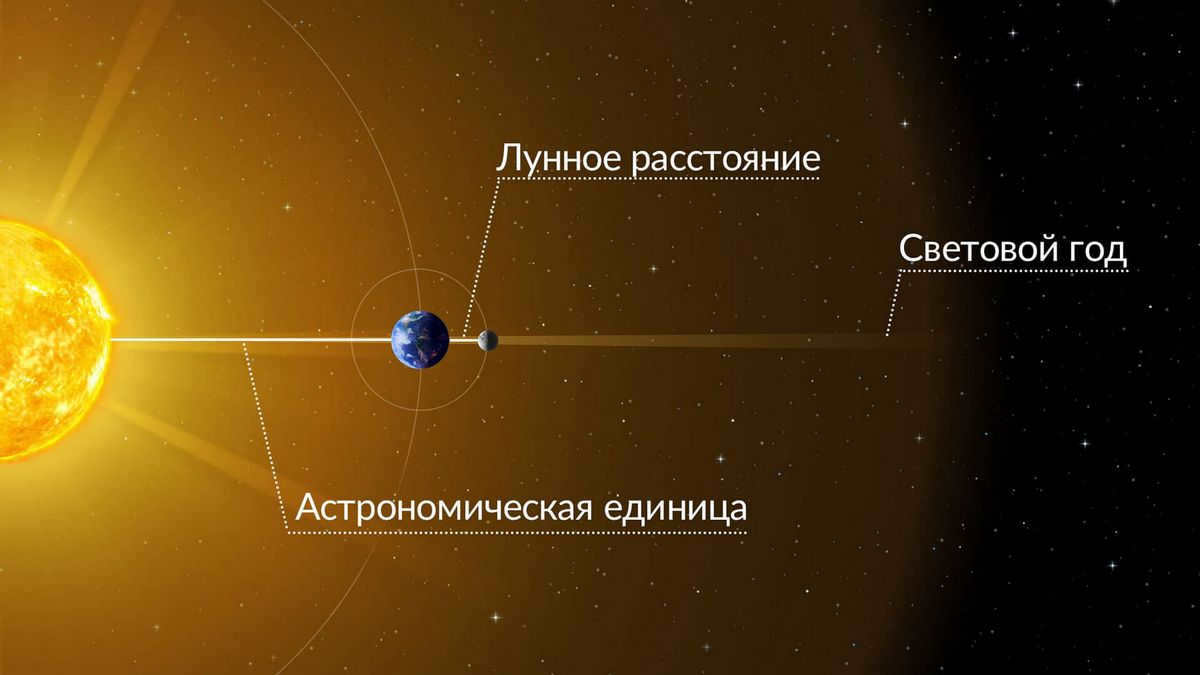
In the early stages of astronomy, distances to celestial bodies were measured using kilometers and other familiar units of measurement on Earth. However, as people began to realize that they and their world were not the center of the universe, and that the cosmos was much larger than it appeared, it became impractical to measure cosmic distances using conventional values. As a result, astronomers devised specialized units of measurement. The first of these was the astronomical unit. The astronomical unit (abbreviated as a.e.; internationally known as au since 2012, with the older designation ua used in previous sources) represents the average distance between the Earth and the Sun’s centers. This unit allows individuals to visualize the distance between the Earth and the Sun’s centers.

Light-years and parsecs.

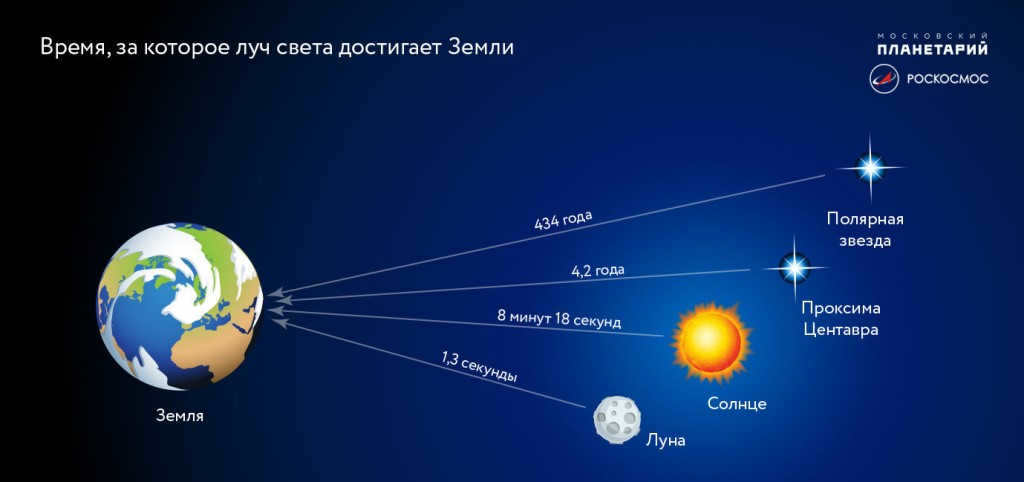
To determine the distance to a nebula star and other objects in deep space, astronomers commonly rely on the concept of a light-year (known as sv.let. in Russian and abbreviated as ly in international usage). A light-year is defined as the distance that light travels in one year. When studying nearby stars, scientists can estimate their distance by measuring their annual parallax or by examining the orbits of double or multiple star systems.

When it comes to even greater distances, scientists rely on novae and supernovae as indicators of distance. These celestial events, novae and supernovae, have a consistent true (absolute) luminosity. By comparing the absolute luminosity to the observed luminosity, scientists can determine the distance to the supernova or the galaxy in which it is located. However, let’s return to the concept of the light year. Astronomers frequently utilize the light year as a unit of measurement for distances within the Milky Way. For instance, the distance from the Sun to the Alpha Centauri system is 4.3 light-years, while the distance from the Solar System to the Crab Nebula is 6300 light-years. Unfortunately, the light year is not without its limitations. While it is intuitive for many, it is primarily applicable to stellar distances and is rarely used for measurements involving galaxies.

The famous Andromeda Nebula is located at a distance of nearly 2.5 million light years. Located 2.5 million light years awayAnd this is where the parsec comes into play. Parsec (Russian: пк.; international: pc) serves as a cosmic unit of measurement that astronomers commonly employ to determine the distance to extremely distant objects in the Universe. The term “parsec” is a combination of two words: parallax and second. However, it’s not just any second. It is an angular second.. As you may be aware, angles are measured in degrees, each of which is divided into 60 parts, and each part is further divided into 60 seconds.

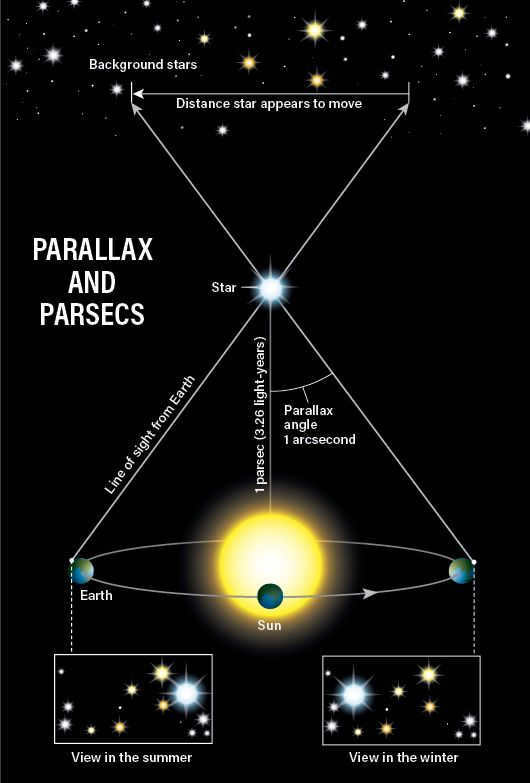
The position of the observer determines the displacement of a celestial object relative to the background (starry sky), a phenomenon known as parallax.

Astronomers study three types of parallax – diurnal, annual, and centennial. The annual parallax is utilized in determining the parsec. By measuring the annual parallax of a celestial object, astronomers can calculate its distance from Earth. To do this, they construct an imaginary right triangle. The hypotenuse represents the distance from the observed star to the Sun, while one of the catheti represents the distance from Earth to the Sun (AU). The angle within this triangle is determined by the annual parallax of the observed star. The distance to a star where this angle measures one second is defined as one parsec. Amateur astronomers are likely familiar with the fact that one parsec is equivalent to 3.2616 light-years. This unit serves not only a practical purpose in calculating distances in the Universe but also provides convenience for astronomers in their calculations. It is much simpler to denote the distance from the Sun to the nearest star as 1.3 pc (parsecs) rather than 40.7 trillion kilometers. Therefore, the invention of the parsec greatly simplifies computational processes in astronomy.
For instance, the distance from the Sun to Arcturus in parsecs is 11.3 or 36.7 sv. years. One might think that the light-year is more convenient, so why create a new unit of measurement? However, if we measure the distance from the Solar System to a distant red dwarf OGLE-2018-BLG-0567L in light-years, it would be approximately 23,000 light years, whereas in parsecs, it would be “only” about 7000. Thus, the parsec proves more convenient as distances increase.
Nevertheless, even the parsec is insufficient for the needs of space exploration, prompting scientists to introduce derivative units such as the kiloparsec (kpc), which represents a thousand parsecs, and the megaparsec (Mpc) and gigaparsec (Gpc), representing a million and billion parsecs, respectively. As such, the distance proposed to be traversed in the Soviet science fiction cartoon “The Mystery of the Third Planet” – 100 parsecs, equivalent to 326 light-years – pales in comparison to the mind-boggling distances known in modern astronomy.
For example, the distance to the Virgo cluster, the closest cluster of galaxies to Earth, is 18 Mpc, and that is considered a relatively nearby object in deep space.

Cosmic Shift

This intricate yet convenient measurement system was utilized to ascertain the distance to GN-z11, the most remote galaxy within our knowledge. Its name itself indicates the distance – 11 z, or 33.2 billion years. Currently, cosmological redshift stands as the most extensive scale system for gauging cosmic distances. It serves as the most practical metric for galactic and universal scales. However, scientists refuse to halt their progress and are actively pursuing methods to reach far beyond the boundaries of the known universe. The most recent and cutting-edge suggestion involves the quest for lenses constructed from enigmatic dark matter, which could be employed as highly specialized telescopes to observe objects from 100 z-1000 z and even beyond. To grasp the enormity of these distances, we are talking about spans of over a trillion light years!

It is possible that there are alternative universes that would be measured using entirely unfamiliar units of measurement. However, regardless of the case, it would be an entirely different narrative.

The vast distances between celestial bodies cannot be compared to that of Earthly objects, and attempting to measure them in kilometers would result in an overwhelming number of zeros. This is why astronomers require specialized units of measurement, such as the parsec, to accurately gauge these distances.

Definition of the Term

The term “parsec” is a combination of two words: parallax and second.

In this context, a second refers to an angle, rather than a unit of time. Angles are measured in degrees, which are further divided into 60 parts called minutes, and each minute is subdivided into 60 seconds.

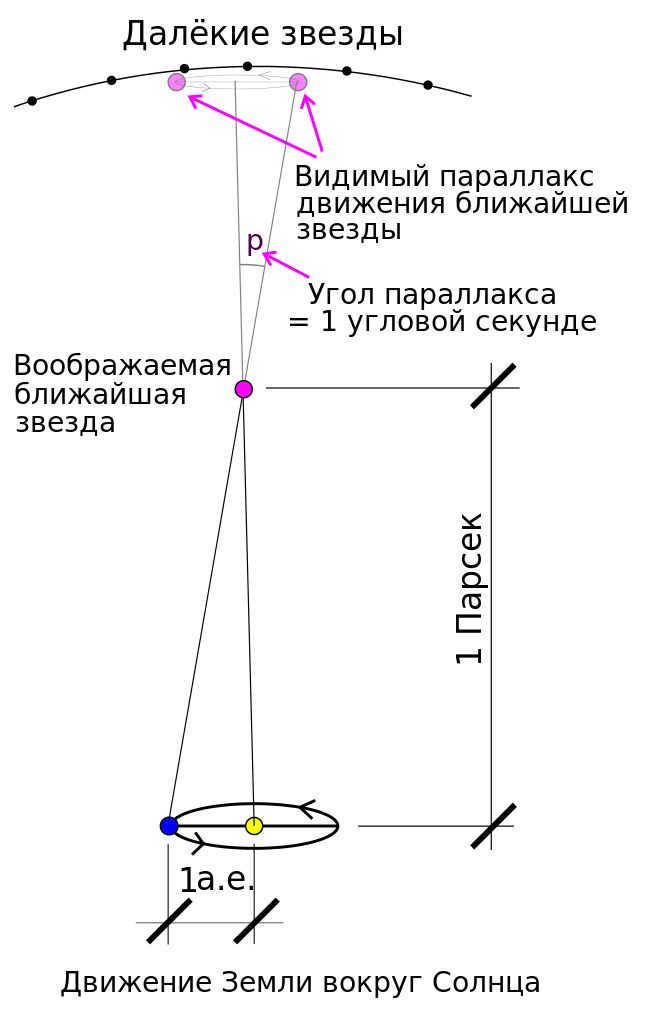
Parallax refers to the displacement of an object in relation to the background, as determined by the observer’s position. Astronomers commonly deal with three types of parallax – diurnal, annual, and centennial. When it comes to the parsec, the annual parallax is particularly significant.

Astronomers use the annual parallax of a star to calculate its distance from Earth. This involves creating an imaginary right triangle, with the hypotenuse representing the distance from the star to the Sun, and one of the catheti representing the major semi-axis of Earth’s orbit. The angle in this triangle that corresponds to the star is known as the annual parallax.
The distance to a star where this angle measures one second is known as a parsec. This unit is internationally denoted as pc, and in Russian it is represented as pc.

Understanding the Parsec Measurement

When discussing vast distances in the cosmic realm, it is common to utilize a unit known as a parsec. This particular measurement represents the distance that a beam of light can travel within the span of one year, amounting to an astonishing 9,460,730,472,580.8 kilometers. However, the parsec itself is even more expansive!

A parsec is equivalent to 3.2616 light-years, which translates to approximately 30.8568 trillion kilometers. It is the parsec, rather than the light-year, that is predominantly employed by professional astronomers. The usage of light-years is more prevalent in popular scientific literature or works of science fiction.

Nevertheless, even the parsec measurement was insufficient for the requirements of space exploration. This led to the introduction of units such as the kiloparsec (kpc) and megaparsec (Mpc), which are equal to one million parsecs.

So, the distance that the heroes of “The Mystery of the Third Planet” had to overcome turns out to be quite impressive. 100 parsecs – this is more than 326 light years! However, modern astronomy is aware of even greater distances. For instance, the distance to the Virgo cluster – the closest cluster of galaxies to Earth – is 18 megaparsecs.

Image source: mattbodnar.com

Due to its uniqueness, every person who has seen this cartoon has memorized this word.

“It’s not far, just a hundred parsecs!” – this is how Gromozeka, one of the characters in “The Mystery of the Third Planet,” described the distance to the planet he recommended Prof. Seleznev and his team to fly to.

However, not many people know exactly what a parsec means, what distance it refers to, and how far the characters of the popular cartoon had to travel.

Definition of the term “parsec”

The term “parsec” is derived from the combination of the words “parallax” and “second”. However, in this context, “second” does not refer to a unit of time, but rather to an angular second, which is a non-systematic astronomical unit equivalent to the second of a plane angle.

Parallax refers to the change in the apparent position of a celestial body based on the observer’s location.

Within modern astronomy, various types of parallax are recognized:

Diurnal – The disparity in orientation towards a specific luminary in both geocentric and topocentric directions. This angle is directly influenced by the elevation of the celestial body above the horizon.
When it comes to annual parallax, alterations in orientation towards a specific object are directly influenced by the Earth’s orbit around the Sun.
Regarding century parallax, it provides a means to ascertain the disparity in orientation towards a celestial body based on its movements within the Galaxy.

What Does “Parsec” Mean?

Essentially, a “parsec” is a unit of measurement used to determine the distance between celestial bodies located outside of our solar system. The parsec is commonly utilized when calculating distances within the Milky Way galaxy. These distances are often expressed in multiples of the parsec unit, such as kiloparsecs, megaparsecs, and gigaparsecs. However, parsecs are not typically used in everyday astronomical calculations, as it is more convenient to utilize standard astronomical units instead.
Parsecs greatly simplify calculations for astronomers, as it is much easier to express the distance from the Sun to a particular star as one and a half parsecs, rather than over 46 trillion kilometers.

Who was the inventor of the parsec?

In 1838, Friedrich Bessel, a German astronomer, became the first person to successfully measure distances to celestial objects. He achieved this by accurately calculating the annual parallax of the Swan star. Bessel utilized a traditional method of calculating the disparity in angles obtained from two separate measurements to determine the distance from the star.

Image source: bigslide.ru

To determine the distance to stars, the parallax method was employed. This involved taking measurements when the Earth was facing the Sun with one side and repeating the measurements six months later when the Earth was facing the Sun with the opposite side.

It wasn’t until 1913 that the term “parsec” was officially coined by the English astronomer Herbert Turner.

What is the calculation for a parsec and what is its equivalent?

Schematic representation of a parsec (not to scale) Image source: wikipedia.org

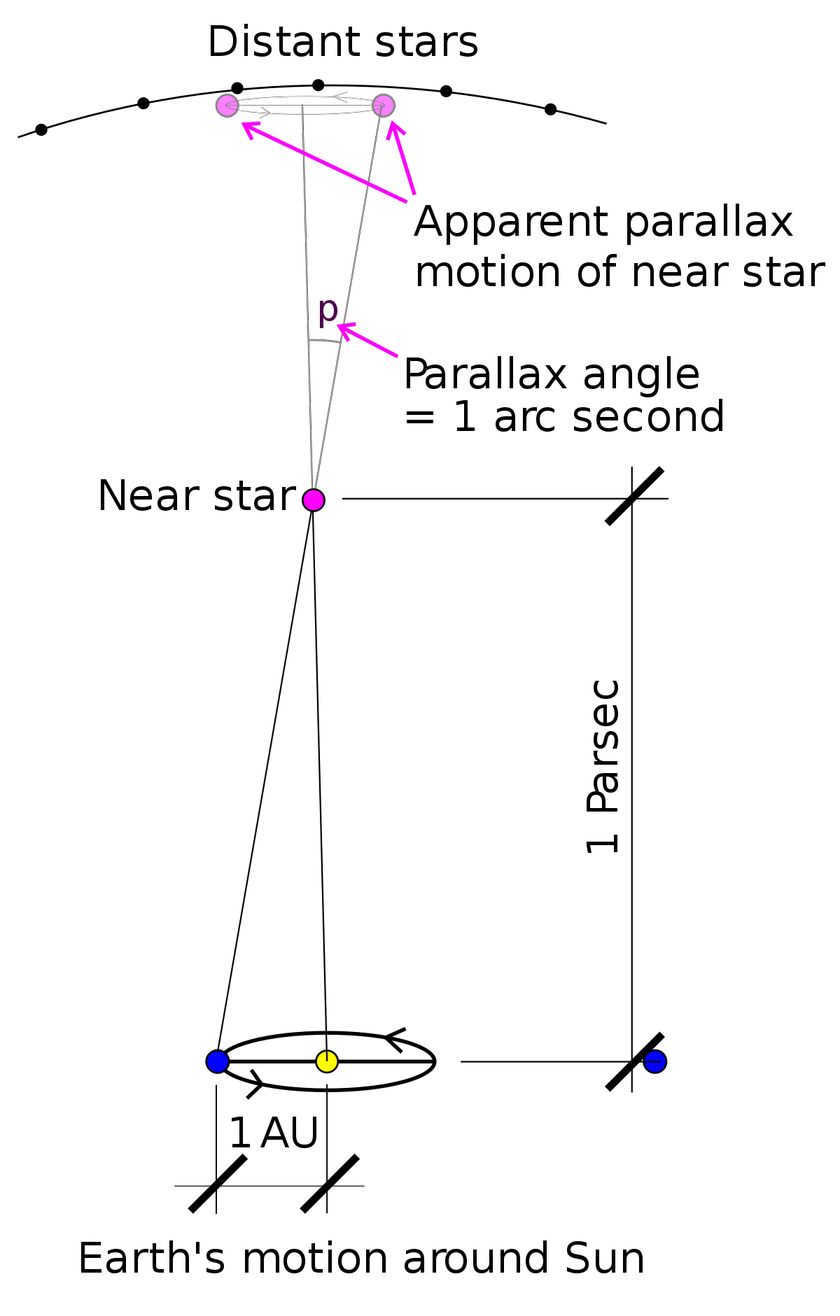
A parsec is determined by the distance at which one astronomical unit (the average distance between the Earth and the Sun) creates an angle of one arc-second.

To calculate the parsec, the annual parallax is utilized. By imagining a right-angled triangle, the distance to a star can be determined assuming its parallax is 1 arc-second.
A parsec is equivalent to 3.26 light-years or approximately 30 trillion kilometers. It is one of the initial methods for measuring distances to stars and is abbreviated as “pc”.

The concept of the parsec revolves around utilizing the principle of parallax to ascertain the distance to celestial bodies in space based on their minute shift as the Earth orbits the Sun.

There are some measurements of distances to celestial objects:

Proxima Centauri, the closest star to the Sun, is located at a distance of 1.3 parsecs.

The center of the Milky Way is approximately 8 kiloparsecs away from the Sun.

The Andromeda Nebula is situated at a distance of 0.77 megaparsecs from the Sun.

If you found this article interesting, please show your support and subscribe to the channel . Stay tuned for more fascinating content!

The term parsec is derived from the words “parallax” and “second,” and it represents the distance to an object whose annual parallax is equal to one arcsecond.

According to the similar definition, a parsec is the measurement of distance equivalent to the average radius of Earth’s orbit (which is equal to 1 a.u.), when viewed perpendicular to the line of sight at an angle of one arc second (1″).

1 pc = a.u. ≈ 206 264.8 a.u. = 3.085677776-10 16 = 30.8568 trillion kilometers (petameters) = 3.2616 light-years .

There are also larger units of measurement used: kiloparsec (kpc, kpc), megaparsec (Mpc, Mpc), gigaparsec (Gpc, Gpc).

Various Distances

Additional Resources

Important Points

The Journey of Discovery

When it comes to measuring the distance to objects in space, a radio telescope can do the job with remarkable accuracy, even down to a few centimeters. However, things get much more challenging when it comes to measuring the distance to far-flung corners of the Universe. Nonetheless, scientists were determined to find a way to calculate this value and thus turned to the method of horizontal parallax, a well-known technique in geometry.

The concept behind the horizontal parallax method is straightforward: when observing a far-off object from different locations, its position will appear to shift in relation to other, more distant objects. By knowing the distance between the observation points and the angle of displacement of the object against the backdrop of distant objects, it becomes possible to calculate its distance using geometric calculations. Astronomers embraced this principle, which formed the foundation for the identification of a novel unit of measurement known as the parsec.

Calculating a parsec

If you’re observing a star and wish to calculate its distance in parsecs, you first need to understand the measurement of a parsec. A parsec is defined as the distance at which one astronomical unit (AU) subtends an angle of one arcsecond when observed from Earth. An astronomical unit is the average distance between the Earth and the Sun, which is approximately 149.6 million kilometers (93 million miles). So, to determine the distance to a star in parsecs, you would measure the angle it subtends and calculate the corresponding distance based on the known distance of one AU.

By knowing the distance between the points where the observations were taken (which is equivalent to 1 astronomical unit – the distance from the Earth to the Sun or the radius of the Earth’s orbit) and the displacement of the star compared to the background of more distant stars and galaxies, we are able to calculate its distance. If the star has moved by 1 arc second within the observed range, its distance is one parsec; if it has moved by half a second, it is two parsecs. Contrary to popular belief, the smaller the parallax (displacement) of a celestial object, the greater its distance in parsecs.

When it comes to performing calculations in astronomy, scientists rely on unique units of measurement that may not be easily understandable to the general public. This is understandable, as if cosmic distances were measured in kilometers, the sheer number of zeros involved would be overwhelming. As a result, astronomers use larger units of measurement such as the astronomical unit, light year, and parsec to quantify cosmic distances.

It is quite common to use measurements to describe distances within our solar system. For example, the distance from Earth to the Moon can be expressed in kilometers (384,000 km). However, when it comes to measuring the distance to Pluto, the numbers become much larger and more difficult to comprehend. The closest distance to Pluto is approximately 4.25 billion kilometers, which is already a challenging concept to grasp. This is why astronomers use a different unit of measurement called an astronomical unit (a.u.). An astronomical unit is defined as the average distance from the Earth’s surface to the Sun, which is about 150 million kilometers. By using this unit, it becomes easier to understand the distances involved. For instance, we can say that the shortest distance to Pluto is 28 a.u., while the longest journey would be 50 a.u., making it much more manageable to visualize.

The light-year is the next largest unit of measurement, and despite its name, it does not refer to time. Instead, it is the distance that a beam of light travels in one year. Astronomers have determined that it takes over 10 billion years for light to reach us from the farthest reaches of the universe. To put this immense distance into perspective, it can be expressed as 63,240 astronomical units or approximately 95 billion trillion kilometers.

Since 1676, scientists have hypothesized that light does not travel instantaneously, but at a specific speed. This discovery was made by Danish astronomer Ole Remer, who noticed that the eclipses of one of Jupiter’s satellites were starting to lag. This lag coincided with the Earth’s movement in its orbit to the opposite side of the Sun, the opposite direction of Jupiter. As time passed and the Earth started to move back, the eclipses gradually returned to their previous schedule.

Therefore, a discrepancy of approximately 17 minutes in time was observed. This discovery led to the conclusion that it takes 17 minutes for light to traverse a distance equal to the diameter of Earth’s orbit. Given that the diameter of the orbit is estimated to be around 186 million miles (939,120,000 kilometers), it can be deduced that the speed of light is roughly 186,000 miles per second.

In the present era, thanks to the efforts of Professor Albert Michelson, who embarked on a mission to ascertain the precise measurement of a light year, a different approach was utilized to determine the final figure: 186,284 miles in one second (approximately 300 km/s). By calculating the number of seconds in a year and multiplying it by this value, we arrive at the conclusion that a light year measures 5,880,000,000,000,000,000 miles, equivalent to 9,460,730,472,580.8 kilometers.

For practical purposes, astronomers often employ the parsec as a unit of distance. This unit is defined as the displacement of a star against other celestial bodies by 1″ when the observer is offset by 1 radius.

Ways to Study Distances in the Universe

Parallax Method
Laser Measurements
Radar Measurements
Standard Candles
Measuring Rods
Hubble’s Law
And approximately 30 others.

Understanding Parallax

In the field of astronomy, parallax refers to the phenomenon where the apparent position of an object in the celestial sphere appears to change when observed from different locations due to the observer’s displacement.

Parallax is an apparent shift in the position of an object caused by the movement of the observer, specifically, a change in the observer’s position.

The concept of parallax is applicable in various systems:

The diurnal parallax, also known as geocentric equatorial parallax, is caused by the Earth’s rotation.
The meridional geocentric parallax is associated with the observer’s change in latitude.
The annual parallax, also referred to as heliocentric parallax, is connected to the Earth’s orbit around the Sun.

Explanation of a parsec

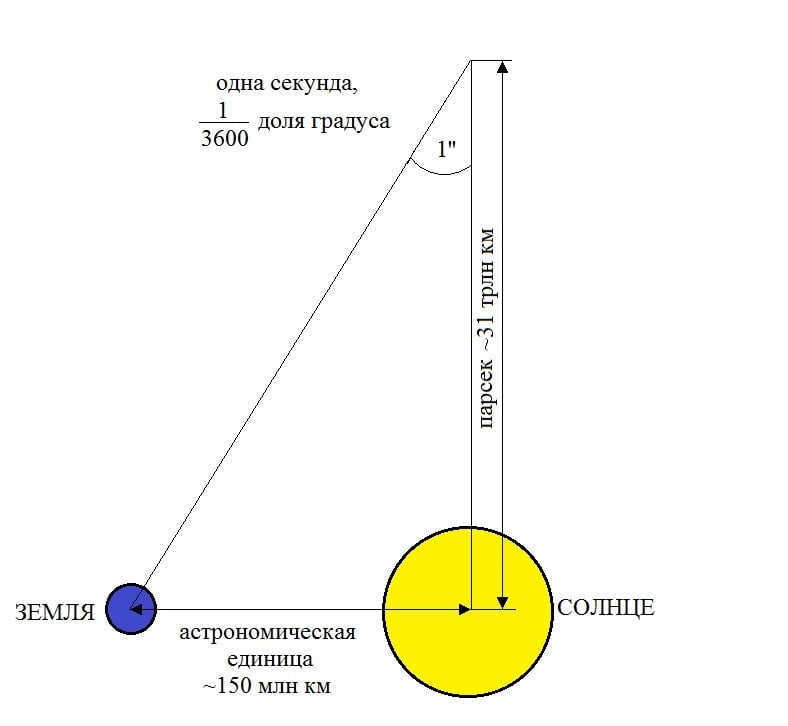
If the parallax angle remains constant, it is possible to calculate the distance to a star by applying trigonometric principles (given that the distance from the Earth to the Sun is already known). In 1913, Turner introduced the term parsec, which represents the distance from the Sun to a star with a parallax angle of 1 arc second, as a unit of measurement.

Light Year (LY)

Light has a finite speed of 299,792,458 m/s, allowing it to cover approximately 300,000 km in one second. By multiplying this distance by the number of days in a year (365 days), we can determine that light travels about 946,800,000,000,000,000 km in a single year. This measurement is known as one light-year.

Astronomical unit (AU)

1 AU is the average distance between the Earth and the Sun, which measures approximately 149.6 million km or 149,597,870,700 meters. The International Astronomical Union determined this constant value in Beijing in 2012.

Distances in the Universe

1 km = 0.00000000000006684587 AU
1 light-year = 63241 AU
1 parsec = 206265 AU
The distance from the Earth to the Sun is 1 AU
Mercury’s distance from the Sun = 0.39 AU
The distance to Venus from the Sun = 0.72 AU
distance to Mars from the Sun = 1.52 AU
Distance of Jupiter from the Sun = 5.2 AU
Saturn’s distance from the Sun = 9.58 AU
Distance of Uranus from the Sun = 19.23 AU
The distance from the Sun to Neptune is 30.1 astronomical units.
The distance from the Sun to the center of the Milky Way is 1,700,000 astronomical units.

The distances of the individual planets from the Sun in light-years are:

Mercury – 0.000006121
Venus – 0.000011437
Mars – 0.000024094
Jupiter – 0.000082279
Saturn – 0.000150806
Uranus – 0.000303463
Neptune – 0.000475467.

It is also the unit of measurement for distances in the universe. However, defining the concept of time in space is much more complex and contentious. A light year is the distance that light travels in a vacuum during a Julian year, which is equivalent to 365.25 days and 31,557,600 seconds. In other units, 1 light year is equal to 63,241 astronomical units, 0.3066 parsecs, or approximately 9.4607 x 10^15 meters, which is roughly equivalent to 9.4 trillion kilometers. The time it takes for light to travel from the Sun to the Earth is approximately 8 minutes and 20 seconds. Light can travel from the Moon to the Earth in just 1.3 seconds. This phenomenon, among other factors, caused communication delays during the Apollo manned mission. The Milky Way galaxy has a diameter of approximately 100,000 light years.

One light-year takes you 6 trillion miles into space. A light-year is a unit of measurement that represents the distance between Earth and objects in space. However, how did this unit come to be and how does it assist us in space exploration?

Within our solar system, the planet Saturn holds the distinction of being the most distant planet visible to the naked eye from Earth. In the event that this ringed planet were to be obliterated by an asteroid during the course of observation, whether aided by a telescope or not, it would continue to remain in view for approximately 80 minutes. This is due to the fact that the average distance separating Saturn and Earth is approximately 0.00015 light-years, necessitating a span of roughly 80 minutes for light emitted from Saturn to traverse the distance and reach Earth.

Promotion

Therefore, if you happen to observe any star that is situated 100 light-years away from the Earth, what you are actually witnessing through a telescope is not its present condition, but rather its state from a century ago. This is why a telescope is often referred to as an astronomical time machine. Attempting to measure astronomical distances in either miles or kilometers is simply impractical due to the vast size and scale of the numbers involved. By utilizing light-years as a unit of measurement, astronomers are able to peer into the past. Since it takes a specific amount of time for light to reach our eyes, everything that we are able to perceive in space has already occurred. Consequently, when you observe an object located precisely two light years away, you are viewing it as it existed two years in the past.

The speed of light remains constant. When traveling through a vacuum, light moves at a rate of 670,616,629 miles per hour (1,079,252,849 kilometers per hour). Over the course of one Earth year, which consists of 364.25 days (8,766 hours), light covers a staggering distance of 5,878,625,370,000 miles (9.5 trillion kilometers). This enormous distance is referred to as a light year.

Given that distances between celestial bodies are typically in the millions or billions of kilometers, it became necessary to have a more practical unit of measurement for expressing such vast distances. This need ultimately led to the development of the light-year as the preferred unit of measurement for astronomical distances.

In accordance with its nomenclature, a light-year (plural light-years) serves as a measure of distance. One prevalent misconception regarding the light-year revolves around the notion that it represents a unit of time, an idea that is fundamentally incorrect. The light-year is frequently employed to convey the vast expanse separating Earth from celestial entities beyond our solar system.

The velocity of light and the discovery of the light year

For scientists to accurately compute the light year, it was imperative for them to ascertain the value of the velocity of light. The ancient Greek philosophers held divergent views on the essence of light’s velocity. Empedocles, the philosopher, posited that light is in motion and therefore must possess a speed. On the other hand, Aristotle argued that light is instantaneous.

In the mid-1600s, Galileo Galilei carried out experiments aimed at determining the velocity of light by employing individuals stationed on hills approximately a mile apart, each holding a lantern. However, the distance proved inadequate to measure its velocity, leading to the deduction that light travels faster than sound.

In 1676, a Danish astronomer named Ole Rømer accidentally discovered a new estimate for the speed of light while attempting to create a reliable astronomical clock for sailors at sea. By observing eclipses of Jupiter’s moon, Io, Rømer estimated that the speed of light was 124,000 miles per second (200,000 kilometers per second).

However, this estimate differed from the speed of light that is known today, which is 299,792 kilometers per second. This discrepancy was not due to any flaws in Rømer’s method, but rather because the actual diameter of the Earth (12,742 kilometers) was unknown at the time. It was later discovered by Dutch mathematician Christiaan Huygens, who used the correct value of Earth’s diameter in Rømer’s calculations, resulting in a more accurate estimate of the speed of light at 220 million miles per second.

English astronomer James Bradley presented his theory on the deviation of light (a change in the direction of light propagation) to the Royal Society in 1729. In his research, he calculated the speed of light to be 185,000 miles per second (301,000 km/s), which is roughly 1% off from our modern understanding.

In the mid-1800s, two French physicists, Hippolyte Fizeau and Leon Foucault, made separate attempts to approach the speed of light, with Fizeau reaching a speed of about 1,000 miles per second (1,609 kilometers per second) and Foucault achieving a similar result.

In 1879, physicist Albert A. Michelson conducted an experiment using mirrors and lenses to measure the speed of light, which was found to be 186,355 miles per second (299,910 kilometers per second). Forty years later, Michelson attempted to create near-vacuum conditions using mile-long pressurized tubes in order to obtain a more precise measurement, which was only slightly smaller than the current accepted value.

The concept of the “light year” was initially introduced in 1851 in a German publication called Lichtjare. When Einstein formulated the theory of special relativity (E=mc 2 ), which posits that light always travels at a finite speed, the light-year had already established itself as a widely used unit for measuring astronomical distances within the scientific community.

Astronomical Units: Light-year, Lunar Distance, and Parsec

Besides the light-year, there are other units that astronomers use to measure distances in space. These include the astronomical unit (AU), lunar distance (LD), and parsec (pc).

When it comes to measuring the distance between the Earth and the Moon, astronomers use the concept of lunar distance. It represents the mean semi-major axis of the geocentric lunar orbit and is approximately 400,000 kilometers, a quarter of a million miles, or 1.28 light seconds. Lunar distance is often used to describe the proximity of objects in our solar system.

An astronomical unit (AU) is another important unit of measurement. It is defined as the average distance from the center of the Earth to the center of the Sun.

The measurement of distances within our solar system is commonly done using the lunar distance and astronomical units. On the other hand, when it comes to measuring distances outside our solar system, the light-year and parsec are the preferred units of measurement. These units are especially useful when dealing with distances between galaxies.

A parsec is a unit of measurement that is derived from the angle formed by Earth’s orbit. Specifically, it is the distance at which the radius of Earth’s orbit creates an angle of one second of arc. This angle is formed when two rays pass through the endpoints of an arc. As a result, the parallax of a star located one parsec away can be measured as one second. In comparison, one light-year is equivalent to 63,241 astronomical units and one parsec is equal to 3.26 light-years or 206,265 astronomical units.

Some fascinating information regarding light years

A light year can be divided into light hours, light minutes, light seconds, and even light nanoseconds. As an illustration, it takes eight minutes for light from the Sun to reach Earth, signifying that the Sun is also eight light minutes away from Earth. Below are a few captivating facts concerning light years:

In November 2021, the Voyager 1 space probe, which was launched by NASA in 1977, transmitted a signal from a distance of 21.31 light hours (14.45 billion miles). This achievement makes it the farthest distance traveled in space by any human-made object.

The nearest dwarf galaxy to our galaxy, the Milky Way, is located 25,000 light-years away from the Sun. The dwarf elliptical galaxy Sagittarius is positioned 70,000 light years from the Sun. The most distant galaxy known to us is called GN-z11, which was identified by the Hubble telescope in 2016 in the constellation of the Big Dipper. Initially, it was estimated to be 13.4 billion light years away from Earth, or approximately 134 nonillion kilometers (that’s 134 followed by 30 zeros).

To determine the distance of a flying airplane, a radar system utilizes radio waves and measures time in nanoseconds. This is because radio waves travel at the speed of light. A nanosecond is equivalent to one billionth of a second, and light can travel approximately 1 foot (30 cm) within that time frame.

NASA has recently made an exciting announcement about its Parker Solar probe, stating that it has successfully made contact with the Sun. This incredible spacecraft is not only the fastest man-made object in space, but it is also projected to reach speeds of 430,000 miles per hour (690,000 kilometers per hour). To put that into perspective, it can travel from Philadelphia to Washington, D.C. in less than a second.

Renowned American astronomer Edwin Hubble once expressed that the quest for knowledge will always persist and cannot be suppressed. Space exploration can be viewed as a continuous search for what lies beyond our planet and the stars. Additionally, the concept of a light-year serves as a reminder of the immense scale of the universe and how much there is still to discover for humanity and science.

However, it’s not surprising, is it? One doesn’t need to be an expert in every domain!

Nevertheless, in order to avoid being misled by sensational newspaper headlines, it’s advisable to have a basic understanding of key concepts.

A catchy title proclaiming: Just a Stone’s Throw Away – 10 Parsecs!

1. astronomical unit (a.u., internationally known as au)

An astronomical unit is approximately 150 million kilometers, which is quite a substantial distance. To put it into perspective, if a car were traveling at a speed of 80 km/hour, it would take over 200 years to cover such a vast distance.

As observational astronomy progressed and our understanding of the Universe deepened, it became clear that the astronomical unit was too small and not very practical for measuring long distances.

As a result, larger units of measurement were introduced.

2. What is a light-year?

The speed of light in a vacuum is the fastest possible speed, reaching 299,792,458 meters per second.

A light-year is a unit of distance that represents how far light can travel in one year in a vacuum. In other words, it is the distance that electromagnetic waves can travel in a vacuum without the influence of gravitational fields over the course of one Julian year.

To give you a sense of scale, a light-year is approximately 9,460,730,472,580,800 meters long. This is equivalent to more than 63,000 astronomical units, or about 13.5 million years of travel by car.

However, in the world of professionals, the light-year as a unit of measurement is seldom utilized; it is typically reserved for popular science literature and media.

When astronomers need to gauge vast distances, they rely on another popular unit of measurement and its corresponding prefixes (kilo-, mega-).

3. Parsec

The parsec is the most commonly used unit of measurement in astronomy when estimating large distances.

Unfortunately, it is also the most complex to comprehend without proper training.

The parsec is defined as the distance to an object that has an annual trigonometric parallax equal to one arcsecond.

Over time, the concept of the parsec has been refined, and in 2015 it was officially defined as 648,000 divided by Pi and multiplied by one astronomical unit.

The Andromeda Nebula (the closest large galaxy) is located at a distance of over 770 thousand parsecs from us.

However, to calculate the distance in parsecs, it is only necessary to understand its relationship to more familiar units such as kilometers and light years.

One parsec is roughly equivalent to 3.262 light years, which is approximately 206 thousand astronomical units, or just under 31 trillion kilometers, or more than forty million years of travel by car.

And in order to comprehend the immense distances within the Universe, here is a concise compilation of various examples.

The distance between the Earth and the Sun is equivalent to 1 astronomical unit (AU).
The solar system’s diameter measures approximately 1 light-year.
The distance to our closest star amounts to 1.3 parsecs.
The Milky Way galaxy’s diameter spans about 100,000 light-years or 30 kiloparsecs.
The Andromeda Nebula, which is our nearest large galaxy, is situated at a distance of 2.5 million light-years or approximately 772,000 parsecs.

Laniakea (center and left) is a conglomeration of galaxies that encompasses the Virgo supergroup along with the Local Group of galaxies as one of its components. The span of Laniakea measures approximately 520 million light years.

Therefore, when the media proclaims the discovery of a planet in ten parsecs that closely resembles Earth, keep in mind that although ten parsecs may not be significantly distant on a cosmic scale, it equates to three hundred trillion kilometers. It would take half a billion years to travel that distance by car!

The size of the Universe is enormous, and objects within it are separated by vast distances. A light-year (abbreviated as ly) is a unit of measurement used to describe the distance that light can travel in a vacuum over the course of one Julian year, which consists of 365.25 days. This measurement is calculated by multiplying the speed of light by the length of one year.

To determine the distance of one light-year in meters, you can multiply the speed of light (measured in meters per second) by the number of seconds in a Julian year:

299,792,458 m/s × 31,557,600 s = 9,460,730,472,580,800 m (approximately 9.46 × 10^15 meters)

In other units of measurement, a light-year is equal to:

9.46 trillion kilometers (9.46 × 10^12 km);
5.88 trillion miles (5.88 × 10^12 miles);
63,241,077 astronomical units;
0.306601 parsecs.

By using the light-year as a measurement of distance, we can understand that light does not travel instantaneously. If a galaxy is a million light years away from us, it means that it took light a million years to reach Earth. Therefore, when an observer from Earth looks at a galaxy that is a million light years away, they are actually seeing what it looked like a million years ago.

Here are the distances from Earth to some astronomical objects in light-years:

The term “parsec” is a combination of the words “parallax” and “second”. In this context, a second does not refer to a unit of time, but to a unit of angular measurement (arc second).

Meaning of the term

The term parsec is derived from the combination of two words, Parallax and.

In this particular context, a second does not refer to time but rather to an angle. As you may be aware, angles are measured in degrees, each of which is divided into 60 parts, which are further divided into 60 seconds.

Parallax refers to the displacement of an object in relation to its background, determined by the observer’s position. Astronomers encounter three types of parallax: diurnal, annual, and centennial. For parsecs, the annual parallax is of particular significance.

By measuring the annual parallax of a star, astronomers are able to determine the distance from the Earth to that particular star. This calculation involves creating an imaginary right triangle, with the hypotenuse representing the distance between the star and the Sun, and one of the perpendicular sides representing the semi-major axis of the Earth’s orbit. The angle in this triangle that corresponds to the star is known as the annual parallax. A parsec is defined as the distance from a star at which this angle is equal to one second. The international unit of measurement for parsecs is pk, which is referred to as pk in Russian.

What is a parsec

When it comes to vast distances in the cosmos, they are often expressed in parsecs. A parsec is the distance that a beam of light travels in one year and it equals 9,460,730,472,580.8 kilometers. That’s an impressive value, but the parsec is even larger!

The length of a parsec is 3.2616 light years or 30.8568 trillion kilometers. This unit of measurement is commonly used by professional astronomers instead of light-years. Distances in light-years are often mentioned in popular science publications or in novels and science fiction movies.

However, even this unit of measurement proved insufficient for the needs of space exploration. It became necessary to introduce units equivalent to a million parsecs – kiloparsecs (kpc) and megaparsecs (MPc).

Thus, the heroes of “The Mystery of the Third Planet” face a truly impressive challenge in terms of distance. The distance they must traverse is a staggering 100 parsecs, which is equivalent to over 326 light years! However, it is worth noting that modern astronomy has discovered even greater distances. For instance, the Virgo cluster, which is the nearest cluster of galaxies to Earth, is located at a distance of 18 megaparsecs.

Image source: mattbodnar.com

Due to its distinctive nature, the word has become ingrained in the memory of everyone who has watched this animated film.

“It’s not a considerable distance, just a hundred parsecs,” remarked Gromozeka, one of the characters in “The Mystery of the Third Planet,” when discussing the distance to the planet that Professor Seleznev and his team were advised to travel to.

Nonetheless, only a few individuals are truly familiar with the precise meaning of parsec, the specific distance it represents, and just how far the beloved heroes of this popular cartoon had to journey.

Understanding the concept of “parsec”

The term “parsec” is composed of the words “parallax” and “second”, but in this context, they do not refer to a unit of time. Instead, they denote an angular second, which is an astronomical unit outside of our solar system that is equivalent to a plane angular second.

Parallax refers to the shift in the position of a celestial body based on the observer’s point of view.

In contemporary astronomy, various forms of parallax are recognized:

The diurnal angle is the disparity between the orientations to a specified heavenly body in both the geocentric and topocentric orientations. This angle is closely linked to the elevation of the celestial body above the horizon. When it comes to annual parallax, the alteration in orientation to a specific object is directly associated with the Earth’s orbit around the Sun. In the case of annual parallax, the divergence in orientation of a celestial body can be ascertained by its movement in the Milky Way.

The Definition of Parsec

In simple terms, a “parsec” denotes a unit of measurement that quantifies the change in distance between celestial bodies located outside of our solar system. Parsecs are commonly employed to compute distances within the Milky Way galaxy. These distances are often expressed in multiples of kiloparsecs, megaparsecs, and gigaparsecs. Larger units are typically not used as it is more convenient to utilize standard astronomical units. The parsec greatly facilitates calculations for astronomers, as it is much simpler to state that the distance from the Sun to a star is one and a half parsecs rather than over 46 trillion kilometers.

Who invented the parsec?

In 1838, Friedrich Bessel, a German scientist, became the first person to measure the distances between celestial objects. He accurately calculated the 61-year parallax of the star Swan to determine its distance. Bessel used the traditional method of calculating the difference in angles between two measurements.

Image source: bigslide.co.uk

The measurements were initially taken with one side of the Earth facing the Sun and then repeated six months later, with the other side of the Earth facing the Sun.

However, it was Herbert Turner, an English astronomer, who coined the term “parsec” in 1913.

How do you calculate a parsec and what is its value?

Schematic representation of a parsec (not to scale) Image source: wikipedia.org

A parsec is defined as the distance at which one astronomical unit (the average distance between the Earth and the Sun) equals an angle of one arc second.

The parsec is calculated using the annual parallax. By using an imaginary right-angle triangle, a parsec is the distance to a star when its parallax is 1 arc second. The length of a parsec is 3.26 light-years or approximately 30 trillion kilometers. It is one of the earliest methods used to measure distances to stars and is denoted as “pc”.

The essence of the parsec lies in applying the principle of parallax to determine the distances of celestial bodies in space based on their minute displacement as the Earth orbits the Sun.

The distance between the Sun and Proxima Centauri, the closest star, is 1.3 parsecs.

The distance from the Sun to the center of the Milky Way is approximately 8 kiloparsecs.

Parallax

Parallax is an astronomical phenomenon that refers to the apparent shift in the position of an object on the celestial sphere relative to other objects. This shift occurs as a result of a change in the observer’s observation position caused by their movement.

Parallax is the apparent change in an object’s position due to the movement of the observer.

The concept of parallax is applicable in various systems:

Diurnal parallax (geocentric equatorial parallax), which is related to the Earth’s rotation
Meridional geocentric parallax, which is associated with the change in the observer’s latitude
The parsec is a unit of length used in astronomy to measure the distance of objects in space.

What is the parsec?

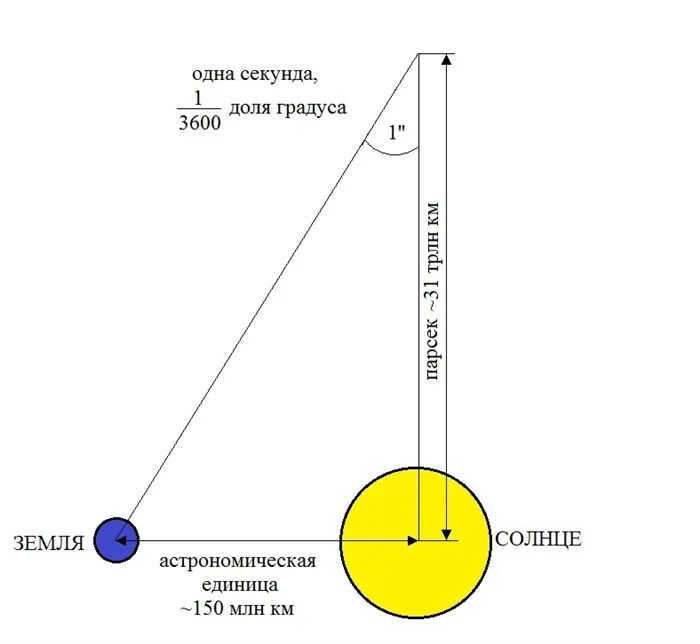
If the parallax angle remains constant, it is possible to calculate the distance to a star by applying trigonometry principles (given that the Earth’s distance from the Sun is known). In 1913, Turner introduced the term “parsec” to designate the distance from the Sun to a star with a parallax angle of 1 arc second, thus establishing it as a unit of measurement.

The term “parsec” is derived from the combination of “parallax” and “second”. Parallax refers to the Earth’s rotation (diurnal parallax), the observer’s change in latitude (geocentric meridian parallax), or the Earth’s orbital motion around the Sun (annual parallax). According to its definition, 1 parsec (pc) is the distance at which half of the Earth’s orbit’s major axis is visible as a 1-second arc. This distance is the reciprocal of the body’s heliocentric parallax. Parsec is now abbreviated as pc, previously known as ps. The reason for this abbreviation change is currently unknown, as it coincides with the abbreviation for picosecond.

The Measurement of Distance: Light Year (LY)

The speed of light is finite, clocking in at 299,792,458 meters per second. In just one second, light can travel approximately 300,000 kilometers. By multiplying this distance by the number of days in a year (365 days), we find that light covers a staggering 946.8 million kilometers in a single year. This incredible distance is known as 1 light year.

Another unit of measurement used in astronomy is the astronomical unit (AU), which represents the average distance between the Earth and the Sun. This distance amounts to about 149.6 million kilometers or 149,597,870,700 meters. The value of the astronomical unit was officially established in Beijing in 2012 by the International Astronomical Union.

In simple terms, a parsec is a unit of measurement that defines the distance between celestial bodies beyond our solar system. The parsec is commonly used for calculating distances within the Milky Way galaxy. When determining distances on a larger scale, multiples of parsecs such as kiloparsecs (1000 parsecs), megaparsecs (one million parsecs), and gigaparsecs (one billion parsecs) are utilized.

This particular tool not only serves a practical purpose, but also offers astronomers added convenience. It is much more convenient to state that the distance between the Sun and a star is 1.5 parsecs rather than 46.27 trillion kilometers.

Who first discovered the parsec?

In 1838, German astronomer Friedrich Wilhelm Bessel made the initial accurate measurements of distances to celestial bodies. As a result, he was able to perform the first reliable calculation of the annual parallax for the star known as 61 Swan.

The scientist employed one of the oldest techniques in astronomy to calculate the distance to a star by recording the difference in angle after two measurements. Initially, measurements were captured when the Earth was positioned on one side of the Sun, and after six months, the same measurements were taken when it was positioned on the opposite side of the Sun. The British astronomer Herbert Hall Turner introduced the term “parsec” in 1913.

What is the equivalent of a parsec?

Parallax is utilized to determine parsecs. To calculate the distance to an object, astronomers create an imaginary right triangle where the hypotenuse represents the distance of the celestial body from the Sun, and the perpendicular represents the semi-major axis of the Earth’s orbit. The acute angle in this triangle is the annual parallax, and in this case, a parsec is the distance to the star whose parallax corresponds to 1 arc second.

Aside from parsecs, kilometers and light-years are also utilized to measure the distance between celestial objects. The conversion ratios between these units have long been computed. The symbol for parsec is “pc” in Russian and “rs” in English.

When discussing distances, astronomers typically use parsecs as their preferred unit. A parsec is defined as the distance an object must be from the Sun in order to have a parallax angle of 1 ” (one arc-second). As a result, any measurement obtained through parallax will be expressed in parsecs. Parsecs serve as a convenient standard unit for measuring vast distances in space.

On the other hand, a light-year represents the distance that light travels in one year. This measurement not only informs us of the distance traveled by light, but also the duration of its journey. Light-years are more commonly utilized in popular science as they are easier for individuals unfamiliar with parallax measurements to comprehend.

# 1 “parsec” is equivalent to 3.1 * 10 ^ 13 “km” or 1.9 * 10 ^ 13 “mi” #

# 1 “light-year” is equivalent to 9.5 * 10 ^ 10 ^ 12 “km” or 5.9 * 10 ^ 12 “mi” # #

# 1 “parsec” is equivalent to 3.3 “light years” #

Please note that the provided numbers are rounded and may not be exact.

What is a parsec and why is it necessary considering that a light year also serves as a unit of distance measurement?

A parsec is a unit of distance that is used in astronomy. It is defined as the distance at which one astronomical unit (AU) subtends an angle of one arcsecond. More precisely, one parsec is equal to 206264.8 AU or approximately 3.27925 light years. The concept of parsec is important because it offers a convenient way to measure distances in space.

Although a parsec is not very large compared to a light year, it is still a significant distance. In fact, one parsec is approximately equal to 2.0 x 10^5 AU. To put it in perspective, a megaparsec is equal to one million parsecs. So, converting distances to megaparsecs is a straightforward way to approximate distances with a few significant digits.

Another way to understand the concept of parsec is to consider the arc of a circle that is one parsec away from the Sun. This arc would measure 3600 AU, which is equivalent to one degree on the Sun. This explanation provides a basic understanding of what a parsec is and why it is needed in astronomy.

What is the correct order from shortest to longest for these units of measurement? Angstrom, astronomical unit, centimeter, kilometer, light-year, micron, nanometer, parsec?

What is the proper sequence for arranging these units of measurement from smallest to largest? Angstrom, astronomical unit, centimeter, kilometer, light-year, micron, nanometer, parsec?

Let’s arrange these units of measurement from shortest to longest:

Angstrom -> 10 ^ -10 "m"
Nanometer -> 10 ^ -9 "m"
Micron -> 10 ^ -6 "m"
Centimeter -> 10 ^ -2 "m"
Kilometer -> 10 ^ 3 "m"
Astronomical unit -> 1.496 xx 10 ^ 11 "m"
Light-year -> 9.461 xx 10 ^ 15 "m"
Parsec -> "3.26 light-years", or 3.08 xx 10 ^ 16 "m"

Related Posts: