Determining Equatorial Coordinates: A Step-by-Step Guide

The Equatorial Coordinate System: An Introduction

In astronomy, the equatorial coordinate system is commonly used to locate celestial objects in the sky. It is based on the concept of spherical coordinates, where the Earth’s equator serves as the fundamental plane.

The Celestial Equator: A Projection of Earth’s Equator

To establish the celestial equator, we project the Earth’s equator onto the celestial sphere. This imaginary line divides the celestial sphere into two equal halves – the northern and southern hemispheres.

The Ecliptic: Tracing Earth’s Orbit in the Sky

Another important component of the equatorial coordinate system is the ecliptic. By projecting the Earth’s orbit onto the celestial sphere, we define the ecliptic. The ascending node of the ecliptic is set on the celestial equator, creating the point of the vernal equinox.

Direct Ascension: Measuring Eastward Along the Celestial Equator

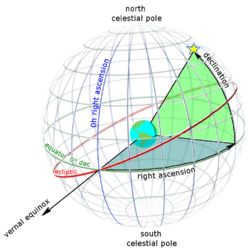
To determine direct ascension, we measure eastward along the celestial equator starting from the vernal equinox point. This coordinate tells us the angular distance of a celestial object from the vernal equinox, in the eastward direction.

Declination: Measuring North of the Celestial Equator

Declination is the angular distance of a celestial object from the celestial equator, measured in the northward direction. A positive value indicates a position north of the celestial equator.

The North and South Celestial Poles: Projections of Earth’s Poles

Lastly, the north and south celestial poles are formed by projecting Earth’s north and south geographic poles onto the celestial sphere, respectively. These poles serve as reference points for celestial navigation.

The equatorial coordinate system is a widely used system of celestial coordinates for determining the position of celestial objects. It can be expressed in either spherical or rectangular coordinates, with the coordinate origin located at the center of the Earth. The fundamental plane of this system is formed by projecting the Earth’s equator onto the celestial sphere, creating the celestial equator. Additionally, the primary direction is defined as the point of the vernal equinox, and the system follows a right-handed agreement.

The coordinates at the center of the Earth have their origin, which means that they are geocentric, or viewed from the center of the Earth as if it were transparent. The coordinate system, aligned with the Earth’s equator and pole, remains relatively stationary with respect to the background stars, as it does not rotate with the Earth. In addition, the coordinates increase north of the principal plane and east of it, following a right-handed agreement.

The primary direction

This explanation of the orientation of the frame of reference is somewhat simplified; the orientation is not completely fixed. The gradual movement of the Earth’s axis, known as precession, causes the coordinate system to slowly rotate in a westward direction around the poles of the ecliptic, completing one full revolution approximately every 26,000 years. Overlaying this movement is a smaller shift in the position of the ecliptic and a slight wobble of the Earth’s axis, known as nutation.

In order to determine the exact primary direction, these movements rely on the equinox point of a specific date, referred to as the epoch, when specifying the position. The three most commonly utilized epochs are:

The standard reference epoch (typically J2000.0, but can also include B1950.0, B1900.0, etc.) is a fixed point of reference that allows for direct comparison of positions measured at different times. The reference epoch for a specific date is the point where the ecliptic of that date intersects with the mean equator (an equator adjusted for precession to its position on that date, but without the small periodic nutation oscillation). This is commonly used in the calculation of planetary orbits. The true equinox date is the point where the ecliptic of that date intersects with the true equator (the mean equator plus nutation). It represents the actual intersection of the two planes at any given moment, taking into account all motions.

The position in the equatorial coordinate system is typically determined by the actual equinox and the equator of the current date, the average equinox and equator of J2000.0, or a similar reference point. It is important to note that there is no concept of a “mean ecliptic” in this context, as the ecliptic does not experience minor periodic variations.

Coordinates in a spherical form

Application in astronomy

When it comes to celestial bodies, their spherical coordinates are often represented by a combination of direct ascension and declination, without taking into account the distance coordinates. The direction of objects that are located far enough is the same for all observers, which makes it convenient to establish this direction using the same coordinates for everyone. On the other hand, in the horizontal coordinate system, the position of a star varies from one observer to another depending on their location on the Earth’s surface and constantly changes due to the Earth’s rotation.

Telescopes that are equipped with equatorial mounts and mounting circles utilize the equatorial coordinate system for locating objects. With the help of setting circles and either a star chart or ephemeris, it becomes effortless to direct the telescope towards known objects on the celestial sphere.

Declination

Declination, represented by the symbol δ (lowercase “delta”) and abbreviated as DEC, is a measurement of the angular distance to an object perpendicular to the celestial equator. It is positive when measured to the north and negative when measured to the south. For instance, the declination of the North Pole is +90 degrees. The celestial equator serves as the reference point for declination, as it is the projection of the Earth’s equator onto the celestial sphere. In a similar manner, declination can be thought of as the celestial equivalent of Earth’s latitude.

Direct Ascent

The method of Direct Ascent involves ascending to space in a single step, without any intermediate stops or stages. This approach is in contrast to the more common method of staging, where multiple stages are used to reach space.

Direct Ascent offers several advantages over staging. Firstly, it simplifies the rocket design and reduces the number of components needed. This can lead to cost savings and increased reliability. Additionally, Direct Ascent allows for a quicker journey to space, as there are no pauses or separations between stages.

However, Direct Ascent also has some drawbacks. One major challenge is the need for a larger and more powerful rocket to carry the entire payload to space in one go. This can make the launch vehicle more expensive and difficult to develop. Additionally, the forces experienced during Direct Ascent can be more extreme, which may require additional engineering considerations.

Despite these challenges, Direct Ascent has been used successfully in certain space missions. For example, the Apollo program used a Direct Ascent approach to send astronauts to the Moon. The Saturn V rocket carried the Apollo spacecraft directly from Earth to lunar orbit, without the need for staging.

In conclusion, Direct Ascent is a method of reaching space in a single step, without any intermediate stops or stages. While it offers advantages such as simplified design and quicker journey times, it also presents challenges such as the need for a larger and more powerful rocket. Overall, Direct Ascent has been used successfully in certain missions and continues to be an area of interest for space exploration.

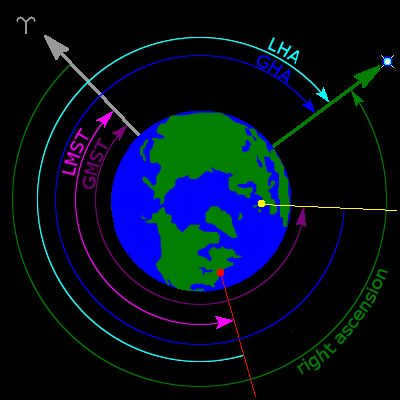
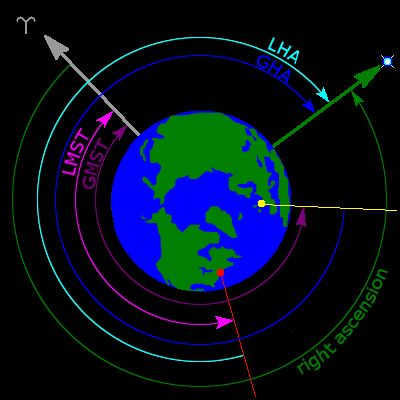
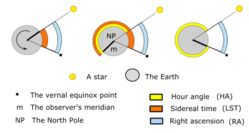
The image above displays Earth’s northernmost point and the local hour angle (LHA) of stars for an observer in the vicinity of New York City. Additionally, it illustrates the stellar right ascension and the Greenwich Mean Time Angle (GMT), local mean sidereal time (LMST), and Greenwich Mean Stellar Time (GMST). The symbol ʏ represents the direction of the vernal equinox.

The direct ascension symbol α (also known as lower case “alpha” and abbreviated as RA) represents the angular distance of an object moving eastward along the celestial equator, from the vernal equinox point to the hour circle that passes through the object. The vernal equinox point is one of the points where the ecliptic intersects the celestial equator. Direct ascension is typically measured in sidereal hours, minutes, and seconds, rather than degrees. This is because direct ascension is determined by timing the passage of objects through the meridian as the Earth rotates. There are 360° / 24 h = 15° for one hour of direct ascension, and 24 hours of direct ascension around the entire celestial equator.

When combined, direct ascension and declination are commonly abbreviated as RA / Dec.

Hour angle

Instead of using direct ascent, the hour angle (HA or LHA, local hour angle) is a different approach to measure the angular distance of an object towards the west along the celestial equator, starting from the observer’s meridian to the hour circle that passes through the object. In contrast to direct ascent, the hour angle consistently increases as the Earth rotates. The hour angle can be considered as a way to measure time from the point of upper culmination, which is the moment when an object crosses directly overhead on the observer’s meridian.

The star that reaches its highest point in the sky above the observer is described as having a zero hour angle (0 h). Once approximately 0.9973 solar hours have passed, the Earth’s rotation will cause the star to move to the west of the observer’s meridian, resulting in an hour angle of 1 hour. When calculating topocentric events, it is possible to convert the star’s right ascension to hour angle as an intermediate step.

Rectangular coordinates

Geocentric equatorial coordinates

Rephrase:

Rectangular coordinates

Coordinates in a rectangular form

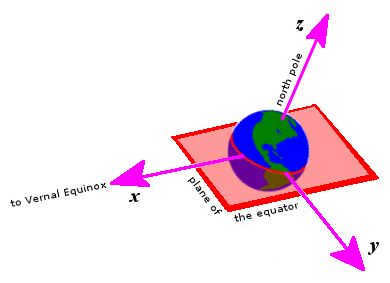
Coordinates for geocentric equatorial system are determined with respect to certain reference frame. The reference frame has its origin at the center of the Earth and its principal plane is aligned with the plane of the Earth’s equator. The principal direction is defined by the vernal equinox. In this right-handed convention, the y-axis represents the east direction in the principal plane, while the z-axis represents the north polar axis. Unlike the Earth, the reference frame itself does not rotate; instead, the Earth rotates about the z-axis.

There are various rectangular variants of equatorial coordinates, but all of them share the following characteristics:

• Origin is located at the center of the Earth.
• The primary plane coincides with the plane of the Earth’s equator.
• The primary direction (axis x) points to the vernal equinox, which is the point where the Sun crosses the celestial equator in a northerly direction along its annual apparent circle around the ecliptic.
• Using the right hand convention, the у axis points 90° eastward in the principal plane, and the г axis aligns with the north polar axis.

Reference frames remain fixed and do not rotate with the Earth (unlike Earth-centered, Earth-fixed frames), always pointing towards the equinoxes and shifting over time due to precession and nutation movements.

• In the field of astronomy:
• The location of the Sun is frequently specified using geocentric equatorial rectangular coordinates X, Y, Z, and a fourth coordinate, R (= √ X 2 + Y 2 + Z 2), measured in astronomical units.
• The positions of planets and other celestial bodies in the solar system are often given in geocentric equatorial rectangular coordinates ξ, η, ζ, and a fourth distance coordinate Δ (equal to √ ξ 2 + η 2 + ζ 2), measured in astronomical units.
• The location of Earth’s artificial satellites is specified in geocentric equatorial coordinates, also referred to as geocentric equatorial inertial system (GEI), geocentric inertial system (ECI), and conventional inertial system (CIS), which are essentially equivalent to the astronomical geocentric system. These coordinates are represented in equatorial rectangular frames, as shown above. Within the geocentric equatorial frame of reference, the axes x, y, and z are commonly denoted as I, J, and K, respectively, or the basis of the system can be defined by unit vectors Î, Ĵ, and K̂.
• The Geocentric Celestial Reference Frame (GCRF) is the geocentric version of the International Celestial Reference Frame (ICRF). It is aligned with the equinox from J2000.0 and remains fixed in space, unaffected by precession and nutation. However, it is otherwise identical to the aforementioned systems.

Summary of notations for astronomical equatorial coordinates
Rectangular
Right Ascension
Declination
Distance
General
Special purpose
Geocentric

Heliocentric

α	Δ	ξ, η, ζ	X, Y, Z (Sun)
x, y, y

Heliocentric equatorial coordinates

In the field of astronomy, there is an alternative representation of equatorial coordinates known as the heliocentric rectangular system, which is represented by x, y, z. This system has the following characteristics:

• The origin is located at the center of the Sun.
• The main plane coincides with the Earth’s equatorial plane.
• The primary direction (axis x) points towards the vernal equinox.
• Following the right-hand convention, the y axis points 90° eastward in the main plane, and the z axis aligns with the Earth’s north polar axis.

This reference frame is identical to the coordinate system of ξ, η, ζ described above, except that the origin is relocated to the center of the Sun. It is commonly utilized in the calculation of planetary orbits. The three astronomical rectangular coordinate systems are interconnected by the equation

ξ symbol equals X + X η symbol equals y + Y ζ symbol equals z + Z \ xi & = x + X \\\ eta & = y + Y \\\\ zeta & = z + Z \ end >>

Related content

Recommended reading

Additional resources

• MEASURING THE SKY An easy-to-follow handbook on understanding the celestial sphere by James B. Kahler from the University of Illinois
• Celestial Equatorial Coordinate System A comprehensive guide to the celestial equatorial coordinate system from the University of Nebraska-Lincoln
• Celestial Equatorial Coordinate System Researchers A compilation of research materials on the celestial equatorial coordinate system from the University of Nebraska-Lincoln

The equatorial coordinate system refers to a celestial coordinate system that uses the plane of the celestial equator as its fundamental plane. There are two forms of the equatorial coordinate system: the first equatorial system, which is tied to the rotation of the Earth, and the second equatorial system, which remains fixed relative to distant stars [1].

Used Coordinates

One of the coordinates used is known as declination [math]\displaystyle< \delta >[/math], or, less commonly, it can be referred to as the polar distance [math]\displaystyle< p >[/math].

The declination of the luminary lies within the range of -90° to +90°. It represents the angle between the equatorial plane and the direction towards the luminary. In the case of luminaries located in the northern hemisphere, the declination value is positive, while in the southern hemisphere it is negative.

The polar distance, on the other hand, measures the angle between the luminary and the north pole of the world. Its value can vary from 0° to +180°. It is worth noting that declination and polar distance are interchangeable and closely related: [math]\displaystyle< \delta + p = 90^\circ >[/math] [1].

One option is to use the hour angle [math]\displaystyle< t >[/math], while another option is to use a direct ascent [math]\displaystyle< \alpha >[/math].

The hour angle represents the distance along the equatorial arc from the celestial meridian to the luminary’s declination circle, and it is measured in the direction of the celestial sphere’s rotation. There is also the concept of the “Greenwich hour angle,” which utilizes the Greenwich meridian instead of the celestial meridian.

The length of the equatorial arc from the vernal equinox to the circle of declination of the luminary is known as direct ascent, and it is measured against the direction of rotation of the celestial sphere. In navigation, the stellar complement, denoted as \displaystyle<\tau^\star>, is also connected to the direct ascent. It represents the arc length from the vernal equinox to the declination circle of the luminary, but measured in the direction of rotation of the celestial sphere. Therefore, \displaystyle<\tau^\star + \alpha = 360^\circ> [1].

Usually, these measurements are taken in hours and range from 0 h to 24 h, excluding the endpoints. Similarly, in terms of degrees, they range from 0° to 360°. However, they are occasionally regarded as ranging from 0° to 180° (0 h to 12 h ) in the west and 0° to -180° (0 h to -12 h ) in the east [1] [2].

Original: First equatorial coordinate system

The first equatorial coordinate system uses declination (or polar distance) and hour angle. In this system, the coordinates of the fixed stars are not constant: their hour angle changes due to the daily rotation of the Earth. However, unlike horizontal coordinates, the hour angle varies uniformly with time, while declination remains constant. In addition, the hour angle of the vernal equinox point is equal to local sidereal time by definition [1] [3].

Rephrased: Introduction to the initial equatorial coordinate system

The initial equatorial coordinate system employs declination (or polar distance) and hour angle. In this system, the coordinates of the stationary stars are not static: their hour angle shifts due to the Earth’s daily rotation. Nevertheless, unlike horizontal coordinates, the hour angle changes consistently with time, whereas declination remains unchanging. Additionally, by definition, the hour angle of the vernal equinox point equals the local sidereal time [1] [3].

The alternative equatorial coordinate system

The alternative equatorial coordinate system employs declination (or polar distance) and right ascension. In contrast to the initial equatorial system, the alternative equatorial system remains unaffected by diurnal motion, as the vernal equinox point remains fixed. Consequently, it is advantageous to store and document the celestial bodies’ coordinates in the alternative equatorial coordinate system [1].

Relationship between the initial and subsequent equatorial coordinate systems

The primary factor in determining the relationship between the first and second equatorial systems is the correlation between the hour angle and right ascension. These quantities are connected to sidereal time [math]\displaystyle< s >[/math] : [math]\displaystyle< s = t + \alpha >[/math] . Technically speaking, the sum of the hour angle and right ascension can exceed 24 hours, in which case the equation holds true modulo 24 hours [1].

Relation to other coordinate systems

The parallactic triangle is utilized to establish a connection with various other coordinate systems, such as the horizontal or ecliptic [4].

General characteristics

• Declination is measured in degrees, minutes, and seconds of arc. The positive direction indicates north of the celestial equator, while the negative direction indicates south. Declinations should indicate the sign accordingly.
• An object located on the celestial equator possesses a declination of 0°.
• The declination of the north pole of the celestial sphere is +90°.
• The declination of the south pole is -90°.
• The declination of a celestial object that passes through the zenith is equivalent to the observer’s latitude.

In the Northern Hemisphere of the Earth, for a given latitude [math]\displaystyle< \varphi >[/math]:

• Celestial objects with a declination of [math]\displaystyle< \delta > 90^\circ – \varphi[/math] do not pass below the horizon.
• If the declination of an object is [math]\displaystyle< \delta < \varphi - 90^\circ[/math], then that object will not be visible at that latitude.

Because the position of the plane of the celestial equator gradually changes due to precession, the equatorial coordinate system always specifies the epoch, which determines the specific location of the main plane and, therefore, the direction to the vernal equinox point.

Notes

1. ↑ 1.01.11.21.31.41.51.6Kononovich E. V., Moroz V. I. General course of astronomy. – 2nd edition, corrected. – URSS, 2004. – P. 19-28. – ISBN 5-354-00866-2.
2. ↑ Astronomical coordinates(unpublished). Astronet. Astronet.
3. ↑ Systems of celestial coordinates(unpublished). Astronet. Astronet.
4. ↑ Conversion of coordinates from one system to another(unpublished). Astronet. Astronet.

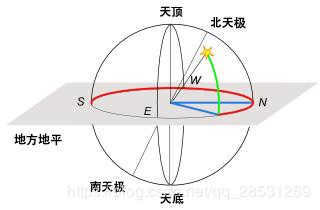
In the system of the horizon or altitude azimuth, an observer is located on the Earth, which rotates around its rotational axis every sidereal day (23 hours 56 minutes) relative to a fixed stellar background. This system is mainly used to determine the short time interval between the sunrise and sunset by calculating the positions of celestial bodies. In the past, it was also utilized for navigation purposes, such as determining the altitude and azimuth of a planet’s position, as well as calculating the accurate longitude and latitude of a ship based on time. Nowadays, many telescopes employ theodolite mounts and computers to calculate the position (altitude and azimuth) of celestial bodies on the horizon, taking into account time and geographic location.

The celestial coordinate system

The equatorial coordinate system, which is centered on the Earth, serves as a reference point for the sky that surrounds us. It gives the impression that the sky is fixed to the Earth, and we are rotating on our axis on the Earth’s surface. Equatorial coordinates are used to describe the sky, including the visible solar system. Nowadays, almost all star charts are created using equatorial coordinates. Ancient astronomers in the East have been using these coordinates for centuries to draw star charts. The equatorial system is the most commonly used coordinate system among professional astronomers. Even amateur astronomers utilize the equatorial system to track the movement of the night sky. When celestial objects are detected using telescopes or other instruments, their positions are marked by comparing them to equatorial coordinates.
The fundamental coordinates of the equatorial coordinate system are as follows:

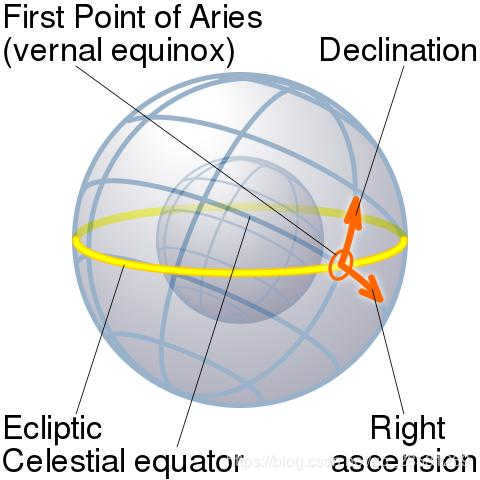
How to Determine Equatorial Coordinates
• Declination: The declination, which is abbreviated as Dec, is one of the two sets of coordinates used in the equatorial coordinate system in astronomy. Similar to latitude on Earth, declination represents the projection of latitude onto the celestial sphere. The unit of measurement for declination is degrees, with smaller units referred to as “angular minutes” and “angular seconds”. The celestial equator has a declination of 0 degrees, while the northern hemisphere has positive declination and the southern hemisphere has negative declination. The north celestial pole has a declination of +90°, while the south celestial pole has a declination of -90°. It is important to note the positive sign as well.
  Changes in Declination:
  Due to the movement of celestial bodies and changes in the Earth’s axis, the declination of celestial bodies is not a constant value but rather continuously changing. The polar star has a declination of either +90° or -90°. If the observer’s latitude is denoted as “l”, any celestial body with a declination greater than 90° – l will remain above the horizon throughout the day. Such celestial bodies are known as circumpolar constellations. The sun, which never sets, is referred to as the midnight sun.
  The Sun’s declination is equal to the angle between the incident sunlight and the Earth’s equator. Since the angle between the Earth’s axis of rotation and the plane of its orbit is roughly the same, the Sun’s declination varies with the seasons. These variations are periodic, with a period equal to one year, which is the Earth’s rotation period. The maximum declination of the sun is 23°26′, occurring during the summer solstice, while the declination during the winter solstice is -23°26′. During the spring and fall equinoxes, the declination of the sun is 0°. Due to the Earth’s orbit having a very low eccentricity, it can be approximated as a circle. The solar declination can be calculated using the following two formulas:
  δ = -23.44° × cos(360/365 × (N + 10)) angle degree \ delta = -23.44 \ deg \ times \ cos (\ frac \ times (N + 10)) angle δ = -23.44° × cos(2π/365 × (N + 10)) arc degree \ delta = -23.44 \ deg \ times \ cos (\ frac \ times (N + 10)) radian
  Here, N represents the number of days in a year, with January 1 being assigned a value of 1.
• Direct Ascension: In astronomy, direct ascension is a coordinate value in the celestial equatorial coordinate system. It is a line that passes through the celestial poles and is perpendicular to the celestial equator. Similar to longitude in geographic coordinates, direct ascension on the celestial sphere is used to determine the position of celestial objects. The zero point of direct ascension is the vernal equinox, which is the point where the Sun enters the northern celestial sphere at the end of March. It is also the Earth’s ascending node. Direct ascension is measured in hours, minutes, and seconds, or sometimes in degrees, east of the vernal equinox. It is both a unit of time and a unit of angle. 1 hour of direct ascension is equal to 15 degrees, 1 minute is equal to 15 arcminutes, and 1 second is equal to 15 arcseconds. The relationship between direct ascension and sidereal time is inseparable. Direct ascension is used to calculate the position of celestial bodies on the celestial sphere and to determine the time when a celestial body reaches a certain point in the sky. For example, if a celestial body has a position of 13 hours and 30 minutes in direct ascension, it will pass the meridian circle in 6.5 hours of sidereal time.
• The ecliptic coordinate system is a coordinate system commonly used for representing the positions and movements of celestial objects in the solar system.
• In this coordinate system, the reference plane is the ecliptic, which is the plane of Earth’s orbit around the Sun.
• The two primary coordinates used in this system are the ecliptic longitude and the ecliptic latitude.
• The ecliptic longitude measures the angular distance of an object eastward along the ecliptic from the vernal equinox.
• The ecliptic latitude measures the angular distance of an object north or south of the ecliptic plane.
• By using these coordinates, astronomers can accurately locate and track the positions of planets, asteroids, comets, and other celestial objects in the solar system.

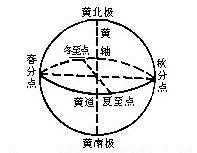
Ecliptic coordinate system

The primary purpose of the celestial coordinate system, which uses the ecliptic as a reference plane, is to analyze the movement of celestial objects within the solar system. The ecliptic system describes the path of the planets as they orbit around the Sun, with the Sun itself serving as the center of gravity for the entire system. The major plane of this system aligns with the Earth’s orbit, known as the ecliptic plane. This system is commonly utilized in planetology to determine various parameters of a planet’s orbit, such as inclination, ascending node, descending node, and perihelion position. Additionally, the ecliptic represents the apparent path of the Sun across the celestial sphere over the course of a year from the perspective of Earth. It can be visualized as the projection of the Sun’s orbital plane onto the celestial sphere. The ecliptic intersects with the celestial equator at two points known as the vernal equinox and the autumnal equinox, while its associated poles are referred to as the North Yellow Pole and the South Yellow Pole. A small circle parallel to the ecliptic is called the latitude of the ecliptic (symbolized as β), where a positive value indicates a direction towards the North Yellow Pole (ranging from 0° to 90°), and a negative value indicates a direction towards the South Yellow Pole. The longitude along the vertical plane of the ecliptic is known as ecliptic longitude (symbolized as λ), measured in a west-to-east direction starting from the vernal equinox point (ranging from 0° to 360°). Similar to the equatorial coordinate system, the vernal equinox is used as the reference point for measuring ecliptic longitude. Due to the precession of the Earth’s axis, the coordinate values of the two yellow poles in this system will gradually shift over time. Therefore, the specific epoch to which the coordinate system pertains must be specified during calculations. The epoch J2000.0 is commonly used, although some previous publications utilized epoch B1950.0. For higher precision calculations, such as astronomical calendars, the instantaneous equinox of the day or month is often employed. This coordinate system is particularly useful for determining the positions of celestial bodies within the solar system. Most planets (excluding Mercury and Pluto) and many asteroids possess orbital planes that closely align with the ecliptic, resulting in small values for ecliptic latitude (β).



How to Determine Equatorial Coordinates

• The Galactic coordinate system

  is a celestial coordinate system in which positions on the celestial sphere are defined relative to the Milky Way galaxy.

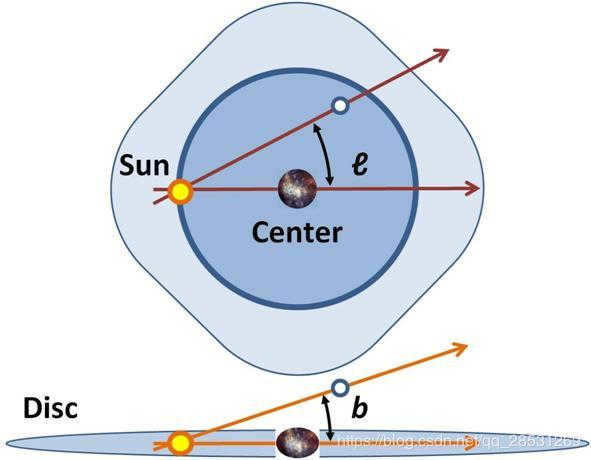
The super galaxy’s coordinate system

The supergalactic coordinate system is one of the celestial coordinate systems, with its equator aligned with the plane of the supergalaxy. This system is employed in the terrestrial universe and primarily pertains to neighboring galaxy clusters such as the Virgo galaxy cluster, the Giant Attractor, and the Perseus-Pisces supercluster in the two-dimensional space. While William Herschel observed the distribution of galaxies in this plane as far back as 200 years ago, the original supergalactic coordinate plane was not officially recognized until Gerard Foculius included it in the Sharpie-Enchie catalog in 1953, pending confirmation. It was determined during a meeting that the supergalactic longitude and latitude correspond to the galactic longitude (l) and galactic latitude (b) in the galactic coordinate system, and are denoted as SGL and SGB, respectively. They intersect at the galactic plane.

One can determine the precise position of a particular point on planet Earth, or any other spherical planet, by employing geographic coordinates – latitude and longitude. The intersection points of circles and arcs at perpendicular angles form a corresponding grid, which facilitates the unambiguous determination of the coordinates. An excellent illustration of this concept can be found in a typical school globe, featuring horizontal circles and vertical arcs. The following section will provide instructions on how to effectively utilize a globe.

The measurement system used in this context is based on degrees of angle. The angle is determined by calculating the distance from the center of the sphere to a specific point on its surface. In terms of orientation, the latitude angle is calculated vertically relative to the axis, while the longitude angle is calculated horizontally. To accurately determine coordinates, specific formulas are employed. In some cases, there may also be a value for altitude, which is primarily used to represent three-dimensional space and aids in calculating a point’s position relative to sea level.

Definitions and explanations of latitude and longitude

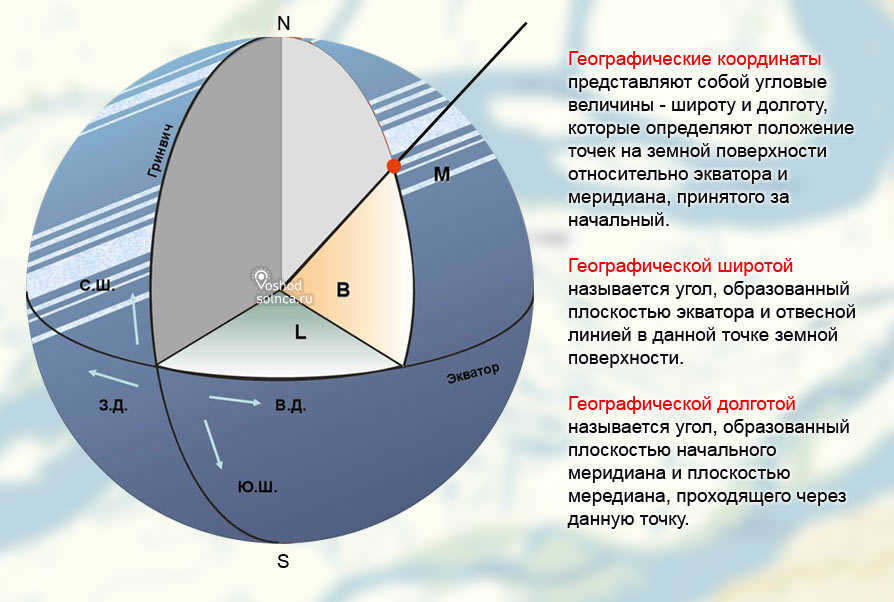
The Earth is divided into two equal parts – the northern and southern hemispheres – by an imaginary horizontal line known as the equator. This division gives rise to the definitions of northern and southern latitudes. Latitude is represented by circles parallel to the equator, known as parallels. The equator itself, with a value of 0 degrees, serves as the starting point for measuring latitude. As the parallels move closer to the north or south pole, their diameter decreases and the angular degree increases. For instance, the city of Moscow is situated at a latitude of 55 degrees north, indicating that it is approximately equidistant from both the equator and the north pole.

Unlike latitude, which uses the equatorial line as its reference point, any meridian can be set as zero. However, for the sake of convenience, particularly in terms of keeping track of time, the Greenwich meridian was established.

Geographic coordinates – location and time

Geographic coordinates enable the precise determination of a location’s address on the planet by using latitude and longitude, which are measured in degrees. Degrees can be further divided into smaller units such as minutes and seconds. Each degree is divided into 60 minutes, and each minute is divided into 60 seconds. For instance, if we take Moscow as an example, its coordinates are 55° 45′ 7″ N, 37° 36′ 56″ E, indicating that it is located at 55 degrees, 45 minutes, and 7 seconds of north latitude, and 37 degrees, 36 minutes, and 56 seconds of east longitude.

It is important to note that there is a 15-degree interval between meridians and approximately 111 kilometers along the equator. This is the distance that the Earth covers in one hour while rotating. It takes 24 hours for the Earth to complete a full revolution, which corresponds to one day.

Utilizing a globe

The globe accurately depicts the Earth, with detailed illustrations of continents, seas, and oceans. Auxiliary lines, such as parallels and meridians, are included on the globe map. A serpentine meridian arc is commonly found in the construction of globes, serving as a helpful tool for measurement.