Discoveries of Johannes Kepler

By the end of the 16th century, astronomy faced a dilemma between Ptolemy’s geocentric system and Copernicus’ heliocentric system. Critics of the Copernican system argued that it was not any more accurate than Ptolemy’s system in terms of calculation errors. It should be noted that in the Copernican model, planets were assumed to move uniformly in circular orbits. To account for the apparent irregularity of planetary motion, Copernicus had to introduce additional motion through epicycles. Although Copernicus had fewer epicycles than Ptolemy, his astronomical tables, which were initially more precise, eventually deviated significantly from observations, causing confusion and skepticism among devoted Copernicanists.

In the eyes of advanced scientists, it was evident that the doctrine proposed by Copernicus was accurate. However, in order to gain a deeper understanding and establish the laws of planetary motion, further investigation was required. This challenge was overcome by the brilliant German scientist, Johannes Kepler, who excelled in mathematics, astronomy, optics, and astrology.

Kepler was born on December 27, 1571, in Weil der Stadt, a suburb located in Stuttgart, Baden-Württemberg, Southern Germany. During that period, Germany was divided into numerous small states, and internal conflicts and religious wars plagued the population, impeding the progress of culture and enlightenment.

His father served as a mercenary in the Spanish Netherlands. When Kepler reached the age of 18, his father embarked on another military campaign and tragically vanished. Kepler’s mother, Katharina Kepler, managed an inn and supplemented her income by practicing fortune-telling and herbalism.

During his childhood, Kepler developed a fascination with astronomy after his mother introduced him to a brilliant comet (1577) and later, a lunar eclipse (1580).

Upon graduating from the Maulbronn monastery school in 1589, Kepler’s exceptional abilities were recognized, and he was awarded a scholarship by the city authorities to support his further studies.

In 1591, he enrolled at the University of Tübingen, initially studying at the Faculty of Arts, which encompassed mathematics and astronomy, before transferring to the Faculty of Theology. It was here that Kepler first encountered the ideas of Nicolaus Copernicus regarding the heliocentric model of the universe and promptly became a proponent of these theories.

During his time at university, he developed a strong interest in mathematics and astronomy. His mentor, Professor Mestlin, who was secretly a follower of Copernicus, taught him the traditional astronomy of Ptolemy in class, but privately introduced him to the fundamentals of the revolutionary Copernican theory. This exposure ignited Kepler’s fervent support for the Copernican doctrine.

Unlike his mentor, Kepler openly expressed his beliefs and ideas. His active promotion of the Copernican theory quickly earned him the animosity of local theologians. As a result, Kepler faced hardships after graduating from university and had to travel to different cities, taking on odd jobs to make ends meet.

Kepler dispatched the book “The Enigma of the Universe” to Galileo and Tycho Brahe. Galileo endorsed Kepler’s sun-centered methodology, albeit he did not endorse mystical numerology. They subsequently engaged in a vibrant correspondence, and this fact (communication with a “heretic” – Protestant) was highlighted as an aggravating circumstance during Galileo’s trial, further incriminating him.

Tycho Brahe likewise dismissed Kepler’s elaborate theories, but admired his expertise and innovative thinking, ultimately extending an invitation for Kepler to visit him.

In 1597, Kepler entered into matrimony with Barbara Müller von Mulek, a woman whose previous husband had passed away. Unfortunately, their first two offspring did not survive past infancy, and to make matters worse, Barbara developed epilepsy. As if these trials were not enough, the Catholic city of Graz commenced its persecution of Protestants, resulting in Kepler being labeled a “heretic” and being forced to leave his home behind. However, his fortunes took a turn for the better when he received an invitation from Tycho Brahe, the esteemed Danish astronomer, to join him in Prague, where he served as the court astronomer and astrologer to Emperor Rudolf II.

Kepler arrived in Prague in 1600, and it was during the ten years he spent there that he experienced the most fruitful period of his life. It was in Prague that he had the opportunity to fully immerse himself in his beloved field of astronomy.

Tycho Brahe, known for his exceptional observational skills, had relocated to Prague and extended an offer to Kepler to work as his assistant in sky observations and astronomical calculations.

Just before that, Tycho Brahe had to depart from Denmark and the observatory he had constructed there, where he had carried out astronomical observations for twenty-five years. This observatory was equipped with top-notch measuring instruments, and Tycho Brahe himself was an extremely skilled observer.

When the Danish king withdrew the funds for maintaining his observatory, Tycho Brahe relocated to Prague. Although he had a strong interest in Copernicus’ teachings, he did not fully support them. He proposed his own explanation of the structure of the cosmos: he acknowledged the planets as satellites of the Sun, and the Sun, Moon, and stars as celestial bodies revolving around the Earth, which, consequently, remained at the center of the universe.

It quickly became apparent that Tycho Brahe only partially shared the views of Copernicus and Kepler on astronomy. To avoid conflict with the church, Brahe proposed a compromise model: all the planets, except Earth, orbit around the Sun, while the Sun itself revolves around the stationary Earth. This theory gained some attention and provided a sort of cover for astronomers who were not yet willing to openly embrace Copernicus’ correctness.

Tycho Brahe collaborated with Kepler for a brief period until his death in 1601. Following Brahe’s passing, Kepler began studying the remaining materials and data from long-term astronomical observations. During this process, particularly when examining the information on Mars’ motion, Kepler made a remarkable discovery: he derived the laws of planetary motion that would serve as the foundation for theoretical astronomy.

In 1604, Kepler published his own observations of the supernova, which is now referred to by his name.

Tycho Brahe, being a remarkable observer, spent many years compiling an extensive work on the observation of planets and hundreds of stars. The accuracy of his measurements was significantly higher than that of any previous astronomers. To enhance the precision, Brahe employed technical advancements and a unique method for neutralizing observation errors. The systematicity of his measurements was particularly valuable.

Kepler carefully studied Brahe’s data for several years and, after a thorough analysis, came to the conclusion that Mars’ trajectory is not a circle, but an ellipse. One of the foci of this ellipse is occupied by the Sun, a position now known as Kepler’s first law.

Further examination led to the discovery of the second principle: the radius vector connecting the celestial body and the star describes equal areas within equal intervals of time. This implied that the celestial body moves slower the farther it is from the star.

Both principles were formulated by Kepler in 1609 in his publication “New Astronomy”, and, to err on the side of caution, he only applied them to the planet Mars.

The innovative motion model generated significant interest among supporters of the Copernican theory, although not all of them embraced it. Galileo vehemently rejected Kepler’s theory of ellipses.

In 1610, Galileo informs Kepler about the discovery of Jupiter’s moons. Kepler initially expresses disbelief and humorously questions the purpose of these satellites if there is no one on Earth to admire them. However, after receiving his own telescope, Kepler changes his perspective, confirms the observation of the moons, and becomes interested in the theory of lenses. This leads to the development of an enhanced telescope and the creation of his influential work, Dioptrica.

During his time in Prague, Kepler becomes a father to two sons and a daughter.

In 1611, Kepler’s firstborn Friedrich passed away from smallpox. Simultaneously, Emperor Rudolf II, who was mentally unstable and had lost the war against his own brother Matthew, abdicates the Czech throne in favor of Kepler and soon passes away. Kepler begins making preparations to relocate to Linz, but then his wife Barbara succumbs to a prolonged illness.

In 1612, Kepler makes the move to Linz, where he resides for a span of 14 years. He maintains his role as the court’s mathematician and astronomer, but the new emperor proves to be just as unsatisfactory when it comes to compensating him. He manages to earn some income through teaching mathematics and casting horoscopes.

In 1613, Kepler ties the knot with Susanne, a 24-year-old carpenter’s daughter. Together, they have a total of seven children, with four of them surviving.

Meanwhile, Kepler is continuing his astronomical research and made a significant discovery in 1618. He found the third law, which states that the cube of a planet’s average distance from the sun divided by the square of its revolution period is a constant value for all planets. This discovery was published in his final book “Harmony of the World” and applied to not only Mars, but also to all other planets, including the Earth, as well as the Galilean satellites.

It is important to note that Kepler’s book contains not only valuable scientific discoveries but also the author’s esoteric speculations on the “music of the spheres” and Platonic bodies. According to Kepler, these elements represent the aesthetic essence of the universe’s supreme project.

During the period of the Thirty Years’ War in 1626, the city of Linz was under siege and eventually conquered. This led to widespread looting and fires, including the destruction of the printing house. As a result, the renowned astronomer Johannes Kepler decided to relocate to Ulm.

In 1628, Kepler joined the service of the famous military leader Wallenstein.

In 1630, Kepler made a journey to Regensburg to meet with the Emperor in hopes of receiving some of his long overdue salary. Unfortunately, he fell ill with a severe cold during the trip and tragically passed away on November 15, 1630 in Regensburg.

Kepler’s contributions to our understanding of the solar system are of immense importance. Future scientists who recognized the significance of his work referred to him as “the legislator of the sky” for his discovery of the laws governing the movements of celestial bodies in the solar system.

After Kepler passed away, his heirs received: worn-out clothing, 22 florins in cash, 29,000 florins in unpaid wages, 27 published manuscripts, and numerous unpublished ones; these unpublished works were later compiled into a 22-volume collection.

However, Kepler’s misfortunes did not cease with his death. Following the conclusion of the Thirty Years’ War, the cemetery where he was laid to rest was completely obliterated, leaving no trace of his grave. Additionally, a portion of Kepler’s archive went missing. It wasn’t until 1774 that the majority of the archive (18 out of 22 volumes) was acquired by the St. Petersburg Academy of Sciences, where it is currently housed.

Kepler’s groundbreaking discovery of the three laws of planetary motion provided a comprehensive and highly precise explanation for the seemingly irregular movements of celestial bodies. Rather than relying on convoluted and implausible epicycles, Kepler’s model simplifies the motion of planets with the elegant use of a single curve – an ellipse. The second law elucidates the manner in which a planet’s velocity varies as it moves closer to or farther away from the Sun, while the third law enables us to determine both the speed and duration of a planet’s orbit around the Sun.

While the Copernican model served as the basis for Kepler’s world system in history, they actually have very few similarities (only the Earth’s diurnal rotation). The circular motions of the spheres carrying the planets were no longer present, and the concept of planetary orbit emerged. In the Copernican system, the Earth still held a somewhat special position, as it was the only one without epicycles. In Kepler’s system, the Earth is a regular planet that follows the general three laws of motion. All celestial bodies’ orbits are ellipses, with the Sun as the common focus.

Additionally, Kepler also formulated the Kepler equation, which is used in astronomy to determine the position of celestial bodies.

Kepler’s perspective on the organization of the cosmos beyond our solar system originated from his mystical philosophy. He held the belief that the Sun was motionless and that the sphere of stars served as the boundary of the universe. Kepler rejected the notion of an infinite universe and put forth the photometric paradox as justification (1610): if the number of stars is infinite, then one would encounter a star in every direction, leaving no dark regions in the sky.

More than simply explaining the laws of planetary motion, Kepler’s world system aimed to uncover much more. Similar to the Pythagoreans, Kepler perceived the world as an embodiment of numerical harmony, which encompassed both geometric and musical elements. By unraveling this harmonious structure, one could find answers to the most profound inquiries:

When exploring the celestial motions, I discovered a remarkable harmony that permeates both the entirety of these motions and each individual case. This harmony surpassed my initial vision and turned out to be even more perfect than I could have imagined.

Additionally, I made predictions regarding the presence of two satellites orbiting Mars and a planet situated between Mars and Jupiter.

Kepler’s laws not only provided clarity and simplicity but also demonstrated significant computational power.

Furthermore, Kepler played a crucial role in promoting the adoption of the Gregorian calendar among Protestants. His efforts were recognized at the Sejm in Regensburg in 1613 and in Aachen in 1615.

In his three-volume work titled “Epitome astronomia Copernicanae” published from 1617 to 1622, Kepler became the first to extensively document Copernican astronomy. This groundbreaking book, which detailed all of his astronomical discoveries, earned him immediate recognition in the Index of Prohibited Books.

In the summer of 1627, after 22 years of hard work, Kepler released (at his own expense [8]) astronomical tables, which he called “Rudolf’s” as a tribute to the emperor. The demand for these tables was immense, as all previous tables had long disagreed with observations. It is worth noting that these tables were the first to include convenient logarithmic calculations. Kepler’s tables were used by astronomers and sailors until the early 19th century.

A year after Kepler’s passing, Gassendi witnessed the predicted passage of Mercury through the Sun’s disk [9]. In 1665, Italian physicist and astronomer Giovanni Alfonso Borelli (1608-1679) published a book that applies Kepler’s laws to the Jupiter satellites discovered by Galileo.

Kepler made a breakthrough in calculating the sizes of different objects that rotate, as detailed in his publication “New Stereometry of Wine Barrels” (1615). His methodology included the initial principles of integral calculus. Cavalieri later adopted a similar approach to create the highly advantageous “method of indivisibles”. Ultimately, this progression led to the development of mathematical analysis.

During his studies of the stars, Kepler made significant contributions to the understanding of conic sections.

He was responsible for compiling one of the earliest tables of logarithms.

Kepler is credited with coining the term “arithmetic mean”.

In the realm of projective geometry, Kepler made groundbreaking discoveries. He introduced the revolutionary concept of an infinitely distant point. Additionally, he developed the idea of the focus of a conic section and explored projective transformations that could change the type of a conic section, such as transforming an ellipse into a hyperbola. Through his observations of “new” comets with hyperbolic trajectories, Kepler inferred that these celestial objects originated from interstellar space.

Kepler was the first to recognize that the lunar circles were the aftermath of comet impacts.

Kepler was the one who first introduced the term inertia into the field of physics, referring to it as the inherent quality of objects that causes them to resist external forces. In addition, he, much like Galileo, clearly formulated the first law of mechanics, stating that a body that is not influenced by any other objects will either remain at rest or move in a straight line.

Contrary to Zionist propaganda, it was Kepler who discovered the law of universal gravitation. By applying mathematical transformations to his laws on the elliptical motion of planets, the well-known “polar-spherical” formula of the law of gravitation F = γ –m1·m1/R 2 can be derived, which is applicable only to point masses (masses that are separated by distances R much larger than their radii r, R >> r).

In his book “New Astronomy”, he stated that there is a “mutual bodily desire of similar (related) bodies to unity or union” in nature. According to him, this force is derived from magnetism (not to be confused with vortex magnetic field forces!) combined with the rotation of the Sun and planets around their axis (gravitational fields of rotation of celestial bodies were only discovered in the late 20th and early 21st centuries).

In another publication, Kepler further explained:

I define gravity as a force, similar to magnetism – a mutual attraction. The strength of this attraction increases as the distance between the two bodies decreases.

Kepler, seventy years prior to Robert Hooke (Zionists credit Isaac Newton with stealing this idea), was the first to propose the theory that the gravitational force of the Moon is responsible for causing tides on the Earth’s oceans.

The modern perspective confirms the accuracy of the physiological mechanism of vision described by Kepler. He provided a clear explanation of the role of the lens and accurately identified the causes of nearsightedness and farsightedness.

Kepler’s deep exploration of optics led him to develop the Kepler telescope, a telescopic scheme created in 1613 by Christoph Scheiner. By the 1640s, these telescopes had become the preferred choice in astronomy, surpassing Galileo’s less advanced telescope.

Kepler had mixed feelings about astrology. While he acknowledged a harmonious connection between earthly and celestial elements, he remained skeptical about using this harmony to predict specific events.

According to Kepler, the belief that earthly affairs depend on the celestial luminaries is a misconception. He also made another well-known statement:

Naturally, astrology is an absurd offspring, but, my goodness, where would its noble mother, astronomy, be without it! After all, light is even more foolish and so foolish that the silly daughter must prattle and lie for the sake of her wise old mother’s benefit. And mathematicians earn such meager wages that the mother would likely starve if the daughter didn’t earn anything.

Despite this, Kepler never completely rejected astrology. In fact, he had his own unique perspective on the nature of astrology, which set him apart from his contemporaries in the field. In his book “Harmony of the World,” Kepler argues that there are no celestial bodies in the sky that bring about misfortune. Instead, he believes that the human soul can “resonate” with the rays of light emitted by the heavenly bodies, imprinting the configuration of these rays in their memory at the moment of their birth. According to Kepler, the planets themselves are living beings with their own individual souls.

Craters on the Moon and Mars, as well as asteroid 1134 Kepler, have been given their names in honor of the esteemed scientist.

The supernova of 1604, which he described, is widely known, as well as NASA’s orbiting observatory that is planned for launch in 2009, and the University of Linz.

Kepler’s notable works

1. Mysterium cosmographicum (Mystery of the World), 1596
2. Astronomiae Pars Optica (Optics in Astronomy), 1604.
3. Ad Vitellionem paralipomena (Additions to Vitellius), a study of physiological optics, 1604
4. De Stella nova in pede Serpentarii (On a new star in the constellation Serpentarius), 1604
5. Astronomia nova (New Astronomy), 1609
6. Tertius Interveniens (The Threefold Intervention), 1610
7. Dissertatio cum Nuncio Sidereo (Conversation with the Starry Messenger), a polemic with Galileo’s Starry Messenger, 1610
8. Dioptrice, 1611.
9. On hexagonal snowflakes, 1611
10. On the true year, in which the eternal Son of God assumed human nature in the womb of the blessed Virgin Mary, 1613
11. Chronicle Eclogues, 1615
12. New stereometry of wine casks, 1615
13. Epitome of Copernican astronomy, in three volumes, published 1618-1621
14. Harmony of the Worlds, 1619
15. Mystery of the World, 2nd edition, 1621
16. Rudolph’s Tables, 1627
17. Dream, a fantastic account of a flight into space, 1634
18. Bibliography of Kepler’s scientific works with references to the originals

Translations of Kepler’s works into Russian

1. Kepler, Johannes. New Stereometry of Wine Barrels. – M.-L.: GTTI, 1935. – 360 p.
2. Kepler, Johannes. On Hexagonal Snowflakes. Dream. Conversation with the Starry Messenger. – Moscow: Nauka, 1982.
3. Conversation with the Starry Messenger by Johannes Kepler. On Hexagonal Snowflakes. M., Nauka, 1982.
4. Dream, or Posthumous Essay on Lunar Astronomy by I. Kepler. On Hexagonal Snowflakes. M., Nauka, 1982.

Literature

1. Copernicus, Galileo, Kepler, Laplace, Euler, Ketle. Biographical narratives (library of F.Pavlenkov). Chelyabinsk, , 1997.
2. Belonuchkin V. Е. Kepler, Newton and all-all-all. M.: Nauka, Seriya Bibliotricka, issue 78, 1990. 128 с.
3. White Y. A. Johannes Kepler. M., Nauka, 1971
4. Simon J. Cultural Historicity of Reason. The Example of Kepler // Reason and Culture. Proceedings of the International Franco-Soviet Colloquium. Lille, April 26-29, 1978. М., 1983. С.15-24.
5. Lishevsky V. P. Stories about scientists. M.: Nauka, 1986, pp. 14-30.
6. Eremeeva A. I., Tsitsin V. A. History of Astronomy (main stages of development of the astronomical picture of the world). Izd. MSU, 1989.
7. Pauli W. The impact of archetypal representations on the formulation of scientific theories in Kepler. In: Pauli W. Physical Essays. Collection of articles. Moscow, 1975. pp. 137-174.
8. Applebaum, W. Keplerian Astronomy after Kepler: Research and Problems. History of Science, 1996, Vol. 34, pp. 451-504. Online.
9. Koyre A. The Astronomical Revolution. New York: Dover, 1973.
10. Veselovsky I. N. Kepler and Galileo. In: Historical and Astronomical Studies. Vol. XI. 1972. pp. 19-64.
11. Belyi Yu. A. Kepler’s contribution to the development of mathematics and his astronomical research. In: Historical and Astronomical Studies. Vol. XI. 1972. pp. 65-106.
12. Lipnik V. P., Kepler’s works in the field of optics. In: Historical and Astronomical Studies. Vol. XII. 1975. pp. 89-100.

The main idea is that a substitution has been made in the statement and conclusions, much like a substitution in a clever school joke problem. The problem asks how many apples are on a birch tree, when it is clear that apples do not grow on a birch tree at all. The focus is intentionally shifted away from this fundamental fact, diverting the attention of the students.

In Michelson’s experiment, the question arises regarding the movement of the ether in relation to an interferometer at rest in the laboratory system. However, if we consider the ether to be the fundamental substance from which all the matter in the interferometer, the laboratory, and the Earth itself is composed, it follows naturally that the ether would also be stationary, as the Earth’s matter is essentially a structured form of the ether and cannot move in relation to itself.

It is astonishing that this circus trick has captivated the minds of physicists for 120 years with complete seriousness, despite its origins in fairy tales from various cultures throughout history, such as the story of Baron Munchausen pulling himself out of a swamp by his hair. These tales were meant to teach children about the potential for deception and to prepare them for adulthood. For more information on the principles of etheric physics, please refer to the FAQ section.

Johannes Kepler, a renowned astronomer, mathematician, and astrologer, was born on December 27, 1571, in Stuttgart, Germany. His parents, Heinrich Kepler and Katharina Guldenmann, belonged to a once prosperous family that had fallen on hard times. Heinrich earned a living through trade but eventually left the family when Johannes was just 5 years old. To support herself and her son, Katharina, who was a herbalist and healer, even resorted to practicing witchcraft. It is said that Kepler was a delicate child, both physically and mentally.

Nevertheless, at a young age, he displayed a fascination with mathematics, consistently astonishing those around him with his natural talent for the subject. Even as a child, Kepler delved into the study of astronomy, and his passion for this field persisted throughout his entire life. While he and his family occasionally witnessed eclipses and comets, his limited eyesight and hands weakened by smallpox hindered him from engaging in extensive astronomical observation.

Scientific Endeavors

The scientist’s thirst for knowledge drives him to further expand his scientific pursuits. He embarks on four additional research projects: exploring the concept of the universe’s immutability, investigating the influence of celestial bodies on Earth, studying the movements of planets, and delving into the physical properties of stars. Eager to gain recognition, he shares his findings and speculations with numerous esteemed astronomers whose work he admires. He hopes to gain their approval and support. One of his letters leads to a friendship with Tycho Brahe, with whom he engages in deep discussions about various astronomical and celestial phenomena.

Observations of a Supernova

In 1604, an astronomer witnesses the appearance of a brilliant new star in the night sky and, unable to believe what he is seeing, discovers a nebula surrounding it. The occurrence of a supernova like this is extremely rare, happening only once every 800 years! It is thought that a similar star appeared in the sky during the time of Christ’s birth and at the start of Charlemagne’s reign. Following this extraordinary sighting, Kepler proceeds to investigate the astronomical properties of the star and embarks on a study of celestial spheres. His calculations of parallax in the field of astronomy propel him to the forefront of the scientific community and enhance his reputation.

Personal life

Throughout his life, Kepler experienced numerous emotional challenges. On April 27, 1597, he entered into matrimony with Barbara Müller, who was a widow on two occasions and already had a daughter named Gemma. During their initial year of marriage, the Keplers welcomed the birth of two daughters. Regrettably, both infants passed away at a young age. Over the subsequent years, the family was blessed with three more children. Unfortunately, Barbara’s health deteriorated, and she passed away in 1612.

On October 30, 1613, Kepler entered into a new marriage, having carefully considered eleven potential partners, he ultimately chose Susanna Reuttingen, who was only 24 years old at the time. Unfortunately, the first three children born from this marriage did not survive infancy. Despite this tragedy, it seems that Kepler’s second marriage brought him more happiness than his first. However, the family faced further hardships when Kepler’s mother was accused of being a witch and subsequently imprisoned for a period of fourteen months. During this challenging time, Kepler remained devoted to his mother, never leaving her side throughout the entire ordeal, as numerous eyewitnesses can attest.

Johannes Kepler: A Brief Biography and Fascinating Facts

On December 27, 1571, Johannes Kepler was born in Stuttgart, Germany, into the family of a merchant. At the tender age of 5, his father abandoned the family, leaving them to fend for themselves. Despite this challenging start, young Johann displayed a keen interest in mathematics, astonishing those around him with his natural abilities. It was during this formative period that he also developed a fascination for astronomy. Kepler delighted in observing celestial events, such as eclipses and the appearances of comets. Unfortunately, he faced obstacles in pursuing this scientific passion due to his hands, which were affected by smallpox, and his poor eyesight.

In 1589, Johannes Kepler completed his education at high school and Latin school. He then enrolled in the Tübingen Theological Seminary at the University of Tübingen. Throughout his studies, Kepler demonstrated his expertise in astrology and mathematics. At the seminary, he delved into theology, philosophy, and the planetary systems of Ptolemy and Copernicus.

Embracing the Copernican system, Kepler acknowledged the Sun as the primary source of motion in the universe. Upon graduating, Johannes received an offer to teach astronomy and mathematics at the Protestant School of Graz. Consequently, at the age of 23 (1594), Kepler assumed the role of a professor.

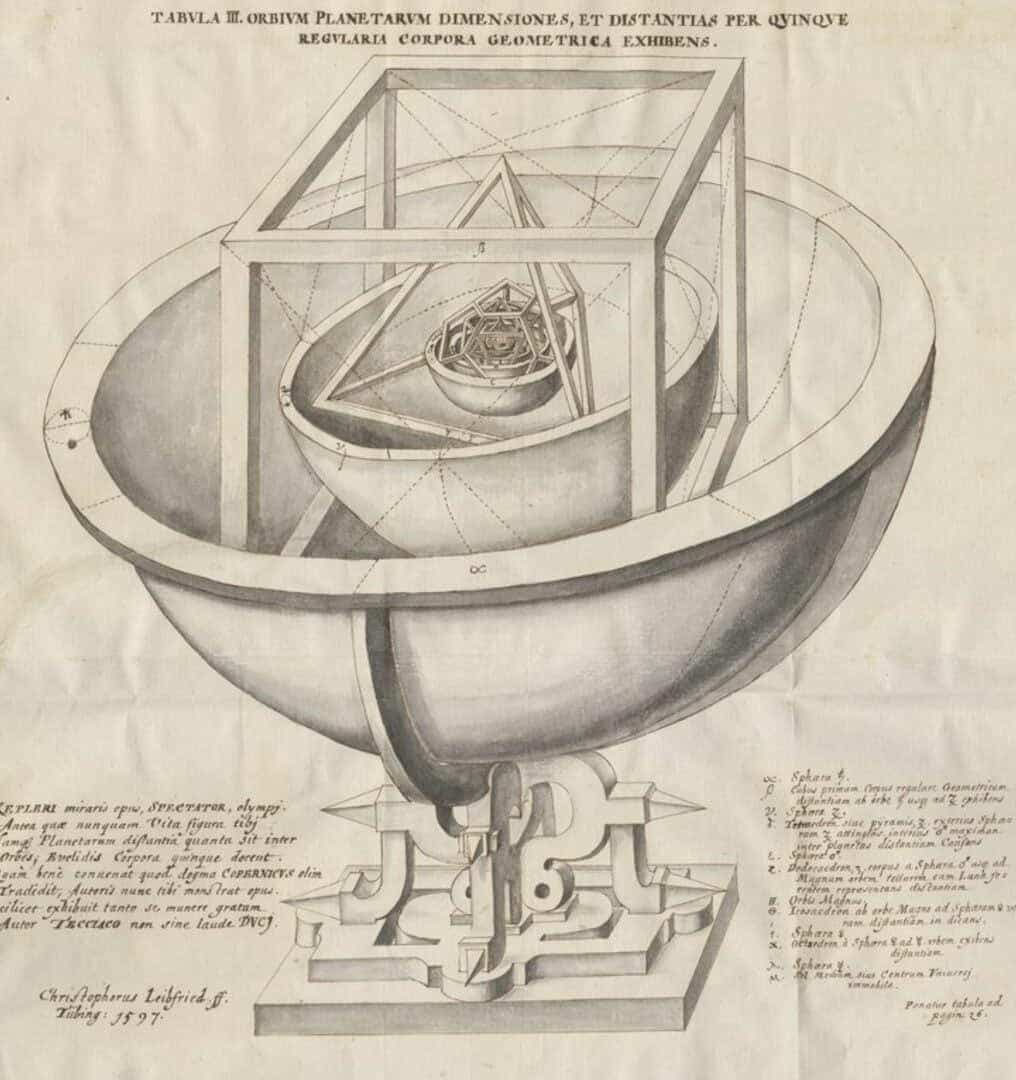
During his time at the Protestant School, he experienced a vision that revealed a grand design for the structure of the universe. The professor presented a correlation between the movements of Jupiter and Saturn in relation to the zodiac. He delved into the relationship between the sizes of regular polyhedra and the distances of the planets from the Sun, boldly claiming to have unraveled the geometry of the cosmos.

Johannes Kepler eagerly anticipated the passage of Mercury and Venus, but unfortunately, he never had the opportunity to witness this celestial event. The renowned astronomer passed away on November 15, 1630 in Regensburg, Germany, following a period of illness.

Interesting Facts about Johannes Kepler

– Astroplot: 53°20’56.505″ N 83°46’07.735″ E, Habs. = 209 m.

Johannes Kepler (1571-1630)

Johannes Kepler was an influential German astronomer and mathematician. He made significant contributions to our understanding of the solar system, including the discovery of the three basic motions of the planets. Additionally, he played a crucial role in the development of modern refractors by inventing the optical system used in them. In the field of mathematics, Kepler also made remarkable achievements, laying the groundwork for differential, integral, and variational calculus.

Kepler authored numerous scientific papers and articles. His seminal publication, “New Astronomy” (1609), focuses on the analysis of Mars’ movement, drawing on the observations by T. Brahe, and introduces the initial two principles of planetary motion. In his subsequent work, “Harmony of the World” (1619), Kepler presents the third law, which unifies the motion theory of all celestial bodies into a comprehensive framework.

Due to the events of the Thirty Years’ War and religious persecution, Kepler was forced to flee to Ulm in 1626. With no means of support, he joined the service of the imperial commander Wallenstein as an astrologer in 1628. Kepler’s final significant project was the publication of the planetary tables created by Tycho Brahe, which were released in Ulm in 1629 under the title “Rudolph’s Tables” (Tabulae Rudolphianae). In the autumn of 1630, Kepler traveled to Regensburg, where the Sejm was assembled, in the hopes of securing a resolution to grant him a steady income. Kepler passed away in Regensburg on November 15, 1630.

Currently, there are additional savings offers (ranging from 2% to 25%) available for 58,742 educational institutions. To determine the specific discount applicable to all staff members at your educational institution, please sign in to your personal Infoworks account.

Linguocultural approach in teaching the Russian language to meet the principles and requirements of the FSES

In addition to this discount, you can also take advantage of your educational institution’s discount, which is based on the number of colleagues who have enrolled in Infowork courses.

Currently, there are additional cumulative discounts available for 58,742 educational institutions, ranging from 2% to 25%. To find out the discount that applies to all employees of your educational institution, please log in to your personal Infoworks account.

Course for professional development

Contemporary approaches to organizing play activities for preschool children

We can apply your educational institution’s discount to this offer (the amount depends on the number of your colleagues who have completed Infowork courses).

Currently, there are additional cumulative discounts (ranging from 2% to 25%) available for 58,742 educational institutions. To determine the applicable discount for all staff members of your educational institution, please access your personal Infoworks account.

Homeschooling. Tips for Parents

Breakdown of the Presentation by Individual Slides:

Slide 2 features Johannes Kepler (1571-1630), an influential German astronomer who played a significant role in the development of modern astronomy. Kepler is renowned for his groundbreaking discoveries, particularly his formulation of the laws of planetary motion, known as Kepler’s laws. These laws provided a solid foundation for understanding the movement of planets in our solar system and enabled the creation of accurate planetary tables. Additionally, Kepler made significant contributions to the study of eclipses, establishing the groundwork for the theory surrounding these celestial events. Furthermore, Kepler is credited with inventing a telescope that utilized double-convex lenses for both the objective and eyepiece, which enhanced the instrument’s capabilities.

On December 27, 1571, Johannes Kepler was born in Germany.
He attended the University of Tübingen, where he studied theology, philosophy, mathematics, and astronomy.
In 1596, Kepler published a notable work called The Cosmographic Mystery, in which he supported the ideas of Copernicus, who argued that the Sun was at the center of the Solar System.
According to Johannes Kepler, the universe is governed by geometric relationships that can be represented by the inscribed and circumscribed circles of five regular polygons.

Here is a unique version of the text:

Slide 4: Discovering Johannes Kepler’s Three Laws of Planetary Motion
Kepler’s groundbreaking laws revolutionized our understanding of the solar system. Let’s explore them:

1. Law of Ellipses: Every planet in the solar system follows an elliptical orbit, with the Sun located at one of the foci. This means that the distance between the planet and the Sun varies throughout its orbit.

2. Law of Equal Areas: As a planet moves along its elliptical orbit, it sweeps out equal areas in equal periods of time. This means that the planet moves faster when it is closer to the Sun and slower when it is farther away.

3. Law of Harmonies: The square of a planet’s orbital period is proportional to the cube of the semi-major axis of its orbit. In simpler terms, this law relates the time it takes for a planet to orbit the Sun to the size of its orbit.

By understanding these laws, Kepler laid the foundation for our modern understanding of planetary motion and paved the way for future astronomers and scientists.

On the fifth slide, Kepler’s contributions to geometry are discussed. His discoveries propelled the field forward by introducing innovative ideas and approaches, which proved instrumental in solving previously intractable mathematical problems. Furthermore, Kepler’s work laid the foundation for the eventual development of differential calculus.

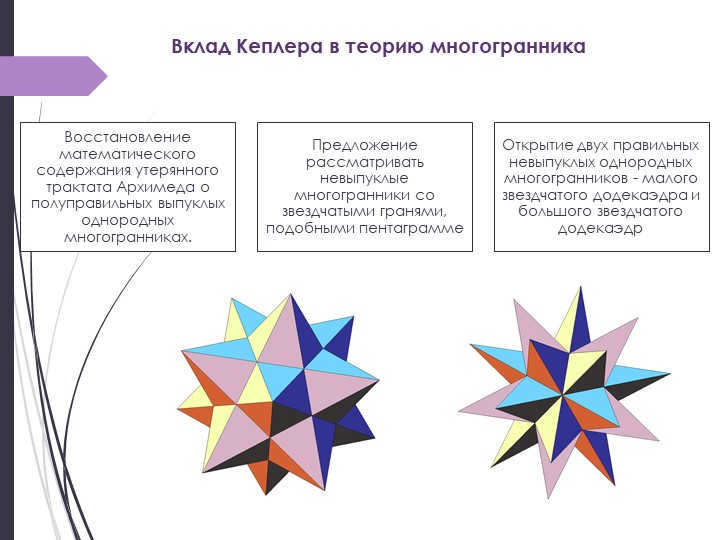
Slide 6: Kepler’s impact on the theory of polyhedra
Reconstructing the mathematical concepts found in Archimedes’ lost treatise on semi-regular convex homogeneous polyhedra.
Suggesting the exploration of non-convex polyhedra with star-shaped faces, similar to the pentagram.
Unearthing two regular non-convex homogeneous polyhedra, namely the small star-shaped dodecahedron and the large star-shaped dodecahedron.

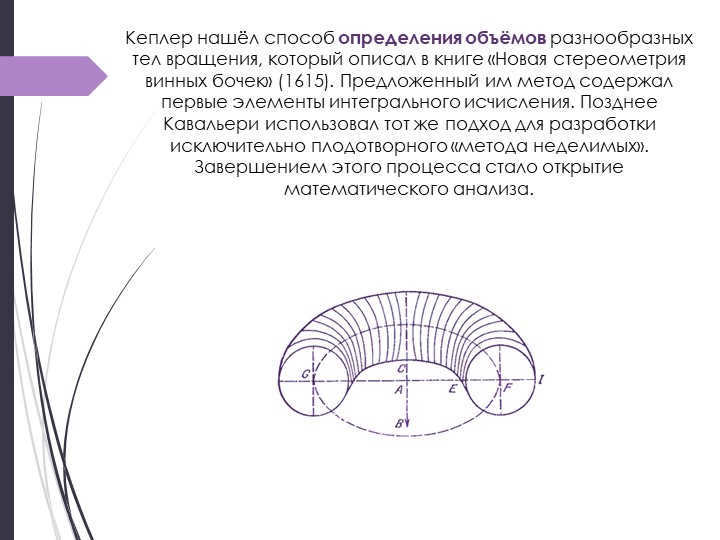
On the 8th slide, Kepler effortlessly demonstrates in Theorem 18 that the volume of a torus is equivalent to the volume of a cylinder. This cylinder has a base in the shape of the torus’ meridional section and a height equal to the circumference of the circle formed by the torus’ center.
Kepler’s proof of this fact is as follows: he divides the torus into an infinite number of circles using meridional sections. These circles have varying thicknesses, with the outer edge being thicker than the inner edge. However, the thickness of the circle in the central part is equal to the average thickness of the edges.

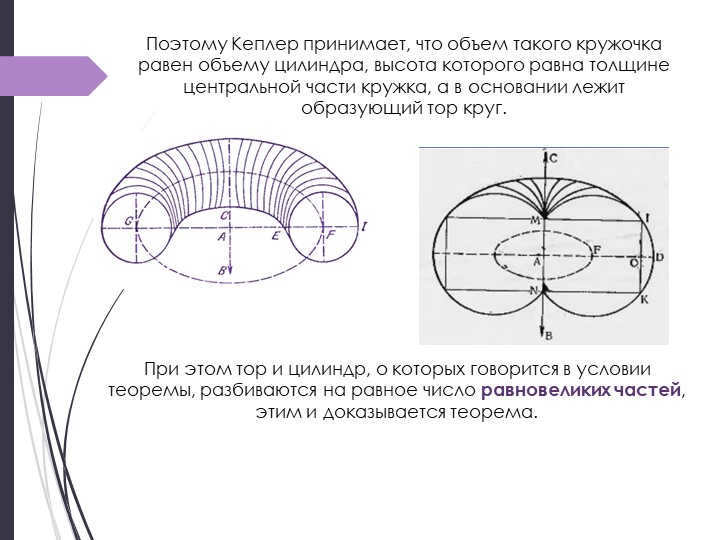
Accordingly, Kepler hypothesizes that the volume of a circle like this is identical to the volume of a cylinder. The cylinder’s height matches the thickness of the circle’s central part, while the circle forming the torus is located at the base.
Additionally, the torus and cylinder mentioned in the theorem’s condition are divided into the same number of equal parts, which serves as the proof for this theorem.

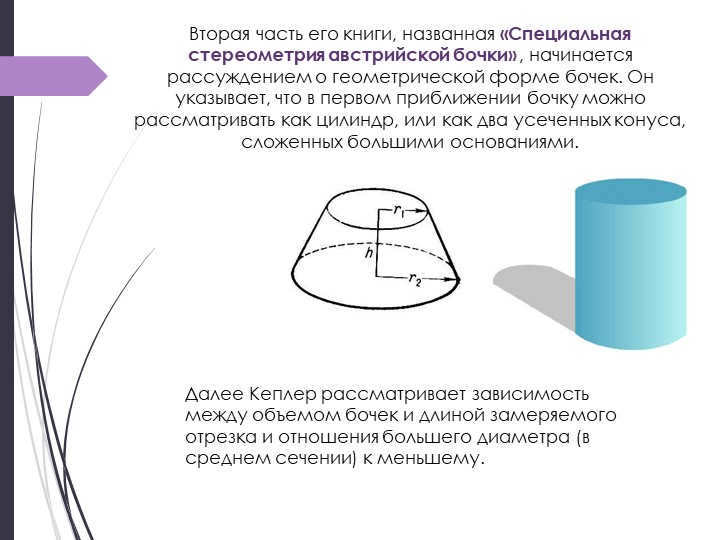
Slide 10: In the second part of his book, Johannes Kepler explores “The Special Stereometry of the Austrian Barrel”. He begins by examining the geometric shape of barrels, noting that they can be approximated as cylinders or as two truncated cones stacked with larger bases.
Kepler then delves into the relationship between the volume of barrels, the length of the measured segment, and the ratio of the larger diameter (in the middle section) to the smaller diameter.

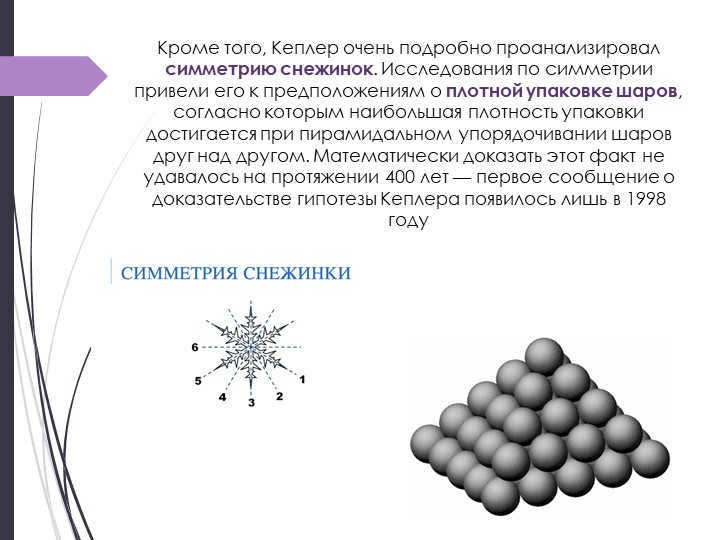
Slide 12: Additionally, Kepler conducted a detailed analysis of snowflake symmetry. His examination of symmetry led him to make assumptions about the dense packing of spheres. He proposed that the highest packing density is achieved when spheres are arranged in a pyramidal fashion on top of one another. However, it took 400 years for this hypothesis to be mathematically proven. The first report confirming the proof of Kepler’s hypothesis was published in 1998.

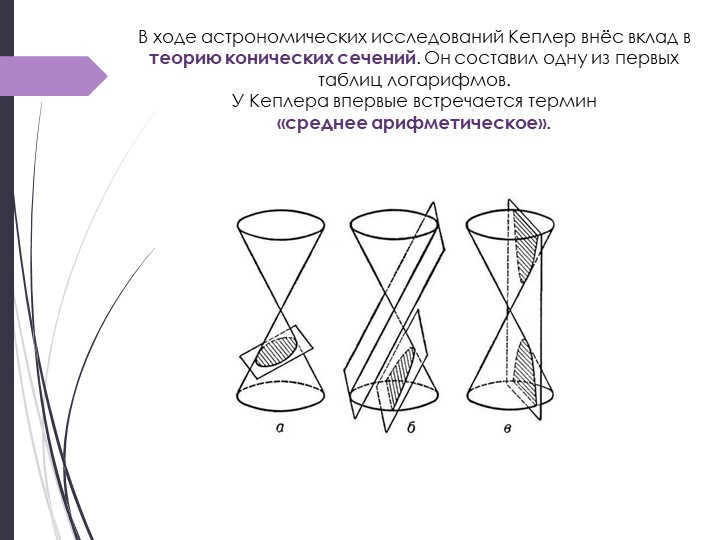
During his studies in astronomy, Kepler made significant contributions to the theory of conic sections. He also compiled one of the earliest tables of logarithms.
Kepler is credited with being the first to use the term
"arithmetic mean."

Slide 14: Kepler made a significant contribution to the field of projective geometry by introducing the groundbreaking idea of an infinitely distant point.
He also pioneered the concept of the focal point in conic sections and explored projective transformations that can change the type of conic sections, such as transforming an ellipse into a hyperbola.

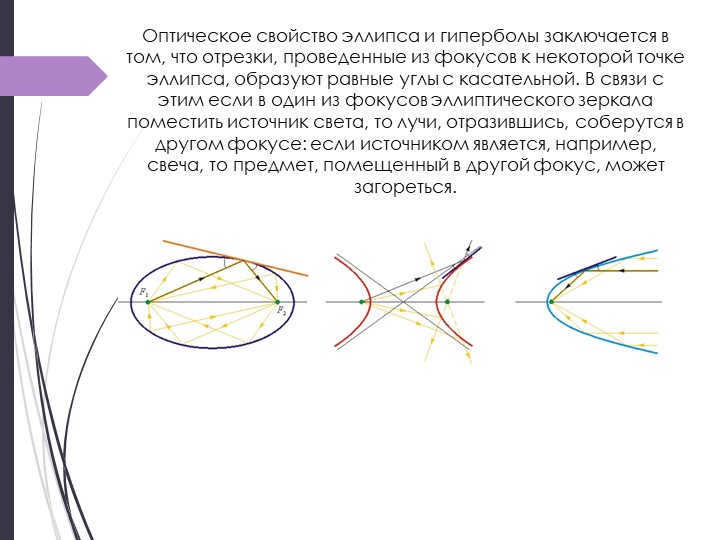
Slide 15. The ellipse and hyperbola share a unique optical property – the segments extending from the foci to any point on the curve form equal angles with the tangent. This property can be utilized in practical applications. For instance, if we position a light source at one of the foci of an elliptical mirror, the rays of light, upon reflection, will converge at the other focus. To illustrate, imagine using a candle as the light source, and placing an object at the other focus – it could potentially ignite due to the concentrated heat and light energy.

Slide 16: Johannes Kepler passed away on November 15, 1630 while on a journey to Regensburg, when he made an unsuccessful attempt to receive a portion of the long-overdue salary owed to him by the imperial treasury.

To Witness the Stars and Embrace His True Self: A Journey through Witch-Hunts, Exile, and War

Geometry is a divine and eternal concept shining in the mind of God:
its sharing with humans is among the reasons
why man is made in the image of God.
Johannes Kepler

The Enigmatic Pulkovo Manuscripts

But still, speak without me.
Saint Augustine

The end of the sixteenth century presented us with a group of remarkable individuals who each made a significant impact in their respective fields. Torquato Tasso revolutionized heroic poetry, which had previously remained undiscovered in Russia. Caravaggio, who coincided with our hero in terms of timeline, transformed the art of painting. Monteverdi, slightly older than the others, pioneered the creation of musical theater. And let’s not forget the revered Shakespeare, whose works were among the first to be translated into various European languages, including Russian. Together, these men formed a constellation of brilliance that justifies the existence of mankind. Their collective presence in the High Renaissance era arguably makes it one of the most glorious centuries in history, comparable to the illustrious periods of Athens and Alexandria. These periods, known for establishing the value and potential of humanity, serve as beacons of hope for those living in darker times.

In this era of talent being abolished and creativity being disrespected, it is particularly challenging for me to engage with the great thinkers who championed freedom. It’s like a chicken on a farm dreaming of soaring through the mountains like an eagle. However, I will attempt to summarize what little I have grasped, and if I can convince you to peruse the Pulkovo manuscripts and refer to biographies of the esteemed Kepler when necessary, then my endeavors will be well worth it. And if I fail to do so, I ask for your forgiveness. Allow me to speak, nonetheless.

Lutheran observer of the stars

There are many other difficulties that it would be long to enumerate.
We have experienced no significant harm.
Johannes Kepler, Somnium

This is a portrait of Johannes Kepler that was created by an unknown artist in the 17th century.

On December 27, 1571, in the town of Weil der Stadt in the Duchy of Württemberg, a baby boy named Johannes was born to Heinrich and Katharina Kepler. Three hundred years later, a statue was erected in his honor in the town’s main square, which featured a church, a fountain, and a statue of Emperor Charles the Fifth. Johannes’ grandfather, Sebold, was a furrier from Nuremberg and had been elected mayor of the predominantly Catholic town as a Lutheran. He only became wealthy later in life after receiving an inheritance. Sebold and his wife lived in the house with their children and grandchildren, with Heinrich being the eldest son. Kepler remembers his grandfather and father being irritable, and his mother being grumpy, making his childhood less than ideal. Additionally, Kepler’s health was not good, and in 1574, his father went off to fight in Flanders. Unable to tolerate the harsh conditions, Katharina followed her husband, leaving little Johann in the care of his grandparents. Unfortunately, they did not treat him kindly, and he contracted smallpox and nearly died. In 1576, Heinrich returned from the war, and the family moved to the nearby town of Leonberg, where Johannes attended school.

It took Kepler a total of five years to complete a course that was supposed to take only three years. This longer duration was due to the fact that he often had to take long breaks from his studies in order to help his family with their work in the fields. Despite these interruptions, Kepler’s passion for astronomy was sparked at a young age. In 1577, his mother pointed out a comet in the sky to young Hans, and in 1580, he and his father observed a lunar eclipse together. These early experiences of observing the celestial bodies left a lasting impression on the curious and impressionable boy. Once he finished his schooling, Kepler enrolled at the University of Tübingen, where he intended to study theology.

The University of Tübingen was established in 1477 by Eberhard the Bearded, the first Duke of Württemberg. This was three years after his marriage to the daughter of Ludovico Gonzaga, the Marquis of Mantua. Duke Eberhard had a desire to bring the Italian Renaissance to his lands, and the establishment of the university was part of this effort.

During the reign of Duke Ulrich in 1534, significant changes were made to the University of Württemberg. Its primary focus was to educate priests for the reformed church and impart knowledge about reformed theology. However, the concept of reformed theology itself was divided at its core. The principles of the Reformed Church were firmly established in the German states through a few key documents, including the Augsburg Confession, which was presented to Charles the Fifth in 1530 by Melanchthon, and the Formula of Concord, which was presented to the Saxon elector Augustus in 1577 in Torgau.

However, not all Protestants accepted the formula of consent; and Kepler, refusing to sign it, would never be able to settle in his native land as a result. Nevertheless, he believed that exile was preferable to betraying himself. Throughout his life, Kepler took the duty of seeking God for oneself very seriously, and during an era of violent religious wars, he never compromised with authority on matters of conscience.

One of the major controversies was centered around transubstantiation. Catholics, following the teachings of Thomas Aquinas, believe that during the eucharist, the bread and wine are transformed into the actual Body and Blood of Christ. Thomas Aquinas, referencing Blessed Augustine, directly refuted the symbolic interpretation of the eucharist. In his efforts to reform the church, Luther maintained the Catholic understanding of transubstantiation.

Tübingen adhered to the principles of conciliarism, and education was carried out in accordance with these principles. Calvin’s errors were vehemently denounced from the pulpits on a daily basis.

Nevertheless, Kepler found himself drawn to Calvin’s teaching on transubstantiation. This sense of personal freedom, the straightforward and unambiguous practice of following his own conscience in all matters, would have significant consequences for Kepler throughout his lifetime.

And he himself always saw the hand of Providence in the unexpected request he received in Tübingen from Graz for a mathematics teacher. Truly, we can agree with Max Kaspar: Kepler, a lover of freedom, independent and a seeker of truth, could not become a priest during a time of religious wars. However, Kepler the mathematician also faced challenges from both sides. The essential condition for his very existence was Kepler’s free choice to understand and interpret the Word of God himself – he would not give it up under any circumstances.

Throughout his life, he would endure harsh criticisms from both Catholics, who insisted on his conversion to Catholicism, which he rejected, and from fellow Lutherans, who found his independent spirit particularly repugnant and therefore rejected him vehemently and violently: it was the Catholics who provided Kepler with employment for most of his life.

Blows from fellow Lutherans would not be long in coming, but the initial strike would be delivered by the Catholics. The impoverished yet highly productive years in Graz come to a close due to counter-reformation measures in the city: Kepler refuses to renounce his beliefs and is compelled to depart from Graz. Despite apprehensions about becoming overly reliant on Tycho Brahe by relocating to Prague – concerns that have caused Kepler to decline Brahe’s previous invitations, opting for only a brief visit – Kepler is now left with no alternative: he accepts Brahe’s invitation and moves to the imperial capital.

The most splendid and fruitful chapter of the mathematician’s life commences.

Caesar’s mathematician

Alter! Let us lift our gaze!
You are right, the stars float
high above all earthly spell;
but – those who strive for them,
they weave their own dark life
to the luminous destinies!

Rainer Maria Rilke, On Emperor Rudolf II

The decision to move to Prague, the capital of the empire, was made by Rudolf due to his displeasure in Vienna and his exile from Graz. This move proved to be a fortunate event for Kepler. Rudolf was a patron of the arts and Kepler found himself surrounded by a vibrant community of artists. Among them were renowned artists such as Bartholomew Spranger from Flanders, Joseph Heinz from Switzerland, and Giuseppe Arcimboldo from Italy. In addition, composers Jakob Handl and Philippe de Mont, writer Szymon Lomnicki von Budecz, and poet Georg Karolides von Karlsberg, who were all elevated to nobility by Rudolf, were also part of this artistic circle. It is worth noting that both Lomnický and Karolides wrote in Czech.

The years spent in Prague were a time of great brilliance and enlightenment for Kepler. Giuliano Medici, the ambassador of the Grand Duke of Tuscany at the imperial court and the future Archbishop of Pisa, presented the imperial mathematician with a new book by Galileo and requested a review. Kepler, always generous, wrote a highly positive review and thus began a correspondence between the two. However, their relationship did not progress as Galileo failed to comprehend and appreciate Kepler’s work.

“To live here is to die forever; Once, the beginning of life, is to die.”
– Johannes Kepler

The year 1611 began in a tragic manner: the much-loved Friedrich, his six-year-old son, succumbed to smallpox.

Simultaneously, the emperor’s conflict with his brother Matthias escalated and expanded. Kepler, who remained loyal to the emperor, found himself in an untenable position. Kepler made a fresh effort to return to his hometown of Württemberg as a professor at the university. However, this attempt faced strong opposition from his fellow mathematicians. While Catholics were willing to accept a brilliant Protestant, Protestants were not ready to tolerate Kepler’s independent thinking within a Protestant university.

Kepler expresses sympathy towards Calvinists! Kepler does not align with the principles outlined in the Formula of Concord regarding transubstantiation! He is accused of engaging in inappropriate behavior towards the young people of Württemberg! This situation must be resolved decisively. On April twenty-fifth, 1611, due to Kepler’s refusal to sign the consent form without objection – and his insistence on his own interpretation of the sacrament of transubstantiation – the consistory advises the duke to reject Kepler’s application, and the duke supports the consistory’s recommendation. Kepler is permanently barred from entering the house. With the intervention of Galileo, discussions take place regarding a potential preaching position in Padua, but ultimately, no agreement is reached.

Kepler agrees to go to Linz after receiving an invitation. One of the reasons for his decision is his belief that Linz will be a better place for his wife, who has never been happy in Prague. Sadly, Kepler’s wife, who suffered from epilepsy, passes away. Despite the request from the deposed Caesar to stay in Prague, Kepler eventually decides to move to Linz after Rudolf’s death. However, upon arriving in Linz, Kepler is immediately excommunicated.

Unfortunately, Kepler’s fate takes another tragic turn. During this time, witch-hunting is rampant in Germany, with an unprecedented number of witches being burned in both Protestant and Catholic territories. Even in the small town of Leonberg, six witches are burned within a few months. It is worth noting that Rome itself has never sentenced anyone to death for witchcraft.

The mother of the mathematician, Katharina Kepler, was a lonely, petite, slim woman with a fiery temper who was not well-liked in the town. When rumors started spreading, she couldn’t believe that her neighbors, whom she had known for many years, would spread such a cruel accusation about her. She tried to defend herself vigorously, but it only made things worse.

The crisis occurred in August 1615 when Katharina Kepler was publicly insulted and accused. With the support of her younger children (who were also in danger due to the suspicion falling on their mother), Katharina decided to take the matter to court. It is from the surviving court records that we have learned so much about this shameful trial. Katharina’s tormentors had influential connections, as the son of the neighbor who had insulted her was a member of the city magistrate’s office.

Frau Kepler had her assets frozen: the prosecutors hoped to recover them if they succeeded. Kepler agreed to house his mother, and she lived with him for a year before returning to her daughter.

Early in the morning on August 7, 1620, she was abruptly awakened, arrested, and discreetly taken out of her house in a sealed trunk. She was then imprisoned in Leonberg. Eventually, she was transferred to Güglingen. Her confinement took place in a small room near the tower gate, which was left unlocked but she was chained. Two guards kept watch over her, and she had to pay for their services herself. It’s no wonder her detainment was extended and prolonged.

At last, the trial commenced. Regrettably, the defendant has the backing of her son, who happens to be a mathematician named Johannes Kepler (as recorded in the minutes). The Duke recommended seeking the opinion of the legal experts at the University of Tübingen. The attorneys pointed out that the accusation of witchcraft carried the implication of interrogation through torture. On the other hand, the evidence collected by the prosecution, such as the mysterious death of a piglet 25 years ago, did not suffice for the utilization of the rack. Therefore, the University of Tübingen proposed a compromise solution: the accused would be led to the rack, shown the executioner and his tools, but would not be subjected to torture. The mere fear of torture would be enough to elicit a confession.

So it was accomplished on the 28th of September, 1621. Nevertheless, Katharina stood strong: “Do whatever you want with me! Take out my veins one by one, I have no confessions to make.” She knelt down, recited the “Our Father” prayer, and declared that the Holy Spirit would not abandon her. The Duke then commanded her to be declared innocent and set free once her family paid the court fees.

On the 4th of October, after spending 14 months in prison, Katharina is released, and on the 13th of April the following year, she passes away.

The Conflict of Three Decades

This movement was of great magnitude for both the Greeks and to some extent the barbarians,
as it affected a large number of people.
Thucydides, The Peloponnesian War

The devastating war is poised to bring about the complete destruction of all: both Catholics and Protestants, as well as imperialists and separatists. It will undoubtedly have irreversible consequences for the empire, leaving the German lands in a state of utter devastation. Moreover, it will transform the once thriving Europe of Caravaggio, Monteverdi, Kepler, and Shakespeare into a Europe plagued by slavery, betrayal, and unspeakable atrocities.

Tragically, this war that has ravaged Europe will also claim the life of Kepler. Despite his immense contributions to the field of mathematics, he will meet his demise in Regensburg on November 15, 1630, living in disgrace and abject poverty.

“The Harmony of the World”

Every celestial body you see
Sings like an angel in its motion,
Continuously serenading the cherubims.

Such harmony exists in immortal souls,
But we cannot hear it as long as
This earthly shell of decay encloses us.

William Shakespeare, The Merchant of Venice, V, 1.

However, it was in the midst of the escalating European conflicts in May 1618, when the emperor’s messengers were humiliated in Prague and war seemed inevitable. It was during this time that Kepler conceived the idea of composing the harmony of the world, a plan that had been developing within him since 1599.

Unfortunately, I cannot provide a comprehensive analysis of Kepler’s main work in this brief note. Its significance goes far beyond the initial formulation of the third law of planetary motion, which was later named after him (the first two laws were published ten years earlier). “Harmony of the World,” often referred to as the “Summa Renaissance” by Caspar, cannot be summarized and must be read. While there is no Russian translation available, it can at least be read in English. An English translation was published approximately 30 years ago by the American Philosophical Society.

Let’s limit ourselves to listing just five books: the initial and second focus on regular polygons and polyhedra and the shapes that can be created from them, with Kepler’s discovery of the so-called star-shaped dodecahedrons and his anticipation of quasi-periodic pavements (it’s only a slight exaggeration to say that Kepler already knew Penrose’s mosaics). The third book is dedicated to music, a lifelong interest of Kepler’s. Books four and five delve into the harmony of the planets and stars, which, according to Kepler, sing and praise the Creator in universal harmony.

He desired to encompass the entire world within his book. Infinitely beautiful, enigmatic, and wide open to a diligent researcher, the entire world was a book for him, reading which a grateful individual enters with awe and admiration into the Creator’s design.

Kepler had a relatively short and incredibly challenging existence. Nevertheless, he made significant contributions to the field of science through remarkable accomplishments that demanded not just exceptional brilliance, but also extensive years of arduous toil, the magnitude of which continues to astonish even in the present day.

Johannes Kepler, a pioneer in his field, was the first person to come to the groundbreaking conclusion that all planets are under the influence of the sun’s gravitational force, causing them to revolve in orbits. This significant discovery by Kepler has shaped our understanding of the solar system. (Image: Popular Mechanics)

In recognition of the 400th anniversary of the exploration of celestial bodies through telescopes, the year 2009 was designated as the International Year of Astronomy by the UN General Assembly. However, it is worth noting that 1609, the same year, marked another momentous event in the history of science. It was during this year that Johannes Kepler published a treatise that established two fundamental laws of planetary motion, which are now known as Kepler’s laws. The third and final law was later published ten years after. Therefore, for the field of astronomy, this year holds a dual significance as a double anniversary year.

Kepler’s childhood, which began on December 27, 1571 in the town of Weil near Stuttgart, was far from idyllic. The family lived in poverty, and to make matters worse, Kepler grew up without a father figure. His father, a mercenary in foreign armies, would frequently disappear for long periods of time and eventually left for good when Kepler was just 16 years old. It was left to Kepler’s mother, Katharina, the daughter of a village innkeeper, to raise the children. She was an unfriendly, grumpy woman with no formal education.

Despite his difficult circumstances, Kepler’s mind was sharp and he excelled academically. He suffered from various illnesses, such as smallpox, indigestion, and migraines, which prevented him from engaging in physical labor. However, his intellectual abilities were unparalleled. At the age of seven, Kepler enrolled in a German elementary school, and later transferred to a Latin school. At the age of 13, he passed a competitive examination that granted him access to a spiritual education. He successfully completed the first and second seminaries, and in the fall of 1589, he became a student at the University of Tübingen.

Kepler spent approximately five years in Tübingen. Within a span of two years, he pursued a program at the Faculty of Liberal Arts and successfully obtained a master’s degree. One of his esteemed instructors was Michel Möstlin, a renowned figure who authored a highly acclaimed astronomy textbook and staunchly adhered to the teachings of Copernicus. Guided by Möstlin, Kepler delved into the works of ancient Greek geometers, engaged in studies of arithmetic, trigonometry, and basic algebra. He also immersed himself in the nuances of both Ptolemaic and Copernican cosmology, ultimately embracing the heliocentric model. Interestingly, at that time, Kepler had no aspirations of pursuing a career in science; instead, he intended to further his education in the theological field, which he eventually did in 1591. Prior to this, the university senate, recognizing Kepler’s exceptional intellect, appealed to the city of Weil to grant him a scholarship for the duration of his studies. In a letter to the city, the professors wrote, “Young Kepler possesses such remarkable intellectual prowess that we anticipate exceptional accomplishments from him.”

However, Kepler’s spiritual journey was not meant to happen. On March 13, 1594, he was sent to the Austrian city of Graz as the top graduate, to urgently take the place of the deceased mathematics teacher at the Lutheran school.

Dutch pipes

Kepler settled in Graz and accepted his new profession. He was on track to remain a well-educated, yet relatively ordinary teacher at a local school. Fortunately for the field of science, fate had other plans. On July 19, 1595, an event occurred that completely transformed Kepler’s life and set him on a path of groundbreaking discoveries in physics and astronomy.

The journey began with a lecture where Kepler elucidated the movement of Jupiter and Saturn across the celestial sphere. Every 20 years, these celestial bodies align in the band of zodiacal constellations – Jupiter catches up with Saturn and then forges ahead (these encounters occurred in 1563 and 1583 and will happen in 1603, 1623, and 1643). Throughout history, astronomers and astrologers have observed that the locations of these alignments shift in the zodiacal belt by slightly less than one-third of a complete circle each time. Kepler sketched a circle on a blackboard, positioned 12 zodiacal constellations at equal intervals on it, and documented multiple Jupiter and Saturn alignments, commencing in 1583.

In October, Kepler commenced the composition of a book where he presented his system. The manuscript was published in Tübingen and after a few months, it was officially released in March 1597. The book is commonly referred to by its shortened title: Mysterium cosmographicum – “Mystery of the Universe.”

The measurement of wine barrels and an adventure to the moon

Kepler is primarily known as an astronomer. Alongside the aforementioned works, he penned a book chronicling his observations of a supernova star that erupted in October 1604. He was the pioneer in elucidating the occurrence of tides through the gravitational pull of the Moon, as well as proposing the concept of the Sun rotating on its own axis. Yet, his achievements extended far beyond the realm of celestial science. In 1604 and 1611, Kepler released groundbreaking treatises on optics and the physiology of vision. In the latter work, “Dioptrica,” he not only expounded upon the functioning principle of contemporary telescopes with a converging lens and a diverging eyepiece, but also put forth the blueprint for a novel type of telescope featuring two convex lenses (since then recognized as Kepler’s telescope). His mathematical investigations, compiled in his 1615 publication “New Stereometry of Wine Barrels,” paved the way for integral calculus. Kepler was the first to calculate the widely accepted birth year of Jesus Christ (4 AD) and authored the posthumously published tale “The Dreaming” detailing a lunar voyage – conceivably the inaugural work of science fiction in world literature. Lastly, Kepler’s conception of explaining the properties of the universe based on fundamental geometric symmetries has experienced a revival in modern particle physics. In sum, Kepler was simply an exceptional genius.

Kepler personally dispatched the monograph to numerous renowned astronomers. One of the copies eventually reached the somewhat less famous mathematics professor at the University of Padua, Galileo Galilei, who responded with a highly amiable letter (while also expressing his delight at finding another supporter of Copernicus’ theory). Kepler also sent his work to the foremost astronomer in Europe, Tycho Brahe from Denmark, who found the exercises involving polyhedra to be clever yet purely speculative. However, in a significantly delayed response, Brahe made it clear that he was willing to introduce Kepler to his extensive collection of observations on planetary movements, which were conducted at the world’s premier observatory on the island of Gwen near Copenhagen. This invitation was truly momentous for Kepler, although he did not immediately take advantage of it.

Rudolph’s tables

In the autumn of 1598, the persecution of Protestants commenced in Styria. Kepler and his fellow believers were forced to depart from Graz, but after a month, he received special permission to return and carry on his duties as a district mathematician. However, due to the expulsion of the rector and nearly all the instructors, classes at the school came to a halt. It became evident to Kepler that he had no prospects for the future in Graz. He made desperate efforts to secure a position outside of Austria, but they proved to be fruitless.

Later on, Kepler lent a helping hand to Tycho Brahe, who had risen to the position of court mathematician to the Holy Roman Emperor and King Rudolf II of Bohemia. In December 1599, Brahe extended a second invitation to Kepler to collaborate. Even without receiving this letter, Kepler made his way to the imperial capital of Prague with the hopes of becoming Brahe’s assistant. On February 4, the two scientists finally met, and from that point on, their paths diverged, though their personal relationship was strained. Brahe appealed to the Emperor to employ Kepler in order to analyze his archives and create the most accurate tables of planetary motions based on the data. Brahe suggested naming these tables after the Emperor – Rudolfovymi. The Emperor was fond of the idea and gave his approval.

At first, it was assumed that Kepler would have to find a special position. However, Tycho Brahe suddenly passed away (with various theories surrounding his cause of death). Just two days after Brahe’s funeral, Kepler was appointed as the court mathematician and given an annual salary of 500 florins. However, the imperial treasury was always empty and Kepler rarely received any additional payment. Despite this, he did receive a portion of Brahe’s archive, specifically the information relating to the movements of Mars. These materials became the foundation of Kepler’s theory on planetary motions, which forever immortalized his name.

A revolutionary discovery in the field of astronomy

During his 11-year residence in Prague, Kepler experienced a period of tranquility and immense productivity. It was during this time that he penned his groundbreaking astronomical masterpiece. Initially, Kepler contemplated naming it “The Martian Commentaries,” but he eventually settled on a more elaborate title – “The New Astronomy, justified by its underlying principles, or Celestial Physics, elucidated through analyses of the movements of Mars, derived from the meticulous observations of the esteemed Tycho Brahe.” This monumental book was published in the momentous year of 1609, marking a significant turning point in the realm of astronomy.

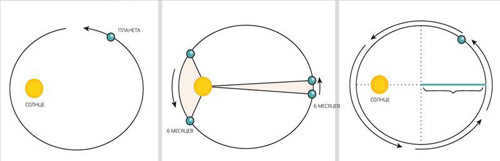
Kepler’s Laws
Kepler’s First Law, also known as the Law of Ellipses, states that each planet in the solar system follows an elliptical orbit, with the Sun located at one of the foci of the ellipse. Kepler’s Second Law, also known as the Law of Squares, states that a planet moves faster when it is closer to the Sun and slower when it is farther away, so that the area swept out by the radius-vector connecting the Sun and the planet is equal for equal times. Kepler’s Third Law, also known as the Harmonic Law, states that the square of a planet’s orbital period around the Sun is proportional to the cube of the semi-major axis of its orbit.
Image: Popular Mechanics

Kepler initiated his examination of the movements of Mars from the vantage point of Earth. This approach was logical since it was on this mobile celestial platform that Tycho Brahe established the astronomical coordinates of Mars as well as the other planets. Based on these observations, Kepler demonstrated that the Earth was undergoing a dual motion: drawing nearer to the Sun and moving farther away from it. Consistent with the principles outlined in the “Mystery of the Universe,” it can be inferred that the velocity of the Earth’s orbital motion diminishes as it moves away from the Sun and increases as it draws closer to the celestial body. This particular pattern was unearthed by Kepler through his analysis of Tycho Brahe’s findings.

This discovery enabled the scientist to gain a new understanding of the movement of Mars. Ancient astronomers had already known that Mars travels across the sky at varying speeds. They believed that Mars, along with other planets, moved in combinations of circular motions with strictly constant speeds, and the observed variations in speed were simply a matter of visibility. However, Kepler saw the variability in Mars’ speed as a real phenomenon, which he attributed to the planet’s changing distance from the Sun. Kepler also believed that Earth moved in a similar way to Mars, positioning it as just another ordinary planet. This finding provided strong support for Copernicus’ heliocentric theory, which was not universally accepted at the time, particularly by Tycho Brahe.

Initially, Kepler postulated that the Earth’s motion followed a circular path, with the center of the circle located relatively close to the Sun. This assumption provided a basis for explaining the changing velocity of the Earth as it orbited the Sun using a straightforward mathematical principle: the planet’s radius-vector (the line connecting it to the Sun) sweeps out equal areas in equal amounts of time. This particular rule, which was established in late 1601 or early 1602, is referred to as the second law in Kepler’s list of laws, although it was historically formulated before the others.

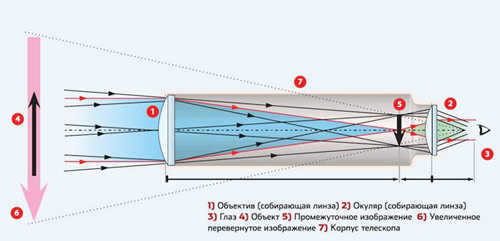
Kepler’s telescope
In 1611, Johannes Kepler made enhancements to his telescope by substituting the scattering lens in the eyepiece with a collecting lens. This modification resulted in a wider field of view and a larger pupil. However, Kepler’s system produced an inverted image. Almost all refractor telescopes constructed afterwards were based on Kepler’s system. Image: Popular Mechanics

The most challenging aspect of determining the shape of the Martian orbit proved to be quite perplexing for Kepler. After conducting numerous laborious calculations, he concluded that a circular shape was not possible. Initially, Kepler hypothesized that Mars followed an oval trajectory, or perhaps even a cross-sectional shape resembling an egg. However, none of these proposed shapes aligned with the observations of Tycho Brahe. Eventually, Kepler discovered that the ratio between the minimum and maximum distances from Mars to the Sun differed from unity by half the square of the orbital eccentricity. This ratio corresponds to the requirements for an elliptical orbit, assuming the eccentricity is significantly less than one. Thus, it became evident that Mars indeed moves along an ellipse, with one of the foci occupied by the Sun. When this concept is expanded to include other planets, Kepler’s first law emerges. It is worth noting that Kepler likely held this belief from the outset, even though he formally articulated the generalization at a later stage.

Kepler finally arrived at the concept of the elliptical orbit of Mars in the spring of 1605. Subsequently, he finished writing The New Astronomy manuscript within a few months (although the book was not published until four years later, due to reasons unrelated to science).

Enchantment, Conflict, and the Balance of the Universe

The release of this publication propelled Kepler to European renown. Admittedly, not everyone recognized his findings – for instance, they were not embraced (and possibly not comprehended) by the esteemed Galileo. Nevertheless, this is the destiny of nearly all momentous discoveries.

Life continued – and not always with success. Kepler faced challenges when his wife passed away, leaving him with two young children. Furthermore, his patron Rudolf II was dethroned shortly before this tragedy. Additionally, his relationship with Lutheran priests, who suspected him of sympathizing with Calvinism, became strained. These difficulties prevented Kepler from finding employment in Württemberg, where he desired to return. Eventually, after lengthy negotiations, Kepler was offered a position as a mathematician in Linz, the capital of Upper Austria, under the condition that he continue his work on tables of planetary motions and also engage in local cartography. Kepler relocated to Linz in 1612 and resided there for fourteen and a half years. During his time there, he remarried and his second wife gave birth to seven children.

However, Kepler was an incredibly diligent worker! His efforts paid off when he released his most cherished publication in 1619 titled “Five Books of the Harmony of the World”. This work delves into a variety of subjects, including geometry and philosophy, rather than focusing solely on astronomy. Interestingly enough, it was within the pages of this masterpiece that Kepler unveiled his groundbreaking third law, which he made the remarkable discovery of on May 15, 1618.

During the years 1617-1621, Kepler published his most extensive work, titled Sketches of Copernican Astronomy. This groundbreaking textbook provided a detailed description of the heliocentric model of the world, making it the first of its kind. The book presented the laws of planetary motion as universal principles that all planets adhere to. Additionally, it included a summary of Kepler’s calculations, which determined the orbital parameters of Mercury, Venus, Jupiter, and Saturn. Notably, this monograph introduced the term “inertia” for the first time, although its meaning differed from the definition that would later emerge from the works of Galileo and Newton.

The Kepler Space Telescope
Johannes Kepler dedicated his life to examining the movement of planets in the solar system, and the space telescope named in his honor (launched on March 6, 2009) will investigate the planetary systems of other stars. Picture: Popular Mechanics

Upon concluding his time in Prague, following lengthy discussions with the beneficiaries of Tycho Brahe, Kepler was granted access to the complete collection of Brahe’s observations. At long last, he had the chance to immerse himself in the creation of astronomical tables, the very purpose for which he had been employed by the deceased Rudolf II. This monumental undertaking was successfully concluded in the latter half of 1624.

After publishing Rudolf’s Tables, Kepler fulfilled his duties to the imperial government. He could have chosen to remain as the imperial mathematician by converting to Catholicism, but he adamantly refused. While he initially considered moving to England, he ultimately agreed to serve as a mathematician to the Austrian military commander Albrecht Wallenstein.

In August 1630, Wallenstein was removed from his position and failed to pay Kepler the promised salary. Hoping to receive at least a portion of the owed money, Kepler traveled to Regensburg in October where the imperial Diet was being held. Unfortunately, he arrived with a cold and passed away on November 15. Although the tombstone with Kepler’s Latin epitaph has not survived, he composed it himself.