A regular polygon is a convex polygon where all sides and angles between adjacent sides are equal.
In simple terms, to create a polygon, we need a circle. By dividing 360 degrees by the desired number of vertices, we can determine the angle at which the rays will be displaced, and this angle will be the same for all adjacent sides. By connecting the points where the rays intersect with the circle, we can form the desired regular polygon. Since we are working with a circle, which can be seen as a circle inscribed in a square, we can conclude that the sides of the polygon will also be equal.
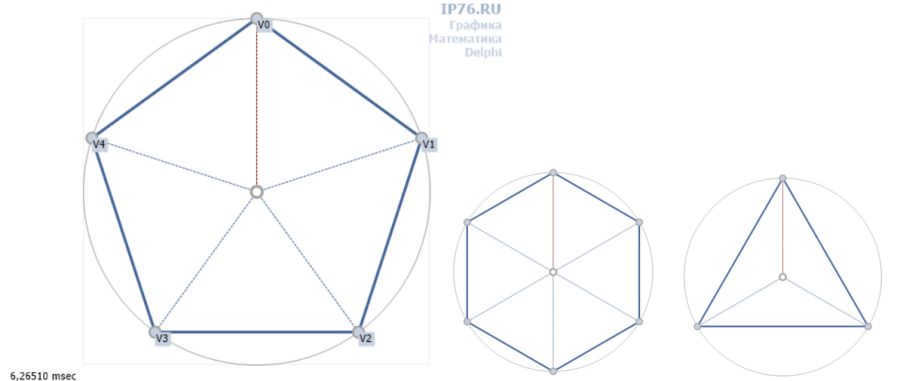
Drawing a polygon is not a complicated task. The challenge lies in calculating the coordinates of its vertices. Taking into account the offset angle is essential if we want to rotate the figure.
Calculating the coordinates of the intersection between a line and a circle is the most challenging part. There is an entire article dedicated to this topic. The xIPTrig module includes the necessary function:
Below is a description of the types used. Instead of TxPoint, TPointF can be used. The other types used have equivalents in modern versions of Delphi. These equivalents are so similar that converting from one to another does not pose any difficulties or questions for the compiler.
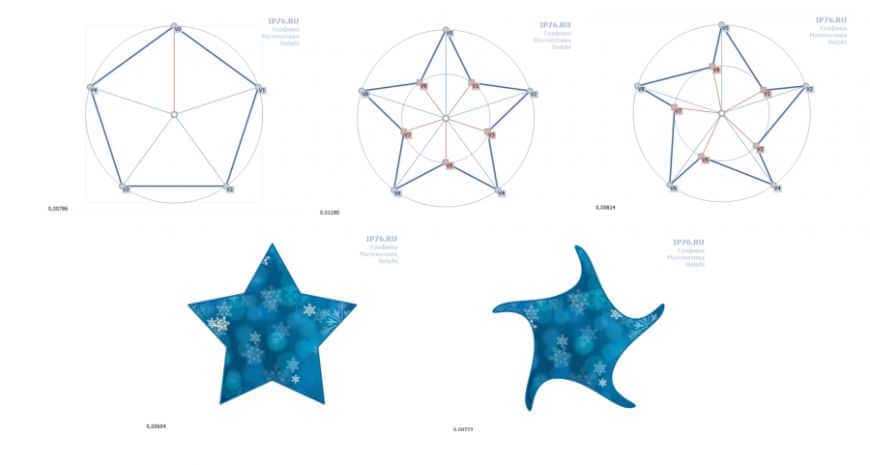
A Perfect Star
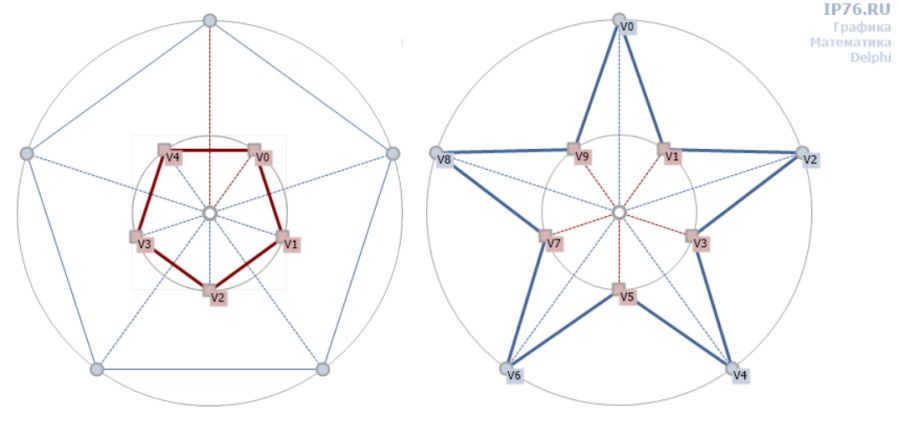
Why not create a stunning star by nesting a smaller polygon within the main one? This inner polygon should be rotated at half the angle obtained by dividing 360 degrees by the number of vertices. In simpler terms, rotate it halfway between each adjacent vertex. Finally, connect all the resulting vertices one by one.
The end result is a remarkably beautiful star!
Discovering the set of points that form a regular star:
By adjusting the dimensions of the inner ellipse and the quantity of vertices, you can create various adorable shapes.

To create unique New Year’s stars, we utilize GDI+. Specifically, we employ TxIPCanvas, which is integrated into GDIPCanvas (included in the demo project). By initializing the texture brush, the fill operation proceeds seamlessly, retaining the current brush settings. Whether it’s a solid color or an image, the result remains consistent.
The perfect “ruthless” celestial body
The celestial bodies depicted on the Chinese and American flags are known for their “ruthless” appearance. Similarly, the star on the Russian Federation’s army symbol embodies this same quality. Unlike other stars, it lacks any internal ellipses and is constructed solely from the intersection of lines connecting its vertices. This star’s design adheres strictly to the principles of geometry, showcasing its straight and unapologetically brutal nature, much like the renowned actor Jason Statham.
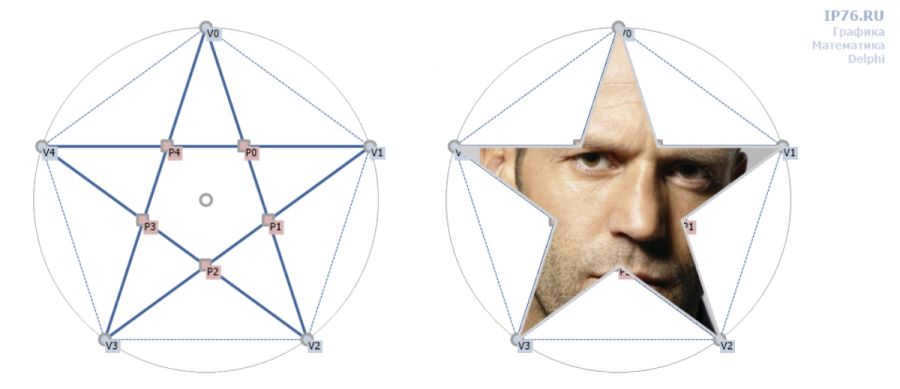
Our task now is to determine the points of intersection. Let’s examine Figure 4. The coordinates of point P0 are obtained by intersecting lines (V0, V2) and (V1,V4). To generalize, we can express it as follows:
Where F represents the function that calculates the intersection of vectors defined by two points. A detailed article is dedicated to the topic of line intersection. As usual, the function for calculating the intersection coordinate is located in the xIPTrig module.
The actual function is within the xIPTrig module:
Incorrect celestial bodies
Why don’t we return to the gentle, festive celestial bodies? Within the angle formed by neighboring vertices, we can introduce an offset parameter. This parameter does not necessarily have to divide the angle in half. Let’s assign it a different value, perhaps 90%. As a result, we will obtain a somewhat timid disco star.
If we replace polygons with curves, we can achieve even more fascinating outcomes. In GDI+, this can be achieved using the Curve function. It is specifically designed for individuals who prefer not to calculate the control points of Bézier curves manually. The Tension parameter (0..1) determines the “tension” of the curve. It is best to experiment with different values, as it is difficult to describe in words.






However, it does resemble a bacterium that can be found in the remnants of a New Year’s olivier salad.
Drawing
I nearly forgot regarding the drawing procedures themselves. The algorithm is straightforward. First, we locate arrays of vertex coordinates. The functions for this are all specified above. Then, we perform the drawing with one of the techniques – Polygon or Curve. For Curve, an additional parameter called “tension” is available. In case this parameter is set to 0.0, it will resemble the usage of Polygon instead of Curve.
All functions utilize the current ACanvas settings. This implies that the color, line thickness, and brush must be configured prior to the function call. Moreover, there is no square calculation performed. It is left to the discretion of the programmer whether to input a pre-calculated square or an ellipse. In the instance of an ellipse (not a circle), neither a polygon nor a star would be appropriate. Nevertheless, the author might have some artistic intentions.
The parameters of the functions are the same as the parameters used to calculate vertex coordinates, which is why I didn’t provide a description for them.
During the testing of the program that converts equatorial coordinates of a celestial object to ecliptic coordinates, it was discovered that if the calculation table is populated with data, it becomes possible to convert time from hours, minutes, and seconds to decimal fractions of an hour, and vice versa. Additionally, it is also possible to convert angular magnitudes from fractional-angular values to degrees, minutes, seconds, and even radians.
Currently, the primary worldwide recognized astrometric system for describing the position of celestial objects is the second equatorial coordinate system [1].
Within this coordinate system, celestial luminaries’ ephemeris [2] is typically represented in the following formats:
1. The angular distance from the vernal equinox point to the point where the luminary’s meridian line intersects the equatorial line, known as the direct ascension α – hh mm ss,ss.
2. The angular distance along the meridian from its intersection with the equatorial line to the luminary, known as the declination δ – (°) (‘) (“,”).
This is the adopted format used to recognize the coordinates of celestial objects in line input positions (Table 1). You have the option to input the coordinates of celestial objects copied from spreadsheets into these position windows.
In many instances, a single string consisting of two coordinate values will be recognized, such as this: 03h 24m 19.35c +49° 51′ 40.5″The most crucial aspect is that the correct designations for the angular coordinates are present. Along with the designations h – hours, m – minutes, s – seconds, the program will not “complain” about data presented with the designations h – hours, m – minutes, s – seconds.
The ecliptic coordinate system [3] is the oldest method of recording the position of celestial objects, dating back to the times of Hipparchus and Bayer. This system is currently used for calculating planetary motion and dividing the celestial sphere into zodiacal sectors. The accepted format for recording ecliptic coordinates is as follows:
longitude λ – (°) (′) (″,″); latitude β – (°) (′) (″,″).
The program utilized on this platform enables us to carry out instant calculations in response to data updates, but not all the essential values have been provided yet.
To initiate the calculation, it is imperative to input or modify both sets of coordinate values for the celestial object. If the required coordinate value is 0.0000°, it is preferable to initially enter a non-zero value in the corresponding field, and subsequently, after the green signal for calculations is activated, reset it to 0 again (you can simply append a dot or comma after the zero, as long as the program identifies that all coordinates are entered deliberately)..
Table 1: Conversion of celestial object coordinates from equatorial to ecliptic reference frame
α – right ascension
δ – declination
There was an issue. Right ascension cannot exceed 24 hours, minutes, and seconds cannot exceed 60, and the absolute value of declination must not exceed 90°.
Design by Sergey Ov for abc2home.ru
For the convenience of transferring data to other sources, the following output formats are available:
Object: Regulus
Constellation: Leo, Leo (Leo)
Equatorial coordinates:
Standard – (10h 08m 22s; 11° 58′ 12″);
Fractions of an hour – (10.13953h; 11.97000° );
Degrees – (152.09300°; 11.97000°) or (152.09300, 11.97000)°;
Radians – (2.65452 rad; 0.20892 rad) or (2.65452, 0.20892)rad
Ecliptic coordinates:
Standard – (149° 49′ 42″; 0° 28′ 05″);
Degrees – (149.82820°; 0.46810°) or (149.82820, 0.46810)°;
Radians – (2.61500 rad; 0.00817 rad) or (2.61500, 0.00817) rads
After entering the coordinates of both celestial objects (planets, stars), the orange prompt will disappear and the green color will activate, initiating the automatic calculation of the angular distance. If this does not occur, simply click on the green field labeled “Calculation” or “OK”.
Calculating the angular distance between two celestial objects whose positions are specified in the second equatorial coordinate system.
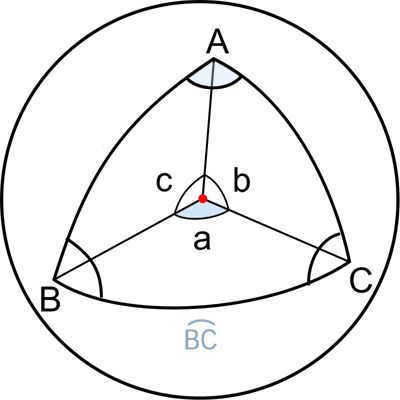
Figure 1: Spherical triangle
The fundamental property of the arc of a circle serves as the foundation for deriving all equations in spherical trigonometry – the radian measure of an arc is equal to the ratio of the arc’s length to the radius of the circle (as shown in Figure 1):
Therefore, all subsequent calculations are carried out solely using angular quantities.
The theorem of sines and cosines serves as the basis for expressing the relationships between angular quantities in both spherical trigonometry and ordinary trigonometry.
Spherical cosine theorem
The cosine of angle A is equal to the cosine of angle B multiplied by the cosine of angle C, plus the sine of angle B multiplied by the sine of angle C multiplied by the cosine of angle A.
The cosine of angle B is equal to the cosine of angle C multiplied by the cosine of angle A, plus the sine of angle C multiplied by the sine of angle A multiplied by the cosine of angle B.
The cosine of angle C is equal to the cosine of angle A multiplied by the cosine of angle B, plus the sine of angle A multiplied by the sine of angle B multiplied by the cosine of angle C.
Spherical sine theorem
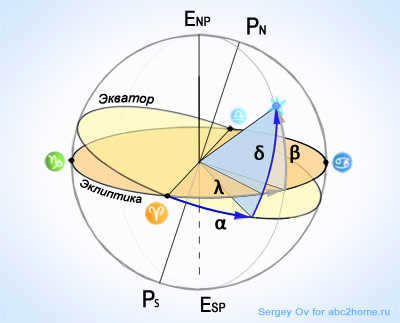
In the second equatorial coordinate system, the position of objects is determined by two angular parameters called the direct ascent α and declination δ, in the ecliptic coordinate system, similar angular quantities, but referenced to the ecliptic are longitude λ and latitude β (Fig.2).
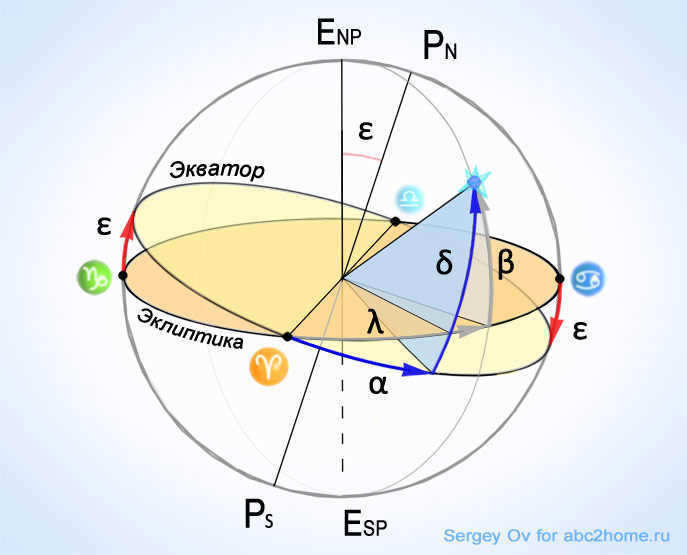
Figure 2: The celestial sphere, along with the angular equatorial coordinates and ecliptic coordinates, provides a means to locate celestial bodies in the night sky.
From the diagram, we can observe that α and δ represent the direct ascension and declination, which indicate the celestial object’s position in relation to the equator, respectively. Meanwhile, λ and β denote the longitude and latitude, determining the object’s position relative to the ecliptic.
Declination is determined by the angle between the celestial equator and the object in a plane perpendicular to the equator.
Direct Ascension is determined by the angle between the vernal equinox point and the declination reference point.
It’s important to note that direct ascension is measured in the opposite direction to the clockwise direction from the vernal equinox point. (the Sun enters Aries at the vernal equinox) and its value is expressed in hours rather than degrees. In the diagram, the approximate value of α is 2 hours, and δ slightly exceeds 45°.
The equation sin(β) = cos(ε)*sin(δ) + sin(ε)*sin(α)*cos(δ),
sin(λ)*cos(β) = sin(ε)*sin(δ) + cos(ε)*sin(α)*cos(δ),
cos(λ)*cos(β) = cos(α)*cos(δ),
The value of ε is equal to 23.439281° and represents the angle at which the Earth’s axis is inclined to the ecliptic. This angle indicates the inclination of the Earth’s equator plane with respect to the plane of the Earth’s orbit as it revolves around the Sun.
P.S.. This page utilizes the Beta version of the celestial sphere point’s ecliptic coordinates calculation program based on the given equatorial coordinates. If you come across any deficiencies or have any suggestions, please report them in the forum section of the website. (the forum input window is located at the bottom of the page)..
1. Ephemerides are tables that summarize the coordinates of celestial luminaries and other variable astronomical quantities calculated for a series of consecutive moments of time. This term is commonly used in astronomy to refer to the calculations and data collected for various celestial objects.
2. Direct ascension and declination are the names given to the coordinates in the second equatorial reference frame.
In order to determine the position of a celestial body, a line is drawn across the celestial equator and the Р (the pole of the world). This line is known as the hour circle, or the circle of declination. The distance along this circle from the equator to the celestial body is the first coordinate, known as the declination of the celestial body (d or δ). The declination is measured from the equator in both directions, ranging from 0° to 90°. For celestial bodies in the Southern Hemisphere, the declination is represented as a negative value.
The ascension of the celestial body (a or α) is the arc α1 on the celestial equator (as shown in Fig. 1), measured from the vernal equinox point in the opposite direction of the celestial sphere’s rotation to the declination circle of the specific celestial body. It represents the spherical angle between the declination circles passing through the equinox point and the specific celestial body. The ascension of the celestial body is typically expressed in hours, minutes, and seconds of time and can range from 0h to 24h.
2. The ecliptic reference frame uses the terms longitude and latitude to describe coordinates. In this system, the primary circle is known as the ecliptic and its pole is referred to as the ecliptic pole EPN. To determine the position of a celestial body, a large circle called the circle of latitude is drawn from the ecliptic to the body, intersecting at the point EPN. The arc from the ecliptic to the body is known as the ecliptic, celestial, or astronomical latitude b (β), which serves as the first coordinate. The latitude b (β) is measured from the ecliptic towards its North or South Poles, with negative values assigned to the latter. The second coordinate is the ecliptic, celestial, or astronomical longitude l (λ), which represents the arc from the vernal equinox point on the ecliptic to the circle of latitude of the celestial body. This arc is measured in the direction of the Sun’s annual motion and can range from 0 to 360.
4. Asterism refers to a collection of stars that come together to form a distinct pattern and are given a separate name. An asterism can either be a component of a constellation, like the Throne, or connect multiple constellations, like the Winter Triangle.
Large Russian Encyclopedic Dictionary. 2012

Note: h1 — represents the altitude of the celestial body at the first vertical as indicated in Table 21 of the MT-75 Navigational Tables.
Sun’s Coordinates
Table 6.4. Equatorial coordinates of the Sun
Right ascension
a®. degrees
The Sun’s declination d® varies by 0.4 ° during the month before and after the vernal and autumnal equinoxes, and by 0.1 ° during the month before and after the summer and winter solstices. During the second month after the dates 21.03, 22.06, 23.09, and 22.12, the variation is -0.3 °.
The direct sunrise a® varies by 1° throughout the year.
The exact coordinates for any given moment can be obtained from the Naval Astronomical Yearbook (MAE).
Using the provided data, we can calculate an approximate meridional height H® of the Sun for a given date in the ship’s latitude. To do this, we calculate the declination d® for the given date, and then find
THE NIGHT SKY
6.2.1. Important star groupings and star designations
Table 6.5. Star groupings
Table 6.6. Designations of stars in star groupings
Number on the table of observable locations of the Museum of Astronomy and Exploration
Locating the primary stars
When studying the night sky, it is recommended to use star charts that are created using specific cartographic projections. It is important to consider the distortions in these projections when comparing the sky to the map.
Stars are classified into different categories known as stellar magnitudes, based on their apparent brightness. It is worth noting that this classification does not indicate the actual size of the stars.
Stars with a magnitude of 6 or lower can be seen with the naked eye. The brighter stars have magnitudes of zero or even negative values. For instance, the Sun has a magnitude of -27, the full Moon has a magnitude of -12, and Venus has a magnitude of -4.
The brightest star, Sirius, has a magnitude of -1.6. Other notable stars include Canopus with a magnitude of -0.9, Bega with a magnitude of +0.1, Capella with a magnitude of +0.2, Rigel with a magnitude of +0.3, Arcturus with a magnitude of +0.2, Procyon with a magnitude of +0.5, Ahernar with a magnitude of +0.6, Alpha Centauri with a magnitude of +0.1, Altair with a magnitude of +0.9, R Centauri with a magnitude of +0.9, and Polaris with a magnitude of +2.1.
One of the most well-known constellations in the northern hemisphere is the Big Dipper. It consists of seven prominent stars that have similar magnitudes. These stars are bright enough to be used for astronomical observations and can serve as reference points for locating other navigational stars.
Diagram depicting the celestial bodies within the constellations
Ursa Major and Ursa Minor
By extending the line connecting the stars b and a of the Big Dipper beyond a by approximately 5 distances between them, we can determine the position of Polaris (a of the Little Dipper). Polaris is located near the North Pole of the world. The altitude of Polaris above the horizon is roughly equal to the latitude of the observer’s location.
The constellation Cassiopeia can be easily identified in the night sky by the distinct arrangement of its stars, which resemble the letter W. Cassiopeia is located at the same distance from Polaris as the Big Dipper, but in the opposite direction (Fig. 6.2).
By extending a line from Polaris through b Cassiopeia to the distance between them, we can locate the star Alpheras (a Andromeda). Alpheras acts as a connection between the constellations Andromeda and Pegasus, as it forms the fourth corner of a large square with the stars of Pegasus (Fig. 6.3). If we continue the diagonal a of Pegasus – a of Andromeda to a distance equal to the length of one side of the square, we will find the star Mirach (b of Andromeda), and further along the continuation of the diagonal is the star Alamak (g of Andromeda).
The arrangement pattern of stars belonging to the constellations Pegasus and Perseus.
If we continue the diagonal of the large square to Pegasus – Andromeda, extended by approximately 2 distances between these stars, we will discover the star Mirfak (in the Perseus constellation). The Perseus constellation can also be found by extending the line of stars g-a from the Big Dipper by 5.5 distances between them (see Fig. 6.2).
By extending the line connecting the stars d and a of the Big Dipper beyond star a by around 5 distances between them, we will locate the star Capella (in the Ascendant), which lies at the intersection of this line with the continuation of the line of the Andromeda constellation – Perseus.
By extending the arc formed by the curved handle of the Big Dipper by the length of the handle (Fig. 6.4), we will come across the star Arcturus (also known as Volopassus), which is equally bright as Capella. Continuing this arc further in the same direction, we will discover the star Spica (in the Virgo constellation) with a magnitude of plus 1.2.
Following a line from g of the Big Dipper through the end of the dipper’s handle (h of the Big Dipper). (h of the Big Dipper), we encounter the Northern Crown constellation, composed of seven relatively faint stars forming a semicircle facing convexly towards Arcturus. The middle and brightest star, Alphacca (in the Northern Crown), is known as the Pearl of the Crown.
Figure 6.5 displays a visual representation of the stars that make up the constellation Orion, along with the prominent star Sirius.
In Figure 6.6, a schematic diagram showcases the stars that form the constellations Southern Cross and Centauri.
The constellation Orion can be used as an additional point of reference for locating the star Capella, which is situated between this constellation and Polaris.
If we continue the line of Orion’s belt to the left at the same distance as the diagonal between Betelgeuse and Riegel, we will once again come across the star Sirius.
By extending the line from Procyon to Sirius by the distance between them, we will find the star a Dove (with a magnitude of plus 2.7). If we now draw a line from the star Rigel through the star a of the Dove constellation and extend it further by half the distance between them, we will discover the star Canopus (a Argo) with a magnitude of plus 1.0.
By extending the side of the great square b – a of the Pegasus constellation beyond the star a by three distances between b and a of Pegasus, we will come across the star Fomalhaut (a of the South Pisces constellation).
One of the most distinct constellations in the southern sky is the Southern Cross, and the brightest star in this constellation is the star Acrux a with a magnitude of plus 1. The northernmost star of the Southern Cross g has a sidereal magnitude of plus 1.5.
On the extension of the line of stars d – b of the Southern Cross constellation, there is a pair of stars b and a of the Centaurus constellation (Figure 6.6).
One of the brightest stars, Ahernar (a Eridanus), can be found in the middle of the line segment that connects the stars Fomalhaut and Canopus.
Get a downloadable file (word) containing illustrations.
All the files are exclusively available for registered users. The registration process will only take a few minutes.
osnovnie_tablici.doc (204.0 KiB, 63 hits)
Sorry, you do not have the permission to download this file.
Table 6.2: Basic tables
Definition of coordinate signs and values
Coordinate signs
Coordinate signs and their meanings
Trigonometric function signs
Latitude f (N or S)
Always “+”, less than 90°
All functions “+ “
Monotonically increasing with f “+ “
All functions “+ “
Declination d (N or S)
Different from f (in IV quarter) “-“
cos and sec “+”, …
The celestial sphere is constantly rotating for an observer on Earth. If you are in the Northern hemisphere of the planet, on a night without a moon and without clouds, and you gaze long enough into the northern part of the sky, you will notice that the entire sparkling array of stars revolves around one unremarkable faint star (although experts tell us that Polaris is the brightest). Some of the stars disappear below the horizon in the western part of the sky, and others take their place.

The carousel continues spinning until dawn. However, come the next day, at precisely the same hour, every single star returns to its original position. The relative coordinates of the stars alter at such a sluggish pace that they appear timeless and motionless to human observers. It is no coincidence that our predecessors envisioned the sky as a solid vault, with the stars serving as perforations within it.
A peculiar star – a point of reference
In ancient times, our predecessors took notice of a peculiar star. What makes it unique is its lack of movement along the celestial slope. It appears to be suspended in a single point above the northern edge of the horizon. All the other celestial bodies orbit around it in perfect concentric circles.

Ancient astronomers had various interpretations of this star. For instance, the Arabs believed it to be a golden stake driven into the sky. They imagined a golden stallion racing around this stake (known as the Big Dipper), connected to it by a golden harness (known as the Little Dipper).
These observations laid the foundation for celestial coordinates. It was only natural and logical for astronomers to use the fixed star, known as Polaris, as the reference point for determining the position of celestial objects.
Incidentally, those of us residing in the Northern Hemisphere are incredibly fortunate to possess a celestial compass. By a stroke of luck, one in a million, our Polaris lies precisely on the planet’s axis of rotation, enabling us to effortlessly ascertain our precise location in relation to the cardinal directions from any point within the hemisphere.
Technical means for accurately measuring angles and distances did not immediately appear, but people have long sought ways to systematize and categorize the stars. Although the ancient astronomical devices did not allow for determining the coordinates of stars in the digitized form we are familiar with, imagination more than made up for it.
Throughout history, people from all parts of the world have divided the stars into groups known as constellations. These constellations were often named based on their resemblance to various objects. For example, the Slavs referred to the constellation of the Big Dipper as simply a dipper.
However, the most commonly used names for constellations were derived from the figures in ancient Greek mythology. It can be argued, albeit with some degree of tension, that these names serve as their initial rudimentary coordinates within the celestial sphere.
Heavenly Jewels
Astronomers paid homage to the magnificent celestial bodies by bestowing them with names inspired by ancient Greek gods and heroes. For instance, the two brightest stars in the Gemini constellation are known as Castor and Pollux, after the twin sons of Zeus, the mighty god of thunder, who were born following one of his amorous escapades.
The star Algol, which is the alpha star of the Perseus constellation, is a fascinating celestial object. According to ancient mythology, Algol represents the eye of Medusa, the fearsome Gorgon from Tartarus. Medusa’s gaze was said to turn all living beings into stone, and after her defeat in a mortal battle, her head was taken as a weapon (even with her head severed, her eyes continued to have an effect). The positioning of Algol in the constellation Perseus, as the eye of Medusa, is not simply a coincidence. The ancient Greek astronomers were able to observe periodic changes in Algol’s brightness, as it is a binary star system where the two components periodically align with each other from the perspective of Earth.

Naturally, the "winking" star transformed into the eye of the mythical creature in fairy tales. The coordinates of Algol, the winking star, in the celestial sphere are: right ascension – 3 h 8 min, declination +40°.
Celestial almanac
However, it is important to remember that the Earth not only rotates on its axis but also revolves around the Sun. Every 6 months, the planet finds itself on the opposite side of the Sun, resulting in changes to the night sky. This phenomenon has long been utilized by astronomers to accurately determine the seasons. For instance, in ancient Rome, students eagerly awaited the appearance of Sirius in the morning sky (known as “Vacation” in Roman times) as it signaled the start of their holiday break. As we can observe, the celestial moniker for these student vacations has endured through the ages.
In addition to school breaks, the arrangement of celestial bodies played a crucial role in marking the start and end of sea and river voyages, initiating military expeditions, and guiding agricultural practices. The creators of the earliest comprehensive calendars across various regions of the globe were astrologers, astronomers, and temple priests, who developed the ability to precisely calculate the positions of the stars. Across all continents that house remnants of ancient civilizations, one can find elaborate stone structures constructed specifically for astronomical observations and measurements.
Coordinate System for Horizontal Positioning
This system displays the positions of stars and other celestial objects in the “here and now” mode, relative to the horizon. The first coordinate represents the vertical angle of the object above the horizon. This value is measured in degrees. The maximum value is +90° (zenith), indicating that the object is directly overhead. A coordinate value of zero indicates that the object is located on the horizon. Conversely, a minimum altitude value of -90° means that the object is positioned at the nadir point or directly beneath the observer’s feet – the opposite of the zenith.
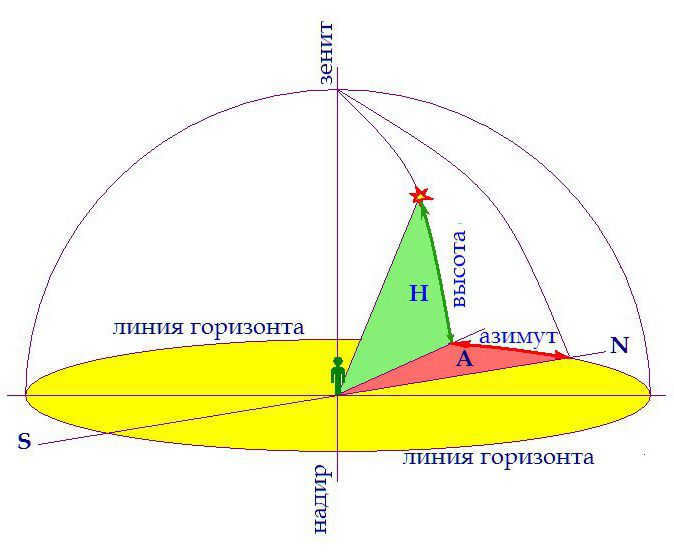
The azimuth, which is the angle between the horizontal lines pointing towards the object and north, represents the second coordinate in this system. It is also known as topocentric as it is tied to a specific point on the globe.
However, this system is not without its drawbacks. Both coordinates for each star in this system change every second, making it less suitable for describing the positions of stars in constellations, for example.
Stellar GLONASS and GPS
So how can we utilize this system? As we travel across the globe over long distances, the arrangement of stars in the sky will inevitably alter. This phenomenon was even observed by ancient sailors. For instance, an individual standing at the North Pole will witness Polaris directly overhead at the zenith. However, someone residing at the equator will only be able to see Polaris on the horizon. Moreover, while moving along the parallels from east to west, a voyager will observe a shift in the sunrise and sunset times of specific celestial bodies.

Despite its complexity and approximation, the described system of determining spatial location has faithfully and accurately assisted travelers for over two centuries.
The initial system of star coordinates
In this system, celestial coordinates are linked to both the Earth’s surface and celestial landmarks. The first coordinate is declination, which is measured as the angle between the line pointing to the celestial body and the equatorial plane (the plane perpendicular to the Earth’s axis – the line pointing towards Polaris). As a result, this coordinate remains constant for fixed objects in the sky, such as stars.
The angle between the direction to the star and the celestial meridian (the plane where the world axis and the plumb line cross) will serve as the second coordinate in the system. Therefore, the second coordinate is influenced by the observer’s position on the planet and the current moment in time.
This system has a particular application. It is utilized in the installation and adjustment of telescopes mounted on rotating platforms. Such a mechanism can track objects that are rotating with the celestial dome. This is done to enhance exposure time when capturing portions of the sky in photographs.
Equatorial #2 stellar.
What is the method used to determine the celestial coordinates of stars? The second equatorial system is designed for this purpose. Its axes remain fixed relative to distant cosmic objects.
Similar to the first equatorial system, the first coordinate represents the angle between the star and the plane of the celestial equator.
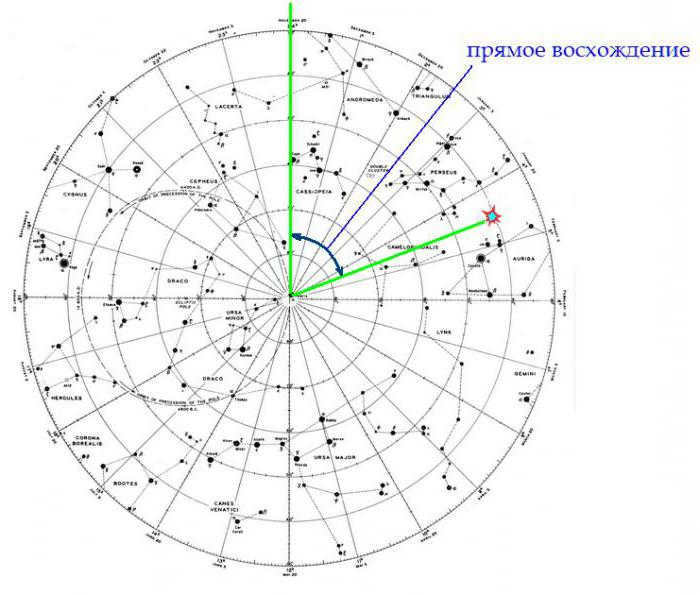
The second coordinate, known as the right ascension, is the angle between two lines that lie on the plane of the celestial equator and intersect at the point where it intersects with the celestial axis. The first line is drawn towards the vernal equinox point, while the second line is directed towards the point where the star is projected onto the celestial equator.
The direct ascension is measured along the arc of the celestial equator in a clockwise direction. It can be quantified in degrees from 0° to 360° or in the “hours:minutes” format. Each hour corresponds to 15 degrees.
The diagram illustrates the process of measuring the direct ascension of a celestial body.
What are the other coordinates of the stars?
None of the aforementioned systems are appropriate for establishing our position relative to other stars. Scientists calculate the position of the closest celestial bodies using the ecliptic coordinate system. This system differs from the equatorial coordinate system as it uses the ecliptic plane (the plane in which the Earth orbits the Sun) as the reference plane.
Additionally, the galactic coordinate system is employed to determine the location of even more distant entities, such as galaxies and nebulae. It is not difficult to surmise that this system is based on the plane of the Milky Way galaxy (our home spiral galaxy).
Is everything absolutely perfect?
Not exactly. The coordinates of Polaris, specifically its declination, are 89 degrees 15 minutes. This means that it is nearly one degree away from the pole. While this location is ideal for orienting oneself on land when looking for direction, it requires a correction when planning the course of a ship that will have to travel thousands of miles.
Furthermore, the apparent stillness of the stars is not quite what it seems. A thousand years ago (which is relatively recent in cosmic terms), the constellations had significantly different shapes.