Kepler’s Laws are a set of physical laws that were discovered by Johannes Kepler and describe the movement of planets around the Sun.
Kepler’s First Law of Ellipses
Each planet in the solar system moves along an elliptical path, with the Sun located at one of the foci of the ellipse.
Here, c represents the distance from the center of the ellipse to its focus (half of the interfocal distance), a represents the major semi-axis, and e is known as the eccentricity of the ellipse. When c = 0 and e = 0, the ellipse becomes a perfect circle.
According to Newton’s Law of Universal Gravitation, each object in the cosmos pulls every other object toward itself in a way that is directly related to the mass of each object and inversely related to the square of the distance between them. This means that the acceleration a can be expressed as follows:
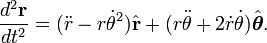
The movement of each planet can be described by the equation above.
Substituting and into the second equation yields
After integrating, we can express this as
for a given constant , which represents the unique angular momentum ().Allow
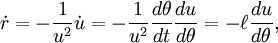
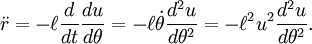
Equating to
This equation represents a conic section with eccentricity e and the coordinate system centered at one of the focuses. Therefore, Kepler’s first law can be directly deduced from Newton’s law of universal gravitation and Newton’s second law.
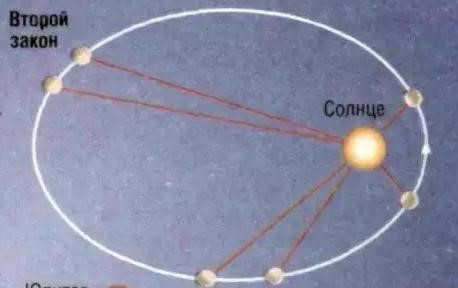
Kepler’s Second Law (Law of Squares)
Every planet orbits in a plane that passes through the center of the Sun. Additionally, when equal amounts of time pass, the radius-vector that connects the Sun and the planet sweeps through sectors of equal area.
When it comes to our solar system, this law is associated with two key concepts: perihelion – the point in the orbit that is closest to the Sun, and aphelion – the point in the orbit that is furthest from the Sun. Consequently, Kepler’s second law implies that the planet’s movement around the Sun is not uniform, as it has a higher linear velocity at perihelion compared to aphelion.
Every year in early January, the Earth moves faster as it passes through perihelion, resulting in a faster apparent movement of the Sun along the ecliptic to the east compared to the average for the year. In early July, the Earth moves slower as it passes through aphelion, causing the Sun’s movement along the ecliptic to slow down. The law of areas states that the force governing the orbital motion of the planets is directed towards the Sun.
Angular momentum of a point particle with mass m and velocity is defined as:
.
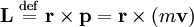Here, a is the radius-vector of the particle, and p is the momentum of the particle.
.
Let’s take the time derivative of both parts of the equation:
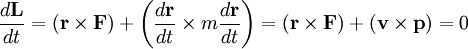
where \(\mathbf{L}\) is constant.
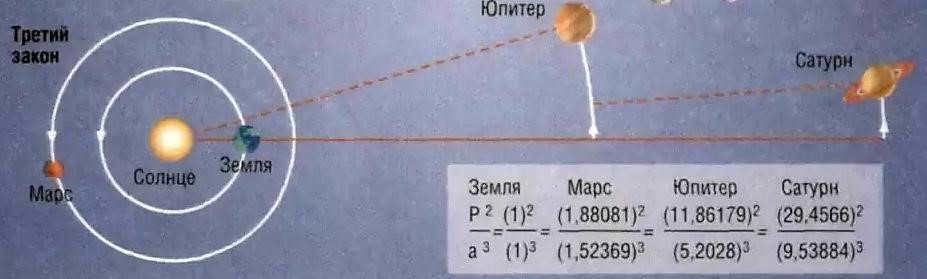
Kepler’s Third Law (Harmonic Law)
The cubes of the major semi-axes of the orbits of the planets are directly proportional to the squares of the periods of their orbital revolution around the Sun.
where T1 and T2 are the orbital periods of two planets around the Sun, and a1 and a2 are the lengths of the major semi-axes of their orbits.
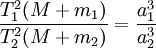where M represents the mass of the Sun, and m1 and m2 represent the masses of the planets.
Given that motion and mass are interconnected, this combination of Kepler’s harmonic law and Newton’s law of gravitation is employed to determine the masses of planets and satellites if their orbits and orbital periods are known.
According to Kepler’s second law, the orbiting body’s radius-vector sweeps equal areas in equal time intervals. If we consider tiny time intervals when the planet is at points A and B (perihelion and aphelion), we can estimate the area using triangles. These triangles have heights equal to the distance from the planet to the Sun and a base equal to the product of the planet’s velocity and time.
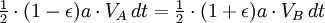
Applying the principle of energy conservation to the overall energy of the planet at points A and B, we can express this as
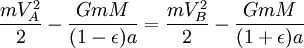
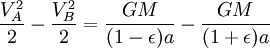
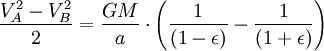
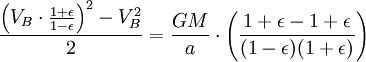
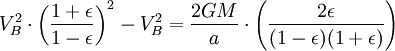
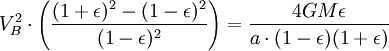
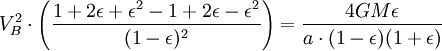
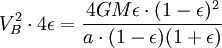
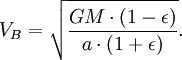
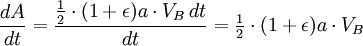
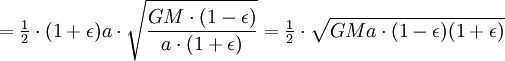
However, the combined surface area of the ellipse is (which is equivalent to πab due to ). Therefore, the total time taken for one complete revolution is equal to
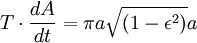
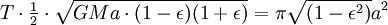
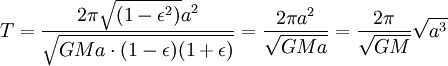
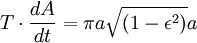
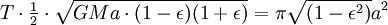
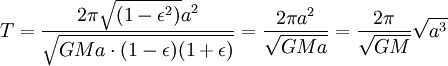
Note that if the mass m is not negligibly small in comparison with Mthen the planet will orbit the Sun at the same speed and in the same orbit as a material point orbiting the mass of M M + m (see reduced mass). Thus the mass M in the last formula should be replaced by M + m :
Wikimedia Foundation . 2010 .
This article is currently being reviewed by Skysmart methodologists.
If you happen to come across any mistakes, kindly report them through the online chat
(located at the bottom right corner of your screen).
The Earth’s Geometric Form
It is quite astonishing to think that there was a time when individuals believed that the Earth was a flat surface. The ancient Greeks, for instance, envisioned a plane suspended in the air and encircled by ice formations. Meanwhile, in India, it was believed that the planet was supported by three elephants standing on the back of a giant tortoise. While some individuals still adhere to these notions, there is an abundance of evidence indicating that our planet is anything but flat. Here are a few examples to help stimulate conversation on this topic.
Gravity
Gravity is responsible for attracting all objects towards the center of mass. The Earth, being a sphere, has its center of mass located at its center.
Gravity acts on all objects on the Earth’s surface, pulling them towards the Earth’s core, causing them to move in a downward direction, regardless of their position. This is a phenomenon that we consistently observe.
However, if we were to envision the Earth as a flat surface, gravity would still pull all objects towards the center of this plane. So, if someone were to find themselves at the edge of this flat Earth, gravity would pull them towards the center of the disk, rather than downwards.
For the flat Earth proponents to support their theory, they would need to identify a location on the planet where objects fall sideways instead of downwards.
If the Earth were not flat, and even with elephants and a turtle, we would witness a different phenomenon during a lunar eclipse, rather than a uniformly expanding shadow:
However, it is possible that this scenario diverges greatly from reality.
On a flat Earth, sunlight would behave similarly to a flashlight beam. In other words, tall objects located in the opposite direction of the Sun would remain in darkness after sunset.
Conversely, on a spherical Earth, skyscrapers or mountains would still be bathed in sunlight after sunset or prior to dawn.
This is precisely what one would observe when witnessing a sunrise or sunset in the mountains – or examining photographs.
Alright, it is now established that the Earth is not actually flat. However, it cannot be described as a perfect sphere either: the Earth has an ellipsoidal shape.
An ellipsoid is a compressed sphere with an elliptical cross-section. It is along the elliptical path that all satellites orbit.
Ellipse
An ellipse is a closed curve in a plane, a special type of oval. An ellipse has two axes of symmetry – horizontal and vertical, which are made up of two semi-axes.
An ellipse also has two focal points, which are points where the sum of distances from any point P(x,y) is a constant value.
F1 and F2 – foci
c – half the distance between F1 and F2
a – major semi-axis
b – minor semi-axis
r1 and r2 are known as focal distances.
Now we have the necessary understanding to comprehend the essence of Kepler’s laws.
Experience the USE physics preparation courses with a skilled instructor at Skysmart online school!
Kepler’s First Law
Each planet in the solar system orbits the Sun in an elliptical path, with the Sun positioned at one of its foci.
The Sun is situated at one of the foci of the ellipse. The point B, which is closest to the Sun along the trajectory, is referred to as the perihelion, and the point A, which is farthest from the Sun, is known as the aphelion.
Kepler’s first law is relatively straightforward, yet significant, as it made significant advancements in the field of astronomy during its era. Prior to this breakthrough, astronomers held the belief that planets only move in circular orbits. In instances where observations conflicted with this belief, scientists incorporated smaller circles into the main circular motion, which depicted the planets’ movement around specific points on the main circular orbit. With access to Tycho Brahe’s extensive collection of observations, Kepler was able to surpass these outdated notions through careful study.
Kepler’s second law (the law of areas)
The planet’s radius-vector traces out equal areas in equal time intervals.
Each planet orbits in a plane that passes through the center of the Sun. Meanwhile, the radius-vector connecting the planet to the Sun traces out equal areas. As a result, the bodies move around the Sun at varying speeds: they have the highest velocity at perihelion and the lowest at aphelion.
This phenomenon can be observed in the Earth’s movement. Every year, in early January, our planet reaches perihelion and accelerates. Consequently, the Sun moves faster along the ecliptic during this time compared to other parts of the year. In early July, the Earth reaches aphelion, causing the Sun to move slower along the ecliptic. This is why daylight hours are longer in summer than in winter.
Kepler’s Third Law
The relationship between the squares of the orbital periods of the planets and the cubes of the major semi-axes of their orbits is expressed by Kepler’s third law.
Kepler’s third law establishes a connection between the orbital periods of the planets around the Sun and the average distance from the Sun to a planet or satellite. This law holds true for both planets and satellites with an accuracy of less than 1%.
Kepler’s Third Law
T1 and T2 – represent the orbital periods of the two planets [c]
a1 and a2 – represent the major semi-axes of the orbits of the planets [m]
By utilizing this principle, we have the ability to determine the duration of a year (the time it takes for a complete revolution around the Sun) for any given planet, provided we have knowledge of its distance from the Sun.
Conversely, it is also possible to calculate the orbit by knowing the period of revolution.
The Principle of Universal Gravitation
Kepler’s laws are the result of careful observations and generalizations. Isaac Newton theoretically justified these laws through the principle of universal gravitation, which states that all objects are attracted to one another. The force of universal gravitation is directly proportional to the product of the masses of the objects and inversely proportional to the square of the distance between them.
The formula for the force of gravitation, according to this principle, is as follows:
The Principle of Universal Gravitation
F – gravitational force [N]
M – the mass of the first body (often a planet) measured in kilograms [kg]
m – the mass of the second body measured in kilograms [kg]
R – the distance between the bodies measured in meters [m]
G – the gravitational constant
G = 6.67 × 10 -11 m^3 kg^-1 s^-2
Newton was the first scientist to deduce that gravitational forces act between all bodies in space, and it is these forces that govern the motion of these bodies.
The primary and secondary cosmic velocities
Kepler’s principles are applicable not only to the movement of planets and other celestial objects in our solar system, but also to the motion of man-made satellites and spacecraft. In this scenario, the Earth serves as the center of gravity.
In the Hitchhiker’s Guide to the Galaxy book series by Douglas Adams, it is stated that flying is essentially a matter of avoiding contact with the Earth. To successfully become an artificial satellite and orbit the Earth, one must attain the initial speed known as the primary space velocity, which is 7.9 km/s. Here is an explanation of the process:
An artificial satellite – is a spacecraft that revolves around the Earth in a geocentric orbit. To achieve this, the vehicle must possess an initial velocity that is equal to or greater than the primary space velocity.
The primary space velocity
v1 – initial velocity in space [m/s]
g – gravitational acceleration on this celestial body [m/s2]
R – radius of the celestial body [m]
On planet Earth, the gravitational acceleration is approximately 10 m/s2.
There are also second and third space velocities. The second space velocity is the velocity required for a spacecraft to enter into orbit around the Sun, and the third space velocity is the velocity required to travel beyond the boundaries of the solar system.
Second space velocity
v2 – second space velocity [m/s]
g – gravitational acceleration on the celestial body [m/s2]
Kepler’s Laws
Observing the effects of gravitational interaction is easiest when dealing with massive cosmic objects. In our daily lives, it’s challenging to detect the gravitational pull between objects, even if they have a weight of hundreds or thousands of kilograms. In the realm of the microcosm, gravitational forces are so minuscule that they can be disregarded, and other types of interactions between elementary particles and atoms take precedence.
Gravity is responsible for keeping living beings and objects grounded on the planet’s surface, as well as determining the planetary motion around the Sun. It’s the gravitational influence that ensures planets remain in orbit around their stars, while satellites are unable to escape into outer space and instead continue to orbit their respective planets.
The theory of gravitation, also known as the law of universal gravitation, was actually discovered through the observation of the planets in our solar system.
When observing the movement of celestial bodies from Earth, it may appear that these bodies follow complex trajectories. For instance, ancient scientist Ptolemy, who discovered the laws of planetary motion, believed that the Earth was at the center of the universe and that other planets and stars revolved around it in various orbits.
Figure 1 . 24 . 1 . A hypothetical representation of Mars’ observed motion against a backdrop of fixed stars.
Ptolemy’s laws of planetary motion remained unchallenged for 14 centuries until Copernicus introduced the heliocentric system in the middle of the 16th century. This revolutionary model proposed that all planets revolve around the Sun.
The heliocentric system greatly simplified the explanation of celestial body trajectories. Building on Copernicus’ work and the observations of Danish astronomer Brahe, German astronomer Kepler established three empirical laws of planetary motion within the solar system.
Kepler’s First Law
The planets of the solar system follow elliptical paths. An elliptical orbit has one focus at the Sun.
We have provided a visual representation of Kepler’s first law. It depicts a planet with a lower mass compared to a star. The star is positioned at one of the foci of the elliptical orbit that the planet traverses. The point P represents the closest distance to the star, known as the perihelion. Point A, on the other hand, represents the farthest distance from the star, which is called the aphelion. The major axis of the ellipse lies between the aphelion and perihelion points.
Figure 1 . 24 . 2 . Elliptical orbit of a planet with mass m M M. ‘a’ represents the length of the major semi-axis, while F and F’ are the foci of the orbit.
In the solar system, all planets, except for Pluto, orbit in paths that closely resemble circles.
Kepler’s second law, also known as the law of areas
The planetary radius vector traces out equal areas in equal time intervals.
Figure 1.24.3. The law of areas represents Kepler’s second law.
The law of conservation of momentum is equivalent to Kepler’s second law. The diagram above illustrates the momentum vector of an object p → and its components p r → and p ⊥ → . The area swept out by the radius vector in a small time interval Δ t is approximately equal to the area of a triangle with base r Δ θ and height r:
∆ S = 1/2 r^2 ∆ θ or ∆ S/∆ t = 1/2 r^2 ∆ θ/∆ t = 1/2 r^2 ω; ( ∆ t → 0 ).
Here ω = ∆ θ/∆ t; ( ∆ t → 0 ) represents the angular velocity.
The momentum L is equal in absolute value to the product of the magnitudes of the vectors p r → and p ⊥ → :
L = r p ⊥ = r ( m v ⊥ ) = m r^2 ω since v ⊥ = r ω.
It can be deduced from these connections:
Hence, if Kepler’s second law states that ∆ S ∆ t = co n s t, then it can also be inferred that the momentum L remains constant throughout the motion.
Specifically, because the velocities of the planet at perihelion v P → and aphelion v A → are perpendicular to the radius vectors r P → and r A →, it can be concluded based on the principle of conservation of momentum:
Kepler’s Third Law
The relationship between the squares of the orbital periods of the planets and the cubes of the major semi-axes of their orbits can be described by Kepler’s third law.
The formula for Kepler’s third law is:
T2a3 = const or T12a13 = T22a23
The accuracy with which Kepler’s third law holds true for all the planets in the solar system is greater than 1%.
The diagram illustrates two orbits in which celestial bodies revolve around a star. One orbit is circular with a radius R, while the other is elliptical with a major semi-axis a. If R = a, then according to Kepler’s third law, the periods of the planetary orbits are equal.
Figure 1.24.4. Circular and elliptical orbits. If R = a, the periods of orbital motion for the bodies in these orbits are the same.
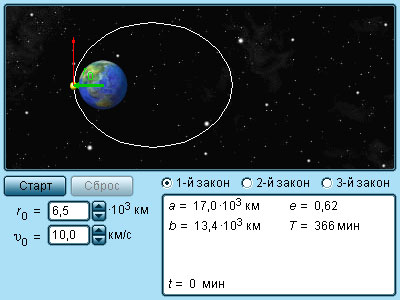
Figure 1 . 24 . 5 . Model of Kepler’s laws.
For a long time, Kepler’s laws were rules that were derived empirically from observations of the motion of celestial bodies. However, there was a lack of theoretical justification for these laws in order to rely on them to create working theories.
The discovery of the law of universal gravitation by Isaac Newton provided such justification:
The Law of Universal Gravitation:
Where M and m are the masses of the Sun and the planet, r is the distance between them, and G = 6.67 x 10^-11 N m^2/kg^2 is the gravitational constant.
Newton was the first researcher to discover that gravitational forces exist between any bodies in space, and these forces determine the motion of these bodies. A specific example of this interaction is the force of gravity acting on objects located on or near planets’ surfaces.
For objects in circular orbits, Kepler’s first and second laws are automatically satisfied, and the third law states that T2 = R3, where T is the period of the orbit and R is the radius of the orbit. This relationship allows us to derive the dependence of gravitational force on distance. When a planet moves along a circular path, it experiences a force due to the gravitational interaction between the planet and the Sun:
The property of gravitational forces being conservative allows us to introduce the concept of potential energy. In the case of universal gravitation, it is convenient to measure potential energy relative to an infinitely distant point.
The potential energy of a mass m located at a distance r from a stationary mass M is equivalent to the work done by gravitational forces in moving mass m from that point to infinity.
To calculate the potential energy of a body in a gravitational field, the mathematical procedure involves summing up the work done over small displacements.
Figure 1.24.6. illustrates the process of calculating the potential energy of a body in a gravitational field.
The law of gravitation that is universal is applicable not solely to masses that are point-like, but also to bodies that have a spherical symmetry. The work ∆ A i done by the force F → of gravity on the small displacement ∆ s i → = ∆ r i → is:
The complete work done in moving a mass m from its initial position to an infinite distance is determined by adding up the work Δ A i at small displacements:
In the limit as Δ r i → 0, this sum transforms into an integral. Consequently, the expression for the potential energy is derived:
The negative sign indicates that gravitational forces are attractive forces.
If an object is situated in a gravitational field at a distance r from the center of gravity and has a velocity v , its total mechanical energy is given by
E = E k + E p = m v 2 2 – G M m r = c o n s t
As per the principle of energy conservation, the total energy of an object within a gravitational field remains constant.
The total energy can be positive, negative, or zero. The sign of the total energy determines the type of motion exhibited by a celestial object (Fig. 1 . 24 . 6 ).
When E = E 1 0 , the object is unable to move beyond a distance r > r m a x from the center of gravity. In such cases, the celestial object follows an elliptical orbit (such as planets in the solar system and comets).
Figure 1 . 24 . 7 . Energy diagram illustrating a body with mass m within the gravitational field produced by a spherically symmetrical body with mass M and radius R .
When E = E 2 = 0, the object can move infinitely far away. The velocity of the object at infinity will be zero. The object follows a parabolic trajectory.
When E = E 3 > 0, the motion follows a hyperbolic trajectory. The object is moving away towards infinity with a surplus of kinetic energy.
The first and second cosmic velocities
Kepler’s laws are applicable not only to the orbital motion of planets and other celestial bodies within the solar system, but also to the movement of artificial satellites and spacecraft. In this case, the Earth serves as the center of gravity.
The first cosmic velocity refers to the velocity of a satellite orbiting in a circular path near the Earth’s surface.
m v 1 2 R 3 = G M m R 3 2 = g m , thus v 1 = G M R 3 = g R 3 = 7 , 9 – 10 3 m / s .
E = m v^2 – G M m / R^3 = 0, so v^2 = 2 G M / R^3 = 2 g / R^3 = 11.2 – 10^3 m/s.
We have demonstrated the concept of first and second space velocity using a diagram. If the speed of the spacecraft is v1 = 7.9 – 10^3 m/s and is aligned parallel to the Earth’s surface, then the spacecraft will travel in a circular orbit at a low altitude above the Earth. For initial velocities greater than v1 but less than υ2 = 11.2 – 10^3 m/s, the ship’s orbit will be elliptical. At an initial velocity v2, the ship will follow a parabolic path, and at an even higher initial velocity, it will follow a hyperbolic path.
Figure 1.24.8. Space velocities. Velocities in the vicinity of the Earth’s surface are shown. 1: v = v1 – circular path; 2: v1 v v v 2 – elliptical path; 3: v = 11,1 – 10^3 m/s – highly elongated ellipse; 4: v = v2 – parabolic path; 5: v > v2 – hyperbolic path; 6: path of the Moon.
Kepler’s laws
Late 16th century astronomy witnessed the confrontation between two models of our solar system: the geocentric system, as proposed by Ptolemy, where the Earth is considered the center of rotation for all celestial objects, and the heliocentric system, advocated by Copernicus, which places the Sun at the center.
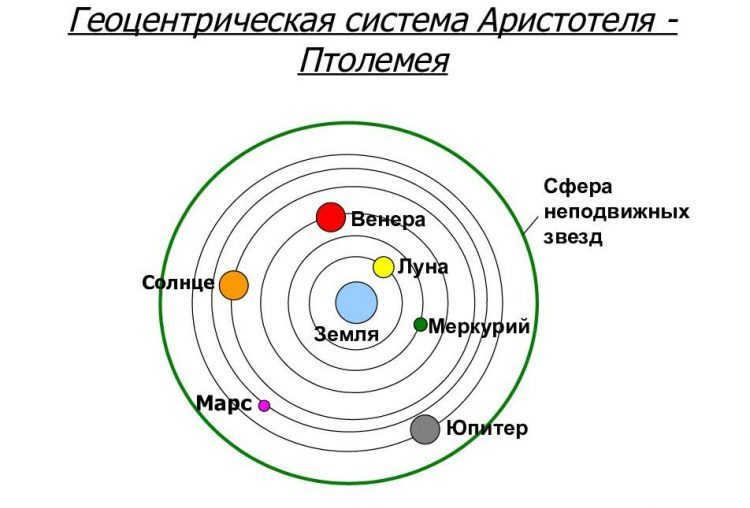
Despite being closer to the true nature of the solar system, Copernicus’ work had its flaws. One of the main shortcomings was his claim that the planets orbit the Sun in circular paths. This belief, however, was inconsistent with the observations, making the Copernican model almost as flawed as the Ptolemaic system. To address this inconsistency, the Polish astronomer introduced an additional circular motion called an epicycle, with its center already moving around the Sun. However, this adjustment did not fully resolve the discrepancies in the model.
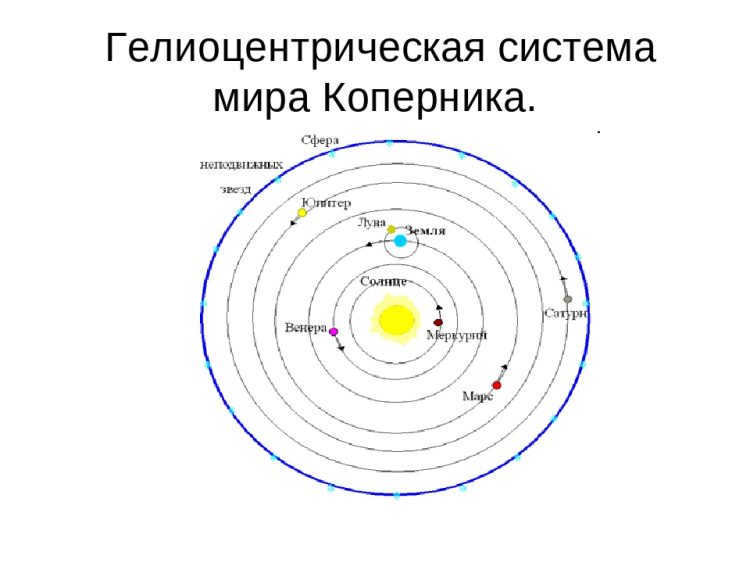
During the early 17th century, the renowned German astronomer Johannes Kepler delved into the study of Nicolaus Copernicus’ system and meticulously analyzed the astronomical observations made by the Danish scientist Tycho Brahe. Through his research, Kepler formulated what are now known as Kepler’s Three Laws.
Tycho Brahe, who possessed exceptional observational skills, dedicated many years to compiling a comprehensive body of work on planetary observations and the study of hundreds of stars. The meticulousness of his measurements far surpassed that of any of his predecessors.
The Sun is located at one of the foci of the elliptical orbits in which the planets of the solar system move.
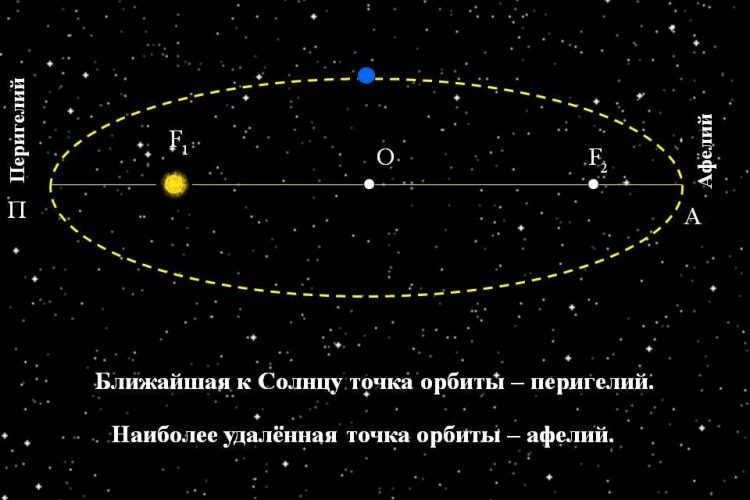
As per the initial law proposed by Kepler, each planet within our solar system adheres to a closed curve known as an ellipse. Our star is situated at one of the focal points of this curve. There exist only two focal points within the curve, and the sum of the distances from these points to any spot on the ellipse remains constant.
After extensive observations, scientists have determined that the orbits of all planets within our solar system are nearly aligned within the same plane. Some celestial bodies follow elliptical orbits that are close to being circular, while only Pluto and Mars move along more elongated paths. Therefore, Kepler’s first law has been named the law of ellipses.
Kepler’s second law, also known as the law of areas.
According to this law, the planet’s radius-vector covers equal areas during equal time intervals.
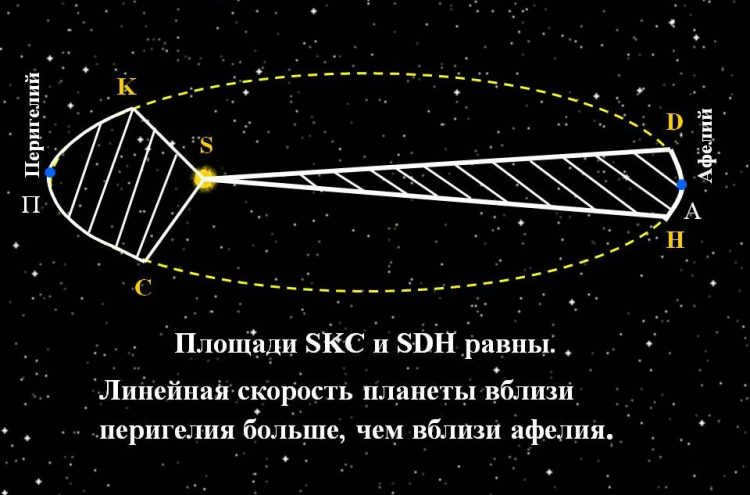
According to the second law of Kepler, each planet orbits in a plane that passes through the center of the Sun. Additionally, the radius-vector connecting the Sun and the planet sweeps out equal areas in equal amounts of time. This means that the celestial bodies move around the Sun in an uneven manner, with the highest velocity occurring at perihelion and the lowest velocity at aphelion.
We can observe this phenomenon in the Earth’s motion. Every year in early January, as the Earth reaches perihelion, its speed increases. As a result, the Sun appears to move faster along the ecliptic compared to other times of the year. In early July, the Earth reaches aphelion, causing the Sun to move more slowly along the ecliptic.
The relationship between the squares of the orbital periods of the planets and the cubes of the major semi-axes of their orbits is evident.
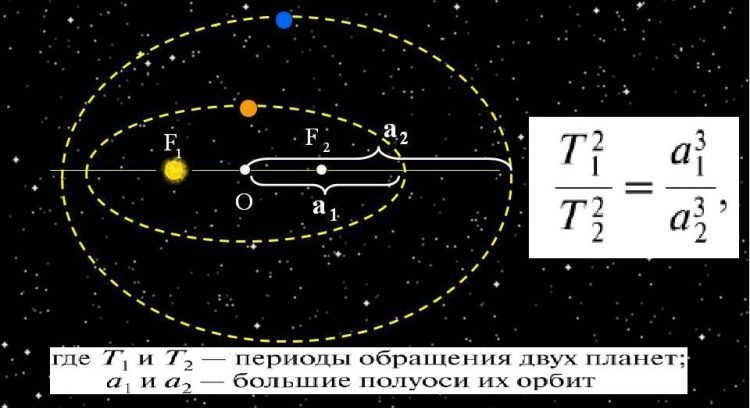
Kepler’s third law establishes a connection between the orbital period and the average distance of a planet or satellite from its central luminary. This law holds true for both planets and satellites, with an accuracy of less than 1%.
Based on this law, it is possible to calculate the length of a planet’s year (the time it takes to complete one orbit around the Sun) if its distance from the Sun is known. Conversely, the same law can be used to determine the orbit of a planet if its period of revolution is known.
Additional progress
Despite the fact that Kepler’s laws had a relatively small margin of error, they were still derived through empirical means. They lacked a theoretical basis. This issue was subsequently resolved by Isaac Newton, who in 1682 introduced the law of universal gravitation.
Kepler’s laws constituted a significant breakthrough in comprehending and explaining the movement of celestial bodies.
Video
Before the 17th century, many scientists held the belief that celestial bodies moved in a uniform manner along the circle, which was considered the “most perfect” curve.
However, Kepler challenged this prejudice and was able to determine the actual shape of planetary orbits, as well as the regularity of changes in the speed of planets as they orbited the Sun.
In his pursuit, Kepler followed the principle that “number rules the world”, a concept that originated with Pythagoras. He sought to discover relationships between the different quantities that describe planetary motion, such as the size of the orbits, the orbital period, and the speed.
Kepler conducted his research purely empirically, without any prior assumptions or biases.
When constructing the orbit of Mars, Kepler utilized his own observations of the planet, along with numerous years of calculations of the coordinates and arrangements of Mars, performed by his mentor Tycho Brahe.
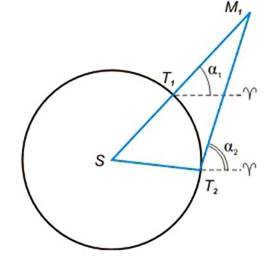
Kepler regarded the Earth’s orbit (in a preliminary approximation) as a circle, which aligned with the observed data.
We need to determine the angular distance of Mars from the vernal equinox during one of the planet’s oppositions (α1), where T1 and M1 represent the orbital positions of Earth and Mars.
After 687 days (the period of Mars’ orbit around the Sun), the planet will return to the same position in its orbit. At this point, the Earth is at T2 and the angle α2 represents the direct ascent of Mars.
By repeating similar calculations for multiple oppositions of Mars, Kepler obtained several data points. By plotting a smooth curve through these points, he was able to construct the orbit of the planet.
Kepler approximated the orbit of the Earth as a circle, which aligned with observations.
When constructing the path of Mars, Kepler was confronted with a decision between two possibilities:
1) Assuming that Mars’ orbit is a circle, and that in certain parts of the orbit, the calculated coordinates of the planet deviate from observations (due to observational errors) by 8′.
2) Assuming that the observations are error-free and that the orbit is not a circle.
Kepler, having confidence in the accuracy of Tycho Brahe’s observations, opted for the second solution.
Kepler discovered that Mars’ orbit is not a circle but rather a curve known as an ellipse, and that the Sun is not located at the center of the ellipse.
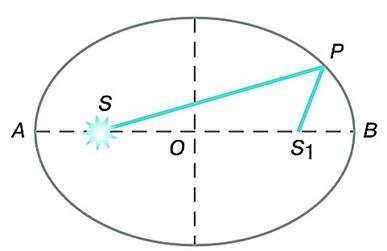An ellipsis is a curve where the sum of the distances from any point to its focal points remains constant.
Each celestial body revolves around the Sun in an ellipsis, with the Sun located at one of its focal points.
An illustration of Kepler’s first law using the motion of Earth’s satellites as an example.
The semi-major axis represents the magnitude of the planet’s orbit.
Perihelion is the point in the orbit closest to the Sun.
Aphelion is the point in the orbit that is farthest from the Sun.
The radius vector of a planet describes equal areas in equal time periods.
According to the principle of energy conservation, the total amount of mechanical energy in a closed system, where gravitational forces are present between bodies, remains constant throughout the motion of the bodies within the system. Therefore, the combined kinetic and potential energies of a planet orbiting the Sun remain constant at every point along its orbit and equal to the total energy.
As the planet gets closer to the Sun, its speed increases, leading to an increase in kinetic energy. However, the potential energy decreases due to the decreasing distance between the planet and the Sun.
The squares of the orbital periods of the planets are proportional to the cubes of the major semi-axes of their orbits.
An illustration of Kepler’s third law, using the motion of Earth’s satellites as an example.
"After 16 years of searching, I have finally found what I was looking for, and this discovery has exceeded all of my expectations. "
The third law enables us to determine the relative distances between the planets and the Sun, by utilizing the already known periods of their orbits around the Sun.
It is not required to ascertain the distance from the Sun for each planet, as measuring the distance from the Sun of at least one planet is sufficient.
The value of Earth’s orbit’s major semi-major axis, known as the astronomical unit (a.u.), serves as the foundation for calculating all other distances within the solar system.
Task. The oppositions of a certain planet recur every two years. What is the semi-major axis of its orbit?
Determine the major semi-major axis of the planet:
1. State Kepler’s laws.
2. What happens to the velocity of a planet as it moves from aphelion to perihelion?
3. When does the planet have:
– maximum kinetic energy;
– maximum potential energy?
1. Mars is 1.5 times farther from the Sun than Earth. How long is a year on Mars? Assume the orbits of the planets are circular.
2. If the synodic period of a minor planet is 500 days, what is the major semi-major axis of its orbit and the stellar period of orbit?
The principles governing the planetary motion within the solar system
Countless researchers have observed that every planet in our solar system moves in such a way that the radius vector
Kepler operated with limited knowledge, relying solely on practical experience.
Kepler observed the Earth’s movement and, despite the lack of concrete evidence, theorized that its orbit could be approximated as a circle.
By performing similar procedures for multiple other oppositions.
Kepler discovered that Mars does not follow a circular orbit, but instead moves along a curved path known as an ellipse.
Kepler’s First Law states that every planet orbits around the sun.
Aphelion, the farthest point in the orbit of the Sun.
The total energy of the Sun remains constant at all points in its orbit.
My Pursuit from 16 Years Ago
Back when I was just starting out on my scientific journey, I made a decision that would shape my entire career. I decided to investigate the concept of planetary motion and how it relates to the conservation of energy. Specifically, I wanted to explore the idea that the total energy of the Sun remains constant at all points of an orbit and is equal to the total energy of the Sun itself.
By utilizing the third law, it becomes possible for us to determine the proportional distances between the planets and the Sun.
Which arrangement of the planets is suitable for solving the problem?
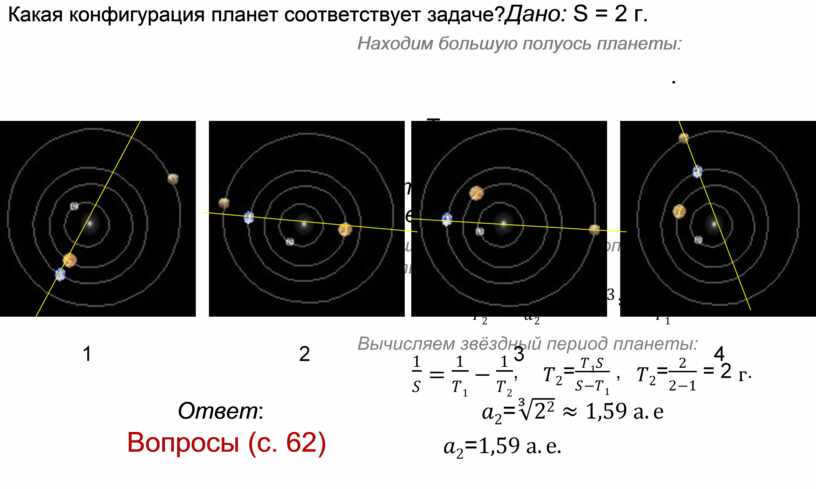
Explain Kepler’s second laws. 2
The synodic period of a minor planet is 500 days
The information presented on this page has been sourced from publicly available materials or has been submitted by users in accordance with the terms and conditions of the website. If you believe there has been a violation, please report it.
Staying on course: uniform rotational motion
If an object maintains a consistent speed while moving in a circular path, it is referred to as uniform rotational motion. Some examples of this type of motion include a race car navigating a circular track and the hands of a clock. Figure 7.1 illustrates a golf ball that is attached to a pole by a string and is moving in a circular motion. Although the ball maintains the same velocity, its direction changes continuously. Hence, this type of motion is referred to as uniform rotational motion.
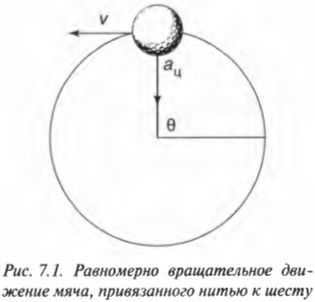
The period of the ball (or any other object) completing a full circle is known as the period, which is represented by the symbol \( T \). The period and linear velocity can be easily connected if we have information about the distance traveled, specifically the circumference of the circle (\( 2\pi r \)), and the radius (\( r \)). Therefore, the linear velocity of the ball (\( v \)) is:
and the rotation period (\( T \)) is:
Assuming the length of the thread is 1 m and the rotation period is 0.5 s, we can calculate the linear velocity of the ball by substituting the given values into one of the previous equations:
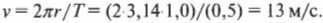
So, the sphere is in motion with a linear speed of 13 m/s!
The meaning of dwarf planets
When astronomers classified all the objects that orbit the Sun in 2006, they divided them into three categories:
The objects known as dwarf planets occupy an intermediate position. They do not have the large size and orbit of bodies like Mars or Jupiter, nor can they be classified as asteroids.
The International Astronomical Union has defined dwarf planets as celestial bodies in the shape of a sphere that revolve around the Sun. However, they have a small mass and lack gravitational dominance. They are held in their orbit by smaller celestial objects.
Kepler’s Third Law
The third principle concerning the movement of celestial objects within the solar system pertains to the notions of perihelion and aphelion. When a line is drawn between these two points, it represents the major axis of a planet’s orbital path. Consequently, the major semi-axis is equal to half of this line segment.
Kepler made observations that led him to formulate his laws. According to his findings, the ratio between the total number of revolutions around the central star for any two planets and the squared ratio of the major semi-axes of their orbital paths is always the same.
Proving and accepting Kepler’s three laws was challenging because he derived them empirically. However, in the late 17th century, Newton discovered the classical theory of gravitation. This theory supported the German astronomer’s conclusions and explained the planets’ motion around the sun in an elliptical orbit. Newton also established that, apart from an object’s mass and distance from the star, no other properties affect the gravitational attraction.
Johannes Kepler’s laws played a crucial role in determining the path of the planets, calculating their orbital period, velocity, and how these factors change as they approach or move away from the Sun. By removing the Earth from its special position in the solar system, Kepler discovered that it follows the same laws as other planets in our star system.
Retrograde motion beyond the Solar System
In recent years, advancements in technology have made it possible for scientists to observe planetary systems outside of our own solar system, as well as the disks of material surrounding them. To date, over 4,000 exoplanets have been discovered, revealing that it is common for stars to have small planets orbiting close to them, even within the orbit of Earth.
By measuring the radial velocities of stars that have known transiting planets, scientists can determine the angle between the star’s equator and the plane of the transiting planet’s orbit. This phenomenon, known as the Rossiter-McLaughlin (RM) effect, has been observed in 134 transiting planets so far.
Fluctuations in Seasons
As observed, the Earth’s orbit around the Sun is referred to as its trajectory.
One significant aspect to consider is the tilt of the Earth’s axis, which is responsible for the occurrence of all four seasons throughout the year. This tilt is at an angle of 23.4 degrees.
As a result of this tilt, astronomical science recognizes two important phenomena: the equinox and solstice.
The Earth’s axis remains fixed and unchanging, leading to variations in the distribution of solar radiation. When the northern hemisphere tilts away from the Sun, it experiences winter, while the southern hemisphere experiences summer. After six months, this pattern reverses. The winter solstice falls on December 21, and the summer solstice occurs in June. The vernal and autumnal equinoxes take place on March 20 and September 23, respectively.
The angle of inclination of the axis of rotation to the orbit is responsible for the seasonality on the planets of the solar system. When the angle is smaller, the weather on the celestial body is more stable and there are no changes in seasons. Celestial bodies with an inclination angle of more than 90° do not experience seasonality.
Objects with an axis inclination angle within 20-30 degrees undergo changes in seasons, specifically “summer” and “winter”. Mercury, despite its almost non-existent axial tilt, also experiences summer and winter due to the high eccentricity of its orbit. The temperature difference between the points at perihelion and aphelion on Mercury is 620 degrees Celsius.
Therefore, the size and form of the orbit that characterizes the object’s movement around the Sun profoundly impact the creation of temperature conditions on it. The Earth’s motion, with its low eccentricity and short distance, combined with the optimal tilt angle of its axis, ensures that its temperature is most suitable for the survival of living organisms.
The exploration of the solar system
For a considerable period, humanity firmly believed that all stars and planets orbited around the Earth. The geocentric model of the universe, with a stationary Earth at its center, was developed by the Greek scientist Ptolemy in the 2nd century BC and persisted for over fifteen centuries.
In 1453, the Polish astronomer Nicolaus Copernicus demonstrated that not only the Earth but also the other planets (known to be six at that time) revolve around the Sun. However, it wasn’t until the 17th century that the Church ceased regarding this theory as heretical and stopped persecuting its adherents.
One of these followers was the Italian monk Giordano Bruno. In 1584, he published a treatise arguing that the universe was infinite and that the Sun, like the other stars, was simply much closer to Earth. Bruno was subsequently apprehended by the Inquisition and condemned to death by burning at the stake for heresy.
Galileo Galilei, an Italian scientist, was another follower of Copernicus. He is known for inventing the first telescope, which enabled people to observe the craters on the Moon, sunspots, and discover the four moons of Jupiter. Furthermore, Galileo’s observations also led him to establish the heliocentric model, demonstrating that the planets revolve around their own axes. Unfortunately, in order to avoid facing the same fate as Giordano Bruno, Galileo was compelled to renounce his ideas.
In the 17th century, Johannes Kepler, a German astronomer, made significant discoveries regarding the motion of planets. He formulated the laws that connected a planet’s speed of rotation with its distance from the Sun. These groundbreaking ideas were later expanded upon by the renowned English physicist, Isaac Newton, who developed the theory of universal gravitation.
During the 18th and 19th centuries, advancements in optics led to the development of more advanced telescopes, which enabled scientists to gain a deeper understanding of the solar system. As a result of these advancements, the planets Uranus and Neptune were discovered.
In 1951, the Soviet Union successfully launched the first artificial satellite into orbit around the Earth, marking the beginning of the Space Age and the start of practical exploration of the solar system.
In 1961, Yuri Gagarin became the first person to venture into space, and in 1969, the Apollo 11 spacecraft transported astronauts to the Moon.
During the 1970s, there was a significant exploration of Mars, Venus, and Mercury by both the Soviet Union and the United States. Additionally, the Voyager 1 and Voyager 2 spacecraft, launched in the 1980s, provided valuable data on Jupiter, Saturn, Uranus, Neptune, and their satellites. The launch of the Hubble Space Telescope in 1990 also played a crucial role in studying our solar system.
In the present decade, various space agencies from around the world are planning a manned mission to Mars. This expedition to another planet will undoubtedly be a monumental event in the history of solar system exploration. However, it’s important to note that humanity is still in the early stages of its journey into space.
The celestial paths of stars
Star formations seem stationary in the celestial sphere from the perspective of human eyesight. This is due to their immense distances from Earth, which cause imperceptible movement. In actuality, stars revolve around the central point of their galaxy.
Stars that have a retrograde orbit compared to the overall rotation of a disk galaxy are more likely to be located in the galactic halo rather than the galactic disk. The outer halo of the Milky Way contains numerous globular clusters that exhibit retrograde orbits or have no rotation. The structure of the halo is currently a topic of debate, with some studies suggesting the existence of two distinct components. These studies propose the presence of a “double” halo, consisting of an inner component with a higher metallicity and direct rotation (stars orbiting the galaxy similar to the disk rotation), and an outer component with lower metallicity and retrograde rotation (rotating opposite to the disk). However, these findings have been contested by other studies that argue against this duality. These studies argue that the observational data can be explained without the need for a duality, by employing improved statistical analysis techniques and accounting for measurement uncertainties.
The Kapteyn star, located nearby, is believed to have obtained its high-speed retrograde orbit around the galaxy by becoming separated from a dwarf galaxy that merged with the Milky Way.
The movement of objects in outer space
By understanding the concept of an orbit and its possibilities, scientists have been able to explain the paths taken by various celestial bodies. Comets, satellites, planets, and stars usually follow elongated trajectories. For instance, there are comets with highly elongated paths that can intersect with a planet’s orbit. If the planet and the comet align at a certain point, a collision may occur or the comet’s orbit may be altered, trapping it within the planet’s gravitational pull. It is believed that this is how some planets acquired rings of comets and satellites.
The principles governing the motion of celestial bodies
“Awesome! Physics” – available on Youtube
In the late 16th century, the Danish astronomer I. Kepler made significant discoveries regarding the movement of planets, uncovering three fundamental laws. These laws served as the basis for I. Newton’s formulation of the law of universal gravitation. Utilizing the principles of mechanics, Newton successfully tackled the two-body problem and established the laws governing the motion of one celestial body within the gravitational field of another. Consequently, he managed to derive Kepler’s three generalized laws. As a result of the gravitational force, a celestial body moves along one of the conic sections, which include the circle, ellipse, parabola, or hyperbola.
The planets revolve around the Sun in an elliptical path (Fig. 15.6). The perigee is the point in the orbit closest to the Sun, while the apogee is the point farthest from it. The radius vector is the line that connects any point on the ellipse to the focus.
Both comets and asteroids also follow elliptical orbits. A circle has an eccentricity (e) of 0, while an ellipse has an eccentricity between 0 and 1.
The motion of natural and artificial satellites around planets, as well as the motion of one star around another in a double system, also adhere to this first generalized law of Kepler.
Each planet moves in a way that the radius vector of the planet covers equal areas in equal time intervals.
A planet travels from point A to point A’ and from point B to point B’ in the same amount of time.
The constant value is obtained by dividing the cube of the major semi-axis of a body’s orbit by the square of its orbit period and the sum of the masses of the bodies.
If T represents the period of revolution for one body orbiting another body at an average distance a, Kepler’s third generalized law can be expressed as:
where M1 and M2 are the masses of the attracting bodies, and G is the gravitational constant. In the case of the solar system, the mass of the Sun is equal to the mass of any planet, resulting in:
For all bodies in the solar system, the right-hand side of the equation remains constant, as stated by Kepler’s third law, which was derived from scientific observations.
The movement of celestial bodies, including the planets, around the Sun is governed by the force of gravity and follows Kepler’s three laws. These laws provide a framework for calculating the positions of planets and determining their masses based on the orbit of their satellites.
For more information on the Earth-Moon system, please visit the next page. To explore other topics in astronomy, you can go back to the “Astronomy – notes” section.
These notes on astronomy are specifically designed for Grade 11 students and are based on the textbook “Physics-11” by Myakishev, Bukhovtsev, and Charugin. They are intended to supplement the class’s physics curriculum.
Observable movements of celestial objects – Principles governing the motion of planets – The relationship between Earth and the Moon – The physical properties of planets and other small objects in the solar system – The Sun – Key features of stars – The internal composition of the Sun and stars in the main sequence. The progression of stars – The Milky Way – Our galaxy – Galaxies – The structure and development of the Universe – A brief overview of the solar system and the structure of the Universe
The Astrophysical Characteristics of the Milky Way
When attempting to comprehend the cosmic scale of the Milky Way, one must compare it to other parts of the Universe. Our galaxy belongs to a subgroup within the larger Local Group. In close proximity to our cosmic metropolis are the Andromeda and Triangle galaxies, along with over 40 smaller galaxies. The Local Group itself is just a component of the even larger Virgo supergroup. However, some argue that these estimations are merely rough approximations of the Milky Way’s actual location. The size of these formations is so vast that it is nearly impossible to fully visualize. Currently, we have knowledge of the distances to our nearest neighboring galaxies, but many other objects in deep space remain beyond our perception. Their existence is only allowed by theoretical and mathematical calculations.
Our galaxy is classified as a spiral galaxy with a SBbc junction according to star maps. The Milky Way’s galactic disk has a diameter of approximately 50-90 thousand light years or 30 thousand parsecs. To put it into perspective, the Andromeda galaxy’s radius on the universal scale is 110 thousand light years, making it significantly larger than our own galaxy. The nearby dwarf galaxies are much smaller in size compared to the Milky Way. For example, the Magellanic clouds have a diameter of only 7-10 thousand light years. Within this massive stellar system, there are an estimated 200-400 billion stars, which are organized into clusters and nebulae. One of the Milky Way’s arms contains our solar system.
Dark matter makes up the majority of the contents in interstellar space, while cosmic gas and bubbles fill the rest. As you approach the center of the galaxy, the number of stars increases and outer space becomes more compressed. Our Sun resides in a region of space that consists of smaller cosmic objects, spread out and separated.
The Milky Way is incredibly massive, weighing in at 6×10^42 kilograms, which is trillions of times the mass of our Sun. The majority of the stars in our galaxy are concentrated in a single disk, estimated to be around 1000 light-years thick. Determining the exact mass of our galaxy is challenging, as much of the visible spectrum of stars is obscured by the Milky Way’s arms. Additionally, the mass of the dark matter that fills the vast interstellar spaces remains unknown.
The core of the galaxy spans 1000 parsecs and comprises a central region with a captivating configuration. The core takes the shape of a bulge, where the largest stars and a cluster of luminous gases are concentrated. It is within this area that a tremendous amount of energy is emitted, surpassing the combined output of the billions of stars that populate the galaxy. This segment of the core is the most vibrant and brilliant section of the galaxy. Encircling the core is a bridge that marks the beginning of the galaxy’s arms. This bridge forms as a result of the immense gravitational force generated by the galaxy’s rapid rotation.
It seems paradoxical to consider that in the heart of the Milky Way, scientists long struggled to comprehend its true nature. However, it has been discovered that a supermassive black hole, with a diameter of approximately 140 km, resides at the very core of this stellar realm. Within this boundless abyss, stars disintegrate and perish, while the majority of the galactic nucleus’ energy is consumed. This revelation reveals that the existence of a black hole within the Milky Way’s center signifies the eventual culmination of all universal formation processes. Ultimately, matter will transform into antimatter, and the cycle will repeat anew. As for the behavior of this colossal entity in the coming millions and billions of years, the black abyss remains silent, signifying that the processes of matter absorption are only gathering momentum.
Earth’s Non-Circular Path
Contrary to popular belief, the Earth does not follow a perfectly circular path in its orbit. Instead, our planet travels along an elongated ellipse. This phenomenon was first explained by the renowned astronomer Johannes Kepler. To better understand the Earth’s orbital motion, refer to the accompanying diagram.
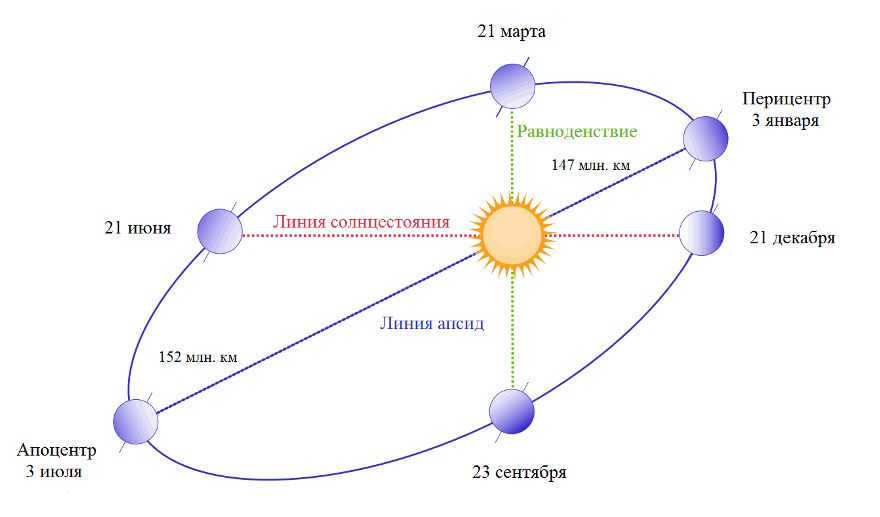
The scientist conducted measurements of the Earth and Mars orbits and made an observation that they undergo periodic changes in speed, alternating between acceleration and deceleration. This observation corresponds to the occurrence of aphelion and perihelion, which are points in the orbit where the distance from the star is determined by the orbital velocity (rather than a perfectly circular orbit).
In order to describe the shape of elliptical orbits, scientists utilize the concept of eccentricity, which ranges from 0 to 1. When eccentricity is close to 0, the orbit is nearly circular. The Earth, for example, has an eccentricity of 0.02, indicating that its orbit is very close to being circular.
Aspirants vying for the designation of dwarf planets
Entities that come close to meeting the criteria for being classified as dwarf planets can be considered contenders for this title. Among these contenders is Sedna, which some astronomers have already classified as a “dwarf” planet. These astronomers argue that Sedna possesses sufficient mass and brightness to assume a spherical shape. However, the International Astronomical Union (IAU) has yet to fully endorse this classification. The main objection is that Sedna has not “cleared” its orbit of other celestial bodies.
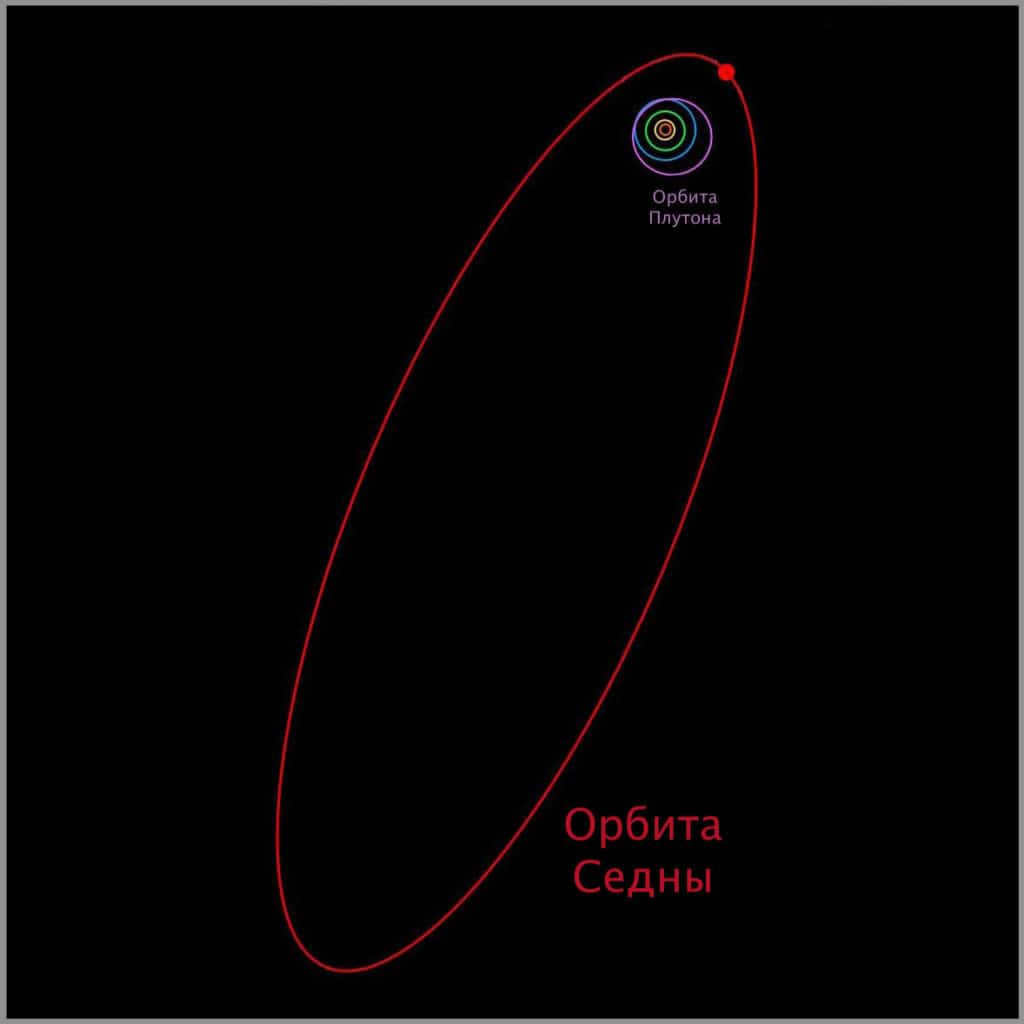
The orbit of Sedna
Possible candidates include Ork (90482), a massive celestial object found in the Kuiper belt. Its orbit closely resembles that of Pluto. Ork consistently maintains a position directly opposite to Pluto. It possesses a luminous exterior adorned with ice crystals comprising of methane and ammonia compounds.
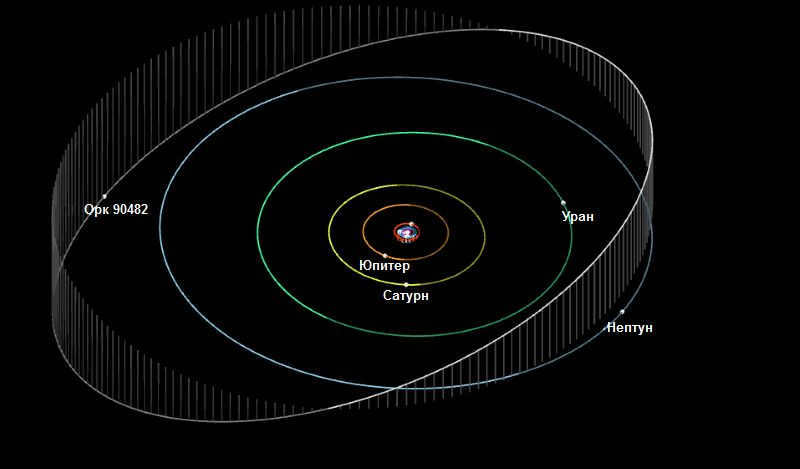
The orbit of Ork 90482 is in relation to the movement of the planets within the solar system.
There are currently over 250 celestial bodies that have the potential to be recognized as independent objects. The majority of these bodies are currently unnamed. In order to be classified as dwarf planets, they must possess all the necessary characteristics.
§ 54. Visible motion of planets
Anything that goes beyond geometry is incomprehensible to us. – B. Pascal
How can we chart the paths of the planets in the solar system from both a geocentric and heliocentric perspective? Why do the planets appear to move in a looping pattern on the celestial sphere? What factors determine the angular size of a planet’s loop? How did Copernicus calculate the relative distances between the planets and the Sun?
Lesson on Practicing
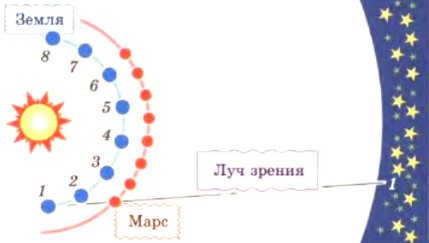
The movement of each planet is so unique that it can be compared to the radius vector. These celestial objects have been observed and documented throughout history. One such observation is depicted in this engraving from Hevelius’ treatise “Selenography, or Description of the Moon.”
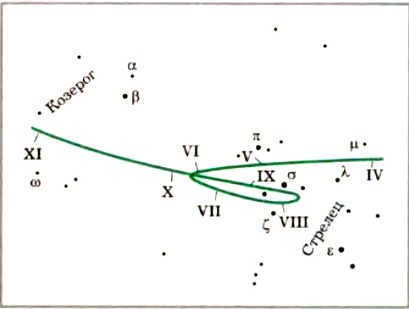
The trajectory of Mars in orbit
OBJECTIVE. Gain knowledge in constructing trajectories of celestial bodies in various reference systems.
WORK PLAN. Analyze observational data to determine the relationship between a planet’s distance from the Sun and its orbital speed. Create a visual representation of Mars’ apparent motion on the celestial sphere.
- What is the correlation between a planet’s linear velocity in orbit and its distance from the Sun?
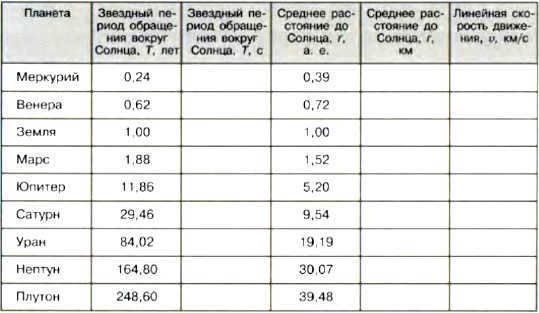
- Approximate the linear speed of planetary motion around the Sun. Draw a conclusion about the relationship between a planet’s distance from the Sun and its orbital speed. Complete the table.
PRO TIP. The velocity can be determined by using the formula V = 2πr/T, where V represents velocity, r is the radius of the circle, and T is the period. To obtain accurate results, it is important to convert distances into kilometers and periods into seconds before performing the calculation.
2. Create a geometric representation of the retrograde motion of Mars on the celestial sphere, taking into account the perspective of an observer on Earth, considering that the planets revolve around the Sun (according to Copernicus).
- Why does the planet on the celestial sphere appear to trace an inverted loop instead of simply moving back and forth, as depicted in our previous illustration for task 2?
- What factors determine the angular size of the apparent loop of planetary motion? To answer this question, create a loop representing the apparent motion of Saturn as observed from Earth and compare it to the angular size of Mars’ retrograde loop.
TIP. In order to accomplish this, you can create a diagram that illustrates the Sun’s position, the Earth’s circular orbit, and the orbit of Mars. According to the provided data, Mars is located at a distance 1.5 times greater than the Earth’s distance from the Sun. When the Earth overtakes an outer planet like Mars in its motion, or when an inner planet like Venus overtakes Earth in its orbital motion, it appears as though the planet is describing a loop. Plot the orbits of Earth and Mars close to this position, and mark several points along their trajectories – 1, 2, …, 8 – which correspond to the eight positions of the planets. Keep in mind that Mars moves slower than Earth by a factor of approximately 1.2. Also, mark the sphere of fixed stars and depict the series of visible positions of the planets from the perspective of an observer on Earth (1, 2…..8). To do this, use a straight line (known as the ray of vision) to connect the corresponding positions of Earth and Mars at specific times (1, 2,…, 8).
