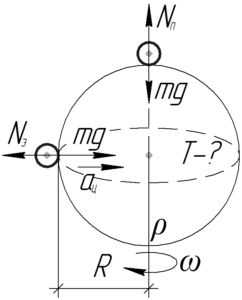
On a certain planet, bodies at the equator have half the weight compared to the poles. The density of the planet’s substance is 3000 kg/m3. Calculate the rotation period of the planet around its own axis.
Problem № 2.5.16 from “Collection of problems for preparation for entrance exams in physics UGNTU”
Given:
Solving the problem:
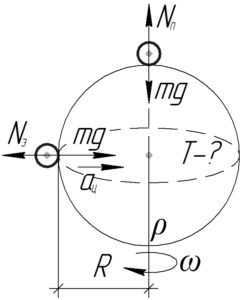
The planet’s equator has a rotating body on a circle of radius \(R\), so we can express Newton’s second law as follows:
The planet’s pole has a rotating body around its own axis, with the planet’s axis of rotation passing through its center of mass. Newton’s first law for this body can be stated as:
According to Newton’s third law, the force of the support reaction is equal to the weight of the body, so \(N_e=P_e\) and \(N_p=P_p\). Rewriting the equations we obtained previously, we get the following system:
Dividing the first equation by the second equation and considering \(P_e=\fracP_n\), we have:
The formula for finding the free-fall acceleration \(g\) on the planet’s surface is:
The planet’s mass can be calculated by multiplying its average density and volume:
The volume of a spherical planet can be determined using a mathematical formula:
The centripetal acceleration au depends on the angular velocity ω and the radius R.
The angular velocity ω is related to the period T by the following formula:
Let’s substitute equations (2) and (3) into the previously derived equation (1):
Answer: 161.7 min.
If you are having trouble understanding the solution and have any questions or if you have found a mistake, please don’t hesitate to leave a comment below.
Density is a physical measurement that compares the mass of an object to the amount of space it takes up.
The density of planet Earth is 5500 kg/m3.
You can use an online density calculator (if you know the mass and volume) to determine density.
Density data is important in both scientific and practical applications.
– performing calculations for specific tasks
– assessing the impact of density on the subject of study
In design work, it is essential to support decisions with scientifically validated data.
Using density data is beneficial for performing calculations or completing tasks in applied contexts.
Calculate the density of a spherical planet given that the weight of an object at the pole is double the weight at the equator
Calculate the density of a spherical planet given that the weight of an object at the pole is two times greater than at the equator. The planet has a rotational period of 2 hours and 40 minutes.
Problem №2.5.15 from “Collection of problems for preparation for entrance exams in physics UGNTU”
Problem Solution:
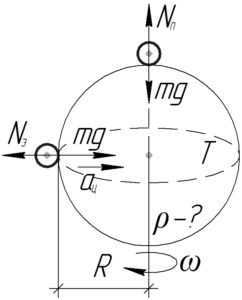
A celestial object positioned on the equator rotates alongside the planet on a circular path with a radius of (R) which represents the radius of the planet. To solve this problem, let us utilize Newton’s second law:
At the planet’s pole, the celestial object is situated on the rotation axis, resulting in it rotating solely around itself. Newton’s first law of motion for this object can be expressed as:
According to Newton’s third law of motion, the supportive reaction forces (N_e and N_n) are equivalent to the gravitational force acting on the object (P_e and P_n, correspondingly). It is important to note that while these forces possess equal magnitudes, they act in opposite directions and are exerted on different objects. Taking this into account, we can express equations (1) and (2) in the following system:
Dividing the upper equality by the lower one gives us:
Since we need to find the average density of the planet ρ, let’s write down the following formulas: firstly, the formula for finding the acceleration due to gravity g on the planet’s surface, secondly, the formula for finding mass using density and volume, and thirdly, the formula for finding the volume of a sphere.
Substituting equation (6) into equation (5), and the result obtained in equation (4), we get:
To express the centripetal acceleration au in terms of the planet’s rotation period T, let’s write down the following formulas: the formula for finding the acceleration au using angular velocity ω, and the formula for relating the latter to the rotation period T.
By substituting expressions (7) and (8) into the previously derived equation (3), we can simplify it:
To convert the given rotation period \(\Theta\) into the SI system (in seconds):
\(\Theta = 2h40min = 2 \cdot 3600 + 40 \cdot 60\) s = 9600 s.
Answer: 3.07 g/cm 3 .
If you have any questions about the solution or if you find any mistakes, please feel free to leave a comment below.

Planets in the Solar System. Authors and rights: CC0 Public Domain.
It is a well-known fact that the size of the planets in the solar system varies greatly.
For instance, the inner planets of our system are smaller but denser compared to the gas or ice giants located in the outer part of the solar system. Additionally, there are cases where planets can be smaller than certain satellites. However, the size of a planet does not necessarily correspond to its mass.
We appreciate your interest in the website!
You have the option to support the Universe Today project in any way that is convenient for you:
5599 0020 1641 0583
9112 3930 4027 6490
Z215342785781
Although Mercury is smaller in size compared to Ganymede, Jupiter’s satellite, or Titan, Saturn’s satellite, it is more than twice as massive as these satellites. Additionally, while Jupiter is 318 times more massive than Earth, its radius is only 11.21 times that of Earth.
Now, let’s examine each planet individually and observe their unique characteristics.
Mercury
Mercury, the smallest planet in the solar system, has an average diameter of 4,879 kilometers (3,031.67 miles). It is also the second most dense planet, with a density of 5.427 g/cm3, second only to Earth.
Similar to other terrestrial planets, Mercury is composed of silicate rocks and minerals, with a large iron core that is disproportionately large compared to its crust and mantle. The planet’s mass is approximately 0.330*1024 kg, which is equivalent to 0.055 times the mass of Earth. The gravitational force on Mercury is only 3.7 m/s2.

Mercury. The credit for the image goes to NASA / Johns Hopkins University Applied Physics Laboratory / Carnegie Institution of Washington.
Venus
Venus, also known as “Earth’s twin” due to its similar composition, size, and mass, possesses a density of 5.243 g/cm3. It is positioned as the second planet from the Sun, with an average radius of approximately 6050 kilometers (3759.3 miles). Consequently, the planet’s mass amounts to 4.87*1024 kg, which is equivalent to 0.815 times the mass of Earth. Considering its density and size, Venus has a gravitational force comparable to that of Earth, measuring around 8.87 m/s2.

This is a real image of Venus, captured by the Mariner probe. The original photos are freely available to the public. Credits: NASA / Ricardo Nunes.
About Earth
Similar to other planets in the inner solar system, Earth is primarily made up of metals and silicates. It has an average radius of 6,371 kilometers (3,958 miles) and an average density of 5.514 g/m 3 , making it the largest and most dense planet in the Earth group. The Earth’s mass is approximately 5.97*10 24 kg, and its gravitational force is commonly known to be 9.8 m/s 2 .
To put it briefly, Mars has a weight of 0.642*10 24 kg, which is equivalent to approximately 0.11 times the mass of Earth. Considering its dimensions and density (which is 3.9335 g/cm 3), the gravitational pull on Mars is not more than 3.8 m/s 2.

The Mars rover Curiosity captured this self-portrait on January 23, 2018, while exploring the slopes of Mount Sharp. The credits for the image go to NASA JPL-Caltech.
Jupiter
Jupiter, the largest planet in our solar system, has a diameter of 142,984 kilometers. In fact, it’s so big that it could easily contain all the other planets in our system, except for Saturn. But what’s even more impressive is its mass. With a weight of 1,898 * 10^24 kilograms, Jupiter is about 2.5 times more massive than all the other planets combined. Despite its size, Jupiter has a lower overall density compared to the terrestrial planets. Its average density is 1.326 g/cm^3.
Saturn
Saturn is the second largest gas giant in our solar system. It has an average diameter of 120536 kilometers, making it just a bit smaller than Jupiter. However, it is not as heavy as Jupiter. Its mass is about 569*10 24 kg, which is 95 times greater than the mass of Earth. Despite its size, Saturn has a density of only 0.687 g/cm 3 , which is lower than that of water (1 g/cm 3 ). This makes it the only planet in our solar system with a lower density than water.

The clouds of Saturn, which are captured in this image taken by NASA’s Cassini spacecraft, exhibit a mesmerizing beauty.
With an average diameter of 120,536 kilometers, Uranus ranks as the third largest planet in our solar system. It has a mass of 86.8*10 24 kilograms, making it the fourth most massive planet. As a result, its average density stands at 1.271 g/cm 3 .
Neptune
Neptune has a diameter of 49528 kilometers, making it about four times larger than Earth. Its mass is 102*10 24 kg, and as a result, its density is greater than that of any other gas giants, measuring 1.638 g/cm 3.
From the information above, it is evident that the planets in the solar system have a significant variation in mass. However, when considering density, size is not always directly proportional. In other words, some planets may be only a few times larger than others, yet they can still be significantly more massive.
Did you find this information interesting? Share it with your friends:

Introducing Zhurong, China’s Mars rover

Scientists detect peculiar reduction in brightness of a recently-formed celestial object

Universe could be 1.2 billion years younger
Comments 4
Astronomers have discovered an intriguing revelation: they determine the dimensions of rocky planets (such as Mars, Earth, Venus, and Mercury) and the moons of Jupiter and Saturn based on the solid aggregate phase of matter, disregarding the extent of the atmosphere surrounding these planets and the satellites of large gas giants. However, the dimensions of gas giants are measured based on the boundaries of the outer clouds in their atmospheres. Similarly, the sizes of stars, including the Sun, are measured based on the visible outer boundary of their photospheres-atmospheres.
In 1927, Abbot Georges Lemaître proposed the idea of the universe’s creation through a single super big Big Bang event, which occurred approximately 14 billion years ago. This event marked the birth of all matter, energy, and the primary volume of space vacuum and ether in the universe, originating from nothing.
However, it is now understood that the universe has always existed and will continue to exist. This is due to its self-sufficiency, maintained by the inherent processes that sustain its existence. These processes operate with an efficiency coefficient of 1.000000000000000000000000000000000000069 per second, known as the Hubble Volume-Mass Constant.
The increase in the observed volume of space by astronomers serves as evidence supporting this concept. This phenomenon is quantified by Hubble’s Linear Constant, which measures a rate of 2.3*10-18 per second, equivalent to 1.0000000000000000000000000000023 per second.
Approximately 4.155 million new neutrons are generated per gram of substance every second. The vast majority of these neutrons are absorbed into the nuclei of atoms that make up various isotopes of different elements…
A comparison chart illustrating the masses of the planets in our solar system reveals that Jupiter accounts for 71% of the total mass, while Saturn contributes 21%. In contrast, the terrestrial group of planets has a negligible mass, with Mercury’s mass measuring a mere 0.1% – too small to be visible on this scale.
The density of an object can be calculated by dividing its mass by its volume. Density is typically measured in units like pounds per cubic foot, grams per cubic centimeter, or kilograms per cubic meter. To determine the density of a planet, you need to consider its mass and radius. The radius is the distance from the surface to the center of the planet. Since planets are roughly spherical, you can calculate the volume of the sphere using the radius. Then, divide the mass of the planet by the volume of the sphere to obtain its density.
To find the mass and diameter of a planet, you will need to perform additional measurements or research.
Input the radius into the calculator. Multiply it by 1,000 to convert kilometers into meters. To cube this value, press the “x ^ 3” button. Alternatively, you can press the “x ^ y” button, enter the number three, and then press “equals”. Multiply the result by the value of pi – or 3.1416 – then multiply it by four, and finally divide by three. Save the final answer by pressing the “M+” button or any other memory key. The displayed figure represents the volume of the planet in cubic meters. Continuing with the given example, 6300 km times 1000 meters/km equals 6300000 meters. Cubing this value yields 250,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000. Multiplying it by a factor of 4/3 results in 1,047,400,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 cubic meters.
Input the planet’s mass into the calculator. Divide by the volume value stored in the calculator’s memory. Press the equals key. The result will be the density of the planet in kilograms per cubic meter.
hints
How to determine the density of a floating object

By dropping a pound of feathers and a pound of lead from the second story, we can observe that one object falls to the ground, while the other falls much faster and could potentially harm pedestrians. This discrepancy in their falling speeds can be attributed to a characteristic of matter known as “density.” One method of measuring density is through the displacement of water.
Methods for determining the density of gasoline

To determine the density of gasoline or diesel fuel, you can make calculations or take measurements using mass, volume, or specific gravity. One way to measure these properties is by using an areometer. It is important to understand the distinctions between various liquids, such as diesel and gasoline. Additionally, finding the specific gravity of gasoline is crucial. The density of diesel fuel in kg/m3 will vary depending on its intended purpose.

Measuring the density of a liquid is much simpler compared to measuring the density of a solid or gas. Obtaining the volume of a solid can be challenging, while directly measuring the mass of a gas is rarely possible. However, you can directly measure both the volume and mass of a liquid, usually simultaneously. This makes it easier to determine the density of a liquid.
Can you please provide me with a formula for calculating the average density of a planet based on its radius and the gravitational acceleration near its surface?
The density should be expressed in grams per cubic centimeter (g/cm³). I need the formula!

To compute it yourself would be quite satisfactory.
Let’s attempt to deduce the equation.
The gravitational force exerted on another object (c) by a planet with mass Mp and radius R is given by:
G is the gravitational constant 6.67 * 10^(-11) (H * m^2) / (kg^2).
The acceleration of an object is equal to the force divided by the object’s mass.
As can be observed, it does not rely on the object’s mass.
The planet’s mass can be represented as:
ρ is the desired density.
Now, we can express the density from equation (3).
In equation (4), the volume V is unknown, but it can be determined by knowing the radius.
Therefore, if the planet is a sphere (not a disc or a box), the volume of the sphere (planet) is:
By substituting the given values into equation (4), we can finally determine the result.
Let’s consider formula (5) with the radius given in meters, G as provided, and g in m/s^2. In this case, the density will be measured in kg/m^3.
However, if you want to convert it to g/cm^3, you will need to apply the appropriate conversion factors.
What is the acceleration of free fall on the surface of our planet with a radius of 200 km and an average density of 8 * 10^3 kg/m^3?
Determine the acceleration of free fall on the surface of our planet with a radius of 200 km and an average density of 8 * 10^3 kg/m^3.
What is the average density of Venus given a radius of 6100 km and an acceleration of free fall of 8.8 m/s?
Calculate the average density of Venus using the given radius of 6100 km and the acceleration of free fall of 8.8 m/s.

What is the constellation in which the small planet with a radius of 250 km and an average density of 3 g/cm3 is located?
The small planet has a radius of 250 km and an average density of 3 g/cm3.
Find the value of the gravitational acceleration g on the surface of the planet.
Discover the gravitational acceleration experienced during free fall on the surface of a celestial body with a radius measuring 200 km.
The mean mass density of the celestial body is 8 * 10 in 3 kg / m in a cube.

Can you assist me in solving physics 54?
I need help with solving the physics 54 problem.
The planet has a radius that is 10 times larger than the Earth’s radius, and the average density of the planet’s matter is 2 times lower than the average density of the Earth.
What is the ratio of the acceleration of free fall on the planet’s surface compared to the Earth’s surface?

What is the acceleration of free fall on the surface of a planet with a radius 10 times greater than that of the Earth and an average density 2 times less than that of the Earth?
Given that the radius of the planet is 10 times that of the Earth and the average density of the planet is 2 times less than that of the Earth, we need to find the acceleration of free fall on the surface of the planet.

What is the constellation in which a small planet with a spherical shape is located with a radius of R = 250 km?
The radius of a small planet in the shape of a sphere is R = 250 km.
If the absolute value of the acceleration due to gravity near the surface of the planet is g = 0.21 m/s^2, then what is the average density of the planet’s matter?

The small planet has a radius of 250 km and an average density of 3 g/cm3?
The small planet has a radius of 250 km and an average density of 3 g/cm3.
What is the value of the free fall acceleration at the surface of the planet?

What is the gravitational acceleration on the surface of the Sun, given that its radius is approximately 110 times larger than that of the Earth, and the average density of the Sun is 4 times lower than the average density of the Earth?
What is the gravitational acceleration on the surface of the Sun, considering that its radius is approximately 110 times larger than that of the Earth, and the average density of the Sun is 4 times lower than the average density of the Earth?

What is the average density of Venus and the radius of the planet?
Venus has an average density of 5200 kg/m³ and a radius of 6100 km.
Determine the acceleration of free fall on the surface of Venus.
This page provides the solution to the query: Could you kindly provide me with the formula for determining the average density of a planet when given its radius and the value of the gravitational acceleration near its surface?, within the field of Physics, suitable for students in grades 10 – 11. To explore different solutions, utilize the “smart search” feature: input relevant keywords to discover related questions and answers in the Physics category. By using the user-friendly interface, you can discover an answer that precisely meets your search criteria: simply click on the button located at the top of the page and rephrase your inquiry. Take note of the various responses from other users, which you can not only view but also provide comments on.

It is likely that the location is in a specific constellation at 74 degrees.

The size of the upper base of the cone doesn’t matter. On the table, there is a force mg acting on the side of the lower base, distributed over an area Sa. The only thing is to convert the area into square meters, so Sa = 4 cm² = 4 / 10000 m² = 0.0004 m². P = mg / Sa.
For the period, the weight will travel a distance equal to four amplitudes: L₀ = 4 * 3 = 12 cm or 0.12 m. Then the number of oscillations is calculated as: n = L / L₀ = 0.36 / 0.12 = 3. The answer is 3 oscillations.

The energy calculation is given by the equation Q = λ * m = 4 * 330000 = 1320000J or 1320 kJ.

The mass of 0.1 kg 100 grams of lead can be found using the formula Q = m * λ, where Q is the solution. Therefore, the mass m = Q / λ = 0.1 kg 100 grams.

The velocity is equal to 72 km/h, which is equivalent to 20 m/s. The acceleration can be calculated using the formula a = V² / R, where V is the velocity and R is the radius. Substituting the values, we get a = 20² / 500 = 0.8 m/s². The force can be calculated using the formula N = m(g – a), where m is the mass, g is the acceleration due to gravity, and a is the acceleration. Substituting the values, we get N = 500×(10 – 0.8) = 4600 N (4500 N if we take g as 9.8 m/s²).

0, 3 times m1 equals N times 0, 2. 0, 1 times N equals 0, 3 times M. m1 equals 2M. M equals 1, 2 kilograms.

The reason for this is that displacement, velocity, and acceleration are all vector quantities, which makes them more challenging to manipulate than projections.