Upon viewing this instructional video, you will acquire knowledge regarding the Earth’s form and dimensions. You will familiarize yourself with the methodology of triangulation for gauging the length of the meridian arc. Additionally, we will explore the concept of horizontal parallax and angular radius of a celestial object, and discover their utility in ascertaining the proportions of celestial bodies within the solar system and calculating the distances to these entities.

Currently, it is not possible to view or share the instructional video with students
In order to watch this and other video lessons included in the package, you will need to add it to your personal account.
Unlock amazing possibilities

Outline of the Lesson “Calculating Distances and Sizes of Celestial Bodies in the Solar System”
As you may be aware, in ancient times, scholars and intellectuals in Greece determined that our planet is not flat, but rather has a spherical shape. The concept of the Earth as a sphere floating freely and unsupported in the vastness of outer space stands as one of the most remarkable achievements of the ancient world.
One of the earliest scientific methods employed to ascertain the size of the Earth was devised by the Greek scientist Eratosthenes, who resided in Egypt. His approach was rather straightforward. Eratosthenes selected two cities – Alexandria and Siena (now known as Aswan) – situated along the same meridian on the Earth.
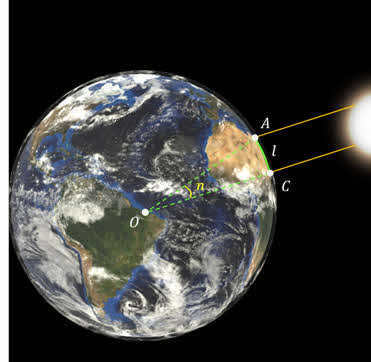
He denoted the distance between the two cities as l and its angular value in degrees as п.
Then the distance of the arc in 1 degree of the selected meridian is equal to
And the distance of the entire circumference of the meridian: L = 360 degrees ∙ l0.
On the other hand, he was aware that the length of the circumference is equal to: L = 2πR.
By setting the right sides of the last two equations equal to each other, it is simple to obtain the desired radius of the globe:
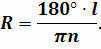
In order to determine the length of the meridian arc in degrees, it became necessary. It is obviously the difference in geographic latitudes between Alexandria and Siena. So, in order to determine this difference, Eratosthenes came up with an ingenious method. He knew that at noon on the day of the summer solstice in Siena, the Sun is directly overhead and illuminates the bottoms of the deepest wells. However, in Alexandria, the sun does not reach the zenith, so a vertically driven pole will cast a shadow. By measuring the length of this shadow, one can easily determine the desired length of the meridian arc, which for Eratosthenes was equal to 7.2 degrees.
Now, the distance between Alexandria and Siena was already known to him: it was five thousand Greek stadia.
When Eratosthenes plugged all the data into the equation for the circumference of the meridian, he obtained a measurement of 250,000 stadia.
Stadia is a unit of distance that is open to interpretation. However, it was generally understood to represent the distance that a lightly armed warrior could travel from the first appearance of sunlight at sunrise until the entire sun was above the horizon.
If we take into account that the straight-line distance between Alexandria and Aswan is approximately 844 kilometers, we can estimate that one stadia is roughly 169 meters.
Based on this, the total circumference of the meridian would be around 42,250 kilometers, which is quite impressive for that era.
Modern science has advanced techniques for accurately measuring distances on the surface of the Earth. One such method is triangulation, which relies on the phenomenon of parallactic displacement.
Parallactic displacement refers to the shift in an object’s direction as the observer moves. This phenomenon can be used to calculate distances by measuring the length of one side of a triangle, known as the base, as well as the two adjacent angles.

During the 18th century, the application of triangulation measurements in latitudes near the equator and the northern polar circle revealed that the length of the arc in the 1st meridian is not uniform and actually increases as it approaches the poles. This discovery led to the realization that our planet is not a perfectly spherical shape, and that its polar radius is approximately 21 kilometers shorter than its equatorial radius. As a result, in the field of geodesy, the Earth is considered to have a geoid shape, which means it is a body with a surface that closely resembles the surface of a calm ocean and extends beneath the continents.
Currently, the physical characteristics that commonly define the shape of the Earth are as follows:
– The polar compression is 0.0033528;
– The equatorial radius is 6378.1 km;
– The polar radius is 6356.8 km;
– The equatorial circumference is 40,075.017 kilometers.
For a long time, astronomers were puzzled by the true distance from the Earth to the Sun. It was only in the late 18th century that they were able to measure it, thanks to the determination of the Sun’s horizontal parallax. This parallax measures the apparent displacement of an object outside the Earth, with the Earth’s radius serving as the baseline.
Horizontal parallax refers to the angle at which the Earth’s radius, perpendicular to the line of sight, is observed from the celestial body.
By knowing the horizontal parallax of the celestial body, it is possible to determine its distance from the center of the Earth using trigonometric relations:
It is evident that the further the celestial body is situated, the smaller its horizontal parallax becomes. For instance, the Moon, being the Earth’s satellite, possesses the largest parallax, averaging 57ʹ. The Sun, on the other hand, possesses a significantly smaller parallax, approximately 8.794ʹʹ. This parallax corresponds to an average distance of approximately 149.6 million kilometers from the Earth to the Sun.
In one of the previous lessons, we have discussed the fact that this distance is considered as one astronomical unit in the field of astronomy. It proves to be a convenient method for measuring distances between celestial bodies within the solar system.
However, let’s return to our equation. Consequently, you must be aware from geometry that when an angle has small measurements, its sine is roughly equivalent to the angle itself, but in radians. Taking into account that one radian equals 206,265ʹʹʹ, you can effortlessly deduce a formula that is convenient for computations:
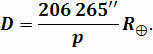
As an illustration, let’s collaborate to calculate the separation between Earth and Jupiter during the opposition if its horizontal parallax was 2.2ʹʹ. We will assume the Earth’s radius to be 6371 kilometers.

There is another way to tackle the same issue.
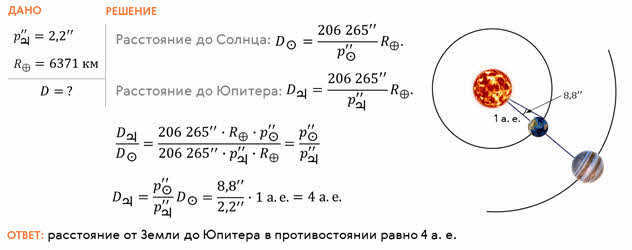
In modern times, a more precise technique called radar is used to accurately measure the distances to objects in the solar system. By calculating the time it takes for a radar signal to travel to a celestial body, bounce back, and return to Earth, scientists can determine the distance using the formula:
where c represents the speed of light in a vacuum.
As methods for determining distances to celestial bodies in the solar system have advanced, scientists have also been able to devise ways to measure their sizes. For example, when observing a celestial body from Earth, it is possible to measure the angle at which it appears to the observer, known as its angular size (or angular diameter), and subsequently calculate its angular radius.
By determining the angular radius and the distance to the luminary, we are able to compute its linear radius.
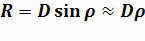
.
In this equation, it is necessary to express the angular radius in radians.
If we substitute the formula for calculating distances using the method of horizontal parallax into the given equation and simplify it, taking into account that the values of the angles ρ and р are small, we obtain a formula that allows us to determine the linear dimensions of celestial bodies:
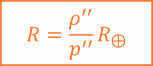
However, keep in mind that you can utilize it only when the disks of the celestial bodies are observable.
For instance, let’s tackle this particular issue together. When we observed the transit of Mercury across the Sun’s disk, we found that its angular radius is 5.5 arcseconds, and the horizontal parallax is 14.4 arcseconds. Now, what is the linear radius of Mercury?
The determination of distances to nearby celestial bodies is directly based on the phenomenon of parallactic displacement. This phenomenon occurs when a close object is observed from different vantage points and is projected onto distant objects. For example, if we hold a pencil vertically in front of a distant apartment building, we would see it against different windows with our left and right eyes. In the case of objects within the Solar System, this displacement against the background of stars becomes noticeable when observed from points that are separated by a distance similar to the radius of the Earth. For nearby stars, this displacement becomes noticeable when observed from points that are separated by a distance similar to the radius of the Earth’s orbit.
11.1 Equatorial Parallax in the Horizontal Plane
The topocentric coordinates, which are determined from various locations on the Earth’s surface, are generally different from each other. These coordinates are specific to celestial bodies within the solar system. To remove this discrepancy, all coordinates of solar system bodies are adjusted to the Earth’s center and are referred to as geocentric coordinates. The angle between the directions to a celestial body from a specific point on the Earth’s surface and from the Earth’s center is known as the daily parallax p’ (Fig. 22). This daily parallax is zero when the celestial body is at the zenith and reaches its maximum value when the celestial body is at the horizon. The maximum parallax is called the horizontal parallax p. The horizontal parallax is related to the diurnal parallax by a simple equation: (37). In this equation, the sines of the angles are approximated as the angles themselves due to their small values. Essentially, p represents the angle at which the Earth’s radius is observed from a particular celestial body. However, the Earth is not a perfect sphere and is flattened towards the poles. Consequently, the Earth’s radius varies at different latitudes, leading to different horizontal parallaxes for the same celestial body. To account for these differences, it is customary to calculate the horizontal parallax using the equatorial radius of the Earth ( R0 = 6378 km) and refer to it as the horizontal equatorial parallax p0.
11.2 Annual parallax
Annual parallax, also known as stellar parallax, is an astronomical measurement technique used to determine the distance to nearby stars. It is based on the principle of triangulation, where the apparent shift in position of a star is observed from two different points in Earth’s orbit around the Sun. By measuring this shift, astronomers can calculate the distance to the star.
The annual parallax is caused by the Earth’s motion around the Sun. As the Earth orbits the Sun, nearby stars appear to shift their positions relative to more distant stars. This shift can be measured by observing the position of a star in the sky at different times of the year.
To measure the annual parallax, astronomers use a technique called astrometry. They take precise measurements of the position of a star in the sky and compare these measurements at different times of the year. By comparing the apparent shift in position, astronomers can calculate the parallax angle and, consequently, the distance to the star.
The annual parallax method can only be used for stars within a certain range of distances. Stars that are too far away have a parallax angle that is too small to measure accurately. Conversely, stars that are too close have a parallax angle that is too large to measure accurately. Therefore, the annual parallax method is most effective for stars that are relatively nearby.
The measurement of annual parallax has been used since the 19th century to determine the distances to nearby stars. This technique has provided invaluable information about the size and scale of the universe, as well as the properties of individual stars. It continues to be an important tool in modern astronomy.
The annual parallax of a star, which is the angle at which the radius of the Earth’s orbit a is visible from the star, provided that it is perpendicular to the direction to it, is referred to as the star’s annual parallax (Fig. 23). Fig. 23. Annual parallax By using the annual parallax, similar to the horizontal equatorial parallax, it is possible to determine the distances to the stars: Instead of measuring distances to stars in kilometers, it is more convenient to use a non-standard unit called a parsec (pc), which is defined as the distance at which the parallax is equal to 1″. The name parsec is derived from the syllables “parallax” and “second”. It is worth noting that 1 pc = 206,265 astronomical units (a.u.) = 3.086 x 10^18 cm. Another unit, less commonly used, for measuring distances to stars is the light-year, which is defined as the distance traveled by light in one year (1 pc = 3.26 light-years). The distance to a star in parsecs can be determined simply by knowing the value of the annual parallax (40) Problems 60. (477) The parallax of the Sun is p0 = 8″.8, and the apparent angular radius of the Sun is . How many times is the radius of the Sun greater than the radius of the Earth? Solution: Since the parallax of the Sun is equal to the angular radius of the Earth seen from the Sun, the radius of the Sun is as many times greater than the radius of the Earth as its angular diameter is greater than its parallax 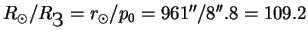 .
.
61. (482) During the highest point, the observed zenith distance of the center of the Moon ( p 0 =57′) was 50 o 00′ 00″. Adjust this observation to account for refraction and parallax effects.
| SOLUTION: As a result of refraction, the observed topocentric zenith distance is smaller than the | |
| true topocentric zenith distance, i.e. | . |
| The true topocentric zenith distance is greater than the geocentric zenith distance by the amount of | |
| daily parallax | . |
| 62. (472) What is the horizontal parallax of Jupiter when it is 6 a.u. Horizon parallax is equal to the horizontal parallax of Jupiter when it is 6 a.u. from Earth. | |
| at a distance of 6 a.u. The horizontal parallax of the Sun is p 0 =8″.8. |
63. (474) The distance between Earth and Venus is currently 40 million kilometers, with Venus having an angular diameter of 32".4. Find the linear radius of Venus. 64. (475) Given that the Moon’s p 0 is 57'02".7 and its angular radius r L is 15'32".6, compute the distance to the Moon and its linear radius in terms of Earth radii, as well as the Moon’s surface area and volume relative to those of the Earth.
| 65. | (483) The measured zenith distance of the upper boundary of the Sun is 64 o 55′ 33″, while the | ||||||
| apparent radius of the Sun | needs to be determined. Calculate the geocentric zenith distance of the Sun’s center | ||||||
| taking into account refraction and parallax. | |||||||
| 66. | By observing the annual parallaxes of the stars Vega | Sirius | , | and Deneb | , | ||
| we can calculate their distances | |||||||
12. Physical characteristics of stars and galaxies
12.1 Fundamental parameters of stars
A star possesses three fundamental characteristics: mass, radius (R*), and luminosity (L*). Luminosity represents the amount of energy emitted by a star per unit time, similar to the concept of power, and is measured in erg/sec in the GHS units commonly used in astrophysics. For the Sun, the values of these parameters are: mass – g, luminosity – erg/sec, and radius – 700,000 km. In addition to these fundamental parameters, derived quantities such as the free-fall acceleration at the star’s surface (41) and the effective temperature (Teff) determined by relation (42) are employed to describe stars.
The value represents the radiation flux emanating from the star and is defined as the amount of energy emitted by the star per unit of surface area and per unit of time (erg/(cm sec)). Regarding T eff , we can provide the following explanation: The effective temperature of a star corresponds to the temperature of a completely black body that emits the same amount of energy per unit of surface area and per unit of time as the star. The fundamental parameters of stars are often expressed in terms of solar values, such as luminosity (solar luminosities), mass (solar masses), and radius (solar radii). Therefore, it is helpful to be aware of the following relationship: (43) The radiation flux from a star at a distance d from it is (44). Consequently, a particular radiation flux aligns with the physical concept of illuminance E *. Hence, from a physics standpoint, the apparent brightness or brilliance of stars should be characterized by the luminosities they generate. Nevertheless, this approach is not particularly convenient.

At present, there are extra cumulative discounts (ranging from 2% to 25%) that can be availed by 58,742 educational establishments. To ascertain the discount applicable to all staff members of your educational institution, kindly access your personal Infoworks account.


Professional development course
Fundamentals of construction estimation
We can apply your educational institution’s discount to this offer (the amount of discount depends on the number of your colleagues who have enrolled in Infoworks courses).
Currently, there are additional cumulative discounts (ranging from 2% to 25%) available to 58,742 educational institutions. To determine the discount available for all employees of your educational institution, please log in to your personal Infoworks account.


Professional development course
Development of intellectual abilities of schoolchildren through the use of chess
We can apply your educational institution’s discount to this offer (the specific discount amount depends on how many of your colleagues have already taken Infowork courses).
Currently, we are offering additional cumulative discounts (ranging from 2% to 25%) to 58,742 educational institutions. To determine the discount available to all employees of your educational institution, please log in to your personal Infoworks account.


Visual representation of the relationship between a teacher and a student: areas of connection
Outline of the presentation broken down by individual slides:

In the field of astronomy, one of the fundamental tasks is to determine the distances and sizes of bodies in the solar system. This topic is covered in Grade 10 of the astronomy curriculum. Lesson No. 14 specifically focuses on this topic. The lesson was compiled by Sergey Viktorovich Levchenko, a physics teacher at MBOU SOSH No. 9 of Timashevsky district, in 2017.

Slide 2: What is the importance of understanding the distance between celestial bodies and ourselves?
One reason is to gain insight into the composition of the Universe.
Additionally, this knowledge allows us to study the characteristics of celestial bodies.
Furthermore, it enables us to determine the sizes of these celestial bodies.
Lastly, it aids in calculating the trajectories of spacecrafts.

3 slide The initial efforts to determine the distance to celestial objects
During a lunar eclipse, ancient astronomers compared the angular size of the Earth’s shadow with the known angular sizes of the Sun and the Moon. They discovered that the distance to the Moon was approximately 30 times the diameter of the Earth, which is in line with modern measurements.
Image “Aristarchus’ Method.” Byzantine reproduction from the 10th century

Slide 4: The initial efforts to compute the distances to celestial bodies
In the 16th century, Nicolaus Copernicus proposed a straightforward approach to determine the relative distances of the planets from the Sun (with the Earth-Sun distance serving as a reference unit).
The approach involves calculating the sine of the angle between the Earth-Sun and Earth-Object lines and using this value to determine the relative distance.
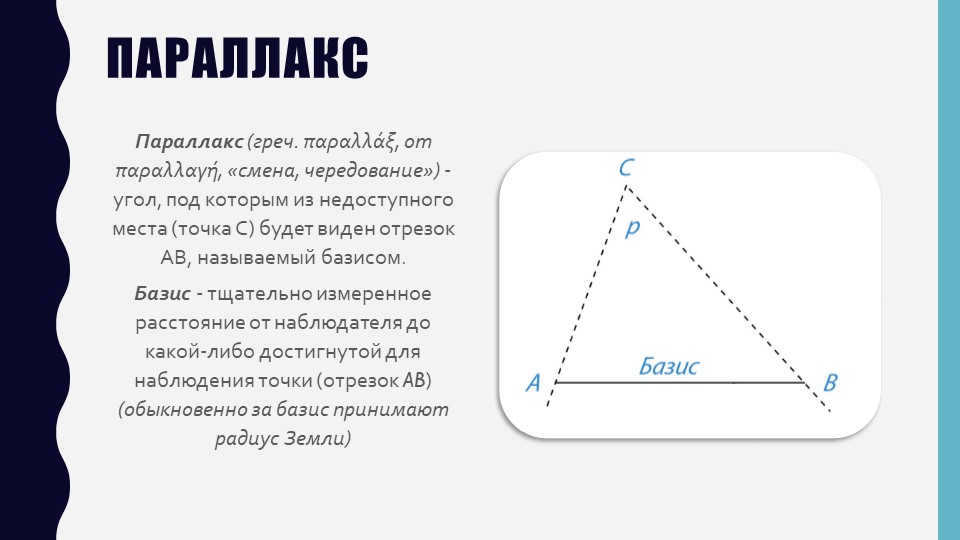
Parallax is an optical phenomenon where an object appears to change its position when viewed from different angles. It is derived from the Greek word παραλλλάξ, meaning “change, alternation”. In parallax, there is a baseline, which is the distance between the observer and a point of observation. The angle at which the baseline is seen from an inaccessible location determines the amount of parallax observed. Typically, the radius of the Earth is used as the baseline for measuring parallax.


Slide 6 Horizontal Parallax of a luminary
The horizontal parallax refers to the angle at which the radius of the Earth, perpendicular to the line of sight, is observed from a luminary.
The distance from the Earth to the Sun is approximately 150,000,000 km, which is equivalent to an astronomical unit (1 a.u.)

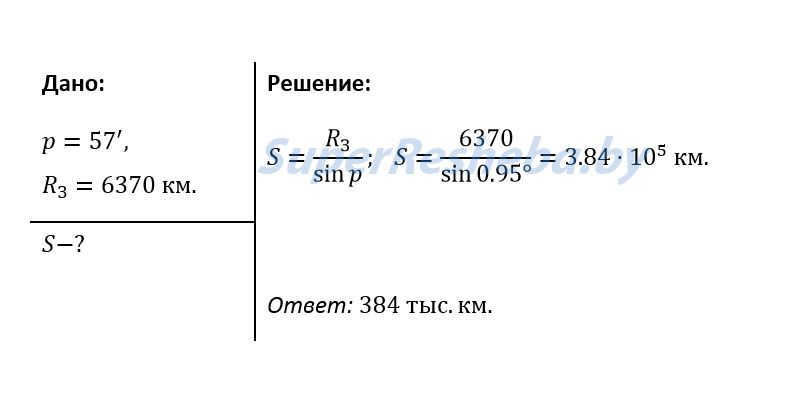
Problem 7: Find the Moon’s distance by using its horizontal parallax of p = 57′.
Solution:
S = θ * z sin ϕ
S = 6370 km * sin 0.95° = 3.84 * 10^5 km.
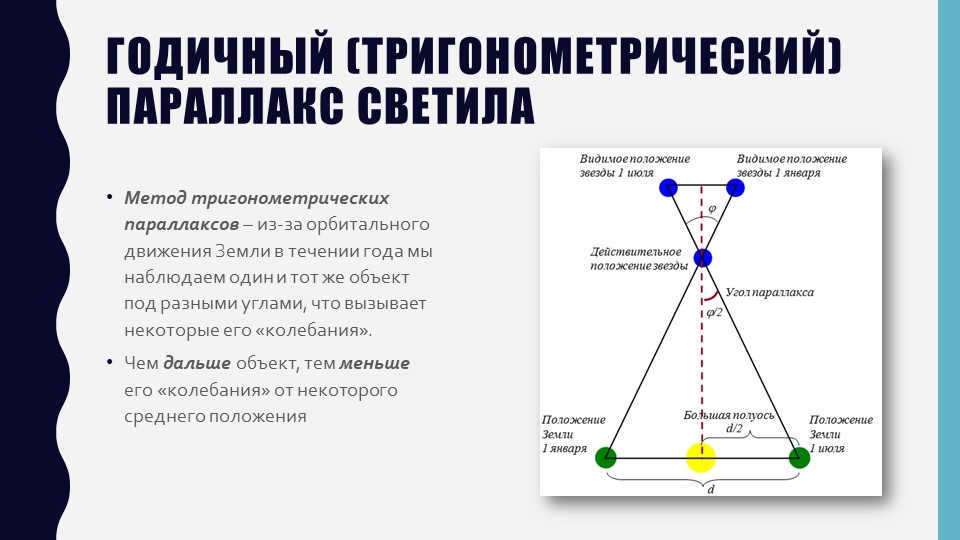
Slide 8 The Annual Trigonometric Parallax of a Star
The Trigonometric Parallax Method – due to the Earth’s orbit, we see the same star from different angles during the year, resulting in its apparent “oscillations”.
The further a star is, the less noticeable its “wobble” is from a certain average position.
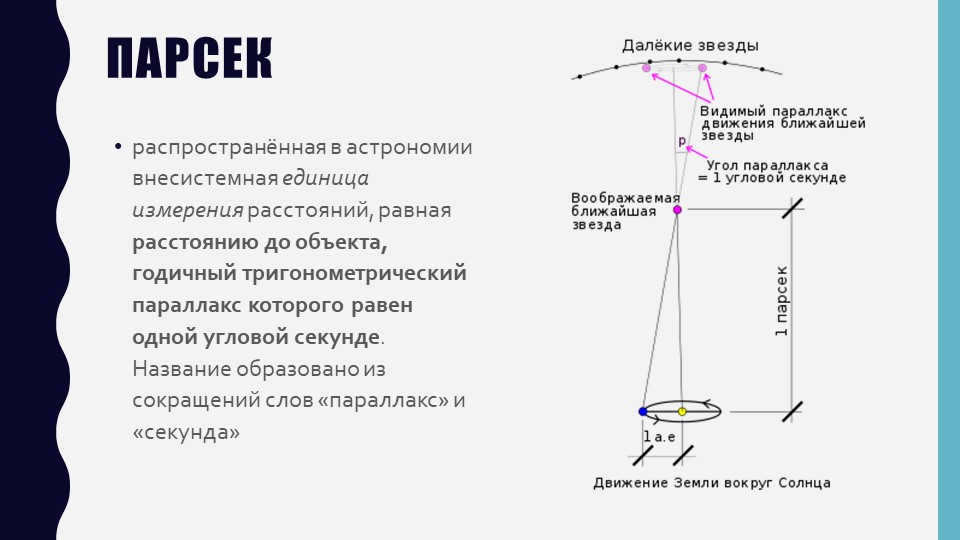

On slide 9, we have the parsec. This is a widely used unit of distance measurement in astronomy. It is defined as the distance to an object that has an annual trigonometric parallax of one arcsecond. The name “parsec” is a combination of the words “parallax” and “second”.

Slide number 10: Radar technique for measuring distances
By transmitting a short pulse, we can receive it back after it reflects off an object.
The speed of radio wave propagation in a vacuum is the same as the speed of light, which is equal to C = 299,792,458 m/s.
Based on our observations, we have determined that 1 astronomical unit (a.u.) is equal to 149,597,868 ∓0.7 km.
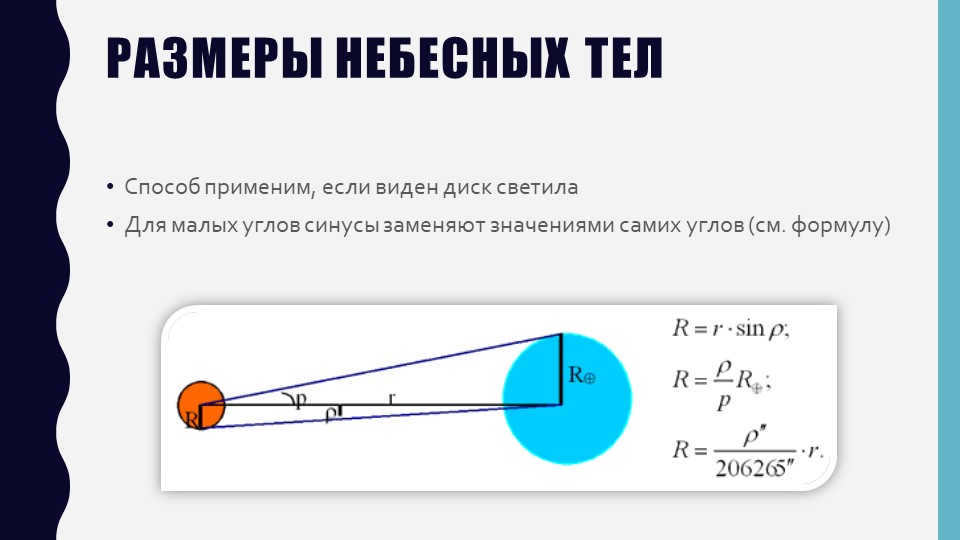
Slide number 11: Celestial bodies’ measurements
This technique works when the luminary’s disk is visible
For small angles, you can replace the sines with the actual angle values (refer to the formula)
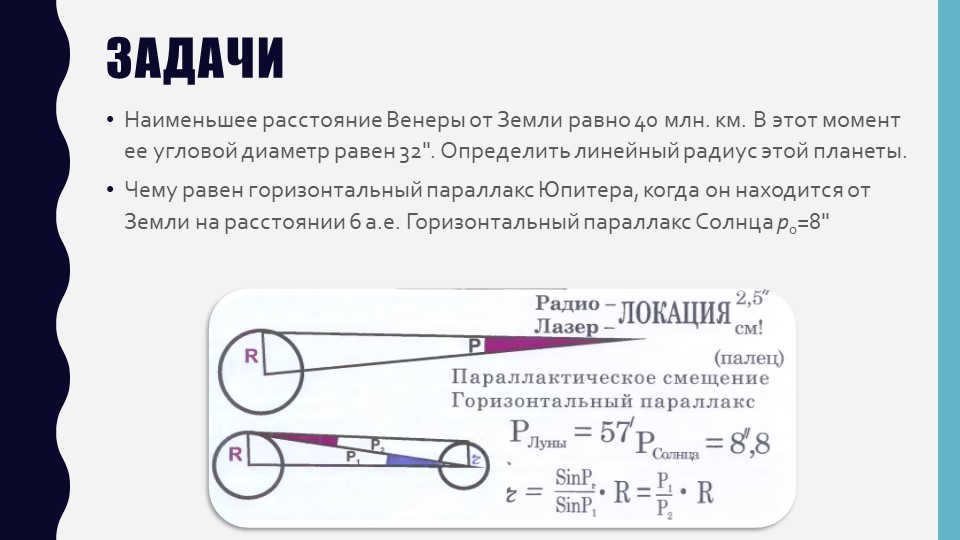
There are 12 issues with the slide.
Venus is located 40 million kilometers away from Earth at its closest point. At this distance, the planet’s angular diameter measures 32 inches. Calculate the linear radius of Venus.
If Jupiter is 6 astronomical units away from Earth, what is its horizontal parallax? The Sun has a horizontal parallax of p0=8 inches.

Summary of Lesson 13
Assigned Work
Prepare a 2-minute presentation on a method of measuring the distance to a celestial object and its dimensions that has not been studied
Section (paragraph number), inquiries
Issue: Through observations, it has been determined that the angular radius of Mars is p = 9.0″, and the horizontal parallax is p = 16.9″. Calculate the linear radius of Mars.


Slide number 14. I appreciate your attention!
The presentation includes the following materials:
The Diafilm named ‘Determination of distances to celestial bodies’ by Studio ‘Diafilm’, released in 1960.
B.A. Vorontsov-Vel’yaminov. Astronomy. 10th grade. Textbook. – M.: Drofa-Ventana
http://www.astronet.ru/db/msg/1175352/node12.html
V.F. Shatalov. Astronomy – M.: CJSC ‘Dortranspechat’, 2009.
The images used in this presentation are from open sources.
Description of the document:
This document provides a concise overview of the presentation created for a lesson about determining distances and sizes of celestial bodies in the solar system. The presentation includes various materials sourced from open sources, such as images. It can be utilized by physics and astronomy teachers as-is or as a valuable resource for developing a lesson on this topic or reviewing the material covered.
- Proof for portfolio
- Unlimited access for only 99 rubles
- Over 3,800 video lectures available for everyone
In the second half of the 18th century, scientists were finally able to determine the distance from the Earth to the Sun by measuring the horizontal parallax of the Sun. This measurement involved observing the parallactic displacement of an object located outside of the Earth, with the baseline being the radius of the Earth.
By examining the triangle OAS, we can calculate the distance OS, denoted as D:
The distance in Earth radii can be calculated using the formula provided, where R represents the radius of the Earth. By determining the magnitude of the distance, we can then convert it to kilometers.
As an object is located further away, its parallax becomes smaller. The Moon has the highest parallax, which fluctuates due to its elliptical orbit, averaging at 57′. The parallaxes of the planets and the Sun are significantly smaller. For example, the Sun has a parallax of 8.8″. This parallax corresponds to a distance of approximately 150 million kilometers to the Sun. This distance is known as one astronomical unit (1 a.e.) and is used as a unit of measurement for distances within the solar system.
It is a well-known fact that when dealing with small angles, the sine of the angle p is approximately equal to the angle itself, as long as the angle p is expressed in radians. One radian is equivalent to 206,265 arcseconds. By substituting the sine of p for p and converting the angle into radians, we can derive a formula that is more convenient for calculations.
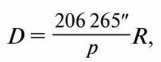
or (with enough precision)
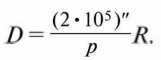
During the latter half of the 20th century, advancements in radio engineering allowed for the calculation of distances to celestial bodies within the solar system using radiolocation techniques. The Moon was the first object to be measured, followed by Venus, Mercury, Mars, and Jupiter using radar methods. By utilizing Venus radar, scientists were able to determine the value of the astronomical unit with an accuracy of approximately one kilometer. This high level of precision in distance calculations is crucial for plotting the trajectories of spacecraft that explore planets and other solar system bodies. In present times, optical localization of the Moon is made possible through the use of lasers. Distances to the lunar surface can now be measured with centimeter-level accuracy.
Astronomy 11th grade – Lesson #10 Workbook: Determining Distances and Sizes of Celestial Bodies in the Solar System
Astronomy 11th grade – Lesson #10 Workbook: Determining Distances and Sizes of Celestial Bodies in the Solar System
1. Fill in the blanks.
To calculate distances within the solar system, we utilize an astronomical unit (a.e.), which represents the average distance between the Earth and the Sun.
The distance to an object can be determined using the transit time of a radar signal with the formula , where S = 1/2-ct, where S represents the distance to the object, c is the speed of light, and t is the transit time of a luminary.
2. Define “parallax” and “baseline”; illustrate these quantities in Figure 10.1.
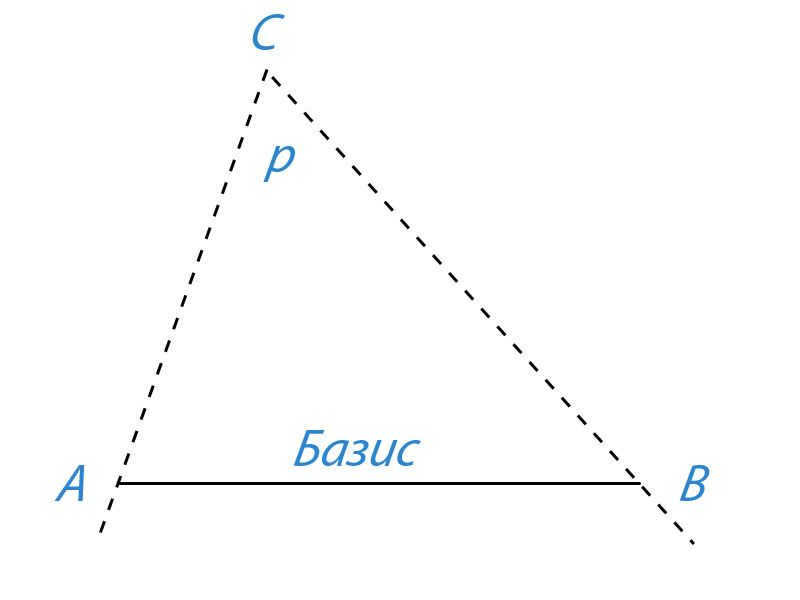
Parallax can be defined as the angle p at which the baseline, represented by segment AB, is observed from an inaccessible location (point C).
The baseline, also known as the basis, is the carefully measured distance from point A (the observer) to a specific point B, which is reached for the purpose of observation.
3. How can parallax and baseline help determine the distance to a distant object C (Fig. 10.1)?
To find the distance AC, one can utilize the magnitude of the baseline and the adjacent angles of triangle ABC. This method, known as triangulation, is commonly used for measurements on Earth.
4. The horizontal parallax p (Fig. 10.2) refers to the angle at which the radius of the Earth, perpendicular to the line of sight, is observed from the celestial body S. Calculate the following distances: a) to the Moon, given its horizontal parallax p = 57′; b) to the Sun, with a horizontal parallax p = 8.8″.
5. Enhance Figure 10.3 by including the appropriate diagrams and derive the equation that enables the calculation of the radius of a celestial luminary (in terms of Earth radii) when the angular radius p and horizontal parallax p are given.
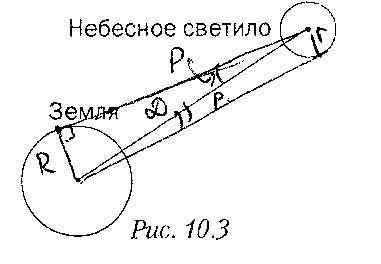
The equation to find the distance, r, from the Earth to an asteroid is given by r = D – sin(ρ). Another equation to find the distance, R, is R = D – sin(ρ)/sin(p) – R. And finally, r can also be calculated using the equation r = ρ”/p” – R.
6. Solve the following problems (when calculating, consider that c = 3 – 10 5 km/s, R3 = 6370 km).
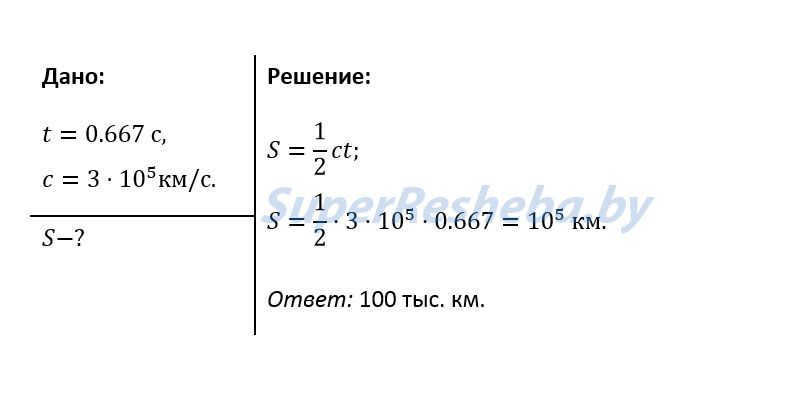
1. A radar detected a reflected signal from an asteroid passing near the Earth in t – 0.667 seconds. At what distance from the Earth was the asteroid at this time?
2. Calculate the Earth-to-Mars distance during the significant opposition, when the horizontal parallax p is equal to 23.2″.
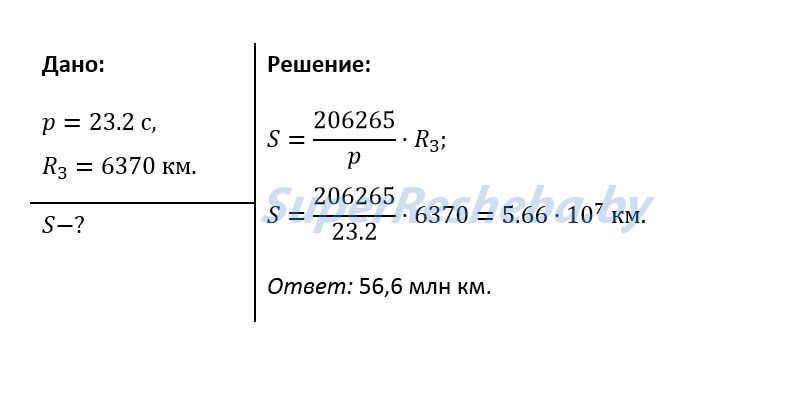
3. When observing the transit of Mercury across the Sun’s surface, it is found that the angular radius of Mercury is p = 5.5″ and its horizontal parallax is p = 14.4″. Calculate the linear radius of Mercury.

1. What was the distance of Venus in its lower conjunction at the time when a radar signal sent to Venus returned back after t – 4 min 36 s?
2. If the horizontal parallax of the asteroid Icarus at this time was p = 18.0″, what distance was it approaching Earth from?
3. By making observations, we were able to determine that Mars had an angular radius of p = 9.0″ and a horizontal parallax of p = 16.9″. Calculate the linear radius of Mars.
How to calculate the Earth’s horizontal parallax
The direct determination of distances to relatively close celestial bodies is based on the phenomenon of parallactic displacement. The concept is as follows: when observing a nearby object from different locations, it appears to be projected onto different background objects that are located far away. To illustrate this, imagine holding a pencil vertically in front of a distant apartment building. When looking at it with our left eye and then our right eye, the pencil appears to be against different windows. The same principle applies to objects in the Solar System. The displacement against the background of stars becomes noticeable when observing from points that are separated by a distance similar to the radius of the Earth. For nearby stars, the displacement becomes noticeable when observing from points that are separated by a distance similar to the radius of the Earth’s orbit.
11.1 The Parallax of Celestial Bodies at the Equator
Coordinates of celestial objects determined from various points on the Earth’s surface are generally different and are known as topocentric coordinates. However, this discrepancy is only noticeable for objects within the solar system. In order to eliminate this ambiguity, all coordinates of solar system objects are adjusted to the Earth’s center and referred to as geocentric coordinates. The angle between the directions to a celestial body from a specific point on the Earth’s surface and from the Earth’s center is referred to as the daily parallax. This parallax is denoted as diurnal parallax p‘ for the celestial body (Fig. 22). It is evident that the daily parallax is zero when the celestial body is at the zenith and reaches its maximum value when the body is at the horizon. This maximum parallax is known as the horizontal parallax of the celestial body p. The horizontal parallax can be related to the diurnal parallax through a simple equation:
Basically, the angle p represents the perspective from a specific celestial body at which the Earth’s radius is observed. However, due to the Earth’s non-perfect spherical shape and its flattening towards the poles, the radius varies at different latitudes, resulting in different horizontal parallaxes for the same celestial body. To standardize these differences, it is common practice to calculate the horizontal parallax using the equatorial radius of the Earth (R0 = 6378 km) and refer to it as the horizontal equatorial parallax p0.
When measuring the altitudes and zenith distances of celestial bodies within the Solar System and making corrections to align the observations with the center of the Earth, the daily parallax must be taken into consideration:
After determining the horizontal equatorial parallax of the celestial body p0, it becomes possible to calculate the distance d to it, as
By substituting the sine of the small angle p0 with the value of the angle itself, expressed in radians, and considering that 1 radian is equal to 206265″, we obtain the desired formula:
Substituting the sine of the angle with the angle itself is acceptable because the maximum known horizontal equatorial parallax of the Moon is 57′ (the Sun has a p0=8″.79).
Currently, radar is used for measuring distances to objects within the solar system with significantly higher precision.
11.2 Annual parallax
The annual parallax of a star refers to the angle at which the radius of the Earth’s orbit is visible from that star, assuming it is perpendicular to the line of sight (Fig. 23).
Similar to the equatorial parallax in the horizontal plane, knowledge of the annual parallax allows us to calculate the distances to stars:
When it comes to measuring distances to stars, using kilometers can be quite inconvenient. That’s why we often turn to a different unit of measurement called the parsec (pc). This unit is defined as the distance at which parallax equals 1″. The name “parsec” is actually a combination of the first syllables of the words “parallax” and “secunda”. In terms of conversion, it’s worth noting that 1 pc is equal to 206,265 astronomical units (a.u.) or 3.086 x 10^18 centimeters. Another unit that is sometimes used to measure distances to stars is the light-year. A light-year represents the distance that light travels in one year (1 pc = 3.26 light-years).
To determine the distance to a star in parsecs, we can simply rely on the value of its annual parallax.
60. (477) The Sun has a parallax value of p0=8″.8, and its apparent angular radius is . How many times larger is the Sun’s radius compared to that of the Earth?
Solution: The Sun’s radius is proportional to the Earth’s radius, as its angular diameter is greater than the parallax.
61. (482) When the Moon’s center was at its highest point, the observed zenith distance (p0=57′) was 50 o 00′ 00″. This observation needs to be adjusted for refraction and parallax effects.
Solution: Refraction causes the observed topocentric zenith distance to be smaller than the true topocentric zenith distance, i.e. . The true topocentric zenith distance is greater than the geocentric zenith distance by the daily parallax amount.
62.(472) What is the horizontal parallax of Jupiter when it is 6 astronomical units away from Earth? The horizontal parallax of the Sun is p0=8″.8.
63. (474) Venus is at its closest distance to Earth, which is 40 million kilometers. At this point, its angular diameter is 32″.4. Find out the linear radius of this planet.
64. (475) Given that for the moon, p0=57'02".7, and its angular radius at this time is rL=15'32".6, calculate the distance to the Moon and its linear radius in terms of Earth radii, as well as the surface area and volume of the Moon compared to those of the Earth.
66. The distances to the stars Vega (), Sirius (), and Deneb () can be determined using their annual parallaxes. These distances can be measured in pc (parsec) and in a.u (astronomical units).
How to calculate the horizontal parallax of the Earth
§ 13. Measuring distances and sizes of objects in the solar system
The idea that the Earth is a spherical object, floating freely and unsupported in outer space, is one of the remarkable accomplishments of ancient science.
The Greek scientist Eratosthenes (276-194 B.C.) who resided in Egypt is credited with the initial accurate determination of the Earth’s dimensions. Eratosthenes’ approach to measurement was quite straightforward: calculate the length of the Earth’s meridian arc using linear units and determine its proportion to the total circumference. With this information, it becomes possible to calculate the arc’s length in 1° increments, and subsequently the length of the entire circle and its radius – in other words, the radius of the globe. It is evident that the length of the meridian arc in degrees is equivalent to the difference between the geographic latitudes of two given points: ϕB – ϕA.
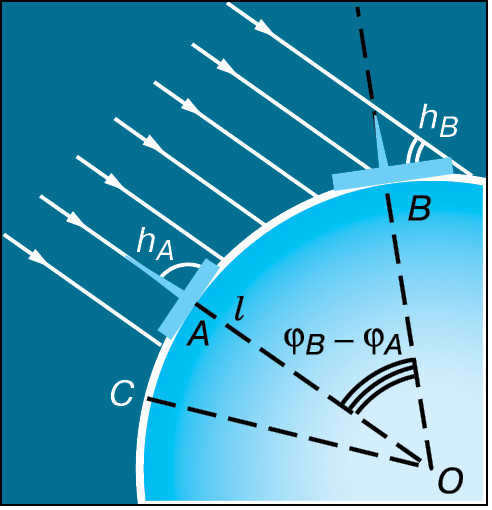
To determine this discrepancy, Eratosthenes compared the midday altitude of the Sun on the same date in two cities on the same meridian. By measuring the height of the Sun h B (Fig. 3.8) at noon on June 22 in Alexandria, his place of residence, Eratosthenes deduced that the Sun is 7.2° away from the zenith. On the same day at noon in the city of Siena (now Aswan), the Sun is directly overhead, illuminating the bottom of the deepest wells, which means it is at the zenith ( h A = 90 ° ). Consequently, the length of the arc is 7.2 ° . The distance between Siena ( A ) and Alexandria ( B ) is approximately 5000 Greek stadia – l .
In ancient Greece, “stadia” referred to the distance covered by a lightly armed Greek warrior from the moment the Sun’s lower edge touched the horizon until it completely disappeared behind the horizon.
Despite the seemingly inconvenient nature of this unit and the cumbersome verbal definition, its introduction was deemed justified due to the predictable regularity of celestial phenomena, which allowed for the measurement of time.
If we denote the circumference of the Earth as L, we can express it as:
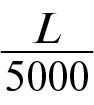 =
= 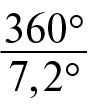 ,
,
From this, we can conclude that the circumference of the Earth is 250 thousand stadia.
The precise measurement of a stage in modern units remains unknown, however, based on the fact that the distance between Alexandria and Aswan is 800 km, it can be assumed that 1 stage is equal to 160 meters. Eratosthenes’ findings closely align with modern data, which suggests that the Earth’s circumference is approximately 40,000 kilometers.
Eratosthenes is credited with introducing the terms “latitude” and “longitude”. These terms likely originated from the unique characteristics of maps during that time period, which depicted the Mediterranean coast. The coast appeared longer in the east-west direction (longitude) compared to the north-south direction (latitude).
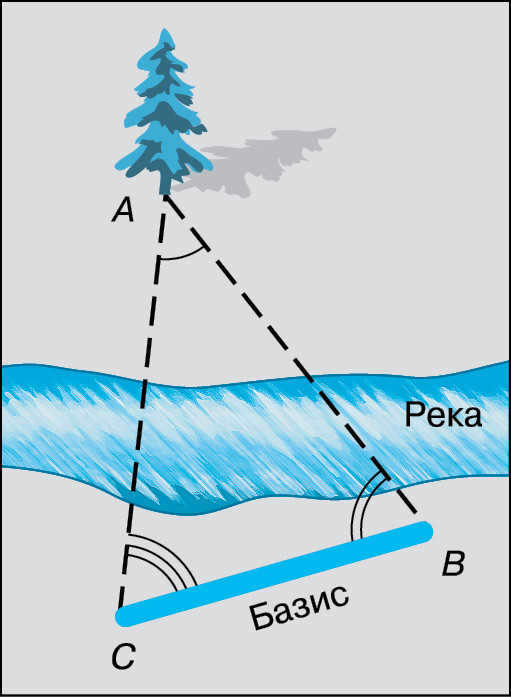
Figure 3.9. Parallactic displacement
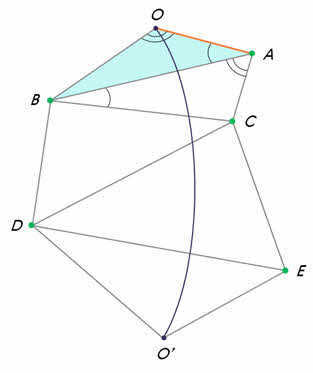
Measuring the distance between two points can be challenging due to natural obstacles such as mountains and rivers. However, determining the geographic latitude of these points is comparatively easier. To overcome this challenge, a method based on parallactic displacement is used. This method involves calculating the distance by measuring the length of one side (base – BC) and two angles B and C in triangle ABC (Fig. 3.9).
Parallactic displacement refers to the change in direction to an object as the observer moves.
The parallactic displacement of an object is smaller when it is located farther away. On the other hand, the observer’s movement (measurement basis) results in a greater parallactic displacement.
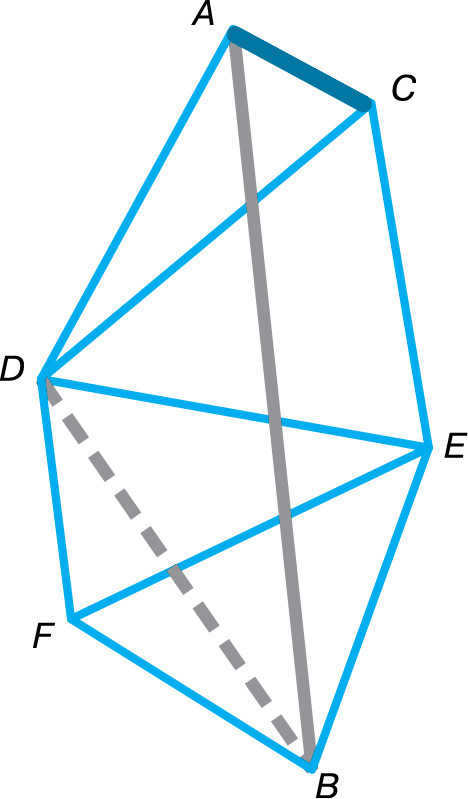

Figure 3.10 presents a scheme of triangulation.
The arc length is determined using the triangulation method, which was first employed in 1615. Points are selected at the vertices of triangles on both sides of the arc, with a distance of 30-40 km between each point. It is ensured that each point has at least two other visible points. The AC baseline (Fig. 3.10) serves as the basis for calculating the lengths of the sides in these triangles. The accuracy of measuring a 10 km long baseline is approximately 1 mm. Geodetic signals, which are towers several tens of meters tall, are installed at all points. From the top of the signal, using a theodolite, the angles between the directions to two or three neighboring points are measured. By measuring the angles in a triangle, with one side being the baseline, surveyors can calculate the lengths of the other two sides. By measuring the angles from the points whose distance is being calculated, the lengths of the next two sides of the triangle can be determined. With knowledge of the side lengths of these triangles, the length of the arc AB can be determined.
The late 18th century unveiled the degree to which the Earth deviates from a perfect sphere. In order to elucidate the Earth’s shape, the French Academy of Sciences orchestrated two expeditions. One expedition operated in the equatorial latitudes of South America, specifically in Peru, while the other expedition took place near the Arctic Circle in Finland and Sweden. Measurements indicated that the length of one degree of the meridian arc in the northern regions exceeded that near the equator. Subsequent investigations substantiated that the length of one degree of the meridian arc grows as the geographic latitude increases. This signified that the Earth’s shape is not perfectly spherical, but rather flattened at the poles. The polar radius is 21 kilometers shorter than the equatorial radius.
For a 1:50,000,000 scale school globe, the discrepancy in these radii would amount to only 0.4 mm, rendering it indiscernible.
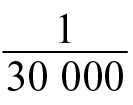
In the 20th century, precise measurements with an accuracy of 15 m revealed that the Earth’s equator is not a perfect circle. Its flattening is only one-hundredth the amount of the flattening of the meridian. To accurately describe the shape of our planet, we use an ellipsoid, which is a figure where any plane section passing through the Earth’s center is not a circle.
Currently, the shape of the Earth is commonly described by the following measurements:
– Ellipsoid compression: 1 : 298.25;
– Average radius: 6371.032 km;
– Length of the equatorial circumference: 40075.696 km.
2- Determining distances in the solar system: Horizontal parallax.
Measuring the distance from the Earth to the Sun became feasible during the latter half of the 18th century when the first determination of the Sun’s horizontal parallax was made. This measurement essentially calculates the parallactic displacement of an object located beyond the Earth, with its radius serving as the reference point.
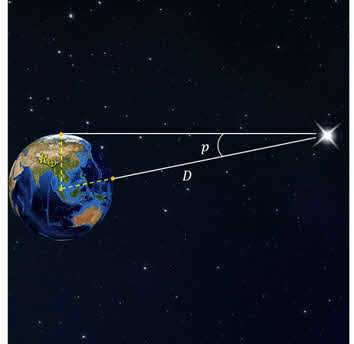
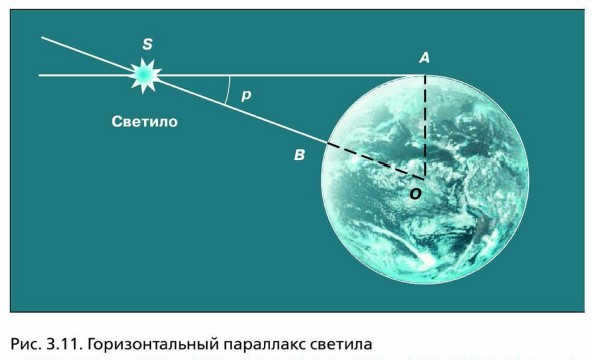
The horizontal parallax ( p) refers to the angle at which the Earth’s radius, perpendicular to the line of sight, is observed from the celestial body (Fig. 3.11).
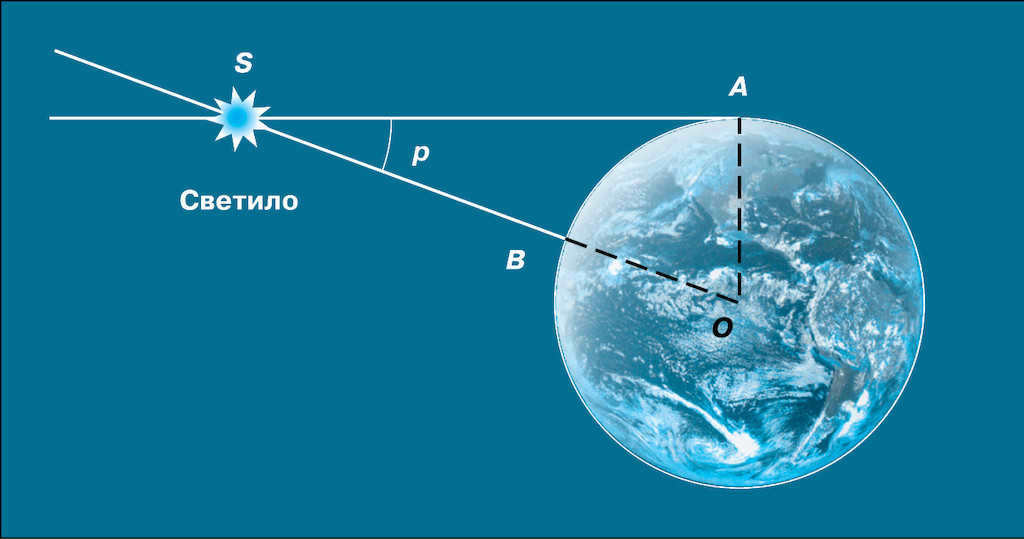
Figure 3.11 shows the horizontal parallax of the luminary.
By considering the triangle OAS, we can calculate the distance OS (represented by D):
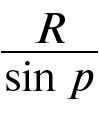
The formula for calculating the parallax is D = , where R represents the radius of the Earth. By using this equation, we can determine the distance in terms of Earth’s radii and then convert it to kilometers.
It is evident that the parallax decreases as the object moves farther away. The Moon has the highest parallax, which varies due to its elliptical orbit and has an average value of 57 ʹ. On the other hand, the parallaxes of the planets and the Sun are much smaller, with the Sun’s parallax measuring 8.8 ʺ. This parallax value corresponds to a distance of approximately 150 million km, known as one astronomical unit (1 a.e.), and is used as a unit of measurement for distances between celestial bodies within the solar system.
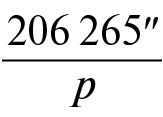
The equation is D equals R, or, with enough precision.
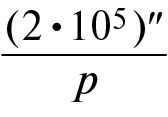
D = R .
During the latter part of the 20th century, advancements in radio engineering enabled the measurement of distances to celestial bodies within our solar system through the use of radiolocation. The first body to have its distance determined in this way was the Moon. Subsequently, radar methods were employed to establish the distances to Venus, Mercury, Mars, and Jupiter. By utilizing radar techniques on Venus, the value of the astronomical unit was determined with a precision of approximately one kilometer. This level of accuracy in distance measurement is crucial for calculating the flight trajectories of spacecraft that explore planets and other celestial bodies within our solar system. Presently, optical localization of the Moon can be carried out using lasers, allowing for distance measurements to the lunar surface accurate to within centimeters.
What is the distance from the Earth to Saturn when its horizontal parallax is 0.9 ʺ?
We know that the Sun has a parallax of 8.8 ʺ at a distance of 1 a.e.
By writing the formulas for the distance to the Sun and to Saturn and dividing them, we can calculate:
D1 = 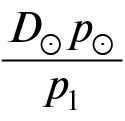 =
= 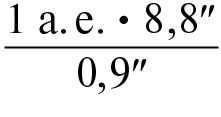 = 9.8 a.e.
= 9.8 a.e.
3 Determination of the sizes of the luminaries
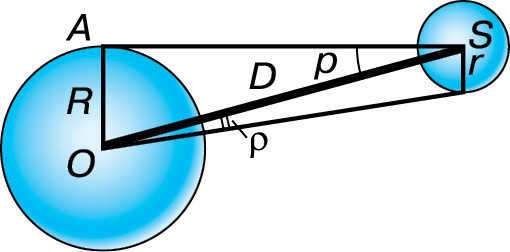
Fig. 3.12. Angular measurements of a celestial body
By knowing the distance to the celestial body, we can calculate its linear measurements by measuring its angular radius ρ (Fig. 3.12). The equation that relates these quantities is similar to the equation for finding parallax:
D = .
Considering that the angular diameters of even the Sun and Moon are approximately 30 ʹ , and all planets appear as points to the naked eye, we can use the approximation: sin ρ ≈ ρ . Therefore:
D = and D = .
r = R .
If the distance D is known, then
where the value of ρ is given in radians.
What is the linear diameter of the Moon if it is observed from a distance of 400,000 km at an angle of about 30 ʹ ?
If ρ is given in radians, then.
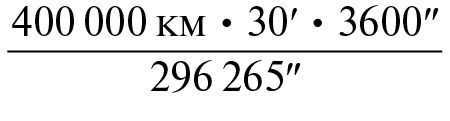
The distance is 3490 kilometers.

Queries 1. Which Earth measurements indicate its shrinkage? 2. Does the Sun’s horizontal parallax vary throughout the year and why? 3. What is the current technique for calculating the distance to the nearest planets?

Exercise 11 1. If Jupiter is 5 times farther from the Sun than Earth, what is the observed horizontal parallax of Jupiter from Earth in opposition? 2. At the closest point in its orbit (perigee), the Moon is 363,000 km away from Earth, and at the farthest point (apogee), it is 405,000 km away. Calculate the horizontal parallax of the Moon at these positions. 3. If the Sun and the Moon have the same angular diameter and their horizontal parallaxes are 8.8ʺ and 57ʹ respectively, how many times larger is the Sun compared to the Moon? 4. What is the angular diameter of the Sun as seen from Neptune?
A tool can be used to calculate the distance to a nearby star in light-years and parsecs if the annual parallax of that star is known in angular seconds. The parallax can also be determined if the distance is known.
For example: Let’s calculate the distance in light-years to the brightest star in the northern hemisphere starry sky, Arcturus (α Volopassus) in the constellation Volopassus, if its parallax is known to be 88.83 angular milliseconds.
The phenomenon known as parallax refers to the apparent shift in position of an object when viewed from different vantage points. This shift is measured as the angle (or half angle) between the observer’s line of sight and the object. In the case of stars, the annual stellar parallax is determined by observing the star from two widely separated points in Earth’s orbit, as illustrated below. By using the parallax of a celestial body, astronomers can calculate its distance using the following formula:
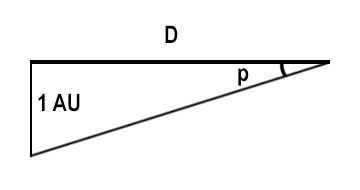
Here D represents the distance to the celestial body, which is measured in parsecs, and p represents the observed annual parallax, which is measured in arc seconds. This formula is utilized for the computations in our calculator. A parsec is defined as the distance to an object whose annual stellar parallax is equal to 1 arc second. In simpler terms, a parsec is the distance at which a disk with a size of 1 a.u. would have an angular size of 1 arc second.
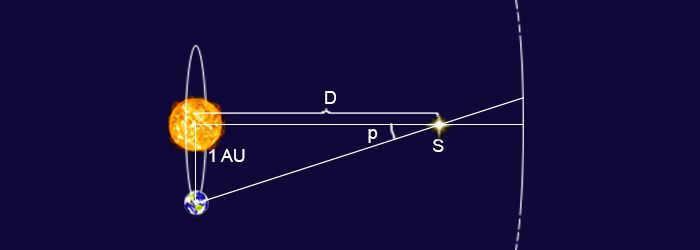

Annual parallax of the star (drawing not to scale); 1 – astronomical unit (a.u.), which is the distance from the Earth to the Sun; D – distance from the center of the Earth’s orbit to the star S; p – parallax measured in angular seconds (")

Overview

The vastness of space makes it necessary to use different methods for measuring distances compared to those used on Earth. In our previous article on lengths and distances, we focused mainly on measuring relatively small distances that are easy to visualize. However, the scale of distances in space is so immense that conventional units like meters and kilometers are not suitable. Traditional measuring tools like tape measures or rulers are inadequate for measuring the vast distances between planets and galaxies. Additionally, satellite navigation systems do not function in space. As a result, new units of measurement and innovative measuring techniques must be developed specifically for space exploration.
Radar measurements: paraphrasing the text while preserving HTML markup
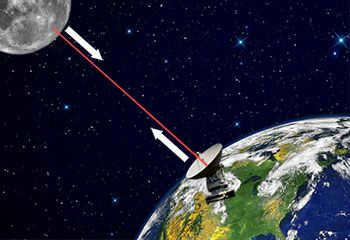

A radar station (radar) located on Earth transmits microwave radiation towards an astronomical object for which the distance needs to be calculated. The duration it takes for the signal to reach the object and return to the radar station is then measured. By knowing this time and the speed of light in a vacuum, the distance can be determined by multiplying the speed by the time.
This technique is specifically applicable to celestial bodies that are in close proximity to Earth. It can be regarded as appropriate for entities within the solar system. The reason for this is that radio signals become weakened and dispersed over significant distances. Furthermore, the farther the distance, the larger an entity must be in order to be detectable by a radar station.
Annual stellar parallax
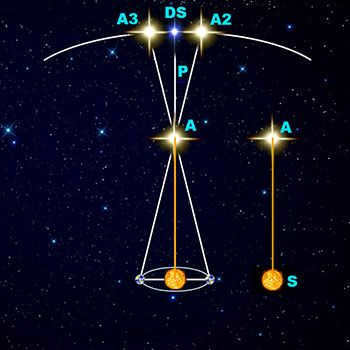
In this illustration, the blue circles represent the two locations of the Earth, while the Sun is depicted in orange. The star whose distance needs to be determined is denoted as point A. A2 and A3 represent the apparent positions of this star as observed from two different vantage points in relation to the distant white star DS. The parallactic angle is denoted as P. If the angle P measures one arc second, the distance between the Sun and the star, indicated by the orange AS line, is defined as one parsec.
For a more detailed explanation of how to measure distance using parallax, please refer to the length and distance article. In general, distances should be measured when the Earth is at two opposite points in its orbit around the Sun (at six-month intervals, as the Earth completes one revolution around the Sun in one year). We can utilize the known distance from Earth to the Sun (which is accurately measured and referred to as an astronomical unit) and determine the angle formed by the line connecting the Earth at the first measurement point, the star whose distance is being measured, and the Earth’s position during the second measurement. In reality, we only need to know half of this angle, known as the parallactic angle and labeled as P in the diagram. With this information, we can calculate the distance from Earth to a star using trigonometric equations.
By utilizing the described technique, the measurement of distance can be conducted utilizing an array of length units, although astronomers have a preference for the parsec. A parsec is defined as the distance between the Sun and the star in question when the parallactic angle reaches 1 arc second. Alternatively, the light-year can be employed as a unit of length (1 parsec is equivalent to 3.26 light-years), although this particular unit is more frequently utilized by journalists. In the realm of astronomy, parsecs are the preferred choice.
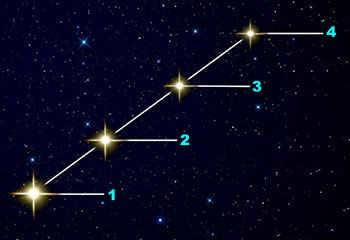
 The four stars are of equal size but are situated at differing distances from us. The star at position 1 is the closest, whereas the star at position 4 is the farthest away. As a result, the stars that are nearer to us appear brighter, while those that are further away appear less bright. If we know their true brightness, we can compare it to their apparent brightness and thus ascertain their distance from us.
The four stars are of equal size but are situated at differing distances from us. The star at position 1 is the closest, whereas the star at position 4 is the farthest away. As a result, the stars that are nearer to us appear brighter, while those that are further away appear less bright. If we know their true brightness, we can compare it to their apparent brightness and thus ascertain their distance from us.
Cepheids
Cepheids, a specific kind of stars, offer a unique opportunity to gauge distances in the vast expanse of space. These stars pulsate, with their brightness intricately linked to their pulsation period. In other words, the longer the period, the more radiant the Cepheid becomes. This relationship between pulsation period and luminosity is widely recognized, and all Cepheids adhere to this pattern. Consequently, by observing the pulsation period, which is a relatively straightforward task, we can ascertain the luminosity of the star. It is a well-established fact that the farther a star is, the dimmer its luminosity. By comparing the actual brightness to the apparent brightness, we can effectively calculate the distance to the star.
Cepheids pulsate as a result of their contraction and expansion. Their luminosity fluctuates, and the interval between the peaks of maximum luminosity needs to be measured in order to ascertain the period. The size of a star’s core remains constant, but its external gas layers expand and contract due to variations in gas pressure within these layers. The contraction and expansion occur as a result of two forces: gravitational attraction, which causes gas molecules to move closer towards the star’s center, and gas pressure, which leads to expansion of the outer layer.


Schematic representation of a pulsating Cepheid with a period of two days. Luminosity peaks on December 1, 2010, when the star starts to slowly dim. On December 2, the brightness is at its minimum. The star then reaches its maximum luminosity again on December 3 and decreases in brightness on December 4, and so forth.
When a star is in a state of compression, its photons possess significant energy, leading to an increase in pressure that causes the star’s outer shell to expand. Subsequently, when this pressure diminishes and falls below the gravitational forces that compress the envelope, the star undergoes contraction. This cycle then repeats.
Cepheids offer the ability to measure distances of up to 40 million parsecs, a scale that surpasses the limitations of the parallax method. However, it should be noted that Cepheids are relatively uncommon, which poses a disadvantage to this measurement technique.
Type Ia supernovae: a closer look
Alternative approaches for measuring distances
There are various other techniques for measuring distances in space. One method relies on the premise that the universe is undergoing expansion at a known rate. By determining the rate at which galaxies are moving away from our own galaxy, we can utilize Hubble’s law to ascertain their distance. Hubble’s Law states that the distance to a galaxy is equal to the velocity of the galaxy divided by the Hubble constant, a fixed value. The velocity of a galaxy can be determined by analyzing its spectrum and considering the Doppler effect. The Doppler effect, also known as the Doppler shift in astronomy, refers to the alteration in frequency of electromagnetic radiation (in this case, light) emitted by an object in motion relative to an observer. As the galaxy moves away from the observer, its spectrum shifts towards lower frequencies, or towards the red end of the spectrum, with the degree of shift dependent on the galaxy’s velocity and distance. By analyzing this shift, we can calculate the velocity and subsequently determine the distance.