At times, we find ourselves pondering over seemingly odd and insignificant questions. We often have a curiosity about numerical values of certain parameters and compare them to other known values. These questions frequently arise in the minds of children, leaving parents with the responsibility to provide answers.
What is the Earth’s volume? It can be a challenging question to answer, as our brains tend to resist memorizing values that are rarely applicable in our daily lives. Even if you once knew the answer to this question, chances are that you have forgotten it since it hasn’t been of use to you since then.
Before we provide an exact response and compare the Earth’s volume with established measurements, let us delve into the history of geometry. After all, this field of study was initially developed to quantify diverse attributes of our planet.

Origins of Geometry
Geometry has its roots in ancient Egypt, where people often found themselves in need of measuring distances between cities, determining the size of objects, and calculating the area of land they owned. These practical needs gave rise to the development of a specialized field of study known as geometry, derived from the Greek words “geo” meaning Earth and “metros” meaning to measure. Initially, geometry was primarily used for practical purposes. However, as more complex calculations became necessary, philosophers and scientists such as Pythagoras and Euclid emerged at the forefront of this evolving discipline.
When constructing even seemingly simple structures, it is important to have the ability to measure the amount of material that will be used, calculate distances between points, and determine angles between straight planes. It is also necessary to have knowledge of the properties of basic geometric shapes. The Egyptian pyramids, built in the 2nd-3rd century BC, are a testament to the precision of their spatial relationships, demonstrating that their builders possessed a deep understanding of various geometric principles and had a solid foundation for accurate mathematical calculations.
As time went on and geometry developed, it expanded beyond its original purpose and found applications in various fields. Nowadays, it is impossible to imagine any industry without calculations that involve geometric methods.
In the following section, we will discuss methods for measuring specific geometric characteristics of different objects.

Body Measurements
When it comes to measuring rectangular bodies, determining their volume and area is quite straightforward. All you need to know are the dimensions – width, length, and height – and you can easily calculate the essential properties of the figure. The volume of a rectangular body can be found by multiplying these three measurements together. On the other hand, the area of such a figure can be determined by adding up twice the product of each pair of sides. Mathematically, these formulas can be represented as follows: for volume, V=abc, and for area, S=2(ab+bc+ac).
However, when it comes to a ball, these equations can be quite inconvenient. To determine the diameter (and subsequently the radius) of a ball, one would have to enclose it within a cube, ensuring that it is in contact with the cube at six points. The length (or width or height) of this cube would then represent the diameter of the ball. Nonetheless, a much simpler method involves determining the volume of the ball by submerging it into a vessel filled to the brim. By measuring the volume of the water displaced, we can ascertain the volume of the ball itself. Moreover, since the formula for the volume of a ball is V=4/3* π*R 3 , we can use this equation to calculate the radius, which in turn assists in determining additional properties of the object.
Another intriguing approach to measuring the volume of a ball will be discussed in the subsequent section.

What is the method for determining the mass of the Earth?
When dealing with objects of astronomical proportions, such as planets, it becomes more challenging to accurately measure their volume and surface area. In such cases, more intriguing and advanced techniques must be utilized.
This is a method for determining the volume of sizable objects, such as celestial bodies. The ancient Greeks employed it in the past to gather additional information about the Earth. It enabled them to calculate the Earth’s volume. However, it’s important to note that these measurements are only approximations, as this method does not account for numerous errors.
Prior to addressing the primary question, let’s explore how modern techniques allow for the measurement of intricate quantities with the least margin of error.

Contemporary Techniques for Determining Earth’s Mass
In the present day, there exist numerous advanced technologies that enable us to refine the calculations made by ancient scientists regarding various characteristics of the Earth. In the previous century, humanity utilized orbiting satellites for this purpose. These satellites possess the ability to measure the Earth’s circumference with the utmost precision. By extrapolating from this data, it becomes possible to calculate the radius. As we have already discovered, once the radius is known, determining the Earth’s volume becomes a straightforward task.
Now is the time to uncover the precise figure and compare it to the values we are already familiar with.

What is the size of the Earth?
So, we are getting closer to the main question of this article. The size of the Earth is 1,083,210,000,000,000 km 3 . Is that a significant amount? It depends on what we compare it to. Out of the objects that we can compare to this value, only one other celestial body comes close. Therefore, we can state that the size of the Moon is only two percent of the Earth’s size.
There are also planets, like Jupiter, which have a massive size due to their low density and large surface area. The size of the Earth could also be larger if it consisted mainly of gases instead of solids and liquids.
Application
We require these quantities primarily out of curiosity. However, they find extensive practical use in various fields. For instance, in the field of astronomy, the volume, mass, and radius of the Earth are employed to calculate the orbital trajectory of satellites launched from our planet’s surface. Moreover, these data hold significance in more profound scientific investigations. In geography and geology, the utilization of this information is intriguing as it aids in determining the Earth’s volume, which is crucial for geological exploration and providing approximate assessments of mineral reserves.
As is well-known, errors are present everywhere. And when it comes to calculating the volume of the Earth, there are quite a myriad of them. To be more precise, only one error plays a major role in these measurements, but it is the most significant one. This error stems from the fact that the Earth is not a perfect sphere. It is flattened at the poles and also features surface irregularities in the form of depressions and mountains. While the planet is enveloped by an atmosphere that tends to mitigate these effects on measurements, determining density remains a highly intricate task.

Summary
The Earth’s physical attributes have always been a popular subject of interest. People often wonder about the percentage of the planet’s surface covered by oceans and the overall volume of the Earth. In this article, we not only provide the precise answers to these questions but also explain the methods and tools used for their calculation.
It is well-known that two objects are drawn towards each other due to their mass. This gravitational attraction also applies to other forms of matter, such as fields and radiation, which possess mass. The presence of gravity is the most well-known manifestation of this attraction, as it influences all objects on Earth.
The attractive force between two bodies is known as gravitational force. The magnitude of this force is determined by Newton’s law of universal gravitation.
Here:
– F represents the gravitational force between two bodies in Newtons,
– m1 is the mass of the first body in kilograms,
– m2 is the mass of the second body in kilograms,
– r is the distance between the centers of masses of the bodies in meters,
– G is the gravitational constant, which is approximately 6.67 × 10^-11 m^3/(kg·sec^2).
It is important to note that the mutual attraction of masses should not be confused with the forces of magnetic or electric attraction, as these forces have entirely different natures.
Gravitational forces are always attractive and cannot be repulsive. Additionally, no screen can weaken or eliminate gravitational interaction.
By plugging in the values for the mass of the Earth, the mass of the body, and the distance from the center of mass of the body to the center of the Earth into the numerator and the denominator r of the gravity formula, we can calculate the force of gravity:
| The force of gravity, | Newton |
| mass of the Earth 5.97 – 10^24 | kg |
| body mass | kg |
| free fall acceleration at the Earth’s surface 9.81 | meter / second2 |
| distance from the center of mass of the body to the center of the Earth | meter |
| gravitational constant 6.67 – 10-11 | m3/(kg – sec2) |
At the surface of the Earth, the force of gravity is calculated using a simplified formula.
The force of gravity F does not reach zero at finite distances r, it only approaches zero at infinite distances between bodies.
Free fall acceleration
The acceleration of free fall at any distance from the Earth, as well as on other planets, can be determined using the formula for the Earth’s gravitational force. By dividing by the mass of the object, we can obtain:
The acceleration of free fall decreases in inverse proportion to the square of the distance from the center of the Earth. The formula for the acceleration of free fall also applies to other celestial bodies.
Gravitational field, field of gravity
Every object (like the Earth) generates a force field around itself – the gravitational field. The magnitude of this field at any point within it indicates the force exerted on another object at that point.
g – strength of the gravitational field
F – gravitational force acting on an object with mass m
m – mass of the object within the gravitational field
The strength of the field, g, is a vector quantity with its direction determined by the direction of the gravitational force, F, and its numerical value determined by the formula for the acceleration due to gravity.
The magnitude, direction, and units of measurement of the gravitational field strength align with the acceleration of free fall, although they are distinct physical quantities. While the field strength describes the state of space at a specific point, the force and acceleration only manifest when a test body is present at that point.
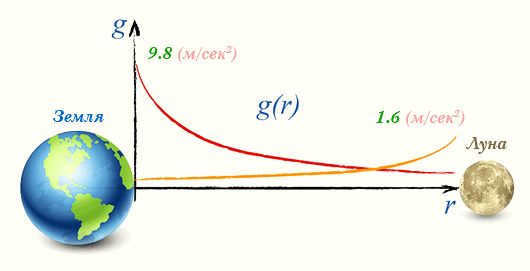
By observing the graph of the function g=g(r), it becomes evident that as the distance r approaches infinity, the gravitational field strength g approaches zero. Therefore, any claims stating that a satellite has completely escaped the Earth’s gravitational field are incorrect.
The gravitational fields of celestial bodies overlap with one another. If one were to travel along a straight line connecting the centers of the Earth and the Moon, at a certain point, the gravitational field strength of the Moon would become dominant.
The initial orbital velocity is the speed at which a body must travel in order to maintain a constant altitude above the planet’s surface.
By utilizing the equation for gravitational acceleration during free-fall, we have the ability to calculate the velocity of a man-made satellite orbiting the Earth (or any other planet) at any given distance above its surface.
The gravitational force acting upon the satellite is equivalent to the centrifugal force, as follows:
Where:
Uk – initial orbital velocity (in meters per second)
h – distance of the satellite from the planet’s surface (in meters)
gZem – initial separation between the centers of mass of the objects (the Earth’s surface) (in meters)
mZem – mass of the Earth (in kilograms)
m – mass of the satellite (in kilograms)
g – gravitational acceleration at a specific distance from the Earth’s surface (in meters per second squared)
gEarth – gravitational acceleration at the Earth’s surface (9.81 meters per second squared)
? – gravitational constant (6.67 × 10^-11 cubic meters per kilogram per second squared)
The formulas stated above are applicable to the scenario where the Moon orbits around the Earth. They are also valid for the planets orbiting around the Sun, as long as their trajectory deviates slightly from a perfect circle and instead follows a path with a minor eccentricity.
Escape velocity (second space velocity)
Escape velocity is the minimum speed required for a body to overcome the gravitational pull of the Earth and move infinitely far away without any additional force.
If:
m – mass of the body (kg)
M – mass of the Earth (kg)
h – height of the satellite above the Earth’s surface (m)
gEarth – initial distance between the centers of mass of the bodies (surface of Earth) (meter)
r – final distance between the centers of mass of the bodies (meter)
G – gravitational constant 6.67 × 10-11 (m3/(kg·s2))
Ve – escape velocity (second space velocity) (m/s)
So, in order to overcome the force of gravity, the body’s kinetic energy must be equal to the work done:
After simplifying and rearranging, the second velocity in space can be expressed as:
Essentially, the second velocity in space for a rocket launch from the planet’s surface is the velocity that a body would need to have at the surface when h is small and the gravitational force is large. As we move further away from the source of gravitational force, the escape velocity decreases because the gravitational force decreases, resulting in a decrease in the required kinetic energy for escape.
The mass of the Earth is an astonishing 5.9736 x 10 24 kg. Incredible!
What is the method for determining the Earth’s mass?

However, the more intriguing question is how scientists were able to determine the Earth’s mass in the first place? The answer lies in the gravitational pull that our planet exerts on nearby objects.
According to the laws of physics, any object with mass is attracted to other objects. If you were to place two billiard balls next to each other, they would naturally move towards each other. Although this force is invisible to the naked eye, sensitive instruments are able to detect it. By measuring this force, scientists can calculate the mass of both objects.
Sir Isaac Newton hypothesized that the mass of spherical objects is concentrated at their centers. Using this assumption, we can utilize the following equation:
- F represents the force of gravity between the objects.
- G is a constant equal to 6.67259 × 10 -11 m 3 /kg s 2 .
- -M1 and M2 represent the masses of the objects attracting each other.
Let’s imagine that one of the masses corresponds to the planet Earth, while the other is a kilogram sphere. The magnitude of the force between them is 9.8 kg * m/s 2 . The radius of the Earth is 6,400,000 meters. By plugging these values into the equation, we obtain a mass of 6 x 10 24 kg.
It is worth noting that it is accurate to utilize the term “mass” instead of “weight” in this context, as the latter signifies the force required to calculate the gravitational field. If you were to weigh a ball on both the Earth and the Moon, the reading would differ. However, mass remains constant, and the mass of the Earth remains unchanged.
We are fortunate to have the highest planetary density in the system, measuring at 5.52 g/cm3. This value is derived from the presence of a metallic core, surrounded by a layer of rocky mantle. In contrast, less dense planets such as Jupiter are primarily composed of hydrogen and other gases. Thus, we now have an understanding of the Earth’s mass.
How is the mass of the Earth and other planets determined by scientists?
Scientists can determine the mass of the Earth by using a barometer.
In general, the mass of the Earth is determined using Newton’s second law F=mg and the law of universal gravitation F=G*m*M/R^2, where F represents the force with which the Earth attracts the barometer, G is the gravitational constant, m is the mass of the barometer, M is the mass of the Earth, and R is the radius of the Earth.
Using these equations, the mass of the Earth can be calculated using the formula M = g*R^2/G. The challenge is to find the appropriate values for the variables in the equation.
To begin, the acceleration of free fall, g, needs to be measured. This can be done by dropping the barometer from a tall structure and timing its fall. The height of the structure can also be measured using a barometer, although this topic is not covered in this lecture.
The subsequent stage involves determining the radius R of the Earth. During the summer solstice, when the Sun is positioned directly above the Tropic of Cancer, we must measure the length of the shadow cast by a barometer of known height, located in Moscow. Once we have the distance from Moscow to the tropic, it becomes a matter of technique to calculate the Earth’s radius.
The most challenging task is calculating the gravitational constant G. To accomplish this, we require a device known as a torsion scale. This apparatus enables us to measure the force exerted on the barometer by a heavy lead ball of a predetermined mass.
If we have not engaged in any deception, we should obtain values for the acceleration due to gravity g = 9.8 m/s/s^2, the Earth’s radius R = 6371 km, and the gravitational constant G = 6.67*10^-11 m^3/(kg*s^2).
Therefore, the Earth’s mass is approximately 6*10^24 (6 and 24 zeros) kilograms.
In order to determine the mass of other planets, scientists employ astronauts equipped with barometers to visit these celestial bodies.
[1] The experiment on free-fall conducted by Galileo: wikipedia.org
[2] Eratosthenes and his calculation of the Earth’s radius: wikipedia.org
[3] Torsion scales and the Cavendish Experiment: wikipedia.org
[5] The Law of Universal Gravitation: wikipedia.org
[6] Utilizing a barometer to measure the height of a building: lyceum1502.ru
What is the weight of planet Earth?
In the field of astronomy, the mass of the Earth represents a unit of measurement. Remarkably, scientists have already determined the exact mass of our planet. The mass of the Earth is equivalent to 1 M Earth=(5.9722±0.0006)×10²⁴ kg.
Here are a few intriguing facts:
- Firstly, researchers have established that the mass of the Earth is approximately 5.97×10 ²⁴ kg;
- Secondly, the mass of the Moon is 81 times smaller than that of our planet;
- Thirdly, the weight of the Earth is constantly fluctuating.
Earth’s Mass Distribution
It is common knowledge that the distribution of weight within any object is not uniform, especially if it is not made up of a single, homogeneous substance. However, even in cases where the object is homogeneous, there can still be exceptions.
As we know, the Earth is comprised of various layers including the core, mantle, crust, hydrosphere, and atmosphere. It is safe to assume that each of these parts has a different weight.
Let’s examine how the mass of the Earth is distributed.
The mantle, or outer shell, carries the most weight, with a mass of 4.043 x 10²⁴ kg.
The core, on the other hand, has a mass of 1.93 x 10²⁴ kg.
The crust, which is the Earth’s surface, weighs 0.026 x 10²⁴ kg.
Lastly, the atmosphere has a mass of approximately 0.0000051 x 10²⁴ kg.
What causes fluctuations in the Earth’s mass?
The mass of our planet is not a constant value, as it is influenced by numerous factors.
For instance, the weight of the Earth is affected by the presence of various celestial objects and elements. Space dust, meteors, comets, and other particles from the universe all contribute to the increase in its mass. These objects settle on the Earth’s surface, thereby significantly impacting its overall weight. As a result, the Earth’s mass increases by an average of 40 thousand tons each year.
However, there are certain occurrences in the world around us that actually decrease the planet’s weight index. For instance, gases in the Earth’s atmosphere are lost as they evaporate into outer space. This phenomenon is caused by an increase in the molecular thermal motion. Moreover, the heating of the Earth due to human activities and global warming also contributes to the release of substances from the atmosphere. Additionally, artificial satellites that are launched into outer space don’t return to Earth’s orbit, which clearly impacts the overall mass.
Consequently, the decrease in the planet’s weight and mass results in a reduction in Earth’s gravity. This, in turn, weakens the ability to retain particles and substances in the atmosphere.
As you are aware, within the group of planets in the Earth’s solar system, our home planet is the largest in terms of mass. In comparison, the other planets have significantly less weight: Venus has a mass that is 0.815 times that of Earth, Mercury’s mass is only 0.055 times, and Mars is approximately 0.108 times.
However, when it comes to the gas planets, they are greatly overshadowed in terms of weight. For instance, Uranus is 14.5 times heavier than Earth, Neptune is 17.2 times heavier, and Saturn is a staggering 95.1 times heavier. Nonetheless, all of these planets pale in comparison to Jupiter, which is the clear champion in this category. It weighs a colossal 317.8 times more than Earth!
It’s not possible to measure the weight of a planet. Because we are unable to place it on a scale. However, this limitation does not hinder our scientists. They find ways to overcome the impossible…
Investigating and discovering one’s own home is more than just a matter of curiosity and principle. One could argue that it is a duty of sorts. This is because knowledge leads to understanding, and understanding is crucial for comprehending everything that surrounds us. This understanding is vital for the preservation and sustenance of life.
There is no god-creator, but there is a cosmos that gives rise to suns, planets, and living beings. There is no all-powerful god, but there is the Universe, which governs the destiny of all celestial bodies and their inhabitants.
Konstantin Eduardovich Tsiolkovsky
How to Estimate the Weight of the Earth with Balls and String
In order to calculate incredibly large magnitudes, it is necessary to work with extremely small numbers.
Illustration: Daniel Grizely / Getty Images
Contemplating the methods by which we acquire knowledge can be quite fascinating. Consider, for instance, the weight of the Sun, which is approximately 2 x 10 30 kilograms. This figure is so immense that it is difficult to grasp. And if we struggle to comprehend such enormous numbers, how do we determine these values? Well, the original approach involved employing small masses, a stick, and a rope. This method is a crucial step in determining the weights of both the Sun and all the planets in our solar system. It is known as the Cavendish experiment, which was first conducted by Henry Cavendish in 1798. This experiment is truly remarkable, so let me explain how it functions.
Objects with mass experience a gravitational pull toward each other. For example, a basketball is attracted to the Earth due to their respective masses. This gravitational attraction causes the basketball to accelerate as it falls when released. The concept of objects falling when released has been known for a long time. However, it was not until around the time of Isaac Newton that people realized this gravitational attraction also applies to astronomical objects like the Earth, Moon, and Sun. This understanding led to Newton’s law of universal gravitation, which describes the interaction of forces between objects. It is important to note that Newton’s law of universal gravitation was likely a collaborative effort involving multiple contributors.
Illustration: RHETT ALLAIN
Let’s take a look at this gravitational force model. Firstly, the strength of this force is determined by the multiplication of two masses that interact with each other (m1 and m2). Secondly, the strength decreases in correlation with the square of the distance between the two entities ( r ). Lastly, we have G. This represents the universal gravitational constant, which plays a crucial role in calculating the mass of the Earth.
Imagine this experiment. Let’s say I have a liter of water (which I know weighs 1 kilogram) and I want to measure the gravitational force exerted by the Earth on it. If I know the Earth’s radius (which the Greeks calculated accurately) and the gravitational constant G, I can solve the equation for gravitational force to find the mass of the Earth (as mentioned earlier). However, determining the value of G is a bit tricky. Here’s how you can do it.
Interestingly, the gravitational constant is extremely small. This means that the attraction between two regular objects, like water bottles, is almost negligible. To observe a significant gravitational force, one of the masses involved needs to be enormous (like the Earth). Nevertheless, there is a method to figure it out – by using a torsion scale.
Let’s begin with a straightforward physics demonstration that you can experiment with in the comfort of your own home. Take a pencil and position it on the perimeter of a table so that approximately half of the pencil hangs over the edge, as if it is on the verge of falling, yet it manages to remain in place. At this particular moment, the pencil is essentially teetering on the brink of the table. It is only supported by this minuscule point of contact, rendering friction force incapable of preventing it from rotating. Even the tiniest amount of force exerted against the end of the pencil will set it into motion. It requires nothing more than a mere gust of air to initiate the rotation of the pencil.
I enjoy placing my fingers in close proximity to the pencil and pretending that I possess superhuman abilities that enable me to manipulate its movement. Now, let’s substitute the pencil with a lengthier stick and, instead of placing it on a surface, let’s suspend it from a string. As it hangs in the middle, even a slight force is capable of causing it to rotate, mirroring the behavior of the pencil. Instead of utilizing air pressure, we could employ a minimal gravitational force to initiate its motion. Allow me to explain the mechanics behind this phenomenon.
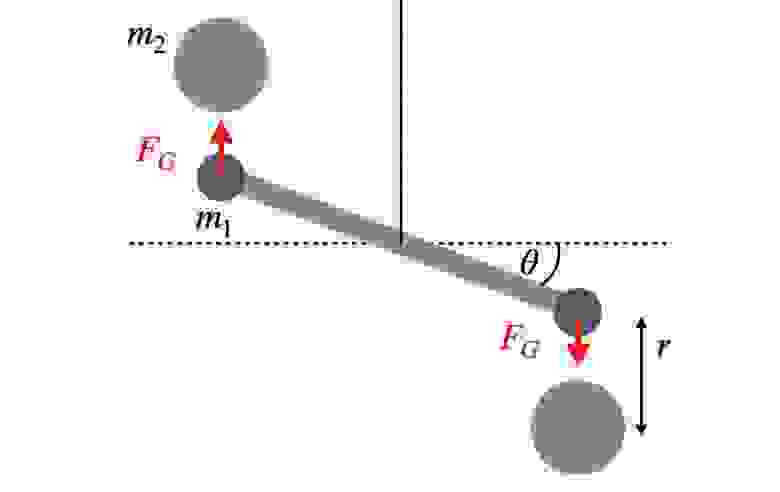
Picture: RHETT ALLAIN.
In this scenario, we obtain the value of the gravitational constant G as 6.67 x 10 -11 N*m 2 kg 2 . It is evident that this constant is extremely minuscule. To illustrate, let us demonstrate the procedure for calculating it. Imagine you are an individual positioned 1 meter away from another individual with an identical mass (approximately 75 kg). What will be the magnitude of the force exerted on you as a result of gravitational attraction? By substituting these values (along with the constant) into the equation for force, we obtain:
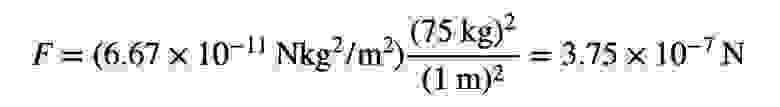
Illustration: RHETT ALLAIN.
However, this concept is not logical. It is impossible for anyone to perceive a force of such minuscule magnitude. Let us attempt to conceive of a scenario involving a force comparable to the gravitational attraction between two individuals. Consider this: imagine placing a small object in your hand. Since your hand must exert an upward force to counterbalance the gravitational force, you can perceive the Earth’s gravitational force acting upon this object. What mass would this object need to possess in order to generate an Earth-induced gravitational force equal to the force between two people? Certain values on the Earth’s surface remain constant, such as the gravitational constant, the Earth’s mass, and the distance from the Earth’s center. We can aggregate all of these values into a single numerical value.
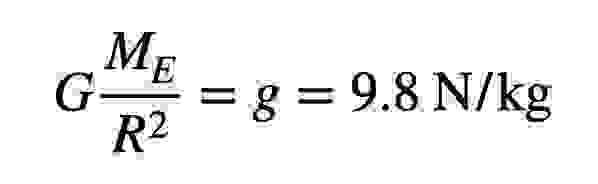
Image credit: RHETT ALLAIN
The gravitational force (weight) can be calculated by multiplying the mass by the local-Earth gravitational constant. To avoid confusion with the other gravitational constant, we use the lowercase letter “g”. So, to find the weight, simply multiply the mass by “g”. In the case of the gravitational force between two people, an object with a mass of approximately 4 x 10 -11 grams would be needed. Though it may seem small, consider this: a human hair can have a linear mass density of 6.5 grams per kilometer. This means that a hair as short as 6 x 10 -6 millimeters long would have a weight equal to the attraction between two people. It’s truly mind-boggling! As a bonus, here are my calculations if you wish to change the values.
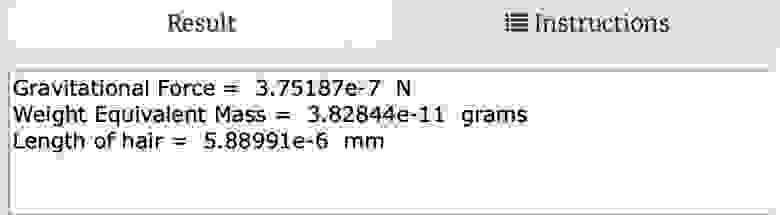
Illustration: RHETT ALLAIN
Indeed, it is possible to perform the same computation, but this time by utilizing a known weight to determine the weight of the Earth. The outcome will be approximately 5.97 x 10 24 kilograms. Nevertheless, why limit oneself to this? It is also feasible to apply the G value to ascertain the weight of the sun. Allow me to provide a brief explanation of the procedure involved in this calculation.
Consequently, let’s consider a planet such as Mercury, which revolves around the sun. Given that the orbit is circular, Mercury is exposed to a gravitational force emanating from the Sun.
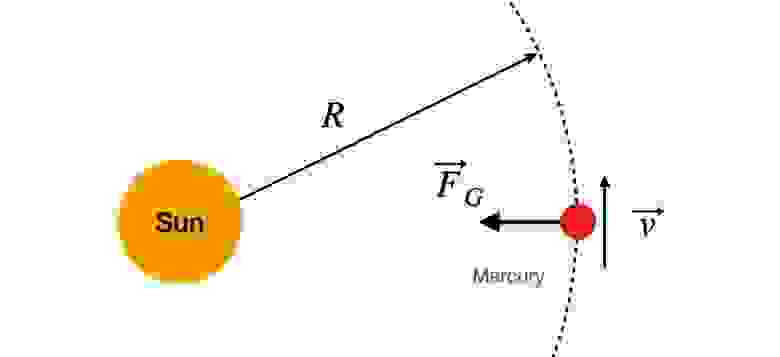
Illustration: RHETT ALLAIN
The planet’s mass can be determined using the formula provided. It is important to note that the gravitational force is responsible for the planet’s acceleration and its movement in a circular path, referred to as centripetal acceleration. However, this centripetal acceleration is influenced by two factors: the angular velocity (ω) and the orbital distance (R). As the gravitational force is the only force acting on the planet, it can be determined by multiplying the mass with the acceleration. This relationship can be expressed as follows.
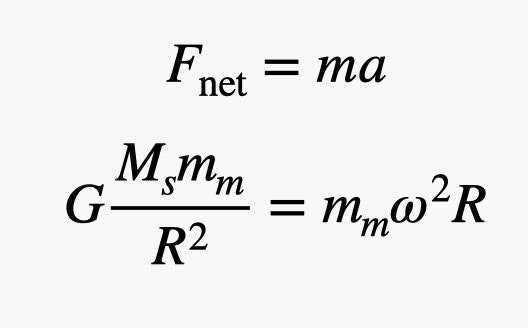
Image: RHETT ALLAIN
To determine the mass of the sun, it is assumed that the sun is stationary, which is generally true. The mass of the sun is incredibly large compared to the mass of Mercury, making the mass of Mercury irrelevant. Thus, the formula for finding the mass of the sun is:
Image: RHETT ALLAIN
Now all you have to do is determine the distance between the orbital point and the center of Mercury. This can be accomplished by initially considering the Earth’s radius. Next, ascertain the angular velocity by observing the time it takes for Mercury to complete one full revolution around the sun. Once you’ve obtained this information, you’re ready to proceed. You have access to the gravitational constant and can calculate the mass of the Sun. It’s remarkable that all of this originates from a few small masses on a horizontally rotating rod, but it’s undeniably true.
Prior to utilizing the law of universal gravitation, it’s crucial to address a significant detail.
The law of universal gravitation F = ?(m1m2/r 2 ) can be strictly applied in cases where there are no doubts. To apply the law to two close bodies, the distance between them should be much larger than their dimensions, allowing us to treat them as points. However, when dealing with two close bodies, we need to mentally divide them into small pieces, calculate the force F for each pair, and then vectorially add all the forces.
In theory, this process is simple, but in practice, it can be quite challenging.
However, nature has provided us with assistance. The calculation reveals that if the particles of an object interact with a force that is proportional to 1/r^2, then spherical objects possess the property of being attracted to each other as if they were point masses located at the centers of the spheres. For two spheres that are close to each other, the formula F = ?(m1m2/r^2) holds true, just as it does for spheres that are far apart, if r is the distance between the centers of the spheres. We have previously employed this principle when calculating the acceleration due to gravity on the surface of the Earth.
Now, we are permitted to utilize the formula for gravitation to determine the force of attraction between a body and the Earth. In this context, r represents the distance from the center of the Earth to the body.
If we consider M as the Earth’s mass and R as its radius, we can calculate the gravitational force exerted by a body with mass m on the Earth’s surface.
However, the body’s weight is always expressed as mg. Thus, the gravity acceleration
Now we can explain how the Earth is measured. g, ? and R – are known quantities, and the Earth’s mass can be calculated using this equation. The Sun’s mass can be determined in a similar manner.
But can we call this calculation weighing? Absolutely, we can; indirect measurements are just as important in physics as direct ones.
Now let’s solve an intriguing problem.
In the plans to create world television, the creation of a “hovering” satellite plays a significant role, i.e. a satellite that would constantly remain in the same position on the equatorial plane above the Earth’s surface. Would such a satellite experience friction? This depends on how far it would need to rotate from the Earth.
By equating the values of accelerations, we can derive the following equation:
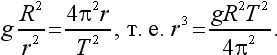
By substituting the approximate values g = 10 m/s 2 , R = 6-10 6 m, and T = 9-10 4 s, we obtain: r 2 = 7-10 22 , which means that r ? 4-10 7 m = 40,000 km. At such an altitude, there is no atmospheric resistance, and the potential “hovering” satellite, if it were to be created, would not experience any deceleration in its “stationary orbit”.
Related Articles
Expanding the Earth’s Size
Expanding the Earth’s Size At first glance, it may appear that Newton’s law, which is simple and straightforward, would not permit such a possibility even in theory: gravity is determined by the Earth’s mass, which cannot be decreased. However, this is not entirely accurate. We are referring to the gravitational pull exerted on the Earth’s surface.
To speed up the rotation of the Earth.
Mechanics also suggests an alternative method to lessen the Earth’s gravitational pull. This method involves increasing the velocity of the Earth’s rotation around its axis. Currently, the centrifugal force generated by the Earth’s rotation already reduces the weight of objects.
3. Earth Astrology Do you remember what a horoscope is? Let me remind you – it’s a beautifully crafted piece of paper containing predictions about one’s destiny. The author anticipates that the reader will come across this piece of paper on their own, but the initial stage of this document is of utmost importance, so to speak.
4. Earth Questionnaire
4. Earth Survey And now, to conclude the discussion about our home planet, and to assess our knowledge of it, the author suggests a familiar and reliable method: referring to an authoritative source.
4. Earth’s Distance
4. Earth’s Distance The average distance between the Earth and the Moon is 384,400 kilometers. This is approximately 30.14 times the diameter of the Earth. We use the term “average distance” because the Moon’s orbit is an ellipse (as stated in Kepler’s law), and at its farthest point (apogee), the Moon is approximately 405,500 kilometers away.
18. What is the method used to determine the age of the Earth?
18. What is the method used to determine the age of the Earth? The inquiry into the age of the Earth is intertwined with the age of the Sun, as the Earth cannot be older (otherwise it would be frozen). The duration of the Sun’s brightness is contingent upon the amount of heat it has emitted and the origin of its energy. The earliest
42. Is the Earth’s climate influenced by the Sun?
42. Does the Earth’s climate depend on the Sun? The Earth’s climate is regulated by solar energy. Even small variations in solar radiation can have significant impacts on weather patterns and overall climate conditions. Throughout its existence, the Sun, similar to other stars, has gradually become more intense and hotter. Looking ahead, this trend is expected to continue in the distant future.
Chapter 15. Cecilia Payne’s research has revealed that our Sun and other celestial stars function as enormous energy generators, operating according to the principle of E=mc2. However, the process of hydrogen fusion into helium can potentially lead to
4.1 The Threat of Comets to Earth
4.1 The Threat of Comets to Earth Comets, much like asteroids, are small celestial bodies within our solar system. The nuclei of known comets are generally quite minuscule, typically not exceeding 50 km in diameter, though it is possible for some nuclei to reach hundreds of kilometers in size. For instance, the diameter of
8.4 Objects at risk on the Earth’s surface
As human civilization advances, new aspects of asteroid danger continue to emerge. This includes high hydroelectric dams, large chemical plants, and powerful structures that are vulnerable to potential asteroid impacts.
From the Earth to the Sun
What can be more fragile and exquisite than the silk thread spun by a spider? Its delicate nature has earned it a legendary reputation, and not without cause: a single strand of spider silk is ten times thinner than a human hair, with a cross-section measuring a mere 0.005 mm. This incredible thinness accounts for the ethereal quality of the spider’s web, as the material itself is weightless and delicate.





