
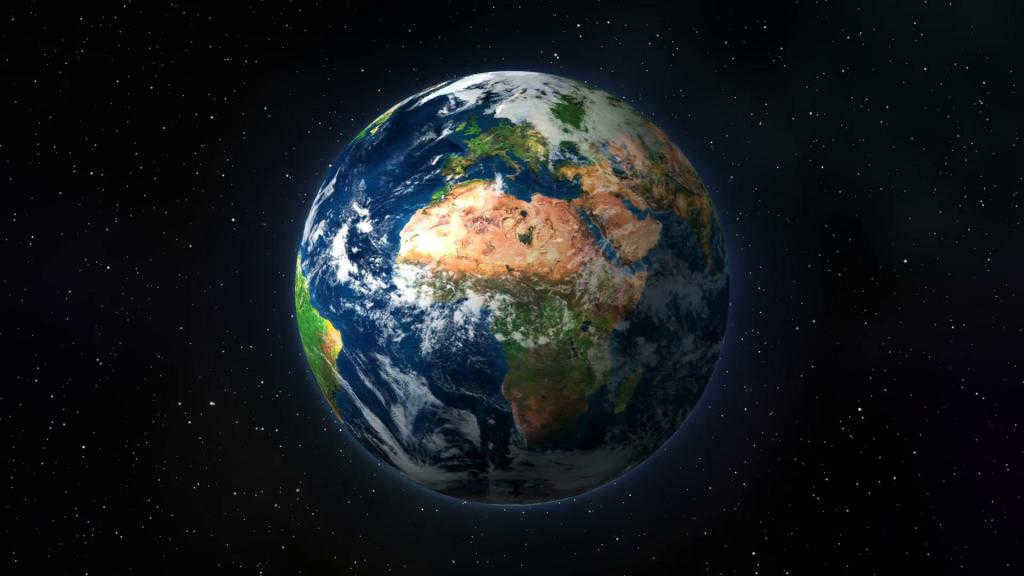
Earth is a one-of-a-kind planet within our solar system. It may not be the smallest, but it certainly isn’t the largest either – it holds the fifth position in terms of size. Among the planets within the Earth group, it reigns supreme in terms of mass, diameter, and density. This celestial body resides in the vast expanse of outer space, making it quite challenging to determine its weight. Placing it on a scale simply isn’t an option, so scientists calculate its weight by adding up the mass of all the various substances that compose it. This calculation amounts to approximately 5.9 sextillion tons. To truly grasp the magnitude of this figure, let’s write it out mathematically: 5 900 000 000 000 000 000 000. The sheer number of zeros can be quite overwhelming.
The quest to determine the magnitude of the planet throughout history
Throughout the ages, scientists from various cultures and time periods have embarked on a mission to uncover the true weight of planet Earth. In ancient times, it was widely believed that the Earth was a flat disc supported by massive whales or turtles. In certain civilizations, elephants were thought to bear the weight instead of whales. Regardless, diverse societies across the globe shared the common notion that our planet was flat and possessed definitive boundaries.

Shape and weight concepts underwent changes in the Middle Ages. G. Bruno was the first to discuss the spherical shape, but his beliefs led to his execution by the Inquisition. Another significant contribution to scientific understanding of Earth’s radius and mass was made by the explorer Magellan, who proposed that the planet was round.
Initial findings
The planet Earth is a tangible entity with distinct characteristics, one of which is its mass. This revelation initiated a plethora of investigations. According to the principles of physics, weight is the resultant force exerted by an object on its support. Given that the Earth lacks any support, it can be deduced that it lacks weight, but possesses a substantial mass.
For the initial occasion of ascertaining the magnitude of the planet, Eratosthenes, an ancient Greek scientist, made an attempt. He conducted measurements of shadows in various Greek cities and subsequently compared the acquired data, aiming to compute the planet’s volume. Following Eratosthenes, G. Galileo, an Italian scientist, endeavored to perform calculations. It was Galileo who unveiled the principle of gravitational free fall. The responsibility of determining the Earth’s weight was then assumed by I. Newton, who, through his attempts at measurement, succeeded in establishing the law of gravity.

The weight of planet Earth was successfully determined for the first time by the Scottish scientist N. Makelin. Based on his calculations, the planet’s mass is estimated to be around 5.9 sextillion tons. However, it is important to note that this figure is not static and has increased over time. The variations in weight can be attributed to the accumulation of cosmic dust on the planet’s surface. Approximately thirty tons of dust settle on Earth each year, contributing to its overall weight.
Mass of the Earth
In order to determine the exact weight of the Earth, it is necessary to have knowledge of the composition and weight of the various substances that make up the planet.
- Mantle. The weight of this layer is approximately 4.05 X 10 24 kg.
- Core. This layer has a lower weight compared to the mantle – only 1.94 X 10 24 kg.
- Crust of the Earth. This part is very thin and has a weight of only 0.027 X 10 24 kg.
- Hydrosphere and atmosphere. These layers have weights of 0.0015 X 10 24 and 0.0000051 X 10 24 kg, respectively.
By summing up all of these data, we can determine the weight of the Earth. However, different sources provide different estimates for the mass of the planet. So, how much does planet Earth weigh in tons, and what are the weights of other planets? The weight of the planet is 5.972 X 10 21 tons. It has a radius of 6,370 kilometers.

The weight of the Earth can be easily determined based on the principle of gravity. To do this, one can use a thread and suspend a small weight from it, measuring its precise location. Next to it, a ton of lead is placed, resulting in an attraction between the two bodies. This attraction causes the weight to deflect to the side by a small distance. Even a deviation as small as 0.00003 mm allows for the calculation of the planet’s mass. By measuring the force of attraction between the weight and the force of attraction between the small weight and the large weight, it is possible to obtain the necessary data for calculating the mass of the Earth.
The weight of Earth and other planets
Earth is the biggest planet in the Earth group. In comparison, Mars weighs about 0.1 times the weight of Earth, while Venus weighs 0.8 times. Mercury’s weight is approximately 0.05 times that of Earth. The gas giants are significantly larger than Earth. When comparing Jupiter to our planet, the giant is 317 times bigger, while Saturn is 95 times heavier and Uranus is 14 times heavier. There are planets that weigh 500 times or even more than Earth. These are enormous gas bodies situated outside of our solar system.

Ever since 2005, the consensus has been that there are a total of eight planets in our solar system. This conclusion was reached after the groundbreaking discovery made by M. Browne, which conclusively proved that Pluto is indeed a dwarf planet. Naturally, there is some debate among scientists regarding the classification of Pluto, with some arguing that it should not be considered a true planet.

Based on the most recent calculations in astronomy, the Earth’s mass is determined to be 5.97×1024 kilograms. Regular measurements of this quantity clearly indicate that it is not fixed. However, it would be inaccurate to suggest that the planet is expanding.

This article provides a comprehensive overview of Saturn, including its mass, size, description, and a comparison with Earth. It offers a wealth of information that may introduce you to new and intriguing facts about the gas giant.
This article provides information about the surface area of planet Earth, including the proportion of the world’s oceans and landmasses. It also explores the remarkable convergence of favorable conditions that led to the formation of our planet and the subsequent development of water bodies, such as seas and continents.

The gas giants of our Solar System, much like their counterparts elsewhere, are primarily made up of gases. These planets possess such distinct physical and chemical properties from the rest of our surroundings that they inevitably pique the curiosity of even the most indifferent observers.
Mars, the fourth planet in our solar system, has served as the backdrop for countless works of science fiction. Many authors and filmmakers have chosen to populate Mars with extraterrestrial civilizations, some of which are hostile while others are friendly towards humanity. However, extensive research has conclusively shown that Mars does not harbor advanced forms of life. Nevertheless, this does not diminish the intrigue and fascination surrounding the Red Planet. In fact, numerous scientists are captivated by Mars and devote their efforts to unraveling its mysteries and understanding its unique characteristics.

Scientists have been pondering the question of the Earth’s formation for countless centuries. Throughout history, various theories have emerged, ranging from religious explanations to contemporary ideas based on data collected from the depths of space. However, due to the lack of first-hand observation, researchers must rely solely on indirect “evidence” to piece together the puzzle.

Jupiter is located at an average distance of 778 million kilometers from the Sun, which is equivalent to 5.2 astronomical units. It takes approximately 43 minutes for light to travel from the Sun to this massive gas planet.
Galileo Galilei, an Italian scientist, philologist, mechanic, critic, poet, astronomer, and physicist, had a profound impact on the advancement of scientific knowledge during his era. He emphasized the importance of empirical evidence and vehemently opposed scholastic doctrines. Galileo is credited with inventing hydrostatic scales, the thermoscope, and making significant improvements to the telescope.

Our magnificent planet Earth, nestled in the vast expanse of the universe, is truly one-of-a-kind. It possesses the perfect conditions for organic life to thrive, with its unique chemical composition, atmosphere, and magnetic field all playing crucial roles in its emergence and diversity.
Once considered boundless, we now realize that our planet has its limits. However, long before it became crowded, humans were able to determine the size and weight of their home planet.
How was it determined – you don’t weigh the planet, do you (which would require scales)?
But you don’t have to put it on a scale.
First we had to calculate the size of the Earth – this was accomplished in ancient Greece by Eratosthenes, who compared the length of the shadow of a stick stuck in the ground in different cities.
The next step was taken in the 17th century: Galileo Galilei determined the acceleration of free fall.
Then it was necessary to “plug in” the data into the formula.
The mass of the Earth was first calculated in 1774 – and it was done by a Scottish scientist named Dr. N. Makelin. He arrived at a figure of 5,879,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 tons – 5.879 sextillion tons (that’s how it’s written).
Currently, the estimation of the Earth’s mass differs slightly – 5.976 sextillion tons, not due to miscalculations, but due to the continuous increase in weight: the accumulation of space dust occurs constantly, with an approximate annual amount of 30 thousand tons.
The composition of the Earth is not uniform. How is the distribution of its mass organized?
The mantle, consisting of silicates of iron, magnesium, and calcium, bears the majority of the Earth’s mass, which amounts to 4.043 1024 kg. Following it is the core, primarily composed of iron (possibly iron and nickel), with a weight of approximately 1.93,1024 kg. The Earth’s crust, where we reside, is significantly lighter, weighing only 0.026,1024 kg, while the oceans, crucial for the existence of life, account for 0.0014 1024 kg. The atmosphere, in conjunction with water, which played a vital role in enabling life on our planet, is even lighter, weighing a mere 0.0000051 1024 kg.
How does the Earth compare to its “siblings” in the Solar System in terms of mass?
Let’s be honest – it’s not in first place. It falls far behind the gas giants: it’s even smaller than the “smallest” of them – Uranus – by a factor of 14.5, Neptune – by a factor of 17.2, Saturn’s mass is 95.1 times greater than Earth’s, and Jupiter is a whopping 317.8 times heavier than our planet (but this record holder is far ahead of all the other planets in the solar system: its mass is 2.47 times greater than all of them combined).
But where our planet really shines is among the rocky planets of the Earth group (these are the planets that have a solid surface – unlike the gas giants, with high density and consisting mainly of iron and silicates – unlike the rocky and icy dwarf planets): Mars has a mass of 0.108 Earth mass, Venus – 0.815, Mercury – 0.055. No matter what, it’s nice to know that our home planet is at least somewhere – in first place!
It’s quite a fascinating question, and it leads to another equally intriguing one – how did scientists manage to measure the mass of our planet?
But let’s dive into it.
Based on their calculations, the Scottish scientist determined that the Earth’s weight is 5,879,000,000,000,000,000,000. That’s an astonishing number.
Modern scientists have replicated the calculations and arrived at a figure of 5,976,000,000,000,000,000,000 (5.976 sextillion tons).
As you can see, the difference compared to the 18th-century calculations is “only” 97 sextillion tons, which is relatively small.
It’s worth noting that the weight of our planet increases every year. The culprit is space dust, which deposits around 30,000 tons on the Earth’s surface annually.
How was the measurement conducted?
Naturally, scientists were unable to physically place the entire cosmic body on a massive scale to obtain the result.
Instead, they had to employ more complex methods that were equally precise. To determine the mass of the Earth, they utilized the force of gravity, which is responsible for the attraction between any objects in our universe.
The scientists suspended a minuscule and lightweight object from a string and meticulously recorded its position within space. They then positioned a substantial lead cube weighing one ton adjacent to the object. As we are aware (aren’t we?), the greater the mass of an object, the more potent its gravitational field and subsequent attraction to surrounding bodies.
The gravitational field generated by the one-ton lead cube attracted the small object by a minuscule 0.000.02 millimeters, a measurement sufficient for the scientists to calculate the mass of our Earth using mathematical formulas.
Every individual, regardless of age, is aware that the Sun is a star situated at the core of our solar system. This celestial body, known as the Sun, serves as the focal point around which all other objects orbit. It is worth mentioning that the Sun holds the distinction of being the largest entity within our planetary system, accounting for an impressive 99.866% of its total mass. To put things into perspective, consider the white dot depicted in the image, which represents Earth. Now, let us calculate the ratio between the mass of the Sun and the mass of our home planet.
The Sun is the sole star within our solar system. All of the planets, including Earth, orbit around it, as well as thousands of meteorites, hundreds of comets, and other small celestial bodies. Our star is truly immense, being hundreds of times larger than any of the planets, including Jupiter. Additionally, it is the most massive object in our system. Not only is the Sun enormous, but it is also composed of numerous heavy elements…
What would occur if all of the water on Earth were gathered into one colossal sphere? The image depicts the size of the sphere in relation to the size of our planet. The diameter of the resulting sphere is 1.385 kilometers, while the volume of water is 1.386.000.000.000 cubic kilometers. This sphere encompasses all the water found in the seas, oceans, glaciers, rivers and lakes, as well as groundwater and atmospheric water, water found in plants, animals, and even within yourself.
We are all familiar with the sight of the Moon, our natural satellite, in the sky every day. However, it did not always exist. Like any other object in the Universe, the Moon was formed as a result of a specific event. Today, I invite you to learn about the event that gave birth to the Moon. According to the current prevailing theory, the history of Earth’s satellite can be described as follows: 4.5 billion years ago…
One might wonder how to determine the weight of the Earth when it is suspended in outer space. After all, we can’t simply put it on a scale! However, it is possible to calculate the Earth’s weight by adding up the weight of the substances that compose it.
What is the weight of the Earth in tons?
According to scientists, the weight of planet Earth is about 6.6 sextillion tons. To put it in full, the weight of the Earth is 6 600 000 000 000 000 000 000 000 000 000 000 000 000 tons.
Scientists have determined the Earth’s mass by observing the gravitational force between objects. The principle of Earth’s gravity states that the more massive and closer objects are to each other, the stronger the gravitational pull. Conversely, objects with less weight and farther apart have a weaker gravitational force.
The method of “measuring the mass of the Earth”
- Take a small object with a known weight;
- Suspend the object in a stable position;
- Measure the exact position of the suspended object;
- Bring a heavy object close to the suspended weight;
- Observe the deflection of the weights from their original position due to the gravitational attraction between them;
- Calculate the weight of the Earth based on the angle of deflection.
The same technique is applied to determine the mass of the Earth. To accomplish this, it is necessary to determine the gravitational force between our planet and the weight, as well as between the heavy object and the weight. The relative difference between these two forces will provide us with the Earth’s mass.
The ancient Greek scientist Erastostosthenes made the first attempt to determine the weight of the Earth in kilograms. He conducted measurements of shadows using a regular stick in various Greek cities and compared the results. As a result, Eratosthenes derived a formula for calculating the Earth’s volume.
However, it was Henry Cavendish who accurately calculated the weight of the Earth. He conducted experimental calculations using lead balls, torsion scales, and his own intelligence. Surprisingly, in the late seventeenth century, Cavendish achieved remarkably precise results! Although there is evidence suggesting that Dr. N. Makelin also made calculations in 1774 and shared the credit with Cavendish. According to Makelin’s data, the weight of the Earth was 5,870 sextillion tons.
While it is nearly impossible to ascertain the exact weight of planet Earth, it is practically unfeasible to determine its precise mass, which is estimated to be around 6.6 sextillion tons.
How was this figure determined? This fascinating revelation, along with numerous other astounding findings, will be explored further in the following discussion.
How was the weight of planet Earth determined?
The planet’s weight was determined through the calculation of its mass, which is based on the universally recognized property of bodies attracting each other. This property serves as the foundation for the Earth’s own gravitational attraction.
By relying on the principles of this law, scientists have established that the force of attraction between two bodies directly depends on their mass and the distance between them.
In conclusion, scientists have observed that larger objects have a higher force of attraction, while objects that are farther apart have a weaker force of attraction.
Conducting Practical Research with Small Masses
To determine the mass of the planet, scientists conducted an experiment using a relatively small weight compared to the Earth’s mass. They suspended this weight on a cable and carefully measured its precise position in space. Additionally, a ton of metal (used as a reference weight) was attached to the weight, which remained motionless on the cable. Over time, both the weight and the metal began to attract each other.
During the attraction process, the weight deviated from its original position by a minuscule amount. This deviation was within the range of a millionth of a centimeter, highlighting the need for highly accurate and practical measurements to be made.
After determining the extent of the current deviation in weight, the scientists were able to commence the analytical calculation of the requisite weight of the planet. The only requirement was to establish the gravitational force between our planet and the cargo, as well as between the cargo and the metal itself.
The key point is the relative difference that was established between the two.
What is typically meant by the term “Earth’s mass”
Many individuals are unaware of the full extent of what is encompassed within the mass of our planet. Upon closer examination, it becomes evident that the planet’s surface is comprised of a crust composed of relatively solid rocks. Beneath the crust lies the mantle, which is also comprised of solid rock, while at the center resides the planetary core. It is important to note that the core is characterized by extremely high temperatures, which accounts for its molten composition.
There has been a significant amount of controversy and debate within the scientific community regarding whether the Earth is undergoing expansion, if the continents are moving, or if they are in a fixed position.
As a result of this expansion and movement of the continents, it raises the question of whether there is an increase in the planet’s mass. On one hand, it is worth noting that if we examine the edges of Africa, Europe, and America and combine them, they form a single continent.
These findings have been supported by mathematical studies, providing clear evidence of the former unity of all continents. Therefore, it can be concluded that the continents are expanding and moving, causing changes in the shape of the planet and an increase in its weight.
P.S.. The piece of writing – what is the weight of planet Earth was released in – .
Earth is situated in the vastness of outer space, making it incredibly challenging to determine the planet’s weight. Placing it on a scale is simply not an option! Consequently, we will focus on the weight of the substances that compose the Earth, which is its mass. The Earth’s mass is approximately 6.6 sixtillion tons. To grasp the magnitude of this number, let’s write it out: 6 600 000 000 000 000 000 000. So how did scientists ascertain the mass of the Earth? They based their calculations on the well-known principle that all bodies experience gravitational attraction towards one another. It is this characteristic that forms the basis of the Earth’s gravitational pull. According to the law of Earth’s gravitation, the attractive force between two bodies depends on their masses and the distance separating them. The larger the objects, the stronger the force of attraction, and conversely, the greater the distance, the weaker the attraction. Let’s delve into how scientists “weighed” the Earth. To accomplish this, they utilized a large weight, suspending it and precisely measuring its position. They then brought a ton of metal in proximity to the suspended weight. The weight and the metal started to attract each other. The weight deviated slightly from its initial position (the extent of deviation is approximately one millionth of a centimeter. This is why measurements must be executed with utmost precision). By determining the magnitude of the weight’s deviation, scientists were able to commence calculating the Earth’s mass. To do this, it is necessary to ascertain the gravitational force between the Earth and the weight, as well as between the metal and the weight. The relative difference between the two will provide us with the mass of the Earth. What comprises the Earth’s mass? The Earth’s surface is coated with a solid rock crust, beneath which lies the Earth’s mantle, also composed of solid rock. In the very center resides the planet’s core. The temperature at the Earth’s core is exceedingly high, resulting in the core being composed of molten substances.
The Earth’s mass ( M E or M 🜨 where 🜨 is the recognized astronomical symbol for Earth), is a measurement of mass that corresponds to the mass of the planet Earth. The current most accurate estimation of Earth’s mass is M 🜨 = 5.9722 × 10 24 kg, with a standard uncertainty of 6 × 10 20 kg (relative error 10 -4 ). The recommended value in 1976 was (5.9742 ± 0.0036) × 10 24 kg. This is equal to an average density of 5515 kg.m -3 .
The Earth mass serves as a standard unit of mass in the field of astronomy, specifically when referring to the mass of other planets, including both solid Earth-like planets and exoplanets. One solar mass is approximately equivalent to 333,000 Earth masses. It is important to note that when calculating the mass of the Earth, the mass of the Moon is excluded. The Moon’s mass accounts for roughly 1.2% of the Earth’s total mass, resulting in a combined mass of the Earth and Moon system of approximately 6.0456 × 10 24 kg.
The majority of the Earth’s mass is comprised of iron and oxygen, each contributing about 32% to the total mass. Magnesium and silicon make up roughly 15% each, while calcium, aluminum, and nickel account for approximately 1.5% each.
Measuring the mass of the Earth accurately is a challenging task as it involves measuring the gravitational constant, which is a fundamental physical constant that is known with the least accuracy due to the relatively weak gravitational force. The first attempt to measure the mass of the Earth with some degree of accuracy (within approximately 20% of the correct value) was made in the Schiehallion experiment in the 1770s. Subsequently, the Cavendish experiment carried out in 1798 achieved a measurement within 1% of the modern value.
Mass unit in astronomy
The estimated mass of the Earth is:
M⊕ sign equals (5.9722 ± 0.0006) × 1024 kilograms = (5.9722 ± 0.0006) times 1024 k grams = > > > > >
which can be expressed in terms of the Sun’s mass as:
M⊕ sign equals 1,332,946.0487 ± 0.0007 M⊙ ≈ 3.003 × 10-6 M⊙ = > > >>
The ratio of the mass of the Earth to the mass of the Moon has been measured with great precision. Current best estimate:
M⊕ / ML sign is equal to 81.3005678 ± 0.0000027 / ML = 81.3005678 ± 0.0000027>
The geocentric gravitational constant for Earth, known as derivation G M 🜨, is referred to as the geocentric gravitational constant and has a value of (398,600,441 0.8 ± 0.8) × 10 6 m 3 s -2 . It is determined through the utilization of laser location data obtained from Earth-orbiting satellites like LAGEOS-1 . The calculation of the G M 🜨 product is also feasible by observing the movement of the Moon or the period of a pendulum at various heights. Nevertheless, these approaches are less precise compared to the observations made on artificial satellites.
The uncertainty of the geocentric gravitational constant is incredibly small, only 2 × 10-9, which is 50,000 times smaller than the uncertainty for M itself. M can only be calculated by dividing the product GM by G, and the value of G is known with a relative uncertainty of 4.6 × 10-5 (the 2014 NIST recommended value). Therefore, M would have the same level of uncertainty at best. Because of this, astronomers prefer to use the unreduced product GM or mass ratios when comparing and contrasting planetary objects, rather than using mass in kilograms.
The density of Earth varies significantly, ranging from less than 2700 kgm -3 in the upper crust to 13,000 kgm -3 in the inner core. The inner core, which accounts for 15% of Earth’s volume, contains more than 30% of its mass. The mantle, on the other hand, makes up 84% of the volume and nearly 70% of the mass. The crust, in contrast, represents less than 1% of the total mass. The Earth’s mass is primarily composed of iron-nickel alloy (95% iron) in the core (30%), silicon dioxides (about 33%) and magnesium oxide (about 27%) in the mantle and crust. Iron (II) oxide contributes 5%, aluminum oxide accounts for 3%, and calcium oxide contributes 2%. Additionally, there are numerous trace elements, with iron and oxygen each making up 32% in elemental terms, magnesium and silicon each representing 15%, and calcium, aluminum, and nickel each accounting for 1.5%. Carbon makes up 0.03% of Earth’s mass, water comprises 0.02%, and the atmosphere represents about one part per million.
Evolution of measurement systems

The Mendenhall gravimeter, created in 1890 by Thomas C. Mendenhall, revolutionized the field of measuring the Earth’s local gravitational field. This portable device provided the most precise relative measurements to date.
Calculating the mass of the Earth is an indirect process that involves determining various quantities, such as density, gravity, or the gravitational constant. Early experiments, like the Schiehallion experiment in the 1770s, underestimated the Earth’s mass by approximately 20%. However, the Cavendish experiment of 1798 yielded a much more accurate measurement within 1%. Over time, advancements in technology and methodology reduced the uncertainty to 0.2% in the 1890s and further down to 0.1% by 1930.
Since the 1960s (WGS66), the accuracy of the Earth’s shape has been known to be superior to four significant figures. As a result, the main source of uncertainty in the Earth’s mass has been the measurement of the gravitational constant. In the 1970s, the relative uncertainty was 0.06%, which improved to 0.01% (10 -4 ) by the 2000s. At present, the relative uncertainty is 10 -4, equivalent to 6 × 10 20 kg in absolute terms, which is comparable to the mass of a small planet (70% of the mass of Ceres).
Initial calculations
Before the direct measurement of the gravitational constant, approximations of the Earth’s mass were limited to approximations of the Earth’s average density based on observations of the crust and approximations of the Earth’s volume. In the 17th century, approximations of the Earth’s volume were derived from an approximated circumference of 60 miles (97 km) in terms of latitude degrees, which corresponded to a radius of 5,500 km (86% of the Earth’s actual radius of approximately 6,371 km). As a result, the estimated volume was about one-third smaller than the actual value.
In the 18th century, scientists utilized Newton’s law of universal gravitation to indirectly determine the Earth’s average density by estimating the gravitational constant (as it is known today). Early attempts at estimating the Earth’s average density involved observing the slight deviation of a pendulum near a mountain, much like the Schiehallion experiment. Newton himself examined this experiment in his work “Beginnings,” but he pessimistically concluded that the effect would be too minuscule to be accurately measured.
In an expedition that took place from 1737 to 1740, Pierre Bouguer and Charles Marie de la Condamine aimed to determine the Earth’s density by measuring the pendulum’s period and the force of gravity at different altitudes. They conducted experiments at Pichincha volcano and Mount Chimborazo in Ecuador and Peru. In a paper published in 1749, Bouguer noted that they were able to observe a deviation of 8 angular seconds. Although the accuracy was not sufficient to accurately calculate the average density of the Earth, Bouguer stated that it was enough to prove that the Earth was not hollow.
Schiehallion experiment
In 1772, Neville Maskelyne, the Astronomer Royal, proposed a new experiment to the Royal Society. He believed that this experiment would bring honor to the nation where it was conducted. Maskelyne suggested that either Whernside in Yorkshire or the Blencathra-Skiddaw massif in Cumberland would be suitable locations for the experiment. To further explore this idea, the Royal Society established a Committee of Attention, which included Maskelyne, Joseph Banks, and Benjamin Franklin as members. The committee then enlisted the help of astronomer and surveyor Charles Mason to search for a mountain that would be suitable for the experiment.
In the summer of 1773, Mason made a report after an extensive search and identified Schiehallion as the most suitable candidate. Schiehallion, located in the central part of the Scottish Highlands, stood isolated without any neighboring hills, minimizing their gravitational influence. The mountain’s symmetrical east-west ridge made calculations simpler. The experiment was carried out by Nevil Maskelyne, Charles Hutton, and Reuben Burrow, and by 1776, it was completed. Hutton (1778) concluded that the average density of the Earth was equivalent to that of Mount Schiehallion. This indicated an average density about 4 1/2 times higher than that of water (approximately 9.5 g/cm3), which was about 20% lower than the present-day value. However, it still remained significantly higher than the average density of typical rock, suggesting for the first time that the Earth’s interior might be predominantly composed of metal. Hutton estimated that this metallic portion occupied around 65% of the Earth’s diameter, which is slightly higher than the modern value of 55%. With the determined average density of the Earth, Hutton was able to assign specific values in Jerome Lalande’s planetary tables, which previously only provided relative densities of major objects in the solar system.
Henry Cavendish (1798) was the first scientist to make an attempt at directly measuring the gravitational attraction between two objects in a laboratory setting. By combining Newton’s Second Law and Newton’s law of universal gravitation, he was able to determine the mass of the Earth.
In contemporary terms, the mass of the Earth is calculated using the gravitational constant and the average radius of the Earth.
Cavendish’s experiment revealed the average density of the Earth to be 5.45 g/cm3, which is approximately 1% lower than the present-day value.
The 19th century
was a time period that spanned from 1800 to 1900.

The density of the Earth was determined by Francis Bailey and Henry Foster using the Cavendish method.
Although the mass of the Earth can be inferred from the radius and density, it was not commonly expressed in absolute terms until the late nineteenth century when scientific notations using powers of 10 were introduced. This was because using absolute numbers would be too inconvenient. In Ritchie’s (1850) study, the mass of the Earth’s atmosphere is given as “11,456,688,186,392,473,000 lbs.” (1.1 × 10^19 lb = 5.0 × 10^18 kg, modern value 5.15 × 10^18 kg). Ritchie also states that “compared with the weight of the globe, this enormous sum becomes negligible.”
The mass of the Earth was first quantified in the second half of the 19th century, primarily in popular literature rather than scientific texts. Initially, it was referred to as “14 septillion pounds” (14 quadrillion pfunds) [6.5 × 10^24 kg] in Mazius’ work (1859). Beckett (1871) cites the “weight of the earth” as “5842 quintillion tons” [5.936 × 10^24 kg]. The New Volumes of the Encyclopedia Britannica (Vol. 25, 1902) provides the measurement of “Earth’s mass in gravitational measure” as “9.81996 × 6370980^2,” with the logarithm of the Earth’s mass expressed as “14.600522” [3.98586 × 10^14]. It’s important to note that this value represents the gravitational parameter in m^3-s^-2 (modern value: 3.98600 × 10^14), not the absolute mass of the Earth.
Continued experimentation with pendulums persisted throughout the initial half of the 19th century. However, by the latter half of the century, their effectiveness had diminished in comparison to the repeated trials of Cavendish’s experiment. Consequently, the current value of G (and consequently the Earth’s mass) is still determined through remarkably precise repetitions of the Cavendish experiment.
Contemporary significance
The uncertainty surrounding the current estimation of the Earth’s mass is solely attributed to the uncertainty of the gravitational constant G, particularly since the 1960s. The measurement of G is notoriously challenging, and various high-precision measurements conducted between the 1980s and 2010s have produced contradictory outcomes. Zagitov (1969) determined the value of M 🜨 to be 5.973 (3) × 10 24 kg (with a relative error of 5 × 10 -4 ) based on the measurements of G by Heylem and Chrzanowski (1942).
Since that time, there has been only a slight improvement in accuracy. Most modern measurements are repeated versions of the Cavendish experiment, producing results (within the standard uncertainty range) between 6.672 and 6.676 × 10 -11 m 3 kg -1 s -2 (with a relative error of 3 × 10 -4 ) for results reported since 1980. However, the recommended value by NIST in 2014 is close to 6.674 × 10 -11 m 3 kg -1 s -2 with a relative uncertainty below 10 -4 . The Internet Astronomical Almanac in 2016 suggests a standard uncertainty of 1 × 10 -4 for the mass of the Earth, M 🜨 5.9722 (6) × 10 24 kg
Variability
The mass of the Earth can vary due to a combination of factors, including the accretion of material and the loss of material. This loss can occur through the accretion of falling particles, such as micrometeorites and cosmic dust, as well as the loss of hydrogen and helium gas. Overall, it is estimated that the Earth loses approximately 5.5 × 10 7 kg (5.4 × 10 4 long tons) of material per year. This represents about 10-17% of the total mass of the Earth. The annual net loss of 5.5 × 10 7 kg is primarily due to atmospheric emission, which accounts for about 100,000 tons, and the accretion of falling dust and meteorites, which accounts for an average of 45,000 tons. It’s important to note that these figures have a margin of error of 0.01% (6 × 10 20 kg), but this does not significantly impact the calculated value of the Earth’s mass.
There are additional variations in mass that occur as a result of the principle of mass-energy equivalence, although these variations are relatively insignificant. It is estimated that there is a loss of mass, approximately 16 tons per year, due to a combination of nuclear fission and natural radioactive decay.
Furthermore, there are additional losses of mass from spacecraft on escape trajectories, estimated at around 65 tons per year since the mid-20th century. In the first 53 years of the space age, Earth lost approximately 3,473 tons, but currently, there is a downward trend.
Also check out

The Earth has a weight of 5.97 to 10.24 kilograms. In the solar system, it ranks fourth in terms of mass.
Mass and Density of the Earth:
The weight of the Earth is 5.97-10.24 kilograms or, to be more precise, 5.9722 ± 0.0006 – 10 24 kg.
In the field of astronomy, the weight of the Earth is represented by M⊕, where ⊕ is the symbol for the Earth.
In astronomy, the weight of the Earth is used as a non-system unit of weight. Therefore, 1 M⊕ = 5.9722 ± 0.0006 – 10 24 kg.
As a result, the weights of the other planets in the solar system can be expressed in terms of the Earth’s weight.
The weight of the Moon, which is the Earth’s natural satellite, is approximately 0.0123 times the weight of the Earth.
Jupiter’s mass is about 317.8 times greater than the Earth’s mass.
The Sun’s mass is incredibly massive, approximately 333,082 times the mass of the Earth.
Among all the celestial bodies in our solar system, Earth ranks as the fourth heaviest planet, following Jupiter, Saturn, and Neptune.
Mass, as a fundamental physical quantity, represents the gravitational properties and the inertia of an object. It is important to note that in the realm of modern physics, gravitational mass and inertial mass are considered to be equivalent.
Due to the gravitational properties and the law of universal gravitation, when two bodies have greater masses, they are attracted to each other with a stronger force. In other words, the force with which a body attracts other bodies increases as its mass increases. The measure of this gravitational attraction, or gravitational force, is determined by the gravitational mass.
According to the law of universal gravitation, the force of gravitational attraction between two masses, m1 and m2, separated by a distance r, is directly proportional to both masses and inversely proportional to the square of the distance:
where G is the gravitational constant, approximately equal to 6.67⋅10 -11 m³/(kg-s²).
The mass of a body remains constant for all processes and is not affected by the body’s velocity.
Derived from the mass of the Earth, various other properties of our planet can be determined, such as density, gravitational acceleration, first and second escape velocities, and more. The average density of the Earth (ρ) is calculated to be 5.5153 g/cm³.
The average density of the Earth (ρ) is 5.5153 g/cm³ or 5,515.3 kg/m3.
The force of gravity and the rate of free fall on Earth:
The rate of free fall on Earth (g) is 9.81 m/s² and varies from 9.832 m/s² at the poles to 9.78 m/s² at the equator.
The rate of free fall is determined using the equation:
r² is the square of the radius of the planet, m.
The weight and mass of an object on Earth are equivalent. This implies that an individual with a mass of 72 kg will have a weight of 72 kg on Earth. To be more precise, the weight of an individual on Earth is 72 kg – 9.81 m/s² = 706.32 N.
Weight refers to the amount of force exerted on an object by the gravitational pull of a celestial body, such as the Earth or the Sun. It is the force that prevents an object from freely falling. The weight of an object at rest in a frame of reference is equal to the force of gravity acting on it. Gravity, in turn, is the attractive force between an object and a celestial body.
The weight, or force of gravity, can be calculated using the formula F = m * g, where g is the acceleration of free fall, measured in m/s^2.
If we were to consider other planets in the solar system, a person with a mass of 72 kg would have different weights:
On the Sun, a person would weigh approximately 2,010.96 kg, which is equivalent to about 2 tons.
Primary orbital velocity and secondary orbital velocity on Earth:
The primary orbital velocity (v1) on Earth is 7.91 km/s.
The primary orbital velocity, also known as the circular velocity, is the minimum horizontal velocity that must be given to an object at a certain height above the planet’s surface in order for it to orbit the planet in a circular path.
The primary orbital velocity depends on the mass and radius of the celestial body, as well as the altitude above its surface.
The primary orbital velocity can be calculated using the following formulas:
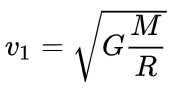
How to determine the mass of the Sun?
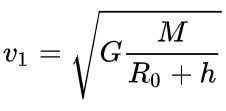
,
h is the altitude above the planet surface, m.
The second orbital velocity (v2) on Earth is 11.186 km/s.
The second orbital velocity (also known as the parabolic velocity or escape velocity) is the minimum velocity required for an object (such as a spacecraft), with negligible mass compared to the celestial body (such as a planet), to overcome the gravitational pull of the celestial body and escape its orbit.
The second orbital velocity depends on the radius and mass of the celestial body.
The second orbital velocity can be calculated using the following formulas:
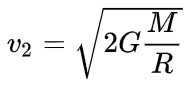
,
.
Variation in Earth’s Mass:
Earth’s mass is not constant and currently experiences a net loss. This decrease in mass leads to a weakening of Earth’s gravitational pull, affecting its ability to retain the atmosphere.
There are various factors that contribute to the change in Earth’s mass.
Factors that contribute to an increase in Earth’s mass:
– Space debris such as meteors, dust, and comets, add approximately 40 thousand tons to Earth’s mass each year.
Factors that contribute to a decrease in Earth’s mass:
– The dissipation of atmospheric gases includes the release of hydrogen (3 kg/sec, or 95000 tons per year) and helium (1600 tons per year). Moreover, some of the electrons from the atoms of atmospheric gases escape at a faster rate than the atoms themselves;
– Artificial satellites, orbiting at a distance, have the capability to exit the vicinity of Earth (approximately 65 tons per year);
– The heating of the Earth, caused by both human activities and global warming, along with solar radiation, can intensify the thermal movement of molecules, thus contributing to the escape of matter from the atmosphere.
Mass Distribution of Earth:
The planet Earth is composed of various layers, including the lithosphere, which consists of the core, mantle, and crust, as well as the hydrosphere and atmosphere.
The distribution of mass on Earth can be described as follows:
– The core has a mass of approximately 1.93 × 10^24 kg.
– The mantle has a mass of around 4.043 × 10^24 kg.
– The crust accounts for about 0.026 × 10^24 kg.
– The hydrosphere contributes to a mass of approximately 0.0014 × 10^24 kg.
– Finally, the atmosphere, which makes up a minuscule portion, weighs about 0.0000051 × 10^24 kg.
It is not widely known that people had concrete beliefs about the Earth’s shape and size before the start of our era. For example, the renowned Greek philosopher Aristotle (384 – 322 BC) was convinced that the Earth was spherical. As evidence, he pointed to the circular shadow cast by the Earth during lunar eclipses, as only a sphere can consistently produce a round shadow when illuminated from any angle.
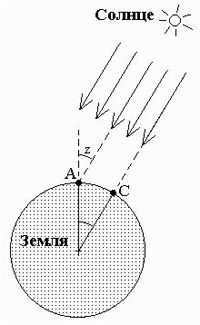
Based on the latest definitions, there is a 7°7' latitude difference between Alexandria and Assouan, and these two cities are not located on the same meridian (Assouan is approximately 3° east of Alexandria). However, Eratosthenes’ astronomical calculations were remarkably accurate given the time period. Unfortunately, the exact length of the Egyptian stage was not known, with different scientists estimating it to be between 158 and 185 meters. As a result, it is currently impossible to determine the true accuracy of Eratosthenes’ initial degree measurement. Nevertheless, the fundamental principles of Eratosthenes’ method remain valid and are still used today.
It is perplexing to consider that over a millennium and a half later, Christopher Columbus made such a significant error in estimating the size of the Earth that he mistakenly believed the American continent to be a part of India!
The size of the Earth was next attempted to be determined by Posidonius. (Posidonius of Apamea in Syria, a stoic philosopher, mathematician, and astronomer, BC. Chr. In philosophy, he represented syncretism; as an astronomer, he is known for his attempt (the second, the first belonging to Eratosthenes) to determine the size of the globe.) Alexandria and the island of Rhodes were selected as the extreme points of the meridian arc. The angular distance was calculated based on observations of the star Canopus. (Canopus (Argus), a first-magnitude star in the constellation “Argo’s ship”; visible in our southern hemisphere below 37.5°N latitude). It reaches a height of 7.5° at Alexandria and is barely visible on the horizon at Rhodes, indicating that its height there is almost 0°. The linear distance is estimated from the travel time of ships and is assumed to be 5,000 stages (800 km). Therefore, the Earth’s circumference is determined to be 240,000 stadia (38,400 km). Posidonius’ result is considered less satisfactory than Eratosthenes’ conclusion because the heights of the celestial bodies near the horizon are significantly affected by atmospheric refraction, which was still unknown at that time, and the estimation of linear distance by sea could not be dependable. It is now understood that the difference in latitude between Alexandria and Rhodes is only 5°, and they are not located on the same meridian.
It’s quite fascinating that Ptolemy, the renowned astronomer from Alexandria, did not mention anything about calculating the Earth’s size in his works, despite the fact that his “Geography” implies its spherical shape. Instead, he assumed that one degree is equivalent to 500 stadia (80 km), resulting in a circumference of 180,000 stadia (28,800 km) for the entire Earth. This estimation is significantly smaller than the measurements made by Eratosthenes and Posidonius.
Following the destruction of the Alexandrian library during the tumultuous years of the first centuries A.D., all scientific endeavors came to a halt. It wasn’t until 827 that the Arabs, who had gained political power through their caliphs, made a new attempt to measure degrees. Caliph Almamum, the son of Harun, took a keen interest in the advancement of the exact sciences and instructed his astronomers, Kalid and Izp, to measure the arc of the meridian in the plain of Sinjar, which lies to the west of the Tigris River and the present-day city of Mosul. The starting point they chose was at approximately 35 degrees north latitude.
Using Arabic cubits as their measuring units, the Arab scientists split into two groups and headed in opposite directions along the meridian. They measured the meridian by observing the altitudes of the stars with the angular measuring instruments available at that time. Each party continued their measurements until they had traveled along the meridian for a distance of 1 degree.
One group calculated the value of the meridian degree to be 56 miles, while the other group arrived at a slightly higher value of 56⅔ miles, equivalent to 4,000 cubits. The latter measurement was deemed to be more accurate and was accepted as the value for the meridian degree.
Until the length of the Arab cubit was discovered, it was impossible to gauge the accuracy of Arab measurement. All that was known was that the Arab cubit was 27 inches in length, with each inch being equivalent to six barley grains arranged in a line. However, recent findings on the Nile island of Rhoda, near Cairo, have shed light on this matter. On a meticulously carved stone column, markings representing the divisions of the Arabic cubit into inches were discovered. These markings revealed that an Arabian cubit is approximately 49⅓ centimeters in length. Consequently, the length of an Arabian mile is approximately 1973 meters or 926.3 fathoms. When this figure is multiplied by 56⅔, it results in a length of 104.8 versts (111.088 km) for a degree of latitude at 35°, which closely aligns with modern definitions.
In the Middle Ages, the knowledge of the Greeks and Arabs regarding the Earth’s spherical shape and its size was lost. It was not until the early 16th century, following the era of great sea voyages, that a new attempt to measure the Earth’s size was made. This endeavor was undertaken by Fernel, a French scientist and physician to King Francis, in the year 1528. Fernel measured the meridian arc near Paris, using a triangle with dioptres to determine the angular heights of the Sun. One side of the triangle was divided into parts corresponding to minutes of the arc, while Fernel calculated the linear distance by counting the revolutions of his wagon wheel. The length of the meridian degree, under the latitude of Paris, was found to be 56,746 toazes or approximately 51,838 sazhens (110.41 km).
Therefore, initially the form and dimensions of our planet have been familiar for quite some time. However, is it achievable, while situated on its surface, to authenticate its rotation? Surprisingly, it is indeed feasible, and even through multiple means.
The Rotation of the Earth
In 1672, a discovery was made by Frenchman Richet. He observed that pendulum clocks at the equator run slower compared to those in Paris. This phenomenon was later explained by Isaac Newton, an English physicist, astronomer, and mathematician (1643 – 1727). Newton proposed that the rotation of the Earth results in the generation of centrifugal force that is perpendicular to the axis of rotation (not the surface!) and directed opposite to this axis. In regions closer to the equator, the magnitude of the centrifugal force is smaller (due to the shorter distance to the axis of rotation) and it is also inclined at an angle to the horizon. On the other hand, at the equator, the centrifugal force reaches its maximum value, causing a decrease in the force of gravity (g) and consequently, a slower oscillation (increased period T) of a pendulum with length (l). This can be expressed mathematically as T = 2p(l/g)1/2 .
One more proof of the Earth’s rotation is the impact of rotational or Coriolis acceleration on the movement of air and water masses. This phenomenon is observed as a deviation from the north-south direction of winds and ocean currents, as well as in the erosion of one of the river banks that flow in a north-south direction. The concept behind this phenomenon is quite straightforward. For instance, when a river flows from south to north, its waters, due to inertia, tend to maintain the linear rotational velocity (perpendicular to the flow direction) that they had when flowing to the south. This causes them to deviate towards the east (since the Earth rotates from west to east). Consequently, the eastern bank of the river will experience erosion.
Yet another evidence of the rotation of the Earth is the deflection of objects that fall from the vertical line. The reasoning behind this phenomenon is the following: the rotational speed increases as you move higher above the Earth’s surface, and this speed remains constant during the fall. Meanwhile, the point directly above the initial location of the falling object will shift eastward, but to a lesser extent than the object itself when it eventually lands. As a result, the object will fall in an eastward direction.
A more precise description of the Earth’s shape
By considering the Earth’s rotation period (24 hours) and radius, we can easily calculate the linear velocity of rotation at the equator: v0 = w R, where w = 2p/86400 r/sec. With R = 6378 km, we find that v0 is approximately 460 m/s (at latitude j, this velocity will be v = v0*cos(j)). The centrifugal force, Fc = m*w2*R, and the gravity force, according to the law of universal gravitation, Fg = G*M*m/R2, where M is the mass of the Earth and R is its radius. The ratio of Fc to Fg for a spherical Earth is:
If we substitute the actual values of M and R, we obtain Fc / Fg = 3.45×, meaning that at the equator, any object should weigh approximately 0.3% less than at the poles. In reality, this difference does not exceed 0.55%.
It is now time to recall that the Earth’s shape deviates from that of a sphere. Newton himself demonstrated theoretically that if two interconnected tunnels were drilled to the Earth’s core – one from the North Pole and the other from the equator – and filled with water, the water levels would not be the same. In the polar tunnel, only the force of gravity affects the water, whereas in the equatorial tunnel, the centrifugal force also comes into play. In order for both columns of water to exert equal pressure on the Earth’s core (i.e., possess equal weight), the water level in the equatorial tunnel must be higher. According to Newton’s calculations, this disparity should amount to 1/230th of the Earth’s average radius.
This calculation is not too difficult. The weight of each small volume of matter at the pole and at the equator must be equalized. This means that for balance at any distance r from the center of the Earth, the following relationship holds true:
The dependence of acceleration due to free fall on radius is the same at the poles and at the equator: gp(r) = ge(r) = GM/r2 , where M is the mass enclosed within radius r : M(r) = r*4*p*r3/3 , where r is the density of the substance filling the wells. If we substitute all of this into the equation of balance (3), divide by m, and integrate over the entire radius of the Earth (the left part – from 0 to the polar radius Rp, the right part – from 0 to the equatorial radius Re), the result is the following ratio:
By substituting the average density of the Earth, which is 5.52 g/cm3 (mainly consisting of substances other than water), and the equatorial radius Re=6378140 m into equation (4), we can calculate that the polar radius Rp is approximately 6356130 m. This means that the polar radius is about 22 km less than the equatorial radius, and the ratio f=()/Re=1/289.8. This ratio, known as the compression of the Earth, is actually equal to 1/298.257. Therefore, our theoretical calculation aligns well with the actual shape of the Earth’s surface, despite not considering the density’s dependence on radius and instead using the average density.
Thus, Newton demonstrated that the Earth’s shape should be altered at the poles. The same conclusion was drawn from observations of the rapidly rotating gas giants Jupiter and Saturn. However, it proved challenging to empirically verify this phenomenon on Earth. It wasn’t until the following century that several expeditions were organized specifically to measure the lengths of two meridian arcs spanning 1° each, one as close as possible to the equator and the other near the pole. Eventually, it was discovered that the 1° arc in equatorial latitudes (measured between 1735 and 1743 in Peru) is indeed shorter than in polar latitudes (measured in Lapland), providing direct evidence of the Earth’s compression towards the poles. It should be noted, however, that these measurements do not provide the Earth’s radius (i.e., the distance from the surface to the center), but rather the radius of curvature of the surface. This radius of curvature represents the radius of the circle that corresponds to the meridian arc in a given region. Since the meridians at the poles have a more gradual curve compared to those at the equator, their radii of curvature are larger in the former case.
When it comes to units of length, it’s important to mention another one. The meridian’s full length is considered to be 40,000 km, so 1° of this length would be approximately 1/360th of it, which is equivalent to 111,111 km. Additionally, 1 ' is equal to 1,852 km, and this unit is known as the nautical mile. The nautical mile has proven to be extremely useful for navigation, especially in previous centuries. This is because the latitude of a given area is determined by the height of celestial bodies (such as the Sun when it reaches its highest point) above the horizon. A change in the height of a celestial body by 1 ' (due to movement north or south) corresponds to a movement of the observer by 1 nautical mile along the meridian.
It should be noted that the shape of the Earth, when examined more closely, deviates from an ellipsoid of rotation and, on a smaller scale, has a highly complex surface known as a geoid. It is important to clarify that the term “surface of the Earth” in this context does not refer to the actual topography with mountains, hills, and valleys, but rather to the average level of water in the oceans, which can be extended to land through leveling (measuring height above sea level). This surface is considered to be level, meaning it is perpendicular to gravity in all directions, and it differs from the ellipsoid of rotation by only a few hundred meters. If we take a triaxial ellipsoid as the Earth’s shape (with the equator represented as an ellipse with a semi-axis difference of approximately 200m), the difference between the geoid and this ellipsoid will not exceed 100 meters. This difference is due to the uneven distribution of mass on the Earth’s surface (continents and oceans) as well as within the Earth, which affects the magnitude and direction of gravity. The study of the geoid’s shape is one of the main objectives of geodesy and gravimetry.
Mass of the Earth
In 1797, Henry Cavendish accurately measured the mass of the Earth using torsion scales with lead balls at the ends. To determine the mass, Cavendish observed the twisting angle of the scales when two large lead balls approached a smaller ball from different sides. By comparing the gravitational forces between the balls and the Earth, Cavendish calculated that the Earth’s mass is approximately 6×1021 tons, a value that is still accepted today.
Now, let’s revisit the law of universal gravitation. The acceleration experienced by an object on the Earth’s surface due to gravity is known as the acceleration of gravity. This acceleration is directed towards the center of the Earth and has an approximately equal magnitude:
The equation (5) is an exact expression if the Earth is a non-rotating sphere with a spherically symmetric distribution of masses. However, in reality, the Earth’s shape is ellipsoidal and these conditions are not fully met.
The direction of gravity on the Earth is slightly different from the direction to the geometric center of the ellipsoid. This difference is most pronounced at latitudes of +-45 degrees, where the deviation is at its maximum value of 5.7 degrees. At the equator, the gravitational force due to the Earth’s ellipsoidal shape is approximately half of that at the poles, which is about 1/600 of a fraction.
Furthermore, the gravitational acceleration also takes into account the centrifugal acceleration that arises due to the Earth’s daily rotation. This acceleration is perpendicular to the axis of rotation and lies in the plane of the parallel circle formed by it. The centrifugal acceleration can be calculated as w2*r, where w is the angular velocity of rotation with a period of T, and for the Earth, T is the duration of stellar days, which is 86146 s. The maximum centrifugal acceleration occurs at the equator and is equal to 3.39 cm/s2, which is 1/288th of the gravitational acceleration of 983.42 cm/s2 at the equator. At the equator, the centrifugal force opposes the gravitational force and is subtracted from it, resulting in a net free-fall acceleration of 980.03 cm/s2. At the poles, there is no centrifugal force and thus no lateral component.
At intermediate latitudes, the centrifugal force is proportional to the radius of the parallel r = r*cos(ja), where r is the current distance to the center of the Earth (radius-vector) and ja is the geocentric latitude. The difference ja from the usual geographic latitude j is j – ja = 11'.6*sin(2*j). Therefore, the centrifugal acceleration w2*r = w2*r*cos(ja) can be separated into a vertical component w2*r*cos(ja)*cos(j) and a horizontal component w2*r*cos(ja)*sin(j), pointing towards the meridian to the equator. If we disregard the small difference between ja and j, the horizontal component of centrifugal acceleration w2*r*cos(j)*sin(j) will be at its maximum at latitude +-45°, reaching a value of 1.7 cm/s2, which corresponds to a plumb bob deviation of 5'9 to the south in angular measure. The vertical component of centrifugal acceleration w2*r*cos(j) (if we neglect the difference between the direction of the plumb line and the direction to the center of the Earth) at the equator will be w2*r, at latitudes +-45° – 0.5*w2*r and zero at the poles. Thus, at the equator, the acceleration of gravity is reduced by f due to the centrifugal force and by f/2 due to the reduction of the gravitational force. Altogether, these two effects cause the acceleration of gravity at the equator to be f/2+f = 1.5*f ~ 1/200 less than at the poles.
The specific relationship between the acceleration of gravity and altitude was discovered in 1743 by French mathematician A. Clero:
g = g0*(1+b*sin2(j)), where g0 represents the acceleration of gravity at the equator, gp is the acceleration of gravity at the pole, and the coefficient b = (g0 – gp)/g0 (6).
In this equation, q represents the ratio of centrifugal acceleration to the acceleration of gravity at the equator (w2*r/g0), and f represents the compression of the Earth. In modern terms, Clero’s formula can be written as:
By measuring the acceleration of gravity in different locations, we can determine the numerical value of b and, subsequently, the compression of the Earth f. These values align closely with measurements of meridian arcs. There are multiple methods for measuring the acceleration of gravity, with the simplest being the period of swing of a pendulum with a known length l:
T = 2*p*(l/g)1/2 , therefore g = 4*p2*l/T2 (8)
Gravimetry, a specialized field of astronomy, focuses on measuring and analyzing the variations in gravity acceleration across the Earth’s surface. These variations provide valuable insights into the Earth’s compression, deviations of the geoid shape from the ideal ellipsoid, and even the internal structure of our planet.
The acceleration of gravity allows us to easily determine the mass and average density of the Earth. For instance, at a latitude of 45° using Clerot’s formula (7), the acceleration of gravity is 980.62 cm/s2. At this latitude, the vertical component of centrifugal acceleration is 1.7 cm/s2, which means that the acceleration of the gravitational force is 982.32 cm/s2. By plugging in this value and the average radius of the Earth, which is 6.370×108 cm, into Newton’s formula (5), we can calculate the mass of the Earth, which is 5.98×1027 g. To determine the average density of the Earth, we divide the mass M by the volume of the Earth, resulting in a value of 5.52 g/cm3.





