Parsec (designation: pc) – a unit of length used to measure large distances to astronomical objects outside the solar system, approximately equal to 3.26 light-years or 206,000 astronomical units (a.u.), that is, 30.9 trillion kilometers (19.2 trillion miles). The parsec is obtained using parallax and trigonometry and is defined as the distance at which 1 a.e. forms an angle of one angular second (1 / 3600 degree). This corresponds to 648,000 / π astronomical units, t. The nearest star, Proxima Centauri, is about 1.3 parsecs (4.2 light-years) from the Sun. Most stars visible to the naked eye are within a few hundred parsecs of the Sun, and the most distant stars are a few thousand parsecs away. 1 ps sign is equal to 1 / tan (1 arsses) a you = 1 / \tan \left(\mathrm
ight), \mathrm>
The term “parsec” was coined by British astronomer Herbert Hall Turner in 1913 to simplify the calculation of astronomical distances based solely on observational data. It is derived from the combination of “one second parallax”. While the light-year is still commonly used in popular science and everyday language, parsecs are the preferred unit of measurement in astronomy and astrophysics. Kiloparsecs (kpc), megaparsecs (Mpc), and gigaparsecs (Gpc) are used for larger scales in the Universe, including objects within and around the Milky Way, medium distant galaxies, and the most distant galaxies, respectively.
Resolution B2, adopted by the International Astronomical Union (IAU) in August 2015, included a standardized scale for absolute and apparent bolometric magnitude. As part of this definition, the IAU referred to the existing explicit definition of the parsec, which is approximately 3.085,677,587,581,491,361,3673 × 10 16 meters. This definition is based on the IAU’s 2012 precise definition of the SI astronomical unit and corresponds to the small-angle definition of a parsec found in numerous astronomical reference books.
History and origin
The parsec has its roots in an intriguing concept of an elongated imaginary right-angled triangle in space. It is defined as the length of the neighboring cathetus, with the opposite cathetus measuring 1 astronomical unit. The shorter side of this triangle is equivalent to the average distance between the Earth and the Sun, while the vertex opposite this side is measured in one arc second. Through the application of trigonometric principles to these measurements, we can derive the unit of length for the other cathetus, known as the parsec.
The utilization of the parsec as a measurement of distance is a logical outcome of the Bessel technique, as the distance in parsecs can be easily determined as the reciprocal of the parallax angle in angular seconds (for example, if the parallax angle is 1 angular second, the object is 1 pc distant from the Sun; if the parallax angle is 0.5 angular seconds, the object is 2 pc distant, and so on). This correlation does not necessitate trigonometric functions, given that the exceedingly small angles involved permit an approximate solution of the thin triangle to be employed.
Despite the fact that it may have been previously employed, the phrase parsec was initially introduced in a scientific journal in 1913. The renowned astronomer Frank Watson Dyson was troubled by the absence of a designated term for this particular unit of measurement. He proposed the name astron, however, he acknowledged that Charles Charlier had put forward the syriometer, and Herbert Hall Turner had suggested parsec. It was Turner’s proposition that gained popularity.
Calculation of the parsec value
In 2015, it was defined that 1 astronomical unit (a.u.) of arc length creates an angle of 1″ at the center of a circle with a radius of 1 pc. This means that 1 pc is equal to 1 a.u. divided by the tangent of 1″, which is approximately 206,264.8 a.u. By converting from units of degrees/minute/second to radians,
1 pc = 1 a.u. × (180 × 60 × 60) π = 149,597,870,700 m (exactly as defined in 2012).
π pc = (180 × 60 × 60) a.u. = (180 × 60 × 60 × 60 × 60 × 149,597,870,700) = 96,939,420,213,600,000 m (exactly as defined in 2015).
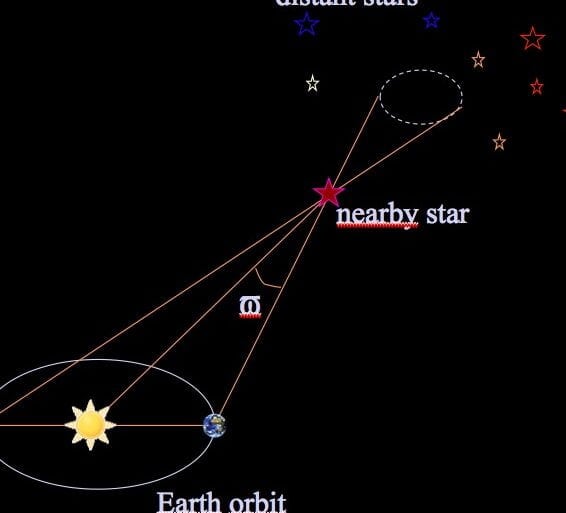
In the diagram shown above (not to scale), the Sun (S) and Earth (E) are depicted at a specific point in Earth’s orbit. Therefore, the distance between the Sun and Earth (ES) is equivalent to one astronomical unit (a.u.). The angle SDE represents one angular second (1/3600 degree), which means that point D is located one parsec away from the Sun. By applying trigonometry, we can determine the distance SD using the following formula:
CD = ES * tan(1″) ≈ EC * 1″ = 1 a.u. * (1/60 * 60 * π/180) ≈ 648,000 * π a.u. ≈ 206,264.81 a.u. & \ mathrm = > > > \ [8pt] & \ mathrm \ approximately > > = >> > > \ times >>> = > \, > \ approximately 206 \, 264.81 >. \ end >>
Given that the astronomical unit is defined as 149,597,870,700 meters, we can calculate:
Therefore, if one light ≈ 9.46 × 10 15 meters,
then one parsec ≈ 3.261,563,777 sv . years.
The implication is that a parsec is also the distance at which a disk with a diameter of one astronomical unit must be observed in order for it to have an angular diameter of one angular second (by positioning the observer at point D and the diameter of the disk at point ES).
Mathematically, to compute the distance given the angular measurements of the instruments in angular seconds, the formula would appear as follows:
The length of the parsec, as defined by IAU Resolution 2015 B2 (which is exactly 648,000 / π astronomical units), is equivalent to the result obtained through the calculation of small angles. This varies by approximately 200 km from the traditional definition of arctangency, or in other words, only after the 11th significant digit. Since the astronomical unit was defined by IAU (2012) as the precise length in the SI system in meters, the parsec now corresponds exactly to the length in the SI system in meters. Rounded to the nearest meter, a parsec calculated using small angles corresponds to 30,856,775,814,913,673 m.
Usage and measurement
The parallax method is the primary calibration step for determining distance in astrophysics. However, the precision of parallax angle measurements by telescopes on the ground is limited to approximately 0.01″. This limitation means that stars cannot be more than 100 pc away, as the Earth’s atmosphere affects the sharpness of the star’s image. In contrast, space telescopes are unaffected by this atmospheric interference and can accurately measure distances to objects beyond the reach of ground-based observations.
Between 1989 and 1993, the European Space Agency (ESA) launched the Hipparcos satellite, which measured the parallaxes of approximately 100,000 stars with an astrometric accuracy of about 0.97 msec. arc. This mission obtained precise measurements of stellar distances up to 1,000 stars.
The Gaia satellite, launched by the European Space Agency (ESA) on December 19, 2013, has been specifically developed to accurately measure the distances to a billion stars. It is capable of achieving an astounding accuracy of 20 angular microseconds, which results in a maximum error of 10% when measuring distances to the center of our galaxy, located approximately 8000 parsecs away in the Sagittarius constellation.
Measuring Distances in Parsecs
Distances smaller than a parsec
Fractions of a parsec are commonly used to describe distances within the same star system. For instance:
- An astronomical unit (AU), which is the distance from the Sun to Earth, is slightly less than 5 × 10-6 pc.
- The farthest space probe, Voyager 1, was 0.000703 pc away from Earth as of January 2019. It took Voyager 1 41 years to cover that distance.
- The diameter of the Oort Cloud is estimated to be approximately 0.6 pc.

Based on observations from the Hubble Space Telescope, scientists have determined that the astrophysical jet originating from the active galactic nucleus M87 measures 20″ in length and is estimated to be 1.5 kiloparsecs (equivalent to 4892 light days) long. It should be noted that the jet appears slightly smaller when viewed from Earth’s perspective.
Distances are measured in parsecs (pc) which include distances between stars in the same spiral arm or globular cluster. When the distance is 1,000 parsecs (3,262 light-years), it is called a kiloparsec (kpc). Astronomers use kiloparsecs to express distances within a galaxy or between groups of galaxies. For example:
- One parsec is approximately equal to 3.26 light-years.
- Proxima Centauri, the closest star to Earth after the Sun, is about 1.3 parsecs (4.24 light-years) away based on direct parallax measurements.
- The Pleiades star cluster is located at a distance of 130 ± 10 pc (420 ± 30 light-years) from us, according to parallax measurements by Hipparcos.
- The distance between Earth and the center of the Milky Way is over 8 kiloparsecs or approximately 26,000 light-years. The Milky Way itself spans about 34 kiloparsecs or 110,000 light-years.
- Earth is roughly 780 kiloparsecs or 2.5 million light-years away from the Andromeda Galaxy (M31).
Megaparsecs and gigaparsecs
Astronomers commonly express the distances between neighboring galaxies and galaxy clusters in megaparsecs (mpc). A megaparsec is equivalent to one million parsecs or approximately 3,260,000 light-years. Galactic distances are occasionally given in units of Mpc/h (e.g., “50/h Mpc”, also written as “50 Mpc/h – 1 »). h – constant (“dimensionless Hubble constant”) falls within the range 0.5 < h < 0.75, representing the uncertainty in the value of the Hubble constant H for the expansion rate of the Universe: h = HOUR / 100 km/s/Mpc. The Hubble constant becomes relevant when converting the observed redshift z into a distance d using the formula d ≈ c / HOUR × g.
One billion parsecs is equivalent to one gigaparsec (Gpc), which is a commonly used unit of length. A gigaparsec is approximately 3.26 billion light-years or about 1/14th of the distance to the observable Universe’s horizon, as determined by cosmic background radiation. Astronomers frequently utilize gigaparsecs to describe the size of large-scale structures, such as the Great Wall of China CfA2, the distance between galaxy clusters, and the distance to quasars.
- The Andromeda Galaxy is located approximately 0.78 Mpc (2.5 million light-years) away from Earth.
- The nearest large cluster of galaxies, known as the Virgo cluster, is situated around 16.5 Mpc (54 million light-years) from Earth.
- The galaxy RXJ1242-11, which contains a supermassive black hole core similar to that of the Milky Way, is positioned approximately 200 Mpc (650 million light-years) away from Earth.
- The galaxy Hercules-Corona Borealis Great Wall contains a filament that is currently the largest known structure in the universe. Its diameter measures approximately 3 Gpc, which is equivalent to 9.8 billion light-years.
- Within the observable Universe, the particle horizon serves as its boundary. It has a radius of around 14 Gpc, which is equivalent to 46 billion light-years.
Units of volume
To calculate the quantity of stars within the Milky Way galaxy, measurements are taken in cubic kiloparsecs (kpc 3 ) along various directions. These measurements sample volumes and involve counting all stars within them, allowing for statistical determination of the total number of stars. Similarly, the number of globular clusters, dust clouds, and interstellar gas are determined using this method. To determine the quantity of galaxies within superclusters, volumes in cubic megaparsecs (Mpc 3 ) are utilized. All galaxies within these volumes are classified and counted, enabling statistical calculation of the total number of galaxies. The immense void known as Botes is measured in cubic megaparsecs.
The measured size of gravitational wave interferometers (such as LIGO and Virgo) is given in cubic megaparsecs (mpc3) and represents the cubic value of the effective distance.
In popular culture
In the first movie “Star Wars,” Han Solo mistakenly referred to the parsec as a unit of time when he stated that his ship, the Millennium Falcon, traveled the Kessel path in less than 12 parsecs. This statement was repeated in “The Force Awakens,” but Han Solo clarified in Star Wars that he was referring to the ship’s speed and maneuverability. In the series “The Mandalorian,” parsec is also used ambiguously as a unit of space.
In the book “The Time Warp,” “megaparsec” is Mr. Merry’s nickname for his daughter Meg.
In the 1955 science fiction short story “Risk” by Isaac Asimov, the groundbreaking hypersonic spacecraft is called “Parsec”.
Additional Information
Important Details
Recommended Reading
External References
- Guidry, Michael. “Astronomical distance scales” . Astronomy 162: stars, galaxies, and cosmology . University of Tennessee, Knoxville. Archived from the original on December 12, 2012 . Checked March 26, 2010.
- Merrifield, Michael. “PC Parsec” . Sixty characters . Brady Haran for the University of Nottingham .
The unit of length known as the parsec is utilized to measure vast distances to celestial objects beyond our solar system. It is roughly equivalent to 3.26 light-years or 206,000 astronomical units (a.e.), which is approximately 30.9 trillion kilometers (19.2 trillion miles). The parsec is determined through the utilization of parallax and trigonometry, and it represents the distance at which 1 a.e. forms an angle of one angular second (1/3600 degree). This equates to 648,000/π astronomical units. An example of a star that is about 1.3 parsecs (4.2 light-years) away from the Sun is Proxima Centauri. The majority of stars that are visible to the naked eye are situated within a few hundred parsecs of the Sun, while the most distant stars are located several thousand parsecs away. The mathematical representation of 1 p s is equal to 1/tan (1 a r s s e s) a you = 1/ \ tan \ left( \mathrm \ right) \ , \mathrm >
The term “parsec” was created by British astronomer Herbert Hall Turner in 1913 by combining “one second parallax”. Its purpose was to facilitate the calculation of astronomical distances based solely on observational data. Due to this, it has become the preferred unit of measurement in the fields of astronomy and astrophysics. However, the light-year is still widely used in popular science texts and everyday conversations. While parsecs are commonly used for shorter distances within the Milky Way, larger scales in the Universe require multiples of parsecs. For instance, kiloparsecs (kpc) are used for more distant objects in and around the Milky Way, megaparsecs (MPc) for medium-distant galaxies, and gigaparsecs (Gpc) for extremely distant quasars and galaxies.
In August 2015, the International Astronomical Union (IAU) implemented Resolution B2, which included a standardized scale of absolute and apparent bolometric magnitude. This scale referred to the well-established definition of the parsec as precisely 648,000 / π a.u. or approximately 3.085,677,587,581,491,361,3673 × 10 16 meters (based on the IAU 2012 precise definition of the SI astronomical unit). This definition aligns with the small-angle definition of a parsec commonly found in numerous astronomical reference books.
History and origin
The concept of the parsec was developed based on the measurements of an elongated imaginary right-angled triangle in space. This triangle has two dimensions – a shorter side that is equivalent to one astronomical unit (the average distance between the Earth and the Sun), and a constricted angle at the vertex opposite this side, measured in one arc second. Utilizing trigonometry, the length of the other cathetus of the triangle, known as the parsec, can be calculated.
One of the oldest techniques employed by astronomers to determine the distance to a star involves measuring the difference in angles between two observations of the star’s position in the sky. The initial observation is taken from Earth on one side of the Sun, while the second observation is taken approximately six months later when Earth is on the opposite side of the Sun. The distance between the two Earth positions at the time of the observations is twice the distance between Earth and the Sun. The disparity in angles between the two observations is equal to twice the parallax angle, which is formed by the lines extending from the Sun and Earth to the star at the distant vertex. By utilizing trigonometry, the distance to the star can be calculated. The first successful documented direct measurements of an object at interstellar distances were performed by the German astronomer Friedrich Wilhelm Bessel in 1838. Bessel utilized this approach to determine a distance of 3.5 parsecs from the star 61 Cygni.
The distance measurement in parsecs can be easily derived from the Bessel method, which is based on the calculation of the inverse of the parallax angle in angular seconds. For example, if the parallax angle is 1 angular second, the object is located 1 pc away from the Sun. If the parallax angle is 0.5 angular seconds, the object is positioned 2 pc away, and so on. This relationship eliminates the need for trigonometric functions due to the small angles involved, allowing for an approximate solution using a thin triangle.
Even though it might have been utilized previously, the expression parsec was initially cited in an astronomical publication in 1913. The Royal Astronomer Frank Watson Dyson was worried about the necessity for a designation for this measurement unit. He proposed the term astron but acknowledged that Charles Charlier had suggested the syriometer, and Herbert Hall Turner put forward parsec. It was Turner’s proposition that gained popularity.
Calculation of the parsec value
In 2015, it was defined that 1 astronomical unit (a.u.) of arc length constrains an angle of 1″ at the center of a circle with a radius of 1 parsec (pc). This means that 1 pc is equal to 1 a.u. divided by the tangent of 1″, which is approximately 206,264.8 a.u. By converting from units of degrees/minute/second to radians,
1 pc = 1 a.u./tan(1″) ≈ 206,264.8 a.u.
Furthermore, 1 a.u. is equal to 149,597,870,700 meters (as defined in 2012).
Therefore, π pc = 180 × 60 × 60 a.u. = 96,939,420,213,600,000 meters (exactly as defined in 2015).
One PC sign is equivalent to 96,939,420,213,600,000 π sign, which is equal to 30,856,775,814,913,673 meters (accurate to the meter).
In the diagram above (not to scale), S represents the Sun, and E represents Earth at a specific point in its orbit. Therefore, the distance ES is defined as one astronomical unit (a.u.). The angle SDE is equivalent to one angular second (1/3600 degree), which means that D is a point in space located one parsec away from the Sun. By utilizing trigonometry, the distance SD can be calculated in the following manner:
The equation CD sign equals ES tan 1″ CD ≈ EC 1″ sign equals 1 au 1 60 × 60 × π 180 sign equals 648,000 π au ≈ 206,264.81 au. & \ mathrm = > > > \ [8pt] & \ mathrm \ approximately > > = >> > > \ times >>> = > \, > \ approximately 206 \, 264.81 >. \ end >>
Given that the astronomical unit is defined as 149,597,870,700 meters, we can calculate:
| Thus, 1 parsec | ≈ 206,264 0.806 247,096 astronomical units |
| ≈ 3.085 677 581 × 10 16 meters | |
| ≈ 30,856,775,815 trillion kilometers | |
| ≈ 19,173,511,577 trillion miles. |
Therefore, if 1 light ≈ 9.46 × 10 15 meters,
then 1 pc ≈ 3.261,563,777 sv. years.
The corollary postulates that a parsec is additionally the distance from which a disk having a diameter of one astronomical unit must be observed so as for it to own an angular diameter of 1 angular second (by putting the observer at a degree of D and also the diameter of the disk at the purpose ES ).
Mathematically, to calculate the gap given the angular measurements of the instruments in angular seconds, the formula would appear as if this:
where θ – represents the angle measured in angular seconds, Distance Earth-Sun – remains constant (1 a.u. or 1.5813 × 10-5 sv years). The calculated distance of the star will be in the same units of measurement as the Earth-Sun distance Earth-Sun (for example, if the Earth-Sun distance Earth-Sun = 1 a.u., the unit of measurement for the distance to the star will be in astronomical units; if the Earth-Sun distance is Earth-Sun = 1.5813 × 10 -5 light-years, the unit of distance to a star will be in astronomical units. star is measured in light-years).
The length of the parsec as defined in IAU Resolution 2015 B2 (exactly 648 000 / π astronomical units) is equivalent to the result obtained using the calculation of small angles. This is different from the traditional definition of arctangency by approximately 200 km, or only after the 11th significant digit. Since the astronomical unit was defined by IAU (2012) as the exact length in the SI system in meters, the parsec now corresponds to the exact length in the SI system in meters. Rounded to the nearest meter, a parsec calculated using small angles corresponds to 30,856,775,814,913,673 m.
The parallax method is the primary calibration step used in astrophysics to determine distance. However, the precision of parallax angle measurements taken by telescopes on the ground is limited to approximately 0.01″, restricting the range of observable stars to within 100 parsecs. This limitation is due to the Earth’s atmosphere, which blurs the image of the star. Space telescopes, on the other hand, are not subject to this effect and can accurately measure distances to objects beyond what is possible with ground-based observations. From 1989 to 1993, the European Space Agency (ESA) launched the Hipparcos satellite, which measured the parallaxes of around 100,000 stars with an astrometric precision of about 0.97 msec. arc. This mission provided precise measurements of stellar distances for up to 1,000 stars.
The European Space Agency (ESA) launched the Gaia satellite on December 19, 2013. Its main objective is to accurately measure the distances to one billion stars, achieving an accuracy of 20 angular microseconds. However, this precision still results in an error of about 10% in measurements to the center of the Galaxy, which is approximately 8000 parsecs away in the constellation Sagittarius.
Measurement Units
Distances within a parsec
Distances expressed as fractions of a parsec typically refer to objects that are part of the same star system. For example:
- An astronomical unit (AU), which is the distance from the Sun to Earth, is approximately 5 × 10 -6 pc .
- The farthest space probe, known as Voyager 1, was located at a distance of 0.000703 pc from Earth as of January 2019. It took Voyager 1 41 years to travel that far.
- The estimated diameter of the Oort Cloud is around 0.6 pc.

Based on the data collected by the Hubble Space Telescope, it has been determined that the astrophysical jet originating from the active galactic nucleus M87 measures 20″ in length and is estimated to be around 1.5 kiloparsecs (equivalent to 4892 light days) long (although its size appears slightly smaller when viewed from Earth).
Parsec and Kiloparsec
Distances that are measured in parsecs (pc) represent the distances between stars that are in close proximity to each other, such as those that are found in a single spiral arm or globular cluster. When we refer to a distance of 1000 parsecs (3262 light-years), we use the term kiloparsec (kpc). Astronomers commonly use kiloparsecs to express distances between different parts of a galaxy or within groups of galaxies. Therefore, for example:
- One parsec is roughly equivalent to 3.26 light-years.
- Proxima Centauri, which is the closest known star to Earth after the Sun, is approximately 1.3 parsecs (4.24 light-years) away according to direct parallax measurements.
- The distance to the Pleiades star cluster is approximately 130 ± 10 pc (420 ± 30 light-years) from us, as determined by parallax measurements conducted by Hipparcos.
- The distance between Earth and the center of the Milky Way is over 8 kiloparsecs (equivalent to approximately 26,000 light-years), while the width of the Milky Way spans about 34 kiloparsecs (or around 110,000 light-years).
- When it comes to the Andromeda Galaxy (also known as M31), it is located approximately 780 kiloparsecs away from Earth, which is equivalent to around 2.5 million light-years.
Megaparsecs and gigaparsecs
A gigaparsec (Gpc) is equivalent to one billion parsecs, making it one of the most commonly used units of length. In terms of distance, a gigaparsec is approximately 3.26 billion light-years, or roughly 1/14th of the distance to the observable Universe’s horizon, as determined by cosmic background radiation. Astronomers frequently employ gigaparsecs to quantify the size of large-scale structures, such as the dimensions and distance of the Great Wall of China CfA2, the gaps between galaxy clusters, and the distance to quasars.
- The Andromeda Galaxy is situated approximately 0.78 Mpc (2.5 million light-years) away from Earth.
- The nearest major galaxy cluster, the Virgo cluster, is roughly 16.5 Mpc (54 million light-years) distant from Earth.
- The galaxy RXJ1242-11, which possesses a supermassive black hole core akin to that of the Milky Way, is located approximately 200 Mpc (650 million light-years) away from Earth.
- The galaxy Hercules-Corona Borealis Great Wall, which is currently the largest known structure in the universe, has a diameter of approximately 3 Gpc (equivalent to 9.8 billion light-years).
- The observable Universe’s particle horizon, which marks its boundary, has a radius of around 14 Gpc (equivalent to 46 billion light-years).
Quantities of Capacity
To calculate the quantity of stars in the Milky Way, different directions are surveyed, sampling volumes measured in cubic kiloparsecs (kpc 3 ). The stars contained within these volumes are tallied, allowing for a statistical determination of the total number of stars. In a similar fashion, the quantity of globular clusters, dust clouds, and interstellar gas is ascertained. Volumes measured in cubic megaparsecs (Mpc 3 ) are chosen to calculate the number of galaxies in superclusters. All galaxies within these volumes are categorized and counted, enabling a statistical determination of the total number of galaxies. The expansive void known as Botes is measured in cubic megaparsecs.
In the field of physical cosmology, the distribution of matter in the visible universe and the count of galaxies and quasars are determined by choosing volumes of cubic gigaparsecs (Gpc3). Currently, the Sun is the lone star within its cubic parsec (pc3), but in globular clusters, the stellar density can range from 100 to 1000 pc-3.
The cubic megaparsecs (mpc3) measurement is used to express the observed volume of gravitational wave interferometers such as LIGO and Virgo. This measurement essentially represents the cube of the effective distance.
In popular culture
The measurement of a parsec was used incorrectly by Han Solo in the first movie “Star Wars” when he claimed that his ship, the Millennium Falcon, traveled the Kessel path in less than 12 parsecs. This claim was also mentioned in “The Force Awakens,” but was clarified in Han Solo: Star Wars. It is also ambiguously used as a spatial unit in “The Mandalorian.”
In the book “The Time Warp,” the term “megaparsec” is Mr. Merry’s nickname for his daughter Meg.
In Isaac Asimov’s 1955 science fiction short story “Risk,” the first hypersonic spacecraft is named “Parsec.”
Notes
References
External Links
- Guidry, Michael. “Astronomical distance scales”. Astronomy 162: stars, galaxies, and cosmology. University of Tennessee, Knoxville. Archived from the original on December 12, 2012. Accessed March 26, 2010.
- Merrifield, Michael. “PC Parsec”. Sixty characters. Brady Haran for the University of Nottingham.
The parallax method is the primary calibration step for determining distance in astrophysics; however, the precision of parallax angle measurements by ground-based telescopes is limited to approximately 0.01″, meaning that it can only accurately measure distances to stars within 100 parsecs. This limitation is due to the Earth’s atmosphere, which affects the sharpness of the star image. In contrast, space telescopes are not affected by atmospheric interference and can accurately measure distances to objects beyond the range of ground-based observations. From 1989 to 1993, the European Space Agency (ESA) launched the satellite Hipparcos, which measured the parallaxes of around 100,000 stars with an astrometric precision of about 0.97 msec. Arcs, providing accurate measurements of stellar distances up to 1000 parsecs away.
The European Space Agency (ESA) launched the Gaia satellite on December 19, 2013. Its primary purpose is to accurately measure the distances of one billion stars with a precision of 20 microseconds. This level of accuracy allows for a margin of error of 10% when measuring distances to the center of the Galaxy, which is approximately 8000 pc away in the constellation Sagittarius.
Additional Sources
Recommendations
- (refer to August 19, 2015) .
- ↑ and and and
- ↑ and notes , on terminology and linguistic database in the Government of Canada (consulted onAugust 19, 2015) .
- ↑ and (en) Entries , in Mohammad Heidari-Malayeri , Etymological Dictionary of Astronomy and Astrophysics , Paris, Observatoire de Paris , 2005 -2015.
- ↑ and Frédéric Arenou , " The birth of the parsec ", L'Astronomie , vol. 124, p o 23 , January 2010, pp. 20-23 .
- (De) Hermann Kobold , Der Bau des Fixsternsystems , Brunswick, Friedrich Vieweg und Sohn, coll. "Wissenschaft" ( p o 11)1906, XI -256 pp. ( OCLC ) , pp. 74.
- (in) Frank Watson Dyson, “The spatial distribution of stars in Carrington’s catalog”, Monthly Notices of the Royal Astronomical Society, Vol. 73, March 1913, pp. 334-342.
- (in) “Meeting of the Royal Astronomical Society (Friday, March 14, 1913)”, Observatory, Vol. 36, April 1913, pp. 160-174.
- (in) W. W. Campbell and Joel Stebbins, “Report on the Formation of the International Astronomical Union”, Proceedings of the National Academy of Sciences of the United States of America, Vol. 6, No. 6, 1920, pp. 349-(360-361).
- ↑ and
- (in) Introduction of Oxford University Press (accessed August 19, 2015)..
Here are some fascinating examples:
1 example is approximately equal to 4.8481368×10-6 parsecs.
As of October 14, 2019, the Voyager 1 spacecraft has covered a distance of 30.3 pc from the Sun and is still moving away at a rate of about 0.74255 pc/yr. It holds the record for being the farthest object created by humans from Earth.
The distance between the Sun and the nearest star, Proxima Centauri, is 1.3 parsecs.
The time it takes for light to travel a distance of 10 pc is 32 years, 7 months, and 6 days.
The distance from the Sun to the center of our Galaxy (Milky Way) is approximately 8 kpc.
The diameter of our Galaxy (Milky Way) is estimated to be around 30 kpc.
The distance to the Andromeda Nebula is 0.77 Mpc.
Note: Photo credits to https://www.pexels.com and https://pixabay.com
The distance in kilometers that one parsec unit in astronomical years is equal to in light years is how much? What is the equivalent of 1 60 parsec star parallax in thousands of astronomical units in parsecs?
The demand factor is 920.
Application
This apparatus is the outcome of implementing a trigonometric technique known as the “parallax method” to determine the separation between an observer and any remote object, for measuring the distance to celestial entities. For practical purposes, astronomers frequently present distances to astronomical objects in parsecs instead of light-years. This contrivance enables the direct conversion of observed measurements into distances: if a star is gauged in arc seconds, then the distance between that star and the Sun, stated in parsecs, is the reciprocal of that measurement. In terms of absolute value and modulus, the distances are two units derived from parsecs, and expressing distances in parsecs eases the manipulation of such information.
The closest star to the Sun, α Cen C (Proxima Centauri), is located 1.316 parsecs (4.28 light-years) away. Distances to other celestial objects beyond our solar system are much larger and are typically measured in kiloparsecs (symbol kpc) or megaparsecs (symbol Mpc).
The parallaxes have relatively small values: 0.76″ for Proxima Centauri. Additionally, the parallax method is not able to accurately determine distances to stars that are greater than approximately 100 parsecs, which corresponds to parallax measurements of less than ten milliseconds of arc.
Between the years and , the Hipparch satellite, launched by the European Space Agency, measured the parallax of approximately one hundred thousand stars with a precision greater than milliseconds of arc. This enabled the determination of distances to distant stars that are more than a kiloparsec away from us.
General information
Parsec (short for “parallax second”) is a non-standard unit of measurement used in cosmology to measure distances to extremely distant objects in outer space. This unit serves not only a practical purpose – it helps calculate the distance to various objects in the Universe – but also provides a level of convenience for astronomers. Consider this: it is much simpler to state that the distance from the Sun to the nearest star is 1.3 parsecs rather than 40.7 trillion kilometers. A person who regularly deals with numbers with such an enormous number of zeros would inevitably go insane. Therefore, by introducing the parsec, scientists have greatly simplified the computational processes in astronomy.
Parsec, a widely used unit of measurement in astrophysics, is equivalent to 3.2616 light-years. Enthusiasts of this field are knowledgeable about the distances to various remote objects in parsecs. However, not everyone comprehends the origins of this measurement unit and the correct method of calculating it.
The significance of the term “parsec”
This expression was derived from the terms “parallax” and “second”, where the latter does not refer to a unit of time, but rather an angular second – a non-standard astronomical unit that is equivalent to a second of a plane angle.
In present-day astronomy, there are several types of parallax:
Diurnal – The discrepancy in the direction towards a specific celestial body along both geocentric and topocentric directions. This angle is directly influenced by the altitude of the celestial object above the horizon. Annual parallax – variations in the direction towards a particular object are dependent on the Earth’s orbital motion around the Sun. Century parallax – It enables the determination of the difference in direction towards a celestial body based on its movements within the Milky Way galaxy.
Parsec – the definition of the term
Put simply, a “parsec” is a unit of measurement for the distance between celestial bodies located outside of our solar system. Typically, parsecs are used to calculate distances within the Milky Way galaxy. These distances are often expressed in multiples of units such as kiloparsecs, megaparsecs, and gigaparsecs. Smaller units are generally not used because it is more convenient to use standard astronomical units instead. The parsec greatly simplifies calculations for astronomers, as it is much easier to say that a certain star is one and a half parsecs away from the Sun, rather than stating a distance of over 46 trillion kilometers.
Who was responsible for the invention of the parsec?
In the year 1838, it was the German scientist Friedrich Bessel who achieved the breakthrough in measuring distances to celestial objects. He was the first person to accurately calculate the 61 annual parallax of the Swan star. Bessel utilized the traditional method of calculating the disparity in angles derived from conducting two separate measurements in order to determine the distance from this particular star.
Image source: bigslide.ru
The process involved taking measurements when the Earth was positioned facing the Sun on one side, and then repeating the measurements six months later (when the Earth was positioned facing the Sun on the opposite side).
However, it was not until 1913 that the term “parsec” was coined, all thanks to the contributions made by the English astronomer Herbert Turner.
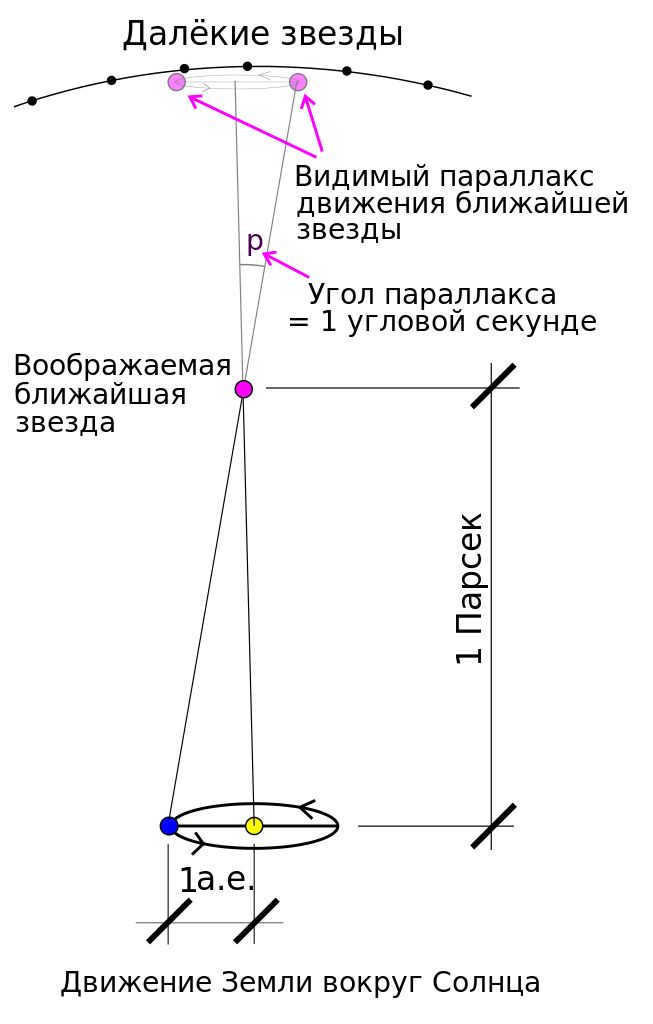
Schematic representation of a parsec (not to scale) Image source: wikipedia.org
A parsec is a unit of distance used in astronomy, defined as the distance at which one astronomical unit (the average distance between the Earth and the Sun) subtends an angle of one arc-second.
To calculate the parsec, we apply the annual parallax. By imagining a right-angled triangle, we can determine the distance to a star based on its parallax, which is measured in arc-seconds. A parsec is equivalent to 3.26 light-years or approximately 30 trillion kilometers. It was one of the first methods used to measure distances to stars and is represented as “pc”.
The concept of the parsec relies on the principle of parallax, which allows us to measure the distance to celestial bodies by observing their slight shift as the Earth orbits the Sun.
There are some distances to objects in space that are measured in parsecs:
The closest star to the Sun, Proxima Centauri, is located at a distance of 1.3 parsecs.
The distance from the Sun to the center of the Milky Way is approximately 8 kiloparsecs.
The distance from the Sun to the Andromeda Nebula is about 0.77 megaparsecs.
" – A parsec is defined as the distance to an object that has an annual trigonometric parallax of one angular second.
According to the alternative definition, a parsec is the distance from which a segment of one astronomical unit length (which is nearly equal to the average radius of Earth’s orbit) that is perpendicular to the line of sight is observed at an angle of one angular second (1″).
1 piece.
not found; View. math/README – configuration assistance): \frac<\operatorname1 inch»>
Unable to interpret the expression (No executable file found; View math/README – setup assistance.): \frac<2\pi>
Multiples are also utilized: kiloparsec (kpc, kpc), megaparsec (Mpc, Mpc), gigaparsec (Gpc, Gpc). Dolal units are generally not utilized because astronomical units are utilized instead .
What is the definition of the term “parsec”?
The term “parsec” is derived from the combination of the words “parallax” and “second”. However, in this context, the word “second” does not refer to a unit of time, but rather to a unit of measurement for plane angles, specifically an angular (or arc) second.
Parallax is a metric used to determine the change in position of a celestial object in relation to an observer. In the field of astronomy, daily, annual, and century parallax are distinguished.
The diurnal parallax is a measurement that determines the disparity in the direction to a celestial body from a specific point on Earth compared to the center of the Earth. On the other hand, the annual parallax takes into consideration the Earth’s rotation around the Sun while determining the same parameters. Lastly, the century parallax allows observers to ascertain the discrepancy between the observed object and the observer, considering the proper movements of the object within the galaxy.
Distances measured in parsecs
Distances below one parsec
Distances expressed as fractions of a parsec are commonly associated with objects within the same star system. For instance:
- One astronomical unit (a.e.) – the distance from the Sun to Earth – is slightly less than 5 × 10 -6 pc.
- The farthest space probe, Voyager 1, was 0.000,703 pc away from Earth as of January 2019. “Voyager 1” took 41 years to cover that distance.
- The estimated diameter of the Oort Cloud is approximately 0.6 pc.
According to observations made by the Hubble Space Telescope, the astrophysical jet emanating from the active galactic nucleus of M87 contracts by 20″ and is believed to be 1.5 kiloparsecs (4892 sv. years) in length (the perspective from Earth somewhat shortens the jet).
Distances in the universe are often measured in parsecs (pc), which represent the distances between nearby stars, such as those in a single spiral arm or globular cluster. When we talk about distances of 1000 parsecs (3262 light-years), we use the term kiloparsecs (kpc). Astronomers commonly use kiloparsecs to refer to distances within galaxies or groups of galaxies. For example:
- A parsec is approximately equal to 3.26 light-years.
- Proxima Centauri, the closest known star to Earth after the Sun, is located 1.3 parsecs (4.24 light-years) away, as determined by direct parallax measurements.
- The Pleiades cluster is situated at a distance of 130 ± 10 pc (420 ± 30 light-years) from us, based on parallax measurements from the Hipparcos mission.
- The distance between Earth and the center of the Milky Way is over 8 kiloparsecs (26,000 light-years), and the Milky Way itself spans about 34 kiloparsecs (110,000 light-years).
- Andromeda (M31) is approximately 780 kiloparsecs (2,500,000 light-years) away from Earth.
Megaparsec and gigaparsec
Astronomers often use megaparsecs (Mpc) to measure the distances between neighboring galaxies and galaxy clusters. A megaparsec is equivalent to one million parsecs, or approximately 3,260,000 light-years. Occasionally, galactic distances are given in GPC / h units (such as “50 / h Mpc” or “50 Mpc h -1″). Here, h represents a constant known as the dimensionless Hubble constant, which falls within the range of 0.5 < h H for the rate of expansion of the universe: h =HOUR100 km / s / Mpc. The Hubble constant becomes relevant when converting the observed redshift z into a distance d using the formula d ≈cHOUR× z.
One gigaparsec (Gpc) is equivalent to one billion parsecs, making it one of the largest units of length commonly used. Approximately, one gigaparsec is equal to 3.26 billion light-years or about 114 times the distance to the observable Universe, which is determined by the cosmic background radiation. Astronomers frequently utilize gigaparsecs to describe the size of large-scale structures, including the dimensions and distance to the Great Wall of CfA2, the distance between galaxy clusters, and the distance to quasars.
- Andromeda is situated approximately 0.78 Mpc (2,500,000 LY) away from Earth.
- The closest major cluster of galaxies, known as the Virgo cluster, is roughly 16.5 Moc (54,000,000 LY) away from Earth.
- The galaxy RXJ1242-11, which possesses a supermassive black hole core similar to that of the Milky Way, is located approximately 200 Mpc (650 million light-years) away from Earth.
- The Hercules-Corona Borealis Great Wall filament galaxy is presently recognized as the largest structure in the Universe, measuring approximately 3 GPH (98 trillion years) in diameter.
- The particle horizon, which marks the boundary of the observable Universe, has an estimated radius of 14 GPH (46 billion years).
Depiction in popular culture.
It appears that Han Solo in “A New Hope”, the first Star Wars movie, mistakenly used Parsec as a unit of time. In the movie, he claimed to have completed the Kessel run in less than 12 parsecs. This claim was later repeated in “The Force Awakens”, but in the movie “Solo: A Star Wars Story”, it was clarified that the Millennium Falcon traveled a shorter distance, not a faster one, due to its more dangerous route through hyperspace. The term Parsec is also ambiguously used as a spatial unit in the show “The Mandalorian”.
In the novel “A Wrinkle in Time”, Mr. Murray gave his daughter Meg the nickname “megaparsec”.
Volume Units
In order to calculate the quantity of stars within the Milky Way, cubic kiloparsecs (kpc^3) volumes are selected in different directions. The total number of stars within these volumes are then counted and statistically determined. Similarly, the number of globular clusters, dust clouds, and interstellar gas are calculated. To determine the quantity of galaxies within superclusters, cubic megaparsecs (Mpc^3) volumes are chosen. All galaxies within these volumes are classified and counted. From there, the total number of galaxies can be determined statistically. The extensive void of Botes is measured in cubic megaparsecs.
In the field of physical cosmology, scientists use cubic gigaparsecs (Gpc3) to measure the distribution of matter in the visible Universe and determine the number of galaxies and quasars. Currently, the Sun is the only star within its cubic parsec (pc3), but in globular clusters, the density of stars can range from 100 to 1000 pc-3.
Gravitational-wave interferometers, such as LIGO and Virgo, observe a volume expressed in cubic megaparsecs (mpc3). This volume represents the effective distance of a cube that encompasses the observed region.
Handy estimations
Within the depiction presented, the measurement of a single second possesses a significantly higher numerical value, consequently resulting in a hypotenuse that is evidently lengthier than the adjacent side. In reality, for such a minuscule angle, the disparity in length between the two sides is comparatively negligible, and ultimately, the hypotenuse is scarcely greater than a parsec (or, more precisely, the distance from the Sun to a remote star, rather than the distance from the Earth to a remote star).
There are various ways to measure distances in astronomy, one of which is the parsec (pc). The parsec is a unit commonly used to measure vast distances in space, particularly within our own galaxy, the Milky Way.
A parsec is equivalent to approximately 3.26 light years or roughly 30.857 quadrillion kilometers. This implies that a parsec represents an incredibly long distance.
The term “parsec” is derived from the English phrase “parallax second.” A parallax second refers to an angular distance that corresponds to 1/3600 degrees. Parallax is a phenomenon in which the apparent position of an object in the sky changes due to a shift in the observer’s perspective.
By measuring the parallax, which varies depending on the observer’s location, it is possible to determine the distance to an object in the sky.
The parsec is a significant unit of measurement in the field of astronomy due to its ability to accurately measure large distances. Scientists utilize parsecs to estimate the distances to various celestial bodies, such as stars, galaxies, and other objects found in space.
What exactly is a parsec?
A parsec represents a specific distance measurement used within the realm of astronomy to determine the relative remoteness of objects in space. This unit is particularly valuable when it comes to calculating the distance to stars and galaxies positioned at vast distances from our planet.
Symbolized by “pc”, a parsec is defined as the distance at which an astronomical unit (a.u.), equal to the average distance between the Earth and the Sun, subtends an angle of one arcsecond.
The angular second is the tiniest unit of angular measurement, equivalent to one 3600th of a degree or one minute of angle. A parsec corresponds to approximately 3.09 × 10^16 meters or roughly 3.26 light-years.
By utilizing the parsec, astronomers are able to estimate the distances to the most remote celestial objects, enabling precise measurements of astronomical distances and facilitating comparisons of the remoteness of objects at various distances.
The introduction of the parsec as a unit of measurement for stellar distances was driven by the inadequacy of other units of measurement for such vast distances.
The parsec holds significant importance in the field of astronomy as it aids astronomers in comprehending the scale of the universe and the vast distances separating celestial objects, thus paving the way for new explorations and discoveries.
Understanding the Parsec
The parsec, a unit of measurement used in astronomy, provides a way to gauge the vast distances between celestial objects within our galaxy.
Specifically, a parsec is equivalent to approximately 3.26 light-years or 9.46 trillion kilometers. This measurement is derived from the distance at which an astronomical unit (AU) creates an angle of one ten-millionth of an arc second.
The primary purpose of the parsec is to calculate distances to stars and subdwarfs within our galaxy, as well as in nearby galaxies like the Nebula in the Magellanic Clouds. Additionally, it is utilized to determine distances to more remote galaxies that alternative measuring techniques cannot accurately assess.
The parsec is a convenient unit of measurement as it relies on the principle of triangulation, enabling astronomers to determine distances based on parallax, which is the apparent shift in the position of an object in the sky due to the change in the observer’s position on Earth.
It is worth mentioning that although the parsec is utilized in professional astronomy, it is not a commonly used or widely recognized unit of measurement in everyday situations.
When it comes to the vast distances between stars in the universe, astronomers rely on a unique unit of measurement known as the parsec (pc).
A parsec is defined as the distance at which an astronomical unit (a.u.) creates an angle of one second of arc. In other words, one second of arc is equal to 1/3600 of a degree.
To be more precise, a parsec is determined by the annual parallax of a star, which is the angular displacement of its position on the celestial sphere caused by its motion around the Sun. This displacement is measured in units of angular seconds over the course of one year.
Overall, the parsec serves as one of the fundamental units for measuring interstellar distances.
Typically, astronomers utilize parsecs or another measurement unit called the light-year (ly) to gauge interstellar distances. A light-year corresponds to the distance that light covers within a span of one year.
In cosmology, larger units like megaparsec (Mpc) or gigaparsec (Gpc) are employed to denote interstellar distances.
The cosmos is immense, and the gaps between stars serve as a highly coveted subject of exploration and examination for astronomers.
What is the measurement equivalent to a parsec?
A parsec (pc) is a unit of measurement used in astronomy to quantify vast distances in outer space. It is derived from parallax, which refers to the apparent shift in the position of a star in the sky due to the Earth’s orbit around the Sun.
One parsec is defined as the distance at which the parallax of a star is equal to one arc second (1 arc second or 1/3600 of a degree). This value is approximately equivalent to 3.26 light years or about 30.86 trillion kilometers.
The determination of a parsec is based on the triangulation method, which involves using two observation points in Earth’s orbit at different times of the year to measure the parallax of a star in the sky. The accuracy of parsec measurements has significantly improved with the advancements in space astronomy, enabling more precise calculations of distances to distant stars and galaxies.
By utilizing the parsec, astronomers have the capability to gauge distances in space that extend beyond our solar system. It proves to be quite valuable when it comes to measuring distances to stars, as well as estimating the size and scale of galaxies, quasars, and other celestial objects.
Calculating in terms of light-years
A light-year serves as a unit of length that astronomers use to measure immense distances in the universe. It is defined as the distance that light, when traveling in a vacuum, covers within one year, at a rate of approximately 299,792,458 meters per second.
The measurement in light-years proves to be especially advantageous when describing the distances between stars and galaxies. In fact, the expanse of the universe is so vast that measuring it in kilometers, local light seconds, or minutes would be highly inconvenient. The light-year provides us with a more intuitive understanding of the scale and the time it takes for light to reach these entities.
As an instance, the nearest celestial body to our planet, known as Proxima Centauri, is situated approximately 4.24 light-years away. This implies that the light emitted from this celestial body requires 4.24 years to traverse the immense distance and eventually reach Earth. If, for instance, this celestial body were to suddenly erupt at this very moment, we would not witness this extraordinary event until a span of 4.24 years has elapsed.
Furthermore, the distances between various galaxies and other celestial objects within our vast Universe are also measured in light-years. To provide an example, the Andromeda galaxy, a sprawling spiral galaxy, is located approximately 2.5 million light-years away from our planet Earth.
Utilizing light-years as a unit of measurement assists scientists in comprehending the immense scale of the universe and the considerable amount of time it takes for light to traverse from one point to another. This method also grants them the opportunity to investigate the history and evolution of celestial objects within the universe, based on the data collected from vast distances.
Mathematical definition of a parsec
Parsec is a unit of measurement used in astronomy to determine distances. It is based on fundamental constants, such as the Earth’s geometric properties and certain properties of light.
One of the key components in the definition of a parsec is the concept of a “tired second,” which is derived from the length of a year on Earth. A tired second is exactly equal to 9,192,631,770 periods of radiation corresponding to the transition between the two hyperfine states of the ground state of the cesium 133 atom.
Mathematically, a parsec can be defined as:
1 parsec (pc) =
- The distance that light travels in one tired second (299,792,458 meters)
- (1/3600) degree of the Earth’s elliptical circumference
- One tired second in a vacuum would cover a distance of approximately 30.857 million kilometers for light.
Astronomers can utilize the parsec to quantify and depict immense distances in the universe, as kilometers or light-years are not practical for such scales.
Applications of the parsec in the field of astronomy
The parsec, which is short for “parallax second,” is a unit used in astronomy to measure distances. It is based on the concept of parallax, which involves the apparent shift in the position of objects against the backdrop of the starry sky due to the motion of the Earth around the Sun.
The application of the parsec in astronomy allows scientists to determine the distances to various celestial objects, such as stars and galaxies. This information is crucial for gaining insights into the structure and evolution of the Universe.
The fundamental principle behind the utilization of the parsec is to measure parallax, which refers to the angle at which an object is observed from two different vantage points – the Earth at different positions as it orbits the Sun throughout the course of a year.
When it comes to objects that are further away, astronomers rely on parallax-based methods like the “parallax method” and “dynamic parallax”. These methods establish a correlation between the quantity being measured, such as brightness, and the distance to the object.
The parsec serves as a convenient and practical unit of measurement in astronomy. It is approximately equal to 3.262 light years or about 30.857 trillion kilometers. This means that an object located 1 parsec away will be visible from Earth at an angle of 1 arc second.
By utilizing parsecs, scientists are able to achieve more precise measurements of distances in space. This is particularly useful for calculating the actual sizes and luminosities of stars, galaxies, and other celestial objects within the universe.
Q&A
What exactly is a parsec?
A parsec is a unit of measurement used in astronomy to calculate distances to objects in space. It is equivalent to approximately 3.26 light years or about 30.86 trillion kilometers.
How do astronomers use parsecs to measure distance?
Parsecs are utilized by astronomers as a way to determine the distance to extremely faraway objects in space. This unit of measurement, which is equivalent to about 3.26 light-years or about 30.86 trillion kilometers, helps provide valuable information about the vastness of the universe.
What is the method for calculating distances in parsecs?
The calculation of distances in parsecs involves the use of parallax. Parallax refers to the apparent shift in the position of a star on the celestial sphere caused by the Earth’s movement around the Sun. By measuring the parallax angle of a star, one can determine its distance in parsecs.