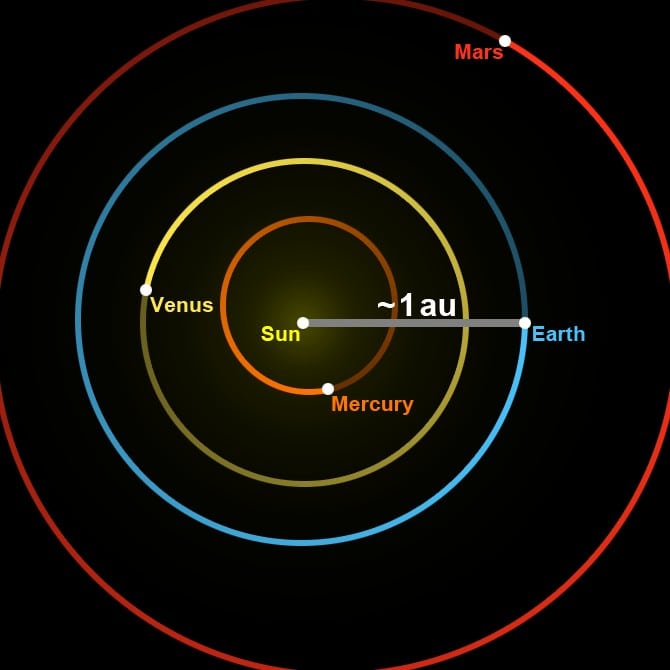
An astronomical unit (a.u.), also known as an au, is a unit of distance commonly used in astronomy. It is approximately equal to the average distance from the Earth to the Sun.
Light takes about 500 seconds (or 8 minutes and 20 seconds) to travel this distance.
The astronomical unit is primarily used to measure distances between objects in extrasolar systems, as well as between components of double stars.
In September 2012, the 28th General Assembly of the International Astronomical Union in Beijing made the decision to establish a connection between the astronomical unit and the International System of Units (SI). The definition of the astronomical unit states that it is precisely equal to 149,597,870,700 meters. Furthermore, the IAU also standardized the international designation for the astronomical unit as “au”. The designations “a. u.” or “AU” can be used. There is also a recommended international standard, ISO 80000-3, which suggests the use of the designation “ua”.
In the Russian Federation, the astronomical unit is permitted for use as a non-system unit within the field of “astronomy” without any time limitations. As per GOST 8.417-2002, it is not allowed to use the name and designation of the astronomical unit with SI prefixes of fractions and multiples.
Previous explanations
In light of the resolution made at the 10th IAU General Assembly in 1976, the astronomical unit was established as the radius of a circular path followed by a selected celestial body in isotropic coordinates. This path would have an angular velocity of exactly 0.017 202 098 95 radians per ephemeris day, while disregarding all other celestial bodies in the solar system aside from the Sun. In the IERS 2003 constant system, the astronomical unit was approximated to be 149,597,870,691 kilometers.
The story of the past
Ever since the heliocentric system was introduced, particularly with Kepler’s study of celestial mechanics, we have had a fairly accurate understanding of the relative distances within our solar system (excluding those that are too close). Given that the Sun is the central body and the Earth orbits it in a nearly circular path, it made sense to use the radius of this orbit as our unit of measurement. However, there was no reliable way to determine the exact magnitude of this unit and compare it to the Earth’s scale. The Sun is simply too far away for us to measure its parallax from Earth. While we did have knowledge of the distance to the Moon, it was impossible in the 17th century to estimate the ratio of distances between the Sun and the Moon based on the available data. Observing the Moon did not provide the necessary accuracy, and we also did not have knowledge of the Earth’s and Sun’s masses to calculate the ratio.
The radar was used to refine the astronomical unit. In 1961, Venus was located and the astronomical unit was determined to be 149,599,300 km. The margin of error did not exceed 2000 km. Further radiolocation of Venus in 1962 helped to decrease this uncertainty and provide a more precise value for the astronomical unit: it was found to be 149,598,100±750 km. Prior to the 1961 location, the value of the astronomical unit was known with an accuracy of 0.1%.
Long-term measurements have shown that the distance from the Earth to the Sun is slowly increasing at a rate of approximately 15 meters per century (which is significantly higher than the accuracy of modern measurements). One possible explanation is the Sun’s mass loss, but the observed effect is much greater than what has been calculated.
Several Distances
- The orbital radius of the most distant planet in the solar system is approximately 30 astronomical units (a.e.).
- As of April 23, 2016, the planet was 134.75 a.e. away from the Sun, moving away from it at a rate of 3.6 a.e. per year. It holds the record for being the farthest from Earth and the fastest moving human-made object.
- The distance to our closest star, Proxima Centauri, measures around 270,000 a.e.
Previous definitions
In line with the resolution passed during the 10th IAU General Assembly in 1976, the astronomical unit was officially defined as the radius of the circular orbit in isotropic coordinates, where the angular velocity of the orbit, without considering any other celestial bodies in the solar system apart from the Sun, would be precisely 0.017 202 098 95 radians per ephemeris day. In the IERS 2003 Constant System, the astronomical unit was assumed to be 149,597,870,691 km.
Following that, further accurate measurements of the astronomical unit were conducted using Venus’ transits across the surface of the Sun. Additionally, the close proximity of the asteroid Eros to Earth in 1901 and subsequent measurements of its parallax provided even more precise estimations.
The measurement of the astronomical unit was further refined through the use of radar to track the positions of the planets. In 1961, the location of Venus allowed scientists to determine that the astronomical unit was 149,599,300 km, with a possible error of only 2000 km. Further radar measurements of Venus in 1962 helped to reduce this uncertainty and provide a more precise value for the astronomical unit: 149,598 100±750 km. Prior to the 1961 measurement, the accuracy of the astronomical unit was known to within 0.1%.
Long-term observations of the astronomical unit, as defined in 1976, have shown a slow increase at a rate of approximately 15 centimeters per year. This rate of change exceeds the accuracy of modern measurements by a significant margin. One possible explanation for this phenomenon is the Sun’s loss of mass through solar wind, although the observed effect is much larger than predicted.
Read also
Remarks
Wikimedia Foundation . 2010 .
Take a look at “Astronomical unit” in alternative dictionaries:
ASTRONOMICAL UNIT – ASTRONOMIC UNIT, a unit of measurement utilized in astronomy (primarily for calculating distances within the solar system). It is equivalent to the average distance from the Earth to the Sun; 1 astronomical unit=149.6 million kilometers … Modern Encyclopedia
Astronomical unit – ASTRONOMIC UNIT, a unit of measurement utilized in astronomy (primarily for calculating distances within the solar system). It is equivalent to the average distance from the Earth to the Sun; 1 astronomical unit=149.6 million kilometers. … Illustrated Encyclopedic Dictionary
ASTRONOMICAL UNIT – length (a. e.) unit of distance in astronomy, equivalent to the average distance of the Earth from the Sun. 1 a. e. = 149.6 million km … Large Encyclopedic Dictionary
ASTRONOMICAL UNIT – (a.e.) is the standard unit of distance used in astronomy, particularly for measuring distances within the solar system. It represents the average distance from the Earth to the Sun, which is approximately 149,598,000 km. This definition can be found in the Scientific and Technical Encyclopedic Dictionary.
ASTRONOMICAL UNIT – also known as length (a.e., AE), is defined as the distance from the Earth to the Sun. It is equivalent to 1.49600 x 10^11 meters. This information is provided in the Physical Encyclopedic Dictionary, published by Soviet Encyclopedia in 1983.
ASTRONOMICAL UNIT – refers to the average distance between the Earth and the Sun, which is also the major semi-axis of the Earth’s orbit. It is approximately equal to 149,500,000 km. This definition can be found in Samoilov K. I.’s Marine Dictionary.
Astronomical unit – (a. e.), a unit of length used in astronomy, representing the average distance between the Earth and the Sun. 1 astronomical unit is approximately equal to 149.6 million kilometers. * * * * * ASTRONOMIC UNIT Astronomical unit Astronomical unit is a unit of measurement used in astronomy, which is defined as the average distance between the Earth and the Sun… … Encyclopedic Dictionary
Astronomical unit – a unit of measurement in astronomy, known as an astronomical unit, which is equal to the average distance between the Earth and the Sun. It is approximately equal to 149.6 million kilometers. * * * Astronomical unit Astronomical unit is a unit of measurement used in astronomy, and it represents the average distance between the Earth and the Sun… Penkiakalbis aiškinamasis metrologijos terminų žodynas
Astronomical unit is a unit of distance in astronomy that is equal to the average distance between the Earth and the Sun. It is recommended by the International Astronomical Union for astronomical research. According to the list of fundamental constants of astronomy, it is approximately equal to 149.6 million kilometers.
General information
An astronomical unit, also known as AU, is defined as the average distance that a sunbeam travels to reach the Earth. Another definition states that it is equal to the major semi-axis of the elliptical orbit of our planet. Both of these definitions are accurate. There are several approaches to calculating the distance in kilometers of an astronomical unit. In this context, Earth and the Sun can be considered as points A and B, respectively, using a geometric perspective. There are traditional methods as well as modern techniques for measuring this distance. The most precise value for the length of 1 astronomical unit is currently accepted as 149,597,870 + 2 kilometers. In common calculations, the value of 149,600,000 kilometers is often used. This value was determined relatively recently. Let’s now explore the classical methods of measurement, followed by an examination of the newer approaches for obtaining this information.
Traditional Approaches to Measurement

Before proceeding with their assistance, it was imperative to ascertain the average radius of the Earth. The most recent techniques no longer necessitate knowledge of this parameter. A comprehensive range of geodetic methods were employed to establish the average radius of the Earth. Now let us discuss the simplest approach for measuring an astronomical unit. It is akin to the serif method, but with a relatively smaller baseline value. Consequently, it becomes imperative to ensure the utmost precision when measuring small angles. This often resulted in relatively imprecise data. The second approach entails utilizing the asteroid Eros in the computations. It periodically passes in close proximity to the Earth. During these instances, its parallax nearly reaches an angular minute. The sides of the ZEC triangle are then determined, with one of them representing the astronomical unit.

Summary

It is now common knowledge that an astronomical unit represents the distance between the Earth and the Sun. Unfortunately, even to this day, humans face challenges in covering such relatively short distances (although this does not hinder our mechanical automated counterparts). It is worth mentioning that this is not the sole unit of measurement used. Alongside it, the light-year and the parsec are widely employed. The former is frequently used and requires no further explanation. The latter refers to a little over 206 thousand astronomical units. Alternatively, it can be expressed as 3.26 light-years. The focus is primarily on their magnitudes. For example, the center of our galaxy is a mere 8 kiloparsecs away. Nevertheless, us humans still have to conquer the task of traveling to even these relatively small cosmic distances, such as the astronomical unit.
The astronomical unit serves as a means for people to comprehend the distance to various celestial objects in our solar system.
Essentially, the astronomical unit represents the distance between our planet and a cosmic entity.
The rationale behind this concept is straightforward. Specifically, the astronomical unit is derived from the average radius of Earth’s orbit or the distance from Earth to the Sun. It can be challenging to fathom the distance from Earth to a star system when given a value of 1.3. However, if you are informed that this distance is equivalent to 270,000 astronomical units, you can readily envision the gap between the Sun and Earth and mentally magnify it by 270,000. This enables you to vividly picture this immense distance and grasp its vast magnitude.
Despite its clarity, the astronomical unit is not widely used in professional astronomy. This is because it is only convenient to calculate distances to nearby objects in the Universe, such as the planets in our Solar System. When trying to determine the distance to more distant objects in astronomical units, the numbers become so large that it becomes impractical for mathematical calculations. Instead, astronomers use another measurement called the parsec, along with its derivatives, to determine distances to objects in the observable Universe.
The discovery of the astronomical unit was made possible by the realization that the Earth orbits the Sun, as well as the application of Keplerian celestial mechanics, which enabled scientists to calculate a relatively precise distance from Earth to various planets in the solar system, including the Sun. Further investigations by astronomers from the 17th to the 20th century led to refinements in these initial calculations and the acquisition of even more accurate data regarding the positions of these celestial bodies. One particular method that played a significant role in determining distances during this period was the horizontal parallax technique, which continues to be widely utilized in both astronomy and geometry to this day.
In 1962, astronomers were able to determine the precise distance from Earth to the Sun using radar signals. The average measurement, which is 149597870.7 km, was adopted as the standard unit known as the astronomical unit (AU). This definition is included in the International System of Units SI.
In recent times, scientists have made the intriguing discovery that the value of the astronomical unit is not constant. It actually increases slightly each year. Through observation, scientists have noted that the length of the AU expands by one meter every 7 years. This means that over the course of 100 years, the Earth moves 15 meters further away from the Sun. Several theories have been proposed to explain this phenomenon, with the most popular one suggesting that the Sun is gradually losing mass due to the solar wind.
Astronomers utilize specialized units of measurement that may not always be readily comprehensible to the general public. This is understandable since if cosmic distances were measured in kilometers, the sheer magnitude of zeros would be overwhelming. Hence, it is customary to employ significantly larger units of measurement such as the astronomical unit, light year, and parsec to gauge cosmic distances.
Commonly used to indicate distances within our solar system. If we were to express it in kilometers, the closest distance to Pluto would be about 4,250 million km, which would be difficult to comprehend. For distances of this magnitude, it is more appropriate to use an astronomical unit (a.u.), which is defined as the average distance from the Earth’s surface to the Sun. In other words, 1 a.u. corresponds to the length of the major semi-axis of Earth’s orbit, which is approximately 150 million kilometers. Therefore, if we state that the shortest distance to Pluto is 28 a.u. and the longest journey could be 50 a.u., it is much easier to visualize.

Scientists have hypothesized for centuries that light does not propagate instantaneously, but rather at a finite speed. This notion was first proposed in 1676 by Danish astronomer Ole Remer, who observed a peculiar phenomenon during the eclipses of one of Jupiter’s satellites. Remer noticed that the timing of these eclipses appeared to lag when the Earth was on the opposite side of the Sun, relative to Jupiter’s position. However, as the Earth gradually moved closer to Jupiter once more, the eclipses resumed their normal schedule.
Therefore, a discrepancy of approximately 17 minutes in time was observed. This finding led to the conclusion that it takes 17 minutes for light to traverse a distance equal to the diameter of the Earth’s orbit. Given that the diameter of the orbit is approximately 186 million miles (or 939,120,000 kilometers), it follows that the speed of light is around 186,000 miles per second.

In our modern era, with the guidance of Prof. Albert Michelson, an endeavor was undertaken to determine the precise measurement of a light year. Through meticulous calculations, it was determined that a light year is equivalent to 186,284 miles per second (approximately 300 km/s). By multiplying this speed by the number of seconds in a year, we find that a light year spans a distance of 5,880,000,000,000,000,000 miles, which is equivalent to 9,460,730,472,580.8 kilometers.
For practical purposes, astronomers often utilize another unit of measurement known as the parsec. This unit represents the displacement of a star relative to other celestial bodies by 1 arcsecond when the observer is situated at a distance of 1 astronomical unit.
Scientists are actively conducting research on the four planets within our solar system. One particular area of interest for scientists is determining the precise distance to Mars.

Calculating the Distance from Earth: A Complex Task
Measuring the distance between Earth and other celestial objects can be a challenging endeavor.
Within the solar system, distances are often measured using an astronomical unit (a.u.), which represents the average distance between the Sun and the third planet. This value is approximately 149.6 million kilometers and is primarily used for interplanetary measurements.
On a cosmic scale, distances are calculated using two main units of measurement: light-years and parsecs. A light-year corresponds to the distance traveled by light in one year, equivalent to about 9.460 trillion kilometers. A parsec, on the other hand, is approximately 3.26 light-years. These units allow for calculations on a much larger scale, encompassing the vastness of the universe.
When determining the distance between Mars and Earth, the positions of both celestial bodies must be taken into account.
However, there are various factors that complicate these calculations:
- The orbits of celestial bodies are elliptical, not circular.
- Mars moves at a slower speed than Earth.
- The orbits do not revolve around the Sun.
As a result, the distance between celestial bodies varies at different points, meaning that the distance between Earth and Mars is not constant.
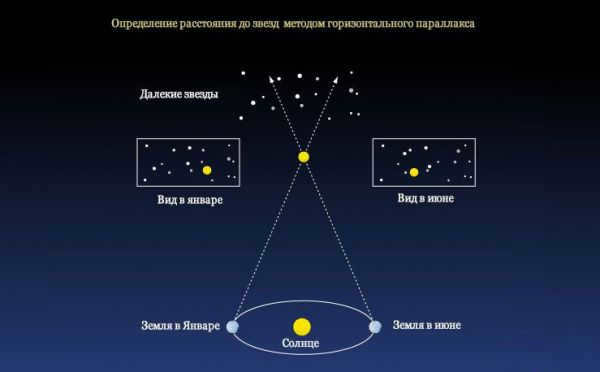
The technique of parallax measurement for determining the distance to Mars
A crucial method for calculating astronomical distances involves the utilization of the parallax technique, which can be summarized as follows:
- Two distinct points are selected on Earth (preferably with a significant separation). The line segment connecting these points is known as the baseline.
- A celestial body, such as a star or planet, whose distance needs to be determined, acts as the third point, forming the vertex of an abstract triangle.
- Subsequently, the angle with a vertex at the third point is computed, which corresponds to the angle opposite the baseline. This angle is referred to as the horizontal parallax.
- Trigonometric calculations are then conducted to establish the distances to astronomical objects.
Giovanni Domenico Cassini first employed this method in the 17th century.
Different Points in Mars’ Orbit and Distance
Due to the complexity of calculating the exact distance between Earth and Mars, astronomers commonly refer to maximum, minimum, and average values.
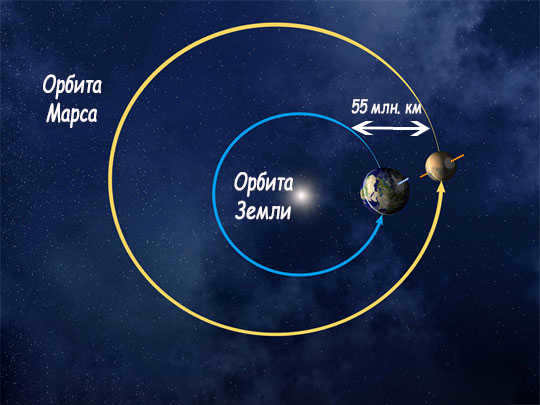
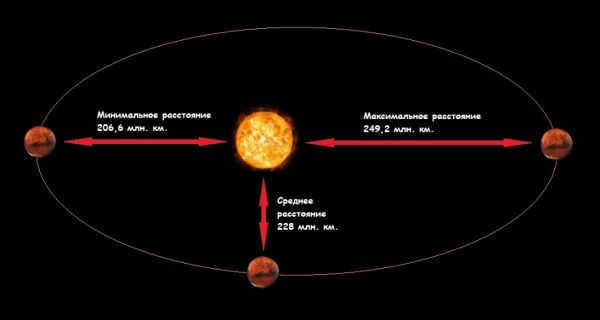
The closest distance between the two planets in the Solar System is 54.55 million kilometers. This occurs when Earth is at its farthest point from the Sun and Mars is at its closest point to the Sun. However, the closest Mars has been to Earth in the past 50,000 years was in 2003, at a distance of 56 million km.
The average distance between these two celestial bodies is 225 million km. This figure is calculated based on the greatest and least distances between Earth and Mars.
The largest separation between Earth and Mars occurs when both planets are positioned on opposite sides of the Sun (measuring approximately 401.3 million km).
Distance from Mars to the Sun
Mars is the fourth furthest planet in our Solar System. Its distance from the Sun is not constant due to its elliptical orbit, causing it to move closer to and farther away from the Sun, resulting in a constantly changing distance between the two celestial bodies.
For instance, when Mars is at aphelion, the farthest point from the Sun, the maximum distance is 249 million kilometers. Conversely, when Mars is at perihelion, the closest point to the Sun, the distance between the two objects is 206 million km.
How much does it cost to travel from Earth to Mars?
Mars is currently being studied from various angles, including:
- its potential as a source of natural resources and minerals;
- its suitability for human colonization;
- its potential as a tourist destination.
One important factor to consider for each of these scenarios is the duration of the journey from Earth to Mars. The length of the trip depends on the relative positions of the two planets. The shortest possible route is a direct flight, when Mars and Earth are as close to each other as possible. On average, this journey would take approximately 39 days and 5 hours.
However, in reality, such a direct flight is not currently possible due to several factors:
- Mars and Earth are constantly moving, following elliptical orbits of different sizes.
- The gravitational pull of the Sun affects the paths of both planets.
As a result, there are 3 flight trajectories that have been developed by scientists for the journey to Mars: parabolic, Homans (elliptical), and hyperbolic.
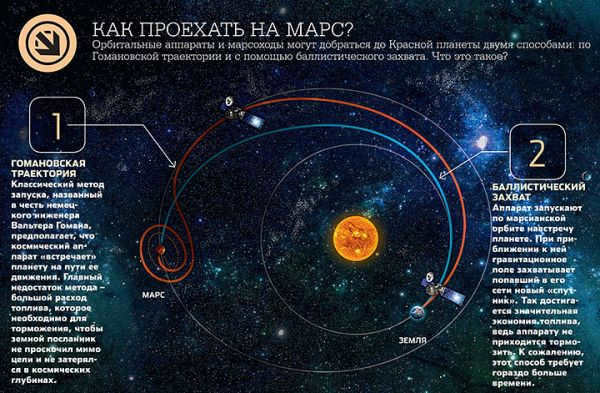
The most efficient trajectory for a flight to Mars is the elliptical trajectory, which requires the least amount of fuel. This trajectory was first proposed in 1925 and is known as the Goman trajectory. It takes the form of an elliptical orbit, allowing the spacecraft to transition between two other orbits. The approximate travel time for this trajectory is between 150-260 days, depending on the initial speed of the spacecraft.
In order to fly to Mars along a parabolic trajectory, the spacecraft needs to reach an initial velocity of 16.7 km/s, which is equivalent to the third space velocity. With this velocity, the estimated flight time is 70 days. The trajectory is plotted along a half segment of a parabola.
An hyperbolic trajectory is based on the assumption that the spaceship will initially pass by Mars and then alter its course due to the gravitational pull of the planet. The challenge of executing such a path lies in the requirement for the spacecraft to surpass speeds of 16.7 km/s.
Current rockets employ chemical engines that are not capable of achieving such velocities. This necessitates the utilization of ion engines, which scientists are actively working on. The total duration of a trip along a hyperbolic trajectory can range from 1 to 1.5 months.
Thus, the selection of a Mars flight path is influenced by various factors: the type of spacecraft propulsion system, the desired (optimal) travel time, and the distance between Earth and Mars.
Throughout the history of space exploration, around 50 missions involving unmanned probes have been dispatched to Mars. Presently, programs for crewed missions to the Red Planet are under development.
The astronomical unit is a measurement that provides a visual representation of the distance to various objects within our solar system.
Overview
An astronomical unit serves as a reference point for conceptualizing the distance between our planet and celestial bodies.
Additional Resources
How far away is our celestial body?
The reason behind this is quite simple. Essentially, the astronomical unit represents the average radius of Earth’s orbit, or the distance between Earth and the Sun. It can be challenging to comprehend the distance between Earth and the Alpha Centauri star system when expressed as 1.3 parsecs. However, if you were to hear that this distance is equivalent to 270,000 astronomical units, you would immediately picture the distance between the Sun and Earth and mentally multiply it by 270,000. This visualization allows you to truly grasp the magnitude of this distance and understand its tremendous length.
Despite its clarity, the astronomical unit is rarely used as a measurement value in professional astronomy. The reason for this is that it is only convenient for calculating distances to nearby objects in the Universe, such as the planets in our Solar System. When it comes to determining the distance to extremely distant objects in astronomical units, the numbers become so large that they are impractical for mathematical calculations. Instead, astronomers rely on another unit of measurement, the parsec, and its derived quantities, to determine distances to far-off cosmic objects in the observable universe.
Discovery’s History
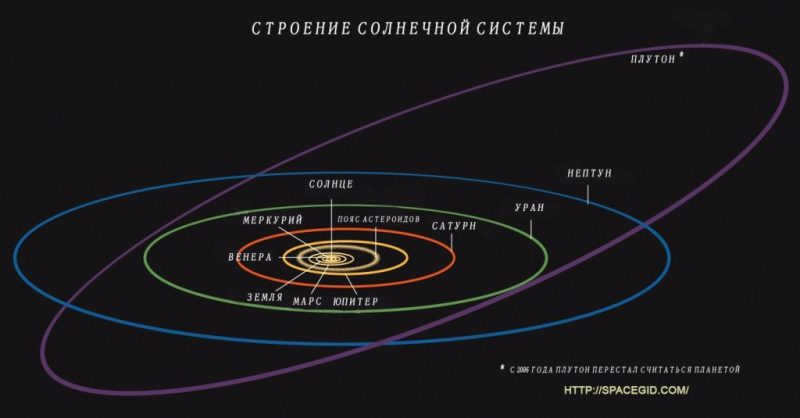
The Composition of the Solar System
The discovery of the astronomical unit was made possible by the realization that the Earth orbits around the Sun, along with the principles of Keplerian celestial mechanics. These principles allowed for a relatively precise calculation of the distance between the Earth and various celestial bodies within the solar system, including the Sun. Over time, further research by astronomers from the 17th to the 20th century led to the refinement of initial measurements and the acquisition of even more accurate data regarding the positions of these bodies. During this period, the technique of horizontal parallax played a significant role in determining distances, and it continues to be widely employed in the fields of astronomy and geometry.
Resources about the subject
Visualization of our solar system

In 1962, astronomers were able to determine the exact distance from Earth to the Sun using radar signals. The average measurement, which is 149597870.7 km, was established as a standard reference point. This measurement is known as the astronomical unit and is defined in the International System of Units SI.
In recent times, scientists have made the intriguing discovery that the astronomical unit is not a constant value. It actually increases slightly each year. Researchers have observed that every 7 years, the length of the astronomical unit grows by one meter. This means that over the course of 100 years, the Earth moves 15 meters farther away from the Sun. Various theories have been proposed to explain this phenomenon, with the most popular one suggesting that the Sun is gradually losing mass due to the effects of solar wind.
Astronomical unit
The astronomical unit (AU) is a unit of length used in astronomy to measure distances within the Solar System. It is defined as the average distance from the Earth to the Sun, approximately 149.6 million kilometers (93 million miles). The AU is a convenient way to express the vast distances involved in astronomical measurements, as it provides a reference point that is familiar and easily understood. It is commonly used to describe the distances between planets, moons, and other celestial bodies within our solar system.


The Astronomical Unit (AU) is a unit of measurement used to determine distances to celestial objects. It is defined as the average distance from the Earth to the Sun, which is approximately 149,597,870,700 meters. The AU is commonly denoted as “a.e.” in Russian and “au” internationally.
Astronomical unit: a measurement unit in astronomy
Astronomical unit is a unit used to measure distances in astronomy.
Astronomical unit represents the radius of a circular orbit of a test body in isotropic coordinates. It is defined as the angular velocity of the orbit, neglecting all other bodies in the Solar System except the Sun, which would be exactly 0.017 202 098 95 radians per ephemeris day (as decided by the 10th General Assembly of the International Astronomical Union in 1976).
The definition of the astronomical unit has evolved as astronomical measurement techniques have advanced.
In 1672, Giovanni Cassini and his collaborator Jean Richet determined the value of the astronomical unit by measuring the parallax of Mars. They found it to be approximately 140 million kilometers.
Due to the Earth’s orbit around the Sun, the distance between them varies throughout the year, from its maximum point (aphelion) to its minimum point (perihelion). To account for this, a new definition of the astronomical unit was established in 2012, which is now tied to the International System of Units (SI).
The astronomical unit is precisely 149,597,870,700 meters (according to the decision made by the 28th General Assembly of the International Astronomical Union in 2012).
Astronomical unit is denoted in Russian as a.e. and internationally as au.
The astronomical unit is listed as a non-system unit approved by the International Bureau of Weights and Measures, and is recognized for use alongside the units of the International System of Units (SI).
According to the resolution of the Russian Federation government dated October 31, 2009, No. 879 “On the Approval of the Regulations on the Acceptable Units for Use in the Russian Federation,” the astronomical unit can also be used as a non-system unit of length in the field of astronomy without any time limitations.
1 a.u. is equal to exactly 149,597,870,700 meters.
Application of the astronomical unit:
The astronomical unit is primarily utilized for measuring distances within the solar system or in proximity to other stars. Additionally, it serves as a basis for defining other units of astronomical length, specifically the light-year and the parsec.
Conversion of an astronomical unit to other units of measurement:
1 astronomical unit equals exactly 149,597,870,700 meters.
1 astronomical unit is approximately equivalent to 499,004,783.84 light seconds.
Multiples and fractions of an astronomical unit:
Using divisible and multiple prefixes from the International System of Units (SI) with the astronomical unit is not acceptable.
Interesting examples:
Electromagnetic radiation, including visible light, travels approximately 1 astronomical unit in 499 seconds (or 8 minutes and 19 seconds).
The major semi-axis of Neptune’s orbit, which is the farthest planet in the solar system, is approximately 30.1 a.u.
As of October 14, 2019, the Voyager 1 spacecraft has traveled a distance of 147.17 a.u. from the Sun and is continuously moving away from it at a rate of about 3.6 a.u. per year. It is currently the farthest man-made object from Earth.
1 light-year is approximately equal to 63,241 a.u.
The distance to the nearest star (after the Sun) to Earth, Proxima Centauri, is approximately 268,400 a.u.
Original source: https://ru.wikipedia.org/wiki/Astronomical_unit
Disclaimer: © Image credits go to https://www.pexels.com and https://pixabay.com


What is the distance of the largest astronomical unit AE from Earth? How many kilometers are equal to one light year?
One astronomical unit is equal to the distance between the Earth and the Sun.
How can we convert astronomical units to the measurement distance of planets?
What is the distance from the Sun to the solar system in astronomical units?
What is the value of an astronomical unit?

When considering the relative sizes of the planets in our solar system, it is common to use a unit of measurement known as the astronomical unit. This unit represents the average distance between the Earth and the Sun, which is approximately 93 million miles or 150 million kilometers.
The Origins of the Astronomical Unit
Over the course of centuries, scientists, particularly those studying Keplerian celestial mechanics, have discovered that each planet in our solar system orbits around the Sun. Additionally, the stars we see in the night sky are located at such vast distances from Earth that it’s difficult to comprehend. As our understanding of the Universe expands through new scientific discoveries, it becomes increasingly apparent that its size is beyond our current comprehension. The field of astronomy continues to rapidly progress and is now one of the most advanced scientific disciplines.
The idea behind the astronomical unit
300 years ago, scientists reached the conclusion that the Earth is not and has never been the center of the universe. Through extensive observations and repeated verifications, astronomers began to uncover the true scale of our celestial abode – the solar system. It turns out that its dimensions are so vast that the Earth’s conventional units of measurement fall short. The distances to the nearest planets were expressed in numbers with numerous zeroes, and nobody, except for the scientists themselves, had a clue about what to call these numbers. This prompted astronomers to introduce a specialized unit for measuring distances within the Solar System, known as the astronomical unit. This unit is defined as the average distance between the Earth and the Sun, which is approximately 150 million kilometers (more precisely, 149,597,870,691 km). In practical astronomical calculations, a rounded value of 149,600,000 kilometers is commonly used.
Considering that the longest path on our planet, the Earth’s equator, is approximately 40,000 kilometers in length, it becomes evident that the Moon, which is the Earth’s closest celestial body and satellite, orbits the Earth at a distance exceeding 380,000 kilometers.
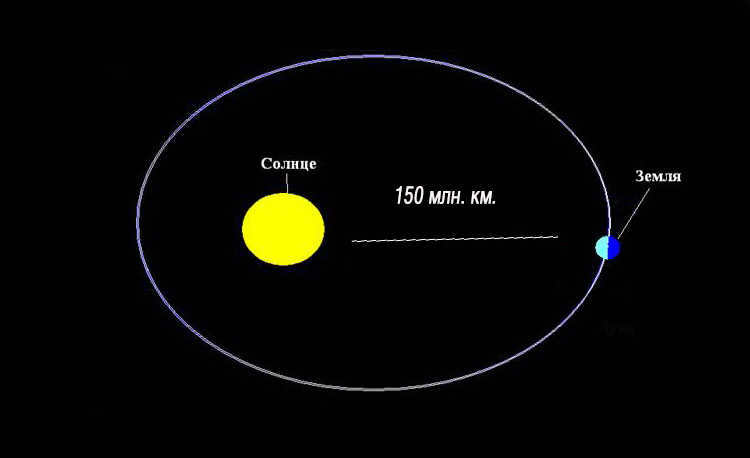
Why is the distance from the Earth to the Sun used as a standard? Well, the Sun serves as the central body in the solar system, and the Earth functions as the location for observers and orbits in an almost circular (elliptical) trajectory. Therefore, the radius of this orbit was chosen as the unit of measurement.
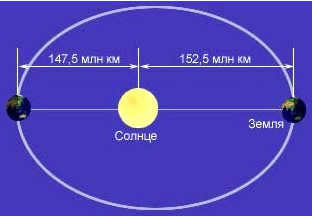
The above concept is exemplified by the subsequent diagram:
Explanation of an astronomical unit
Hence, an astronomical unit is a unit of measurement for distances to celestial bodies, which is equivalent to the major semi-axis of Earth’s elliptical orbit and, in accordance with the characteristics of the ellipse, the average distance between the Earth and the Sun. This definition satisfies not only enthusiasts but also the majority of professional astronomers.
Therefore, the astronomical unit is approximately 400 times larger than the distance between the Earth and the Moon. It is also highly suitable for measuring the distances between planets. For instance, the average distance from Earth to Mars is 0.3 astronomical units. Mars is situated farther from the Sun compared to Earth. Consequently, it is simple to calculate that the distance from the Sun to Mars is 1.52 astronomical units. Even the distant Jupiter is only a little over 5 astronomical units away from the Sun. The distance between Earth and Uranus is around 20 astronomical units. The orbital radius of Neptune, which is one of the most remote objects in the solar system, is 30 astronomical units. Sirius is a binary star. The companion stars Sirius A and Sirius B revolve around each other at a distance of 20 astronomical units.
It takes approximately 500 seconds (or 8 minutes and 20 seconds) for light to travel from Earth to the Sun. What is fascinating is that this distance has a consistent tendency to gradually expand, at a rate of roughly 15 meters per 100 years. This phenomenon could potentially be attributed to the loss of solar mass caused by the solar wind. However, the effect of this increase in the astronomical unit is so minuscule that it can easily be disregarded, as it is significantly smaller than the calculated values.
Over the years, numerous scientists have made use of the astronomical unit with great success. The distances within our solar system, when expressed in this unit of measurement, were relatively small and proved to be convenient and easy to work with. Most importantly, they were comprehensible to all. Any schoolchild, upon observing distances in astronomical units, could quickly discern that Venus is closer to the Sun than Earth. Additionally, it is common knowledge that Jupiter is situated approximately halfway between the Sun and Saturn.
However, our joy was short-lived. Once we were able to determine the distances to the nearest stars, it became evident that within the vast expanse of the stellar realm, the astronomical unit is simply too minuscule, rendering it unsuitable for measurement purposes.
ASTRONOMICAL UNIT
Check other dictionaries for “ASTRONOMIC UNIT”:
ASTRONOMICAL UNIT – ASTRONOMIC UNIT, a unit of measurement used in the field of astronomy (primarily for measuring distances within the solar system). It is equivalent to the average distance between the Earth and the Sun; 1 astronomical unit = 149.6 million kilometers … Modern Encyclopedia
Astronomical unit – ASTRONOMIC UNIT, a unit of measurement used in astronomy (primarily for measuring distances within the solar system). It is equal to the average distance between the Earth and the Sun; 1 astronomical unit = 149.6 million kilometers. … Illustrated Encyclopedic Dictionary
ASTRONOMICAL UNIT – a unit of distance (a.e.) used in astronomy, which is equal to the average distance from the Earth to the Sun. 1 a.e. = 149.6 million km … Large Encyclopedic Dictionary
ASTRONOMICAL UNIT is a unit of length (a. e., AE) that represents the average distance from the Earth to the Sun. It is equivalent to 1.49600-1011 m. This measurement is commonly used in astronomy to describe distances within the solar system. The concept of the astronomical unit has been documented in various encyclopedias and dictionaries, such as the Physical Encyclopedic Dictionary edited by A. M. Prokhorov in 1983 and the Marine Dictionary by Samoilov K. I. The term “astronomical unit” is also mentioned in the online encyclopedia Wikipedia.
Astronomical unit (a. e.), is a distance unit used in astronomy that represents the average distance between the Earth and the Sun. It is equivalent to 149.6 million kilometers. * * * * * ASTRONOMIC UNIT Astronomical unit is a unit of length (a. e.) used in astronomy to measure the distance between celestial bodies, specifically the average distance from the Earth to the Sun… … Encyclopedic Dictionary
Astronomical unit is a unit of measurement in astronomy that is equal to the average distance from the Earth to the Sun. It is also known as astronominis vienetas in Lithuanian. For more information, refer to the definition in the appendix. Appendix( es) Graphical format equivalents: English astronomical unit German astronomische Einheit Russian astronomical unit French unité … Multilingual explanatory metrology glossary
An astronomical unit is a unit of distance used in astronomy that represents the average distance between the Earth and the Sun. It was defined by the International Astronomical Union in 1964 as 1 a. e. equals approximately 149.6 million kilometers. This measurement is crucial for astronomical research and is widely used in calculations and observations. The concept of the astronomical unit helps scientists understand the vast distances in our solar system and beyond.
Astronomical unit
The International Astronomical Union (IAU) made a significant decision in September 2012 during the 28th General Assembly held in Beijing. They determined that the astronomical unit would be tied to the International System of Units (SI). As a result, the astronomical unit is now defined as precisely 149,597,870,700 meters. Moreover, the IAU also standardized the international abbreviation for the astronomical unit, which is now universally recognized as “au”. The abbreviations “a. u.” or “AU” are no longer used.
Similar concepts
References in scientific literature
Continuation of similar concepts
The habitable zone, also known as the HZ, is a concept in astronomy that refers to a specific region in space. This region is defined based on the assumption that any planets within it will have conditions on their surface that are similar to Earth, allowing for the presence of liquid water. Planets or moons located in the habitable zone are considered to be potentially suitable for the development of life similar to what exists on Earth. The highest likelihood of life originating is believed to be within the habitable zone around a star, also known as the circumstellar habitable zone.
There are three classifications of stars that bear some resemblance to the Sun: a solar-type star, a solar analog star, and a solar double. The investigation of these stellar bodies holds great significance in enhancing our comprehension of the Sun’s characteristics, determining whether it is unique or typical among its stellar counterparts, and exploring the potential habitability of planets in other solar-type stars.
Spectral double – is a system of binary stars that can be detected through spectral observations. Typically, these systems consist of two stars that are located very close to each other and have large velocities, making it impossible to observe them separately with modern telescopes. Due to the orbital motion of the stars around their center of mass, one star moves towards us while the other moves away, resulting in unequal radial velocities (along the observer’s line of sight).
Hot Jupiters are a type of exoplanet with masses similar to that of Jupiter (1.9⋅1027 kg). Unlike Jupiter, which is located about 5 astronomical units (a.u.) away from the Sun, hot Jupiters are typically found at distances of about 0.05 a.u. from their host star. This means they are one order of magnitude closer to their star than Mercury is to the Sun, and two orders of magnitude closer than Jupiter. All known hot Jupiters are located outside of our solar system.
To calculate the distance between points on a tourist map in kilometers, you can multiply the number of degrees by the length of the arc of 1 degree in longitude and latitude (in the system of geographic coordinates). The exact values for these arcs can be found in tables or approximated using a formula or calculator. This method is commonly used in school geography lessons, both in older textbooks and in textbooks for elective courses.
Determine the scale of a small-scale map of the Earth’s surface, specifically in the area of Kazan and Yekaterinburg. Both cities are located at approximately latitude 56°N.
Kazan has a longitude of 49°E, while Yekaterinburg has a longitude of 60°E. On the map, the distance between the two cities is measured to be 1.1 cm using a measuring circle and a ruler with millimeter divisions.
The length of an arc of parallel at latitude 56°N is 62,394 meters.
The difference in longitude between Kazan and Yekaterinburg is 11°. Therefore, the calculated distance between the two cities on the map is 686,334 meters or 68,633,400 cm.
Using this information, the scale of the map can be determined. The scale (m) is approximately 1 / 62,400,000, or in other words, 624 kilometers in 1 cm.
So, the private scale of this small-scale map is 624 kilometers in 1 cm.
The major scale (indicated on the backstrip of this map) is 1 / 75,000,000 (1 cm equals 750km).
The secondary scale may vary in size compared to the main scale, depending on the position of the selected area on the map.
Here’s an example of converting geographic coordinates from tenths to degrees and minutes.
The approximate longitude of Sverdlovsk city is 60.8° (sixty degrees and eight tenths) East.
8 / 10 = X / 60
X = (8 * 60) / 10 = 48 (find the numerator of the right fraction using the proportion).
Total: 60.8° = 60° 48' (sixty degrees and forty-eight minutes).
To insert the degree symbol ( ° ), you can press Alt+248 on your keyboard. On a laptop, you can press Fn+Alt+248 or turn on the NumLk function. This method works for Windows and Linux operating systems. For Mac operating systems, you can use the Shift+Option+8 keys.
When specifying coordinates, it is important to note that latitude coordinates are always mentioned before longitude coordinates, whether you are typing on a computer or writing on paper.
Task: Calculate the length of a parallel at a specific latitude, such as 50°, using arc length tables. You can find these tables on Krasovsky’s reference ellipsoid website: www.kakras.ru/mobile/book/dlina-dugi.html
Resolution. By referring to the table titled “Arc length of the parallel in 1°”, we can determine that for a latitude of 50 degrees, the corresponding value for the arc of 1° is 71697 meters.
Since there are 360 degrees in a circle, we can calculate the total arc length by multiplying the tabular value by 360.
71697 * 360 = 25,810,920 meters.
The rules define the supported formats in the maps.google.ru service
Here are some examples of how the correct format should be:
For the full form of angle record (degrees, minutes, seconds with fractions):
41° 24′ 12.1674″, 2° 10′ 26.508″
For abbreviated forms of angle record:
Using degrees and minutes with decimal fractions – 41 24.2028, 2 10.4418
Using decimal degrees (DDD) – 41.40338, 2.17403
The Google map service provides an online converter to convert coordinates and place them in the desired format.
When using numerical values as decimal separators on internet sites and in computer programs, it is recommended to use a dot.
F.N.Krasovsky’s reference ellipsoid, which was utilized in the USSR in the SK-42 and RF (SK-42) reference systems since 1942.
It was also used in the RF (SK-42/95) reference system until January 1, 2017.
The semi-major axis of this ellipsoid is 6,378,245.
GSC-2011 is an ellipsoid and a Russian geodetic coordinate system established in 2011.
It is primarily used for geodetic and cartographic works.
The semi-major axis of this ellipsoid is 6,378,136.5.
WGS-84 is a modern International Universal Reference System ellipsoid, which is nearly identical to ITRF(2008).
The semi-major axis of this ellipsoid is 6,378,137.
Tables of arcs in 1°, 1′, 1″
To ensure that the table is calculated based on Krasovsky, let’s calculate for zero latitude (equator), knowing the numerical value of the large equatorial semi-major axis for the Krasovsky reference ellipsoid a = 6 378 245 meters
1 degree of parallel arc at latitude 0° (equator) = (2 * 3.14159 * 6378245) / 360 = 111321
The tables provided on the page will still be relevant as educational materials (for available textbooks) when using old, Soviet-era maps and for approximate calculations.
Length of the parallel arc in 1°, 1′, and 1″ in longitude (on the west-east line), meters
| 0 | 111321 | 1855 | 31 |
| 1 | 111305 | 1855 | 31 |
| 2 | 111254 | 1854 | 31 |
| 3 | 111170 | 1853 | 31 |
| 4 | 111052 | 1851 | 31 |
| 5 | 110901 | 1848 | 31 |
| 6 | 110716 | 1845 | 31 |
| 7 | 110497 | 1842 | 31 |
| 8 | 110245 | 1837 | 31 |
| 9 | 109960 | 1833 | 31 |
| 10 | 109641 | 1827 | 30 |
| 11 | 109289 | 1821 | 30 |
| 12 | 108904 | 1815 | 30 |
| 13 | 108487 | 1808 | 30 |
| 14 | 108036 | 1801 | 30 |
| 15 | 107552 | 1793 | 30 |
| 16 | 107036 | 1784 | 30 |
| 17 | 106488 | 1775 | 30 |
| 18 | 105907 | 1765 | 29 |
| 19 | 105294 | 1755 | 29 |
| 20 | 104649 | 1744 | 29 |
| 21 | 103972 | 1733 | 29 |
| 22 | 103264 | 1721 | 29 |
| 23 | 102524 | 1709 | 28 |
| 24 | 101753 | 1696 | 28 |
| 25 | 100952 | 1683 | 28 |
| 26 | 100119 | 1669 | 28 |
| 27 | 99257 | 1654 | 28 |
| 28 | 98364 | 1639 | 27 |
| 29 | 97441 | 1624 | 27 |
| 30 | 96488 | 1608 | 27 |
| 31 | 95506 | 1592 | 27 |
| 32 | 94495 | 1575 | 26 |
| 33 | 93455 | 1558 | 26 |
| 34 | 92386 | 1540 | 26 |
| 35 | 91290 | 1522 | 25 |
| 36 | 90165 | 1503 | 25 |
| 37 | 89013 | 1484 | 25 |
| 38 | 87834 | 1464 | 24 |
| 39 | 86628 | 1444 | 24 |
| 40 | 85395 | 1423 | 24 |
| 41 | 84137 | 1402 | 23 |
| 42 | 82852 | 1381 | 23 |
| 43 | 81542 | 1359 | 23 |
| 44 | 80208 | 1337 | 22 |
| 45 | 78848 | 1314 | 22 |
| 46 | 77465 | 1291 | 22 |
| 47 | 76057 | 1268 | 21 |
| 48 | 74627 | 1244 | 21 |
| 49 | 73173 | 1220 | 20 |
| 50 | 71697 | 1195 | 20 |
| 51 | 70199 | 1170 | 19 |
| 52 | 68679 | 1145 | 19 |
| 53 | 67138 | 1119 | 19 |
| 54 | 65577 | 1093 | 18 |
| 55 | 63995 | 1067 | 18 |
| 56 | 62394 | 1040 | 17 |
| 57 | 60773 | 1013 | 17 |
| 58 | 59134 | 986 | 16 |
| 59 | 57476 | 958 | 16 |
| 60 | 55801 | 930 | 16 |
| 61 | 54108 | 902 | 15 |
| 62 | 52399 | 873 | 15 |
| 63 | 50674 | 845 | 14 |
| 64 | 48933 | 816 | 14 |
| 65 | 47176 | 786 | 13 |
| 66 | 45405 | 757 | 13 |
| 67 | 43621 | 727 | 12 |
| 68 | 41822 | 697 | 12 |
| 69 | 40011 | 667 | 11 |
| 70 | 38187 | 636 | 11 |
| 71 | 36352 | 606 | 10 |
| 72 | 34505 | 575 | 10 |
| 73 | 32647 | 544 | 9 |
| 74 | 30780 | 513 | 9 |
| 75 | 28902 | 482 | 8 |
| 76 | 27016 | 450 | 8 |
| 77 | 25122 | 419 | 7 |
| 78 | 23219 | 387 | 6 |
| 79 | 21310 | 355 | 6 |
| 80 | 19394 | 323 | 5 |
| 81 | 17472 | 291 | 5 |
| 82 | 15544 | 259 | 4 |
| 83 | 13612 | 227 | 4 |
| 84 | 11675 | 195 | 3 |
| 85 | 9735 | 162 | 3 |
| 86 | 7791 | 130 | 2 |
| 87 | 5846 | 97 | 2 |
| 88 | 3898 | 65 | 1 |
| 89 | 1949 | 32 | 1 |
| 90 | 0 |
The simplified formula for determining the parallel arcs (without considering any distortions caused by polar compression) is as follows:
The length of the meridian arc in 1°, 1' and 1" of latitude (along the north-south line) is measured in meters.
| 0 | 110579 | 1843 | 31 |
| 5 | 110596 | 1843 | 31 |
| 10 | 110629 | 1844 | 31 |
| 15 | 110676 | 1845 | 31 |
| 20 | 110739 | 1846 | 31 |
| 25 | 110814 | 1847 | 31 |
| 30 | 110898 | 1848 | 31 |
| 35 | 110989 | 1850 | 31 |
| 40 | 111085 | 1851 | 31 |
| 45 | 111182 | 1853 | 31 |
| 50 | 111278 | 1855 | 31 |
| 55 | 111370 | 1856 | 31 |
| 60 | 111455 | 1858 | 31 |
| 65 | 111531 | 1859 | 31 |
| 70 | 111594 | 1860 | 31 |
| 75 | 111643 | 1861 | 31 |
| 80 | 111677 | 1861 | 31 |
| 85 | 111694 | 1862 | 31 |
| 90 |

Figure. Calculation of the lengths of meridian and parallel arcs using a simplified formula.
Here is a practical example of how tables can be used. Let’s say you have a map without a numerical scale or a scale bar, but it does have lines of a degree grid. In this case, you can determine distances graphically by calculating that one degree of arc corresponds to a certain length value from the table. In the “north-south” direction (between horizontal lines of the geographical grid on the map), the length of arcs changes slightly from the equator to the poles of the Earth, approximately equal to 111 kilometers per degree. By calculating how much is contained in a centimeter segment, you can then determine the length of any given profile.