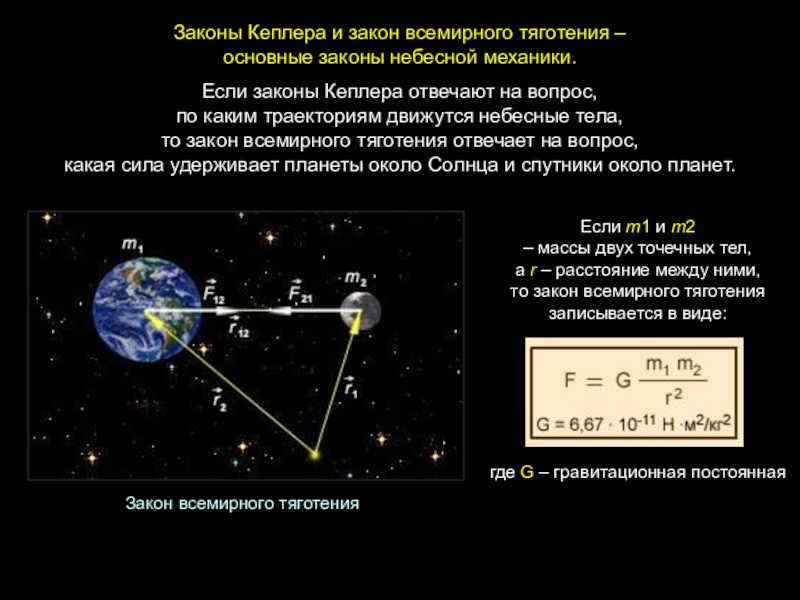
Kepler’s laws and the principle of universal gravitation serve as the fundamental principles of celestial mechanics. While Kepler’s laws provide insight into the paths that celestial bodies take, the principle of universal gravitation explains the force that keeps the planets in close proximity to the Sun and the
Newton’s Recapitulation and Enhancement of Kepler’s Principles


Slide 2 – Kepler’s laws and the law of universal gravitation are the fundamental principles of celestial mechanics.
Kepler’s laws provide an explanation for the trajectories followed by celestial bodies. On the other hand, the law of universal gravitation explains the force that keeps planets close to the sun and satellites near the planets.
Law of Universal Gravitation
If m1 and m2 represent the masses of two point bodies, and r is the distance between them, the law of universal gravitation can be expressed as:
where G is the gravitational constant.

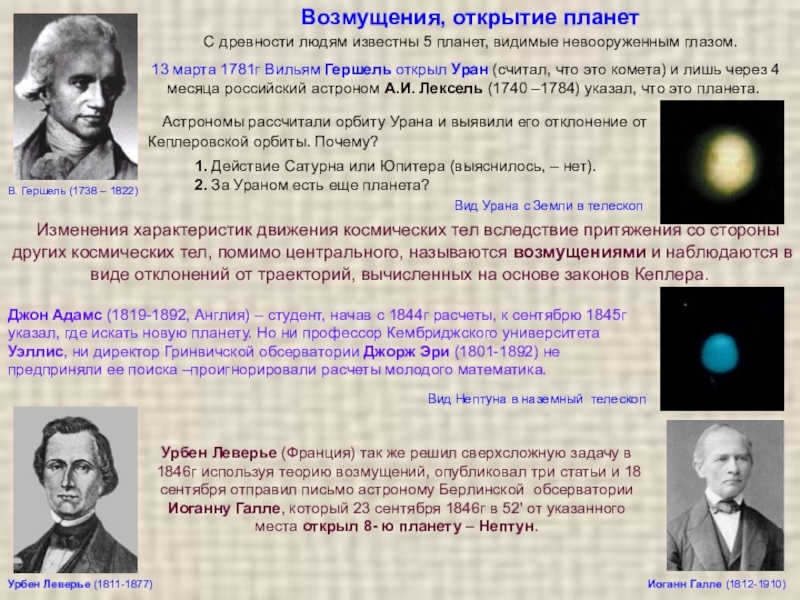
Slide 3William Herschel (1738-1822) utilized a telescope in 1781 to make the groundbreaking observation of the planet Uranus, a celestial body that cannot be seen without the aid of optical instruments.
This is its appearance.

Slide 4After the detection of Uranus, astronomers observed an anomaly in its orbit, which defied Newton’s law of universal gravitation.
This observation sparked the hypothesis that there might be an additional planet located further out from Uranus, exerting a gravitational influence that caused the deviation in the seventh planet’s trajectory. Neptune was eventually discovered using a telescope on Earth.

Disturbing the movement of Uranus.
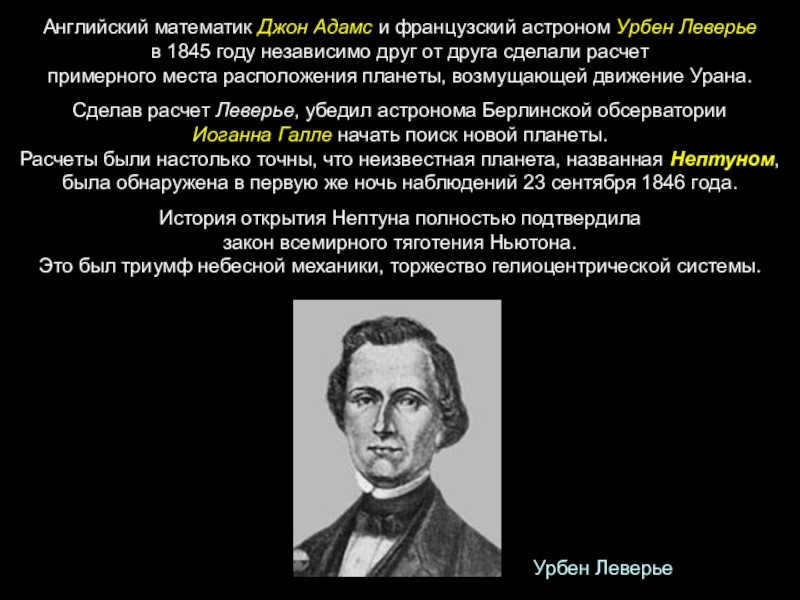
Using Leverrier’s calculations, he convinced the astronomer at the Berlin Observatory, Johannes Galle, to begin searching for a new planet. The calculations were so precise that the unidentified planet, called Neptune, was found on the initial night of observations on September 23, 1846.
The tale of Neptune’s discovery fully validated Newton’s law of universal gravitation. It was a victory for celestial mechanics and the heliocentric system.
The International Astronomical Union made the decision to strip Pluto of its planetary status within the solar system. From now on, it can only be referred to as a “dwarf planet”.
During the assembly, approximately 2.5 thousand astronomers established the following criteria for a planet:
the object must orbit a star, but it cannot be a star itself;
it must have enough mass for its own gravity to maintain a more or less spherical shape;
there should be no other celestial bodies in its orbit.
Pluto, which was discovered in 1930, fails to meet the third criterion as its orbit intersects with that of the planet Neptune.
Consequently, there are now only eight planets remaining in the solar system: Jupiter, Saturn, Uranus, Neptune, Earth, Venus, Mars, and Mercury.

Conic sections and orbital paths in space

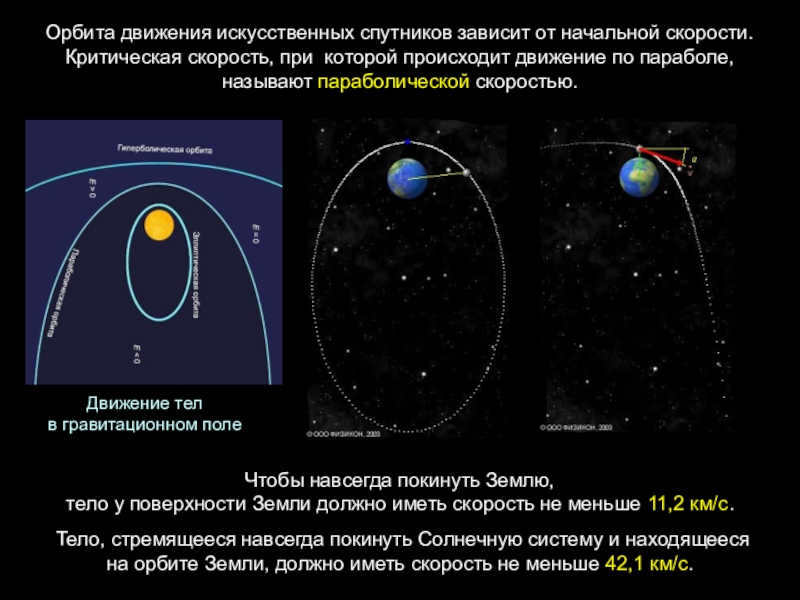
Slide 8The initial velocity determines the orbit of man-made satellites. The critical velocity required for parabolic motion is known as the parabolic velocity. To escape the gravitational pull of Earth and enter into a permanent orbit around the Sun, a body must have a velocity of at least 11.2 km/s.
A body that is attempting to permanently leave the solar system and is currently in orbit around the Earth,
The movement of objects
within a gravitational field
In order to determine the masses of celestial bodies, Newton’s generalization of Kepler’s third law to any system of circulating bodies is used.
Kepler’s third law, in its generalized form, is typically expressed as:
The periods of revolution of two bodies around the Sun (T12 and T22), multiplied by the sum of the masses of each body and the Sun (M1+ M☉ and M2+ M☉ ), are related to the cubes of the major semi-axes of their orbits (a13 and a23).

The planetary system comprises a central body and orbiting satellites that interact based on the principle of universal gravitation.
Typically, the planet’s mass significantly outweighs that of the satellite. Therefore, we can reasonably estimate the mass ratios of the two celestial bodies using the following formula:

Slide 11Problem. Calculate the mass of Jupiter, by knowing the mass of one of its satellites (Io)
Given: Solution:
M2=1
T2=27.32d
a2=3.84*105 km M1= (T2/T1)2 (a1/a2)3 M2
T1=1.77d M1= (27.32/1.77)2 * (422000/384000)3 * M2
a1=4.22*105 km M1≈ 316 M2
Johannes Kepler empirically discovered his lawsI. All the planets in the solar system orbit around the Sun in elliptical paths with the Sun at one of the foci. II. The radius-vector of a planet covers equal areas in equal time intervals: velocity of motion
Slide 1: Newton’s Advancement and Enhancement of Kepler’s Laws
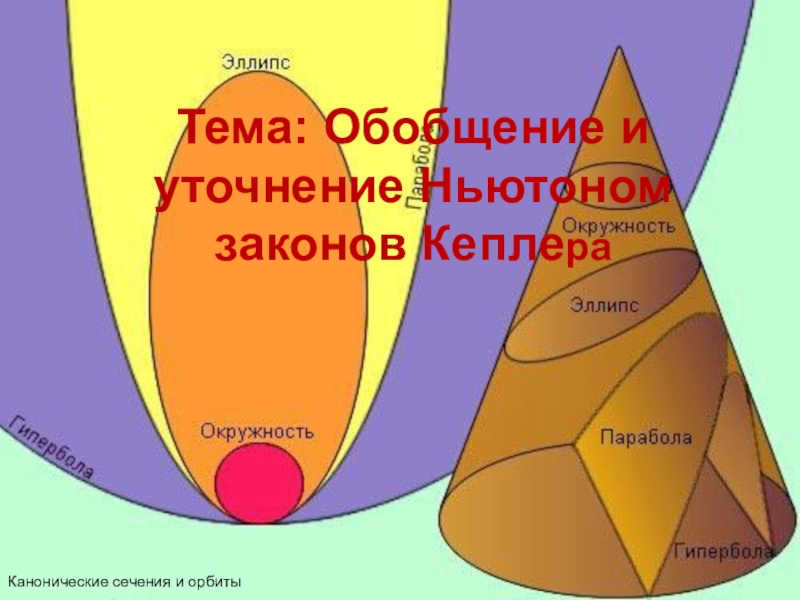
Canonical Sections and Orbits

Slide 2Johannes Kepler empirically discovered three laws that describe the motion of planets in the solar system:
I. The planets in the solar system orbit the Sun in elliptical paths, with the Sun located at one of the focal points of the ellipse.
II. The radius vector of a planet sweeps out equal areas in equal time intervals, meaning that the velocity of the planet is highest when it is closest to the Sun (perihelion) and lowest when it is farthest from the Sun (aphelion).
III. The square of the period of orbital motion for each planet is proportional to the cube of its average distance from the Sun.
Gravity is an inherent characteristic of all natural entities.
When it comes to celestial bodies, it accounts for
virtually all movements
and numerous phenomena related to the creation and evolution of celestial bodies

Slide 3Kepler’s Laws ► how things move,
ZW ► why they move this way
The concept of celestial mechanics
The concept of celestial mechanics was first introduced in 1799 by Pierre Simon Laplace (1749-1827, France). Laplace, an astronomer, extensively studied the complex cases of perturbed motion of cosmic bodies, such as the perturbations of Jupiter, Saturn, the Moon, as well as planetary figures, the motion of the Earth’s poles, the first theory of motion of Jupiter’s satellites, and dynamic theory of tides. His work, the five-volume “Treatise on Celestial Mechanics,” became a classic in the field and served as the main guide for astronomers for 50 years.
The fundamental principles of Celestial Mechanics, which study the movement of celestial bodies influenced by gravitational forces, consist of four laws: three Kepler’s laws and three W laws.

Slide 4John Adams (1819-1892, England), a student, began calculations in 1844, and by
By September 1845, John Adams, a student from England, had identified the precise location to search for a new planet. However, his calculations were disregarded by Professor Wellis of Cambridge University and George Erie, the director of the Greenwich Observatory (1801-1892).
Perturbations and the discovery of planets
Astronomers have made calculations regarding the orbit of Uranus and have determined that it deviates from the expected Keplerian orbit. The reason for this deviation is due to perturbations caused by the gravitational influence of other celestial bodies. These perturbations cause the observed deviations from the trajectories predicted by Kepler’s laws.
There were a couple of hypotheses regarding the cause of these perturbations. One hypothesis was that the gravitational pull of Saturn or Jupiter was responsible for the deviations. However, further analysis showed that this was not the case. Another hypothesis was the existence of an undiscovered planet beyond Uranus.
In 1846, Urbain Leverrier, a French astronomer, successfully solved this complex problem using perturbation theory. He published three articles on the subject and on September 18, he sent a letter to Johann Galle, an astronomer at the Berlin Observatory. In his letter, Leverrier predicted the existence and location of the 8th planet, Neptune. Just a few days later, on September 23, 1846, Galle discovered Neptune at the exact location specified by Leverrier.
Here is a telescope view of Uranus as seen from Earth:
Observing Neptune using a telescope located on the Earth’s surface.
Slide 5Kepler’s First Law.
Newton proves that, assuming one body is stationary, a celestial body can move along a circle, ellipse, parabola, or hyperbola under the influence of gravitational force (types of canonical section).
The shape of the orbit of artificial celestial bodies, which is determined by the modulus and direction of the initial velocity, follows the first law.
Each planet’s orbit is an ellipse, with the Sun located in one of the foci.
The eccentricity of the ellipse determines its shape.
Kepler’s laws in Newton’s formulation
By formulating the problem of two bodies (m1, m2) with velocities (v1, v2) and solving it using advanced mathematics to find the coefficients of the bodies under the influence of gravitational force, Newton was able to derive all of Kepler’s laws from the Law of Universal Gravitation. In the process, he also discovered and developed differential and integral calculus.
Satellites of celestial objects are objects that orbit around them (with a common center of gravity) due to the force of gravity.
There are different types of satellite orbits: the first type is circular with a velocity (υo) of 7.91km/s; the second type is elliptical with velocities (υ) of 9km/s and (υυ) of 11.1km/s; and the third type is parabolic with a velocity (υ2) of υo√2, which is equal to 11.19km/s.

Slide 6Dependence of the orbit of an ISV on initial velocity
Second space velocity υ2= υ1.√2 =11.19
km/s. The object follows a parabolic trajectory and moves away from Earth indefinitely, becoming a satellite of the Sun. The first instance of this was with “Luna-1” on January 2, 1959.
First cosmic (circular) velocity. For Earth, υ1=7.91 km/s. The object becomes an ISR. The first instance of this was with “Sputnik-1” on October 4, 1957.
Elliptical (orbit of varying eccentricity): ranging from υ1=7.91 km/s to υ2=11.19 km/s. At υ = 11.1 km/s, the Moon’s orbit is highly elongated. On October 7, 1959, a spacecraft orbited the Moon for the first time, utilizing gravitational maneuvering and capturing photographs of the far side of the Moon (“Luna-3″/SSR) for the first time.
To travel to the closest planets, a speed of υ3 = υ2.√2 = 16.67 km/s is required (initially achieved by “Venus-1” on 12.02.1961). To enable a spacecraft launched from Earth to exit the Solar System, the third velocity of space (which is the combination of Earth’s velocity around the Sun and the spacecraft’s second velocity relative to Earth) must be created. υIII = 42 km/s.


Slide 7: Alteration of Orbit (Shape and Velocity) in the Gravitational Field of the Planet.
Regarding the Influence of the Law
Modification of circular orbits by impulses directed “in the direction of velocity” and “opposite to velocity”. The orbit undergoes the most significant geometrical displacement in the area opposite to the point where the impulse was applied to the object.
Deceleration in a sparsely populated atmosphere results in a reduction in the major semi-axis of the orbit, and with each revolution of the spacecraft, the elliptical orbit approaches a circular orbit.


Slide 8 Kepler’s Second Law The planet’s radius vector describes equal areas in equal time intervals.
As the planet orbits: when it approaches the Sun, its velocity increases, kinetic energy increases, potential energy decreases, and vice versa when the planet moves away. The law did not require further clarification.
Kepler’s Third Law The squares of the sidereal periods of revolution of two planets are related as the cubes of the major semi-axes of their orbits.
Isaac Newton tackled the problem of two bodies revolving around a shared center, determining their resulting accelerations based on the law of universal gravitation and the angular velocity of centripetal acceleration. As a result, he derived a refined version of Kepler’s third law that takes into account the masses of the bodies.
Kepler’s laws as formulated by Newton
Orbiting around the Sun
Newton’s Second Law
Newton’s Laws are a set of three laws that form the foundation of classical mechanics. They allow us to write down the equations of motion for any mechanical system, provided we know the forces acting on its constituent bodies. These laws were first fully formulated by Isaac Newton in his book “Mathematical Principles of Natural Philosophy” (1687).
Newton’s first law introduces the concept of inertia, which is also referred to as the Law of Inertia. Inertia is the phenomenon where a body maintains its velocity (both in magnitude and direction) in the absence of any external forces. To alter the velocity of a body, it must experience a force. Naturally, the effect of forces of equal magnitude on different bodies will vary. Therefore, bodies are said to possess inertial properties. Inertial properties refer to the ability of bodies to resist changes in their current state. The mass of a body determines the magnitude of its inertial properties.
Contemporary statement
In contemporary physics, the first law of Newton is typically expressed in the subsequent manner [1] :
There exist reference frames known as inertial frames, with respect to which an object, in the absence of external forces, will maintain both the magnitude and direction of its velocity indefinitely.
This law also holds true even in scenarios where external forces are present, but mutually cancelled out (this can be inferred from Newton’s second law, as compensated forces result in zero net acceleration of the object).
Origin of the concept
In his renowned work “Mathematical Principles of Natural Philosophy,” Sir Isaac Newton initially proposed the fundamental law of mechanics in the subsequent manner:
Each object persists in its current position of stillness or consistent and straight motion unless and until external forces coerce it to modify its state.
From a contemporary perspective, this statement is deemed unsatisfactory. Firstly, the term “body” ought to be substituted with the term “material point” as a body of limited dimensions can undergo both translational and rotational motion in the absence of external forces. Secondly, and most importantly, Newton’s work was based on the assumption of the existence of an absolute stationary frame of reference, which encompasses absolute space and time, a concept that is refuted by modern physics. Conversely, in an arbitrary (such as a rotating) frame of reference, the principle of inertia is invalid. Consequently, the Newtonian formulation necessitates further elaboration.
Newton’s second law of motion is a differential equation that defines the correlation between the force exerted on an object and the resulting acceleration of that object. Specifically, Newton’s second law establishes mass as a measurement of an object’s resistance to changes in motion within a specific reference frame.
Contemporary Statement
In a frame of reference that is not affected by external forces, the acceleration experienced by a material point is directly proportional to the inverse of all forces exerted on it and inversely proportional to its mass.
By selecting appropriate units, this principle can be expressed as an equation:

where  represents the acceleration of the material point;
represents the acceleration of the material point;
 denotes the force applied to the material point;
denotes the force applied to the material point;
 signifies the mass of the material point.
signifies the mass of the material point.
Alternatively, in a more familiar form:

When the mass of a material point changes over time, Newton’s second law is expressed using the concept of momentum:
In a frame of reference that is not accelerating, the rate at which the momentum of a material point changes is equal to the sum of all the forces applied to it.
where 𝒿 is the momentum of the point,
 where
where  – is the velocity of the point;
– is the velocity of the point;
t – time;
– the derivative of the momentum with respect to time.
When multiple forces act on a body, taking into account the principle of superposition, Newton’s second law can be written as:

Newton’s second law is applicable only to velocities significantly lower than the speed of light and in frames of reference that are not accelerating. When dealing with velocities closer to the speed of light, the principles of relativity theory are employed.
 ) of the second law as being equivalent to the first law, since the first law assumes the existence of an inertial frame of reference, while the second law is formulated within the framework of an inertial frame of reference.
) of the second law as being equivalent to the first law, since the first law assumes the existence of an inertial frame of reference, while the second law is formulated within the framework of an inertial frame of reference.
Newton’s initial statement:
The alteration in the amount of motion is directly proportional to the exerted propulsive force and takes place in the same direction as that force.
Curiously, if we introduce the stipulation of an inertial frame of reference, then within this formulation, this principle remains applicable even in the realm of relativistic mechanics.
Newton’s Third Law
This principle describes the behavior of two interacting objects. Let’s consider a closed system consisting of two objects as an example. The first object can exert a certain force  on the second object, and the second object can exert a force
on the second object, and the second object can exert a force  on the first. How are these forces related? According to Newton’s third law, the magnitude of the action force is equal to the magnitude of the reaction force, but they act in opposite directions. It is important to note that these forces are applied to different objects and therefore cannot cancel each other out.
on the first. How are these forces related? According to Newton’s third law, the magnitude of the action force is equal to the magnitude of the reaction force, but they act in opposite directions. It is important to note that these forces are applied to different objects and therefore cannot cancel each other out.
Contemporary statement
Interactions between material points occur through forces that possess identical characteristics, with a direction along the line connecting the points and a magnitude that is equal but opposite in direction:
This law embodies the concept of pairwise interaction, signifying that all forces in the natural world are created in pairs.
Historical formulation
Action always has an equal and opposite counteraction, otherwise, the interactions of two bodies on each other are equal and directed in opposite directions.
For the Lorentz force, Newton’s third law is not satisfied. Its validity can only be restored by reformulating it as the law of conservation of momentum in a closed system of particles and electromagnetic field [2].
 then there arises the law of conservation of total mechanical energy of interacting bodies:
then there arises the law of conservation of total mechanical energy of interacting bodies:

The fundamental principles of mechanics are Newton’s laws. These laws serve as the basis for deriving the equations of motion for mechanical systems. It is important to note, however, that not all principles of mechanics can be deduced from Newton’s laws. For instance, the law of universal gravitation and Hooke’s law are not direct consequences of Newton’s three laws.
Remarks about Newton’s principles
The concept of inertia
Newton’s laws are applicable only in inertial reference frames. If we accurately express the equation of motion of an object in a non-inertial frame of reference, it will appear different from Newton’s second law: , where – represents the observed acceleration in the reference frame being considered, and – represents the acceleration of a specific point in this non-inertial reference frame relative to any inertial reference frame. However, in many cases, in order to simplify the analysis, a fictional “inertial force” is introduced, and then these equations of motion are reformulated in a manner that is identical to Newton’s second law. Mathematically, everything is correct here, but from a physics standpoint, the new fictional force cannot be regarded as something real, resulting from an actual impact on the object. It is important to emphasize once again that the “inertial force” is merely a convenient parameterization of how motion differs in inertial and non-inertial reference systems.
Newton’s Laws and Lagrangian Mechanics
The formulation of classical mechanics goes beyond Newton’s laws. Within the framework of Lagrangian mechanics, there is a single formula known as the record of mechanical action, and a single postulate that states bodies move in a way that the action is stationary. From these principles, it is possible to derive all of Newton’s laws, but only for Lagrangian systems. It’s worth noting that all known fundamental interactions are described by Lagrangian systems. Additionally, the Lagrangian formalism allows for the consideration of hypothetical situations where the action takes on a different form. In such cases, the equations of motion will no longer resemble Newton’s laws, but classical mechanics will still be applicable.
The second derivative of time is the acceleration, which makes it a differential equation. This implies that the displacement of a mechanical system over time can be uniquely determined if its initial coordinates and initial velocities are known.
It is important to recognize that if the equations governing our universe were first-order equations, we would not observe phenomena such as inertia, oscillations, and waves.
Retelling of the Past

In his book “Mathematical Beginnings of Natural Philosophy,” Newton presented the fundamental principles of mechanics in the following manner.
1. Any object remains at rest or continues to move in a straight line with constant speed unless acted upon by external forces.
(2) The change in an object’s motion is directly proportional to the applied force and occurs in the direction of the force.
3. For every action, there is an equal and opposite reaction; otherwise, the interactions between two objects are equal and opposite in direction.
Galileo was the first to publish the law of inertia (also known as the first law) in a slightly different form. It is worth mentioning that Galileo not only allowed for free motion in a straight line, but also on a circular path, possibly due to his interest in astronomy. Another important contribution by Galileo was his formulation of the principle of relativity, which Newton did not include in his axiomatics. Newton considered this principle to be a direct consequence of the equations of dynamics for mechanical processes. Furthermore, Newton believed that space and time were absolute concepts that were unified throughout the entire universe, as explicitly stated in his work “Beginnings”.
Newton also provided precise definitions for physical ideas such as quantity of motion (which Descartes did not clearly use) and force. He brought in the concept of mass as a measure of inertia and, simultaneously, gravitational properties (previous physicists had utilized the concept of weight).
Euler and Lagrange achieved the full mathematization of mechanics.
Related Articles
Additional Information
- ↑ Yavorsky B.M., Seleznev Y.A. Physics. Reference Manual. 5th ed. Fizmatlit, 2006. p.39.
- ↑Matveev A.N. Mechanics and Theory of Relativity. – 3rd ed. – M. Vyshaya Shkola 1976. – С. 132.
Sources
Recommended Reading
- Leach J.W.Classical Mechanics. Moscow: Foreign Literature, 1961.
- Spassky B. I.. History of physics. M., “Vysshaya Shkola”, 1977.
- Volume 1. Part 1-ya; Part 2-ya
- Volume 2. Part 1-ya;Part 2-ya
| Newton’s Laws – Law of universal gravitation – Kepler’s laws – Two-body problem – Three-body problem – N-body gravitational problem – Bertrand’s problem – Kepler’s Equation |
| Celestial Coordinate SystemGalactic – Horizontal – First Equatorial – Second Equatorial – Ecliptic – International Celestial Coordinate System – Spherical Coordinate System – World Axis – Celestial Equator – Direct Ascension – Declination – Ecliptic – Equinox – Solstice – Fundamental Plane. |
| Keplerian Orbital Elements: Eccentricity – Major Semi-Axis – Mean Anomaly – Longitude of Ascending Node – Pericenter Argument – Apocenter and Pericenter – Orbital Velocity – Orbital Node – Epoch |
| Motion of the Sun and Planets on the Celestial Sphere – Ephemerides Planetary Configurations: Opposition – Quadrature – Parade of Planets – Culmination – Sidereal Period – Orbital Resonance – Rotation Period – Pre-Eclipse of Equinoxes – Synodic Period – Convergence Eclipse: Solar Eclipse – Lunar Eclipse – Saros – Methone Cycle – Coverage – Passage – Libration – Elongation – Kozai Effect – Yarkovsky Effect – Janibekov Effect |
| Space Velocity: First (Circular) – Second (Parabolic) – Third – Fourth Tsiolkovsky’s Formula – Gravitational Maneuver – Goman Trajectory – Osculating Element Method – Tidal Acceleration – Change of Orbital Inclination – Docking – Lagrangian Points – Pioneer Effect |
| Geostationary Orbit – Heliocentric Orbit – Geosynchronous Orbit – Geocentric Orbit – Geo-Transition Orbit – Low Reference Orbit – Polar Orbit – Tundra Orbit – Sun-Synchronous Orbit – Lightning Orbit – Osculating Orbit |
8. Can you identify the most luminous star in the sky, its stellar magnitude, and the constellation it is located in?
9. Why is there a star that remains stationary throughout the day?
10. Describe what the ecliptic is and list the constellations it passes through.
- Get Link
- Other apps
Feedback
Leave your feedback
Top articles on this website
Task for the 9th grade students in the field of Information Technology: Create a document using a word processor and reproduce the given text, ensuring that the text layout remains intact. The text should be typed in a regular 14 point font, Times New Roman. The first line of the first paragraph should be indented 1 cm. The line spacing should be set to 1.5 intervals. In the main text, some words are bold, italicized, and underlined. The first column of the table should be left-aligned, while the second and third columns should be left-centered. The table width should be narrower than the width of the main text. The table should be horizontally centered on the page. Please note that the width of your document may differ from the example due to variations in page size and margins. In such cases, line breaks should be adjusted to fit the standard paragraph width. The spacing between lines should be consistent throughout the document.
IT Assignment for 9 B is due on December 20, 2022! Enter the text and insert formulas. To insert formulas, go to Menu – Insert – Formula. In the window that appears, select Insert New Formula at the bottom. Start typing the formula in the formula box. To print a fraction, select Fraction. To print a degree, select Index. Borodina S. is assigned to assignment #2, Golovanova V. to assignment #3, Kachuev A. to assignment #4, Kruchinin A. to assignment #5, Knysh V. to assignment #6, Sorokina E. to assignment #7, Stekhina E. to assignment #10, Tikhomirova M. to assignment #11, Trofimov A. to assignment #12, Tolmacheva A. to assignment #13, Tuganova A. to assignment #14, Kharitonov A. to assignment #15, Shcherbakova N. to assignment #16. Here is the link to the folder with assignments: Assignments Folder.





