The equation of time represents the discrepancy between mean solar time and true solar time at any given moment. This difference arises because the Sun’s movement along the ecliptic is not uniform throughout the year. The duration of a true solar day varies due to the Earth’s orbital eccentricity, resulting in longer days in the northern hemisphere during winter and shorter days during summer, and vice versa in the southern hemisphere. To account for this variation, the concept of an average solar day was introduced, defined as 24 hours year-round. To establish the concept of mean solar days, an additional concept of the “mean Sun” was introduced – an imaginary point that moves uniformly along the celestial equator (not the ecliptic!). The equation of time enables the conversion between true solar time and mean solar time.
The relationship between true solar time and average solar time is important for understanding time zones in the Northern Hemisphere (or vice versa in the Southern Hemisphere). This blog discusses time zones in Russia and around the world.
The field of aeronautical astronomy utilizes the equation of time to estimate the hour angle of the true Sun when an AAU (Astronomical Almanac Unit) is not readily available. This estimation is based on the readings of a clock that is set to mean time.
There are various methods to determine the correction needed.
Visualization
Data in a table
Solution using analysis
By utilizing the empirical equation, we can determine the correction:
η=7.8*sin(D-2)+10*sin(2D+10) where
D=(d*360/365) – represents the change in longitude of the average Sun from the start of the year;
d – signifies the numerical position of the day within the year.
Let’s calculate the exact time of noon on November 1 for a location with an east longitude of 87 degrees in the Northern Hemisphere, in the +7 GMT time zone. To do this, we need to convert the longitude into a time measurement. One hour corresponds to 15 degrees of longitude (360/24 hours). Therefore, 87 degrees of longitude correspond to 5 hours and 48 minutes. Taking into account the time zone difference, the total difference will be 1 hour and 12 minutes.
So, according to the local mean solar time, noon will not be at 12 o’clock, but at 13:12, with an additional adjustment for the Equation of Time.
On November 1, there is a 16-minute adjustment. Let’s establish the direction of the adjustment. Remember that in the winter months in the northern hemisphere, the day is longer than 24 hours. This means that the actual movement of the Sun is faster than the “average” Sun, causing noon to occur earlier. By subtracting the adjustment, we find that noon will be at 12:56 pm according to standard clocks, which display the average solar time.
Analemma
Practically, it is also convenient to utilize a representation of the equation of time in the form of a curve known as the analemma. This curve enables the determination of the Sun’s declination, in addition to the time correction.
The analemma is a path that connects a series of consecutive positions of the Sun in the sky at the same time throughout the year. In other words, if you capture photographs of the Sun from the same location and at the same time over the course of a year, you will obtain a similar image, depending on the latitude and chosen time:
A graph representing the equation of time (shown as a blue line) and its two components when the equation is defined as UW = SSV – ISV.
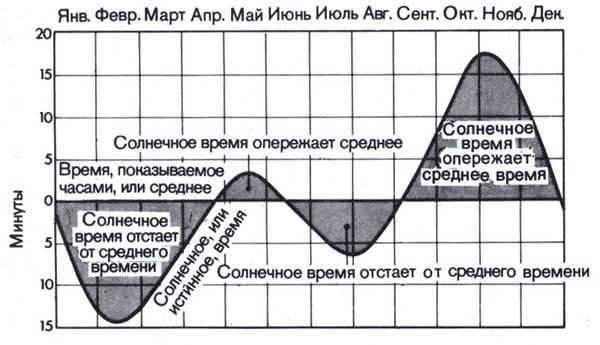
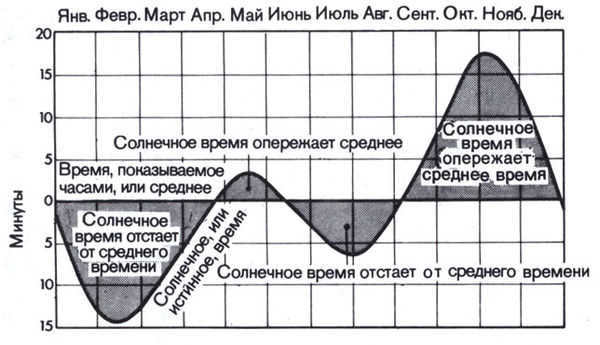
The equation of time, as defined in the English-language literature, is displayed in the graph above. When the value is above zero, the sundial is “rushing”, and when it is below zero, the sundial is “lagging”.
Definition of the equation of time: It is the difference between mean solar time (MSW) and true solar time (TSW), which can be calculated using the formula EQ = MSW – TSW [1]. This difference remains constant for observers at any point on Earth. The equation of time can be obtained from specialized astronomical publications, astronomical programs, or by using the formula provided below.
In the publication “Astronomical Calendar”, the equation of time is described as the discrepancy between the hour angles of the mean equatorial sun and the actual sun. In this definition, EE is equal to EEH minus EEH [2].
In English publications, a distinct definition of the equation of time (referred to as the “inverted” definition) is frequently employed: UW equals ISV minus SSV, which signifies the difference between true solar time (TSV) and mean solar time (MSV).
One can define the equation of time as the discrepancy between “local apparent solar time” and “local mean solar time” (also referred to as “local apparent solar time” and “local mean solar time” in the English literature). This definition is technically more accurate, but it doesn’t change the outcome since this discrepancy remains constant for any given location on Earth.
Furthermore, it’s important to note that neither “local true solar time” nor “local mean solar time” should be mistaken for zone time, which represents the time displayed by “official” clocks (such as “Moscow time”).
While the apparent daily motion of the stars remains relatively constant and is solely due to the Earth rotating on its axis, the daily motion of the Sun is more complex. This is because the Sun’s movement is influenced by the Earth rotating on its axis, the Earth orbiting around the Sun, and the tilt of the Earth’s axis in relation to the ecliptic plane.
The Earth’s orbit around the Sun is not a perfect circle, but rather an elliptical shape. Kepler’s second law states that this means the Earth’s motion is not constant; it is faster when it is closest to the Sun (perihelion) and slower when it is farthest away (aphelion). This irregular motion is observed by people on Earth as the Sun appearing to move faster or slower along the path of the ecliptic compared to the fixed stars.
The Earth’s axial tilt causes unevenness
Due to the inclination of the ecliptic plane to the plane of the celestial equator, a particular phenomenon occurs:
- During the solstices (winter and summer), the Sun moves almost parallel to the celestial equator, resulting in minimal change in the hour angle of the Sun due to the subtraction of its movement speed from the daily motion of the celestial sphere.
- During the equinoxes (autumn and spring), the Sun moves at a maximum angle to the celestial equator, resulting in a maximum change in the hour angle of the Sun due to only partially subtracting its movement speed from the daily motion of the celestial sphere.
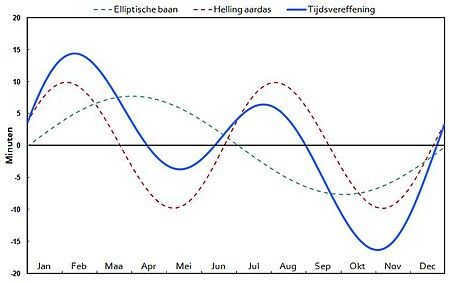
Equation of time expressed as the combination of two irregularities
1. Influence of eccentricity 2. Impact of the inclination of the ecliptic 3. Combined result – Equation of time 4. The position of the true Sun in relation to the mean Sun.
(The graphs are presented based on the “inverted” definition of the equation of time adopted in English-language literature)
The Equation of Time curve is formed by the addition of two periodic curves – one with a yearly period and the other with a six-month period. The nearly sinusoidal curve with a yearly period is caused by the Sun’s irregular motion along the ecliptic. This component of the equation of time is referred to as the equation of center or the equation arising from eccentricity. The sinusoidal curve with a six-month period represents the time difference caused by the inclination of the ecliptic relative to the celestial equator and is known as the equation arising from the tilt of the ecliptic [1].
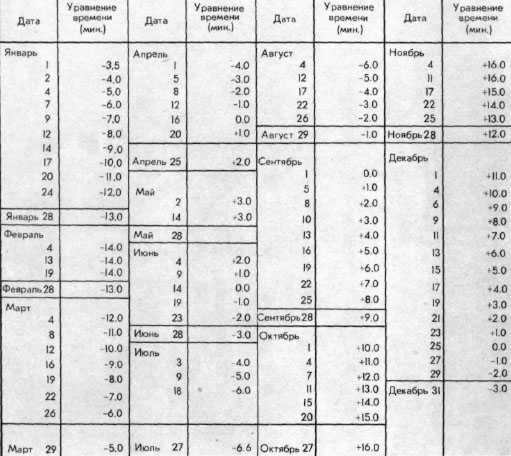
The equation of time experiences four instances of reversing to zero each year: April 14, June 14, September 2, and December 24.
Consequently, during each period of the year, there exists a distinct maximum value for the equation of time: approximately +14.3 min on February 12, -3.8 min on May 15, +6.4 min on July 27, and -16.4 min on November 4. The precise values for the equation of time can be found in astronomical yearbooks.
It can serve as an additional feature in certain clock models.
Calculation
The calculation can be approximated by a segment of a Fourier series, which is the combination of two sine curves with periods of one year and six months, respectively:

if the angles are given in degrees.
 if the angles are given in radians. Where
if the angles are given in radians. Where  – represents the number of days, for instance: on January 1
– represents the number of days, for instance: on January 1  on January 2
on January 2
- ↑ 12 Kononovich E. V., Moroz V. I. “General course of astronomy” Textbook, edited by V. V. Ivanov. V. Ivanov. 2nd edition, revised. Moscow: Unitorial Urss, 2004. – 544 p. ISBN 5-354-0866-2, 3000 copies.
- ↑ Astronomical calendar. Permanent part / Editor-in-Chief Abalakin V.K.. – 7th edition. – M .: Nauka, 1981. – p. 19.
As a result, the mean solar time in the center of Moscow will be 10:30:28 when it is 8:00:00 UTC. By using Greenwich time, it is possible to determine the civil time and local mean solar time on any meridian. For urban dwellers, true time is more of an abstract concept that doesn’t have much relevance in their daily lives because it is irregular (see Solar Day).
In certain countries, official time is adjusted forward by one hour for the summer season. The Earth is divided into 24 meridians, with each meridian representing a time zone, and the time in each zone is averaged.

Suppose you reside in Moscow, where the geographic longitude is 37 degrees. The current time zone in Moscow is GMT+3 (post October 26, 2014). If you multiply 15 degrees by 3, you obtain 45 degrees. Moscow is located at an eastern longitude of 37 degrees, 36′. To simplify the calculation in this example, let’s “round” the longitude to 37 degrees. The disparity between the prime meridian and the longitude of Moscow is roughly 45 – 37 = 8 degrees.
We calculate the difference between Moscow time and real solar time by multiplying the value of 8 degrees by 4, resulting in 32 minutes. It is important to adjust the solar time to the local time when choosing the hour. Hello Denis! Could you please explain where you obtain the longitude for local time calculations? I need help understanding how to determine the solar time for Warming the Money Star in April 2014 in Pyatigorsk, Stavropol region. I’m quite confused… Wishing you blessings and prosperity.
Also, don’t miss out on our article about the top 10 best models of solar panels, including their features, specifications, and prices.
Am I correct in my calculation that there is a 58-minute (equivalent to 14.5 degrees) difference between maternity time and astronomical time? Therefore, if I intend to create a horizontal sundial, I would have to rotate it 14.5 degrees clockwise in order for it to display maternity time accurately under the sun? Thank you in advance! Denis, I would greatly appreciate your assistance as I am unable to comprehend this: does the statement “local time is less than solar time” imply that the event will take place earlier? I reside in GMT -5 (Toronto).

What is the process of determining the planetary positions in a natal chart?
In order to construct a horoscope, you will need the following information: the date of birth (day, month, year), the time of birth, and the coordinates of the city where the individual was born.
For instance, let’s determine the positions of the Sun, Moon, and Mercury for December 5, 1965, at 17:38 (local time) in the city of Riga. The coordinates of Riga are N = 56 degrees 57 minutes, E = 24 degrees 06 minutes. We will calculate the Greenwich Mean Time (GMT). Riga is situated in the second time zone (minus 2 hours), in 1965 there was a decree time (minus 1 hour), and there was no summer time (minus 0 hours). Thus, GMT = 17:38 – 2 – 1 – 0 = 14:38.
1. We can extract the information from the ephemeris for the midnight of December 5, 1965. The day was Sunday and the Stellar Time (ST) was 4 hours 54 minutes 20 seconds. The Sun was at 12 degrees 38 minutes 31 seconds in the sign of Sagittarius, while the Moon was at 25 degrees 33 minutes 32 seconds in the sign of Aries. Additionally, Mercury was at 8 degrees 18.4 minutes in the sign of Sagittarius, and it was retrograde (indicated by the letter R). Note that 18.4 minutes is equivalent to 18 minutes and 24 seconds (calculated by subtracting 18 from 18.4, which equals 0.4, and then multiplying 0.4 by 60 to obtain 24).
2. Let’s write down the data from the ephemeris for December 6, 1965, at midnight (a full day has passed). The day is Monday and the Stellar Time (ST) is 4 hours 58 minutes 16 seconds (with a difference of 3 minutes 56 seconds compared to the previous day). The Sun is at 13 degrees 39 minutes 24 seconds in the sign of Sagittarius, while the Moon is at 8 degrees 42 minutes 29 seconds in the sign of Taurus. Furthermore, Mercury is at 7 degrees 3.4 minutes in the sign of Sagittarius.
The calculation of the rest of the planets follows the identical algorithm; however, there are slight variations when it comes to computing retrograde planets, which we will explore using Mercury as an example.
Firstly, let’s determine the Moon’s position. Throughout the day, the Moon has transitioned from the Aries zodiac sign to the Taurus zodiac sign. Therefore, we must consider the translation of values in terms of absolute longitude. On December 5th, the Moon was at 25 degrees 33 minutes 32 seconds in Aries (25.5589). On December 6th, the Moon reached 8 degrees 42 minutes 29 seconds in Taurus (8.7081). To calculate the absolute longitude, we need to add 30 degrees to the Aries value of 8 degrees (representing the transition from zero degrees in Aries to zero degrees in Taurus), resulting in 8.7081 + 30 = 38.7081. Let’s perform the following calculations:
- 38.7081 – 25.5589 = 13.1492 (Moon’s speed in a day)
- 13.1492 : 24 = 0.5479 (Moon’s speed per hour)
- 0.5479 x 14.6333 = 8.0176 (path per GMT)
- 8.0176 + 25.5589 = 33.5765 (Moon’s natal position in absolute value)
- 33.5765 – 30 = 3.5765 degrees in the Taurus zodiac sign
- 3.5765 can be expressed as 3 degrees 34 minutes 35 seconds in the Taurus zodiac sign
Calculating the positions of retrograde planets involves determining their velocity. In the case of Mercury, which is moving backwards, we need to subtract the smaller value (on December 5) from the larger value (on December 6) to find its velocity. On December 5, Mercury was at 8 degrees 18.4 minutes of Sagittarius (8.3067), while on December 6, it was at 7 degrees 3.4 minutes of Sagittarius (7.0567). The calculation is as follows:
- 8.3067 – 7.0567 = 1.25 (Mercury’s speed for the day)
- 1.25 : 24 = 0.0521 (Mercury’s speed per hour)
- 0.0521 x 14.6333 = 0.7624 (path per GMT)
- 8.3067 – 0.7624 = 7.5443. This corresponds to 7 degrees 32 minutes 40 seconds of the sign of Sagittarius.
Again, because the planet is retrograde, we need to subtract the planet’s path from the greater value (as of December 5). The desired natal position of the planet should be between the two original positions on December 5 and 6.
The position of the sun determines the actual time
Hello Denis, good afternoon. I appreciate your hard work. I have a favor to ask – can you please verify my calculations as well? 10×15 equals 150 degrees. When we subtract 143 from 150, we get 7. Multiplying 7 by 4 gives us 28 minutes. This represents the difference between the local time and the solar time. Should we only subtract or add to the local time? In reality, all time conversions are taken into consideration, and based on this, each territory is assigned a specific time zone (GMT+).
I reside in Baku. I attempted to calculate the difference with solar time. I live in Novokuznetsk, Kemerovo region. I am somewhat confused about the concept of summer/winter time in our area. In Kirov, like many other cities in the Volga region, the time is not the original local time, but rather Moscow time, which was adopted during the period of perestroika. During the Soviet era, the day in the Volga region started an hour earlier than in Moscow.
Determining the Local Time: A Formula
At present, all settlements abide by their respective time zones. If people strictly followed solar time, chaos and confusion would ensue worldwide. Within a single time zone, all settlements have the same time on their clocks. Additionally, Russia has long implemented a decree time policy (such as orienting according to Moscow time). This principle has been widely adopted since 1960. It entails advancing all clocks by 1 hour. Therefore, if Moscow has 12 hours, the time at the 30th meridian would be calculated as 12-1=11 hours. By knowing both the actual time (corresponding to the time zone) and the time at the 30th meridian, one can easily determine the geographic longitude.
Specifically, if the meridian time is 11 hours and the actual time is 11:20, you can determine the longitude. Researchers have demonstrated that the Earth rotates 1 degree every 4 minutes. Therefore, the settlement will be situated 5 degrees east of the 30th meridian, resulting in a geographic longitude of 35 degrees E.
Discover the definition of “True solar time” in various dictionaries:
The concept of True solar time refers to the time in which the length of the day is considered to be equal to the interval between two consecutive culminations of the Sun. This term is particularly relevant in aeronautical astronomy, as it is crucial to determine the local time for accurate astronomical observations.
Additional related topics to explore include Geographic models, Geographic map, terrain plan. These subjects delve into the fundamental parameters and elements of these models, such as scale, conventional signs, methods of cartographic representation, and degree network.
It is important to note that each meridian has its own unique local time, which can be categorized into stellar, true solar, and mean solar time. This relationship holds true for both solar and sidereal time, regardless of the specific time measurement system being used.
You should be aware of the distinction between local time and Greenwich Mean Time. For instance, you can input a city here along with the date and time. It will indicate the offset from local time that you need to subtract (for our hemisphere). Additionally, all astrological software programs that I currently possess, including ZET, incorporate this offset. In terms of measuring geographical or astronomical coordinates, minutes and seconds are commonly used.
As you can observe, there is a direct correlation with those minutes and seconds, which have always been more associated with measuring time rather than angles and coordinates. We have the inhabitants of Babylon to thank for this convenient standardization of units, from whom modern civilization inherited hours, minutes, and seconds.
Calculation of accurate timeRight
Since we rely on the Chinese calendar of cosmic energies for selecting dates and hours, the determination of time is not based on government regulations but on the actual solar time, when the Earth is at a specific angle to the Sun. This serves as the reference meridian. Additionally, there are occasions where choosing a time on the cusp of a day becomes necessary. Incorrectly identifying the hour could lead to selecting the wrong day, resulting in a completely different energy.
I thoroughly enjoy reading your articles and strive to abide by the principles of feng shui. I would appreciate it if you could confirm whether I have accurately calculated the time for Krasnoyarsk: 112 minutes after solar time?
Hello, Denis! Have I correctly calculated the data: City of Tiraspol, TMR1. Geographic longitude 29°.2. Time zone: GMT +2:003. I am perplexed as some sources state that the GMT of Barnaul (Altai region) is +3, while others claim it to be +4. This discrepancy in calculations, albeit small (4 minutes), requires clarification! Currently, we are observing daylight saving time. In the winter, will the GMT shift to -4? Is that correct? Thank you! Previously, it was +1.5 hours, but now it seems to be about 30 minutes. Can you confirm if this is accurate or if it will be 2.5 hours in the opposite direction? Thanks.
SOLAR TIME is determined by the change in the hour angle of the Sun. I was born in Prokopyevsk, which is located in the 6th time zone… However, maternity time was later abolished. To calculate the average solar time in Moscow, we need to convert the longitude of the location (approximately 38°) into hours. The reference point for determining the movement of the International System of Solar Time (ISST) is the center of the Sun, and the calculation is based on the moment of the Sun’s highest point in the sky (true noon)… This information is related to Natural History.
Belt, Decretal and Ship’s time
Belt time.
Belt time is the average local time of the central meridian in a specific time zone, which is used throughout the zone. The time offset is calculated from the moment when the mean Sun reaches its highest point at the central meridian to a specific moment.
The diagram demonstrates the conceptual framework of time zones:
Determining the N belt based on longitude. To determine the N belt, divide the longitude by 15°. If the remainder is less than 7° 30/, the quotient represents the N belt. If the remainder is greater than 7° 30/, add one unit to the quotient.
The time remains the same within each belt, so clocks do not need to be adjusted when moving between locations. However, when crossing the eastern boundary of a belt, clocks should be moved forward by 1 hour. Conversely, when crossing the western boundary, clocks should be moved back by 1 hour.
Converting from local time to zone time.
Also, check out: Calculating the length of parallels and meridians on the Krasovsky ellipsoid, accounting for distortions caused by the Earth’s polar compression.
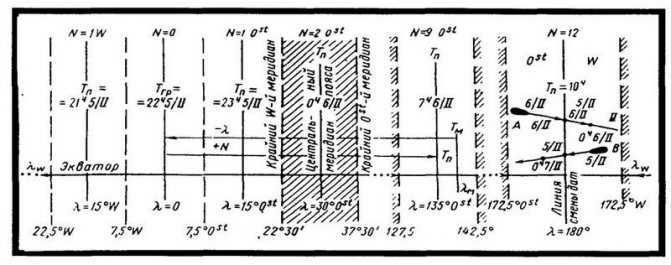
To introduce the correction for the difference in longitudes between the local and central meridians (Dl in hours), it is necessary to adjust the local time for the transition to the belt time. However, for a moving ship, it is more convenient to solve the problem “through Greenwich”. Let Tm represent the time for the meridian lm (see Fig.); by converting the longitude into hours, we can obtain the local time for the zero meridian, Tgr, which is also the belt time for the zero belt. By using the value N for the belt (which represents the central meridian in hours), we can then determine the time Tp for the central meridian of this belt:
Tgr = Tm + l 0stw; Tp = Tgr ± N 0stw
The reverse transition from Tp to Tm is done similarly, but using the following formulas:
Tgr = Tp + N 0stw; Tm = Tgr ± l 0stw
Example. 17/VIII 1977 d. in l = 82°10′ W we have TM = 5h38m. Find, Tp:
Solution. The calculation is performed “via Greenwich”.
| Tm + | 5Ch38m 17/VIII |
| lw | 5 29 … |
| 11 07 | |
| – Nw | 5 |
| Tp | 6h07m |
Translate l = 5h28m40s and round to 1m, since Tm is given to 1m.
Belt times: Many belt times have their own names; for example, the time of the first belt (N = 1 Ost) is referred to as Central European, while the time of the second belt is referred to as Eastern European.
Belt time Td in Russia is calculated by adding 1 hour to the belt time, i.e.
Belt N = 13 Ost extends to the date change line in the Bering Strait (l = 1690 W), the clock shows the time N = 11 W, but the date differs by 1 day.
Ship’s time.
Ship’s time Tc refers to the time of the time zone where the ship’s watch is set. The zone number is provided by the captain and recorded in the logbook, for example, 22.00, N = 10 Ost , or N = -10. The zone number given by the captain often does not correspond to the computed longitude, so it is chosen from the logbook for calculations instead of being determined by longitude. Ship’s time is typically measured to the nearest minute, which is sufficient for the purposes of ship life, operation, and navigation (at speeds up to 15 – 16 knots).
Tgr = Tm + lOstW ; Tc = Tgr ± N OstW ;
where l – represents the longitude of the ship’s current position;
N – indicates the belt number used to set the ship’s watch (recorded in the logbook);
For example, 23/11 1977 d. at l = 13040′ Оst sunset Tm = 17h15m. Find Tc, (# = 3 0st).Solution.
| Tm | 17Ch15m 23/I I |
| lOst | 0 55 |
| Tgr | 16 20 |
| № | 3 |
| Tc | 19h20m |
Time equation – the distinction between mean solar time (MSW) and true solar time (TSW), specifically UV = MSW – TSW. This distinction at any specific moment is consistent for any observer on Earth. The equation of time can be obtained from specialized astronomical publications, astronomical software, or computed using the formula below.
In publications like the Astronomical Calendar, the equation of time is described as the discrepancy between the hour angles of the average equatorial sun and the actual sun, meaning that in this definition, EE = SSV – ISV.
English publications frequently employ a “reversed” interpretation of the equation of time: UW = ISV – SSV, which signifies the difference between true solar time and average solar time.
Explanation of the concept
The equation of time can be defined as the discrepancy between “local apparent solar time” and “local mean solar time” (also referred to as “local apparent solar time” in English literature). This definition is technically more accurate, but it has no impact on the outcome, as this difference remains constant for any specific location on Earth.
Furthermore, it is important to note that neither local true time nor local mean solar time should be mistaken for the official local time (referred to as “standard time”).
Contrary to the stars, which have a nearly uniform apparent daily movement caused solely by the Earth’s rotation on its axis, the Sun’s daily motion is non-uniform. This is due to the combination of the Earth’s rotation on its axis, its revolution around the Sun, and the tilt of the Earth’s axis in relation to the plane of its orbit.
Influence of the ellipticity of the orbit
The Earth’s revolution around the Sun takes place in an elliptical trajectory. As per Kepler’s second law, this movement is non-uniform, with a faster pace at perihelion and a slower pace at aphelion. This phenomenon is noticeable to an observer on Earth through the accelerated or decelerated apparent motion of the Sun along the ecliptic in relation to the fixed stars.
The impact of the Earth’s axial tilt
Due to the tilt of the Earth’s axis in relation to the ecliptic plane, the following phenomenon occurs:
- During the solstices (winter and summer), the Sun moves nearly parallel to the celestial equator, resulting in minimal change in the hour angle of the Sun due to the daily motion of the celestial sphere;
- During the equinoxes (autumn and spring), the Sun moves at a maximum angle to the celestial equator, resulting in the maximum change in the hour angle of the Sun due to the daily motion of the celestial sphere.
The equation of time is a combination of two periodic curves – one with a yearly period and another with a six-month period. The sinusoidal curve with a one-year period is a result of the Sun’s irregular motion along the ecliptic. This component of the equation of time is known as the equation of center or the equation arising from eccentricity. The sine wave with a six-month period represents the time difference caused by the inclination of the ecliptic to the celestial equator and is referred to as the equation arising from the tilt of the ecliptic.
The equation of time reaches zero four times throughout the year, approximately on April 15, June 13, September 1, and December 25.
Consequently, there is a distinct peak of the equation of time during every period of the year: approximately on February 12th – +14.3 minutes, May 15th – -3.8 minutes, July 27th – +6.4 minutes, and November 4th -16.4 minutes. The precise values of the equation of time can be found in astronomical yearbooks.
This feature can be utilized as an extra feature in certain clock models.
Calculation
The calculation can be estimated by a segment of a Fourier series as the combination of two sine curves with periods of one year and six months, respectively:
B = 360 ( N – 81 ) / 365 , if the angles are given in degrees,
B = 2 π ( N – 81 ) / 365 , if the angles are given in radians.
Here, N represents the number of days in a year, for example:
Ruby program for calculating the current date
#!/usr/bin/env ruby =begin Equation of Time calculation *** No guarantees are implied. Use at your own risk *** Written by E. Sevastyanov, 2017-05-14 Based on "Equation of time" WikiPedia article as of 2016-11-28 (which describes angles in a bewildering mixture of degrees and radians) and Del Smith, 2016-11-29 It appears to give a good result, but I make no claims for accuracy. =end pi = (Math::PI) # pi delta = (Time.now.getutc.yday – 1) # (Current day of the year – 1) yy = Time.now.getutc.year np = case yy #The number np is the number of days from January 1 to the date of the Earth's perihelion. (http://www.astropixels.com/ephemeris/perap2001.html) when 2017 ; 3 when 2018 ; 2 when 2019 ; 2 when 2020 ; 4 when 2021 ; 1 when 2022 ; 3 when 2023 ; 3 when 2024 ; 2 when 2025 ; 3 when 2026 ; 2 when 2027 ; 2 when 2028 ; 4 when 2029 ; 1 when 2030 ; 2 else; 2 end a = Time.now.getutc.to_a; delta = delta + a[2].to_f / 24 + a[1].to_f / 60 / 24 # Correction for fractional part of the day lambda = 23.4372 * pi / 180; # Earth’s inclination in radians omega = 2 * pi / 365.25636 # angular velocity of annual revolution (radians/day) alpha = omega * ((delta + 10) % 365) # angle in (mean) circular orbit, solar year starts 21. Dec beta = alpha + 0.03340560188317 * Math.sin(omega * ((delta – np) % 365)) # angle in elliptical orbit, from perigee (radians) gamma = (alpha – Math.atan(Math.tan(beta) / Math.cos(lambda))) / pi # angular correction eot = (43200 * (gamma – gamma.round)) # equation of time in seconds puts “EOT =” + (-1 * eot).to_s + ” seconds”