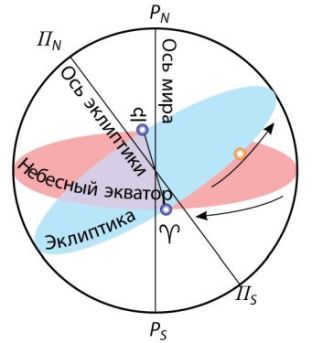
The celestial equator, represented by the blue circle in the diagram, is formed by extending the Earth’s equator onto the celestial sphere. Similarly, the north and south poles of the Earth also extend onto the celestial sphere. The yellow circle represents the ecliptic, which is the plane of the Earth’s orbit around the Sun. The hour circle, or meridian, of a star is a large circle that passes through both the poles and the star itself. The intersection of the ecliptic and the celestial equator defines two points. The vernal point, which is located in the constellation of Pisces, is one of these points. From the vernal point, we establish the right ascension on the celestial equator, represented by the horizontal red line in the diagram. The declination of an object is determined by its position along the meridian, represented by the vertical red line.
The equatorial coordinate system is a celestial coordinate system that is independent of the observer’s position. It is based on a projection of the Earth’s equator onto the celestial sphere as a reference plane. This projection is known as the celestial equator and it divides the sky into two hemispheres. Each hemisphere has a reference axis that is a projection of the Earth’s pole perpendicular to the celestial equator. The equatorial coordinate system is defined by two angular coordinates: right ascension and declination.

- Ascension (α) refers to the angle measured from the celestial equator, starting from a reference point like the vernal equinox, which is the point where the celestial equator intersects with the ecliptic. This angle is measured eastward and divided into 24 hours, with each hour further divided into minutes and seconds.
- Declination (δ) is the angle measured perpendicular to the celestial equator and represents the position of a celestial object. It is measured in degrees, with positive values indicating objects in the northern hemisphere and negative values indicating objects in the southern hemisphere. The range of declination extends from -90° (the south pole) to +90° (the north pole), with 0° representing the celestial equator.
Direct Ascension and declination are the celestial equivalents of Earth’s longitude and latitude. In professional terms, direct ascension is sometimes expressed in degrees. This corresponds to the equatorial coordinate of direct ascent (α or AD) with 1 hour of direct ascent being equivalent to 15 degrees. For instance, a direct ascent of 77.5° corresponds to 5 h 10 m. As scientists explored the universe and the sky, they discovered that everything around them was in motion.
The history of the origin of the coordinate system dates back to ancient times. The development of a coordinate system is primarily linked to the need for orientation on the ground and understanding the structure of the celestial surface.
To determine the location and movement of objects, humanity has devised a comprehensive system of methods and techniques. Additionally, special numerical and symbolic designations have been created. In reality, there are several systems that determine the points of object positioning. They mainly differ in the choice of the main plane and the point of reference.
Since we observe the sky as a sphere from Earth, the coordinates in astronomy are also spherical. Moreover, they represent specific arcs of circles on the sphere. It is important to note that they are measured in degrees, and sometimes in hours.
Horizontal coordinate system
The main plane of the horizontal coordinate system is determined by the mathematical horizon. The zenith and nadir are represented by the poles. This coordinate system is commonly employed for observing celestial objects from Earth, whether using the naked eye or a telescope, particularly within the solar system. Continuous observation and measurement are necessary due to the ongoing movement of celestial bodies.
Several explanations of the coordinate system
The initial equatorial coordinate system
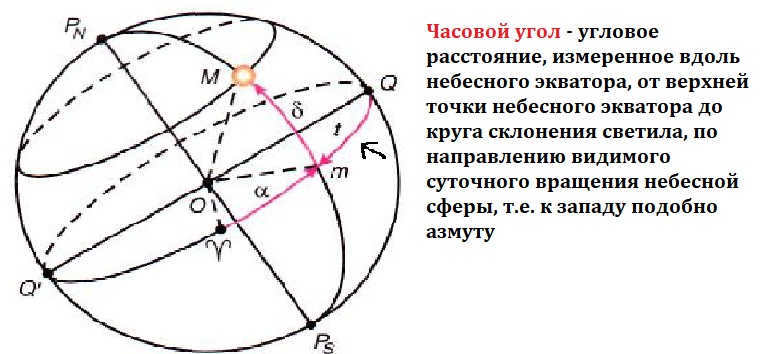
In this system, the flat region representing the surface of the equator of the sky is taken as the point of reference, denoted as Q. The coordinates in this system represent the declination and hour angle.
To understand what declination is, you can find more information here.
The hour angle is the arc located between the celestial meridian and the circle of declination. Its measurement ranges from 0° to 360°.
It is worth mentioning that the first equatorial coordinate system is used due to the constant movement of our planet throughout the day. As a result, the starting point was set as the point of vernal equinox, which remains constant relative to the stars.
Hour angle
Another equatorial coordinate system
The concept behind the equatorial system of celestial coordinates
The declination of a celestial object δ is the angle between the plane of the celestial equator and the direction to the object from the center of the celestial sphere. The declination of a celestial object is measured from 0 to ±90°.
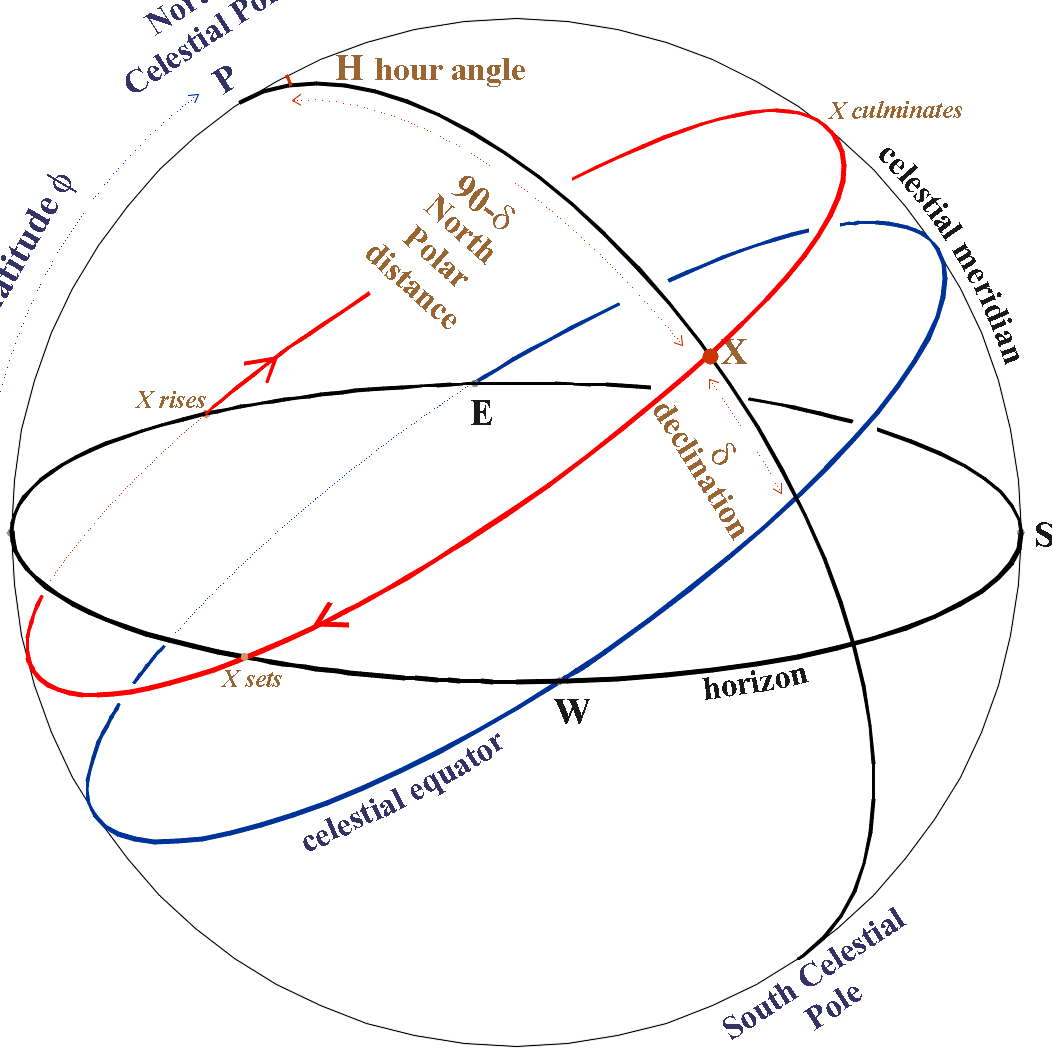
Positive declination is counted towards the North Pole of the world, and negative declination is counted towards the South Pole. The declination of the Sun, Moon, and planets are usually obtained from the aeronautical astronomical yearbook for each hour of Greenwich Mean Time, while the declination of navigational stars is taken from a table of equatorial coordinates of stars at the beginning of each year due to its yearly change by 1-2 degrees. Sometimes, instead of declination, another coordinate called polar distance P is used. Polar distance P is the angle in the plane of the declination circle, enclosed between the world axis and the direction to the object from the center of the celestial sphere. Polar distance is counted from the North Pole of the world to the South Pole from 0 to 180°. The relationship between polar distance and declination is given by: P + δ = 90°, thus P = 90° – δ; δ = 90° – P Celestial objects that lie on the same daily parallel have the same declination and polar distance. The declination or polar distance determines the position of the object on the declination circle. The position of the declination circle on the celestial sphere is determined by the hour angle of the object. The hour angle of the object t is the dihedral angle in the plane of the celestial equator, enclosed between the plane of the celestial meridian and the plane of the object’s declination circle.
The hour angle is counted from the southern direction of the celestial meridian clockwise (to the west) to the circle of the object’s declination from 0 to 360°. It is important to note that the hour angle of the object is counted in the direction of the daily rotation of the celestial sphere. In some calculations, the hour angles of objects are counted from 0 to 180° to the west and east, denoted as t3 and tB respectively. In the Aeronautical Astronomical Yearbook, the western hour angles of objects are given from 0 to 360°, while in the calculation tables for the Sun, Moon, and planets, hour angles are given from 0 to 180°. The relationship between the hour angle of the object and the longitude of the observer’s location is significant. As mentioned earlier, the hour angle of the object is usually counted to the west of the celestial meridian. Since the plane of the celestial meridian coincides with the observer’s geographic meridian, the hour angles of the same object will differ for observers located on different meridians.
It is evident that at the same moment in time, the difference in local hour angles of the object is equal to the difference in longitudes of the observers t2-t1=λ2-λ1. If we take λ1=0 in this relation, then t1 = tgp. Taking λ1=λ and t2=t, we obtain t=tgr±λ b 3. As can be seen from the formula, the local hour angle of the object differs from the Greenwich hour angle by the value of the observer’s longitude. In practice, instead of the object’s hour angle, another coordinate is often used – the right ascension of the object. The right ascension of an object α is the angle between the plane of the declination circle of the vernal equinox (the initial declination circle) and the plane of the object’s declination circle. The vernal equinox is the point of intersection of the plane of the celestial equator with the center of the Sun (March 21) in its apparent annual movement on the celestial sphere. This point is usually denoted by the symbol of the constellation Aries, in which it was located during the birth of astronomy. The right ascension of the object is counted in the plane of the celestial equator from the vernal equinox counterclockwise (to the east) to the circle of declination of the object from 0 to 360°. The right ascension of the object and its hour angle can be measured not only by the angle but also by the arc of the celestial equator, and the declination and polar distance of the object by the arc of the declination circle.
Characteristics of the equatorial system of celestial coordinates
- Illustration 1. The luminary’s western hour angle is t3 = 230°; the luminary’s declination is δ = +60°.
- Illustration 2. The luminary’s right ascension is α = 300°; the luminary’s declination is δ = -60°.
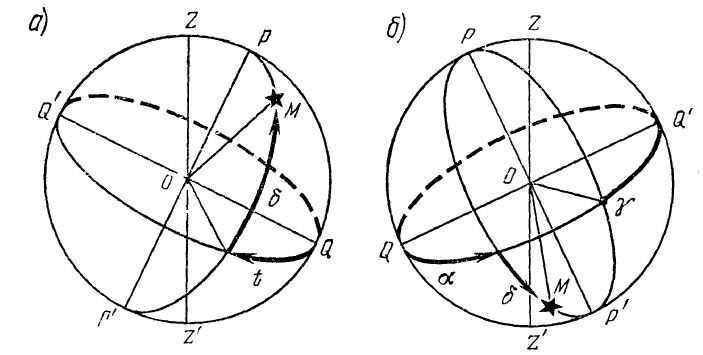
Example illustrating how the equatorial celestial coordinate system is used to determine the coordinates of an object (as shown above)

2. The stars exhibit an observable daily motion. When we observe the night sky for a period of one to two hours, we can clearly see that it rotates as a whole, with stars rising on one side and setting on the other. From our perspective in the Northern Hemisphere, the stars appear to rise from the eastern part of the horizon and then shift towards the right. Eventually, they reach their highest point in the southern part of the sky before descending in the western part of the horizon. Over the course of a day, the entire starry sky completes one full revolution. Therefore, the visible daily rotation of the night sky occurs in a clockwise direction when facing south.
The northern part of the sky is where Polaris is located (Fig. 10). It appears as though the entire sky revolves around it. In reality, the Earth rotates on its axis from west to east, while the entire sky rotates in the opposite direction, from east to west. The polar star remains nearly still and at a consistent height above the horizon for a given area. The daily movement of the stars, known as the apparent rotation of the firmament, is a reflection of the Earth’s actual rotation around its axis.
A film about the celestial sphere and how to determine stellar equatorial coordinates.
3. The celestial sphere is a concept that helps us understand the arrangement of stars in the sky. Although it may appear that all the stars are located on a single spherical surface and are equidistant from us, this is not the case. In reality, the stars are at varying distances from us. However, we can still imagine a spherical surface, known as the celestial sphere, to represent the sky. The celestial sphere is an imaginary sphere with a chosen center, which can be aligned with different points in space depending on the specific problem being studied. This center could be the observer’s eye, the center of the Earth, or even the Sun. The celestial sphere is particularly useful for making angular measurements and studying the relative positions and movements of objects in the sky.
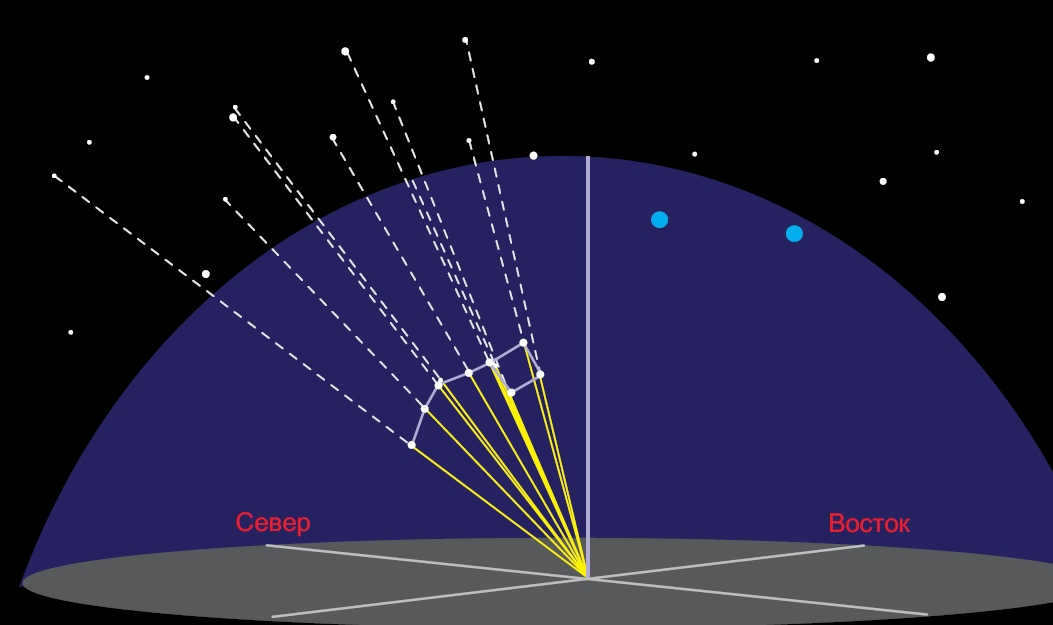
Fig. 11. A diagram illustrating how stars in the Big Dipper constellation are projected onto the celestial sphere
The plumb or vertical line is a straight line that runs through the center of the celestial sphere (Fig. 12) and aligns with the direction of the plumb line at the observation site. It intersects the celestial sphere at the zenith (the highest point where the plumb line intersects the celestial sphere) and the nadir (the point on the celestial sphere directly opposite the zenith). The plane that passes through the center of the celestial sphere and is perpendicular to the plumb line is known as the plane of the true or mathematical horizon.
The circle of altitude, also known as the vertical circle or simply the vertical of the luminary, is the great circle of the celestial sphere that passes through the zenith, the luminary, and the nadir.
The celestial sphere is intersected by the world axis, which is a straight line passing through the center of the sphere and running parallel to the Earth’s axis of rotation. These two points of intersection are diametrically opposed to each other.
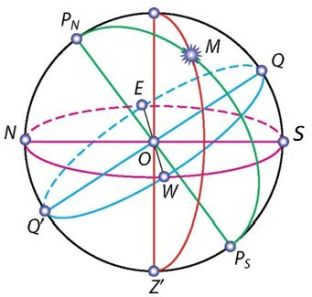
Illustration 12 – The celestial sphere: O – the center of the celestial sphere (the observer’s position); PN – the North Pole of the Earth; PS – the South Pole of the Earth; PNPS – the axis of the Earth; Z – the zenith; Z’ – the nadir; E – the east; W – the west; N – the north; S – the south; Q – the upper point of the celestial equator; Q’ – the lower point of the celestial equator; ZZ’ – the vertical line; PNMPS – the declination circle; NS – the noon line; M – a celestial body on the celestial sphere.
The point where the celestial sphere intersects with the axis of the world, and where Polaris is located, is known as the North Pole of the world. The opposite point is called the South Pole of the world. Polaris is positioned approximately 1 degree away from the North Pole of the world (to be more precise, it is 44 minutes away).
The celestial equator is a great circle that runs through the center of the celestial sphere and is perpendicular to the axis of the world. It divides the celestial sphere into two parts: the Northern Hemisphere, with its apex at the North Pole of the world, and the Southern Hemisphere, with its apex at the South Pole of the world.
The circle of declination of a celestial body is a large circle on the celestial sphere that passes through the poles of the world and the celestial body.
The daily parallel is a small circle on the celestial sphere whose plane is perpendicular to the world’s axis.
The celestial meridian is a large circle on the celestial sphere that passes through the zenith, nadir, and poles of the world. It intersects with the true horizon at two diametrically opposite points. The point where the true horizon and the celestial meridian closest to the North Pole of the world meet is known as the north point. The point where the true horizon and the celestial meridian closest to the South Pole of the world meet is known as the South point. The line that connects the north and south points is called the noon line. It lies on the plane of the true horizon. At noon, the shadows of objects fall in the direction of the noon line.
The celestial equator intersects with the true horizon at two opposite points: the east point and the west point. If you are standing in the center of the celestial sphere and facing north, the east point will be on your right and the west point will be on your left. Remembering this rule will help you easily orient yourself on the ground.
The annual path of the Sun among the stars is known as the ecliptic. The Earth’s orbit around the Sun, also known as its ecliptic plane, is inclined at an angle of 23° 27′ to the celestial equator. It intersects with the celestial equator at the vernal equinox (Γ), which occurs around March 21, and the autumnal equinox (Ω), which occurs around September 23 (Figure 13).
There are various coordinate systems employed in astronomy, each of which is defined with respect to different circles on the celestial sphere. Celestial coordinates are measured by the arcs or central angles that span these circles.
Celestial coordinates refer to the central angles or arcs of the great circles on the celestial sphere, which are utilized to ascertain the location of celestial bodies relative to the primary circles and points on the celestial sphere.
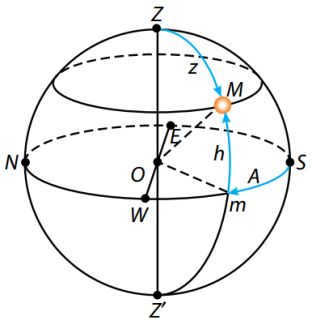
Figure 14 – The Horizontal Coordinate System: h represents the height of a luminary above the horizon, while z represents the zenith distance. A denotes the azimuth.
The Horizontal Coordinate System is employed during astronomical observations to determine the position of luminaries in relation to the horizon. This system utilizes the true horizon as the reference circle. In this system, the coordinates are represented by altitude (h) and azimuth (A).
The altitude of a celestial body refers to its angular distance from the true horizon, as measured along the vertical circle (Figure 14). This measurement is expressed in degrees, minutes, and seconds. If the celestial body is visible in the sky, the altitude is measured from 0 to +90 degrees towards the zenith. If the celestial body is below the horizon, the altitude is measured from 0 to -90 degrees towards the nadir.
To determine azimuths, the south point is used as the reference. The azimuth of a celestial body is the angular distance along the true horizon, measured from the south point to the point where the horizon intersects with the vertical circle passing through the celestial body (refer to Fig. 14). Azimuth values range from 0 to 360 degrees, with measurements taken west of the south point.
The use of the horizontal coordinate system is common in topographic surveying and navigation. As the celestial sphere rotates daily, the altitude and azimuth of a celestial body change over time. Consequently, horizontal coordinates only have a specific value for a given moment in time.
The zenith distance (z) is the angular distance from the zenith to a celestial body, measured along a vertical circle. It is measured from 0 to +180° towards the nadir. The altitude and zenith distance are connected by the equation: z + h = 90°.
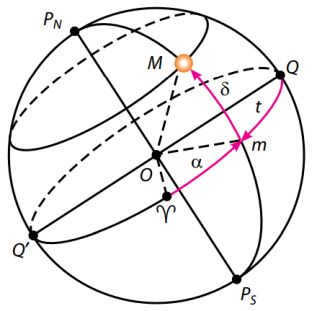
Figure 15 – Equatorial celestial coordinate system: δ – declination of luminary M; α – right ascension; t – hour angle
The equatorial coordinate system is used for the construction of star maps and star catalogs, and it is based on the celestial equator as the main circle of the celestial sphere (Fig. 15). The equatorial coordinate system uses declination (δ) and right ascension (α) as its coordinates.
Declination is the angular distance of a luminary M from the celestial equator, measured along the declination circle. It is measured from 0 to +90° towards the North Pole of the world and from 0 to -90° towards the South Pole of the world.
The starting point for the celestial equator is defined as the vernal equinox point γ, which occurs around March 21st when the Sun is positioned there.
The right ascension of a celestial body refers to the angular distance measured along the celestial equator from the vernal equinox point to the intersection point of the celestial equator with the declination circle of the body. Right ascension is measured in the opposite direction of the daily rotation of the celestial sphere, and it ranges from 0 to 360 degrees or 0 to 24 hours.
Instead of using direct ascension (a) for certain astronomical tasks involving time measurement, the hour angle (t) is used instead (see Fig. 15). The hour angle is the angular distance measured along the celestial equator, starting from the highest point of the celestial equator and extending to the declination circle of the celestial object. The hour angle is measured in the direction of the apparent daily rotation of the celestial sphere, which is towards the west. It is measured on a scale of 0 to 24 hours.
Star charts and catalogs make use of the coordinates (α, δ) in the equatorial coordinate system which are independent of the daily motion of the celestial sphere and change at a slow rate. As a result, they are utilized for creating star charts and catalogs. Star charts are representations of the celestial sphere projected onto a plane and feature objects plotted in a specific coordinate system. An online star map is available for reference. A star atlas consists of a collection of star maps that cover either the entire sky or specific sections of it. Star catalogs, on the other hand, include specialized lists of stars that provide their coordinates on the celestial sphere, stellar magnitude, and other relevant parameters. The Hubble Guide Star Catalog (GSC) is a notable example, containing a vast array of approximately 19 million objects.
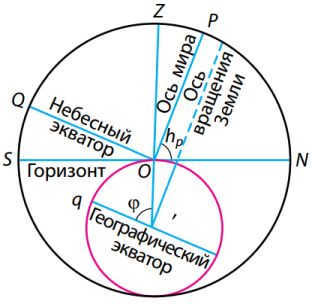
Figure 16 – Elevation of the global pole relative to the horizon
2- The precession of the Earth’s axis is caused by the gravitational pull of the Moon and the Sun, as well as the uneven distribution of mass within the Earth. This causes the axis to trace out a cone over time. As the axis changes direction, the equatorial plane perpendicular to it also shifts, leading to a displacement of the vernal equinox point. This phenomenon is known as luni-solar precession. The vernal equinox point moves towards the apparent annual motion of the Sun at a rate of 50.3″ per year or 1° in 71.6 years, completing a full revolution along the ecliptic in 25,770 years. The Earth’s poles also shift their position among the stars. Currently, the North Pole is close to Polaris, but in 10,000 years it will move towards Vega in the constellation Lyra.
3. The elevation of the Earth’s North Pole above the horizon is determined by the geographic latitude of the observer’s location. It is well-known that Polaris, which is situated near the North Pole, maintains a relatively constant height above the horizon due to the daily rotation of the starry sky. However, as one travels from north to south, where the geographic latitude decreases, Polaris gradually descends towards the horizon. Thus, there exists a correlation between the height of the Earth’s North Pole and the geographic latitude of the observer’s position.
The diagram in Figure 16 shows the globe and the celestial sphere in a section view, specifically the plane of the celestial meridian of the observation site. An observer at point O sees the North Pole at a height of hP. The Earth’s axis, represented by Ð OO, is parallel to the world axis. The angle Ð OO'q, which is centered at the Earth, corresponds to the geographical latitude f of the observation site. As the radius of the Earth at the observation point is perpendicular to the plane of the true horizon, and the world axis is perpendicular to the plane of the geographical equator, Ð NOP and Ð OO'q are equal to each other as angles with sides that are mutually perpendicular. Therefore, the angular elevation of the North Pole above the horizon is equal to the geographical latitude of the observation site:
On the contrary, it can be inferred from Figure 16 that the zenith declination dZ is determined by Ð QOZ. Thus, it can be expressed as
The relationship between the geographic latitude of the observation site and the corresponding horizontal and equatorial coordinates of the luminary is characterized by equality (2).
The movement of the celestial sphere on a daily basis at locations near the equator

The starry sky at the Earth’s equator undergoes a daily rotation.
As an observer moves towards the Earth’s North Pole, the North Pole of the World emerges above the horizon. At the Earth’s pole, the pole of the world is directly overhead. The stars in this region move in circular paths parallel to the horizon, which aligns with the celestial equator. The celestial meridian becomes indistinguishable, and the concepts of north, south, east, and west lose their significance.
On the equator of our planet, the axis of the Earth aligns with the line of noon, while the poles of the Earth align with the points of north and south. The celestial equator intersects with the points of east, west, zenith, and nadir. The paths that stars trace across the sky are at right angles to the horizon, and each star remains visible above the horizon for half of the day.
The celestial coordinate system is utilized to determine the positions of celestial objects by using the equatorial coordinate system and spherical coordinates. The fundamental plane is created by projecting the Earth’s equator onto the celestial sphere, resulting in the formation of the celestial equator. The primary direction is established by projecting the Earth’s orbit onto the celestial sphere, forming the ecliptic, and positioning the ascending node of the ecliptic at the celestial equator, thus creating the vernal equinox. Direct ascension is measured by moving eastward along the celestial equator from the equinox point, while declination is measured in a positive direction north of the celestial equator. (Two sets of such coordinates are displayed here.) The projections of Earth’s north and south geographic poles form the north and south celestial poles, respectively.
The equatorial coordinate system is a popular method for determining the positions of celestial objects. This system can be represented using either spherical or rectangular coordinates. The starting point is located at the center of the Earth, and the fundamental plane is formed by projecting the Earth’s equator onto the celestial sphere. This creates the celestial equator. Additionally, there is a principal direction that points towards the vernal equinox, and a right-handed convention is followed.
The geocentric coordinates are based on the origin located at the center of the Earth, as if it were transparent. The coordinate system is aligned with the Earth’s equator and pole, and remains relatively stationary relative to the background of the stars. The right-handed agreement dictates that the coordinates increase north of and east of the primary plane.
This explanation of how the reference frame is oriented is a bit simplified; it’s not exactly fixed. The Earth’s axis moves slowly, causing the coordinate system to slowly rotate westward around the poles of the ecliptic. This rotation takes about 26,000 years to complete and is known as precession. In addition to precession, there is also a smaller movement of the ecliptic and a slight wobble of the Earth’s axis called nutation.
In order to accurately determine cardinal directions, these movements require a specific date, known as an epoch, to be used as a reference point. The three most commonly used epochs are:
The standard reference point for comparing positions set on different dates is known as the standard epoch mean equinox. This reference point, typically J2000.0 but occasionally including B1950.0, B1900.0, and others, provides a fixed standard direction. The mean equinox of a specific date is determined by the intersection of the ecliptic of that date (i.e., the position of the ecliptic at that specific date) with the mean equator. The mean equator is the equator that has been adjusted for precession to its position at the given date, while also being free from small periodic variations caused by nutation. This measurement is commonly used in the calculation of planetary orbits. In contrast, the true equinox of a date is determined by the intersection of the ecliptic of that date with the true equator. The true equator is the mean equator plus any nutation that occurs. It represents the actual intersection of the two planes at any given moment, accounting for all motions.
Therefore, a location in the equatorial coordinate system is typically determined by the actual equinox and equator of the current date, the average equinox and equator of J2000.0, or a similar reference point. It is important to note that there is no concept of a “mean ecliptic” because the ecliptic does not experience small periodic fluctuations.
Polar coordinates
Applications in astronomy
Astronomers often utilize spherical coordinates to express the position of stars. This is typically done by using two coordinates: right ascension and declination. Unlike other coordinate systems, such as the horizontal coordinate system, the direction of distant objects remains the same for all observers. This makes it convenient to use the same coordinates for everyone. In contrast, the position of a star varies for each observer depending on their location on Earth and changes as the Earth rotates.
Telescopes equipped with equatorial mounts and setting circles rely on the equatorial coordinate system to locate objects in the sky. By combining setting circles with a star map or ephemeris, astronomers can easily point their telescopes at known objects on the celestial sphere.
The δ symbol (also known as “delta” or DEC) is used to measure the angular distance from an object to the celestial equator, with positive values for objects to the north and negative values for objects to the south. For instance, the declination of the North Pole is +90°. The celestial equator, which is the projection of the Earth’s equator onto the celestial sphere, serves as the reference for declination. In a way, declination is similar to latitude on Earth.
Direct Ascent
Ascend Directly
Direct Climb
Straightforward Ascent
Vertical Climbing
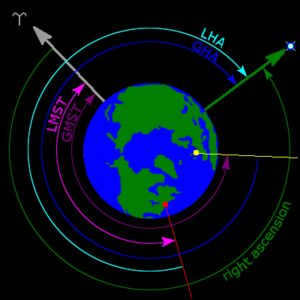
From an aerial perspective, the coordinates of stars at the equator can be determined. This can be seen by examining the North Pole of Earth, where the local hour star angle (LHA) is calculated for an observer located near New York City. Additionally, the direct ascension and Greenwich hour angle (GHA) are depicted, along with the local mean sidereal time (LMST) and Greenwich Mean Star Time (GMST). The symbol ʏ is used to indicate the direction of the vernal equinox.
The α symbol (also known as “alpha”) represents the direct ascension (abbreviated as RA), which indicates the angular distance of an object moving eastward along the celestial equator from the vernal equinox to the hour circle passing through the object. The vernal equinox point is one of the two points where the ecliptic and the celestial equator intersect. Similar to the longitude on Earth, direct ascension is commonly measured in sidereal hours, minutes, and seconds instead of degrees. This is due to the method of measuring direct ascension, which involves tracking the time it takes for objects to move along the meridian as the Earth rotates. In one hour of direct ascension, there are 15 degrees, and a full 24 degrees of direct ascension around the entire celestial equator.
When used in conjunction, direct ascension and declination are usually abbreviated as RA / Dec.
Instead of directly ascending, the hour angle (HA or LHA, local hour angle), a system that measures the angular distance to an object in the west along the celestial equator from the observer’s meridian to the hour circle passing through the object, can be used as an alternative. Unlike direct ascension, the hour angle always increases as the Earth rotates. The hour angle can be seen as a way to measure time from the moment when the object touches the meridian overhead, known as upper culmination.
The star that culminates on the observer’s meridian is considered to have a hour angle of zero (0). After one sideric hour (approximately 0.9973 solar hours), the Earth’s rotation will move the star to the west of the meridian, resulting in an hour angle of 1. When calculating topocentric, direct ascension can be converted to hour angle as an intermediate step.
Rectangular coordinates
Geocentric equatorial coordinates
can be restated in a unique way using the English language while preserving the HTML markup as follows:
Rectangular coordinates
Geocentric equatorial coordinates
can be rephrased in a distinctive manner while maintaining the HTML formatting.
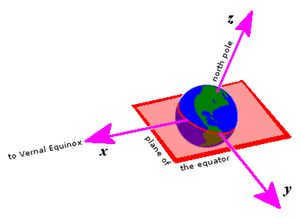
Geocentric equatorial coordinates are a system of celestial coordinates that have their origin at the center of the Earth. The primary plane in this system is the plane of the Earth’s equator, and the primary direction is defined by the vernal equinox. In this system, the y-axis is oriented 90° to the east in the primary plane, while the z-axis represents the north polar axis. It is important to note that the reference frame of this coordinate system does not rotate with the Earth; instead, it is the Earth that rotates around the Z axis.
There are various rectangular variations of equatorial coordinates, all of which share the following characteristics:
- An origin located at the center of the Earth.
- A fundamental plane that coincides with the plane of the Earth’s equator.
- The vernal equinox marks the principal direction (x-axis) where the Sun crosses the celestial equator in a northern direction in its annual visible path. It forms a circular contour around the ecliptic.
- There is a right-handed convention that establishes the y-axis at 90° east in the fundamental plane and the az-axis along the north polar axis.
Reference frames do not rotate with the Earth (unlike Earth-centered, Earth-fixed frames). They always point towards the equinoxes and gradually drift over time due to the movements of precession and nutation.
- In astronomy:
- The position of the Sun is often described using geocentric equatorial rectangular coordinates X, Y, Z, and the fourth distance coordinate R (= √ X + Y + Z), measured in astronomical units.
- Geocentric equatorial rectangular coordinates ξ, η, ζ, and the fourth distance coordinate δ (equal to √ξ + η + ζ) are commonly used to describe the positions of planets and other solar system bodies. These coordinates, measured in astronomical units, are related to spherical coordinates in the following way: XR = ξ Δ = cos δ cos α YR = η Δ = cos δ cos α ZR sign equals ζ Δ sign equals sin δ > = >> = \ cos \ delta \ cos \ alpha \ > = >> = \ cos \ delta \ sin \ alpha \ > = >> = \ sin \ delta \ end >>
- The coordinates of artificial Earth satellites are provided in geocentric equatorial coordinates, also known as geocentric equatorial inertial (GEI), (ECI), and conventional inertial system (CIS), which are defined as being equivalent to the astronomical geocentric equator. In the geocentric equatorial reference frame, the x, y, and z axes are often represented as I, J, and K, respectively, or the basis of the system is determined by the unit vectors Î, Ĵ, and K̂.
- The Geocentric Celestial Reference Frame (GCRF) corresponds to the geocentric version of the International Celestial Reference Frame (ICRF). Its primary reference point is the equinox at J2000.0, and it remains fixed in relation to precession and nutation, while still being equivalent in the aforementioned systems.
Heliocentric equatorial coordinates
Astronomy also utilizes a heliocentric rectangular version of equatorial coordinates, denoted as x, y, z, which possesses the following properties:
- The coordinates have their origin situated at the center of the Sun.
- The fundamental plane lies within the plane of the Earth’s equator.
- The primary direction (x-axis) points towards the vernal equinox.
- The y-axis is defined as “a to the right,” with a notation indicating 90° east in the fundamental plane, while the az-axis aligns with Earth’s north polar axis.
This coordinate system is identical in all aspects to the ξ, η, ζ reference frame mentioned above, except that the origin is shifted to the center of the Sun. It is commonly employed in the calculation of planetary orbits. The three astronomical rectangular coordinate systems are interrelated through the following equation:
ξ = x + X η = y + Y ζ = z + Z \ xi = x + X \\ eta = y + Y \\\ zeta = z + Z \ end >>
See Also
Links
External links
- MEASUREMENT OF THE SKY A brief guide to the celestial sphere James B. Kahler, University of Illinois
- Celestial Equatorial Coordinate Explorers University of Nebraska-Lincoln
Determine the equatorial coordinates of the celestial bodies and, conversely, find a celestial body using the given coordinates. Test yourself using an electronic planetarium.
1. Determine the coordinates of stars:
2. Identify the stars based on the approximate coordinates:
3. Determine the equatorial coordinates and constellations they belong to:
1) the point of the fall equinox
2) The purpose of the winter solstice.
To accomplish the following tasks, let’s recall how to determine the position of the Sun. It is evident that the Sun always lies on the ecliptic line. Connect the calendar date with a straight line to the center of the map and the point where this line intersects the ecliptic is the Sun’s position at noon.
4. The Sun’s equatorial coordinates are α = 15 h, δ = -15°. Determine the calendar date and constellation in which the Sun is located.
A) November 21, Scorpio B) November 6, Libra C) October 22, Virgo
5. Determine the equatorial coordinates of the Sun on February 5.
A) α = 21 h, δ = 0° B) α = -15°, δ = 21 h C) α = 21 h, δ = -15°
6. The Sun’s right ascension is α = 10h 4min. Which bright star is near the Sun on this day?
A) α of Sextant B) α of Hydra C) α of Leo
To ascertain which celestial bodies are visible above the horizon at a specific moment, overlay a rotating circle onto the diagram. Align the time displayed on the circumference of the rotating circle with the date indicated on the periphery of the diagram, and the constellations that appear within the “window” will be those visible above the horizon during that time.
Throughout the course of the day, the celestial sphere completes a full rotation from east to west, while the observer’s horizon remains unchanged. By rotating the overhead circle in a clockwise direction to mimic the daily rotation of the celestial sphere, it becomes apparent that certain celestial bodies are rising above the horizon while others are setting.
As you continue to rotate the overhead circle clockwise, take note of the position of the circle when Aldebaran first becomes visible above the horizon. By determining the time indicated on the overhead circle for the desired date, you can ascertain the exact time of sunrise.
Additionally, you can determine on which side of the horizon Aldebaran rises. Similarly, you can establish the time and location of the star’s setting, and calculate the duration of time that the celestial body remains above the horizon.
- Which constellations above the horizon in our latitudes at 22 hours on June 25 cross the ecliptic?
9. Find the time of sunrise and sunset, as well as the duration of the day on June 22.
Remember the relationship that allows us to calculate the height of a luminary at its upper culmination based on its equatorial coordinates. Let’s consider the problem. Let’s write down the conditions: the latitude of Moscow ϕ = 55°; since we know the date – March 21 – the day of the vernal equinox, we can determine the declination of the Sun – δ = 0°.
- Does the Sun culminate to the south or north of the zenith? (Since δ < ϕ, the Sun culminates to the south).
- Which formula should be used to calculate the altitude?
- (h = δ + (90° – φ).
Practical work #1: Interactive starry sky map
Find the equatorial coordinates of the stars and vice versa, locate a star using the given coordinates. Verify your answers using an electronic planetarium.
1. Determine the coordinates of the stars:
2. Identify the stars based on the approximate coordinates:
3. Find the equatorial coordinates and indicate the constellations they belong to.
To complete the following tasks, let’s review how to determine the position of the Sun. We know that the Sun is always on the ecliptic line. Draw a straight line from the calendar date to the center of the map, and the point where this line intersects with the ecliptic represents the Sun’s position at noon.
4. The Sun is located in the constellation Aquarius on February 20.
5. The bright star α Virgo (Spica) is near the Sun on October 12.
6. The bright star α Gemini is close to the Sun on the day when the Sun’s direct ascension α is 7h 50min.
To determine which luminaries are above the horizon at a given time, you can use a moving circle overlaid on a map. By matching the time indicated on the edge of the moving circle with the calendar date marked on the edge of the map, you can see the constellations above the horizon at that time through the “window”.
Throughout the course of a day, the celestial sphere completes a full revolution from the east to the west, while the observer’s horizon remains fixed. If you were to rotate the circle above your head in a clockwise direction to simulate the daily rotation of the celestial sphere, you would observe certain stars and celestial bodies rising above the horizon while others set. As you continue to rotate the circle clockwise, take note of the moment when Aldebaran first becomes visible above the horizon. Look for the corresponding time marker on the circle overhead to determine the exact time of sunrise. Also, determine on which side of the horizon Aldebaran emerges. In a similar fashion, establish the time and location of the star’s setting and calculate how long it remains above the horizon.
7. The constellations that cross the equator and are above the horizon in our latitudes at 22 hours on January 25 are:
A) Sextant B) Gemini C) Orion D) Aries
8. Find out the time of sunrise and sunset and the duration of the day on September 21?
9. Find out the time of sunrise and sunset and the duration of the day on June 22?
Let’s recall the relationship that allows us to calculate the height of a luminary in its upper culmination based on its equatorial coordinates. Let’s consider the problem and write down the given conditions: the latitude of Moscow is ϕ = 55°, and the date is March 21, the day of the vernal equinox. Therefore, we can determine the declination of the Sun, which is δ = 0°.
- Does the Sun culminate to the south or north of the zenith? (Since δ < ϕ, the Sun culminates to the south).
- What is the appropriate equation for determining the altitude?
- (h = δ + (90˚ – φ).
- Compute the altitude of the Sun. h = 0 ° + 90 ° – 55 ° = 35 °
Regarding: methodical developments, presentations, and notes

Development of a segment of hands-on activity for 7th grade students. The subject of the educational hands-on activity: Analyzing the characteristics of major landforms on maps and comparing the Earth’s crust structure map with the physical map
Creation of a segment of hands-on activity for 7th grade students. Curriculum: Sample curriculum for fundamental geography education “Geography of the Earth” (6-7 grades) / compilation of regulatory documents: Г.
Practical exercise “A funny sequence of images”
Acquiring skills in using Microsoft Word. Incorporating visual elements within the document.

Practical exercise: “Navigating with Maps”
This hands-on activity is divided into two sections. The initial section is a quiz, while the second section focuses on problem-solving techniques such as determining geographical coordinates and identifying geographical landmarks. This exercise can be utilized during a classroom session.

Practical exercise “Determining geographical coordinates and distances on maps and globes”.
Calculating geographical coordinates and distances using maps and globes.

Practical work on a contour map: a necessary requirement.
This guide is intended for 6th grade students who are engaged in working on a contour map.

Practical exercise “Russia’s Time Zone Placement”
The practical exercise “Russia’s Time Zone Placement” offers a way to assess the understanding students have gained on this particular subject.

Practical exercise “Measuring distances between points on maps in degrees and kilometers”
Measuring distances between points on maps in both degrees and kilometers.
The equatorial coordinate system is based on spherical coordinates. It is defined by projecting the Earth’s equator onto the celestial sphere, creating the celestial equator. The primary reference direction is established by projecting the Earth’s orbit onto the celestial sphere, resulting in the ecliptic. The ascending node of the ecliptic is set on the celestial equator, creating the point of the vernal equinox. To measure positions in this system, right ascension is measured eastward along the celestial equator from the vernal equinox point, while declination is measured positively north of the celestial equator. (Two sets of coordinates are displayed here.) The projections of the Earth’s north and south geographic poles form the north and south celestial poles, respectively.
The equatorial coordinate system is a popular method for determining the position of celestial objects. This system can be represented using either spherical or rectangular coordinates, with a coordinate origin at the center of the Earth. The fundamental plane of this system is formed by projecting the Earth’s equator onto the celestial sphere, creating the celestial equator. Additionally, the primary direction is defined as the point of the vernal equinox, and the system follows a right-handed agreement.
The primary direction of cardinal points
This description of the orientation of the reference frame is somewhat simplified; the orientation is not exactly fixed. The gradual movement of the Earth’s axis, known as precession, causes the coordinate system to slowly rotate, continuously moving westward around the poles of the ecliptic, completing one revolution in approximately 26,000 years. Overlaying this movement is a smaller shift of the ecliptic and a slight wobble of the Earth’s axis, referred to as nutation.
In order to determine the precise primary direction, these movements necessitate the use of the equinox point on a specific date, referred to as the epoch, when specifying the position. The three most commonly utilized are:
The standard epoch mean equinox (usually J2000.0, but may include B1950.0, B1900.0, etc.) serves as a fixed reference point that enables direct comparison of positions determined on different dates. The mean equinox of a specific date represents the point where the ecliptic of that date (i.e., the position of the ecliptic at that specific date) intersects with the mean equator (i.e., an equator adjusted for precession to its location on the given date, without the small periodic nutation oscillation). This concept is commonly employed in the calculation of planetary orbits. On the other hand, the true equinox date refers to the point where the ecliptic of the specific date intersects with the true equator (i.e., the mean equator plus nutation). It represents the actual intersection of the two planes at any given moment, taking into account all motions.
The usual method for determining the position in the equatorial coordinate system is by using either the true equinox and equator of the date, mean equinox and equator of J2000.0, or a similar reference point. It’s important to note that the equatorial coordinate system does not include a “mean ecliptic” because the ecliptic does not experience small periodic fluctuations.
Coordinates in the shape of a sphere
Application in astronomy
When discussing the spherical coordinates of a star, it is common to represent them as a pair known as right ascension and declination, without including distance coordinates. For all observers, the direction of objects that are sufficiently far away remains the same, making it convenient to establish uniform coordinates for this direction. In contrast, the horizontal coordinate system shows that the position of a star varies for each observer depending on their location on Earth’s surface, and it also changes continuously due to Earth’s rotation.
Telescopes equipped with equatorial mounts and mounting circles utilize the equatorial coordinate system to locate objects. By using setting circles in conjunction with a star chart or ephemeris, it becomes effortless to point the telescope towards known objects on the celestial sphere.
Parallax
Parallax symbol p (lowercase “pi”, abbreviated PAR) calculates the horizontal distance to an object perpendicular to the celestial meridian, positive to the east and negative to the west. For instance, the prime meridian has a parallax of + 0°. The origin of parallax is the celestial meridian, which is the projection of the Earth’s meridian onto the celestial sphere. Parallax is similar to Earth’s longitude.
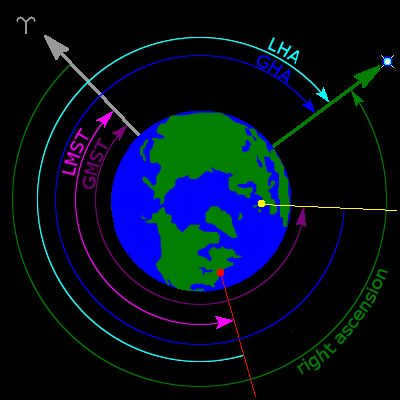
The image above depicts the North Pole of the Earth, along with the Local Hour Angle (LHA) of the stars for an observer near New York City. It also illustrates the Direct Ascension of the stars and the Greenwich Mean Time Angle (GMT), as well as the Local Mean Sidereal Time (LMST) and the Greenwich Mean Stellar Time (GMST). The symbol ʏ indicates the direction of the vernal equinox.
The symbol for direct ascension α (lower case “alpha”, abbreviated RA) represents the angular distance of an object moving eastward along the celestial equator from the vernal equinox point to the hour circle that passes through the object. The vernal equinox point is one of the two points where the ecliptic intersects the celestial equator. Direct ascension is typically measured in sidereal hours, minutes, and seconds instead of degrees, which is the outcome of timing the passage of objects through the meridian as the Earth rotates. There are 360° / 24 h = 15° for one hour of direct ascension and 24 hours of direct ascension around the entire celestial equator.
When used in combination, direct ascension and declination are usually abbreviated as RA / Dec.
Hour angle
Instead of using direct ascent, the hour angle (abbreviated HA or LHA, local hour angle) is a method of measuring the angular distance of an object in the left-hand system that is located westward along the celestial equator from the observer’s meridian to the hour circle passing through the object. Unlike direct ascent, the hour angle always increases as the Earth rotates. The hour angle can be seen as a way of measuring time from the point of upper culmination, which is the moment when an object reaches the meridian directly overhead.
The star that reaches its highest point in the sky directly above the observer is known as the culminating star. At this point, the star has a zero hour angle (0 h). As the Earth continues to rotate, the star will move to the west of the observer’s meridian after approximately one sidereal hour (equivalent to 0.9973 solar hours). At this time, the star’s hour angle will be 1 hour. When calculating topocentric phenomena, it is possible to convert the star’s right ascension to hour angle as an intermediate step.
Coordinates in a geocentric equatorial system
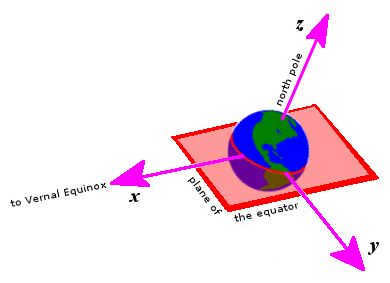
The geocentric equatorial coordinates are determined with the center of the Earth as the origin. The principal plane corresponds to the Earth’s equator. The principal direction is determined by the vernal equinox. In the right-handed convention, the y axis is set to the east in the main plane, while the z axis represents the north polar axis. Unlike the Earth, the reference frame does not rotate; instead, the Earth rotates about the z axis.
There are several variations of rectangular equatorial coordinates, all of which share the following characteristics:
- The origin is located at the center of the Earth.
- The primary plane coincides with the Earth’s equator.
- The primary direction (axis x) is towards the point of the vernal equinox, which is where the Sun crosses the celestial equator in a northerly direction along its annual apparent circle around the ecliptic.
- Using the right hand convention, point the у axis 90° eastward in the principal plane and the г axis along the north polar axis.
Reference frames do not rotate with the Earth (in contrast to Earth-centered, Earth-fixed frames), but instead always point towards the equinoxes and drift in time with the movements of precession and nutation.
- In astronomy:
- The position of the Sun is commonly represented by geocentric equatorial rectangular coordinates X, Y, and Z, as well as the distance coordinate R (= √X^2 + Y^2 + Z^2), measured in astronomical units.
- Planets and other bodies in the solar system are often described using geocentric equatorial rectangular coordinates ξ, η, and ζ, along with a distance coordinate Δ (equal to √ξ^2 + η^2 + ζ^2) in astronomical units.
- The Geocentric Celestial Reference Frame (GCRF) is a geocentric version of the International Celestial Reference Frame (ICRF). It is oriented with respect to the equinox from J2000.0 and remains fixed with respect to precession and nutation. However, it is otherwise identical to the aforementioned systems.
| α | Δ | ξ , η , ζ | X , Y , Z (Sun) |
| x , y , y | |||
Heliocentric equatorial coordinates
In the field of astronomy, there is an alternative form of equatorial coordinates known as the heliocentric rectangular system. This system is represented by the variables x, y, and z, and it possesses the following characteristics:
- The origin is located at the center of the Sun.
- The main plane coincides with the plane of the Earth’s equator.
- The primary direction (axis x) points towards the vernal equinox.
- By convention, using the right-hand rule, the y axis points 90 degrees eastward in the primary plane, while the z axis aligns with the Earth’s north polar axis.
This frame of reference is identical to the coordinate system of ξ, η, ζ described above, except that the origin is shifted to the center of the Sun. It is commonly utilized in the calculation of planetary orbits. The three astronomical rectangular coordinate systems are interconnected by the equation
ξ equals X + X, η equals y + Y, ζ equals z + Z \ xi & = x + X \\\ eta & = y + Y \\\\ zeta & = z + Z \ end >>