
The Moon is the biggest celestial body in the night sky. The ancient Greeks were able to estimate the rough size of the Moon.
The Moon is the fifth largest natural satellite in our Solar System, coming after the three satellites of Jupiter and one satellite of Saturn in terms of size. The Moon is slightly smaller than Mercury, which is the smallest planet, and half the size of Mars. When compared to its planet, the Moon is the largest among all satellites.
Size
Due to its rotation, the Moon is somewhat compressed at the poles, with a diameter of 3471.94 km at the pole line and 3476.28 km at the equator line. This is approximately one-fourth the size of the Earth’s diameter. As the Moon is spherical in shape, we can also determine other geometric measurements: the circumference of the Moon’s equator is 10920 km, the volume of the Moon is one-fiftieth that of the Earth, and the surface area is thirteen times smaller than that of the Earth.
Angular size

Dimensions of the Moon at its farthest and closest points
As the Moon follows its elliptical orbit, its angular diameter ranges from 33'40" at perigee, the closest point, to 29'24" at apogee, the farthest point. When the Moon is positioned low on the horizon, it appears larger than when it is directly overhead, a phenomenon that is still not fully understood. Interestingly, the Moon’s angular size is almost the same as that of the Sun, which allows for total solar eclipses when the Moon completely obscures the Sun’s disk.
How the size of the Moon was determined
In the 3rd century BC, Aristarchus of Samos became the first person to attempt to measure the diameter of the Moon. He used measurements taken during a solar eclipse and applied Euclidean geometry to calculate its size. However, due to measurement error, his calculations turned out to be inaccurate.
One hundred years later, Hipparchus made a new calculation and determined that the diameter of the Moon is 3.5 times smaller than that of the Earth. If you found this post interesting, don’t forget to share it with your friends!

- The Solar System
The moon is the Earth’s sole natural satellite. It is the closest planetary satellite to the Sun, as Mercury and Venus, the planets closest to the Sun, do not have any. It is the second most luminous object in the Earth’s sky, right after the Sun. Furthermore, it is the fifth largest natural satellite of a planet in the entire solar system. The average distance between the centers of the Earth and the Moon is 384,467 kilometers (0.00257 astronomical units, approximately 30 Earth diameters).
The Russian word Luna originates from the term for “light.” The Greeks referred to the Earth’s satellite as Selene, while the ancient Egyptians called it Yah, and the Babylonians named it Sin.
The Moon possesses numerous unique characteristics: its luminosity in the sky, its gravitational impact on our planet, its lesser-known hidden side, and its origin.
The majority of the legal matters pertaining to lunar exploration were resolved with the adoption of the Treaty on Principles Governing the Activities of States in the Exploration and Use of Outer Space, including the Moon and Other Celestial Bodies in 1967.
Furthermore, the legal standing of the Moon is delineated in the Moon Agreement of 1979.
As the nearest and most extensively researched celestial entity, the Moon is considered a potential site for human colonization.
Research History
Astronomers from the Ancient World have been observing the Moon’s movements in the sky for a long time. Hipparchus, in the 2nd century BC, was one of the first to study the Moon’s motion across the starry sky. He determined the inclination of the lunar orbit in relation to the ecliptic, as well as the Moon’s size and distance from Earth. Additionally, he identified several features of the Moon’s motion.

During the medieval era, explorers utilized the telescope to examine various regions of the moon’s surface and create the initial lunar map.
Giovanni Riccioli was one of the pioneers in lunar mapping, producing his first map in 1651 and referring to the vast dark areas as “seas”.
In the 19th century, the first photographic images of the moon’s surface were captured, leading to the compilation of a photographic atlas.
The advent of spacecraft technology significantly expanded our understanding of the moon. Starting in 1958, both Soviet and American explorers sent numerous automated and manned vehicles, satellites, and lunar rovers to the moon, which marked the famous “Moon Race” in history.
In 1959, the back side of the moon became visible for the first time when the Soviet station Luna-3 flew over the Moon and captured images of a portion of its surface that was not visible from Earth.
The American initiative to send astronauts to the Moon was known as the “Apollo” program. The initial landing took place on July 20, 1969, with subsequent landings occurring until December 1972.

Neil Armstrong, an American astronaut, became the first person to step foot on the Moon on July 21, 1969. His fellow astronaut, Edwin Aldrin, followed shortly after, making him the second person to do so. The third member of their crew, Michael Collins, remained in the orbiter.
Years later, in August 1976, the Soviet station Luna-24 successfully transported lunar soil samples back to Earth. However, it wasn’t until 1990 that the next spacecraft, the Japanese Hiten satellite, made its journey to the Moon.
Fast forward to January 3, 2019, when history was made once again. The Chinese landing module Chang’e-4, along with the Chinese lunar rover Yutu-2, successfully achieved a soft landing on the far side of the Moon, marking the first time this had ever been accomplished.

An exclusive biological experiment was conducted by the landing module, focusing on the cultivation of potatoes, Arabidopsis, rapeseed, cotton (only cotton was able to be germinated), and the breeding of Drosophila flies, as well as yeast.
Various nations are currently engaged in lunar exploration through the use of multiple lunar rovers and orbital probes. Additionally, private companies have begun their own investigations of the Moon, with plans to offer space tourism opportunities that include flights around the Moon using Russian spacecraft.
Dimensions and weight of the Moon

It is important to analyze the characteristics and parameters of the Moon. In terms of shape, the Moon closely resembles a sphere, with an average radius of 1738 kilometers, which is approximately 3.68 times smaller than the radius of the Earth.
The volume of the Moon is 2.2 × 1010 km3, and its surface area is 3.769 × 107 km2. The mass of Earth’s satellite is 7.3476*1022 kg, which is 81.3 times less than the mass of the Earth. The angular radius of the Moon’s disk visible from Earth (at the average distance between them) is 31’05”.
The density index of the Moon is 3.35 g/cc, which is the second highest among all moons, second only to Io. The acceleration of free fall at the Moon’s surface is g = 1.63 m/s.q., which is approximately 17% of Earth’s. It is believed that the Moon did not have an atmosphere, as its gravity was not strong enough to hold one.
Movement of the Moon
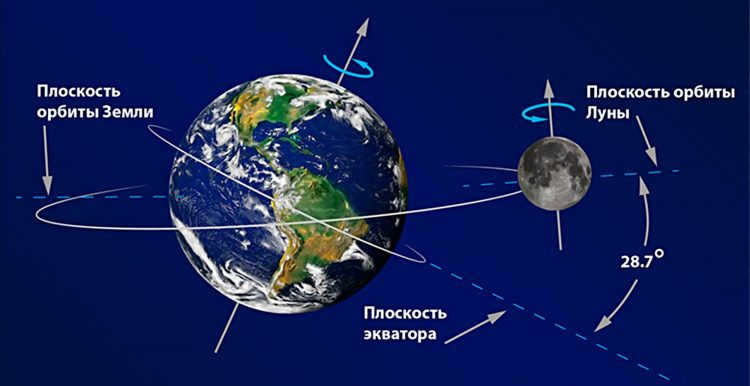
The Moon revolves around the Earth in an orbit with a major semi-axis of 383,000 km (eccentricity 0.055). The inclination of the lunar orbit to the ecliptic plane is 5°09.
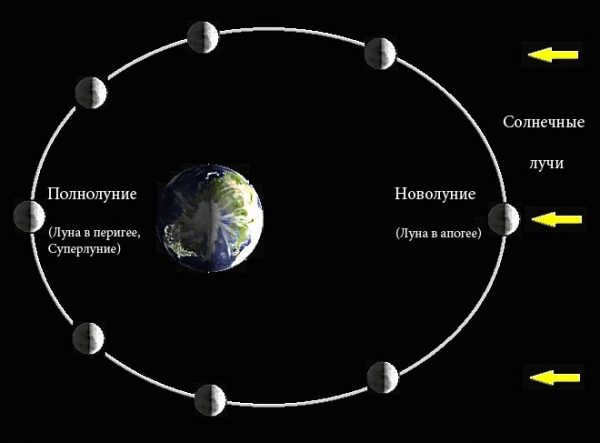
The size of the lunar orbit changes periodically: perigee is 363.10 thousand kilometers, apogee is 405.70 thousand kilometers.
The rotation period is 27 days, 7 hours, 43 minutes. This is the sidereal period. The synodic period – the period of lunar phases is 29 days 12 hours 44 minutes.
The rotation period of the Moon around its axis is equal to the sidereal period.
Due to the fact that the duration of one complete rotation of the Moon around the Earth is precisely equal to the duration of one complete rotation of the Moon around its own axis, the Moon consistently presents the same side towards the Earth.
After the Sun, the Moon is the most prominent celestial object in the sky. It has a stellar magnitude of up to 12.7m.
The Moon has an eccentricity of 0.0549, and its orbital path spans from Z56400 to Z70400 km at perihelion and from 40400 to 406700 km at aphelion. It takes approximately 27.Z21582 days for the Moon to complete one orbit around the Earth. Additionally, the Moon is tidally locked, meaning that it always presents the same face to us.
Surface Characteristics of the Moon
The Moon’s surface can be classified into two distinct types:
- An ancient mountainous region with a vast number of craters, resembling lunar continents.
- Relatively flat and comparatively young lunar seas.
Lunar seas, comprising approximately 16% of the Moon’s surface, are large impact craters that were subsequently filled with lava.
Researchers at the Paris Institute of Physics of the Earth hypothesize that about 3.9 billion years ago, a collision between the Moon and a massive asteroid resulted in a significant transformation of the Moon’s surface.
A significant part of the lunar surface is coated with regolith, which is a blend of fine particles and rocky debris resulting from meteorite crashes. The depth of the regolith layer varies from a few centimeters to several meters.
Curiously, the lunar maria are predominantly located on the near side of the Moon, for reasons that have yet to be discovered.

The majority of the craters located on the far side are named after prominent figures in the fields of science, physics, and astronomy, such as Tycho Brahe, Copernicus, and Ptolemy. The geographical features on the far side have more contemporary names like Apollo, Gagarin, and Korolev – predominantly Russian names, as the initial photographs were captured by the Russian Luna-3 spacecraft.
Within the far side of the Moon lies a massive crater basin that spans 2,250 kilometers in diameter and reaches a depth of 12 kilometers – making it the largest impact basin within the entire solar system.
Additionally, the lunar furrows, which include domes, ridges, plains, and fissures, help to distinguish the smaller details of the lunar terrain.
Until lunar soil samples were collected, scientists had limited knowledge about the formation of the Moon, including the time and manner in which it was formed.
Map
The moon’s terrain is one-of-a-kind and unlike any other. It is adorned with craters of varying dimensions – ranging from minuscule to hundreds of kilometers wide. For a considerable duration, researchers were unable to gather data about the far side of the Moon. This only became feasible with the arrival of spacecraft.
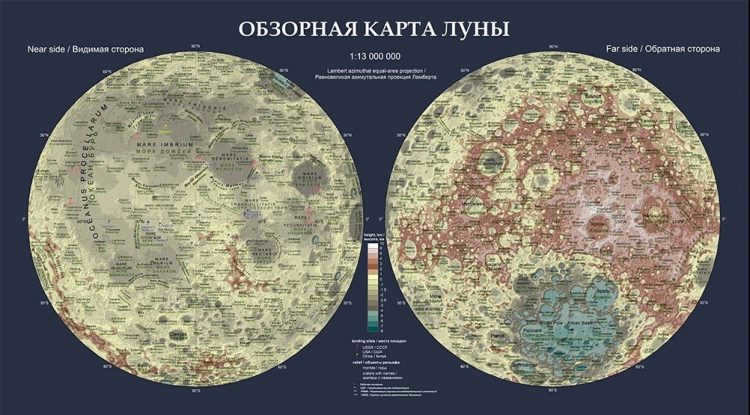
There are now highly detailed maps available for both the northern and southern hemispheres of the moon. The creation of these detailed lunar maps is essential in order to properly plan for future human missions to the moon, including the establishment of lunar bases, telescopes, transportation systems, and the search for valuable minerals.
Internal composition
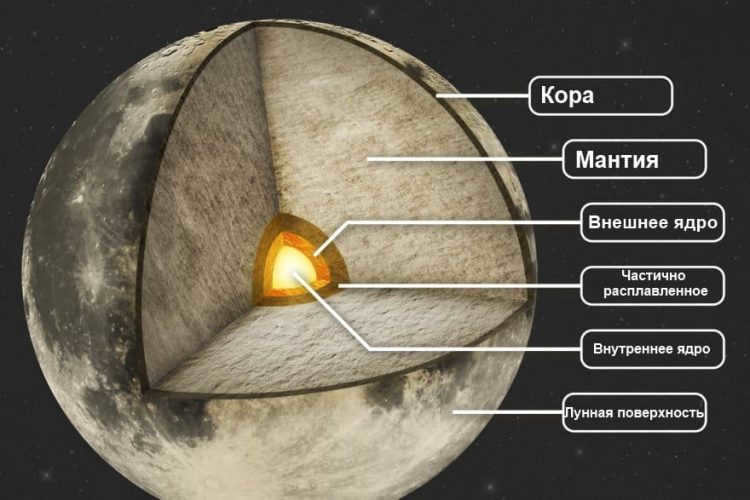
Because of its size and composition, the Moon is sometimes classified as a member of the earth group of planets. By examining the geological makeup of the Moon, we can gain valuable insights into the structure and evolution of the Earth.
The Moon’s density is similar to that of the Earth’s mantle, suggesting that it has either a minimal or nonexistent iron core. Scientists have studied the internal composition of the Moon using seismic data collected by devices from the Apollo space missions. The Moon’s crust has an average thickness of 68 km, ranging from 0 km beneath the lunar Crisis Sea to 107 km in the northern part of Korolev Crater on the far side.
The upper part of the Earth’s mantle is approximately 400 kilometers thick. Within this layer, seismic velocities change depending on depth and decrease with distance. The middle portion of the mantle has a thickness of about 600 kilometers, and within it, seismic velocities remain constant. The lower mantle is located below a depth of 1100 kilometers.
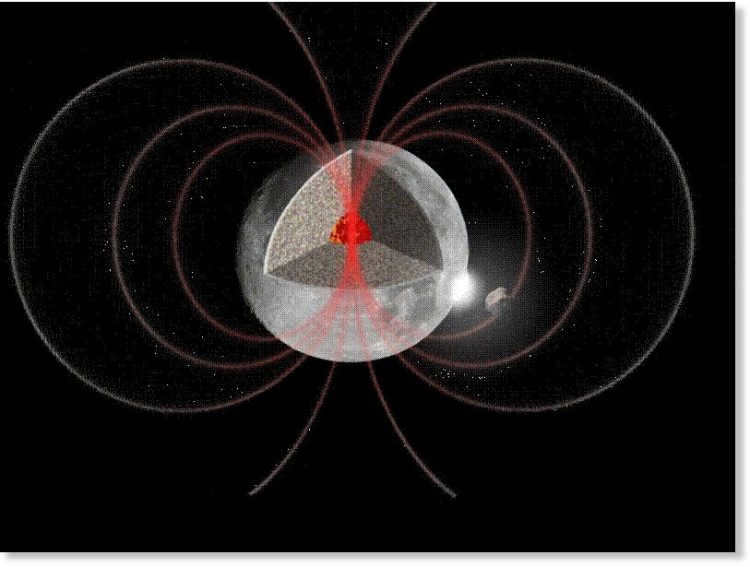
Starting at a depth of 1500 kilometers, the core of the Moon is believed to be in a liquid state. Interestingly, it contains very little iron, resulting in a weak magnetic field that is only about one ten-thousandth of the Earth’s magnetic field. Some localized magnetic anomalies have also been detected.
The composition of the lunar soil varies significantly between the Moon’s marine and continental regions. Lunar rocks contain very little water and are also depleted in iron and volatile elements.
Caves
In 2009, a hole in the Moon’s surface near the volcanic plateau of Marius Hills was discovered by the Japanese Kaguya probe. This hole is thought to lead to a tunnel beneath the surface and has a diameter of approximately 65 meters with a depth of around 80 meters.
It is believed that these tunnels are created when streams of molten rock cool and solidify, forming a central core of lava. These geological processes took place during a period of volcanic activity on the Moon.

Tunnels like these can be used for colonization purposes since they provide protection from solar radiation and a controlled environment that makes it easier to sustain life support conditions.
Similar openings can also be found on Mars.
Moonquake
The fluctuations on the lunar surface can last for over an hour, making them long-lasting.
There are four categories of lunar shaking:
- Tidal quakes occur twice a month and are caused by the tidal forces of the Sun and Earth;
- Tectonic quakes are irregular and caused by ground motions on the Moon;
- Meteoric quakes happen due to impacts from meteorites;
- Thermal quakes are a result of the sudden heating of the lunar surface during sunrise.
The most significant risk to potential manned stations on the moon is posed by tectonic lunar tremors. Over the course of five years of research, NASA seismographs have detected a total of 28 of these lunar tremors. Some of these tremors have reached a magnitude of 5.5 and have endured for more than 10 minutes. In contrast, earthquakes of this magnitude on Earth typically last no longer than two minutes.
The Atmosphere of the Moon

The Moon possesses a delicate exosphere, giving rise to a wide range of temperature variations, spanning from -15Z°C to 107°C. Scientific examination discloses the existence of helium, neon, and argon. Helium and neon are primarily generated by solar winds, while argon is produced through the decay of potassium. Furthermore, there are indications of frozen water within the lunar craters.
Physical characteristics of the Moon
The gravitational field of the Moon has been extensively researched, as it provides valuable insights into the Moon’s structure and is essential for space exploration. These studies have revealed that the gravitational field is not centrally located, which is attributed to variations in subsurface density.
The surface gravity of the Moon is approximately 1,623 m/s2, which is about six times weaker than that of the Earth.
The Moon’s magnetic field is relatively weak, estimated to be around 0.1% of the Earth’s magnetic field. This translates to a magnetic field strength of no more than 0.5 gamma.
There is currently no available data on the measurement of the electric field at the surface of the Moon. However, theoretical predictions suggest that due to the strong gravitational pull from the Earth, there may be a redistribution of electric charges within the Moon. This redistribution could potentially lead to the formation of an electric field over the Moon’s surface, with certain points experiencing a strength of around a kilovolt per meter.
The Moon emanates brightness by reflecting sunlight from its surface. The Moon’s visual spherical albedo is measured to be 0.075, indicating that it reflects only 7.5% of the sunlight that reaches it.
The brightness of the Moon is most pronounced when it reflects light from an external source, such as during a full moon. The Moon’s own thermal radiation is minimal, with a temperature not exceeding 100 K.
Theories regarding the origin of the Moon
Hypothesis of a significant collision
This is the predominant concept that garners the greatest amount of support.

The Earth originated from a cloud composed of dust and gas. During that time, the solar system experienced intense celestial battles, with objects constantly colliding, merging, and altering their orbits. One of these objects collided with the Earth, which was still in the process of formation.
The impactor responsible for this event is known as Teia.
This collision caused fragments of the Earth’s crust to separate. Gravity then began pulling these fragments back together until they formed a solid mass. This phenomenon explains why the Moon is composed of lighter elements and is less dense compared to the Earth.
As the material concentrated around the remaining core of Teia, it remained close to the plane of the Earth’s ecliptic and eventually became the Moon.
Co-formation
can be restated as the process of creating something together.
Both a planet and a satellite can come into existence simultaneously. This means that gravitational forces caused the fragments to coalesce, resulting in the formation of two objects in tandem.
In such a scenario, the satellite would possess a composition akin to that of the planet and would be situated in close proximity. However, the Moon is still less dense, which defies expectations if they indeed share the same abundance of heavy elements in their cores.
Seize

The Moon’s history suggests that Earth’s gravity might have captured a passing celestial body, similar to what happened with the Martian moons Phobos and Deimos. This rocky object could have originated from another part of our solar system and subsequently been pulled into Earth’s orbit.
This theory helps to explain the differences in composition between the Moon and Earth. However, there are some inconsistencies, as objects captured in this way often have irregular shapes rather than being spherical. Additionally, the orbital path of the Moon does not align with the ecliptic plane.
Astrological Significance of the Moon
Although the Moon is technically a satellite of the Earth, it is often referred to as a planet in astrology to prevent any confusion. The Moon plays a significant role in shaping our lives and influences our moods, emotions, and sense of devotion. It is particularly associated with femininity and motherhood and is a dominant factor in the natal chart.

The emotional response to global events is depicted by the Moon, as it influences and motivates actions. The Moon is also a symbol of the mother-child relationship, and in men’s horoscopes, it represents the spouse, pregnancy, and intuition.
By paying attention to the Moon, one can gain a holistic understanding of the world rather than focusing on individual parts. The Moon encourages individuals to strive for their dreams instead of conforming to societal expectations.
The Moon is particularly influential in occupations related to navigation and maritime professions.
All the female reproductive organs are under the influence of the Moon. The health conditions that occur in women are directly related to the characteristics of the Moon. The cycle and duration of the Moon’s orbit around each zodiac sign is 28 days.
The Moon holds significant importance in Vedic astrology. It brings financial prosperity and comfort, and it governs an individual’s life. The position of the Moon at the time of birth influences one’s perception of reality. The Moon’s phase at birth, whether it was decreasing or increasing, is also very important.
Fascinating information
- The Moon has an average diameter of 3475 kilometers, making it the fifth largest satellite in the solar system. It is smaller than Ganymede, Titan, Callisto, and Io.
- The Moon has a mass that is 81 times less than that of the Earth and a volume that is almost 50 times smaller.
- The Moon has a surface area of 58 million square kilometers, which is larger than Africa but smaller than Asia.
- Based on radioisotope analysis of lunar samples, Tycho Crater and its famous ray system formed approximately 108 million years ago, during the time of the dinosaurs on Earth.
- Although the Moon may appear as a luminous celestial object, its actual surface reflectivity, known as albedo, is only 13%. This is nearly three times lower than the Earth’s albedo. Consequently, photographers often intentionally enhance the Moon’s brightness in their pictures.

- More than 40% of the visible side of the Moon is covered by lunar seas, which are dark areas with frozen lava deposits.
- The far side of the Moon is significantly different from the visible side. It has higher elevation on average and is home to most of the largest lunar craters, but it only has two lunar seas.
- Currently, the Moon does not have a magnetic field. However, analysis of lunar soil samples has revealed that it had a magnetic field in the past, which was even stronger than Earth’s.
- The Moon experiences lunar tremors, although they are much weaker compared to those on Earth. The strongest recorded lunar tremor had a magnitude of 5.5 on the Richter scale. The causes of these lunar “earthquakes” are still unknown.
- The Soviet spacecraft Zond-5, launched on September 15, 1968, carried a diverse group of organisms on its mission to the Moon. Among the passengers were Central Asian steppe turtles, Drosophila flies, beetles, various plants, seeds, and microorganisms.

- Throughout history, a mere 12 individuals have had the opportunity to step foot on the Moon. A grand total of 24 astronauts have been fortunate enough to partake in expeditions to our celestial neighbor.
- The sole individual laid to rest on the Moon is the renowned American astronomer and geologist Eugene Shoemaker. Unfortunately, health complications prevented him from embarking on interplanetary voyages. Following his passing, his ashes were transported to the Moon in 1998 via the Lunar Prospector interplanetary research station.
- The Moon is gradually distancing itself from our planet at a rate of approximately 3.8 centimeters per year. In approximately 600 million years, its apparent size in the sky will diminish to such an extent that observing total solar eclipses from Earth will become an impossibility.
- Moisture is absent on the Moon and the soil is entirely devoid of moisture, thereby preventing any growth. However, examination of lunar soil samples returned to Earth reveals that it possesses the necessary qualities for cultivating plants.
- In comparison to the computers utilized during the Apollo moon landing, present-day smartphones possess significantly greater power.
Video
can be rephrased as
Visual content
The vertical angle above the horizon of the celestial body a is defined as the altitude, and it is measured by the angle with its vertex at O and resting on the arc XB. The horizontal angle A is known as the azimuth, and it is measured by the angle with its vertex at O and resting on the arc NB. Therefore, the altitude indicates the “height” of the celestial body in degrees (with altitude below the horizon considered negative), while the azimuth indicates the direction of the celestial body relative to the northward direction; the azimuth is also measured in degrees.
The angle A increases from O to 360° as you turn in the north-east-south-west direction. At a northerly point, the azimuth is 0°, at a southerly point it is 180°, and so on.
Coordinates in the equatorial system
Equatorial coordinates, as their name implies, are determined with respect to the plane of the Earth’s equator (refer to the figure). The observer is located at point O, the horizon is the plane that contains the NESW circle, and point Z represents the zenith.
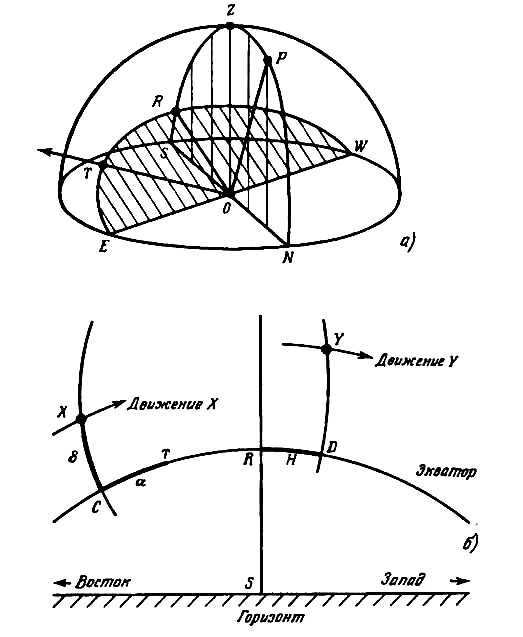
Figure 6. Equatorial coordinates: a on the celestial sphere; b as seen from Earth.
Let’s imagine that our illustration represents a view of the Earth from a very far distance. The Earth, along with the person observing it, becomes a point at the center of the illustration. The equatorial plane can be extended to intersect the celestial sphere at the great circle E♈RW. This plane is known as the equatorial plane and it is inclined to the horizon plane at an angle of (90° – ϕ), where ϕ represents the geographic latitude of the observer. For instance, if the observer is located at a northern latitude of 52°, this angle would be 38°. The Earth’s axis of rotation, which is perpendicular to the equatorial plane and crosses the celestial sphere at point P – the North Pole, can be found along the line OR. Since the Earth rotates around this line, it appears to us that all the stars move in circular paths around point P. Figure 6, b illustrates what an observer O sees when looking at the sky. In addition to the point south S on the horizon, the figure also displays an imaginary equatorial line C♈RD. The arc that runs downward through points R and S is a part of the large NPZRS circle shown in Fig. 6, а. The arc XC is part of another large circle that is not labeled in Fig. 6, a, and it passes through points R, X, and C. Let’s consider a star located at point X. The arc XC, or the angle centered at O that rests on this arc, is referred to as the declination δ of point X. It determines “how high” or “how far north” the star is located from the plane of the equator. The other coordinate, which determines “how far apart”, is measured from a specific point in the sky denoted by the symbol ♈. This point is known as the vernal equinox, and its position is determined by the intersection of the Earth’s equator and the ecliptic – the Earth’s orbit around the Sun. However, we won’t need this definition for now. Just remember that the position of the point ♈ remains constant in relation to the stars, and it is from this point that we measure the second coordinate. This coordinate is called the right ascension a and is determined by the size of the angle centered at O that rests on the arc ♈C. As time goes by, the star X moves westward along a circle centered at P, completing one revolution every 24 hours in sidereal time. Since the plane of this circle is parallel to the equator, the declination remains unchanged. Furthermore, since the point ♈ maintains a fixed position in the sky, it must move along the equator at the same angular velocity as the star X along its circle. As a result, the right ascension of star X also remains constant. Thus, α and δ are considered to be ideal coordinates for describing the position of stars and other “fixed” celestial bodies.
Aside from the direct ascent, there is another measure known as the hour angle. This measure, denoted as H, indicates the lateral position of a point (refer to Fig. 6, b). For star Y, the hour angle is determined by the angle formed at point O, resting on arc RD. It represents the star’s distance traveled along the equator from point R in the southern direction. In essence, the hour angle H serves as a measurement of the time elapsed since the star crossed the meridian. As time progresses, the value of H increases uniformly and reaches zero when the star intersects the great circle NPZRS (refer to Fig. 6, a). This great circle is known as the meridian, and the point where the star intersects it is referred to as its culmination or passage through the meridian. At this moment, the celestial body’s altitude is at its maximum, and the azimuth measures 180° (assuming the star’s declination is lower than the geographic latitude).
Declination is a measurement that is expressed in degrees and is considered positive when north of the equator and negative when south of the equator. Hour angle and right ascension can also be measured in degrees, ranging from 0 to 360°. The angle a is measured in a way that increases eastward from the point ♈, with the value 0 at the point ♈ itself. (It is important to note that this direction is opposite to the direction in which H is counted). However, it is more commonly measured in hours, minutes, and seconds, ranging from 0 to 24 hours. A complete revolution (360°) corresponds to 24 hours of sidereal time, meaning that 1 hour corresponds to 15°. The statements “the right ascension of star X is 90°” and “the right ascension of star X is 6 hours” are completely equivalent. To convert between units, it is sufficient to divide or multiply the corresponding values by 15.
The convenience of measuring the direct ascension in hourly intervals is determined by the fact that at the moment of culmination, the local sidereal time is equal to the direct ascension.
The planet’s phase
The measurement of a planet’s phase is based on the ratio of the illuminated area of its visible disk to its total area. The phase angle is the angle between the direction from the planet to the Sun and the Earth. When the phase angle is f = 180° (the planet is between the Sun and the Earth), the phase is zero, as the half of the planet facing the Earth is not illuminated at all (this is known as a new moon for the Moon).
When the Earth and the Sun are on the same side of the planet (at phase angle f = 0), the phase is equal to 1, which means that the visible disk of the planet is fully illuminated. This moment is known as a full moon for the Moon. In the general case, the relationship between phase F and phase angle f is determined by the following formula:
The phase angle for the lower planet ranges from 0° (upper conjunction) to 180° (lower conjunction), resulting in phases ranging from zero to one.
On the other hand, the phase angle for the upper planets never exceeds the maximum value, which occurs at quadrature moments when the Earth is seen from the planet at its greatest distance from the Sun.
For Mars, this maximum value is no more than 48°, for Jupiter it is 11°, and for all other planets it is less than 11°.
As a result, the phase for Mars is always at a minimum of 0.84, while for the other outer planets it is very close to one.
Syntax
For XMPP clients, astroda is used;
A date can be specified in the format DD.MM.YYYY.HH.mm.ss
where DD represents the date, MM is the month, YYYYY is the year, mm is the minute, and ss is the second.
and city refers to any populated area in the world.
–> Astronomical parameters of the Moon. This includes the phase, distance to Earth, declination, moon azimuth, phase, and coordinates.
- Russian and English alphabets combined in one line
- Online hour and minute hand. Find the angle between them.
- Online calculation of mass fraction for chemical substances
- Decode text\u0xxx online
- Online calculator for universal complex numbers
- Shuffle letters in online text
- Analyze the frequency of text online
- Rotate points to any angle online
- Calculate proportions and ratios
- Decode numbers using reverse and additive methods online
- Calculate the area of a polygon using coordinates online
- Find the residue of a number in modulo degree online
- Learn how to convert degrees to minutes and seconds
- Calculate percentages online
- Discover the solubility of metals in different liquids
- Locate an object using geographic coordinates
- Customize DameWare Mini Control
- Find the time of sunrise and sunset for a specific area
- Use a geographic coordinates calculator
- Calculate the value of the Euler function
- Create an arbitrary triangle using given parameters
- Explore graph theory using an online adjacency matrix
- Find the greatest common factor (GCF) of two polynomials
- Converting a number to Gray’s code and vice versa
- Animal Community. What are the names of the animals?
- Calculating the area of intersection of circles on a plane
- Geographic coordinates of any city worldwide
- Continuous fractions, chain fractions online
- Online projection of a point onto a plane
- From exponential to algebraic: a detailed explanation
- Online definition of equivalent resistance
- Online calculator for calculating the number of working days
- Solving a system of complex linear equations
- Calculating the capacitance of a step-down capacitor
- Calculating the charge and discharge of a capacitor through a resistance
- Gold deposits and their associated satellites
- Defining the formula for the tangent to a circle
- The canonical equation of a two-point hyperbola
- Returning to work after vacation or online maternity leave
- Creating a matrix-based undirected graph
Angular diameter, also known as angular dimension, apparent diameter, or apparent size, is a measurement of the angle that describes how large a sphere or circle appears from a specific viewpoint. In the field of vision science, this is referred to as the angle of view, and in optics, it is known as the angular aperture (from the lens). Alternatively, angular diameter can be understood as the angle by which the eye or camera must rotate in order to view from one side of the visible circle to the opposite side. The angular radius is half of the angular diameter.
- 1. Formula
- 2. Estimating the angular diameter manually
- 3. Applications in astronomy
- 3.1. Non-circular objects
- 3.2. Illumination defect
Formula
Rephrase the text, making it unique, using the English language and keeping the HTML markup:
Formula
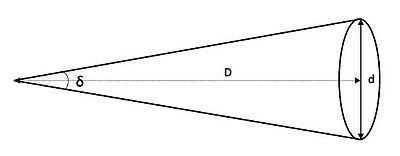
Angular diameter diagram
To find the angular diameter of a circle with a plane perpendicular to the displacement vector between the observer and the circle’s center, you can use the following formula:
, where δ represents the angular diameter, d is the actual diameter of the object, and D is the distance to the object. When the distance D is much greater than the diameter d, we can approximate the angular diameter as δ ≈ d / D, with the result being expressed in radians.
For a spherical object with an actual diameter of dact, where the distance to the center of the sphere is D, the angular diameter can be determined using the following formula:
The distinction lies in the fact that the perceptible boundaries of the sphere consist of tangent points that are in closer proximity to the observer than to the center of the sphere. In practical terms, this distinction is only significant for spherical objects that are relatively close, as the small angle approximation holds true for x ≪ 1:
Approximating the angular size using the arm
An estimation of the angular size can be derived by positioning the hand perpendicular to the fully extended arm, as illustrated.
Astronomical Applications
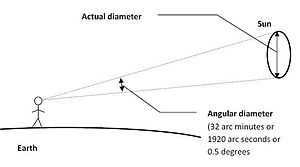
Angular size: the measurement of the angle created by an object
In the field of astronomy, the sizes of celestial objects are often described in terms of their angular size when observed from Earth, rather than their actual physical size. Due to the smallness of these angular sizes, they are commonly measured in angular seconds (″). An angular second is equal to 1/3600 of a degree (1°), and a radian is 180 / π degrees. As a result, one radian is equivalent to 3600 * 180 / π arcseconds, which is approximately 206,265 angular seconds (1 rad ≈ 206,264.806247 inches). Consequently, the angular size of an object with a physical diameter d at a distance D, expressed in arc seconds, is defined as:
These objects have an angular size of 1″:
- an object with a diameter of 1 cm at a distance of 2.06 km
- An object measuring 725.27 km in diameter located at a distance of 1 astronomical unit (AU)
- An object with a diameter of 45,866,916 km located at a distance of 1 light year
- An object with a diameter of 1 AU (149,597,871 km) located at a distance of 1 parsec (pc).
Thus, when viewed from a distance of 1 pc, the Earth’s orbit around the Sun has an angular diameter of 2″, as 1 a.u. represents the radius of the Earth’s orbit.
The Sun has an angular diameter of 0.03″ when viewed from a distance of one light year, while the Earth has an angular diameter of 0.0003″. The Sun’s angular diameter of 0.03″ mentioned earlier is approximately the same as that of a human body at a distance equal to the Earth’s diameter.
This table displays the angular sizes of notable celestial bodies as observed from Earth:
| Andromeda Galaxy | 3 degrees 10 minutes by 1 degree | About six times the size of the Sun or Moon. No long exposure photography. |
| Sun | 31 minutes 27 seconds – 32 minutes 32 seconds | 30-31 times the maximum value for Venus (below) / 1887-1952 seconds |
| Moon | 29 minutes 20 seconds – 34 minutes 6 seconds | 28-32.5 times the maximum value for Venus (orange band at bottom) / 1760-2046 seconds |
| Helix Nebula | approximately 16 seconds by 28 seconds | |
| Spire in the Eagle Nebula | 4 minutes 40 seconds | 280 seconds long |
| Venus | 9.7 seconds – 1 minute 6 seconds | |
| Jupiter | 29.8 seconds – 50.1 seconds | |
| Saturn | 14.5 seconds – 20.1 seconds | |
| Mars | 3.5 seconds – 25.1 seconds | |
| Mercury | 4.5 seconds – 13.0 seconds | |
| Uranus | 3.3-4.1 inches | |
| Neptune | 2.2-2.4 inches | |
| Ceres | 0.33-0.84 inches | |
| Vesta | 0.20-0.64 inches | |
| Pluto | 0.06 seconds – 0.11 seconds | |
| R Doradus | 0.052 seconds – 0.062 seconds | |
| Betelgeuse | 0.049 seconds – 0.060 seconds | |
| Eris | 0.034 seconds – 0.089 seconds | |
| Alphard | 0.00909 seconds | |
| Alpha Centauri A | 0.007 seconds | |
| Canopus | 0.006 seconds | |
| Sirius | 0.005936 seconds | |
| Altair | 0.003 seconds | |
| Deneb | 0.002 seconds | |
| Proxima Centauri | 0.001 seconds | |
| Alnitak | 0.0005 seconds | |
| Event horizon of the black hole M87 * at the center of the galaxy M87, obtained by the Event Horizon Telescope in 2019. | 0.000025 seconds |

Comparing the angular size of the Sun, Moon, and planets can give you a better understanding of their relative sizes. To accurately gauge their sizes, you can view the image from a distance that is 103 times the width of the “Moon: max” circle. For instance, if the circle measures 5 cm wide on your screen, you should view it from a distance of 5.15 meters. The photo below showcases the apparent size of Jupiter and its four Galilean satellites (Callisto at maximum elongation) in comparison to the apparent diameter of the full Moon during their conjunction on April 10, 2017.
The table presented above reveals that the angular diameter of the Sun, as observed from Earth, is approximately 32 ‘ (1920″ or 0.53°).
Therefore, the Sun’s angular size is approximately 250,000 times greater than that of Sirius. (Sirius has twice the diameter and is located at a distance 500,000 times farther away; the Sun is 10 times brighter, which results in an angular size ratio of 10, so Sirius is roughly 6 times brighter per unit solid angle.)
Similarly, the Sun’s angular size is approximately 250,000 times larger than that of Alpha Centauri A (it has a similar diameter and is located 250,000 times farther away; the Sun is 4 times brighter, resulting in an angular size ratio of 200,000, so Alpha Centauri A is slightly brighter per unit solid angle).
The Sun has a similar angular diameter as the Moon. (The Sun’s diameter is 400 times larger, as well as its distance; the Sun is 200,000-500,000 times brighter than the full Moon (numbers may vary), which corresponds to an angular diameter ratio of 450 to 700. This means that a celestial body with a diameter of 2.5-4″ and the same brightness per unit solid angle would have the same brightness as the full Moon.)
While Pluto is physically larger than Ceres, when observed from Earth (such as through the Hubble Space Telescope), Ceres appears much larger in apparent size.
Angular sizes, measured in degrees, are useful for large sections of the sky. (For example, the three Belt stars cover an angular size of approximately 4.5°.) However, measuring the angular size of galaxies, nebulae, or other objects requires much more precise units of measurement in the night sky.
As a result, degrees can be divided into the following categories:
To give you an idea, when we look at the full Moon from Earth, it appears to be about 1/2 degree or 30 seconds of arc (or 1800 seconds of arc). We can measure the Moon’s movement across the sky by its angular size, which is approximately 15 degrees per hour or 15 inches per second. If we were to draw a line one mile long on the Moon’s surface, it would appear to be about 1 inch long when viewed from Earth.
Here is the minimum, average, and maximum distance from the Moon to the Earth, taking into account its angular diameter when observed from the Earth’s surface, to scale.
In the field of astronomy, determining the exact distance to an object can often be a challenging task. However, it is possible to establish the physical size of an object, especially if it resembles a closer object with a known distance, and measure its angular diameter. By employing the inverse of the angular diameter formula, we can calculate the angular diameter distance to remote objects.
It is important to note that in a non-Euclidean space like our expanding universe, the angular diameter distance represents just one of many ways to define distance. As a result, different “distances” may exist for the same object. Further information can be found in the section on Distance measurements (cosmology).
Objects with Irregular Shapes
Many celestial objects, such as galaxies and nebulae, have irregular shapes and are not perfectly round. As a result, they are often measured using two dimensions: a major axis and a minor axis. For instance, the Small Magellanic Cloud appears to be 5° 20′ in width and 3° 5′ in height.
Defect in Illumination
Illumination defect refers to the maximum angular width of the unilluminated area of a celestial body visible to an observer. For example, if an object has a diameter of 40 arc inches and is 75% illuminated, the illumination defect would be 10 inches.
Related Articles
Citations
Additional Resources
Angular dimension, angular measurement, apparent dimension, or apparent measurement is the measurement of the angular distance that determines the perceived size of a large sphere or circle from a specific vantage point. It is referred to as the field of view in the field of visual sciences, and it is known as the angular aperture in the field of optics. Alternatively, angular dimension can be defined as the angular displacement required for the human eye or a camera to shift its gaze from one side of the visible circle to the opposite side. The angular radius is half of the angular dimension.
Formula
Rephrase the text, making it unique, using the English language and preserving HTML markup:
Formula
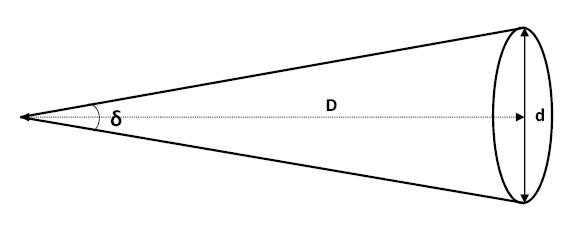
The formula for calculating the angular diameter of a circle, whose plane is perpendicular to the vector between the point of view and the center of the circle, can be expressed as follows:
where δ represents the angular diameter, d is the actual diameter of the object, and D is the distance to the object. When the value of δ is much greater than d, the approximation δ ≈ d / D can be used to obtain the result in radians.
For a spherical object, the actual diameter is equal to d act, and the distance to the center of the sphere is denoted as D. In this case, the formula to find the angular diameter is d act >> D.
The discrepancy arises from the fact that the apparent boundaries of the sphere are formed by its points of tangency, which are closer to the viewer than the sphere’s center. This distinction becomes noticeable primarily for spherical objects with a substantial angular diameter, as for smaller values, the following approximations based on small angles hold true: Ix
Arcsin X ≈ arcsin X ≈ X .
Estimation of Angular Diameter Using the Arm
The arm can be used as a tool to estimate the angular diameter by extending it fully and holding the hand at a right angle, as demonstrated in Figure.
Applications in the Field of Astronomy
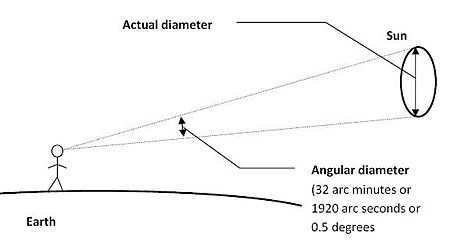
In the field of astronomy, the sizes of celestial objects are often given in terms of their angular diameters as observed from Earth, rather than their actual sizes. Due to the small nature of these angular diameters, they are typically measured in angular seconds (″). An angular second is equivalent to 1/3600th of a degree (1°), and a radian is 180 / π degrees. Therefore, one radian is equal to 3600 × 180 / angular second, approximately 206,265 angular seconds (1 rad ≈ 206,264.806247 inches). As a result, the angular diameter of an object with a physical diameter of d at a distance D expressed in angular seconds is defined as follows: π
δ sign is equal to 206,265 (d / D) angular seconds >.
These objects have an angular diameter of 1 in:
- an object measuring 1 cm in diameter at a distance of 2.06 km
- an object measuring 725.27 km in diameter at a distance of 1 astronomical unit (a.u.)
- an object measuring 45,866,916 km in diameter at a distance of 1 light year
- an object measuring 1 a.u. (149,597,871 km) in diameter at a distance of 1 parsec (pc)
Thus, when viewed from a distance of 1 pc, the Earth’s orbit around the Sun has an angular diameter of 2 inches, as the average radius of the Earth’s orbit is 1 a.u.
The angular diameter of the Sun is 0.03 inches from a distance of one light-year, while the Earth’s angular diameter is 0.0003 inches. The given angular diameter of the Sun, 0.03 inches, is approximately equal to that of a human body at a distance equal to the Earth’s diameter.
This table displays the angular dimensions of significant celestial bodies as seen from Earth:
| Magellanic Stream | over 100° | |
| Gum Nebula | 36° | |
| Milky Way | 30° (at 360°) | |
| Snake-Aquila Rift | 20° by 10° | |
| Canis Major superdensity | 12° by 12° | |
| Smith Cloud | 11° | |
| Large Magellanic Cloud | 10.75° by 9.17° | Note: the brightest galaxy in the night sky, apparent magnitude 0.9 (V). |
| Barnard’s Loop | 10° | |
| Zeta Serpens Nebula Sh2-27 | 10° | |
| The dwarf spheroidal galaxy Sagittarius | 7.5° by 3.6° | |
| Coal Sack Nebula | 7° by 5° | |
| Rho Serpens cloud complex | 4.5° by 6.5° | |
| Hyades | 5° 30′ | Note: brightest star cluster in the night sky, apparent magnitude 0.5 (V) |
| Small Magellanic Cloud | 5° 20′ by 3° 5′ | |
| Andromeda Galaxy | 3° 10′ by 1° | About six times the size of the Sun or Moon. Without long exposure photography, only the much smaller nucleus is visible. |
| Veil Nebula | 3° | |
| Heart Nebula | 2.5° by 2.5° | |
| Westerhout 5 | 2.3° by 1.25° | |
| Ш2-54 | 2.3° | |
| Keel Nebula | 2° by 2° | Note: brightest nebula in the night sky, apparent magnitude 1.0 (V) |
| North America Nebula | 2° by 100′ | |
| Orion Nebula | 1° 5′ at 1° | |
| sun | 31′27 ″ – 32′32 ″ | 30-31 times the maximum value for Venus (orange band below) / 1887-1952″ |
| Moon | 29′20 ″ – 34′6 ″ | 28-32.5 times the maximum value for Venus (orange band at bottom) / 1760-2046 ″ |
| Spiral Nebula | approximately 16′ by 28′. | |
| The spire in the Eagle Nebula | 4′40 ″ | 280″ long. |
| Venus | 9.7 ″ – 1′6 ″ | |
| Jupiter | 29.8 ″ – 50.1 ″ | |
| Saturn | 14.5-20.1″ | |
| Mars | 3.5-25.1 inches | |
| Mercury | 4.5-13.0 inches | |
| Uranus | 3.3 inches to 4.1 inches | |
| Neptune | 2.2 ″ – 2.4 ″ | |
| Ceres | 0.33-0.84 inches | |
| Vesta | 0.20-0.64 in. | |
| Pluto | 0.06-0.11 in. | |
| R Doradus | 0.052 ″ – 0.062 ″ | |
| Betelgeuse | 0.049 ″ – 0.060 ″ | |
| Eris | 0.034 ″ – 0.089 ″ | |
| Alphard | 0.00909 ″ | |
| Alpha Centauri A | 0.007 ″ | |
| Canopus | 0.006 ″ | |
| Sirius | 0.005936 ″ | |
| Altair | 0.003 ″ | |
| Deneb | 0.002 ″ | |
| Proxima Centauri | 0.001 ″ | |
| Alnitak | 0.0005 ″ | |
| Event horizon of the black hole M87* at the center of the galaxy M87, obtained by the Event Horizon telescope in 2019. | 0.000025 ″ |
Comparing the angular diameter of the Sun, Moon, and planets is an interesting exercise. In order to truly grasp their size, it is recommended to view the image at a distance that is 103 times the width of the “Moon: max” circle. For instance, if the circle measures 5 cm wide on your monitor, you should view it from a distance of 5.15 meters.

This photograph illustrates the relative size of Jupiter and its four Galilean moons (Callisto at its farthest point) compared to the apparent size of the full Moon during their conjunction on April 10, 2017.
The table indicates that the angular diameter of the Sun, as observed from Earth, is approximately 32 arcminutes (1920 arcseconds or 0.53 degrees) as depicted above.
Consequently, the angular diameter of the Sun is roughly 250,000 times greater than the diameter of Sirius. (Sirius has twice the diameter and a distance 500,000 times greater than the Sun; the Sun is 10^10 times brighter, corresponding to an angular diameter of 10^5, so Sirius is about 6 times brighter per unit solid angle).
The Sun’s angular diameter is roughly 250,000 times larger than that of Alpha Centauri A. This is because the Sun and Alpha Centauri A have similar diameters, but the Sun is much further away from us, around 250,000 times the distance. Additionally, the Sun is about 4 x 10^10 times brighter than Alpha Centauri A, which corresponds to an angular diameter ratio of 200,000. Therefore, Alpha Centauri A is slightly brighter per unit solid angle.
Comparing the Sun to the Moon, their angular diameters are approximately the same. However, the Sun’s diameter is 400 times larger than the Moon’s, and it is also much further away from us. The Sun is also 200,000-500,000 times brighter than the full Moon, depending on the specific numbers. This corresponds to an angular diameter ratio of 450 to 700. This means that a celestial body with a diameter of 2.5-4″ and the same brightness per unit solid angle would have the same brightness as the full Moon.
While Pluto appears larger than Ceres when observed from Earth (for example, through the Hubble Space Telescope), Ceres has a significantly larger apparent size.
Angular sizes, which are measured in degrees, are useful for large areas of the sky. (For instance, the three Belt stars have an angular size of approximately 4.5°.) However, measuring the angular sizes of galaxies, nebulae, or other objects in the night sky requires more precise units.
Therefore, degrees are divided as follows:
For comparison, the full Moon, when viewed from Earth, is about 1/2° or 30 feet (or 1800″). The Moon’s movement across the sky can be measured by its angular size: approximately 15° every hour, or 15 inches per second. A line one mile long drawn on the surface of the Moon will appear to be about 1 inch long from Earth.
The minimum, average, and maximum distance from the Moon to the Earth with its angular diameter when observed from the Earth’s surface, to be shown accurately
In the field of astronomy, it is often challenging to directly determine the distance to an object. However, an object may possess a known physical size (possibly similar to a closer object with a known distance) and a measurable angular diameter. In such cases, the formula for angular diameter can be reversed to obtain the angular diameter distance to remote objects.
Within a non-Euclidean space like our expanding Universe, the angular diameter distance represents just one of the various definitions of distance. As a result, there may be different “distances” to the same object. For further information, refer to Distance measures (cosmology).
Objects with Irregular Shapes
Many celestial objects in deep space, such as galaxies and nebulae, often have non-circular shapes, resulting in the need for two measurements of their size: a major axis and a minor axis. For instance, the Small Magellanic Cloud appears to have dimensions of 5° 20′ × 3° 5′.
Flaw in Illumination
The flaw in illumination refers to the maximum angular width of the unilluminated section of a celestial body that is visible to a particular observer. For example, if an object has a diameter of 40 arc inches and is 75% illuminated, the flaw in illumination would measure 10 inches.






