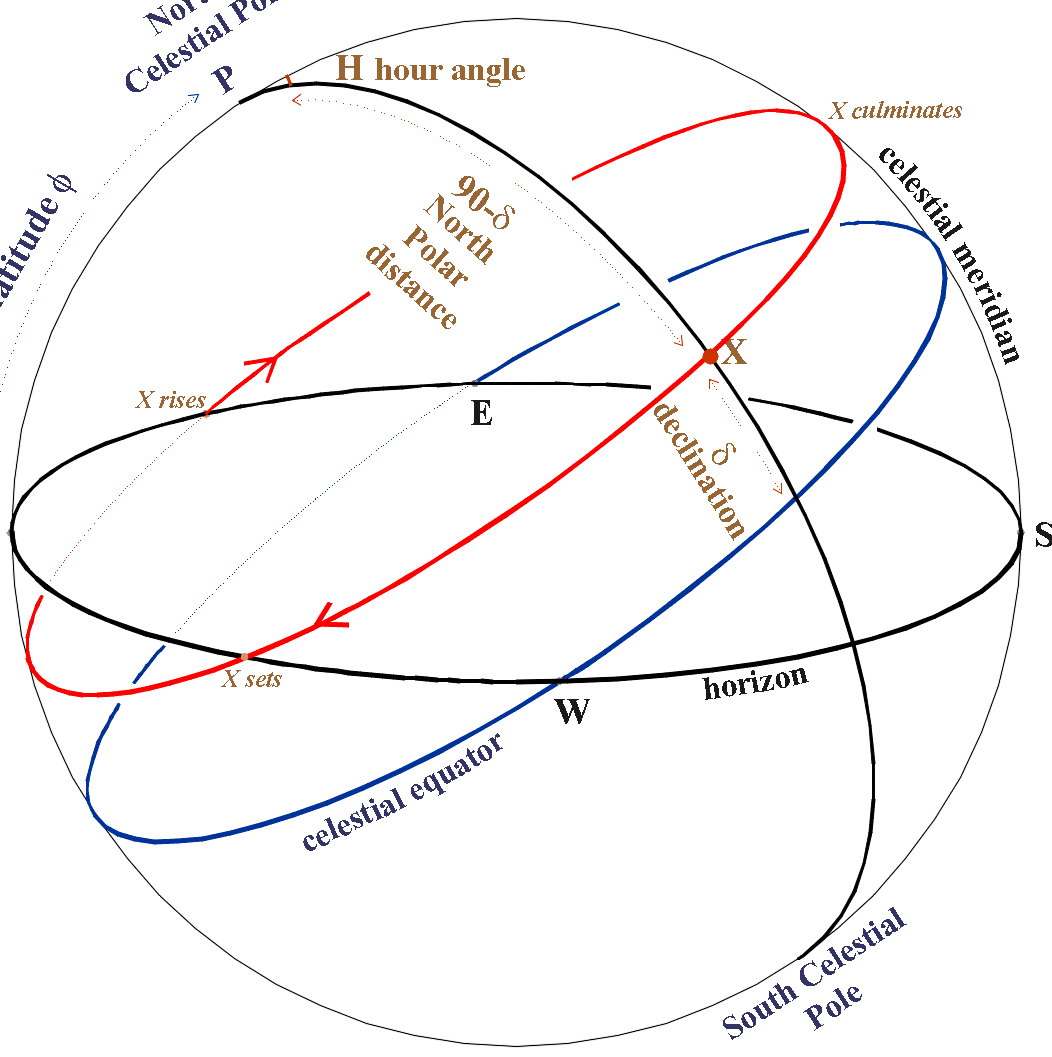
With a high level of precision, the time it takes for the celestial sphere to complete a full revolution can be calculated by measuring the time between two consecutive culminations of a star or a specific point on the celestial sphere, such as the vernal equinox (T).
Duration of TimeThe duration of time between two successive occurrences of the highest point of the vernal equinox is referred to as a sidereal day.
A sidereal day is divided into 24 sidereal hours, with each hour consisting of 60 minutes and each minute consisting of 60 seconds. The position of point T relative to the meridian determines the fraction of the day from the start of the day to the current moment. This position is measured by the arc of the celestial equator between the meridian and point T, in the direction of the daily rotation of the celestial sphere (indicated by a green arrow). In other words, this arc represents the time at the current moment. The arc is equal to the hour angle, which is the spherical angle formed by the meridian, the great circle passing through the pole and point T (shown by a red arrow), and called the hour angle. Therefore, the sidereal time S at a given moment is equal to the hour angle of the vernal equinox point. Since there are 24 hours in a day and 360 degrees in a circle, we can express this relationship as:
Because the hour, minute, and second are used to measure the hour angle, the labels for these units are also placed at the top right of the corresponding digit, similar to how the units of degree measure are labeled. Therefore, the representation of the time moment will be as follows: S = 14h06m27s.
Astronomical observations use stellar time. However, for everyday purposes, it is not convenient as our lives are based on the Sun.
Solar time
Similar to the concept of stellar days, we introduce the notion of a true solar day, which refers to the duration between two consecutive upper culminations of the center of the solar disk.
The true solar time corresponds to the hour angle (/0) of the center of the Sun. Due to the Sun’s annual movement along the ecliptic in the opposite direction of its daily movement, at a rate of approximately 1° per day, the true solar day is on average about 4 minutes longer than the sidereal day.
Constructing a clock based on true solar time is very challenging because the hour angle of the Sun changes unevenly. This is primarily due to the Sun’s uneven movement along the ecliptic and the inclination of the ecliptic to the equator. The Sun’s movements along the ecliptic near perihelion and aphelion for equal time intervals will be unequal, and equal movements of the Sun along the ecliptic near the equinox and solstice points will result in unequal changes in the hour angle (Fig. 38).
Average Ecliptic and Average Equatorial Sun
To address the issue of inconsistent true solar time, the notion of the “mean Sun” is introduced, referring to a hypothetical point in motion. The “average ecliptic Sun” represents a point that moves steadily along the ecliptic, coinciding with both perihelion and aphelion at the same time as the center of the true solar disk. By replacing the actual Sun with this “ecliptic mean,” the irregularity in solar time caused by the varying speed of the Sun’s movement along the ecliptic is eliminated. In order to neutralize the impact of the inclination of the ecliptic to the equator, the concept of the “mean equatorial sun” is introduced. This point moves uniformly along the equator and aligns with the vernal and autumnal equinoxes simultaneously with the “mean ecliptic sun.”
The fictional “average equatorial sun” takes part in the daily rotation of the celestial sphere in a similar manner to the actual sun. The period of time between two consecutive identical culminations of the “average equatorial sun” is known as the average day. To establish the start of the average day, we consider the moment of peak culmination of the “average equatorial sun”. The angular distance of the “average equatorial sun” determines the average time at any given moment. The average day is divided into 24 average hours, each hour consisting of 60 minutes and each minute consisting of 60 seconds.
Time Zones
Every location on the Earth’s surface has its own unique local time, which varies depending on longitude. This means that the time in one location can differ from the time in another location by hours, minutes, and seconds. Using local time for transportation and communication purposes can be highly inconvenient in practical life. To address this issue, there is a need to standardize time measurement across the entire globe. This is achieved through the implementation of a system known as time zones.
The entire world is divided into 24 belts, with each belt spanning 15 degrees of longitude. The center of the “initial or zero” belt passes through the Greenwich meridian, and the local time at the Greenwich meridian is considered the standard for this belt. In the next eastern belt, the local time is one hour ahead of the standard world time, and so on. This local time, denoted as Ta, is referred to as belt time, and the belts themselves are known as time zones.
On any point of the Earth, the local time varies from the zone time by approximately half an hour (maximum). The implementation of zone time results in a one-hour difference in time for a number of settlements that are located in close proximity to each other. However, this is offset by the fact that minutes and seconds are the same across the entire globe when using zone time, and the time of different points only differs by a whole number of hours.
The borders of time zones are delineated, in some cases deviating from the meridians, along state, administrative, or natural (rivers, mountain ranges) boundaries.
Date line
The date line is a line on the Earth’s surface that marks the change in date as one travels east or west across it. It is based on the concept of local or zone time, which increases in proportion to longitude. When counting east of the prime meridian (passing through Greenwich), the local time will increase, while counting to the west of the zero meridian will result in a decrease in local time. This means that when crossing the date line, the date will change. This is an important consideration when traveling across different time zones.
Imagine three observers standing at the same location on a middle latitude. They decide to start counting days, marking each day by the time of sunrise. The first observer stays in place, while the second observer embarks on a journey around the world, traveling eastward along a parallel. The third observer also takes a round-the-world trip, but in the opposite direction, traveling westward along a parallel. After some time, all three observers meet again at the same location. The first observer, who remained in place, will note that N days have passed between their initial meeting and the reunion. However, the second observer, who traveled eastward, will claim that (N + 1) days have passed. This discrepancy occurs because the second observer, traveling eastward, experiences the culmination of the Sun slightly earlier each time, compared to the stationary observer.
To ensure consistency in counting days for both stationary observers and travelers, an international agreement was established to implement a “date line”. This line spans the surface of the ocean and roughly follows the 180th meridian from Greenwich. When crossing this line in the westward direction, one day is skipped in the count (e.g., the second day is immediately followed by the fourth day). Conversely, when crossing the date line in the eastward direction, an extra day is added to the count (for example, a number is repeated twice in record-keeping).
Using the meridian count from Greenwich is convenient because it aligns the date line with the easily memorable figure of 180° longitude. This would not be the case if the count was based on any other observatory.

Currently, 58,748 educational institutions have the opportunity to benefit from additional cumulative discounts ranging from 2% to 25%. To determine the specific discount applicable to all staff members of your educational institution, please access your personal Infoworks account.


A course on professional development
Marketing Strategies in the Field of Education
We have the option to include a discount for your educational establishment (the discount percentage varies based on the number of your colleagues who have enrolled in Infowrok courses).
Currently, there are 58,748 educational institutions benefiting from additional discounts (ranging from 2% to 25%). To determine the available discount for all staff members at your educational institution, please sign in to your personal Infoworks account.


Enroll in our professional retraining course
Specialization in Industrial Design
We can apply an additional discount to the already discounted price of our course for your educational institution. The amount of the discount will depend on the number of your colleagues who have previously taken Infowrok courses.
Currently, we offer additional cumulative discounts ranging from 2% to 25% for a total of 58,748 educational institutions. To find out the specific discount that applies to all employees of your educational institution, please log in to your personal account on “Infoworks”.


The importance of studying the academic subject “Concepts of contemporary natural science”. What does science mean?
Overview of the presentation through individual slides:



Slide 3: The definition of the basic unit of time, known as the second, has evolved over time based on experimental capabilities. Originally, it was defined as 1/86400th of the Earth’s rotation period until the discovery of irregularities in the Earth’s rotation. In 1956, a new definition called the ephemeris second was introduced, which is equal to 1/31556925.9747 of the Sun’s rotation period relative to the spring point at the epoch of 1900.0. Currently, the atomic second is accepted as 9192631770 periods of oscillation of the electromagnetic wave emitted by a 133Cs atom in its ground state.
The three distinct intervals of time defined by these points are known as stellar, true solar, and mean solar days. The time measured by each interval is referred to as stellar, true solar, and mean solar time, respectively.


Slide 4 After observing for many years, it has been established that a tropical year consists of 365.2422 mean solar days. Due to the slow movement of the vernal equinox point, caused by precession, in relation to the stars, the Sun appears at the same position in the sky after a time interval of 20 minutes and 24 seconds longer than the tropical year. This is known as a sidereal year and contains 365.2564 average solar days.


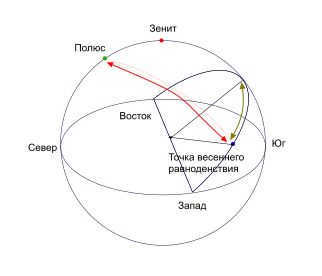
On the 6th slide, practically speaking, in order to establish the start of the sidereal day or sidereal time at any given moment, one must measure the hour angle t of a known luminary M with a known direct ascension α (Fig. 1). Then, since t = Qm, α=ϒt, and the hour angle of the vernal equinox point tϒ = Qϒ and, as defined, is equal to sidereal time s,
s = t + α, which means that
Stellar time at any given moment is equal to the direct ascension of any luminary plus its hour angle.
At the moment of the luminary’s upper culmination, its hour angle t = 0, and therefore
s = o.(1.1)
At the time of the luminary’s lower culmination, its hour angle t = 12h, and sidereal time
s = α + 12h.(1.2)



Slide 9: The difference between the average time and the actual solar time at the same moment is referred to as the equation of time η:
η = Tm – Tʘ.(1.4)
From the above equation, we can conclude that:
Tt = Tʘ + η, which means that (1.5)
the average solar time at any given moment is equal to the actual solar time plus the equation of time.
Therefore, by directly measuring the hour angle of the Sun, we can determine the actual solar time using equation (1.3), and with knowledge of the equation of time η at that particular moment, we can calculate the average solar time using formula (1.5)
Tm = t ʘ + 12h + η.


Kepler’s Laws of Planetary Motion:
1. All planets orbit the Sun in elliptical paths.
2. The line connecting a planet to the Sun sweeps out equal areas in equal time intervals.
3. The square of the time it takes for a planet to complete its orbit is proportional to the cube of the length of the major axis of its elliptical orbit.
These laws can be expressed mathematically as:
T1^2/a1^3 = T2^2/a2^3 = (M/(m1+m2))^2/3
where T1 and T2 are the periods of two planets orbiting the Sun, a1 and a2 are the lengths of their major axes, M is the mass of the Sun, and m1 and m2 are the masses of the planets.


Slide 13, paragraph 4. The primary half-axis a of an elliptical trajectory, which establishes the sidereal period T of the celestial body. It is frequently provided in conjunction with it as a component of the average daily motion n=3600/T=2π/T, i.e. the mean angular velocity of the celestial body per day.
Where a and b represent the semi-major axes of the elliptical trajectory. The primary half-axis and eccentricity determine the size and shape of the trajectory.
Slide 6. The time of passage through perihelion t0, or the position of the celestial body in orbit at a specific moment in time t (longitude at epoch t).
Each star of the Big Dipper during the day describes a circular path around Polaris (the entire constellation rotates).
A direct line from Polaris to stars 1 and 2 of the Big Dipper will be referred to as the Dipper’s arrow.
When stars 1 and 2 align directly beneath Polaris, the arrow points straight down. We can say that it indicates 6 hours, according to the conventional count. This will be position I in the diagram.
As we continue to observe, it becomes apparent that in this particular position, the Big Dipper shifts towards the right, or eastward, and gradually ascends in a circular motion, with Polaris as its center. Within a span of six hours, or a quarter of a day, the hand of the Medusa will have completed a quarter of a revolution around the circle, resulting in a horizontal placement rather than a vertical one, thus bringing us to position II. At this point, the hand of the Medusa indicates three hours based on conventional counting, and so on.
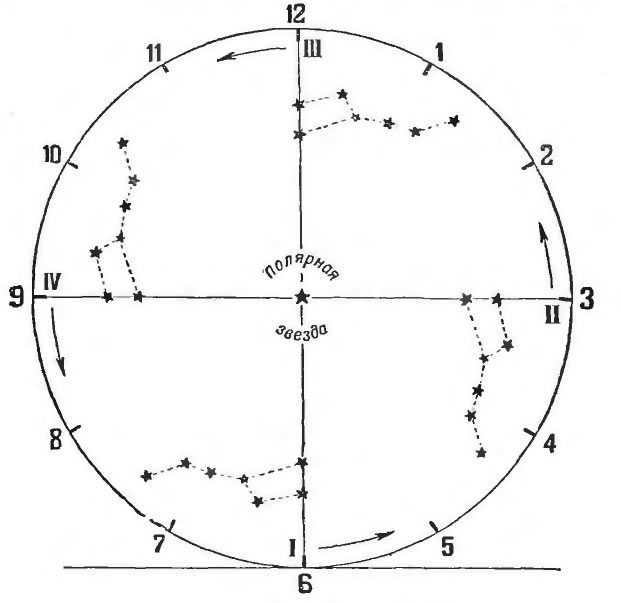
"Star Dial" and "Sidereal Time"
Due to the consistent movement of the Big Dipper around Polaris, we can consider the Big Dipper and Polaris as a traditional star dial. The indicator of this celestial timepiece is an imaginary line that stretches from Polaris to stars 1 and 2 of the Big Dipper, although there is no physical dial present. However, the absence of a dial is inconsequential. When we glance at a clock, we often determine the time based on the position of the hands without needing to read the numbers they point to.
The hand of a celestial clock rotates counter-clockwise, unlike the hand of a regular clock. Once it reaches position II, it surpasses the imaginary figures that represent 2 o’clock, 1 o’clock, 12 o’clock, 11 o’clock, and so on. It is important to note that this clock is not real, but rather a conventional representation of our imaginary hand.
Here are some examples of the tasks that can be accomplished with the assistance of this imaginary celestial clock.
What is the method to determine the duration of a night reconnaissance using the Big Dipper?
Task 1: Imagine a scenario where a fighter goes on a night reconnaissance without a watch, while the Big Dipper has not yet reached its lowest position. By visually observing the position of the Big Dipper’s arrow, he determines that it is at 6.5 conventional hours. After completing the mission, he looks at the Big Dipper again and notices that its hand now indicates 4.0 notional hours. How much time did he spend on the reconnaissance?
To find the answer, subtract 4.0 from 6.5, resulting in 2.5 notional hours.
To convert the notional hours into actual hours, multiply the result by 2. Therefore, 2.5 x 2 = 5 hours (actual hours).
Hence, the night reconnaissance lasted approximately 5 hours.
In order to subtract 10.5 hours from 2 hours, we need to first add 12 hours to 2 hours (remember, “conditional hours” go in the opposite direction of true hours):
2 conditional hours + 12 conditional hours = 14 conditional hours. Now subtract:
14 conditional hours – 10.5 conditional hours = Z.5 conditional hours. To convert conditional hours into true hours, multiply 3.5 conditional hours by 2 and you will get 7 true hours.
Therefore, we can establish the following rule:
To calculate the amount of time that has passed based on the position of the Big Dipper, you must:
1) Observe the position of the “arrow” of the Big Dipper on an imaginary celestial clock at the beginning and at the end.
2) Subtract the second number from the first (if the first number is smaller than the second, add 12 to the first and then subtract the second).
3) Double the resulting number.
How can you determine that it is midnight by observing the Big Dipper?
This particular task is more challenging compared to the previous one because the stars in the Big Dipper, just like all other stars, complete a full revolution not exactly in 24 hours, but 4 minutes earlier.
In simpler terms, our celestial clocks advance each day by 4 minutes ahead of the regular clocks. Consequently, the lowest position of the Big Dipper according to regular clocks will be 4 minutes earlier tomorrow compared to today, 8 minutes earlier the day after tomorrow, and so on. After 30 days, it will be 120 minutes earlier than today, equivalent to a full two hours. Despite the intricacy involved, this task can be effortlessly comprehended with the assistance of the following information.
On the 22nd of September, the arrow of the Medusa points directly downward at midnight (0:00 a.m. on our clocks) and indicates 6 conventional hours on the celestial clock.
A month later, on the 22nd of October, the arrow will already be two true hours ahead of midnight in the plumb position. Therefore, at midnight on the 22nd of October, the celestial arrow will no longer be pointing straight down, but will be angled to the east (to the right) as if it were pointing towards the number 5 on the imaginary celestial clock. Continuing this reasoning, we can determine the following:
The arrow of the Big Dipper at midnight indicates:
| September 22 | 6 hours (ordinary) |
| October 22 | 5 hours |
| November 22 | 4 hours (conditional) |
| December 22 | 3 hours (conditional) |
| January 22 | 2 hours (conditional) |
| February 22 | 1 hour (conditional) |
| March 22 | 12 hours (conditional) |
| April 22 | 11 hours (notional) |
| May 22 | 10 hours (notional) |
| June 22 | 9 hours (notional) |
| July 22 | 8 hours (notional) |
| August 22 | 7 hours (notional) |
| September 22 | 6 hours (ordinary) |
Calculating these numbers without the table is not a challenging task, given that we remember the initial reading and the fact that the conventional hours decrease by one every month.
Let’s consider solving a specific problem:
Problem 3. How can we determine that it is midnight on November 7 by observing the Big Dipper?
November 7 falls exactly between October 22 and November 22. Hence, referring to the table, we can conclude that at midnight on this day, the Dipper’s hand should indicate a decrease of 4.5 conventional hours.
Therefore, midnight will occur when the Big Dipper is positioned precisely between position I (6 conventional hours) and position II (3 conventional hours) in Figure 10.
How can I determine the time by observing the Big Dipper?
Knowing the time involves calculating the elapsed time since midnight. This can be easily done using the provided table.
Task 4: On November 7, the Big Dipper’s hand displayed 4.5 conventional hours. What is the actual hour?
In the previous problem, we found that at midnight on November 7, the Big Dipper’s hand showed 4.5 conventional hours. To determine the time, we need to subtract 2 conventional hours from 4.5 conditional hours and then multiply the result by 2: 4.5 – 2 = 2.5 conditional hours.
Multiplying the result by 2: 2.5 x 2 = 5 true hours (morning).
Task 5: On October 20, the Big Dipper’s hand showed 7 conventional hours. What is the true hour?
According to the data from the table on October 20th, it can be concluded that at midnight, the Medusa’s hand indicates approximately 5 conventional hours. To calculate the difference of 7 hours from 5 hours, first add 12 hours to 5 hours:
5 + 12 = 17 notional hours; 17 notional hours – 7 notional hours = 10 notional hours. Multiply the result by 2:
10 x 2 = 20 true hours (evenings).
To determine the time based on the position of the Big Dipper’s hand, follow these steps:
1) Use the table to find the indication of the Big Dipper’s hand at midnight on the given day;
2) Subtract the observed arrow reading from this number (if the first number is smaller than the second, add 12 hours to the first number and then subtract the second number);
3) Double the obtained number.

Let’s illustrate the celestial sphere on the plane of the celestial equator. Take point C to represent the position of a certain star on the sphere at a given time; – the position of the vernal equinox point (the point of Aries); t – the western hour angle and – the right ascension of the star. From the diagram, we can observe that the sidereal time at a specific moment is equal to the sum of the right ascension and the hour angle of the star at that same moment, i.e.
This expression is known as the fundamental time formula. It establishes a relationship between the coordinates of celestial bodies and time, enabling us to convert from sidereal time to solar time and solve other significant problems. In the field of nautical astronomy, this formula is frequently employed to calculate the hour angles of stars:
To simplify the calculations, we can replace subtraction with a more convenient addition by introducing the stellar complement:
Stellar complement – refers to the section of the celestial equator that extends from the point of Aries to the meridian of the luminary, and it is measured in the direction of the daily rotation of the celestial sphere.
In navigational astronomy manuals written in English, this coordinate is commonly referred to as SHA, which stands for Sideral Hour Angle, or Stellar Hour Angle.
Average duration
Solar time or actual 24-hour period refers to the duration between two sequential highest or lowest points of the Sun’s core on the identical longitude. The lowermost point of the Sun is generally regarded as the commencement of the solar day, consequently, the precise solar time represents the duration between two consecutive highest or lowest points of the Sun’s core on the identical longitude. Actual solar time (T) indicates the duration from the lowest point of the Sun to the current moment.
| However, the disadvantage of true time is that it changes in an uneven manner. This can be understood by referring to Kepler’s second law, which states that the radius-vector of a planet describes equal areas in equal time intervals. As a result, the daily change in the direct sunrise is not consistent throughout the year, ranging from 53.8′ to 66.6′. Therefore, the difference between the longest and shortest solar day is 66.6′ – 53.8′, which equals 12.8′ or 51s (almost 1 minute). |
In order to ensure that the days have equal duration, they are measured based on the mean Sun. The mean Sun is an imaginary point that moves uniformly along the celestial equator, unlike the actual Sun.
A mean day is the time interval between two consecutive lower culminations of the average Sun on the observer’s meridian.
| The average time is the interval between the lower culmination of the mean Sun and a specific point in time. It is calculated by measuring the arc of the celestial equator from the midnight section of the observer’s meridian to the meridian of the mean Sun. Average time is typically measured in hours. |
Due to the uniform movement of the mean Sun and the uneven movement of the true Sun, the true Sun will either surpass or fall behind the average Sun.
The equation of time and the relationship between mean and true time.
The equation of time represents the disparity between mean time and true time, which is equivalent to the discrepancy in hour angles between the mean Sun and the true Sun.
| The equation of time can be derived from either the MAE or the graphical representation. The graph reveals that the equation of time reaches zero on four occasions throughout the year (April 16, June 14, September 1, and December 25), while it also exhibits four extreme values: (February 11 +14.3 m, May 15 -3.8 m, July 26 +6.4 m, and November 3 -16.4 m). This knowledge proved instrumental in determining the longitude of the characters in Jules Verne’s novel “The Mysterious Island.” |
- Calculating the hour angle of the Sun based on the given time.
t = T ± 12 – - Determining the time of the Sun’s culmination.
For the upper culmination, t = 0, so from the previous formula we can derive
Tin.k = 12 hours +
This correlation is clearly visible in the provided excerpt from the MAE (bottom right corner of the daily pages).
The correlation between the average and sidereal time
Utilizing the fundamental time equation for the mean Sun S = t + , however, considering that the time equation t = T ± 12 h, thus
Save as a solitary document (word) with illustrations.
All documents are exclusively accessible for registered users. The registration process will not exceed a few minutes.
zvezdnoe_vremia.doc (147.0 KiB, 44 hits)
Regrettably, you lack the required permissions to download this file.
Stellar time is of great significance in nautical astronomy. A sidereal day refers to the duration it takes for the Earth to complete one full revolution relative to the point of Aries. The initiation of a sidereal day is determined by the moment when the vernal equinox point reaches its highest point. As a result, a sidereal day is defined as the time interval between two consecutive upper culminations of the vernal equinox point. This interval is measured in stellar units and represents the elapsed time from the start of a sidereal day to a specific point…
Rating of the Article
Please provide your rating for this article!
Explore more on the subject: