Methods for calculating the sun’s altitude at midday

Currently, there are additional cumulative discounts (ranging from 2% to 25%) available for a total of 58,742 educational institutions. In order to determine the specific discount that applies to all staff members of your educational institution, please log in to your personal Infoworks account.

Professional development course

Innovative technologies in teaching geography to children with disabilities.

We have the option to provide a reduced price for your educational institution on this course (the amount will depend on the number of your colleagues who have already completed Infowork courses).

Currently, 58,742 educational institutions are benefiting from additional discounts ranging from 2% to 25%. To discover the specific discount available to all staff members at your educational institution, please sign in to your personal Infoworks account.

Course for professional growth

Specifics of preparing for the USE in geography with the implementation of the FSES SOO

We can apply your educational institution’s discount to this special offer (it depends on how many of your colleagues have completed Infoworks courses)

Currently, 58,742 educational institutions are eligible for additional discounts (ranging from 2% to 25%). To find out the discount available for all staff members of your educational institution, please log in to your personal Infoworks account.

Using game techniques to teach geography in schools

Breakdown of the presentation by slide:

Slide 2. Objectives for establishing the elevation of the Sun above the horizon at various points situated on the identical parallel
The Earth revolves in an anticlockwise direction, and the further eastward a point is positioned, the earlier the Sun will ascend above the horizon.

To calculate the Sun’s altitude above the horizon at various points on the same parallel, it is necessary to determine the meridian of noon using the data of the Greenwich meridian time.

The meridian of noon can be calculated using the following formula:
(12 hours – Greenwich meridian time) – 15 degrees
if the meridian is in the Eastern Hemisphere;
(Greenwich meridian time – 12 o’clock) – 15 degrees
if the meridian is in the Western Hemisphere.

The Sun’s altitude will be higher in the meridians that are closer to the meridian of noon, and lower in the meridians that are farther away.

Slide number 6.
Problem number 1.
Find out the location on the world map where the Sun will be at its lowest point above the horizon at 3 a.m. GMT. Please describe your thought process.

Algorithm for finding the solution in 7 steps:
1. Calculate the meridian at noon using the formula
(12h – Greenwich meridian time) – 15º.

2. Examine the location of the points with respect to the noon meridian.

3. The point that is farthest from the noon meridian will have the lowest sun altitude.

Slide number 8

The second method involves determining the solar time for each point and comparing the values.

Local (solar time) refers to the time at a specific moment along a single meridian line.

One revolution of the Earth around its axis is equal to 360 degrees.

The Earth completes one revolution around its axis in 24 hours.

One hour (60 minutes) is equal to 15 degrees (the length of one time zone).

Therefore, 1 degree is equal to 4 minutes.

Slide 9 Solution Algorithm:
1. The solution accurately calculates the solar time for each of the specified points.
For instance, for point A:
3h.+80-4min=8h. 20min.
etc.
2) The correct point is determined by comparing the time of day at the specified points provided in the condition.

Content elements of the correct response (alternative phrasings of the response are acceptable without distorting its meaning)

1) The Sun is at its lowest point above the horizon at point A.
2) The calculation of (12 – 3) x 15 degrees is utilized to determine the meridian at noon.
OR
At this point on the 135-degree East meridian, it is noon.
OR
The response correctly calculates the solar time for each of the points mentioned in the given scenario.
3) The point is the farthest from the meridian at noon.
OR
The point is determined by comparing the time of day at the specified points in the given scenario.

Slide 11. The objective is to calculate the Sun’s elevation above the horizon at various locations that are not on the same latitude, while also taking into account the date of either the winter (December 22nd) or summer (June 22nd) solstice.

In order to analyze the situation presented in the task and determine the duration of day (night) in relation to the Earth’s axial tilt, certain tasks need to be performed.
For instance, in regions with long day lengths (such as in June in the northern hemisphere), the length of the day increases the closer the territory is to the Arctic Circle, while it decreases the farther away it is.

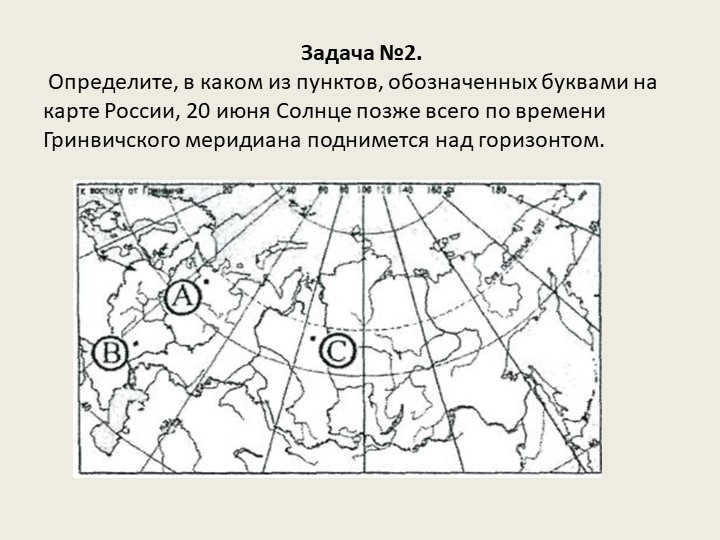
Task #2.
Determine the specific location on the map of Russia where the Sun will reach above the horizon on June 20 according to Greenwich meridian time.

15 slide Solution Algorithm:
To solve tasks of this nature, certain steps need to be followed:
1. Begin by recalling the characteristics of Earth’s illumination on the day of the summer solstice;
2. Analyze the positions of the specified points in relation to the polar circle; draw conclusions regarding the duration of the day.
3. Keep in mind that the Earth moves counterclockwise, and the further east a point is located, the earlier the Sun will rise above the horizon.

Slide 16
Elements of a valid response
(alternative phrasings that do not alter the meaning are acceptable)

1)June 20th is a date near the summer solstice in the northern hemisphere.
2)point B is situated south of point A, therefore the sunrise will be later there.
point B is positioned west of point C, so the sunrise is delayed there.
The sunrise occurs later than the horizon at point B

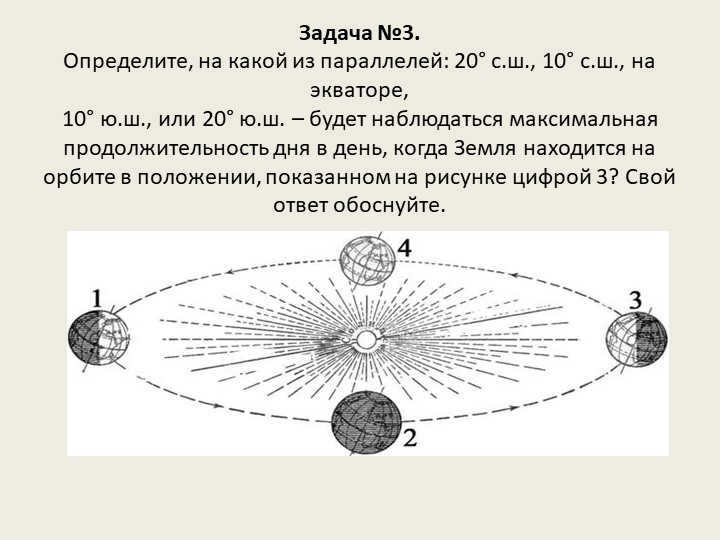
Task #3.
Identify the parallel, either 20°N, 10°N, on the equator,
10°S, or 20°S, that will experience the longest day length when the Earth is in the position indicated as number 3 in the diagram. Provide a rationale for your choice.

Slide 18: Elements of a valid response
(alternative phrasings of the response that do not alter its meaning are acceptable)
Examine the Earth’s location at point 3.
At point 3, the Earth is positioned on the day of the winter solstice – December 22, experiencing longer daylight hours – in the Southern Hemisphere.
2. The latitude of 20 S will have the longest duration of daylight, as this parallel is located furthest south.

Question #4.
Among the parallels labeled with letters in the diagram, which one has the shortest duration of daylight hours on December 22?
1) A 2) C 3) C 4) D
Please provide a rationale for your answer.

20 slide Content elements of a correct answer
(other wording of the answer that does not distort its meaning is allowed)

1) The Southern Hemisphere experiences its shortest day at parallel A, where the Sun is directly overhead at noon. Alternatively, this day marks the summer solstice for the Southern Hemisphere.

2) On this specific day, the length of the day increases in the Southern Hemisphere and decreases in the Northern Hemisphere as you move away from the equator. Alternatively, parallel A, located furthest from the equator in the Northern Hemisphere, experiences the shortest day length.

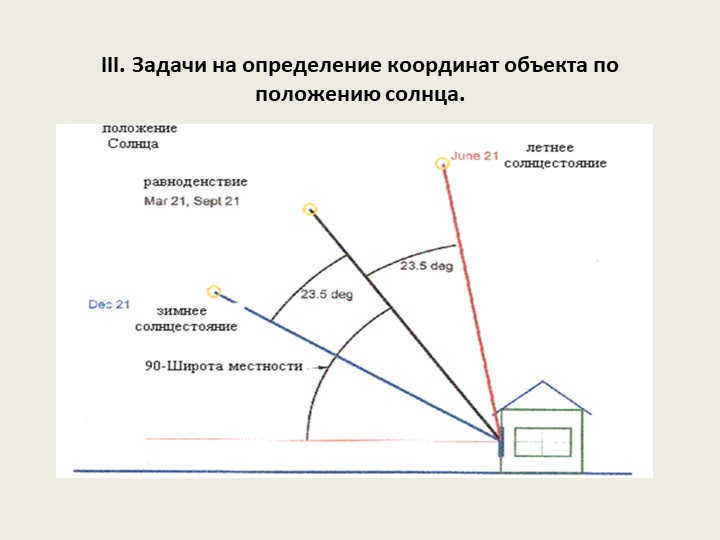
Slide 22
To calculate the geographical latitude, we consider the relationship between the angle of incidence of the sun’s rays and the latitude of the area.

During the equinoxes (March 21 and September 23), when the sun’s rays fall directly on the equator, we use the following formula to determine the geographical latitude:

90º – angle of incidence of the sun’s rays = latitude of the area (north or south determined by the shadow cast by objects).

During the solstices (June 22 and December 22), we need to take into account that the sun’s rays fall directly (at an angle of 90º) on the tropics (23.5º N and 23.5º S).
Therefore, to determine the latitude of an area in the illuminated hemisphere.
(for example, June 22 in the Northern Hemisphere), we use the following formula:

90° – angle at which the sun’s rays hit the surface + 23.5° = latitude of the area

To find out the latitude of a place in the dark hemisphere (e.g., December 22 in the Northern Hemisphere), the following formula is used:

90° – angle at which the sun’s rays hit the surface – 23.5° = the latitude of the area

Slide 23: For example, let’s determine the geographical latitude of a place given that on June 22nd, the midday Sun is positioned above the horizon at an angle of 35 degrees. To calculate this, we can use the formula: 90 degrees – 35 degrees – 23.5 degrees = 78.5 degrees North.

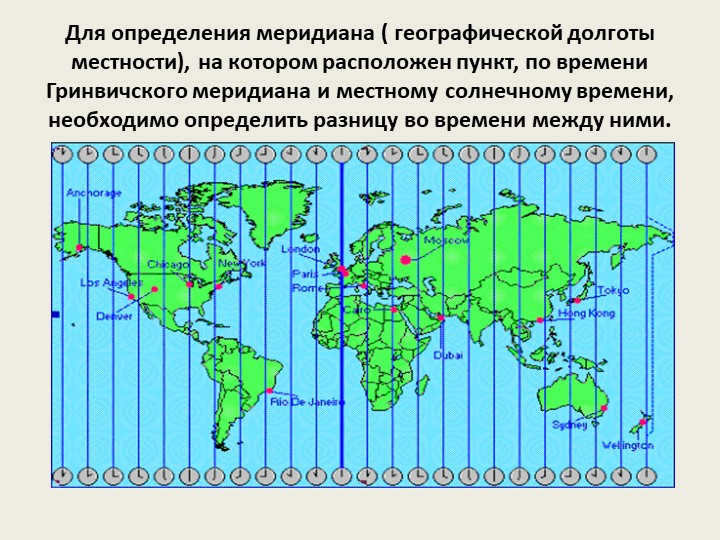
24 slide
To ascertain the meridian (geographic longitude of a location) on which a specific point lies in relation to the Greenwich meridian time and the local solar time, it is necessary to calculate the time discrepancy between the two.

For instance, let’s consider a scenario:
It is exactly 12:00 PM (noon) at the Greenwich meridian, and the local solar time at the specific location is 8:00 AM.
The time difference between the two is 4 hours.
Now, each time zone covers a span of 15 degrees.
To find out the meridian required, the calculation would be 4 x 15 degrees = 60 degrees.
To determine the hemisphere where this meridian is situated, we must keep in mind that the Earth rotates in a counterclockwise direction from west to east.
Therefore, if the time at the Greenwich meridian is ahead of the given location, then the location falls in the Western Hemisphere.

If it is known that on March 21 at 17:00 GMT the Sun is at 50° above the horizon and it is noon, it is possible to determine the geographic coordinates of a point in the United States. To do this, we can use the concept of solar noon, which is when the Sun reaches its highest point in the sky. By knowing the time of solar noon and the angle of the Sun above the horizon, we can calculate the latitude of the point. The latitude is the angle between the equator and the point, measured in degrees. Since we know that the Sun is at 50° above the horizon at solar noon, we can calculate the latitude using the following equation: Latitude = 90° – Sun’s altitude above the horizon. Therefore, the latitude of the point in the United States can be determined by subtracting 50° from 90°, resulting in a latitude of 40°. However, to determine the exact longitude of the point, additional information is needed, such as the time zone or the longitude of a reference point. Without this information, it is not possible to determine the exact geographic coordinates of the point.

Slide 27 Algorithm:
1. To find the latitude of a specific location, you can use the following formula:
90º – the angle at which the sun’s rays hit the Earth’s surface = latitude of the location
(north or south is determined by the shadow cast by objects).
2. To determine the longitude, you can use the following formula:
(Greenwich meridian time – 12 hours) – 15º
since the prime meridian is located in the Western Hemisphere.

Problem #6 on slide 28.
To find the geographic coordinates of the point, we need to consider the conditions during the equinoxes. During this time, the noon Sun stands above the horizon at a height of 40 degrees, with the shadow of the object falling to the north. Additionally, the local time is 3 hours ahead of the Greenwich meridian time. Let’s calculate the coordinates based on these factors.

Slide 29 Problem 7
Calculate the sun’s elevation at noon on the day of the winter solstice for Inta (66°N).
Does our settlement experience the phenomenon known as the “polar night”?

Findings and resources for educators and teachers

Over 10,000 educational materials for school and home learning

It is commonly believed that the Sun is always directly south at noon, as indicated by clocks, or more precisely, in a southerly direction. This belief forms the basis of the Sun and Clock method of navigation.

However, this notion is mistaken. And today we will endeavor to comprehend this rather challenging inquiry, centering on scientific evidence and rationality.

Factors influencing the position of the Sun in the sky

Several factors influence where the Sun will be located at noon on the celestial sphere. Let’s examine a few of them.

Longitude of the region

The moment of true noon, or solar noon, often does not align with the official noon time. To clarify this, let’s first understand the definitions.

Noon, according to official time, is the time of 12:00 determined by a precisely set clock. However, true noon is the specific moment when the sun reaches its highest point in its trajectory as observed from the Earth’s surface, also known as the zenith.

It is important to note that during true noon, the Sun is directly south for an observer situated in the middle latitudes of the northern hemisphere. We will explain why this is the case for middle latitudes shortly.

If you observe our planet from the top, specifically from the North Pole, you will notice that its rotation around its own axis is in a counterclockwise direction. Considering that the Earth orbits around the Sun and not the other way around, it can be inferred that the Sun primarily illuminates the Earth from areas further to the east. Therefore, two straightforward conclusions can be drawn:

Conclusion #1. Irrespective of whether one is in the northern or southern hemisphere, the Sun rises in the east and sets in the west for an observer on the Earth’s surface.

Conclusion #2. Two observers situated at different geographic longitudes will experience the Sun being at its zenith at different times: the first observer, located in the east, will reach solar noon before the observer in the “western” region.

One must understand that in order to make it more convenient for people to use, the time within each time zone is averaged. This is done to avoid having different times on clocks in two cities within the same country, which would be impractical. Therefore, even though two different cities may have different longitudes, their time can be the same.

From the information above, it can be concluded that for two observers located in different longitudes but within the same time zone, true noon may occur at different times. The actual time of noon may be either ahead or behind the time defined by the hours. This fluctuation can be up to fifteen minutes or even more. In reality, time zones do not always align perfectly with longitudes and are instead based on the political map of the world.

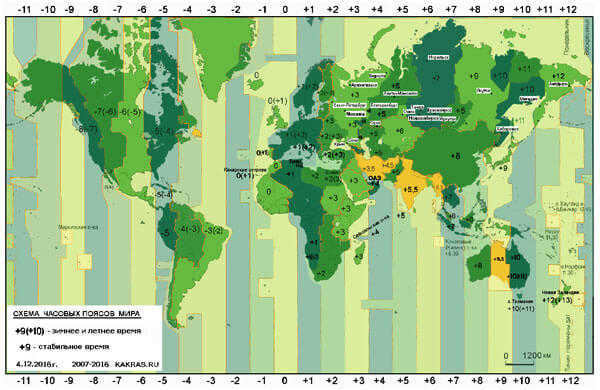
Mapping the time zones across the globe

Since the solar noon does not consistently align with 12 o’clock (referred to as 12:00), it cannot be assumed that the Sun is always precisely due south at this time.

You can observe the varying position of the Sun in the sky simultaneously in different cities within the same time zone.

Now, let’s revisit the topic of average latitude and examine its impact on the Sun’s position in the sky.

Latitude of the region

As mentioned earlier, in the moderate latitudes, the Sun always travels southward during true noon. However, let’s explore if this pattern changes when the observer is located north or south of these latitudes. To do so, let’s consider a few key scenarios.

Scenario #1 – moderate latitudes in the southern hemisphere. In this case, during true noon, the Sun will be situated directly in the north.

Regrettably, it is not mentioned in all tourism textbooks that the Sun at noon is not only in the south, but also in the north. However, thanks to various airlines, contemporary travelers have the opportunity to explore not only their homeland, but also effortlessly reach the antipodal point on the planet, where the guidelines for navigation, as described in the literature, may not be accurate.

Simultaneously, the Sun will have varying elevations at the same latitudes in different hemispheres.

Variant #2 – the upper limit of the tropical zone in the northern hemisphere. In these areas, throughout the year, except for the summer solstice, the Sun will be in the south during true noon, and on the described day, it will be directly overhead. As you may understand, it will not be possible to determine the south, and consequently, the other directions based solely on the method of orienting oneself using the Sun at noon.

Option 3 – the southern hemisphere’s tropical zone lower limit. In this area, throughout the year, except for the winter solstice, the Sun will be in the north at true noon, similar to the middle latitudes of this hemisphere. However, on the specified day in December, it will be directly overhead at the zenith, making it difficult to quickly orient oneself.

Option 4 – the equator line. In this zone, there are three possible variations that alternate throughout the year. From the autumn equinox to the spring equinox, the Sun will be in the south at true noon, and from the spring equinox to the autumn equinox, it will be in the north. During the equinoxes, it will be directly overhead, posing challenges for orientation.

It appears that the Sun reaches its highest point in the sky, known as the zenith, only once a year at the points where tropical zones meet temperate zones. This means that it is directly overhead the observer. However, in regions closer to the equator, this unique occurrence can be witnessed twice a year.

It is nearly impossible to determine if the Sun is directly overhead without knowing your own location on the Earth’s surface.

There is a belief that at the equator, the Sun is always at its zenith at noon throughout the entire year. However, this assumption is incorrect. In reality, the Sun is only at its zenith at noon for half of the year in the northern hemisphere and the other half in the southern hemisphere. Even if we define the zenith as the highest point of the Sun’s trajectory, this belief still doesn’t hold true. In this case, the Sun would be at its zenith every day of the year at noon, not just at the equator but also at any other point on the planet.

In certain tropical cities, a fascinating phenomenon can be observed: around noon, vertical objects like poles and fences cease to create shadows. This occurs because the Sun is directly overhead at that time, causing its rays to fall straight down and eliminating any shadow projection. The following video provides a detailed explanation of this intriguing occurrence:

Another possibility exists – the high latitudes of the northern and southern hemispheres. In these regions, the Sun will behave similarly to how it does in middle latitudes. However, during the polar night, it will not be visible above the horizon, making it impossible to use it for orientation purposes.

It is evident that without comprehending the underlying processes that cause these disparities, it is simple to become disoriented and make grave errors, even to the extent of confusing north and south. For a traveler without access to modern navigation tools in the wilderness, this can be perilous and even fatal at times.

Daylight saving time and winter time

Daylight saving time is often implemented by moving the clocks forward by one hour. The purpose of this practice is to conserve electricity used for lighting. However, numerous studies have demonstrated that there is no economic benefit gained from these adjustments. Nevertheless, that is not the focus of our discussion at present.

Disregarding the act of changing the clocks for winter and summer time can lead to a significant error when relying on both the Sun and clocks for orientation. In regions with middle latitudes, this error can be as much as 30 degrees, while in tropical areas it can be even greater. Consider the distance one can stray from their intended destination if a one-degree deviation results in a deviation of approximately twenty meters for every kilometer traveled.

While some countries have chosen to eliminate daylight saving time and maintain a consistent time throughout the year, others still adhere to the practice. Additionally, there are certain countries that have never had the pleasure (or perhaps the annoyance) of adjusting their clocks.

For instance, as of the current year (2017) in Ukraine, midday in the winter coincided with solar noon, while in the summer, the Sun reaches its highest point only at 13:00 according to the clock. However, in Russia, the time change was abolished and the clock was set to stay on summer time, so now solar noon for Russians occurs at 13:00, disregarding other factors that may affect the discrepancy between true noon and local time noon.

Movement of the Earth in Orbit around the Sun

The Earth doesn’t move in a perfect circle around the Sun, but rather in an elliptical orbit. As it travels, the Earth gets closer to the Sun at certain points and farther away at others. When summer arrives in the northern hemisphere, the Earth is at its farthest point from the Sun, and during winter, it moves closer.

As a result of this elliptical path, the length of a solar day, which is the time between two solar noons, changes throughout the year. When the Earth is closer to the Sun, the solar day becomes longer, while it becomes shorter when the Earth is farther away.

This variation in solar day length is further influenced by the tilt of the Earth’s rotation axis.

An interesting picture is produced as a result. If an individual, positioned at a specific point on the Earth’s surface (for instance, the middle latitudes of the northern hemisphere), were to mark the Sun’s position on the celestial sphere every day at 12:00 throughout the year, they would observe an elongated figure eight instead of the anticipated vertical line (with the Sun being higher in summer and lower in winter). This implies that the Sun’s position at noon, as determined by a clock, can either be to the left or to the right of the southward direction. The extent of these deviations on any given day of the year can be determined by the equation of time, which is conveniently summarized in a table or graph format.

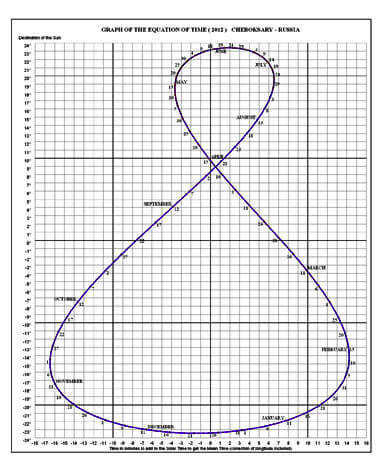
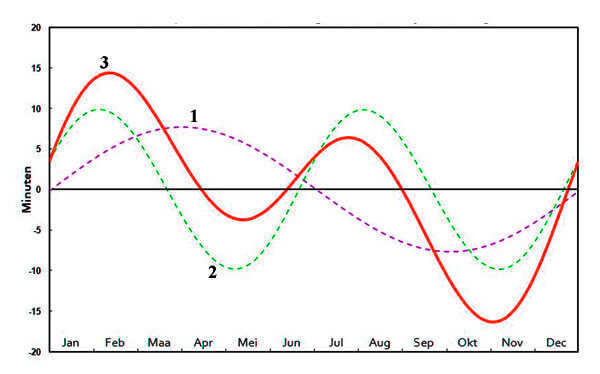
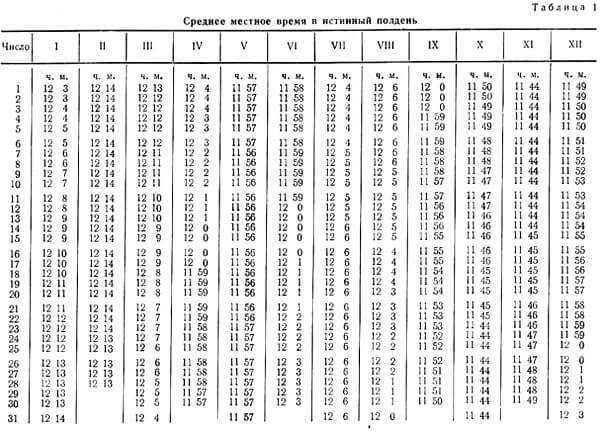
If you disregard this phenomenon, when navigating in high latitudes, there is a possibility of experiencing an error of approximately four degrees, while in the tropics, the error can be as high as ten degrees or more.

How to ascertain the exact time of noon

By determining the precise time of noon, you can establish the cardinal directions, as it is during this moment that the Sun will be directly south or north, depending on the Earth’s hemisphere. By knowing at least one cardinal direction, you can deduce the remaining directions.

There are various methods to ascertain the true time of noon. Presented below are a few simple techniques that do not necessitate advanced expertise or knowledge.

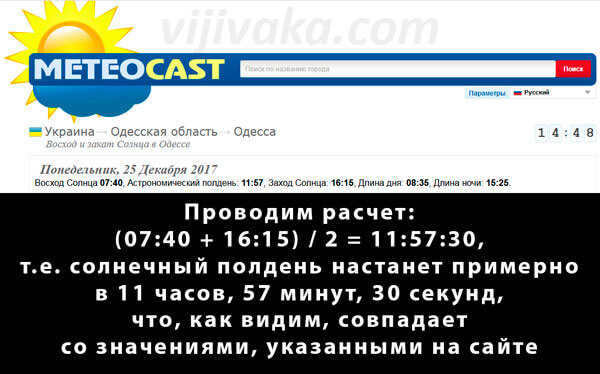
There is a method that can be used to determine the true noon with the assistance of astronomical data. This data is commonly included in weather forecasts found in various print and online publications. To find the true noon, one must locate the sunrise and sunset times for the specific area in question. By adding these times together and dividing by two, the resulting value will indicate the time of true noon.

Approach #2 – utilizing a sundial (gnomon). When properly designed, marked, and installed, a sundial can accurately indicate the time of solar noon. The gnomon aligns with twelve o’clock during the moment of solar noon.

Approach #3 – using a navigator. By indicating the direction towards the geographic north, a navigator can aid in determining the onset of true noon. To do this, identify the moment when the center of the solar disk is directly above the southern or northern direction (depending on the Earth’s hemisphere), as determined with the assistance of a navigator. This moment will signify true noon.

The use of a magnetic compass is limited in this method, as it indicates the direction to the magnetic poles rather than the geographical poles, resulting in significant errors. We have explained the true and magnetic poles, as well as their differences, in a separate article.

Method No. 4 – using the shadow from a pole. A level pole is inserted into the ground vertically on a level horizontal surface. Prior to noon, the length of the shadow cast by the pole is measured. Initially, the shadow will decrease and then increase. The moment when the shadow starts to lengthen corresponds to solar noon.

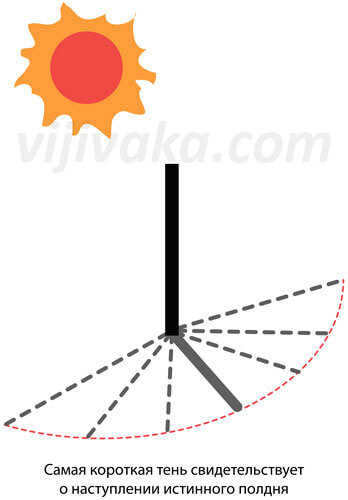
One way to determine the sides of light on the ground in sunny weather is by noting the time at which the shadow is shortest. This method of orientation is often recommended in literature and relies on the levelness of the ground and the chosen pole. The accuracy of the method can be increased by using a longer pole, typically 1-2 meters in length.

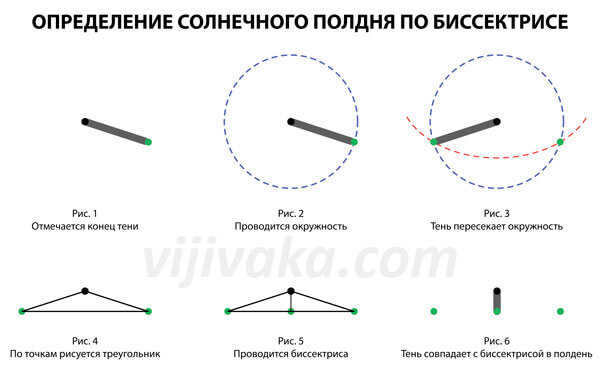
Another method, known as Method #5, involves using the bisector. This method requires measurements to be taken as early as possible in the morning for increased accuracy. Here’s how it works:

1. Install a pole on level ground, similar to the previous method, and mark the end of its shadow.
2. Measure the distance from the placement of the pole to this marked point.
3. A circle is created with a radius equal to the mentioned distance and positioned at the point where the pole is installed. Now we just need to wait for the pole’s shadow to cross this circle again, but in a different location (towards the east).
4. Once this happens, the second point is marked.
5. The first and second points are then connected by a line, forming a sort of isosceles triangle with the third vertex being the location of the pole installation.
6. A bisector is drawn from the point of pole installation, dividing the previously drawn line segment between the two points in half.
7. The following day, when the shadow from the pole aligns with the bisector, it can be concluded that true noon has arrived.

This method, similar to the previous one, is also a technique for orienting oneself using the sun.

Out of all the different options available, only the first one can be used in any weather conditions, at any time of the day, and provide quick results. The other options, on the other hand, can only be used during daylight hours, are dependent on the weather, and are generally slower.

Now, taking into consideration all of the information mentioned above, along with other data, let’s come to some general conclusions.

Conclusions

The sunrise occurs in the eastern direction, while the sunset takes place in the western direction. By following the time displayed on clocks, which closely aligns with astronomical time, we can estimate that the Sun will be positioned towards the east at around 6 a.m., gradually moving towards the west by 6 p.m., and reaching a southern point around noon. However, it is important to account for any necessary adjustments when translating the time displayed on clocks.

In the northern hemisphere, if one were to face away from the Sun, their front side would be oriented towards the north, the south would be behind them, the west would be on their left, and the east would be on their right. Conversely, in the southern hemisphere, facing away from the Sun would result in the front side pointing towards the south, the north would be behind, the east would be on the left, and the west would be on the right.

In order to improve the precision of Sun and clock-based orientation, it is necessary to consider and make appropriate adjustments for all factors that can cause deviations in the readings of “terrestrial” clocks from astronomical ones.

Orientation by the Sun can only be done during daylight hours when the weather is clear or slightly cloudy.

Overall, the methods of using the Sun for orientation, and specifically determining the true noon, enable individuals to identify the different sides of the world, orient maps, and maintain their desired direction of movement even in the absence of a compass, GPS, and visible landmarks. This is a highly valuable skill not only for tourists and hunters, but also for regular individuals who occasionally venture into nature to escape the noise and chaos of the city.

A shadow pointing north at noon can be observed in the northern hemisphere.

It is imperative to not only memorize the techniques, but also comprehend the underlying mechanisms on which they rely. By doing so, one can always adapt the method to the specific circumstances at hand. Failing to do so may result in errors and emergencies in certain situations.

To illustrate, numerous online articles and textbooks mention the technique of orienteering using mechanical clocks and the Sun, which we will delve into further below. However, it is rarely mentioned that this particular method only works in the northern hemisphere, specifically above the tropical zone. If someone is unaware of the origins of this method, they can easily make an error and, while in the southern hemisphere, incorrectly identify the directions of the world, leading to getting lost.

Therefore, what is this fundamental knowledge that is essential for determining the directions of the world based on shadows?

The Foundations of Theory

All the techniques for orienting oneself using the Sun’s shadow are based on well-established facts. Let’s take a closer look at them.

Fact #1: The Sun always rises in the east and sets in the west. However, in high latitudes during the polar day, it remains above the horizon for several weeks without setting, while during the polar night, it doesn’t rise above the horizon at all.

Fact #2: In the middle and high latitudes of the northern hemisphere, the Sun is in the southern direction at noon, or as it is commonly referred to, “in the south.” In the southern hemisphere, at the same distance from the equator, the Sun’s disk moves northward at noon. At the equator, the Sun is in the north half of the year, the south half of the year, and passes directly overhead for two days a year. We discussed this extensively in a separate article.

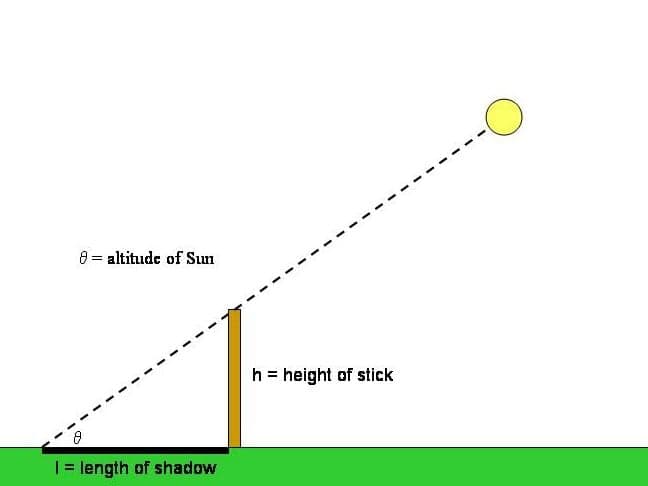
Fact #3. During astronomical noon, the length of the shadow cast by objects placed vertically on a flat horizontal surface is at its minimum. This occurs because the Sun is positioned directly overhead, at its highest point in the sky.

Fact #4. The Sun traverses the celestial sphere at an angular velocity of approximately 15 degrees per hour.

Fact #5. When facing north, the south will be behind you, the east will be on your right, and the west will be on your left.

Exclusively, this system will only function in the northern hemisphere in middle and high latitudes.

Naturally, it must be comprehended that it is not the Sun itself that ascends in the east and traverses the sky, and this apparent motion is connected to the Earth’s rotation and the existence of an observer on its surface. However, for the sake of simplicity, we will discuss the Sun’s movement rather than the Earth’s rotation.

And now, I suggest proceeding directly to the techniques of orienting oneself using the Sun’s shadow.

Methods for Determining Cardinal Directions Using Shadows

As promised, we will now discuss several popular methods for determining the cardinal directions.

Method #1: The Shortest Shadow from the Pole

This method is based on the observation that shadows from objects are shortest at noon. Follow these steps:

1. Insert a vertical pole into a flat horizontal surface.
2. Before noon, mark the end of the shadow cast by the pole on the surface.
3. Make these marks at regular intervals.
4. Once the shadow begins to lengthen after noon, connect all the marks with a smooth curve.
5. Identify the point on the curve that is closest to the pole and mark it.
6. Draw a line from the pole to this point. This line represents the north-south direction.
7. People position themselves on this line in such a way that it runs parallel to their feet, with the sunrise marks on the left side. At this moment, the north is in front of them, the south is behind them, the east is to the right, and the west is to the left.

If the shadow starts to lengthen from the moment the first point is marked, it indicates that noon has already passed, and one must wait until the next morning to repeat the process.

There is a need for additional constructions in most methods of orienting by the Sun.

Method #2. Utilizing the shadow of a pole at the center of the segment. This approach is founded on the principle that the Sun ascends in the east and descends in the west, and the right portion of its trajectory across the sky mirrors the left portion. To employ this method:

1. Similar to the previous method, a pole is inserted vertically into the ground.
2. In the morning, a mark is made on the ground representing the end point of the shadow cast by the pole.
3. The distance from the pole to this mark is measured.
4. A line is drawn straight between the initial mark and the second mark, representing the east-west direction.
5. The individual positions himself in a way that the initial mark is to his left and the second mark is to his right. Thus, we can determine that north is in front of him, south is behind him, east is to his right, and west is to his left.

You can find information about other variations of these techniques in the article on the position of the sun at noon…

These two techniques allow for relatively precise orientation based on the shadow of the Sun anywhere on Earth (excluding polar regions and the poles themselves) during daylight hours. However, they are time-consuming and not practical for individuals who need to navigate while on the move.

Method #3. Utilizing the shadow cast by a pole at two specific points. This particular technique is based on the understanding that the sun ascends in the east and descends in the west, causing shadows to move from west to east, albeit not always in a linear fashion. To orient oneself using this method:

1. As previously mentioned, a pole is inserted vertically into a level, horizontal surface.
2. A marker, such as a stone, peg, or any other convenient object, is used to denote the end of the shadow cast by the pole.
3. After approximately 15 minutes, a second marker is placed to correspond with the new position of the shadow’s end.
4. By positioning one’s left foot on the initial marker and the right foot on the second marker, the individual will be facing north, with south at their back, east to their right, and west to their left.

This technique, similar to the ones mentioned earlier, can be employed anywhere in the world during daylight hours, but it distinguishes itself in terms of speed. Nevertheless, this approach may encounter challenges in terms of precision.

The issue lies in the fact that the shadow cast by the pole typically forms a curved line throughout the day, rather than a straight one. Furthermore, the shape of this line can be either concave or convex, depending on the latitude and time of year in relation to the position of the pole. Neglecting these factors can result in significant errors, which is why I will provide my recommendations to ensure the maximum efficiency when utilizing this method. There are only two such recommendations.

My first recommendation is to utilize this technique during the months of March and September. These months provide the highest level of accuracy throughout the entire day, particularly during the spring and fall equinoxes when the shadow forms a perfectly straight line. As you move further away from these equinoxes on the calendar, the margin of error will increase.

For my second recommendation, it is best to rely on this method during the midday hours. Regardless of the time of year, this technique yields the most accurate results around lunchtime. The further you move away from solar noon, the greater the potential for error. For instance, if you were to orient yourself three hours before noon and then repeat the measurements three hours after noon, the margin of error could double.

Technique #4. Using shadow and clock to determine orientation. This technique is based on the concept that at 12 noon, the Sun is approximately in the south in the northern hemisphere, and in the north in the southern hemisphere. At 6:00, the Sun is approximately in the east, and at 18:00, it is approximately in the west. Consequently, a person’s shadow is cast in the opposite direction of the Sun.

For instance, if you face the Sun at noon in the northern hemisphere, your shadow will point towards the north, while in the southern hemisphere, it will point towards the south. If you face away from the Sun at 6 a.m., your shadow will point towards the west, and if you do the same at 6 p.m., your shadow will point towards the east. By determining one direction in this manner, you can determine all the other directions as well.

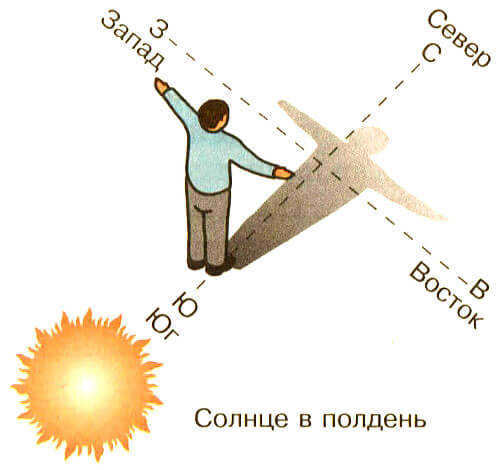
A typical image representing the northern hemisphere.

If one needs to navigate, there is no need to constantly search for a flat surface to stick a stick into and wait for fifteen minutes. Once you have oriented yourself, it is sufficient to determine the direction of the Sun and choose a path based on its position in the sky. For instance, if the Sun is on the right side when turning in the correct direction, one should continue to keep it on the right side during the journey. Over time, adjustments can be made for the Sun’s speed, and the method described can be used to confirm the direction during breaks.

When using this technique, it is crucial to bear in mind that certain countries observe daylight saving time and that the position of the Sun at noon in tropical and equatorial regions can vary throughout the year, as we discussed in a separate article. Furthermore, we also discussed other factors that can impact the accuracy of this method.

Method #5. Utilizing the shadow of a matchstick and a traditional clock with hour and minute hands. This technique is documented in various military manuals and is based on the understanding that in the northern hemisphere, the Sun moves in a clockwise direction across the sky, covering an angular distance of 15 degrees per hour. To orient oneself using this method in the northern hemisphere:

1. Place the clock horizontally with the face pointing upwards.
2. Position a matchstick between the hour hand of the clock and the number “12” on the dial from a side perpendicular to the face. For instance, if the clock displays 8:00, place the matchstick near the “10” mark, and if the clock displays 20:00, place it near the “4” mark.
3. The match should be turned on the clock until the shadow of the match crosses the center of the dial.
4. Once the shadow of the match aligns with the center of the dial, the number “12” will indicate the approximate southern direction.

This technique is effective only when the Sun is low above the horizon, particularly during noon. The higher the Sun is at noon, the more inaccurate this method becomes.

This is because the speed at which the Sun’s projection moves along the horizon does not align with the Sun’s angular velocity and varies throughout the day. These variations are more significant as the Sun’s zenith position increases.

That is why this method of orientation is most effective in regions with high latitudes. In areas with middle latitudes, it is preferable to use this method during the winter season, when the Sun is positioned at a lower altitude above the horizon. In tropical regions and at the equator, this method is generally not utilized due to the fact that the Sun is positioned at a high altitude above the horizon throughout the year, resulting in significant inaccuracies.

In this approach, similar to the previous one, it is necessary to consider the adjustment of clocks for daylight saving time. Other factors are typically not taken into account since the method still yields a relatively large margin of error and is primarily intended for rough estimation of cardinal directions.

When using this technique in the southern hemisphere, it is necessary to make adjustments to ensure accurate results. In my personal approach, I visualize a dial with numbers arranged in a counterclockwise direction. For instance, if the time is 10 am, I imagine the hour hand pointing to the number “2”, and if it is 16:00, I imagine the hand pointing to “8”. From there, I follow the steps outlined in the method, but instead of relying on the actual hand position, I use the imaginary one.

This approach is particularly useful for approximating cardinal directions and may have larger margin of error compared to previously discussed methods. However, it offers the advantage of quickly orienting oneself within seconds, making it highly practical for on-the-go navigation.

How to Calculate Time Using Shadows

The techniques for determining time using shadows rely on the same principles as orienteering methods.

The sundial is one of the oldest tools used to determine the time of day based on the shadow’s direction.

There are several methods to determine the time based on the shadow cast by an object illuminated by the Sun. Let’s explore some of them, but before we do, it’s important to consider the factors that affect the discrepancy between astronomical and “terrestrial” time in order to enhance accuracy.

Method #1. Using the shortest shadow. On a flat horizontal surface, a flat object placed vertically, like a pole stuck in the ground, will cast the shortest shadow at 12 noon.

Alternative Approach #2. East and West. The shadow will indicate the direction of the west around 6 am and the direction of the east around 6 pm. This technique becomes increasingly precise when the day in question is closer to the vernal or fall equinox.

Procedure No. 3. By north and south. The sun’s disk will traverse either the northern or southern direction (depending on the hemisphere, and in the tropics and on the equator – based on the time of year) precisely at noon.

Let’s talk about the Polar Regions separately. In the northern hemisphere, during the polar day, the Sun will pass to the south at 12 o’clock in the afternoon. However, it can also pass to the north without dipping below the horizon, which will correspond to 12 o’clock at night. In the southern hemisphere, it’s the opposite: the Sun will pass to the north at noon and to the south at midnight.

Method #4. Changing the angle of the shadow. This approach involves determining the angle between the pole’s shortest shadow, which occurs at solar noon, and the shadow at a specific time. By dividing this angle by the speed at which the Sun moves across the sky, we can calculate the time. If the shadow is on the west side, indicating that solar noon has not yet occurred, we subtract the calculated time from 12 hours. If the shadow is on the east side, we add the calculated time to 12 hours.

The last method is effective in regions with high latitudes (especially during the polar day near the poles). However, it produces significant errors near the equator, so it is not recommended for use in such areas. Nonetheless, out of all the previously described methods, this one allows for determining the time not only at 6 am, 6 pm, and noon, but also at any time in the middle of the day.

Of course, it is possible to create a simple “disposable” sundial by inserting a stick into the ground and marking the end of the shadow every hour on a sunny day. This type of sundial would still provide fairly accurate time readings for several weeks, until the vertical shift of the solar zenith becomes significant. However, implementing this method would require an additional day and a regular clock, which seems unnecessary. Why bother creating a sundial when there is already a regular clock available?

There are actually many more ways to determine and track time using shadows, but it wouldn’t make sense to go into detail about all of them. Today, I will simply focus on the essence of these methods, the underlying mechanisms, and demonstrate them using popular techniques. By understanding these mechanisms, individuals can not only utilize the described methods and verify their effectiveness, but also create their own methods that are convenient for specific situations.

When it comes to the aforementioned methods, it is impossible to determine the best one: each method has its own strengths and weaknesses. That’s why it is crucial to utilize all of them and choose the most suitable one based on the prevailing conditions.

Fascinating video: and an alternative method of telling time without a wristwatch….

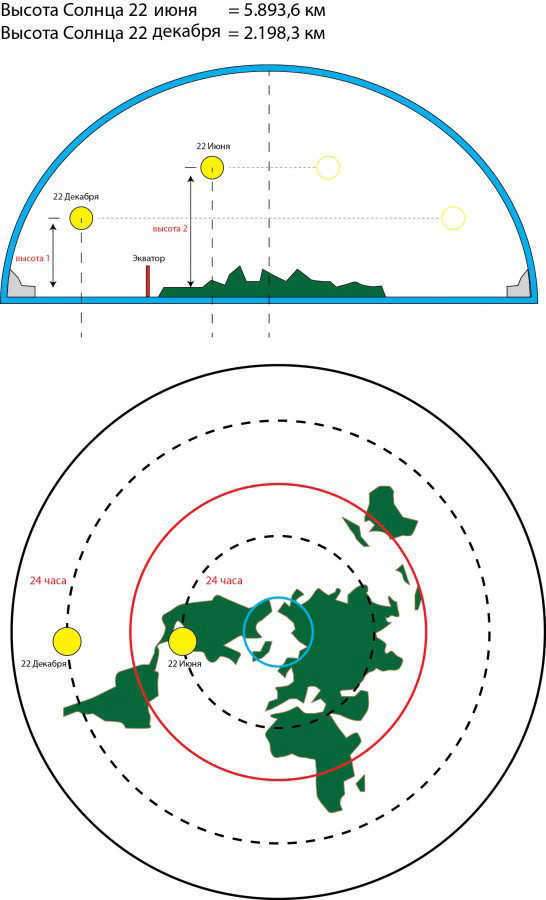
Every day, the Sun traverses a complex spiral path above the flat earth, altering its height, circumference, and speed.

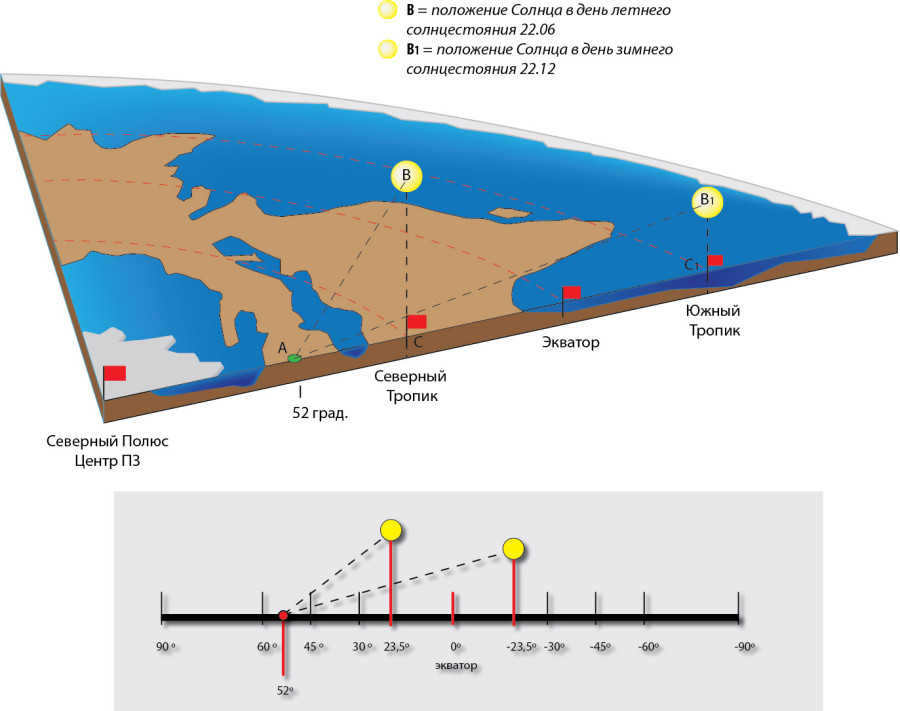
December 21-22 marks the point in the year when the Sun’s orbit reaches its maximum length, as it reaches the Southern Tropic known as the Tropic of Capricorn.

During this time, the Sun not only has the lowest altitude above the Earth and the longest orbit, but also the highest speed.

Within the Tropic of Capricorn, the Sun remains stationary for a period of 3 days. After December 24-25, it begins its new path, symbolizing a rebirth. This is why Christmas is celebrated worldwide on December 24-25. The Sun embarks on a new spiral journey around the center of the Earth, the North Pole.

The climax of this expedition will occur on June 21-22, during the summer solstice, at the furthest point north along the Tropic of Cancer.
During this time, the Sun reaches its highest point above the Earth’s surface on the flat Earth model, and the orbit itself is at its shortest length with the slowest speed of passage.

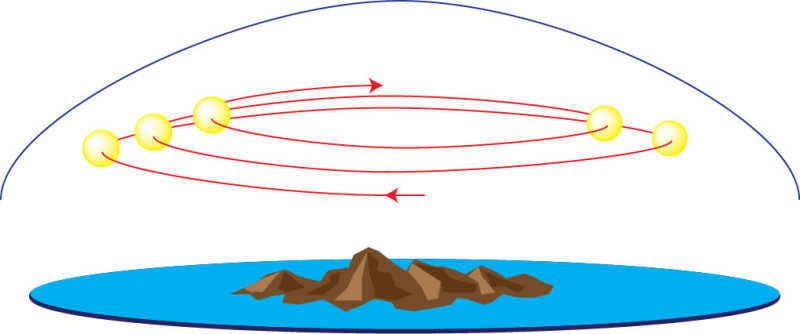
The most precise way to determine the height of the Sun at noon is by measuring it twice a year, specifically on December 22 and June 22.

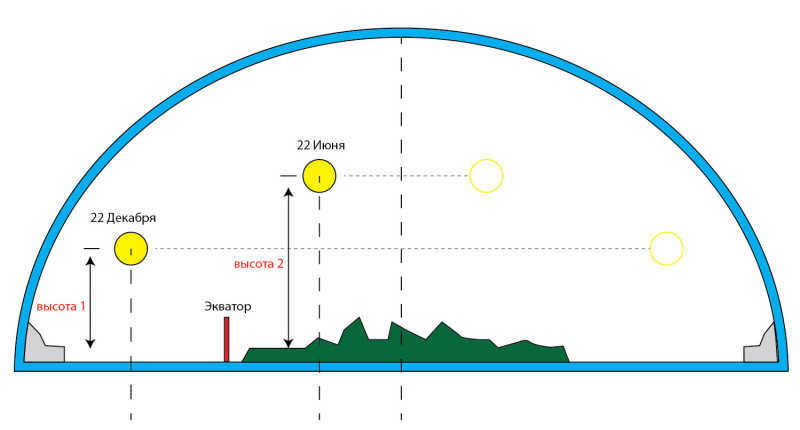
On this particular day, the sun will reach its lowest point in the sky, resulting in the shortest shadow at noon. If we place an object with a height of 1 meter in Berlin, the angle of the shadow cast will be approximately 14.5 degrees, which corresponds to the latitude of the city.

To conduct an experiment, take a 1-meter long rail and go outside on December 21 at exactly 12:00. Measure the length of the shadow cast by the rail.

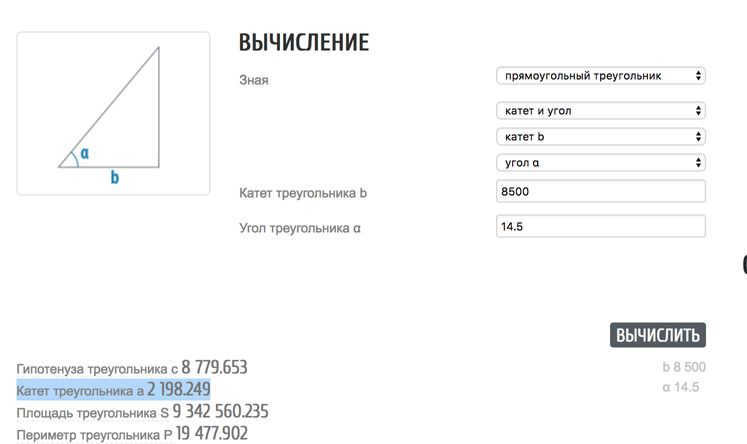
Knowing that the distance from Berlin to the Southern Tropic is 8,500 kilometers (cathetus B) and the angle of the cast shadow is 14.5 degrees, we can calculate the unknown cathetus A, which represents the altitude.

To determine the height of the sun at noon, we will make use of a calculator.

Using the identical method, we can determine the height of the sun at noon on the northernmost point, specifically on the summer solstice which falls on June 21-22.

The distance from Berlin to the Northern Tropic is 3,200 km (Cathetus B).

The cast shadow at noon on June 22 in Berlin, at a latitude of Berlin, has an angle of 61.5 degrees when the object height is 1 meter.

We can calculate the altitude of cathetus “A” to be 5.893.6 km using a calculator.

By dividing the difference by 180 days (6 months), we can determine the distance the sun descends in one day.

The sun descends approximately 20.53 kilometers per day during the winter and rises in the summer, completing one revolution in its orbit. This means that the vertical step of the sun’s spiral orbit is equal to 20.53 kilometers.

Recent Posts from This Journal

Mikhalkov’s perspective on Bucha, based on verifiable FACTS !

The Four Horsemen of the Apocalypse

So, you have already determined whether the rays in the Earth’s atmosphere propagate in a straight line or follow intricate curvilinear paths due to the complex laws of “refraction” above and below the dome, which result in the clockwise twisting of the celestial sphere in the southern hemisphere, and so on.
Additionally, if you use more than two sun sighting points, it immediately undermines all of your theories. This is because there is no practical way for observations from three locations to converge on a single point representing the Sun’s position.

Edited at 2019-11-12 10:48 pm (UTC)

Anyone can calculate the distance from the Earth to the Sun over the equator in just a couple of minutes, without the need for any measurements. And this calculation can be done with very high accuracy.

Twice a year, the sun crosses the equator as it moves from the northern tropic (23.5 degrees) to the southern tropic (-23.5 degrees). Surprisingly, this phenomenon can be explained using the spherical-vertex model, where the earth tumbles in a specific way, similar to a wolfcart on its last breath (precession).

So, if you have a satellite dish, you might have noticed that when the sun is directly above the equator, the satellite dish, the geostationary satellite, and the sun align in a straight line, causing the signal on your TV to disappear momentarily. This phenomenon is known as solar interference or backlighting.

Now, imagine a rectangular triangle with known angles of 90 degrees at the equator and the antenna elevation angle, let’s assume it is @.

There is a known measurement called a cathetus, which represents the distance between your antenna and the equator (you can use Google to find it). Using a trigonometry formula, you can calculate the height of the sun above the equator by multiplying the distance from the antenna to the equator by the tangent of the elevation angle of the antenna (@). You can determine the elevation angle by using a water level or a satellite antenna tuning program (such as Satellite-Antenna-Alignment-install-2.36.8.rar, which can be downloaded from the internet). In the program, input your geographical coordinates and use Google to find the name of the satellite you are watching (e.g., NTV+ and Tricolor have a 36-degree angle). This calculation should give you an approximate distance of about 3000 kilometers.

This solar interference phenomenon completely masks geostationary satellites located 36,000 km away, whether on the spherical (SH) or flat earth (FL) model. This occurs because the sun, satellite, and antenna can align on a single line, particularly on the equator, but not in the northern hemisphere where we view NTV+ and Tricolor packages for SH. Similarly, in the case of FL, it is impossible for the sun and satellite to occupy the same point simultaneously. This unique occurrence simultaneously reveals the deception surrounding cosmic affairs.

Your post is insignificant.

After carefully examining your post, I have concluded that your “evidence” is inconclusive and holds no significance. It is clear to me, and hopefully to you as well, that the shadow cast by your rail in a heliocentric system is a result of the Earth’s rotation axis tilt. While it is true that the length of the shadow on a curved surface would be longer than on a flat surface, in the context of a spherical Earth, the size of your rail is negligible compared to the Earth’s radius. Therefore, whether you measure using a ruler or apply geometric theorems, the length of the shadow will be approximately the same in both scenarios (with a minuscule margin of error).

During your travels, you might have come across the notion that the sun is “directly overhead” at noon. However, unless you happen to be on or north of the Arctic Circle, this statement is technically incorrect. In fact, even if you don’t reside on the Earth’s equator, the sun’s highest position above the horizon, known as its altitude, slightly fluctuates from day to day throughout the year.

The sun’s altitude, which is measured in degrees, is influenced by two factors: your proximity to the equator and the date.

Step 1: Understand

Your latitude is a numerical value that ranges between 0 degrees (if you reside on the equator) and 90 degrees (if you reside at either the north or south pole). In the United States, the majority of individuals are situated between 25 degrees north latitude and 45 degrees north latitude. Considering that the Earth’s circumference is roughly 25,000 miles and a full circle is comprised of 360 degrees, each degree of latitude measures slightly less than 70 miles.

If you are unsure of your latitude, you can utilize NASA’s Latitude/Longitude Finder (refer to “Latitude/Longitude Finder” under Resources) to determine your location. For instance, Boston, Massachusetts, USA is positioned at a latitude of 42 degrees north.

Step 2: Determining the Altitude of the Solar Equinox

The Earth is tilted at an angle of 23.5 degrees from a line that is perpendicular to its plane of rotation. This tilt can be visualized as a wolf that is slightly off balance. The Earth’s tilt is responsible for the changing seasons and it also affects the highest altitude at which the sun appears in the sky. On approximately March 22 or 23 and again on September 22 or 23, the Earth passes through the equinox, which is a Latin term meaning “equal night.” During these two days, the Earth experiences 12 hours of daylight and 12 hours of darkness. At this time, the sun rises to an altitude that is equal to (90 – L) degrees above the horizon. For Boston, this translates to an altitude of (90 – 42.36) = 47.64 degrees relative to the horizon. This is just over halfway to the zenith, which is the point directly overhead.

Step 3: Calculate the Altitudes of the Sun during the Solstices

Starting from the vernal equinox in the northern hemisphere on either March 22 or 23, which marks the first day of spring, the duration of daylight gradually increases and the sun rises to a higher position each day. Three months later, around June 22, we reach the summer solstice, which is the first day of summer and commonly known as the “longest day of the year.” Due to the aforementioned tilt of 23.5 degrees, at noon in Boston, the sun is now positioned at (90 – 42.36 + 23.5) degrees, which is equivalent to 71.14 degrees above the horizon. This is approximately 80 percent of the distance from the horizon to the zenith (71.14 ÷ 90 = 0.790).

After a span of six months, around December 22 or 23, the autumnal equinox has passed, and the winter solstice has arrived. This day marks the beginning of winter and is known as the “shortest day of the year.” During this time, the situation with summer is completely reversed, and the sun only reaches an altitude of approximately 24.1 degrees (90 – 42, 36 – 23, 5). This is just a little over a quarter of the distance from the horizon to the zenith (24, 14 ÷ 90 = 0.268).

The phenomenon caused by the Earth’s tilt is known as declination. It assumes a positive value during the spring and summer months and a negative value during the fall and winter months, fluctuating between 23.5 and -23.5 degrees.

The formula for determining the altitude above the horizon on any given day is (90 – L + D). In our previous examples during the equinoxes, the value of D was zero and thus not explicitly mentioned.

To calculate the declination and altitude of the Sun for today, there are a few online tools available such as the NOAA Solar Calculator or the Kiesan Calculator. However, if you don’t have access to these tools, you can still make a reasonable estimation by knowing the date and approximate latitude. For instance, if you are in Miami, Florida in early May, you can assume that the Sun’s declination is roughly halfway between 0 and 23.5 degrees because spring is halfway through, and your latitude is around 25 degrees. Therefore, you can estimate that the Sun will rise to an altitude of approximately 76.5 degrees by subtracting your latitude from 90 and adding 11.5 degrees.

What is the method for determining the height of a structure?

One can ascertain the elevation of a structure without descending to the ground by employing basic trigonometric or geometric examination. The shadow cast by the edifice during a sunlit day when the sun is positioned at its zenith can be utilized, or alternatively, a sextant can be employed to gauge the angle to the apex of the building. The former methodology possesses certain advantages over the latter.

There are different methods to determine the height of a structure that is too tall to measure directly, like a flagpole or a building. You can use geometric or trigonometric techniques for this purpose. In the geometric method, you compare the shadow of the measured structure with the shadow of a directly measured object. On the other hand, in the trigonometric method, you observe the top of the object.

Converting a slope height to a regular height: a step-by-step guide