
At present, there are 58,741 educational establishments that qualify for extra combined markdowns (ranging from 2% to 25%). To determine the applicable discount for all staff members at your school, please sign in to your personal Infoworks account.


Professional course for retraining
Library and bibliographic and information knowledge in the educational process.
In addition to this discount, you can also take advantage of the discount offered by your educational institution, which is based on the number of your colleagues who have already completed Infowork courses.
Currently, 58,741 educational institutions are eligible for additional discounts ranging from 2% to 25%. To find out the discount available for all staff members of your educational institution, please log in to your personal Infoworks account.


Professional training program
Management of librarian activities in the field of professional education
In addition to this discount, we can also apply your educational institution’s discount (the amount depends on the number of your colleagues who have completed Infoworks courses)
Currently, 58,741 educational institutions are eligible for additional discounts (ranging from 2% to 25%). To determine the specific discount applicable to all employees of your educational institution, please login to your personal Infoworks account.




Emergency assistance during outdoor adventures
Breakdown of the presentation, slide by slide:

Slide 2: Calculating the Distance to an Unreachable Object
With
A
B
Baseline
The angle ASV, which represents the view of the baseline from an unreachable position, is known as parallax.
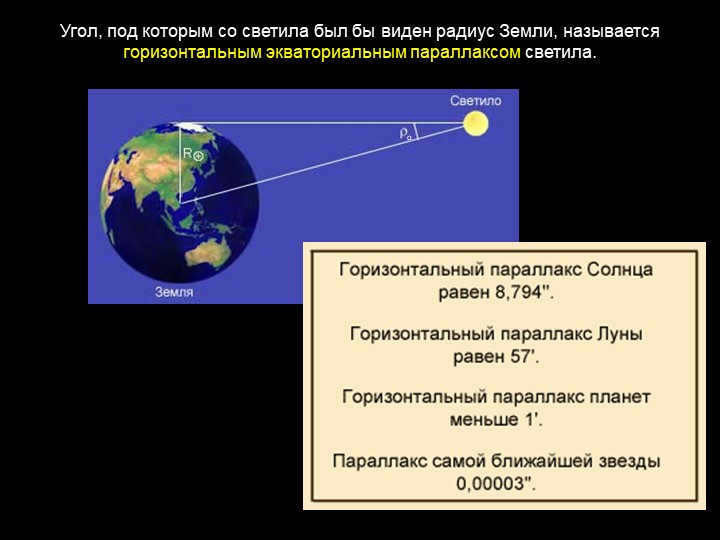

Slide 3: The horizontal equatorial parallax of a luminary is the angle at which the radius of the Earth becomes visible from that luminary.
о
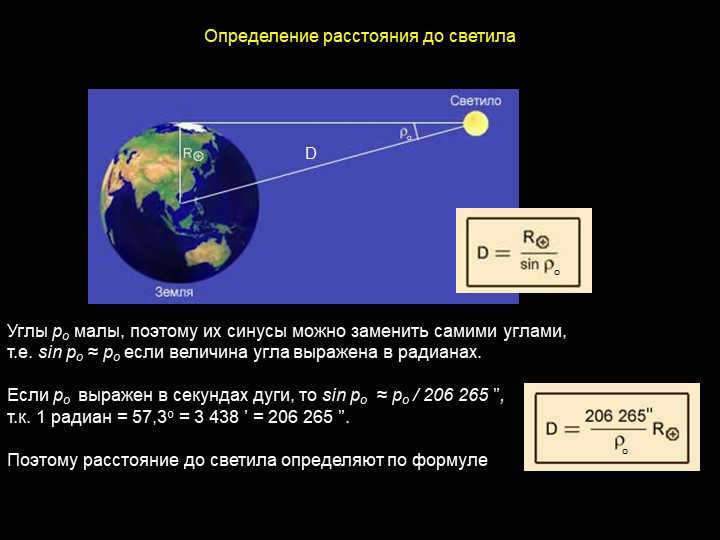
Slide 4 D
The small angles of ro can be approximated by their sines, meaning that sin ro ≈ ro when ro is expressed in radians.
When ro is expressed in arc seconds, sin ro ≈ ro / 206 265, as 1 radian is equal to 57.3 degrees, which is also equal to 3,438 arc minutes or 206,265 arc seconds.
Therefore, the distance to the luminary can be determined using the formula for the determination of the distance to the luminary.
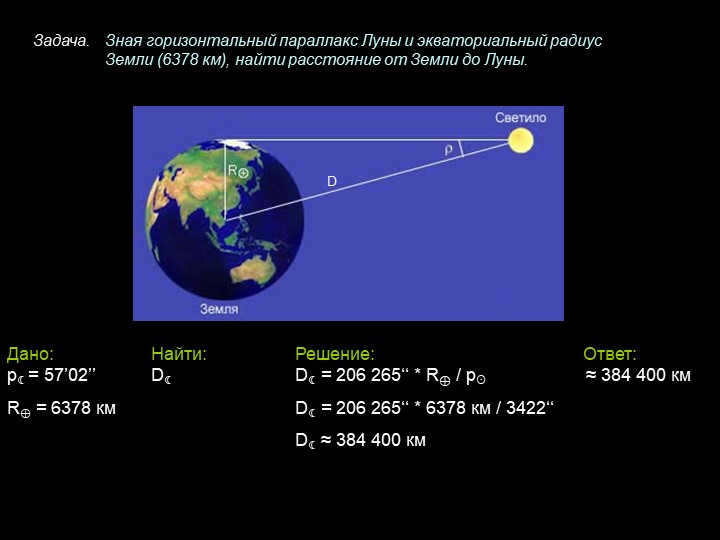
On the fifth slide, we are given the following information: we need to find the solution and answer. Let p be equal to 57'02'' and D be equal to 206,265'' * R⊕ divided by p, which is approximately 384,400 km. Given that R⊕ is equal to 6378 km, we can calculate D by multiplying 206,265'' by 6378 km and dividing it by 3422''. The approximate value of D is 384,400 km. The task is to find the distance from the Earth to the Moon, given the horizontal parallax of the Moon and the equatorial radius of the Earth (6378 km).

Slide 6: The radar technique for measuring distances to planets.
A short pulse is transmitted and then received after reflection.
The speed of radio wave propagation is equivalent to the speed of light in a vacuum:
c = 299,792,458 m/s.
By conducting radar observations of Venus, the following value for an astronomical unit is obtained:
1 a.u. = 149,597,868 ± 0.7 km

7 slide Determining the Earth’s radius
A
B
O
R
l
n
l / n = 2 π R⊕ / 360
R⊕ = 180 l / (π n)
Method for calculating the radius of the Earth:
Assuming the Earth is a sphere with radius R⊕, measure the linear (l) and angular (n) distances between two points on the Earth’s surface that are on the same line of longitude.
Then, calculate the arc length corresponding to 1 degree of this line of longitude:
The radius of the Earth can be determined using the following formula:

During his time in Siena (Aswan), Eratosthenes made an observation of the Sun passing directly overhead on the day of the solar solstice. This phenomenon could even be observed in deep wells. Moreover, he utilized a special instrument called a scaphysis to determine that the Sun deviated from the vertical by 1/50th of a circle (7.2°) when observed from Alexandria, which was located 5,000 stadia away. Based on this information, he was able to calculate the Earth’s radius to be 40,000 stadia (6,400 km). Eratosthenes’ estimation of the Earth’s size was groundbreaking in the 3rd century BC.

9 slide Calculation of the linear dimensions of the celestial bodies of the solar system
R = D sin ρ
R
о
ρ
о
R
D
ρ – angular radius of the celestial body
Task. How many times is the linear radius of the Sun greater than the radius of the Earth,
If the angular radius of the Sun is 16′?
Given: Find: Solution:Answer:
ρ∀ = 16′ R∀ R∀ = R⊕ ρ∀ / p∀ ≈ 109 R⊕
p∀ = 8.8 “R∀ = (16*60″/8.8”) R⊕ ≈ 109 R⊕

Assignment questions: Numbers 2 to 4 and 6 on page 52
There is no single, universally accepted method for determining distances in the field of astronomy. As we venture further away from celestial bodies that are closer to us, we must rely on different methods to calculate distances, with each method building upon the previous one. The accuracy of our distance estimations is limited by either the least accurate method used or by the accuracy of the astronomical unit of length (a.e.), which is determined through radar measurements with an average error of 0.9 km. The current value of the astronomical unit is 149597867.9 ± 0.9 km. Taking into consideration various adjustments, the International Astronomical Union established in 1976 that 1 a.e. is equal to 149597870 ± 2 km.
Measuring the distances to the planets.
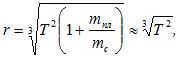
The orbital period T of a planet, measured in Earth years, can be used to calculate its average distance r from the Sun (expressed in fractions of a. e.):
where r is the average distance in a. e., and T is the orbital period in Earth years. The mass of the planet m can be disregarded compared to the mass of the sun mc. This formula is derived from Kepler’s third law, which states that the squares of the orbital periods of planets around the Sun are proportional to the cubes of their average distances from the Sun.
Precise measurements of distances to the Moon and planets can also be obtained using radiolocation methods.
Parallax method.
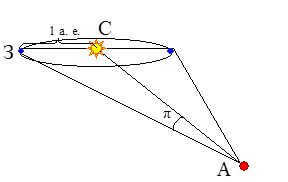
The slight movement of nearby stars in relation to distant “fixed” stars is due to the annual orbital motion of the Earth. Over the course of a year, a star traces a small ellipse on the celestial sphere. The size of this ellipse decreases as the star gets farther away. In terms of angular measurement, the major semi-major axis of the ellipse is approximately equal to the maximum angle at which the star can be seen, 1 a.e. (the major semi-axis of the Earth’s orbit), perpendicular to the direction of the star. This angle, known as the annual or trigonometric parallax (p), is equal to half of the star’s apparent displacement per year. It is used to calculate the distance to the star using trigonometric relations between the sides and angles of the WSA triangle. In this triangle, the angle p and the base, which is the major semi-axis of the Earth’s orbit, are known (see Fig. 1).
The distance to the star, which is determined by the trigonometric parallax value p, can be calculated as:
r = 206265''/p (a. e.),
Here, the parallax value p is measured in angular seconds.
Figure 1: The parallax method for determining the distance to a star (A – star, Z – Earth, S – Sun).
For the purpose of determining distances to stars using parallaxes in the field of astronomy, a unique unit of length called the parsec (ps) is utilized. A star situated at a distance of 1 ps exhibits a parallax equal to 1”. In accordance with the aforementioned equation, 1 ps is equivalent to 206265 astronomical units (a. e.) or 3.086-10 18 centimeters.
In addition to the parsec, another specialized unit of distance known as the light-year (i.e., the distance traversed by light in the span of 1 year) is employed, equivalent to 0.307 parsecs or 9.46-10 17 centimeters.
The nearest star to the Solar System, a red dwarf of 12th magnitude called Proxima Centauri, possesses a parallax of 0.762, indicating that its distance amounts to 1.31 parsecs (4.3 light-years).
The trigonometric parallaxes have a lower measurement limit of approximately 0.01”, allowing them to accurately measure distances up to 100 ps with a relative error of 50%. (For distances up to 20 ps, the relative error is no more than 10%.) Using this method, scientists have successfully determined the distances to around 6000 stars so far. However, for stars that are farther away, the photometric method is predominantly used to determine their distances.
Table 1. The Twenty Nearest Stars.
Parallax in seconds of arc
Visible stellar magnitude, m
Absolute stellar magnitude, М
The first mention of the Earth’s size can be traced back to Aristotle. In his book “On the Sky,” he mentions that mathematicians attempted to calculate the Earth’s circumference and arrived at an estimated figure of around 400,000 stadia. It is unclear whether Aristotle used Egyptian or Babylonian data, and the method by which this value was obtained remains unknown. In the ancient world, stadia varied in length, ranging from 157 to 210 meters. For the purpose of estimation, we will assume a stadion length of 180 meters, although there are ongoing debates regarding which stadion measurement different authors used. Taking the value of 180 meters for the stadion, let us calculate the Earth’s circumference according to Aristotle’s anonymous “mathematicians” to be approximately 70,000 kilometers.
This estimation is greatly inflated and the manner in which it was derived remains unknown.
Eratosthenes
Eratosthenes, also known as Eratosthenes of Cyrene, was a Greek mathematician, geographer, poet, astronomer, and music theorist. He lived in the third century BCE and is best known for his work in mathematics and geography. Eratosthenes is credited with being the first person to accurately calculate the circumference of the Earth, using a method that involved measuring the angle of the sun’s rays at two different locations. He also made significant contributions to the field of geography, creating the first known map of the world and introducing the concept of latitude and longitude. Additionally, Eratosthenes was a prolific writer and poet, and his works on various subjects have been highly regarded throughout history.
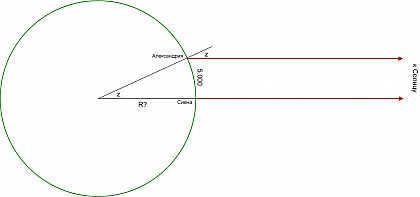
Eratosthenes employed the subsequent technique. Siena (currently Aswan) and Alexandria are situated along the same meridian and are separated by a distance of 5,000 stadia, with Siena positioned on the Tropic of Cancer: on the day of the summer solstice at noon, the sun is precisely at its highest point directly above, as observable from the well. By measuring the midday altitude of the sun above the horizon at Alexandria on this day (Eratosthenes suggested using a scaphis – a special type of sundial), it is feasible to ascertain the circumference of the Earth. This approach is effective as long as there is no topographic parallax of the Sun, a condition that Eratosthenes specifies and that is generally acknowledged among ancient writers.
According to Eratosthenes, the Earth’s circumference measures 250,000 stadia, which is equivalent to 45,000 kilometers using our conventional stadia of 180 meters.
Eratosthenes’ method, although methodologically flawless, relied on a certain degree of luck to accurately estimate the size of the Earth. Along the way, he encountered various errors that, surprisingly, canceled each other out. The measurement based on caravan travel time and the zenith distance of the midday sun from a well may not inspire complete confidence. By the way, Siena is located just north of the tropic.
Posidonius
could be rephrased as:
The philosopher Posidonius
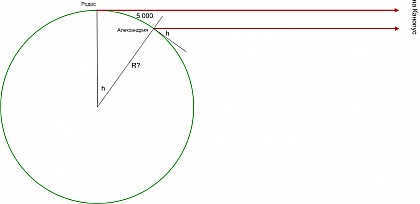
Posidonius makes his calculations based on another observation in astronomy: the star Canopus is exactly at the horizon on the island of Rhodes when it reaches its highest point (this can only be seen from the mountain, not from the plain). In Alexandria, the star reaches a height of 1/4 sign at its highest point (this is mentioned by Pliny the Elder, among others). Since Alexandria is located 5,000 stadia south of Rhodes, the circumference of the Earth is calculated to be 240,000 stadia, which is equivalent to 43,000 kilometers.
Cleomedes provides the method and results of Posidonius, but other authors have different data. I will not include them at this time.
Cleomedes (c. 1st century A.D.) calculates the size of the Moon and Sun and their distances.
Aristarchus of Samos
Aristarchus of Samos, who lived in the 3rd century B.C., was the first person to make an effort to calculate the distance to the celestial bodies such as the Moon and the Sun. This groundbreaking work is found in his only surviving piece of writing, titled “On the Magnitudes and Distances of the Sun and Moon.”
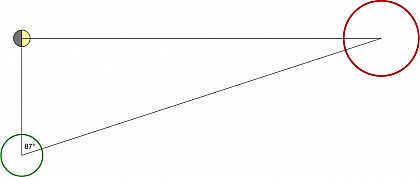
Initially, he calculates the proportion of distances to both the Moon and the Sun. This calculation is based on the fact that during the quarter phase of the Moon, the apparent angle between the Moon and the Sun is 87°. Aristarchus defines this ratio as:
Aristarchus, however, was mistaken in his calculation. In reality, the angle is actually 89° 50', resulting in a ratio of 1/400. It is worth noting that during that time, astronomers did not have the necessary instruments to accurately determine the precise moment of the quarter phase. Unfortunately, this error was due to technological limitations and not anyone’s fault.
But this ratio of distances is only the beginning. Aristarchus then proceeds to determine the actual values of these distances with the following statements:

Based on the given information, Aristarchus concludes that the Sun is 7 times bigger than the Earth, and the Moon is 3 times smaller. By using Eratosthenes’ estimate, we can determine that the diameter of the Sun is 90,000 kilometers and the diameter of the Moon is 5,000 km.
By understanding the actual dimensions of the Moon as well as its apparent size of 2°, it is possible to calculate the distance to the Moon, which is approximately 10 times the diameter of the Earth. However, Aristarchus does not utilize this method. If he had, based on Eratosthenes’ estimation, he would have arrived at a figure of 150,000 kilometers for the distance to the Moon. Therefore, the distance to the Sun would be 20 times greater, totaling 3,000,000 kilometers.
Exploring the mathematical concepts of Aristarchus of Samos
Incidentally, in this undertaking, Aristarchus Samosky incorporates trigonometric motifs and, specifically, articulates his own theorem.
In conclusion, let us summarize the outcomes of Aristarchus of Samosky and compare them with contemporary findings.
- The proportion of distances to the Moon and the Sun is 1/19, which is twice overestimated.
- The diameter of the Moon is overestimated by a factor of 1.5.
- The diameter of the Sun is underestimated by a factor of 15.
- The distance to the Sun is underestimated by a factor of 50.
- The distance to the Moon is underestimated by a factor of two.
Cleomedes, calculation of lunar size
Cleomedes, similar to Aristarchus of Samos, uses a lunar eclipse to estimate the magnitude of the moon. However, Cleomedes’ approach is much simpler and lacks the intricate astronomical and geometric complexities employed by Aristarchus. Perhaps this is because Cleomedes’ work serves as a basic textbook on general astronomy.
Like Aristarchus, Cleomedes deduces from lunar eclipse observations that the moon’s diameter is half that of the Earth, or 40,000 stadia, which is approximately 7,000 kilometers instead of the previously believed 3,500 kilometers. However, there are two notable differences. Firstly, the moon’s shadow is not twice the size of the Earth’s shadow, but rather two-thirds of it. Secondly, the Earth’s shadow is not a cylinder, as Cleomedes assumes, but a cone.

Cleomedes and the Phenomenon of Solar Eclipse
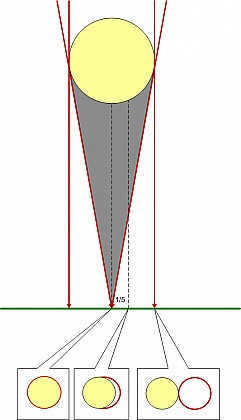
Cleomedes proposed an alternate approach to determine the size of the Moon. This method relies on a solar eclipse observation. During a solar eclipse in the Hellespont (Dardanelles Strait), the centers of the sun and moon were displaced by 1/5 of the diameter. Although Cleomedes does not provide a direct calculation, it is possible to estimate the moon’s diameter using his method and assuming a distance of 7,000 stadia between the observation points, as was common among geographers at the time. This estimation would yield a diameter of approximately 40,000 stadia, which aligns with the results of the initial method.
By measuring the size of the moon, which is 40,000 stadia, Cleomedes is able to calculate the distance to the moon as 5,000,000 stadia or 900,000 kilometers (in reality it is 390,000 kilometers). However, this calculation is not accurate. Cleomedes mistakenly assumes that the diameter of the moon is 1/750 of the full circumference of 360°, while in reality it is larger – 31' corresponds to 1/700 of the full circumference. Cleomedes justifies his use of the 1/750 value by measuring the time it takes for the moon to rise above the horizon using a klepsydra. However, this method of measurement is likely to be insufficiently precise.
Distance and size of the sun
Cleomedes
Cleomedes also provides an estimation for the Sun, using the assumption that all planets, including the Sun and Moon, move at the same linear speed. By considering the equality of the apparent sizes of the moon and sun, and taking into account the duration of the year and month, Cleomedes calculates the key ratio to be 1/13. From this, he deduces that the diameter of the sun is 520,000 stadia (equivalent to 93,000 kilometers), and the distance to the Sun is 65,000,000 stadia (equivalent to 12,000,000 km), rather than the previously accepted values of 1,400,000,000 and 150,000,000 km respectively.
Therefore, the measurements of the Moon Cleomedes were inaccurately calculated, with an overestimation of its parameters and an underestimation of both its size and distance from the Sun by a factor of ten. However, it should be noted that these calculations are a conservative estimate, as it would be naive to assume that the planets move at a uniform speed in their complex orbits. Additionally, the estimates of the Sun’s size provided by Cleomedes were unprecedented and unmatched by any previous physicists or astronomers.
Posidonius
can be rephrased as follows:
The philosopher Posidonius
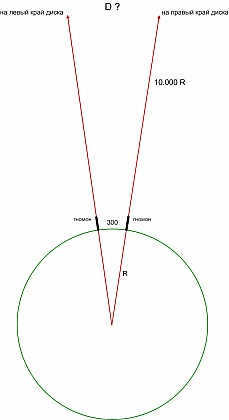
Around a hundred years before Cleomedes, Posidonius provided an estimation of the Sun’s size. We previously mentioned him when discussing the Earth’s dimensions.
Based on observations in Siena (Aswan), which is located on the Tropic of Cancer, during the equinox at noon, the gnomon casts no shadow on a 300 stadia wide area, indicating that the Sun is directly overhead. By estimating the distance to the Sun as 10,000 times the radius of the Earth, Posidonius calculated the Sun’s diameter to be 3,000,000 stadia or 540,000 kilometers (although the actual value is 1,400,000).
It seems audacious, no doubt, to employ a gnomon for measuring such angles. By the way, we possess an a priori evaluation of the Sun’s distance as well. It amounts to 70,000,000 kilometers..
Posidonius made erroneous calculations only twice when determining the magnitude of the Sun and its distance, but naturally, this is merely a fortuitous occurrence.
Cleomedes attempts to determine the physical dimensions of the stars, specifically the planet Venus, by assuming its apparent size is 1/6 of the sun. However, this estimate is greatly exaggerated and should actually be 1/30. Cleomedes reasons that since the sphere of Venus is smaller than the sphere of the Sun, the actual size of Venus must be proportionally smaller.
Cleomedes does not provide specific calculations due to the uncertainty of his assumptions, but he asserts that the stars, especially the fixed stars on the outer sphere known as the “sphere of stars,” are either similar in size to or even larger than the Sun.
Aratus on the planets
It is impossible to predict where and when to find the planets using other celestial bodies – their positions are constantly changing.
Cleomedes, “The Doctrine of the Circular Nature of Celestial Bodies”.
- If we observe the Earth from the distance of the Sun, it would appear as a star of the smallest magnitude, and it would not be visible from the sphere of fixed stars.
- The Sun itself, when observed from the distance of the fixed stars, would have a magnitude comparable to that of the stars, indicating their similar brightness to the Sun.
In ancient Greece, there were early attempts to estimate the distance between the Earth and the Sun and make predictions about related events. These initial calculations laid the foundation for the advancement of astronomy. Today, thanks to advanced technologies, modern scientists are able to accurately determine the distance to the Sun, with an error margin of just a few fractions of a centimeter.

An up-to-date calculation of the precise distance
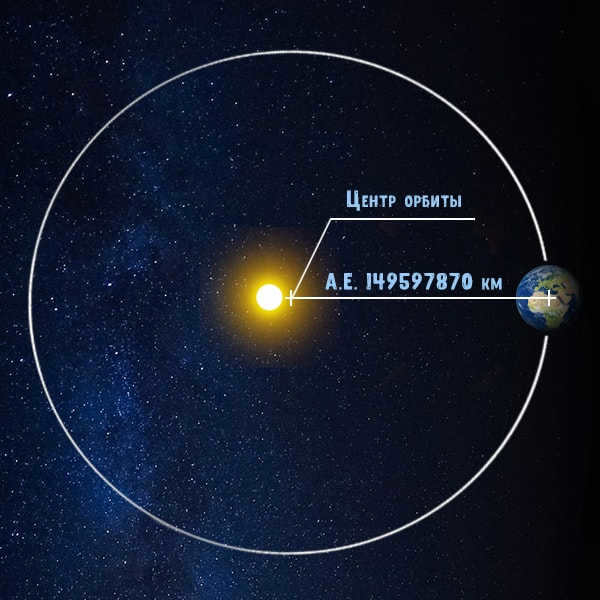
The measurement of the distance between the Earth and the Sun is commonly accepted as 149,597,870 km, although this value is merely an approximation. Due to the elliptical path of the planet’s orbit, its distance from the star is in a constant state of flux.
The concept of a celestial unit
The distance between the Earth and the Sun is known as a celestial unit. It is utilized for measuring the distances between celestial bodies. The Russian term for this unit is a.e., while the international abbreviation is au.
As of 2012, the International Astronomical Union has decided to align the celestial unit with the International System of Units (SI), making it equal to 149,597,870,700 meters. This value is employed for calculations that do not necessitate high precision. Otherwise, the specific value for the given moment in time is computed.
Impact of Tidal Forces on Distance
According to a team of Japanese astrophysicist Takaho Miura, the separation of celestial bodies can be attributed to the influence of tidal forces. Despite its relatively small size compared to the Sun, the planet generates tides within the star due to the fact that the closer regions of the star experience slightly stronger gravitational attraction compared to the more distant regions. These tidal forces propagate across the star’s surface and result in a slowing down of its rotation. As the total momentum of the Earth-Sun system remains constant, there is a slight expansion of the heliocentric orbit.
A similar interaction occurs between the Earth and the Moon. Deviations in the Moon’s orbit lead to daily oceanic tides on the planet, which in turn cause the lengthening of the day by 1.7 milliseconds per century. Additionally, the distance between these two celestial bodies increases by 4 centimeters annually.
Aphelion and Perihelion Explained
Aphelion and perihelion are terms used to describe the Earth’s maximum and minimum distances from the Sun. These distances are determined by the elliptical shape of the Earth’s orbit.
Aphelion, also known as apogelion, refers to the farthest point in the Earth’s heliocentric orbit, which is approximately 152,098,233 km away from the Sun. Astrophysicists use the term “aphelion” to describe the point in the orbit of any celestial body that is farthest from the star it revolves around. For the Earth, this occurs between July 3 and July 7 each year.
On the other hand, perihelion refers to the closest point in the Earth’s orbit, which is approximately 147,098,291 kilometers away from the Sun. The Earth reaches this point annually between January 2 and January 5.
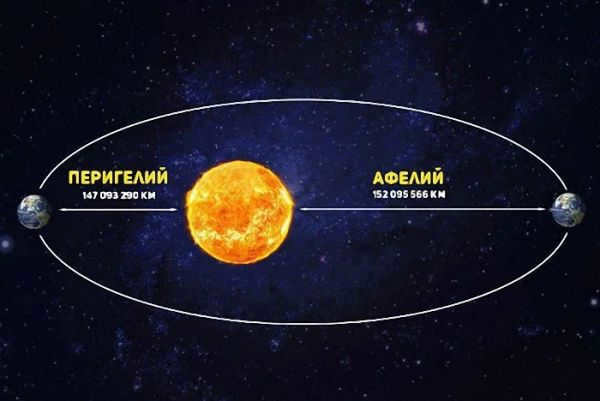
The parameters of aphelion and perihelion represent the maximum and minimum distances from the Sun. Acknowledgement: avatars.mds.yandex.net.
Calculating the distance from the Sun in ancient Greece
Ancient Greek scientists were the first to determine the distance from the Earth to the Sun. During that period, they had access to only basic tools and relied on geometric methods.
The postulations of Aristarchus of Samos
Ancient Greek astronomer Aristarchus of Samos, who lived in the 3rd century B.C., was the pioneer in the endeavor to estimate the distance to the Sun. He expounded on the heliocentric model of the cosmos and employed principles of geometry to ascertain the magnitudes of celestial entities and the gaps that separate them.
His calculations were based on the assumption that the round moon reflects sunlight. When it is in its half-phase, we can draw a right angle between the Earth-Moon-Sun. In this scenario, the side from Earth to Moon is the cathetus, and the side from Earth to Sun is the hypotenuse. According to Aristarchus’ theory, the distance to the star can be expressed as the ratio of the cathetus to the hypotenuse, which is 1:19. However, this result differs from the actual values by a factor of 20, indicating inaccurate calculations. Aristarchus relied on visual observations, which are always prone to significant errors.

Aristarchus of Samosia proposed the idea that the distance from the Earth to the Sun can be determined by comparing the length of the cathetus to the length of the hypotenuse. Credit: wikireading.ru.
Observations made by Hipparchus of Nicaea
Hipparchus of Nicaea, a prominent mathematician from ancient Greece in the 2nd century B.C., is considered one of the greatest astronomers of antiquity. He introduced more precise techniques to astronomical calculations based on the methods used by the ancient Babylonian explorers.
Hipparchus’ method was based on his understanding of the reason behind lunar eclipses: the moon is in the shadow of the Earth. The shadow takes the form of a cone, with the tip closer to the Moon. Using basic measuring instruments, the astronomer calculated the radii of the objects he was studying. By applying the principles of triangle similarity, he was able to determine the distance to the Sun. This distance was calculated to be 382 thousand kilometers. Hipparchus’ findings were considered the most precise of their time in ancient history.
Calculations in the Modern Era
Scientists in the modern era have taken a more meticulous approach to calculating cosmic distances. Many of their studies have achieved a high level of accuracy and have been acknowledged by the scientific community of the time.
Christian Huygens’ Approach Using Right-Angled Triangles
In 1653, the Dutch scientist Christiaan Huygens made his own calculations. His methodology closely resembled the one used by Aristarchus of Samos. Huygens also employed the right triangle method, but focused on the Earth-Venus-Sun system. By chance, he accurately estimated the size of Venus and conducted his calculations. However, the scientific community did not take Huygens’ measurements seriously and regarded them as mere speculation.
Cassini and Richet’s findings
In 1672, while in Paris, Giovanni Cassini conducted observations on the movement of Mars across the celestial sky. He assigned similar research to his assistant Jean Richet, while also sending a colleague to Guiana.
Cassini utilized the positions of the stars surrounding Mars for his measurements, comparing these data with Richet’s observations. Through this, he was able to determine the length of the Earth-Mars segment, which allowed him to calculate the distance between the Earth and the Sun. The astronomer employed scientific methodologies, which lent credibility to his findings.
The parallax technique
During their experiments, Cassini and Richet utilized the phenomenon of parallactic displacement, which refers to the apparent change in the position of a celestial object in relation to background objects situated at a certain distance. This change becomes noticeable when the observer alters their perspective.
This method enables us to determine the distance to the celestial object through straightforward geometric calculations. All that is required is knowledge of the observer’s displacement magnitude and the angle of displacement of the object being studied in relation to its background.
Trigonometric parallaxes are utilized to ascertain the distances to nearby celestial objects. In order to gauge the distances of objects that are far away, the standard candles method is employed. This method takes into consideration the principle that illumination diminishes in inverse proportion to the square of the distance.
Stars act as standard candles. Given that stars of the same temperature and size radiate the same amount of energy, similar stars are utilized to determine distances. By knowing the distance of the Sun and the magnitude of its energy emission, the distance to similar stars can be computed.
In the realm of astronomical research, the advent of modern technology has brought about a revolution, particularly in the realm of distance measurement. This is made possible through the utilization of the radar method, which involves the transmission of pulses towards celestial bodies. These waves are then reflected back and subsequently analyzed to determine their intensity and travel time, allowing for the calculation of the distance traveled.
The Radar Method
However, the radar method does present certain challenges. Specifically, the intensity of the waves diminishes in inverse proportion to the fourth power of the distance to the object under investigation. Consequently, the creation of powerful transmitters and large antennas becomes necessary to overcome this obstacle. Despite the associated costs, the accuracy of the data obtained justifies the investment, with the margin of error being only a few kilometers.
Measuring distance using laser technology
There are various methods available to determine the distance to a celestial body within the solar system. Credit: marsplaneta.ru.
The laser location technique operates under the same principles as the radio wave method. A high-powered transmitter emits a beam of light towards the heavenly body, which then reflects back to Earth. The intensity and duration of the beam’s travel are considered when calculating the distance.
This approach offers exceptional precision and allows for data acquisition with an error margin of mere fractions of a centimeter. However, it requires technologically advanced and costly equipment.
Units for Measuring Distances in Space
When it comes to vast cosmic distances, Earth-based measurements just won’t cut it. In the field of astronomy, there are three primary units of measurement:
- The astronomical unit (AU) – equivalent to 149.6 million kilometers.
- The light-year – approximately 9,460,730,472,580,800 meters, representing the distance traveled by a light wave in one Julian year.
- The parsec – roughly equal to 3.26 light-years, and defined as the distance at which the radius of the Earth’s orbit subtends an angle of one second of arc. This unit is commonly used by professional astronomers instead of light-years.
While the astronomical unit is primarily used for measuring distances within the solar system, the light-year and parsec are employed to estimate interstellar cosmic distances.
There are numerous potential scenarios for the apocalypse, such as global climate change, a supervolcano eruption, a meteorite impact, or nuclear war. While the Earth itself would likely survive, it would no longer be habitable for humans. In order to prepare for such a threat, scientists from around the world are currently searching for a safe haven where humanity can escape. Some researchers are exploring the idea of terraforming Mars or constructing underground habitats on the Moon. However, others are looking even further into the future. Exoplanets, also known as extrasolar planets, which are planets located in other star systems, could potentially serve as a refuge. The only challenge that remains is figuring out how to reach these distant worlds.
Unseen Satellites of Stars
It has long been speculated that the Earth is not the only planet of its kind. Even the ancient Greek philosopher Epicurus mentioned in a letter to his student Herodotus that “there are infinite worlds, both similar and dissimilar to our own.” This insight dates back to the 4th and 3rd centuries BC. Later, other thinkers shared similar notions, but without the invention of the telescope, they couldn’t be proven.
It wasn’t until the 19th century that scientists began actively searching for exoplanets. By then, they had a good understanding of how celestial bodies interact with one another. Astronomers were hopeful that they could observe peculiarities in the movement of stars across the sky using their telescopes.
It was indeed discovered. However, the discovery had nothing to do with exoplanets – the path was affected by extremely faint companion stars that could not be seen without a telescope. These companion stars were later named white dwarfs. As for planets, their impact on the movement of stars was so minimal that it was undetectable with the telescopes available at that time.
The astrometric method
If a star has a nearby planet, both objects orbit around a shared center of mass. The larger the planet’s mass, the greater its influence on the star. This causes the star to appear to sway slightly back and forth to an external viewer, creating a wavelike motion in the sky. The astrometric method of exoplanet detection is based on observing these movements of stars across the celestial sphere.
In the 20th century, scientists attempted to accomplish what their 19th-century counterparts were unable to achieve. One of the most well-known examples is the story of astronomer Pieter van de Kamp. Throughout much of his scientific career, he focused on studying the star Barnard, which is a red dwarf located in the Serpentine constellation and is only 5.96 light-years away from Earth. Van de Kamp hypothesized that this relatively low-mass star, approximately 6-7 times lighter than the Sun, would experience noticeable changes in its trajectory due to the influence of other celestial bodies.
In the late 1960s, the astronomer made an announcement that he had successfully detected not just one, but two exoplanets. Based on his calculations, these exoplanets were gas giants with masses equivalent to 0.7 and 0.5 times that of Jupiter.
When considering the future, it can be said that astronomers remain optimistic about the possibility of discovering planets near Barnard’s star. In late 2018, a team of international scientists made an exciting announcement. Although it was not the gas giant previously reported by van de Kamp, they had discovered an Earth-like planet with a mass approximately 3.2 times that of Earth. Sadly, the fate of this discovery took a turn for the worse as another scientific group refuted its reliability three years later. Therefore, the question of whether or not planets exist around Barnard’s star remains unanswered.
The dawn of discovery
By the late 1980s, there was a widespread consensus among experts that the discovery of exoplanets was imminent. Numerous scientific teams across the globe were diligently searching for them using state-of-the-art optical spectrometers. However, it was the radio astronomers, who weren’t even actively seeking planets, who ultimately struck gold.
In 1991, the Polish scientist Alexander Wolszczan made an observation that his observed neutron star, the radio pulsar PSR 1257+12, undergoes variations in the frequency of its pulses, resembling waves. This discovery indicated that the pulsar is being influenced by another celestial body. The validity of this finding was later confirmed by Wolszczan’s colleague Dale Freil. In January 1992, the scientific community announced the discovery of two planets orbiting the radio pulsar, which were named PSR B1257+12 c and PSR B1257+12 d. These planets were later given the names Poltergeist and Phobetor, respectively. Subsequently, a third planet was also found and named PSR B1257+12 b, known as Draugr. The pulsar itself, often referred to as the “father” of this eerie planetary system, was assigned the equally menacing name Leach.
Among the discovered exoplanets, Draugr has the lowest mass, measuring only 0.02 times that of Earth.
The discovery made by radio astronomers has puzzled scientists. When the star underwent a supernova outbreak, the planets that were orbiting it were forced to scatter in different directions due to the decrease in the mass of the star and, consequently, the weakening of its gravity. As a result, Draugr, Poltergeist, and Phobetor were formed after the star transformed into a pulsar. However, the process of how and from what these planets were formed remains a mystery to science. So far, only six pulsars have been found to have exoplanets, even though there are over two thousand known pulsars.
While the rest of the scientific community was learning about the planets discovered by Volshchan and Freil, astronomers from the scientific groups in California and Geneva turned their attention to the star 51 Pegasus. Their instruments detected oscillations in the spectral lines of the star with a period of 4.23 days.
The technique of measuring radial velocity
Stars emit electromagnetic radiation, and when the distance between the star and the observer remains constant, the frequency of the waves remains unchanged. However, if a star and a planet orbit a common center of mass, the spectral lines of the star’s light will shift towards the violet edge when approaching the observer and towards the red edge when moving away. This phenomenon is known as the Doppler effect, and scientists have utilized this effect to search for exoplanets using a method called the Doppler method or the radial velocity method.
By analyzing the spectrum of 51 Pegasus, astronomers discovered significant shifts that could only be explained by the presence of a massive planet. Furthermore, this planet had to be located very close to the star, which contradicted previous observations in our own solar system, where smaller planets were found closer to the star and larger planets were found farther away.
Actually, the award slipped away from the Californian group’s grasp simply because the astronomers lacked the scientific boldness to publish such an unusual finding.
It turned out that the surface of 51 Pegasi b was scorching hot, reaching temperatures of 1300 K, leading astronomers to categorize it as a new kind of planet known as a hot Jupiter. Scientists were puzzled by how a gas giant could have formed so close to its parent star, as there should not have been enough material for it. However, a plausible explanation was soon discovered. In 1996, astronomer Douglas Lin and his colleagues proposed that the planet originally formed at a distant location from the star but migrated towards it over time, gradually accumulating matter from the remnants of the surrounding disk. This phenomenon seems to occur with other hot Jupiters as well.
The residents of the “zoo”
Following the detection of 51 Pegasi b, the radial velocity technique remained the sole successful approach to hunt for exoplanets for several years. Nevertheless, in 2000, scientists had the opportunity to witness the initial “eclipse” of a star by an exoplanet: the scorching Jupiter known as Osiris (HD 209458 b), discovered a year earlier using the Doppler method, passed directly in front of the disk of the yellow dwarf HD 209458.
Currently, Osiris is regarded as the most extensively researched exoplanet. It is notable, for instance, for its perpetual tidally locked state, with one side constantly facing its star, resulting in scorching temperatures ranging from 1,000 to 1,300 K. Conversely, the opposite side experiences significantly lower temperatures. This temperature disparity gives rise to a powerful storm system on the gas giant, with wind speeds reaching up to 7,000 km/h. Furthermore, Osiris holds the distinction of being the first exoplanet where the presence of oxygen, carbon, and water vapor in its atmosphere was confirmed.
The method of transit
A transit occurs when a planet passes in front of a star, causing a slight decrease in the star’s brightness. The transit method involves detecting these changes in luminosity. However, a single transit is not sufficient to confirm the presence of an exoplanet, as other factors can also cause variations in the star’s brightness. Similarly, two transits may be inconclusive, as they could be caused by different planets. It is only with the observation of three transits, occurring at regular intervals, that a new exoplanet can be confidently identified.
The transit method has also proven effective in the search for previously unidentified celestial objects. One notable discovery is OGLE-TR-56 b, which is among the hottest exoplanets identified by scientists. Its surface temperature reaches a scorching 2000 K, leading to the formation of iron vapor clouds in its atmosphere, which then precipitate as rain.
As technology has advanced, the rate of planet discoveries has increased exponentially. While each new finding initially caused excitement within the scientific community, the past fifteen years have seen the annual addition of dozens, and even hundreds, of new names to the list of discoveries.
The primary techniques for exoplanet detection are still radial velocity and transit methods, which have led to the discovery of 95% of known exoplanets. Interestingly, astrometry has only resulted in one discovery, but it has been instrumental in confirming many planets found through other means. However, the most unique and effective method of detection has been gravitational microlensing, which enables the detection of non-luminous objects such as distant cold planets, free-floating planets, and solitary black holes.
When a star is eclipsed by a planet passing behind it, the gravitational field of the planet bends the rays of light. This creates a lens-like effect, where the star’s light is focused by the planet’s massive celestial body. By analyzing specific characteristics of the resulting light curve, scientists can calculate the mass of the planet and its distance from the star. Albert Einstein originally proposed this method of searching for planets in his groundbreaking general theory of relativity.
During the early years, the primary focus of astronomers was on hot Jupiters. They discovered such a large number of these planets that it almost seemed like they comprised the majority of planets in our Universe. However, this is not the case. According to data gathered by the Kepler space telescope, only one out of every two hundred sun-like stars has a hot Jupiter in orbit. It was relatively simple to find massive planets in close orbits that caused significant disruptions in the motion of their parent stars. However, astronomers have now developed the ability to detect objects that are located far away from their parent stars.
The method of direct observation
Scientists are currently unable to directly observe planets in the visible range due to the overpowering brightness of the stars. However, with the use of a specialized infrared telescope, it is possible to detect a young and hot planet that is situated far from its star. This telescope is equipped to register thermal radiation. In some cases, scientists resort to clever techniques, such as employing a special opaque disk called a coronograph, to block out the star’s light and make the planet’s dim light more discernible.
The exoplanet “zoo” is filled with an incredible array of diversity. There are gas dwarfs and super-Earths, planets that are devoured by their star, and rogue planets that wander without any star to call home. Some planets have nearly perfect circular orbits, while others have elongated orbits resembling comets. There are planets with oceans 100 kilometers deep, and others with lava oceans on their constantly sun-facing side. Some planets are made entirely of iron, while others are 10 times less dense than water. There are planets as white as snow and others as black as coal. The possibilities seem endless.
Comparatively, our own Solar System seems rather ordinary and even boring, with its four rocky planets, two gas giants, and two ice giants.
In the near future, the exoplanet “zoo” will undoubtedly be enriched with new and fascinating specimens, thanks to space observatories. Scientists are placing great expectations on the James Webb telescope, which is set to be launched at the end of 2021. This groundbreaking project is a collaboration between NASA, the Canadian Space Agency, and the European Space Agency. The James Webb telescope is expected to not only discover exoplanets that are significantly distant from their stars but also exolunas. Furthermore, astronomers have begun analyzing the data collected by the Gaia telescope of the European Space Agency since 2014. While some preliminary findings have already been made, it is anticipated that the overall data will contribute to the discovery of at least 10 thousand exoplanets.
In the pursuit of leaders
Russian scientists are actively involved in the search for extrasolar planets. For instance, there is a scientific group at the Special Astrophysical Observatory of the Russian Academy of Sciences (in the Karachay-Cherkessia Republic) that has been dedicated to this pursuit for the past decade. Using the radial velocities method, they have successfully confirmed the existence of seven exoplanets that were previously discovered through the transit method on space telescopes like Kepler and TESS. Furthermore, there are at least 10 more celestial bodies that have been identified as potential exoplanets and are currently being observed by these domestic specialists. The Crimean Astrophysical and Pulkovo Observatories are also actively involved in the search for exoplanets.
A collaborative project called EXPLANATION (EXoPLANet And Transient events InvestigatiON) was launched in 2022 by Russia and South Korea with the aim of studying exoplanets and transient events. However, at this stage, it is premature to discuss any interim findings from the project.
As of July 11, 2023, a total of 5470 exoplanets have been discovered according to available data.
Russian astronomers have contributed to the discovery or confirmation of approximately 10 exoplanets. It is challenging to provide an exact number as most of these findings were made using foreign telescopes, and some discoveries lack sufficient observations and are not recognized by other groups or international databases.
The number of exoplanets discovered by our scientists may appear small in comparison to the discoveries made by Western astronomers, but there are valid reasons for this. According to the Institute of Space Research of the Russian Academy of Sciences, the blame for this situation lies in the catastrophic state of domestic science during the 1990s. It was during this time that the scientific world experienced an “exoplanet revolution”, but Russian scientists became involved in these studies relatively late.
Furthermore, Russia faces the challenge of lacking modern instruments necessary for the search of extrasolar planets.
In Russia, there are only a few large telescopes capable of studying and discovering exoplanets, and these telescopes are located in areas with limited clear nights for observations. In fact, there are no locations in Russia with optimal astroclimate conditions.
Russia currently lacks its own space telescopes capable of observing Earth-like planets in the habitable zone of stars in the optical or infrared ranges beyond Earth’s atmosphere.
A Different Planet
Although planets with iron rain or lava oceans may be fascinating and captivating to the imagination, the ultimate aspiration for most exoplanetologists has always been the identification of an Earth-like twin.
If we were to scan the cosmos beyond our solar system using our current technology, we would only come across Jupiter and possibly Saturn. If we were incredibly fortunate, the Kepler telescope might also detect the presence of Venus. However, it would be impossible to spot our own planet, Earth.
When the space observatory Kepler was launched in March 2009, astronomers held great expectations. Its primary purpose was to search for Earth-like planets using the transit method, focusing on stars similar to our Sun. Unfortunately, the telescope’s precision fell short – even if it did manage to observe the transits of Earth’s doppelgängers, the measurements were indistinguishable from the instrument’s background noise.
During the transit of Earth, the Sun’s light would only be diminished by a mere 0.0084%.
If Kepler had worked for ten years, there is a high probability that he would have discovered planets similar to ours. Due to the extensive collection of data, even a small signal could have been detected amidst the noise. This is evident in the case of the twin planets Venus: these planets, which are similar in size to Earth, complete their orbits around stars in a shorter period of time, resulting in more frequent transits recorded by the telescope. Unfortunately, Kepler experienced a malfunction just four years after its launch, preventing it from finding Earth’s twin. Although NASA engineers were able to fix the device in 2014, it was no longer capable of observing the same region of the sky.
Ultimately, the telescope concluded its operations on November 15, 2018, coinciding with the passing of astronomer Johannes Kepler, for whom it was named. While the primary objective of the mission was not fully realized, its scientific significance cannot be overstated: Kepler’s planets account for roughly two-thirds of the exoplanets presently known.
However, the discovery of an Earth-sized celestial entity is merely the tip of the iceberg. A habitable planet necessitates Earth-like conditions.
Water has the ability to exist in a liquid state only within specific temperature ranges. When planets are located near stars, the intense heat causes the water to evaporate. On the other hand, when planets are far from stars, the water freezes and becomes ice. However, there exists a particular region surrounding a star where the water on a planet’s surface can potentially remain liquid. This area is referred to as the zone of life or the zone of habitability by scientists. In addition to these terms, the English-language scientific literature also uses another term to describe this region – the Goldilocks Zone.
Aside from water and a source of light, life requires organic compounds and certain chemical elements to originate and survive. Furthermore, the atmosphere must have a specific density, as being too dense would result in a potent greenhouse effect, while being too rarefied would be detrimental as well. In essence, a planet’s properties are just as crucial as its distance from a star. Interestingly, the moon falls within the habitable zone, but unfortunately, it hasn’t benefited much from this fact.
The notion of the habitable zone has faced scrutiny on multiple occasions, and in recent years, critics’ arguments have grown increasingly persuasive. A team of Russian scientists suggests that the habitable zone may not have an outer boundary at all, but rather only an inner one – the region near stars where temperatures are too high for life to thrive.
Deep within Enceladus, one of Saturn’s moons, lies an underwater ocean filled with warm and salty water that is rich in organic matter. Astronomers became aware of this discovery through geysers that continuously erupt from cracks in the moon’s icy surface. Similar intermittent geysers have also been observed on Europa, one of Jupiter’s moons. It is entirely plausible that other moons orbiting gas giants may harbor warm subglacial oceans as well.
Europa and Enceladus are situated far outside the habitable zone, lacking the necessary solar heat. Instead, their interiors are warmed by powerful tidal forces. While it may be futile to expect the presence of an advanced civilization beneath their icy surfaces, the failure to discover even microbial life would challenge the notion of a clearly defined habitable zone.
Nevertheless, the moons of Jupiter and Saturn are unsuitable as potential new homes for humanity, as we cannot inhabit the depths of the ocean. If we ever find ourselves needing to leave Earth, our journey will take us beyond the boundaries of our solar system.
Unfortunately, the current state of affairs leaves us with limited options. The spacecrafts currently developed by humans are ill-equipped for interstellar travel, as they are too slow and the journey to the nearest star would take tens of thousands of years. The crew simply does not have the luxury of that much time.
Currently, scientists are engaged in the development of cutting-edge devices. One such project is the Breakthrough Starshot, which involves the creation of a starship that utilizes a sailing mechanism. Renowned physicist Stephen Hawking and Russian billionaire Yuri Milner, who has already invested $100 million in the project, are among the driving forces behind this initiative.
The initial phase of the project involves testing the technology on miniature prototypes, which will be connected to a four-meter mirror sail using slings. Subsequently, laser installations will be used to propel the sail from Earth, utilizing the pressure exerted by light to accelerate the spacecraft to approximately 20% of the speed of light. If all goes according to plan, the spacecraft is expected to reach the nearest star system, Alpha Centauri, approximately 20 years after its launch.

The concept of constructing a spacecraft that runs on antimatter seems equally promising and even more fantastical. When antimatter is combined with regular matter, an immense amount of energy is unleashed, enabling the starship to reach incredibly high velocities – possibly even a fraction or even tens of a fraction of the speed of light, as scientists have projected.
However, let’s envision a scenario where an interstellar vessel has already been fabricated. Who would pilot it? Who would be willing to embark on such an extraordinary journey? After all, for every crew member and passenger, it would be a one-way expedition, with no possibility of returning to our beloved Earth.
Flying with a limited number of individuals, ranging from five to seven, lacks practicality. Even if the settlers manage to successfully land on another celestial body, their lack of support will inevitably result in a rapid regression to a primitive state, resembling the Stone Age, and eventually succumbing to illness or old age – hardly a comprehensive plan for space exploration, is it? It is imperative that an interstellar expedition be comprised of thousands, if not tens of thousands, of individuals. These pioneers will bring along entire factories and intricate production facilities, ensuring their ability to establish a sustainable presence in a new environment without relying on assistance from Earth or being constrained by the conditions of an alien planet.
The team responsible for resettlement should consist of individuals with expertise in scientific research as well as those skilled in physical labor, such as construction or resource extraction. It is important to have a diverse group of people in terms of gender and age among the passengers of the starship to ensure natural growth of the colony.
Obviously, none of us who are currently reading this text are likely to embark on an interstellar journey. However, perhaps our future generations, specifically our great-grandchildren or even great-great-grandchildren, will have the opportunity to fulfill our aspirations and witness the beauty of distant planets firsthand.
- Anderson D., Hellier C., Gillon M., Triaud A., Smalley B. WASP-17b: an Ultra-low Density Planet in a Probable Retrograde Orbit. The Astrophysical Journal, 2010.
- Bhathal R. Searching for ETI. Journal & Proceedings of the Royal Society of New South Wales, 2008.
- Brown T. Distant Planet is the Hottest Yet. Nature, 2003.
- Charbonneau D., Berta Z., Irwin J., Burke C., Nutzman P. A Super-Earth Transiting a Nearby Low-mass Star. Nature, 2009.
- Cocconi G., Morrison P. Searching for Interstellar Communications. Nature, 1959.
- Cromie W. New, Far-out Planet is Discovered: Would take 5,000 Years to Travel There at 186,000 mps. The Harvard Gazette, 2003.
- Deming D., Wilkins A., McCullough P., Burrows A., Fortney J. Infrared Transmission Spectroscopy of the Exoplanets HD 209458b and XO-1b Using the Wide Field Camera-3 on the Hubble Space Telescope. The Astronomical Journal, 2013.
- Ehrenreich D., Lecavelier des Etangs A., Hebrard G., Desert J.-M., Vidal-Madjar A. New observations of the Extended Hydrogen Exosphere of the Extrasolar Planet HD 209458b. Astronomy & Astrophysics, 2018.
- Frisbee R. Building an Interstellar Antimatter Rocket: Key Considerations in Advanced Propulsion Technology Vehicle Design. Proceedings of the 39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, 2003.
- Hershey J. Astrometric Analysis of AC +65° 6955 Field Using Sproul 24-inch Refractor Plates. The Astronomical Journal, 1973.
- Lin D., Bodenheimer P., Richardson D. The Orbital Migration of 51 Pegasi’s Planetary Companion. Nature, 1996.
- Lubin J., Robertson P., Stefansson G., Ninan J., Mahadevan S. Explaining Barnard b as a False Positive: Stellar Activity Manifestation at a One-year Alias. The Astronomical Journal, 2021.
- Ribas I., Tuomi M., Reiners A., Butler R., Morales J. A Super-Earth Planet Candidate in the Snow-line of Barnard’s Star. Nature, 2018.
- Snellen I., R. de Kok, E. de Mooij, S. Albrecht. Nature, 2010. “The Orbital Motion, Absolute Mass, and High-altitude Winds of Exoplanet HD209458b.”
- G. Valyavin, G. Beskin, A. Valeev, G. Galazutdinov, S. Fabrika. Photonics, 2022. “EXPLANATION: Exoplanet and Transient Event Investigation Project — Optical Facilities and Solutions.”
- A. Wolszczan, D. Frail. Nature, 1992. “A Planetary System Around the Millisecond Pulsar PSR1257+12.”
- P. van de Kamp. The Astronomical Journal, 1969. “Alternate Dynamical Analysis of Barnard’s Star.”
- P. van de Kamp. The Astronomical Journal, 1968. “Astrometric Study of Barnard’s Star from Plates Taken with the 24-inch Sproul Refractor.”
- P. van de Kamp. Vistas in Astronomy, 1982. “The Planetary System of Barnard’s Star.”
- Ananyeva V., Tavrov A., Petrova E., Korablev O. Habitable Zones. From the Solar System to exoplanets. Earth and the Universe, 2020.
- Valyavin G., Beskin G., Valeev A., Galazutdinov G., Fabrika S. EXPLANATION: a project for investigating exoplanets and transient events. Astrophysical Bulletin, 2022.
- Gadelshin D., Valyavin G. Exoplanets of other stars: significant advances in the exploration of extrasolar planets. Earth and Universe, 2020.
- Materialists of Ancient Greece (collection of texts by Heraclitus, Democritus, and Epicurus). Moscow: Politizdat, 1955.
- Surdin V. Exploration of remote planets. M.: Fizmatlit, 2017.
- NASA Exoplanet Archive website
- Open Exoplanet Catalogue website
- Central Bureau for Astronomical Telegrams website
- ESA website
- IAU website
- NASA website
- Official website of the SETI Institute
- Swarthmore College’s official website
- The website of the Planetary Habitability Laboratory
- Website of the IKI RAS
- Author: Anton Zaritovsky
- Infographics Editor: Sofya Shandybina
- Editorial staff: Sabina Vakhitova, Daria Donina
- SMM editors: Daria Kalinina, Ekaterina Fedotova, Anna Yakusheva
- Illustrator: Anastasia Zotova
- Art director and developer: Anton Mizinov





