
As we gaze up at the sparkling night sky, the vastness of the space between the stars becomes apparent. Although they may appear as tiny specks, in reality, the stars are not small at all. In fact, the distance between us and them is akin to a colossal abyss. Moreover, the gap between the stars themselves is also immense. While it may seem unfathomable to us, it is not so for the vastness of the cosmos.
Long ago, people held the belief that all celestial bodies were equidistant from one another. However, through the exploration of outer space, our understanding has evolved over time.

How do scientists measure the distance to stars?
I often wonder about the units used by astronomers to measure the distance to stars. It turns out that the distance to stars, as well as any other celestial bodies, is not measured in kilometers, but in light-years or parsecs.
A light-year is the distance traveled by a beam of light in one year, assuming it travels at a speed of 300,000 kilometers per second. Just imagine, one light-year corresponds to 9.5 trillion kilometers.
Using meters and kilometers to determine the distances between stars and the distance from Earth to them is very challenging and problematic.
While the use of light years can be inconvenient for measuring the degree of remoteness of astronomical objects due to their immense distances, another unit of measurement called a parsec is used. A parsec is equal to 3.26 light years.
Furthermore, a unit of measurement known as a megaparsec can also be utilized. A megaparsec is one million times larger than the standard unit, equivalent to 3,260,000 light years.

Techniques and approaches to measuring the distance to celestial bodies
In all aspects of life, humans seek to identify properties, characteristics, and unique attributes. Currently, we possess the ability to calculate any distance using both practical and theoretical methodologies.
However, how do scientists determine the distance to stars? The prevailing method employed for this purpose is known as the parallax method.
Parallax refers to the alteration in the apparent position of an object in relation to the background, which is directly determined by the observer’s location.
If a celestial object were positioned at a distance of 3.26 light-years or 1 parsec from our planet, its parallax would measure 1 second of arc. However, it is most likely a stroke of luck that there are unlikely to be any other celestial objects in such close proximity to us.
Alternative methods for calculating the distance to stars
Of course, there are other techniques available. One approach is to use the photometric method to determine the distance to stars. This method measures the level of illumination produced by sources of equal strength and power. The level of illumination is inversely proportional to the square of the distance between objects.
An alternative way to determine the distance to stars is by analyzing their spectra. This involves studying the chemical composition and physical characteristics of the objects, as well as examining their spectra.
Therefore, we have now gained knowledge about the units of measurement and techniques used to calculate the distance to stars.
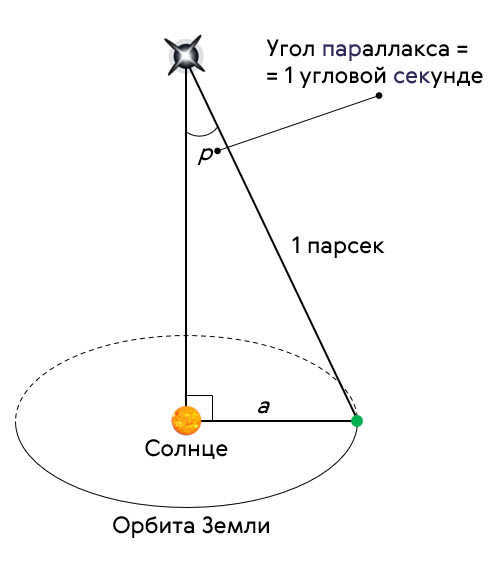
It is common knowledge that the Sun is the nearest star to us. Hence, its distance is often measured in kilometers (149.6 million kilometers), which is equivalent to 8.3 light minutes.
The vastness of the distances between the stars and planets in our solar system is truly awe-inspiring. For instance, the planet Pluto is approximately 5 light hours away from Earth, while the closest planet to us, Proxima Centauri, is located 4.2 light years away.
Just think about how much we already know and have access to, and yet there is still so much more to discover about our Universe!

Determining distances to remote celestial objects, like stars, is not a direct measurement process. Instead, scientists rely on measurable characteristics of these objects, such as their brightness or the periodic variations in their coordinates, to calculate their distances. Various methods have been developed to calculate stellar distances, each with its own limitations. Now, let’s delve deeper into the techniques scientists use to determine the distance to stars.
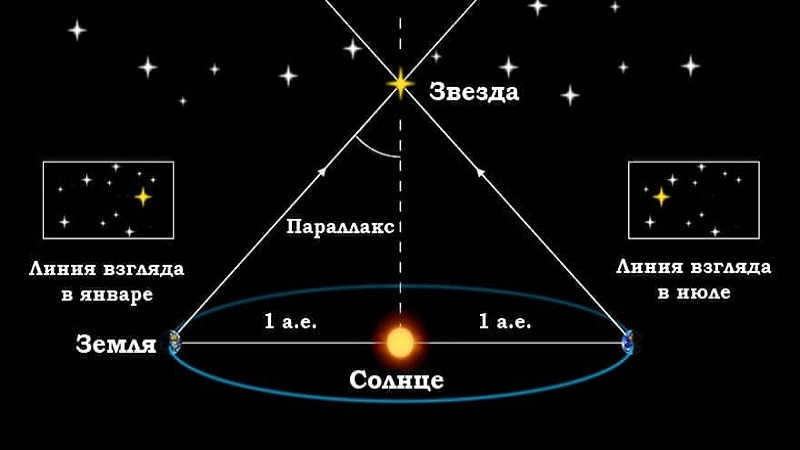
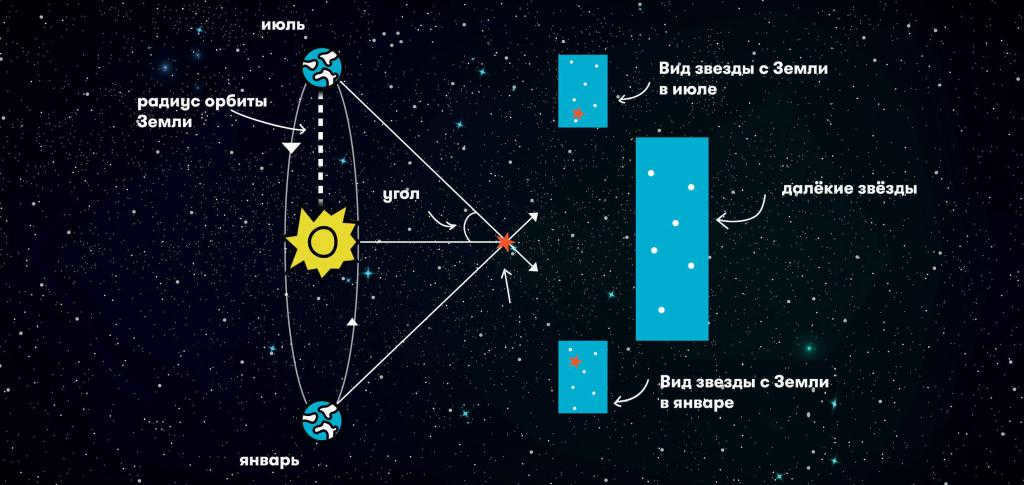
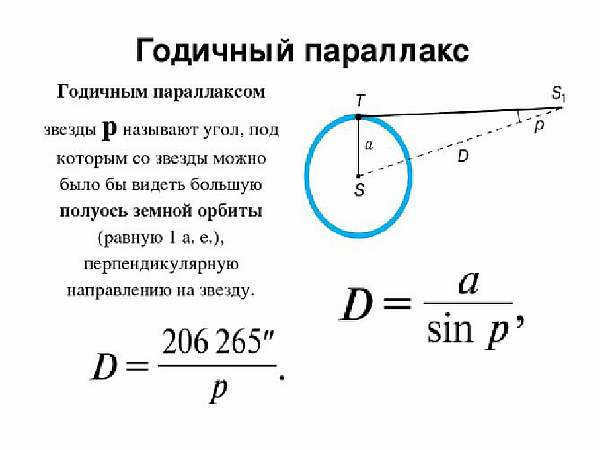
Parallax refers to the shift in position of an observed object in relation to a distant background when the observer’s position changes. By knowing the distance between the observation points (known as the parallax baseline) and the angular displacement of the object, it is possible to easily calculate its distance. When the offset value is smaller, it indicates that the object is farther away. Since interstellar distances are immense, the largest possible baseline is used to increase the angle, and this is achieved by measuring the position of a star at opposite points of the Earth’s orbit. This particular method is known as stellar annual parallax.
Understanding how the stellar annual parallax method measures the distance to stars is now simple. The method calculates the distance as one side of a triangle formed by the observer, the Sun, and the distant star. This distance, denoted as r, is equal to a divided by the sine of the annual parallax, p. Here, a represents the distance from the Earth to the Sun. Since all star parallaxes are less than 1 arc second (1”), we can approximate the sine of the small angle with the magnitude of the angle itself in radian measure: sin p ≈ p”/206265. By substituting this approximation, we obtain the equation: r = a∙206265/p”, or, in units of astronomical distance, r = 206265/p”.
Interstellar Distance Units
It is evident that the resulting equation is impractical, as expressing vast distances in kilometers or astronomical units is cumbersome. Hence, the parsec (‘parallax-second’; abbreviated as pk) is universally adopted as the standard unit in stellar astronomy. This unit represents the distance to a star with an annual parallax of 1 second. In this scenario, the equation becomes simple and convenient: r = 1/p pc.
206265 astronomical units or approximately 30.8 trillion kilometers is equivalent to one parsec. In popular literature and articles, the light-year is frequently used as a measurement – it represents the distance that electromagnetic waves travel in a vacuum over the course of a year, unaffected by gravitational fields. About 9.5 trillion kilometers, or 0.3 parsecs, is equal to one light year. As a result, one parsec is roughly equivalent to 3.26 light-years.
At present, ground-based conditions only allow for the measurement of parallax with an accuracy that permits the determination of star distances up to 200 parsecs. The use of space telescopes further enhances the accuracy of these observations.


Consequently, the launch of the European satellite known as “Hipparchus” (HIPPARCOS) in 1989 not only expanded the distance capability to 1000 pc, but also greatly enhanced the precision of already established stellar distances. The introduction of the European satellite Gaia in 2013 further improved measurement accuracy by two orders of magnitude. Gaia’s data has enabled astronomers to determine star distances within a 40 kiloparsec radius and holds the potential for discovering new exoplanets. The Hubble Space Telescope also achieves a comparable level of accuracy to Gaia, and is likely reaching the limits of what is possible for optical measurements.
Despite this limitation, the trigonometric annual parallax serves as a calibration basis for other methods of measuring distances to stars.
The concept of stellar magnitude in Photometry
Photometry in astronomy focuses on measuring the intensity of electromagnetic radiation emitted by a celestial object, including in the optical range. Various methods use photometric parameters to determine the distance to stars and other distant objects like galaxies. Stellar magnitude, or luminosity (represented by the index m ), is one of the fundamental concepts employed in photometric methods.
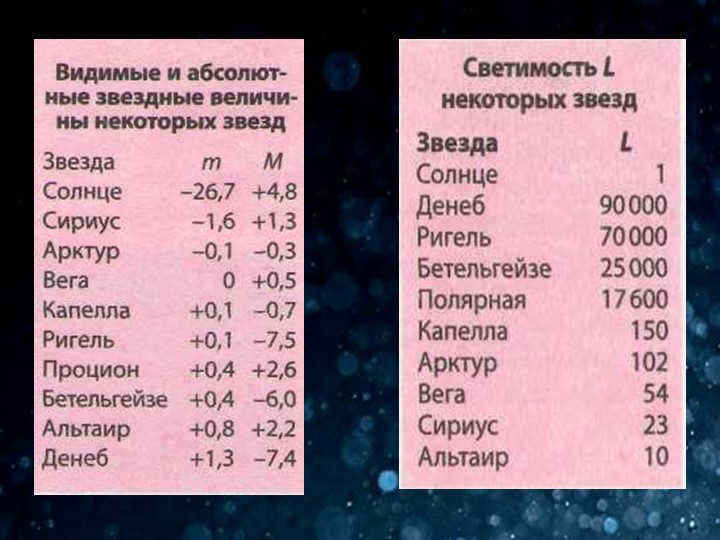
The magnitude of a star, which is visible or relative (for the optical range – visual), is directly measured from its brightness. This magnitude is characterized by a scale in which an increasing magnitude indicates a decrease in brightness (historically). For instance, the Sun has a stellar magnitude of -26.7 m, Sirius has a magnitude of -1.46 m, and Proxima Centauri, the closest star to the Sun, has a magnitude of +11.05 m.

The absolute stellar magnitude is a calculated value that represents the apparent magnitude of a star if it were located at a distance of 10 parsecs. This parameter is used to compare the brightness of different stars, taking into account their distances. For example, the Sun has an absolute magnitude of +4.8m, Sirius has an absolute magnitude of +1.4m, and Proxima has an absolute magnitude of +15.5m. These stars are located at distances of approximately 0.000005 parsecs, 2.64 parsecs, and 1.30 parsecs, respectively. The variation in absolute magnitude between these stars is directly related to their luminosity, a key astrophysical characteristic.
Spectra and brightness of stars
Astronomers define brightness, or luminosity (L), as the total amount of energy that a star (or any other object) emits per unit of time. Luminosity can be determined using the absolute magnitude of a star, but unlike absolute magnitude, it is not affected by distance.
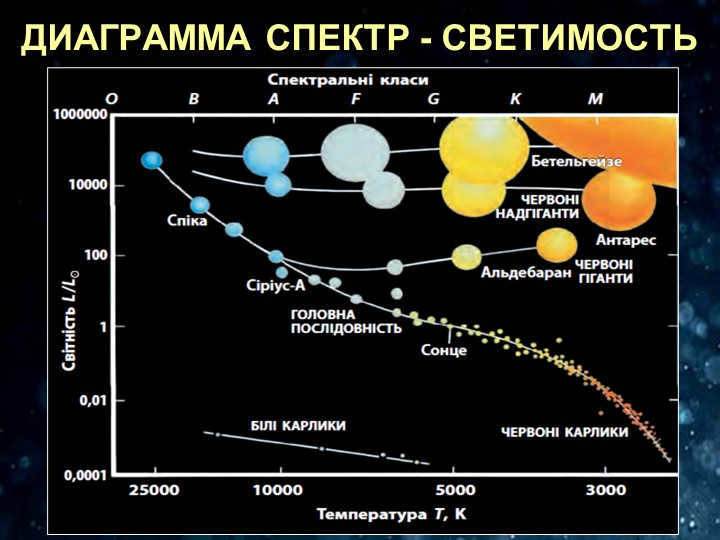
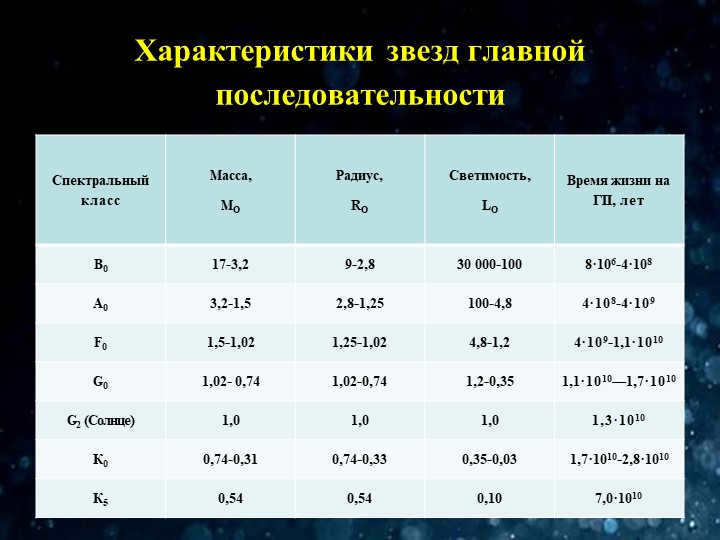
Stars are classified into various spectral classes based on their emission spectrum, which primarily indicates their temperature (with color being a visible manifestation of temperature). Stars of the same spectral class usually have similar luminosity (although there are exceptions, which can be identified by peculiarities in their spectra). The relationship between “spectrum – luminosity” (or “color – stellar magnitude”) is depicted on the Hertzsprung-Russell diagram.
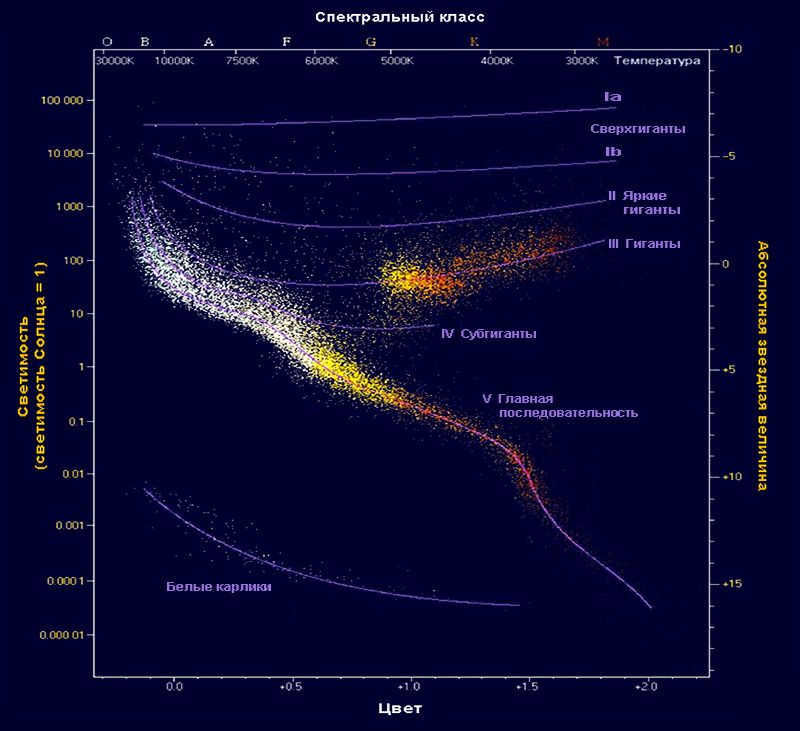
The Hertzsprung-Russell diagram provides a means of approximating the absolute brightness of stars based on their spectral classifications. By establishing a straightforward relationship between absolute brightness, visible magnitude, and distance, we gain insight into how to calculate the distance to stars. The equation is as follows: lg r = 0.2(m – M)+1. In this equation, r represents the distance, m represents the apparent magnitude of the star, and M represents the absolute magnitude. While this method does not offer absolute precision, it does allow for estimation of distance.
Standard candles in astronomy
In the field of astronomy, there exist certain stars whose brightness is uniquely correlated to a specific physical parameter. This correlation allows astronomers to accurately determine the distance to these stars by observing the drop in luminosity based on the inverse squares law. The smaller the apparent magnitude of a star, the greater its distance from us. Examples of these standard candles include Cepheids and Type Ia supernovae.
Cepheids are a type of variable star that exhibit a predictable relationship between their luminosity and pulsation period. By measuring the luminosity and period of a Cepheid, scientists can easily calculate its distance. These stars are exceptionally bright, and with the help of modern telescopes, astronomers can even observe Cepheids in other galaxies, allowing them to determine the distance to these galaxies as well.

Type Ia supernovae are explosions that occur when a specific type of star in binary systems reaches a critical mass. These explosions always have the same brightness and rate of decay, which enables us to determine their distance. The luminosity of supernovae is so intense that it can rival the brightness of an entire galaxy. This makes them valuable tools for astronomers to estimate distances on cosmological scales, spanning billions of parsecs.
The most distant
Most individuals are aware of Proxima Centauri, the nearest star to us. However, have you ever wondered about the farthest known star?
Recently, astronomers made a groundbreaking discovery – the most distant star within our own Galaxy. This star is situated beyond the spiral disk of the Milky Way, on the outskirts of the galactic halo, approximately 122,700 pc or 400,000 light-years away, in the constellation Libra. It is a red giant with a magnitude of 18 stars. Naturally, there may be even more distant stars, but determining their exact location within our Galaxy is a challenging task.

So, what is the most remote star known in the cosmos? It bears the romantic title MACS J1149+2223 Lensed Star-1, or more simply LS1, and resides a staggering 9 billion light-years away. Its discovery is a celestial stroke of luck, as observing a star at such an immense distance was only made possible by a gravitational microlensing phenomenon in a distant galaxy, which was in turn magnified by a closer cluster of galaxies. A different technique was utilized to calculate the distance – through cosmological redshift. This approach is employed to determine distances to the farthest objects in the Universe, which cannot be discerned as individual stars. And LS1 stands as one of the most awe-inspiring and exquisite illustrations of how astronomers ascertain the distances to stars.

The concept that stars are distant suns has been proposed since ancient times. However, due to the immense distances separating them, the discs of stars remain invisible even through the most advanced telescopes. Consequently, in order to establish means of comparing stars both with each other and with the Sun, it became necessary to devise methods of determining their distances. In this lesson, we will acquire an understanding of the annual parallax of a star. We will acquaint ourselves with the units used to express distances to stars. We will gain insight into the definition of absolute stellar magnitude and how it varies from apparent stellar magnitude. Additionally, we will ascertain the meaning of stellar luminosity.
Unfortunately, at the moment, you are unable to view or share the instructional video with your students.
In order to access this and other video lessons in the package, you will need to include it in your personal account.
Unlock amazing possibilities


Outline for the Lesson on “Determining Distances to the Stars: Visible and Absolute Stellar Magnitudes”
The Sun is often referred to as a typical star. However, there are numerous stars in the universe that differ significantly from the Sun in terms of their physical characteristics and chemical composition. In order to have a comprehensive understanding of stars, we need to consider the following definition:
A star is a massive sphere of gas that emits light and maintains its equilibrium through the interplay of gravitational forces and internal pressure. Deep within a star, thermonuclear fusion reactions take place or have previously occurred.

Ancient civilizations had a belief that stars were actually distant suns. However, due to the immense distances between us and the stars, we are unable to see their disks even with the most advanced telescopes. Therefore, in order to compare stars with one another and with our own Sun, scientists needed to develop methods for determining their distances.
Even Aristotle hypothesized that if the Earth orbits around the Sun, then by observing a star from two opposite points on Earth’s orbit, we would notice a change in the star’s direction – its parallactic (or apparent) displacement.
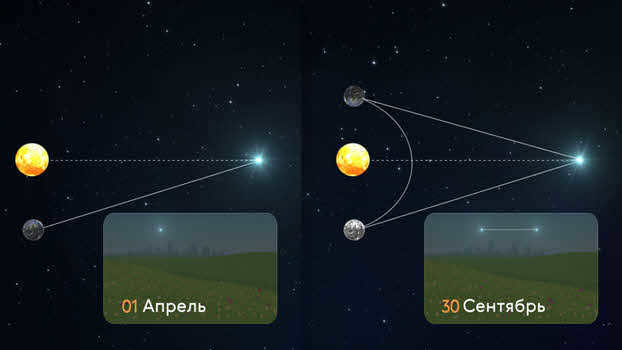
After Nicolaus Copernicus introduced the heliocentric system of world order, he proposed a similar method for measuring distances. However, neither Copernicus nor Aristotle were able to observe this displacement.
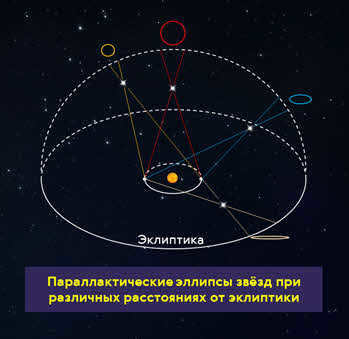
It wasn’t until the mid-19th century, when telescopes became equipped with advanced tools for accurately measuring angles, that scientists were able to measure this displacement in nearby stars. They discovered that the apparent displacement of a closer star against a background of very distant stars forms an elliptical pattern with a one-year period, reflecting the observer’s motion with Earth around the Sun. This elliptical path traced by the star is known as the parallactic ellipse. parallactic ellipse.
The major semi-major axis of the Earth’s orbit, when viewed from a star, is equal to the angular measurement known as the annual parallax. This measurement, denoted by the Greek letter π or the Latin letter р, represents the angle between the star and the perpendicular direction to the Earth’s orbit.
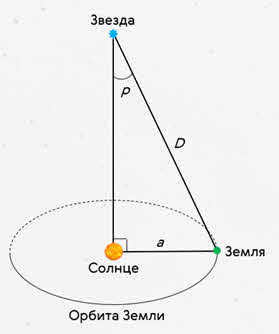
By understanding the star’s yearly parallactic displacement, we can effortlessly calculate its distance:
In the given equation, a refers to the average radius of the Earth’s orbit.
If we consider that star’s annual parallaxes are measured in ten-thousandths of a second, and the Earth’s orbit has a major semi-major axis equal to one astronomical unit, we can derive a formula for determining the star’s distance in astronomical units:
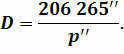
The initial accurate calculations of yearly parallax were conducted nearly at the same time in Germany, Russia, and England in 1837.
Within Russia, Vasily Yakovlevich Struve was the first to measure yearly parallax for the prominent star Vega in the Northern Hemisphere. We can employ his findings to estimate the distance to this particular star.

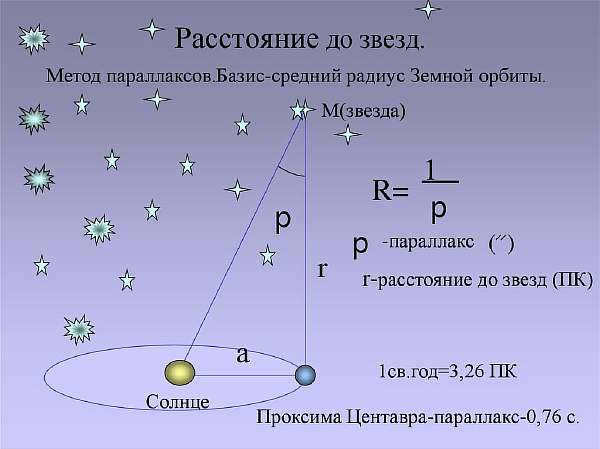
It is widely accepted that the astronomical unit is insufficient for measuring distances to stars. Even the nearest star to us, Alpha Centauri, is located more than 273.5 thousand astronomical units away. Therefore, in astronomy, a special unit of length called a parsec (abbreviated as pk) is used to conveniently determine star distances. The term “parsec” is derived from the words “parallax” and “second”.
A parsec is defined as the distance from which the average radius of the Earth’s orbit, perpendicular to the line of sight, subtends an angle of one arc second:
1 pc = 206,265 astronomical units = 30.8586 trillion kilometers.
According to the given definition, the distance to stars can be measured in parsecs by taking the reciprocal of the annual parallax:
Now, let’s revisit our initial problem and calculate the distance to Vega in parsecs using the equation we derived.

In addition to the parsec, astronomy also uses another unit of distance measurement outside of our solar system – the light-year.
The light-year is defined as the distance that light travels in a vacuum in one year:
1 pc = 3.26 sv. yr. = 206,265 a. e. = 3 ∙ 10,13 km.
In 1989, the European Space Agency launched the Hipparcos satellite, which was able to measure the annual parallaxes of over a million stars during its 37-month mission. The accuracy of measurements for more than one hundred thousand of these stars was within one angular millisecond.
However, once astronomers acquired the knowledge to calculate the distances to the stars, a new challenge emerged. It was discovered that stars that are nearly equidistant from Earth can exhibit different levels of apparent brightness. This apparent brightness does not accurately depict the star’s actual radiance. For instance, the Sun appears to be the brightest object in the sky simply because it is much closer to Earth than other stars. Consequently, in order to make a fair comparison of a star’s true brightness, it became necessary to establish their stellar magnitudes at a standardized distance from Earth. This standardized distance is referred to as 10 pc. The apparent stellar magnitude that a star would possess if it were situated at a distance of 10 pc from Earth is known as the absolute stellar magnitude.
What was the reason behind selecting 10 parsecs as the standard distance? It was chosen for the sake of simplicity in calculations. Let’s assume that the apparent stellar magnitude of a star at a certain distance D is denoted as т, while its luminosity is represented by I.
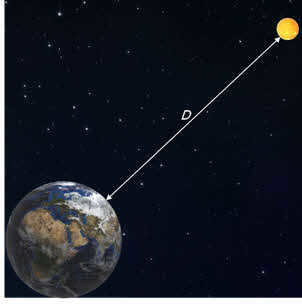
Remember that the brightness of two sources with a difference of one in their stellar magnitudes is 2.512 times. In other words, for two stars with stellar magnitudes т1 and т2 respectively, the ratio of their brightness is given by the ratio:
By definition, the apparent stellar magnitude of a star at a distance of 10 pc will be the same as its absolute stellar magnitude M. If we symbolize the star’s luminosity at this distance as I0, then the equation for the apparent and absolute stellar magnitudes of the star can be written as follows:
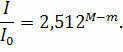
Simultaneously, we possess knowledge from the realm of physics that the brightness changes in an opposite manner to the square of the distance:
Allow us to replace this statement into the preceding equation, considering the fact that:
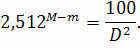
Let’s now introduce the acquired equation:
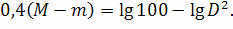
By considering that the star’s distance is inversely related to its annual parallax, we can derive an equation that allows us to determine the absolute stellar magnitude of nearby stars.
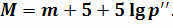
Now, we can apply the equation to determine the absolute magnitude of our Sun. Considering that its apparent magnitude is 26.8 and the average distance to it is one astronomical unit.

That means, the Sun appears to be a dim star with an approximate magnitude of fifth magnitude.
By knowing the absolute magnitude of a star, we can determine its actual total emission or brightness.
Brightness refers to the total energy radiated by a star per unit of time. It can be measured in watts, but it is more commonly expressed in terms of the Sun’s brightness.
Using Pogson’s formula, we can establish the relationship between the brightness and absolute magnitude of a star and the Sun:
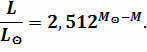
If we consider the Sun’s luminosity as a standard and its absolute stellar magnitude as 4.8 m, we can rephrase this equation.
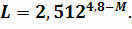
Stars exhibit significant variations in terms of luminosity, or the power of radiation they emit. For instance, certain supergiant stars have a radiation power that exceeds that of the Sun by 330 thousand times. On the other end of the spectrum, some dwarf stars have the lowest luminosity and emit light that is 480 thousand times weaker than our Sun.

Currently, there are extra cumulative discounts (ranging from 2% to 25%) available for 58,740 educational establishments. To determine the discount applicable to all staff members of your educational institution, please access your personal Infoworks account.


Professional retraining course
Learn the theory and methodology of teaching history and social science in educational organizations with our professional retraining course.
Take advantage of our special discount offer! We can apply an additional discount for your educational institution based on the number of colleagues who have already completed Infowork courses.
Currently, 58,740 educational institutions have received extra discounts ranging from 2% to 25%. To find out the specific discount available for all employees of your institution, simply log in to your personal Infoworks account.


Course for professional development
Current challenges in teaching physics in schools implementing the FSES
In addition to this discount, you may also qualify for a discount from your educational institution (based on the number of colleagues who have taken Infoworks courses).
At present, there are 58,740 educational institutions that receive additional discounts ranging from 2% to 25%. To determine the discount applicable to all staff members at your educational institution, please log in to your personal Infoworks account.


Resource state, emotional sphere, effective parenting – debunking myths and facing realities
Elaboration on the presentation through individual slides:

On the second slide, we will explore the methods used to measure the distances to the stars. Additionally, we will uncover the significance of stellar magnitudes and how they are determined. Lastly, we will discover how it is possible to measure the temperature of stars without the use of a traditional thermometer.


slide 3 slide DISTANCE TO STARS.
To calculate the distances to stars, astronomers use the method of annual parallax, which is based on the Earth’s orbit around the Sun. The distance from Earth to a star can be found using the formula:
r = 1a.e./sinp
The annual parallax allows us to determine the angle at which the major semi-axis of Earth’s orbit would be seen from a star in a direction perpendicular to the line of sight

4 Slide The distance to stars is measured in light-years, however astronomers still utilize the unit parsec (pk), where the yearly parallax p = 1″ (parsec is abbreviated for parallax-second).
1 pc ≈ 3.26 sv years.

Slide 5 VISIBLE STAR VOLUMES
In the 2nd century BC, the Greek astronomer Hipparchus categorized all stars based on their brightness, dividing them into 6 classes known as stellar magnitudes. The stars with the highest brightness were referred to as stars of the 1st stellar magnitude, while the ones with the lowest brightness, barely visible in the sky, were labeled as 6th magnitude stars.
Hipparchus
(circa 190 BC – after 126 BC).

Slide number 6
The English astronomer Norman Pogson expanded upon the definition of stellar magnitude by introducing an additional criterion:
Stars of 1st magnitude should be 100 times brighter than those of 6th magnitude.
Norman Robert Pogson
(1829 – 1891) – An astronomer from England


Slide number 7
The letter m represents the apparent stellar magnitude. The ratio of the brightnesses E1 and E2 will be true for stellar magnitudes m1, m2:
According to this criterion, stars that are barely visible to the naked eye have a magnitude of +6m.
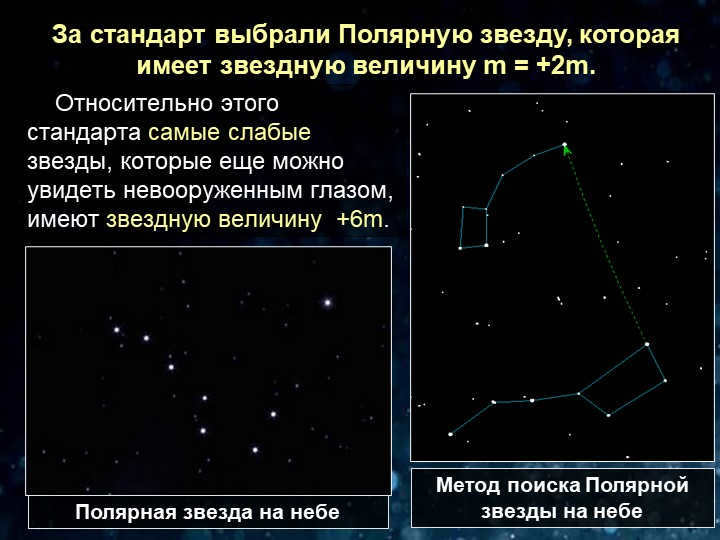
In the celestial sphere, Polaris is commonly used as a reference point.
There is a specific technique for locating Polaris in the sky.
We have selected Polaris as the standard because it has a magnitude of +2m.


Slide 9 ABSOLUTE STAR magnitudes
If the Sun were located 10 parsecs away, it would appear as a relatively faint star with a magnitude of fifth stellar magnitude. In other words, the absolute magnitude of the Sun is M = +5m. The absolute magnitude M refers to the magnitude a star would have if it were at a standard distance of 10 pc.


Slide number ten
The luminosity of a star, denoted as L, is responsible for determining the quantity of energy that a star releases per unit of time, also known as the star’s radiative power. In the field of astronomy, the luminosity of the Sun is considered as the standard unit, with a radiative power of 4∙1026 W.
In 1665, Isaac Newton (1643-1727) broke down light into a spectrum and provided an explanation of its properties.
The spectra of stars serve as a unique identifier, providing a comprehensive description of their characteristics. By analyzing the spectrum of a star, we can determine its luminosity, distance, temperature, size, chemical composition of the atmosphere, rotational speed, and specific motion around the center of gravity.

Typically, each star’s spectrum features dark absorption lines known as Fraunhofer lines. These lines are created in the star’s thin atmosphere as well as in Earth’s atmosphere, and they reveal the atmosphere’s chemical makeup. This is interesting because all stars share a nearly identical chemical composition due to the prevalence of hydrogen and helium, which are the primary chemical elements in the universe.

Slide 14 – COLOR AND TEMPERATURE OF STARS
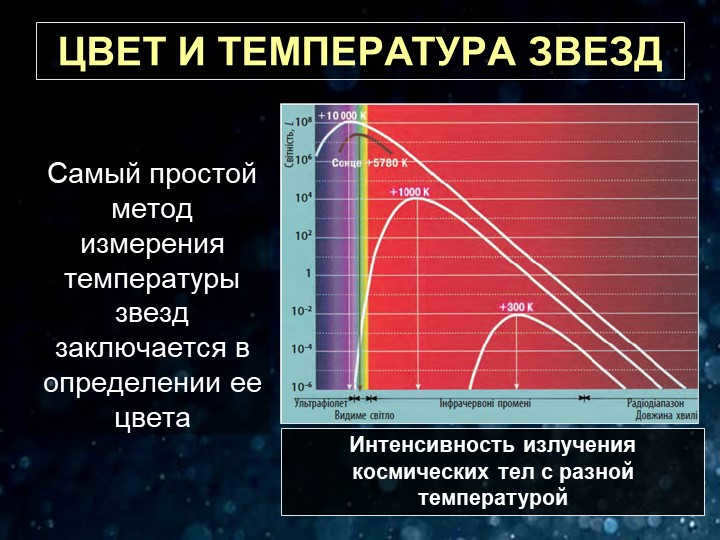
One of the most straightforward approaches to determine the temperature of stars is by observing their color.
The radiation intensity emitted by celestial bodies varies depending on their temperature.
Slide number 15 SPECTRAL CLASSES
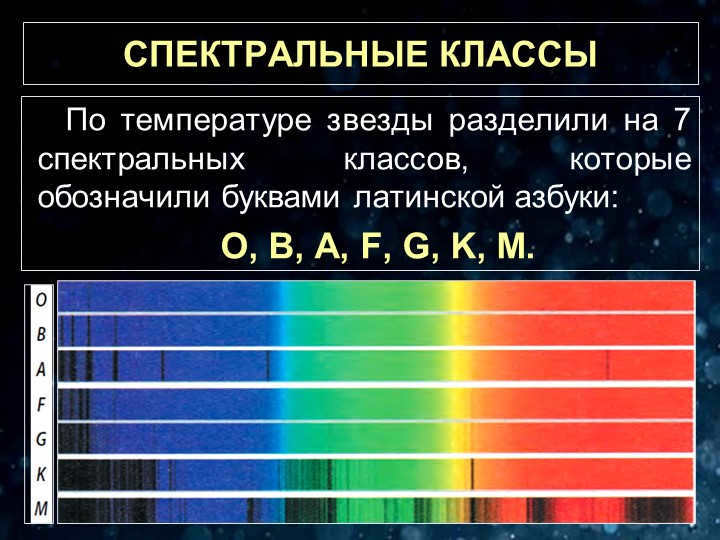
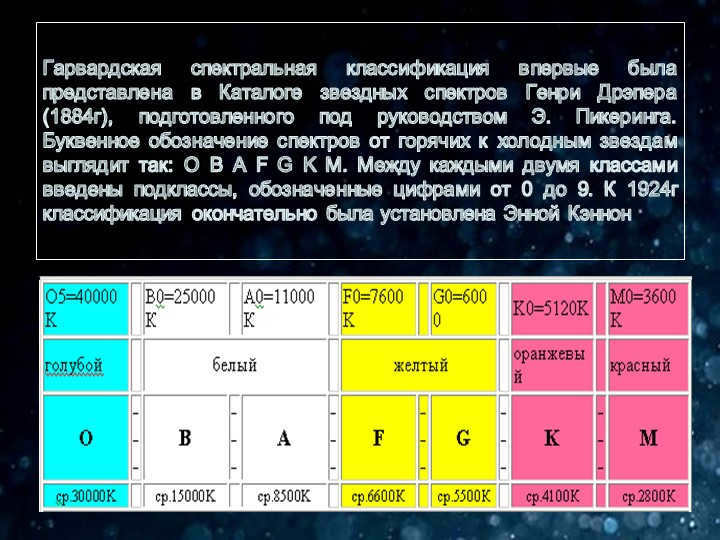
Stars have been categorized into 7 spectral classes based on their temperature, with each class represented by a letter from the Latin alphabet:
O, B, A, A, F, G, K, M.


slide 17 STELLAR RADII
The size of a star can be calculated by measuring its brightness and surface temperature. Scientists use the Stefan-Boltzmann law to calculate the radius of a star:
Q = σ-T4
where Q represents the amount of energy emitted by a single unit of the star’s surface over a specific time period; σ is the Stefan-Boltzmann constant; T is the absolute temperature of the star’s surface.
Comparison of star sizes with the Sun’s radius:

Slide 18: The energy emitted by a star is calculated using the formula E = 4πR2-Q = 4πR2-σ-T4. This equation represents the power radiated by the star based on its surface area and temperature.
It is interesting to note that there are stars with radii hundreds of times larger than the radius of the Sun, as well as stars with radii smaller than the radius of the Earth. These stars can be classified into different categories based on their size:
- Supergiants (I)
- Bright giants (II)
- Giants (III)
- Subgiants (IV)
- Main-sequence dwarfs (V)
- Subdwarfs (VI)
- White dwarfs (VII)

The Beta Pegasus, a red giant classified as M2.3 II-III, can be found within the globular cluster M15 in the constellation of Pegasus.


21 Slide If you put Betelgeuse, a red supergiant situated 640 light-years from here, in the heart of our solar system, the gas plume reaches beyond the orbit of Jupiter.

There are 22 STARS in the WHITE CARLISTS slideshow. This presentation showcases a binary system consisting of two white dwarfs. The larger of the two dwarfs, NLTT 11748, is actually lighter in weight compared to the smaller dwarf.

Slide 26: Final Remarks
While stars may appear similar, they possess distinct physical traits such as luminosity, temperature, radius, and density that set them apart from one another.
The Sun, for instance, falls into the category of yellow stars, which remain in a stable state and maintain a consistent size over billions of years.
Space is also home to colossal giant stars that are a thousand times larger than the Sun, as well as dwarf stars with a radius smaller than that of Earth.


Slide 27: Identify the star (1 b)
Which constellation does this star belong to? (1 b)
Apparent magnitude of the star (1 b)
Distance to the star in parsecs and light years (2 b)
How many times is the luminosity greater than that of the Sun? (1 b)
What is the energy E emitted by the star per second? (2 b)
What is the spectral class of your star in terms of temperature? (1 b)
What is the size classification of your star (dwarf, normal, giant, supergiant)? (1 b)
Calculate the radius of your chosen star if the radius of the Sun is approximately 7-105 km. (2 b)
QUESTIONS




Homework assignment for slide 32
1) Section 22, page 152, Assignment 18.
2) Investigate the scientists mentioned in Section 22 and assess their impact on the field of astronomy. Produce a presentation with one slide dedicated to each scientist.

Determining the distance to the stars is a fascinating topic for those who enjoy reading popular literature on astronomy but may not have a specialized education or access to the necessary information for calculating such measurements. Ancient astronomers relied on simple methods which involved angular measurements from multiple points. Additionally, they used formulas that incorporated time, the calculated speed of celestial bodies’ movement, and the observer’s movement along with the planet Earth. These methods enable us to estimate the distance to nearby astronomical objects. However, calculating the distance to stars using these methods is highly challenging.

Context
For countless years, brilliant scientists have been captivated by the quest to discover reliable methods for measuring the distance to the nearest star. These individuals have dedicated their lives to studying the vast expanse of the night sky and the enigmatic objects that inhabit it. A groundbreaking milestone in this field of human knowledge occurred with the introduction of telescopes.

It is important to also note the following facts:
- The accumulation of knowledge did not always result in the ability to draw conclusions. Lack of information exchange led to simultaneous discoveries in various regions of the world. If information could have been shared as easily as it is today, scientists would have had an easier time making discoveries. They would not have had to measure different quantities based on their own misunderstandings and reach incorrect conclusions.
- The first successful determination of stellar distances occurred in 1838, with separate discoveries made in various locations across the globe. Renowned German astronomer Friedrich Bessel was able to ascertain the distance to the star 61 Cygni. Similarly, esteemed Russian scientist V. Struve became the first person to measure the distance to Vega, while British scientist Thomas Henderson successfully determined the distance to Alpha Centauri.
- This marked a significant milestone in the field of astronomy, representing the culmination of existing knowledge and the beginning of a new era in scientific exploration. These measurements were only possible due to the substantial distances separating the planets, which could be measured in easily comprehensible kilometers.
- By 1838, the methodology for determining stellar distances was already established, albeit limited to relatively close stars. This involved measuring the angular distance and calculating parallax.

The success of astronomers can be attributed to their ability to collaborate and share knowledge. In the past, this was achieved through printed publications, and later through the World Wide Web of Information.
However, in the field of modern astronomy, there is still no universal method for determining accurate distance measurements.
Scientists use various methods to calculate these measurements. As distances increase, new methods are developed and built upon the existing ones.

The astronomical unit (a. e.) has taken the place of kilometers and meters, which were previously used to measure distances on Earth. These units were also used to calculate the distances of celestial bodies and planets that are relatively close by cosmic standards.
Even when measuring distances to our closest neighbors, the astronomical unit can be used. It has a relatively stable value and was officially defined as 149597870 km in 1976, with a margin of error of 2 km.

Measuring the Distance to Stars
However, the distance between the Sun (which is measured in astronomical units) and the nearest alien star is too insignificant to accurately measure the vastness of outer space, especially deep space. This discrepancy led to the development of concepts like the parsec (pc) and the speed of light.

These calculations can be used for objects that are not visible to the naked eye. And it is difficult to comprehend the concept of a light year, such as how long it would take for a spaceship to reach even the closest galaxy.
The most straightforward solution to the problem of determining distances in the Universe applies to both humans and the solar system. Nowadays, any student can write an essay or give a presentation on this topic. However, they may not consider the origins of these formulas or how the distance to the Earth’s satellite and other objects was determined.
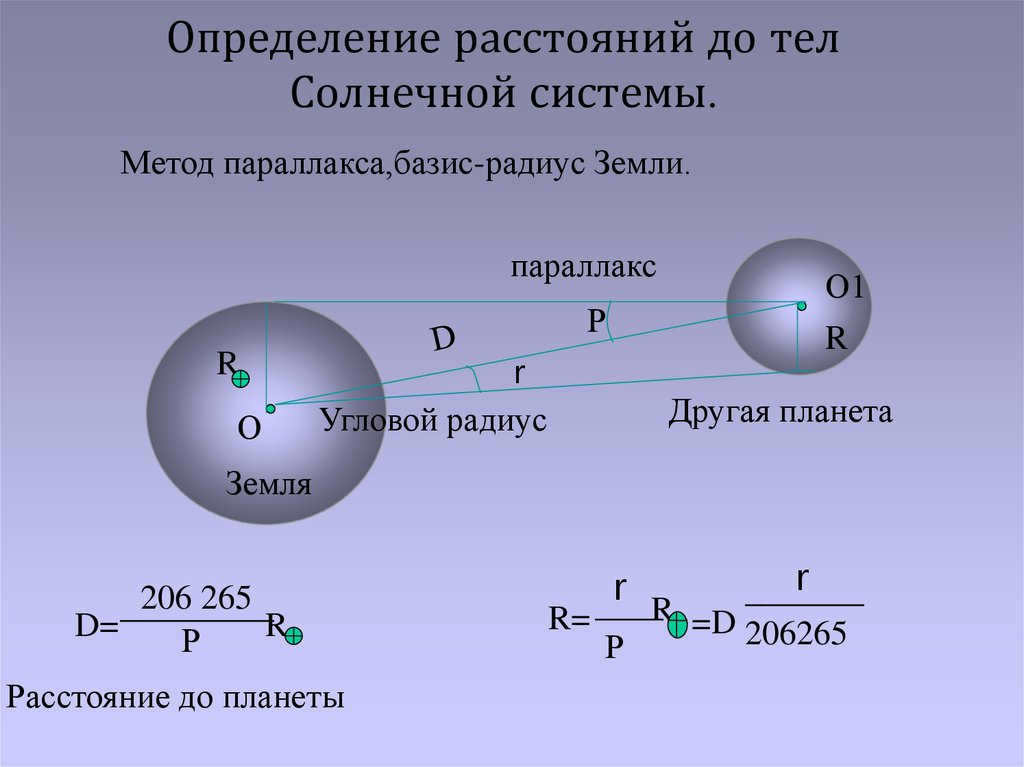
The Third Law of the renowned astronomer Johannes Kepler has played a vital role in determining the distances between distant planets and the Sun. According to Kepler’s law, the square of the planets’ orbital period is proportional to the cubes of their average distances from the center of the solar system.
The distances to the Moon and the nearest yellow dwarf star have been accurately calculated using radar technology, although it requires some time to obtain precise results.

Measuring the Distance to Stars: Techniques and Methods
Calculating the distance to stars involves employing a variety of measurement techniques. The selection of each method depends on the distance being measured and the desired level of accuracy for the observations.
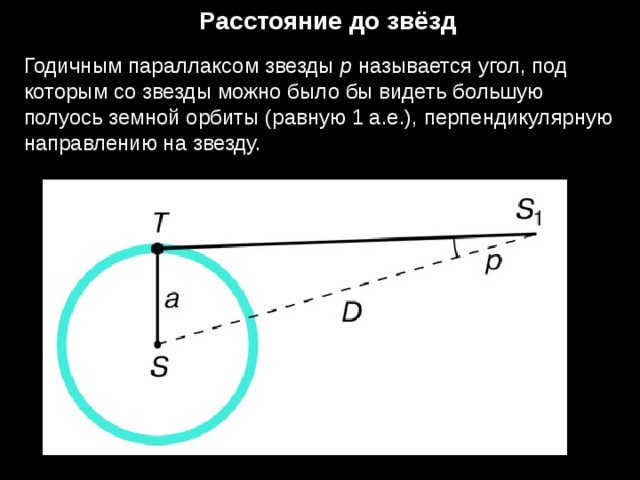
The parallax method allows for the determination of distances up to 100 parsecs, with some margin of error (approximately 50%). The accuracy of the measurements decreases as the distance increases. Using this method, scientists have been able to calculate distances up to 6,000 parsecs from stars. For instance, the distance to Proxima Centauri (a red dwarf) is estimated to be around 1.31 parsecs.
This method is based on the apparent displacement of nearby stars compared to distant stars, which appear to be stationary.
This visual effect is caused by the actual movement of the Earth in its annual orbit. Despite its complex verbal description, the parallax method can be expressed in simple trigonometric terms and does not pose any difficulties in its solution.
If you want to get a better understanding of the process, you can check out videos created by popularizers. There are many videos available that are specifically tailored for astronomy classes. One such video is provided below as an example.
Calculating Distance
Cepheids are celestial bodies that can be utilized as a point of reference to determine distances. Their size allows them to pulsate with a specific period, which in turn affects their brightness. By observing these pulsations, scientists can calculate the distance to Cepheids using specialized calculations. This technique is centered around the luminosity of these stars.

The advent of super-modern telescopes has enabled the differentiation of a cluster of individual stars in a relatively nearby galaxy, thanks to its periodicity and power. This innovative method allows scientists to determine the approximate distance. However, it is not applicable to distant galaxies.
While redshift is not a highly accurate method, it can be recalculated according to the cosmological model. This makes it suitable for estimating phenomena that are beyond the reach of the human eye. The vast distances (10 million light years) that light must travel to reach these objects make it challenging to comprehend their current state at the observed boundary of the Universe.
Calculations can also utilize a thermonuclear explosion resulting from supernovae, specifically double white dwarf stars, which release an immense amount of energy. The precision of these calculations may rely on the rate at which the mass limit is reached. However, comprehending how distance can be conveyed necessitates additional understanding and specialized techniques for analyzing the acquired data.
The concept of the photometric method is grounded in a basic comprehension of the principles governing the movement of light. When the radiance of a star or any other source of light matches that of another, it signifies that they are at an equivalent distance. By determining the amount of light emanating from one object, it is possible to ascertain that this figure is equivalent to the distance to another object with comparable illumination. This calculation is accomplished using a specialized formula for photometric distances.

Determining Distances to Stars
Measurements have been carried out to determine the distances to the closest visible stars. By calculating the time it takes for a light beam to travel to these stars, scientists have been able to identify their approximate spectrum, color, and proximity. It’s important to note that optical illusions can sometimes make objects appear closer than they actually are in relation to other objects.

However, the situation with Alpha Centauri and its Proxima is quite complex. It is approximately 270,000 times farther from the Sun and has a mass that is nearly 7 times smaller. Despite its close proximity, it is nearly imperceptible to the naked eye. Additionally, there are some intriguing facts to consider:
- Barnard’s star, the fourth most distant, is also relatively nearby, at a distance of almost 2 parsecs. Like Alpha Centauri, it is also barely visible in the night sky and was only discovered at the beginning of the last century;
- Sirius, the brightest star, is located 8.6 light-years away but can be seen from almost any hemisphere. While not as close as Barnard’s star or Proxima, its brightness allows it to be easily observed;
- Polaris, which is located in close proximity to the Big Dipper, is situated at a distance of over 447 light-years. Despite its location being as far as 137 parsecs away, it is visible much more prominently than other stars like Proxima. This is due to the fact that Polaris is a supergiant and is part of a triple star system.

Polaris is a fascinating natural phenomenon, resembling a carefully calibrated tool for calculations and observations. Its position above the horizon corresponds to the latitude of the Earth’s surface at the specific moment of observation.
Furthermore, when traveling north, the direction often aligns with that of the supergiant star.
It’s no wonder that ancient navigators assigned special significance to Polaris. Despite being a physical object located at a great distance, it holds a certain mystique. The pattern it creates is likely coincidental, resulting from the cyclic alignment of celestial motion, and the visible sphere of Polaris undergoes constant changes in luminosity. These fluctuations are attributed to variations in temperature and the presence of older and younger stars within its triad.

The fallaciousness inherent in the visual perception of the celestial sky is easily elucidated when humanity possesses not only the bare minimum, but rather concrete knowledge. Each of the novel advancements in the exploration of the celestial sky and its distances serves as a sort of trial, surmounted prior to the commencement of the subsequent phase. At present, humanity has successfully completed four stages in investigating and determining the distances to the stars and stands at the cusp of the fifth, which promises to be even more arduous.





