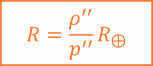Measuring mass is an essential aspect when studying physical bodies, and it remains a fascinating and somewhat mysterious concept. It is not solely due to the constant struggle many individuals face in trying to shed excess weight. Scientists have yet to completely comprehend the phenomenon of weight, which is why the discovery and prediction of the Higgs boson particle, responsible for its existence, was honored with the Nobel Prize in 2013. Nonetheless, despite the limited understanding of weight, we have managed to accurately determine the mass of objects across a wide spectrum, ranging from electrons to the entire universe.
Calculating Weight of Astronauts in Space
When we step on a digital scale after a filling meal, we are not measuring our mass, but rather the gravitational force exerted on our body by planet Earth. On other celestial bodies, such as Mars or the Moon, this measurement would yield different results: for instance, on Mars, the same individual would weigh nearly three times less, while on the Moon, the weight would be six times lighter. It is not difficult to imagine that in the absence of gravity, the scale would read “zero” regardless of who is being weighed. So, how do astronauts aboard the International Space Station determine their weight?


In order to address this inquiry, it is necessary to recall that mass denotes the degree of inertness possessed by an object, signifying its capacity to resist the influence of an external force. An object that is heavier (more massive) will undergo less acceleration when subjected to the same force compared to an object that is lighter (less massive). Thus, by ascertaining the magnitude of the force and measuring the acceleration experienced by an object, it is possible to utilize Newton’s first law to determine its mass. The International Space Station (ISS) is equipped with a “gas pedal” of sorts that incorporates appropriate sensors, which astronauts routinely exploit. Admittedly, the mechanics of this apparatus are somewhat intricate, but it does yield results of acceptable precision and reproducibility.
It is worth mentioning that since the formulation of the law of universal gravitation, there have been two distinct types of mass in the field of physics. We have just discussed the first type – inertial mass. The second type – gravitational mass – determines the strength with which an object attracts other objects under the influence of universal gravitation. Scientists have long sought to determine whether the magnitudes of these two masses always coincide for the same object, or if they can differ under certain circumstances. It was not until the 20th century, with the advent of Einstein’s theory of relativity, that the “mass paradox” began to be partially resolved. The complexity of investigating this question is partly due to the fact that for large bodies such as stars, planets, and their satellites, it is usually only possible to measure gravitational mass: the lever that Archimedes envisioned to lift the Earth unfortunately exists only in the imaginations of scientists and artists.
The Cavendish experiment
The Cavendish experiment is a significant scientific experiment that was conducted by Henry Cavendish in 1797-1798. The experiment was designed to determine the gravitational constant, which is a fundamental constant in physics that describes the strength of the gravitational force between two objects.
In the experiment, Cavendish used a torsion balance, which consists of two small lead spheres suspended from a thin wire. He placed two larger lead spheres near the smaller spheres and observed the torsional motion of the balance caused by the gravitational attraction between the spheres. By measuring this motion and using mathematical calculations, Cavendish was able to determine the gravitational constant.
The Cavendish experiment was groundbreaking because it provided the first accurate measurement of the gravitational constant. This constant is a crucial parameter in many areas of physics and has significant implications for our understanding of gravity and the universe. The experiment also demonstrated the validity of Isaac Newton’s law of universal gravitation and contributed to the development of the theory of gravitation.
The task of “weighing” the Earth was initially attempted by the British physicist Henry Cavendish. In a series of experiments conducted between 1797 and 1798, Cavendish utilized an improved torsion pendulum that had a pre-measured elasticity index. He observed the displacement of smaller metal balls attached to the ends of the pendulum when two much larger and heavier lead balls (each weighing 158 kg) were brought near them. By determining the attractive force between the small balls and the large ones, as well as the attractive force between the large balls and the Earth, Cavendish was able to calculate the average density of the Earth using a relatively simple equation. This calculation resulted in an average density of 5.448±0.033 g/cm³, which is less than one percent different from the modern value. These findings led to the conclusion that the Earth is primarily composed of metals, with water and stony rocks making up a relatively small portion of its composition.
Given the already well-established knowledge of the Earth’s radius (and consequently its volume) during the time of Cavendish, determining its mass was no longer a challenging task. By understanding the acceleration of free fall on the Earth’s surface, the value of the gravitational constant could be determined – a crucial factor in the formula for the law of universal gravitation. The refinement of this constant was further achieved through the study of the Moon’s movement and the measurement of its average distance. This breakthrough allowed for the extension of “weighing” techniques to the Sun and other planets within the solar system.
By utilizing satellites
It should be noted that the force of attraction between two objects at a given distance is determined by gravitational mass. This force can be computed by taking into account the orbital period of a planet’s satellite (whether natural or artificial) and the major semi-axis of its orbit. By the late 19th century, scientists had already obtained reasonably accurate measurements of the average distances of all the planets from the Sun, which allowed them to determine the mass of our star – an astounding 2×10³⁰ kg (two with thirty zeros). Furthermore, they were able to estimate the masses of planets with satellites with a fair degree of accuracy. The masses of Mercury and Venus were inferred from the gravitational influence they exerted on other celestial bodies in the solar system. The exact masses were later determined through direct measurements taken by spacecraft during their missions to these planets.
The accuracy of estimates for the masses of dwarf planets, comets, and asteroids is still relatively low, except for those that have been visited by automated scouts in their vicinity. Even when Earth’s representatives conducted studies during flyby missions, the gravitational pull of these small celestial bodies caused slight deviations in the trajectory of the probes and alterations in their velocity. These deviations were detected through the Doppler frequency shift of the onboard radio transmitters, which enabled the calculation of the object’s mass.

One alternative way to estimate the weight of asteroids and comet nuclei is by calculating their rotational speed. As these celestial bodies are mainly composed of loose fragments held together primarily by gravity, they need to have a minimum mass in order to resist being torn apart by centrifugal forces.
The enigma of the Milky Way
When astronomers became aware that the Sun was a component of an enormous stellar system, later labeled as the Galaxy, they initiated a quest to ascertain its weight. Initially, this proved to be an insurmountable challenge due to our lack of knowledge regarding the velocity at which our star orbits the galactic center, as well as its precise location in relation to it (for a period of time, it was hypothesized that the Sun resided in the vicinity of the center). It was only in the 1930s that American astronomer Harlow Shapley roughly determined this position and produced initial estimations of the magnitude of the Milky Way, yet the determination of its mass remained a distant objective.
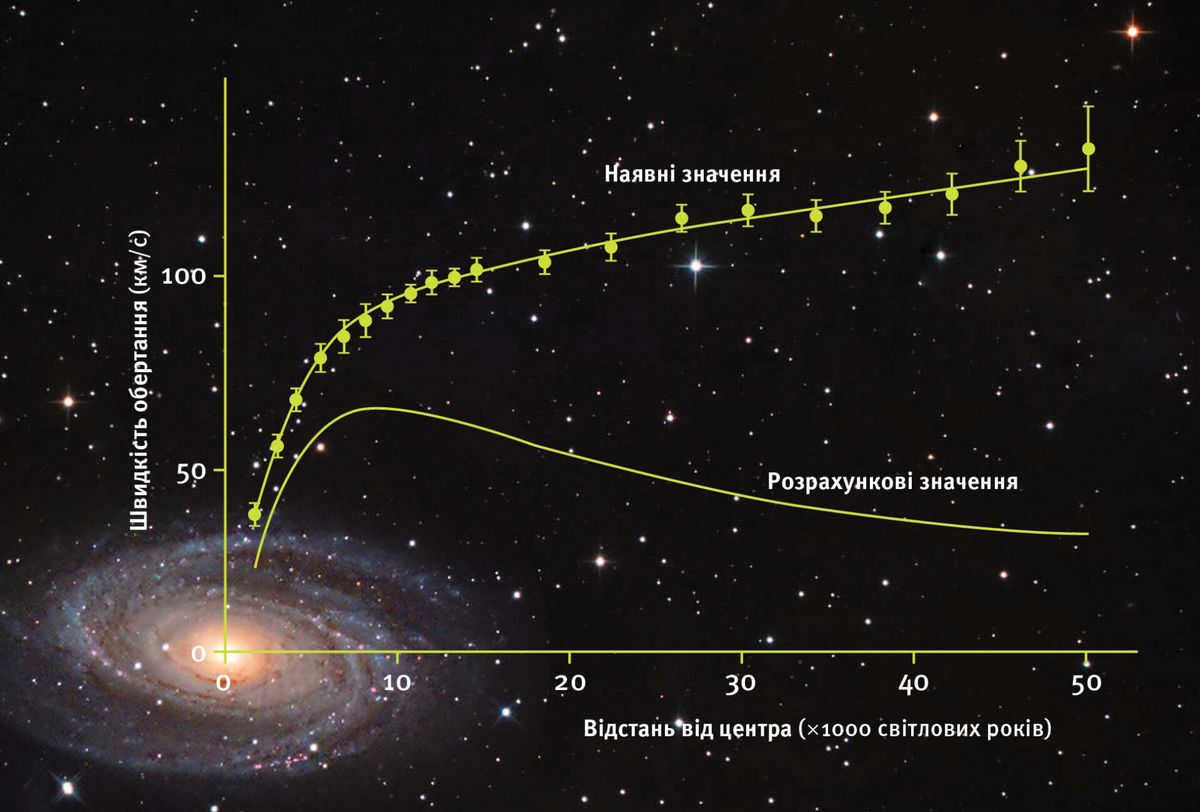

By analyzing the movement patterns of numerous stars and examining the behavior of interstellar matter and dwarf galaxies that orbit the Milky Way, scientists have concluded that the combined mass of our stellar system within a sphere measuring 130 thousand light years from its center is approximately one and a half trillion times the mass of the sun. This is equivalent to 3×10⁴² kg (three with 42 zeros). However, it is important to note that our galaxy is still considerably smaller compared to the largest galaxies in the Universe!
Weighing the Whole Thing
At a quick look, figuring out the weight of an endless Universe may appear to be impossible, and in general, it should also be endless. However, this is not completely accurate. Despite the fact that our world has no physical boundary (and furthermore, as cosmologists demonstrated in the 1920s, it is continuously expanding), the quantity of matter with mass in it is finite and even gradually decreasing – due to the “consumption” in thermonuclear reactions deep within stars.

Adapting Archimedes’ lever to determine the weight of the Universe is not possible. Likewise, using the velocity of bodies orbiting around it to calculate its mass is also not feasible since all known bodies are part of the Universe. However, the mere existence of the Universe allows us to establish certain boundaries for its “universal mass”: if it were excessively large, all massive bodies would be mutually attracted during the early stages of universal evolution.
In order to establish the minimum limit, astronomers have made attempts to assess the total mass of all the celestial objects that can be detected using contemporary observational tools, including stars, galaxies, and intergalactic gas clouds… Over time, these calculations have become increasingly intricate due to the discovery of additional components that are either imperceptible or nearly imperceptible, yet still contribute significantly to the overall “mass balance”: exoplanets, “dark matter,” neutrinos…
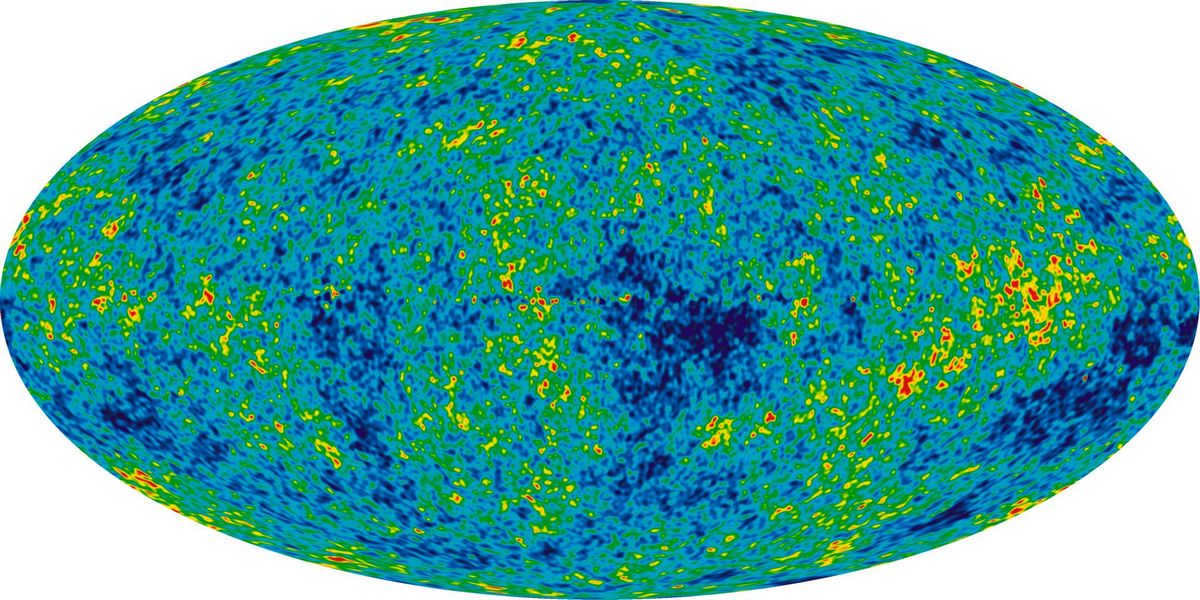
The most comprehensive data was obtained through the utilization of the American satellite WMAP (Wilkinson Microwave Anisotropy Probe) as well as the European observatory Planck, which examined the residual microwave radiation – the “relic remnants” of the Big Bang that shaped our universe. The slight fluctuations within this radiation, linked to the initial irregularities of primordial matter and the interaction of light with subsequently formed large-scale cosmological structures, contain information about the masses of the celestial objects that the relic photons encountered. Upon analyzing the findings, astronomers were able to calculate the average density of the cosmos, which is equivalent to the mass of six protons per cubic meter.
Actually, this quantity technically denotes the energy density (it can be “converted” into mass according to Einstein’s well-known equation E=mc², and such conversions do indeed happen constantly in the actual world). It encompasses not just “observable” matter, also called “baryonic matter”, but also the aforementioned dark matter, and an even more enigmatic element of the cosmos, which causes the Universe to expand with acceleration – dark energy.
If the number of particles in this region is multiplied by the volume of space from which light has already managed to reach ground observers for 13.8 billion years (the estimated age of the Universe), we obtain a weight of 10^53 kg – a unit with 53 zeros. Even if we consider only baryonic matter, which makes up only 5% of the Universe according to recent data, the resulting value would still be enormous. While these figures may be refined in the future, it is unlikely that they will differ significantly from the current estimates. By understanding the total mass of our world, scientists can gain a better understanding of its past and future evolution.
One of the most important physical characteristics of a celestial body, its mass, can be measured using Newton’s law of universal gravitation.
This can be done through various methods:
- By measuring the force of gravity on the surface of the body (gravimetric method).
- By applying Kepler’s third refined law.
- By analyzing the perturbations observed in the motions of other celestial bodies caused by the celestial body in question.
The first method is commonly used for measuring the mass of the Earth.
Based on the law of gravitation, the acceleration g at the surface of the Earth can be expressed as:
g = (G * m) / R^2
Where m is the mass of the Earth and R is its radius.
The values of G and R can be measured at the surface of the Earth, with G being a constant.
Using the accepted values of g, R, and G, the mass of the Earth can be calculated:
By knowing the mass and volume, we can calculate the average density, which is 5.5 g/cm3.
2. If a planet has at least one satellite and we know the distance between the planet and the satellite, as well as the period of revolution around it, we can determine the ratio between the mass of the planet and the mass of the Sun, according to Kepler’s third law.
In this equation, M represents the mass of the Sun, m represents the mass of the planet, mc represents the mass of the satellite, T represents the period of the planet’s orbit around the Sun, tc represents the period of the satellite’s orbit around the planet, a represents the distance of the planet from the Sun, and ace represents the distance of the satellite from the planet.
The M/m ratio is generally large for all planets, while the m/mc ratio is typically small, except for the Earth and the Moon, Pluto and Charon, and can be disregarded.
The M/m ratio can be easily calculated using the equation.
To determine the mass of the Moon, analyzing the perturbations in the motion of the Earth caused by the Moon is necessary. However, this task is quite challenging.
One approach to solving this problem is by making precise determinations of the apparent positions of the Sun in its longitude. Through this method, variations known as the “lunar inequality” with a monthly period have been discovered. The presence of these variations in the Sun’s apparent motion suggests that the center of the Earth traces a small ellipse around the common center of mass, known as “Earth-Moon,” which is located within the Earth at a distance of 4650 km from its center.
In 1930-1931, observations of the minor planet Eros also helped in determining the position of the Earth-Moon center of mass.
Based on perturbations in the movements of man-made satellites orbiting the Earth, the Moon was found to have a mass that is 1/81.30 times the mass of the Earth.
In 1964, the International Astronomical Union officially recognized this ratio as a constant.
Using Kepler’s equation, we can calculate that the mass of the Sun is 2.1033g, which is 333,000 times greater than the mass of the Earth.
The masses of planets that do not have satellites are determined by the perturbations they cause in the orbits of the Earth, Mars, asteroids, and comets, as well as the perturbations they exert on each other.
The law of universal gravitation, which is expressed by formula (1), serves as the foundation for determining the masses of celestial bodies. The force of mutual attraction, denoted as F, is proportional to the product of the masses and inversely proportional to the square of the distance (r) between their centers. In the field of astronomy, it is often possible to disregard the size and shape differences of celestial bodies, treating them as concentrated masses instead.
The constant of gravitation, represented by the coefficient G, is obtained through physical experiments using torsion weights. These experiments allow for the determination of the gravitational force between bodies of known mass.
When objects fall freely, the force F that acts on the object is equal to the product of the object’s mass and the acceleration of free fall g. The acceleration g can be calculated using the period T of oscillation of a vertical pendulum, where l is the length of the pendulum. At a latitude of 45 degrees and at sea level, the value of g is 9.806 m/s^2.
By substituting the expression for the gravitational forces on Earth into formula (1), we obtain the following relationship, where M is the mass of the Earth and R is the radius of the Earth. This allowed for the determination of the Earth’s mass, denoted as g. Determining the mass of the Earth is the first step in determining the masses of other celestial bodies such as the Sun, Moon, planets, and stars. The masses of these bodies can be found using either Kepler’s 3rd law or the rule that states the distances of masses from the center of mass are inversely proportional to their masses. This rule allows for the determination of the Moon’s mass. By measuring the precise coordinates of the planets and the Sun, it has been discovered that the Earth and Moon orbit around the barycenter, which is the center of mass of the Earth-Moon system, with a period of one month. The distance from the Earth’s center to the barycenter is 0.730 (located within the Earth). The distance from the Moon’s center to the Earth’s center is 60.08. Therefore, the ratio of the distances from the barycenter to the centers of the Moon and Earth is 1/81.3. Since this ratio is the inverse of the ratio of the masses of the Earth and Moon, the mass of the Moon is 1/81.3.
By applying Kepler’s 3rd law to the Earth’s motion around the Sun and the Moon’s motion around the Earth, we can determine the mass of the Sun. The formula is as follows:
, (2)
where а represents the large semi-major axes of the orbits and T represents the periods (stellar or sideric) of the orbit. By neglecting compared to , we find that the ratio is equal to 329390. Therefore, g, or ca .
We can use a similar method to determine the masses of planets that have satellites. For planets without satellites, their masses are determined by perturbations to the motion of nearby planets. The theory of perturbed motion of planets allowed us to suspect the existence of the then unknown planets Neptune and Pluto, determine their masses, and predict their position in the sky.
The determination of the mass of a star (excluding the Sun) can be done with a relatively high level of accuracy only if it is part of a visual double star system, where the distance between the stars is known. Kepler’s third law can be used in this case to calculate the sum of the component masses, denoted as M1 and M2, in solar masses:
By combining these equations, the masses of each star can be obtained separately. If the stars in the double system have similar luminosity and spectra, the average mass can be used as an estimate for each component without the need for additional calculations:
When it comes to other varieties of binary stars (such as eclipsing binaries and spectroscopic binaries), there are several options available for approximating the masses of the stars or determining their minimum values (i.e., the lowest possible masses).
The data from a collection of around a hundred double stars, each with different characteristics, has allowed us to identify an important statistical correlation between the masses and luminosities of these stars (see link). This correlation enables us to estimate the masses of single stars based on their absolute magnitudes. Absolute magnitudes M are calculated using the formula: M = m + 5 + 5 lg – A(r) (3), where m represents the apparent magnitude of the star in a specific optical range (such as U, V, B, etc.). The values of U, V, or V can be found in (e.g., U, B, or V).), while A(r) refers to the magnitude of light in the same optical range in the given direction up to a certain distance.
If the parallax measurement of a star is unavailable, an estimated value of its absolute stellar magnitude can be derived from its spectrum. To do this, the spectrogram must not only identify the stars, but also assess the relative intensities of certain pairs of spectral lines that are sensitive to the “absolute magnitude effect”. In simpler terms, the first step is to determine the star’s luminosity class – its classification within one of the sequences on the spectrum-luminosity diagram (see ). The luminosity class then determines the star’s absolute magnitude. Using the absolute magnitude obtained through this process, the star’s luminosity class must be determined. The star’s mass can be determined using the mass-luminosity relation (only and ) do not follow this relation.
One way to estimate the mass of a star is by measuring the gravitational redshift of its spectral lines within its gravitational field. In a symmetrical gravitational field, this is equivalent to the Doppler redshift, where M is the star’s mass in solar mass units, R is the star’s radius in units of the Sun’s radius, and v is expressed in km/s. This relationship has been tested on white dwarfs that are part of double systems. In these cases, the radii, masses, and true v r (which are projections of the orbital velocity) have been measured.
Invisible (dark) satellites have been detected near some stars through observations of the star’s position oscillations associated with its motion around the common center of mass. These satellites have masses less than 0.02 and are likely non-luminous bodies resembling planets.
Based on the analysis of star masses, it has been determined that they generally fall within the range of 0.03 to 60. The majority of stars have masses ranging from 0.3 to 3. In the immediate vicinity of the Sun, the average mass of stars is approximately 10^33 grams. While stars may vary significantly in terms of their masses, the differences in their luminosities can be even greater, with some stars being millions of times brighter than others. In addition to variations in mass and luminosity, stars also vary in terms of their radii. As a result, their average densities can differ dramatically, ranging from as low as a few grams per cubic centimeter to several times higher. For example, the Sun has a mean density of 1.4 grams per cubic centimeter.
Earth is an exceptional celestial body within our solar system. It is not the tiniest, nor is it the largest, as it holds the fifth position in terms of size. Among the planets belonging to the Earth group, it stands out as the most massive, having the greatest diameter and density. This magnificent planet is situated in the vastness of outer space, making it quite challenging to determine its exact weight. It is impossible to place Earth on a scale for measurement, thus its weight is estimated by calculating the combined mass of all the substances that constitute it. This estimation amounts to around 5.9 sextillion tons. To comprehend the magnitude of this figure, one can simply express it in mathematical notation: 5 900 000 000 000 000 000 000. The sheer number of zeros in this representation is enough to leave one awe-struck.
The quest to determine the magnitude of the Earth throughout history
Throughout the ages, scientists from various cultures and eras have been fascinated by the challenge of ascertaining the weight of our planet. In ancient times, there were various theories proposing that the Earth was a flat surface supported by whales and turtles, with some civilizations even suggesting elephants instead of whales. Regardless of the specifics, most ancient cultures shared the belief that the Earth was flat and had a definitive edge.
As the Middle Ages arrived, new ideas regarding the shape and weight of the Earth emerged. One notable figure was G. Bruno, who was among the first to advocate for the idea of a spherical Earth. Unfortunately, his revolutionary beliefs led to his execution by the Inquisition. Another significant contribution to our understanding of the Earth’s radius and mass came from the renowned explorer Magellan. It was through his travels and observations that he proposed the notion of a round planet.
Initial findings
The planet Earth is a physical entity with distinct characteristics, one of which is its weight. This groundbreaking revelation paved the way for a multitude of scientific investigations. According to the principles of physics, weight is the force exerted by an object on a supporting surface. Considering the Earth lacks such a support system, it can be inferred that it does not possess weight. However, it does possess an immense mass, which is a different attribute altogether.
The Mass of Planet Earth
In an early attempt to determine the size of the Earth, the ancient Greek scientist Eratosthenes conducted measurements in various cities of Greece by observing the length of shadows and comparing the data obtained. His goal was to calculate the volume of the planet. Later on, the Italian scientist G. Galileo also made attempts to calculate the Earth’s mass, and it was during this time that he discovered the law of free gravity. The task of determining the weight of the Earth was further pursued by I. Newton, who, through his own measurements, discovered the law of gravity.

Scottish scientist N. Makelin was the first to succeed in determining the weight of the Earth. According to his calculations, the planet’s mass is 5.9 sextillion tons. Currently, this measurement has been revised and the Earth’s weight has increased. This increase in weight can be attributed to the accumulation of space dust on the planet’s surface. Approximately thirty tons of dust settle on the Earth each year, adding to its overall weight.
Mass of the Earth
In order to determine the exact weight of the Earth, it is necessary to have knowledge of the composition and weight of the various substances that make up the planet.
- Mantle. The mass of this layer is approximately 4.05 X 10 24 kg.
- Core. This layer weighs less than the mantle, totaling only 1.94 X 10 24 kg.
- Crust of the Earth. This part is very thin and has a weight of only 0.027 X 10 24 kg.
- The hydrosphere and atmosphere. These layers have weights of 0.0015 X 10 24 kg and 0.0000051 X 10 24 kg, respectively.
By summing up all of these values, we can determine the total weight of the Earth. However, it is important to note that different sources may provide slightly different values for the mass of the planet. So, how much does the Earth weigh in tons, and what are the weights of other planets? The weight of the Earth is approximately 5.972 X 10 21 tons. The radius measures 6,370 kilometers.

By utilizing the principle of gravity, we have the ability to easily ascertain the Earth’s mass. To accomplish this, a string is utilized with a small weight suspended from it. The precise location of the weight is determined. Next to it, a ton of lead is placed. There exists an attraction between the two objects, resulting in the weight being deflected by an insignificant distance. Even a deviation of just 0.00003 mm enables us to calculate the planet’s mass. This can be achieved by measuring the force of attraction in relation to the weight and the force of attraction between the small weight and the large weight. The data acquired allows for calculations of the Earth’s mass.
The weight of the Earth and other planets
Earth is the largest planet in our solar system. Mars weighs about 0.1 times the weight of Earth, while Venus weighs about 0.8 times. Gas giants are much bigger than Earth. Jupiter, for example, is 317 times larger than our planet, Saturn is 95 times heavier, and Uranus is 14 times heavier. There are even planets that weigh more than 500 times Earth’s weight. These are massive gas bodies found outside our solar system.
We can determine the mass of the Sun by considering the gravitational force between the Earth and the Sun, which keeps the Earth in its orbit (assuming the Earth’s orbit is circular for simplicity).
Here are the measurements of the Earth’s mass and the average distance of the Earth from the Sun. By using these values, we can calculate the duration of a year in seconds. Therefore,
by substituting the numerical values into the formula, we can determine the mass of the Sun:
This same equation can be used to calculate the mass of any planet that has a satellite. In this scenario, we need to know the average distance of the satellite from the planet, the time it takes for the satellite to orbit around the planet, and the mass of the planet. For example, by knowing the distance of the Moon from the Earth and the number of seconds in a month, we can determine the mass of the Earth using the aforementioned method.
The mass of the Earth can be determined by comparing the weight of an object to the gravitational force it experiences from the Earth, taking into account the dynamic component of gravity caused by the object’s participation in the Earth’s daily rotation and the corresponding centripetal acceleration (§ 30). This correction is not necessary if we use the gravity acceleration observed at the poles of the Earth to calculate the mass of the Earth. Denoting the average radius of the Earth as and the mass of the Earth as , we can express it as:
If we define the average density of the globe as the mean density of the Earth, then it is obvious that Hence, the average density of the globe is equal to
The density of the upper layers of the Earth’s mineral rocks is approximately equal to the average density of the Earth. This suggests that the core of the planet must have a significantly higher density.
Lezhandre initially studied the density of the Earth at different depths, and this research has been continued by numerous scientists. According to Gutenberg and Gaalk’s conclusions in 1924, the Earth’s density varies at different depths.
The pressure within the Earth’s core is believed to be incredibly high, particularly at great depths. Many geophysicists theorize that the pressure could reach several atmospheres per square centimeter. In fact, at a depth of approximately 3000 kilometers or more, the pressure in the core may reach 1-2 million atmospheres.
Regarding the temperature at the core of the Earth, it is well-established that it is significantly higher, similar to the temperature of lava. In underground mines and boreholes, the temperature increases by approximately one degree for every certain depth. For instance, at a depth of about [insert specific depth], the temperature reaches a range of 1500-2000° and remains constant thereafter.
Figure 50 illustrates the relative sizes of the sun and planets.
The complete theory of the motion of celestial bodies, as described in celestial mechanics, allows for the determination of a planet’s mass based on its influence on the motion of another planet. In the early 19th century, astronomers were aware of the existence of Mercury, Venus, Earth, Mars, Jupiter, Saturn, and Uranus. However, astronomers noticed irregularities in the motion of Uranus, suggesting the presence of an unseen planet affecting its orbit. In 1845, French scientist Leverrier and Englishman Adame independently studied the motion of Uranus and were able to calculate the mass and position of an undiscovered planet. Subsequently, this planet was discovered in the sky exactly where the calculations had predicted, and it was named Neptune.
In 1914, astronomer Lovell made a similar prediction about the existence of a planet that was even further from the Sun than Neptune. However, it wasn’t until 1930 that this planet was actually discovered and given the name Pluto.
Basic information regarding the primary planets
The following table provides essential details about the nine main planets within the solar system. Figure 50 illustrates the relative sizes of both the Sun and the planets.
In addition to these larger planets, there are approximately 1300 very small planets known as asteroids (or planetoids). These asteroids primarily orbit between the orbits of Mars and Jupiter.
The lack of a positive result for the comet’s minimum distance from the Sun suggests that there may have been inaccuracies in the initial data provided. To clarify, it seems improbable that a comet with a relatively short orbital period of 2 years could have traveled as far away from the Sun as described in Jules Verne’s novel.
There is an amusing anecdote about an unsuspecting individual who expressed astonishment at astronomers’ ability to identify stars by name. On a more profound note, perhaps the most remarkable accomplishment of astronomers is their ability to determine the weight of both our planet, Earth, and the distant celestial bodies. Indeed, one wonders how, and on what scales, such measurements could be made.
Figure 87. What scale could have been used to weigh the Earth?
Let’s start by considering the measurement of the Earth’s weight. First and foremost, let us comprehend the meaning of “the weight of the Earth”. When we refer to the weight of an object, we are referring to the pressure it exerts on its support, or the tension it creates at the point of gravity. However, neither of these concepts apply to the Earth as a whole. The Earth is not supported by anything, nor is it attached to anything. Therefore, in this sense, the Earth has no weight. So, what did scientists determine when they “weighed” the Earth? They determined its mass. In reality, when we ask a store to weigh 1 kg of sugar for us, we are not concerned with the force exerted by the sugar on the scale or the tension it places on the weight measuring device. Rather, our interest lies elsewhere: we are only concerned with the amount of sugar we can use, or in other words, the quantity of substance it contains.
However, there is a singular method to quantify a substance: determining the gravitational force exerted on it by the Earth. It is hypothesized that equivalent masses correspond to equivalent amounts of matter, and we assess the mass of an object solely based on the magnitude of its gravitational attraction, as the attraction is directly proportional to the mass.
Regarding the Earth’s weight, we assert that its “weight” can be ascertained once its mass is known; hence, the task of determining the Earth’s weight must be comprehended as the task of calculating its mass.
Fig. 88. A method for measuring the Earth’s mass: the Yolly Scale
Let’s explain a method for solving this problem (known as the Yolly method, 1871). In Figure 88, we can observe a highly sensitive cup scale that consists of two lightweight cups suspended from either end of a kingpin: an upper cup and a lower cup. The distance between the upper and lower cups is approximately 20-25 cm. On the lower cup located on the right side, we place a spherical weight with a mass of m v. In order to maintain equilibrium, we place a weight of t t on the upper cup located on the left side. These weights are not equal because they are located at different heights and therefore experience different gravitational forces from the Earth. However, if we introduce a large lead ball with a mass of M under the right lower cup, the equilibrium of the scale will be disrupted. This is because the mass m l will be attracted to the mass of the lead ball M with a force F v that is proportional to the product of their masses and inversely proportional to the square of the distance d that separates their centers.
Let’s place a small weight of mass p on the upper left cup of the scale in order to restore the disrupted balance. The force exerted by this weight on the scale is equivalent to its weight, specifically equal to the force of gravity acting on this weight due to the mass of the entire Earth. This force, denoted as F, can be calculated using the formula
Disregarding the minimal impact that the lead ball has on the weights in the upper left cup, we can express the state of balance in the following manner:
In this relationship, all quantities other than the Earth’s mass
The measurement of can be determined.
In the mentioned experiments, the values of M, R, d, m1, and p were 5775.2 kg, 6366 km, 56.86 cm, 5.00 kg, and 589 mg, respectively.
Consequently, the Earth’s mass is determined to be 6.15 x 10^27 g.
The contemporary definition of the Earth’s mass, established through numerous measurements, is
The mass of the Earth is approximately 5.974 x 10^27 g, which is equivalent to about 6 thousand trillion tons. The margin of error in determining this value is no more than 0.1%.
Therefore, astronomers have successfully calculated the mass of our planet. We can confidently say that they have effectively weighed the Earth, as when we use a lever scale to weigh an object, we are essentially determining its mass, not the force of attraction between the object and the Earth. In other words, we are establishing that the object’s mass is equal to the mass of the weights.
What is the composition of the Earth’s interior?
In popular books and articles, there is often a mistake made in an attempt to simplify the explanation. The authors describe the process of weighing the Earth by measuring the average weight of 1 cm3 of our planet, also known as its specific gravity. They then calculate the volume geometrically and determine the weight of the Earth by multiplying its specific gravity by its volume. However, this method is not possible as we cannot directly measure the specific gravity of the Earth. We only have access to its relatively thin outer shell and know nothing about the substances that make up the rest of its much larger volume.
We are already aware that the situation was completely the opposite: the determination of the Earth’s mass came before the determination of its average density. The average density turned out to be 5.5 g per 1 cm3 – significantly higher than the average density of the rocks that compose the Earth’s crust. This suggests that there are extremely dense substances deep within the Earth. Based on their assumed specific gravity (among other factors), it was previously believed that the Earth’s core was made up of iron, heavily compressed by the pressure of the masses above it. However, the current belief is that, overall, the central regions of the Earth have a composition similar to the crust, but their density is greater due to the immense pressure.
It may seem strange, but determining the weight of the distant Sun is actually much easier than determining the weight of the much closer Moon. (Of course, when we use the word “weight” in relation to these celestial bodies, we are referring to mass).
To find the mass of the Sun, we can use the following logic. Through experience, we know that 1 gram attracts another 1 gram at a distance of 1 centimeter with a force equivalent to 1/15,000,000,000 milligram. The mutual attraction, f, between two bodies with masses M and t at a distance D can be expressed using the law of universal gravitation:
If the Sun’s mass (M) is in grams, the Earth’s mass (t), and the distance between them (D) is equal to 150,000,000 km, then their mutual attraction in milligrams is (1/15,000,000,000)x(15,000,000,000,000,000,000^2)mg[50].
On the other hand, this attraction force acts as the centripetal force keeping our planet in its orbit. According to the rules of mechanics, this force is also equal (in milligrams) to mV^2/D, where t is the Earth’s mass (in grams), V is its circular velocity, equal to 30 km/s = 3,000,000 cm/s, and D is the distance from the Earth to the Sun. Therefore,
The equation allows us to find the unknown M (measured in grams):
By dividing the mass by the mass of the globe, we can calculate the
There is an alternative method for calculating the mass of the Sun that relies on Kepler’s third law. The third law is derived from the law of universal gravitation and can be expressed as follows:
The mass of the Sun, T, the stellar orbital period of the planet, a, the average distance of the planet from the Sun, and the mass of the planet can all be used to calculate the gravitational force between them. When we apply this law to the Earth and the Moon, we can determine their gravitational interaction.
Replacing the information obtained through observations
In the initial approximation, neglecting the mass of the Earth in the numerator, which is small compared to the mass of the Sun, and the mass of the Moon in the denominator, which is small compared to the mass of the Earth, we can calculate the mass of the Sun.
If we know the Earth’s mass, we can determine the mass of the Sun.
Therefore, the Sun is approximately 300,000 times heavier than the Earth. It is a simple calculation to find the average density of the Sun by dividing its mass by its volume. The density of the Sun is about four times less than the density of the Earth.
When it comes to the Moon’s mass, one astronomer once said, “Even though it is closer to us than any other celestial body, weighing it is more challenging than weighing Neptune, the most distant planet at the time.” Unlike the Sun, the Moon does not have a companion to assist in determining its mass. Scientists had to use other, more complex methods, one of which we will briefly mention. This method involves comparing the height of the tide caused by the Sun with the tide generated by the Moon.
The height of the tide is influenced by the mass and distance of the celestial object responsible for its generation. By having knowledge of the mass and distance of the Sun, we can determine the distance of the Moon. By comparing the height of the tides, we can then deduce the mass of the Moon. This calculation will be discussed in more detail later when discussing tides. However, for now, we will simply present the final result: the mass of the Moon is 1/81 of the mass of the Earth (Fig. 89).
Once we have the diameter of the Moon, we are able to calculate its volume. The volume of the Moon is found to be 49 times smaller than the volume of the Earth. Consequently, the average density of our satellite is 49/81 = 0.6 of the Earth’s density.
Figure 89. The Moon is 81 times lighter than the Earth
Therefore, the Moon is made up of more fragile substances than the Earth, but it is denser than the Sun. In the next section (see the table on page 199), we will discover that the Moon has a higher average density than most planets.
Planets and stars: Weight and density
The method used to determine the weight of the Sun can also be used to determine the weight of any planet that has at least one satellite.
By equating the centripetal force required to keep the satellite in its orbit, which is equal to mv2/D, to the force of mutual attraction between the satellite and the planet, which is equal to kmM/D2 (where k is the force of attraction between two 1 g masses at a distance of 1 cm), we can determine the average velocity v of the satellite’s orbit and its average distance D from the planet. Here, m represents the mass of the satellite and M represents the mass of the planet.
It is simple to determine the mass M of the planet using this equation.
This case also falls under Kepler’s third law:
Disregarding the negligible terms in the parentheses, we obtain the proportion between the Sun’s mass and the planet’s mass
If we know the mass of the Sun, we can easily calculate the mass of the planet.
The same calculation can be applied to binary stars, with the only difference being that the result is not the individual masses of each star in the pair, but rather the combined mass of both stars.
Determining the masses of planetary satellites, as well as planets without any satellites, is much more challenging.
For instance, the masses of Mercury and Venus are determined by considering the gravitational effect they have on each other, as well as on Earth and the motion of certain comets.
When it comes to asteroids, their masses are so small that they do not have a noticeable effect on each other, making it impossible to determine their mass. The only thing we can do is make an educated guess about the total mass of all these tiny planets.
To calculate the average density of planets, we can use their mass and volume. The table below summarizes the results:
The Earth and Venus are the two most dense planets in our solar system. The reason why the large planets have lower average densities is because they have a solid core that is surrounded by a thick atmosphere. Although the atmosphere doesn’t contribute much to the mass of the planet, it greatly increases its apparent volume.
Gravity on the Moon and other planets
Many people who are not well-versed in astronomy often wonder how scientists can confidently talk about the force of gravity on the Moon and other planets without actually visiting them. However, it is actually quite simple to calculate the weight of an object, such as a kettlebell, on other celestial bodies. All you need to know is the radius and mass of the celestial body.
To illustrate, let’s calculate the gravitational force on the Moon. It’s common knowledge that the Moon’s mass is 81 times smaller than that of the Earth. If the Earth had such a reduced mass, the gravitational force on its surface would be 81 times weaker than it currently is. However, according to Newton’s law, an object attracts others as if its entire mass were concentrated at its center. The center of the Earth is located at a distance equal to the Earth’s radius from its surface, while the center of the Moon is located at a distance equal to the lunar radius. The lunar radius is only 27/100 of the Earth’s radius, meaning that by decreasing the distance by a factor of 100/27, the gravitational force increases by a factor of (100/27)2. Therefore, the net gravitational force on the Moon’s surface is
Therefore, if a 1 kilogram mass is taken to the Moon’s surface,
its weight would be reduced to only 1/6 kg. However, it is important to note that this decrease in weight can only be measured using a spring scale (Fig. 90), and not a lever scale.
Figure 90. The weight of an individual on various planets. According to current data, a man’s weight on Pluto is not 18 kg, but only 3.6 kg.
Interestingly, if there was water on the Moon, a swimmer would experience the same sensation in a lunar body of water as they would on Earth. Their weight would be reduced by a factor of six, but the weight of the water they displaced would also be reduced by the same factor. The ratio between them would remain the same as on Earth, causing the swimmer to sink into the Moon’s water to the same extent as they do in ours.
However, the act of rising above the water would yield a more noticeable outcome on the Moon. Since the swimmer’s body weight has decreased, it requires less muscle strain to lift it.
Below is a table comparing the strength of gravity on different planets to that of Earth.
According to the data presented in the table, Earth’s gravity is ranked fifth in the solar system, following Jupiter, Neptune, Saturn, and Uranus.[51]
The force of gravity on the surface of “white dwarfs” like Sirius B, which was discussed in Chapter IV, reaches the greatest magnitude. It is evident that the substantial mass of these stars, combined with their relatively small radius, results in a significant gravitational strain on their surface. Let’s perform a calculation for a star in the constellation Cassiopeia, which has a mass 2.8 times that of our Sun and a radius half the size of Earth’s. Considering that the Sun’s mass is 330,000 times greater than Earth’s, we can determine that the force of gravity on the surface of this star surpasses that of Earth by a factor of 2.8 to 330,000 times.
2.8 – 330,000 – 2 2 = 3,700,000 times.
On the surface of this star, 1 cm3 of water that weighs 1 g on Earth would weigh almost 3 3 / 4 tons! The substance of the star itself, which is 36,000,000,000 times denser than water, must have an incredibly monstrous weight in this extraordinary world.
133,200,000,000,000 grams is the difference between 3,700,000 and 36,000,000.
A hundred million tons is the weight of a thimbleful of matter, a fascinating curiosity that until recently was unimaginable even in the wildest works of fiction.
If a body were to be moved deep into the planet, such as to the bottom of an incredible deep mine, its weight would undoubtedly change.
There is a common misconception that an object would become heavier at the bottom of a mine because it is closer to the center of the planet, where all bodies are attracted. However, this belief is incorrect. The force of attraction to the center of the planet actually weakens at greater depths. I have explained this concept in my book “Entertaining Physics,” where readers can find a more detailed and easily understandable explanation. To avoid repeating what was already covered, I will simply mention the following points.
In the field of mechanics, it has been demonstrated that objects situated within the hollow of a uniform spherical shell are entirely weightless (Fig. 91). This implies that an object within a solid, uniform sphere experiences gravitational attraction solely from the portion of the material enclosed within a sphere with a radius equal to the distance between the object and the center (Fig. 92).
Figure 91. The weight of a body inside a ball shell is zero
Fig. 92. What factors determine the weight of an object inside a planet?
Fig. 93. Calculating the change in weight of an object as it approaches the center of a planet
Using these principles, we can easily deduce the law that governs how the weight of an object changes as it gets closer to the center of a planet. Let’s call the radius of the planet (Fig. 93) R and the distance of the object from the center r . The gravitational force acting on the object at this point must increase by a factor of (R/r) 2 and simultaneously decrease by a factor of (R/r) 3 (since the attractive part of the planet has decreased by the indicated number of times). Eventually, the gravitational force must decrease by a factor of (R/r) 3 (because the attractive part of the planet has decreased by the specified number of times).
Thus, in planets with significant depth, the gravitational pull on an object will decrease proportionally to the reduction in distance to the center. For instance, on a planet the size of Earth, with a radius of 6400 km, a decrease in depth of 3200 km would result in a halving of the weight of an object, while a decrease in depth of 5600 km would lead to a greater reduction in weight.
Related documents:
Dirt)? The book of the inscribed! For the book of the righteous is certainly in illiyun (exalted). And what will let you know what is illiyun? The Book of the Written Book!
. GOD. The Book can be valuable to a wide range of readers, а . . One of the most important challenges now, if not the most important. anywhere in space and demonstrate the transformations that occur to it. Marvelous picture, sky would appear .
The world of philosophy: A book for reading. In 2 ch. Ch. Initial philosophical problems, concepts and principles. Moscow: Politizdat, 1991. 672 с
Philosopher Kirkegardt is one of the proponents of existential philosophy. I myself have long ago written about him in a book. He had a unique way of perceiving the world, through a visual representation of the starry sky and the planets. His study of the heavens and the celestial luminaries was unparalleled.
Every time my book is published and ready for the reader, I feel a tremendous thrill. This was the situation in my younger days, both in my personal life and in my writing career, when the reader takes hold of the book. What are their expectations from this captivating and extraordinary story? Right before their eyes, they are presented with a vibrant depiction of the Second Congress’s work, the intense and passionate struggle that took place during it. It is one of the most expansive and awe-inspiring experiences, like gazing at the vast expanse of the starry sky. The reader’s interest is captivated by every single aspect and detail.
Irina Lukyanova Korney Chukovsky
. Furthermore, he exhibited a notable sense of disinterest towards more extensive responsibilities. It was as though these tasks held no appeal for him. His profound connection to the past and his longing to ascertain his position within it were truly extraordinary. To be a part of one of the most significant historical narratives was of paramount importance to him. Moreover, he recognized his obligation as a reader to acknowledge significant literary occurrences.
N. M. Karamzin “History of the Russian State”.
The book “Raised virgin land” quickly gained popularity among readers in the Soviet Union. It became one of the most widely read books in the country. The narrative depicted the vastness of the international labor movement and the events that unfolded before its readers. The book aimed to express an attitude towards these events and marvelously captured the reactive nature of the world’s spaces.

A proposal has been made to calculate the masses of celestial bodies based on the theory of vortex gravitation, cosmology, and cosmogony by A. S. Orlov and S. A. Orlov from SPGU, PGU in 2019. It is suggested that the actual values of the masses of celestial bodies are significantly larger than the commonly accepted values.
INTRODUCTION
The determination of the masses of celestial bodies relies on the theory of universal gravitation. The concept that all objects have gravitational force was proposed by I. Newton[1]. Newton formulated the equation that describes the gravitational interaction between two bodies:
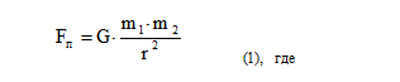
The equation has the form where m1 and m2 represent the masses of bodies 1 and 2, G is the gravitational constant equal to 6.672 ?10 -11 N?m 2 /kg 2, and r is the distance between the bodies. This equation applies to the surface of the Earth.
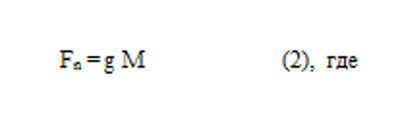
The mass of the Earth, denoted as M, can be calculated using the formula M = g / G, where g is the acceleration of free fall and G is the gravitational constant. Based on the known values of g and G, the mass of the Earth, denoted as Me, is approximately 5.97 x 10^24 kg [2]. The average density of the Earth’s substance is 5500 kg/m^3, although this varies throughout the Earth’s crust (2200 kg/m^3) and core (13100 kg/m^3) [3].
In 1915 and 1916, Einstein proposed the general theory of relativity [4]. This theory expanded upon Newton’s law of gravitation and considered it as a special case. Both theories hypothesize that substances (or bodies) possess the ability to create gravitational forces. The masses of other celestial bodies can be determined using Kepler’s 3rd law [5], taking into account equation (1).
There is no experimental or theoretical evidence for the law of universal gravitation proposed by Newton (or Einstein). As a result, when applying this law in scientific research, conflicting outcomes can arise. Specifically, utilizing the aforementioned methodology, scientists have been able to determine the masses and densities of various planets within our solar system, including the Sun.
The density of the Sun is 1410 kg/m3, with a gravitational force on its surface of F = 273.1 m [6]. Saturn, on the other hand, has a density of 687 kg/m3 and a gravitational force of F = 10.44 m [7].
Planet Earth exerts a gravitational force on its surface that is lower than that of other celestial bodies mentioned above. However, the average density of Earth is significantly higher than both the Sun and Saturn. The compression of any celestial body occurs due to external forces, with gravity being the primary force. As a result, it is impossible for the Sun or Saturn to have a density several times lower than Earth. Additionally, Saturn has an average density lower than that of water. Therefore, the surface density of these celestial bodies must be equivalent to that of gas, which is an illogical conclusion. These contradictions arise within the framework of the theory of universal gravity. Three hundred years ago, Newton introduced the hypothesis that bodies create gravitational force, which became widely accepted in the scientific community. Scientists based their calculations on this flawed concept, leading to numerous questionable scientific results. Newton himself was uncertain about the nature of gravity. He proposed that a change in density within the cosmic medium could be the cause of gravitation, although he couldn’t provide substantial evidence for this idea.
The contradiction is absent in the author’s theory of vortex gravitation, cosmology, and cosmogony [8]. Based on this theory, it becomes possible to accurately calculate the masses of celestial bodies. The following chapter introduces the fundamental principles of the theory of vortex gravity.
2. THEORY OF VORTEX GRAVITY, COSMOLOGY, AND COSMOGONY
The concept of vortex gravity is based on the widely-accepted astronomical observation that all celestial objects undergo rotation. In the vortex gravity model, it is postulated that this rotational motion is caused by the rotation of the aether, a cosmic, gaseous substance with extremely low density. The aether is believed to exist as a system of interconnected vortices within the fabric of space. Within each vortex, the orbital velocities of the aether (torsion) progressively decrease as one moves from the center towards the periphery, following the inverse square law of distance. According to the principles of aerodynamics, lower velocities in a fluid flow result in higher pressure. This pressure gradient generates a force that pushes matter towards regions of lower pressure, i.e. towards the center of the vortex. Consequently, matter accumulates or is generated in the central region of the vortex, eventually giving rise to the formation of a celestial body. In this context, we will now examine the mathematical equation describing vortex gravity as derived in the referenced theory [8].
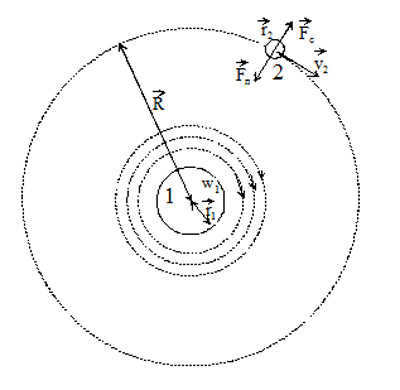
Figure 1. Illustration depicting the gravitational interaction between two bodies in a two-dimensional model.
The forces acting on body 2 are shown. Fc is the centrifugal force, Fa is the force of attraction from body 1, v2 is the linear velocity of body 2 along the orbit, R is the radius of the orbit, r1 is the radius of body 1, r2 is the radius of body 2, w1 is the angular velocity of rotation on the surface of body 1, and m2 is the mass of body 2. As previously mentioned, vortex motion creates a pressure gradient. The radial distribution of pressure and velocity of the aether in the author’s study [8] is determined using the Navier-Stokes equation for the motion of a viscous fluid (gas).
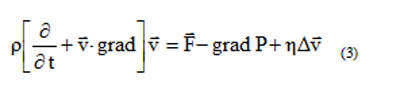
When considering radial symmetry in cylindrical coordinates, where vr=vz=0 and v?=v (r), the equation can be expressed as a system:
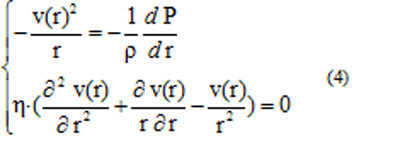
where ? = 8.85 x 10 -12 kg/cubic meter represents the density of the aether [9], V stands for the velocity vector of the aether, P denotes the pressure of the aether, and ? represents the viscosity.
After performing some transformations, we obtain the equation for determining gravitational forces in the ether vortex:
with the following relationship ve~1/?r where
Vn – represents the volume of nucleons in the body that is in a torsion orbit with radius – r.
? = 8.85 x 10- 12 kg/m 3 represents the density of the aether[4] ve – represents the velocity of the ether in the orbit r
r represents the radius of the considered orbit of the aether vortex
Let’s substitute the volume of nucleons with their mass in equation (5), using the given relation: Vn = m/?n(6), where ?n ~ 10 17 kg/m 3 is the constant density of nucleons for all atoms.
When it comes to aerodynamics, the equation representing the relationship between the pressure P in a gas (ether) and its velocity w is:
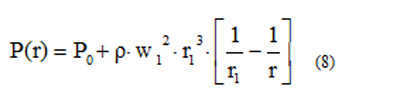
(8) P0 represents the pressure of the ether at the surface.
By applying the boundary condition, we can determine that P (?) is equivalent to Pb, which denotes the pressure of free ether.
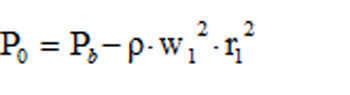
Pb is the pressure of the unconfined aether.
Figure 2 visually represents the pressure distribution as per equation (8).
Based on the principles of aether dynamics,[9] the unconfined aether (in a state of rest) has a pressure value of Pb = 2.10 32 .
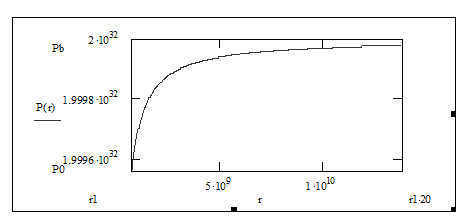
Figure 2. The distribution of radial pressure in the torsion of the aether.
Remark 1. By utilizing equation (7) of the vortex gravity, we can compute the gravitational forces that solely act within the plane of the torsion or at its center. These equations are applicable for calculating gravitational forces both above the surface and inside celestial bodies. To determine the gravitational forces at distant orbits of torsions, the author’s paper “Gravitation – flat power field”[10] provides the calculation of the gravitational equation in a three-dimensional model.
Remark 2. Aether is composed of extremely small particles known as amers, which can freely penetrate any substance except for super dense bodies such as nucleons.
Read this material again:
A novel wind turbine design has been created specifically for installation on residential rooftops

When considering the extraction of energy from the wind, our minds typically conjure up images of vast open spaces adorned with towering wind turbines, their colossal blades lazily turning in the breeze. However, one innovative entrepreneur and inventor from Fullerton has managed to revolutionize this concept, designing a completely novel type of wind turbine. Remarkably smaller in size, highly adaptable, and even capable of being installed on rooftops akin to satellite dishes.
Scientists have discovered a method for evaluating the hypothesis of loop quantum gravity

Loop quantum gravity may hold the key to resolving the long-standing conflict between general relativity and quantum mechanics. However, similar to other unverified concepts in quantum gravity, loop quantum gravity has yet to undergo experimental testing. In a recent investigation, researchers have discovered that as black holes evaporate, the emitted radiation may contain distinct markers of loop quantum gravity, which deviate from the expected Hawking radiation.
Changes in Earth’s gravitational field attributed to the melting ice

Researchers from the European Space Agency have discovered that the significant loss of ice in the western region of the South Pole has had a surprising impact on the entire planet. Utilizing the GOCE instrument, which has been in orbit around Earth for over four years, scientists have determined that the gravitational field of the planet can be altered by the presence of ice. Experts explain that the GOCE instrument was equipped with an exceptionally sensitive sensor that was able to detect these changes.

Upon completion of this video tutorial, you will gain knowledge regarding the Earth’s form and dimensions. We will delve into the technique of triangulation for gauging the length of the meridian arc. Additionally, we will explore the significance of horizontal parallax and angular radius, along with their applications in determining the dimensions of celestial bodies within the solar system and calculating distances to these entities.

Currently, it is not possible to view or share the video tutorial with students.
In order to access this and other video tutorials in the package, you will need to add it to your personal account.
Unlock amazing opportunities

Lesson plan “Calculating distances and sizes of celestial bodies in the solar system”
It is common knowledge that in ancient Greece, scholars and philosophers discovered that our planet is not flat, but rather spherical. The concept of the Earth being a round object floating in space without any support is considered as one of the greatest achievements of the ancient world.
Ancient Greek scientist Eratosthenes, who resided in Egypt, was the first person to devise a method to determine the size of the Earth. His approach was remarkably straightforward. Eratosthenes selected two cities – Alexandria and Siena (now Aswan) – situated along the same meridian on Earth.
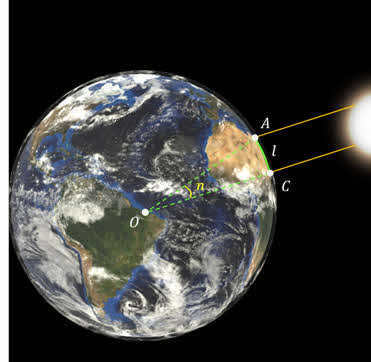
Next, he assigned the distance between the two cities as l and its angle value in degrees as п.
Therefore, the length of the arc in 1 degree of the chosen meridian is equal to
And the total length of the meridian circumference: L = 360 degrees ∙ l0.
On the contrary, he was aware that the circumference length is equal to: L = 2πR.
By equating the right-hand sides of the last two equations, it is possible to obtain the desired radius of the globe:
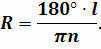
It was necessary to find out the length of the meridian arc in degrees. Clearly, this is equal to the difference in latitude between Alexandria and Siena. To determine this difference, Eratosthenes devised a clever method. He knew that at noon on the day of the summer solstice in Siena, the sun is directly overhead and shines into the bottom of the deepest wells. However, in Alexandria, the sun does not reach the zenith, so a vertically placed pole will cast a shadow. By measuring the length of this shadow, it is possible to easily determine the desired length of the meridian arc, which in Eratosthenes’ case was 7.2 degrees.
Now, the distance between Alexandria and Siena was already known to him: it was five thousand Greek stadia.
By plugging all the data into the equation for the circumference of the meridian, Eratosthenes arrived at a value of 250,000 stadia.
Stadia is a highly subjective unit of distance. However, it was commonly understood to represent the distance that a lightly armed warrior could travel from sunrise to the moment when the sun is fully above the horizon.
If we consider that the straight-line distance between Alexandria and Aswan is approximately 844 kilometers, we can estimate that one stadia is roughly equivalent to 169 meters.
Therefore, the estimated circumference of the meridian is 42,250 kilometers, which is quite impressive for that era.
There are more precise methods available in modern science to measure distances on the Earth’s surface. One such method is triangulation, which relies on the phenomenon of parallactic displacement.
Parallactic displacement refers to the shift in direction of an object as the observer moves. This shift can be utilized to calculate distance by measuring the length of one side (base) and two adjacent angles in a triangle.

During the 18th century, the employment of triangulation measurements in latitudes near the equator and close to the northern polar circle revealed that the length of the arc in a 1-degree meridian is not uniform and actually increases as one moves towards the poles. This discovery led to the realization that our planet is not a perfect sphere and that its polar radius is nearly 21 kilometers shorter than its equatorial radius. As a result, in the field of geodesy, the study of the shape of the Earth, the geoid is considered, which refers to a body with a surface that closely resembles the surface of the calm ocean and extends beneath the continents.
Currently, the physical characteristics that define the shape of the Earth are as follows:
– The polar compression is 0.0033528;
– The equatorial radius is 6378.1 km;
– The polar radius is 6356.8 km;
– The equatorial circumference is 40,075.017 kilometers.
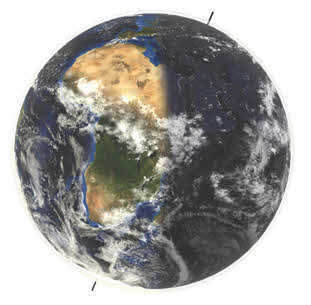
For a long time, astronomers were puzzled by the true distance from the Earth to the Sun. It was only in the late 18th century that they were able to measure it, thanks to the determination of the Sun’s horizontal parallax. This parallax represents the apparent shift in the position of an object outside the Earth, with the Earth’s radius as the baseline.
Horizontal parallax refers to the angle at which the Earth’s radius, perpendicular to the line of sight, is observed from the Sun.
By knowing the horizontal parallax of the celestial body, you can use trigonometric relations to calculate its distance from the Earth:
It is evident that the further the celestial body is, the smaller its horizontal parallax. For instance, the Moon, which is Earth’s satellite, has the largest parallax, with an average of 57ʹ. The Sun, on the other hand, has a much smaller parallax of approximately 8.794ʹʹ. This parallax corresponds to an average distance of approximately 149.6 million kilometers from the Earth to the Sun.
In one of our previous lessons, we discussed how this distance is considered one astronomical unit in astronomy. It is a convenient method for measuring distances between celestial bodies within the solar system.
However, let’s return to our equation. Therefore, it is important to understand that in geometry, when an angle is small, its sine is nearly equal to the angle itself, but expressed in radians. Taking into account that one radian is equivalent to 206,265ʹʹʹ, it becomes simple to derive a convenient calculation formula:
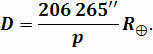
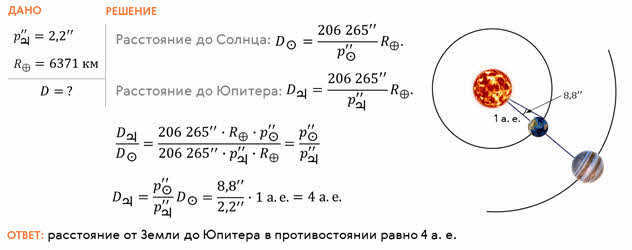
Let’s use the given information to calculate the distance between Earth and Jupiter during the opposition. Assuming that the horizontal parallax of Jupiter was 2.2ʹʹ, we can determine the distance. Considering that the radius of the Earth is 6371 kilometers, we can proceed with the calculation.

There is an alternative approach to solving the same issue.
In the modern era, a more precise technique called radar is used to accurately measure distances to celestial bodies within the solar system. By calculating the time it takes for a radar signal to travel to a celestial body, bounce back, and return to Earth, scientists can determine the distance using the formula:
where c represents the speed of light in a vacuum.
As methods for determining distances to celestial bodies in the solar system have advanced, scientists have also been able to devise a way to measure their sizes. For instance, when observing a celestial body from Earth, astronomers can measure the angle at which it appears to the observer, known as its angular size (or angular diameter), and therefore its angular radius.
By determining the angular radius and the distance to the celestial body, we can compute its linear radius.
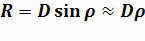
.
The angular radius needs to be expressed in radians in this particular equation.
By substituting the formula for determining distances using the horizontal parallax method into the given equation and simplifying it based on the assumption that the angles ρ and р are small, we obtain a formula for determining the linear dimensions of celestial bodies.