Measuring the mass of celestial bodies can be a challenging task, especially when it comes to objects as massive as stars or galaxies. Unlike small earthly objects, these celestial bodies cannot simply be placed on a scale. So how do scientists determine their mass? And where is the fulcrum that Archimedes once suggested for rolling heavenly bodies?
In the past, Isaac Newton defined the mass of a body as the amount of matter it contains. However, our understanding of the problem has evolved over time, and now mass is determined by the inertia of bodies. The greater the mass, the more difficult it is to accelerate them. As a result, various methods have been developed to measure the mass of celestial bodies.
By utilizing geodetic methods, scientists were able to accurately measure the linear length of a degree of the meridian arc. This measurement, combined with the law of universal gravitation, allowed them to determine the mass of the Earth, which was found to be 6 x 10^24 kg. With this knowledge, they were then able to apply the third Keplerian law to calculate the mass of the Moon, which was determined to be 7.3477 x 10^22 kg. This breakthrough discovery also enabled them to calculate the mass of our own celestial body, the Sun, which was found to be 1.9891 x 10^30 kg. Armed with this information, scientists were then able to easily calculate the masses of other objects within the solar system.
- One technique, known as gravimetric analysis, involves utilizing data from gravity measurements to determine the mass of a celestial body. By measuring the force of gravity and the radius of the body, such as the Earth, scientists can accurately calculate its mass.
- By utilizing Kepler’s third principle, it is feasible to calculate the proportion of the mass of the star and the planet by considering the presence of at least one satellite orbiting the planet, along with the known values of the distance between the satellite and the planet, as well as the period of revolution around the planet.
- By examining the apparent disruptions exhibited by specific celestial entities in relation to the movement of other celestial entities.
Determining the mass of a star
It is not always possible to determine the mass of a star with sufficient accuracy. In order to do so, two conditions must align: the star must have a companion and the distance to it must be known. First, the total mass of both stars is calculated, and then, depending on certain factors, such as brightness, the mass is divided proportionally.
The data that has been calculated for a hundred double stars of different types has revealed an important pattern: the masses of stars and their brightness are directly correlated. This allows us to estimate the mass of stars based on their luminosity – stellar magnitude.
To determine the mass of a star, it is essential to identify its luminosity class. This approach is not applicable to white dwarfs and pulsars alone. Alternatively, one can measure this parameter by analyzing the redshifts in the star’s gravitational field. The gravitational shifts of spectral lines are then quantified.
The value of this parameter is determined by the sum of the masses of all the companions. However, in the case of globular clusters, it is more complicated. It is not always possible to accurately count the members of the cluster and determine their luminosities. Therefore, statistical methods are used, taking into account the cluster’s radius and the deviations in the radial velocities of individual stars from the average values.
The weight of a galaxy
The weight measurement for a galaxy, like our own, is established by observing its actual rotation. Every star, including the Sun, experiences a centripetal acceleration caused by the gravitational pull of galactic matter within its orbital boundaries. By knowing certain values such as the distance from the star to the galactic core and its orbital velocity, we can also determine the weight of the galaxy.
Illustrations
The weight of a galaxy is a more concrete measurement. For instance, the weight of our Milky Way is defined as 3 x 10^12 solar masses, and the enigmatic Andromeda galaxy is only 1.5 times as heavy as ours. Presumably, the largest galaxy ever discovered is IC 1101. It resides in the Serpent constellation and is situated 1.07 billion light years away. With an astonishing diameter of 6 million light years, it is light-years ahead in size, with a weight 24.5 trillion times greater than that of the Sun! If this super galaxy were to take the place of our galaxy, it would effortlessly consume both the Magellanic Clouds, Andromeda, and the Triangle.
The primary way to determine the mass of a Galaxy is by measuring the velocity of globular clusters at the outer edges of the Galaxy.
By utilizing data from multiple spacecraft, such as Hubble and Gaia, astronomers have concluded that the mass of our Galaxy is approximately 1.5 trillion solar masses. The portion of this mass that is comprised of dark matter (assuming it does exist) makes up around 85-90% of the total estimated mass.
To provide a clearer understanding of this concept, let’s consider a simple example. If we measure the orbital velocity of a planet and its distance from the Sun, we can calculate the mass of the central body that generates the gravitational field (the Sun).
Therefore, in order to determine the mass of the entire Galaxy, we must ascertain the orbital velocity of the celestial bodies that orbit the entirety of the Galaxy, as well as estimate their distance from the Galaxy’s center. The most suitable candidates for this task are globular clusters, as they are the objects that are farthest from our Galaxy. It should be noted that solving such a problem is much more complex than the provided example and the method described here.
Globular clusters are the oldest and most distant entities within the Galaxy. They originated from the condensation of gas during the formation of the galaxy and consist of hundreds of thousands to millions of stars.

This stunning image was captured by the Hubble spacecraft and shows a globular cluster, a tightly packed group of stars. The Hubble spacecraft has contributed greatly to our understanding of the universe by capturing breathtaking images like this one. The cluster is composed of thousands of stars and is held together by gravity. By studying the properties of globular clusters, scientists can learn more about the formation and evolution of galaxies.
In 2018, a team of researchers from the Moscow University Astronomical Institute (GAISH MSU) released a collection of articles regarding the proper movements of globular clusters and their trajectories (Astrophysical Bulletin, 2018, vol. 73, issue 2, pp. 168-189. A. Rastorguev et al.).
The researchers utilized six star catalogs spanning 65 years of observations from various epochs, with the initial Gaia catalog serving as a baseline. Within each examined globular cluster, they tracked the changes in coordinates for selected stars over time and estimated their proper motions. The average accuracy of the proper motions for each globular cluster was 0.004 seconds of arc per year. Over the course of the 65-year interval, multiple points were obtained for the orbits of each of the 115 clusters studied. These findings enabled the determination of the orbital parameters. Notably, it was discovered that the elliptical orbits of globular clusters undergo significant changes due to the influence of density inhomogeneities within the Galaxy. These investigations will be ongoing and are expected to yield a more precise estimation of the Galaxy’s mass.

Gaia Space Observatory
The researchers utilized information on 34 globular clusters situated within 65,000 light-years of our Sun and observed by the Gaia spacecraft over a span of 22 months. This dataset was supplemented by an additional 12 globular clusters within a radius of 130,000 light-years observed by the Hubble spacecraft over a duration of 10 years. The orbital velocities were computed for all of the clusters. Four clusters were found to be present in both datasets, and their orbital velocities were found to be consistent.
By analyzing the orbital velocities of 46 globular clusters, the researchers were able to estimate the total mass of all components in our Galaxy to be approximately 1.5 trillion solar masses within a volume with a radius of 129,000 light-years. The exact outer boundary radius of the Galaxy remains unknown. Baryonic matter, which makes up about 10-15% of the mass, is the only known component, while the remaining 85-90% of the mass is composed of dark matter, the nature of which is still a mystery.
Upon reviewing this article by the esteemed RMR_astra, a few points caught my attention.
1. The Astronomical Institute of Moscow University (GAISH MSU) continues to conduct important scientific research. Having some insight into the individuals and numbers involved in GAISH’s current activities, it is reassuring to see that science and genuine scientists cannot be suppressed or eliminated.
Is there any record of similar calculations being performed elsewhere?
About 85-90% of the mass is composed of dark matter, which is of an enigmatic nature.
The most groundbreaking discoveries have been made when physicists, particularly astrophysicists, openly acknowledge their lack of understanding and inability to explain something.
Dear Polina! Your question is very pertinent, as it addresses a sensitive issue. The mass of the Galaxy has been estimated multiple times, yielding a wide range of results, from 0.5 trillion to 3 trillion solar masses.
It is beneficial that the authors provide detailed explanations of the techniques employed, enabling comprehension of the significant disparities in the calculations. The earlier publications failed to account for the masses of brown dwarfs, small black holes that result from the death of some stars, as well as other constituents of the Galaxy that are only observable through infrared or shortwave bands from space. It is commendable that numerous authors specify the portion of the Galaxy they have “captured,” i.e., the extent to which they have been able to “observe.” More recent investigations incorporate a dark matter disk, although its precise dimensions remain uncertain. Consequently, in the latest study outlined in my article, the authors specify the radius of the region in which they estimated the mass: 129,000 light-years.
Estimations of the mass of galaxies are based on extensive observational data, employing various methods and approaches, and utilizing the outcomes of observations for computer simulations. Each scientific article includes evaluations of the credibility of the findings.
Astronomers eagerly anticipate the outcomes of new space studies, which may lead to further refinements.
The article elucidating the process of ascertaining the mass of our Galaxy completely transformed my perspective. I was compelled to respond immediately, but unfortunately, time constraints prevented me from doing so, and I had to patiently await inspiration.
I must admit that I used to have a negative outlook on popular science lectures about the life of stars, including the Sun, over billions of years. It didn’t seem worth it to contemplate or worry about something that has such a long lifespan compared to our own. What truly matters is what’s happening in the present moment.
However, I’ve come to realize that it’s important for ordinary people to understand the constant dependence of humanity’s survival on the Cosmos. For instance, a massive solar flare from the Sun could potentially annihilate mankind or drastically alter life in a way that would make billions of years irrelevant.
Within a volume encompassing a radius of 129,000 light-years, our galaxy possesses a mass equivalent to 1.5 trillion solar masses.
The vastness of our galaxy’s mass, measured in trillions of suns, serves as a humbling reminder of humanity’s place within the Universe. This magnitude makes it implausible for life to be confined to a single planet.
This realization instills in me the belief that human existence on Earth must inevitably evolve and expand, venturing into other forms in order to explore and comprehend the vastness of the Universe. Astronomers and astrophysicists, who employ scales of billions and trillions when constructing models of our world, are seemingly beckoned from above to broaden our perceptions. In doing so, life becomes infinitely more captivating and the apprehension of the future dissipates.
This fact has been made evident by actual scientists who have studied the cosmos throughout history.
Thank you for your response, dear RMR_astra! It is always nice to receive feedback that shows understanding.
The challenges we face in our daily lives seem insignificant in comparison to the vastness of the universe. I didn’t mention it earlier, but I wanted to convey the idea that the soul may not die, but instead wander through the endless expanse of the cosmos.
In the Middle Ages, during the time of Kepler and Galileo, people already had some knowledge about the characteristics of the planets in our solar system. They were able to estimate the masses of the planets using simple methods and instruments. Nowadays, modern astronomy has developed various methods for determining the characteristics of planets, stars, clusters, and galaxies.
The planets in our solar system
Here’s an intriguing tidbit: The Sun holds a whopping 99.9% of the entire mass of our solar system. The collective mass of all the planets, on the other hand, amounts to a mere 0.01%. Within that 0.01%, though, the gas giants dominate with 99% of the mass, with Jupiter and Saturn alone accounting for a staggering 90%.
Calculation of Earth and Moon Masses
In order to determine the masses of planets in our solar system, it is convenient to start with Earth. As we recall, the acceleration due to gravity can be calculated using the formula F=mg, where m represents the mass of the object and F is the force acting upon it.
Simultaneously, we must consider Newton’s law of universal gravitation:
By comparing these two formulas and utilizing the known value of the gravitational constant, 6.67430(15)-10-11 m³/(kg-c²), we can compute the mass of Earth. The acceleration due to gravity on Earth is known to be 9.8 m/s2, as is the planet’s radius. By substituting all of these values into the equation, we arrive at an approximate mass of 5.97 x 10²⁴ kg.

By knowing the Earth’s mass, we can easily calculate the parameters for other celestial bodies within the solar system, such as the Moon, planets, and even the Sun. When it comes to the Moon, the calculation is relatively straightforward. It involves considering that the distances from the centers of bodies to the center of mass are inversely proportional to their masses. By plugging in the specific measurements for the Earth and its satellite, we can determine that the Moon has a mass of 7.36 × 10²²² kilograms.
Next, let’s explore the methods used to measure the masses of other planets within the Earth’s group, such as Mercury, Venus, and Mars. Following that, we will delve into the gas giants, and, finally, conclude with exoplanets, stars, and galaxies.
Methods for calculating the masses of planets
One popular method for determining the masses of planets is to utilize Kepler’s third law. According to this law, the squares of a planet’s orbital period are proportional to the cubes of the semi-major axes of its orbit. Newton made a slight adjustment to this law by incorporating the masses of celestial bodies into the equation. As a result, the following formula was derived –
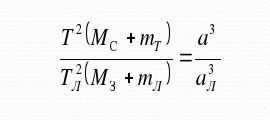
By utilizing astronomical methods that do not require sophisticated instruments, we can determine the masses of all the celestial bodies in the Solar System, including the planets and the Sun itself. The periods of revolution and the major semi-major axes of the planets’ orbits can be easily measured. With the mass of the Earth already calculated, we can input the values into the formula and obtain the final result.
When it comes to exoplanets and double stars, the field of astronomy typically relies on analyzing visible perturbations and oscillations. This method is based on the fact that all massive bodies have an effect on each other’s orbits.
The calculations of the planets Neptune and Pluto led to their discovery even before they were visually observed, as they say “by the stroke of a pen.”
The Masses of the Planets in the Solar System
Therefore, we have covered the general methods of calculating the masses of various celestial bodies and determined the values for the Moon, Earth, and Galaxy. Now, let’s create a ranking of the planets in our system based on their masses.
Topping the list with the greatest mass in the solar system is Jupiter, which falls just short of doubling our system by one order of magnitude. Instead of Jupiter, we could have had a second sun. The mass of this gas giant is 1.9 × 10²⁷ kilograms.
It is interesting to note that Jupiter is the sole planet in our solar system where the center of mass of its rotation with the Sun is situated outside the surface of the star. Specifically, it is approximately 7% of the distance between them from the surface of the Sun.
Following Jupiter, the second most massive planet is Saturn, boasting a mass of 5.7 × 10²⁶ kg. Subsequently, Neptune takes the third spot with a mass of 1 × 10²⁶. The fourth most massive planet is Uranus, a gas giant with a mass of 8.7 × 10²⁵ kg.
The remaining planets belong to the terrestrial group, characterized by their rocky composition, in contrast to the gas giants which possess a larger radius and relatively lower density.

In terms of mass, our planet is the heaviest among this group, and we have already calculated its mass. Venus is the next in line, with a mass of 4.9 × 10²⁴ kg. Following Venus is Mars, which is nearly 10 times lighter, with a mass of 6.4 × 10²³ kg. Finally, Mercury takes the last spot in terms of mass, weighing in at 3.3 × 10²³ kg. It is interesting to note that Mercury is even lighter than two satellites in the solar system, Ganymede and Callisto.
To determine the characteristics of individual star systems, scientists employ the gravimetric method. This technique involves measuring the gravitational redshift of the star’s light. The redshift is quantified using the equation ΔV = 0.635 M/R, where M represents the mass of the star, and R denotes its radius.
Alternatively, the mass of a star can be indirectly determined by analyzing its visible spectrum and luminosity. First, the star’s luminosity class is established based on the Hertzsprung-Russell diagram. Then, the mass/luminosity relationship is utilized to calculate the star’s mass. It should be noted that this approach is not applicable to white dwarfs and neutron stars.
When it comes to determining the mass of galaxies, scientists primarily rely on the rotational velocity of the stars within them (or the relative velocity of the stars in non-spiral galaxies). Newton’s Universal Law of Gravitation provides a formula that expresses the centrifugal force of the stars in a galaxy:
On this occasion, we substitute the measurement from the Sun to the center of our galaxy and its mass into the equation. This is how we can compute the mass of the Milky Way, which is 2.2 × 10⁴⁴⁴g.
We need to keep in mind that this value represents the mass of the galaxy excluding the stars whose orbits are located beyond the orbit of the Sun’s rotation. Therefore, for more precise calculations, the outermost stars of the arms of spiral galaxies are considered.
For elliptical galaxies, the approach to determining the mass is similar, however, in this case, the relationship between the angular size, the velocity of stars, and the total mass is taken into account.


The rotation of galaxies holds the key to determining their masses. In each part of the galaxy, the centrifugal force caused by rotation is balanced by the centripetal force caused by the attraction towards the center of the galaxy, and the strength of attraction depends on the distribution of masses within the galaxy. Therefore, by observing the radial velocity curve, we can ascertain how the density of matter changes within the galaxy and estimate the total mass of the galaxy.
Extragalactic astronomy has achieved a significant milestone with the determination of stellar system mass, which is a critical parameter in understanding these celestial objects.
Regrettably, constructing a velocity curve for elliptical galaxies and dwarf galaxies I II proves to be impracticable. These galaxies exhibit a slower rotation rate and consist of type II stellar populations, lacking hot giants, supergiants, or hydrogen clouds that would form bright clumps of matter with measurable radial velocities. Consequently, an alternative method had to be devised for galaxies E and I II, which, while less precise, still permits estimation of their masses. This method relies on the observation that in stellar systems that either do not rotate or rotate at a sluggish pace, the stars move to a similar or nearly similar extent in all directions. This behavior parallels the movement of air molecules around us, where within any small volume, there is always a molecule moving vertically upward, one moving vertically downward, and others moving in various other directions.
In a stellar system that does not rotate, the average speed of stars can be determined using the spectral method. No matter where the slit of the spectrograph is pointed, there will be stars moving towards us, stars moving away from us, and stars moving in other directions. Each of these stars has a different radial velocity relative to us, and if we could obtain the spectra of each star individually, the line shifts in the spectra would be different due to the Doppler effect. However, the spectrum of a galaxy is the combined spectrum of all the stars within it. If we add together all the spectra with different line positions caused by different radial velocities, the lines in the combined spectrum will appear broader. In this scenario, the broadening of the lines will be more pronounced as the velocities of stars in the galaxy increase.
There exists a correlation between the mass of a non-rotating galaxy, its volume, and the average velocity of stars moving in all directions within it. In the case where two stellar systems have equal volumes but one has a greater mass, the velocities of stars within that system must be higher. This is due to the fact that, under the influence of stronger gravitational forces, the stellar system with the greater mass would otherwise begin to contract. The correlation between mass, volume, and average velocity of stars has been the subject of theoretical investigation. Therefore, if two out of these three quantities are measured, it is possible to calculate the third using the established relationship between them. The volume of an E or I II galaxy can be determined by measuring its angular size and determining its distance. The average velocity of stars can be derived from the broadening of spectral lines. As a result, the mass of the galaxy can also be determined.

The data presented in the table illustrate the findings of determining the masses of galaxies through either the rotation velocity curves or the broadening of spectral lines. These findings were predominantly achieved by American astronomers Berbidge.
The remarkably low mass of the I and II dwarf galaxies is notable. One of these galaxies has a mass of merely 2 million solar masses, while the other has a mass of 20 million solar masses. The mass of the elliptical companion NGC 221 in the Andromeda Nebula is also considerably small. Conversely, all the other galaxies listed are considered non-dwarf galaxies. It is evident that the average masses increase as we transition from type II galaxies to Sc, and subsequently to Sb and Sa.
The mass champion among galaxies with measured masses is the NGC 4466 elliptical galaxy of the E0 type, which means it has no visible compression.
It has a mass equivalent to 1,000 billion solar masses. NGC 4486 is also notable for its abundant system of globular clusters that surround it. In fact, it is a champion among galaxies in this regard, with the number of these globular clusters exceeding 4000. Many of them are so bright that they can be clearly seen, creating a magnificent and awe-inspiring spectacle along with NGC 4486. It is worth noting that the Andromeda Nebula and our star system, both supergiant galaxies, have approximately 300 and 132 globular clusters, respectively.
In the table’s final column, the ratios of galaxy masses to their luminosities are provided, with both measurements expressed in solar masses and luminosities. Upon comparing these values, it becomes evident that the mass of NGC 4486 is three times greater than that of the Andromeda Nebula (NGC 224), although its luminosity is lower than that of the Andromeda Nebula.
Within these galaxies, there still exists some gas matter, which can potentially serve as material for future star formation. However, as previously mentioned, the small quantity of gas matter in the Galaxy, representing approximately 2% of the total mass, does not align well with the ongoing intensive star formation observed within it. Nevertheless, this is substantiated by the significant presence of hot giants and supergiants.
We cordially invite you to engage in a discussion regarding this publication on our space forum.
The mass of the Sun can be determined by considering the Earth’s gravitational force towards the Sun as a centripetal force that keeps the Earth in its circular orbit.
To find the mass of the Sun, we need the mass of the Earth and the average distance between the Earth and the Sun. By denoting the duration of a year in seconds as , we can use the following equation:
Substituting the appropriate numerical values, we can calculate the mass of the Sun:
This formula can also be used to calculate the mass of any planet that has a satellite. In this case, we need to know the average distance between the satellite and the planet, the time it takes for the satellite to orbit the planet, and the mass of the planet. For example, using the distance between the Moon and the Earth and the number of seconds in a month, we can determine the mass of the Earth using the same method described above.
The mass of the Earth can also be determined by comparing the weight of any object to its gravitational pull towards the Earth, taking into account the dynamic gravitational component caused by the body’s participation in the Earth’s daily rotation, resulting in the corresponding centripetal acceleration (§ 30). The need for the aforementioned correction can be avoided by calculating the Earth’s mass using the gravitational acceleration observed at the Earth’s poles. Therefore, if we denote the average radius of the Earth and the mass of the Earth as:
If the average density of the Earth is denoted as, then it is evident that Hence, the average density of the Earth is equal to
The exploration of Earth’s density at different depths was initiated by Lezhandre and continued by numerous scientists. According to the findings of Gutenberg and Gaalk (1924), the Earth’s density varies at various depths:
The pressure within the planet, at great depths, is evidently immense. Many geophysicists speculate that the pressure should already reach atmospheres per square centimeter at certain depths. In the Earth’s core, which is approximately 3000 kilometers deep or more, the pressure likely exceeds 1-2 million atmospheres.
Regarding the temperature at the planet’s depth, it is known to be higher (lava temperature). In mines and boreholes, the temperature increases by an average of one degree for every Assume that at a depth of around the temperature reaches 1500-2000° and remains constant thereafter.
Figure 50 depicts the comparative sizes of the sun and the planets.
In the field of celestial mechanics, the complete theory of planetary motion enables us to determine the mass of a planet by studying its influence on the motion of another planet. In the early 19th century, scientists were familiar with the planets Mercury, Venus, Earth, Mars, Jupiter, Saturn, and Uranus. However, they noticed some irregularities in the motion of Uranus, suggesting the presence of an undiscovered planet beyond Uranus that was affecting its motion. In 1845, French scientist Leverrier and Englishman Adame independently studied the motion of Uranus and used their calculations to predict the mass and location of this yet-to-be-observed planet. Subsequently, astronomers located the planet exactly where the calculations had indicated, and it was named Neptune.
In 1914, astronomer Lovell made a similar prediction about the existence of a planet that was even further away from the Sun than Neptune. However, it wasn’t until 1930 that this planet was actually discovered and given the name Pluto.
Here is some basic information about the major planets:
The table provided below includes basic details about the nine largest planets in our solar system. Fig. 50 provides a visual representation of the relative sizes of the Sun and these planets.
In addition to the aforementioned large planets, there are approximately 1300 known small planets, commonly referred to as asteroids or planetoids. These asteroids’ orbits are primarily located between the orbits of Mars and Jupiter.
The History of Efforts to Determine the Size of a Planet
Throughout various time periods and cultures, scientists have embarked on a quest to unravel the mystery of the Earth’s weight. In ancient civilizations, it was commonly believed that the planet was a flat plate supported by whales and turtles, although some cultures substituted elephants for whales. Regardless, the prevailing view was that the Earth was flat and had a discernible edge.
As the Middle Ages dawned, perceptions regarding shape and weight began to shift. One notable figure who championed the idea of a spherical Earth was G. Bruno, although he paid the ultimate price for his beliefs at the hands of the Inquisition. Another pivotal contribution to scientific understanding of the Earth’s radius and mass was made by the intrepid explorer Magellan, who proposed that the planet was indeed round in shape.
Initial findings
The planet Earth is a tangible entity possessing various characteristics, one of which is its weight. This revelation sparked the commencement of numerous investigations. As per the principles of physics, weight is the force exerted by an object on its support. Given that the Earth lacks any support, it can be inferred that it possesses no weight, although it does possess a substantial mass.
The magnitude of the Earth’s mass
Eratosthenes, an ancient Greek scientist, was the first to attempt to determine the size of our planet. He conducted shadow measurements in various cities in Greece and compared the data obtained in order to calculate the Earth’s volume. Following in his footsteps, Italian scientist G. Galileo made his own calculations and discovered the law of free fall. Later, I. Newton took up the challenge of determining the Earth’s weight and, through his measurement attempts, discovered the law of gravity.

The Scottish scientist N. Makelin was the first to successfully calculate the weight of the Earth. According to his calculations, the planet weighs 5.9 sextillion tons. However, this figure has since increased due to the accumulation of cosmic dust on the planet’s surface. Approximately thirty tons of dust settle on the Earth each year, causing its weight to increase.
To determine the exact weight of the Earth, one must have knowledge of the composition and mass of its constituent substances.
- The mantle, which comprises the largest portion of the Earth, has a mass of roughly 4.05 X 10 24 kg.
- The core, on the other hand, is lighter than the mantle, weighing only 1.94 X 10 24 kg.
- The Earth’s crust, while thin, is still significant and has a weight of only 0.027 X 10 24 kg.
- The hydrosphere and atmosphere, which exist as shells around the planet, have weights of 0.0015 X 10 24 kg and 0.0000051 X 10 24 kg, respectively.
By summing up these values, we can determine the weight of the Earth. However, it’s worth noting that different sources may provide different values for the mass of the planet. So, how much does Earth weigh in tons, and what about the other planets? The weight of Earth is approximately 5.972 X 10 21 tons, with a radius of 6,370 kilometers.

By utilizing the principle of gravity, it is possible to easily determine the mass of the Earth. To accomplish this, a thread is utilized and a small weight is suspended from it. The precise location of the weight is determined. Then, a ton of lead is placed beside it. There is an attractive force between the two objects, resulting in the cargo being deflected by a minuscule distance. However, even a deflection of 0.00003 mm is sufficient to calculate the mass of the planet. To do so, it is only necessary to measure the attraction force in relation to the weight and the attraction force between the small weight and the large weight. The obtained data enable the calculation of the Earth’s mass.
The weight of the Earth and other planets
Earth is the biggest planet in the Earth group. In comparison, Mars weighs about 0.1 times the weight of Earth, while Venus weighs about 0.8 times. It is approximately 0.05 times the weight of Earth. Gas giants are much larger than Earth. If we compare Jupiter to our planet, the giant is 317 times bigger, while Saturn is 95 times heavier and Uranus is 14 times heavier. There are planets that weigh 500 times or more than Earth. These are massive gas bodies situated outside our solar system.
The law of universal gravitation, expressed by the formula
(1)
states that the force of attraction between two masses F is proportional to their product and inversely proportional to the square of the distance r between their centers. In astronomy, it is often possible to disregard the size and shape of celestial bodies and treat them as point masses, where all their mass is concentrated.
The constant of proportionality, denoted as G, is known as the gravitational constant. It is determined through a physical experiment involving torsion weights, which allows for the calculation of the gravitational force between bodies of known mass.
When bodies fall freely, the force F exerted on the body is equal to the mass of the body multiplied by the acceleration of free fall g. The acceleration g can be calculated using the period T of oscillation of a vertical pendulum: , where l represents the length of the pendulum. At a latitude of 45 degrees and at sea level, the value of g is 9.806 m/s2.
The mass of the Sun can be calculated by applying Kepler’s third law to the movement of the Earth (along with the Moon) around the Sun and the movement of the Moon around the Earth:
, (2)
where а – is the major semi-major axes of the orbits, T – is the periods (stellar or sideric) of the orbit. By neglecting compared to , we can determine the ratio , which is equal to 329390. Therefore, g, or ca.
In a similar manner, we can determine the masses of planets that have satellites. The masses of planets without satellites are determined by perturbations in the movement of their neighboring planets. The theory of perturbed planetary motion allowed for the suspicion of the existence of the then unknown planets Neptune and Pluto, as well as the determination of their masses and prediction of their positions in the sky.
The mass of a star (apart from the Sun) can only be reliably determined if it is part of a visual double star system, where the distance is known. Kepler’s third law can be used to calculate the sum of the masses of the components in this case, using the formula:
,
where а is the major semi-axis (in seconds of arc) of the true orbit of the satellite around the main (usually brighter) star, which is considered stationary, Р is the orbital period in years, and is the angular separation of the components (in seconds of arc). The value represents the major semi-axis of the orbit in astronomical units (a. e.). If the angular distances of the components from the center of mass are known, their ratio can be used to determine the ratio of their masses: . By using the sum of the masses and their ratio, the mass of each star can be calculated individually. If the double star components have similar luminosity and spectra, then the average of the masses can provide an accurate estimate of each component’s mass without needing to determine their ratio separately.
For alternative categories of binary stars (eclipsing binaries and spectroscopic binaries), there are several options available for approximating the stellar masses or estimating their minimum values (i.e., the masses below which their magnitudes cannot be).
The collection of data on the combined masses of approximately one hundred double stars of various types has provided us with valuable statistical information regarding the relationship between their masses and luminosities. This finding has enabled us to estimate the masses of individual stars based on their absolute stellar magnitudes. The absolute stellar magnitudes, denoted as M, can be calculated using the formula: M = m + 5 + 5 lg – A(r) (3), where m represents the apparent stellar magnitude in a specific optical range (such as U, V, B, etc.), U, V, or V, and A(r) denotes the magnitude of light in the same optical range in a given direction up to a certain distance.
There is another technique for estimating the mass of a star that involves measuring the gravitational redshift of spectral lines within its gravitational field. This can be thought of as similar to the Doppler redshift in a spherically symmetric gravitational field. In this case, the mass of the star is denoted by M in solar mass units, the radius of the star is denoted by R in units of the Sun’s radius, and the redshift is expressed in km/s. This relationship has been verified for white dwarfs that are part of binary systems, where the radii, masses, and true velocity v r (which are projections of the orbital velocity) can be determined.
In addition, there have been observations of invisible (dark) satellites near certain stars, which have been detected through fluctuations in the star’s position caused by the motion near the common center of mass (see ). These satellites have masses less than 0.02 , and are likely non-self-luminous bodies that resemble planets.
From the determination of stars’ masses, it has been discovered that they fall within a range of approximately 0.03 to 60. The majority of stars have masses ranging from 0.3 to 3. The average mass of stars in close proximity to the Sun is 10^33 g. Although there is a significant difference in the masses of stars, their difference in luminosities is much greater (reaching tens of millions). Stars also vary greatly in terms of their radii, resulting in a noticeable disparity in their mean densities, ranging from up to g/cm^3 (with the Sun’s mean density being 1.4 g/cm^3).
Newton’s law of universal gravitation enables the measurement of one of the most important physical characteristics of a celestial body – its mass.
a) through measurements of the gravitational force on the surface of a given body (gravimetric method),
b) utilizing Kepler’s third law, which has been refined.
c) The method of determining the mass of a celestial body can be done by analyzing the observed perturbations it produces in the motions of other celestial bodies.
1. The first technique is applied specifically to the Earth.
Based on the law of gravitation, the acceleration g at the Earth’s surface is given by:
Where m represents the mass of the Earth and R is its radius.
The values of G and R are measured at the Earth’s surface, with G being a constant.
By using the accepted values of g, R, and G, we can calculate the mass of the Earth:
Once we have the mass and volume, we can determine the average density, which is found to be 5.5 g/cm3.
2. Kepler’s third law allows us to find the ratio between the mass of a planet and the mass of the Sun, provided that the planet has at least one satellite and we know its distance from the planet and the period of its revolution around it.
where M, m, mc – are the masses of the Sun, the planet, and its satellite, T and tc – are the periods of orbits of the planet around the Sun and the satellite around the planet, a and ace – are the distances of the planet from the Sun and the satellite from the planet, respectively.
The ratio of M/m for all planets is extremely large; however, the ratio of m/mc is very small (except for the Earth and Moon, Pluto and Charon) and can be ignored.
The M/m ratio can be easily determined using Eq.
In the case of the Earth and the Moon, the first step is to calculate the mass of the Moon, which is a challenging task. This difficulty is overcome by studying the disturbances in the Earth’s motion caused by the Moon.
3. The lunar inequality, which refers to variations in the apparent positions of the Sun in its longitude over a monthly period, has been discovered through precise determinations. This phenomenon suggests that the center of the Earth follows a small elliptical path around the common center of mass known as “Earth-Moon”, which is located within the Earth at a distance of 4650 km from its center.
Observations of the minor planet Eros between 1930 and 1931 also allowed for the determination of the position of the Earth-Moon center of mass.
Studies on the movements of artificial satellites of the Earth have revealed that the ratio of the masses of the Moon and the Earth is approximately 1/81.30.
In 1964, the International Astronomical Union officially recognized this ratio as constant.
According to Kepler’s equation, the mass of the Sun is estimated to be 2.1033g, which is 333000 times greater than the mass of the Earth.
The mass of planets that do not have satellites is calculated based on the disturbances they create in the orbits of the Earth, Mars, asteroids, and comets, as well as the perturbations they have on each other.
 Lyrics by Rem Digga – I am injured, pleasant, but not dead, but during the flight Lazarev is not angry at Zakharchuk
Lyrics by Rem Digga – I am injured, pleasant, but not dead, but during the flight Lazarev is not angry at Zakharchuk Who was Pavlik Morozov really?
Who was Pavlik Morozov really? How does Russian language develop?
How does Russian language develop? Who invented the first parachute?
Who invented the first parachute? How do insects travel. Insect Class. Overview of their characteristics and diversity. The significance of insects in ecosystems and their importance to humans. A brief summary of the class
How do insects travel. Insect Class. Overview of their characteristics and diversity. The significance of insects in ecosystems and their importance to humans. A brief summary of the class- The implicit formula for finding the derivative of a function
 Understanding relatively prime numbers
Understanding relatively prime numbers- Polynomials over the field of rational numbers
- Polynomials over the field of complex numbers
The mass of the Sun can be determined by considering the Earth’s gravitational force towards the Sun as a centripetal force that keeps the Earth in its orbit (we will simplify by assuming the Earth’s orbit is a circle).
Here we have the mass of the Earth and the average distance between the Earth and the Sun. Let’s denote the duration of the year in seconds as . Thus,
Therefore, by substituting the numerical values , we can calculate the mass of the Sun:
The mass of any planet that has a satellite can be calculated using the same formula. In this scenario, you would need the average distance between the satellite and the planet, the duration of the satellite’s orbit around the planet, and the mass of the planet. For instance, by knowing the distance between the Moon and the Earth, as well as the number of seconds in a month, you can determine the mass of the Earth using the aforementioned method.
If we let the mean density of the Earth represent the average density of the planet, then it is clear that the average density of the globe is equivalent to
The average density of the upper layers of the Earth’s mineral rocks is approximately Thus, it can be inferred that the core of the planet must have a significantly higher density than the average density of the Earth.
The examination of the Earth’s density at different depths was initiated by Lezhandre and continued by numerous scientists. Based on the findings of Gutenberg and Gaalk (1924), the Earth’s density can be observed to have the following values at various depths:
The pressure at great depths inside the globe is believed to be extremely high by many geophysicists. It is estimated that the pressure could reach several atmospheres per square centimeter even at shallow depths. In the Earth’s core, which is approximately 3000 kilometers deep or more, the pressure is likely to be around 1-2 million atmospheres.
As for the temperature at different depths inside the globe, it is known to increase significantly. In mines and boreholes, the temperature rises by an average of one degree for every certain depth. It can be assumed that at a depth of about 1500-2000° the temperature reaches its peak, which is comparable to the temperature of lava. After reaching this peak, the temperature remains constant.

Celestial mechanics allows us to determine the mass of a planet by studying its influence on the motion of other planets. During the early 19th century, scientists knew about the existence of Mercury, Venus, Earth, Mars, Jupiter, Saturn, and Uranus. However, they noticed some irregularities in the motion of Uranus, suggesting the presence of an unseen planet. In 1845, both the French scientist Leverrier and the Englishman Adams independently studied the motion of Uranus and successfully calculated the mass and location of the yet-to-be-discovered planet. Following their calculations, the planet Neptune was discovered exactly where they predicted.
Astronomer Lovell made a prediction in 1914 about the existence of a planet that was even further from the Sun than Neptune. However, it wasn’t until 1930 that this planet, named Pluto, was actually discovered.
The following table provides basic information about the nine major planets in our solar system. Figure 50 shows the relative sizes of the Sun and these planets.
Aside from these large planets, there are also approximately 1300 very small planets known as asteroids (or planetoids). These asteroids primarily orbit between Mars and Jupiter.
The constant of gravitation, also known as the coefficient of proportionality, is denoted as G. It is determined through a physical experiment involving torsion weights, which allows for the calculation of the gravitational force between objects of known mass.
When objects fall freely, the force F acting on the object is equal to the product of its mass and the acceleration due to gravity, denoted as g. The value of g can be determined by measuring the period T of oscillation of a vertical pendulum, where l represents the length of the pendulum. At a latitude of 45 degrees and sea level, g is approximately equal to 9.806 m/s^2.
By substituting the expression for the gravitational forces of the Earth into formula (1), we can derive the following relationship, where M is the mass of the Earth and R is the radius of the globe. Thus, the mass of the Earth, g, can be determined. This determination of the Earth’s mass serves as the initial step in a series of calculations to determine the masses of other celestial bodies such as the Sun, Moon, planets, and stars. The masses of these bodies are determined either by applying Kepler’s 3rd law (see link), or by utilizing the principle that the distances between any masses and their common center of masses are inversely proportional to the masses themselves. This principle allows for the determination of the Moon’s mass. By measuring the precise coordinates of the planets and the Sun, it has been found that the Earth and Moon orbit around the barycenter, which is the center of mass of the Earth-Moon system, with a period of one month. The distance from the Earth’s center to the barycenter is 0.730 (located within the globe), while the distance from the Moon’s center to the Earth’s center is 60.08. Therefore, the ratio of the distances between the centers of the Moon and the Earth to the barycenter is 1/81.3. Since this ratio is the inverse of the ratio of the masses of the Earth and Moon, the mass of the Moon can be determined as 1/81.3.
г.
The mass of the Sun can be calculated by using Kepler’s 3rd law to analyze the movement of the Earth (along with the Moon) around the Sun and the movement of the Moon around the Earth:
, (2)
where a – represents the major semi-major axes of the orbits, T – represents the periods (stellar or sideric) of the orbit. By disregarding compared to , we can determine the ratio , which is equal to 329390. As a result, g, or approximately .
In a similar manner, we can determine the masses of planets that have moons. The masses of planets without moons are determined by the disruptions they cause in the movement of their neighboring planets. The theory of disrupted planetary motion enabled the suspicion of the existence of the then unidentified planets Neptune and Pluto, the determination of their masses, and the prediction of their location in the sky.
The determination of a star’s mass (excluding the Sun) is most reliable when it is part of a visual double star system, where the distance is known. Kepler’s third law can be applied in this scenario to calculate the sum of the component masses (in units ):
,
where а "" represents the major semi-axis (in seconds of arc) of the orbit of the companion star around the main star (typically the brighter one), which is considered stationary in this context. Р denotes the orbital period in years, and represents the major semi-axis of the system’s orbit (in seconds of arc). The value represents the major semi-axis of the orbit in astronomical units (a. e.). If the angular distances of the components from the common center of mass can be measured, their ratio provides an inverse estimate of the mass ratio: . By knowing the sum of the masses and their ratio, the mass of each star can be determined individually. In cases where the double star components have similar luminosity and spectra, the half-sum of the masses provides an accurate estimation of each component’s mass without the need for additional calculations.
When it comes to other kinds of double stars, such as eclipsing doubles and spectral doubles, there are various methods available to approximate the masses of the stars or to determine their minimum limit (i.e., the lowest possible value for their masses).
By analyzing data from a large sample of double stars, consisting of about a hundred stars of various types, we have made an interesting discovery regarding the relationship between the masses and luminosities of these components (see ). This finding allows us to estimate the masses of individual stars based on their (or, more precisely, their abs. ). The absolute magnitude of a star, denoted as M, can be calculated using the formula: M = m + 5 + 5 lg – A(r) (3), where m represents the apparent magnitude of the star in a specific optical range (e.g., U, V, B, etc.) and A(r) represents the magnitude of light in the same optical range in a specific direction up to a certain distance. The specific optical ranges used are typically denoted as U, V or V (e.g., U, B, or V).
There is another way to estimate the weight of a star, which involves measuring the gravitational redshift of spectral lines in its gravitational field. In a gravitational field that is spherically symmetrical, this is equivalent to the Doppler redshift. Here, M represents the mass of the star in units of the Sun’s mass, R is the radius of the star in units of the Sun’s radius, and v is expressed in km/s. This relationship has been tested with white dwarfs that are part of binary systems. For these stars, we can determine the radii, masses, and true v values, which are the projections of the orbital velocity.
Invisible (dark) satellites, which have been detected near certain stars through the observed oscillations of the star’s position associated with its motion near the common center of mass (see ), have masses that are less than 0.02 . These satellites are likely not self-luminous objects and are more similar to planets.
It has been determined that stars have masses ranging from approximately 0.03 to 60. The majority of stars fall within the range of 0.3 to 3. The average mass of stars near the Sun is 10^33 g. Although the difference in masses between stars is relatively small, their differences in luminosities can be significant, reaching up to tens of millions. Stars also vary greatly in terms of their radii, resulting in a noticeable disparity in their densities, ranging from [density range] (in comparison to the Sun’s density of 1.4 g/cm^3).
Newton’s law of universal gravitation allows for the measurement of a celestial body’s mass, which is one of its most important physical characteristics.
a) This can be done through the gravimetric method, which involves measuring the force of gravity on the surface of the body.
b) Another approach is to use Kepler’s third refined law.
c) The analysis of perturbations caused by the celestial body in the movements of other celestial bodies is a method used to determine certain characteristics of the celestial body.
1. The first method is specifically applied to the Earth.
Based on the law of gravitation, the acceleration g at the Earth’s surface can be expressed as:
Where m represents the mass of the Earth and R is its radius.
The values of G and R are measured at the Earth’s surface, with G being constant.
Given the accepted values of g, R, and G, the mass of the Earth can be calculated:
Once the mass and volume are known, the average density can be determined, which is approximately 5.5 g/cm3.
2. Kepler’s third law provides a means to determine the ratio between the mass of a planet and the mass of the Sun, given that the planet has at least one satellite and the distance between the planet and the satellite, as well as the period of revolution around the planet, are known.
where M, m, and mc represent the masses of the Sun, the planet, and its satellite, while T and tc denote the periods of the planet orbiting the Sun and the satellite orbiting the planet, respectively. The distances of the planet from the Sun and the satellite from the planet are denoted as a and ace, respectively.
The ratio of M/m is significantly large for all planets, whereas the ratio of m/mc is negligible (excluding the Earth and the Moon, Pluto and Charon).
The M/m ratio can be easily determined by using Eq.
In the case of the Earth and the Moon, the mass of the Moon needs to be determined first. However, this is a challenging task. The problem is resolved by analyzing the disturbances in the Earth’s motion caused by the Moon.
3. The discovery of variations in the apparent positions of the Sun in its longitude, known as “lunar inequality”, has been made through precise determinations. This phenomenon indicates that the Earth’s center traces a small ellipse around the common center of mass “Earth-Moon” during a month. The “Earth-Moon” center of mass is located within the Earth, at a distance of 4650 km from the Earth’s center.
The position of the “Earth-Moon” center of mass was also determined through observations of the minor planet Eros in 1930 – 1931.
Through the study of perturbations in the movements of artificial satellites of the Earth, the ratio of the Moon’s mass to the Earth’s mass was found to be 1/81.30.
In 1964, the International Astronomical Union officially recognized this ratio as a constant.
Using Kepler’s equation, we can calculate that the mass of the Sun is 2.1033g, which is 333000 times larger than the mass of the Earth.
The masses of planets that do not have satellites are determined by the disturbances they create in the orbits of the Earth, Mars, asteroids, and comets, as well as the disturbances they have on each other.
The quest to determine the magnitude of our planet throughout history
Throughout the ages, scholars from various civilizations have endeavored to unravel the elusive mystery of the Earth’s weight. In ancient times, it was commonly believed that our planet was a flat expanse, supported by the backs of gigantic whales or turtles. Some cultures even imagined colossal elephants in place of whales. Regardless, the prevailing notion was that the Earth was flat, with a discernible edge.
As the Middle Ages dawned, perspectives on the Earth’s shape and weight underwent a transformative shift. It was the visionary G. Bruno who first dared to propose the notion of a spherical Earth, though his audacity cost him his life at the hands of the Inquisition. Another pivotal figure in the annals of scientific discovery, the intrepid explorer Magellan, contributed to our understanding of the Earth’s radius and mass. It was he who postulated that our planet was indeed round.
Initial breakthroughs
The planet Earth is a physical entity with distinct characteristics, one of which is its weight. This significant revelation served as a catalyst for numerous groundbreaking investigations. As per the principles of physics, weight is the measure of the body’s gravitational pull towards its support structure. Considering that the Earth lacks any form of support, it can be inferred that it does not possess weight. However, it does possess an immense mass.
The Mass of Planet Earth
Eratosthenes, an ancient Greek scientist, was the first to attempt to determine the size of the planet. He measured shadows in different cities of Greece and compared the data in order to calculate the planet’s volume. Following him, the Italian scientist G. Galileo made his own calculations and discovered the law of free gravity. The task of determining the weight of the Earth was then taken up by I. Newton, who made further measurements and ultimately formulated the law of gravity.

In a groundbreaking discovery, Scottish scientist N. Makelin has successfully calculated the weight of planet Earth. His calculations revealed that the planet’s mass is approximately 5.9 sextillion tons. However, it is important to note that this figure is subject to change. The variations in weight can be attributed to the accumulation of cosmic dust on the planet’s surface. It is estimated that around thirty tons of dust settle on Earth each year, contributing to its increasing weight.
To determine the precise weight of the Earth, we must ascertain the composition and mass of the various components that constitute the planet.
- Mantle. The mass of this layer is approximately 4.05 X 10^24 kg.
- Core. This layer is lighter than the mantle, weighing only 1.94 X 10^24 kg.
- Crust. This portion is exceedingly thin and has a weight of merely 0.027 X 10^24 kg.
- Hydrosphere and atmosphere. These layers have respective weights of 0.0015 X 10^24 kg and 0.0000051 X 10^24 kg.
By summing up all of these values, we arrive at the overall weight of the Earth. However, different sources provide varying estimates for the planet’s mass. So how much does the Earth weigh in tons, and what about the weights of other planets? The Earth’s weight amounts to 5.972 X 10^21 tons, with a radius of 6,370 kilometers.

By utilizing the force of gravity, it is possible to ascertain the mass of the Earth quite easily. To accomplish this, a thread is utilized and a small weight is suspended from it. The precise location of the weight is determined. Next to it, a ton of lead is placed. There is an attraction between the two objects, which causes the weight to deflect to the side by a small distance. Even a deviation as small as 0.00003 mm can be used to calculate the mass of the planet. This can be achieved by measuring the force of attraction between the weight and the Earth, as well as the force of attraction between the small weight and the large weight. The resulting data can then be used to calculate the mass of the Earth.
The weight of the Earth and other planets
The Earth is the largest planet in the Earth group. In comparison, Mars weighs about 0.1 times the weight of Earth, while Venus weighs about 0.8 times the weight of Earth. On the other hand, gas giants are significantly larger than Earth. For instance, Jupiter is 317 times larger than our planet, Saturn is 95 times heavier, and Uranus is 14 times heavier. There are also planets that weigh 500 times or more than Earth, and these massive gas bodies are located beyond our solar system.
The law of universal gravitation is the foundation for determining the masses of celestial objects, as expressed by the following equation:
(1)
where F is the force of attraction between the masses, which is proportional to their product and inversely proportional to the square of the distance r between their centers. In the field of astronomy, it is often possible to disregard the size and shape of celestial bodies and treat them as point masses, where all of their mass is concentrated.
The constant of gravitation, denoted as G, is the coefficient of proportionality in the equation. It is determined through physical experiments using torsion weights, which allow the measurement of gravitational forces between bodies with known masses.
When objects fall freely, the force F that acts on them is equal to the mass of the object multiplied by the acceleration of free fall g. The acceleration g can be calculated by measuring the period T of oscillation of a vertical pendulum, using the equation , where l is the length of the pendulum. At a latitude of 45 degrees and at sea level, the value of g is 9.806 m/s2.
The Sun’s mass can be calculated by using Kepler’s 3rd law to study the movement of the Earth (along with the Moon) around the Sun and the Moon’s movement around the Earth:
, (2)
where а – represents the major semi-major axes of the orbits, and T – is the period (stellar or sideric) of the orbit. By disregarding compared to , we derive the ratio , which equals 329390. Consequently, g, or about .
The masses of planets with moons are determined in a similar manner. The masses of planets lacking moons are determined by analyzing the perturbations they cause in the orbits of nearby planets. The theory of perturbed planetary motion helped identify the then unknown planets Neptune and Pluto, determine their masses, and predict their locations in the sky.
The determination of the mass of a star (excluding the Sun) is most reliable when it is part of a visual double star system, where the distance between the stars is known. Kepler’s third law can be applied in this case to calculate the sum of the masses of the components, denoted as M1 and M2 (in units M☉).
,
Here, a represents the major semi-axis (in seconds of arc) of the true orbit of the companion star around the main star, which is assumed to be stationary. P is the orbital period in years, and θ is the angular separation of the stars in seconds of arc. By measuring the angular distances, we can determine the ratio of masses, which is the inverse of the ratio of angular separations: . With the sum of the masses and their ratio, we can calculate the individual mass of each star. If the double star system has similar luminosity and spectra for both components, then the half-sum of the masses provides an accurate estimation of each star’s mass without the need for additional measurements.
When it comes to other kinds of binary stars such as eclipsing binaries and spectroscopic binaries, there are various methods available to approximate the masses of the stars or to determine their minimum values (i.e., the values that the masses cannot go below).
By analyzing data from approximately one hundred double stars of various types, we have been able to uncover a significant statistical correlation between their masses and luminosities (see source). This correlation enables us to estimate the masses of individual stars based on their absolute magnitudes. The absolute magnitude M of a star can be calculated using the formula: M = m + 5 + 5 lg – A(r), where m represents the apparent magnitude of the star in a specific optical range (such as U, V, B, etc.). The values for U, V, or V can be found in the respective photometric systems (e.g., U, B, or V). Additionally, the formula takes into account the star’s parallax and the magnitude of light A(r) in the same optical range along a particular direction up to a certain distance.
There is another technique for determining the mass of a star, which involves measuring the gravitational redshift of spectral lines within its gravitational field. In a spherically symmetrical gravitational field, this is equivalent to the Doppler redshift. The mass of the star can be represented as M, measured in solar mass units, while the radius of the star can be represented as R in terms of the Sun’s radius. The relation is expressed in units of km/s. This relationship has been examined in relation to white dwarfs that are part of binary systems. In these cases, the radii, masses, and actual v r (which are projections of the orbital velocity) have been studied.
Dark satellites, which cannot be seen and have been detected near certain stars due to observed oscillations in the star’s position as it moves around the common center of mass (see ), have masses that are less than 0.02 . It is likely that these satellites are not self-luminous and resemble planets more than anything else.
It has been determined that stars have masses ranging from approximately 0.03 to 60. The majority of stars fall within the mass range of 0.3 to 3. This can be compared to the mass of stars in the Sun’s immediate vicinity, which is about 10^33 grams. Although stars vary greatly in terms of mass, their differences in luminosity can be even more pronounced, reaching tens of millions. Additionally, stars exhibit significant variations in their radii, resulting in striking differences in their average densities, which can range from up to g/cm^3 (the Sun’s average density is 1.4 g/cm^3).
The mass of the Sun can be determined by considering the gravitational force between the Earth and the Sun, which acts as a centripetal force to keep the Earth in its orbit (assuming a circular orbit for simplicity).
Below you can find the weight of our planet, the average gap between the Earth and the Sun. By using the duration of a year in seconds, we can establish:
By substituting the numerical values into the equation, we can determine the weight of the Sun:
This same equation can be used to calculate the weight of any planet that has a moon. In this case, we would need to know the average distance between the moon and the planet, the time it takes for the moon to orbit the planet, and the weight of the planet. For example, by using the distance between the Moon and the Earth and the number of seconds in a month, we can determine the weight of the Earth using this method.
The weight of an object can be used to calculate the mass of the Earth by subtracting the component of gravitational force that is due to the Earth’s rotation. This correction is not necessary if we use the acceleration of gravity observed at the poles of the Earth. Using the average radius of the Earth and the mass of the Earth, we can calculate the mass as follows:
If we define the average density of the Earth as the mean density of the globe, then it is clear that the average density of the globe is equal to
The average density of the mineral rocks in the upper layers of the Earth is approximately equivalent to. This implies that the density of the Earth’s core must be significantly higher than the average density of the planet.
Lejeandre and subsequent scientists have conducted research on the density of the Earth at different depths. Based on the findings of Gutenberg and Gaalk (1924), the Earth’s density varies at different depths:
The pressure within the Earth’s core at great depths is immensely high. Many geophysicists speculate that at certain depths, the pressure could reach atmospheres per square centimeter. In the core, which is approximately 3000 kilometers deep or more, the pressure is estimated to reach 1-2 million atmospheres.
Figure 50. The Sun and planets in relation to their sizes.
The complete theory of celestial mechanics allows us to determine the mass of a planet by studying the impact it has on the motion of another planet. In the early 19th century, scientists were aware of the existence of Mercury, Venus, Earth, Mars, Jupiter, Saturn, and Uranus. However, they noticed that Uranus exhibited irregularities in its motion, suggesting that there was another planet located beyond Uranus that was affecting its trajectory. In 1845, the French scientist Leverrier and the Englishman Adame independently studied the motion of Uranus and successfully calculated the mass and position of a previously unseen planet. This planet, which was later named Neptune, was then observed in the sky precisely where the calculations had indicated.
In 1914, astronomer Lovell made a similar prediction regarding the existence of a planet that would be located even farther from the Sun than Neptune. It wasn’t until 1930 that this planet, now known as Pluto, was actually discovered and given its official name.
Here is some basic information about the nine major planets in our solar system:
The table below provides essential details about these planets, while Figure 50 offers a visual representation of the Sun’s size relative to that of the planets.
In addition to the larger planets mentioned earlier, there are approximately 1300 smaller celestial bodies known as asteroids (or planetoids). These asteroids primarily orbit between Mars and Jupiter.
Newton’s law of universal gravitation allows us to determine one of the most crucial physical attributes of a celestial body: its mass.
a) This can be achieved by measuring the force of gravity exerted on the surface of the given celestial body (gravimetric method).
b) Kepler’s third refined law states that
c) The analysis of observed perturbations produced by the celestial body in the motions of other celestial bodies provides insight.
1. The Earth is subject to the first method.
Based on the law of gravitation, the acceleration g on the Earth’s surface can be expressed as:
Where m represents the mass of the Earth and R is its radius.
The values of g and R are measured at the Earth’s surface. G = constant.
By utilizing the current accepted values of g, R, and G, the mass of the Earth can be determined:
Once the mass and volume are known, the average density can be calculated. It is equivalent to 5.5 g/cm3.
2. Kepler’s third law states that if a planet has at least one satellite and we know the distance between the planet and the satellite, as well as the period of revolution around it, we can determine the ratio between the mass of the planet and the mass of the Sun.
In this equation, M represents the mass of the Sun, m represents the mass of the planet, and mc represents the mass of the satellite. T and tc represent the periods of the planet’s orbit around the Sun and the satellite’s orbit around the planet, respectively. a and ace represent the distances of the planet from the Sun and the satellite from the planet.
The ratio M/m is generally very large for all planets, while the ratio m/mc is typically very small (except for the Earth and the Moon, Pluto and Charon) and can be ignored.
We can easily calculate the M/m ratio using the equation above.
When it comes to the Earth and the Moon, determining the mass of the Moon is a challenging task. However, there is a solution – analyzing the perturbations in the Earth’s motion caused by the Moon.
3. Accurate determinations of the Sun’s apparent positions in its longitude have revealed monthly variations known as “lunar inequality”. This finding suggests that the center of the Earth describes a small ellipse during the month around the shared center of mass “Earth-Moon”, which is located inside the Earth at a distance of 4650 km from the Earth’s center.
The position of the Earth-Moon center of mass was also deduced from observations of the minor planet Eros between 1930 and 1931.
Based on disturbances in the movements of man-made satellites orbiting the Earth, the ratio of the Moon’s mass to the Earth’s mass was found to be 1/81.30.
This finding was officially recognized by the International Astronomical Union in 1964.
Applying Kepler’s equation, we can calculate that the mass of the Sun is 2.1033g, which is 333000 times greater than the mass of the Earth.
The masses of planets that do not have natural satellites are determined by the disturbances they cause in the orbits of the Earth, Mars, asteroids, and comets, as well as the disturbances they exert on each other.
The quest to determine the dimensions of our planet throughout history
Throughout the ages and across various cultures, scientists have embarked on a mission to unravel the mystery of Earth’s weight. In ancient times, it was commonly believed that the planet rested on the backs of whales and turtles, although some cultures envisioned elephants instead of whales. Regardless, the prevailing notion was that the Earth was a flat surface with a distinct edge.
As the Middle Ages unfolded, there emerged a shift in perceptions regarding shape and weight. G. Bruno was among the first to propose a spherical Earth, but his ideas were met with resistance and ultimately led to his execution by the Inquisition. Another key figure in the scientific exploration of Earth’s dimensions was the intrepid traveler Magellan, who boldly asserted that our planet was indeed round, shedding light on its radius and mass.
Initial findings
The planet Earth is a tangible entity with distinct characteristics, one of which is its weight. This breakthrough led to the initiation of a multitude of investigations. As per the laws of physics, weight is the exertion of force by an object on its surroundings. Considering that the Earth lacks any external support, it can be inferred that it lacks weight, although it possesses a substantial mass.
The Earth’s Mass: Unraveling its Secrets
Eratosthenes, a pioneering Greek scientist, embarked on a groundbreaking quest to unveil the true dimensions of our planet. Across various Greek cities, he meticulously measured shadows and compared the resulting data, aiming to ascertain the Earth’s volume. Building upon Eratosthenes’ efforts, the Italian genius G. Galileo delved into the realm of calculations, ultimately unraveling the enigmatic law of free gravity. Stepping into the realm of measuring the Earth’s weight, the baton was then passed to I. Newton. Through relentless attempts to quantify this mysterious force, Newton unveiled the revolutionary law of gravity.

The Scottish scientist N. Makelin was the first to calculate the weight of the Earth. According to his calculations, the planet’s mass is 5.9 sextillion tons. Currently, this value has been updated. Variations in weight occur as a result of cosmic dust settling on the Earth’s surface. Approximately thirty tons of dust accumulate on the planet every year, contributing to its increased weight.
To determine the exact weight of the Earth, it is necessary to have knowledge of the composition and mass of the various components that constitute the planet.
- Mantle. The mass of this layer is approximately 4.05 X 10 24 kg.
- Core. This layer has a lesser weight compared to the mantle, amounting to only 1.94 X 10 24 kg.
- Crust of the Earth. This segment is extremely thin and weighs merely 0.027 X 10 24 kg.
- The hydrosphere and atmosphere. These layers have respective weights of 0.0015 X 10 24 kg and 0.0000051 X 10 24 kg.
By summing up these measurements, we can establish the weight of the Earth. Nevertheless, there exist discrepancies among different sources regarding the mass of the planet. Consequently, what is the precise weight of planet Earth in tons, and how much do the other planets weigh? The weight of the planet is 5.972 X 10 21 tons. Additionally, the radius measures 6,370 kilometers.

By utilizing the concept of gravity, one can easily ascertain the mass of the Earth. To accomplish this, a thread is taken and a small weight is hung from it, with its precise position being determined. A ton of lead is then placed adjacent to it. There exists an attraction between these two objects, causing the weight to be deflected slightly to the side. Even a minuscule deflection of 0.00003 mm is sufficient to calculate the mass of the planet. This can be achieved by measuring the force of attraction between the weight and the Earth, as well as the force of attraction between the small weight and the large weight. The obtained data enables the calculation of the Earth’s mass.
The mass of Earth and other planets
Earth is the largest planet in the group of planets called the Earth Group. In comparison, Mars has a mass that is approximately 0.1 times that of Earth, while Venus has a mass that is approximately 0.8 times that of Earth. However, gas giants are significantly larger than Earth. For example, Jupiter is 317 times bigger than our planet, Saturn is 95 times heavier, and Uranus is 14 times heavier. There are even planets that weigh 500 times or more than Earth, and these are gigantic gas bodies located outside of our solar system.
I have always been fascinated by the phenomenon of weightlessness. It is similar to the feeling of flying, which is something that many people desire. Prior to studying the topic, I only knew that weightlessness is experienced in space, particularly on spaceships, where objects float and astronauts cannot stand on their feet like they can on Earth.
Weightlessness is not just an anomaly, but a significant concern for the field of astronautics. The absence of gravity can lead to various health issues during spaceflights, and astronauts often have to undergo rehabilitation to regain their ability to walk and stand once they return to Earth. Therefore, it is crucial to understand the concept of weightlessness and its impact on the well-being of individuals in space. Consequently, it is imperative to develop initiatives aimed at mitigating the potential negative effects of weightlessness on the human body.
My objective is to present the idea of weightlessness in a comprehensive manner, exploring it from various perspectives. I aim to highlight the significance of this concept not only in the exploration of outer space and its detrimental effects on human beings, but also in the potential application of Earth-derived technologies to mitigate these effects. Additionally, I intend to demonstrate the execution of certain technological processes that would be challenging or even impossible to achieve under terrestrial conditions.
Imagine this scenario: a situation where an astronaut ventures out of a spaceship into space and, utilizing a personal rocket engine, takes a stroll around the vicinity. Upon returning, the astronaut inadvertently applies too much force to the engine, resulting in an excessive speed as they approach the ship and accidentally collide with it using their knee. Would this collision cause any harm?
The answer is no: in a weightless environment, an astronaut is as light as a feather, as some may say.
However, this answer is incorrect. When you fall from a fence on Earth, you also experience a state of weightlessness. Yet, when you make contact with the Earth’s surface, you experience a noticeable force, which becomes even more significant if you fall onto a heavier surface or have a higher velocity at the moment of impact.
Therefore, weightlessness and weight are not relevant when it comes to impact. It is the mass and velocity that truly matter, not the weight.
However, the astronaut’s experience of pain will be less intense when the spacecraft touches down compared to when it impacts the Earth (assuming all other factors are the same: equal masses, relative velocities, and equal hardness of obstacles). The spacecraft has a much smaller mass than the Earth, so when the astronaut collides with the spacecraft, a significant portion of the kinetic energy will be transferred to the spacecraft, resulting in a smaller amount of deformation. This will cause the spacecraft to gain extra velocity and reduce the severity of the astronaut’s painful sensations.
Weightlessness and Measuring the Mass of Bodies
If a body, along with its support, is in free fall with an acceleration of g, then according to the equation
P = m (g – a), it follows that P = 0.
The absence of weight when the support experiences only the force of gravity and moves with an acceleration of gravity is referred to as weightlessness.
There are two types of weightlessness. The loss of weight that occurs when far away from celestial bodies and due to the weakening of gravity is known as static weightlessness. On the other hand, the state experienced by a person during orbital flight is referred to as dynamic weightlessness.
Both types of weightlessness manifest in the same way, with similar human perceptions. However, their causes are different.
Astronauts in space deal exclusively with dynamic weightlessness.
The term “dynamic weightlessness” refers to “weightlessness resulting from motion.”
We experience the gravitational pull of the Earth only when we oppose it. It is only when we resist the urge to fall that we become aware of gravity. And as soon as we give in to the force of gravity and allow ourselves to fall, the sensation of gravity instantly vanishes.
Just picture yourself taking your dog for a walk, holding onto him with a harness. The dog suddenly darts off, tugging on the harness. You can only feel the tension of the leash “pulling” on the dog as long as you resist its pull. And if you start running after the dog, the leash will slacken and the feeling of tension will disappear.
Gravity is also at play on Earth. As the airplane soars through the sky, two skydivers in the cockpit prepare for their jump. The force of gravity pulls them towards the ground, but they resist. They can feel the Earth’s gravity as their feet press against the floor of the airplane, reminding them of their weight. “The belt is tight,” they note.
However, they soon decide to surrender to the Earth’s pull. Standing on the edge of the hatch, they take the plunge. “The belt is slack,” they remark. In an instant, the sensation of Earth’s gravity vanishes and they become weightless.
One individual extended his arm, grasped the box that sailed past, unlocked a portal within it, and reached within.
At present, out of the pair of individuals, one is soaring externally of the container while the other is positioned inside. They will encounter entirely contrasting sensations. The individual soaring externally perceives and experiences the sensation of rapidly descending. The wind howls in their ears. The nearing Earth can be observed in the distance.
Contrarily, the individual soaring inside the container has secured the portal and initiates by propelling off the walls, “floating” on the container. It appears to them that the container is serenely situated on the Earth, and they, having reduced weight, glide through the atmosphere akin to a fish in an aquarium.
Technically speaking, there is no distinction between the two parachutists. They both descend towards the Earth at the same velocity, resembling a stone in motion. However, one will exclaim, “I am soaring through the sky,” while the other will claim, “I am suspended in mid-air.” The reality is that one is influenced by the gravitational force of the Earth, while the other is influenced by the container within which they are flying.
This is precisely how the phenomenon of dynamic weightlessness occurs within the cockpit of a spacecraft.
Initially, this may appear perplexing. It might seem that the spacecraft is flying parallel to the Earth, similar to an airplane. Yet, in an airplane flying horizontally, weightlessness is absent. However, we understand that the spacecraft satellite is continuously descending. It is more akin to a box released from an airplane than an actual airplane.
There are instances on Earth where individuals experience dynamic weightlessness. One example is when divers and swimmers launch themselves off a tower and enter the water, momentarily experiencing weightlessness. Similarly, skiers feel weightless for a brief period when they leap off a ski jump. Skydivers also encounter weightlessness as they plummet towards the ground before opening their parachutes. In the realm of astronaut training, weightlessness is simulated in an aircraft for approximately thirty to forty seconds. This is achieved through a technique known as a “slide,” where the pilot accelerates the plane, ascends rapidly, and then shuts off the engine. The plane proceeds to move through the air purely due to inertia, resembling a stone hurled by hand. Initially, it ascends slightly, traces an arc while descending, and eventually dives towards the Earth. Throughout this entire sequence, the plane is in a state of free fall, resulting in a weightless environment within the cabin. Subsequently, the pilot reactivates the engine and gently guides the plane out of the dive, returning it to regular level flight. Once the engine is restarted, the weightlessness promptly dissipates.
When in a state of weightlessness, all the particles of the body experience the effects of gravity, but there are no external forces (such as support reactions) acting on the body’s surface that would result in mutual pressure between the particles. This phenomenon is also observed with bodies located on an artificial Earth satellite (or a spaceship); these bodies and their particles, having been given an appropriate initial velocity along with the satellite, move along their orbits under the influence of gravitational forces with equal accelerations. It’s as if they are free and not exerting any mutual pressure on each other, thus experiencing weightlessness. Similar to a body in an elevator, gravity still affects them, but there are no external forces on the body surfaces causing mutual pressure between the bodies or their particles.
In general, if a body is subjected to external forces, it will experience a state of weightlessness under the following conditions: a) the only external forces acting on it are gravitational forces; b) the gravitational field is locally uniform, meaning that the acceleration imparted to all particles of the body at any given position is the same in magnitude and direction; c) all particles of the body have the same initial velocities, moving forward. Therefore, if the dimensions of a body are small compared to the radius of the Earth, and it is undergoing free translational motion in the Earth’s gravitational field without any other external forces, it will be in a state of weightlessness. The same principle applies to motion in the gravitational field of any other celestial bodies.

Weightlessness offers the opportunity to achieve certain technological processes that are challenging or even impossible to accomplish under normal Earth conditions. Examples of these processes include creating composite materials with a consistent structure throughout, shaping molten materials into precise spherical forms using surface tension forces, and more. The first-ever experiment involving welding different materials under vacuum conditions of weightlessness took place during the flight of the Soviet spacecraft “Soyuz-6” in 1969. Additionally, a range of technological experiments such as welding, studying the flow and crystallization of molten materials, and more were conducted on the American orbital station Skylab in 1973.
Scientists carry out a variety of experiments in space, establishing and conducting experiments, although their ultimate outcomes remain largely unknown. However, once an experiment yields a specific result, it still necessitates extensive testing over an extended period of time in order to ultimately elucidate and apply the acquired knowledge.
Provided below are descriptions of several experiments and intriguing news concerning weightlessness that are yet to be undertaken.
We are accustomed to our own gravitational force. We are accustomed to all objects surrounding us possessing weight. We cannot fathom anything different. Weightlessness has never been experienced in our lives. The entire history of life on Earth has transpired under the same circumstances. Gravity has persisted for millions of years without ever ceasing. Therefore, all organisms inhabiting our planet have long since adapted to maintaining their own gravitational pull.
Since ancient times, animals have developed bones as a means of support for their bodies. Without these bones, animals would be forced to crawl on the ground due to the pull of gravity, similar to a jellyfish being pulled out of the water onto the shore.
Over millions of years, all of our muscles have adapted to move our bodies and overcome the force of gravity on Earth.
Furthermore, every aspect of our bodies has adapted to the conditions of weight. The heart, for example, possesses powerful muscles that are capable of continuously pumping several kilograms of blood. While blood easily flows down into the legs, it requires force to be pumped up into the head. Strong ligaments suspend all of our internal organs, preventing them from descending and piling up in a heap.
Due to the constant gravitational force, a unique vestibular organ has developed deep within the cranial region, specifically located behind the ear. This intricate structure allows us to perceive the orientation of our surroundings relative to the Earth’s gravitational pull, distinguishing what is considered “up” and “down”.
The vestibular apparatus is a small chamber filled with a specialized fluid, containing minuscule stones known as otoliths. When an individual assumes an upright position, these stones settle at the bottom of the chamber. Conversely, when a person reclines, the otoliths shift and rest against the chamber’s sidewall. Through this mechanism, the human brain is able to detect positional changes, enabling an individual to accurately discern the location of the “bottom” even without visual cues.
Hence, every aspect of human physiology is finely tuned to adapt to the specific conditions experienced on the Earth’s surface.
Living Conditions in Zero Gravity
When it comes to the flight of manned spacecraft, it is crucial to consider the unique nature of weightlessness. Living conditions in a state of weightlessness differ significantly from those on Earth, which leads to changes in several vital functions. The central nervous system and receptors of various analyzing systems, such as the vestibular apparatus, musculoarticular apparatus, and blood vessels, are exposed to unfamiliar conditions in weightlessness. As a result, weightlessness acts as a specific integral stimulus that affects both human and animal organisms throughout the entire orbital flight. The response to this stimulus involves adaptation processes in physiological systems, with the extent of manifestation depending primarily on the duration of weightlessness and, to a lesser extent, on individual organism characteristics.
A bicycle ergometer was used to perform high-intensity exercise for one hour daily, resulting in a heart rate increase of 150-170 beats per minute. Five days after completion, recovery of circulatory and respiratory function was observed. Although metabolic changes, statokinetic, and vestibular disturbances were present, they were not significantly pronounced.
One possible solution could be to implement an artificial “gravitational” force within the spacecraft. This could be achieved by designing the station in the shape of a large rotating wheel, with work areas positioned along its outer edge. As the wheel rotates, the centrifugal force would push objects towards the outer surface, effectively creating a “floor” and simulating the effects of gravity. By incorporating this artificial “gravity” system, it would be possible to counteract the negative impacts of weightlessness on both animals and humans.
In order to address various theoretical and practical issues in the field of space medicine, laboratory techniques for simulating weightlessness are commonly employed. These methods involve restricting muscle activity, removing the typical vertical support for the body, and reducing hydrostatic blood pressure. This reduction is achieved by placing the individual in a horizontal position or at an angle (with the head positioned lower than the legs), subjecting them to long periods of continuous bed rest, or immersing them in a liquid medium for several hours or days (known as “immersion”).
A recent article in the journal Acta Astronautica, written by French scientists, highlights the impact of weightlessness on astronauts’ ability to accurately perceive object size and distance. This impairment can lead to difficulties in orienting oneself in space and potentially cause accidents during missions. The study conducted by scientists from the National Center for Scientific Research in France involved an experimental test in which subjects experienced artificially created weightlessness on a parabolic flight lasting approximately 20 seconds. Volunteers were provided with special goggles and shown an incomplete image of a cube, then asked to complete the correct geometric shape. Interestingly, in normal gravity, the subjects drew all sides of the cube the same, but in weightlessness, they were unable to accurately complete the task. This experiment suggests that weightlessness, rather than prolonged adaptation to it, is the key factor in distorting perception.
Weightlessness occurs when an object falls freely with no support, meaning that the acceleration of the object and the support is the same as the acceleration of gravity.
There are two types of weightlessness: static and dynamic.
Weightlessness can be utilized to achieve certain technological processes that are challenging or impossible to achieve under normal Earth conditions.
The examination of flames in weightlessness is essential for evaluating the fire resistance of spacecraft and for the development of specialized fire extinguishing methods.
A comprehensive understanding of the process of liquid boiling in space is of utmost importance for the successful operation of a spacecraft carrying tons of liquid fuel.
Artificial gravity can be implemented on spacecraft to counteract the negative effects of weightlessness on the body. This includes limiting muscle activity and other measures.
A groundbreaking study led by Prof. Dominique Martin and his team of French doctors from Bordeaux has successfully demonstrated that surgical procedures can be performed in space under weightless conditions.
So, there is a wealth of information available on the topic of weightlessness, but I believe that my paper provides a comprehensive analysis, considering it from both a physical and medical perspective. Additionally, the abstract includes descriptions of various experiments conducted under weightless conditions by scientists. I think this effectively presents an understanding of weightlessness, its mechanism, the unique aspects of this phenomenon, and its impact on the human body. The combination of the physical and medical viewpoints on weightlessness complements each other, as medicine cannot exist without physics!
Feel free to submit assignments at any time to ➔
Visit the official website of Natalia Valeryevna Brilyonova, a teacher at the Department of Informatics and Electronics of the Ekaterinburg State Institute.





