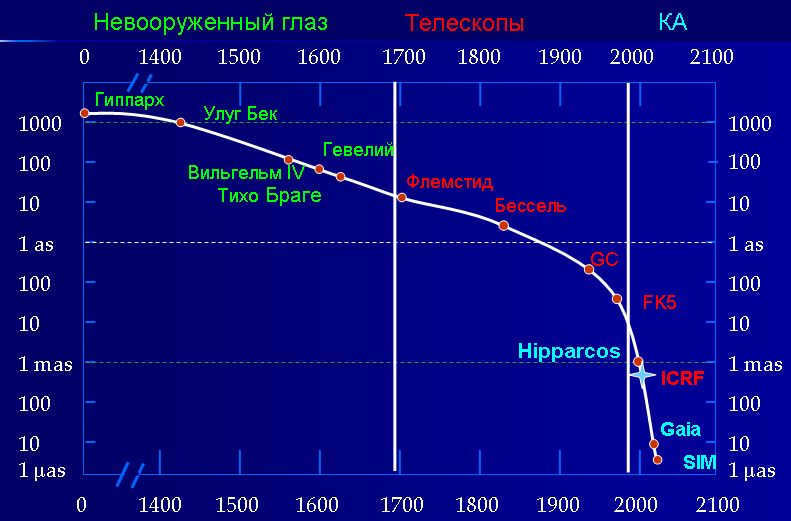
Astrometry serves as the foundation for astronomical observations and the measurement of coordinates and time. The primary objective of astrometry is to establish a reference frame, which corresponds to the inertial reference frame described in Newton’s first law. Throughout history, astronomers have compiled star catalogs to achieve this goal. These catalogs have enabled the discovery of various phenomena, such as the Earth’s axis precession and nutation, the proper motions and parallaxes of stars, and the orbital motion of binary stars. The International Celestial Reference Frame (ICRF), which serves as the basis for modern navigational systems like GPS or GLONASS, relies on observations of quasars – extremely distant objects detected in both radio and optical ranges. The 21st century has witnessed remarkable advancements in astrometry, thanks to the computational power available. Star catalogs with over a billion objects have been created, marking a significant milestone. However, space observations have truly revolutionized astrometry. Two spacecraft have already generated star catalogs of unprecedented accuracy, enabling us to tackle problems that were previously unimaginable. This article provides an overview of the progress in astrometry over the past two millennia, highlighting mass star catalogs and space astrometric projects.
Aims and Historical Background of Astrometry

Always existing, possibly in equatorial and/or galactic coordinate systems. Provided for a specific time period of observation.
Modifications in coordinates over time. Almost always included in contemporary star catalogs.
Distances to stars. Included in specialized catalogs and catalogs of cosmic astrometry.
The brightness of stars on one or more widely accepted scales. Although it is an astrophysical quantity, it is almost always present.
It is often provided to indicate the presence of features in astrometric data.
Star numbers from alternative catalogs.
Beneficial information for combining and comparing data from diverse catalogs.
Miscellaneous data is typically of astrophysical nature, often derived from other catalogs. For instance, radial velocities – velocities of a star along the line of sight obtained from spectral measurements.
Proper motions, also known as proper motions, refer to the velocities at which stellar coordinates change. Having this information enables us to convert star coordinates to a different time period, whether it be in the past or future. By analyzing proper motions, we can gain insights into the movement of stars, both in the vicinity of the sun and throughout the entire galaxy. The credit for the discovery of proper motions goes to the renowned English astronomer Edmund Halley, who observed in 1718 that certain bright stars in the Hipparchus-Ptolemy catalog had noticeably shifted positions compared to other stars (Kiselev, 2002).
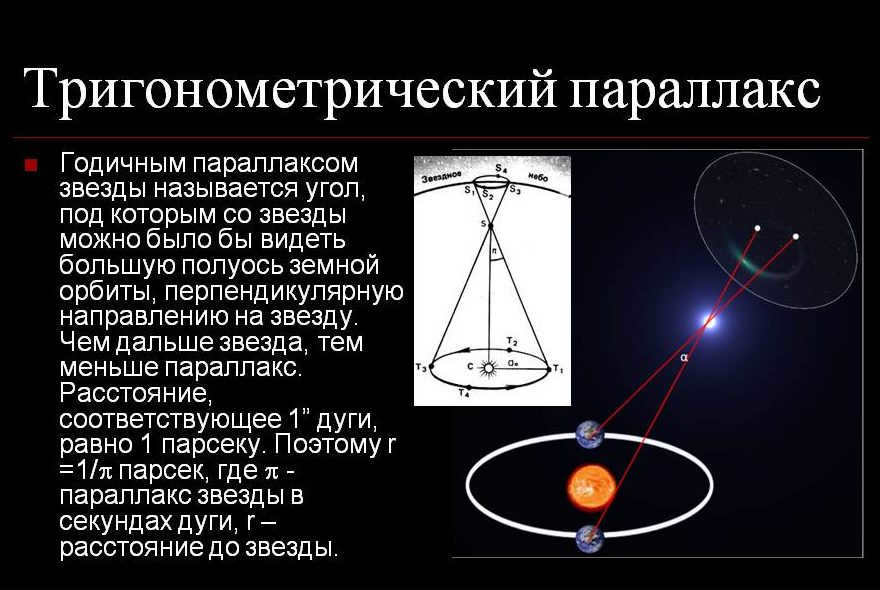
The task of determining the distances to stars has always been a challenging and momentous one. Since ancient times, there have been attempts to observe the parallax shifts of stars caused by the Earth’s orbit around the Sun. The absence of such shifts (due to their minuscule magnitude) was used as an argument against the heliocentric model of the universe. Eminent scientists like Tycho Brahe, Galileo Galilei, and Robert Hooke were involved in the pursuit of detecting parallax in the Renaissance era. It was during this quest that James Bradley discovered the phenomenon of light aberration and the Earth’s axis nutation in 1728, while William Herschel observed the orbital motion of double stars in 1804 (Kovalevsky, 2004).
In 1837, V.J. Struve at the Derpta Observatory, along with Friedrich Bessel at the Königsberg Observatory and Thomas Henderson at the Cape of Good Hope Observatory, were the first to accurately estimate the parallaxes of nearby stars. These measurements were only fractions of a second of arc (Sokolovskaya, 1972). For example, Altair’s parallax was found to be 0.181″ ± 0.094″ by Struve. To better understand the smallness of these angles, we can refer to the following table, which shows the distances and angles at which a ruble coin with a diameter of 2 cm would be visible:
0.1″ – parallaxes of the nearest stars
4,000 km (Moscow – Lisbon)
0.001″ or 1 millisecond of arc (mas) – accuracy of Hipparcos
Determining trigonometric parallaxes (i.e., distances to stars obtained through geometric methods) using ground-based observations is an incredibly time-consuming task. The Earth’s atmosphere places limitations on observing small angles. The highest achievable statistical accuracy for terrestrial observations is typically limited to 0.05″, which would result in a 100% error in parallax determination at a distance of 20 pc. As a result, only 8000 stars had their parallaxes measured with significant uncertainty between 1838 and 1991 (van Altena, 1991+). It is important not to confuse trigonometric parallax with photometric or spectral parallaxes. The latter refers to indirect estimates of star distances based on their astrophysical characteristics. However, in order to determine distances to stars of certain types using a “true” trigonometric method, it is necessary to have this information available. This information can then be used to calculate distances to stars that are beyond the reach of direct trigonometric measurements.
The catalog of one of the greatest observers, Tycho Brahe, from the pre-telescopic era, should be regarded as the final catalog. It was created between 1570 and 1600 (Volodarov, 1996). The precision of the positions in this catalog is approximately 1 minute of arc. It was this particular catalog that enabled Johannes Kepler to formulate his renowned laws, ultimately leading to Isaac Newton’s discovery of the law of universal gravitation.
The observation accuracy during the 18th and 19th centuries gradually improved, eventually reaching an accuracy of around 0.1″. The FK5 Basic catalog, which was published in 1988 by Fricke et al., included 1535 stars. These stars had positions and proper motions that were already at the limit of ground-based observation accuracy, and their observational histories dated back over a century. The FK series catalogs (FK3, FK4, FK5) established the fundamental coordinate system for many years. The methodology of these observations ensured that each star’s coordinates were determined individually, without any dependence on other stars. This is why the fundamental catalogs contain a relatively small number of stars.
In order to expand the scope of the foundational systems to encompass a greater number of stars, relative catalogs such as PPM (Position and Proper Motions) (Röser & Bastian 1988), which included approximately 400 thousand stars but with decreased accuracy, were employed. These catalogs, known as relative catalogs, introduced inaccuracies into the reference system used for propagation.
Radio astrometry
Radio astrometry progressed alongside optical observations, and the advent of ultra-long-base radio interferometers (ULDB, VLBI) greatly enhanced the precision of measurements to 0.001″ (Vityazev, 1999).

As it is widely known, quasars are celestial objects located at vast distances from us. Even if we were to assume unrealistically high velocities of their transverse movement, even then we would not be able to detect their own motion. This means that quasars create a “sphere of fixed stars” that can be used as a frame of reference. However, not all quasars are suitable for this purpose. Some quasars have a variable structure caused by internal physical processes, resulting in a displacement of the center of the radio image. That is why a total of 667 stable radio sources were chosen to create the reference frame, with 212 of them having a detection error.
Determining the distances to faraway celestial objects, like stars, is not feasible through direct measurement. Instead, scientists rely on calculated values based on various parameters of these objects, such as their brightness or the periodic changes in their coordinates. Numerous techniques have been developed to calculate these distances, each with their own specific limitations. In this article, we will delve deeper into the methods scientists employ to determine the distance to stars.
Utilizing parallax
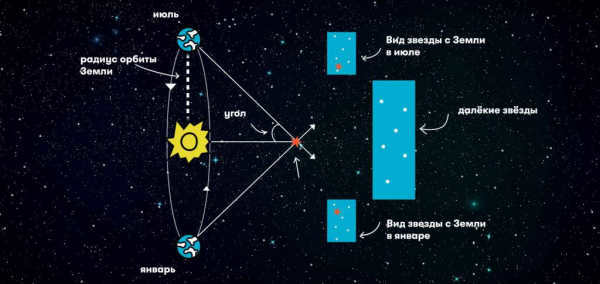
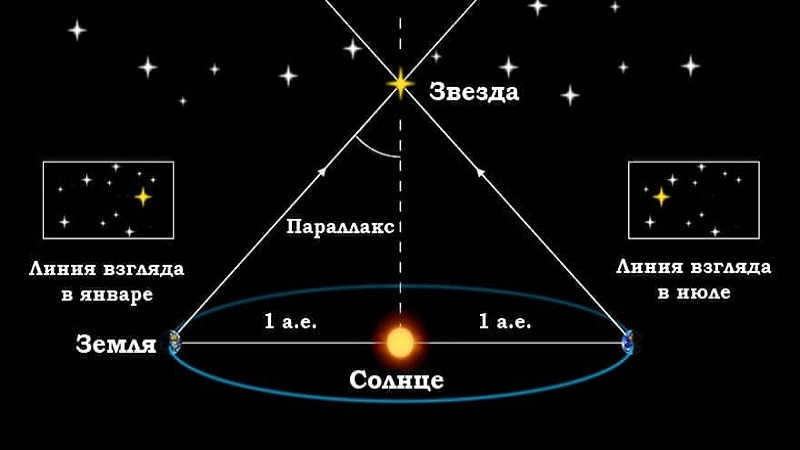
Parallax refers to the apparent shift in the position of an object when the observer’s viewpoint changes relative to a distant background. By determining the distance between observation points (known as the parallax baseline) and measuring the angular displacement of the object, it becomes possible to calculate the object’s distance. A smaller parallax offset indicates a greater distance to the object. Given the vast distances involved in interstellar space, astronomers employ the maximum possible baseline by measuring the position of a star from opposite points in Earth’s orbit. This technique is known as stellar annual parallax.
Units of interstellar distances
The formula obtained is clearly inconvenient, as are the expressions of immense distances in kilometers or astronomical units. Hence, the parsec (abbreviated pc) – derived from “parallax-second” – is widely adopted as a standard unit in stellar astronomy. It represents the distance to a star with an annual parallax of 1 second. Using this unit, the formula simplifies to: r = 1 / p pc.
One parsec is equivalent to 206,265 astronomical units, or roughly 30.8 trillion kilometers. In literature and popular articles, the light-year is often used as a unit of measure. It signifies the distance traveled by electromagnetic waves in a vacuum within a year, unaffected by gravitational fields. A light-year corresponds to approximately 9.5 trillion kilometers, or 0.3 parsecs. Thus, one parsec is approximately equal to 3.26 light-years.
Reliability of the parallactic technique
At present, the precision of parallax measurements carried out from the Earth’s surface enables scientists to calculate the distances to stars that are within a range of 200 parsecs. To enhance the accuracy even further, astronomers rely on observations made by space telescopes.

Therefore, the European satellite named Hipparchus (HIPPARCOS), which was launched in 1989, had two significant achievements. Firstly, it managed to increase the distance to stars up to 1000 pc (parsec). Secondly, it greatly enhanced the accuracy of previously known stellar distances. Another European satellite called Gaia, which was launched in 2013, has further improved the precision of measurements by two orders of magnitude. By utilizing data from Gaia, astronomers are able to determine the distance to stars within 40 kiloparsecs and have high hopes of discovering new exoplanets. The Hubble Space Telescope’s accuracy is comparable to that of Gaia, making it one of the most advanced optical measurement devices available.
Despite the limitations, the annual trigonometric parallax serves as a calibration basis for other methods of determining distances to stars.
Photometry: Understanding Stellar Magnitude
Photometry, a crucial aspect of astronomy, focuses on quantifying the intensity of electromagnetic radiation emitted by celestial objects, particularly in the optical range. Through the use of photometric parameters, scientists can determine the distance to stars and other astronomical entities, including galaxies. An essential concept in photometric analysis is magnitude, also known as brightness, denoted by the symbol m.

Absolute magnitude is a parameter that is calculated to determine the apparent magnitude of a star if it were located at a distance of 10 parsecs. This value is used to establish the relationship between the brightness of an object and its distance from an observer. The absolute magnitudes for the stars mentioned are as follows: the Sun has an absolute magnitude of +4.8, Sirius has an absolute magnitude of +1.4, and Proxima has an absolute magnitude of +15.5. These stars are located at distances of 0.000005, 2.64, and 1.30 parsecs, respectively. This parameter is crucial in understanding the brightness of these celestial bodies.
Spectra and Luminosity of Stars
The total energy emitted by a star (or any other object) per unit time, known as luminosity (L), is referred to by astronomers as the star’s power. Luminosity can be measured using absolute magnitude and is independent of the distance to the star.
Stars are classified into different spectral classes based on their emission spectra, which primarily reflects their temperature (with color being a visual indicator). Generally, stars within the same spectral class have similar brightness levels (with some exceptions that can be identified through their spectra). The relationship between “spectrum – brightness” (or “color – magnitude”) is represented on the Hertzsprung-Russell diagram.
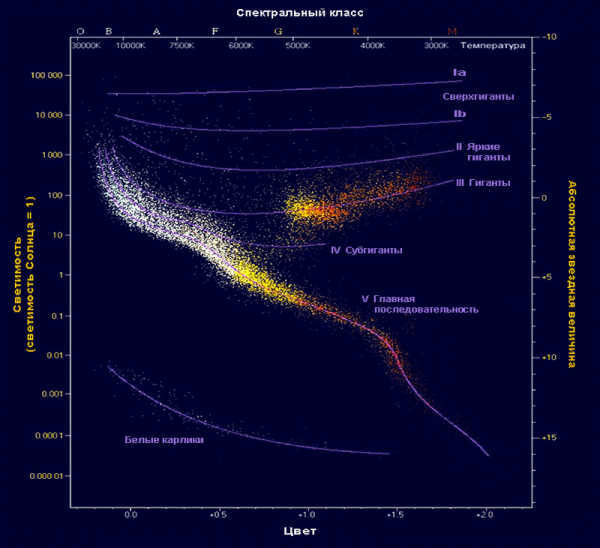
This diagram enables scientists to approximate the absolute magnitudes for different spectral classes of stars. By using a simple relationship between absolute magnitude, apparent magnitude, and distance, we can determine the distance to the stars. The formula is as follows: lg r = 0.2 (m – M) +1. In this equation, r represents the distance, m represents the apparent stellar magnitude, and M represents the absolute stellar magnitude. While this method is not highly accurate, it provides us with an estimation of the distance.
Standard candles used in the field of astronomy
In the vast realm of the universe, there exists a diverse range of stars, each possessing its own unique brightness. This brightness is closely linked to a specific physical attribute, allowing astronomers to accurately gauge the distance to these celestial bodies. By employing the law of inverse squares, astronomers can utilize the decline in brightness to determine the distance to the stars. Remarkably, the smaller the apparent magnitude of a star, the greater its distance from us. Two prime examples of such stars are Cepheids and Type Ia supernovae.
Cepheids, known as variable stars, showcase a fascinating connection between their brightness and pulsation period. By meticulously measuring both the brightness and period of these stars, scientists can effortlessly compute their distance. It is worth mentioning that Cepheids emanate an extraordinary level of brightness, making them easily detectable by modern telescopes even in distant galaxies. This invaluable ability enables astronomers to accurately ascertain the distance between galaxies.

Scientists determine the distance to stars using a method called Type Ia supernovae. These explosions occur in certain types of stars that are part of double systems located nearby. When the star reaches a specific critical mass, it explodes, and the resulting supernova always has the same brightness and brightness decay. This consistent behavior allows astronomers to accurately calculate the distance to the star. The brightness of Type Ia supernovae can be equivalent to the brightness of an entire galaxy, making them useful for estimating distances on a cosmological scale. Astronomers can use these supernovae to estimate distances on a scale of billions of parsecs.
Most individuals are aware of Proxima Centauri, which is the closest star to us. However, do you know which star is currently recognized as the farthest away?
Recently, scientists made a groundbreaking discovery regarding the farthest star within our galaxy. This star is situated outside the spiral disk of the Milky Way, specifically on the outer edge of the galactic halo, within the constellation Libra. It can be found approximately 122,700 pc away, which is equivalent to 400,000 light-years. This star is classified as an 18th magnitude red giant. While there may be more distant stars, it is challenging to accurately determine if they truly belong to our galaxy.

So, which star in the Universe is the most remote from us? It is known as MACS J1149 + 2223 Lensed Star-1, or simply LS1, and it is located 9 billion light-years away from us. The discovery of this star is a remarkable achievement in the field of astronomy. It was found that this star can only be observed from such a great distance because of a gravitational microlensing event in a distant galaxy, which is itself illuminated by a closer cluster of galaxies. Additionally, another method called cosmological redshift was used to calculate the distance. This is how scientists determine the distances to the most distant objects in the Universe, which cannot be observed as individual stars. LS1 serves as a shining and captivating example of how astronomers measure the distances to stars.
Related notes:
When we gaze up at the glittering night sky, it may seem that the stars are not very far away. They appear as tiny specks in the vastness of the universe. However, this is merely an illusion.
In reality, the stars are not small at all, and the distance between them and us is like an unfathomable chasm. Furthermore, the space between the stars themselves is also immense. It may be difficult for us to comprehend, but in the grand scale of outer space, it is not surprising.
In ancient times, people held the belief that all celestial bodies were equidistant from each other. However, as our understanding of space has evolved through scientific study, these views have undergone a transformation.
How do astronomers measure the distance between stars?
Have you ever wondered how astronomers measure the vast distances to the stars? It turns out that they use a different unit of measurement – light years or parsecs – rather than the usual kilometers.
A light year is the distance that a ray of light travels in one year, assuming it maintains a speed of 300,000 kilometers per second. To put it into perspective, one light year is equivalent to 9.5 trillion kilometers.
Using meters and kilometers to measure the distances between stars and the distance from Earth to them is incredibly challenging and problematic.
Furthermore, a megaparsec can serve as a unit of measurement, being one million times greater than the standard one (equivalent to 3,260,000 light years).

Flying star
Methods and techniques for determining star distances
In all aspects of life, humans seek to understand properties, characteristics, and unique qualities. Currently, we possess the ability to calculate any measurement using practical and theoretical approaches.
However, how does one determine the distance to stars? The most commonly employed method for this purpose is the parallax method.
Parallax refers to the apparent shift in an object’s position in relation to the distant background, which directly correlates with the observer’s position.
When it comes to calculating the distance to stars, scientists conduct observations from opposite sides of the Sun, with a 6-month interval between them. This allows them to measure the apparent shift in the position of the star and estimate its distance.
If a star was located 3.26 light-years or 1 parsec away from Earth, its parallax would be 1 second of arc. However, it is unlikely that there are any other stars in such close proximity to our planet. Thankfully, this means that the method of parallax measurement can be used to determine the distances to more distant stars.
Measuring the distance to a star can be done in various ways. One such approach is the photometric method, where the illumination produced by sources of equal strength and power is measured. The obtained value of illumination is inversely proportional to the squares of the distance between the bodies.
Another method involves analyzing the spectrum of objects. By studying the chemical composition, physical characteristics, and spectra of the body, the distance to stars can be determined.
Thus, there are different methods available for determining the distance to the stars.
It is common knowledge that the Sun is the nearest star to us. Hence, the distance to it is often measured in kilometers (149.6 million kilometers), which is equivalent to 8.3 light-minutes in terms of light-years.
The distances between the stars and planets in our solar system are truly astounding. For instance, the planet Pluto is approximately 5 light hours away from Earth, and the closest planet to us (Proxima Centauri) is 4.2 light years away.
Just ponder on the vast amount of knowledge and discoveries that we already possess, and consider how much more there is to unravel about our vast Universe!


Calculating the Distances between Stars
A Brief History
As we construct our staircase to the outer reaches of the universe, we often overlook the foundation upon which it is built. The parallax method provides distances not in standard meters, but in astronomical units, which are based on the Earth’s orbit. However, determining the size of this orbit was not an immediate feat. Let’s take a moment to reflect and descend the cosmic distance ladder back to Earth.
Aristarchus of Samos, who formulated the heliocentric model of the universe over a millennium and a half before Copernicus, was likely the initial proponent of measuring the distance between the Earth and the Sun. He determined that the Sun was 20 times more distant from us than the Moon. However, this calculation, which we now know was a significant underestimate, persisted until the time of Kepler. Despite not directly measuring the astronomical unit himself, Kepler recognized that the Sun must be considerably farther away than Aristarchus had proposed, a sentiment shared by subsequent astronomers.
What are the methods of measuring the distance to the stars and how is a light year defined?

The vast distances between galaxies make measuring them in traditional units like kilometers or miles impractical. Instead, astronomers use specialized units of measurement that are better suited to the immense scale of the cosmos. One commonly used unit is the light-year, which measures the distance that light travels in one year. Another unit is the parsec, which is based on the parallax method of measuring distances.
The astronomical unit is a unit of measurement that is used for objects within the solar system and nearby celestial bodies. It is defined as the average distance between the Earth and the Sun, which is approximately 149,598,100 kilometers (+-
The average distance of the Earth from the Sun is approximately 93 million miles (150 million km), which is roughly equal to 1 astronomical unit (AU). Modern observations have recorded a gradual increase in this value by about 15 cm per year. This phenomenon is believed to be caused by the Sun’s possible loss of mass due to the solar wind.
A light-year is a unit of distance that represents the distance light travels in one year. In terms of meters, it is approximately 9,460,730,472,580,800. When we look at the stars on a clear night, we are actually seeing light that has traveled for many centuries to reach us. Some of these stars may no longer exist.
A parsec, also known as the “parallax of an angular second,” is a unit of distance that is defined as the distance from which the average radius of the Earth’s orbit is seen at an angle of one arc second. In simpler terms, a parsec is equivalent to 3.26 light-years.
The farthest galaxy from Earth is Galaxy UDFj-39546284, located 13.3 billion light-years away, and it appears as a small red dot in an image captured by the Hubble telescope.
In comparison, the closest star to our planet is Alpha Centauri, which is only 4.37 light-years away. However, the distance between Earth and the farthest known galaxy, as of December 2012, is a staggering 13.3 billion light-years. This means that if the sun of this particular galaxy were to extinguish, humanity would not become aware of it for a significant amount of time.
Distances measured in numerical values
Techniques for determining the distances to stars?
The technique of laser positioning and radiolocation

These two contemporary techniques are utilized to ascertain the precise distance to an entity within the solar system. The procedure is as follows: utilizing a powerful radio transmitter, a directional radio signal is transmitted towards the object of observation. The object then reflects the received signal and sends it back to Earth. The time it takes for the signal to travel the path determines the distance to the object. The accuracy of radiolocation is limited to a few kilometers. In the case of laser location, a light beam is transmitted instead of a radio signal, which enables the determination of the object’s distance using similar calculations. Laser location achieves accuracy down to fractions of a centimeter.
The trigonometric parallax method is the most basic way to measure the distance to faraway objects in space. It relies on principles of geometry taught in school and involves the following steps. First, we draw a line (called a baseline) between two points on the Earth’s surface. Then, we choose an object in the sky that we want to measure the distance to and designate it as the vertex of a triangle. We then measure the angles between the baseline and the lines drawn from the selected points to the object in the sky. By using the side length and two adjacent angles of a triangle, we can calculate all of its other properties.
The accuracy of the measurement depends on the chosen baseline. If the star is located far away, the measured angles will be close to perpendicular to the baseline. Any error in measuring these angles can greatly affect the accuracy of calculating the distance to the object. Therefore, it is important to select the most distant points on Earth as the baseline. Initially, the radius of the Earth was used as the baseline. Observers at different locations on the globe would measure the angles mentioned, and the angle opposite the baseline was called horizontal parallax. Later, a greater distance – the average radius of the Earth’s orbit (an astronomical unit) – was used as the baseline. This allowed for the measurement of distances to even more distant objects. In this case, the angle opposite the baseline is referred to as the annual parallax.
This method is not very feasible for studying objects from Earth because the Earth’s atmosphere interferes and prevents the determination of annual parallax for objects located beyond 100 parsecs.
However, in 1989, the European Space Agency launched the Hipparcos space telescope, which enabled the determination of stars up to 1000 parsecs away. Through the data obtained, scientists were able to create a three-dimensional map of the distribution of these stars around the Sun. In 2013, ESA launched the Gaia satellite, which has a measurement accuracy 100 times better, allowing for the observation of all stars in the Milky Way. If human eyes had the same precision as the Gaia telescope, we would be able to see the diameter of a human hair from a distance of 2,000 km.
The method of using standard candles

The standard candle technique is utilized for determining the distances to stars in other galaxies and the distances to those galaxies themselves. It is common knowledge that the further away the light source is from the observer, the fainter it appears. In other words, the brightness of a light bulb at a distance of 2 meters will be four times lower than at a distance of 1 meter. This principle is employed in measuring the distance to objects using the standard candle method. Therefore, by drawing a parallel between a light bulb and a star, it becomes feasible to compare distances to light sources with known luminosities.
Standard candles in astronomy refer to objects whose luminosity, which is equivalent to the power emitted by the source, is known. These objects can be various types of stars. In order to determine the luminosity of a star, astronomers measure its surface temperature based on the frequency of its electromagnetic radiation. By knowing the temperature, which enables us to determine the star’s spectral class, we can then find its luminosity using the Hertzsprung-Russell diagram. Once we have the luminosity values and measure the brightness (apparent magnitude) of the star, we are able to calculate its distance. Utilizing such a standard candle allows us to obtain a general estimate of the distance to the galaxy in which it is located.
Nevertheless, this approach requires a significant amount of effort and does not possess a high level of precision. Hence, astronomers find it more convenient to employ cosmic entities with distinctive characteristics as standard candles, whose luminosity is initially known.
Utilizing Redshifts
This technique, known as the “long-range” method, enables the calculation of distances to the most remote corners of the Universe by measuring redshifts.
Edwin Hubble, the namesake of the renowned space telescope, was able to piece together the larger picture and demonstrate, by comparing the spectra of galaxies with their distances, that the rate at which a galaxy moves away is directly proportional to its distance.
The emergence of cosmological redshift can be visualized as follows: imagine light, an electromagnetic wave originating from a faraway galaxy. As the light traverses through space, space itself expands. Consequently, the wave expands as well. The wavelength of the wave adjusts accordingly. If space has expanded twofold during the journey of the light, then the wavelength of the wave will double.
Hubble himself substantiated the expansion of the Universe through the red shift. Hence, the longer humanity postpones interstellar travel, the greater the distance we will have to cover in the future.

Astronomers from the United Kingdom have devised a remarkably simple and ingenious method for gauging the distances between celestial bodies and our planet. This groundbreaking technique enables scientists to determine the exact distance from Earth to any star within the Milky Way by utilizing its “twin,” which possesses identical dimensions and spectrum.
In a study published in the Monthly Notices of the Royal Astronomical Society, British astronomers detail their innovative approach to measuring distances in outer space. By exploiting the characteristics of a star’s “twin” with matching size and spectrum, researchers can now accurately calculate the vast distances between Earth and distant stars.
"Our concept is incredibly straightforward, it’s astonishing that nobody has conceived of it previously. The further a star is from us, the fainter it will appear in the night sky. If this star and another celestial object have the exact same spectrum, we can utilize the disparity in brightness between them to determine the distance to one of them, given the distance to the other star," explains Jofre Pfeil from the University of Cambridge.
According to Pfeil and his colleagues, astronomers presently compute the distance to distant celestial objects using parallax, which is the measurement of how much the star of interest moves relative to objects behind it as the Earth orbits the Sun and revolves around it.
A technique of such precision is highly accurate, but it is only effective for stars that are relatively close to us, approximately 1-2 thousand light-years away from Earth. As a result, astronomers have only determined the precise distance for 100,000 out of the Milky Way’s 100 billion stars.
Measuring distances to more distant stars is feasible, but current methods, as Pfeil explains, rely on various statistical models and assumptions regarding the star’s temperature or chemical composition, which can introduce significant errors in the measurements.
In an effort to reduce these potential errors and inconsistencies, Pfeil’s team stumbled upon a groundbreaking yet straightforward idea – to identify spectral “twins” of stars among those that have had their parallax accurately measured, and determine their distance based on the difference in their brightness.
Scientists have conducted a test on 175 pairs of stars with the same spectrum, one of which was located far away from Earth, while the other was within a range of 1-2 thousand light years. The distances calculated for the further “twin” stars were almost identical to the results obtained from other techniques, which confirms the potential of this method for determining distances to distant stars.
In the near future, Pfeil and his colleagues have plans to create a catalog of twin stars and also attempt to calculate the exact size of the Galaxy, spanning from one end to the other.
Conversations Between Stars
Exploring the Measurement of Space Distances
You may already be familiar with the terms light-years and parsecs, which are used to describe astronomical distances. These measurements are often associated with objects that are incredibly far from us, such as galaxies that exhibit redshift and are located near the edge of the Universe. In this article, we aim to provide a comprehensive overview of how astronomers measure these vast distances and determine the distances of objects that are beyond our reach, both currently and perhaps indefinitely.
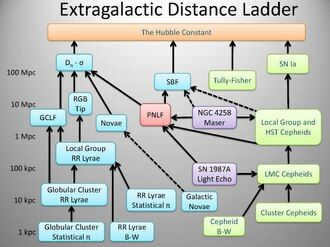
If you find it too cumbersome to read the entire article, we have a simplified representation that effectively presents all the information. This is known as the “cosmic distances ladder”, which illustrates the distances between different celestial bodies – ranging from objects within our Solar System to clusters of galaxies – and, more significantly, the methods employed to measure these distances. In the event that the diagram appears overly intricate, our article will provide assistance in comprehending it.
The ladder of cosmic distances that guides us from the closest stars (below) to the vast structure of the Universe (above). The measurement methods based on the understanding of star formation laws are represented by the color pink, while the methods relying on low-mass and variable stars are depicted in light green. Geometric methods for determining distances are indicated by the color blue, and methods for measuring distances from supernovae outbursts are represented by maroon. Additional methods, such as the Syunyaev-Zel’dovich effect or gravitational waves, are shown in dark green. It is crucial to note that all these methods are interconnected, enabling cross-checking and refinement.
First and foremost, let’s commence by acknowledging that conventional measurements, such as meters or kilometers, are solely utilized in limited aspects of astronomy. This is particularly applicable when examining the closest celestial entities, such as determining the Sun’s radius, the dimensions of Jupiter’s red spot, the characteristics of Saturn’s rings, or distinctive compact objects within the Universe, like neutron stars.
If we consider the distances of objects from us, the largest measurements in kilometers are the distances to other planets in the solar system. This is primarily because these distances were determined using radio radar technology, which involves sending signals of known frequency and recording the time it takes for the signal to bounce back from the surface of a planet. Radars are commonly used on Earth, so there was no need to invent a new method to measure the distance to Venus, for example, and thus, the standard unit of measurement used is kilometers. The laws governing the motion of celestial bodies enable us to determine the distance to more distant bodies based on the distances to closer ones. Therefore, once we know the distance to Venus, it becomes relatively easy to accurately calculate the distance to the Sun. This can be achieved by applying basic trigonometry and visualizing the Earth, Sun, and Venus as the vertices of a right triangle. However, it is worth mentioning that meters and kilometers are not frequently used as distance scales, although an experienced astrophysicist will convert all distances into these units before delivering a popular science lecture.
The next step on the distance scale is the astronomical unit (a.u.), which was previously defined as the average distance from the Sun (remember that the Earth’s orbit is elliptical, so the distance varies throughout the year). Nowadays, the astronomical unit is defined as the distance from the Sun at which a certain gravitational potential is generated, and it is approximately equal to 149597870700 meters (or roughly 150 million kilometers). The measurement of the astronomical unit became possible after Kepler discovered the laws of celestial motion and Huygens observed Venus passing across the Sun’s surface. As a result, the designation “a.u.” is now used in scientific papers to describe the positions of objects in the Solar System (e.g., Jupiter is located at a distance of 4.95 a.u., the asteroid belt has a diameter of 6.4 a.u., and the hypothetical Oort cloud is located 20000-50000 a.u. away from us) or the positions of objects orbiting other stars (e.g., the nearest Earth-like exoplanet, Proxima B, is only 0.05 a.u. away from its star). Occasionally, these units are also used in specific areas of astrophysics, such as the study of protoplanetary disks or nebulae, but in those cases, there must be a central star (or its remnant) from which these units are measured. The value of the astronomical unit is known with an accuracy of +/-3 meters, but it is not sufficient for measuring distances on a truly cosmic scale. To explore distances to other stars and galaxies, a larger measuring tool is needed.
The Parallax Technique
This ancient measuring tool has been in existence for centuries and only requires basic knowledge of trigonometry. It utilizes the parallax method, which can be easily understood by extending your index finger in front of you and alternately closing your left and right eyes to observe the shift in position relative to a more distant object, such as a wall switch. By measuring the positions of stars in the sky during different months, specifically in January and July, we can observe that some stars have shifted while others have remained fixed. We can assume that the stars that have remained in place are much farther away and can serve as reference points, similar to a wall switch. By understanding the Earth’s orbit around the Sun over a six-month period, we can calculate the distance to the stars that have moved across the sky. It’s a simple and straightforward process. Don’t hesitate to grab a piece of paper and a pencil to derive a formula that can convert the angle of star movement into its distance. Along with the provided information, all you need to remember is the definition of sine. We are confident that you will be able to obtain the formula, as it is both simple and elegant in its own way. However, if you still find it challenging, you can find the formula here.
The parsec is defined as the distance at which a star needs to be positioned for the Earth’s orbit to shift by 1 arcsecond, making it a geometric measure.
Astronomical Distance Measurement – A comprehensive term for issues related to determining distances in astronomy.
Creating the Measurement Scale
Trigonometric Parallax Method
The annual parallax is the angle at which the average radius of the Earth’s orbit is observed from the star’s center of mass. The existence of the annual parallax is solely due to geometric laws and nothing else, making this method similar to using a ruler and independent of any specific models. According to the same geometric laws, the distance to the star can be calculated as:

When it comes to practical application, it is widely acknowledged that this assumption does not hold true due to the small angle of parallax. In the case of small angles, the sine of α is approximately equal to α. Thus, in practice, the formula used is:
– where the angle α is measured in radians. As the distance to the star increases, the value of parallax decreases, greatly restricting the range of situations where this method can be applied.
Technique for Estimating Distance from Cepheids and RR Lyrae-type Stars
Cepheids and RR Lyrae-type stars are types of variable celestial objects. While cepheids are considered young, RR Lyrae stars have already evolved from main sequence giants of spectral classes A-F. These stars are characterized by their Pulsation Period – Absolute Stellar Magnitude relationship.
There are two main challenges associated with this estimation method:
- The inherent low luminosity of these objects, making it extremely difficult to detect a Cepheid in a distant galaxy.
- The need to account for light absorption caused by dust, both in calibrating the relationships and in measuring distances.
Type Ia supernovae occur when a white dwarf in a close binary system explodes. Cepheid measurements have revealed that all supernovae of this type have a similar level of brightness at their peak.
The process behind this phenomenon is relatively straightforward: matter from the companion star builds up on the surface of the white dwarf through accretion. Eventually, the pressure from the degenerate gas can no longer support the weight of the accumulated matter, leading to a collapse. The mass of the white dwarf at this moment is known as the Chandrasekar limit. Theorists propose that this limit is what causes the consistent luminosity at the peak of the supernova.
Then, if you observe a sudden burst of light at its highest intensity, you can calculate the distance to the supernova, and by analyzing the lines in the spectrum, determine the redshift. In a similar manner, in 1998, two groups of scientists discovered the phenomenon of the universe’s accelerating expansion.
A technique for determining distance using gravitational lenses
 where d is the distance between the images, and c is the speed of light.
where d is the distance between the images, and c is the speed of light.
By measuring the angular separation between the images and applying principles of geometry, it is feasible to determine the distance to the lens. Nevertheless, the drawback of this approach is the lack of prior knowledge about the lens’s gravitational potential and structure. This can introduce a considerable margin of error in precise measurements.
Relation of the problem of the scale of distance to important issues in astrophysics
Background
References
- Scale of distance in the universe
- Igor DrozdovskyMethods for determining distances to galaxies. Archived from the original source on August 11, 2011.
- Distances to celestial objects (methods of determination) // Physics of Space / edited by R. A. Syunyaev. – 2nd ed. – M .: Soviet Encyclopedia, 1986. – С. 569-573.
How often do we find ourselves captivated by the night sky, mesmerized by the beauty of shimmering stars! They appear to be scattered across the heavens, enticing us with their enigmatic glow. This raises numerous inquiries, but one thing is certain: the stars are situated at significant distances from us. However, what does the term “significant” truly entail? How distant are the stars from our reach? How can we accurately gauge their distance?
Understanding the Definition of the Term “Star”
A star refers to a celestial entity that exists in outer space and undergoes thermonuclear reactions. These reactions involve the fusion of lighter atomic nuclei into heavier ones, driven by the kinetic energy resulting from their thermal motion.
Our Sun serves as a prime example of a typical star.
In essence, stars can be described as colossal luminous spheres composed of plasma, which primarily consists of hydrogen and helium. They form through gravitational compression and boast immensely high temperatures, reaching millions of kelvins in their core. If desired, these temperatures can be converted to degrees Celsius using the formula °C = K-273.15. On their surface, the temperature is comparatively lower, typically measuring in the thousands of kelvins.
Stars hold a significant role in the Universe as they house the majority of the luminous matter found in nature.
With our unaided eyes, we can observe approximately 6000 stars. All of these stars that are visible to us (including those that are observable through telescopes) are part of the local group of galaxies, which includes the Milky Way, Andromeda, and Triangle galaxies.
The star that is closest to our Sun is Proxima Centauri. It is situated 4.2 light-years away from the center of our solar system. When this distance is converted to kilometers, it amounts to 39 trillion kilometers (3.9-10 13 km). A light year is equivalent to the distance that light travels in one year, which is approximately 9,460,730,472,580,800 meters (or 200,000 km/sec.).
What is the method used to determine the distance to the stars?
As we know, stars are located at vast distances from us, appearing as tiny bright dots despite being much larger than our own Sun. Manipulating such large numbers can be inconvenient, so scientists have devised a different, relatively straightforward method to measure the distance to stars, although it may be less accurate. This method involves observing a specific star from both the northern and southern poles of the Earth. During this observation, the star appears to shift slightly in position when viewed from different locations. This shift is known as parallax, which is the apparent change in position of an object against a distant background based on the observer’s viewpoint.
The photo captures an interesting phenomenon known as parallax, where the reflection of the lantern in the water appears to be shifted compared to the stationary position of the Sun.
By knowing the distance between the observation points D (base) and the angle of displacement α in radians, it is possible to calculate the distance to the object.
When it comes to measuring the distance to stars, it is more convenient to utilize the concept of annual parallax. The annual parallax refers to the angle at which the Earth’s orbit, specifically the major semi-axis, is observed from a star located perpendicular to its direction.
Annual parallaxes are measurements used to determine the distances to stars. These distances are commonly expressed in parsecs (ps). A distance with an annual parallax equal to 1 arc second is referred to as a parsec (1 parsec = 3.085678-10 16 m). The nearest star, Proxima Centauri, has a parallax of 0.77″, which means its distance is approximately 1.298 pc. The distance to the star α Centauri is 4/3 pc.
Galileo Galilei proposed that if the Earth orbited around the Sun, we would observe variations in parallax for distant stars. However, at that time, it was impossible to detect the parallactic displacement of stars or accurately determine their distances with the available instruments. Additionally, the Earth’s radius is too small to serve as a reliable basis for measuring parallactic displacement.
By using the method of annual parallax, scientists are able to determine the distances to stars that are no more than 100 parsecs, or 300 light years, away. For stars that are farther than this, other methods are currently used to calculate their distances.
In May 2015, the Hubble telescope made a remarkable discovery when it detected an outburst from the farthest known galaxy to date. The light from this galaxy, which is also the oldest known, took an astonishing 13.1 billion years to reach Earth and be detected by our instruments. This means that the galaxy was formed approximately 690 million years after the Big Bang, according to scientists’ calculations.
It might be logical to assume that the distance to the galaxy EGS-zs8-1 (as it is formally known) is equal to the distance that light would travel in 13.1 billion years, since that is how long the light took to reach us.

Galaxy EGS-zs8-1 holds the record for being the most remote galaxy ever discovered.
However, it is important to consider certain characteristics of the structure of our universe that have a significant impact on distance calculations. One such characteristic is the expansion of the universe, which is happening at an accelerated rate. This means that while light was traveling for 13.1 billion years to reach our planet, the space between us and the galaxy was expanding, causing the galaxy to move away from us at an increasing speed. The figure below provides a visualization of this process.
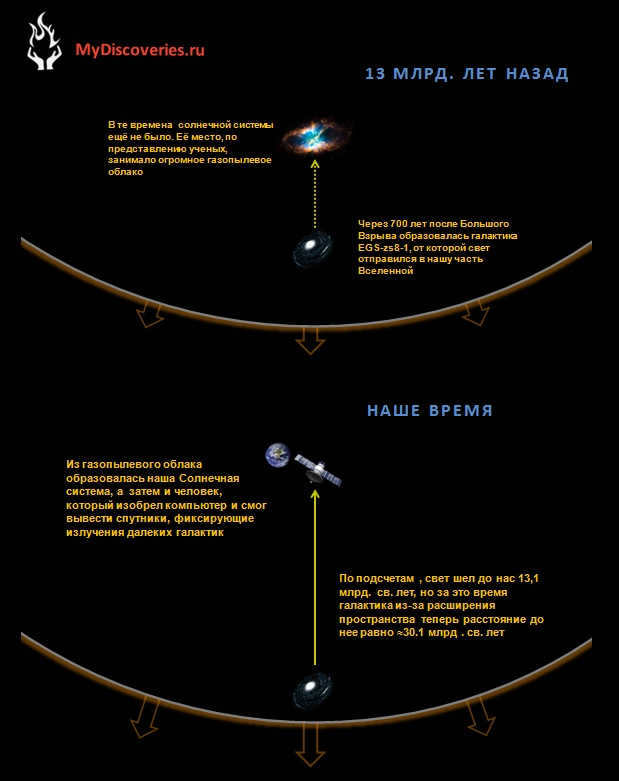
Due to the expansion of the universe, the farthest galaxy known as EGS-zs8-1 is currently situated at a staggering distance of approximately 30.1 billion light-years away from our planet. This achievement stands out as a remarkable feat among all other celestial objects of similar nature. It is worth noting that there are galaxies out there, beyond our reach, whose light is yet to reach us. It is highly likely that the distance record held by the galaxy EGS-zs8-1 will be surpassed in the future.
Here’s something fascinating: there is often a misunderstanding about the magnitude of the cosmos. Its breadth is compared to its age, which is 13.79 billion years. However, this fails to take into consideration the fact that the universe is expanding at an accelerating pace. Based on rough estimates, the visible universe has a diameter of 93 billion light years. Yet, there is also an imperceptible portion of the cosmos that will forever remain beyond our sight. Discover more about the immensity of the universe and imperceptible galaxies in the article “”.
If you come across an error, please select the text and press Ctrl+Enter.
Methods for Measuring the Distance to Objects in Space
How to Determine the Distance to Nearby Planets
Determining the distance to objects in the vast expanse of space can be a challenging task. However, within our solar system, there are established methods for calculating these distances. One such method is using Kepler’s laws, which govern the motion of planets. By applying these laws, we can easily determine the distance to neighboring planets and even asteroids. Additionally, radar measurements provide another reliable way to measure the distance to these celestial bodies. With these techniques, establishing distances becomes a relatively straightforward process.
It is important to note that Kepler’s laws specifically apply within the confines of our solar system.
Methods of Measuring Distances to Stars
When it comes to stars that are relatively close to us, scientists utilize a method called parallax to determine their distance. This involves observing how the position of the star changes as a result of the Earth’s revolution around the sun, in relation to stars that are much farther away. By measuring this parallax with accuracy, we can obtain a fairly precise and direct measurement of the distance.
Another approach to calculating distances is by analyzing the spectrum of the star. By studying the type of star present in the spectrum, scientists can make inferences about its distance based on its true brightness. This method is considered indirect, as it relies on certain assumptions about the star.
Both the parallax and spectrum analysis methods provide valuable tools for measuring distances to stars.
If it is not possible to utilize this method, scientists will attempt to make use of the “distance scale”. In this scenario, they will search for stars within our Galaxy whose brightness has been accurately determined through observations. These stars are referred to as “standard candles”. One example of a standard candle is the Cepheid stars, which exhibit periodic changes in brightness. According to the theory, the rate of these changes is dependent on the star’s maximum brightness.
Distance calculations can be made based on Cepheids
If Cepheids of this nature are discovered in another galaxy and their varying brightness can be observed, their maximum brightness can be determined, allowing for the calculation of their distance from us. Another example of a standard candle is a specific type of supernova explosion, which astronomers believe consistently exhibits the same maximum brightness.
A supernova explosion can serve as a standard candle
Nevertheless, this technique does have its constraints. Subsequently, astronomers employ the redshift observed in galaxies’ spectra.
When the wavelength of light emitted by a galaxy lengthens, it causes the galaxy to appear redder on the spectrum. This phenomenon is known as redshift.
By analyzing redshift, astronomers can determine the velocity at which a galaxy is moving away. According to Hubble’s law, this velocity is directly proportional to the distance between the galaxy and Earth.
We leave the cash register feeling embarrassed, deciding to return at a later time when we have more freedom. The cashier watches us sadly as we walk away. It seems that the flight we were planning to take will not proceed as all the passengers are running away. It turns out that the train is not suitable for interstellar travel. We start to consider the possibility of using a rocket instead. Let’s imagine that a fuel has already been created that allows the rocket to travel at a speed of 20 kilometers per second, which is equivalent to 72,000 kilometers per hour. Now, you and I will calculate the cost-effectiveness of flying a rocket. Since the speed of a rocket is 240 times faster than that of a train, it will take 240 times less time to reach the destination. Let’s divide 15 million by 240 to find out the answer.
Wow! On a rocket, it would take an astonishing 62,500 years to reach the stars! How incredibly far away they are from us!
As we learned from this book, the fastest thing in the world is a beam of light. Every second, it travels a mind-boggling 300,000 kilometers – nearly the same distance from the Earth to the Moon. That’s the kind of journey one would undertake on a beam of light!
If we consider the distance from the Earth to the Sun, also known as one astronomical unit, a light ray would cover that distance in just 8 minutes and 20 seconds. In a day, which consists of 1440 minutes, light travels about 173 astronomical units. Over the course of a year, it would travel a staggering path of 63,000 astronomical units, which is 63,000 times greater than the distance from the Earth to the Sun.
Astronomers have given a name to the distance that light travels in a year – the light-year. This enormous measure of length is used to measure distances in the vast universe.
While the astronomical unit works well for measuring distances within the solar system, it falls short when it comes to measuring stellar distances. Even Proxima, our nearest star, is located 260,000 astronomical units away, and there are stars that are thousands or even millions of times farther from Earth. Trying to measure the distance to such stars in astronomical units is like attempting to measure the distance from Moscow to Vladivostok in millimeters.
Remember this: a year is a unit of time, consisting of 365 and a quarter days; a light-year is a unit of length, consisting of 63,000 astronomical units.
How many light-years away is Proxima? Since there are 63,000 astronomical units in one light-year, and Proxima is located at a distance of 260,000 astronomical units, it means that it is over four light-years away. oskazkah.ru – site
Now, let me share another incredible scenario with you.
An expedition sent from Earth has reached Proxima. The explorers have brought along a powerful radio transmitter and are in communication with Earth.
– Greetings, Earth! Can you hear us? This is Proxima speaking!
– Hello, hello, Proxima! We can hear you loud and clear! How was your journey?
– It went very smoothly! We didn’t encounter any major incidents along the way. We are now awaiting the arrival of personnel and supplies.
– Have you discovered any habitable planets there?
– Not yet. We have temporarily settled on a small planet, but its environment is harsh and the food is not suitable for Earthlings.
– Understood. We will send passenger and transport ships to assist you. This will conclude our conversation. Goodbye, Proxima!
– Goodbye, Earth!
How long do you think this conversation will last? Over 25 years! Each question and its corresponding answer will be separated by more than eight years, due to the fact that radio waves travel through space at the same speed as light.
Even at its colossal speed of 300,000 kilometers per second, light takes over four years to travel from Proxima to us. And there are stars that are unimaginably farther away.
The Universe is vast! It is nearly impossible to comprehend the immense distances that separate us from even the closest stars. Perhaps the stories of trains, rockets, and radio conversations will aid in understanding.
How small the ancient Greeks imagined the Universe to be!
According to one Greek legend, the god Hephaestus dropped an anvil from the sky, and it took nine days and nine nights to reach the Earth. To the ancient Greeks, this distance seemed incredibly vast. However, in reality, the falling object would only travel a distance of 580,000 kilometers in nine days – just a little farther than the distance from the Earth to the Moon.
Even the solar system is thousands of times larger than the entire universe as conceived by the Greeks.
Regardless of how much we gaze up at the dark night sky, mere observations won’t provide us with a response to this query. Clearly, the stars are situated at a great distance – they are farther away than both the sun and moon (as our satellite often obscures the stars), and most likely even farther away than all the planets. However, the question remains: just how far away are they?
Nicolaus Copernicus revolutionized the field of astronomy by introducing a groundbreaking concept. He proposed a theory that challenged the prevailing belief of his time, placing the Sun at the center of the world instead of the Earth. This revolutionary idea not only simplified the understanding of planetary motion but also provided an explanation for some of the peculiarities observed in their behavior. Copernicus postulated that the Earth itself also revolved around the Sun, following a wide orbit that took one year to complete. As a result, the positions of the stars would appear to change when observed from different angles during various seasons, such as spring and fall, when the Earth is in opposite parts of its orbit.
Despite the invention of the telescope, astronomers were unable to solve this question. The minuscule parallaxes presented challenges that surpassed the capabilities of astronomers in the seventeenth and eighteenth centuries. It wasn’t until approximately two hundred years ago, with the introduction of precise observational techniques, that the first parallaxes were successfully measured. These measurements revealed that the stars were astonishingly distant, surpassing even the most pessimistic calculations. Consider this: it takes years for light, which can travel from Earth to the Moon in less than a second and a half, to reach Earth from the stars. Such vast distances are truly unfathomable!
However, within the realm of stars, there are those that are closer to us than others, as well as those that are even farther away.
Let’s use stars – the main pattern of the summer sky – as an example. Two of the three stars – Vega and Altair – are relatively near to us. The journey of light from Vega to Earth takes approximately 25 years. This is equivalent to a distance of 240 trillion kilometers. Altair is even closer – it is one of the Sun’s hundred nearest stars. Its distance is measured at 17 light-years.
Vega, Altair, and Deneb make up the summer triangle, consisting of three stars with similar brightness but varying distances from us. Image: Stellarium
There is a significant distinction in the dimness of the star known as Deneb, which is positioned at the upper left corner of the Summer Triangle. Its distance is so vast that it cannot be accurately measured by conventional means due to the potential for large measurement errors. In order to determine distances for objects in such remote regions of space, astronomers have had to develop specialized and indirect methods. While these methods may not be highly precise for shorter distances, they prove to be quite effective for distances spanning thousands of light years.
Surprisingly, it has been determined that Deneb is located 2,750 light years away. This distance is a staggering 160 times greater than that of Altair and an astonishing 110 times greater than that of Vega!

When comparing the Sun, depicted as a yellow circle, with the blue supergiant star Deneb, it becomes clear that Deneb is a truly remarkable celestial body. In fact, if Vega and Altair were situated in the same position as Deneb, they would be completely invisible to the naked eye. However, Deneb shines brilliantly, emitting less than half the luminosity of Altair. This exceptional brightness sets Deneb apart from other stars. In fact, Deneb’s luminosity is so extraordinary that it is equivalent to 196,000 times the radiation output of the Sun. Just take a moment to gaze at the night sky and you will not find a star that surpasses Deneb’s radiance. With the exception of Rigel, none of the stars visible to the naked eye shine as intensely as this bluish-white star.





