What are the processes that occur within stars, and how can we qualitatively determine the abundance of chemical elements in our surroundings? It is interesting to consider which elements are more abundant and which are less so. We don’t have to look very far for examples: the sands found on beaches and in deserts contain silicon (Si), the air we breathe is composed of oxygen (O) and nitrogen (N), water is made up of hydrogen (H) and oxygen, and fossils and coals contain carbon (C). Ores and minerals provide elements such as iron (Fe), nickel (Ni), magnesium (Mg), and oxygen. These elements are likely to be abundant. However, gold (Au) and platinum (Pt) found in jewelry stores are much more expensive than all of the aforementioned elements, indicating their rarity.
Why is the number of elements exactly as it is? How were they formed and how did they come to exist in our environment?
First of all, let me introduce myself. I am currently a second-year postgraduate student at MIPT, studying physics and astronomy with a specialization in theoretical physics. I have completed both my bachelor’s and master’s degrees in applied mathematics and physics. Currently, my work revolves around astrophysics, specifically focusing on neutron stars.
This article aims to provide a popular science interpretation of our research. As an introductory piece, it will primarily cover the essential concepts necessary for those interested in delving deeper into the subject. However, it will also address and explore the questions that often arise when individuals consume popular science programs, books, and news.
The Origin of Time
Let’s take a step back and delve into the widely accepted cosmological concept known as the Big Bang. At one point in the distant past, there existed an infinitesimally small and dense entity. Why was it a point? Astronomers in the late 1990s made a groundbreaking discovery – the Universe is expanding, and at an accelerating rate. Now, let’s reverse time and envision the Universe contracting. How small would it become? It would shrink down to a singular point known as the singularity, marking the very beginning of time. We are currently about 13.8 billion years removed from that momentous event.
After the initial explosion known as the big bang, the universe started to expand and cool down. At first, the primary building blocks were the quark-gluon plasma. Later on, quarks and gluons combined to create hadrons, which include protons and neutrons, as well as other elementary particles. This phase is referred to as primary nucleosynthesis, as it occurred before the formation of the first stars. Eventually, the universe became a mixture of hydrogen, helium (He), and lithium (Li).
What is important to understand about atomic nuclei? Here is the essential information.
The structure of an atom can be described as follows: it contains a centrally located nucleus, which is composed of protons and neutrons. Surrounding the nucleus are negatively charged electrons, which orbit around it. The charge of an electron is considered as the unit of elementary charge. Unlike protons and electrons, neutrons have no charge and are slightly heavier than protons. It is worth noting that the majority of an atom’s mass is concentrated within its nucleus, accounting for over 99.9% of the total mass.
Atomic nuclei can have varying amounts of neutrons and protons. The composition of a chemical element’s nucleus is determined by the number of protons it contains: hydrogen has 1 proton, helium has 2 protons, iron has 26 protons, and uranium (U) has 92 protons. Now, let’s focus on iron as an example. It has 26 protons, but how many neutrons does it need? The number of neutrons can vary, within certain limits. It could be 30, it could be 40, or any other number. Isotopes are chemical elements with different numbers of neutrons in their nuclei. The positive elementary charge of a nucleus is equal to the number of protons, denoted as Z. The mass of the nucleus is determined by the combined number of neutrons and protons, denoted by the letter A.
For instance, consider the U-235 record (uranium-235 isotope). It indicates that the total number of neutrons and protons in the nucleus is 235. However, since it is uranium, the number of protons should be exactly 92, no more and no less. Therefore, there must be 235-92=143 neutrons. On the other hand, the U-238 isotope has 146 neutrons. Moreover, the properties of these isotopes are distinct! The number of all possible combinations exceeds what is displayed in the Mendeleev table. Each of the 103 chemical elements has more than one isotope. In fact, there are thousands of different nuclei!
New stars are still being formed in the present day. In our very own Milky Way galaxy, approximately 2 solar masses per year (equivalent to 2 brand new Suns every year!) are utilized in the process of star formation. One particular region in our galaxy that is notable for its high rate of star formation is the Kiel Nebula. This stunning nebula was recently observed by the cutting-edge James Webb telescope, a small part of which is even featured on the cover of this review article.
The energy that holds atomic nuclei together
In his book A Brief History of Time, Stephen Hawking stated:
“I was advised that including equations in my book would cut its sales in half. Therefore, I made the decision to exclude any equations. However, I eventually decided to include one equation, which happened to be Einstein’s famous equation. I hope that this will not deter half of my potential readers.”
or
“I was informed that including any mathematical formulas in my book would reduce the number of customers by half. Consequently, I chose not to include any formulas at all. Nevertheless, I did include one equation at the end – the renowned Einstein equation. I trust that it will not discourage half of my potential readers.”
It is important to note that this same equation is essential in explaining most phenomena. Therefore, we will need to present it at the beginning instead of the end, as follows:
The energy at rest of a particle is equal to the product of its mass and the square of the speed of light. To simplify calculations in theoretical physics, it is common to use a value of one for the speed of light (as well as other constants such as the Boltzmann constant), which allows us to measure all velocities in units of the speed of light. In this case, the formula becomes:
We have defined the relationship between mass and energy. What is the significance of this equation? Consider the process of decay of a stationary particle into two smaller stationary particles:
In our system, mass is equivalent to energy. Initially, prior to the decay, there existed a greater amount of energy. In nature, there exists a fundamental principle of energy conservation which asserts that energy within closed systems cannot be created nor destroyed, but can only be transformed. As a result of the aforementioned decay reaction, an equal amount of energy is produced:
Additionally, there cannot exist a scenario in which:
Therefore, the total energy of the decay products cannot exceed the initial energy. Such reactions do not occur without the addition of energy to the initial particle, for instance, through the absorption of a photon:
This type of reaction is already feasible. And the resulting energy is numerically equivalent to:
The converse situation may also arise, wherein:
If there is insufficient initial energy, then additional energy must be obtained from another source. In the event of a reaction, the mnemonic remains consistent: What was before, before minus what it was after. This is the portion that must be performed according to the law of conservation of energy. It represents the energy that is released. If the nuclei are in motion, then each nucleus’s energy is comprised of its resting energy (rest energy) and its energy of motion (kinetic energy). For the sake of simplicity, we have assumed that all nuclei are at rest.
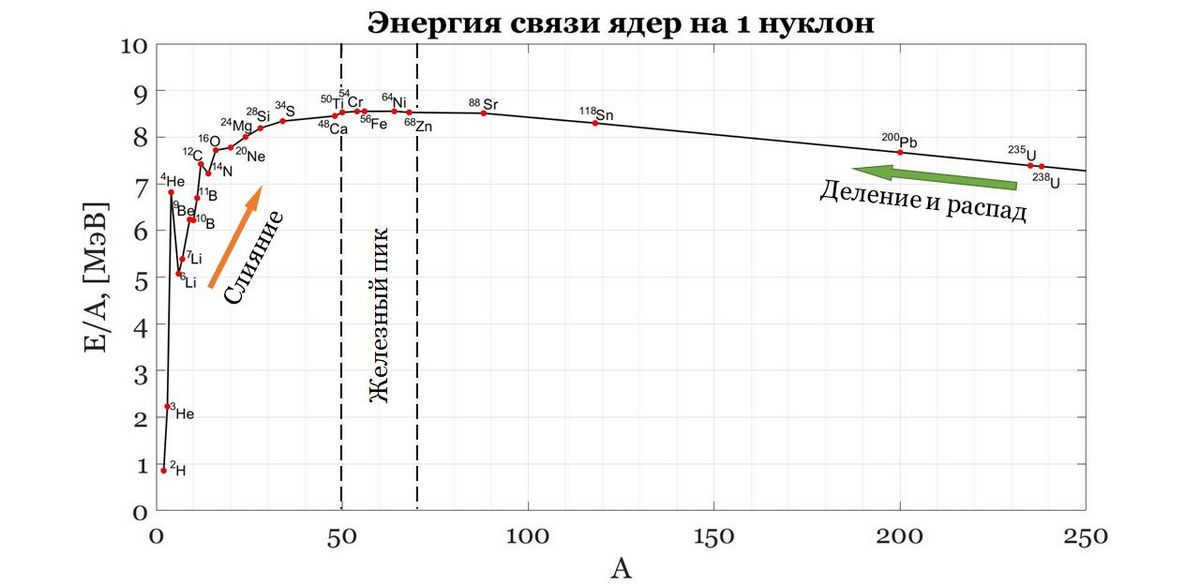
The underlying principle of the statement above is known as the concept of nuclear binding energy. In the natural order of things, objects strive to exist in a state of minimal energy, meaning that processes that release energy are favorable and can occur spontaneously. Quantitatively, nuclear binding energy can be determined by calculating the difference between the rest energies of the individual components (neutrons and protons) and the total energy of the nucleus:
This is the amount of energy required to transfer to the nucleus in order to cause it to split into its individual components. The force of attraction known as binding energy holds the neutrons and protons together. The greater the binding energy, the more energy is needed to break apart the nucleus or, conversely, the more energy is released when the nucleus is formed from (A-Z) neutrons and Z protons. The most preferred “bound state” among nuclei is the Fe-58 isotope of iron (containing 26 protons, since it is iron and 58-26=32 neutrons in the nucleus), which has a binding energy of approximately 8.79 MeV per nucleon (a nucleon refers to both neutrons and protons, and A represents the number of nucleons in the nucleus). It’s worth noting that the electronvolt (eV) is a non-standard unit of energy measurement, but we shouldn’t be concerned about its non-standard nature since the speed of light is already equal to one.
What occurs in stars, such as our Sun? How do the nuclei combine and generate energy? Previously, it was mentioned that specific conditions are required to initiate nuclear reactions: high temperature and density. However, why is this the case?
In nature, there exists the Coulomb force, which causes charges of the same sign to repel each other and charges of opposite signs to attract each other. In its simplest form, in the units of the GHS system, it can be expressed as:
Here, we consider that if the force is greater than zero, the charges repel each other. If it is less than zero, they attract each other. q represents the charges of the particles, while r represents the distance between them.
What is the relevance of that? In order to overcome the repulsive Coulomb force (known as the Coulomb barrier) between two positively charged nuclei, the particles must possess sufficient kinetic energy as they move towards each other. Otherwise, they will simply veer off in different directions, pushing each other away! They need to have some stored energy that they can use to approach each other in spite of the repulsion. This is where the influence of temperature comes into play. The higher the temperature, the faster the gas particles move. Therefore, a high temperature is necessary to accelerate the particles within the medium, allowing them to come into contact with each other as they approach.
Every fusion reaction requires the presence of two or more types of particles. The greater the number of particles of each type in the surrounding medium, the higher the rate of reactions per unit of time. A higher density of the medium also increases the likelihood of reactions. Stars, being naturally dense conglomerates of matter, provide an ideal environment for fusion reactions to occur. When a cloud of gas undergoes shrinkage, its density and temperature rise, along with the pressure exerted by the gas against the surrounding shell. Eventually, this increasing pressure will counteract the force of “self-attraction,” halting the compression process. To ensure the initiation of nuclear reactions, it is crucial for a high temperature to be reached in a timely manner. An example of an object that experienced insufficient compression and failed to attain the necessary temperatures for nuclear reactions to begin is Jupiter, the fifth planet in our solar system.
Now let’s talk about what happens inside stars, specifically in the Sun. Imagine a large amount of hydrogen that is packed tightly together and heated to high temperatures. To start off, two protons combine to form a hydrogen isotope called H-2. This process also produces a positron (an antiparticle to the electron) and a neutrino (one of the fundamental particles). The H-2 isotope then captures another proton to form a helium isotope called He-3, along with the emission of a photon. Next, two He-3 isotopes merge together to create a helium isotope called He-4, as well as two free protons (see Figure 4). Each of these reactions releases a significant amount of energy. It is because of these chains of reactions that life as we know it exists. The Sun transfers this energy to the Earth through the process of radiation. So, the next time you’re sunbathing on the beach, remember that millions of kilometers away, the nuclei of light elements are merging in the Sun and sending warmth your way.
Now let’s examine these processes in relation to the binding energies of the nuclei illustrated in Figure 2. The progressive fusion of a nucleus with neutrons, protons, and other nuclei causes an increase in its mass A and charge Z numbers, pushing it along the curve from left to right (indicated by an orange arrow). At this point, the binding energy of the newly formed elements continues to rise, resulting in the release of energy. However, once the iron peak is reached, the binding energy starts to decrease. From this point onward, no more heat is released. Fusion reactions are only favorable and accompanied by energy release up until the elements of the iron group, which are considered the most stable. Any elements heavier than the “iron peak” release heat through fission (indicated by a green arrow). In other words, if I were to take numerous heavy elements with high Z and A values, expend energy to break them down into free neutrons and protons, and then reassemble only Fe-58 isotopes of iron, I would actually gain energy. This process is similar to what occurs with uranium in nuclear power plants. Under the influence of free neutrons, uranium undergoes nuclear fission, resulting in the formation of smaller nuclei and several free neutrons. These free neutrons then initiate a chain reaction, causing other uranium nuclei to undergo fission as well (as shown in Figure 5). So, what is the purpose of all this? To produce useful energy. However, it is important to note that this is not a simple or risk-free endeavor (as evidenced by events like Chernobyl and Fukushima).
At this point, we have come to understand that there are two methods for creating atomic weapons. One method involves fusing nuclei up to iron, while the other method involves splitting heavy nuclei beyond iron. Alternatively, these methods can be combined. The main objective of this type of weapon is to generate a rapid and substantial release of energy, resulting in a fast-moving shock wave. This shock wave is characterized by changes in pressure, temperature, and density on either side of an imaginary moving surface. The strength of the explosion directly correlates with the intensity of the shock wave and its destructive capabilities. The initial nuclear weapon was developed using the fission of heavy nuclei and was classified as a single-stage weapon. In modern times, we have thermonuclear weapons that utilize both nuclear fission and nuclear fusion. The most powerful nuclear weapons test ever conducted on Earth took place on October 30, 1961, by the USSR on Novaya Zemlya. A video simulation of this test is provided below (I recommend muting the sound).
Furthermore, at the website https://nuclearsecrecy.com/nukemap/, users have the ability to personalize the specifications of the explosive device and virtually deploy it to any desired location. This feature allows individuals to assess the extent of destruction and potential radiation effects, albeit in a purely hypothetical scenario. Overall, I strongly disapprove of the utilization of nuclear weaponry!
The greater the gap between the levels of binding energies of atomic nuclei (Fig. 2), the more energy is released during fusion/separation reactions. It can be observed that after iron, the decline is relatively gradual compared to the steep increase at the beginning. This implies that the energy “exhaust” is more efficient in fusion rather than nuclear fission. This then raises the question, why do we need to split uranium at nuclear power plants when we can simply merge light nuclei, just like in the Sun! However, it’s not as simple as it seems. The Sun has the ideal conditions for this process. The temperature in the Sun’s core reaches tens of millions of Kelvin, which is roughly equivalent to the same number of tens of millions of degrees Celsius. Therefore, we need to recreate these conditions on Earth, fill the vessel with hydrogen, and let it burn while we shut down all nuclear power plants. This approach is known as controlled thermonuclear fusion. The term “controlled” indicates that it is potentially manageable and does not occur explosively like nuclear weapons based on nuclear fusion. The efforts to achieve this level of control are collectively referred to as tokamak (toroidal magnetic coil chamber). The idea is to hold the plasma, which consists of charged particles, not by the walls of the vessel that cannot withstand such temperatures, but by suspending it somehow. Since plasma is composed of charged particles, there must be an electromagnetic field acting upon it. Tokamaks are designed in such a way that the plasma is suspended by the force of the magnetic field exerted on it. This sounds promising. However, there are various physical and engineering challenges to overcome in order to realize this project. Research and development are still ongoing to this day. We have already achieved success in heating up plasma to hundreds of millions of degrees Celsius/Kelvin and maintaining it at that temperature for more than a minute.
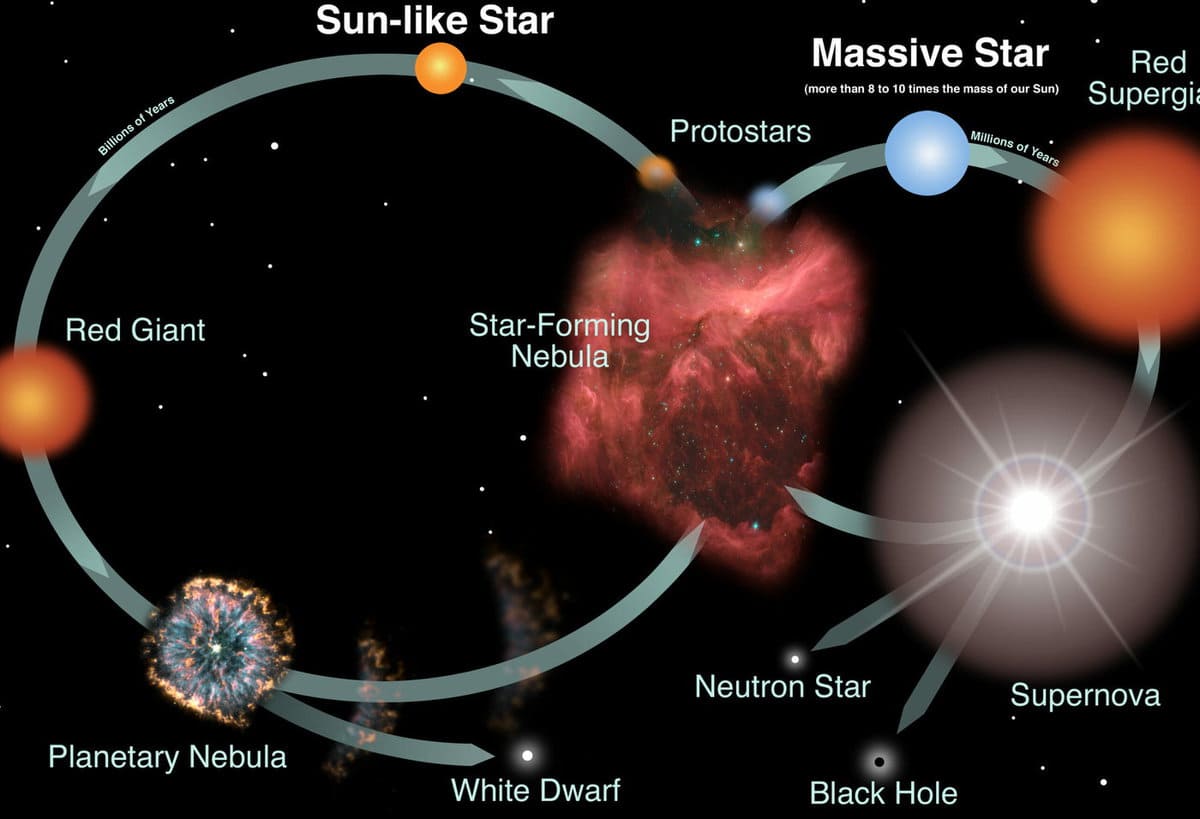
During the final stages of a star’s life, it undergoes either gravitational compression or the shedding of its outer shell by a red giant, resulting in the formation of one of three compact objects: a neutron star, a black hole, or a white dwarf. Some of the star’s matter is expelled into interstellar space and becomes part of the next generation of celestial bodies, including stars, planets, interstellar gas, and even ourselves.
But where is the explanation for the observed abundance of elements? We have now arrived at the formation of chemical elements in the iron group. Where do platinum, gold, and uranium come from? It almost feels like we have been deceived in some way. We have extensively discussed stellar nucleosynthesis throughout most of a star’s life, as well as red giants and compact objects that result from stellar evolution, which have been temporarily set aside.
The prevailing belief is that nuclei heavier than iron were created through what is known as the s- and r-processes, which involve the slow and fast capture of neutrons by nuclei, followed by beta decay. Beta decay is a process in which a neutron is converted into a proton, accompanied by the emission of an electron. In today’s scientific models and theories, the s-process is associated with red giants, while the r-process (which has not been fully understood due to a lack of experimental data on neutron-rich nuclei) is believed to occur in neutron stars. This is a complex topic, and the abundance of information available can often lead to confusion rather than a clear and cohesive understanding.
To further explore this subject, I recommend participating in the poll linked to a potential future post. Thank you for your attention.

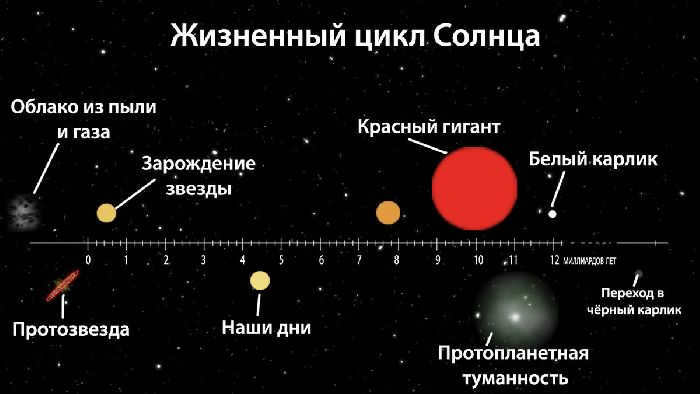
When gazing up into the celestial expanse, one’s eyes are greeted by a multitude of celestial bodies. Among them is our own Sun, a star known as a yellow dwarf in the midst of its cosmic journey. But how did these luminous entities come to be? Let us delve into the intricate life cycle of a star and explore how the size and mass of these stellar entities influence their very existence.
At the beginning
Contrary to what is often depicted in the media, stars do not simply appear fully formed with a series of planets orbiting around them. The process actually takes millions, or even billions, of years, and it all begins with a cloud of interstellar gas.
Each and every star in the sky started its life as a nebula, which is essentially a cloud composed of gas and dust. These nebulae are primarily composed of hydrogen and helium, along with some other trace elements. As time passes, the cloud begins to rotate, forming a center of gravity and attracting all the matter within the nebula towards that point. Gravity continues to increase and become more intense until, at a crucial moment, the pressure causes the nucleus of hydrogen and helium molecules to collapse through a process known as nuclear fusion.
Stars that initiate the process of formation but do not possess enough temperature and compression to instigate nuclear fission are commonly referred to as brown dwarfs. These celestial bodies have a mass approximately twice that of Jupiter, yet they can only be detected from our planet using infrared telescopes.
Once fusion takes place, a star comes into existence – but what unfolds subsequently?
The life cycle of a star
Before we delve into the specifics of each star’s life cycle, it is important to understand the crucial relationship between a star’s mass and its lifespan.
Massive stars, although they may possess a greater abundance of hydrogen, consume it at a much faster rate compared to smaller stars in order to sustain their larger size. On the other hand, smaller stars do not require as much fuel to burn brightly, allowing them to enjoy a longer existence.
It is worth noting that the concept of longevity is relative when it comes to stars, as their average lifespan spans billions of years. For instance, our very own star, the Sun, is estimated to be 4.603 billion years old and is projected to continue burning hydrogen for another 5 billion years. This mass-to-longevity ratio has significant implications for the various types of stars.
O- and B-class stars are among the biggest stars visible in the nighttime celestial expanse. You can classify their lifetime into five distinct phases.

The first stage occurs immediately following the initial merger that creates this new celestial body. The star contains both helium and hydrogen, but it only burns hydrogen at this point. This phase is known as a main-sequence star and is typically the most stable part of its life cycle.
Once the hydrogen supply is depleted, the star enters the second stage. Over millions or billions of years, the core becomes less stable. Instead of burning up helium, the star fuses it with carbon, combining it with elements like iron, sulfur, and neon. The core also transforms into iron during this phase, while the outer helium shell of the star begins to expand.
The third phase lasts for approximately one million years and encompasses a sequence of nuclear reactions that generate additional layers around the iron core of the star.
Phase four is the most tumultuous period in the life cycle of a star. Eventually, the core will implode and produce a massive shockwave known as a supernova. The remnants of the star will expand in all directions, obliterating everything in their path.
From this perspective, there are two distinct pathways by which a massive star can enter the fifth phase. If the remaining material is between 1.5 and 3 times the mass of our Sun, it will undergo further collapse and transform into a neutron star. If it exceeds this threshold, what remains of the star will instead become a black hole.
K- and M-class stars
Low-mass stars do not necessarily have small sizes. When compared to our Sun, most low-mass stars are about 1.4 times its size, or 1.4 solar units. Despite being larger, these stars are significantly lighter than G-class stars like our Sun.
The early stages of a low-mass star’s life are similar to those of high and intermediate-mass stars. They form from dust clouds, undergo nuclear fusion, and exist as part of the main sequence for billions of years. Once these stars deplete their hydrogen fuel, their cores start to collapse, gradually becoming hotter and denser over millions of years. Eventually, the core reaches a temperature of approximately 100 million Kelvin, causing the fusion of helium molecules with carbon. As the star expands, its appearance turns reddish, transforming into a red giant.
Instead of undergoing a supernova explosion, a high-mass star eventually reaches a point where gravity can no longer retain its outer layers. This transformation leads to the formation of a planetary nebula.
After this process, only the star’s core remains, which continues to emit light as a white dwarf. As the white dwarf exhausts its fuel, it eventually cools down and turns into a black dwarf.
G-class stars
We are all familiar with G-class stars – our sun is one of them. It currently serves as the primary star in the sequence, situated in the middle of its life cycle. It remains stable, with the exception of occasional solar flares or coronal mass ejections, and supplies our planet with the necessary heat and light for survival.
The destiny of a medium-mass star, such as our sun, closely resembles that of low-mass stars. It will eventually begin to expand into a red giant – potentially engulfing our planet – and subsequently transform into a planetary nebula, leaving behind a white dwarf.
The future of life on Earth
Although the Sun is still relatively young in astronomical terms, there is no need to worry about it expanding into a red giant within the span of your lifetime or that of your descendants. We can expect another 5 billion years of existence before any drastic changes occur. By that time, it is likely that humanity will have ventured out into the cosmos, leaving behind the distant memory of our home planet.
Stellar evolution refers to the series of transformations that a star goes through over the course of its lifespan, which can span hundreds of thousands, millions, or even billions of years. During these immense timeframes, the changes that take place are truly remarkable.
A star originates from a frigid and sparse cloud of interstellar gas, contracting due to its own gravitational force and gradually assuming a spherical shape. During this compression process, gravitational energy is transformed into heat, causing the object’s temperature to rise. Once the temperature at the core reaches 15-20 million K, thermonuclear reactions commence and the compression ceases. At this point, the object evolves into a fully-fledged star. The initial phase of a star’s life closely resembles that of our own sun, with the dominance of hydrogen cycle reactions. It remains in this state for the majority of its lifespan, residing on the main sequence of the Hertzsprung-Russell diagram, until the fuel reserves in its core are depleted. When all the hydrogen in the star’s core is converted into helium, a helium core forms, and thermonuclear fusion of hydrogen continues at the outer layers of the core.

During this phase, the star undergoes significant transformations. Its brightness increases, the outer layers expand, and the surface temperature decreases. As a result, the star evolves into a red giant, which occupies a specific position on the Hertzsprung-Russell diagram. This phase is relatively short compared to the star’s main sequence. Once the helium core accumulates a substantial amount of mass, it becomes unable to withstand its own gravitational force and starts contracting. If the star is sufficiently massive, the rising temperature can trigger further nuclear fusion reactions, converting helium into heavier elements such as carbon, oxygen, silicon, and ultimately iron.
Studying stellar evolution is not feasible through the observation of a single star – numerous changes in stars occur at such a slow rate that they may not be detectable even after centuries. Hence, scientists analyze multiple stars, each representing a distinct stage in its life cycle. The utilization of computational modeling for understanding stellar structure has gained significant popularity in the field of astrophysics in recent decades.
Thermonuclear fusion occurring within the core of celestial bodies [ ]
It was determined by 1939 that the fusion process occurring within the interior of stars is the source of stellar energy [2]. The majority of stars emit radiation due to the combination of four protons into a single alpha particle through a series of intermediate steps. This fusion process can occur through two primary paths: the proton-proton (p-p) cycle and the carbon-nitrogen (CN) cycle. In stars with lower mass, the first cycle primarily provides the energy release, while in heavier stars, the second cycle is responsible. The nuclear fuel within a star is limited and continuously depleted through radiation. The combination of thermonuclear fusion, which releases energy and alters the composition of the star’s matter, gravity, which causes compression and also releases energy, and surface radiation, which carries away the released energy, are the main driving forces behind stellar evolution.

Maturation [ ]
After a certain period of time, ranging from millions to tens of billions of years (depending on the initial mass), a star exhausts the hydrogen reserves in its core. This process occurs at a much faster pace in larger, hotter stars compared to smaller, cooler stars. The depletion of hydrogen leads to the cessation of thermonuclear reactions.
Without the counterbalancing pressure from these reactions, the star’s internal gravity causes it to contract once again, similar to its earlier stage of formation. However, this time, the temperature and pressure increase to a much higher degree. The collapse continues until helium thermonuclear reactions commence, which typically occurs at a temperature of around 100 million K.
The process of thermonuclear fusion reigniting at a higher intensity triggers a tremendous expansion of the star. The star undergoes a significant increase in size, becoming highly voluminous and loose, expanding by approximately 100 times its original size. Consequently, the star transitions into a red giant phase, characterized by the burning of helium which persists for several million years. It is worth noting that the majority of red giants exhibit variability in their brightness.
The subsequent events following this phase are contingent upon the mass of the star.
Stellar Evolution in the Final Stages [ ]
Aging Low-Mass Stars [ ]
When a star has a mass that is less than 0.5 times the mass of the Sun, it is unable to undergo the process of converting helium even after hydrogen reactions have stopped in its core. This is because the mass of such a star is too small to create enough gravitational contraction to initiate the “ignition” of helium. These types of stars are known as red dwarfs, like [4]. Once the thermonuclear reactions in their cores have ceased, they will gradually emit weaker amounts of infrared and microwave radiation as they cool down.
Stars of average size [ ]
It remains uncertain what exactly occurs after this point, however, the events that transpire within a mere matter of seconds ultimately result in the astonishingly powerful detonation of a supernova star [ ].source not provided for 3276 days].
Strong streams of neutrinos and a rotating magnetic field expel a significant portion of the star’s accumulated material [source not provided 3276 days], known as seedling elements, which include iron and lighter elements. The scattered matter is bombarded by neutrons that escape from the core of the star, capturing them and thus generating a range of elements that are heavier than iron, including radioactive elements like uranium (and potentially even californium). As a result, supernova explosions account for the presence of elements heavier than iron in interstellar matter. However, this is not the sole method of their formation, as evidenced by the neutrino streams that carry matter away from the dying star [source not provided 3276 days] and into interstellar space. Subsequently, as this supernova material cools and traverses through space, it may collide with other cosmic debris and potentially contribute to the formation of new stars, planets, or satellites.
The study of supernova formation is still ongoing, and there is currently no clear understanding of the processes involved. Additionally, the fate of the original star remains uncertain. However, two possibilities are being considered: the formation of neutron stars or black holes.
Neutron stars [ ]
It is known that in certain supernovae, the intense gravitational forces within the supergiant star cause electrons to merge with protons, resulting in the formation of neutrons. This process, known as neutronization, eliminates the electromagnetic forces that separate neighboring atomic nuclei. As a result, the core of the star transforms into a dense sphere comprised of atomic nuclei and individual neutrons.
The Formation of Black Holes
Not all stars, after going through the phase of a supernova explosion, transform into neutron stars. In the case of a star with a significant mass, the collapsing process will persist, and the neutrons will start collapsing inward until the radius becomes smaller than the Schwarzschild radius. At this point, the star transforms into a black hole.
There are still several unresolved questions. Specifically, until recently, the primary question remained unanswered: “Do black holes actually exist?”. After all, in order to definitively determine if an object is a black hole, it is necessary to observe its event horizon. However, this is impossible based on the definition of a horizon alone. Nevertheless, with the use of ultra-long-baseline radio interferometry, it is possible to study the metric around the object by observing the movement of gas in that area, as well as detect rapid, millisecond-scale variability in stellar-mass black holes. These characteristics, observed in a single object, would ultimately serve as conclusive evidence that the object in question is indeed a black hole.
At present, the direct observation of black holes is not possible. However, their mass can be estimated through various indirect methods. One approach is to study the luminosity of the nuclei of active galaxies, which provides an estimation of the mass of the accreting object. The mass can also be determined by analyzing the rotation curve of the galaxy or by studying the frequency of stars near the object using the virial theorem. Another method involves observing the emission lines of gas from the central region of active galaxies, which allows for the measurement of the rotation velocity. In blazars, this velocity can reach tens of thousands of kilometers per second. In many galaxies, the mass of the central object is determined to be too large to be anything other than a supermassive black hole. There are objects that show clear signs of matter accretion, but do not exhibit any specific radiation caused by shock waves. This suggests that the accretion process is not hindered by a solid surface, but rather proceeds in a region with a very high gravitational redshift. According to current concepts and data (as of 2009), no stationary object other than a black hole is capable of existing in such a region.
Related Articles [ ]
Additional Information [ ]
- ↑The Institute of Physics named after Kirenskii SB RAS – The Strohsky Institute of Physics. Kirensky SB RAS – The Structure and Evolution of the Universe
- ↑Shklovsky I. S. Stars: their origin, lifespan, and demise. – Moscow: Nauka, Main Editorial Office of Physical and Mathematical Literature, 1984. – 384 p. (see ISBN )
- ↑ 3,03,1 Burrows, A., Hubbard, W. B., Saumon, D., Lunine, J. I.. An expanded collection of models for brown dwarfs and very low mass stars // (in Russian) rec. scientific journal. – 1993. – Vol. 406. – No. 1. – P. 158-171. – See P. 160.
- ↑ 5.05.1 Paul A. Crowther, Olivier Schnurr, Raphael Hirschi et al. The R136 star cluster contains a number of stars with individual masses that greatly exceed the accepted stellar mass limit of 150 M⊙ // Monthly Notices of the Royal Astronomical Society: a peer-reviewed scientific journal. – 2010. – Vol. 408. – No. 2. – pp. 731-751.. – arΧiv:1007.3284.
- ↑ 6.06.1Paul Crowther, Olivier Schnurr, Henri Boffin.A Star with a Mass of 300 Solar Masses Uncovered (English) . ESO (July 21, 2010). – A 300 solar mass star discovered (Mon. Not. R. Astron. Soc. (English) ). Checked January 10, 2012.Archived from the original source on May 4, 2012.
References [ ]
Formation – Main sequence – Asymptotic branch of giants – Planetary nebula – Bright blue variables – Wolf-Raye star – Supernova star – Hertzsprung-Russell diagram
Red giant – Blue supergiant – Mercury-manganese star – Variable star
List of stellar names – List of largest stars – List of nearest stars – List of brown dwarfs – Chronology of stellar astronomy
In the mid-twentieth century, two hypotheses for the formation of chemical elements emerged:
- Chemical elements are formed in the stars of our Galaxy and then ejected into interstellar space, supplying material for the subsequent evolution of the chemical composition of the Universe;
- Chemical elements were created during the early hot phase of the expanding Universe at the pre-stellar stage.
According to current understanding, the pre-stellar stage of the Universe’s evolution is when the two most abundant chemical elements, hydrogen (approximately 90%) and helium (approximately 9%), were formed. All other elements were produced through the transformation of these elements within stars.
13.1 The distribution of chemical elements
Nucleosynthesis refers to the natural formation of atomic nuclei. These nuclei are created through nuclear reactions that occur at various stages of the Universe’s evolution. There are three primary mechanisms of nucleosynthesis:
- Cosmological (primary or pre-stellar) nucleosynthesis,
- Nucleosynthesis in stars and stellar explosions,
- Nucleosynthesis due to cosmic rays.
The abundance of elements is measured by the number of nuclei of a specific element in a substance, relative to a certain number of nuclei. The prevalence of silicon (Si) is considered to be 10^6. Notable characteristics of elemental abundance include:
- The Universe is primarily composed of hydrogen, which accounts for 91% of all atoms.
- Helium is the second most abundant element, comprising approximately 9% of all atoms.
- There exists a profound minimum that corresponds to lithium, beryllium, and boron.
- Following this, there is a steep increase in the abundance of carbon and oxygen.
- After the oxygen peak, there is a sharp decrease that reaches scandium (Z = 21, A = 40).
- An increased abundance of elements in the iron region (“iron peak”) is observed.
- After A ≈ 60, the decrease in abundance becomes smoother, with local maxima occurring around the magic numbers of protons or neutrons: 50, 82, and 126.
- In general, even-numbered nuclides (even Z and N) have a higher abundance compared to neighboring nuclides with an odd number of nucleons.
- The lightest stable isotopes of several chemical elements (such as 74 Se, 73 Kr, 92 Mo, and 96 Ru) have an abundance two orders of magnitude lower than their neighboring heavier stable isotopes.
Figure 13.1 shows the logarithm of the abundance of nuclides in the Universe plotted against their mass number, based on the data from E. Anders and N. Greaves (1989).
13.2. Nucleosynthesis before stellar formation
When the temperature was much higher than 1010 K (and the kinetic energies were much greater than 1 MeV), neutrons and protons were in a state of thermodynamic equilibrium due to weak interaction reactions.
The probability of a state with energy E being formed is described by the Gibbs distribution.
In conditions of thermodynamic equilibrium, the ratio of neutrons to protons is determined by the difference in mass between the neutron and proton.
Approximately 2 seconds after the occurrence of the Big Bang at T ≈ 10 10 10 K, the average kinetic energies of particles dropped below 1 MeV. At this point, the equilibrium ratio of neutron and proton concentrations nn/np reduced to about 1/6, and prior to the start of primary nucleosynthesis, this ratio mainly decreased due to neutron decay.
Around a minute following the Big Bang, conditions for the synthesis of more complex lightest nuclei appeared in the Universe. As a result of the annihilation of particles and antiparticles, there were 10^9 photons for every 1 proton. The formation of deuterium became possible when the photon energy fell below the photon splitting energy of deuterium, which is 2.2 MeV. The basic chain of reactions for helium synthesis is as follows:
2 H + 3 H → 4 He + n (Q = 17.59 MeV),
2 H + 3 He → 4 He + p (Q = + 18.35 MeV).
Each reaction provides the released energy Q.
Within a time frame of 1-3 minutes, the majority of neutrons became bound in 4 He. This resulted in a decrease in the temperature and density of the Universe, causing a halt in the fusion reactions.
Fig. 13.2 illustrates the changes in the yield of the lightest nuclei and the baryonic density (shown as a dashed line) during the stage of cosmological nucleosynthesis.
13.3. Nuclear fusion in stars
- Hydrogen fusion. This is one of the primary mechanisms that sustain the prolonged release of energy in stars. During the fusion of hydrogen, four hydrogen nuclei combine to form four helium nuclei. This process can occur through the pp-chain or through cyclic nuclear reactions involving heavier nuclei such as carbon, nitrogen, oxygen, neon, and others acting as catalysts. It also includes proton-proton reactions that produce light elements.
- Helium fusion. Once helium accumulates in a star, gravitational forces compress the helium nucleus, causing it to become dense and hot. This leads to the initiation of helium burning, resulting in the formation of carbon-12, oxygen-16, and neon-20 nuclei.
- α-process. The α-process involves the step-by-step addition of α-particles to the nucleus of 20 Ne, resulting in the formation of nuclei such as 24 Mg, 28 Si, 32 S, 36 Ar, and 40 Ca. This process accounts for the increased abundance of elements with the formula Nα, where α represents the nucleus of 4 He and N is an integer.
- e-process. The e-process occurs when elements near the iron maximum are created under conditions of thermodynamic equilibrium.
- s-process. The s-process is responsible for the formation of nuclei heavier than iron through the gradual capture of neutrons. The rate of the s-process is slower than the rate of β-decay of radioactive nuclei that are formed during neutron capture. The s-process typically takes anywhere from 10^2 to 10^5 years to occur and is responsible for the abundance peaks of elements at A ~ 90, 138, and 208.
- The r-process involves the rapid sequential capture of neutrons at a rate significantly higher than the β-decay rate of resulting radioactive nuclei, leading to the formation of nuclei heavier than iron. This process has a characteristic time of 0.01-100 seconds. The r-process is responsible for the appearance of peaks in the elemental abundance curve at A = 80, 130, and 195.
- The p-process is responsible for the formation of the lightest isotopes of nuclei. It involves positron formation and capture, proton capture, neutron photoreduction, and (p,n)-reactions.
- The X-process involves the splitting reactions of cosmic rays, resulting in the formation of isotopes 6,7 Li, 9 Be, 10,11 B.
Combustion of hydrogen in the reaction 4p → α is shown in Figure 13.3.
The spectrum of neutrinos produced in the Sun as a result of hydrogen burning in reaction
4p → α and in the CNO cycle is illustrated in Fig.13.4.
13.5. CNO cycle
12 C + p → 13 N + γ (Q = 1.94 MeV),
13 N → 13 C + e + + νe (Q = 1.20 MeV, T1/2 = 10 min),
13 C + p → 14 N + γ (Q = 7.55 MeV),
14 N + p → 15 O + γ (Q = 7.30 MeV)
15 O → 15 N + e + + νe (Q = 1.73 MeV, T1/2 = 124 с),
15 N + p → 12 C + 4 He (Q = 4.97 MeV).
15 N + p → 16 O + γ (Q = 12.13 MeV),
16 O + p → 17 F + γ (Q = 0.60 MeV),
17 F → 17 O + e + + νe Q = 1.74 MeV, T1/2 = 66 c),
17 O + p → 14 N + α (Q = 1.19 MeV).
17 O + p → 18 F + γ (Q = 6.38 MeV),
18 F → 18 O + e + + νe (Q = 0.64 MeV, T1/2 = 110 min),
18 O + p → 15 N + α (Q = 3.97 MeV).
13.6. α-process in stars
4 He + 4 He + 4 He → 8 Be + 4 He → 12 C* → 12 C + γ
12 C + α → 16 O + γ (Q = 7.16 MeV),
16 O + α → 20 Ne + γ (Q = 4.73 MeV),
20 Ne + α → 24 Mg + γ (Q = 9.31 MeV),
24 Mg + α → 28 Si + γ (Q = 9.98 MeV),
28 Si + α → 32 S + γ (Q = 6.95 MeV).
Figure 13.6 α-Process in stars. The lower levels of 8 Be, 12 C, and 16 O nuclei are given.
13.7: Generation of nuclei in the vicinity of A ≈ 50, e-process
Figure 13.7: Network of nuclear reactions resulting in the production of elements ranging from helium to germanium.
13.8 Generation of heavy elements
s-process. Generation of heavy elements through the reaction (n, γ):
If the nucleus (A+1, Z) formed in a neutron capture reaction is unstable, then at low neutron densities it is more probable that this nucleus will undergo β – – decay rather than capturing the next neutron. The condition for the development of such a process is usually expressed as the ratio τnγ >> τnβ, where τnγ represents the lifetime of the nucleus before neutron capture. This type of process is referred to as a slow or s-process. The characteristic values of τnγ in this process are in years.
Fig. 13.8. The s-process is responsible for the formation of elements with atomic numbers ranging from 26 to 33.
If the density of neutrons reaches values of 10^19 – 10^20 cm-3 , the lifetime of the nucleus before it captures a neutron, τnγ, decreases to approximately 10^-3 s. As a result, the rate of neutron capture by the nucleus becomes much higher than the rate of its β-decay, τnγ nβ. Neutron capture continues until the reaction rate (n,γ) becomes lower than the β-decay rate of the isotope. During this process, the nucleus has enough time to capture around 10-20 neutrons before it undergoes β-decay. This type of process is known as the rapid or r-process.
The line on the NZ-diagram that represents the formation of nuclei in the r-process is shifted away from the stability valley (which is the track of the s-process) toward neutron-depleted isotopes.
Figure 13.9. The s- and r-processes follow different paths (tracks) for the formation of nuclei.
Fig. 13.10. The primary stages of the development of a massive star (M > 25M☉)
| Mass, M☉ | Nuclear fusion reactions in stars of various masses |
| 0.08 | None |
| 0.3 | Hydrogen combustion |
| 0.7 | Hydrogen and helium combustion |
| 5.0 | Hydrogen, helium, carbon combustion |
| 25.0 | All fusion reactions with energy release |
Fig. 13.11. The development of a massive star (M > 25M☉).
Fig. 13.12. The composition of elements in a star with a mass of 25M☉ as a function of the mass of the inner region.
13.9. Cosmic Ray-induced Nucleosynthesis
Isotopes Li, Be, B are created through splitting (spallation) reactions when galactic cosmic rays interact with interstellar matter:
1) The light component of cosmic rays (fast protons and α-particles) split heavy nuclei of the interstellar medium, resulting in the formation of isotopes Li, Be, B, which then mix with the interstellar medium;
2) Fast nuclei C, N, O, which are part of cosmic rays, collide with H and Ne nuclei, transforming into Li, Be, and B.
| Figure 13.13. Primary cosmic rays: the main constituents. | Figure 13.14. Secondary particle cascade in Earth’s atmosphere. |
13.10. Quark-gluon plasma
Quark-gluon plasma, also known as QGP, is a state of matter that is believed to have existed in the early universe, just a few microseconds after the Big Bang. It is a state in which quarks and gluons, which are the fundamental particles that make up protons and neutrons, are no longer confined within individual particles, but instead are free to move and interact with each other.
The formation of quark-gluon plasma is thought to occur at extremely high temperatures and densities, such as those found in the early universe or in high-energy particle collisions. These conditions cause the strong force, which normally binds quarks and gluons together, to weaken and eventually break down, allowing the particles to move freely.
Quark-gluon plasma is a unique state of matter that is not found under normal conditions on Earth. It has properties that are similar to both a liquid and a gas, but it also exhibits behavior that is distinct from either of these states. Scientists study quark-gluon plasma to gain a better understanding of the fundamental forces and particles that make up the universe, as well as to learn more about the early stages of the universe’s evolution.
In recent years, experiments at particle accelerators such as the Relativistic Heavy Ion Collider (RHIC) and the Large Hadron Collider (LHC) have been able to create and study quark-gluon plasma in the laboratory. These experiments have provided valuable insights into the properties of this unique state of matter and have confirmed many of the theoretical predictions about its behavior.
The study of quark-gluon plasma is an active area of research in the field of particle physics, and scientists continue to investigate its properties and behavior. It is hoped that further study of this unique state of matter will help to deepen our understanding of the fundamental nature of the universe.
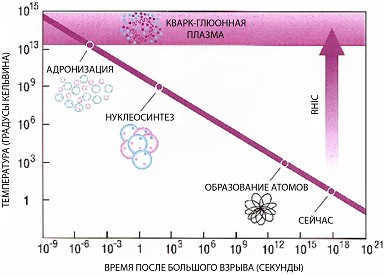
At extremely high temperatures and densities of hadronic matter, a unique state of matter known as quark-gluon plasma is formed. This exotic state is believed to have existed in the first 10^-5 seconds after the Big Bang under natural conditions. It is speculated that similar conditions for the formation of quark-gluon plasma may also exist at the core of neutron stars.
The transition to the quark-gluon plasma state is considered to be a first-order phase transition, occurring at a critical temperature of approximately 200/k MeV (where k is the Boltzmann constant equal to 8.62 x 10^-11 MeV/Kelvin). The production of quark-gluon plasma can be achieved through the collision of relativistic heavy ions, which generates extreme temperatures and densities.
However, one of the main challenges in studying quark-gluon plasma is its identification. Scientists rely on various observables such as the production of anomalous lepton pairs, photon emissions, and the unusually high yield of strange particles to infer the presence of quark-gluon plasma.
Goals
13.1. Calculate the amount of solar neutrinos reaching the Earth’s surface.
13.2. Explain why nuclear fusion reactions in stars start with the reaction p + p → d + νee due to weak interaction, rather than the reaction p + n → d + γ due to electromagnetic interaction or other reactions due to strong interaction.
13.3. Find out the rate at which the Sun is losing its mass, given that the specific power of solar radiation incident on the Earth is wud = 0.14 W/cm 2 . If this rate continues, how long will the Sun exist?
13.4. Calculate the amount of mass δM lost by the Sun over the last t = 10 6 years, given that the Sun’s luminosity W = 4-10 33 erg/s and the Sun’s mass M = 2-10 33 g.
13.5. The formula for determining the gravitational radius of an object with mass M is rG = 2GM/c2, where G is the gravitational constant. Let’s calculate the gravitational radii for the Earth and the Sun.
13.6. We need to calculate the energy released in the p-p chain. The answer is E(pp) = 25.8 MeV.
13.7. In addition to the CNO-cycle in massive stars, there is a hydrogen combustion reaction cycle starting with 24 Mg. Let’s construct the corresponding reaction chain (Mg-Al cycle).
13.8. In addition to the CNO-cycle in massive stars, there is a hydrogen combustion reaction cycle starting with 20 Ne. Let’s construct the corresponding reaction chain (Ne cycle).
13.9. Determine the amount of energy, E(CNO), released in the carbon-nitrogen Bethe cycle:
12 C + p → 13 N + γ
13 N → 13 C + e + + + νe
13 C + p → 14 N + γ
14 N + p → 15 O + γ
15 O → 15 N + e + + νe
15 N + p → 12 C + 4 He
Answer: E(CNO) = 24.8 MeV
13.10. What elements could have been formed during the pre-stellar stage of the Universe’s evolution?
13.11. In what reactions during the pre-stellar stage of the Universe’s evolution could isotopes of helium be formed?
13.12. What characteristics does the distribution of elements in the Universe possess? What mechanisms of element formation are responsible for these characteristics?
13.13. Why are there peaks in the abundances of elements for α-particle nuclei?
13.15. What is the temperature T at which the fusion of deuterium nuclei can occur?
Answer: T ≈ E/(3/2k) = (Ze) 2 /(3/2kR) = 5.4 -10 9 K
13.16. Find the energy released in the following reactions: 1) d + d → 3 H + p, 2) d + t → 4 He + n,
3) d + d → 3 He + n, 4) d + 3 He → 6 He + p.
Answer: 1) 4.03 MeV; 2) 17.59 MeV; 3) 3.27 MeV; 4) 18.35 MeV
13.17. The main source of solar neutrinos is the reaction p + p → d + e + + + νe. Calculate the maximum energy of the electron neutrinos produced in this reaction.
13.18. Solar neutrinos are produced in the reaction e – + 7 Be → 7 Li + νe. Calculate the energies of neutrinos and 7 Li nuclei in this reaction.
Answer: TLi ≈ 0.12 MeV
13.19. What are the primary nuclear reactions that generate neutrons in the r- and s-processes?
13.20. Does the formation of chemical elements occur in the present era? Provide observational evidence to support your answer.
13.21. Explain why there is a greater prevalence of neutron-deficient nuclei compared to neutron-rich nuclei.
13.22. Which reactions produce the neutron-deficient isotopes 74 Se and 92 Mo?
13.23. Describe the nuclear reactions involved in the formation of the beryllium isotopes 7 Be and 10 Be.
13.24. Calculate the magnitude of the nuclear energy reserve in a star with the mass of the Sun.
13.25. How long will the Sun continue to release energy through the p-p chain if its current luminosity is maintained?
Answer: t = NpEpp/(4L) = 7.8-10 10 years
13.26. Calculate the amount of energy Q that is released in the fusion reactions outlined below:
1) d + 6 Li → 2α, 2) p + 11 B → 3α.
Solution: 1) Q = 22.4 MeV; 2) Q = 8.7 MeV
13.27. Determine the maximum energy that is released in the reaction 3 He + p → 4 He + e + + + νe.
Solution: Q = 18.8 MeV

Stars may seem everlasting and unchanging to Earth’s inhabitants, but modern astronomy has proven that stars undergo a gradual evolution. Let’s take a brief look at the stages of stellar evolution.
Phases of stellar evolution
Every evolution is driven by certain factors that prompt the system to change. For stars, gravity and the energy produced by thermonuclear reactions in their cores are the main driving forces. According to theory, the state of a star is determined by the balance between these factors.
The formation of matter in the universe has resulted in the creation of inhomogeneities: some regions contain very little matter, while others consist of sparse gas clouds. Since hydrogen is the most abundant element in the universe, these clouds are primarily composed of hydrogen.
Convective star formation
As gravity takes effect, the clouds start to condense, creating a region of higher density known as a “protostar”.
The more matter that accumulates in the protostar, the stronger its gravitational pull becomes, resulting in a faster formation of a dense object.
As the gas gets compressed, its temperature rises in accordance with the gas laws. This leads to the formation of significant temperature variations within the protostar, which triggers vigorous gas convection. Hot gas rises from the core to the surface, while cooled gas descends back to the core. Gravitational compression primarily drives the energy source at this stage.
Main-sequence star
When the temperature inside the core reaches several million degrees, the thermal energy of the atomic nuclei becomes sufficient to overcome the Coulomb repulsion forces and come close enough together to start fusion reactions of hydrogen nuclei into helium nuclei. These reactions happen with the release of a large amount of energy, and gravitational forces are balanced. The star “ignites” and enters its main phase of evolution.
The brightness of the star and its spectral class are usually closely connected, and as a result, the star falls into a specific position on the graph of these properties (the Hertzsprung-Russell diagram) in the long diagonal region known as the “main sequence”. This is why this stage of stellar evolution is called the main sequence.
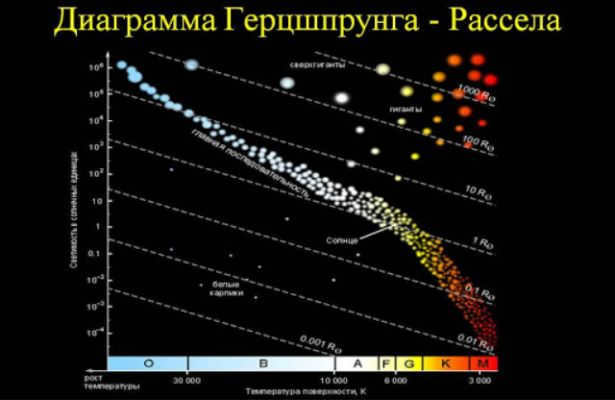
The length of the main-sequence phase is determined by the star’s mass. The larger the mass of the star, the more rapidly it consumes hydrogen. The most massive stars remain on the main sequence for just a few million years. In contrast, the least massive stars can remain in this phase for billions of years.
As the star’s hydrogen supply is exhausted, the internal pressure decreases and it becomes unstable. This triggers the contraction of the inner core, leading to the initiation of new thermonuclear fusion reactions involving helium nuclei, resulting in the formation of carbon, neon, oxygen, and eventually iron nuclei.
In the central region of the star, where the temperature is lower, the burning of helium starts at a later stage. This release of energy causes the outer layers of the star to expand, creating a denser core and a less-dense, expanding outer shell. Consequently, the star evolves into a red giant.
A typical red giant star can have a size of 100-1000 times the radius of our sun. If such a star were placed in our solar system, its outer surface could be located near the orbit of Jupiter. However, the average density of a red giant is often lower than that of Earth’s atmosphere.

Final Phases of Stellar Evolution
The red giant phase, characterized by a denser core and an expanding outer shell, typically lasts between 10 and 100 million years. Subsequently, depending on specific conditions, the outer layers may disperse or undergo a explosive event, resulting in the formation of a nebula with diverse shapes.
Within the nebula, the remnant core persists, which can manifest as a white dwarf, neutron star, or black hole, depending on its mass. This marks the ultimate stage in the life cycle of a star.