In previous lessons, we have learned that just like other stars, the Sun appears to move across the celestial sphere. Similarly, the Moon also moves in relation to the stars, but its trajectory is more complex. In this lesson, we will explore the reason why the Moon always presents the same face to Earth. We will delve into the concepts of the sidereal and synodic month and understand how they differ from each other. Additionally, we will uncover the meaning of the Moon’s phases and examine how they transition.
Currently, you are not able to view or share the instructional video with your students
In order to access this and other video lessons included in the package, you will need to add it to your personal account.
Unlock amazing possibilities


Moon Movement and Phases Lesson Outline
Just like the Sun, the Moon also undergoes motion in relation to the stars. However, its movement is more intricate and consists of two distinct motions: the orbit around the Earth and the orbit of the Earth around the Sun. In the former, the Moon follows an elliptical path as it revolves around the Earth, aligning with the Earth’s axial rotation. As a result, we observe the Moon traversing the stellar backdrop in sync with the sky’s rotation.
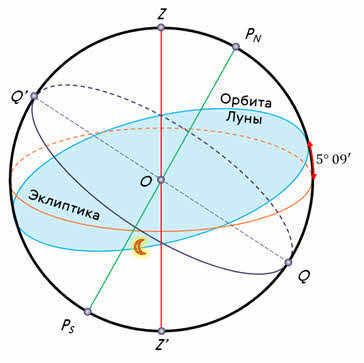
The Moon moves in a consistent direction, always going from west to east. Its visible path in the sky forms a large circle, which is inclined at a slight angle of only 05 o 09′ to the ecliptic plane. This circular path intersects the ecliptic at two specific points known as the nodes or draconic points.
The Moon completes a full orbit around the Earth in 27 days, 7 hours, 43 minutes, and 6 seconds. This is known as the sideric or sidereal month. What makes it even more fascinating is that the Moon also completes one rotation on its axis within the same time frame. This is why we only ever see one side of the Moon from Earth.

The study of the Moon’s motion around the Earth is a highly complex task in celestial mechanics. However, when we observe the Moon from Earth, it is easy to notice changes in its appearance. This is because the Moon does not have its own luminosity; it simply reflects the light of the Sun. As the Moon orbits around the Earth, the amount of illumination we see constantly changes, which is known as the lunar phases.
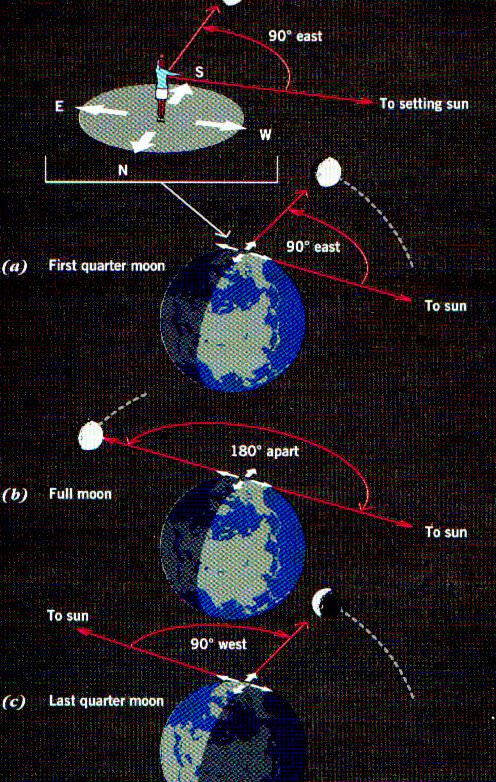
It’s interesting to note that the side of the Moon that is illuminated always faces the Sun, even if the Sun is hidden behind the horizon. The line that separates the illuminated part of the Moon from the unilluminated part is called the terminator.

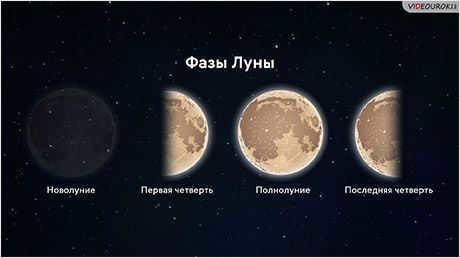
The movement of the Moon across the sky can be divided into four primary phases: new moon, first quarter, full moon, and last quarter. These phases are commonly recognized and used to track the lunar cycle.

The phase of the Moon known as the new moon occurs when the Moon is positioned between the Earth and the Sun. During this time, the Moon’s dark side is facing us, making it invisible as it is located close to the Sun.
After a few days, a thin and bright crescent of the young Moon becomes visible in the western sky and gradually grows in size. Occasionally, you may also observe the remaining part of the Moon emitting a faint grayish glow, referred to as the ashen light. This phenomenon can be explained by the direct illumination of the lunar crescent by the Sun, while the rest of the Moon’s surface reflects sunlight scattered by the Earth.
You have a few more days to observe the Moon’s sickle growing wider and moving farther away from the Sun. Seven days after the new moon, the right half of the lunar disk becomes visible, marking the first quarter phase.
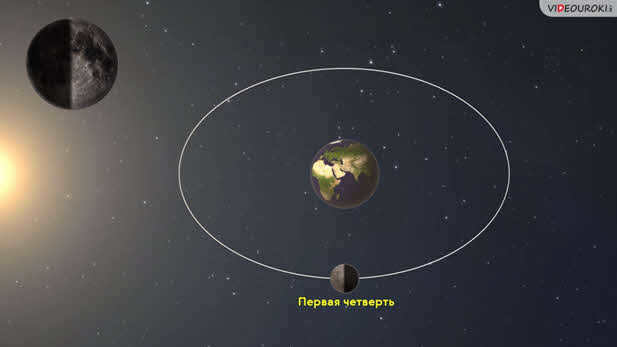
As the lunar cycle progresses, about 14-15 days after the new moon, the Moon reaches a point of alignment with the Sun. This marks the full phase of the Moon, commonly known as a full moon ♪ full moon ♪. During this phase, the Sun’s rays fully illuminate the side of the Moon facing the Earth. As a result, the Moon can be seen above the horizon throughout the entire night, rising at sunset, passing through the southern part of the sky, and setting at sunrise.
After the full moon, the Moon gradually moves closer to the Sun. Initially, a small crescent-shaped section appears on the right side of the Moon, which grows larger over the following days. About a week after the full moon, the Moon enters the third or last quarter phase.
During this stage, we once again witness half of the Moon’s illuminated hemisphere, just like in the first quarter. However, this time it is the portion that was not illuminated previously.
The Moon typically rises around midnight and by the time the Sun rises, it can be found in the southern part of the sky. It then sets in the afternoon.
In the future, the crescent shape of the Moon will be turned convex to the left (east) due to its gradual approach towards the Sun from the west. This results in the Moon being illuminated from the left. Currently, we can only observe the Moon in the morning, shortly before sunrise. Then, it reverts back to being the new moon.
The time interval between two consecutive new moons is not constant and on average lasts for 29 days, 12 hours, 44 minutes, and 3 seconds.
This time interval between two identical phases of the Moon is known as the synodic month.
Now, we will examine the synodic and sideric months and make a comparison:

Astronomy also has its own version of a calendar year, known as a lunar year, which consists of 12 lunar months and lasts about 354 Earth days. This is approximately 11 days shorter than the standard calendar year. As a result of this difference, the phases of the Moon will occur on different dates each year. However, they will align with the same days of the year every 19 years.
To further reinforce the newly learned information, let’s answer a couple of questions together. In one of the books, the night sky is described as follows: “Above the park, hovering low near the ground, is the distinct crescent shape of the Moon, with its curved edges pointing towards the left. The Big Dipper is tilted towards the west. It feels like it is well past midnight, but not quite morning yet.” This description pertains to an autumn sky in Lithuania, which has an average latitude of 55 degrees. Let’s verify the accuracy of this description.
The answer to this question is quite straightforward. If the month resembled a sharp sickle with horns pointing to the left, it would be considered a “young” month. And it has been established that such a Moon does not linger in the sky past midnight. Therefore, the description of the night sky in Lithuania, from an astronomical perspective, is incorrect.
By the way, to differentiate between the first quarter of the Moon and the last quarter, an observer in the northern hemisphere can utilize the following mnemonic rule. If the lunar sickle in the sky resembles the letter “C”, it indicates the Moon is “Aging” or “Descending,” meaning it is the last quarter. If mentally imagining a stick placed against the moon’s sickle forms the letter “R”, then it signifies the moon is “Growing,” indicating it is the first quarter.
Here’s another question from the book: “A river flowed freely, with the moon shining brightly above the calm left bank, and a gleaming strip of light cutting through the water.” Assuming that the moon was most likely at its full phase, let’s determine the direction in which the river flowed.
So, as we have previously discussed, during a full moon, the Moon is near its position at its highest point in the sky, which is on the southern side. Therefore, if we stand along the river, we would be facing south with our left side. As a result, the river was flowing towards the west.

At first glance, it may seem that the Moon simply revolves around the Earth in a specific orbit and at a certain speed.
The forces that cause the Moon’s rotation
In reality, the motion of the Moon is a highly complex process that is difficult to describe scientifically. It is influenced by various factors, such as the shape of the Earth, which is slightly flattened, and the fact that the Sun exerts a gravitational pull on it that is 2.2 times stronger than the pull of our own planet.

Photos of the Deep Impact spacecraft capturing the Moon’s movement
When accurately calculating the Moon’s movement, it’s important to consider the tidal interaction between the Earth and the Moon. The Earth transfers its rotational momentum to the Moon, causing it to move away. However, this gravitational interaction is not constant and decreases as the distance increases. As a result, the rate at which the Moon moves away slows down. The Moon’s rotation around the Earth relative to the stars is known as the sideric month and lasts approximately 27.32166 days.

Here is an image taken by Mars Express showing the Earth and the Moon.
Have you ever wondered about the reasons behind the phases of the Moon? Or why it appears to glow? Let’s uncover the secrets! The Moon reflects a mere 7% of the sunlight that reaches it. This occurs due to specific regions on its surface being capable of absorbing and storing solar energy during periods of intense solar activity, and then emitting it weakly.

Ashen light is the reflected light originating from our planet. It lacks the ability to emit light on its own and instead reflects the sunlight. Consequently, we perceive only the portion of the Moon that has been previously illuminated by the Sun. This celestial body orbits our planet in a specific path, causing the angle between the Moon, the Sun, and the Earth to constantly shift. As a result, we witness various phases of the Moon.
Moon Phases visual representation

The period of time between each occurrence of a new moon is approximately 28.5 days. The reason for the discrepancy in length between calendar months can be attributed to the Earth’s movement around the Sun. When the Moon completes a full orbit around the Earth, the Earth itself has moved approximately 1/13th of its own orbit. This additional movement of the Earth means that the Moon requires an extra couple of days to align with the Sun and Earth once again.
Despite the Moon’s constant rotation on its axis, it always presents the same face towards the Earth. This phenomenon, known as synchronous rotation, is a result of the gravitational forces between the Moon and Earth. These gravitational forces also influence the tides on our planet.

Our satellite orbits around its own axis in a uniform manner, as well as around the Earth in accordance with a specific law. The essence of this law is as follows: the movement is not constant – it is faster near the perigee, but slightly slower near the apogee.
At times, it is possible to observe the Moon’s far side from the east or west. This phenomenon is known as optical longitude libration, and there is also optical latitude libration. The latter occurs due to the tilt of the lunar axis in relation to the Earth, and it can be seen in the north and south.
Did you enjoy reading this article? Share it with your friends!

Having analyzed the movement of the Earth and its impact on our lives, we will now examine the motion of our natural satellite, the moon. The moon also undergoes various types of motion, including rotation around its own axis. The proximity or distance of its position in relation to Earth determines the duration of a day, weeks, months, and even the year, and significantly influences the tides.
Consequently, this article aims to delve into the intricacies of lunar movement and its implications for life on our planet.
What are the Moon’s movements?


Due to the gravitational interaction between the Earth and the Moon, the Moon undergoes natural movements. Similar to our planet, it experiences two distinct motions referred to as rotation on its axis and orbit around the Earth. These motions are unique to the Moon and are closely tied to the tides and the phases of the Moon.
As the Moon goes through its various movements, it requires a certain amount of time to complete them. On average, it takes approximately 27.32 days for the Moon to go through a complete cycle. Interestingly, this is why we always see the same side of the Moon facing us and why it appears to be stationary. This phenomenon is a result of various geometric factors and another type of motion known as lunar libration, which we will explore later on.
The position of the Moon’s nodes is not static and they are located 18.6 light-years away. As a result, the shape of the Moon’s orbit is not fixed, and the Moon reaches its perigee, or closest point to its orbit, once every 8.85 years. During this perigee, the Moon is in its full phase and closest to its regular path. Conversely, the Moon’s apogee is the point at which it is furthest from its orbit.
Rotating and Translating the Moon
The movement of our rotating satellite is synchronized with its translation. This cycle takes 27.32 days, resulting in us always observing the same side of the Moon. This period is known as the sidereal month. Throughout its rotation, it forms an angle of 88.3 degrees relative to the plane of its elliptical orbit. This inclination is due to the gravitational force exerted by the Earth on the Moon.
During its translational motion around the Earth, the Moon is tilted about 5 degrees in relation to its elliptical path. To complete a full revolution, it returns to its original position. This movement around our planet is what leads to the creation of the different tides we experience today.
The Moon also undergoes rotation, which is the rotation of the Moon in relation to the Sun. This rotational motion occurs simultaneously with the Earth’s rotation and orbit around the Sun.
Effects of the Moon’s Rotation

Due to the movements of the moon, there are various types of months that you may be aware of but not very familiar with. Let’s explore each one:
- The sideric month: This month lasts approximately 27 days, 7 hours, 43 minutes, and 11 seconds. It occurs when the moon completes a full revolution in its orbit, and the hour circle reaches its maximum on the celestial sphere.
- Synodic month: Also known as lunation, this month is the time it takes for two equal phases of the moon to pass. It typically lasts around 29 days.
- Tropical Month: This month is approximately the time it takes for the moon to complete two consecutive phases while moving around the circle of the point of Aries. It usually lasts about 27 days.
- Anomalistic month: Lasting approximately 27 days and 13 hours, this month occurs when there are two consecutive phases of the moon at perigee, the point in its orbit closest to Earth.
- Month of the Dragon. This is the duration it takes for the Moon to transition from one phase to the next while passing through the ascending node. It has a duration of 27 days and 5 hours.
Lunar Libration

The moon’s movement results in us being able to see only half of its surface or the same face all the time. There are three types of libration, which we will discuss in more detail.
- Latitude libration. This occurs due to the inclination between the moon’s orbit and the plane of the ellipse. It allows us to see only the northern and southern parts of the moon at the same time. The plane of the moon’s equator is above and below the plane of its orbit, resulting in more surface area being visible from the opposite polar region.
- Daytime libration. The position of the observer plays a significant role in capturing an image of the moon during the daytime. There are various geometric factors that need to be taken into account.
- Librations in length. The rotational motion of the moon is consistent, but its translational motion is not. This results in the moon moving at different speeds at perigee and apogee. The Earth also experiences a similar phenomenon during its orbit around the Sun at aphelion and perihelion. As a result of this motion, we have a westward influence that allows us to only see one side of the moon in the eastern and western regions.
We can describe lunar libration as a point on the moon’s surface where three types of libration occur. This causes the moon to spiral and not return to its original position.
The information presented in this article adheres to our editorial guidelines. If you notice any inaccuracies, please click here to report them.
Summary of the Full Article: Network Meteorology “astronomy” Moon’s movement
Caution: To find basic details about the Moon and its characteristics, refer to the page Moon as a celestial body. For lunar phases, apogee, perigee, and position in the Zodiac, visit the page Moon as a celestial body. Moon factor: data project by Geocosmos Laboratory.
3.1. THE PATH OF THE MOON IN RELATION TO THE ECLIPTIC
If the lunar orbit was aligned with the Earth’s orbit, the Moon’s path across the sky would be identical to that of the Sun, meaning it would follow the ecliptic. However, the lunar orbit is slightly tilted (around 4°59′ to 5°19′) in relation to the Earth’s orbit. As a result, the Moon’s path deviates from the ecliptic, with one part of its journey slightly above and the other part slightly below the ecliptic. It intersects the ecliptic at two points known as the ascending and descending nodes (see Fig. 3.1 and also Fig. 1.2c mentioned earlier in the treatise). This path can be approximated as a sinusoid in the first approximation.
Because of the rotation of the lunar orbital axis, the nodes of the Moon’s orbit shift in the direction of its motion. Over one revolution of the Moon’s orbit, the ascending node shifts by an average of 1.45 degrees, which is approximately three times its apparent angular diameter. As a result, the Moon’s trajectory on the periodic curve it follows has a period slightly less than 360 degrees, causing it to shift to the right with each revolution around the Earth. Simultaneously, due to nutation, the Moon’s path also shifts to the right as a result of periodic changes in the angle of inclination of its orbit axis. These changes in the lunar orbit axis inclination angle also affect the amplitude of the curve. The first harmonic of nutations has a period equal to the precession period, which is 18.6 years. Therefore, once per full rotation of the nodes, the Moon’s trajectory deviates from the ecliptic by the maximum amount, and once by the minimum amount. Additionally, there are higher-order harmonics of nutations, leading to amplitude variations with smaller periods and correspondingly smaller magnitudes.
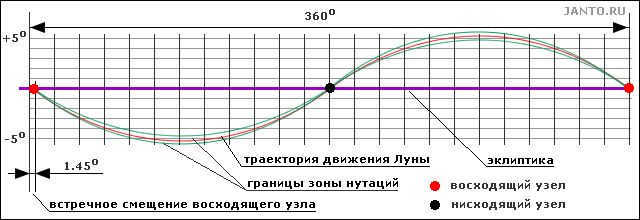

Figure 3.1 showcases the Moon’s path as observed from the Earth’s orbit.
The collection of all potential paths of the Moon.
3.2. MOON’S TRAJECTORY IN RELATION TO THE STARS
To determine the Moon’s trajectory in relation to the stars, one can convert its ecliptic coordinates to equatorial coordinates using the formulas of spherical trigonometry (refer to the Astronet website for more information on converting coordinates between systems). However, for the purpose of illustrating its distinct characteristics, qualitative assessments of “trajectory above the ecliptic,” “trajectory below the ecliptic,” and “trajectory intersecting with the ecliptic” in several typical scenarios will suffice (see Figures 3.2A – 3.2D).
The point where the ascending node is positioned is precisely at the vernal equinox.
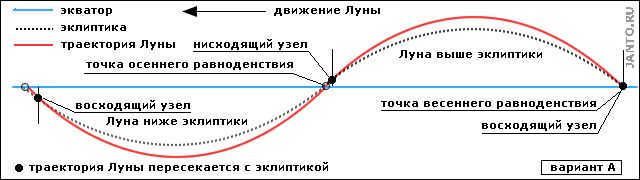
Figure 3.2A illustrates the path of the Moon as observed from the Earth, specifically variant A.
When the Moon is in this particular position, it is situated above the ecliptic as it transitions from the ascending node to the descending node. Conversely, it is positioned below the ecliptic when moving from the descending node to the ascending node. Furthermore, the Moon’s trajectory is generally situated at a greater distance from the equator compared to the ecliptic. This results in the vertical extent of its path being maximized.
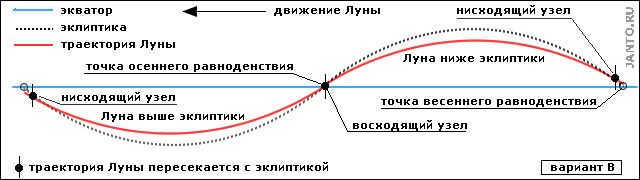
Figure 3.2B. The Moon’s path as seen from Earth – alternate version
In this configuration, the Moon is positioned above the ecliptic as it moves from the ascending node to the descending node, similar to the previous version. Conversely, when transitioning from the descending node to the ascending node, it is positioned below the ecliptic. Nonetheless, the Moon is primarily situated nearer to the equator than the ecliptic, and its trajectory has a negligible vertical span. .
The Ascending Node shifts closer to the point of the autumnal equinox.
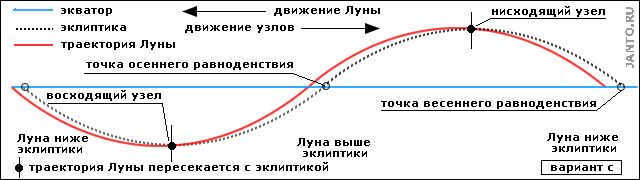
Figure 3.2B shows the path of the Moon as observed from the Earth, specifically variant C.
As the Moon’s ascending node moves closer to the autumnal equinox, the vertical range of its trajectory decreases and reaches its minimum at position B. When the ascending node is positioned between the vernal and fall equinoxes, the magnitude of the lunar trajectory is approximately equal to that of the ecliptic.
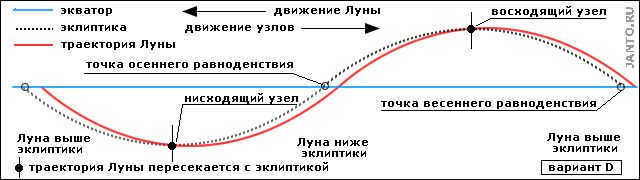
Figure 3.2D. Trajectory of the Moon observable from the Earth – D variation
As the point where the Moon’s orbit crosses the celestial equator moves closer to the point where the Sun crosses the celestial equator during the vernal equinox, the vertical span of the Moon’s trajectory increases, reaching its maximum at position A. When the ascending node is positioned halfway between the autumnal and vernal equinoxes, the span of the Moon’s trajectory is approximately equal to the span of the ecliptic, similar to position C.
3.3. LUNAR TRAJECTORIES CORRIDOR
Considering the information provided, we can affirm that the collection of all potential paths taken by the Moon across the sky is situated within a corridor that has a width equivalent to twice the maximum angle of inclination of the Moon’s orbit in relation to the ecliptic plane, which is 10°38′. The central line of this corridor is formed by the ecliptic line (refer to Figure 3.3). Throughout the complete cycle of the Moon’s nodes, which spans 18.6 years, this corridor becomes densely populated by various trajectories.
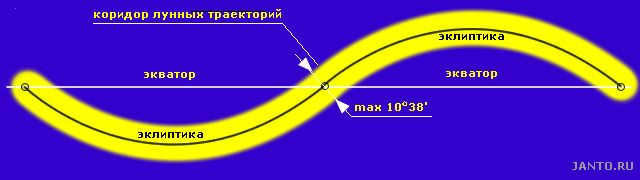
Figure 3.3. Pathway of lunar trajectories
3.4. MOVEMENT OF THE MOON ALONG THE TRAJECTORY
The Moon’s angular velocity along the trajectory is tangential to it and is exactly the same as the angular velocity of the Moon’s orbit described in the previous section. It is not affected by whether the trajectory is represented in the ecliptic or equatorial coordinate system. Throughout the Moon’s complete revolution around the Earth, its angular velocity changes from a maximum at perigee to a minimum at apogee. In other words, the Moon moves along its celestial trajectory with varying speed, either accelerating or decelerating (see Figure 3.4 for calculated values and variations of angular velocities at apogee and perigee, and refer to Table 2.1 and Figure 2.1 for more details from chapter 2).
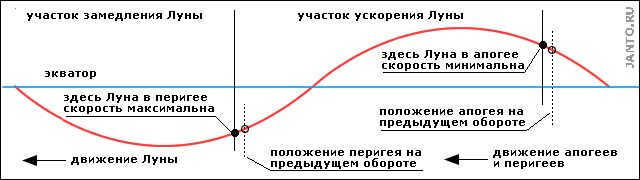

Figure 3.4: Movement dynamics of the Moon along its trajectory (without considering the unique characteristics of the absidal precession).
Due to the phenomenon of absidal precession, which refers to the rotation of the apsidal line (the major axis of the lunar orbit), the apogees and perigees of the Moon should ideally move away from it in a consistent and continuous manner. This means that the angular distance between successive apogees and perigees should always be greater than 360°. As a result, the areas of maximum and minimum angular velocities should constantly shift along the Moon’s trajectory. However, when analyzing lunar calendars, tables, and graphs based on official astronomical data provided in the “Lunar factor: data” section of the Geocosmos Laboratory project, it becomes evident that the distances between successive apogees and perigees are unstable. Furthermore, the movement of apogees and perigees across the signs of the Zodiac is significantly uneven and can even exhibit a reciprocating pattern in certain positions. This peculiar dynamics of the Moon’s motion is often overlooked in popular sources, so the next chapter will provide a detailed modeling and analysis of this phenomenon.
Important Information
For comprehensive details about the Moon’s characteristics, you can refer to the Moon Factor service.
1.1. Overview
The Moon is a substantial celestial body within the realm of planets and satellites in our solar system. It has an average radius of 1737.1 km, which is approximately 27.3% of Earth’s radius. To provide a visual comparison, Figure 1.1 illustrates the Moon alongside Mercury, Venus, Earth, and Mars, as well as the largest satellites of Jupiter and Saturn.

Figure 1.1 shows a comparison of the sizes of the Moon and other celestial bodies in the solar system.
It is evident that the Moon is only slightly smaller than the smallest planet, Mercury, and also larger than the largest satellites, whose parent planets are about ten times larger than Earth. This means that the Moon’s size relative to its parent planet is unusually high for the solar system. The Moon has an average density of 3.346 g/cm3, which is 70-80% higher than that of other major satellites (excluding Io, which has a density of 3.528 g/cm3), and is similar to the density of Mars (3.933 g/cm3).
Due to its relatively large size and density, the Moon exerts a noticeable gravitational force on the Earth, primarily resulting in the formation of tides. Furthermore, the Earth and the Moon together form a system of masses that rotate around a shared center, which is displaced from the center of the Earth by 4750 km. As a result, the Earth’s orbit around the Sun is not perfectly uniform, but rather exhibits oscillating movements.
The Moon’s rotation period on its axis is equal to its revolution period around the Earth, causing it to constantly present the same side to the Earth. This is due to the braking effect of tidal waves in the Moon’s crust, caused by the Earth’s strong gravitational field. The other satellites depicted in Fig. 1 exhibit the same characteristic.
The apparent size of the Moon (29'24" – 33'40") is extremely similar to the apparent size of the Sun (31'29" – 32'31"). As a result, we are able to witness the extraordinary optical event known as a total solar eclipse, during which the Moon completely covers the Sun, revealing the radiant solar corona.
1.2. THE MOON’S ORBIT
Figure 1.2a depicts the movement of the Moon in relation to the Earth when observed from the north pole. It is important to note that everything in this diagram rotates in the same direction: the Moon around its own axis, the Moon around the Earth, the Earth around its own axis, and the Earth around the Sun.
The Moon completes a full orbit around the Earth in 27.32166 Earth days (27 days 7 hours 43 minutes 12 seconds). This duration is referred to as the sidereal lunar month. The term “sidereal” is used because it was initially determined by the Moon’s positional changes relative to the stars.
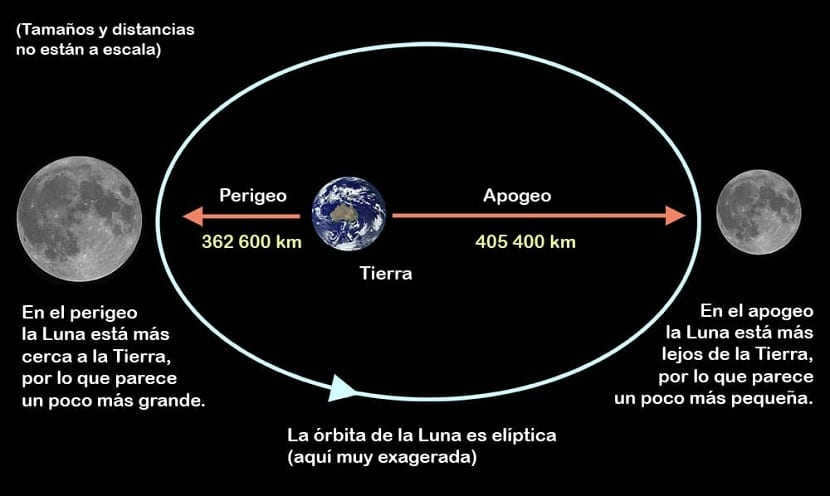
The Moon’s path around the Earth is in the shape of an oval, with one of the focuses being the Earth. Because of this, the distance between the Moon and Earth changes, measuring at 363,104 km at perigee (the point in the orbit closest to Earth) and 405,696 km at apogee (the point farthest from Earth). These measurements are average values, and the actual distances fluctuate over a period of approximately 207 days based on intricate and complex factors. The exact nature of these variations is not completely understood, so we won’t delve into them here. It’s also worth noting that due to the variability of the Moon’s distance, its apparent size in the sky fluctuates by about ±6.7% from the average value. This phenomenon is known as libration.
The apsidal line, which is the line that passes through the points of perigee and apogee, is aligned with the center of the Earth. This line, also known as the apsidal line (derived from the Greek word apsidus meaning arc), coincides with the major axis of the ellipse. In addition, it slowly rotates in the same direction as the other components of the system, completing a full revolution in 8.85 years (see Fig. 1.2b).
The period between the Moon’s perigee passages is referred to as the anomalistic month. It spans 27 days, 13 hours, 18 minutes, and 33 seconds, slightly longer than the sideric month due to the continual movement of the perigee away from the Moon caused by the rotation of the apsidal line.
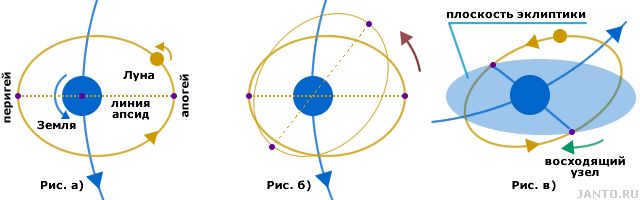
Figure 1.2 showcases the perspective and characteristics of the lunar orbit.
The inclination of the lunar orbit is located at a slight angle to the Earth’s orbit, also known as the ecliptic plane (see Fig. 1.2c). This angle is referred to as the orbital inclination and varies periodically from 4°59′ to 5°19′. The point where the lunar orbit intersects with the ecliptic plane during the Moon’s ascending motion is known as the ascending node (denoted Ω). Unlike other rotations, this node moves in the opposite direction and completes a full revolution every 18.6 years. This motion is caused by the precession of the lunar orbit, which is a change in the axis of rotation that describes a cone-like shape (similar to a spinning top or a fallen coin). As the Moon moves towards the ascending node, it passes through it faster than completing a full revolution in its orbit. This interval is known as the draconic month and is slightly shorter than the sideric month, totaling 27.2 days.
Aside from the sideric, anomalistic, and draconic months, there is also the tropical month, which is defined as the time it takes for the Moon to pass through the same longitude in the system of ecliptic coordinates, such as the longitude of the vernal equinox. Its duration is slightly shorter than that of the sideric month due to the Earth’s axis precession. Occasionally, these concepts and their durations may be mistakenly interchanged, but for the purpose of our research, this distinction is not crucial.
The Moon’s axis of rotation is inclined at an angle of 1.5424° from the vertical, causing it to be tilted relative to the plane of its orbit. As it orbits around the Earth, the Moon slightly rotates, revealing different sides to observers on Earth and allowing a glimpse of a small portion of its backside. Despite always appearing the same to us, the Moon actually has over 50% of its surface available for observation.
It is evident that the Moon follows a complex trajectory around the Earth, with numerous parameters and variables involved. Describing this motion accurately and completely using mathematics is an exceptionally challenging task.
We observe only the portion of the Moon that is facing us and being illuminated by the Sun. This is determined not only by the Moon’s position relative to the Earth during its orbit, but also by the Earth-Moon system’s position relative to the Sun. The shape and orientation of the illuminated part of the Moon that we see at any given moment, which is commonly referred to as “full moon,” “new moon,” “waning moon,” “waxing moon,” etc., is known as its “phase” in the language of astronomers and astrologers. phase.. The phases of our nighttime celestial body change as a result of the changing positions of the Moon, Earth, and Sun, and this process repeats continuously with a period known as the synodic lunar month. This mechanism is illustrated in Figure 1.3.
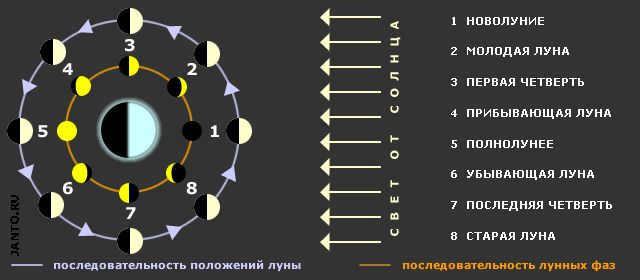
Fig.1.3 The process of lunar phase formation
The duration of the synodic lunar month is commonly defined as the time between new moons. The term itself is derived from the Greek word synodos, meaning “conjunction”, as the Moon and the Sun appear to be joined together during the new moon phase. The synodic month is slightly longer than the sidereal month mentioned earlier. This is due to the fact that as the Moon completes a full revolution around its orbit, the Earth also moves along its own orbit, causing the Sun to shift along the ecliptic and move away from the Moon. As a result, the Moon needs to complete a bit more than one full revolution to “catch up” with the Sun (refer to Fig. 1.4).
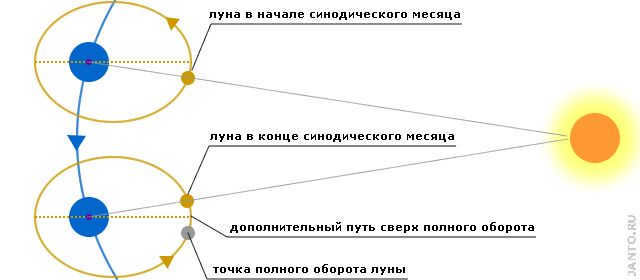
The duration of the synodic month varies due to the influence of various factors. On average, it lasts 29.530588 days (equivalent to 29 days, 12 hours, 44 minutes, and 2.8 seconds), with deviations from the mean value reaching approximately ± 13 hours. The synodic month serves as the fundamental unit for most lunar calendars, as it is measured by observing the moon’s phases without the aid of any instruments. However, we will delve deeper into this topic in the following section. For now, let us continue exploring the mechanics of lunar celestial bodies.
1.4. MOTION ON THE CELESTIAL SPHERE.
Before discussing the movement of the Moon on the celestial sphere, let’s focus on the sphere itself. When we gaze at the sky and witness the celestial bodies in motion, it appears as though they orbit around us. This geocentric perspective has been embraced by civilizations since ancient times until the heliocentric model of Copernicus emerged during the Middle Ages. Nowadays, it is widely known that the luminaries traverse the sky due to the Earth’s rotation. However, for the purposes of celestial mapping, it is more practical to adhere to the traditional, non-scientific approach with an immobile observer at the center of the rotating celestial sphere. Figure 1.5 illustrates one such variation.
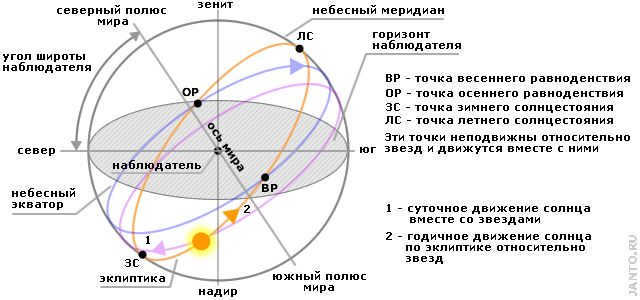
Figure 1.5: The celestial sphere’s geometry and the mechanics behind the apparent movement of the celestial bodies
Due to its movement along the ecliptic, the Sun is continuously shifting towards the east with respect to the stars, meaning it falls behind them by approximately 1° (around two times its angular diameter) each day. The daily displacement in relation to the celestial equator is slightly less, particularly near the solstice points. As a result, during the day, the sun moves almost parallel to the stars. Figure 1.6 illustrates the map of the Sun’s position along the ecliptic in the starry sky.
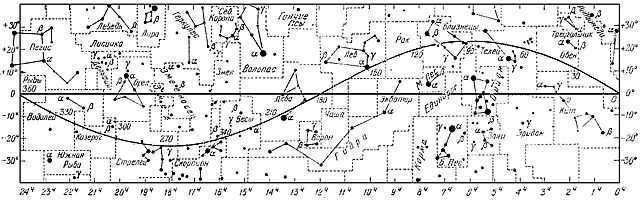
Figure 1.6 shows the representation of the ecliptic on the starry sky map
(V.P.Chekhovich. What and how to observe in the sky. M., Nauka, 1984, fig.29)
On this map, the celestial equator is represented by a straight line, while the ecliptic line resembles a sine wave. The points where the ecliptic intersects with the equator are known as the equinox points, and the points of extreme are referred to as the solstice points. It’s important to note that the Sun moves along the ecliptic from west to east, or right to left, which is contrary to the usual sinusoidal patterns found on process charts. It’s also important to understand that the ecliptic map only displays the path that the Sun traces against the backdrop of stars during one revolution of the Earth. It does not provide specific information about the Sun’s exact position at a given time, as its movement along the ecliptic is not uniform and the Earth completes a full revolution in a non-integer number of days. To determine the precise position, ephemerides are used. These are tables containing coordinates and parameters of celestial objects, which are calculated and published by various scientific organizations and enthusiasts (such as the astronomical yearbook of the Russian Academy of Sciences). Additionally, special computer programs can be used to calculate the position.
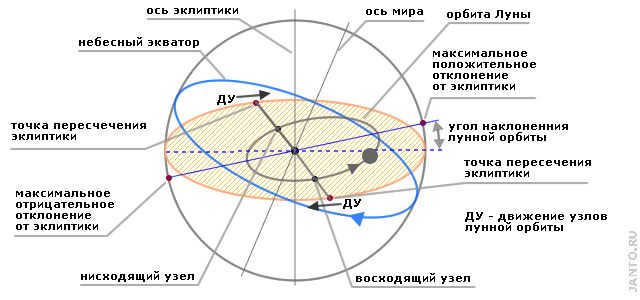
Fig.1.7. To the motion of the Moon in the sky
To simplify things, let’s exclude the horizon from the model and connect the Moon’s coordinates to the ecliptic. In this scenario, the Moon’s movement on the celestial sphere will involve both the motion of the ecliptic and the Moon’s motion in relation to the ecliptic. The maximum deviation of the Moon from the ecliptic will be equal to the inclination of its orbit, which is approximately 5°. At the lunar nodes, the Moon’s path will intersect with the ecliptic. It’s worth noting that the nodes of the lunar orbit shift towards the Moon’s direction, about 5° to the west, at a rate of about 1.5° per revolution. As a result, the Moon’s path will constantly deform, completing a full cycle of node motion in 18.6 years (as mentioned earlier), but always remaining within a ±5° range around the ecliptic. Additionally, the amplitude of the Moon’s path oscillations relative to the equator will change from 28.5° to 18.5°. This is because the angle of inclination of the lunar orbit to the ecliptic plane is combined with the angle of inclination of the ecliptic to the equator, with different signs and coefficients.
Calculating the Moon’s coordinates for a specific date is a much more intricate and challenging task compared to the Sun. This is because the Moon’s movement is affected by a multitude of variables. There exist numerous mathematical models that describe the Moon’s motion in the sky, and just like for the Sun, ephemeris yearbooks are available for reference.
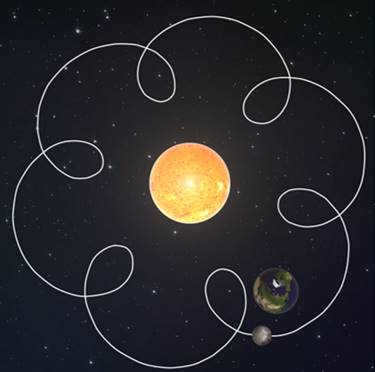
For instance, Fig. 1.8 displays multiple paths of the Moon’s movement across the celestial sphere, graphed using ephemeris tables obtained from the NASA website. It is worth noting that, unlike the standard sinusoids on process charts, the Moon, like the Sun, moves from west to east, or from right to left. Furthermore, these trajectories do not provide precise information about the Moon’s location at a specific time. It is important to consider that while the Sun traverses the ecliptic over the course of one Earth revolution, approximately one calendar year, the Moon completes each of its paths along the ecliptic within a single lunar sidereal month. In other words, these images depict not the actual combined motion of the Sun and Moon, but rather the fixed routes along which they are supposed to travel.
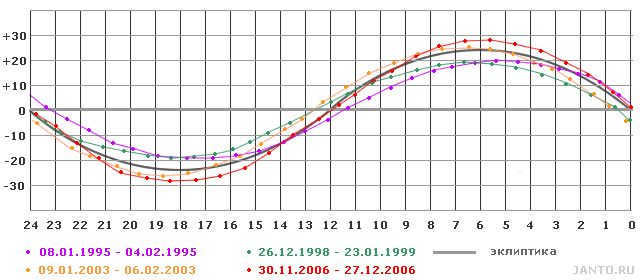
Fig.1.8. Paths of the Moon’s movement on the celestial map
During its daily journey, the Moon falls behind the stars even more than the Sun – by approximately 13° per day, which is equivalent to about 26 (twenty-six!) visible lunar diameters. This can be observed with the naked eye. Throughout the day, the Moon also shifts significantly (up to 5-6° at its peak, or 10-12 diameters) in relation to the celestial equator. As a result, the spiral nature of the Moon’s paths is much more pronounced compared to the Sun’s paths.
Note: The graphs displayed above for the Sun and Moon are applicable to an observer situated at the Earth’s center. However, for an observer located on the Earth’s surface, there is an additional displacement component caused by parallax. Parallax refers to the change in the Sun and Moon’s position relative to an infinitely distant sphere due to the observer’s change in position. In our scenario, the observer’s position changes due to both variations in latitude and the Earth’s rotation. Because of parallax, the Moon’s apparent position can deviate by up to 2 degrees (equivalent to 4 apparent lunar diameters) from its calculated position for the Earth’s center. This deviation is significant, particularly in relation to solar and lunar eclipses.
1.5 ECLIPSES
It is important for everyone to be familiar with solar and lunar eclipses and understand their characteristics. Let’s highlight that a solar eclipse happens exclusively during the new moon phase. In order for a solar eclipse to be considered total, the Moon must align with the ecliptic plane, specifically one of its nodes. Additionally, taking into account parallax and the apparent angular diameter of the Moon, it should be equal to or greater than the angular diameter of the Sun. The combination of all these factors is quite rare, making a total solar eclipse an extremely uncommon event for a specific location. Partial eclipses, where the Moon does not completely block the solar disk, occur more frequently but still not annually.
Lunar eclipses, unlike solar eclipses, can only be seen near the time of the new moon. However, because the Earth’s shadow cone that the Moon falls into is 2.5 times larger than the apparent size of the Moon, total eclipses can be observed from almost anywhere on the night side of the Earth and last much longer. This is why lunar eclipses occur more frequently in a specific area than solar eclipses. It is important to note that during a lunar eclipse, the Moon does not completely vanish, as it is still illuminated by the solar rays that refract through the Earth’s atmosphere.
1.6. BRIEF SUMMARY
To sum up:
1. The Moon is an abnormally large satellite and has a significant gravitational influence.
2. The apparent size of the Moon varies slightly and can coincide with the apparent size of the Sun.
3. The Moon always keeps one side facing the Earth.
4. The parameters of the lunar orbit change periodically with different cycles.
5. The Moon’s paths relative to the stars are located near the ecliptic and undergo modifications with each revolution, repeating every 18.6 years.
- Sidereal (based on the passage of the celestial meridian);
- Anomalistic (based on the passage of perigee);
- Draconic (based on the passage of the ascending node);
- Tropical (based on the passage of the ecliptic longitude);