On January 3, 2010 at 8:53 a.m. local time, a picture was taken of the Sun from Lamlash, Scotland (55° 31′ 47.43″ N, 5° 05′ 59.77″ W).
The Sun’s position in the sky depends on the time and geographic location of the observer on Earth’s surface. Due to the Earth’s orbit around the Sun, the Sun appears to move in relation to the fixed stars in the celestial sphere, following a circular path known as the ecliptic.
The Earth’s rotation on its axis is responsible for the daily movement of the Sun and the fixed stars across the sky. This movement varies depending on the observer’s geographic latitude. The timing of a fixed star passing the observer’s meridian is determined by the geographic longitude.
To determine the Sun’s position at a specific time and location, we can follow these three steps:
- Calculate the Sun’s position in the ecliptic coordinate system.
- Convert the coordinates to the equatorial coordinate system.
- Finally, convert the coordinates to a horizontal coordinate system based on the observer’s local time and location.
Summary
- 1 Approximate position
- 1.1 Ecliptic coordinates
- 1.2 Equatorial coordinates
- 1.3 Horizontal coordinates
- 1.4 Rectangular equatorial coordinates
- 1.5 Ecliptic tilt
- 2.1 Overview
- 2.2 Calculations
- 2.3 Atmospheric refraction
- 6.1 Related articles
- 6.2 External References
Approximate position
Ecliptic coordinates
These formulas, extracted from the Astronomical Almanac, can be utilized to compute the apparent coordinates of the Sun, mean equinox, and ecliptic dates with an accuracy of approximately 0° 0.01′ (or 36 seconds of arc) for dates ranging from 1950 to 2050.
Let’s initiate the calculation by determining n – the number of days (positive or negative) since noon GMT on January 1, 2000 (J2000.0). If we have the Julian calendar date for the desired time,
no sign equals D J – 2 451 545, 0 -2 \, 451 \, 545, 0 >.
The mean longitude of the Sun, adjusted for light aberrations, is:
L sign equals 280, 460° + 0, 9856474° no +0.9856474 ^ n>
The mean anomaly of the Sun (in reality, the Earth in its orbit around the Sun, but it is convenient to express that the Sun orbits around the Earth) is:
Set the value in the range of 0° to 360°, by adding or subtracting multiples of 360° as necessary. L gram
The lambda sign is equal to L + 1 , 915 ∘ sin gram + 0 , 020 ∘ sin 2 gram \ sin g + 0.020 ^ ^ \ sin 2g>
As the ecliptic latitude of the Sun never exceeds 0.00033 °,
and the distance from the Sun to the Earth in astronomical units is equal:
p sign is equal to 1 , 00014 is 0 , 01671 because grams is 0 , 00014 because 2 grams .
Equatorial coordinates
- Ecliptic tilt, ϵ
- Right ascension, which is in the same quadrant as . To obtain the correct quadrant for the right ascension, we use the arc tangent function with two arguments (atan2(y, x) in many computer languages): α sign equals arctan(because ϵ tan λ) α λ α sign equals arctan2(because ϵ sin λ, because λ)
- and declination, . δ sign equals arcsin(sin ϵ sin λ)
Horizontal coordinates
Rectangular equatorial coordinates
In the rectangular equatorial coordinate system, the right ascension axis is aligned with the vernal point, and the declination axis is 90° east in the plane of the celestial equator. The third axis points north of the celestial pole. The coordinates are measured in astronomical units: X, Y, Z.
The X coordinate is positive because lambda is positive. The Y coordinate is positive because epsilon times sine lambda is positive. The Z coordinate is positive because sine epsilon times sine lambda is positive.
Tilt of the ecliptic
When the inclination angle of the ecliptic cannot be determined precisely, it can be estimated as follows:
The symbol ϵ is equal to 23.439° – 0.0000004° multiplied by n>
This approximation can be used in the equations mentioned above.
The Sun’s declination as observed from Earth
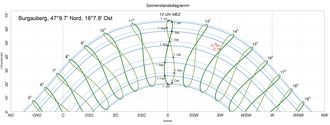
The Sun’s path across the celestial sphere during the day for an observer located at a latitude of 56° north. The Sun’s path varies with its declination throughout the year. The points where the lines intersect the horizontal axis indicate the azimuths in degrees from north where the Sun rises and sets at the summer and winter solstices.
Summary
During the northern spring, the Sun appears to move towards the north and reaches the celestial equator at the March equinox. At the June solstice, the Sun’s declination reaches its maximum, which is equal to the angle of tilt of the Earth’s axis (23.44°). Afterward, the declination gradually decreases and reaches its minimum (-23.44°) at the December solstice, when the tilt of the axis is negative. This variation in the Sun’s declination is responsible for the changing seasons.
When plotted on a linear graph, the Sun’s declination over the year forms a sine wave with an amplitude of 23.44°. However, one lobe of the wave is slightly longer than the other, resulting in some differences in the pattern.
If the Earth were a perfect sphere orbiting the Sun in a circular orbit and its axis were tilted 90° so that the axis itself lay in the plane of the orbit (similar to Uranus), various occurrences would emerge. At one point in the year, the Sun would be directly above the North Pole, resulting in a declination of +90°. Over the following months, the sunspot would progressively move towards the South Pole at a constant rate, traversing circles of latitude at a consistent pace. Consequently, the Sun’s declination would decrease linearly with time. Eventually, the Sun would be directly above the South Pole with a declination of -90°, after which it would begin moving northward at a steady rate. As a result, a graph depicting the solar declination observed from this drastically tilted Earth would resemble a triangular waveform rather than a sine wave, zigzagging between positives and negatives of 90°, with linear intervals between peaks and troughs.
Indeed, the Earth’s path around the Sun is not a perfect circle, but rather an elliptical shape. During the Earth’s closest approach to the Sun, known as perihelion, which occurs in early January, it moves faster than during its farthest point, known as aphelion, which occurs in early July. This difference in speed affects various processes, such as the Sun’s change in declination. In January, the change in declination is more rapid compared to July. When represented on a graph, this results in sharper dips and rises, with the lowest points being more abrupt than the highest points. Additionally, since perihelion and aphelion do not align precisely with solstices, there is a slight offset in the timing of these highs and lows. The rates of change before and after these points are also not exactly equal.
As a result, the plot of apparent solar declination deviates from a typical sine wave in several ways. The accurate calculation of this phenomenon poses certain challenges, as illustrated below.
Mathematical Computations
The solar declination, δ☉, represents the angle formed by the Sun’s rays and the Earth’s equator. The Earth’s axial tilt, also known as the ecliptic tilt, represents the angle formed by the Earth’s axis and a line perpendicular to its orbit. While the Earth’s axial tilt slowly changes over thousands of years, its current value, approximately ε = 23° 26′, remains relatively constant. As a result, the change in solar declination from year to year is nearly identical.
During the solstice, the angle between the Sun’s rays and the Earth’s equator reaches its maximum value of 23° 26′. Consequently, δ☉ equals +23°26′ during the northern summer solstice and -23° 26′ during the southern summer solstice.
During each equinox, the Sun’s center seems to pass through the celestial equator, and δ ☉ is 0°.
The calculation for the Sun’s declination at any given time is as follows:
δ ⊙ sign is equal to arcsin [ sin ( – 23.44° ) ⋅ sin ( LE ) ] = \ arcsin \ left [\ sin \ left (-23.44° \ right) \ cdot \ sin \ left (LE \ right) \ right]>
where LÉ is the ecliptic longitude (essentially the position of the Earth in its orbit). Due to the small eccentricity of Earth’s orbit, it can be approximated as a circle, resulting in an error of up to 1°. This circular approximation causes EL to be 90° before the solstice of Earth’s orbit (at the equinoxes), allowing us to write sin (EL) as sin (90 + NDS) = cos (NDS), where NDS represents the number of days after the December solstice. Additionally, by approximating arcsin [sin (d) – cos (NDS)] as d – cos (NDS), we can derive the following commonly used formula:
δ ⊙ sign equals – 23 , 44 year ∘ ⋅ because [ 360 ∘ 365 ⋅ ( NO + 10 ) ] = – 23.44 ^ ^ \ cdot \ cos \ left [<\ frac <360 ^ > > \ cdot \ left (N + 10 \ true-false]>
By excluding both approximations and utilizing the Earth’s orbital parameters, a more precise determination of EL can be obtained:
The value of δ ⊙ sign can be derived as Arcsin [ sin ( – 23 , 44 year ∘ ) ⋅ because ( 360 ∘ 365 , 24 ( NO + 10 ) + 360 ∘ π ⋅ 0 , 0167 sin ( 360 ∘ 365 , 24 ( NO – 2 ) ) ) ) ] = \ arcsin \ left [\ sin \ left (-23,44 ^ \ right) \ cdot \ cos \ left ( <\ frac <360 ^ > > \ left (N + 10 \ right) + <\ frac <360 ^ > > \ cdot 0,0167 \ sin \ left (<\ frac <360 ^ > > \ left (N-2 \ right) \ right) \ right) \ right]>
This expression can be simplified by evaluating the constants:
δ ⊙ sign is equal to – Arcsin [0.39779 because (0.98565 ∘ (NO + 10) + 1.914 ∘ sin (0.98565 ∘ (NO – 2)))] = – \ arcsin \ left[0.39779 \ cos \ left(0.98565 ^ \ left(N + 10 \ right) +1.914 ^ \ sin \ left( 0.98565 ^ \ left(N-2 \ right) \ right) \ right) \ right]>
N – represents the number of days from midnight (Universal Time) at the start of January 1, accounting for local time variations. The term ( N -2) approximates the number of days after January 1 until the Earth reaches its perihelion. The value 0.0167 signifies the current eccentricity of the Earth’s orbit. Although eccentricity changes gradually over time, it can be considered constant for dates near the present. The equation’s largest errors are less than ± 0.2°, but if the number 10 is adjusted up or down on fractional days based on the distance to the previous year’s December solstice before or after noon on December 22, the errors can be reduced to less than ± 0.03° for a specific year. These accuracies are compared to NOAA’s extended calculations using Jean Meeus’ 1999 algorithm, which achieves an accuracy of 0.01°.
The formula shown above pertains to a rather straightforward and precise computation of the equation of time, which is detailed in this article.
More advanced algorithms account for variations in ecliptic longitude by incorporating additional terms to correct for the eccentricity described earlier. They also account for the 23.44° tilt, which changes ever so slightly over time. These corrections can even take into consideration the influence of the Moon on the Earth’s position in relation to the Sun’s orbit. Once the declination from the Earth’s center is determined, another correction is applied to account for parallax, which depends on the observer’s distance from the Earth’s center. This correction is less than 0.0025 °. The margin of error in calculating the Sun’s position can be as small as 0.00015 °. To put this into perspective, the Sun appears to be about 0.5 ° wide.
Atmospheric refraction
The calculations above for declination do not take into account the impact of atmospheric refraction. As a result, the observed angle of elevation of the Sun is higher than the calculated angle. This is particularly noticeable when the Sun is low on the horizon. For instance, when the Sun is at an altitude of 10°, it appears to be at an elevation of 10.1°. By considering the Sun’s inclination in combination with its direct ascent, it is possible to calculate both its azimuth and true elevation. These values can then be adjusted for refraction in order to determine the Sun’s apparent position.
The sundial would be ahead of the clock showing mean local time above the axis, and behind the sundial below the axis.
In addition to the yearly change in the Sun’s apparent position from north to south, which corresponds to the change in its declination mentioned above, there is also a smaller but more intricate change in the Sun’s position from east to west. This is caused by the tilt of the Earth’s axis and the variations in its orbital speed around the Sun due to the elliptical shape of its orbit. The main effects of this east-west change are alterations in the timing of events like sunrise and sunset, as well as differences in the reading of a sundial compared to a clock that shows the average local time. According to the graph, sundials can be either ahead or behind by approximately 16 minutes. Since the Earth rotates at an average rate of one degree every 4 minutes with respect to the Sun, this 16-minute difference corresponds to a shift of about four degrees in the Sun’s apparent position compared to its average position. The westward shift causes the sundial to be ahead of time.
The oscillation caused by this phenomenon is referred to as the equation of time, using the term “equation” in a somewhat outdated manner to mean “correction”. This oscillation is quantified in units of time, specifically minutes and seconds, which indicate the discrepancy between the time displayed on a sundial and the time shown on a clock. The equation of time can be either positive or negative.
Analemma
The analemma is a figure-eight shaped curve that represents the apparent motion of the sun in the sky over the course of a year. It is a result of the combination of the Earth’s axial tilt and its elliptical orbit around the sun. The term “analemma” comes from the Greek word meaning “support” or “pedestal”, and it was first used by astronomers to describe the shape of this curve.
The analemma is often depicted as a diagram with two loops, one larger and one smaller, joined at a central point. The larger loop represents the sun’s position at noon at different times of the year, while the smaller loop represents the sun’s position at the same time of day but different dates. The central point where the loops intersect represents the sun’s position at the same time and date each year, known as the “mean sun”.
The analemma can be observed by taking a series of photographs of the sun at the same time every day for a year. The resulting images can be overlaid to create a single composite image of the analemma. This image will show the sun in different positions throughout the year, with higher loops in the summer and lower loops in the winter.
The analemma has been used by astronomers and navigators for centuries to determine the time and date based on the sun’s position in the sky. It has also been used to study the Earth’s axial tilt and the accuracy of calendars. Overall, the analemma is a fascinating phenomenon that represents the complex relationship between the Earth and the sun.

An analemma is a visual representation of the Sun’s changing position on the celestial sphere throughout the year, as observed from a fixed location on Earth. This diagram, which resembles the shape of a figure eight, shows how the Sun’s position varies relative to its average position. In other words, it depicts the apparent motion of the Sun over the course of a year. The term “analemma” is occasionally used in other contexts, although infrequently. One way to create an analemma is by overlaying photographs taken at the same time of day, but on different days, throughout the year.
The analemma is a representation of the Sun’s declination and the equation of time. It is typically displayed as a graph with the Sun’s declination plotted vertically and the equation of time plotted horizontally. The scale of the graph is chosen so that equal distances on the diagram correspond to equal angles on the celestial sphere. For example, the 4 angular minutes (or 3 minutes 56 seconds) in the equation of time are represented by the same distance as 1° in declination. This is because the Earth rotates at an average rate of 1° every 4 minutes relative to the Sun.
The analemma is usually depicted as if the observer is looking up at the sky, with north at the top and west on the right. This convention is followed even when the analemma is marked on a geographic globe, where the continents are typically shown from west to east.
Several analemmas are identified to indicate the position of the Sun on a graph on various dates, with a few days’ interval throughout the year. This enables the analemma to be utilized for straightforward calculations of analogous measurements like hours and azimuths derived from sunrise and sunset. Dateless analogs are employed to rectify the displayed time on the sundial.
Recommendations
- ↑ (in) Jean Mius, Astronomical Algorithms, Richmond, Virginia, Willmann Bell, Inc. 1991, 429 p. (ISBN 0-943396-35-2), “Chapter 12: Coordinate Transformations”.
- ↑ ab and c A. Jenkins, “The position of the Sun in the sky”, The European Physical Journal, vol. 34, no. 3, 2013, pp. 633 (DOI 10.1088/0143-0807/34/3/633, Bibcode 2013EJPh. 34..633J, arXiv 1208.1043)
- ↑ U.S. Naval Observatory and U.K. Hydrographic Office, HM Naval Almanac Office, Astronomical Almanac 2010, U.S. Government Printing Office, 2008. (ISBN 978-0-7077-4082-9), p. C5
- ↑ The U.S. Naval Observatory website, https://web.archive.org/web/20160131231447/http://www.usno.navy.mil/USNO, provides a set of equations called “Approximate Solar Coordinates” that cover the period from 1800 to 2200. You can visit this website to access these equations. (Archive – Wikiwix – Archive.is – Google – What to do?), as of January 31, 2016. Additionally, you can compare error plots of these equations with the exact ephemerides.
- ↑ Meeus (1991), page 152
- ↑ The Explanatory Supplement to the Astronomical Almanac: Revision of the Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Marine Almanac, published by the U.S. Naval Observatory Marine Almanac Office, is available in Mill Valley, California. It is a 752-page book (ISBN0-935702-68-7), and it contains valuable information. (University Science Books, Mill Valley, ETO, 1992), page 12
- “Selected Astronomical Constants, 2015”, U.S. Naval Observatory, 2014, K6 – K7
- “Selected Astronomical Constants, 2015”, U.S. Naval Observatory, 2014, K6 – K7
- J. W. Spencer, “Representation of the Sun’s position by Fourier series”, Search, vol. 2, po 5, May 1971, pp. 172 (read online)
- Alistair B. Sproule, “The derivation of the geometrical relations of the Sun by vector analysis” (as of February 28, 2012)
- “SunAlign” (archived March 9, 2012) (as of February 28, 2012)
- “NOAA Solar Calculator,” Earth System Research Laboratory (as of February 28, 2012)
- ↑ “Solar Calculation Details”, Earth System Research Laboratory(as of February 28, 2012)
- ↑ “Astronomical Algorithms”(as of February 28, 2012)
- ↑ Manuel Blanco-Muriel, Diego S. Alarcón-Padilla, Teodoro López-Moratalla and Martín Lara-Coira, “Solar vector computation”, Solar Energy, vol. 70, p o 5, 2001, pp. 431-441 (DOI 10.1016/s0038-092x (00) 00156-0, Bibcode 2001SoEn. 70..431B, read online)
- ↑ Ibrahim Reda and Afshin Andreas, “Sun position algorithm for solar radiation applications”(as of February 28, 2012)
- ↑ “Atmospheric Refraction Approximation”, National Oceanic and Atmospheric Administration(as of February 28, 2012)
Related Links
Articles by Subject
External resources
- Solar Position Algorithm , available at the Renewable Resources Data Center website of the National Renewable Energy Laboratory.
- Solar Position Calculator , available at pveducation.org . A helpful tool that illustrates the sun’s trajectory across the sky.
- NOAA Solar Calculator , accessible on the website of the Global Monitoring Division of the NOAA Earth System Research Laboratory.
- NOAA Sun declination and position calculator
- HORIZONS system on the JPL website . Provides highly accurate positions of solar system objects based on JPL DE series ephemerides.
- General ephemerides of solar system bodies on the IMCCE site . Offers positions of solar system objects based on INPOP series ephemerides.
- Solar position in the R package. Insol.
The Sun serves as the primary provider of heat and stands as the sole star within our solar system. It possesses a magnetic force that attracts all the planets, satellites, asteroids, comets, and other celestial bodies found in space.
The Earth is situated at a distance of over 149 million kilometers from the Sun. This particular separation between our planet and the Sun is commonly known as an astronomical unit.
Despite the considerable gap, this star exerts a tremendous influence on our planet. It determines the alternation between day and night, the change from summer to winter, the occurrence of magnetic storms, and the formation of astonishing auroras. Most importantly, the Sun’s involvement is crucial for the process of photosynthesis, which serves as the primary source of oxygen on Earth.
Our planet revolves around the celestial body that emits light and warmth within a closed trajectory. This trajectory can be depicted as an elongated ellipse. The Sun, however, does not occupy the central position of this ellipse, but is slightly displaced to one side.
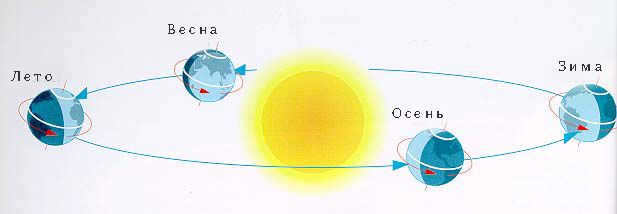
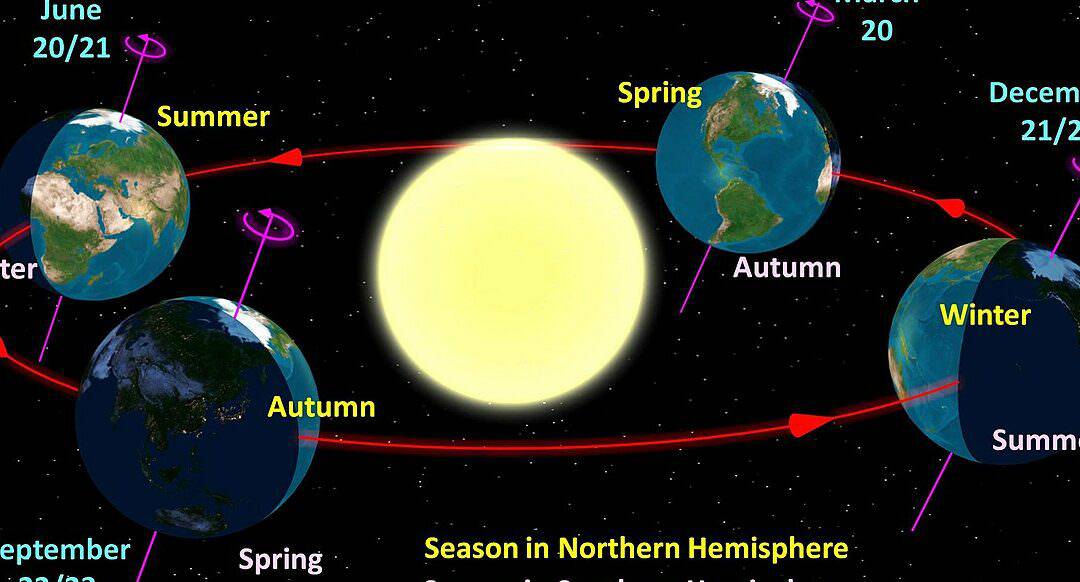
The Sun and Earth have a dynamic relationship, with the Earth moving closer and farther away from the Sun as it completes a full orbit in 365 days. In the month of January, our planet reaches its closest point to the Sun, known as the perihelion, where the distance between the two celestial bodies is reduced to 147 million kilometers.
When the Earth is at its closest to the Sun, the South Pole receives more sunlight, leading to the start of summer in the countries of the southern hemisphere.
As we approach July, our planet reaches its maximum distance from the primary star of our solar system. At this time, the distance between Earth and the Sun exceeds 152 million kilometers. This farthest point in Earth’s orbit is known as the “aphelion”. The greater the distance from the Sun, the more light and heat the countries in the northern hemisphere receive. This is why it is summer in these regions, while winter prevails in places like Australia and South America.
The way in which the Earth is illuminated by the Sun during various seasons
The amount of light that the Earth receives from the Sun during different seasons is determined by two main factors: the distance between our planet and the Sun at any given time, and the specific side of the Earth that is facing the Sun at that particular moment.
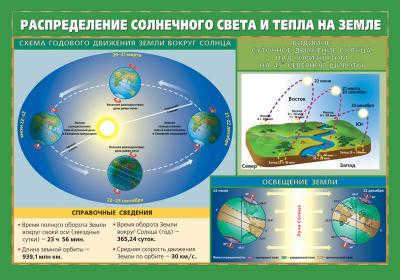
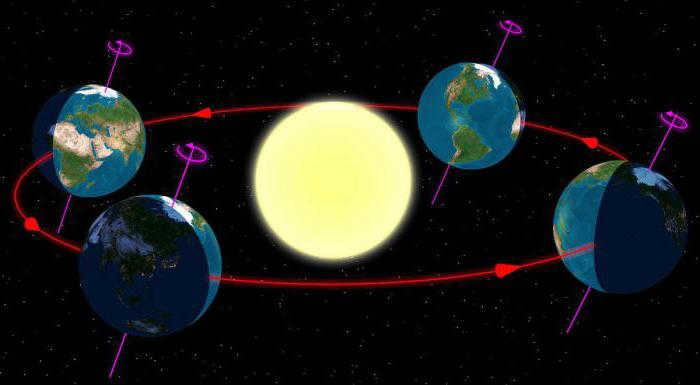
The Earth’s axis is the most crucial factor that influences the alteration of seasons. While our planet orbits the Sun, it also manages to rotate on its own axis. This axis is tilted at an angle of 23.5 degrees in relation to the celestial luminary and consistently points towards Polaris. A complete revolution around the Earth’s axis takes 24 hours. The axial rotation is also responsible for the transition between day and night.
Interestingly, without this tilt, the seasons would remain constant and not change. This means that certain regions would experience perpetual summer, while others would have a continuous spring or autumn. There would be a portion of the Earth that would continuously receive rainfall during the autumn season.
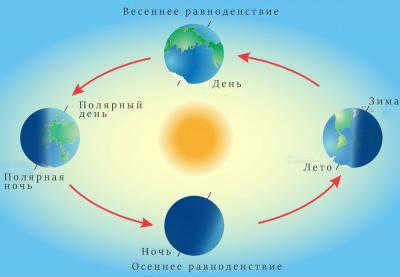
The sun’s rays fall alternately on the poles of the earth. As a result, half of the year is daytime and the other half is nighttime at the poles. When the North Pole is illuminated, it signals the start of spring in the northern hemisphere, which then transitions into summer.
Over the next six months, the scenario reverses. The South Pole now faces the sun, marking the beginning of summer in the southern hemisphere, while the countries in the northern hemisphere experience winter.
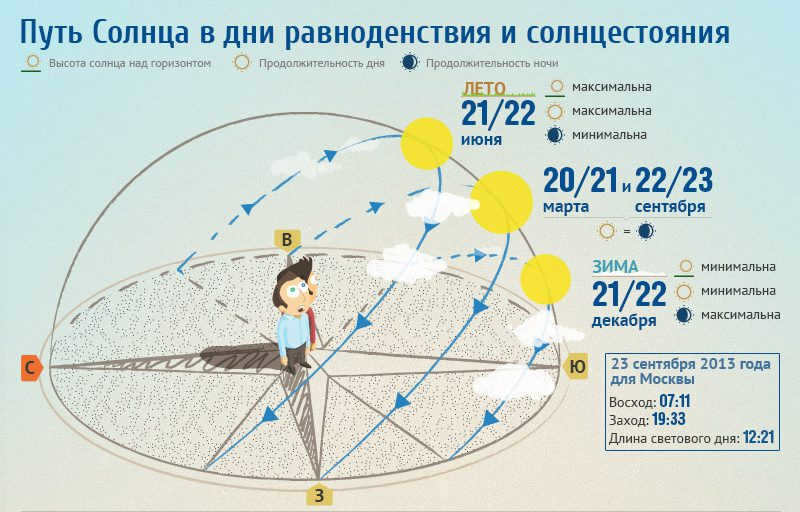
Twice a year, our planet finds itself in a position where the sun’s rays evenly illuminate its surface from the far north to the South Pole. These occasions are known as equinox days. The vernal equinox is observed on March 21, while the autumnal equinox is observed on September 23.
There are also two other significant days known as solstices. During these times, the Sun is either at its highest point above the horizon or at its lowest point.
In the northern hemisphere, the longest night of the year occurs on December 21 or 22 – this is the winter solstice. Conversely, on June 20 or 21, the day is the longest and the night is the shortest – this is the summer solstice. In the southern hemisphere, the opposite is true. There, the days are long in December and the nights are long in June.
Where does the sun rise in the morning hours, on which side of the world? How does the sun move across the globe?
Shift in position along the equator
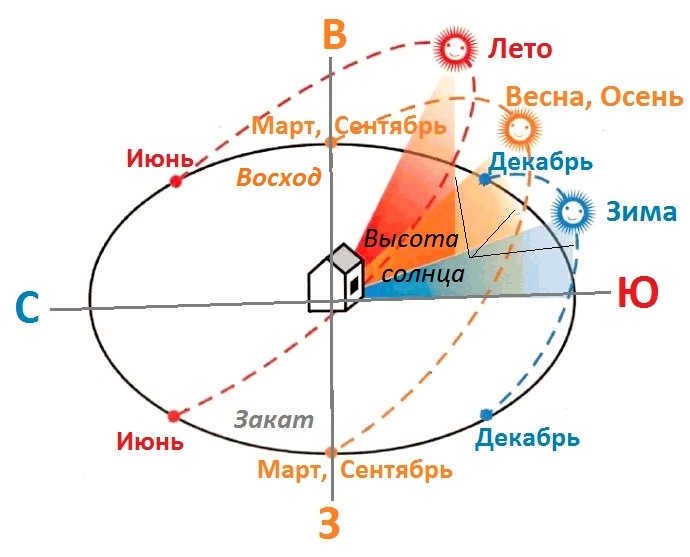
When a star is located in the vernal equinox zone, its ascension is at zero. Over time, the ascension gradually increases and eventually reaches 90 degrees, while the declination reaches its maximum value of +23 degrees 26 minutes. Afterward, there is a noticeable increase in the direct ascension and a complete decrease in the declination. As a result, at the autumnal equinox, the value becomes 180 degrees. Following that, there is a further increase in the direct ascension, and at the peak of the winter solstice, it reaches 270 degrees. The declination, on the other hand, starts at 23 degrees 26 minutes and continues to increase.
According to the Sun and known time
This technique is still relatively new and has not yet become widely used among orienteers. However, it offers the ability to accurately plan the rest of the route with just a watch. Both mechanical and electronic watches can be used for this method.
The method is based on the fact that the celestial body moves at a speed of 15 degrees per hour along the horizon. Additionally, it is important to know the position of the star at specific times: 6, 12, 18, and 24 hours.
Determining the direction using the sun and known time
The process of orienting oneself using the sun and known time is as follows:
- Calculate the time remaining until 12 o’clock noon or, conversely, the time extending past noon. This is considered the pivotal time, as the Sun passes the meridian at its zenith.
- Once the time and location of the star are obtained, the angle is computed with respect to the north-south line.
- In the morning, the calculated angle is adjusted along the path of the sun’s movement. In this case, the observer should position themselves to the left of the sun, with the north ahead and the south behind.
- After noon, the angle is adjusted in the opposite direction, but the observer should stand to the right of the sun.
This method is not ideal for navigating in tropical forests or near the equator, as it can result in significant errors. In these regions, alternative methods such as using a gnomon are recommended for determining directions.
Observable yearly motion of the Sun
The yearly motion of the Sun can be easily explained with a logical and reasonable explanation. There exists a specific system that provides a more detailed description of this phenomenon. It illustrates that depending on the Earth’s position, one can witness the Sun appearing against various constellations. This observation leads to the realization that the Sun is continuously in motion. This motion is a direct result of the Earth revolving around our star. Over the course of a year, the Earth completes a full revolution around the Sun.
The Sun’s constant movement along the ecliptic is accompanied by a similar motion of the planet along its orbit, specifically towards the east. Throughout the year, the star passes through 12 constellations on the ecliptic, giving rise to the zodiacal belt and its well-known signs.
The celestial equator, like the ecliptic, is inclined at an angle to the Earth’s orbit due to the equatorial plane being tilted at 23 degrees 27 minutes. This angle remains constant, but can be influenced by the gravitational forces of the Moon and the Sun, which constantly act on Earth.
Therefore, during the approval process of astronomical constant units in 1896, it was determined that the inclination should be considered at a value of 23 degrees 27 minutes 8 seconds.
Techniques for Sun-based orientation
There are numerous techniques that enable one to orient themselves using the Sun. These include using the position of the clock’s hand or the shadow of a gnomon, as well as simply observing the Sun’s movement along the horizon. By employing these methods, one can chart their future path. In certain situations, this skill can prove to be life-saving, allowing individuals to not only locate specific objects on the ground but also ensure their own survival.
Furthermore, there are certain nuances to Sun-based orientation that depend on the time of year and the observer’s geographical location.
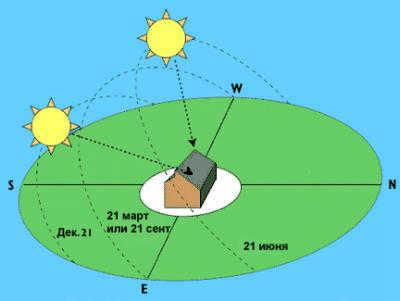
The sun rises precisely in the east and sets precisely in the west during the spring and fall equinoxes, which occur on March 21 and September 23. On other days, the sun’s position shifts towards the north or south, depending on the time of year.
The timing of sunrise and sunset varies depending on the time of year.
Following the vernal equinox, as the Earth moves closer to the sun, the sunrise gradually shifts towards the north each day. On June 21, the summer solstice, it can be accurately determined that the sun rises in the northeast and sets in the northwest. Then, the sun’s movement shifts towards the south, and on the day of the winter solstice (December 22), the sunrise is observed in the southeast, while the sunset occurs in the southwest.
If you are looking for information on the Sun’s position in the Southern Hemisphere, the calculations provided here are specifically for the Northern Hemisphere. The data for the Southern Hemisphere would be completely opposite.
The Celestial Equator and Ecliptic Plane
In order to better understand and explain the movement of the Sun, it is helpful to consider the processes taking place on the celestial equator. The ecliptic intersects with the celestial equator in two specific zones, known as the equinox points. These points occur in March (21) and September (23), and on these days, day and night are of equal length on Earth.
Solstice points are the points on the ecliptic that are 90 degrees away from the equinoxes. These points mark the highest and lowest positions of the star in relation to the sky’s equator. The summer solstice, which occurs on June 22, is when the Sun is at its highest point. On the other hand, the winter solstice, which falls on December 22, is when the Sun is at its lowest point.
The gnomon is considered to be one of the oldest inventions that enabled the determination of both the north-south direction and the height of the Sun through the shadow it casts. A gnomon can be any vertical object (such as a pillar or column) situated on a flat, open surface.
Furthermore, the gnomon serves as the primary component of sundials, which are strictly positioned on the cardinal directions. Throughout ancient times, these timekeeping devices have provided an accurate means of telling time by utilizing shadows.
Utilizing the shadow of the gnomon for measurement
Often, a long object is selected as the gnomon to facilitate more precise measurements, as variations in shadow length are readily discernible. However, longer shadows tend to be less distinct. Hence, the pointed shape is incorporated at the top of the gnomon to enhance clarity.
To make more accurate calculations using the gnomon, it is important to keep in mind a few key points:
- Remember that the shadow from the gnomon moves from west to east, opposite to the motion of the Sun.
- Take note that the shortest shadow indicates the beginning of astronomical noon, while the longest shadows occur at sunrise and sunset.
- When the Sun reaches the zenith, the shortest shadow is observed. At this moment, the solar landmark aligns with the true meridian line.
- Keep in mind that the shadow of the gnomon changes most rapidly at the start and end of the Sun’s path. In the middle of the day, the shadow moves at a slower speed, which can be helpful for measurements.
Orienteering using the gnomon is typically conducted during sunny weather conditions. By identifying the shortest shadow cast by the instrument, the observer can determine the direction of the north. In the Southern Hemisphere, the shadow will indicate the south.
This technique allows for the determination of noon without relying on a clock, as well as the identification of the cardinal directions, and thus, the planning of a route.
Coordinates in the Equatorial System
The position of the Sun in the sky changes unevenly throughout the year due to its erratic movement along the ecliptic, which is tilted towards the equator. During a period of 186 days, from March 21 to September 23, the Sun covers about half of its visible annual path. The remaining half takes 179 days for the rest of the year.
This unevenness is caused by the fact that Earth orbits the Sun at different speeds throughout its revolution. The Sun is located at one of the foci of the ecliptic. According to Kepler’s second law, the line connecting these celestial objects describes the same area in equal periods of time. Therefore, the planet moves quickly in the winter season and slowly in the summer.
Based on mechanical clocks and the Sun
The concept behind this technique is that the Sun’s movement across the sky is half as fast as the movement of the hour hand on a mechanical clock. Thus, if there is a mechanical clock that shows the local time, it is possible to determine the direction towards the south by observing the position of the Sun. Once one direction is established, the others can be deduced.
It is important to note that this method is only accurate in high latitudes. In low and middle latitudes, using clocks to find the cardinal directions can lead to significant errors due to the uneven projection of the Sun. Therefore, if a tourist becomes lost in the forests of this zone, relying on time and the Sun for orientation can only worsen the situation.
The implementation of this technique will enable the determination of the north-south direction. In order to accomplish this, the following steps should be taken:
- Place the mechanical watch horizontally with the dial facing upwards.
- Align the clock hand pointing to the celestial luminary.
- Mentally visualize the angle between the number “12” on the dial and this hand.
- Divide the resulting angle into two equal parts using a straight line, which will indicate the direction of the south.
To conveniently and accurately perform the calculations, it is important to remember:
- If the orientation is done at 6 o’clock in the morning, the bisector should be drawn towards the division equivalent to “9”.
- If the clock displays 6 o’clock, but it is evening, the bisector should be directed towards the number “3”.
- This order is applicable only in the Northern Hemisphere as the Sun moves from left to right in this region. Different conditions apply in the opposite hemisphere.
This method of orientation using clock hands is widely used. And there’s no need to worry if you have a watch without numbers. You can still determine the cardinal directions and navigate to a specific location using them.
Electronic watches can also be used. In this case, it’s not just about knowing the time, but also about depicting a circular dial based on the current position of the Sun.
At 7 am, the Sun rises in the east, then at 1 pm, it reaches its highest point in the south, and towards the end of the day, around 7 pm, it sets in the west. By knowing these key positions of the Sun, it is possible to calculate the intermediate directions.
Solar eclipse
An eclipse of the Sun has always evoked a range of emotions in people who are unaware of its scientific explanation, leading to fear and panic. There have also been individuals who sought to take advantage of the event and gain recognition as fortune tellers and clairvoyants. Interestingly, not only humans but also animals react to the sudden darkness, although they mostly perceive it as the onset of night.
Interesting fact: Why is Mars red? Description, photos, and video
Solar eclipse – diagrams
The simple scientific explanation for this phenomenon is that the Moon moves in front of the Sun, causing an eclipse. This only happens during the new moon phase when the Moon, Sun, and Earth are aligned, and even then it doesn’t happen every time. There are different types of solar eclipses depending on the observer’s position on Earth:
- A “partial” eclipse occurs when the Moon only partially covers the Sun’s disk.
- A “total” eclipse occurs when the Moon completely covers the Sun, blocking out all light.
- An “annular” eclipse occurs when the Moon is farther away from Earth, creating a ring of sunlight around the Moon.
- A “total annular” or “hybrid” eclipse occurs when two observers at different locations see different types of eclipses simultaneously.
Based on the Sun’s position
Regrettably, there are instances when an individual traveler or a group of tourists becomes disoriented in an unfamiliar area without a compass, map, or knowledge of emergency azimuth. It is particularly easy to get lost in a forest.
In such cases, one is faced with the task of selecting a clear and direct path instead of wandering aimlessly. This is where a method comes in handy, which explains how to navigate through a forest by observing the position of the Sun. By doing so, one can quickly reach a significant landmark, such as a highway or a river, and ultimately find their way to a populated area.
There is a step-by-step algorithm for orienting oneself using the Sun’s position:
- Firstly, it is necessary to calculate the azimuth in relation to a solar landmark;
- Locate a distant landmark in the direction of the person’s movement and head towards it.
- Once there, use the previously calculated data to navigate towards the next landmark.
- Continue moving from one landmark to another until the lost person reaches a familiar or residential area.
It is important to note that when calculating the angle, it is done in relation to the luminous star’s projection. If the star is in front of the observer, the angle is calculated on the left or right side. However, if the star is behind the observer, the azimuth should be determined based on the shadow it casts.
Determining azimuth using a compass
The celestial body known as the Sun is visible from all corners of the globe. Each morning, it illuminates the heavens, prompting curiosity among many individuals about the precise location from which it ascends.
What is the origin of the sun?
The sun’s origin can be traced to its appearance in the east and its gradual movement across the sky until it sets in the west. In ancient times, people believed that the Earth was at the center of the universe and that all celestial bodies revolved around it. However, this viewpoint is no longer considered scientific and has been thoroughly disproven.
The Sun, an immovable star, is the center of our solar system. Meanwhile, the Earth, constantly in motion along its orbit, revolves around the Sun, creating a phenomenon we witness every morning – the sunrise in the east and its end in the west.
What is the significance of tracking the Sun’s movement?
As the need to measure time emerged, people sought ways to accomplish this task. In ancient times, it was believed that one could determine the passage of time solely through the movement of the Sun or the Moon during the night. Why are individuals so captivated by this celestial body and why is it vital for some to monitor its trajectory?

- The day starts with the sunrise and ends with the sunset.
- Many organisms on Earth have their biological clocks and rhythms synchronized with these natural phenomena.
- Astrologers and horoscope enthusiasts also consider the sunrise and sunset times for their calculations.
- Astronomers utilize these events for various scientific studies.
- Ancient civilizations relied on the changing position of the sun in the sky to develop the first timekeeping devices, such as stone sundials.
- The measurement of days and months is also determined by the placement of the sun, which is exemplified in the contemporary Gregorian calendar. Here, a day is defined as the time between one sunrise and the next, while a year is symbolized by a complete orbit around the star.
It can be concluded that monitoring the position of the Earth relative to the Sun remains important in the present day. Scientists also continue to monitor its activity, predict magnetic storms, and perform other measurements.
The advantages of the Sun for humans
The significance of the Sun in human life should not be underestimated. However, researchers are still studying its impact on the human body. A team of scientists from Edinburgh discovered that exposure to the Sun can lead to the following processes in the body:

- There is a decrease in blood pressure.
- There is a reduction in the risk of developing thrombosis.
- The body undergoes rejuvenation.
- The metabolism experiences improvement.
- The risk of stroke development is lowered.
- Blood circulation is enhanced.
Furthermore, the sun plays a vital role in preventing heart attacks, cancer, and other diseases. Additionally, it produces a beneficial vitamin D that strengthens bones and detoxifies the body by removing heavy metals.
Some of the advantages of sunlight include:
- It stimulates the production of serotonin, a hormone responsible for blood clotting. Moreover, an adequate amount of this substance enhances mood, earning it the nickname “the happy hormone”.
- Exposure to sunlight releases biologically inert nitrite NO3, which helps lower blood pressure and reduces the risk of heart failure or heart attacks.
- Sun rays possess antibacterial properties, leading to faster wound healing, disappearance of acne and pimples, and overall improved skin health.
However, this is by no means an exhaustive list of the beneficial properties that sunlight possesses. Furthermore, it is important to acknowledge the overall advantages of the sun for all forms of life on Earth.
The sun can pose a threat
It would be incorrect to assume that the sun’s rays are entirely beneficial without any need for caution. In addition to the numerous advantages they offer, they can also inflict significant harm if not handled with care.


- Extended exposure to the sun can result in the appearance of a tan, which is the body’s way of protecting itself from the harmful effects of ultraviolet rays. Failing to take action and protect your skin when it first turns red can easily result in a severe sunburn. In some cases, it can even lead to the development of skin cancer.
- It is not advisable to look directly at the sun without sunglasses, as its intense brightness can lead to blindness or damage to your eyesight.
- Individuals with dry skin should avoid prolonged sun exposure without the use of moisturizing cream, as the rays can further dry out the skin.
Therefore, it is crucial to take precautions when exposed to direct sunlight and shield your head with a hat of light color, hydrate adequately, and wear sunglasses. Additionally, try to avoid being outdoors during the sun’s peak hours.
The sun is a celestial body that provides warmth and illumination to all living beings on Earth, rising in the eastern horizon. However, apart from its benefits, it can also pose risks, and this should not be disregarded.
The sunlight is one of the most vital elements on our planet. It sustains life in every living organism, and without it, our existence would be impossible. But how does it impact us? And what causes the sun to emit light? Let’s explore the mechanisms behind these phenomena.
Yet Another Star in the Celestial Expanse
In times of antiquity, humanity grappled with the enigma of the Sun’s radiant illumination. However, even in those bygone eras, astute observers noticed its arrival at dawn and its departure at dusk, yielding to the radiant splendor of countless stars. Regarded as a celestial deity, it represented luminosity, benevolence, and supremacy. In the present era, scientific progress has afforded us a deeper comprehension of our nearest star. Countless online resources and literary works provide us with a wealth of knowledge, and even esteemed institutions like NASA offer breathtaking imagery captured from the vastness of space.
In this modern epoch, we can confidently assert that the Sun is no longer an enigma but rather a star, akin to the multitude of celestial bodies that grace our nocturnal vista. However, the distance that separates us from these other stars renders them minuscule points of light when observed from our terrestrial perspective.
The Sun is significantly nearer to us, and its radiance is much more apparent. It serves as the hub of the stellar system. Encircling it are planets, comets, asteroids, meteoroids, and other celestial bodies. Each entity follows its unique orbit. Among these, the planet Mercury occupies the closest position to the Sun, while the outermost regions of the system remain uncharted. Sedna, one of the most remote objects, completes a full orbit around the Sun every 3420 years.

What is the reason behind the Sun’s brightness?
Similar to all celestial bodies, the Sun is an enormous sphere of intense heat. It is believed to have originated from the remains of other stars approximately 4.5 billion years ago. The gas and dust released from these stars began to condense into a cloud, gradually increasing in temperature and pressure. As it reached a temperature of around ten million degrees, the cloud transformed into a star, which ultimately became a colossal energy source.

The reason behind the Sun’s shining is the presence of thermonuclear reactions happening inside it. Within the core of our star, hydrogen atoms are constantly being converted into helium atoms due to the extremely high temperatures of around 15.7 million degrees. This conversion process generates an enormous amount of thermal energy, resulting in the Sun’s radiant glow.
Thermonuclear reactions exclusively occur within the solar core. The radiation produced by these reactions spreads throughout the star, creating various outer layers:
- a region of radiative transfer;
- the convective zone;
- the photosphere;
- the chromosphere;
- the corona.
The majority of visible light is generated in the photosphere, an opaque shell that corresponds to the surface of the Sun. The temperature of the photosphere is 5,000 degrees Celsius in Celsius, but there are certain cooler regions known as spots. The temperature increases again in the upper layers.
Our star is a yellow dwarf, not the oldest or largest star in the Universe. It has reached about halfway through its evolution and will remain in this state for approximately five billion years. After that, the Sun will transform into a red giant and eventually shed its outer shell, becoming a faint dwarf.
The light it currently emits appears almost white in color, but from our planet’s surface, it appears yellow due to scattering and passage through the Earth’s atmosphere. The true color of the radiation is most apparent in very clear weather.
Interaction between the Earth and the Sun
The relative position of the Earth and the Sun is in constant flux. Our planet continuously orbits around the star, completing a full revolution in approximately 365 days. Over the course of this orbital journey, the Earth travels a staggering distance of 940 million kilometers. Despite this incredible movement, the sensation of motion is not felt on the planet’s surface, even though it travels an average of 108 kilometers every hour. However, the consequences of this perpetual journey are evident on Earth in the form of the ever-changing seasons.
However, the seasons are not only determined by the Sun’s motion, but also by the Earth’s axis tilt. The Earth is tilted by 23.4 degrees relative to its orbit, causing different parts of the planet to be illuminated and warmed by the Sun differently. When the Northern Hemisphere is facing the Sun, it experiences summer while the Southern Hemisphere experiences winter at the same time. Six months later, the situation is reversed.
We often use the phrase that the Sun appears during the daytime. However, this is simply a way of expressing that the Sun creates the day for us. Its rays penetrate the atmosphere, illuminating the planet from morning until evening. The intensity of its brightness is so powerful that we are unable to see other stars during the day. During the night, the Sun does not cease to shine. Rather, the Earth rotates, causing different sides of the planet to face the Sun at different times. This rotation occurs both in its orbit around the Sun and on its own axis. A complete revolution takes place within a 24-hour period. The side facing the Sun experiences daytime, while the opposite side experiences nighttime. This cycle repeats every 12 hours.
Unreplaceable source of energy
The distance from our planet to the Sun is approximately 8.31 light years or 1.496-10 8 kilometers, which is essential for the existence of life. If the Earth were closer to the Sun, it would resemble the lifeless Venus or Mercury. Nevertheless, in about a billion years, the Sun is expected to become 10% hotter, and in another 2.5 billion years, it has the potential to completely eradicate all life on our planet.

At present, the star’s temperature is ideal for our needs. This has led to a diverse range of life forms on our planet, including plants, bacteria, and humans. All of these organisms rely on sunlight and warmth, and prolonged absence of these elements would result in their demise. The star’s light plays a crucial role in photosynthesis, which is essential for producing oxygen. Additionally, its ultraviolet radiation enhances the immune system, stimulates vitamin D production, and aids in the atmosphere’s self-cleaning process.
The Sun’s uneven heating of the Earth generates the movement of air masses, which subsequently influences the planet’s climate and weather. The star’s light also influences the establishment of circadian rhythms in living organisms, meaning their activity is closely tied to the changing time of day. As a result, some animals are active exclusively during the daytime, while others are active solely at night.
Studying the Sun
Out of the star systems closest to us, the Sun doesn’t hold the highest position in terms of brightness. It actually ranks fourth in this regard. For instance, Sirius, a star that can be easily seen in the night sky, surpasses the Sun’s brightness by a staggering 22 times.
Despite this, it is extremely dangerous to observe the Sun with our bare eyes. Its proximity to Earth means that looking at it without proper instruments can have disastrous consequences for our eyesight. In fact, the Sun appears about 400,000 times brighter to us than the Moon’s reflected light. We can only observe it with our naked eye during sunrise and sunset, when its angle is small and its luminosity decreases by thousands of times.