The path of the celestial bodies

In my recent article discussing the phenomenon of Halley’s Comet, I had a sudden realization that the defining factor of a celestial body’s uniqueness lies within its trajectory. This epiphany came to me unexpectedly, almost in a stream-of-consciousness manner, and now requires further exploration and analysis.

It is important for me to clarify this concept for my readers.

Have you ever pondered the question: “What exactly is an orbit, and is it possible for multiple celestial bodies to occupy the same orbit simultaneously?”

For most individuals, the notion of an orbit is simply a path that resembles a line, often circular or oval in shape. However, for astronomers, the concept of an orbit holds a much more intricate meaning.

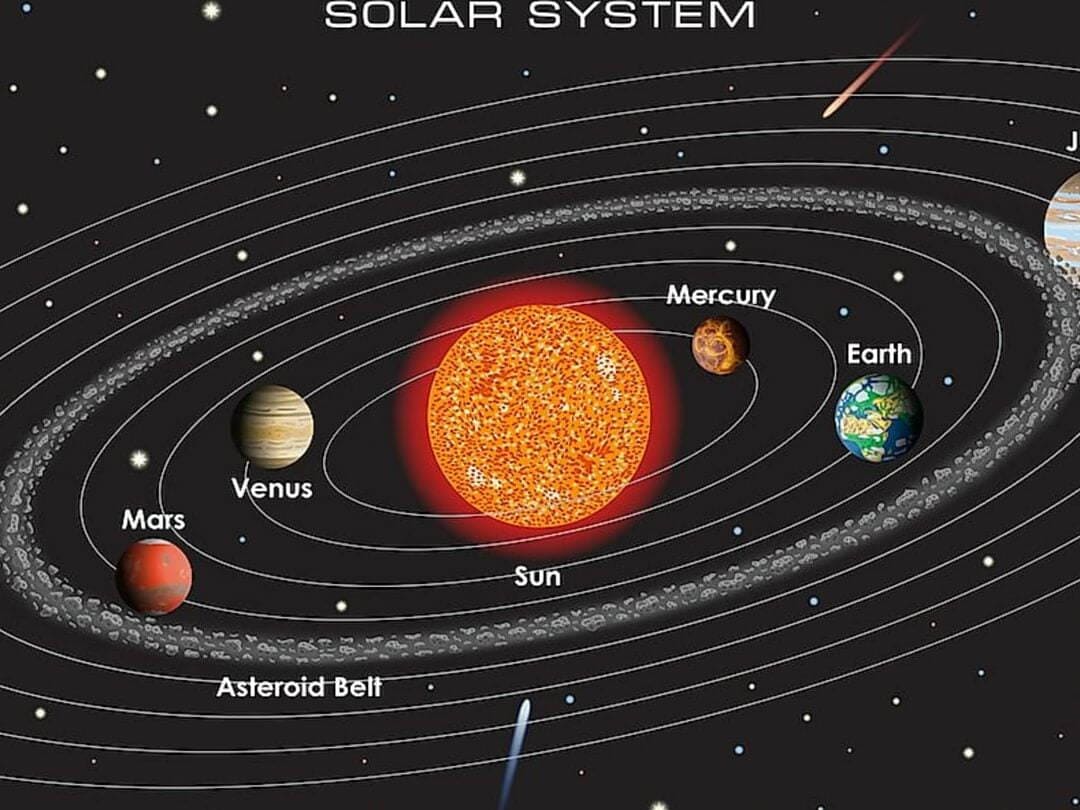
Our solar system consists of eight planets that orbit the Sun. Each planet has its own unique trajectory and path as it travels through space. The trajectory of a planet is determined by its mass, velocity, and the gravitational pull of the Sun. The paths of the planets are not perfectly circular, but rather elliptical, meaning that they are slightly elongated and asymmetrical. This creates a beautiful and dynamic dance as the planets move in their orbits.

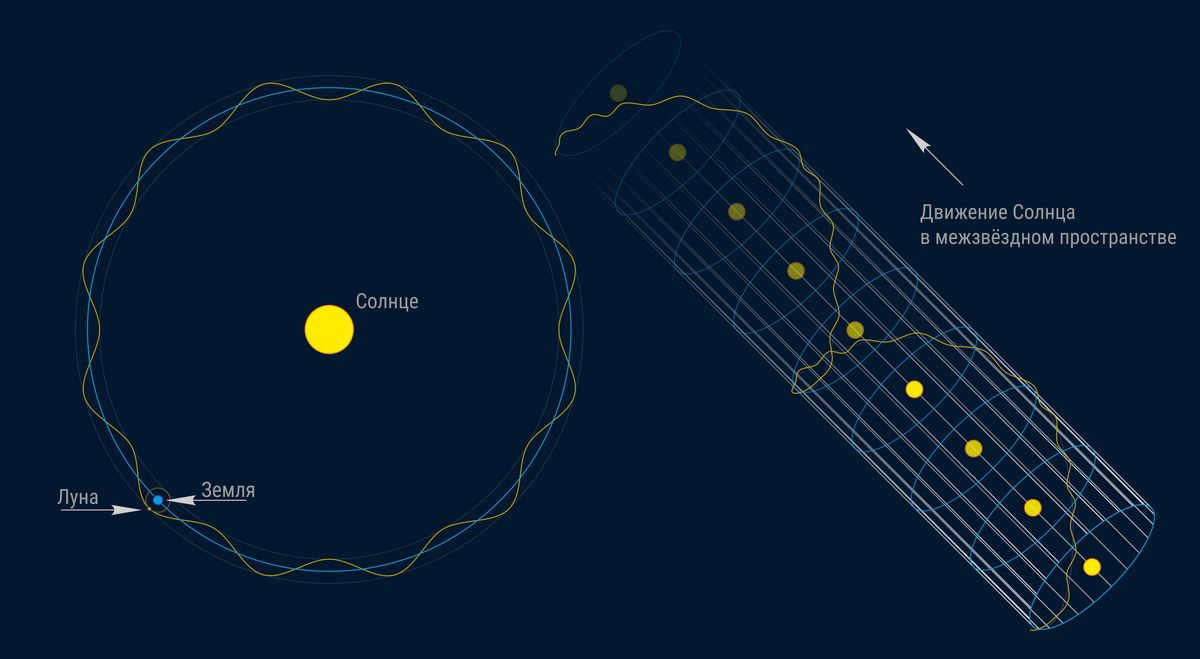
First and foremost. Astronomers establish the parameters of a given orbit within a specific coordinate system, fully aware that the same orbit may appear drastically different when observed from an alternate coordinate system. An excellent example of this phenomenon is the orbit of the Moon, which, when viewed from the Earth’s perspective, takes the form of a slightly elongated ellipse. However, when observed from the Sun’s perspective, the Moon’s orbit resembles a sinuous snake, akin to a “creeper” enveloping the Earth’s orbit. If we distance ourselves from the Sun and examine the Moon’s orbit from a reference frame that is maximally representative of the stellar environment closest to us, we would perceive a highly stretched and mildly undulating spring-like trajectory – a trajectory that remains open, directed towards the distant stars of the Hercules constellation. The choice of reference frame is essentially limitless. For the sake of our current discussion, let us focus on the reference frame that is most pertinent to us – the one oriented around the Sun, taking into account the bodies within our solar system.

Now that we have a better grasp on the concept of “orbit,” let’s focus on how astronomers differentiate between celestial bodies.

While it’s easy to distinguish the Sun from the Moon, there may be some confusion when it comes to the others.

It might appear peculiar to some – well, isn’t it evident – there was an entity that could be seen in the evening twilight, then it descended into the twilight and ceased to be visible, and a few days later something resembling it emerged in the morning twilight. Intuition implies that this is the identical “something”. However, how can we eliminate the possibility that there are two similar but physically distinct entities that alternately change each other in some regular pattern? By the way, there are still individuals who naively hold the belief that the Moon (full) and the slender Crescent are two distinct celestial bodies that, according to certain rules, replace each other in the sky and are even occasionally observed simultaneously.

However, when it comes to Venus and the Moon, it is possible to experience confusion. This raises the question of how we can accurately identify and distinguish between the many asteroids and comets that exist. When observing them through a telescope, even with the highest magnification, they may appear indistinguishable – a star is a star, lacking any discernible details (in the case of asteroids, also known as small planets). On the other hand, comets can constantly change their appearance, sprouting a tail, losing it, exhibiting a fluffy head, and varying in brightness. Over the course of a few nights, they can transform from a faint, foggy spot into something that spans the entire sky. It becomes challenging to ascertain whether we are observing the same object we saw the previous night or if it is a different object that bears a striking resemblance.

Indeed, celestial objects have the ability to move and alter their appearance. This can sometimes be misleading. Take Venus and Mercury, for instance, which can be easily mistaken for one another when observed through a telescope. Both of these planets undergo similar phases and lack obvious surface features. Granted, Venus is larger than Mercury, but in the absence of a direct comparison, there is room for uncertainty. Additionally, Saturn bears a striking resemblance to Jupiter when its rings vanish from view (this occurs every 15 years when the rings align with our line of sight). As a result, an inexperienced observer may easily mix up the two. Distinguishing between Uranus and Neptune can also pose a challenge, as William Herschel himself initially misidentified Uranus as a comet when he first discovered it. These instances demonstrate the potential for confusion.

And there is only one piece of knowledge that allows us to unequivocally identify this object and not another – the fact that it resides in its designated orbit and is situated precisely in the region of the sky where it should be. Neptune was discovered precisely in its orbit, at the exact point in space where it was expected to be, and although it had never been observed before, its position in space indicated that it was indeed the planet we were searching for. A similar narrative applies to Pluto – it was classified as a planet solely due to its pre-calculated orbit. And in spite of its unassuming physical characteristics, it retained its status as a major planet within the solar system for several decades purely because of its orbit.

"Planet X dances in the cosmos!"

At present, scientists are on the lookout for the elusive "Planet X", whose trajectory has already been calculated to some degree (thanks to the computations of Konstantin Batygin and Michael Brown). The main challenge now lies in actually detecting a tangible object following this orbit. Nevertheless, the orbit serves as the primary characteristic of this celestial entity – even though the body itself has yet to be found, the orbit is already established (based on certain assumptions).

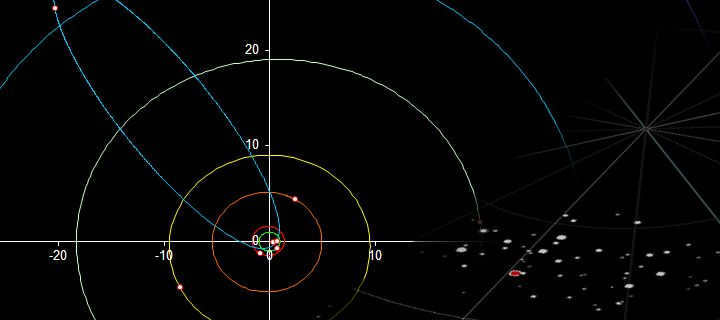
There are certain instances where it may appear that multiple celestial bodies coexist on a single orbit. It is important to note the existence of Lagrangian points, specifically L3, L4, and L5, which are depicted in the image as lying on the primary celestial body’s orbit with considerable accuracy. However, it is crucial to understand that this depiction is only true in the image. In reality, any objects that happen to fall within the gravitational equilibrium of Lagrangian points are involved in at least two orbital motions simultaneously, or their orbits can be viewed as a combination of at least two components.

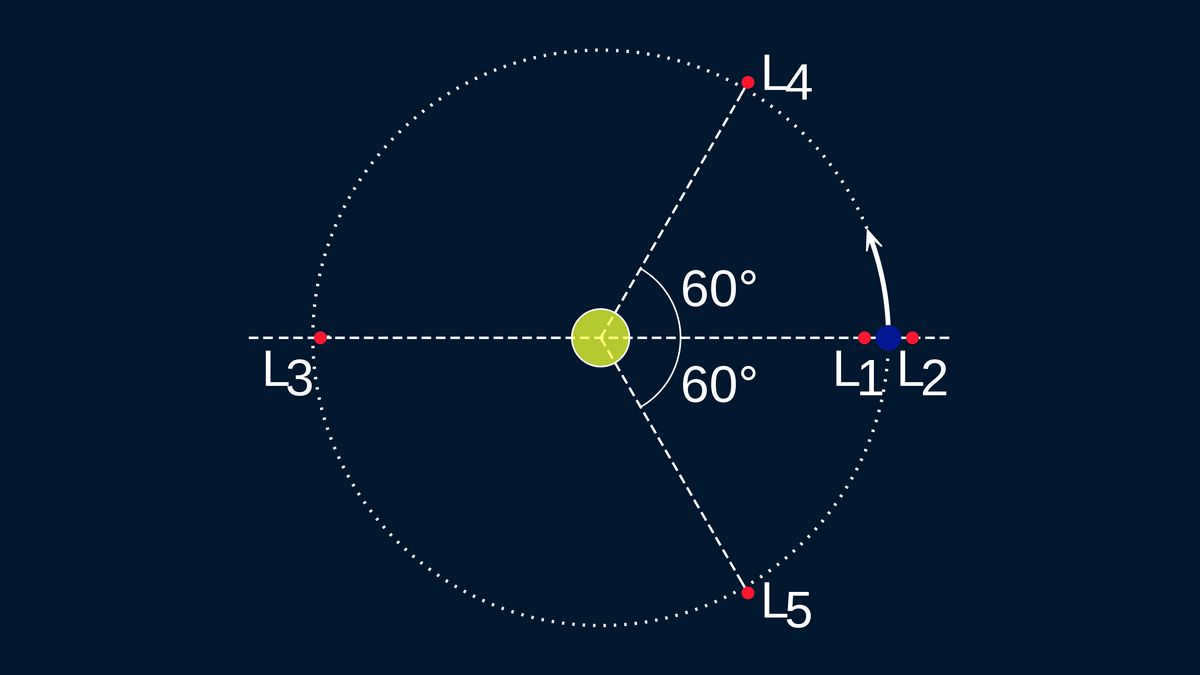
Initially, their radius-vector always slightly exceeds or falls short of the radius-vector of the “parent orbit” (for points L4, L5 – slightly exceeds; for L3 – slightly falls short), however, in the field of astronomy, these slight deviations hold great importance.

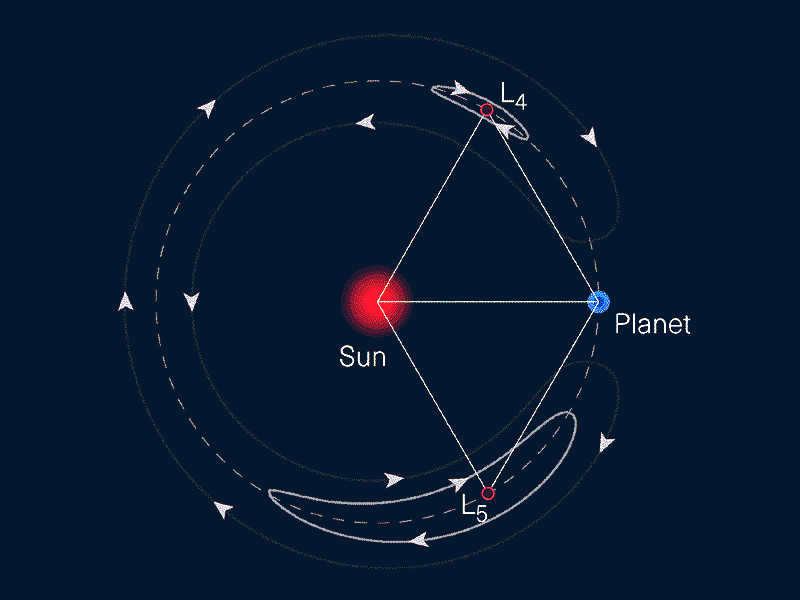
Additionally, having precise knowledge about such closely positioned orbits enables us to dispatch spacecraft to investigate the cluster of Trojan asteroids. In fact, a spacecraft called Lucy has already been launched in 2021. Its mission is to study four asteroids near the L4 point of the Sun-Jupiter system (known as the Greeks) and two asteroids near the L5 point (known as the Trojans). These asteroids form a interconnected gravitational system and revolve around a shared center of mass. Each asteroid follows its own unique orbit, which is meticulously calculated and accounted for with utmost precision. Therefore, astronomers will not mistake these two asteroids, despite their closely aligned orbits in relation to the Sun (although they are still distinct from each other).

In the history of celestial objects, there have been instances where objects underwent significant alterations in their orbits, as orbits are susceptible to change. This is particularly evident in comets – comets are highly reliant on the gravitational influence of massive planets. Occasionally, comets become captured by a massive planet and become its companions. Subsequently, they break free and find themselves in an entirely different orbit around the Sun. Is it reasonable to consider a comet the same comet following such orbital transformations?

The journey of a comet in astronomical history commences with its detection, followed by the assignment of a name – typically derived from the discoverer’s surname or surnames in cases where multiple observers independently spot the same comet. Alternatively, the comet’s name may reflect the moniker of an automated observation system, as an increasing number of comets are being identified using orbiting telescopes. If a comet is temporarily lost but subsequently rediscovered, the name of the astronomer responsible for the rediscovery is appended to the original name. This essentially results in a change in the comet’s name, as if it has undergone a transformation of some sort – a divergence. Often, this change is attributed to the comet’s altered orbit. A different trajectory necessitates a different name, signifying a distinct celestial entity… although it may physically remain an ice block.

Isn’t it incredible?

Occasionally, a celestial entity meets its demise. Planets occasionally collide with comets. Scientists have witnessed several instances of this phenomenon firsthand and have even been able to predict them. One particularly remarkable example is the event known as the Shoemaker-Levy 9 comet’s impact on Jupiter. This event occurred in 1994, and the comet itself no longer exists in its original form. However, its orbit still remains – a specific trajectory in outer space that the comet followed at one point in time. It can be challenging to comprehend the notion of an orbit existing independently from a celestial body!”

Let’s envision a future scenario where our far-off descendants possess the technological capability to relocate a planet to a different orbit. It is possible that one day we may find ourselves needing to do the same for our own Earth, as the Sun gradually continues to heat up, rendering the conditions near its current orbit inhospitable for life.

Would a celestial body that has been towed into a new orbit still be regarded as the same planet and retain its original name?

This is a question of consensus. As individuals make their decisions, so it shall be. However, it is crucial to recognize that it is the present trajectory of the Earth that renders the conditions on its surface suitable for us. If our planet were slightly nearer to the Sun or slightly farther away, everything on its surface would be altered – a distinct composition of the atmosphere, a distinct temperature pattern, a distinct length of the day, for in that case we may not possess the Moon, and the Moon substantially influences the contemporary era of the Earth’s rotation around its axis.

Will it be the same planet? – It will be utterly different!

Take a look at Venus – at first sight, it appears to be Earth’s sibling, but the prevailing conditions on its surface render it inhospitable for life forms similar to ours.

When it comes to deliberately altering the paths of celestial objects, it is not just a figment of the imagination. In the not-too-distant future, individuals will need to adjust the trajectories of certain asteroids to prevent potential collisions. Additionally, it is possible that certain minor planets could be disassembled for their components, utilizing their mineral resources to construct orbital settlements – space cities that will exist as independent entities on their own orbital paths.

To conclude, I would like to direct your attention to a philosophical aspect that parallels our existence. The trajectory of a celestial entity can be likened to the course of its fate. Whether one believes in destiny or rejects it as predetermined is not of utmost importance at present. What truly matters is that an individual’s destiny, their path, is determined not by their appearance, but by their actions. This holds paramount significance for individuals. It often transpires that when a person undergoes a profound transformation in their life – embarks on new endeavors – their surroundings undergo a radical change as well. Those who were acquainted with them in the past lose sight of them, and even if they chance upon them, they fail to recognize them – it is as if they have migrated to a different orbit, where no one anticipates an encounter with them.

And yet another common occurrence: A person who has altered the typical trajectory of their life eventually reaches a juncture where they modify their name. This could involve legally changing their first and last name in their official documents, or it may involve adopting a unique pen name. However, if the alterations to one’s existence are substantial, it is highly probable that they will result in a name change in the realm of humanity. This phenomenon bears a striking resemblance to the celestial and the terrestrial. Oftentimes, grasping this concept aids in making the appropriate influential choice.

A neglected custom of melodic extras

This melody is known as Five Minutes to Fly – it was exclusively issued as a standalone track (it does not appear on any album). However, recently, I created a music video for it (with the assistance of the BlueWillow neural network). Let this serve as an illustration for the concluding chapter of the article, and it shall be an additional speck of dust on the scales that tipped our future towards the promising side.

In this series of articles, I will endeavor to explain, in the simplest terms possible, a complex topic. As a result, we will develop a straightforward software application that can provide information on the locations of the planets in our solar system from any given point on Earth’s surface at a specific time. The objective of this endeavor is to help the reader understand the underlying principles of the Kepler orbit model, without relying on commonly known facts, apart from Newton’s laws and the law of universal gravitation.

For those who have a curious mind, please proceed below the feline creature.

It is important to mention that the subsequent content assumes a certain level of acquaintance with Newton’s laws, fundamental concepts in geometry, vector algebra, and differential calculus.

What is the mechanism behind the movement of planets?

In reality, when considering the mutual influence of planets, the displacement of the solar system’s center of gravity in relation to the sun’s center of gravity, and other factors, the movement of planets becomes incredibly complex and cannot be strictly defined analytically. It’s important to note that even the three-body motion problem cannot be solved using analytical methods. Therefore, we need to specify which models we will be working within. For this discussion, we will focus on the Kepler orbit model. While there are other models available, most of them are semi-analytical and ultimately reduce to determining the parameters of the Keplerian orbit at a specific point in time. In other words, a Keplerian orbit is an approximation of a planet’s complex motion at a given moment. The Keplerian parameters of planetary orbits can be found at nssdc.gsfc.nasa.gov/planetary/factsheet, where the epoch (or specific moment in time) is specified when these Keplerian orbit parameters accurately represent the celestial body’s position. Typically, this initial moment of time is the epoch J2000.0, which corresponds to noon on January 1, 2000. Calculating the motion of bodies over a short period of time using the Kepler model is quite accurate and sufficient enough to not notice any errors visually or through a small telescope. However, more precise models are required for calculating the trajectory of a spaceflight to another planet.

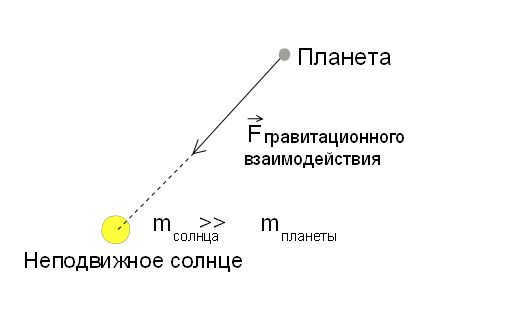
Alright, let’s begin by discussing the fundamental assumptions of this model. We assume that the Sun’s mass is significantly greater than the combined mass of all the planets. This allows us to conclude that the interaction between planets is negligible compared to the interaction between the Sun and each individual planet. As a result, we can simplify the problem to a two-body interaction (meaning we can analyze the interaction between each planet and the Sun separately). Additionally, we assume that the mass of each planet is much smaller than the mass of the Sun, resulting in a one-sided interaction. In other words, the planet’s motion does not affect the Sun’s motion in any way. Therefore, we can treat the planet as a point-like object moving within a stationary gravitational field. This can be summarized as follows:

Interaction of Gravity

What is gravitational interaction? It is a fundamental interaction that occurs between all material bodies. We can discuss gravitation at length, but let’s focus on the key point. According to Newton’s classical theory of gravitation, the gravitational attraction force between two material points of mass m1 and m2 separated by a distance R, is directly proportional to both masses and inversely proportional to the square of the distance between them – as shown in the equation below:

Here, G represents the gravitational constant (a proportionality coefficient). It is important to note that the gravitational force is always directed from the center of gravity of one body to the center of gravity of the other, and it is inversely proportional to the square of the distance between them (known as the law of inverse squares).
It is worth mentioning that on our spherical planet in a vacuum, a material point experiences no other force besides the gravitational force from the Sun. In this case, the gravitational force field is a central force field. In a central field of forces, the direction of the force acting on a body at any point within the field always passes through the center of the field (in our case, the center of gravity of the Sun), and the magnitude of this force depends solely on the distance to this center.

Newton’s second law

What is the motion of a body when a force is applied to it? This question is answered by Newton’s second law. There are several formulations of this law, but the most common one today is:

According to this law, the acceleration of an object is directly proportional to the force applied to it, in the same direction as the force, and inversely proportional to the object’s mass.

The change in momentum is directly proportional to the applied force and occurs in the direction of the force.

This formulation, though less precise (we must express reservations about the reporting systems, but we are not interested in it at the moment), is much more lucid. The amount of motion in this case is defined as the momentum of the object, which is calculated by multiplying the object’s mass by its velocity:

Therefore, let’s express the verbal formulation in symbolic form:

Or, if we express the momentum of an object and treat mass as a constant (mass is not always constant, but in our case it is) outside the differential sign, we obtain the following well-known equation:

Where vector represents the object’s acceleration. It is important to remember that acceleration, momentum, velocity, and force are all vector quantities. Let’s agree that if a vector quantity is indicated by a vector symbol, then it is a vector, otherwise it represents its magnitude.

The second law of Kepler

Each celestial body orbits in a plane that passes through the central point of its star. Additionally, during equal time intervals, the line connecting the star and the celestial body sweeps out equal areas.

Yes, I understand that “got the law” may not sound ideal, but unfortunately, that is the term used. The reason for this is that Kepler did not deduce the law through logical reasoning, but rather he intuitively grasped it based on his observations. In other words, he obtained it empirically, making it fitting to be called a law.
Below, you can find an illustration of this law (the image is sourced from a Wikipedia article).

Differential equation for the path of an object

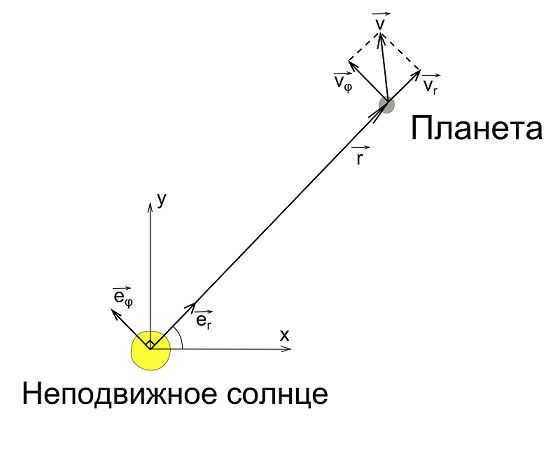
Let’s examine the cross product of the position vector with the velocity vector in more detail. The position vector can be expressed as the product of its magnitude (the distance from the origin to a point) and a unit vector that has the same direction as the position vector:

Then the velocity vector can be written as: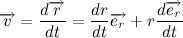

And the cross product of the position vector with the velocity vector is: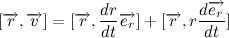

Since the vectors are parallel, we can conclude that the cross product is equal to zero. Therefore:

Now, let’s examine the time derivative of a unit vector:

By examining the diagram, it is evident that over time, the vector undergoes a rotation by the angle . The distinction between vectors and is equivalent to the vector . When dealing with small angles, the following relationship holds true:

As the angle approaches zero, the directions of vectors and align, with the direction of the vector becoming perpendicular to them. We can introduce a unit vector , which is perpendicular to and shares the same direction as the movement of its endpoint. As a result, we can deduce:

By taking the limit, we arrive at: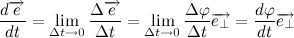

Where denotes the angular velocity of the vector . Let’s denote
Now let’s revisit the calculation of the radius of the vector multiplied by the velocity, yielding: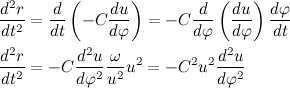

It is evident that vectors and are mutually perpendicular. To further illustrate this, let’s introduce another unit vector , which is perpendicular to vectors and . Hence, the vectors , and form an orthonormal basis. By utilizing the definition of the vector product, we obtain:

Therefore, . Let’s introduce the notation, . Additionally, it’s worth noting: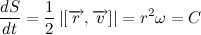

Now let’s return to Newton’s second law. We can describe the force acting on the body as the product of the magnitude of the gravitational force and the orth :

Where m1 and m2 represent the masses of the planet and the sun, respectively. Let’s simplify the mass of the planet to unity, as it has no impact on the trajectory of motion. Therefore, we can assume we are dealing with a body of unit mass. By introducing the notation , we have:

Now let’s describe the acceleration vector: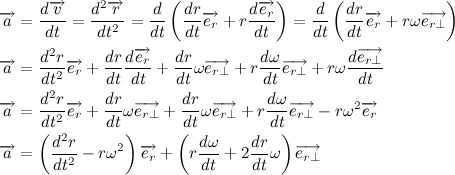

Let’s examine the contents of the second bracket: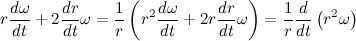

Since we already know , it follows that , resulting in:

Let’s introduce the notation . Recall that we previously introduced the notation , thus it is evident that .
Now let’s express the derivative of the modulus of the radius vector in terms of C: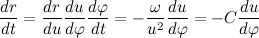

Next, let’s express the second derivative of the modulus of the radius vector using C:

Given the obtained result, let’s rewrite the expression for the acceleration vector: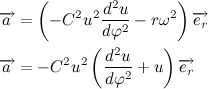

Consequently, Newton’s second law can be expressed as:

Let’s rewrite the obtained differential equation in a more recognizable form:

I believe many of you have already surmised the nature of the obtained differential equation, but I will conclude this first part to avoid overwhelming the reader and myself.

Main point

We have derived a differential equation that describes the trajectory of a material point in a gravitational field, which is highly applicable in describing the paths of planets and other celestial bodies.

Next steps

However, the obtained differential equation lacks a time parameter, leaving us unaware of the nature of the motion. Therefore, we must somehow incorporate time into the equation. Additionally, we will explore different coordinate systems and their transformations to determine the coordinates of planets in an observer-bound system.

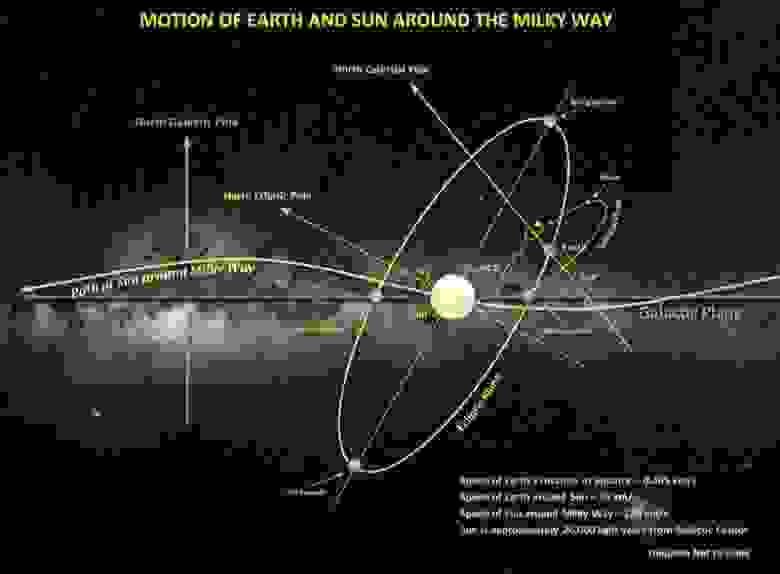
Many of you may have come across a gif or watched a video illustrating the movement of the solar system.

In 2012, a viral video caused quite a stir. I stumbled upon it shortly after its release, back when my knowledge of space was much more limited. What puzzled me the most was the perpendicularity of the planets’ orbits to the direction of their motion. It’s not that it’s impossible, but the solar system can actually move at any angle relative to the plane of the Galaxy. You might wonder why I bring up this long-forgotten story. Well, the reason is that right now, if you’re interested and the weather is clear, anyone can observe the true angle between the planes of the ecliptic and the Galaxy in the night sky.

Verify scientists’ findings

According to the field of astronomy, it has been determined that there is a 63° angle between the planes of the ecliptic and the Galaxy.

However, the illustration itself is uninteresting, and now, with the flat Earth enthusiasts gathering on the fringes of science, we desire a straightforward and comprehensible depiction. Let’s contemplate how we can observe the planes of the Galaxy and ecliptic in the sky, preferably using only our naked eye and without venturing far from the city. The plane of the Galaxy corresponds to the Milky Way, although presently, due to the abundance of light pollution, it is not so effortless to perceive. Is there a line approximately aligned with the plane of the Galaxy? Indeed, there is – it is the constellation of the Swan. It is distinctly visible even within the city, and it can be easily located by referencing the brilliant stars Deneb (alpha Swan), Vega (alpha Lyra), and Altair (alpha Eagle). The “torso” of the Swan roughly coincides with the galactic plane.

Alright, so we’ve got this one plane. But how can we visualize the path of the ecliptic? Let’s consider what the ecliptic actually is. According to the precise modern definition, the ecliptic is the intersection of the celestial sphere with the plane of the Earth-Moon barycenter’s orbit (the center of mass). On average, the Sun moves along the ecliptic, but unfortunately we don’t have two Suns to conveniently trace a line, and we can’t see the constellation of Swan in sunlight. However, if we take into account that the planets in our solar system also move roughly in the same plane, we can use the parade of planets to help us visualize the ecliptic. And at this very moment, Mars, Jupiter, and Saturn are visible in the morning sky, perfectly positioned to demonstrate the plane of the ecliptic.

In the following weeks, during the early morning hours before the sun rises, one can observe a vivid scene similar to the one depicted below:

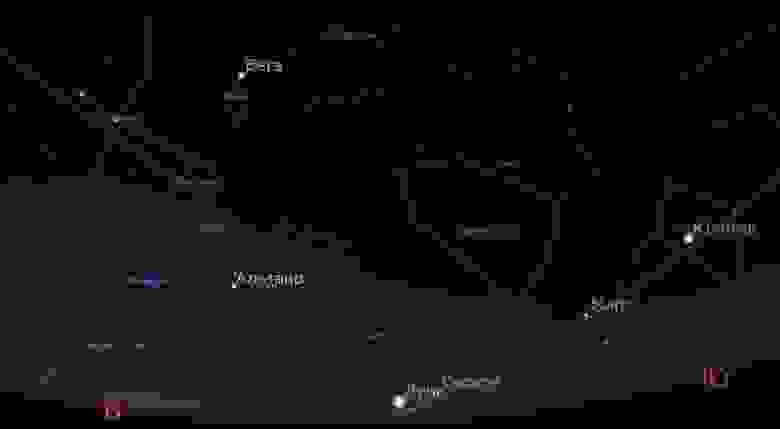
It is quite astonishing that this aligns flawlessly with the information found in astronomy textbooks.

And the animation is more accurately depicted in this way:

Source: astronomer Rhys Taylor’s website rhysy.net

The position of the planes can raise the question. Are we traveling

The path of celestial bodies

The trajectory of a celestial body is the path along which space objects move in outer space: the Sun, stars, planets, comets, spacecraft, satellites, interplanetary stations, and others.

When applied to artificial spacecraft, the term “orbit” is used for those portions of trajectories in which they move with the propulsion system disconnected.

The configuration of the trajectory of celestial objects. Velocity in space

The configuration of trajectories and the pace at which celestial objects traverse them are primarily determined by the force of universal gravitation. When examining the movement of celestial objects within the solar system, their shape and composition are often disregarded, treating them as point masses. This approach is justified by the vast distances between objects, which typically far exceed their dimensions. By treating a celestial object as a point mass, the law of universal gravitation can be applied to analyze its motion. Additionally, it is common to consider only two attracting bodies and neglect the influence of others.

When considering the Earth’s orbital path around the Sun, it can be reasonably assumed that the planet is solely influenced by the gravitational forces exerted by the Sun. Similarly, when studying the orbit of a satellite around a planet, only the gravitational pull of its specific planet is taken into account, disregarding not only the gravitational pull of other planets, but also that of the Sun.

These simplifications have led us to the problem of the two-body system. One solution to this problem was proposed by I. Kepler, and the complete solution was later formulated by I. Newton, who demonstrated that a celestial body attracted by another orbits around it in the shape of an ellipse (or circle, which is a special case of an ellipse), parabola, or hyperbola. The second point is located at the focus of this curve.

• the weight of the object in question;
• the separation between them;
• is the velocity at which one object moves in relation to another.

If an object with a mass of m1 (kg) is situated at a distance of r (m) from an object with a mass of m0 (kg) and is currently moving with a velocity of v (m/s), then the orbit is determined by a constant:

The gravitational constant f = 6.673 x 10-11 m3 kg-1 s-2. If h0 – in a hyperbolic orbit.

The second cosmic velocity – is the minimum initial velocity that must be given to an object in order for it to begin moving near the Earth’s surface, overcome the Earth’s gravitational pull, and permanently leave the planet in a parabolic orbit. It is equal to 11.2 km/s.

The minimum initial velocity required to turn a body into an artificial satellite of the Earth is called the first space velocity. This velocity is calculated to be 7.91 km/s.

Most celestial bodies in the Solar System follow elliptical paths when in motion. However, there are a few exceptions, like comets, which tend to move along parabolic or hyperbolic trajectories. As a result, interplanetary stations are launched on hyperbolic orbits around the Earth and then transition to elliptical paths around the Sun as they travel towards their intended destination.

Distinctive Features of the Motion of Celestial Objects

Orbital Elements – quantities that determine the size, shape, position, orientation of an orbit in space, and the location of a celestial body on it.

Several significant points on the orbits of celestial bodies have their own designated names.

The point on the orbit of a celestial body orbiting the Sun that is closest to the Sun is referred to as the Perihelion (Figure 1).

Conversely, the point on the orbit of a celestial body traveling around the Sun that is farthest from the Sun is known as the Aphelion.

The point on the orbit that is closest to the planet Earth is called the Perigee, while the farthest point is called the Apogee.

When dealing with more abstract scenarios involving multiple celestial bodies, the term used for the point in an orbit that is closest to the center of the Earth is called the pericenter, while the point farthest from the center is referred to as the apocenter.

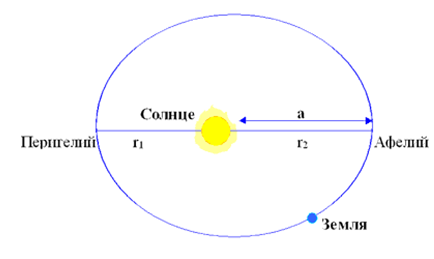
Figure 1. Orbital positions of celestial objects in relation to the Sun and the Earth

The situation involving two celestial bodies is the most basic and rarely occurs (although there are instances where the influence of a third, fourth, etc. body is disregarded). In reality, the situation is much more intricate: every celestial body is subject to the influence of numerous forces. As planets traverse their orbits, they are not only attracted to the Sun, but also to each other. In star clusters, stars exert gravitational attraction on one another.

The movement of man-made satellites is influenced by various forces, such as the irregular shape of the Earth and the resistance of its atmosphere. Additionally, the gravitational pull of the Sun and Moon also play a role. These extra forces are known as perturbing forces, and the resulting effects on the movement of celestial bodies are called perturbations. Because of the impact of these perturbations, the orbits of celestial bodies are constantly and gradually changing.

Celestial mechanics is a field of astronomy that focuses on studying the movement of celestial bodies while considering the influence of perturbations.

Planetary sphere of influence refers to the area of space near a planet (or the Moon) where the planet’s gravity is the dominant force in determining the motion of a satellite, comet, or interplanetary spacecraft, rather than the Sun’s gravity.

Calculations are simplified within the sphere of influence because the perturbation from solar gravity is smaller compared to planetary gravity. However, it’s important to note that both inside and outside the sphere of influence, the body is still influenced to varying degrees by the forces of solar gravity, as well as other celestial bodies such as planets.

The sphere of influence radius is determined by the distance between the Sun and the planet. The celestial bodies’ orbits within this sphere are calculated using the two-body problem. If a body exits the planet’s sphere, its trajectory inside the sphere follows a hyperbolic orbit. The Earth’s sphere of influence has an estimated radius of around 1 million light years. The Moon’s sphere of influence in relation to the Earth has a radius of approximately 63,000 kilometers.

The method of approximating the orbit of a celestial body using the sphere of influence is one technique for estimating orbital paths. If approximate values of the orbital elements are known, other methods can be employed to obtain more precise values. Gradual refinement of the determined orbit is a common approach for calculating orbit parameters with high accuracy. The range of modern orbit determination tasks has expanded significantly, driven by the rapid advancement of rocket and space technology.

To determine how many times the mass of the Sun exceeds the mass of the Earth, we can use the known period of the Moon’s orbit around the Earth, which is 27.2 seconds, and its average distance from the Earth, which is 384,000 kilometers.

Given: T = 27,2 s u t., a = 3,84 – 105 km.

Find: m with m h – ?

The above simplifications reduce us to the 2-body problem. One of the solutions to this problem was proposed by I. Kepler, and the full solution was formulated by I. Newton. Let us use these solutions.

Th = 365 s y t is the period of Earth’s revolution around the Sun.

as = 1,5 – 108 km – the average distance from the Earth to the Sun.

When solving we will be guided by the formula of the law of I. Kepler, taking into account the 2nd law of I. Newton:

ms + mh mh mh + m – T3 2 T2 = a3 3 a3.

Knowing that the mass of the Earth compared to the mass of the Sun and the mass of the Moon compared to the mass of the Earth are very small, let us write the formula in the form:

By using the given expression, we can determine the required mass ratio:

ms / mh = (a3 / 3) / (a3 – T3 / 2T2)

Answer: ms / mh = 0.3 – 106 kg.

Let’s discuss the planetary orbits

The Composition of the Solar System

According to the definition, a planet is a celestial body that orbits around a star. An orbit, on the other hand, is the path that this planet takes in the gravitational field of another body, usually a star. In the case of Earth, this body is the Sun.

All the planets in our solar system move along their orbits in the same direction as the Sun’s rotation. Currently, scientists are only aware of one planet that moves in the opposite direction – an exoplanet known as WASP-17b, located in the Scorpius constellation.

Duration of a Planetary Year

The duration of a planetary year, also known as the sideric rotation period, refers to the time it takes for a planet to complete one revolution around its star. The velocity of the planet is subject to variation based on its proximity to the star. The closer the planet is to the star, the faster it moves, whereas the farther it is, the slower it travels. Consequently, the length of a planetary year is directly influenced by the planet’s distance from its “Sun”. If the distance is smaller, the planetary year is relatively brief. As the planet moves farther away from the star, the gravitational pull diminishes, resulting in slower motion and a longer year.

Perihelion, aphelion, and eccentricity explained

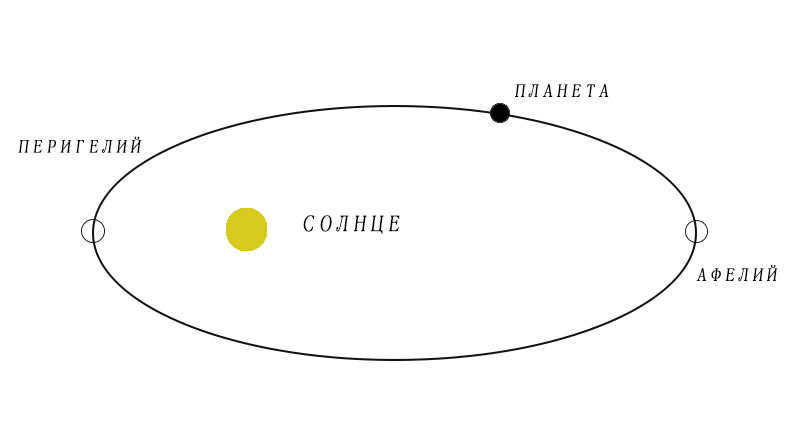
All planets orbit the sun in a circular shape, and the extent of this circularity is determined by eccentricity. If the eccentricity is close to zero, the orbit is nearly a perfect circle. Orbits with an eccentricity close to one take the form of an ellipse. For instance, the orbits of various satellites and exoplanets in the Kuiper belt resemble an ellipse, while the orbits of planets in the Solar System are almost perfectly circular.

The factor that causes the seasons to change.

Photo of the Earth taken from the Electro-L satellite.

The inclination of an orbit is defined as the angle between the orbital plane and the reference plane. In the Solar System, the reference plane is the ecliptic, which corresponds to the Earth’s orbit. The planets in our solar system, including Earth, have orbits that are very close to the ecliptic plane.

All planets in the solar system have an inclination relative to the equatorial plane of their respective stars. For instance, the Earth has an axial tilt of approximately 23 degrees. This tilt is responsible for the variation in light received by the Northern and Southern hemispheres, as well as the changing of seasons.

The Elektro-L satellite has captured the transition between day and night.

If you enjoyed this article, please share it with your friends!

Traditionally, the general belief is that the planets orbit the Sun in circular paths. However, this is not entirely accurate. In the early 17th century, Johannes Kepler examined the observations of Mars and discovered that its orbit actually has the shape of an ellipse, which can be described as an oval. An ellipse has two focal points, with one of them being occupied by the Sun. Subsequent observations have confirmed that all the planets in the solar system, as well as other celestial bodies such as asteroids and dwarf planets, follow elliptical orbits around the Sun. Additionally, the satellites of the planets also move along elliptical trajectories around their respective planets.

It should be noted that an ellipse is a more general shape than a circle. The similarity between them lies in the fact that a circle can be seen as a special case of an ellipse. The degree of deviation from a perfect circle in an ellipse is measured by a specific value called eccentricity. When the eccentricity is zero, the ellipse is indistinguishable from a circle. However, as the eccentricity approaches one, the ellipse becomes increasingly elongated. To illustrate this, consider the Earth’s orbit around the Sun. At the point of closest approach (perihelion), the distance between the Earth and the Sun is approximately 147 million km, while at the farthest point (aphelion), it is about 152 million km. The eccentricity of the Earth’s orbit is calculated to be 0.017. In comparison, the planet Mercury has the highest eccentricity among the planets in our solar system, with a value of 0.206. This means that its orbital radius varies significantly, ranging from 46 to 70 million km.

Indeed, Newton’s laws can be used to mathematically demonstrate the elliptical nature of planetary orbits, taking into consideration the gravitational interactions between the Sun and the planet. However, when we factor in the gravitational interactions between planets, it becomes evident that the shape of the orbits will deviate from the ideal ellipse. These deviations, known as perturbations, prevent us from calculating orbits with absolute precision. As a result, astronomers are unable to predict with certainty the exact position of Pluto in the sky 20 million years from now, although they can make reasonably accurate forecasts for several millennia ahead.

Sources:

Let’s discuss the paths that planets follow in space

The Arrangement of the Solar System

According to the definition, a planet is a celestial object that orbits around a star. An orbit is the path that a planet takes in the gravitational field of another body, typically a star. In the case of Earth, this body is the Sun.

All the planets in the Solar System follow their own trajectories as they orbit in the direction of the Sun’s rotation. Currently, scientists are aware of only one planet that moves in the opposite direction – an exoplanet called WASP-17b, located in the Scorpius constellation.

Planetary year

The sideric rotation period, also known as the planetary year, refers to the time it takes for a planet to complete one revolution around its star. The velocity of the planet varies depending on its position, with closer distances resulting in greater speeds and greater distances leading to slower planetary movement. Consequently, the length of the planetary year is directly influenced by the planet’s distance from its “Sun”. When a planet is located closer to its star, the planetary year tends to be shorter. On the other hand, when a planet is further from its star, it experiences less gravitational influence, resulting in slower movement and therefore, a longer year.

Perihelion, aphelion, and eccentricity explained

All the planets in our solar system revolve around the sun in orbits that are shaped like elongated circles. The degree of elongation, or eccentricity, determines how much the shape deviates from a perfect circle. When the eccentricity is very small, the orbit is nearly circular. On the other hand, if the eccentricity is close to one, the orbit takes the shape of an ellipse. For instance, the satellites and exoplanets in the Kuiper belt have elliptical orbits, while the planets in our solar system have orbits that are almost perfectly circular.

The element accountable for the alteration of the seasons.

The Electro-L satellite provides a unique view of Earth.

The inclination of an orbit is determined by the angle between the reference plane and the orbital plane. In our Solar System, the reference plane is the ecliptic, which is the plane of Earth’s orbit. The orbits of the eight planets in our solar system closely align with the ecliptic plane.

Each planet in the solar system has a tilt relative to its equator, which affects the amount of sunlight received by the Northern and Southern hemispheres and leads to the changing of seasons. For instance, Earth has an axial tilt of approximately 23 degrees.

The change of day and night observed by the Elektro-L satellite.

Did you enjoy this article? Share it with your friends!

Orbits of the solar system and the arrangement of the planets

Firstly, let’s define what orbits are and their purpose.
The orbits of the planets represent their path or trajectory of movement. It is understood that this movement occurs within a predetermined coordinate system.
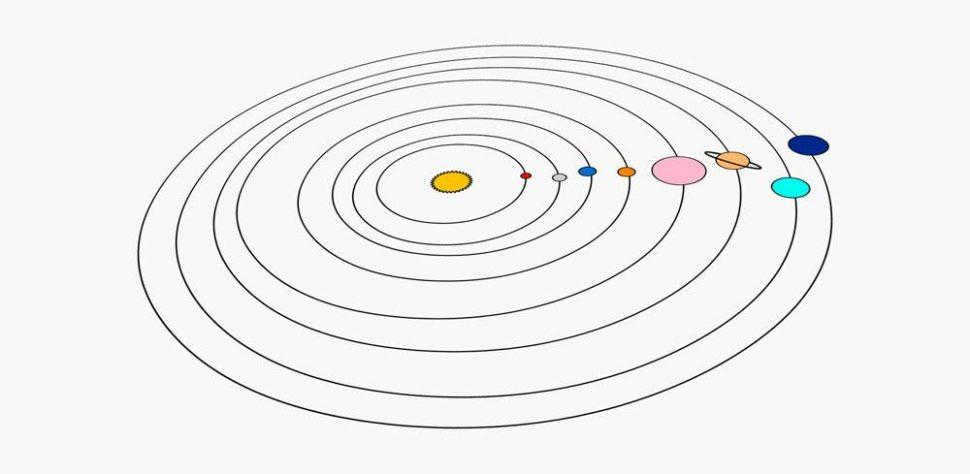
All celestial bodies in the solar system revolve around the Sun. This serves as the given coordinate system. Each celestial body, however, has its own distinct orbit. As we know, these orbits do not align with one another. Furthermore, they differ in length and shape. These differences have an impact on the climate and surface temperatures of these celestial bodies.

The paths followed by the planets in the solar system

Characteristics of an orbit

Every orbit that a planet takes has its own unique characteristics. Moreover, these characteristics determine the shape, size, and position of the orbit in space.
In the field of astronomy, the Keplerian elements of an orbit are commonly used. These elements include:

• Major semi-axis – a geometric characteristic of objects. It is created by the intersection of a plane with the surface of a circular cone.
• Eccentricity – a numerical parameter that indicates the deviation of a conic section from a perfect circle.
• Inclination – the angle between the plane and the orbit.
• The longitude of the ascending node is a mathematical representation of the line of the orbital plane in relation to the reference plane.
• The mean anomaly is the result of the average motion of the object multiplied by the time interval from the pericenter. It maintains a consistent angular velocity.

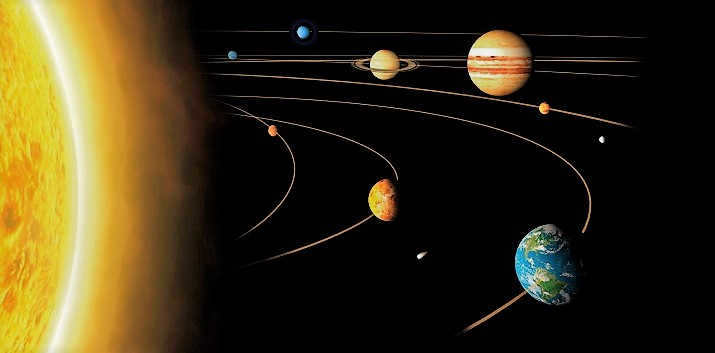
Planetary Orbits in the Solar System

Naturally, the Sun is the central body of our solar system, holding the majority of its mass. Through its gravitational pull, it attracts celestial objects.

The Sun

It is important to note that a significant number of celestial bodies in our solar system orbit in close proximity to each other. This region is known as the ecliptic. However, there are other objects that have a higher inclination angle in relation to the ecliptic.

All the planets and many other celestial bodies orbit the Sun counterclockwise. Interestingly, most planets also rotate counterclockwise around their own axis. However, there are two exceptions to this pattern – Venus and Uranus, which have a clockwise rotation.
As the distance from the Sun increases, the gap between the orbits of these celestial objects also widens.

On the left we have Uranus, and on the right we have Venus.

According to astronomers, celestial objects follow an elliptical trajectory as they travel through space. Essentially, they move along a closed curve in a two-dimensional plane. The Sun is located at one of the points on this ellipse. The closer an object is to the Sun, the faster it rotates around it. As a result, it has a shorter orbital period, or in simpler terms, a shorter year.

The celestial bodies in our solar system

Incidentally, our solar system is commonly classified into two regions: the inner zone and the outer zone.

The inner zone encompasses the asteroid belt and the planets belonging to the terrestrial group: Mercury, Venus, Mars, and, naturally, Earth.
On the other hand, the outer zone lies beyond the initial group and consists of four gas giants.

Furthermore, all entities within the solar system can be categorized into three distinct types:

The composition of the solar system has been officially recognized and approved by the International Astronomical Union. A total of eight planets have been identified: Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, and Neptune.

Planets in the solar system

Arrangement of the planets

You may be wondering, what exactly is a planetary arrangement and why is it so fascinating?
In the field of astronomy, the term “configuration” refers to the relative positioning of the Sun, planets, and other celestial bodies. This concept is especially applicable to the solar system.
There are distinct configurations for the upper and lower planets, based on their respective motions.

When observed from Earth, the lower planets, specifically Mercury and Venus, exhibit changes in their phases.
These planets move relatively close to the Sun, with their maximum distance either to the east or west of it. Depending on the direction of their movement, we distinguish between eastern (evening) elongation and western (morning) elongation.

Elongation refers to the angular position between the Sun and a planet.

The motion of the lower planets can also be retrograde, meaning it occurs from east to west.
In this case, the moment when the planet is positioned between the Earth and the Sun is known as the lower conjunction.
On the other hand, the movement can be direct, or from west to east. When the Sun is positioned between the Earth and the planet, we observe the upper conjunction.

Upper planets’ configuration

The arrangement of the upper planets is quite similar to that of the lower planets. Just like the lower planets, they also exhibit both direct and retrograde motion. However, the main difference lies in the slower pace of their movement. Consequently, a moment arrives when the Sun catches up with these planets, causing them to align. At this juncture, the Sun is positioned between the Earth and the planet in question.
During the retrograde motion, the planet reaches a point directly opposite to the Sun’s position. This particular moment is known as opposition, and it is during this phase that the Earth is positioned between the Sun and the planet.

The eastern quadrature is when the planet is positioned at a 90° angle from the Sun in the eastern direction. Similarly, the western quadrature refers to the planet being positioned at a 90° angle from the Sun in the western direction.

The upper planets exhibit visible motion without undergoing phase changes. They always present their illuminated side towards the Earth.
It’s worth noting that the motion of the Moon follows the same pattern as the upper planets.
However, the movement of the upper planets cannot be observed from Earth.

Planetary Orbit Periods

There are two recognized types of orbital periods in the field of astronomy. The first is the Sidereal Period, which refers to the time it takes for a planet to complete one orbit around the Sun. In other words, it is the duration of a planet’s year measured in Earth days or years.

The duration of a planet’s rotation at the same point from the observer’s perspective is known as the synodic period. This period is measured when the observer is located on Earth, making it more accessible to astronomers. Consequently, the synodic period was calculated before the sideric period.

However, determining the synodic period comes with certain challenges. Firstly, the Earth revolves around the Sun, causing the motion of the planets from Earth to be imprecise and irregular. Additionally, the retrograde motion of the planets must not be overlooked.

The orbits of planets add to the uniqueness of the Universe, making their study and observation truly mesmerizing. Countless astonishing phenomena occur in the cosmos, and it is reasonable to assume that even more captivating discoveries lie ahead.

The eccentricity of Mercury is 0.205. Its orbit extends from 46 million kilometers at the nearest point to the sun to 70 million kilometers at the farthest point. The closest point to the sun in the orbit is known as perihelion, while the farthest point is called aphelion. Mercury holds the title for being the swiftest planet, completing a full revolution around the sun in just 88 Earth days.

Venus has the smallest eccentricity among the planets in our solar system, with a value of 0.007. This means that its orbit is nearly a perfect circle. At its closest point to the sun, called perihelion, Venus is about 107 million kilometers away, while at its farthest point, called aphelion, it is about 109 million kilometers away. It takes Venus approximately 224.7 Earth days to complete one revolution around the sun. Interestingly, a day on Venus is actually longer than a year on Earth because Venus rotates very slowly. Unlike other planets, which rotate counterclockwise when viewed from the north pole, Venus rotates clockwise. This makes Venus the only planet in our solar system with this unique rotation.

Similar to Venus, the Earth also has a relatively small eccentricity, measuring 0.017. On average, the Earth is about 150 million kilometers away from the sun, but this distance can vary slightly between 147 and 150 million kilometers. It takes the Earth approximately 365.256 days to complete one revolution around the sun, which is why we have leap years to account for the extra time.

The orbit of Mars is known for its high eccentricity, with a value of 0.093, making it one of the most elongated orbits in our solar system. The closest point to the Sun, known as perihelion, is approximately 207 million kilometers away, while the farthest point, known as aphelion, is about 249 million kilometers away. Over the course of time, the orbit of Mars has gradually become more eccentric. It takes Mars approximately 687 Earth days to complete one orbit around the Sun.

Jupiter has a slightly oval-shaped orbit, with a closest point to the sun of 741 million km and a farthest point of 778 million km. It takes approximately 4331 Earth days, or 11.86 years, for Jupiter to complete one orbit around the sun.
Saturn’s orbit is also slightly elliptical, with an eccentricity of 0.056. The closest point to the sun in Saturn’s orbit is 1.35 billion km, while the farthest point is 1.51 billion km away. The visibility of Saturn’s rings depends on its position in its orbit, with the rings appearing more prominent at certain points. Saturn takes about 29.7 Earth years to complete one revolution around the sun. Since its discovery in 1610, Saturn has completed only 13 revolutions around the sun in over 400 years.

Uranus has a perihelion distance of 2.27 billion km and an aphelion distance of 3 billion km from the sun. Its eccentricity is 0.047. It takes Uranus approximately 84.3 Earth years to complete one orbit around the sun. What sets Uranus apart is its unique axial tilt, which is nearly 99°, causing it to rotate on its side.

Neptune, on the other hand, has a relatively low eccentricity, similar to that of Venus. It has a perihelion of 4.45 billion kilometers and an aphelion of 4.55 billion kilometers. Since the reclassification of Pluto as a dwarf planet, Neptune now holds the record for being the farthest planet from the sun in terms of orbit.

The Sun is orbited by the planets in a singular direction, following nearly circular orbits that are closely aligned with the Laplace plane, which serves as the fundamental plane of our solar system. Much like the laws of mechanics that govern our daily lives, these planets are held together by the unyielding law of universal gravitation. Given the absence of friction in the vast expanse of interstellar space, it is safe to assume that the relative motion of these planets will remain unchanged, at least for the foreseeable future spanning millions of years. Countless scientists, including the renowned Einstein, have endeavored to predict the future trajectories of these celestial bodies within our system. However, they all arrived at the same conclusion: the planets of our solar system will perpetually maintain their stable existence.

The Configuration of the Planetary Orbits in the Solar System

The orbits of the celestial bodies within the Solar System, depicted in accordance with their respective scales (proceeding clockwise, starting from the upper left).

At the heart of the Solar System lies the Sun, a G2V spectral class main-sequence star, commonly referred to as a yellow dwarf. The Sun encompasses the majority of the system’s mass (approximately 99.866%) and exerts its gravitational force to maintain the planets and other entities within the solar system. The four most substantial bodies, recognized as the gas giants, contribute to 99% of the remaining mass (with Jupiter and Saturn constituting the majority – roughly 90%).

The majority of the significant entities that orbit the Sun are situated within a relatively uniform plane known as the ecliptic plane. Conversely, comets and objects in the Kuiper Belt often exhibit substantial inclinations in comparison to this plane.

All celestial bodies, including planets, follow a similar orbit around the Sun, moving in a counterclockwise direction when observed from the Sun’s north pole. However, there are a few exceptions to this rule, such as Halley’s Comet. One interesting fact is that Mercury has the highest angular velocity among all the planets. It manages to complete a full revolution around the Sun in just 88 Earth days. On the other hand, the most distant planet, Neptune, takes a whopping 165 Earth years to complete one orbit.

When it comes to the rotation of the planets around their own axis, most of them follow the same direction as their orbit around the Sun. However, there are a couple of exceptions. Venus and Uranus have a unique rotation pattern. Uranus, in particular, has an axial tilt of about 90 degrees, making it almost “lying on its side.” This interesting phenomenon can be visually demonstrated using a special device called a tellurium.

Many conventional models of the Solar System depict the planets’ orbits as being evenly spaced, but in reality, this is not the case. In general, the further a planet or belt is from the Sun, the greater the distance between its orbit and the orbit of the previous object. For instance, Venus is roughly 0.33 astronomical units (a. u.) farther from the Sun than Mercury, while Saturn is 4.3 a. u. farther from Jupiter and Neptune is 10.5 a. u. farther from Uranus. Various attempts have been made to establish correlations between orbital distances, such as the Titius-Bode rule, but none of these theories have gained widespread acceptance.

Kepler’s laws describe the paths that objects take as they orbit the Sun. These laws state that each object moves in an ellipse, with the Sun located at one of the focal points. Objects that are closer to the Sun, with a smaller major semi-axis, have a higher angular velocity of rotation. As a result, their orbital period, or year, is shorter. In an elliptical orbit, an object’s distance from the Sun changes throughout the year. The point in an object’s orbit that is closest to the Sun is called the perihelion, while the farthest point is called the aphelion. At its perihelion, an object moves at its fastest speed, while at its aphelion, it moves at its slowest. While the orbits of the planets are mostly circular, many comets, asteroids, and objects in the Kuiper Belt have highly elongated elliptical orbits.

Terminology

The solar system is occasionally segmented into different areas. The inner portion of the solar system encompasses the four planets of the Earth-group and the asteroid belt. The outer portion commences beyond the asteroid belt and encompasses the four gas giants. With the identification of the Kuiper belt, the region beyond Neptune is now regarded as the most remote part of the solar system, housing objects that are positioned even farther out.

There are officially three categories for all objects in the solar system that orbit the Sun: planets, dwarf planets, and small solar system bodies. A planet is defined as a body in orbit around the Sun that has enough mass to form a spherical shape, but not enough to initiate thermonuclear fusion. Additionally, it must have cleared its orbit of planetesimals. Based on this definition, the solar system has eight known planets: Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, and Neptune. However, Pluto does not meet this definition because it has not cleared its orbit of the objects in the Kuiper Belt. On the other hand, a dwarf planet is a celestial body that orbits the Sun and has enough mass to maintain a nearly circular shape due to its own gravitational forces. However, it has not cleared its orbit of planetesimals and is not a satellite of a planet. Currently, there are five recognized dwarf planets in the Solar System: Ceres, Pluto, Haumea, Makemake, and Erida. In the future, other objects like Sedna, Ork, and Kvavar may be classified as dwarf planets. Dwarf planets that orbit in the region of transneptunian objects are called plutoids. Finally, the remaining objects that orbit the Sun are known as the small bodies of the solar system.

What is the method for memorizing the planets?

To remember the planets, you can use the mnemonic “We All Know – Julie’s Mom Sat on the Pill in the Morning” which represents their names in order of their distance from the Sun: Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, Neptune. It is a simple technique that even the youngest child can use to recognize the planets, especially Venus and Mercury.

What is the path of a planet, what shape do the paths of the solar system have?

A comprehensive solution to the final task 1 in geography for fifth grade students, authored by V. P. Dronov and L. E. Savelieva in 2015

1. How can you navigate using the stars?

Navigation can be accomplished by using prominent stars. The 26 brightest stars used for navigation are known as navigational stars. They indicate directions towards specific sides of the horizon. For instance, Polaris always points towards the North.

2. What is the solar system? Which celestial bodies are part of it?

The solar system consists of the Sun and the celestial bodies orbiting around it. The solar system comprises of the Sun and the celestial bodies orbiting around it (planets, satellites, comets, asteroids), as well as the interplanetary space containing tiny particles and gaseous matter.

What is the definition of a planetary orbit? What is the specific shape of the orbits of the planets within our solar system?

A planetary orbit refers to the trajectory that a planet follows around the Sun. The orbits of the planets in our solar system are elliptical in shape.

Which number planet is Earth in relation to the Sun? Between which two planets is Earth situated?

Earth is known as the third planet from the Sun. It is positioned between Venus and Mars.

What are the distinct categories that the planets in the Solar System are classified into? How do these groups of planets differ from one another?

The planets within our solar system are categorized into terrestrial planets and giant planets. These two groups vary in terms of composition and size. Terrestrial planets consist of rocky materials and are relatively small in size, while giant planets are composed of gas and dust and are significantly larger.

How does the Sun impact Earth?

7. List the planets in our solar system. Which ones receive more sunlight and heat from the Sun than Earth, and which ones receive less?

The planets in our solar system include Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, and Neptune. Mercury and Venus receive more sunlight and heat than Earth, while all the other planets receive less compared to Earth.

8. What is considered a 24-hour day? How long is a day on Earth? Under what circumstances can the length of a day change?

A 24-hour day is a natural unit of time measurement. A day on Earth lasts for 24 hours. The length of a day can change when the Earth’s rotation speed around its axis changes: increasing the speed shortens the day, while slowing it down lengthens the day.

9. What are the effects of the Earth’s rotation on its axis on geography?

The Earth’s rotation on its axis has several geographic consequences. One of the most significant effects is the alternation of day and night. As the Earth rotates, different parts of the planet are exposed to sunlight, creating the cycle of day and night. Additionally, the rotation of the Earth influences the shape of the planet. The centrifugal force generated by the rotation causes the Earth to bulge slightly at the equator and flatten at the poles.

Another consequence of the Earth’s rotation is the Coriolis effect. This effect causes moving objects on Earth to be deflected to the right in the Northern Hemisphere and to the left in the Southern Hemisphere. This deflection is responsible for the rotation of large-scale weather systems, such as hurricanes and cyclones, and the formation of ocean currents.

10. What is the definition of a year? How long does it take for the Earth to complete one orbit around the Sun? Why is every fourth year on Earth longer than the previous three by one day? What are these extended years called?

A year is defined as the time it takes for the Earth to complete one orbit around the Sun. This period of time is approximately 365.25 days. To account for this extra fraction of a day, every fourth year on Earth is longer than the previous three by one day. These extended years are called leap years. The additional day, known as February 29th, is added to the calendar to keep it synchronized with the Earth’s orbit around the Sun.

A year is a period of time during which the Earth completes a full revolution around the Sun in its orbit. The duration of an Earth year is 365 days, with every fourth year being one day longer and known as a leap year. This is because the Earth’s day is slightly longer than 24 hours, with an extra 6 hours added to the year. For convenience, a year is considered to be 365 days, and an additional day is added every four years.

11. What is the geographic pole? What is the equator’s length on Earth?

The geographic pole is a designated point on the Earth’s surface where it intersects with the Earth’s axis.

The equator is an imaginary circle drawn on the Earth’s surface at an equal distance from the North and South Poles.

12. What is the reason for the difference in distance from the center of the Earth to the geographic poles and the equator?

The reason for the difference in distance is that the Earth is not a perfect sphere but slightly flattened at the poles, resulting in a smaller polar radius compared to the equatorial radius.

13. What causes the change in seasons on Earth?

The change in seasons on Earth is caused by the tilt of its axis, which results in uneven heating of different areas during the year.

14. What are the geographical effects of the Earth’s orbit around the Sun?

The Earth’s orbit around the Sun leads to the change of seasons and the annual rhythms of both animate and inanimate nature.

The paths of the planets in the solar system have been altered. Planet Nine might have caused the paths of all the planets in the solar system to change

A recent collaborative research conducted by Elizabeth Bailey, Konstantin Batygin, and Mike Brown, the individuals credited with the discovery of Planet Nine, suggests that this phenomenon could have resulted in the adjustment of the paths of the other eight planets in the solar system.

A recent collaborative research conducted by Elizabeth Bailey and Konstantin Batygin and Mike Brown, the individuals credited with the discovery of Planet Nine, suggests that this occurrence could have caused the paths of all the other eight planets in the solar system to shift. If it indeed exists, it might provide an explanation for why the planets are not aligned with the Sun.

The original plane of the protoplanetary disk from which the eight major planets were born still holds true as they continue to orbit our star. Surprisingly, our Sun also spins on its axis, but at a peculiar angle of 6 degrees in relation to a line perpendicular to the planet’s plane.

There are multiple theories attempting to explain this unique tilt, such as the possibility of a passing star billions of years ago or the interaction between the Sun’s magnetic field and the primordial disk of gas and dust that birthed our solar system. However, these theories struggle to fully comprehend why the rotation axis aligns so precisely with the other planets.

Previously, there have been suggestions that Planet Nine, proposed by Michael Brown and Konstantin Batygin of the California Institute of Technology (USA), could explain the irregular movements of icy objects in the outer reaches of our solar system. However, a new theory suggests that this mysterious planet could actually influence the orbits of all the major planets.

“We hypothesize that this recently discovered planet has a significant tilt, and if it does exist, it would cause a gravitational pull that would alter the paths of other celestial bodies. These pieces of the puzzle seem to fit together and provide further evidence for the existence of Planet Nine,” explained Elizabeth Bailey.

This distant planet is estimated to be 5 to 20 times the mass of Earth and has an incredibly eccentric orbit. This suggests that it may have been a captured exoplanet that was once part of another star system before being stolen by our Sun.

“The crucial factor is not the mass but the tilt of Planet Nine. If it were solely a matter of mass, Jupiter would be the primary suspect. What matters is that the disturber is situated outside the general plane. Jupiter is unable to alter its own tilt angle,” stated Alessandro Morbidelli of the Observatoire de la Côte d’Azur (France), who reached a similar conclusion in his separate study.

The tilt of the Sun alone does not confirm the presence of Planet Nine. To begin with, we still require visual confirmation, at the very least, through a telescope.

What is the direction of planetary revolution around the Sun?

The planets in our Solar System all revolve around the Sun in the same direction, which is counterclockwise when observed from the North Pole of Earth. Additionally, the six planets also rotate on their own axes in this same direction.

Why do the planetary ORBITS align in a single plane?

Position of the planets within the Solar System. Overview of the planets in the Solar System

The total count of planets within the solar system is 8, and they are arranged based on their proximity to the Sun:

• The inner planets, also known as the terrestrial planets, consist of Mercury, Venus, Earth, and Mars. These planets are primarily composed of silicates and metals.
• The outer planets – Jupiter, Saturn, Uranus, and Neptune – are commonly referred to as gas giants. These planets are significantly more massive than the terrestrial planets. Jupiter and Saturn, the largest planets in the solar system, are primarily composed of hydrogen and helium. Uranus and Neptune, the smaller gas giants, contain methane and carbon monoxide in their atmospheres, in addition to hydrogen and helium.

Figure 1. Planets in the solar system.

The arrangement of planets in the solar system starting from the Sun is as follows: Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, and Neptune. However, if we arrange the planets from largest to smallest, the order changes. Jupiter is the largest planet, followed by Saturn, Uranus, Neptune, Earth, Venus, Mars, and finally Mercury.

All the planets orbit the Sun in the same direction as the Sun’s rotation, which is counterclockwise when viewed from the Sun’s north pole.

Mercury has the highest angular velocity among all the planets, completing a full revolution around the Sun in just 88 Earth days. On the other hand, the farthest planet, Neptune, takes 165 Earth years to complete one orbit.

The majority of planets rotate in the same direction as they orbit the Sun, but there are two exceptions. Venus and Uranus have unique rotation patterns. Uranus, in particular, has an axis tilt of about 90 degrees, causing it to rotate almost “lying on its side.”

Here is the sequence of the planets in the Solar System, along with their distinctive characteristics.

What is the reason for the alignment of all the planets in the same plane in the solar system?

Upon observing a map of the solar system, it becomes evident that all the planets follow a uniform orbit around the central star. It is not a result of cost-saving measures by the map publisher, but rather a natural arrangement of celestial bodies.

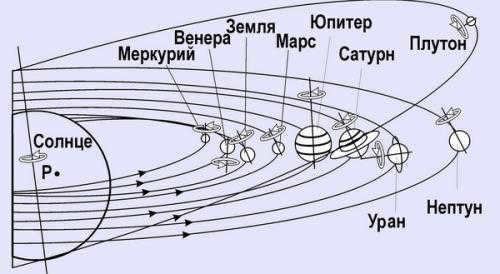
The paths of the planets in our solar system

This observation was made even before telescopes were invented, when people simply noted the Sun and the planets’ positions in the sky. In order to understand why they were all in the same flat plane, we have to go back to the time when the solar system was forming. At that time, there was a massive cloud of gas and dust that was rotating slowly. Then, for some unknown reason, it started to collapse. In simpler terms, it started to shrink. Scientists cannot definitively state what caused this to happen, but it is likely that it was not a supernova explosion that occurred very far away.

Regardless of the circumstances, gravity compelled the gas-dust cloud to increase in density – becoming more and more compact. As this spherical mass decreased in size, its rotational speed increased. This principle is known as the “conservation of momentum” and is a fundamental law of physics governing rotating systems. The momentum of an object is determined by two factors – the distribution of mass and the velocity of rotation. If either of these factors changes, the other must be adjusted accordingly in order to maintain the overall momentum, which remains constant and conserved.

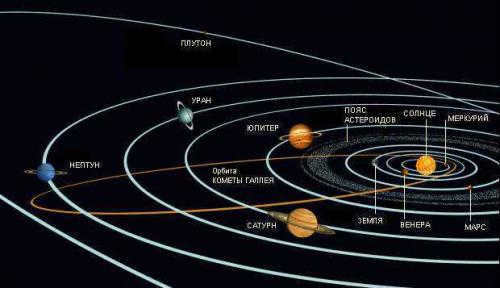
The arrangement and paths of the planets in the solar system

This suggests that as the massive gas-dust cloud decreased in size, it spun more rapidly. Eventually, this spinning generated enough force to flatten the cloud into a disk. Imagine it like this – you have a spherical lump of dough, you begin rotating it quickly on its own axis, and it transforms into a flat pizza bread. Interestingly, this is not just a theoretical concept. We actually observe the formation of these disks around young stars, including those within our own galaxy.

However, let’s travel billions of years back to our beloved planet. Within the disk that was created, particles of dust and gas would continuously collide and adhere to one another, leading to the creation of increasingly larger celestial entities. Most of them remained as small as asteroids, taking on a shape similar to that of potatoes, but a select few would eventually evolve into Earth and the other seven planets within our solar system. As they all originated from a singular rotating disk of matter, which inherently takes on a flat shape, these objects came into existence within a single plane. Furthermore, they all orbit the Sun in the same direction.

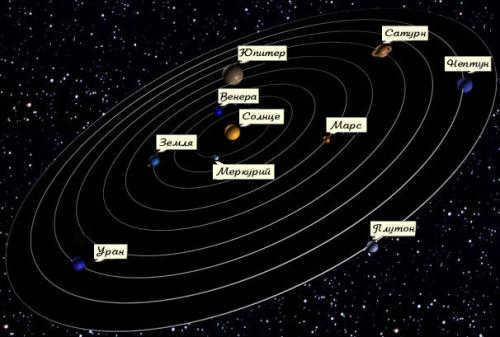
The planets within our solar system

Within the vast expanse of space surrounding the Sun, there are numerous smaller celestial bodies that move in inclined orbits. These include Pluto, comets, and certain asteroids. Initially, it is believed that all of these objects were situated within the same plane as the planets, but due to the gravitational influence of Jupiter or Neptune, they were displaced from this plane and assumed their current positions. Interestingly, these gas giants also had a hand in expelling many smaller celestial bodies from the solar system altogether.

Although it may appear peculiar to some, the fact that all of the planets in our solar system rotate within the same plane is a common occurrence observed in other known star systems. Rather than feeling disheartened by this regularity, we should embrace it. After all, we possess something that has yet to be discovered elsewhere in the vast expanse of the Universe – intelligent life in the form of humans. In that sense, we remain exceptionally unique.