
As you are aware, Nicolaus Copernicus’s groundbreaking concept of a heliocentric system of celestial arrangement provided a tremendous impetus to the advancement of astronomy. However, it is worth noting that Copernicus did not completely discard Aristotle’s notions regarding the “perfection” of the planets’ orbits. It was not until the early 17th century that Johannes Kepler, an Austrian astronomer, discovered the kinematic principles governing planetary motion. In this lesson, we will explore the formulations of Kepler’s three laws and examine the pivotal role they played in the subsequent progress of astronomy.

Currently, it is not possible for you to watch or distribute the instructional video with your students
In order to gain access to this and other video lessons included in the package, you will need to add it to your personal account.
Unlock amazing possibilities

Outline of the lesson “The Laws governing the motion of planets in the solar system”
You are already aware of the groundbreaking concept proposed by Nicolaus Copernicus, which introduced the heliocentric model of the solar system and propelled the progress of astronomy. However, it is important to note that Copernicus did not completely discard Aristotle’s notions of the planets’ orbits being “perfect”. Hence, his theory still incorporated the use of epicycles and deferents to account for various phenomena, including the retrograde motion of the planets.
Simultaneously, numerous scientists held the belief that the movement of celestial entities ought to be uniform and follow the “most perfect curve,” which is to say, the circle. Consequently, until the conclusion of the 16th century, they struggled to accurately predict the relative positions of the planets several years in advance. This theory resulted in a significant discrepancy when compared to observational data.
It was not until the early 17th century that the Austrian astronomer Johannes Kepler uncovered the laws of planetary motion. In his quest, he operated under the assumption that “numbers govern the world,” as expressed by Pythagoras. Kepler sought to correlate the motion characteristics of the planets with the regularities found in the musical scale, the lengths of the sides of polygons inscribed and circumscribed within the planets’ orbits, and so forth.

Unfortunately, every time Kepler compared his model to the observed paths of the planets, he had to acknowledge that their actual behavior did not align with the elegant framework he had outlined. As the contemporary British biologist John Haldane aptly put it, “the notion of the universe as a perfectly geometric work of art turned out to be yet another beautiful hypothesis shattered by unsightly facts.”
Only when he relocated to Prague and became a pupil of the Danish astronomer Tycho Brahe did Kepler encounter the concepts that would truly cement his name in the history of science.
Let’s envision the challenge that Kepler confronted in the following manner. We find ourselves on a celestial body that, firstly, rotates on its axis, and secondly, revolves around the Sun in an orbit that is unfamiliar to us. Gazing into the heavens, we witness other celestial bodies that also traverse orbits that are unknown to us. The query is: how can we ascertain the orbit and velocity of these other celestial bodies based on observations made from our vantage point on this rotating celestial body?
This appears to be quite a complex inquiry, even with the aid of modern computers. Remarkably, Kepler was able to solve this predicament without any such technology!
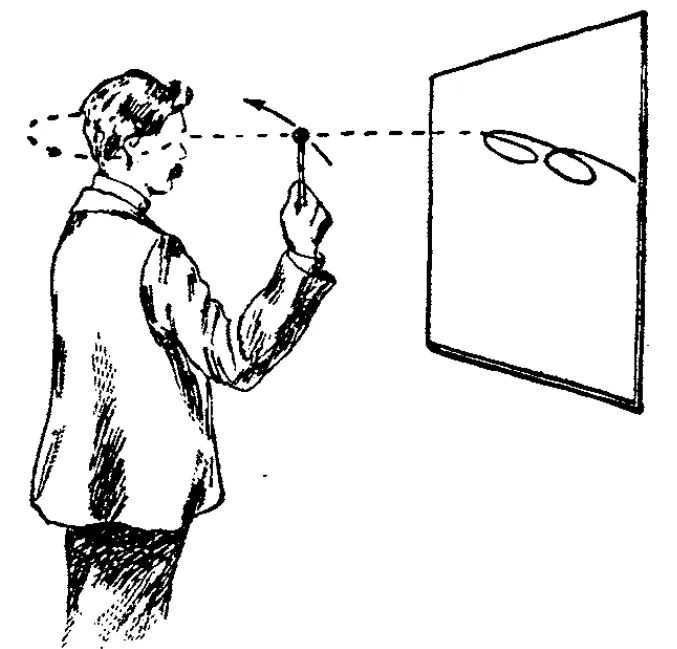
While observing the movement of Mars in space and utilizing the extensive data on its coordinates and configurations collected by Tycho Brahe over the years, Kepler observed that Mars does not move in a uniform manner. In order to determine the orbit of Mars, Kepler made a simplification by assuming that the Earth’s orbit is circular (which was consistent with observations). Based on this assumption, he made the following rough reasoning. Let’s suppose that we know the angular distance of Mars (represented by point M in the diagram) from the vernal equinox point during one of its oppositions, which is the direct ascent α1.
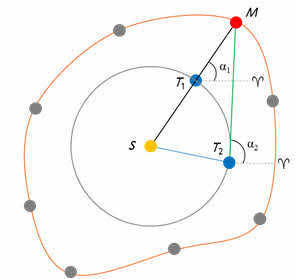
T1 is the Earth’s position during the opposition with Mars.
In order for Mars to return to the same point in its orbit, it takes 687 days (this is Mars’ sidereal period). The Earth’s sidereal period is 365 days. Therefore, it won’t have enough time to reach point T1 and will be at point T2 in its orbit at that moment. As a result, the apparent position of Mars will change for the observer. By studying different oppositions of Mars, Kepler obtained a series of points. Connecting them with a smooth curve, he constructed the orbit of this planet, which turned out to be not a perfect circle.
When faced with a decision, Kepler had two possible options: either assume that the orbit of Mars is a circle and that the calculated coordinates of the planet diverge from observations in certain parts of the orbit, or assume that all observations are correct and that the orbit of the planet is not actually a circle. Kepler, confident in the accuracy of his own observations as well as those of Tycho Brahe, chose the latter option and discovered that the best positions of Mars in its orbit align with a curve known as an ellipse. In this scenario, the Sun is not located at the center of the ellipse. Consequently, he formulated a law which would later be referred to as Kepler’s first law: all planets orbit in ellipses with the Sun situated at one of their foci.
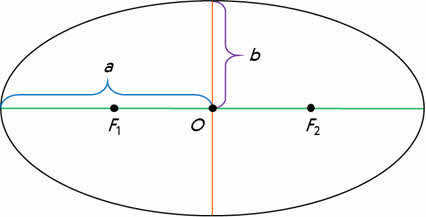
In the diagram, point O represents the center of the ellipse, while F1 and F2 are the focal points.
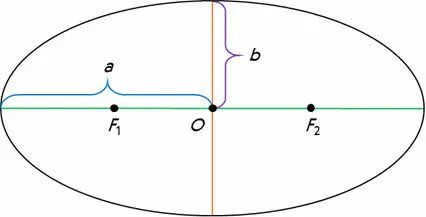
The line that passes through the foci of the ellipse, with its endpoints on the ellipse, is known as the major axis.
Additionally, the line that passes through the center of the ellipse and is perpendicular to the major axis is referred to as the minor axis.
The lines drawn from the center of the ellipse to the vertices on the major and minor axes are respectively called the major semi-axis and minor semi-axis of the ellipse. These are represented by the lowercase letters a and b.
The distinction between an ellipse and a circle lies in the value of its eccentricity. This value is equivalent to half of the ratio of the focal distance of the ellipse to its major semi-axis:
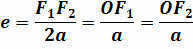
It should be noted that when the eccentricity of the ellipse is zero, the focal points and the center of the ellipse merge into a single point – the ellipse becomes a circle.
Let’s imagine that the Sun is located at the focus of the ellipse, F1. In this case, the point on the planet’s orbit closest to the Sun is called the perihelion. The point farthest from the Sun is called the aphelion.
For instance, the Earth’s orbit has an eccentricity of 0.017, which indicates that the orbit is nearly circular. The perihelion of our planet occurs in early January, with a distance of approximately 147 million kilometers to the Sun. On the other hand, the aphelion of Earth takes place in early July, and the distance at aphelion is slightly over 152 million kilometers.
However, let’s return to Kepler and the trajectory that he constructed for Mars. By analyzing the positions of the points he obtained, he noticed that the orbital velocity of Mars varies. Simultaneously, the radius vector of the planet (which is the line connecting the center of the Sun to the center of the planet) describes equal areas at regular time intervals.
This phenomenon was later named Kepler’s second law, sometimes referred to as the law of areas.
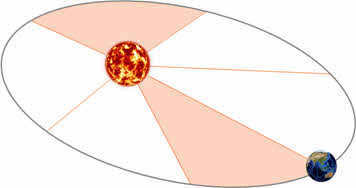
To gain a deeper comprehension of its physical significance, reminisce about your early years. You most likely possessed the ability to rotate around a pole on the playground, holding onto it with your hands. In actuality, planets revolve around the Sun in a comparable manner. As the planet’s elliptical orbit takes it further from the Sun, its motion slows down, whereas when it is closer to the Sun, the planet’s movement speeds up.
Therefore, the velocity of the planet’s revolution varies, reaching its maximum at perihelion and its minimum at aphelion.
Kepler introduced the first and second principles in 1609 in his work “The New Astronomy, or the Physics of the Heavens, set forth in the Investigations of the Motion of the Planet Mars.” However, Kepler’s first law was actually discovered in 1605, and the second law in 1602.

In 1618, Kepler finally formulated his third law. According to this law, the squares of the planets’ sideric periods of circulation are proportional to the cubes of the major semi-axes of their orbits.
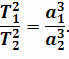
Kepler himself described this discovery in the following way: “What I set out to find 16 years ago has finally been found, and it has exceeded all of my wildest expectations.”
The third law of planetary motion is truly remarkable. It allows us to determine the relative distances of the planets from the Sun by using their known orbital periods. Instead of calculating the distance from the Sun to each individual planet, we can simply measure this distance for one planet, such as Earth. To simplify the calculations, the major semi-axis of Earth’s orbit is taken as one astronomical unit (1 AU). This unit of measurement serves as the basis for calculating all other distances in the Solar System.
Once again, we would like to emphasize that Kepler formulated his laws solely based on his own observations and those made by Tycho Brahe. If one were to inquire about the factors behind the elliptical shape of the orbits or the equal areas of the sectors, Kepler would not have been able to provide an answer. These conclusions simply arose from his analysis. Similarly, if one were to inquire about the orbital motion of planets in other stellar systems, Kepler would have been equally stumped.
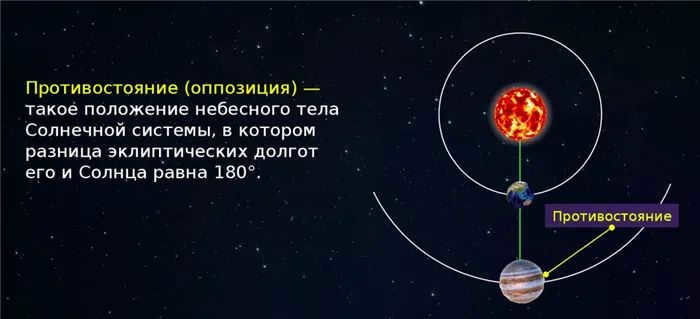
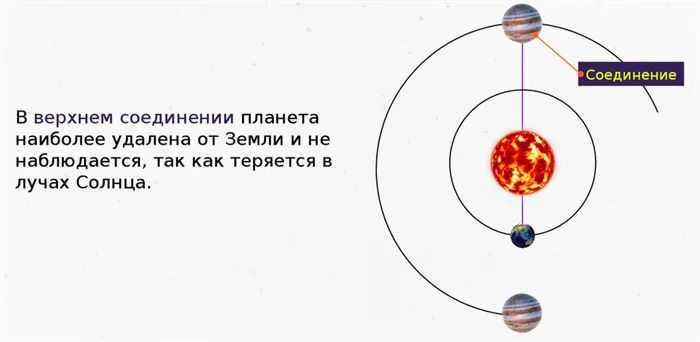
When a planet arrives, it actually becomes undetectable – it reaches the highest conjunction. To put it simply, the Sun is currently positioned between the planet and the Earth, obstructing our view.
Lecture. Planetary Arrangements. Laws Governing Planetary Motion
Planetary arrangements determine the relative positions of the planets with respect to the Earth and the Sun, and dictate their visibility in the sky. Since all planets shine through reflected sunlight, the planet closest to Earth is most visible when its sunlit side is facing us, as it is illuminated by the Sun during the day.
Figure 4.1 depicts Mars in opposition (M1), an arrangement where the Earth lies directly between Mars and the Sun. In this scenario, the planet appears brighter because its entire sunlit hemisphere is facing Earth.
The paths of the two planets Mercury and Venus are situated nearer to the Sun than to Earth, hence they do not come into opposition. When Venus or Mercury is at its closest point to Earth, it cannot be observed as the side of the planet facing us is in darkness (see Figure 4.1). This arrangement is known as a lower conjunction with the Sun. During an upper conjunction, the planet is also not visible as the Sun shines brightly between it and the Earth.
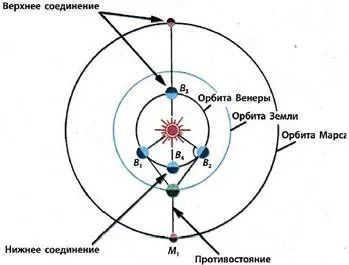
Figure 4.1: Venus and Mars Configurations. Mars, which is the nearest planet to Earth, can be observed throughout the night in the opposite direction of the Sun. Venus is most visible in the evening during its eastern elongation, positioned to the left of the Sun B1, and in the morning during its western elongation, positioned to the right of the Sun.2
Opposite – the planet can be seen from Earth throughout the night in the opposite direction of the Sun
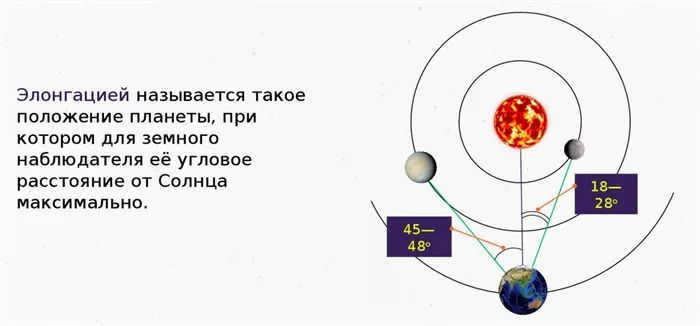
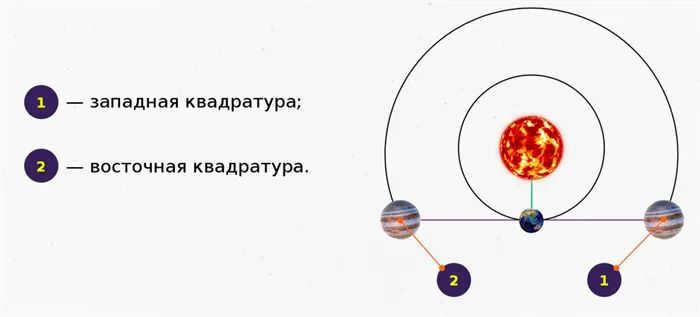
Elongation – the angular distance between the planet and the Sun as observed from the surface of the Earth.
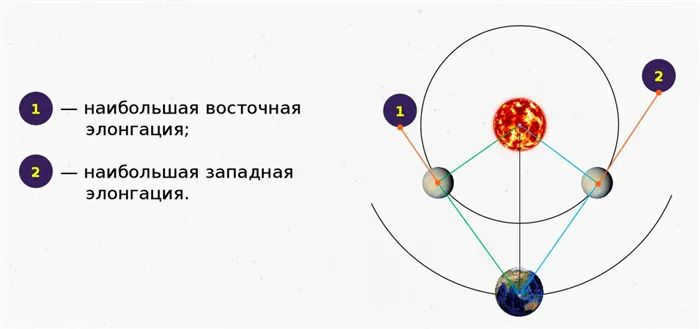
The most favorable conditions for observing Venus and Mercury occur when they are in elongation. Eastern elongation refers to the position when the planet is visible at night on the left side of the Sun. On the other hand, western elongation of Venus can be observed in the morning, as the planet is seen to the right of the Sun on the eastern side.
Explanation: During contrast, the planet is visible throughout the entire night. During conjunction with the Sun, the planet is not visible. Eastern elongation occurs when the planet is visible in the western part of the horizon in the evening, while western elongation occurs when the planet is visible in the eastern part of the sky in the morning.
Sideric and synodic periods of planetary orbital periods
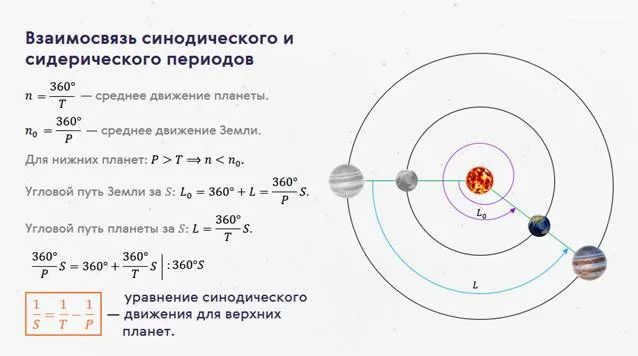
The length of time it takes for a planet to complete one revolution around the Sun determines the orbital period of the planet and its motion relative to the stars (Figure 4.2).
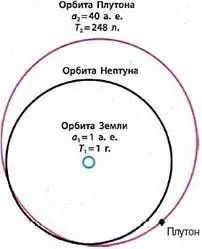
Figure 4.2: The dashed blue line represents the orbit corresponding to the secondary period of Mars’ rotation around the Sun, while the red dashed line represents the coherent period.
The sinusoidal orbital period is responsible for the movement of celestial bodies in relation to the Earth and the Sun. It is the period during which we observe the same configurations of the planets, such as opposition, conjunction, and elongation. Fig. 4.2 illustrates the positions of N-S1-М1 and C-32-М2, which are two consecutive oppositions of Mars. The following equation describes the relationship between the synodic periods S and the secondary periods T of planetary rotation: (4.1)
Johannes Kepler (Figure 4.3) made the groundbreaking discovery that Mars orbits the Sun in an elliptical path. Subsequently, it was demonstrated that other planets also follow elliptical orbits.
Kepler’s initial principle. All planets revolve around the Sun along ellipsoids, with the Sun positioned at one of the focal points of these ellipsoids (Figures 4.4 and 4.5).
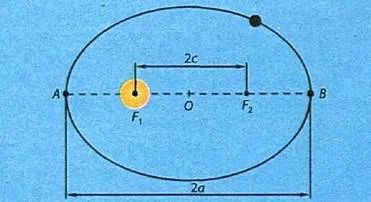
Figure 4.4: The planets orbit the Sun in elliptical paths. AF1=Fmin- at the point of closest approach to the Sun known as perihelion; BF1=Fmax- at the point of farthest distance from the Sun known as aphelion.
The most significant implication of Kepler’s first law is that the distance between a planet and the Sun is not constant but varies within the range: rmax≤ r ≥ rmin
The point at which the planet is closest to the Sun in its orbit is called perihelion (derived from the Greek word “peri” meaning close to the Sun), while the point farthest from the center of the Sun is called aphelion (derived from the Greek word “aro” meaning far away). The sum of the distances from perihelion to aphelion corresponds to the major axis AB of the elliptical orbit: rmax + rmin = 2a. The semi-major axis of the Earth’s orbit (OA or OM) is known as an astronomical unit. 1 AU is equal to 149.6 × 106 km.
During perihelion on January 3 and 4, the Earth is closest to the Sun and has a distance of 147 million km.
During aphelion on July 3 and 4, the Earth is at its farthest distance from the Sun at 153 million kilometers.
Kepler’s Second Law: The radius-vector of the planet describes equal areas at equal distances.
Kepler’s second law states that as a planet moves along its orbit, both its distance from the Sun and its linear and angular velocity change over time.
The planet has its highest velocity at perihelion, when it is closest to the Sun, and its lowest velocity at aphelion, when it is farthest from the Sun.
Kepler’s second law also establishes the well-known principle of conservation of energy: the total energy (kinetic + potential) in a closed system remains constant. The planet’s kinetic energy is determined by its velocity, while its potential energy depends on its distance from the Sun. Therefore, the closer the planet is to the Sun, the greater its velocity (Figure 4.6).
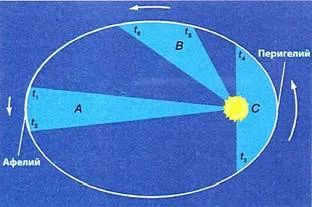
Figure 4.6: As a planet approaches the Sun, its velocity increases, but as it moves away from the Sun, its velocity decreases.
Although it is challenging to confirm Kepler’s first law in a classroom setting since the distance between the Earth and the Sun must be measured during both winter and summer, Kepler’s second law can be easily verified by any student. This can be accomplished by validating the Earth’s varying velocity throughout the year. To conduct this verification, a regular calendar can be utilized to measure the duration of a semester from the vernal equinox to the autumnal equinox (March 21st-September 23rd) and vice versa – from September 23rd to March 21st. If the Earth were to orbit the Sun at a consistent speed, the number of days in these six months would be identical. However, in accordance with Kepler’s second law, the Earth’s velocity is higher in winter and lower in summer. As a result, summer in the northern hemisphere lasts slightly longer than winter, while winter in the southern hemisphere lasts slightly longer than summer.
The Earth’s minimum velocity during the summer season is 29.36 kilometers per second.
During the month of July, the Earth experiences a reduced speed, resulting in a longer duration of summer in the northern hemisphere compared to the southern hemisphere. This phenomenon can be attributed to the higher average annual temperature in the northern hemisphere as compared to the southern hemisphere.
As you are already aware, the groundbreaking concept proposed by Nicolaus Copernicus, which suggested a heliocentric model of the world, had a profound impact on the advancement of astronomy. However, it is important to note that Copernicus did not completely discard Aristotle’s notions regarding the “perfection” of planetary orbits in his teachings. It was not until the early 17th century that the Austrian astronomer Johannes Kepler discovered the laws of planetary motion. In this lesson, we will explore the formulations of Kepler’s three laws and examine their significance in the subsequent progress of astronomy.

Currently, it is not possible for you to view or share the instructional video with students
In order to have access to this and other video lessons included in the package, you must add it to your personal account.
2. Share the video lessons with the personal accounts of your students.
3. Check out the data on the number of video lessons viewed by your students.
Outline of the Lesson “The Laws Governing the Motion of Planets in the Solar System”
You are already aware that Nicolaus Copernicus’ groundbreaking concept of a heliocentric model of the universe propelled the field of astronomy forward. However, it is important to note that Copernicus did not completely discard Aristotle’s notion of the “perfection” of planetary orbits in his teachings. As a result, his theory still incorporated epicycles and deviations to account for various phenomena, such as the periodic motion of the planets.
It wasn’t until the start of the 17th century that Austrian astronomer Johannes Kepler unraveled the laws governing the movement of planets. Kepler’s quest was rooted in the conviction that “numbers govern the universe”, a concept previously espoused by Pythagoras. Kepler endeavored to draw parallels between the characteristics of planetary motion and the principles governing musical scales, the lengths of geometric figures inscribed and circumscribed within planetary orbits, and more.

Regrettably, each time Kepler compared his model with the observed trajectories of the planets, he had to acknowledge that their actual behavior did not align with the intricate framework he had described. As the insightful British biologist John Haldane once remarked, “the concept of the universe as a geometrically flawless masterpiece turned out to be yet another exquisite hypothesis destroyed by unfavorable circumstances.”
It was only after relocating to Prague and becoming a student of the Danish astronomer Tycho Brahe that Kepler formulated the ideas that would eternally immortalize his name in the annals of scientific history.
Imagine the scenario that Kepler had to deal with in the following way. We find ourselves on a planet that rotates on its axis and also orbits the Sun in an orbit that is not known to us. As we gaze up at the sky, we observe other planets that are also moving in orbits that are unknown to us. So, the question arises: How can we determine the orbit and velocity of these other planets by observing a sphere that revolves on its axis and around the Sun?
This question may seem quite complex, even with the advancements of modern computer technology. However, Kepler was able to find the answer despite not having access to such technology!
By observing the movement of Mars in space and utilizing the coordinates and configurations of this planet determined by Tycho Brahe over a span of various years, Kepler made the discovery that Mars moved in an irregular manner. He made the decision to construct an orbit for Mars. To accomplish this, he made a small approximation by assuming a circular orbit for Earth (which did not contradict the observations). His reasoning went as follows. We have knowledge of the angular distance of Mars (point M in the diagram) from the point of the vernal equinox at the time of one of the planet’s oppositions, specifically its direct ascension a1.
T1 represents the specific position of the Earth during Mars’ opposition.
In order for Mars to return to the same location in its orbit, a period of 687 days must elapse (this corresponds to Mars’ lateral rotation period). The solar period of the Earth is 365 days, so there isn’t enough time for it to reach point T1 and it is instead in orbit at temperature T2. As a result, the direct rising of Mars will appear different to observers. Kepler was able to obtain a series of points by analyzing multiple Mars oppositions. By connecting these points with a smooth curve, he was able to map out the orbit of Mars, which was found to be non-circular.
Observable Movement of Planets and the Sun
During your science lessons, you have gained a basic understanding of the composition of the solar system. Now, let’s delve deeper into the arrangement of the solar system and commence by discussing and evaluating the visible movements of the planets. There are five planets that can be observed without the aid of a telescope: Mercury, Venus, Mars, Jupiter, and Saturn.

In the early 16th century, Nicolaus Copernicus was able to determine the movement of the planets within the constellations of the zodiac. This is a result of the Earth and the planets orbiting the Sun at varying speeds. The term “ecliptic” refers to the changing equatorial coordinates of the Moon, Sun, and planets. It represents the apparent annual path of the Sun’s center across the celestial sphere. The Sun’s motion along the ecliptic reflects the Earth’s actual motion around the Sun, which was only confirmed in 1728 with James Bradley’s discovery of the annual deviation.
The path that a celestial object follows as it moves through the universe is known as its orbit. As a planet moves farther away from the Sun, its orbit becomes smaller in size. The orbits of all the planets in our solar system are located close to the ecliptic plane, although they do deviate from it.
The planets generally follow a west-to-east movement, similar to that of the Sun and the Moon, which is known as direct motion. However, at certain points in their orbit, each planet slows down, comes to a halt, and starts moving from east to west, which is referred to as retrograde motion. Eventually, the planet stops again and resumes its forward motion. As a result, the apparent path of any planet in the sky is a intricate series of zigzags and loops. Furthermore, this path changes from one cycle to another, with the planet roughly maintaining its position relative to the stars.
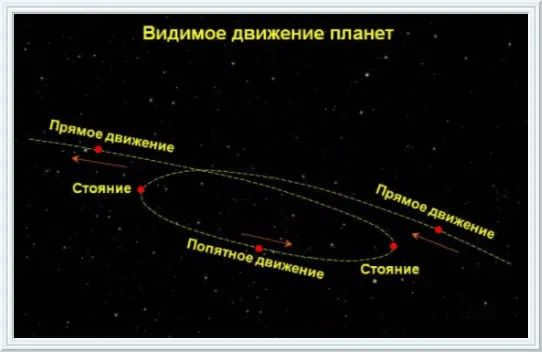
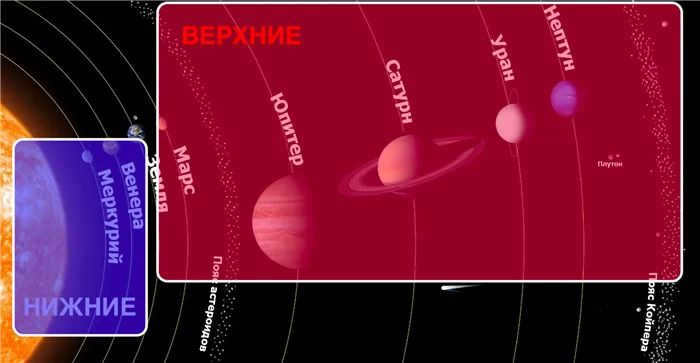
The planets of our solar system can be categorized into two groups based on their orbits and visibility from Earth. The inner planets, which include Mercury and Venus, are closer to the Sun and are typically visible from Earth. On the other hand, the outer planets, such as Mars, Jupiter, Saturn, Uranus, and Neptune, are located farther from the Sun and are also visible from Earth, but with their illuminated side facing us.
The inner planets, similar to the Moon, go through different phases as they orbit around the Sun. In contrast, the outer planets always present the same illuminated side to Earth due to their position in the solar system.
We can also classify the planets based on their orbits with respect to Earth’s orbit. The planets that have orbits inside Earth’s orbit are known as the lower planets, while the planets with orbits outside Earth’s orbit are referred to as the upper planets.
2. Planetary Configurations
Planetary configurations refer to the specific relative positions of the planets, Earth, and the Sun. The configurations of the lower and upper planets vary due to their different visibility conditions. The visibility of a planet is determined by its location in relation to the Sun, which provides illumination, and the Earth, from where the planet is observed.
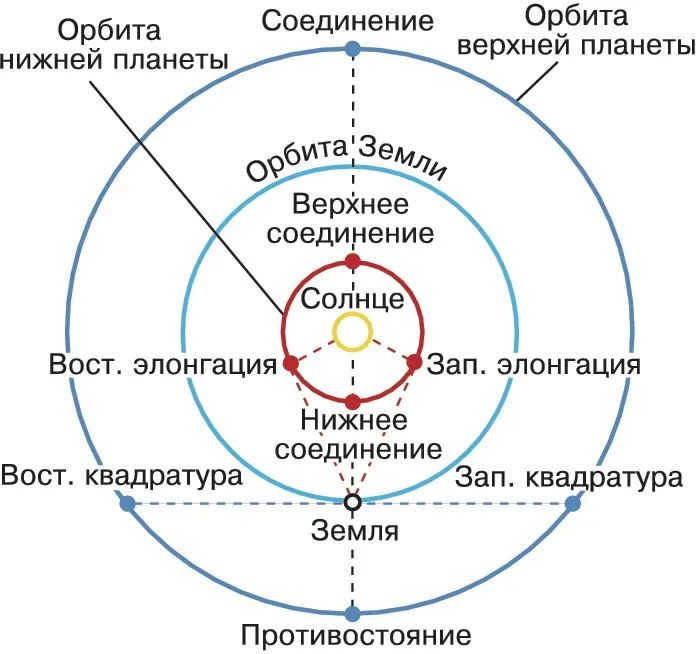
The trajectory of movement for the planets in the solar system can be divided into two categories: cuspids, which are located below and above, and oblates, which are situated to the east and west.


Conjunction, opposition, and square are the three main celestial events that we use to differentiate between the upper planets.


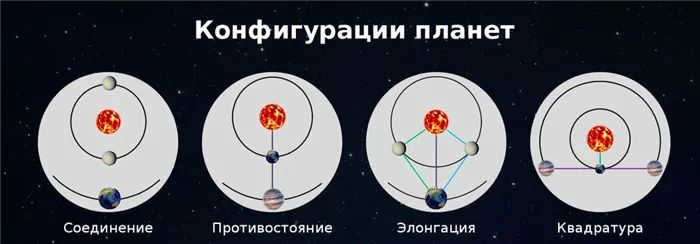
Due to the orbit of the planets around the Sun, they naturally go through recurring configurations. The time period between two consecutive configurations of a particular planet is known as the phinoid period, derived from the Greek word “synopsis”. In simpler terms, it is the duration after which a planet (or any other celestial body in the solar system) returns to its previous position relative to the Sun as observed from Earth.
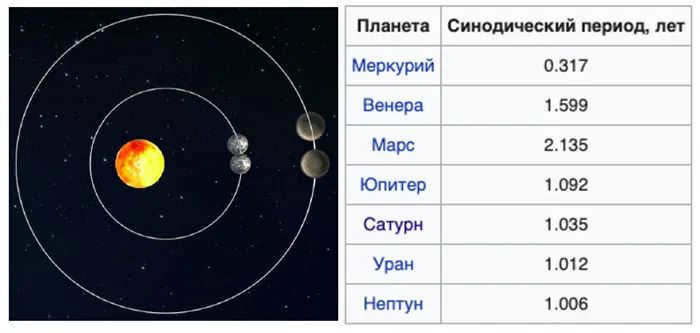
Calculations of planetary periods have been carried out since ancient times, when it was believed that all celestial bodies orbited around the Earth. However, we now understand that the Earth is not static, but rather orbits the Sun alongside the other planets. The length of time it takes for a planet to complete one full revolution around the Sun, while also orbiting the stars, is known as the sidereal period (sidus, derived from the Latin word for star, sideris). In everyday language, this period is often referred to as a year. For instance, we have the Earth’s year, Mercury’s year, Jupiter’s year, and so on.

It is not possible to accurately determine the exact period of a planet’s revolution around the Sun due to the Earth’s constant movement. As the Earth completes its orbit, it shifts to a new position in space and the planet’s projection against the background of fixed stars also shifts. This means that the planet cannot reach or pass the point from which its motion was initially observed. However, there is a correlation between the apparent and actual periods of planets. Let’s explore this relationship:
3. The duration of a day in astronomy
In astronomy, the length of a day on a planet is determined by how fast it rotates. There are different types of twenty-four-hour periods in astronomy, depending on the frame of reference. If a distant star is used as the point of reference, then the duration of a day will be different from that of the central star in the planetary system. On Earth, for instance, there is the average solar day, which lasts 24 hours, and the sidereal day, which lasts approximately 23 hours, 56 minutes, and 4 seconds. These two types of days are not the same because the Earth’s orbit around the Sun causes the Sun to appear to move against the background of distant stars as observed from the Earth’s surface.
A sidereal day is the period of time that a celestial body takes to complete one full rotation on its axis relative to the center of the Sun. In the illustration above: 1-3 represent solar days.
Ecliptic. The path of the Sun along the ecliptic
Ancient astronomers who studied celestial bodies observed that the sun is at varying altitudes at noon throughout the year. If you gaze at the horizon at midnight during summer or winter, spring or fall, you can clearly discern different constellations on the southern side. For instance, what is visible during summer is completely invisible during winter. Conversely, the stars of summer constellations are entirely invisible during winter. Based on these observations, the annual movement of the Sun in relation to the stars was established. This is when the term “ecliptic” was coined in the field of science.
We are already aware that the movement of the Sun is relative. The apparent movement of a star in relation to the movement of the Earth around the Sun. The Earth’s daily movement, which is a complete rotation on its axis, takes 23 hours, 56 minutes, and 4 seconds. In a similar manner, the Sun moves across the sky by 1 degree per day. The period of time it takes for the Sun to complete a full circle in the celestial sphere is known as a year. This equates to 365 days and 6 hours. Every fourth year is a leap year because extra days are added throughout the year. Consequently, a leap year consists of 366 additional days.
Zodiacal constellations
Throughout the course of one year, the Earth follows a circular path as it orbits around the Sun. Along this path, known as the ecliptic, the Sun moves through 13 constellations, commonly known as the signs of the zodiac.
To put it simply, the constellations that line the ecliptic are referred to as zodiacal constellations.
In modern astronomy, there are actually 13 constellations within the zodiac, not just 12 as previously believed. Even ancient astronomers assigned names to each star that remained associated with the respective constellation for many years. The choice of name was often based on their resemblance to certain objects, animals, or images. Today, these names are well-known. The zodiacal constellations include:
- Aries.
- Taurus.
- Gemini.
- Cancer.
- Leo.
- Virgo.
- Libra.
- Scorpio.
- Serpentarius.
- Sagittarius.
- Capricorn.
- Aquarius.
- Pisces.
If you follow the path of the Sun starting from Aries (April 19-May 3), it will return to the same constellation exactly one year later. In just one month, the Moon will traverse all the constellations of the zodiac in a shorter time. This is because it only takes 27 days for the Earth to complete its full orbit. The planets also move through the constellations at varying speeds, which is determined by their distance from the Earth and the Sun. The vernal equinox on March 20 serves as the reference point for the zodiacal constellations.
Every zodiac sign boasts an abundance of brilliant stars that played a crucial role in dividing the sky into distinct regions, with each sign having its own set boundaries. Here are a few examples of the most prominent stars. The constellation Gemini boasts Pollux, Alchena, and Beaver, Scorpio showcases Sargas and Antares, Sagittarius displays Nunki and Kaus Australis, and Leo features Algieba, among others.
It’s important to note that the modern boundaries of these constellations were officially established by the International Astronomical Union in 1928.
The ancient constellations are referred to as Aries, and they were already known in ancient Greece. This constellation can be seen in the northern hemisphere and is particularly visible throughout Russia. The best times to observe Aries are during the summer, fall, and winter. Legend has it that Aries is a magical ram with twisted horns, also known as the Golden Fleece. In Greek mythology, the Argonauts embarked on a quest to find the Golden Fleece, sailing on the ship named “Argo.”
Aries consists of a total of 57 stars that can be seen without the aid of a telescope. In terms of size, Aries is the 39th largest constellation out of the 88 modern constellations. It features several bright stars.

The constellation is associated with ancient civilizations. Many cultures revered and respected this creature. Taurus can be easily spotted across various regions. Even without any astronomical tools, one can observe the 216 stars that form Taurus. This constellation is located in the northern hemisphere. The best time to view it is between November and January. Among its brightest stars is a notable one, which is ranked as the 17th largest star in the night sky.
This group of stars can be found in the northern hemisphere and is characterized by two relatively bright stars, Castor and Polydicea, which are located close to each other. These stars represent the heads of twin brothers, with their feet pointing southwest and situated in the Milky Way. The best time to observe the twins is during the months of December and January. Approximately 70 stars can be seen with the naked eye in this constellation, ranking it 30th in the region.
All the planets in our solar system are subject to the gravitational force exerted by the Sun, similar to the way the Moon and artificial satellites of Earth orbit our planet. This type of movement is referred to as central motion. The principles governing this motion are known as Kepler’s laws.

Kepler’s first law
The planets follow elliptical paths, with the Sun located at one of the foci.
Technically, the Sun and the planets orbit around a shared center of mass. However, this center is positioned within the Sun, as the Sun’s mass far outweighs that of the planets.
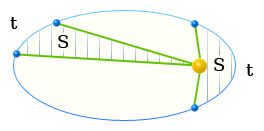
Kepler’s Second Law
The Sun and the planet, when connected by a line, sweep out equal areas in equal time intervals.
Kepler’s second law can be derived from the law of conservation of angular momentum.
Kepler’s third law
The ratio of r 3 to T 2 remains constant for all planetary orbits.
Kepler’s third law is a result of the requirement that the centripetal force must be equal to the gravitational force of attraction.
| represents the radius of the trajectory, | measured in meters |
| represents the angular velocity, | measured in radians per second |
| represents the gravitational constant, | measured in m^3/(kg – s^2) |
| represents the mass of the planet, | measured in kilograms |
| represents the mass of the Sun, | measured in kilograms |
| represents the orbital period, | measured in seconds |
III. Structure of the Solar System
§ 14. The Movement of Celestial Bodies due to the Force of Gravity
Extra Resources for the Lesson
1. The Law of Universal Gravitation
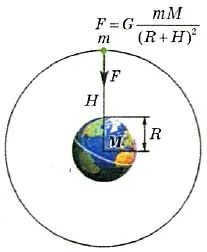
As per the law of universal gravitation, which is studied in the field of physics, all objects in the universe exert an attractive force on each other. This force is directly proportional to the product of their masses and inversely proportional to the square of the distance between them:
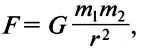
where m1 and m2 denote the masses of the objects; r represents the separation between them; G is the gravitational constant.
The law of universal gravitation was primarily facilitated by Kepler’s laws of planetary motion and other advancements in astronomy during the 17th century. For instance, Isaac Newton (1643 – 1727) was able to establish the equivalence of the force that keeps the Moon in orbit around the Earth and the force responsible for objects falling towards the Earth by utilizing his knowledge of the distance to the Moon.
Considering the law of universal gravitation, which states that the force of gravity is inversely proportional to the square of the distance, it can be concluded that the Moon, being approximately 60 radii away from the Earth, should experience an acceleration that is 3600 times less than the acceleration of gravity at the Earth’s surface, which is 9.8 m/s^2. Therefore, the Moon’s acceleration must be 0.0027 m/s^2.
Additionally, as the Moon moves uniformly on a circular path, it has an acceleration given by the formula:
where ω represents the angular velocity of the Moon, and r is the radius of its orbit. Assuming the radius of the Earth is 6400 km, the radius of the lunar orbit can be calculated as r = 60 – 6,400,000 m = 3.84 ∙ 10^8 m. The orbital period of the Moon, T, is 27.32 days, which is equivalent to 2.36 ∙ 10^6 s. Substituting these values, the acceleration of the Moon’s orbital motion is
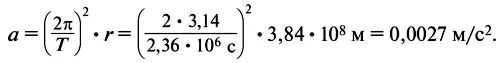
The fact that the acceleration of the Moon and the force of the Earth’s gravity are equal proves that the force keeping the Moon in orbit is the Earth’s gravity, which is 3600 times weaker compared to the force on the Earth’s surface.
Furthermore, we can also confirm that the acceleration of planets and the gravitational force exerted by the Sun on them, in accordance with Kepler’s third law, are inversely proportional to the square of the distance. This can be derived from the law of universal gravitation. Kepler’s third law states that the ratio of the cubes of the major semi-major axes of orbits (d) and the squares of the periods of revolution (T) is a constant value:
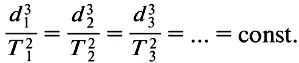
Kepler’s third law can be derived from the following information
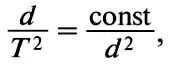
The planet’s acceleration is equivalent to
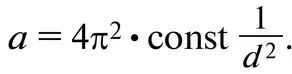
Thus, the gravitational force between the Sun and the planets adheres to the universal law of gravitation.
2. Variations in the movement of celestial bodies in the solar system
If we examine the movement of two separate bodies (the Sun and a planet) solely under the influence of their mutual attraction, Kepler’s laws are accurately upheld. However, since the Solar System contains numerous planets, they not only interact with the Sun but also with one another. Consequently, the movement of planets and other celestial bodies does not precisely follow Kepler’s laws. Deviations from elliptical motion are known as perturbations.
These disturbances are minor, as the Sun’s mass greatly exceeds not only that of a single planet, but of all the planets combined. The most significant disturbances in the movement of the celestial bodies in our solar system are caused by Jupiter, which has a mass 300 times greater than that of Earth. The deviations of asteroids and comets become particularly noticeable when they pass in close proximity to Jupiter.
Currently, the calculations of the positions of planets, their satellites, and other bodies in the solar system, as well as the trajectories of spacecraft sent to study them, take into account these disturbances. However, as far back as the 19th century, the calculation of disturbances allowed for one of the most renowned scientific discoveries to be made “with the stroke of a pen” – the discovery of the planet Neptune.
While conducting a survey of the sky to search for unidentified objects, William Herschel made a groundbreaking discovery in 1781 – a new planet that was later named Uranus. However, it was soon discovered that the observed motion of Uranus did not match up with the calculated motion, even after accounting for the gravitational effects of all known planets. This led astronomers to speculate the presence of another planet, which they referred to as a “sauranic” planet. Independent of each other, John Adams in England and Urbain Leverrier in France solved this problem by calculating the orbit and position of this hypothetical planet in the sky. Leverrier’s calculations guided the German astronomer Johann Halle to the discovery of a previously unknown planet, Neptune, in the constellation Aquarius on September 23, 1846. This momentous discovery was a major triumph for the heliocentric system and provided crucial evidence for the validity of the law of universal gravitation. Subsequently, astronomers noticed perturbations in the motion of both Uranus and Neptune, leading to the hypothesis of the existence of yet another planet in our solar system.
After examining numerous images of the night sky, astronomers made the groundbreaking discovery in 1930 that Pluto was one of several celestial bodies situated beyond the orbit of Neptune.
3 The Earth’s Mass and Density
The law of universal gravitation provided a means to determine the mass of our planet. According to this law, the acceleration due to gravity can be expressed as follows:
By substituting the known values into the equation – g = 9.8 m/s 2 , G = 6.67 ∙ 10 -11 H ∙ m 2 ∕kg 2 , R = 6370 km – we can calculate that the Earth’s mass, M, is approximately 6 ∙ 10 24 kg. With knowledge of the mass and volume of the Earth, we can then calculate its average density, which is approximately 5.5 ∙ 103 kg/m 3 . As one delves deeper into the Earth, density increases due to greater pressure and the presence of heavier elements.
4 Determining the mass of celestial bodies
By using the more precise formula derived by Newton for Kepler’s third law, it is possible to determine the mass of any celestial body. This formula considers the orbits of the planets to be circular in the first approximation.
Consider two bodies with masses m1 and m2, mutually attracted to each other and orbiting around a common center of mass. These bodies are located at distances r1 and r2 from the center of mass and orbit around it with a period of T. The distance between their centers is R = r1 + r2. According to the law of universal gravitation, the acceleration of each body is equal:
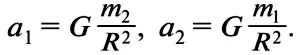
The formula for the angular velocity of rotation around the center of mass is ω = 2 π 2 / T. Next, the centripetal acceleration is calculated for each celestial body using the following expression:
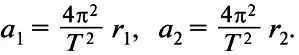
By equating the derived expressions for acceleration and solving for r1 and r2, we can combine them to get:
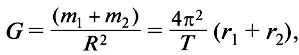
Given that the right side of this equation consists solely of constant values, it holds true for any system of two celestial bodies that interact through the force of gravity and revolve around a shared center of mass. This can include systems such as the Sun and a planet, or a planet and its satellite. To calculate the mass of the Sun, we can derive the following equation:
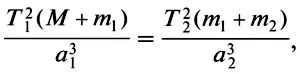
In the given equation, M represents the mass of the Sun, m1 represents the mass of the Earth, m2 represents the mass of the Moon, T1 represents the period of the Earth’s orbit around the Sun (in years), a1 represents the major semi-axis of the Earth’s orbit, T2 represents the period of the Moon’s orbit around the Earth, and a2 represents the semi-major axis of the Moon’s orbit.
By disregarding the negligible mass of the Earth when compared to the mass of the Sun, and considering the fact that the mass of the Moon is 81 times less than the mass of the Earth, we can simplify the equation as follows:
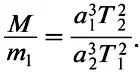
By plugging in the given values into the equation and assuming the mass of the Earth as a unit, it can be concluded that the Sun is approximately 333,000 times the mass of our planet.
When it comes to determining the masses of planets that do not have any satellites, scientists rely on the disturbances they cause to the movement of asteroids, comets, or spacecraft that pass by. For information on how the masses of stars are determined, refer to section 23.
5. Tides
Due to the gravitational attraction between particles, objects have a tendency to assume a spherical shape. However, when these objects rotate, they become deformed, causing a shrinkage at the poles.
Furthermore, changes in their shape are also influenced by the gravitational attraction, which leads to the occurrence of tides. Although tides have been observed on Earth for a long time, their explanation was only possible through the application of the law of universal gravitation.
Now, let’s examine the accelerations produced by the gravitational force of the Moon at different locations on the Earth’s surface (Fig. 3.13).
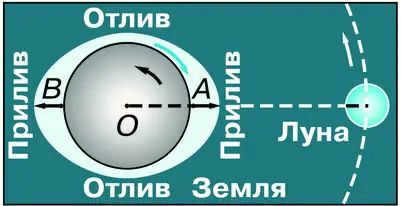
Due to the varying distances between the Moon and points A, B, and O, the gravitational accelerations experienced at each point will differ.
The discrepancy in accelerations resulting from the gravitational pull of another celestial body at a specific location compared to the planet’s center is known as tidal acceleration.
The tidal forces at points A and B result in a pulling effect on the Earth, specifically on its water shell, in the direction away from the center of the Earth. This pulling force occurs along a line that connects the centers of the Earth and the Moon, causing tides to occur at points A and B. Furthermore, along a circular path that is perpendicular to this line, the Earth experiences an ebb tide. Although the Sun’s gravitational pull also contributes to tides, the distance between the Earth and the Sun is greater, resulting in smaller tidal effects compared to those caused by the Moon. Tides are not only observed in the hydrosphere, but also in the Earth’s atmosphere and lithosphere, as well as in the atmospheres and lithospheres of other planets.
Because of the Earth’s diurnal rotation, tidal humps tend to be entrained, while simultaneously, due to the Moon’s gravitational pull as it orbits the Earth in a month, the tidal band must move much more slowly across the Earth’s surface. Consequently, tidal friction occurs between the massive bodies of water involved in tidal events and the ocean floor. This friction decelerates the Earth’s rotation and results in an increase in the length of the day, which in the past was considerably shorter (5 – 6 h). The same phenomenon also accelerates the Moon’s orbital motion and causes it to gradually move away from the Earth. Simultaneously, the tidal forces from the Earth’s side on the Moon have slowed down its rotation, causing it to always show the same face to the Earth. This slow rotation is also observed in numerous satellites of Jupiter and other planets. The intense tides caused by the Sun on Mercury and Venus appear to be the reason behind their extremely sluggish rotation around their axes.
Newton was the first to propose the idea of an artificial Earth satellite. He demonstrated that there exists a specific horizontal velocity at which a falling object will not plummet to the Earth, but instead, will orbit around it, maintaining a constant distance. At this velocity, the object will be attracted to the Earth by its gravitational force just as much as it will be propelled away from it due to the curved surface of our planet (Fig. 3.14).
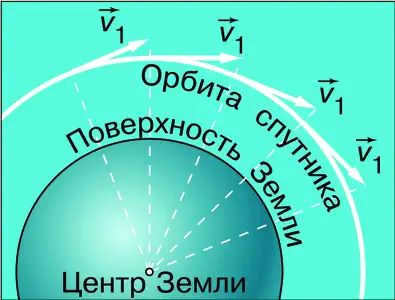
The velocity that goes by the name of the initial cosmic (or circular) velocity is something you are familiar with from your physics class:
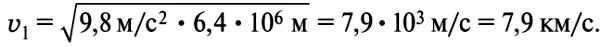
Practically speaking, it took only two and a half centuries after Newton’s groundbreaking discovery for the launch of an artificial Earth satellite to become a reality. This historic event occurred on October 4, 1957, marking the beginning of mankind’s journey into the space age. Since that momentous day, artificial satellites of various types and purposes have played a significant role in our daily lives. They enable us to constantly monitor weather patterns and other natural phenomena, as well as provide television broadcasts, among other things. The GLONASS satellite navigation system and other global positioning systems have revolutionized our ability to accurately determine the coordinates of any location on Earth at any given time. It is safe to say that there is hardly any global issue that has not involved the use of artificial Earth satellites (AES).
When spacecraft (SC) are on their way to the Moon and other planets, they are influenced by the gravitational force of the Sun. According to Kepler’s laws, they move along elliptical paths, similar to the paths of the planets. The Earth has an orbital velocity of approximately 30 km/s. If the sum of the spacecraft’s velocity (given at launch) and the Earth’s velocity is greater than this value, then the spacecraft will move in an orbit that lies outside the Earth’s orbit. If the sum is less than 30 km/s, then the spacecraft will be inside the Earth’s orbit. In the case of the spacecraft traveling to Mars (Figure 3.15) or another outer planet, it is most energy-efficient for the spacecraft to reach the orbit of the planet at its farthest point from the Sun, known as aphelion.
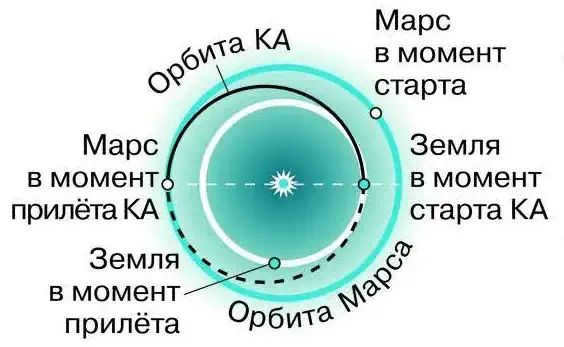
Additionally, it is essential to calculate the spacecraft’s launch time in order for the planet to reach the same point in its orbit. Put differently, the initial velocity and launch day of the KA must be selected in such a way that the KA and the planet, each moving in their respective orbits, converge at the rendezvous point simultaneously. In the case of the inner planet, the rendezvous with the KA should take place at the perihelion of its orbit (Fig. 3.16).
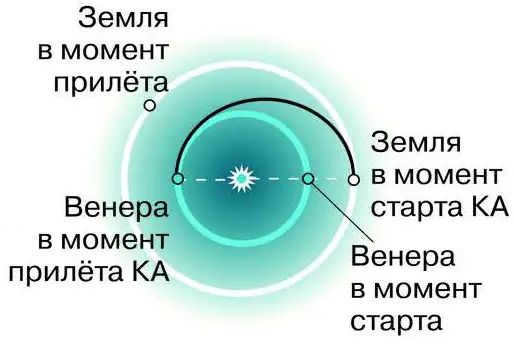
Semi-elliptical flight paths are referred to as such. These ellipses have major axes that pass through the Sun, which is one of the focal points, in accordance with Kepler’s first law.
The design and technology of contemporary spacecraft permits the execution of highly intricate maneuvers – such as entering the orbit of a planet’s satellite, landing on the planet’s surface, and traversing its terrain.
Queries
1. Why do the movements of the planets deviate from Kepler’s laws?
2. How was the position of Neptune determined?
3. Which planet has the greatest impact on the motion of other celestial bodies in the solar system and why?
4. Which celestial bodies in the Solar System experience the most significant perturbations and why?
5. What paths do spacecraft follow when traveling to the Moon and other planets?
6*. Can you explain the causes and periodicity of tides?
7*. If artificial satellites of the Earth and the Moon are equidistant from them, will they have the same revolution periods?
Exercise 12
1. Calculate the mass of Jupiter by using the orbital period of its satellite, which is 422,000 km away from Jupiter and takes 1.77 days to complete one orbit. To compare, refer to the data for the Earth-Moon system.
2. Determine the first space velocity for Mars and Jupiter, considering that the acceleration of gravity on Mars is 3.7 m/s2 and on Jupiter it is 25 m/s2.
3. Estimate the duration of KA’s flight to Mars, assuming it follows an elliptical path with a major semi-major axis of 1.25 astronomical units (a.e.).
Most likely, you have come across a gif or watched a video illustrating the movement of the solar system.
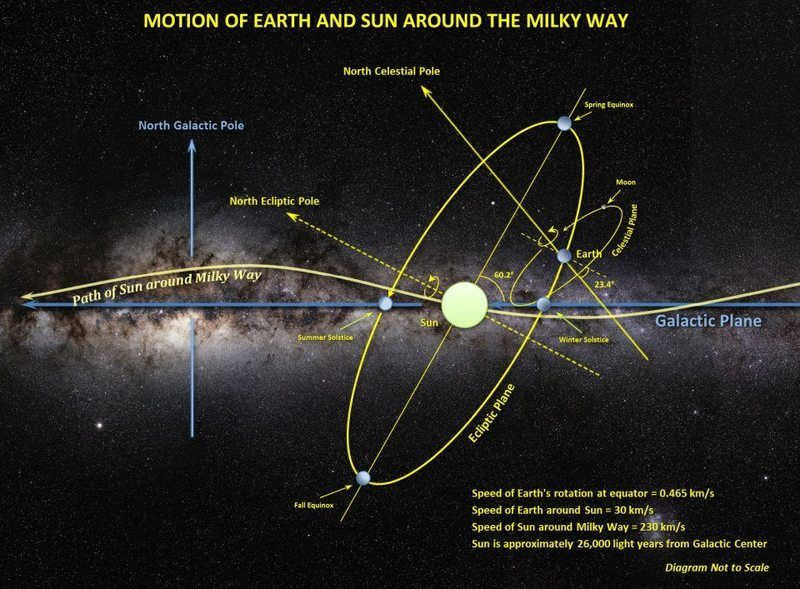
The video, which was released in 2012, quickly gained popularity and generated a lot of attention. I stumbled upon it shortly after its release, back when my knowledge of space was much more limited. What perplexed me the most was the perpendicular alignment of the planets’ orbital plane with the direction of their motion. It’s not that this is impossible, but rather that the solar system can move in any direction relative to the plane of the Milky Way. Now you might be wondering, why recall these long-forgotten stories? Well, the truth is that right now, if you so desire and the weather is clear, anyone can observe the actual angle between the ecliptic and the Milky Way’s plane in the night sky.
Verify scientists
Astronomy affirms that the inclination between the planes of the ecliptic and the Galaxy amounts to 63 degrees.
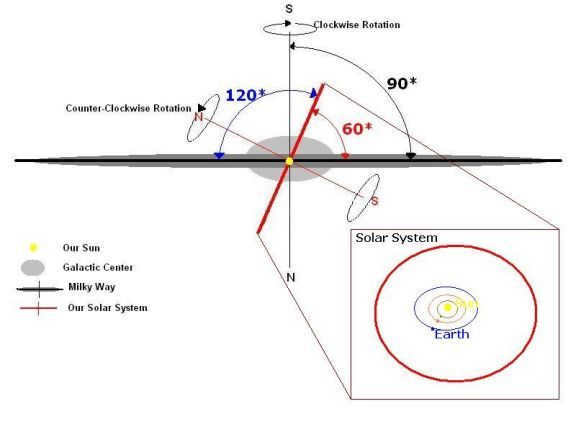
However, the image itself is uninteresting, and now that flat Earth supporters are engaging in pseudoscience, we need a straightforward and comprehensible illustration. Let’s consider how we can observe the planes of the Galaxy and the ecliptic in the sky, preferably without the need for telescopes and close to urban areas. The plane of the Galaxy is known as the Milky Way, but due to excessive light pollution, it has become challenging to see. Is there a line that approximates the plane of the Galaxy? Indeed, there is – it’s the constellation of the Swan. This constellation is visible even within cities and can be easily located by looking for the bright stars Deneb (alpha Swan), Vega (alpha Lyra), and Altair (alpha Eagle). The Swan’s “body” roughly aligns with the galactic plane.
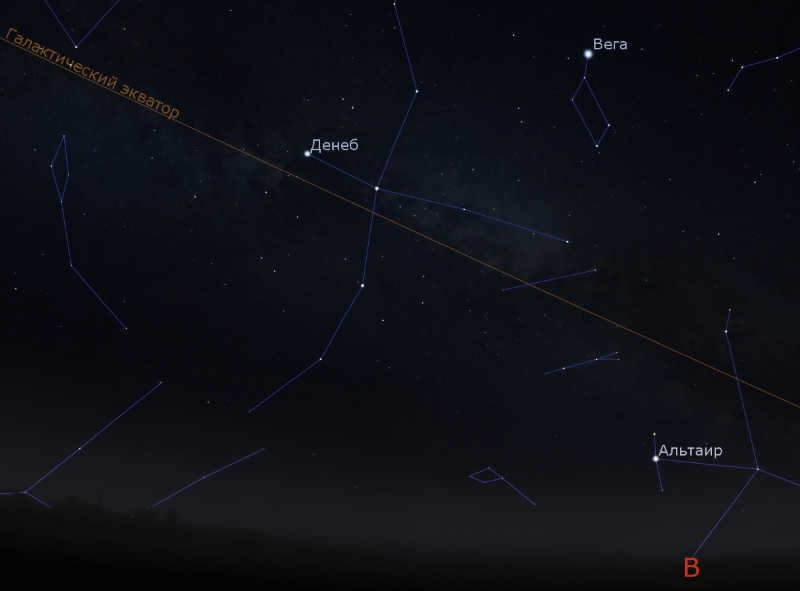
Alright, so we’ve got one aircraft. However, how can we establish a visual reference for the ecliptic? Let’s consider what the ecliptic is in general. By today’s precise definition, the ecliptic is the intersection of the celestial sphere with the orbital plane of the Earth-Moon barycenter (the center of mass). The Sun, on average, moves along the ecliptic. Unfortunately, we don’t have two suns to conveniently draw a line between, and the Swan constellation won’t be visible in sunlight. However, if we take into account that the planets of our solar system also move in a similar plane, it turns out that the parade of planets can give us a good indication of the plane of the ecliptic. And at this very moment, Mars, Jupiter, and Saturn are visible in the morning sky, perfectly aligning with the ecliptic.
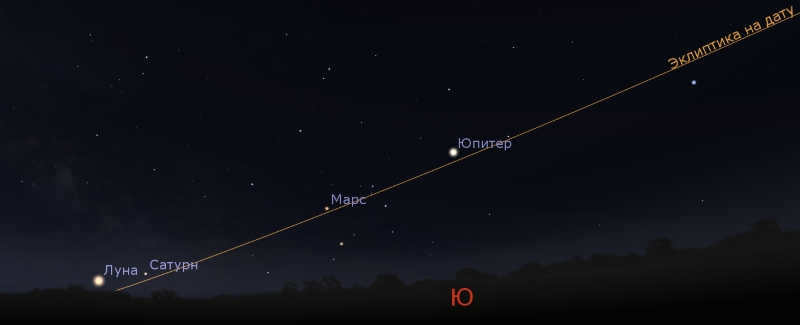
In the next few weeks, it will be possible to observe a striking image similar to this one, just before sunrise:
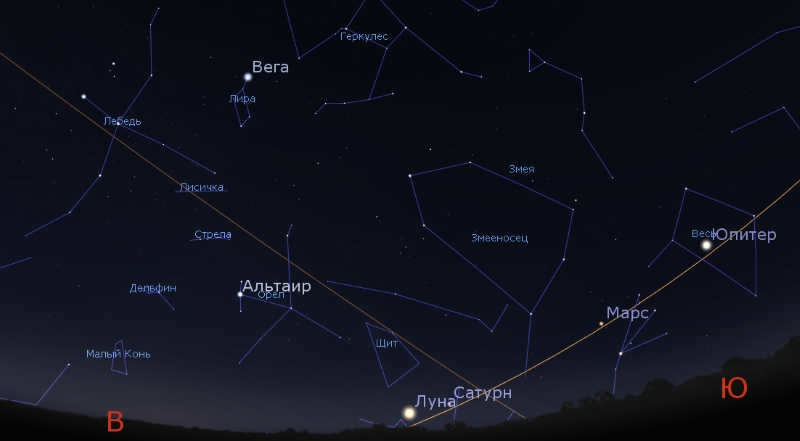
Surprisingly, it aligns impeccably with textbooks on astronomy.
Here’s a more accurate representation of the gif:
Credit: Rhys Taylor, an astronomer who runs the website rhysy.net
Unfortunately, it is impossible to verify this fact easily, as it was done two hundred and thirty-five years ago, relying on the findings of numerous astronomical observations and mathematical calculations.
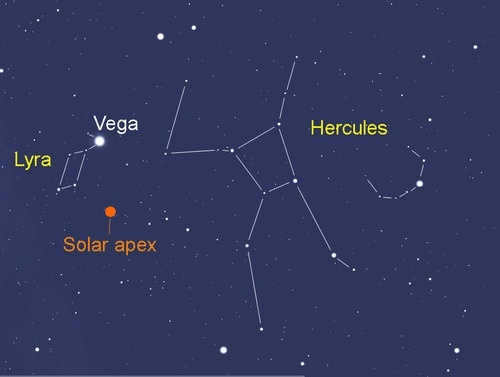
How can we determine the solar system’s current direction relative to neighboring stars? By observing the motion of stars across the celestial sphere over several decades, we can pinpoint the direction in which we are moving in relation to them. This specific point is referred to as the apex. Stars located near the apex, as well as those at the opposite point (known as the anti-apex), will exhibit minimal motion as they are either approaching or moving away from us. Conversely, stars that are further away from the apex and anti-apex will exhibit greater amounts of motion. To illustrate this, imagine driving down a road. The traffic lights at intersections ahead and behind you will not appear to move significantly sideways. However, the lampposts along the road will flicker outside the window, indicating their own substantial movement.
The animated image illustrates the trajectory of Barnard’s star, which exhibits the most significant proper motion. In the 18th century, astronomers possessed historical data documenting the positions of stars within a span of 40-50 years. This valuable information enabled them to ascertain the direction of motion for slower-moving stars. Subsequently, British astronomer William Herschel utilized star catalogs to conduct calculations without direct observation through a telescope. His initial computations based on the Mayer catalog revealed that stars do not exhibit random motion, and that their apex can indeed be determined.
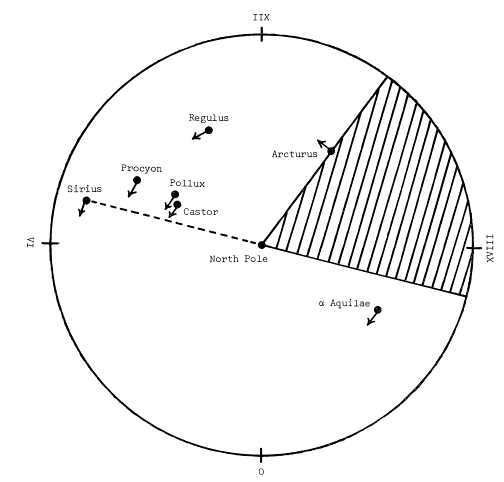
Original source: Hoskin, M. Herschel’s Calculation of the Solar Apex, Journal for the History of Astronomy, Vol. 11, P. 153, 1980
Furthermore, the inclusion of the Lalande catalog information significantly decreased the size of the area.
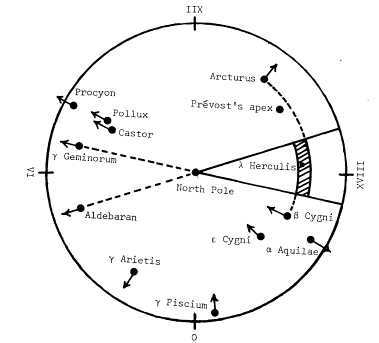
From that point onward.
Further on, regular scientific work was carried out – data clarification, calculations, debates. However, Herschel adhered to the correct principle and made an error of only ten degrees. Data is still being gathered, for instance, just thirty years ago, the velocity of movement was reduced from 20 to 13 km/s. It is important to note that this velocity should not be confused with the velocity of the solar system and other neighboring stars relative to the center of the Galaxy, which is approximately 220 km/s.
So, let’s talk about the speed of movement in relation to the center of the Galaxy. It’s important to note that, just like on Earth, the galactic north pole is chosen arbitrarily by convention. This point is located near the star Arcturus (alpha Volopas) and is roughly in the direction of the wing of the Swan constellation. When we look at a map of the Galaxy, we can see the constellations projected onto it, and it looks something like this:
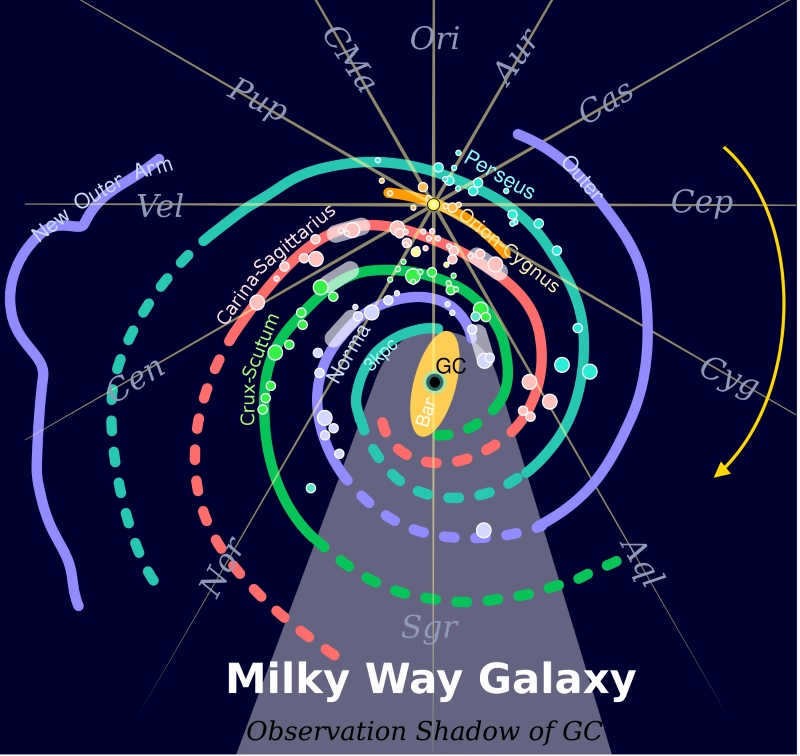
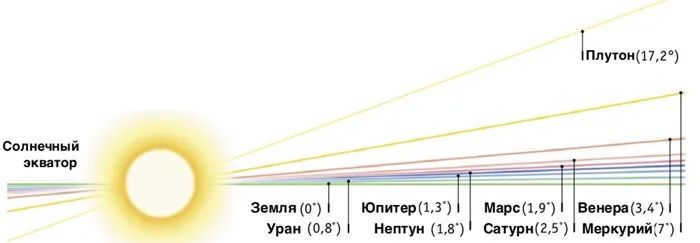
which is the average inclination of the planetary orbits to the ecliptic. This motion is caused by the gravitational pull of the other stars and objects in the galaxy, as well as the motion of the galaxy itself.
It is important to note that this motion is very slow, with the Solar System traveling at a speed of about 230 kilometers per second. Despite this slow speed, over the course of millions of years, it can have a significant effect on the relative positions of the planets and other objects in the Solar System.
This motion also affects the distribution of comets in the Solar System. As the Solar System moves through space, it passes through regions where comets are more abundant, leading to an increase in the number of comets that enter the inner regions of the Solar System and potentially pose a threat to Earth.
The video’s analogy of the solar system to a comet is completely accurate. NASA’s IBEX spacecraft was created with the specific purpose of studying the interaction between the Solar System’s boundary and interstellar space. And based on its data, it has confirmed the existence of a tail.
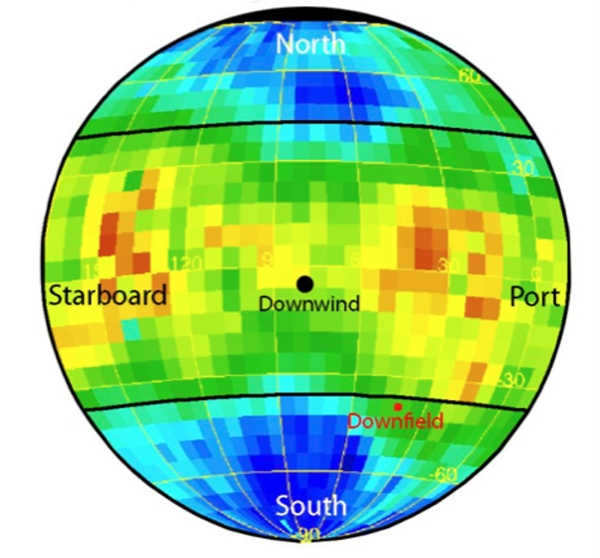
NASA artwork
When it comes to other stars, we have the opportunity to observe astrospheres (bubbles formed by stellar winds) directly.






