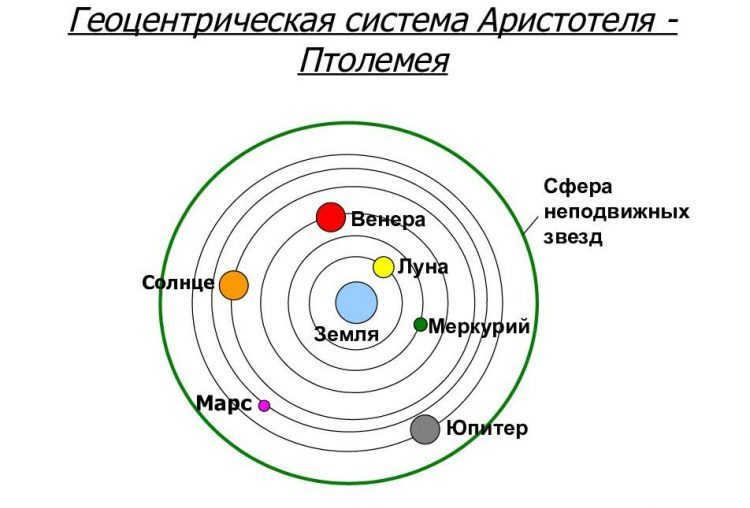
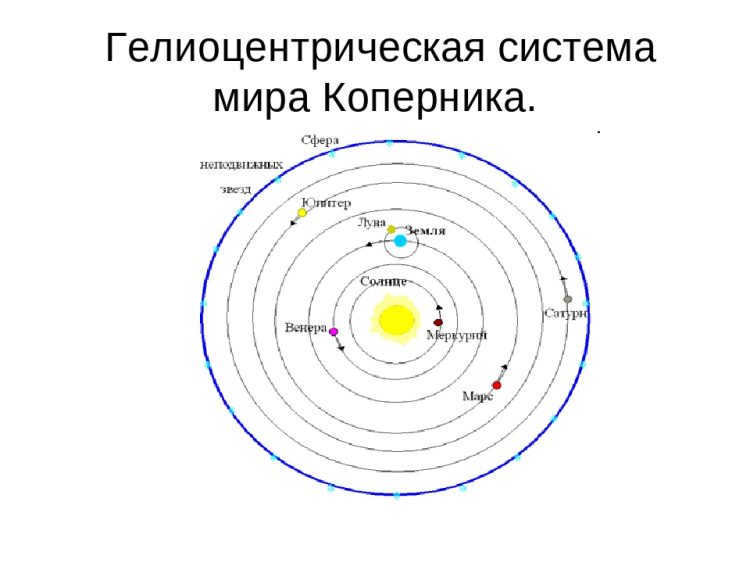
In the late 16th century, the field of astronomy witnessed a clash between two different models of our solar system: the geocentric model, attributed to Ptolemy, which suggests that the Earth is the focal point of all celestial objects’ movement, and the heliocentric model, proposed by Copernicus, which posits that the Sun is the central body.
Even though Copernicus had a better understanding of the solar system, his work still had some flaws. One of the main flaws was his belief that the planets orbit the Sun in perfectly circular paths. This assertion caused his model to be almost as inconsistent with observations as Ptolemy’s system. To address this issue, the Polish astronomer proposed an additional motion of the planets in circular orbits, with the center of these orbits already moving around the Sun – known as epicycles. However, this adjustment did not completely resolve the discrepancies in his model.
In the early 17th century, Johannes Kepler, a German astronomer, examined the system created by Nicolaus Copernicus and analyzed astronomical observations made by Tycho Brahe, a Danish astronomer. Through this research, Kepler formulated the fundamental laws governing planetary motion, which are now known as Kepler’s Three Laws.
Tycho Brahe, known for his meticulous observations of planets and hundreds of stars, compiled a comprehensive body of work over many years. The accuracy of his measurements surpassed that of all his predecessors.
Kepler’s initial principle concerning ellipses.
The celestial bodies within the solar system follow a path of elliptical trajectories, with one of the foci being occupied by the Sun.
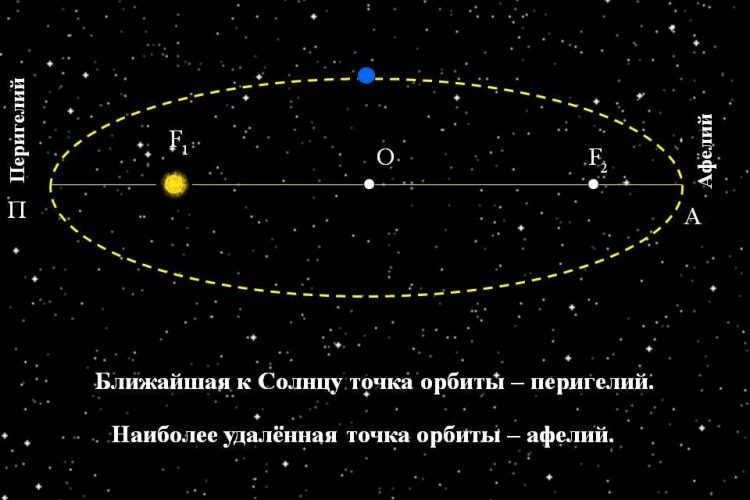
As per Kepler’s initial principle, all the planets within our system follow a closed curve known as an ellipse. Our star is situated at one of the focal points of the ellipse. These focal points are two points within the curve where the sum of the distances to any point on the ellipse remains constant.
After extensive observations, scientists have discovered that the orbits of all the planets in our system are nearly in the same plane. Some celestial bodies move along elliptical orbits that are close to being circular. Only Pluto and Mars have more elongated orbits. Therefore, Kepler’s first law is referred to as the law of ellipses.
The planet’s radius-vector traces out equal areas in equal time intervals.
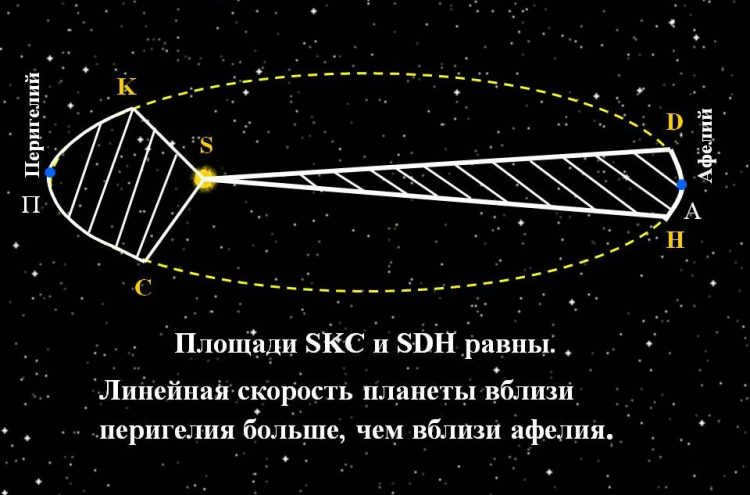
According to Kepler’s second law, each planet orbits in a plane that passes through the center of the Sun. Additionally, the radius-vector that connects the planet and the Sun sweeps out equal areas in equal time intervals. This indicates that the celestial bodies move around the Sun in an uneven manner, reaching maximum velocity at perihelion and minimum velocity at aphelion.
This phenomenon can be observed in the motion of Earth. Every year in early January, our planet speeds up as it approaches perihelion, causing the Sun to move faster along the ecliptic compared to other times of the year. On the other hand, in early July, Earth reaches aphelion and its speed decreases, resulting in a slower movement of the Sun along the ecliptic.
Kepler’s Third Law (harmonic law)
The relationship between the squares of the orbital periods of the planets and the cubes of the major semi-axes of their orbits is described by Kepler’s Third Law.
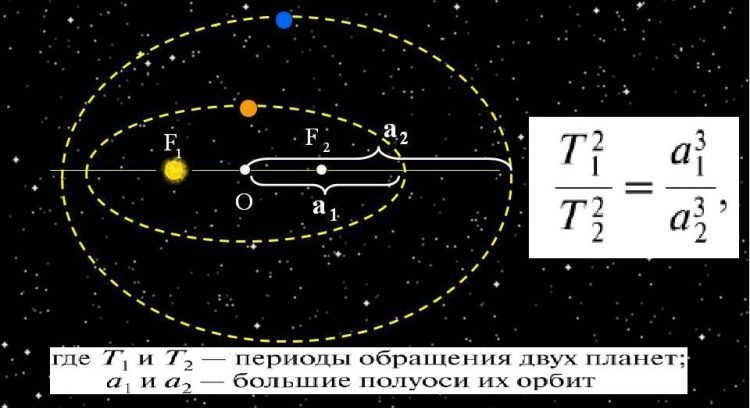
Kepler’s third law establishes a correlation between the orbital period and the average distance of a planet or satellite from its luminary. This law holds true with an accuracy of up to 1%.
By utilizing this law, it is possible to calculate the length of a planet’s year (the time it takes for a complete revolution around the Sun) if the distance from the Sun is known. Conversely, the same law can be used to determine the orbit by knowing the period of revolution.
Continued Progress
Despite having a relatively small margin of error, Kepler’s laws were derived through empirical means and lacked a theoretical basis. However, this predicament was ultimately resolved by the renowned physicist Isaac Newton, who, in 1682, unveiled his groundbreaking discovery known as the law of universal gravitation.
Without a doubt, Kepler’s laws represented a significant milestone in comprehending and delineating the intricate movements of celestial bodies.
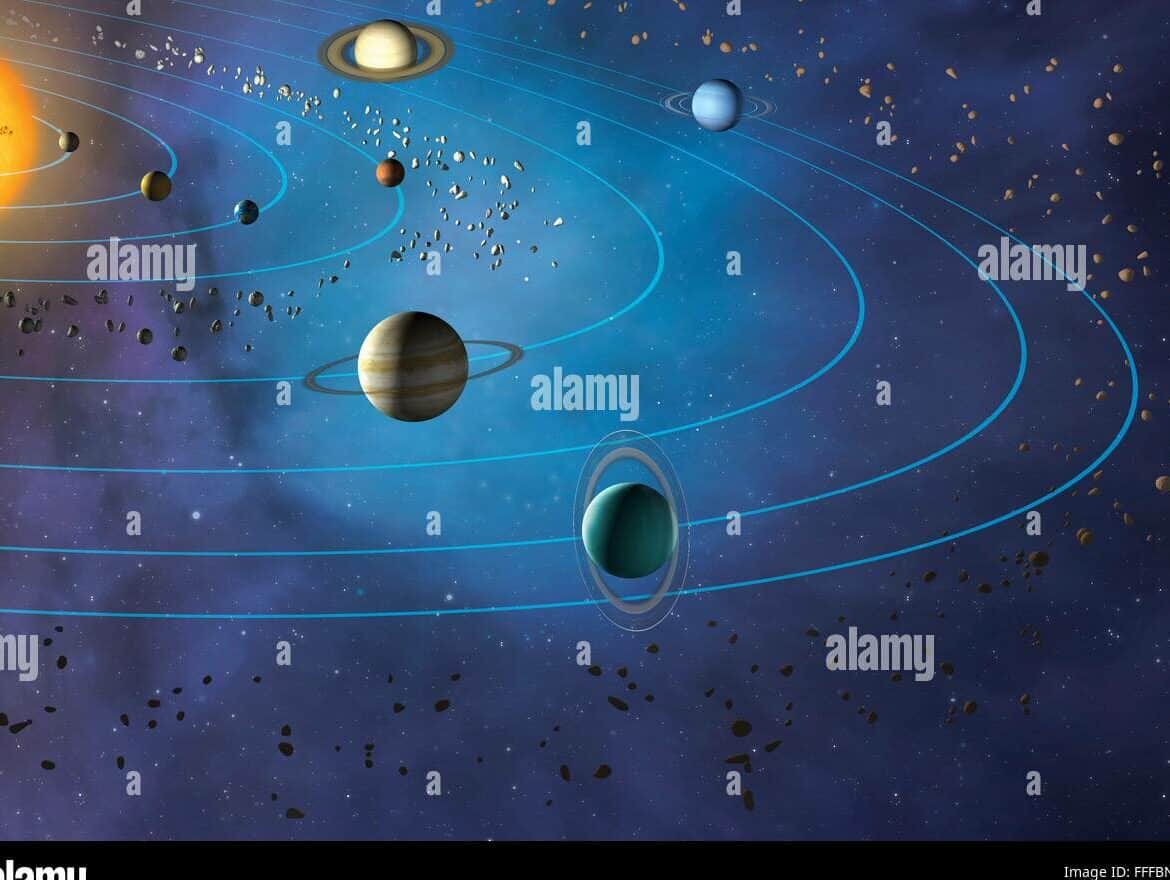
Solar System Orbits and Planetary Configuration
In order to understand the concept of orbits and their purpose, we must first establish a definition.
Orbits refer to the designated path or trajectory of motion that planets follow. These paths are determined within a specific coordinate system.
Within the solar system, all celestial bodies orbit around the Sun. This serves as the central point of reference for the coordinate system. Each celestial body, however, follows a unique orbit. It’s important to note that these orbits are not synchronized or identical. They vary in terms of length and scope, which ultimately impacts the climate and surface temperature of each celestial body.
Orbits of the solar system
Elements of a planetary orbit
Each planetary orbit has its own unique set of parameters. Furthermore, it is these parameters that define the shape, size, and location of the orbit in space.
In the field of astronomy, the Keplerian elements of the orbit are commonly used. These elements include:
- The major semi-axis, which is a geometric characteristic of objects. It is determined by the intersection of the plane and the surface of a circular cone.
- Eccentricity, a numerical parameter of the conic section that indicates its deviation from a perfect circle.
- Inclination, which is the angle between the plane and the orbit.
- The argument of pericenter is the angle between the directions from the center to the ascending node of the orbit. The pericenter is defined as the closest point of the orbit to the attracting center.
- The longitude of the ascending node is a mathematical description of the line of the orbital plane in relation to the reference plane.
- The mean anomaly is the result of the average motion of the body multiplied by the time interval from the pericenter. It has a constant angular velocity.
The paths followed by the planets within the solar system
Undoubtedly, the focal point of our system is the Sun. In reality, it holds the majority of the system’s overall mass. Utilizing its gravitational pull, it draws in celestial objects.

The Sun
It is important to mention that a considerable amount of celestial objects in the solar system orbit around a specific region. This region is known as the ecliptic. There are other objects that have a greater inclination angle with respect to it.
All the planets and many other entities rotate around the Sun in a counterclockwise direction. Interestingly, the central star itself is orbited by almost all the planets in the same direction. Only Venus and Uranus have a different trajectory.
As the distance from the Sun increases, the gap between the orbits of the objects also widens.

The planets Uranus and Venus can be classified as upper planets.
According to astronomers, celestial objects follow an elliptical path as they travel through space. This means that they move along a closed curve on a two-dimensional plane. The Sun is located at one focal point of the ellipse. The closer a celestial object is to the Sun, the faster it rotates around it. As a result, the period of rotation, or year, is shorter for these objects.
The celestial bodies of our solar system
Incidentally, our solar system is frequently categorized into two distinct regions: the inner zone and the outer zone.
The inner zone encompasses the asteroid belt as well as the planets of the terrestrial group, which consist of Mercury, Venus, Mars, and of course, Earth.
On the other hand, the outer zone extends beyond the first group and is comprised of four gas giants.
Moreover, all entities within the solar system can be classified into three different types:
The composition of the solar system has been officially ratified by the International Astronomical Union. In total, there are eight planets: Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, and Neptune.

Planets in the solar system
Arrangement of the planets
You may be wondering, what exactly is a planetary arrangement and why is it intriguing?
In the field of astronomy, the term “arrangement” refers to the relative positioning of the Sun, planets, and other celestial bodies. This concept is particularly relevant to the solar system.
There are two types of planetary arrangements: those of the lower planets and those of the upper planets, each with their own distinct pattern of motion.
When observed from Earth, the lower planets, particularly Mercury and Venus, exhibit a change in their phases as they move.
These planets move relatively close to the Sun, with their farthest distance from it being either to the east or west. Depending on the direction of their movement, we distinguish between eastern (evening) elongation and western (morning) elongation.
Elongation refers to the angular position between a planet and the Sun.
The motion of the lower planets is retrograde, meaning it goes from east to west.
When the planet lies between the Earth and the Sun, it is called the lower conjunction.
On the other hand, the movement can also be direct, or from west to east. When the Sun is positioned between the Earth and the planet, we observe the upper conjunction.
Arrangement of the celestial bodies above
The arrangement of the celestial bodies above is comparable to that of the celestial bodies below. Similar to the lower planets, there is both forward and backward motion. However, the upper planets move at a slower pace. Consequently, there comes a point when the Sun catches up with the planet, causing them to align. Furthermore, during this alignment, the Sun is positioned between the Earth and the planet.
During the backward motion, the planet reaches a point directly opposite to the Sun, which is known as opposition. This period occurs when the Earth is situated between the Sun and the planet.
The planet’s position at a 90° angle from the Sun in the eastern direction is referred to as the eastern quadrature. Similarly, a comparable position on the western side is called the western quadrature.
The upper planets display continuous motion without undergoing any changes in phases. They always present their illuminated side towards the Earth.
Moreover, the motion of the Moon aligns with the arrangement of the upper planets.
However, it is important to note that the movement of the upper planets cannot be observed from Earth.
Planetary Orbits: Different Periods
When it comes to planetary orbits, astronomers recognize two distinct types of orbital periods.
The first one is known as the sidereal period, which refers to the time it takes for a planet to complete one orbit around the Sun. In simpler terms, it’s the duration of a planet’s year as measured by Earth’s days or years.
The period of rotation of a planet at the same point from the observer’s position is called the Synodic period. This period is more accessible to astronomers and was calculated earlier than the sideric period. However, determining the synodic period can be challenging due to a few factors. Firstly, the Earth revolves around the Sun, causing the motion of the planets from the Earth to be inaccurate and uneven. Additionally, the backward motion of the planets should not be forgotten.
The orbits of the planets are one of the many fascinating aspects of the Universe. Studying and observing them is truly mesmerizing, and it is safe to assume that there are even more exciting discoveries to come.
The Sun is located at one of the two focal points of the elongated elliptical orbits that the planets follow as they move around it.
As the planets travel along their paths, the line segment connecting them to the Sun cuts off equal areas in equal periods of time.
The relationship between the squares of the planets’ revolution periods and the cubes of the major semi-axes of their orbits is a significant one.
Johannes Kepler possessed a profound appreciation for beauty. Throughout his entire life, he dedicated himself to demonstrating that the solar system is a remarkable masterpiece. Initially, he endeavored to establish a connection between its structure and the five regular polyhedra of classical ancient Greek geometry. (A regular polyhedron refers to a three-dimensional shape in which all of its faces are identical regular polygons.) During Kepler’s era, there were six recognized planets, which were thought to be positioned on rotating “crystal spheres.” Kepler contended that these spheres were arranged in such a manner that regular polyhedra seamlessly fit between adjacent spheres. Between the two outermost spheres – Saturn and Jupiter – he positioned a cube that was inscribed within the outer sphere, which, in turn, was inscribed within the inner sphere. Between the spheres of Jupiter and Mars, he placed a tetrahedron (a regular tetrahedron), and so forth.* With six spheres representing the planets and five regular polyhedra fitting between them, one would assume that perfection itself had been achieved?
Unfortunately, after comparing his model with the observed paths of the planets, Kepler was forced to acknowledge that the actual behavior of celestial bodies cannot be neatly contained within the framework he had outlined. As the modern British biologist J. Haldane (J. Haldane). B. S. Haldane) aptly remarked, “the notion of the universe as a perfectly geometric work of art has proven to be yet another elegant hypothesis shattered by unsightly facts.” The sole surviving outcome of Kepler’s youthful impulse was a handmade model of the solar system, which he gifted to his patron Duke Frederick von Wurtemburg. Within this exquisitely crafted metal artifact, each of the planets’ orbital spheres and the regular polyhedrons inscribed within them are hollow vessels that do not interconnect. These were intended to be filled with various beverages for the Duke’s guests to enjoy during festive occasions.
Kepler’s name was truly immortalized in the annals of science after he moved to Prague and became an assistant to the famous Danish astronomer Tycho Brahe (1546-1601). Tycho Brahe dedicated his life to collecting astronomical observations and amassed an immense amount of data on the movement of the planets. Upon Tycho Brahe’s passing, Kepler inherited these records, which held great commercial value at the time as they could be utilized to create precise astrological horoscopes (a section of early astronomy that scientists nowadays prefer not to discuss openly).
While analyzing the data from Tycho Brahe’s observations, Kepler encountered a challenge that would still be difficult to overcome even with the aid of modern computers. Kepler had no other option but to manually perform all the calculations. Naturally, like most astronomers of his era, Kepler was already acquainted with Copernicus’s heliocentric system (see The Copernican Principle) and understood that the Earth revolves around the Sun, as demonstrated by the aforementioned model of the solar system. However, the exact mechanisms of the Earth’s and other planets’ rotations remained unclear. Let’s imagine the problem in the following way: you are situated on a planet that, first and foremost, spins on its axis and secondly, orbits around the Sun in an unknown trajectory. When we gaze up into the sky, we observe other planets that also move in undisclosed orbits. Our objective is to deduce the geometry of these orbits and the velocities of the other planets based on observations made from our planet, which is rotating around the Sun. This is the feat that Kepler ultimately accomplished, and it was from these outcomes that he formulated his three laws!
Kepler’s First Law** explains the shape of the paths that planets take around the Sun. In basic geometry, you may have learned that an ellipse is a collection of points in a plane where the sum of the distances to two fixed points – known as the foci – is always the same. If that’s too complicated, here’s another way to think about it: imagine taking a slice out of the side of a cone with a plane that is tilted relative to the base but doesn’t pass through it – that’s also an ellipse. According to Kepler’s First Law, the planets’ orbits are elliptical and the Sun is located at one of the foci. The eccentricities (or how elongated) of the orbits and their distances from the Sun at perihelion (the closest point) and apogee (the farthest point) vary for each planet, but all elliptical orbits share the common feature of having the Sun at one of the two foci. By analyzing the observational data collected by Tycho Brahe, Kepler discovered that the planetary orbits are like a set of nested ellipses, a concept that no other astronomer had considered before him.
The first two laws concern the specific orbital paths of individual planets. Kepler’s Third Law enables the comparison of planetary orbits. It states that the further a planet is from the Sun, the longer it takes for the planet to complete a full revolution and the longer the duration of a “year” on that planet. We now understand that this is a result of two factors. Firstly, the distance between the planet and the Sun determines the length of the planet’s orbit. Secondly, as the planet moves further away from the Sun, its linear velocity decreases.
Kepler’s laws were formulated based on his careful study and summary of observations. When it came to explaining the causes of elliptical orbits or the equality of areas of sectors, Kepler did not provide direct answers. Instead, these phenomena were deduced from his analysis. Similarly, if you were to inquire about the orbital motion of planets in other star systems, Kepler would not have been able to offer any insights. He would have needed to gather observational data, analyze it, and search for patterns all over again. In other words, there would be no basis for him to assume that another planetary system follows the same laws as our Solar System.
One of the greatest accomplishments of Newton’s classical mechanics is its ability to provide a fundamental validation of Kepler’s laws and assert their universality. It has been proven that Kepler’s laws can be derived from Newton’s laws of mechanics, Newton’s law of universal gravitation, and the law of conservation of momentum through rigorous mathematical calculations. As a result, we can confidently state that Kepler’s laws are applicable to any planetary system in the universe. When astronomers search for new planetary systems in outer space (and they have already discovered quite a few), they routinely utilize the Kepler equations to calculate the orbital parameters of distant planets, even when direct observation is not possible.
Kepler’s Third Law has played, and continues to play, a crucial role in contemporary cosmology. When observing distant galaxies, astrophysicists detect faint signals emitted by hydrogen atoms that orbit much further away from the galactic center than stars typically do. By analyzing the Doppler effect in the spectrum of this radiation, scientists are able to determine the rotational velocities of the hydrogen periphery of the galactic disk, and from there, deduce the angular velocities of galaxies as a whole (also known as Dark Matter). It is gratifying to see that the work of the scientist who set us on the right path towards understanding the structure of our solar system, still holds such significance in the study of the vast Universe even centuries after his passing.
* In between the orbits of Mars and Earth, there is a dodecahedron with twelve sides. Between the orbits of Earth and Venus, there is an icosahedron with twenty sides. And between the orbits of Venus and Mercury, there is an octahedron. Johannes Kepler presented this unique structure in a detailed volumetric drawing in his first monograph, The Cosmographic Mystery (Mysteria Cosmographica, 1596). – Translator’s note.
** It is worth noting that Kepler’s laws, similar to the beginnings of thermodynamics, are not numbered according to the chronological order of their discovery, but rather based on their understanding in scientific circles. The first law was actually discovered in 1605 and published in 1609, the second law was discovered in 1602 and published in 1609, and the third law was discovered in 1618 and published in 1619. – Translator’s note.

According to the definition, a planet is a celestial body that orbits a star. The orbit represents the path that the planet follows within the gravitational field of another body, usually a star. The Sun serves as the primary body for the Earth, for example.
All the planets in the Solar System move in the direction of the Sun’s rotation along their respective orbits. Currently, scientists are aware of only one planet that moves in the opposite direction – an exoplanet known as WASP-17b, located in the Scorpius constellation.
The sideric rotation period (planetary year) refers to the time it takes for a planet to complete one orbit around its star. The velocity of the planet varies based on its distance from the star – the closer it is, the faster it moves, while the farther it is, the slower its movement. As a result, the length of the planetary year is directly linked to the planet’s distance from its “Sun”. When the distance is small, the planetary year is relatively short. This is because the gravitational pull on the planet decreases as it moves farther away from the star, causing its movement to slow down and consequently leading to a longer year.
The positions of the Earth in its orbit: perihelion, aphelion, and eccentricity
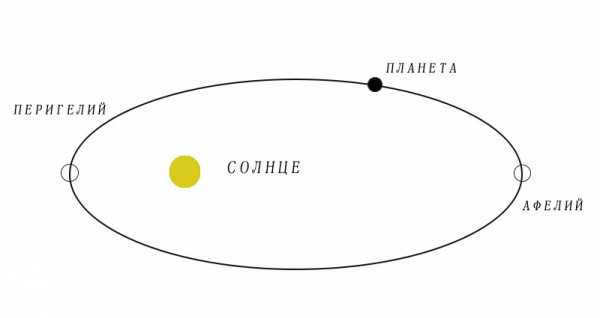
All planets move along orbits that have the form of an elongated circle, and the extent of elongation is determined by the eccentricity. When the eccentricity is very small (close to zero), the shape is most similar to a circle. Trajectories with an eccentricity close to one take the form of an ellipse. For instance, the orbits of many satellites and exoplanets in the Kuiper belt are elliptical, whereas the orbits of all planets in the solar system are nearly perfectly circular.
Due to the fact that none of the known cosmic orbits is a perfect circle, the distance between a planet and its neighboring luminary varies as the planet travels along its orbit. The point at which the planet is closest to the star is referred to as the periastre. In the solar system, this point is known as perihelion. On the other hand, the point farthest from the star on the planet’s trajectory is called apoastrom, and in the solar system, it is referred to as aphelion.

Earth viewed from the Electro-L satellite
The inclination of the orbital plane in relation to the reference plane is known as the orbital inclination. In the Solar System, the reference plane is the plane of Earth’s orbit, also known as the ecliptic. The orbits of the eight planets in the solar system are very close to the ecliptic plane.
All planets in the solar system are tilted at an angle relative to the equatorial plane with respect to the star. For instance, the Earth’s axis is tilted at an approximate angle of 23 degrees. This inclination affects the amount of sunlight received by the Northern or Southern hemisphere of the planet and is also responsible for the change in seasons.
The Electro-L satellite captures the transition from day to night.

The planets in our solar system all have their own unique paths as they revolve around the central star, known as the Sun. These paths, called orbits, come in various sizes and shapes, which play a significant role in determining the climate and surface temperature of each planet. Each orbit follows specific laws and possesses distinct parameters that dictate its individual characteristics, such as its shape, size, and position within the vastness of space.
The idea of an orbit
An orbit is the path followed by a celestial body (such as a planet) under the influence of the gravitational pull of a larger body (like the Sun). In our solar system, all the planets orbit around the Sun in circular paths, forming a coordinate system. The shapes and sizes of these planetary orbits vary, leading to diverse climates on each planet.
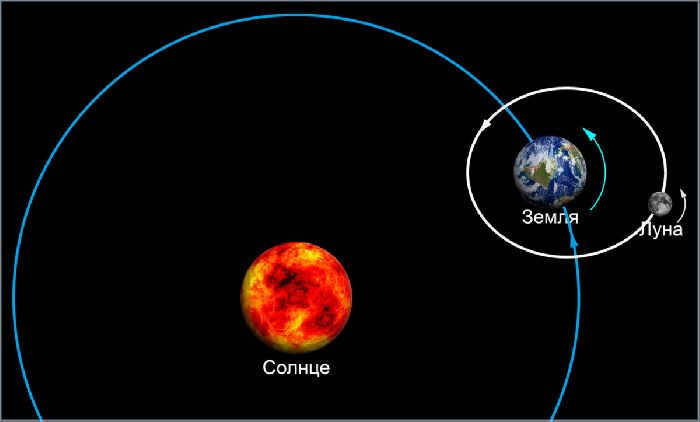
Figure 1. Sideric period.
The planets in our solar system, along with many other celestial bodies, orbit the Sun in a counterclockwise direction. This is true for the star itself as well. Additionally, most planets also rotate on their axes in the same counterclockwise direction. However, there are two exceptions to this: Venus and Uranus, which have the opposite direction of rotation.
Form and dimensions of orbits
All the orbits of the planets in the solar system are uniformly elliptical, resembling elongated circles. The extent of this elongation is known as eccentricity. When the eccentricity is small, the orbit closely resembles a circle, but as the value approaches 1, the orbit takes on the shape of a traditional ellipse.
The planets in the Solar System, as well as the asteroid belt, follow elliptical orbits that are nearly circular and lie in the same plane. On the other hand, objects from the Kuiper belt, situated beyond Neptune’s orbit, exhibit a more pronounced elliptical shape in their trajectories.

Due to the absence of a perfectly circular rotation around the Sun, the distance between each planet and the star is in constant flux throughout their entire path of motion. This gives rise to two distinct points of reference:
- Perihelion – the point at which a planet is closest to the Sun;
- Aphelion – the point at which a planet is farthest from the Sun.
One can find a summary of the characteristics of each planet’s orbit in the table below.
What is responsible for the variation of seasons
The inclination of the orbit, which refers to the angle between the orbital plane and the reference plane, is the primary factor causing the change of seasons. In the Solar System, the reference plane is defined as the ecliptic plane, which corresponds to the Earth’s orbit. The majority of the planets in our solar system have orbits that closely align with the ecliptic plane.
The planets in the solar system all have different angles in relation to the star’s equator. For instance, the Earth’s axis is tilted at an angle of 23.45 degrees. This angle determines how much sunlight the Northern and Southern hemispheres receive and is also responsible for the changing seasons.
Other relevant information:
The arrangement of celestial bodies determines the placement of the planets in relation to the Earth and the Sun, influencing their visibility in the sky. All planets emit a glow from the sunlight they reflect, making the planet closest to Earth the most easily observable, especially when its sunlit side is facing us during the day.
Figure 4.1 showcases the opposition (OA) of Mars (M1), a configuration where Mars and the Sun are directly aligned with the Earth in between. During the opposition, the planet’s brightness is at its peak as its entire illuminated hemisphere is directed towards the Earth.
The paths of two planets, namely Mercury and Venus, are situated nearer to the Sun in comparison to the Earth. As a result, they do not align in opposition. When Venus or Mercury are at their closest point to Earth, they become invisible due to the fact that the side of the planet which is facing away from the Sun is turned towards us (see Figure 4.1). This particular arrangement is known as a lower conjunction with the Sun. Similarly, during an upper conjunction, the planet is also not observable as there is a bright Sun positioned between it and the Earth.
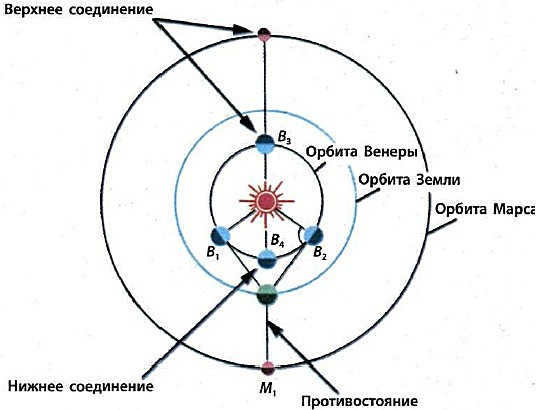
Figure 4.1. Arrangements of Venus and Mars. Mars opposition – the planet is closest to the Earth, it can be seen all night in the opposite direction from the Sun. Venus is most easily observed in the evening during the eastern elongation, located to the left of the Sun B1, and in the morning during the western elongation, located to the right of the Sun B2
The optimal conditions for observing Venus and Mercury occur in arrangements known as elongations. The eastern elongation (EE) refers to the position when the planet is visible in the evening, to the left of the Sun B1. The western elongation (WE) of Venus is observed in the morning, when the planet is visible to the right of the Sun in the eastern part of the sky B2.
Arrangements of prominent planets
The symbols used to represent the movements of planets are as follows: PS indicates opposition, indicating that the planet is visible all night; SP indicates conjunction with the Sun, indicating that the planet is not visible; (EE) represents eastern elongation, signifying that the planet is visible in the evening in the western part of the horizon; WE represents western elongation, indicating that the planet is visible in the morning in the eastern part of the sky.
Sideric and synodic periods of planetary orbits
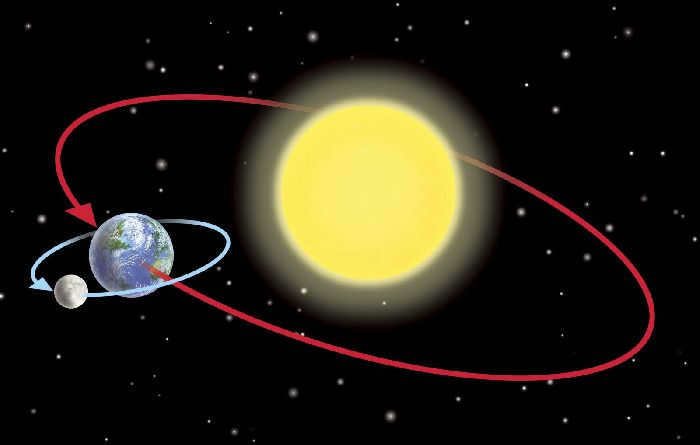
Sidereal orbital period refers to the duration of time it takes for a planet to complete one full revolution around the Sun, as observed relative to the stars (Fig. 4.2).
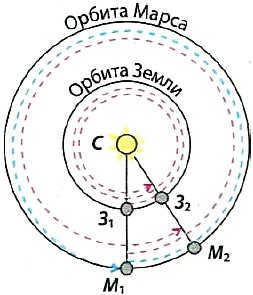
Fig. 4.2. The blue dotted line depicts the path of Mars’ orbit around the Sun corresponding to its sideric period, while the red dotted line represents its synodic period
The synodic period of revolution determines the movement of celestial bodies in relation to both the Earth and the Sun. It refers to the time interval in which we observe the same successive configurations of the planets, such as opposition, conjunction, and elongation. In Fig. 4.2, we can see the positions of S-Z1-М1 and C-32-М2, which are two consecutive oppositions of Mars. The synodic period S and the sideric period T of the planet’s revolution are related as follows:
Kepler’s Laws
Johannes Kepler (Fig. 4.3) established that the path of Mars revolves around the Sun in the shape of an ellipse. Subsequently, it was demonstrated that the orbits of other planets also follow an elliptical trajectory.

Figure 4.3. I. Kepler (1571-1630)
Kepler’s initial principle. The Sun is positioned at one of the foci of the ellipses that all planets travel along as they orbit the Sun (Fig. 4.4, 4.5).
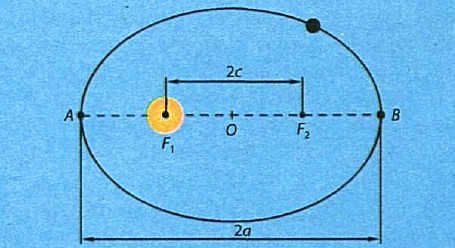
Fig. 4.4. Planets move along ellipses while orbiting the Sun. AF1=Fmin – when the planet is at its closest point to the Sun (perihelion); BF1=Fmax – when the planet is at its farthest point from the Sun (aphelion)
The primary implication of Kepler’s first law is that the distance between the planet and the Sun is not constant and varies within the range: rmax ≤ r ≥ rmin
The point at which the planet comes closest to the Sun in its orbit is known as perihelion (from the Greek words peri – near and helios – Sun), while the furthest point from the Sun’s center is called aphelion (from the Greek word aro – far away). The sum of the distances at perihelion and aphelion is equal to the major axis AB of the ellipse: rmax + rmin = 2a. The major semi-axis of the Earth’s orbit (OA or OB) is referred to as the astronomical unit. 1 a. u. = 149.6×10 6 km.
Figure 4.5. The Correct Way to Illustrate an Ellipse
The extent of elongation of an ellipse can be measured by its eccentricity e, which is the ratio of the distance between the foci 2c to the length of the major axis 2a, that is, e=c/a, 0
The orbit of the Earth has a slight eccentricity of e=0.017 and is almost indistinguishable from a circle, resulting in the distance between the Earth and the Sun varying from rmin=0.983 a. e. at perihelion to rmax=1.017 a. e. at aphelion.
The planets’ satellites also follow elliptical paths, with each orbit having the center of its corresponding planet as the focal point.
Kepler’s second law. The radius-vector of a planet covers equal areas in equal time intervals.
The key implication of Kepler’s second law is that as a planet orbits, not only does its distance from the Sun change over time, but also its linear and angular velocity.
The planet reaches its highest speed at perihelion, when it is closest to the Sun, and its lowest speed at aphelion, when it is farthest away.
Kepler’s second law, which is also known as the law of conservation of energy, states that the total energy in a closed system remains constant. This law can be explained by considering the kinetic and potential energy of a planet. The kinetic energy of a planet is influenced by its velocity, while the potential energy is determined by the distance between the planet and the Sun. As a planet gets closer to the Sun, its velocity increases (Fig. 4.6).
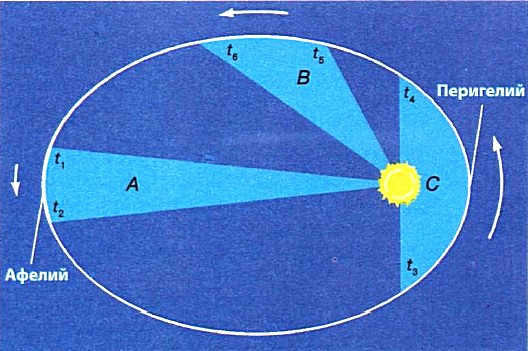
Figure 4.6 illustrates the change in the speed of planets as they approach or move away from the Sun.
While it may be challenging to verify the first law of Kepler in a school setting, as it requires measuring the distance from Earth to the Sun during both winter and summer, the second law of Kepler can be easily tested by any student. To do so, one must observe the changing speed of the Earth throughout the year. This can be accomplished using a regular calendar and calculating the duration of the half-year from the vernal equinox to the autumnal equinox (March 21st to September 23rd) and vice versa, from September 23rd to March 21st. If the Earth orbited the Sun at a constant speed, the number of days in these half-years would be equal. However, according to Kepler’s second law, the Earth’s speed is greater in winter and slower in summer. As a result, summer in the Northern Hemisphere is slightly longer than winter, while in the Southern Hemisphere, winter is slightly longer than summer.
Kepler’s Third Law. The relationship between the squares of the sideric periods of the orbits of the planets around the Sun and the cubes of the major semi-axes of their orbits is expressed by the equation:
T12 / T22 = a13 / a23
where T1 and T2 are the sideric orbital periods of any planets, and a1 and a2 are the major semi-axes of the orbits of these planets.
If you know the major semi-axis of the orbit of any planet or asteroid, you can use Kepler’s third law to calculate the orbital period of the body without having to wait for it to complete a full revolution around the Sun. For instance, in 1930, a new planet called Pluto was discovered in our solar system. It has a large semi-major axis of 40 a.e., and the orbital period around the Sun was immediately determined to be 248 years. However, in 2006, the International Astronomical Union reclassified Pluto as a dwarf planet because its orbit intersects with Neptune’s orbit.
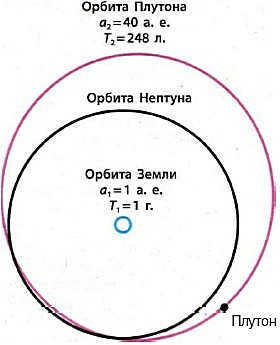
Figure 4.7. The determination of Pluto’s orbit major semi-major axis was based on observations. By considering the parameters of Earth’s orbit as stated in 4.2, we can calculate T2 = 248 л.
Kepler’s Third Law also finds application in astronautics when there is a need to calculate the orbital period of satellites or spacecraft revolving around the Earth.
Law of Universal Gravitation
The fundamental law of universal gravitation, discovered by the renowned English physicist and mathematician Isaac Newton, serves as the physical foundation for Kepler’s laws. This law not only governs the movement of planets within the solar system, but also determines the interactions between stars within the Galaxy. Newton formulated this law in 1687, stating that any two bodies with masses Mum are attracted to each other with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them (Fig. 4.8):
where G represents the gravitational constant, and R represents the distance between the two bodies.
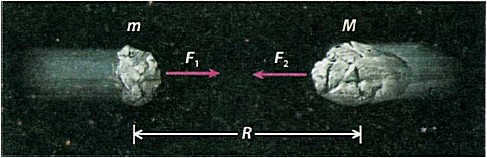
Figure 4.8. Law of universal gravitation
It is important to note that equation (4.3) is only applicable to two individual objects. If an object has a spherical shape and its internal density is symmetrically distributed around the center, the mass of the object can be treated as a single point located at the center of the sphere. For instance, when a spaceship orbits the Earth, the distance from the center of the Earth is used to calculate the gravitational force that attracts the spaceship towards the Earth (Fig. 4.9).
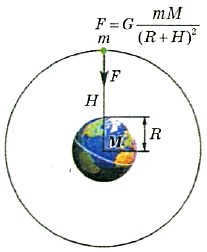
Figure 4.9. The gravitational force acting on a spacecraft depends on the distance R+H between the spacecraft and the center of the Earth
By utilizing equation (4.3), it is possible to ascertain the weight of astronauts on any celestial body given the known values of its radius R and mass M (Fig. 4.10). The law of universal gravitation posits that not only does the planet experience attraction towards the Sun, but the Sun also experiences an equal force of attraction towards the planet. Consequently, the movement of both entities within the gravitational field occurs in orbit around the shared center of mass. In other words, the planet does not fall into the Sun due to its orbiting at a specific velocity, and the Sun does not fall onto the planet due to the same gravitational force, as it too orbits around the common center of mass.

Figure 4.10: The weight of astronauts is determined by the planet’s mass and radius. When on asteroids, astronauts must secure themselves to prevent drifting off into space
In actuality, planets do not move in elliptical orbits because Kepler’s laws only apply to two bodies orbiting a common center of mass. In the solar system, there are large planets and numerous small bodies orbiting around the Sun. Therefore, each planet is not only influenced by the Sun, but also by the gravitational pull of all these other bodies. This interaction results in various forces of different magnitudes and directions, making the motion of each planet quite complex. This type of motion is known as perturbation. The orbit that a planet follows during perturbed motion is not an ellipse.
Due to investigations into the perturbation of Uranus’s orbit, scientists were able to make a theoretical prediction about the presence of an undiscovered planet. In 1846, I. Galle confirmed this prediction by locating and discovering the planet in its calculated position. The newly found planet was given the name Neptune.
For those who are interested
The uniqueness of the universal law of gravitation lies in our lack of understanding of how the attraction between objects is transmitted across vast distances. Despite numerous hypotheses put forth by scientists since the law’s discovery, our current knowledge is not significantly greater than that of Newton’s time. However, physicists have since uncovered three remarkable interactions between material bodies that also occur at a distance: electromagnetic interaction, strong interaction, and weak interaction within atomic nuclei. Among these, gravitational forces are the weakest. For instance, compared to electromagnetic forces, gravitational attraction is 10^39 times weaker. Nevertheless, gravity alone governs the motion of planets and influences the evolution of the Universe. This can be attributed to the fact that electric charges possess different signs (+ and -), resulting in mostly neutral bodies of great mass and hence a relatively weak electromagnetic interaction between them at large distances.
Determining the Distances to Planets
In order to determine the distances to planets, we can utilize Kepler’s third law. However, to accomplish this, we must first establish the distance from Earth to each individual planet. Let’s consider the scenario where we need to calculate the distance, denoted as L, from the center of the Earth (O) to the luminary (S). Using the radius of the Earth (R) as our reference point, we can measure the angle ∠ASO, which is commonly referred to as the horizontal parallax of the luminary. This measurement is crucial as it helps us form a right triangle, with cathetus AS representing the horizon for point A (see Figure 4.11).
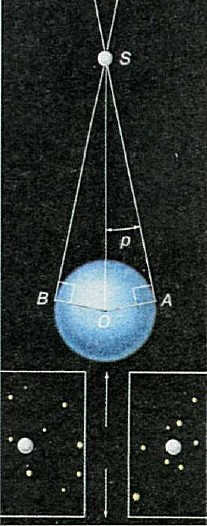
Fig. 4.11. The horizontal parallax p of a celestial object determines the angle at which the radius of the Earth perpendicular to the line of sight would be observed from that celestial object
The horizontal parallax (derived from the Greek word for displacement) of a celestial object is the angle at which the radius of the Earth perpendicular to the line of sight would be observed if the observer were on that celestial object. By using the right-angled triangle OAS, we can determine the hypotenuse OS:
The parallax value decreases as the luminary is observed from a greater distance away from the Earth. For instance, when the Moon is closest to the Earth, it has the largest horizontal parallax, measuring at p = 1°01′. On the other hand, the planets have much smaller horizontal parallax values, which also change as the distances between the Earth and the planets vary. Venus holds the title for the largest parallax among the planets, measuring at 31″, while Neptune has the smallest parallax at 0.21″. To put things into perspective, the letter “O” in this book can be seen at an angle of 1″ from a distance of 100 meters – astronomers have to measure such minuscule angles in order to determine the horizontal parallaxes of celestial bodies in the solar system. For information on how to measure the distance to stars, refer to § 13.
Summary
The law of universal gravitation, discovered by Newton, governs the movement of all cosmic bodies, including planets and galaxies. Kepler’s laws determine the shape of their orbits, the speed of the planets in the solar system, and their periods of orbit around the Sun.
Quizzes
What is the term used to describe the arrangement of planets in outer space in relation to the Earth and the Sun?
A. Configuration.
B. Confrontation. C. Cosmogony.A. Saturn.
B. Venus.
C. Mercury.
D. Jupiter.
A. Saturn.
B. Venus.
C. Mercury.
D. Jupiter.
A. Leo.
B. Capricorn.
C. Orion.
D. Pisces.
E. Aquarius.
A. Perihelion.
B. Perigee.
C. Apogee.
D. Aphelion.
E. Apex.