The planets’ linear and angular velocities around the Sun increase as they get closer to it. The sidereal period refers to the time it takes for the planets to complete one revolution around the Sun relative to the stars.
The Earth’s sidereal year is the time it takes for the Earth to complete one orbit around the stars. Mercury has the shortest sidereal period, while Mars takes about 2 years, Jupiter takes 12 years, and Pluto takes 250 years as its distance from the Sun increases.
The credit for discovering the laws of motion of the planets goes to the remarkable Austrian scientist Kepler. In the early 17th century, Kepler established three laws of planetary motion, known as Kepler’s laws.
Kepler’s first law states that each planet orbits the Sun in an ellipse with the Sun at one of its foci.
The elliptical shape of an ellipse can be described by its eccentricity, which is determined by the ratio of the distance between the focus and the center to the length of the major semi-axis. When the focus and the center coincide, the eccentricity is zero and the ellipse becomes a circle.
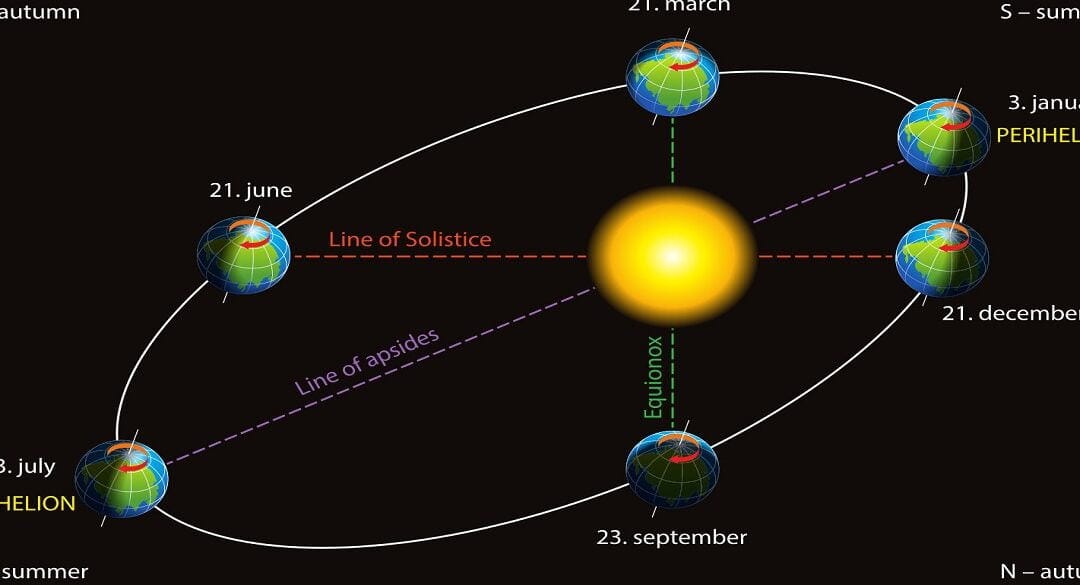
In terms of orbital dynamics, the point on an orbit that is closest to the Sun is known as the perihelion, while the point farthest from it is called the aphelion. Planetary orbits are generally elliptical, although they closely resemble circles with small eccentricities. For example, the Earth’s orbit has an eccentricity value of e = 0.017.
The peculiarities of the paths of comets reach a state of unity. At е=1, the second focal point of the oval shape is eliminated (as it approaches infinity), transforming the oval into an unbounded curve known as a parabola. The two branches of the parabola become increasingly parallel as they extend towards infinity. When е>1, the path becomes a hyperbola. By traversing a parabola or hyperbola, an object orbits the Sun once and then moves away from it indefinitely.
Kepler’s laws were derived from his study of the planets’ periodic revolutions around the Sun. Building upon Kepler’s work, Newton formulated the law of universal gravitation, which revealed that bodies can move in relation to each other along various paths, including ellipses, circles, parabolas, and hyperbolas, under the influence of mutual gravitational forces. Interestingly, certain comets have been observed to orbit the Sun along parabolic or hyperbolic trajectories, eventually leaving the solar system and ceasing to be part of it.
Kepler’s Third Law states that the squares of the periods of the stellar orbits of the planets are proportional to the cubes of the major semi-axes of their orbits.
What is the reason for the elliptical shape of orbits instead of being circular?
What is the explanation for the planets revolving around a star in an elliptical orbit with the star located at one of its foci? Why is the orbit not perfectly circular?
Let’s consider a scenario where the star is significantly more massive than the planet, and both objects are perfectly spherical in shape. Under these assumptions, Newton’s law of gravitation holds true, although this is typically a very accurate approximation. Additionally, we will assume that there are no other forces acting between the star and the planet apart from gravity. If the first condition is not met, then the acceleration of each object will be directed towards the system’s barycenter. In this case, it can be mathematically represented as if the barycenter were exerting a gravitational force on the objects, considering a certain reduced mass. Therefore, the problem can be considered equivalent from a mathematical standpoint.
Imagine a star placed at the origin of a coordinate system. According to Newton’s law of gravitation, the force on a planet can be calculated using the equation F = -mμr^3/r’, where F is the force vector, m is the mass of the planet, μ is the standard gravitational parameter of the star, r is the distance vector, and r’ is the magnitude of the distance vector. Another way to represent the equation is F = -mμr^3/rr’, where r’ is the magnitude of the distance vector. In both equations, μ is equal to GM, where G is the gravitational constant and M is the mass of the star.
Conservation laws
Conservation of momentum is observed in this system because the force acting on the star is purely radial. If the star is at the origin and has a non-zero initial velocity, the orbit must be bounded by the plane defined by all points with vectors from the origin satisfying L ⋅ x = 0. Here, L = r × p ˙ (where r is the position vector and p ˙ is the velocity vector).
The total orbital energy can be defined as the sum of the kinetic energy and the potential gravitational energy of the planet. Its conservation, as well as its ability to produce the correct potential energy, can be proven using the fundamental theorem of calculus for linear integrals.
The Laplace-Runger-Lenz vector, denoted by A ˙, is also conserved in this system.
Simplifying
By utilizing the vector triple product, we are able to express the square of the normalized form. This derivation is straightforward: E2 – r2 = (E + mμ)2
Why ellipses?
Since the energy is relative to infinity, in order to have an orbit that is bound, we require E0. Thus, as mentioned in the previous section, -r = -E-1(Er + mμ) and therefore -r + g = -mμE’0. This implies that -r = -E-1(Er + mμ). This equation defines an ellipse with focus 0.
Why not circles?
A circle is a unique shape where the foci coincide, which can be expressed as E = -1, f = 0.
E > 0, f = 0.
E = 0, f = 0.
e = A / (m^2μ).
Among all the planets in the solar system, Venus has the most circular orbit with an eccentricity of 0.007.
r ˙, ϕ ˙.
Given the multitude of factors that contribute to varying velocities, it is not surprising that only a select few orbits are circular. Furthermore, since the actual orbits undergo changes over time, it is evident that they cannot remain circular indefinitely.
Displayed below is an image depicting the eccentricity of several celestial bodies within the solar system, sourced from this location:
I always find it preferable when answers steer clear of using formulas and instead rely on logical reasoning. In regards to why not all orbits are circular, the reasoning can be summarized as follows:
Imagine a stationary star and a planet in motion. For any given momentum the planet possesses, it is possible to predict the trajectory of its future motion. If this momentum is exactly perpendicular to the line connecting the star and the planet, and if the velocity has a precise value, then the resulting motion can indeed be described by a perfect circle.
However, any deviation from this specific momentum means that the resulting trajectory cannot be a circle:
- If the velocity is too low, the planet will be pulled towards the star (in the extreme case of zero momentum, this pull will be in a straight line).
- If the velocity is too high, the planet will move away from the star (similar to a slingshot).
- If the momentum is not directly perpendicular to the line connecting the planet and the star, the initial movement will either be towards or away from the star, resulting in a non-circular trajectory.
Thus, we can conclude that a circle is a special scenario for the path that a planet can take around a star.
What is the explanation for the elliptical shape of planetary orbits?
The reason behind this phenomenon lies in the force of gravity. As we have learned in our physics classes, gravity is inversely proportional to the square of the distance between objects. Additionally, we understand that the gravitational potential is also inversely proportional to distance. So, when we observe an ellipse in the context of planetary orbits, we are essentially witnessing the path followed by a material point within a central gravitational field.
In short, the history of it goes like this. The ancients, by observing the planets’ movement in the sky, had an inkling that all of them, including the Earth, orbited the Sun. Over time, this knowledge was forgotten, until Copernicus rediscovered it. This sparked a new inquiry: what is the precise path of the planets around the Sun? Do they trace a circular orbit with the Sun at the center, or do they follow a different curve? How swiftly do they traverse their path? And so forth.
It didn’t take much time to discover. Following Copernicus, a period of uncertainty emerged, sparking a great debate about whether the planets, including Earth, revolved around the Sun or if Earth remained at the center of the universe. At this point, a man named Tycho Brahe (Tycho Brahe (1546-1601) was a Danish astronomer) devised a method to address this inquiry. He concluded that the most effective approach involved meticulously observing the planets’ positions in the sky, accurately documenting their movements, and then deciding between the two contrasting theories. This marked the inception of contemporary science, the key to comprehending nature accurately – observing the object, meticulously recording all the particulars, and hoping that the acquired data would serve as a foundation for one interpretation or the other. And so, Tycho Brahe, a wealthy individual who possessed an island near Copenhagen, outfitted his island with expansive bronze circles and specialized observation points, meticulously noting the planets’ positions night after night. It is only through such rigorous labor that any breakthrough reaches us.
After collecting all of this data, it ended up in the possession of Kepler. (Johannes Kepler (1571-1630) was a German astronomer and mathematician who served as Brahe’s assistant) He was attempting to determine how the planets moved around the sun. Kepler was searching for a solution through trial and error. One day, it appeared to him that he had found the answer: he concluded that the planets move in a circular pattern, but the Sun is not located at the center. However, Kepler soon noticed that one of the planets, possibly Mars, deviated from its expected position by 8 angular minutes. This realization led him to understand that his previous answer was incorrect, as Tycho Brahe could not have made such a large mistake. Based on the accuracy of the observations, Kepler decided to revise his theory and ultimately made three significant discoveries.
The movement of the planets around the Sun: laws of motion
Initially, Kepler discovered that the planets orbit the Sun in elliptical paths, with the Sun positioned at one of the foci. An ellipse is a shape familiar to artists, as it resembles a stretched circle. This concept is also known by children, who are often taught that if a string is threaded through a ring, the ends fastened, and a pencil inserted into the ring, it will trace out an ellipse.
Several years later, Kepler came up with a third principle that didn’t focus on the movement of one planet around the Sun, but rather connected the movements of various planets. This principle stated that the duration of a planet’s complete orbit around the Sun is determined by the size of its orbit and is directly proportional to the square root of the cube of this measurement. Additionally, the size of the orbit can be determined by the diameter that passes through the widest part of the ellipse.
Therefore, Kepler made a groundbreaking discovery by formulating three fundamental laws. These laws can be condensed into a single statement: if we define a planet’s orbit as an ellipse, then the radius-vector of the planet will sweep out equal areas in equal time intervals. Additionally, the time it takes for a planet to complete one orbit around the Sun is directly proportional to the size of the orbit raised to the power of three. In other words, it is proportional to the square root of the cube of the orbit’s size. These three laws comprehensively explain the motion of planets as they revolve around the Sun.
Meanwhile, Galileo made a groundbreaking discovery regarding the principle of inertia. Later, Newton came along and concluded that a planet in orbit around the Sun doesn’t require a force to continue moving; if there were no force, the planet would travel in a straight line. However, the planet doesn’t actually follow a straight path. Instead, it consistently ends up closer to the Sun than it would if it were flying freely. In other words, its motion is redirected towards the Sun.
It became evident that the origin of this force (known as gravitational force) was located in close proximity to the Sun.
Observing Jupiter through a telescope, people witnessed its satellites circling around it, creating a miniature solar system. The satellites appeared to be drawn towards Jupiter, just like how the moon revolves around and is attracted to Earth. This led to the natural conclusion that gravity is a universal force. All that was left was to generalize these observations and propose that all bodies attract one another. Therefore, it can be inferred that Earth attracts the Moon in the same manner that the Sun attracts the planets. However, it is well-known that Earth also has the power to attract ordinary objects. For instance, as you sit on a chair, you feel the Earth’s gravitational pull, preventing you from floating in the air. This phenomenon of objects being attracted to Earth was widely recognized. Newton hypothesized that the Moon remains in its orbit due to the same gravitational forces that attract objects to Earth.
Actually, the Earth is engaged in the same activity as the Moon – it is engaged in circular motion. The Earth is subject to a counteracting force from the Moon – but what is this force? Just as the Moon revolves in a circular path to counterbalance the Earth’s gravitational pull, similarly, the Earth also follows a circular path. Both celestial bodies revolve around a common center, and the Earth experiences balanced forces where the water at point x is attracted less by the Moon at point y and more at point z, resulting in bulges of water in both locations. This is the explanation for the occurrence of tides and why they happen twice daily.
The amazing discovery of the speed of light
As scientific knowledge advanced, measurements became increasingly precise and provided more convincing evidence for Newton’s laws. The first highly accurate measurements were made on the moons of Jupiter. It was believed that by carefully observing their orbits, one could verify that everything behaved in accordance with Newton’s laws. However, it was soon discovered that this was not the case. The moons of Jupiter were observed to appear 8 minutes earlier and 8 minutes later than predicted by Newton’s laws. They were found to be ahead of schedule when Jupiter approached Earth and behind schedule when Jupiter and Earth moved apart – a truly perplexing phenomenon.
Rømer (Olaf Rømer (1644-1710) – Danish astronomer) was convinced of the accuracy of the law of gravitation. He came to the intriguing conclusion that it requires a certain amount of time for light to travel from Jupiter’s satellites to Earth. When we observe Jupiter’s satellites, we do not see them in their current position, but rather where they were a few minutes ago – specifically, the same number of minutes it takes for light to reach us. When Jupiter is closer to us, light arrives more quickly, and when Jupiter is farther away, light takes longer to reach us. To account for this time difference, Rømer had to adjust his observations, making them earlier or later depending on the circumstances. By doing so, he was able to calculate the speed of light. This groundbreaking discovery marked the first confirmation that light does not travel instantaneously.
The planet’s discovery
Why do orbits follow an elliptical path instead of a circular one?
What is the reason behind planets revolving around a star in a definite elliptical orbit, with the star positioned at one of the foci? Why is the orbit not a perfect circle?
Let’s consider a scenario where the planet has a negligible mass when compared to the star and both are spherically symmetric (which is usually a good approximation for Newton’s law of gravitation). Additionally, assume that there are no forces acting between them apart from gravity. If the first condition is not met, then both objects will experience an acceleration directed towards the barycenter of the system, as if the barycenter were exerting a gravitational force with a reduced mass on them. This makes the problem mathematically equivalent.
Imagine a star positioned at the origin of a coordinate system. In accordance with Newton’s law of gravitation, the force between the star and a planet can be represented by the equation F = -GMm/r^2, where F is the force, G is the gravitational constant, M is the mass of the star, m is the mass of the planet, and r is the distance between the star and the planet. This equation can also be written as F = -mμ/r^3, where μ is the standard gravitational parameter of the star. In other words, the force between the star and the planet is inversely proportional to the square of the distance between them, and is directly proportional to the product of their masses.
Conservation laws
The conservation of momentum is ensured by the purely radial force. If the star is at the origin and has a non-zero initial velocity, the orbit must be bounded by the plane of all points with vectors from the origin satisfying L ⋅ x = 0, where L = r × p ˙ and L = d ( F ∥ r ) ' role="presentation"> ( F ∥ r ).
The total orbital energy is defined as the sum of the kinetic energy and the potential gravitational energy of the planet. Its conservation, and its ability to produce the correct potential energy, can be proven using the fundamental theorem of calculus for linear integrals.
The Laplace-Runger-Lenz vector, defined as A, is also conserved: ˙ A.
Finally, let’s also consider f, which has the same units as r, and since L ⋅ f = 0, it lies in the same plane as the orbit. Because it is a vector scaled by a scalar, it is possible to demonstrate that f is also conservative as long as E ≠ 0. f = A / (mE) ‘ role=”presentation”> f = A / (mE) r ‘ role=”presentation”> r L ⋅ f = 0 ‘ role=”presentation”> L ⋅ f = 0 f ‘ role=”presentation”> f E ≠ 0 ‘ role=”presentation”> E ≠ 0
Using the vector triple product, we can express the squared magnitude of E minus r as E^2 – r^2 = (E + mμ)^2.
Why do we observe ellipses?
Since the energy is relative to infinity, a bound orbit requires E0. Thus, from the previous section, f – r = -E^-1(Er + mμ) and therefore f – r + g = -mμE’ = E/E0. The equation f – r = -E^-1(Er + mμ) defines an ellipse with focus at the origin (0,0).
Why not use circles?
A circle is a unique shape in which the foci coincide at the same point, which can be expressed as E = -1, f = 0.
E > 0, E = 0, f’.
e = A / (m^2 * μ).
Out of all the planets in the solar system, Venus has the most circular orbit with an eccentricity of 0.007.
r”, φ”.
Due to various factors, it is not surprising that only a small number of orbits end up being circular, and because the actual orbits change over time, we know that they cannot remain that way for long.
Below is an image illustrating the eccentricity of certain celestial bodies in the solar system, obtained from this source:
Personally, I prefer responses that avoid using equations and instead focus on reasoning. When it comes to why not all orbits are circular, the reasoning is as follows:
Imagine a star that is stationary and a planet that is in motion. For every possible momentum that the planet can possess, we can predict the trajectory of its future motion. If that momentum is precisely perpendicular to the line connecting the star and the planet, and if the velocity has a specific value, then the trajectory can be a perfect circle.
However, any deviation from this precise momentum will result in a curve that is not a circle:
- If the velocity is too low, the planet will be pulled towards the star (in the extreme case of zero momentum, this pull will be in a straight line).
- If the velocity is too high, the planet will move further away from the star (similar to a slingshot effect).
- If the momentum is not directly perpendicular to the line connecting the planet and the star, the initial motion will either move towards or away from the star, resulting in a non-circular curve.
Therefore, we can conclude that a circle is a special scenario for the trajectory a planet can have around a star.
Answer:
Conservation laws determine the paths of planets as they travel through space.
Explanation:
Observations made by Johannes Kepler led to the discovery that planets follow elliptical orbits. Later on, Isaac Newton used the law of conservation of energy to prove that a planet’s orbit is in fact an ellipse.
When two celestial bodies orbit each other, they both orbit around a center of mass known as the barycenter. In the case of the Earth and the Moon, they actually revolve around the Earth-Moon Barycenter (EMB), rather than one revolving around the other.
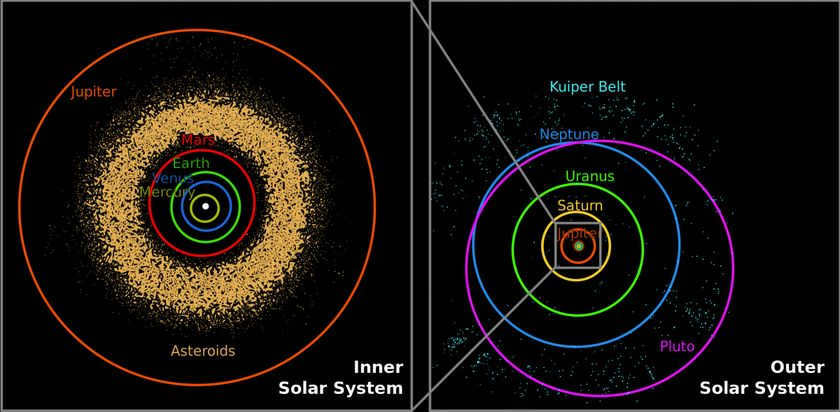
When it comes to something more intricate, like the celestial system, the same principle applies. None of the celestial bodies, including the planets, revolve around the Sun directly. In reality, the Sun, planets, asteroids, comets, and other entities orbit around the center of mass of the celestial system, known as the Solar System Barycenter (SSB).
The SSB is in constant movement and can be located anywhere between the Sun’s center and the outer edge of the Sun. Thus, everything within the celestial system revolves around a constantly moving point.
The illustration demonstrates the trajectory of the SSB over numerous decades. The instances when the SSB is farthest from the Sun occur when the planets are aligned.

Jupiter, the largest planet in our solar system, boasts a diameter of approximately 9 x 10 ^ 4 miles. On the other end of the spectrum, Mercury, the smallest planet, measures in at about 3 x 10 ^ 3 miles in diameter. The question arises: how many times bigger is Jupiter compared to Mercury?

Jupiter is 27,000 times larger than Mercury. To determine this, we can compare the volumes of the two planets. Assuming both planets are perfect spheres, the volume of Jupiter (V_j) is given by:
V_j = (4/3 π (9/2×10^4)^3
The volume of Mercury (V_m) is given by:
V_m = (4/3 π (3/2×10^3)^3
Using the definition of “times larger” above, we can calculate the ratio of the volumes:
V_j / V_m = ((9/2)^3×10^12) / ((3/2)^3×10^9) = (9^3/2^3) × (2^3/3^3) × 10^3 = (3^6/3^3) × 10^3 = 3^3 × 10^3 = 27×10^3 = 27,000
Is it possible to determine the distance of the center of mass of two bodies, with masses m1 and m2 respectively, from mass m1, when they are separated by a distance R? A. (m2R) / (m1 + m2), B. (m1R) / (m1 + m2), or C. (m1m2R) / (m1 + m2)?

Let the distance from the center of mass of the system to m_1 be denoted as x. Therefore, we can express the equation as (m_1 + m_2) x = m_1 * 0 + m_2R, where R is the radial distance. Solving for x, we get x = (m_2R) / (m_1 + m_2).
What is the radial distance of the solar orbit around the center of the galaxy?
The distance between the Sun and the center of the Milky Way is approximately 27000 light years. This information was shared on a photo slide website called share.com.
Through careful observation, Johannes Kepler made the discovery that planets follow elliptical paths in their orbits. Later on, Isaac Newton used the law of conservation of energy to prove that a planet’s orbit is indeed an ellipse.
When two celestial bodies orbit each other, they both rotate around a central point known as the barycenter. This point represents the center of mass. Interestingly, the Moon does not orbit around the Earth alone. In reality, both the Earth and the Moon revolve around a common barycenter known as the Earth-Moon Barycenter (EMB).
When it comes to something more intricate, like the solar system, the same concept applies. None of the planets, etc. actually orbit around the Sun. In reality, the Sun, planets, asteroids, comets, and other celestial bodies orbit around the center of mass of the solar system, which is known as the Solar System Barycenter (SSB).
The SSB is constantly in motion and can be located anywhere from the center of the Sun to just outside the Sun’s radius. Therefore, everything in the solar system revolves around a point that is constantly moving.
The diagram illustrates the trajectory of the SSB over multiple decades. The instances where the SSB is farthest from the Sun occur when the planets are aligned.

With a diameter of about 9 x 10 ^ 4 miles, Jupiter holds the title of the largest planet in the solar system. In contrast, Mercury, with a diameter of about 3 x 10 ^ 3 miles, claims the position of the smallest planet. How much bigger is Jupiter compared to Mercury?

Jupiter is 2.7 times larger than Mercury, which is equivalent to a volume ratio. Assuming both planets are perfect spheres, the volume of Jupiter (Vj) can be approximated as 4/3 π (9 / 2×104)3, and the volume of Mercury (Vm) can be approximated as 4/3 π (3 / 2×103)3. Using this definition, we can calculate the volume ratio: Vj / Vm = (4/3 π (9 / 2×104)3) / (4/3 π (3 / 2×103)3) = ((9/2)3×1012) / ((3/2)3×109) = 93/23 × 23/33 × 103 = 36/33 × 103 = 33 × 103 = 27×103 = 2.7×104.
Is the distance of the center of mass of two bodies, each with mass m1 and m2 respectively, from mass m1 A: (m2R) / (m1 + m2), B: (m1R) / (m1 + m2), or C: (m1m2R) / (m1 + m2)?


A Let’s assume that the center of mass of the system is located at a distance x from m_1. Therefore, we can express this as (m_1 + m_2) x = m_1 * 0 + m_2R, which simplifies to x = (m_2R) / (m_1 + m_2).
What is the distance from the center of the galaxy to the solar orbit?

The radial distance of the solar orbit around the center of the galaxy is approximately 27000 light years. The Sun is located about 28000 light years away from the center of the Milky Way. photo slide share .com.
What is the reason for planets revolving around a star in a specific elliptical orbit where the star is one of its focal points? Why is the orbit not a perfect circle?
Consider a celestial body located at the origin of the coordinate system. According to Newton’s law of gravity, the gravitational force acting on another object is given by the formula , where is the vector pointing from the celestial body to the object, is the mass of the object, and is the standard gravitational parameter of the celestial body. r m μ = G M F = – m μ r 3 r ' role="presentation"> F = – m μ r 3 r r r ' role="presentation"> r m ' role="presentation"> m μ = G M ' role="presentation"> μ = G M
Conservation laws
Conservation laws are fundamental principles in physics that state that certain quantities, such as momentum and energy, are conserved in a closed system. In the case of a radial force, such as the gravitational force in a planetary orbit, the momentum is conserved. If the initial velocity of the planet is not zero and the star is at the origin, then the orbit must be bounded by the plane of all points with vectors from the origin satisfying L ⋅ x = 0, where L = r × p ˙ (cross product of the position vector and the velocity vector).
The total orbital energy is defined as the sum of the kinetic energy and the potential gravitational energy of the planet. This energy is conserved, meaning it remains constant throughout the orbit. This conservation of energy can be proven using the fundamental theorem of calculus for linear integrals.
Another conserved quantity in the system is the Laplace-Runger-Lenz vector, denoted by A. This vector is also conserved over time.
Finally, let’s consider f, which shares the same units as r. Because L ⋅ f = 0, we know that f lies within the orbit plane. Given that f is a conservative vector scaled by a conservative scalar, it can be easily demonstrated that f remains conservative as long as E ≠ 0. This can be expressed as f = A / (mE)’.
Simplification
By utilizing the vector triple product, we can express the normalized square, the derivation of which is straightforward: E^2 – r^2 = (E + mμ)^2
Why ellipses?
Since energy is relative to infinity, in order to have a bound orbit, we require E_0. Therefore, from the previous section, -r + f = -E^(-1)(Er + mμ) and thus -r + f + g = -mμE’EE_0’E -r + f = -E^(-1)(Er + mμ) which defines an ellipse with focus 0.
A circle is a special case where the focuses are the same point, which can be expressed as E = 0 and f = 0. E > 0 can also be stated as E > 0. E = 0 can be represented as E = 0 f. The equation e = A / (m^2μ) can be used to calculate the eccentricity. Among all the planets in the solar system, Venus has the most circular orbit with an eccentricity of 0.007. The variables r ˙ and ϕ ˙ represent the rate of change of radius and angular velocity, respectively.
Since velocities can vary for many reasons, it is not surprising that only a few orbits end up being circular. Additionally, since the actual orbits change over time, we know that they cannot remain circular for long.
Here is an image that displays the eccentricity of certain celestial bodies in the solar system, which was taken from this source:
Personally, I prefer answers that avoid using formulas and instead provide reasoning. As for why not all orbits are circular, the reasoning would be as follows:
Let’s consider a stationary star and a moving planet. For every possible momentum the planet can have, we can predict the path of its future motion. If the momentum is directed exactly perpendicular to the line connecting the star and the planet, and if the velocity has a precise value, then the path of motion can be a perfect circle.
However, any deviation from this precise momentum will result in a curve that is not a circle:
- If the velocity is too low, the planet will be pulled towards the star (in the extreme case of zero momentum, this pull will be in a straight line).
- If the velocity is too high, the planet will move further away from the star (similar to a slingshot effect).
- If the momentum is not directly perpendicular to the line connecting the planet and the star, the initial motion will either move towards or away from the star, causing the curve to deviate from a circle.
Therefore, it can be concluded that a circle is a specific scenario for the path a planet can follow around a star.
A circle is encircled by an elliptical shape
Rosa Maria Ros. “World of Math” #30
“The Music of the Spheres. Astronomy and Math.”
The organization and arrangement of the findings from astronomical observations can only be achieved through the use of mathematics. Additionally, mathematics has played a vital role in the advancement of astronomy. However, astronomy presents its own unique challenges: it is not possible to replicate an experiment in a laboratory and manipulate various conditions at will. How marvelous it would be to be able to orchestrate eclipses at our own discretion!
I desire a partial solar eclipse! No, I long for a total eclipse!
Astronomy originated alongside humanity. Our ancient ancestors, lacking television, likely spent their evenings gazing at the magnificent expanse of the night sky. In fact, they probably observed the sky more frequently than any of us do today. Over time, our forebears began to recognize that certain celestial events occurred in a predictable manner, allowing them to determine optimal times for activities such as sowing crops and hunting.
Undeniably, this knowledge played a crucial role in human survival. It served as the initial demonstration of science’s practical value. Furthermore, ancient civilizations attributed unexplained phenomena to the divine will. These events held great significance and were associated with the performance of sacred rituals, entrusted to priests of various primitive cults.
I find it easier to share astronomical observations compared to other scientific fields due to the highly visual nature of astronomy.
Explaining the most recent breakthroughs in number theory or differential geometry, for instance, is a challenging task, but showcasing the freshest snapshots from the Hubble telescope is a breeze. Who among us hasn’t marveled at the breathtaking images of the cosmos? Furthermore, astronomy, when presented with expertise, evokes emotions and passion just as powerfully as any series. Who wouldn’t be astonished to discover that stars are born, age, and meet tragic ends, with some even exploding? Who wouldn’t feel a sense of connection knowing that it is within the stars that the heaviest chemical elements, which make up our bodies, are forged? Who wouldn’t experience a cosmic kinship upon learning that we are simply the offspring of stars, composed of stardust? The universe is also home to entire galaxies that are in constant motion and occasionally collide. Ultimately, astronomy is an entire realm brimming with magnificent imagery.
There is a growing interest in astronomy, possibly due to its ability to provide insights into the past, the Earth’s rotation, the solar system, the cosmos, and our origins. Astronomy also offers the opportunity to forecast seasonal changes, eclipses, and the positions of planets and stars in the sky. Unfortunately, some individuals misuse this aspect of astronomy to make pseudo-scientific predictions unrelated to celestial bodies. This may stem from human nature itself, as people often seek to alleviate uncertainty about the future by any means necessary, including turning to astrology for guidance.
Speaking of predictions, there is a unique correlation between astronomy and mathematics. This is because astronomical predictions are the outcome of mathematical calculations. In fact, the advancement of new branches of mathematics has facilitated numerous astronomical breakthroughs.
I anticipate that this book will captivate readers and provide them with answers to their queries. It is possible that after perusing its contents, readers will be inspired with fresh ideas – a testament to the progress of science. Every scientist recognizes that they are bound by a certain framework: on one hand, they relish the satisfaction of conquering previously insurmountable challenges or gaining new insights, but on the other hand, they are constantly tormented by more and more unanswered questions.
The book contains five chapters that focus on essential astronomical topics connected to mathematics, particularly the positioning of planets and the measurement of time. The initial two chapters delve into the relative positions of celestial bodies and the distances that separate them. The final two chapters center on the measurement of time. However, the pivotal third chapter explores eclipses, which are astronomical events in which celestial bodies assume unique positions in space.
Chapter 1: Fundamental Angles and Distances: The Basics of Astronomy
Undoubtedly, the primary objective of scientific research dedicated to the observation and examination of entities is the determination of their spatial coordinates. Mathematics, as a pivotal discipline, plays a crucial role in addressing this highly significant problem by enabling the calculation of three parameters: the magnitudes of two angles denoting the position of the entity on the celestial sphere, and the distance between the entity and the observer. While establishing these two angles is relatively straightforward, the computation of distances to celestial bodies, conversely, represents one of the most challenging undertakings in the field of astronomy.
Evaluating Spatial Coordinates based on Two Angles
The position of a celestial body on the Earth’s surface is determined using the coordinate system. Considering Earth coordinates is crucial when working with astronomical data, as the results of observations can vary depending on the observer’s location. Here, we will provide a brief explanation of the method used to calculate the position of celestial bodies.
Our planet rotates around an imaginary line called the axis, which is often used as a reference point to determine the position of locations on the Earth’s surface. For instance, the points where the Earth’s axis intersects the surface are known as the North Pole and the South Pole. If we visualize a plane that is perpendicular to the Earth’s axis and passes through the center of the planet, we can observe that the line where this plane intersects the surface is called the equator. The equator divides the Earth into two halves, known as the Northern Hemisphere and the Southern Hemisphere (with the North and South Poles located at the top of each hemisphere, respectively). If we were to imagine an infinite number of planes that are parallel to the equator and we were to cut the Earth’s surface with these planes, we would obtain smaller circles called parallels.
The circular path is traversed by the ellipse

The greater the distance of the planets from the Sun, the higher their linear and angular velocities as they orbit around the Sun. The period of time it takes for the planets to complete one revolution around the Sun in relation to the stars is known as the sidereal period.
This period of time is also referred to as a stellar year for the Earth’s revolution in relation to the stars. The planet Mercury has the shortest stellar period, while Mars takes about 2 years, Jupiter takes 12 years, and Pluto takes up to 250 years as the distance from the Sun increases.
The credit for discovering the laws of motion of the planets goes to the renowned Austrian scientist Kepler. In the early 17th century, Kepler established three laws of planetary motion, which are now known as Kepler’s laws.
Kepler’s first law states that each planet orbits the Sun in an elliptical path with the Sun located at one of the foci.
The eccentricity of an ellipse determines the extent of its elongation. It is calculated by dividing the distance between the focus and the center by the length of the major semi-axis. When the focus and center coincide, the eccentricity becomes zero, and the ellipse transforms into a circle.
The perihelion is the point on the orbit that is closest to the Sun, while the aphelion is the point farthest from it. Planetary orbits are essentially ellipses with eccentricities that are not significantly different from those of circles. For instance, the Earth’s orbit has an eccentricity of e = 0.017.
The orbits of comets become extremely eccentric. When е=1, the second focus of the ellipse moves infinitely far away, transforming the ellipse into an open curve known as a parabola. As the branches of the parabola extend to infinity, they become parallel. If е>1, the orbit becomes a hyperbola. While moving along a parabola or hyperbola, a celestial body completes one revolution around the Sun and then continues moving away from it indefinitely.
The Earth’s average orbital velocity is 30 kilometers per second. The Earth’s orbit is nearly circular, and its orbital velocity at the Earth’s distance from the Sun is also close to circular. The parabolic velocity for the Earth is calculated as √2*30 km/s, which equals 42 km/s. At this speed relative to the Sun, the object will exit the solar system.
Kepler’s Third Law: the squares of the planetary orbits’ stellar periods are proportional to the cubes of their major semi-axes.
Gravity is a fascinating force. Imagine a massive boulder soaring through space, unaffected by anything in its path. Suddenly, a planet appears in its trajectory. The planet’s gravitational pull comes into play, exerting a force on the boulder. If the boulder is traveling at a high enough speed, it will not be captured by the planet’s gravity and fall onto its surface. It’s a delicate balance of forces at play here. The planet pulls the boulder towards itself, while the boulder continues to move in the opposite direction due to its own momentum. As a result, the boulder ends up moving in the direction where the planet was located a second ago, but it never gets close enough to actually reach the planet. It’s important to note that for this phenomenon to occur, the boulder must be traveling at a velocity equal to or greater than the escape velocity of the planet. Otherwise, the gravitational force would gradually pull the boulder closer and closer to the planet.
Queries and Issues
- At which time do the people on Earth move quicker around the Sun – during noon or midnight?
- During which season does the Earth move faster in its orbit around the Sun – in winter or summer?
- Astronomers have discovered that the speeds of the individual sections of Saturn’s ring are not in proportion to their distances from the axis of rotation. What conclusion should this finding have led to about the structure of the ring?
What is required to provide an object there with the initial cosmic velocity?
A mental experiment of the mind
Interestingly enough, .
. Mark Twain came into this world a mere fortnight following the sighting of Halley’s Comet in 1835, and departed from it the day after its closest approach to the Sun in 1910. Just prior to this moment, Twain playfully informed his companions that due to his birth coinciding with the comet’s reappearance, he would meet his demise immediately after its subsequent return.
. in spite of its inherent cruelty, the Ptolemaic system grants one the ability to accurately foretell celestial phenomena. In a peculiar twist, this ancient model could potentially offer solutions to certain challenges faced by modern astronautics, such as the computation of spacecraft trajectories observable in the heavens.
Mental microexperience
Weightlessness and zero gravity are not caused by impact; instead, they are determined by mass and velocity. Therefore, when working in outer space in the future, it is important to avoid colliding with the spacecraft.
It’s not about going in circles and what causes celestial bodies to move. They are attracted to the sun, so they would naturally fall into it.
The idea is that we have fallen and are lying on the ground, metaphorically speaking. Why an ellipse? If the gravitational force is constant and the centrifugal force is also constant (and for it to be constant, the planet needs to move, but what causes it to move?), then the result is an orbit in the shape of a circle, as far as I understand. And I don’t fall onto you because I am more attracted to the earth, so to speak, and I strive to fall towards its core. I am like you, more attracted to the earth than to each other =))))
Then Commix asks, what is the reason behind the movement of planets? In essence, their motion is influenced by the gravitational pull of the sun, which causes their path to curve.
There is also a mutual attraction between the two of us, much like the attraction between any two objects. However, for some unknown reason, you do not fall onto me (or vice versa). There seems to be something preventing it. In the case of planets, it is inertia. The gravitational force is only strong enough to curve their paths into an ellipse. Why an ellipse and not a circle? Well, a circle is actually a specific type of conic section, and all objects within a gravitational field follow paths that are conic sections. These paths can be not only circles and ellipses, but also parabolas and hyperbolas. Why this is the case, unfortunately, cannot be explained simply. It is a result of the equations that describe our universe.
So, what causes the planets to move? In the past, it was believed that angels or spirits were responsible for pulling the planets. Then Newton introduced his first law, which states that every object remains at rest or continues moving in a straight line at a constant speed unless acted upon by a force. Moving in a straight line is the simplest form of motion, and rest is just a special case of it. In reality, there is no true state of rest; rest can only be relative to something else. We are always in motion, not relative to one thing but rather relative to another. Why the universe is organized in this way, I cannot say. It seems that in another universe where everything comes to a stop, we would simply not exist :).
The reason why planets will never fall into the Sun is because the gravitational force is counterbalanced by the centrifugal force resulting from their rotation.
“Why do planets move in elliptical orbits instead of circular ones?”
An elliptical orbit is actually a more general case that includes circular orbits.
“And what causes planets to move in the first place? Shouldn’t they have fallen into the Sun due to its attraction?”
The motion of planets is determined by inertia and the conservation of momentum.
It’s important to note that there are other celestial bodies in space that possess gravitational forces, not just the Sun. The elliptical shape of the orbit can be explained by the influence of a secondary gravitational source, such as the supermassive black hole at the center of the expanding Milky Way galaxy. This additional gravitational force may be responsible for the Earth’s movement away from the Sun, resulting in an apogee and perigee.
Let me simplify the concept for you. If the Sun didn’t move in space, the planets would have circular orbits. However, because the Sun does have motion, it affects the planets’ orbits and makes them elliptical. Gravity is the force that binds us to this process. There are laws, formulas, and equations that explain the rest.
Gravity is what controls the motion of the planets in our solar system. Without it, the planets would scatter in different directions and get lost in the vastness of space.
People have long been fascinated by the laws of planetary motion. The study of how planets move and the structure of our solar system led to the discovery of the theory of gravitation and the law of universal gravitation.
Looking at it from an Earthly perspective, the planets follow intricate paths as they move through space (Fig. 1.24.1). Ptolemy, around 140 AD, was the first to attempt to create a model of the Universe. According to Ptolemy’s model, the Earth was positioned at the center of the universe, with the planets and stars orbiting it in both large and small circles, in what can be likened to a graceful round dance.
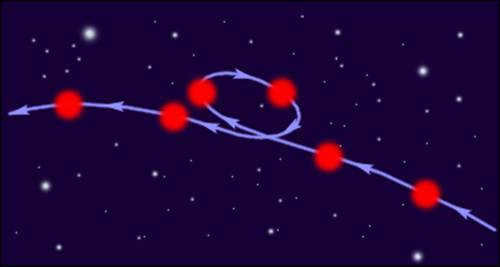 |
| Figure 1.24.1: An artistic representation depicting the observed movement of Mars against a backdrop of fixed stars. |
Kepler’s First Law (1609):
All planets have elliptical orbits with the Sun at one of their foci.
Figure 1.24.2 illustrates the elliptical orbit of a planet with a much smaller mass than the Sun. The Sun is located at one of the foci of the ellipse. The point on the trajectory closest to the Sun, denoted as P, is known as the perihelion, while the point farthest from the Sun, denoted as A, is called the aphelion. The distance between the aphelion and the perihelion represents the major axis of the ellipse.
When it comes to circular orbits, Kepler’s first and second laws are fulfilled automatically. The third law, on the other hand, states that the period of the orbit, denoted as T, is proportional to the cube of the radius, symbolized as R. In other words, we have T 2 ~ R 3. This relationship allows us to derive the gravitational force’s dependence on the distance. As a planet moves along a circular trajectory, it experiences a force resulting from the gravitational interaction between itself and the Sun:
The conservativity characteristic of gravitational forces permits us to introduce the notion of potential energy. It is convenient to measure the potential energy for universal gravitation from an infinitely distant point.
The potential energy of a body with mass m situated at a distance r from a stationary body with mass M is equivalent to the work done by gravitational forces in moving the mass m from this point to infinity.
The mathematical process of determining the potential energy of a body in a gravitational field involves summing up the work done for small displacements (Fig. 1.24.5).
The law of gravitation that is universal is not only applicable to masses that are point-like, but also to bodies that are spherically symmetric. The gravitational force’s work when there is a small displacement can be calculated as follows:
The total work done in moving a body with mass m from its initial position to infinity can be obtained by summing up the work ΔAi for small displacements:
As Δri approaches zero, the sum in question transforms into an integral. By performing calculations for the potential energy, we are able to derive the following expression.
If an object is located at a distance r from the center of gravity and is moving with a velocity υ, its overall mechanical energy can be expressed as
As per the law of energy conservation, the overall energy of an object in a gravitational field remains constant.
The overall energy can be positive, negative, or zero. The direction of the overall energy determines the movement pattern of a celestial object (Fig. 1.24.6).
When E = E1 rmax, the celestial object follows an elliptical orbit (such as planets in the solar system and comets).
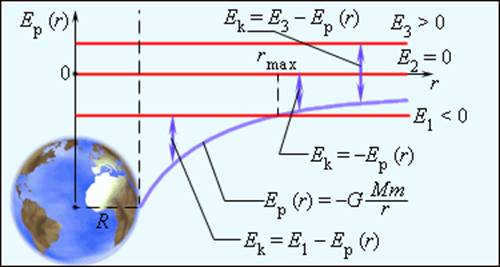 |
| Figure 1.24.6: Energy diagram of a body with mass m in the gravitational field created by a spherically symmetric body with mass M and radius R |
When E = E3 > 0, the object follows a hyperbolic path. It moves away from the Earth indefinitely, retaining a surplus of kinetic energy.
Kepler’s laws are applicable not only to the movement of planets and other celestial bodies within the solar system, but also to the motion of man-made satellites and spacecraft. In this scenario, the Earth serves as the center of gravity.
The initial orbital velocity corresponds to the speed at which a satellite orbits in a circular path near the Earth’s surface.
This velocity is necessary in order to overcome the gravitational pull of the Earth and place an object (such as a satellite) into orbit.for instance, to put a satellite into Earth’s orbit, for example.
Spacecraft must be given a certain minimum speed, known as the second space velocity, near the Earth’s surface in order to overcome the Earth’s gravity and become an artificial satellite of the Sun (or an artificial planet). By achieving this velocity, the spacecraft will follow a parabolic trajectory away from the Earth.