
Blog ❘ Serious Astrology ❘ Mathematics of the celestial sphere ❘ Spherical geometry
A complete revolution of the celestial sphere around its axis is known as a sidereal day. The current portion of a sidereal day is referred to as sidereal time.
The line passing from south to north through the zenith is known as the prime meridian. Any point on the celestial sphere that passes through the prime meridian during its daily motion is situated strictly between the eastern and western horizons, meaning it reaches its highest altitude on the way from sunrise to sunset. This position is called the planet’s culmination or its maximum elevation.
Astrologers have come to an agreement to consider the start of the sidereal day as the moment when the culmination reaches 0° of the celestial equator.
The correlation between sidereal time and RAMC
Let’s say you are somewhere in the middle of a sidereal day. If at the beginning of the sidereal day the culmination is at 0° of the equator, then at this moment the culmination will be at the degree with the coordinate RA (right ascension). This degree is known as the right ascension of the middle of the sky, or Medium Coeli (MC) in Latin. It is represented by the abbreviation RAMC.
Since 24 hours of sidereal time corresponds to a complete revolution of 360 degrees of the celestial sphere, one sidereal hour corresponds to 15 degrees of the celestial equator. Therefore, we can easily determine the current sidereal time by knowing the current culminating degree of the equator:
Distance between the upper and lower meridian and sidereal time
Each planet possesses its own equatorial coordinate known as Direct Ascension (RA). The angular separation between RAMC and RA is referred to as the Upper Meridian Distance (UMD).
If we express this same separation in terms of sidereal time between the planet’s current position and its upper culmination, we obtain the hourly distance, HD.
In the depicted diagram, it is evident that the sum of RA and UMD is equivalent to RAMC:
$$\begin UMD &= RAMC – RA \\ &= \left t_ \times 15 – RA
ight \end\tag$$$.
P.S. When a planet is positioned below the horizon, astrologers make use of the Lower Meridian Distance (LMD), which indicates the distance of the planet from its current position to the descending degree of the equator. It is connected to $UMD$ through a straightforward formula:
$$\begin LMD &= UMD + 180° \\ &= RAIC – RA_P \tag \end$$.
Here $RAIC$ represents the direct ascent of Imum Coeli (bottom of the sky) $RAIC = RAMC + 180°$
RAMC and the inclined ascent of ASC
We already know that the inclined ascent of ASC is the degree of the equator that rises simultaneously with ASC at a given time.
However, we have also learned that the culminating degree at any given time is RAMC. Therefore, if we add 90 degrees to RAMC, we obtain the current degree of the equator that is rising above the horizon. And that is the inclined ascension of the ASC.
The trajectory of any point on the celestial sphere (as the sphere rotates) from the horizon to the prime meridian is referred to as the day/night half-arc.
It is known as the day half-arc, or DSA for the day path (above the horizon), and the night arc, or NSA for the night path (below the horizon).
As depicted in the above diagram, the day half-arc DSA is calculated as
$$\begin{aligned} DSA &= RA – RAMC \\ &= RA – t \times 15 \end{aligned}$$.
For the night half-arc, we use the direct ascent of Imum Coelum, where $RAIC = RAMC + 180^\circ$, instead of $RAMC$:
$$\begin{aligned} NSA &= RA – RAIC \\ &= RA – 180^\circ – t \times 15 \end{aligned}$$.
From the same Figure 4, where $AD$ is negative, we can also observe that
$$ \begin{aligned} DSA &= 90^\circ + AD \\ NSA &= 90^\circ – AD \end{aligned}\tag $$$

The concept of time is not often pondered upon by ordinary individuals. They rely on their clocks, which they synchronize through the use of television or radio. However, even those clocks need to be verified for accuracy. This verification process is carried out by astronomical observatories, which align their clocks with the stars. In the realm of astronomy, stellar time is the standard for conducting observations.

STAR TIME
Star timerefers to the time associated with the Earth’s rotation in relation to a specific point on the celestial sphere – the vernal equinox point. The interval between two consecutive culminations of this point is known as the sidereal day, a concept that has been well-known to us for quite some time.
Therefore, sidereal time serves as the basis for our entire system of timekeeping, although many individuals may not be aware of it, given that our daily lives revolve around solar time.
SOLAR TIME
The concept of solar time is not entirely accurate, as it encompasses two distinct types: true solar time and mean solar time. Among these, there is an intriguing variation known as belt time. In order to grasp the concept of belt time, it is first necessary to comprehend the nature of true solar time.
TRUE SOLAR TIME
True solar time refers to the time measured by a sundial. When the Sun reaches its highest point in the sky, known as the meridian, it is considered noon. The duration between two consecutive crossings of the meridian is known as a true solar day.
A solar day, which begins and ends at noon, has been used for centuries as a simple and natural way of measuring time. However, in our modern age, where exact timekeeping and uniformity are necessary, this method is not suitable because true solar days can vary in length. This is due to the fact that the true 24 hours of the sun can have different durations.
Today, the unit of time known as the second is measured by the duration of 9192631770 oscillations of electromagnetic radiation, specifically the frequency of a certain absorption line in the spectrum of cesium atoms. This method of counting seconds is much more accurate than relying on astronomical observations.
The Sun’s movement across the sky is not consistent throughout the year. At times, it appears to move faster or slower, resulting in varying intervals between two consecutive afternoons. These intervals can differ by nearly a minute. Consequently, if our clocks were synchronized with the Sun, they would need to be adjusted slightly ahead or behind each day, which would undoubtedly be highly inconvenient from a practical standpoint.
This phenomenon occurs because the Earth’s orbit is not a perfect circle, but rather an ellipse, with the Sun located at one of its focal points. As a result, the Earth experiences variations in its distance from the Sun, causing it to orbit at different speeds. Consequently, it appears that the Sun moves across the sky at slightly different rates. The deviation from a perfect circle is relatively small, approximately 3%. At its closest point to the Sun, known as perihelion (from the Greek words peri – about, and Helios – Sun), the Earth is approximately 5 million kilometers closer to the Sun compared to its farthest point, known as aphelion (from the Latin word apo – from). The average distance between the Earth and the Sun is around 150 million kilometers. In the northern hemisphere, there are approximately 186 days from the spring equinox to the fall equinox, and 179 days from the fall equinox to the spring equinox, resulting in a slight difference of about 3%. In our hemisphere, the summer season is approximately one week longer than the winter season.
Furthermore, the solar time is influenced by the location of observation. The exact moment of noon changes by approximately one minute for every quarter of a degree of longitude. To address the first of these challenges, which is the unequal duration of the true solar day, astronomers have introduced mean solar time.
Mean solar time is the average solar day, which is calculated by averaging the length of a solar day over a year.
When we say that a sidereal day is 3 minutes 55.91 seconds shorter than a solar day, we are referring to the average length of a solar day. A sidereal day consists of 24 sidereal hours, which are shorter than solar hours, minutes, and seconds.
In order to make the end of the day at midnight instead of noon, they introduced civil time which was equal to mean solar time plus 12 hours. As a result, the civil day now begins and ends at midnight. If your watch is accurate enough, it will show the time of the average civil day, taking into account the hours, minutes, and seconds of that day. However, there is still one issue – even though the length of the average solar day remains constant, the exact moment of its start and end varies depending on the location of observation. For example, noon in local civil time shifts by one minute with every change of longitude by a quarter of a degree.
Before the introduction of belt time, each city and town had its own local time, which often led to confusion and misunderstandings.
In order to avoid the inconvenience of having to sit down to lunch on Tuesday and get up from the table on Wednesday, we have decided to count our twenty-four hours from midnight.
TIME ZONE
Incidentally, the ancient Mayan calendar, which concludes its largest cycle on December 21, 2012, was remarkably precise compared to our contemporary calendar.
ASTRONOMICAL CHART

- 25 BRIGHTEST STARS
- ALPHABETICAL LIST OF ALL CONSTELLATIONS
- ZODIACAL CONSTELLATIONS
- MAJOR ASTERISMS
The time it takes for the celestial sphere to complete one full revolution can be accurately measured as the interval between two consecutive culminations of the same star or a specific point on the celestial sphere. The vernal equinox point (T) is commonly chosen as this reference point.
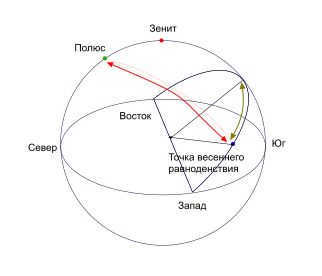
Astronomical MeasurementThe period of time between two successive occurrences of the vernal equinox point reaching its highest point in the sky is referred to as a sidereal day.
Given that the hour, minute, and second are used to measure the hour angle, the labels for these units are placed, just like the labels for degree measurements, at the top right of the respective digit. As a result, the representation of a specific moment in time would appear as follows: S = 14h06m27s.
Stellar time is utilized in astronomical observations. However, for practical purposes, it is not ideal as our daily lives are synchronized with the Sun.
Solar time
By comparing it to sidereal days, we can define the concept of a true solar day, which represents the time between two consecutive upper culminations of the center of the solar disk.
The true solar time is the hour angle (/0) of the center of the Sun. Due to the Sun’s annual movement along the ecliptic in the opposite direction to its daily movement, at a rate of approximately 1° per day, the true solar day is, on average, about 4 minutes longer than the sidereal day.
Irregularity of the flow of accurate solar time
Accurate solar time presents a challenge when it comes to creating a clock that accurately reflects this time, as the Sun’s hour angle changes in an irregular manner. This irregularity is caused by two factors: the uneven movement of the Sun along the ecliptic and the inclination of the ecliptic to the equator. The Sun’s movements along the ecliptic near perihelion and aphelion will result in unequal time intervals, while equal movements along the ecliptic near the equinox and solstice points will lead to unequal changes in the hour angle (Fig. 38).
In order to rectify the irregularity of the actual solar time, the notion of the “average Sun” is introduced, which refers to a supplementary moving point. The “average ecliptic Sun” is a point that moves uniformly along the ecliptic and aligns with the perihelion and aphelion points at the same time as the center of the actual solar disk. By replacing the actual Sun with the “average ecliptic” counterpart, the inconsistency in solar time caused by the varying speed of the Sun’s movement along the ecliptic is eliminated. To counteract the impact of the ecliptic’s inclination to the equator, the concept of the “average equatorial sun” is introduced, which is a point that moves uniformly along the equator and coincides with the vernal and autumnal equinox points at the same time as the “average ecliptic sun”.
Mean solar time
The fictitious “mean equatorial sun” takes part in the daily rotation of the celestial sphere just like the actual sun. The duration of time between two consecutive identical culminations of the “mean equatorial sun” is referred to as a mean day. The moment of the pinnacle culmination of the “mean equatorial sun” marks the start of an average day. The hour angle of the “mean equatorial sun” determines the mean time at any given moment. The average day is divided into 24 average hours, an hour consists of 60 minutes, and a minute is made up of 60 seconds.
Belt time
Every location on the Earth’s surface has its own unique local time, which varies based on longitude and can differ by hours, minutes, and seconds from the time at another location. Using local time can be highly inconvenient in practical situations, particularly for transportation and communication purposes. To address this issue, there is a need to establish a standardized method for keeping time across the entire Earth. Currently, this is achieved through the implementation of the zone time system.
The entire world is divided into 24 belts, each spanning 15 degrees of longitude. The central meridian of the first belt, known as the “initial or zero” belt, passes through Greenwich. The local time at this meridian is considered the world time. In the next belt to the east, the local time is one hour ahead of world time, and so on. This local time, denoted as Ta, is referred to as zone time, and the belts themselves are known as time zones.
Zone time creates a difference of approximately half an hour (at most) from the local time at any given point on Earth. This implementation of zone time results in an hour difference in certain neighboring settlements. However, this discrepancy is balanced by the fact that minutes and seconds remain consistent worldwide when utilizing zone time, with the time in various locations differing only by whole hours.
Time zone boundaries are established, occasionally deviating from meridians, along state, administrative, or natural (such as rivers or mountain ranges) borders.
When it comes to local time, it will increase as we move eastward from the prime meridian, which passes through Greenwich. On the other hand, if we consider local time while moving westward from the prime meridian, it will decrease. This brings us to an interesting point to consider.
Imagine three individuals standing at the same location on a middle latitude, each beginning to count the passing days from sunrise. The first person stays put, while the second person embarks on a journey around the world along the parallel to the east, and the third person sets off on a round-the-world trip along the parallel to the west. When all three individuals reunite at the starting point, the stationary observer will claim that N days have passed since their initial meeting, while the person who traveled eastward will assert that it has been (N + 1) days. This discrepancy arises because the second observer, traveling eastward, consistently witnesses the Sun reaching its highest point slightly earlier than the stationary observer.
The observer who is traveling in a westerly direction will observe that it has been (N – 1) days, as they are moving against the rotation of the Earth and will see the Sun reaching its highest point with a delay compared to a stationary observer.
To ensure that days are counted consistently for both stationary observers and travelers, an international agreement has established a “date line”. This line is located along the surface of the ocean and approximately follows the 180th meridian from Greenwich. When crossing this line in a westerly direction, one day is subtracted from the count (for example, the second day is immediately followed by the fourth day). Conversely, when crossing the date line in an easterly direction, an extra day is added to the count (for example, a number may be repeated twice in the records).
It is convenient to count meridians from Greenwich, as it ensures that the line of date change coincides with a memorable longitude figure (180 °). This would not be the case if meridians were counted from any other observatory.

John Arnold & Son created one of only two sideric angle clocks that are known to still exist in the world. This particular clock was previously owned by Sir George Shuckburgh-Evelyn and is currently on display at the Royal Observatory in Greenwich, London.
Sideric time ( / s aɪ d ɪər i əl / sy- Stag -e-əl ) is a timekeeping system used by astronomers to locate celestial objects. By using sidereal time, astronomers can easily position their telescopes to the appropriate coordinates in the night sky. In essence, sidereal time is a time scale that is based on the Earth’s rotational speed as measured relative to the fixed stars.
If observed from the identical position, a star that is visible in a specific spot in the sky will also be visible in that same spot on another night at the same sidereal time. This concept is akin to how a sundial can be utilized to determine the position of the Sun based on the time it measures. Similar to how the Sun and Moon appear to rise in the east and set in the west due to the Earth’s rotation, the stars also follow this pattern. Both solar time and sidereal time rely on the Earth’s rotation around its polar axis: solar time corresponds with the movement of the Sun, whereas sidereal time roughly aligns with the distant fixed stars on the celestial sphere.
To be more precise, sidereal time refers to the angle that is measured along the celestial equator, starting from the observer’s meridian and extending to the great circle that intersects the March equinox and both celestial poles. This measurement is typically expressed in terms of hours, minutes, and seconds. In contrast, ordinary time on a regular clock measures a slightly longer period, taking into account not only the Earth’s axial rotation but also its orbit around the Sun.
A sideric day is approximately 86164.0905 seconds (23 hours 56 minutes 4.0905 seconds or 23.9344696 hours).
(The term “seconds” used here aligns with the SI definition and should not be confused with ephemeris seconds.)
The Martha Equinox itself moves slowly towards the west in relation to the fixed stars, completing a full revolution in approximately 25800 years. This is why the term “sidereal day” is a misnomer, as it is actually 0.0084 seconds shorter than a true sidereal day, which is the period of Earth’s rotation in relation to the fixed stars. The true sidereal period, known as the Earth rotation angle (ERA), was previously referred to as the star angle. A 360° increase in ERA signifies a complete rotation of the Earth.
Due to the Earth’s annual revolution around the Sun, sidereal time at any given location and time will increase by approximately four minutes compared to the local civil time every 24 hours. As the year progresses, one additional sidereal “day” will have passed compared to the number of solar days that have passed.
Comparison of stellar time and solar time. In the top left corner: a distant star (small orange star) and the Sun reaching its highest point in the sky on the local meridian (m). In the center: only the distant star reaching its highest point (mean sidereal day). On the right: after a few minutes, the Sun once again reaches the local meridian, completing the solar day.
Solar time is determined by the apparent daily movement of the Sun, and local noon in apparent solar time is the moment when the Sun is directly south or north (depending on the observer’s latitude and the season). An average solar day (what we commonly refer to as a “day”) is the average duration between local solar noons (it is “average” because it slightly varies throughout the year).
The Earth completes one full rotation on its axis in a sidereal day, which is the time it takes for the stars to return to their highest point in the sky. However, due to the Earth’s orbit around the Sun, it also moves a small distance (approximately 1°) during this time. As a result, after a sidereal day has passed, the Earth still needs to rotate a bit more to reach local solar noon when the Sun is at its highest point in the sky. This means that an average solar day is about 4 minutes longer than a sidereal day.
Despite the Earth’s motion along its orbit, the stars are so distant that their apparent direction is hardly affected (although parallax is an exception). Therefore, they return to their highest point in the sky on a sidereal day.
To observe this disparity from a different perspective, it can be observed that the Sun, in comparison to the stars, completes a full orbit around the Earth within a year. Consequently, there exists a deficit of one solar day per year in relation to stellar days. As a result, the duration of a stellar day is approximately 365.24 / 366.24 times that of a 24-hour solar day, equating to approximately 23 h 56 min 4.1 s (86,164.1 s).
Impact of precession
The Earth’s rotation is not a simple rotation around a fixed axis. The Earth’s rotation axis itself undergoes a rotation around a perpendicular axis to the Earth’s orbit, and it takes approximately 25,800 years to complete one full rotation. This phenomenon is known as the precession of the equinoxes. Due to this precession, it seems as though the stars have a more intricate motion around the Earth instead of a straightforward, constant rotation.
Contemporary interpretations
In previous times, the measurement of time relied on observations of celestial bodies using various instruments like photographic zenith tubes and Dungeon’s astrolabe. By aligning the passage of stars with specific lines and synchronizing them with an observatory clock, time was determined. This was done by calculating the direct ascension of stars from a star catalog and determining the time at which they should have crossed the observatory meridian. Corrections were then made to the observatory clock’s time based on these calculations. The sidereal time was established in a way that ensured the March equinox would coincide with the observatory meridian at 0 o’clock local sidereal time.
Since the 1970s, radio astronomical techniques such as very long baseline interferometry (VLBI) and pulsar timing have surpassed optical instruments in terms of accuracy for astrometry. As a result, VLBI has been used to determine UT1, which represents the mean solar time at longitude 0°. This has led to the development of a new measure for the Earth’s rotation angle and the establishment of new definitions for sidereal time. These updates were officially implemented on January 1, 2003.
Angle of Earth’s rotation
The angle of Earth’s rotation ( AER ) measures the Earth’s rotation from its starting point at the celestial equator, known as the Celestial Intermediate Origin (CPT), which remains stationary along the equator. Initially, it was referred to as the non-rotating starting point.
The AER, measured in radians, is linked to UT1 through a straightforward linear polynomial.
θ ( t U ) sign is equal to 2 π ( 0.779 057 273 2640 + 1.002 737 811 911 911 354 48 ⋅ t U ) ) = 2 \ pi (0.779 \, 057 \, 273 \, 2640 + 1.002 \, 737 \, 811 \, 911 \, 354 \, 48 \ cdot t_ ) >
where t U = JD-J2000 – represents the Julian date UT1 (JD) relative to the J2000 epoch (JD 2451545.0). The linear coefficient signifies the rate of Earth’s rotation.
The ERA measurement can be converted to different units. For instance, in the Astronomical Almanac 2017, it is presented in degrees, minutes, and seconds.
As an illustration, in the Astronomical Almanac 2017, the ERA measurement at 0 o’clock on January 1, 2017 UT1 is recorded as 100° 37′ 12.4365″.
Types of ERA measurements

A picture of the face of the other remaining sidereal angle clock at the Royal Observatory in Greenwich, England, captured by Thomas Tompion. The face is adorned with an engraving displaying the name of J. Flemsteed and the year 1691.
Even though ERA is meant to supplant sidereal time, it is still important to retain definitions of sidereal time during periods of transition and when dealing with historical data and records.
Each location on Earth has its own local sidereal time (LST), which is determined by its longitude. Since it is impractical to create tables for every longitude, astronomical tables use Greenwich Stardate Time (GST), which represents the sidereal time at the IERS reference meridian, also known as the Greenwich or prime meridian. There are two types of GST: mean sidereal time and apparent sidereal time. Mean sidereal time is calculated using the mean equator and equinox date, while apparent sidereal time takes into account the effect of astronomical nutation. When the choice of location is combined with the decision to include or exclude astronomical nutation, the abbreviations GMST, LMST, GAST, and LAST are used.
The following relationships exist:
New definitions of Greenwich Mean and apparent sidereal time (since 2003, see Above):
where θ – represents the Earth’s rotation angle, E PREC – denotes the accumulated precession, and E 0 – signifies the origin equation, which encompasses the combined effects of precession and nutation. The procedures for calculating precession and nutation were outlined in Chapter 6 of Urban & Seidelmann.
As an illustration, in the Astronomical Almanac 2017. ERA at 0 h on January 1, 2017 UT1 is recorded as 100° 37 ′ 12.4365″. GAST was 6 h 43 m 20.7 – 109 s. For GMST, the hours and minutes remained the same, but the seconds were 21.1060.

These astronomical clocks display dials that indicate both sidereal and solar time.
If a certain interval I is measured in both mean solar time (UT1) and sidereal time, the numerical value will be higher in sidereal time than in UT1 because sidereal days are shorter than UT1 days. The ratio is:
I mean equals sidereal time UT1 sign equals r prime sign equals 1.002 737 909 350 795 + 5.9006 × 10 – 11 t – 5.9 × 10 – 15 t 2 >>> >>> = r prime = r prime = 1.002 \, 737 \, 909 \, 350 \, 795 + 5.9006 \ times 10 ^ t-5.9 \ times 10 ^ t ^ t ^ >
where t represents the number of Julian centuries that have passed since noon on January 1, 2000, in Earth time.
Sideric days compared to solar days on other planets
Out of the eight planets in our solar system, only Venus and Uranus have a retrograde rotation, which means they revolve in the opposite direction compared to the other planets. This results in the Sun rising in the west for these two planets. On the other hand, the remaining six planets have a direct rotation, meaning they revolve more than once a year in the same direction around the Sun, so the Sun rises in the east.
When it comes to calculating the length of a solar day compared to a sidereal day, the formula differs depending on whether the planet has a direct or retrograde rotation. For planets with a direct rotation, the formula is as follows:
solar day length = sidereal day length / (1 – sidereal day length / orbital period).
However, for planets with a retrograde rotation, the formula changes slightly. In this case, the denominator operator in the formula will be a plus sign instead of a minus sign. This is because the orbit of the planet will revolve around its object in the opposite direction.
If the planet rotates in the forward direction and the sidereal day is precisely equal to the orbital period, the formula above yields an infinitely long solar day (division by zero). This scenario refers to the synchronous rotation of the planet, where one hemisphere is in a state of perpetual daylight, while the other hemisphere experiences perpetual darkness, with a “twilight belt” acting as a dividing line.
All planets in the solar system that are farther from the Sun than Earth have a similar characteristic to Earth. This is because they have multiple revolutions per revolution around the Sun, resulting in a small difference between the duration of stellar days and solar days. The ratio of stellar days to solar days is always greater than or equal to Earth’s ratio of 0.997. However, Mercury and Venus are exceptions to this pattern. The sideric day of Mercury is approximately two-thirds of its orbital period, meaning that its solar day lasts two revolutions around the Sun, which is three times longer than its stellar day. Venus, on the other hand, has a retrograde rotation with sideric days lasting about 243.0 Earth days, which is about 1.08 times its orbital period of 224.7 Earth days. According to the retrograde formula, Venus has solar days of approximately 116.8 Earth days, and its orbital period is approximately 1.9 solar days.
As a rule, the planets’ rotation periods are typically given in stellar units unless otherwise specified.
Related Links
Additional Information
Sources
References
- Astronomical Almanac for 2017. Washington and Taunton: U.S. Government Printing Office and the UK Hydrographic Service. 2016. ISBN.978-0-7077-41666.
- Bakich, Michael E. (2000). Cambridge planetary handbook. Cambridge University Press. ISBN0-521-63280-3.
- “Earth’s Angle of Rotation”. International service of Earth rotation and reference frames. 2013. Accessed March 20, 2018.
- Explanatory appendix to ephemerides. London: Her Majesty’s Stationery Office. 1961.
- “Time and frequency from A to Z, C to Tuck”. National Institute of Standards and Technology.
Related Links
The concept of time measurement is established on a recurring natural phenomenon called the day – a period of time in which the Earth completes one full rotation on its axis. The Earth’s daily rotation, which governs the regular alternation of day and night, the cyclic patterns of various processes on our planet, and the organization of human life and activities, serves as the most practical and convenient basis for measuring time. This natural timekeeping system has been utilized by humanity for centuries. The duration of a day can be determined by observing the positions of celestial bodies in the sky and noting the moments when they reach their highest points.
However, there are practical difficulties associated with determining a twenty-four-hour day, which arise from inconsistent requirements for choosing a time unit. In order to establish the duration of a day in our modern era, three auxiliary points are used: the vernal equinox point, the true Sun’s center, and the mean Sun’s point. Each of these points yields a different duration for the day, so it is necessary to utilize all three units of time – the sidereal day, the true solar day, and the mean solar day. These units of time are respectively referred to as sidereal time, real solar time, and mean solar time. While this multitude of methods for determining the day may complicate computational work, it ensures that time calculations align with human life practices and yields greater accuracy in time measurement via astronomical means.
Measurement of short time intervals is done using the concept of day, while long time intervals are measured using the concept of year. The interval between two successive passages of the true Sun through the point of the vernal equinox ( ^ ) is known as the tropical year. Т ^ =365 d , 2422 s.s.d. (average solar days).
Due to the Earth’s axis precession, the point of the vernal equinox slowly moves towards the Sun, which means that the Sun does not come to the same patch of sky in a tropical year, but rather in a sidereal year (sideric period).
The time it takes for the Earth to complete one full revolution around the Sun, as seen from a fixed point, is called the sidereal year. T=365 d , 2568 s.d.m.
During the last thirty years, there has been a significant improvement in the precision of determining the length of a day through astronomical observations of sight. This improvement amounts to a tenfold increase, bringing the accuracy to 0.001 seconds per day. Additionally, there have been advancements in the accuracy of astronomical pendulum and quartz clocks. Moreover, new types of clocks, such as molecular and atomic clocks, have been developed. These clocks are capable of keeping time with an accuracy of 5-10-8 seconds per day, meeting the intricate demands of certain scientific institutions.
Sidereal Day and Sidereal Time
Sidereal Day and Sidereal Time Explained
The Concept of Sidereal Day and Sidereal Time
Understanding Sidereal Day and Sidereal Time
Exploring Sidereal Day and Sidereal Time
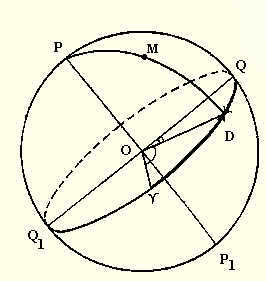
The definition of a sidereal day is based on the apparent rotation of the point of the vernal equinox around the Earth. The start of the day is determined by the point’s upper culmination. The duration of time between two consecutive upper culminations of the vernal equinox on the same meridian is known as a sidereal day.
A sidereal day is divided into 24 sidereal hours, with each sidereal hour further divided into 60 sidereal minutes and each sidereal minute divided into 60 sidereal seconds. The time it takes for the point of the vernal equinox to move from its upper culmination to a specific position, expressed as a fraction of a sidereal day, is called the sidereal hour. It is represented by the Latin letter s.
The hour angle of the vernal equinox point, which is measured in hours, is numerically equal to the sidereal time at a specific moment. The elapsed time since the start of the day is equivalent to the hour angle of the vernal equinox. To determine this, stars with accurately defined coordinates are utilized.
If the hour angle of a star M (Fig.1), then the sidereal hour (arc Q1Q) is the sum of two arcs: arc Q1D (direct ascension of the star) and arc DQ (hour angle of the star). Therefore,
where α represents the direct ascension and t represents the hour angle. When observing the star at the moment of its upper culmination, the hour angle is zero, and thus:
The sidereal time is determined from observations of the culmination of stars using a passing instrument, establishing a connection between the two. Stellar time is commonly used in scientific and engineering works, while solar time was introduced to align with everyday life, as solar days are longer than stellar ones. Solar time is the preferred choice for practical purposes.
THE CURRENT DAYTIME AND THE CURRENT SOLAR TIME
The current solar day is determined by the position of the Sun’s center. The duration between two consecutive instances when the center of the solar disk reaches its lowest point on the same meridian is known as the true solar day.
Unlike starry days, solar days begin during the nighttime, which means that the entire day corresponds to a single calendar date.
The amount of time that has passed since the Sun’s center reached its lowest point to its current position, expressed as a fraction of the true solar day, is referred to as true solar time. It is represented by the letter T. True solar time is measured using the hour angle of the Sun’s center.
The Sun reaches its highest point (at the upper culmination) at 12 hours of the current time, which we define as t = 0. However, the length of a solar day can vary, so we have introduced the concept of the average solar day.
DEFINING THE MEAN SOLAR DAY AND MEAN SOLAR TIME
The irregularity of the current time is caused by the inconsistency of the apparent yearly movement of the Sun along the ecliptic and the inclination of the ecliptic to the plane of the celestial equator. The primary reason for this is the Earth’s movement around the Sun in an elliptical orbit, according to Kepler’s second law, which results in varying speeds. From March 21 to September 23, the Sun moves at a slower pace compared to the period from September 23 to March 21. The second reason is the inclination of the ecliptic. In the diagram, the arcs AB and BC are depicted along the ecliptic near the equinox points.
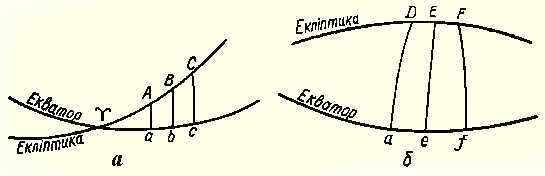
Furthermore, the change in direct ascensions of the Sun can be determined by the projections ab and bc on the equator. It is worth noting that these projections are smaller when compared to the corresponding segments of the ecliptic, namely ab < AB and bc < BC. Interestingly, near the solstice points (part b), the projections of daily segments of the ecliptic onto the equator are actually longer than the segments themselves, indicating that de > DE and ef > EF. Hence, it can be concluded that the position of the Sun on the ecliptic cannot be used as a reliable measure of time due to the inclination of the ecliptic in relation to the equator.
Due to these factors, the length of the present day is longer during the winter season compared to the summer season. December 23rd marks the longest day with a duration of 24 hours, 0 minutes, and 30 seconds, while the shortest day occurs on September 16th with a duration of 23 hours, 59 minutes, and 39 seconds. The maximum difference in duration between these two days is 51 seconds.
The period of time that passes from the lower culmination of the average sun to its position at that specific moment, expressed in units of mean time, is referred to as mean solar time or simply mean time. It is denoted by the symbol Tm.
Observing the average sun directly is not possible, therefore its hour angle cannot be determined through observations. However, by adding η to the equation of time, the mean solar time can be obtained:
The mean solar time at a given meridian is equal to the hour angle of the true sun plus 12 hours, and then adding the equation of time with its corresponding sign.
During a tropical year, the sidereal time will be ahead of the mean time by 24 hours, which is equivalent to a full sidereal day. In other words, throughout a tropical year – consisting of 365.2422 average or true solar days – the Earth will complete 366.2422 rotations around its axis.
CALENDAR.
A system of measuring large intervals of time (chronology) and dividing them into smaller units – years, months, and days – is known as a calendar. When creating calendars, natural time units such as the solar year, synodic month (the time it takes for the moon to go from one new moon to the next, approximately 29 days and 12 hours, but can vary by up to 13 hours due to the moon’s elliptical orbit), and solar day are used as a basis for counting time.
Because these time units are not directly comparable to each other, creating calendars and ensuring their accuracy has been a challenge throughout history. Astronomers have put significant effort into harmonizing these units and resolving discrepancies in the chronology of different cultures.
The existence of three types of calendars, solar, lunar, and luni-solar, is determined by the independence of the basic units of time. In the solar calendar, the length of the tropical year (365.2422 days on average) serves as the basic unit of time. The modern calendar is based on the solar calendar. The monthly calendar, on the other hand, uses the length of a synodic month (29.5 days) as its basis. In this calendar, a year consists of 354 or 355 average solar days, with each month lasting 29.5 days. The luni-solar calendar combines elements of both the solar and lunar calendars.
The numbering of years in calendars starts from a conventional starting point known as an era. There are more than 200 distinct eras that have been identified. The Egyptians counted the eras based on the years when pharaohs ascended to power, while the Chinese counted based on the years when emperors began their rule. The Romans, on the other hand, initially counted years based on the names of consuls and later switched to counting “from the founding of Rome” (which corresponds to 753 BC). In the Christian religion, the years were initially counted “from the creation of the world” (5508 B.C.), but in the 6th century, a new era was adopted, counting from the birth of Christ, which is now widely used in many countries.
The year was composed of 12 months, which were preserved in both European and Russian calendars, and included the months of “July” and “August” in honor of Julius Caesar and Emperor Augustus. The Babylonian seven-day week has endured to this day.
In the Julian calendar, there is a difference of 0.0078 days or 11m 14s between the calendar year and the tropical year; over 128 years, this difference adds up to 1 day. By the end of the 16th century, this difference had already reached 10 days. Italian mathematician Luigi Lilio Garalli proposed a new calendar project, which was approved by Pope Gregory XIII in 1582.
The Gregorian calendar, also known as the “new style,” was introduced as an update to the Julian calendar, which was referred to as the “old style.” A papal bull declared that the day following October 4, 1582, would be recognized as October 15, rather than October 5. This adjustment effectively eliminated a 10-day lag. To prevent future lags, it was agreed upon that leap years would occur every 400 years, rather than every 100 years as in the Julian calendar. Additionally, century years that are not divisible by 4 without a remainder (such as 1700, 1800, 1900) would not be considered leap years. In Soviet Russia, to address a 13-day lag, the day following January 31, 1918, began to be counted as February 14 instead of February 1.
WORLD CALENDAR
As per certain scientists, the Gregorian calendar possesses a few drawbacks: unequal duration of months, varying number of working days each month, and the days of the week change their position in the month from year to year.
In 1954, a novel initiative called the World Calendar was officially adopted by the UN Economic and Social Council. The structure of the World Calendar is as follows: the year comprises of 12 months with identical names; the week remains consistent with seven days; the year is divided into four quarters, each consisting of 91 days; every quarter is composed of three months; the first month has 31 days, while the other two have 30 days each; January 1st always falls on a Sunday; quarters commence on Sunday and conclude on Saturday. The number of working days in each month is 26.
Therefore, the World Calendar divides the year into 4 quarters, each consisting of 364 days, which is one day less than a regular year in the Gregorian calendar. It is suggested that this missing day be designated as a global holiday – the Day of Peace and Friendship among Nations, or New Year’s Day. It falls between December 30 and January 1. In a leap year, an additional non-working day should be inserted into the month – (June 30) – known as Leap Year Day.
The rapid advancement of science and technology in the mid-20th century sparked the emergence of innovative time calculation methods. To achieve this, devices were designed to house autonomous oscillatory processes with exceptional stability. These devices, commonly referred to as frequency standards, rely on counting the number of oscillations that occur within their systems to measure time.
Therefore, in quartz clocks, the quartz plate is oscillated at high frequencies using an alternating electric current, resulting in time calculation with an accuracy of 10 -6 seconds. In atomic clocks, a precise frequency of electromagnetic oscillations emitted by atoms during quantum transitions between energy levels is used, resulting in time accuracy increased to 10 -11 – 10 -12 seconds.
The utilization of these devices has enabled the detection of a slight variation in the Earth’s rotation uniformity, which is caused by:
1. the gravitational influence of the Moon and the Sun (the Earth’s rotation period slowly increases by 0.0014s per 100 years);
2. The Earth experiences a seasonal redistribution of air and water masses, resulting in a fluctuation in the length of a day by ±0.001 s.
3. The Earth’s rotation is occasionally disrupted in an unexpected and irregular manner, leading to variations in the length of a day by ±0.004 s. The exact causes of these disturbances have not yet been determined.
Although the irregularity in the Earth’s rotation is very minor, it still affects the duration of a solar day. Therefore, this unit of time and its derivatives cannot be relied upon as a standard in scientific studies requiring time accuracy of at least 0.000001 s.





