When reading popular science articles about space and astronomy, you may come across the term “ecliptic” which can be somewhat ambiguous. This term is commonly used by both scientists and astrologers to describe the position of objects in the solar system and the orbits of celestial bodies within the system. But what exactly does “ecliptic” mean?
What is the connection between the zodiac and the ecliptic?
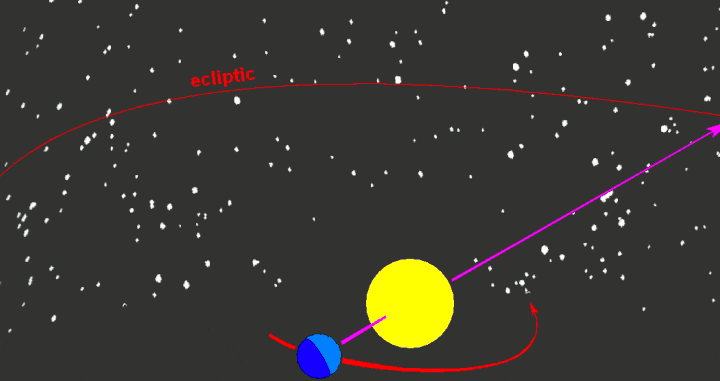
When ancient priests observed the celestial luminaries, they noticed a unique behavior of the Sun. It seemed to move in relation to the stars. By tracking its movement across the sky, they discovered that the Sun always returns to its starting point exactly one year later. Furthermore, the route that it takes is consistent year after year. This path is known as the ecliptic, which is the line along which our main luminary travels throughout the calendar year.
The regions of the stars that the shining Helios, depicted as riding in a golden chariot drawn by golden horses according to the ancient Greeks, passed through were also given attention.


The zodiac is the name given to the path of the Sun as it moves through 12 constellations, and these constellations are known as zodiacal.
If your zodiac sign is Leo, then you won’t be able to see this constellation in the night sky in July, the month of your birth. The Sun is in your constellation during this time, so you would only be able to catch a glimpse of it if you’re fortunate enough to witness a total solar eclipse.
The path of the Sun in the sky
When observing the celestial dome during daylight hours (which can be done not only during a total solar eclipse, but also with a regular telescope), it is apparent that the Sun occupies a specific position within one of the zodiacal constellations. For instance, in November, it is highly likely that the Sun will be found within the boundaries of Scorpio, while in August, it will be situated in Leo. The following day, the Sun’s position will shift slightly to the left, and this pattern will continue daily. After a month (on November 22), the Sun will eventually reach the border of Scorpio and continue its journey into the realm of Sagittarius.

During the month of August, it will be easily observable that the Sun will be situated within the boundaries of the constellation Leo. Similarly, if we were to mark the daily position of the Sun on a celestial chart, after a year we would possess a map displaying a complete ellipse. This particular line is referred to as the ecliptic.
When to Observe
However, to observe their constellations (the zodiac signs under which a person is born), you should do so in the month that is opposite to their date of birth. This is because the ecliptic is the path of the Sun, so if someone is born in August under the sign of Leo, the constellation will be high above the horizon at noon, when the sunlight obscures visibility.
What is the Significance of the Term “Ecliptic Plane”?
Aside from denoting the path of the Sun’s yearly movement, the ecliptic is commonly referred to as a plane. When discussing the location in the cosmos of different celestial bodies and their orbits, you may frequently encounter the phrase “ecliptic plane.” Let’s delve into its meaning.
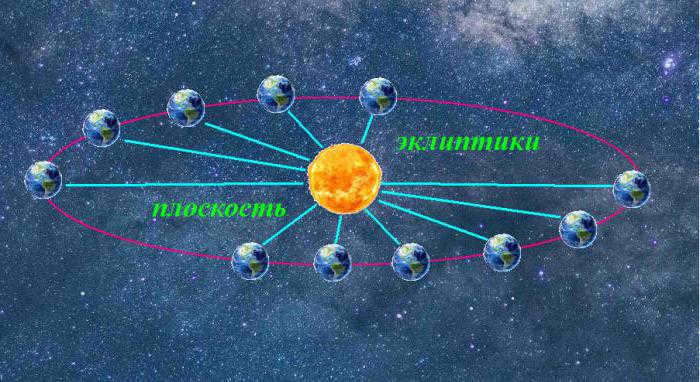
When we consider the orbit of our planet around the Sun and the lines that can be drawn from the Earth to the Sun at different times, we find that they all lie in the same plane known as the ecliptic. The ecliptic can be thought of as an imaginary disk, with the 12 constellations positioned along its sides. If we draw a line perpendicular to the center of the disk, it will intersect with a point on the celestial sphere in the northern hemisphere. This point is located near the constellations of Ursa Major and Ursa Minor, in the constellation of Draco.
As we know, the Earth’s rotation axis is tilted at an angle of 23.44° to the ecliptic axis. This tilt is responsible for the changing seasons on our planet.
And our “neighbors”
Here is a brief overview of what the ecliptic entails. In the field of astronomy, researchers are also intrigued by the movement of other celestial bodies within the solar system. Based on calculations and observations, it has been determined that all of the major planets orbit the sun in a nearly identical plane.
The planet closest to the sun, Mercury, deviates the most from this overall pattern, with an angle of inclination of as much as 7° between its orbital plane and the ecliptic.
Among the outer planets, Saturn’s orbit has the greatest inclination angle (approximately 2.5°), but considering its immense distance from the sun – ten times farther than Earth – this deviation is understandable for the giant of our solar system.
However, the paths of smaller celestial objects such as asteroids, dwarf planets, and comets differ significantly from the ecliptic plane. For instance, Erida, a dwarf planet similar to Pluto, possesses an incredibly elongated orbit.

As it approaches the Sun, this celestial body comes closer to the star than Pluto, which is situated at a distance of 39 astronomical units (an astronomical unit is equivalent to the distance between the Earth and the Sun, which is approximately 150 million kilometers). After this, it then moves away again, ultimately reaching the Kuiper belt. The farthest point of its orbit is nearly 100 astronomical units away. Consequently, the plane of its rotation is slanted at an angle of almost 45 degrees in relation to the ecliptic.
Currently, there are additional cumulative discounts (ranging from 2% to 25%) accessible to 58,742 educational establishments. To ascertain the specific discount applicable to all staff members of your educational institution, kindly sign in to your personal Infoworks account.


Professional training program
The organization of psychologists’ work in the social sphere
We can apply a special discount to your educational institution’s course fee, depending on the number of your colleagues who have already enrolled in Infowork courses.
Currently, a total of 58,742 educational institutions are eligible for additional discounts ranging from 2% to 25%. To find out the specific discount applicable to all employees of your educational institution, please log in to your personal Infoworks account.

Professional development program
Eating disorders in children at various ages
We can apply your educational establishment’s discount to this offer (it depends on the number of your colleagues who have completed Infoworks courses)
Currently, 58,742 educational institutions are eligible for additional discounts (ranging from 2% to 25%). To determine the discount applicable to all staff members of your educational institution, log in to your personal Infoworks account.


Developing Writing Skills in Students through Literature Lessons
Overview of the Presentation by Slide:

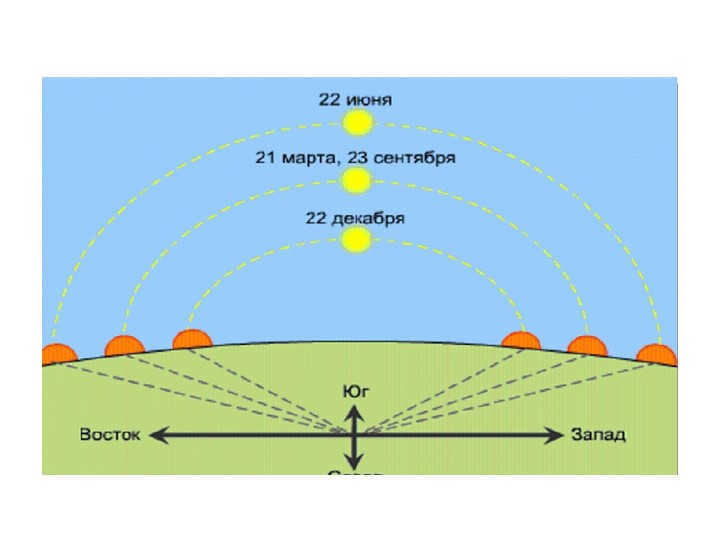
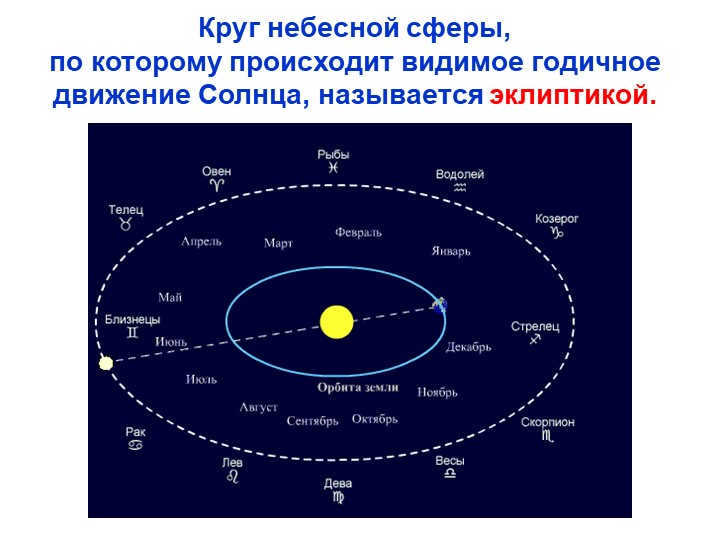
The ecliptic is the path along which the Sun’s visible annual motion takes place, forming a 3-slide circle on the celestial sphere.
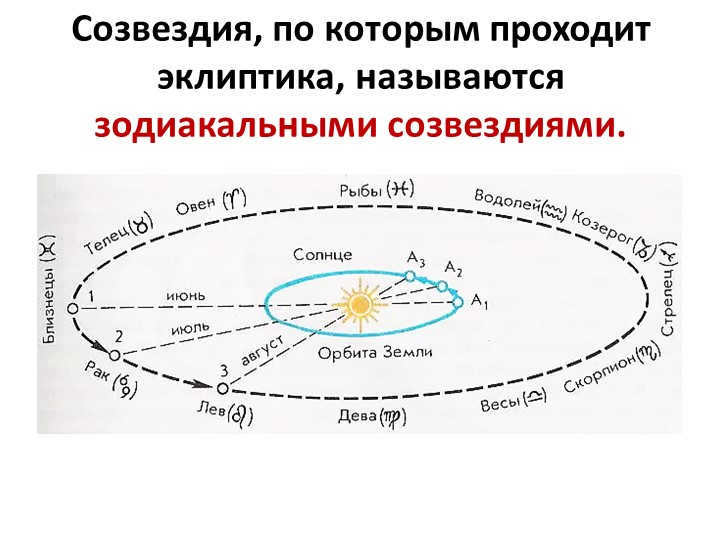

Slide 4: The constellations that the ecliptic passes through are known as zodiacal constellations.
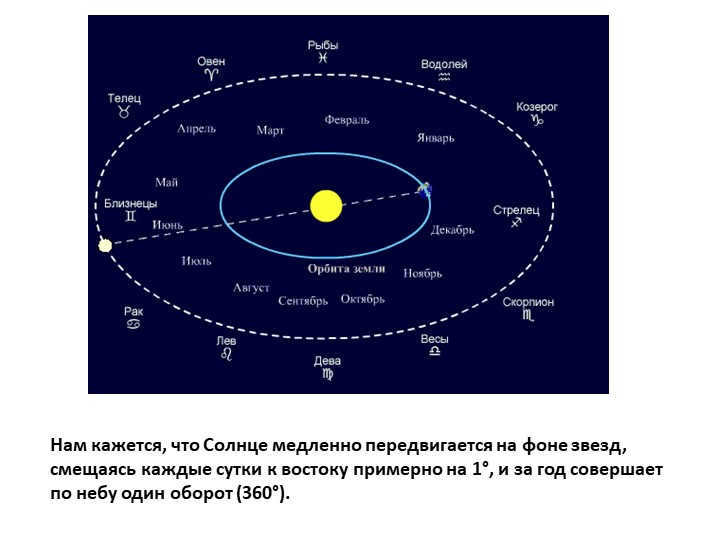

5 slide It appears to us that the Sun moves slowly across the starry background, shifting its position to the east by approximately 1° each day, and completes a full revolution (360°) in the sky over the course of a year.
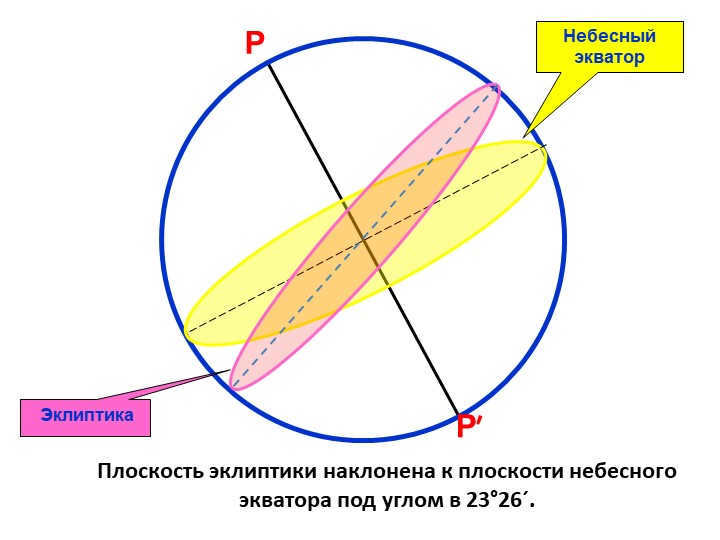
Slide 6 P
P′
Celestial equator
Ecliptic
The angle between the plane of the ecliptic and the plane of the celestial equator is 23°26´.
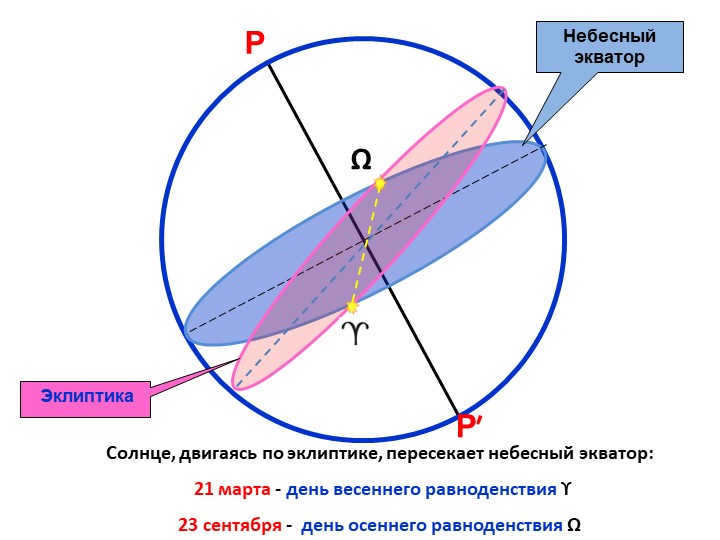

Slide number 7
Point P
The imaginary line called the celestial equator
Another imaginary line called the ecliptic
The Sun, as it moves along the ecliptic, passes over the celestial equator:
On March 21, which is known as the vernal equinox day ϒ
On September 23, which is known as the day of the autumnal equinox Ω
Ω
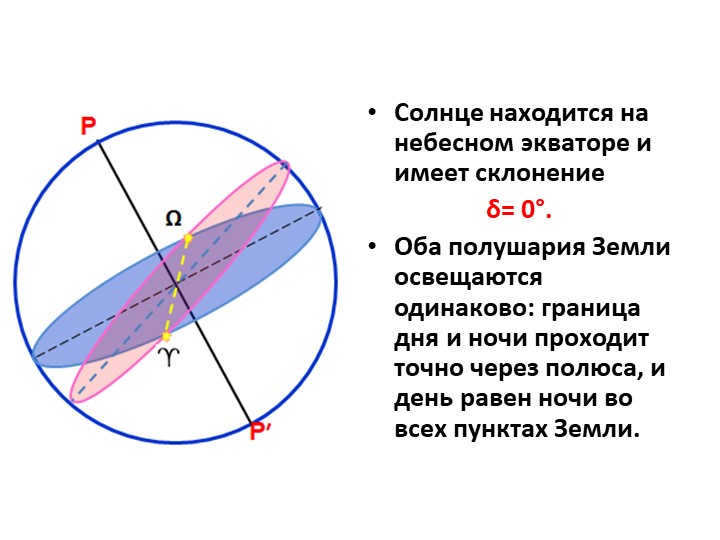

On the eighth slide, the Sun is positioned on the celestial equator with a declination of δ= 0°. This means that both the northern and southern hemispheres of the Earth are equally illuminated. The line dividing day and night passes exactly through the poles, resulting in equal amounts of daylight and darkness at all points on Earth.
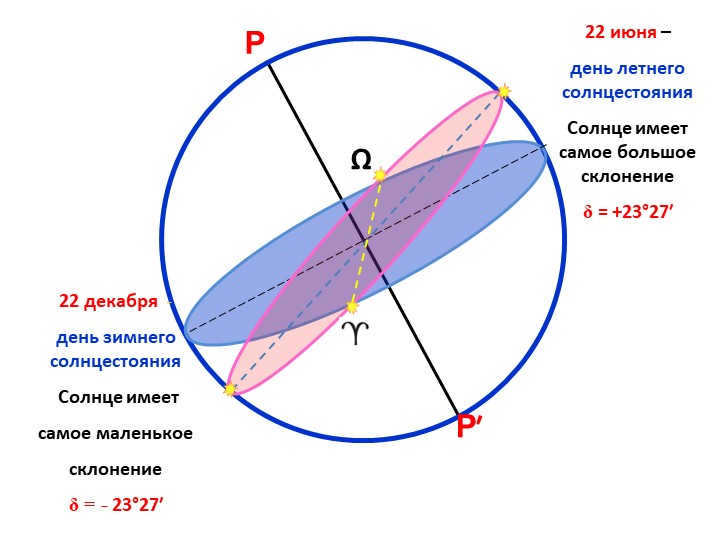
On June 22, we celebrate the summer solstice, which is the day when the Sun reaches its highest point in the sky. This is also the time when the Sun has its greatest declination, which is measured at +23°27′. On the other hand, on December 22, we observe the winter solstice, which is the day when the Sun has its lowest point in the sky. During this time, the Sun has its smallest declination, which is measured at -23°27′.
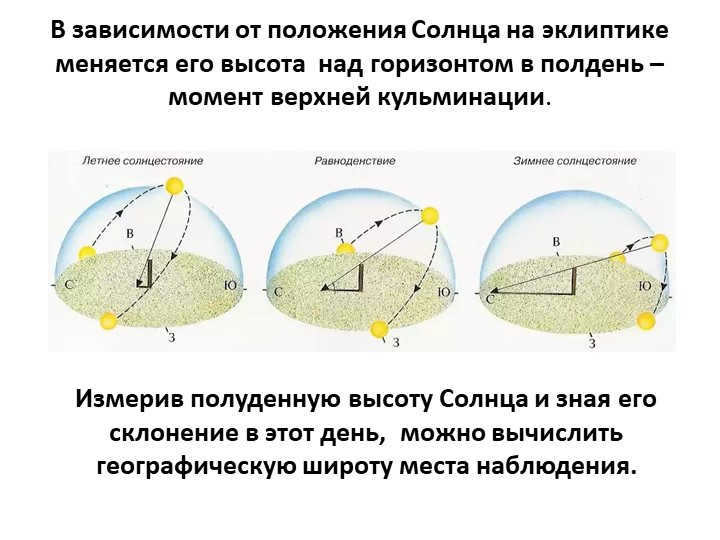
There are 10 different slides available, each representing a different position of the Sun on the ecliptic. The height of the Sun above the horizon at noon, also known as the moment of upper culmination, will vary depending on its position. By measuring this noon height and knowing the declination of the Sun on that particular day, it is possible to calculate the geographic latitude of the observation location.

The altitude of the luminary is represented by the variable h.
The geographic latitude of the observation site is represented by the variable ϕ.
The declination is represented by the variable δ.


Slide 12 To ascertain the Sun’s position, it is imperative to link the calendar date with the map’s center, and the point of convergence of this line with the ecliptic denotes the Sun’s whereabouts.

Slide number 13
a) Calculate the equatorial coordinates of the Sun on August 10th.
b) Find the equatorial coordinates of the Sun on February 25th.

Slide #14
The Sun’s equatorial coordinates are α= 2h28min δ=15°. Find out the specific date and the zodiac sign where the Sun is positioned.

Slide number 15, slide number 3
Find out the exact time when the sun rises and sets and also the duration of the day:
a) September 1
b) June 30.
Discover resources tailored to your lesson by specifying the subject (category), grade level, textbook, and topic:
There are currently 6,330,809 materials in our database
This material is compatible with the UMK
Subject
Additional resources
- Textbook: “Astronomy (basic level)”, authored by Vorontsov-Vel’yaminov B.A. and Straut E.K.
- Topic: Section 12. Laws governing the motion of planets in the solar system
You might find these courses interesting:
- Professional Development Course “Essentials of Local Government and Municipal Services”
- Professional Retraining Course “Tourism Services Organization and Provision”
- Professional Retraining Course “Excursion Management: Introduction to Organizing Excursions”
- Professional Development Course “Foundations of Building Communications in Organizations”
- Advanced Training Course “Marketing in Organizations for Acquiring New Clients”
- Advanced Training Course “Teaching Astronomy in Secondary Schools: Special Considerations”
- Professional Retraining Course “Astronomy: Theory and Methodology of Teaching in Educational Institutions”
- Retraining Program “Effective Secretary Skills with English Language Proficiency”
- Retraining Program “Political Science: Collaborating with Government Authorities, Management Bodies, Non-Governmental and International Organizations”
- Retraining Program “Advanced Techniques for Water Disposal and Wastewater Treatment”
- Retraining Program “Technical Diagnostics and Monitoring of Motor Vehicle’s Technical Condition”
- Advanced Training Program “Global Currency and Credit Relations”
Leave your feedback
If you believe that the content infringes on copyright or should be removed for any other reason, please submit a complaint regarding the material. Remove material
Creator of the content
- Active on the site: 5 years and 9 months
- Subscribers: 0
- Total views: 63211
- Total content: 55
58 minutes ago
42 minutes ago
41 minutes ago
Gift Vouchers
The users who have posted the materials on this website are responsible for resolving any disputes regarding the materials and their content. Nevertheless, the site administration is prepared to offer full assistance in resolving any matters pertaining to the functioning and content of the site. If you happen to come across any unauthorized use of materials on this site, kindly notify the site administration by using the provided feedback form.
All content published on this website is either created by the website’s authors or submitted by users, and is provided for informational purposes only. The copyrights for these materials belong to their respective authors. It is strictly prohibited to copy any part or all of the website’s materials without obtaining written permission from the website administration. The views expressed by the administration may not necessarily align with those of the authors.
From the perspective of Earth’s orbit, the Sun appears to move in relation to the fixed stars, and the ecliptic represents the annual path that the Sun traces on the celestial sphere. This cycle repeats itself in slightly over 365 days.
The ecliptic is a significant plane in the Earth’s orbit around the Sun. When viewed from Earth, the Sun’s movement across the celestial sphere throughout the year creates a path along the ecliptic against the backdrop of stars. The ecliptic serves as a crucial reference plane and forms the basis of the ecliptic coordinate system.
- 1 The apparent motion of the Sun
- 2 Relationship to the celestial equator
- 3 Inclination of the ecliptic
- 4 The plane of the solar system
- 5 The celestial reference plane
- 6 Eclipses
- 7 Equinoxes and solstices
- 8 Constellations
- 9 Astrology
- 10 See Also
- 11 Notes and References
- 12 External links
Movement of the Sun that can be seen
The Sun’s visible path throughout the year is known as the ecliptic.
Because it takes the Earth a full year to orbit around the Sun, the Sun’s apparent position takes one year to complete a full revolution around the ecliptic. With slightly more than 365 days in a year, the Sun moves just under 1° to the east each day. This slight difference in the Sun’s position compared to the stars causes any given location on the Earth’s surface to catch up (and align directly north or south of it) each day about four minutes later than it would if the Earth were not orbiting. As a result, a day on Earth lasts 24 hours, rather than the approximately 23 hours and 56 minutes of sidereal days. However, this is a simplification based on a hypothetical Earth that revolves at a constant speed around the Sun. In reality, the Earth’s orbital velocity varies slightly throughout the year, causing the speed at which the Sun appears to move along the ecliptic to also vary. For instance, the Sun is above the celestial equator for approximately 185 days each year and below it for about 180 days. These changes in orbital velocity contribute to the equation of time.
The link to the celestial equator
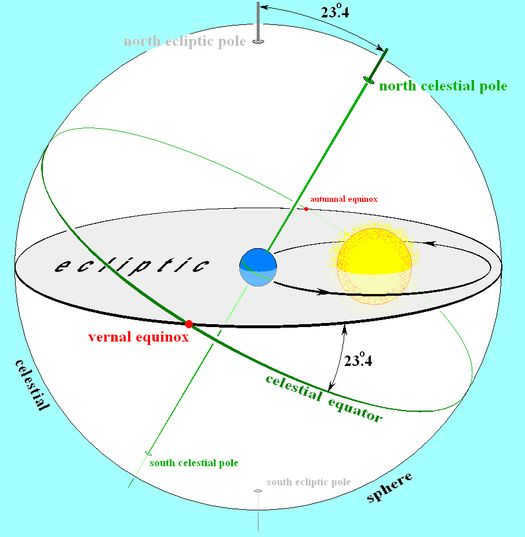
The ecliptic is a reference plane that is formed by projecting the plane of Earth’s orbit in all directions. In the image above, the ecliptic is shown as a gray line projected onto the celestial sphere, along with Earth’s equator and polar axis represented by the green lines. The intersection of the ecliptic plane and the celestial sphere forms a great circle, shown in black, along which the Sun moves as the Earth does. The points where the ecliptic intersects with the equator on the celestial sphere are known as the vernal and autumnal equinoxes, shown in red. These are the times when the Sun appears to cross the celestial equator.
Due to the fact that the Earth’s axis of rotation is not perpendicular to the plane of its orbit, the plane of the Earth’s equator is inclined to the plane of the ecliptic at an angle of approximately 23.4°, which is referred to as the ecliptic tilt. When the equator is projected onto the celestial sphere to create the celestial equator, it intersects with the ecliptic at two specific points known as the equinoxes. These points mark the locations where the sun, in its apparent motion along the ecliptic, crosses the celestial equator. One of these crossings occurs from south to north and is called the vernal equinox, also known as the first point of Aries. At this point, the celestial equator intersects with both the first point of Aries and the ascending node of the ecliptic. The other crossing happens from north to south and is known as the autumnal equinox or descending node.
The position of the Earth’s axis and equator is not static in space, but it revolves around the poles of the ecliptic over a span of approximately 26,000 years. This phenomenon, known as the luni-solar precession, is primarily influenced by the gravitational pull of the Moon and the Sun on the Earth’s equatorial bulge. Similarly, the ecliptic itself is not fixed. Minor gravitational disturbances caused by other celestial bodies in the solar system result in a slight shift in the plane of the Earth’s orbit and, consequently, the ecliptic. This is referred to as the planetary precession. The combined effect of these two movements is referred to as the common precession, which leads to a displacement of the equinox points by about 50 angular seconds (approximately 0.014 degrees) per year.
Once again, this is a simplification. The Moon’s periodic movements and the apparent periodic movements of the Sun (in reality, the Earth in its orbit) cause short-term periodic fluctuations in the Earth’s axis and, therefore, the celestial equator of small magnitude, known as nutation. This introduces a periodic element to the positions of the equinoxes; the positions of the celestial equator and the (vernal) equinox with fully updated precession and nutation are referred to as the the true equator and equinox; positions without nutation are referred to as mean equator and equinox.
Tilt of the ecliptic
The tilt of the ecliptic is the angle at which the Earth’s equator is inclined with respect to the ecliptic, or the Earth’s axis of rotation is inclined to a perpendicular to the ecliptic. Currently, it is approximately 23.4° and is gradually decreasing by 0.013 degrees (47 angular seconds) every hundred years due to the influence of planetary perturbations.
Astronomers determine the angular value of inclination by studying the movement of the Earth and other planets over a long period of time. As observational accuracy and understanding of celestial dynamics improve, astronomers develop new fundamental ephemerides, which are used to derive various astronomical values, including the tilt of the ecliptic.
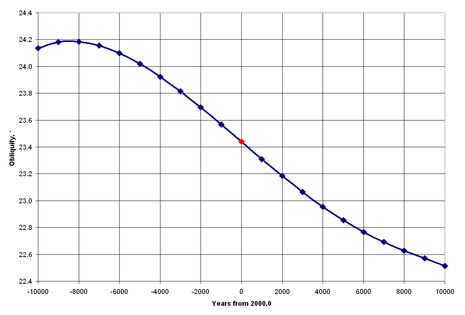
The angle at which the ecliptic is tilted changes slightly over a period of 20,000 years, as shown in the diagram above. It goes from 24.2° to 22.5° during this time. The red dot indicates the year 2000.
Prior to 1983, the slope for any given date was determined using calculations made by Newcomb, who studied the positions of the planets up until around 1895:
ε = 23° 27′08.26″ – 46.845″ T – 0.0059″ T^2 + 0.00181″ T^3
Here, ε represents the slope, and T represents the tropical centuries from B1900.0 to the date being considered.
Since 1984, the main ephemeris used in the Astronomical Almanac has been the DE computer ephemeris series from the Jet Propulsion Laboratory. The angle of inclination based on the DE200 data, which analyzed observations from 1911 to 1979, was calculated:
ε = 23 ° 26′21,45 ″ – 46,815 ″ T – 0,0006 ″ T 2 + 0,00181 ″ T 3
where T represents the Julian ages from J2000.0 and is subject to change.
The JPL ephemerides are continuously updated. The Astronomical Almanac for 2010 provides the following expression:
ε = 23 ° 26′21,406 ″ – 46,836769 ″ T – 0,0001831 ″ T 2 + 0,00200340 ″ T 3 – 0,576 × 10 −6 ″ T 4 – 4,34 × 10 −8 ″ T 5
These equations for the slope angle are designed to provide precise measurements over a relatively short period of time, typically a few centuries. J. Laskar computed an expression of the order T 10 that remains accurate to 0.04 inches / 1,000 years over 10,000 years.
All of these terms refer to the tilt angle for an average position, without considering the equatorial nutation. The actual or instantaneous inclination takes into account nutation.
The orbit of the solar system
 | ||
| The ecliptic plane can be seen from both top and side views, featuring the planets Mercury, Venus, Earth, and Mars. These planets all orbit the Sun in a similar plane to that of the Earth, known as the ecliptic. | In July 2010, four planets were seen aligned along the ecliptic, demonstrating the close alignment of their orbits around the Sun. This photo was taken at sunset in Surakarta, Java, Indonesia, looking west. | |
Most of the large celestial bodies in our Solar System orbit the Sun on a similar plane. This alignment is likely a result of the formation of the solar system from a protoplanetary disk. The current representation of this disk is referred to as the unchanging orbital plane of the solar system. Earth’s orbit, and thus the ecliptic, is tilted slightly more than 1 degree in relation to this orbital plane. Jupiter deviates by a little over half a degree, while the other major planets are within approximately 6 degrees. As a result, most objects in the solar system appear to be very close to the ecliptic when observed from Earth.
The unaltered plane is determined by the aggregate angular momentum of the entire solar system, which is essentially the vector sum of all the orbital and rotational angular momenta of all the celestial bodies in the system; with more than 60% of the total residing in Jupiter’s orbit. This total requires precise knowledge of the position and properties of every object in the system, making it a somewhat uncertain value. Due to the uncertainty surrounding the exact location of the immutable plane, and because the ecliptic is clearly defined by the apparent movement of the Sun, the ecliptic is utilized as the reference plane for the solar system, both for its accuracy and convenience. The only drawback of using the ecliptic instead of a fixed plane is that over geologic time scales, it will shift relative to fixed reference points in the distant celestial background.
The Celestial Reference Plane
The apparent movement of the Sun along the ecliptic (depicted in red) on the inner side of the celestial sphere. The coordinates of the ecliptic are shown in red. The celestial equator (depicted in blue) and its coordinates (also in blue) are tilted in relation to the ecliptic plane, and they seem to waver as the Sun progresses.
The ecliptic is one of the two main planes used as a reference for celestial positions, with the other being the celestial equator. Perpendicular to the ecliptic are the poles of the ecliptic, with the north pole of the ecliptic located north of the equator. Out of the two main planes, the ecliptic is relatively more stationary against the backdrop of the stars, with its motion being approximately 1/100th of the motion of the celestial equator, which is caused by the precession of the planets.
Spherical coordinates, which are also known as ecliptic longitude and latitude or celestial longitude and latitude, are utilized to determine the positions of celestial bodies in relation to the ecliptic on the celestial sphere. Longitude is measured in a positive direction from eastward, ranging from 0° to 360° along the ecliptic, starting from the vernal equinox point, which is the same direction that the Sun appears to move. Latitude is measured perpendicular to the ecliptic, ranging from +90° north to -90° south towards the poles of the ecliptic. The ecliptic itself has a latitude of 0°. In order to fully determine the spherical position, the distance parameter is also necessary. Different units of distance are used depending on the object being measured. Astronomical units are used for objects within the solar system, while Earth radii or kilometers are used for objects near the Earth. Sometimes, the corresponding right rectangular coordinate system is also employed. In this system, the x-axis is directed towards the vernal equinox on the day of the vernal equinox, the y-axis is 90° eastward, and the z-axis points towards the north pole of the ecliptic. An astronomical unit serves as a unit of measurement. The symbols used for representing ecliptic coordinates are somewhat standardized, as shown in the table.
| Summary of symbols for ecliptic coordinates | Rectangular | |||
| Longitude | Latitude | Distance | ||
| Geocentric | λ | β | Δ | |
| Heliocentric | л | б | р | х, у, г |
Ecliptic coordinates are useful for calculating the location of objects in the solar system, as the majority of planets have orbits that are only slightly inclined to the ecliptic. As a result, these objects always appear near the ecliptic in the sky. Due to the minimal movement of the Earth’s orbit and the ecliptic, it serves as a relatively stable frame of reference in relation to the stars.
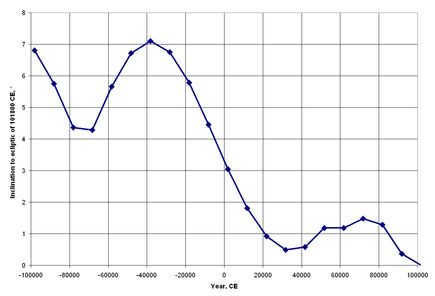
Dzobek (1892) observed that the tilt of the ecliptic changes over a span of 200,000 years. This particular observation is focused on the tilt of the ecliptic in the year 101,800 A.D. It is interesting to note that during this time, the ecliptic only rotates by approximately 7 degrees, while the celestial equator completes multiple cycles around the ecliptic. In comparison, the ecliptic is considered to be a more stable point of reference compared to the celestial equator.
Due to the precessional movement of the equinox point, the positions of celestial objects on the celestial sphere in ecliptic coordinates are constantly changing. To specify a position in ecliptic coordinates, it is necessary to specify a particular equinox, which is the equinox of a specific date known as the epoch. The coordinates refer to the direction of the equinox on that date. For instance, the astronomical almanac provides the heliocentric position of Mars at 0h Earth time on January 4, 2010, as follows: longitude 118° 09'15.8", latitude +-° 43'16.7", true heliocentric distance 1.6302454 AU, mean equinox and ecliptic Date. This determines the mean equinox on January 4, 2010 at 0 h TT as mentioned above, without incorporating nutation.
Eclipses
Due to the Moon’s orbit being inclined by only 5.145° to the ecliptic, and the Sun always being very close to the ecliptic, eclipses consistently take place on or near it. Eclipses do not occur at every conjunction and opposition of the Sun and Moon, but only when the Moon is in close proximity to the ascending or descending node while also being in conjunction (new) or opposition (full). The ecliptic is named as such because it was observed by ancient astronomers that eclipses only happen when the Moon crosses it.
Equinoxes and solstices
| Ecliptic | Equatorial | |
| Longitude | Direct ascent | |
| March equinox | 0 degrees | 0 hours |
| June solstice | 90 degrees | 6 hours |
| September equinox | 180 degrees | 12 hours |
| December solstice | 270 degrees | 18 hours |
The specific points in time when the Sun’s apparent ecliptic longitude is 0°, 90°, 180°, and 270°, taking into account the effects of aberration and nutation, are known as the equinoxes and solstices. However, these dates are not fixed due to perturbations in the Earth’s orbit and calendar anomalies.
Within the star formations
A visual representation of the declination-dependent right ascension of contemporary constellations can be seen in the equirectangular graph. The ecliptic is indicated by a dotted line. Each constellation is assigned a specific color based on its family and the year it was officially established. For a more detailed view, please refer to the provided image.
The constellations that the ecliptic currently intersects with are as follows:
The zodiac is a celestial belt about 20° wide in latitude that is centered on the ecliptic. It is where the Sun, Moon, and planets appear to always move. Traditionally, this region is divided into 12 signs that span 30° longitude each, corresponding to the Sun’s movement in one month. In ancient times, these signs aligned approximately with 12 constellations on either side of the ecliptic. Today, these signs are still occasionally used in modern terminology. The term “The first point of Aries” was originally given to the location where the Sun was during the March equinox in the constellation Aries. However, due to the precession of the equinoxes, it has since shifted to Pisces.
Discover more
Observations and sources
Additional resources
- Ecliptic: the annual path of the Sun in the celestial sphere – Department of Physics, Durham University
- Seasons and ecliptic simulator – University of Nebraska-Lincoln
- MEASURING THE SKY – A concise guide to the celestial sphere – James B. Kahler, University of Illinois
- Seasons of the Earth – US Naval Observatory
- The basics – ecliptic, equator, and coordinate systems – AstrologyClub.Org
- Kinoshita, H.; Aoki, S. (1983). “Definition of the ecliptic”. Celestial Mechanics. 31 (4): 329-338. Bibcode: 1983CeMec..31..329K. DOI: 10.1007/BF01230290. S2CID 122913096. A comparison of the definitions of Leverier, Newcomb, and Standish.
Lesson goals: to clarify how the position of celestial bodies in the sky is determined based on their coordinates; to define the visible yearly movement of the Sun along the ecliptic.
Individual: demonstrate willingness to embrace the history, culture, and customs of diverse societies.
Metacognitive: draw conclusions about the factors influencing the varying length of daylight and nighttime based on a region’s latitude; examine the appearance of the night sky using a dynamic map that factors in the time of year.
It is aimed to define the terms and concepts of “ecliptic” and explain the observed motion of the Sun throughout the year. Additionally, the distinctive characteristics of the Sun’s daily movement at the poles, equator, and middle latitudes of the Earth will be described, along with the reasons for the variation in daylight and nighttime duration at different latitudes throughout the year.
The introduction will present the concepts of “equinox days” and “solstice days” and analyze their astronomical significance. The concept of “ecliptic” will also be introduced. Then, the Sun’s movement throughout the year in relation to the constellations will be examined using an interactive map. Furthermore, the length of day and night will be discussed in relation to the latitude of the location throughout the year.
The lesson’s methodological focus is on offering students a task to determine the height of the luminary during its upper culmination at a specific latitude of the area.
Folk festivals, which have endured over time, correspond to the main dates of the yearly solar cycle – equinoxes and solstices. This raises the question: why isn’t the Sun marked on star charts? Students are led to the conclusion that the Sun’s movement is characterized by its daily and yearly motions. We examine the graphical representation of various daily parallels for different latitudes of observation and different times of the year. As the Earth rotates on its axis, the position of the Sun in relation to the horizon changes throughout the day. Additionally, due to the Earth’s annual orbit around the Sun, our closest luminary moves against the backdrop of stars over the course of the year. We introduce the concept of the ecliptic and analyze its position in relation to other lines and points on the celestial sphere. We also analyze the position of the ecliptic in relation to its projection on the surface of the celestial sphere. To grasp the astronomical significance of the equinox and solstice days, it is recommended to assign students the following tasks in groups.
2. By utilizing a dynamic star map, you can ascertain the precise coordinates of the Sun on June 22 and December 22. These particular days are referred to as the summer and winter solstice due to specific astronomical phenomena.
3. Elaborate on how the duration of both Day and Night fluctuates throughout the year, specifically from March 21 to June 22, June 22 to September 23, September 23 to December 22, and December 22 to March 21.
Visual aids: The use of a moving star map, an educational star atlas, a model of the celestial sphere, a geographical map illustrating the Earth’s hemispheres, and a geographical globe will enhance comprehension.
I. Pupil debriefing [8-10 minutes]
a) Engage students by conducting a survey on the following inquiries at the blackboard:
1. The relationship between the horizontal and equatorial coordinate systems is demonstrated on the prepared blackboard.
2. The motion of celestial bodies throughout the day and at their highest points.
b) Engage in a group discussion about the following questions:
What is the equatorial coordinate system?
What is direct ascent?
What is polar distance?
What is the horizontal coordinate system?
What is zenith distance?
1. On which side of the sky can we find a celestial body with horizontal coordinates: h=28°, A=180°? What is its zenith distance?
2. Identify the three constellations that are currently visible during the daytime.
3. On which side of the sky can we find a star with horizontal coordinates: h=34°, A=90°? What is its zenith distance?
4. Name three bright stars that are visible to us during the daytime.
5. If a star has horizontal coordinates h=53 0 and A=270 o , in which side of the sky is it located? What is its zenith distance?
6. The star is currently at its upper culmination at 21 h 34 m. When will its next lower and upper culmination occur?
(in 12 and 24 hours, precisely at 11 h 58 m and 23 h 56 m).
c ) The task involves working on cards (4 students will do mini-tests).
Plan for presenting new material:
1. Equatorial coordinates (declination and right ascension) and their similarity to geographic coordinates.
2. The apparent motion of the Sun, Moon, and planets against the backdrop of stars. Ecliptic.
Traditional folk festivals that have survived to this day correspond to the main dates of the annual solar cycle – equinoxes and solstices.
So, why isn’t the Sun labeled on star charts? When trying to answer this question, students come to the realization that the Sun’s movement can be described as both diurnal and annual. We examine the graphical representation of diurnal parallels at different latitudes and times of the year. As the Earth rotates throughout the day, the Sun’s position relative to the horizon changes. Additionally, due to the Earth’s annual orbit around the Sun, our closest star appears to move against the backdrop of the stars throughout the year.
The geographic coordinates (φ, λ) uniquely define the position of a point on Earth.
These coordinates were established by Eratosthenes (276-194, Ancient Greece) in 130 BC, referring to the celestial coordinates introduced by Eudoxus of Cnidus (408-355, Ancient Greece).
The position of the luminary in the sky (celestial medium) is also uniquely determined – in the equatorial coordinate system, where the celestial equator is taken as the reference point.
Points E -East, W -West represent the points of intersection of the celestial equator with the points of the horizon. (The points N and S are also mentioned).
All diurnal parallels of celestial luminaries are situated parallel to the celestial equator (their plane is perpendicular to the axis of the world).
Circle of declination is the great circle of the celestial sphere that passes through the poles of the world and the observed luminary (points P, M, P').
Equatorial coordinates:
δ (delta) – the luminary’s declination – the angular distance of the luminary from the plane of the celestial equator (similar to φ ).
α (alpha) – direct ascension – angular distance from the point of vernal equinox ( γ ) along the celestial equator in the opposite direction of the daily rotation of the celestial sphere (during the Earth’s rotation), to the circle of declination (similar to λ , measured from the Greenwich meridian). It is measured in degrees from 0 o to 360 o , but usually in hourly measures.
There are luminaries [Moon, Sun, Planets] that experience rapid changes in their equatorial coordinates. The concept of the ecliptic is introduced.
The ecliptic is the visible annual path of the center of the solar disk on the celestial sphere.
The current inclination of the Earth to the plane of the celestial equator is at an angle of 23 degrees 26 minutes.
The apparent movement of the Sun along the ecliptic is a result of the Earth’s actual motion around the Sun, which was proven in 1728 by J. Bradley with the discovery of annual aberration.
Cosmic phenomena give rise to celestial events.
The Earth rotates on its axis.
Physical phenomena:
1) The eastward deflection of falling bodies;
2) The presence of Coriolis forces.
Manifestations of the Earth’s actual rotation on its axis:
1) The daily rotation of the celestial sphere around the Earth’s axis, moving from east to west;
2) The rising and setting of the celestial bodies;
3) The culmination of the celestial bodies;
4) The alternation of day and night;
5) The diurnal aberration of the celestial bodies;
6) The diurnal parallax of the celestial bodies.
The rotation of the Earth around the Sun.
The group of constellations that the ecliptic passes through are known as zodiacal constellations.
The zodiacal constellations, numbering 12, correspond to the 12 months in a year, with each month associated with the sign of the constellation that the Sun is in during that month. The 13th constellation, Serpentine, is excluded even though the Sun passes through it. “Red Shift 5.1” (Sun’s path).
We work together with the children to complete this table while solving problems using a mobile star map.
1. By using a mobile star map, determine the coordinates of the Sun on October 23 and March 21. Explain why these days are referred to as the vernal and autumnal equinoxes.
2. By utilizing an interactive map of the celestial sphere, ascertain the celestial coordinates of the Sun on both June 22 and December 22. Elucidate the rationale behind labeling these particular days as the summer and winter solstice, respectively.
3. Expound upon the alterations in the duration of Day and Night that occur from March 21 to June 22, from June 22 to September 23, from September 23 to December 22, and from December 22 to March 21.
– The vernal equinox point occurs on March 21 (when day and night are of equal length). The celestial coordinates of the Sun are: α =0 h, δ =0 o
This designation has been retained since the time of Hipparchus, when this point resided in the constellation of Aries. Currently, it lies within the constellation of Pisces, and it will shift to the constellation of Aquarius in the year 2602.
– The summer solstice transpires on June 22 (the day with the longest duration of daylight and the shortest duration of nighttime). The Sun’s celestial coordinates are: α =6 h, =+23 o 26'
The designation of this point has been preserved since the time of Hipparchus, when it was located in the constellation of Gemini. It then moved to the constellation of Cancer, and since 1988 it has been in the constellation of Taurus.
This point marks the day of the fall equinox, which occurs on September 23 and is a day when the length of day and night are equal.
The coordinates of the Sun at this point are α = 12h, δ = 0°.
The designation of the constellation Libra was originally used as a symbol of justice under Emperor Augustus (63 BCE – 14 CE). It is currently located in the constellation of Virgo, but it will move to the constellation of Leo in 2442.
December 22 is the winter solstice, which is the shortest day and longest night of the year. The coordinates of the Sun at this point are α = 18h, δ = -23° 26′.
During the time of Hipparchus, this point was in the constellation of Capricorn. It is now in the constellation of Sagittarius, and it will move to the constellation of Serpentor in 2272.
While the celestial coordinates determine the position of stars in the sky, the view of the starry sky at a specific location and time can change. Observing the culmination of the luminaries at midnight, one can observe different constellations passing near the celestial meridian on different dates. This observation led to the conclusion that the direct ascension of the Sun changes. If we choose a star and fix its position, it will appear in the same place 24 hours later, except it will be 23 hours and 56 minutes later. This is because a day measured relative to distant stars, known as a sidereal day, is slightly shorter than a 24-hour day. The other 4 minutes are accounted for by the Earth’s motion around the Sun, causing a shift of 1° per day against the background of the stars. This shift requires 4 additional minutes for the Earth to “catch up” with the star. As a result, each subsequent night, the stars move slightly to the west and rise 4 minutes earlier. Over the course of a year, the stars will shift a full 24 hours, and the starry sky will repeat itself. This is due to the Earth’s revolution around the Sun, causing the entire celestial sphere to make one revolution in a year.
Therefore, the Earth completes a single rotation around its axis in a duration of 23 hours and 56 minutes. A solar day, which lasts 24 hours, represents the average time it takes for the Earth to complete one revolution in relation to the Sun’s center.
III. Reinforcement of the material (10 min.)
1. Engage in the PCCP (during the presentation of new information)
a) Locate the celestial equator, ecliptic, equatorial coordinates, equinox, and solstice points.
b) Determine the coordinates of the stars: Capella (α Ascendant), Deneb (α Swan) (Capella – α=5 h 17 m , δ=46 o; Deneb – α=20 h 41 m , δ=45 o 17′).
c) Find stars based on given coordinates: (α=14.2 h, δ=20 o) – Arcturus
d) Identify the current location of the Sun, including its position within constellations during the autumn season. (Currently, in the fourth week of September, it is located in Virgo. In early September, it was in Leo and it will move into Libra and Scorpio by November.)
(a) The star reaches its highest point at 2:15 pm. When will it reach its next highest and lowest points? (in 11 hours 58 minutes and 23 hours 56 minutes, that is at 2 hours 13 minutes and 14 hours 11 minutes).
b) A satellite traveled across the sky from the starting point with coordinates (α=18 hours 15 minutes, δ=36 degrees) to the point with coordinates (α=22 hours 45 minutes, δ=36 degrees). Which constellations did the satellite pass through?
a) Why are equatorial coordinates necessary?
b) What is significant about the days of equinoxes and solstices?
c) At what angle is the plane of the Earth’s equator inclined to the ecliptic plane?
d) Can we consider the annual movement of the Sun along the ecliptic as evidence of the Earth’s orbit around the Sun?
Task. Use a moving map of the starry sky to determine the equatorial coordinates of the Sun on October 18. Find the time of its sunrise and sunset on this date.
Homework assignment: §6. Assignment 5(1,2,4). Assignment6,7.
1. The astronomical concept of “twilight”.
2. The Earth’s four “belts” of light and darkness.
3. Astronomical and calendar seasons. 3.
4. “White Nights” – the beauty of astronomy in literature.
5. The bending of light in Earth’s atmosphere.
1. Calculate the latitude of the observation location where Sirius is at an altitude of h = 64° 13′ below the zenith. Write the degrees and minutes with a comma, for example, 38.47 is 38 o 47′.
Write the number: _______________
2. Explain the conditions for observing stars at 55° north latitude.
Match the answers to the choices:
3) Rising and setting stars.
3. Enumerate the requirements for observing the celestial bodies.
Indicate the accuracy of the following statements:
__ If δ ≥ 90° – φ, then a star in the Northern Hemisphere is not visible above the horizon.
__ If δ > 90° – φ, then the star is both rising and setting.
__ If δ ≤ 90° – φ, then a star in the Northern Hemisphere is not rising.
__ If δ ≤ 90° – φ, then the star in the Northern Hemisphere is not descending.
4. By measuring the declination of the celestial body and its altitude at the moments of culmination, it is easy to determine the latitude on which the observer is located. (Insert the missing words).
ROEO CHGEIGFKJUSRSHIAUTU _____________________________
Provide the corresponding options for all 4 answer choices:
__ All stars with a positive declination,
Stars that remain at the same altitude throughout the day can be seen at
__ An observer can see all stars that rise and set during the day.
__ The phenomenon of a celestial body crossing the eastern part of the true horizon.
__ The phenomenon of a celestial body crossing the western part of the true horizon.
1 Find out the geographical latitude of the observation site if Altair passes through the zenith.
Separate the degree and minute values with a comma, for example, 38.47 is 38 o 47′.
Write down the number: _______________
2. The daily paths of the celestial bodies on the celestial sphere are
State whether the answer choices are true or false:
__ circles whose planes are parallel to the celestial equator.
__ ellipses whose planes are perpendicular to the celestial equator.
___ ellipses with planes parallel to the celestial equator.
___ circles with planes perpendicular to the celestial equator.
3. What is the correlation between the elevation of the celestial pole and the geographical latitude of the observation location?
Choose one of the 5 answer options:
1) The elevation of the celestial pole is 180 degrees greater than the geographical latitude.
2) The altitude of the celestial pole is 90 degrees greater than the geographical latitude.
3) The altitude of the celestial pole is 180 degrees less than the geographical latitude.
4) The altitude of the celestial pole is 90 degrees less than the geographical latitude.
4. The specific moment in time when the celestial body in diurnal motion reaches its highest point above the horizon, closest to the zenith.
Choose one of the 4 answer choices:
5. What is the term for the location on Earth where the axis of rotation intersects with the plumb line, and the celestial equator aligns with the horizon?
2) (5 b.) Correct answers: 3; 3; 2;
3) (4 b.) Correct answers: Yes; Yes; No; No; Yes; No;
4) (3 b.) Correct answers: "GEOGRAPHIC LATITUDE".
5) (5 b.) Correct answers: 3; 5; 1; 2;
2) (4 b.) Correct answers: Yes; No; No; No; No;
1. On which side of the sky can a celestial object be found if its horizontal coordinates are h=28° and A=180°? What is its zenith distance?
2. Can you name three constellations that can be seen during daylight?
1. On which side of the sky can a star be located if its horizontal coordinates are h=34° and A=90°? What is its zenith distance?
2. Can you identify three bright stars that are visible during the day?
1. If the star’s horizontal coordinates are h=53 0 and A=270 o, which side of the sky is it located on? What is its zenith distance?
2. The star is currently at its upper culmination at 21 h 34 m. When will it reach its next lower and upper culmination?
(after 12 and 24 hours, more precisely after 11 hours 58 m and 23 hours 56 m)
Textbooks and teaching aids
1. Vorontsov-Vel’yaminov B. A. E.K. Strout. Astronomy. Basic level. 11th grade. Moscow: Drofa, 2018.
2. Kunash M.A. Astronomy. 11 grade. Methodical manual for the textbook B.A.Vorontsov-Veliaminov, E.K.Straut “Astronomy. Basic level. Grade 11” M.: Drofa, 2018.
3. Vorontsov-Vel’yaminov B. A. Collection of tasks on astronomy. – Moscow: Prosveshchenie, 1980.
4. Astronomy/Dagaev M. M., Demin V. G. G., Klimishin I. A., Charugin V. M. – M.: Prosveshchenie, 1983.
5. Dagaev M. M. Book for studying astronomy. – M.: Prosveshchenie, 1980.
About the subject: methodical developments, presentations, and notes

An overview of a public class on the topic of “The Decembrists’ Movement”.
Lesson objectives: 1. To ascertain the factors that led to the Decembrist movement, the objectives of the participants in secret societies, and the importance of the uprising on Senate Square; 2. To foster.
The aim of the lesson is to introduce students to the origins of the Hussite movement in Bohemia, the progression of the Hussite Wars, their ultimate result, and their importance in history.

Lesson Plan – Lesson Topic: “Vast Sky” by R. Rozhdestvensky
This lesson focuses on the poem “Vast Sky” by R. Rozhdestvensky and includes a reading activity led by Z.F.Malysheva. The lesson is designed for 5th grade students in special educational institutions and follows a technological map format.

Lesson plan for the topic “Volunteer Movement”
Objective: Developing essential English communication skills and abilities among Suvorov students. The lesson was designed to meet the requirements of the Federal State Educational Standards.

7th Grade Integrated Lesson Plan: “Mechanical Motion”
This integrated lesson plan offers a unique approach to teaching both physics and English. By studying physics, students will gain an understanding of Newton’s laws and develop their knowledge in the field.

Lesson plan for 5th grade physical education (FSES) on the subject of “Developing skills in stationary and moving ball passing”.
In this article, we will discuss various strategies for enhancing and fortifying students’ physical abilities by means of basketball classes, focusing on the acquisition of ball handling techniques.

A plan for an interactive lesson on “Rules of the Road”.
A lesson plan designed for students in their first or second year of secondary law studies.
From the perspective of Earth, the Sun appears to move across the sky against the backdrop of stars throughout the year. However, it is actually the Earth that is moving around the Sun. Both movements occur in the same direction, and after a little over 365 days, the orbit is completed.
In a more specific sense, the ecliptic refers to the apparent path of the Sun as seen from Earth against the backdrop of fixed stars. In essence, the ecliptic is a plane (known as the ecliptic plane) where the Sun and all the planets (with a few degrees of deviation) are situated. On the celestial sphere, the ecliptic is represented as a great circle.
The observation of the ecliptic occurred in ancient times. Instead of during the day, it was observed at dusk when the position of the sun could be seen against the backdrop of the stars and constellations. The sun passes through a fixed sequence of 12 constellations (according to the previous classification) or 13 constellations (according to the current classification) annually. The zodiac, which is a zone of about 20 degrees width along the ecliptic, is where the orbits of the Moon and all planets also pass through. These constellations along the zodiac are known as the signs of the zodiac.
The two points where the celestial sphere intersects with a straight line perpendicular to the ecliptic plane and passing through the center of the Earth are known as the north and south poles of the ecliptic.
The ecliptic is the representation of the Sun’s position on the celestial sphere, as seen from Earth. It is the projection of the Sun’s path onto the celestial sphere. The angle ε, known as the tilt of the ecliptic, is the angle between the ecliptic plane and the equatorial plane.

The equatorial plane is a plane that is different from the ecliptic plane. It is formed when the Earth’s equator expands freely in all directions due to its daily rotation. The point where this plane intersects with the celestial sphere is known as the celestial equator. Unlike the ecliptic plane, which is determined by the Earth’s annual orbit around the Sun, the equatorial plane is determined by the Earth’s daily rotation on its own axis. The angle at which these two planes are tilted towards each other is referred to as the ecliptic tilt.
Etymology
The term “ecliptica” (Latin “Linea Ecliptica”, “Linea Ecliptica” Eclipse) is derived from the Greek phrase ἐκλειπτική [τροχιά] ekleiptikē [Trochia], meaning “to conceal [orbit]” (before ἔκλειψις ékleipsis, abandonment of the moon, absence, (sun)-darkness). It is also related to the word “eclipse” as a covering (eclipse). The word ékleipsis, meaning absence, disappearance, eclipse, expresses the concept that the earth, moon, and sun align on a straight line in the ecliptic plane during a solar or lunar eclipse.
Introduction
The sun follows two distinct paths in the sky:
- Due to the Earth’s rotation on its axis, the sun appears to move across the sky from east to west during the day. This creates an apparent daily motion of the sun relative to the horizon, known as the diurnal arc.
- Additionally, as a result of the Earth’s yearly orbit around the sun, the position of the sun in relation to the fixed starry sky gradually changes. Over the course of a year, it passes through twelve constellations along the ecliptic.
The ecliptic is the annual path of the Sun’s apparent movement relative to the fixed starry sky. You can track this path by noting the position of the sun on the globe over the course of a year. The location on Earth from which you make these observations doesn’t matter much because the Sun is significantly distant compared to the Earth’s size, resulting in a relatively consistent angle of observation.
Ecliptic plane
The plane of the ecliptic is a fundamental reference plane for astronomical observations. It is the plane that contains Earth’s orbit around the Sun. This plane is inclined at an angle of about 23.5 degrees to Earth’s equator, and it is this tilt that gives us our seasons. The ecliptic plane is used to define the positions of celestial objects in the sky, as well as for calculating the paths of comets, asteroids, and other objects in our solar system.

The planets revolve around the Sun in a similar orbit. This phenomenon can be explained by the formation of a planetary system from a disk of gas and dust.
In the heliocentric model, the Earth and other planets follow a path called the ecliptic, which is the plane of the Sun’s apparent motion in the sky.
Upon closer examination, it is not the Earth that orbits the Sun, but rather the center of mass of the Earth and the Moon (which is located inside the Earth, but not at its center). Therefore, from a geocentric perspective, the Sun does not move exactly along the ecliptic across the sky. Instead, its latitude along the ecliptic varies by about ± 0.7″ on a monthly basis, with an average value of 0.
The ecliptic plane serves as a reference plane for positioning objects within the solar system (Ecliptic coordinate system).
The Earth’s axis, instead of being perpendicular to the plane of the Earth’s orbit, is angled at 66.56347°. This means that the Earth’s equator or celestial equator is tilted at an angle of 23.43653° (23° 26′ 11″51′) to the plane of the ecliptic, a phenomenon known as the inclination of the ecliptic. In Latin, this inclination is called “Obliquus”.
The term “the tilt of the Earth” refers to this angle in relation to the ecliptic plane, within the ecliptic coordinate system.
The difference in the tilt of the ecliptic is a crucial factor in astronomy and geodesy when it comes to establishing coordinate systems and performing calculations. It is commonly represented by the Greek letter ε (epsilon). Due to the gravitational impact of celestial bodies within the solar system, this tilt changes over time. It ranges from 21° 55' to 24° 18', a difference of over 2°, over a span of approximately 40,000 years.
Seasons
While the Earth continues to orbit the Sun, its axis remains relatively fixed in space, with only minor long-term changes. This means that from March to September, the northern hemisphere is slightly tilted towards the Sun, while from September to March, it is the southern hemisphere that is more tilted. These changes in tilt result in variations in the angle at which the Sun’s rays hit the Earth and the length of daylight, which in turn create the different seasons throughout the year.
Astrological Signs

In ancient star charts, such as the Uranography by Hevelius (1690), the constellations in the northern sky and the twelve 30° sections of the zodiac are depicted. These charts use the “stable” pole of the ecliptic as the central point.
Precession
Precession is a phenomenon in which the axis of rotation of a spinning object gradually changes direction. This can occur in a variety of contexts, including celestial bodies such as planets, stars, and even spinning tops. The cause of precession is typically a torque applied to the spinning object, which causes the axis of rotation to shift. The most well-known example of precession is the precession of the Earth’s axis, which causes the position of the North Pole to change over time. Precession has been studied and documented by astronomers and physicists for centuries, and it continues to be an important area of research in these fields.
Constellation Ursa Major with Polaris is depicted at the end of its tail next to the circle on which the north celestial pole in the Platonic year revolves around the northern pole of the ecliptic (Uranographia by Hevelius, 1690)
During the Platonic year, which lasts about 26000 years, two ecliptic poles serve as the centers of two circles on which the northern and southern celestial poles move due to the precession of the Earth’s axis.
Due to the earth’s ellipsoid shape, the gravitational forces exerted by the moon and sun create a torque that attempts to align the tilted axis of the earth, thereby altering its orientation. Similar to an inclined vertex, the earth’s axis, which extends to the two celestial poles, undergoes a precession motion and revolves around the poles of the ecliptic on a conical surface with an angle of 2ε. These poles of the ecliptic are depicted on more precise star charts – the northern pole is located in the constellation Draco, precisely at a right ascension of 18 hours (with a declination of 90° – ε, currently around 66° 34′), while the southern pole is in the constellation Dorado, positioned at 6 o’clock.
“Top of the Earth” moves at a slow pace because of the immense mass of the Earth, which is approximately 6-10^24 kg. It takes about 25,700-25,800 years for the Earth’s axis to complete a precession cycle, also known as the Platonic year. The current North Star, Polaris, is only temporarily serving in this role.
The celestial north pole follows a path (shown in orange) around the ecliptic pole (shown in red), which takes about 26,000 years to complete. Around the year 2000, it is located near Polaris. Additionally, the bright star seen below is Vega.
Similarly, the southern celestial pole also follows a path around the pole of the ecliptic, which takes about 26,000 years to complete. Around the year 2000, it is close to the South Pole. The extremely bright star seen in the picture is Canopus.
Background
In the past, astronomers had limited knowledge about the celestial bodies and their movements. They were able to observe the Moon’s orbit in the night sky and track the rising and setting of the brightest stars. However, they had not yet discovered the connection between the ecliptic and the apparent orbit of the Sun. Nevertheless, the occurrence of solar and lunar eclipses, which are dependent on the Moon’s position in relation to the ecliptic orbit, inspired the development of various myths. For example, early Chinese astronomy developed a myth about a celestial dragon that devours the moon and the sun, while early Indian astronomy spoke of a demon named Rahu who devoured both stars. These myths eventually led to the identification of specific points in the lunar orbit known as dragon points.
However, ancient Egyptian beliefs regarding the celestial realm were intertwined with their mythological traditions, particularly in relation to the celestial bodies, and were based on their careful observation. The concept of the zodiac, which originated in Mesopotamia, was not adopted until the Hellenistic era. The observation of the stars had already commenced in the ancient Babylonian Empire. However, it was during the Assyrian period (1200-630 BC) that ideas closely related to the ecliptic were developed. The MUL-apin texts, a collection of astronomical records, contain the notion of four seasons, as the sun traverses different constellations and moves along a curved path. During the Persian period (539-326 BC), the division of the ecliptic into the 12 signs of the zodiac became established. This progression is evidenced by numerous Babylonian cuneiform tablets, which document astronomical measurements using Babylonian numerals and provide details about the positions associated with the ecliptic.
In ancient times, the Europeans introduced the division of the ecliptic into twelve equal sectors. However, in India, they traditionally divided the lunar orbit into 27 nakshatras (stations of the Moon) based on the groups of stars along the ecliptic. This number corresponds to the approximate duration of a sideric month (27.32 days), during which the Moon typically rises in a different house each day. The system, which has been passed down since the Yajurveda era (around 1000 B.C.), is widely used in Asia. There is ongoing debate about whether the system developed by Chinese astronomers predates it.
Even before the rise of Islam, the Arab world was familiar with the concept of nakshatras, which later evolved into a system known as the Manazil al-Qamar, or lunar houses. This system divided the ecliptic into 28 lunar houses based on groups of stars. However, as powerful caliphates emerged, so too did educational centers and libraries dedicated to the translation of Greek astronomical texts into Arabic. One particularly influential text was Claudius Ptolemy’s Almagest, which was translated in the late 8th century. Arab astronomers not only translated these works, but also expanded upon them. For instance, they made improvements to Ptolemy’s values regarding the asymmetry of the ecliptic, as demonstrated by the work of Al-Battani in the 9th century.