It is common knowledge that throughout history, individuals have relied on star coordinates to navigate their lives. Navigators, for instance, used celestial bodies to orient themselves in space, and this knowledge extended beyond them. Agricultural activities were timed in accordance with the position of the stars, and much more. In fact, calendars were developed that essentially provided advice and guidance to people on when and what to do based on the position of the stars.
Types of Star Coordinates and Systems
Throughout history, humans have gradually organized information about stars, leading to the development of various systems for categorizing them in astronomy.
The Horizontal or Topocentric System
In simple terms, this system represents the position of stars relative to the Earth’s horizon. It involves two key stellar coordinates:
1) Altitude above the horizon: This refers to the height of a star above the horizon and is measured in degrees. Understanding the significance of different positions is crucial:
– The highest point, known as the zenith, is represented by +90 degrees.
– If a star lies on the horizon line, its altitude is zero.
– The position directly opposite the zenith is called the nadir, represented by -90 degrees. In this position, the star appears to be directly beneath the observer.
2) Azimuth – The measurement of the angle between two lines on the horizon, one pointing towards the object and the other pointing north.
The horizontal system is commonly known as topocentric due to the fact that these stellar coordinates are linked to a particular location on the Earth’s surface.
It should be noted that both values are constantly changing, so determining the coordinates of stars on a star map is quite problematic.
The first equatorial system
Unlike the previous system, the equatorial coordinates of stars are associated not only with the Earth’s surface but also with the celestial sphere. In addition, the celestial equator serves as the main plane. There are also two major stellar coordinates:
1) The declination, which remains relatively constant, can be determined by measuring the angle between the equatorial plane and a line pointing towards the star.
Interestingly, the arc of the declination circle is measured from 0 to +90 degrees towards the North Pole, and from 0 to -90 degrees towards the South Pole.
2) The angle of time between the celestial meridian and a line that points to the celestial body. This coordinate is dependent on the observer’s location and time. However, the hour angle is measured in the direction of the sky’s daily rotation, ranging from 0 to 360 degrees (westward).
Celestial meridian – A circle on the celestial sphere that passes through the zenith, the celestial pole, the south pole, and the nadir.
Nevertheless, this system is not entirely convenient for determining the positions of stars.
The alternative equatorial system
In this particular system, it is utilized to establish the precise celestial coordinates of stars. Similar to the original system, the fundamental plane is the equatorial plane of the sky. However, one of its coordinates aligns with the first system, namely declination.
The distinction lies in the second coordinate of the luminary’s position. Referred to as right ascension, it represents the angle between two intersecting lines on the celestial equator, which meet at the intersection of this equator with the axis of the world.
Therefore, it follows that the initial line stretches to the point of the spring equinox, while the second line stretches to the point where the star is projected onto the sky’s equator.
The celestial longitude, or rather its angle, is measured along the equatorial arc. And it is always measured in a clockwise direction. Interestingly, the unit of measurement can be degrees, minutes, or hours. One hour is equivalent to 15 degrees.
By the way, in the second system, the axes remain fixed for distant celestial objects.
The axis of the world is a straight line that corresponds to the Earth’s geographic axis and passes through the celestial dome at the North and South Poles of the world.
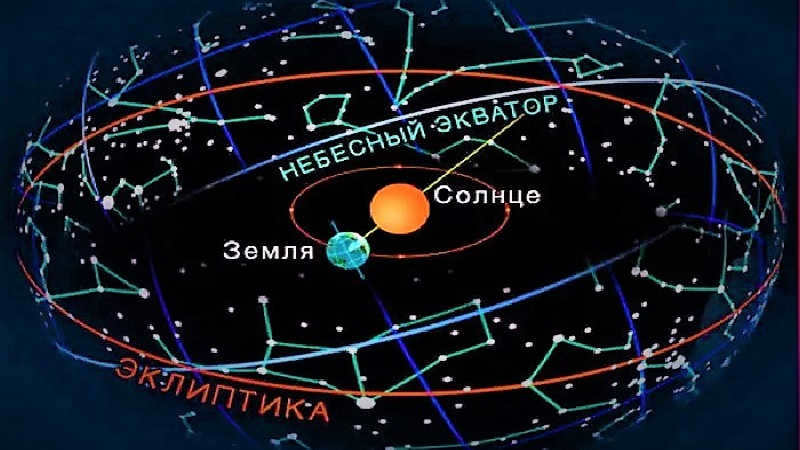
The ecliptic system
To determine the coordinates of stars in close proximity to Earth on a star map of the sky, the ecliptic system is employed. The key distinction of this method lies in taking the ecliptic plane as the principal plane, which is the path traversed by Earth’s orbit as it revolves around the Sun.
Stellar coordinates in the ecliptic system encompass:
- Ecliptic latitude – the arc of the latitude circle that originates from the ecliptic and extends to the celestial body.
- Ecliptic longitude – the arc from the point of the vernal equinox to the latitude circle of the stars.
In addition to providing the means to ascertain the position of nearby celestial entities, the utilization of this approach also reveals Earth’s location in relation to other astronomical objects.
The Galactic Coordinate System
In reality, the galactic coordinate system is essential for conducting searches and calculations on a larger scale. As none of the aforementioned methods are applicable for determining the position of distant celestial objects, such as galaxies and nebulae.
In this system, the fundamental reference is the plane of our own Milky Way galaxy. The coordinates used are galactic latitude and longitude.

Equatorial coordinates of various stars
It is crucial to note the values of declination and right ascension for the stars. To illustrate, let’s examine a few different celestial bodies.
| Star | Declination (degrees/minute) | Right Ascension (h/min) |
| Altair | +8/44 | 19/48,3 |
| Arcturus | +19/27 | 14/13,4 |
| Vega | +38/44 | 18/35,2 |
| Rigel | -8/15 | 5/12,1 |
So, to locate the stars, you can use a search based on their coordinates. These coordinates indicate the position of the stars on the celestial sphere. Furthermore, coordinates or a specific system are used to determine their exact location.
As you can observe, stellar coordinates are represented by two magnitudes or arcs that indicate the star’s position on the celestial sphere. Moreover, there are notable differences between each coordinate system. Firstly, the choice of the central plane varies. Secondly, the difference lies in the selection of the origin.
It is important to note that the sky map does not provide information about the distance to the stars. It simply indicates their location. This is why it is convenient to refer to the neighboring luminous celestial bodies when navigating through the terrain. In fact, people have been doing this for many years.

Scientists have discovered that everything in the universe is in constant motion while studying space and the sky.
The origins of the coordinate system can be traced back to ancient times.
The development of the coordinate system was primarily driven by the need for navigation and a better understanding of the celestial landscape.

To determine the position and motion of celestial objects, humanity has developed a comprehensive system of methods and techniques. Additionally, unique numerical and symbolic designations have been devised.
Indeed, there are multiple systems that establish the coordinates of celestial objects. They primarily differ in the selection of the primary plane and the reference point.
As we observe the sky as a sphere from Earth, the astronomical coordinates are also spherical. Furthermore, they represent arcs of circles on the sphere. It is important to note that they are measured in degrees, sometimes in hours.
Coordinate System in the Horizontal Plane
The primary plane utilized in this system is the mathematical horizon, with the zenith and nadir serving as the poles. The horizontal coordinate system is employed for observations conducted from our planet, Earth. This can be done either through unaided vision or with the assistance of a telescope, enabling the observation of stars and the tracking of celestial objects in the sky, albeit limited to those within our solar system.
Undoubtedly, the process of observing and measuring is constant. This is due to the fact that the movement of celestial objects is uninterrupted.
Several explanations of a coordinate system
A vertical line is a direct line that runs through the center of the celestial sphere. Furthermore, it aligns with the direction of the plumb line from the observer’s perspective. This line intersects the center of the planet and the point of observation in a vertical manner.
Zenith and nadir are two contrasting points. As we are aware, the vertical line intersects with the sky directly above the observer’s position, which is known as the zenith. In reality, the nadir represents the diametrically opposite point.
The mathematical boundary is the celestial sphere’s great circle. Its perpendicular area is parallel to the plumb line. Significantly, it bisects the entire sky’s surface. Furthermore, these bisected portions are referred to as the observable and unobservable to the viewer. The former has its highest point at the zenith, while the latter is located at the nadir.
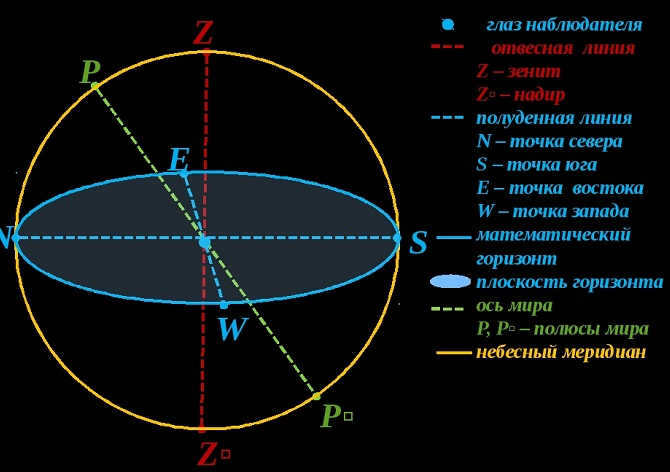
Simultaneously, the mathematical horizon does not align with the observable horizon. This discrepancy arises from two factors. Firstly, the Earth’s surface is uneven, resulting in varying points of observation. Secondly, the curvature of rays in our planet’s atmosphere plays a significant role.
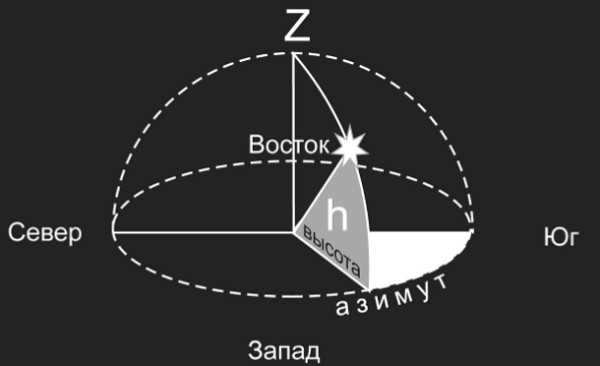
In astronomy, the horizontal coordinates of a celestial object are determined by its altitude, zenith distance, and azimuth.
Altitude refers to the angle between the object’s vertical position and the mathematical horizon. It is measured from 0° to +90° towards the zenith and from 0° to -90° towards the nadir.
On the other hand, zenith distance is the angle between the object and the zenith. It is measured from 0° to 180°.
Azimuth is the angle between the object’s vertical position and the southern point of the horizon. It is measured from 0° to 360°, counting in the westward direction of the daily rotation of the celestial sphere.
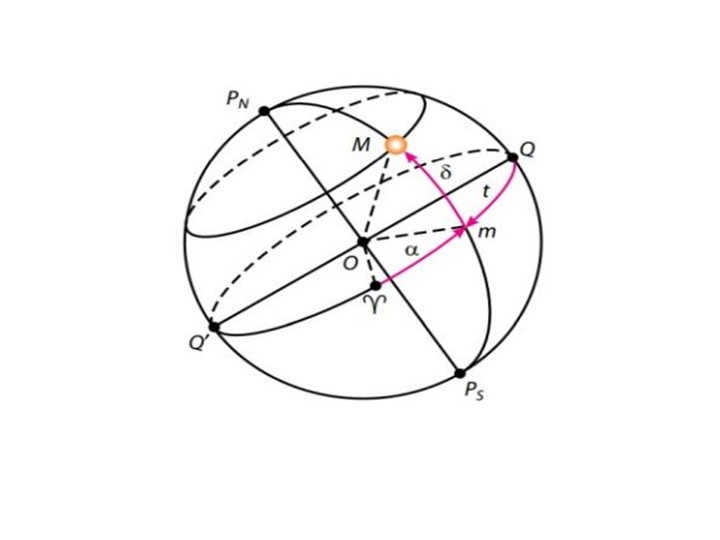
The Initial Equatorial Coordinate System
This system takes the surface of the sky’s equator as a planar region, with the reference point being Q. It uses coordinates that represent declination and hour angle.
For more information on declination, click here.
Hour angle is the arc located between the celestial meridian and the circle of declination. It is measured from 0° to 360°.
It is worth noting that the initial equatorial coordinate system is used because of the constant motion of our planet throughout the day. Therefore, the starting point was set at the vernal equinox, which remains constant relative to the stars.
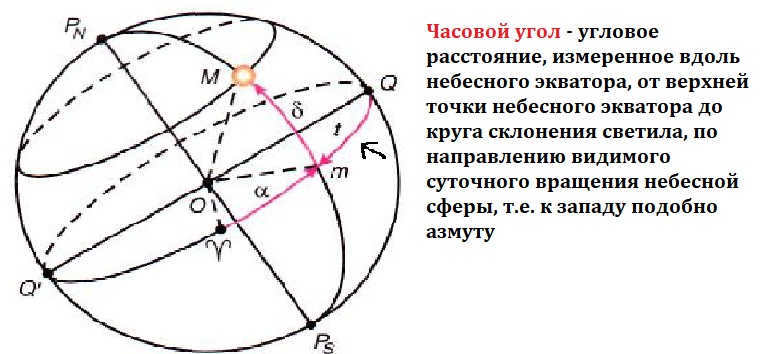
The alternative equatorial coordinate system
Interestingly, the primary plane and the reference point remain the same as the previous system. However, the coordinates are now referred to as declination and right ascension.
What this means is that right ascension is the arc along the celestial equator, running from the vernal equinox point to the circle of the celestial body. Additionally, the measurement is done in hours. However, it is measured in a counterclockwise direction.
On the other hand, the second coordinate system features fixed coordinates for stars. Unlike the first system, the Earth’s rotation during the day does not affect these coordinates. It is used to track the movement of celestial bodies over the course of a year.
It is crucial to understand that the coordinates can vary in every instance. Hence, numerous challenges arise. However, these issues can be addressed by employing a system that is tailored to the specific circumstances. In general, various systems are frequently utilized to resolve problems and determine coordinates.
The establishment of coordinate systems enabled scientists to chart the vast expanse of the night sky. Furthermore, it delineated a particular structure of the celestial realm, which significantly aided the advancement of astronomy and astrology. Moreover, equatorial coordinate systems find utility in numerous scientific disciplines.

Undoubtedly, the advancement and execution of specific systems serve as the foundation for exploring outer space. Our objective is to comprehend this realm to the fullest extent possible. Naturally, the numerous techniques, calculations, and methodologies currently employed aid in expanding our perspectives.

Within this instructional session, we will engage in a discourse regarding the visible daily movement of celestial bodies. We will review fundamental aspects, lines, and planes of the celestial sphere. Moreover, we will examine the coordinate system employed to denote the location of celestial bodies in the atmosphere. Furthermore, we will acquaint ourselves with star charts and acquire knowledge on how to ascertain the coordinates of celestial bodies from a chart.
Currently, it is not possible to view or distribute the instructional video with students
In order to gain access to this and other video lessons included in the package, you must add it to your individual account.
Unlock extraordinary possibilities

Outline of Lesson on Celestial Coordinates and Star Charts
We have all witnessed the Sun rising in the east multiple times. It becomes visible due to distant objects or irregularities on the Earth’s surface. Gradually, it ascends above the horizon and reaches its highest point at noon. In the northern hemisphere, the Sun appears in the south at this time, while in the southern hemisphere, it appears in the north. After noon, the Sun descends towards the horizon and sets in the western part of the sky.
A similar daily movement can be observed in other celestial bodies such as the Moon, stars, and planets. Overall, it appears as though the entire sky rotates around an axis, which we refer to as the axis of the world.
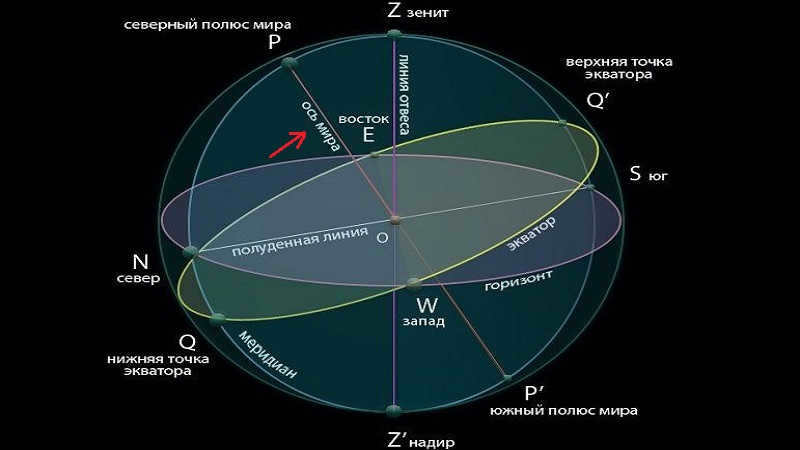
When you look up at the stars on a clear night in the northern part of the sky, you’ll notice that they move in concentric circles around Polaris (the alpha star of the Little Bear), from east to west. This particular point is referred to as the North Pole of the Earth. In the southern hemisphere, you can find a point that is directly opposite to it – the South Pole of the Earth. Additionally, it’s important to remember that the celestial sphere has a great circle that passes through the Earth’s poles and the luminary, known as the circle of declination.
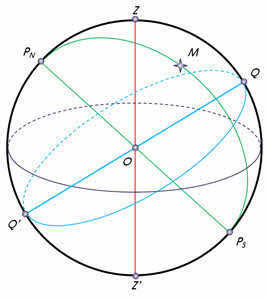
The celestial equator is the name given to the great circle that passes through the center of the celestial sphere and is perpendicular to the axis of the world. This circle divides the celestial sphere into two parts: the Northern Hemisphere, with its apex at the North Pole of the world, and the Southern Hemisphere, with its apex at the South Pole of the world.
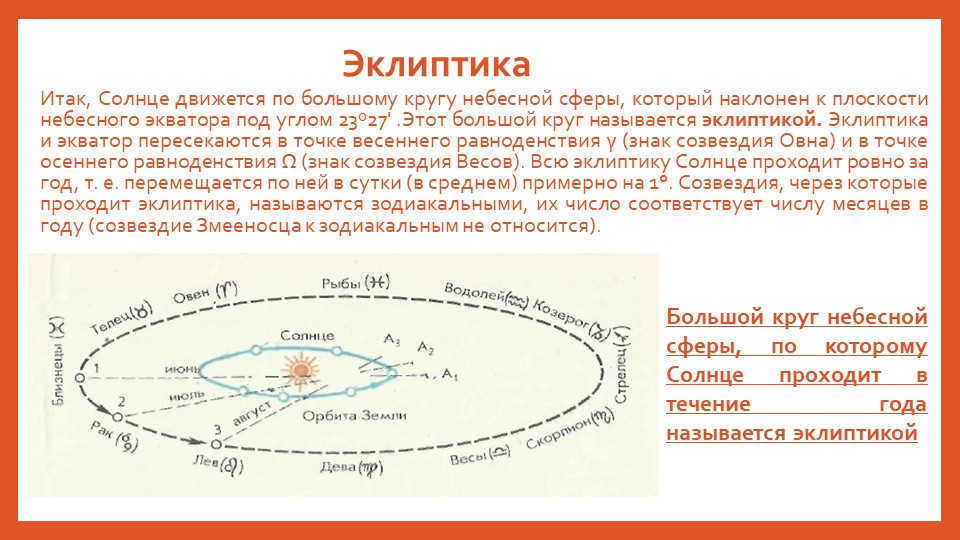
Furthermore, it is customary to represent the visible annual path of the Sun among the stars on the celestial sphere. This path is known as the ecliptic and is inclined at an angle of 23 degrees 27 minutes to the celestial equator. The ecliptic intersects the celestial equator at two points: the vernal equinox (around March 21) and the autumnal equinox (around September 23).
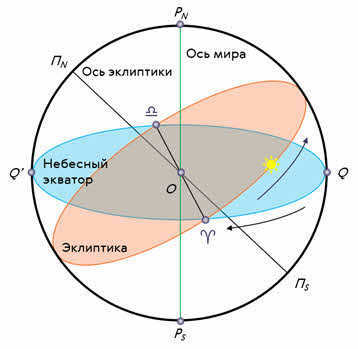
It is now understood that the rotation of the sky is an apparent phenomenon caused by the Earth rotating on its axis from west to east.
The visible movement of the celestial bodies that occurs due to the Earth’s rotation on its axis is known as diurnal motion, and the duration of the Earth’s rotation around its axis is referred to as a day.
In one of our earlier lessons, we discussed how to an observer on the Earth’s surface, it appears that all the stars are situated on a spherical surface in the sky and are equidistant from the observer. This imaginary sphere with an arbitrary radius is known as the celestial sphere.
A coordinate system similar to the one used in geography is employed to indicate the position of celestial bodies in the sky.
As you may already be aware, in geography, geographic coordinates – latitude and longitude – are used to determine the location of a point on the Earth’s surface. Geographic longitude is measured along the equator from the prime (Greenwich) meridian, while geographic latitude is measured along the meridians from the equator to the Earth’s poles.
This coordinate system is known as the equatorial system.
A similar equatorial coordinate system is convenient to utilize in astronomy for indicating the position of celestial bodies in the sky. In this coordinate system, the celestial equator serves as the primary circle of the celestial sphere, and the coordinates used are declination and right ascension.
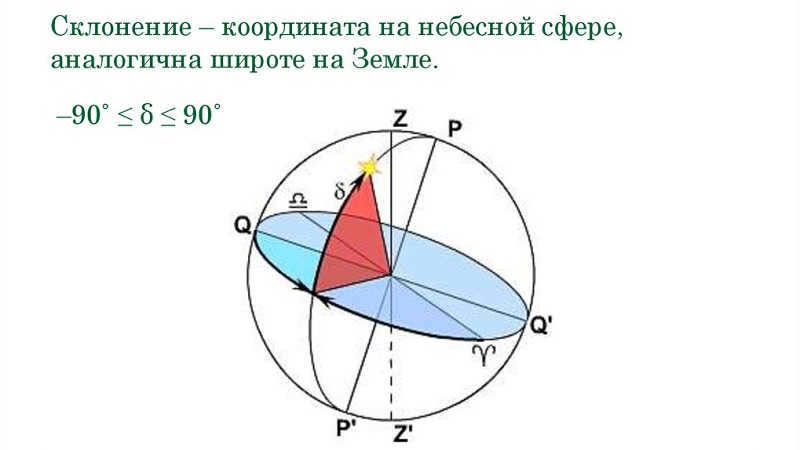
The declination of a celestial body is the angular separation of the body from the celestial equator, measured along the circle of declination. Declination is represented by the Greek letter δ and is analogous to geographical latitude. The only distinction is that for bodies located above the equator, declination is considered positive, while for bodies located below the equator, it is negative. In this case, the starting point for declination on the celestial equator is the vernal equinox.
The second coordinate, right ascension, signifies the position of the celestial body in the sky. It is the angular distance measured along the celestial equator from the vernal equinox to the point where the celestial equator intersects with the declination circle of the body.
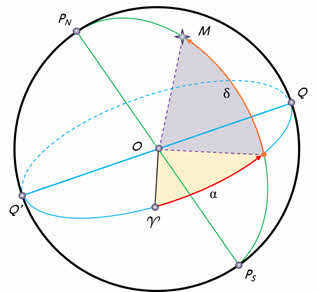
Declination is indicated by the lowercase Greek letter α. It is measured in the opposite direction of the daily rotation of the celestial sphere, ranging from 0 to 360 degrees or 0 to 24 hours. However, in astronomy, declination is typically expressed in hours. Considering that 360 degrees is equal to 24 hours or 1440 minutes, one degree is equal to 4 minutes.
You may be wondering: “What is the main difference between the horizontal coordinate system (which we discussed in one of our earlier lessons) and the equatorial coordinate system?”
The answer is quite simple. In the horizontal system, the coordinates of a celestial object change with time. Therefore, they only have a specific value for a known moment in time.
In the equatorial system, stars do not have coordinates that are affected by the daily motion of the celestial sphere. Instead, their coordinates change slowly over time due to their distance from us. This is why the equatorial coordinate system is commonly used for star globes, maps, and catalogs.
Star maps are representations of the celestial sphere projected onto a two-dimensional plane, with celestial objects plotted according to a specific coordinate system.
A collection of star maps that cover the entire sky or a specific portion of it is known as a star atlas.
Additionally, there are specialized lists of stars known as star catalogs. These catalogs provide information such as the coordinates of stars on the celestial sphere, their magnitude, and other parameters. One well-known example is the Hubble Space Telescope Reference Catalog, which contains over 945.5 million stars.
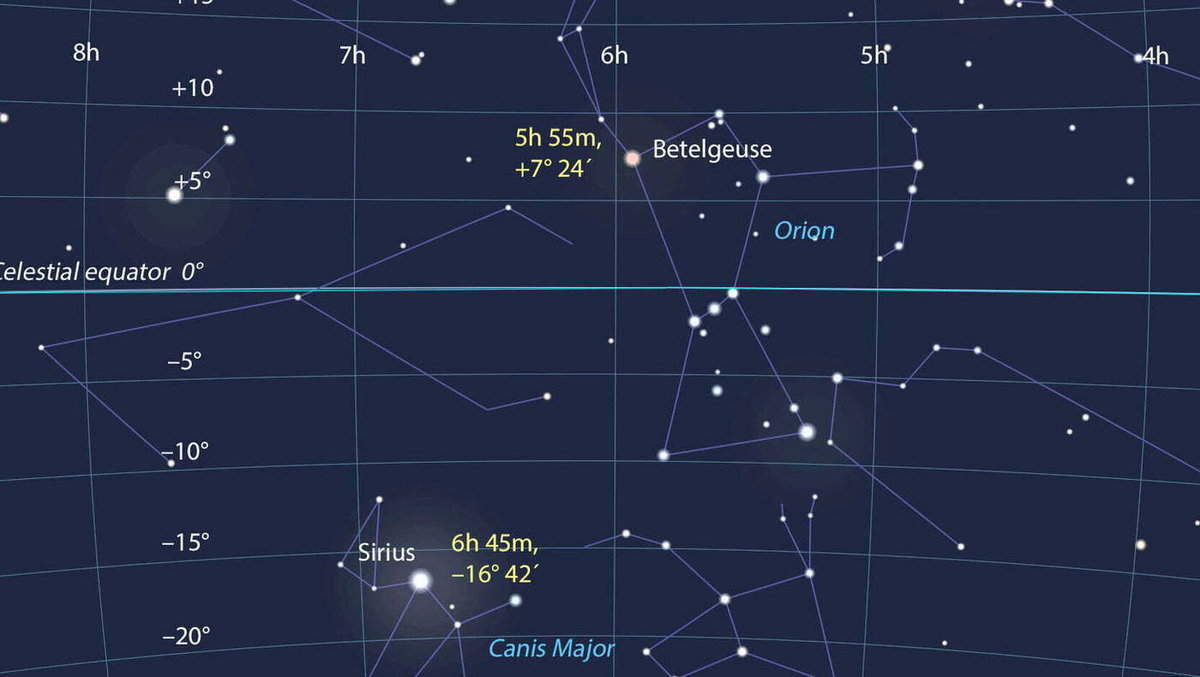
Now, let’s pause and examine the celestial chart more closely. Consequently, right at the heart of our stellar map lies the Earth’s North Pole. Adjacent to it, we find the star Polaris.
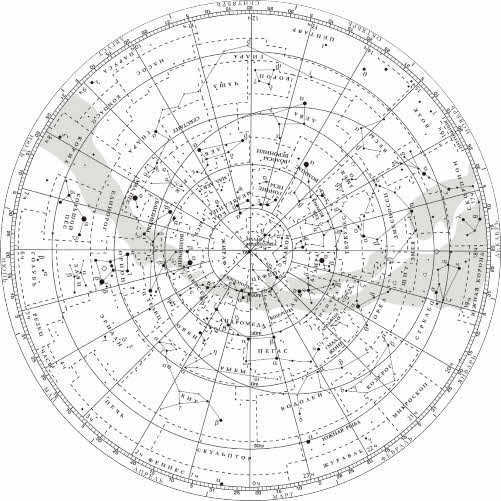

The map displays the equatorial coordinate grid using rays that diverge radially and concentric circles. Alongside each ray, numbers are inscribed to indicate the direct ascension, ranging from 0 to 23 hours.
The ray that marks the starting point of the direct ascension passes through the vernal equinox, which is symbolized by the Aries sign on the map. The declination is measured along these rays from the circle representing the celestial equator, with zero degrees labeled. Other circles are also marked, indicating the declination of the object located on each respective circle.
Stars are represented on the map using circles of varying sizes depending on their stellar magnitude. The stars that combine to form distinct constellation patterns are connected by solid lines, while the boundaries of the constellations are indicated by dotted lines.
Now, let’s explore the process of utilizing a star chart. To begin, we will ascertain the equatorial coordinates of Altair (the alpha star of the Eagle constellation), Sirius (the alpha star of the Big Dog constellation), and Vega (the alpha star of the Lyra constellation).

Let’s now tackle the reverse problem of finding a star based on its coordinates. Suppose the star has a declination of +35 o and a right ascension of 1 h 6 m.
To find the answer to this question, we need to follow the same steps as before, but in reverse order. First, we locate the right ascension of the given star on the map. Then, we draw a mental line (or use a ruler) connecting our point to the center of the starry sky map. Next, we find a circle representing a declination of 30 o and shift it about 5 o upwards. As a result, we have identified the star beta Andromeda.
It is worth mentioning that the celestial map can be utilized not just for locating the coordinates of stars, but also for ascertaining the appearance of the night sky during a specific date of interest. Additionally, it can be used to determine the times at which stars, the sun, or planets rise and set.

Presently, there are extra combined price reductions (ranging from 2% to 25%) accessible to 58,742 educational establishments. To ascertain the applicable discount for all staff members at your educational institution, kindly sign in to your personal Infoworks account.


Course for professional growth
Arranging the cultural adaptation of international students in professional educational institutions.
We can apply your educational establishment’s discount to this offer (the amount depends on the number of your colleagues who have taken Infowork courses).
Currently, there are additional cumulative discounts (ranging from 2% to 25%) available to 58,742 educational institutions. To determine the discount applicable to all staff members of your educational institution, please sign in to your personal Infoworks account.




Professional development course
Designing the object and play space of preschool educational organization in accordance with FSES DO
We can apply the discount for your educational institution to this offer (the amount of discount depends on how many of your colleagues have completed Infowork courses).
Currently, 58,742 educational institutions are eligible for additional discounts (ranging from 2% to 25%). To find out what discount is available for all employees of your educational institution, please log in to your personal Infoworks account.


Developing reading skills in students during classroom instruction
Breakdown of the presentation by individual slides:

2 slide Currently, constellations are identified as specific regions of the night sky that are separated by precise boundaries.
In contemporary astronomy, a constellation is a designated area of the celestial sphere, with its boundaries determined by a specific resolution from the International Astronomical Union (IAU).
During the inaugural Congress of the International Astronomical Union in 1922, the entirety of the celestial sphere was conventionally divided into 88 constellations.

On the third slide, Hipparchus, in the 2nd century BC, implemented a standard system of stellar magnitudes. The most luminous stars were classified as 1st magnitude, while the next level of brightness (approximately 2.512 times fainter) were categorized as 2nd magnitude stars. The dimmest stars that are only visible on moonless nights are considered 6th magnitude stars.
Within the night sky, there are only 12 prominent stars classified as 1st magnitude.
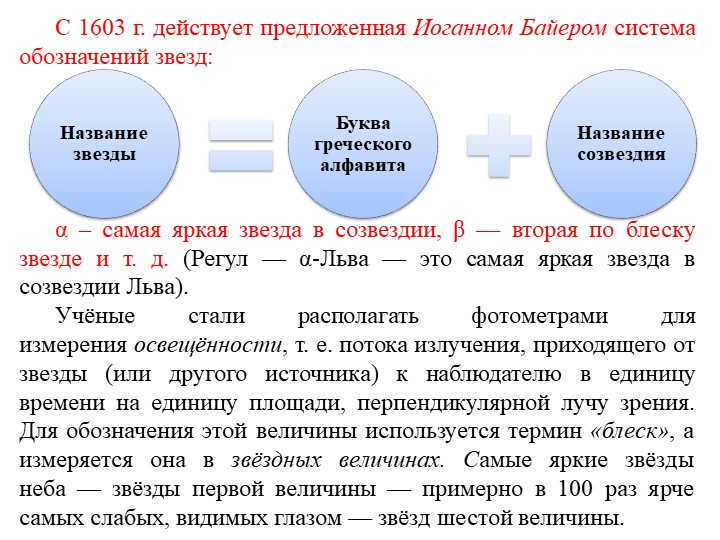
Slide 4: Ever since 1603, the star designation system proposed by Johann Bayer has been utilized.

When facing south, the visible daily rotation of the starry sky is from east to west, which can be described as clockwise. However, in reality, the Earth rotates around its axis from west to east, causing the entire firmament to rotate in the opposite direction, from east to west. This daily movement of stars, also known as luminaries, is an apparent phenomenon that reflects the actual rotation of the globe around its axis.
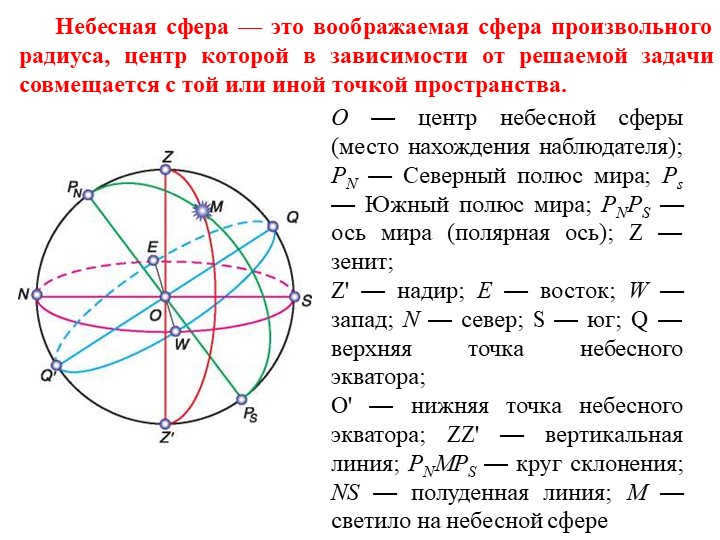
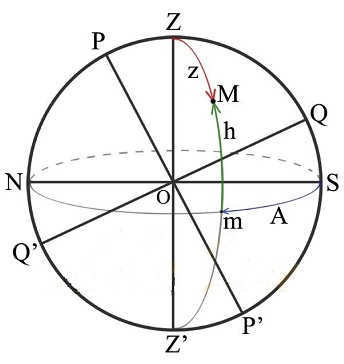
On the sixth slide, we learn about the celestial sphere, which is a hypothetical sphere with a radius that can be adjusted according to the specific problem at hand. It is centered at a point in space, typically where the observer is located.
The center of the celestial sphere is labeled as O, representing the observer’s position. PN represents the North Pole of the world, and Ps represents the South Pole of the world. The line connecting PN and Ps is the world axis or polar axis. Z represents the zenith, which is the highest point in the sky directly above the observer. Z’ represents the nadir, which is the point directly opposite the zenith on the celestial sphere. E represents the east direction, while W represents the west direction. N represents the north direction, and S represents the south direction. Q represents the upper point of the celestial equator, while O’ represents the lower point of the celestial equator. ZZ’ represents a vertical line on the celestial sphere. PNMPS represents a circle of declination, NS represents the noon line, and M represents a luminary on the celestial sphere.

Slide 7: The plumb or vertical line (ZZ’) is the straight line that passes through the center of the celestial sphere and aligns with the direction of the plumb line at the observation point. It intersects the celestial sphere at the zenith (Z), which is the highest point where the plumb line intersects the celestial sphere, and the nadir (N), which is the point on the celestial sphere directly opposite the zenith. The plane that passes through the center of the celestial sphere and is perpendicular to the plumb line is known as the plane of the true or mathematical horizon.
The circle of altitude, also referred to as the vertical circle or luminary vertical, is the great circle of the celestial sphere that passes through the zenith, luminary, and nadir (ZMZ’).
The world axis (PNPS) is a straight line that passes through the center of the celestial sphere and is parallel to the Earth’s axis of rotation.


Slide 9: The true horizon intersects with the celestial equator at two opposite points, known as the east point and the west point.
For an observer positioned in the center of the celestial sphere, facing north, the east point would be on the right and the west point on the left. By following this guideline, it becomes easy to orient oneself on the surface of the Earth.
The ecliptic is the visible annual path of the Sun among the stars. It represents the Earth’s orbit around the Sun, lying in the same plane as the ecliptic. This plane is inclined at an angle of 23°27′ to the celestial equator and intersects it at the vernal equinox (ϓ) around March 21st and the autumnal equinox (♎) around September 23rd.

10 slide Celestial coordinates refer to the central angles or arcs that define the positions of celestial objects in relation to the main circles and points of the celestial sphere. These coordinates are crucial for determining the exact location of stars and other luminaries in the night sky.

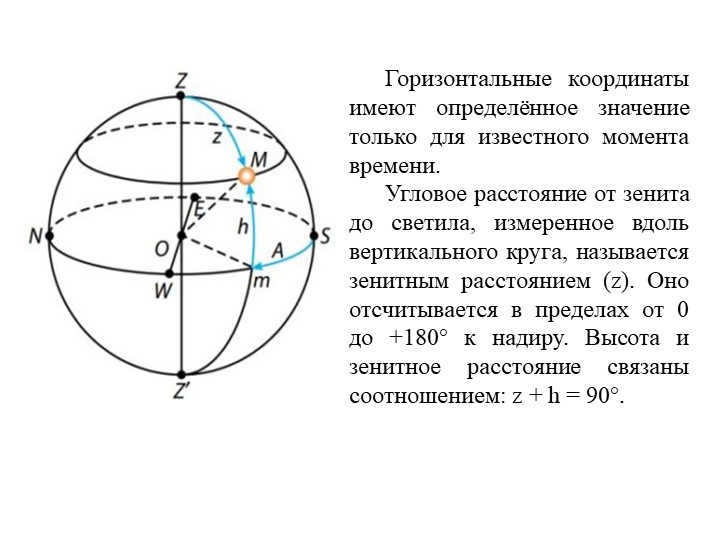
At a certain point in time, the 12 Slide’s horizontal position has a specific value. The zenith distance (z) is the angular distance from the zenith to the luminary, measured along a vertical circle. It is measured between 0 and +180° to the nadir. The relationship between the altitude and zenith distance is expressed as: z + h = 90°.

Teacher and educator resources, including worksheets and materials

At the moment, there are additional cumulative discounts (ranging from 2% to 25%) that can be availed by 58,742 educational establishments. To determine the specific discount applicable to all staff members of your educational institution, kindly access your personal Infoworks account.




Professional development course
Organizing the adaptation of foreign students from different cultures in educational institutions specializing in professional education.
We can apply a discount from your educational institution to this discount (the amount depends on how many of your colleagues have taken Infowork courses).
Currently, there are additional cumulative discounts (ranging from 2% to 25%) available to 58,742 educational institutions. To find out which discount is applicable to all employees of your educational institution, please log in to your personal Infoworks account.


Course for professional growth
Creating the layout and play area of a preschool educational organization in accordance with the Federal State Educational Standard for Preschool Education
We can apply a discount from your educational institution to this special offer (the amount depends on how many of your colleagues have completed Infowork courses).
Currently, 58,742 educational institutions are eligible for additional discounts (ranging from 2% to 25%). To find out the discount available for all staff members of your educational institution, please log in to your personal Infoworks account.


Developing reading skills in students during classroom lessons
Breakdown of the presentation by individual slides:

2 slide Definition and types of stellar coordinates
A stellar coordinate system refers to a system utilized for describing the location of celestial bodies on an imaginary sphere surrounding the earth.
There are various types of star coordinate systems, including:
Horizontal.
1st equatorial.
2nd equatorial.
Ecliptic.
Galactic
Each system is defined in relation to the primary plane that forms the main circle, as well as a reference point known as the zero point.

On the third slide, we can see the Celestial Equator and Circle of Declinations. The Celestial Equator is a line that forms a plane passing through the center of the celestial sphere. It is drawn perpendicular to the axis of the world and intersects the celestial sphere in a great circle.
The great circle of the celestial sphere that passes through the poles of the world and the observed luminary is known as the luminary’s circle of declination.
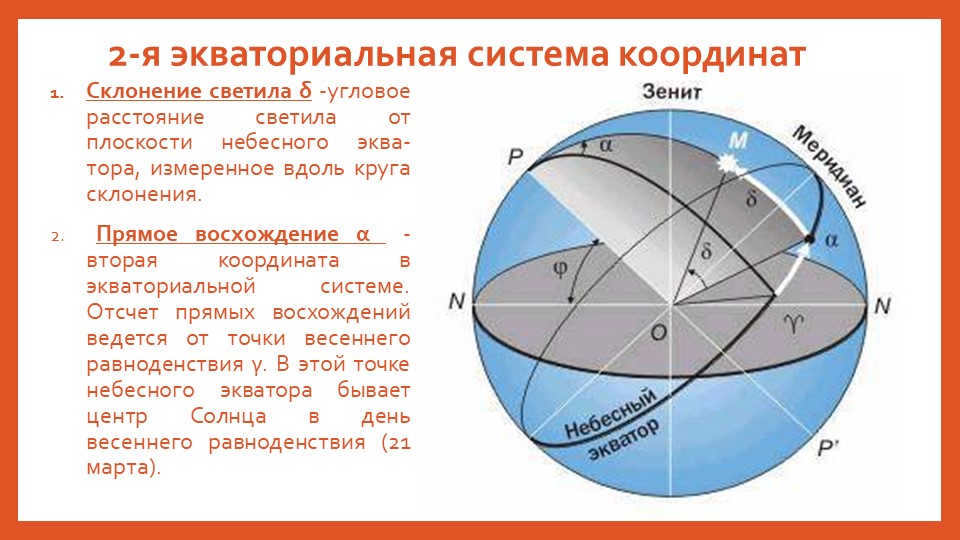
4 slide 2nd equatorial coordinate system
The angular distance of a celestial body δ is its declination, which is measured along the declination circle from the plane of the celestial equator.
The second coordinate in the equatorial system is the right ascension α. Right ascensions are measured from the vernal equinox point γ, which is the center of the Sun on March 21st. This point lies on the celestial equator.


Slide 6 Starry Sky Map
When the celestial sphere rotates daily, the stars’ positions relative to the celestial equator remain unchanged. Therefore, equatorial coordinates are used to create maps, atlases, and catalogs of stars.
With this map, you can estimate the equatorial coordinates of stars or, conversely, plot the positions of stars and other celestial objects on the map using the given α and δ.
For instance: Deneb (α of the Swan)
δ = 𝟒𝟓 𝟓 𝟎; α = 𝟐𝟎 h 𝟑𝟎 m
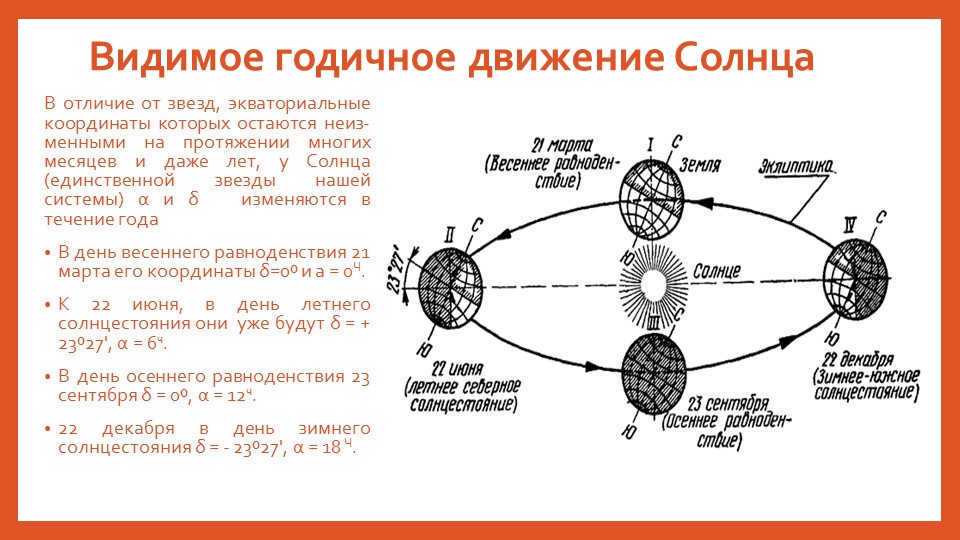
Slide 7: The observable yearly movement of the Sun
Unlike the stars, which have constant equatorial coordinates for extended periods of time, the Sun, being the only star in our solar system, experiences changes in its α and δ values throughout the year
On the day of the vernal equinox, which falls on March 21, the Sun’s coordinates are δ=0º and a=0Ch.
By June 22, which is the day of the summer solstice, its coordinates will have shifted to δ=+23º27' and α=6Ch.
On September 23, at the autumnal equinox, the Sun’s coordinates return to δ=0º and α=12h.
Finally, on December 22, at the winter solstice, the Sun’s coordinates become δ=-23º27' and α=18h.
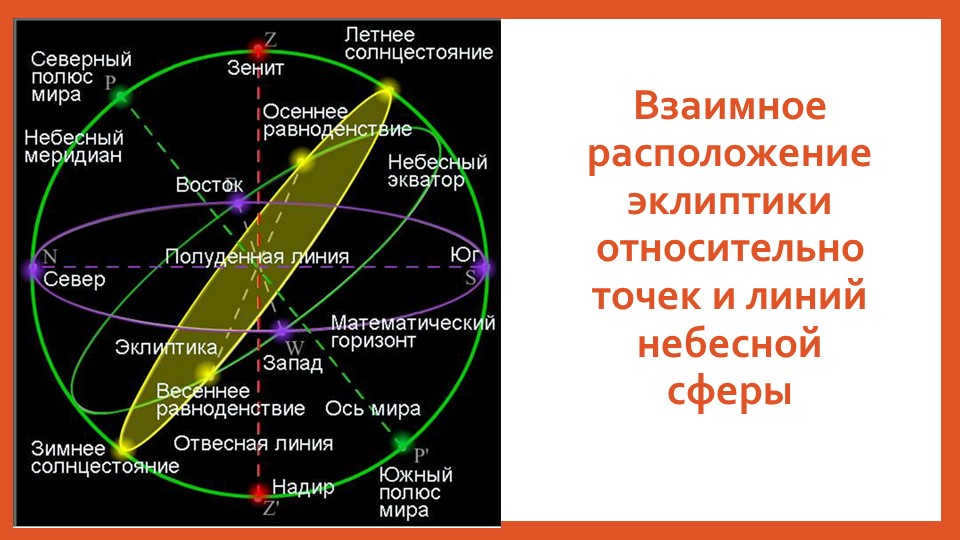
On Slide 9, there is a reciprocal arrangement of the ecliptic relative to the points and lines of the celestial sphere.
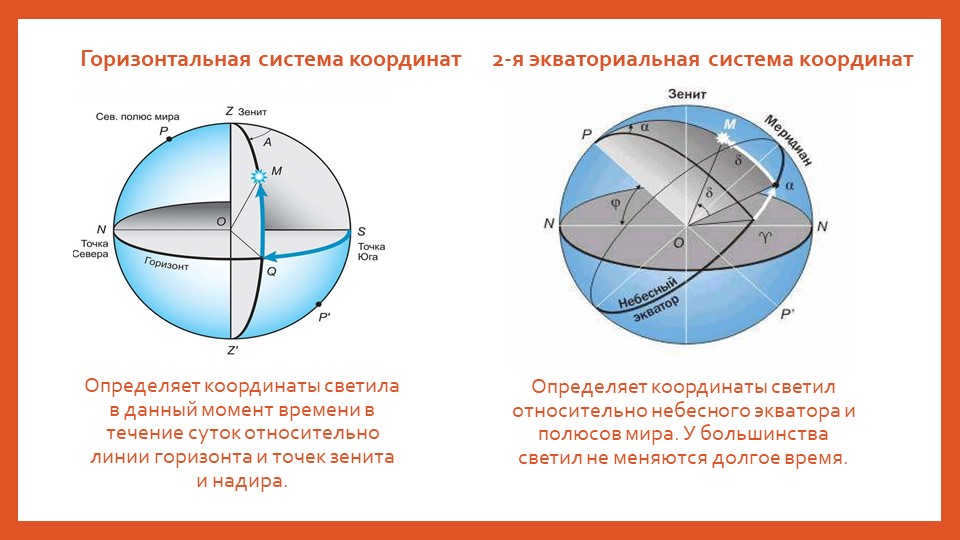
10-slide Horizontal coordinate system
Determines the luminary’s coordinates at a specific time of day in relation to the horizon line, as well as the zenith and nadir points.
Second equatorial coordinate system
Determines the luminary’s coordinates in relation to the celestial equator and the Earth’s poles. For the most part, these coordinates remain unchanged over extended periods of time.


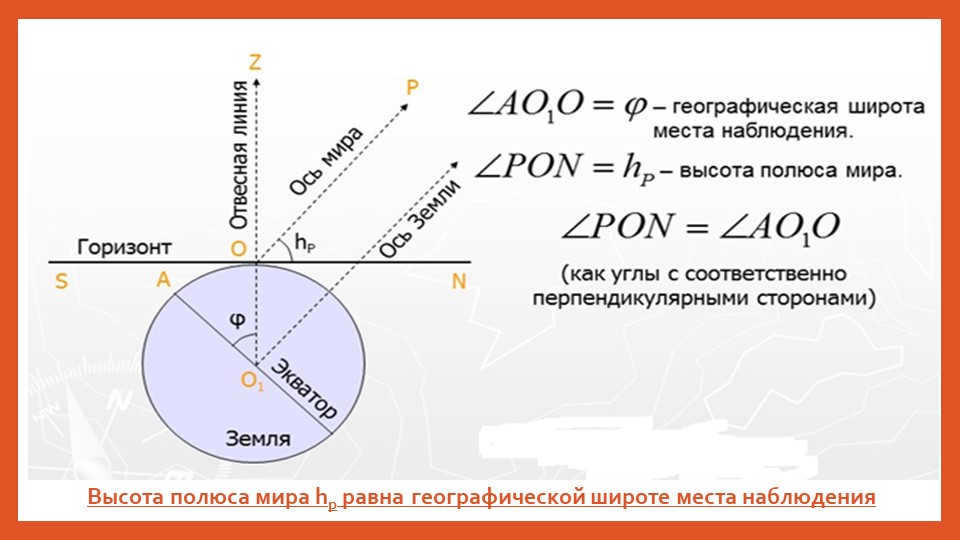
Slide 11: The altitude of the world pole and the geographic latitude.
Polaris, which is located near the South Pole of the world, maintains a relatively constant height above the horizon at a specific latitude during the daily rotation of the starry sky. As an observer moves from north to south, where the geographic latitude is lower, Polaris gradually descends towards the horizon. In other words, there is a correlation between the height of the world pole and the geographic latitude of the observation location.
13 slide Culminations
(repetition).
All celestial bodies cross the celestial meridian twice in a day as they appear to move across the sky. When a celestial body’s center crosses the celestial meridian, it is said to reach its culmination. The word “culmination” comes from Latin and means the highest point. There is a distinction between the highest point and the lowest point of a celestial body’s culmination.
During the highest point of culmination, the celestial body reaches its greatest height, while during the lowest point, it is at its lowest. For celestial bodies that do not rise, both culminations occur above the horizon. For celestial bodies that rise and set, the highest point of culmination occurs above the horizon, while the lowest point occurs below the horizon. For celestial bodies that do not rise, both culminations occur below the horizon and cannot be observed.
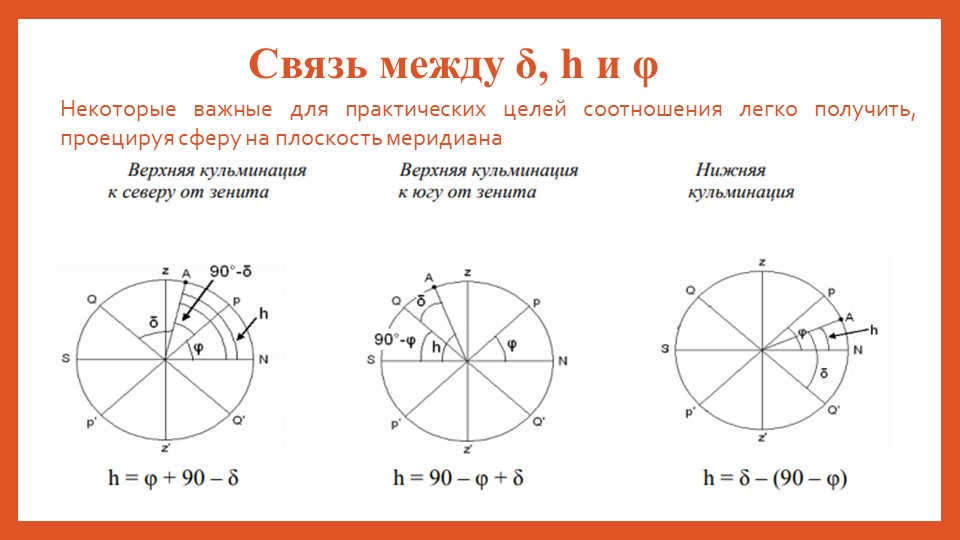
14 Slide The relationship between δ, h, and φ
Some important relationships for practical purposes can be derived by projecting a sphere onto the meridian plane

On the 15th slide, there are formulas available for solving problems. For instance, if the declination of a luminary is less than the geographic latitude (δ< φ), it will culminate south of the zenith at an altitude of
h = 90 0 -φ + δ. On the other hand, if the luminary’s declination is greater than the geographic latitude (δ>φ), it will culminate north of the zenith at an altitude of
h = 90 0 +φ – δ. Lastly, if the luminary is not setting, you can determine its height at the lower culmination using the formula
h=δ – ( 90 0 -φ).

Slide 16 Problem #1
What is the maximum altitude that Vega (δ = +38°47') reaches in Irkutsk (φ = 52°16')?
Given: Solution:
δ = +38°47' The culmination is higher, δ < φ, to solve the problem, apply
φ = 55°45' the formula h = 90o – φ + δ
h = ? h = 90o – φ + δ = 90o – 52°16' + 38°47' = 77°31'

Slide 17, Problem #2
Determine the altitude of the star Algol (β Perseus) when it reaches its highest point in the sky at the northern tropic (φ = 23°27′). Algol has a declination of δ = +26°24′.
Given: Solution:
δ = 26°24′ The culmination is upper, δ > φ , to solve the problem we can use the formula h = 90° + φ – δ
h = ? h = 90° + 23°27′ – 26°24′ = 87°03′

Problem #3 on slide 18
Find the noon altitude of the Sun in Irkutsk (φ = 52°16′) on the day of the summer solstice.
Given: Solution:
φ = 52°16′ On the day of the summer solstice, the Sun’s declination δ = +23°27′.
The noon altitude is at its maximum height, so
h = ? h = 𝟗𝟎 𝟎 -φ + δ = 𝟗𝟗𝟎 𝟎 -52°16′ +23°27′ = 61°11′