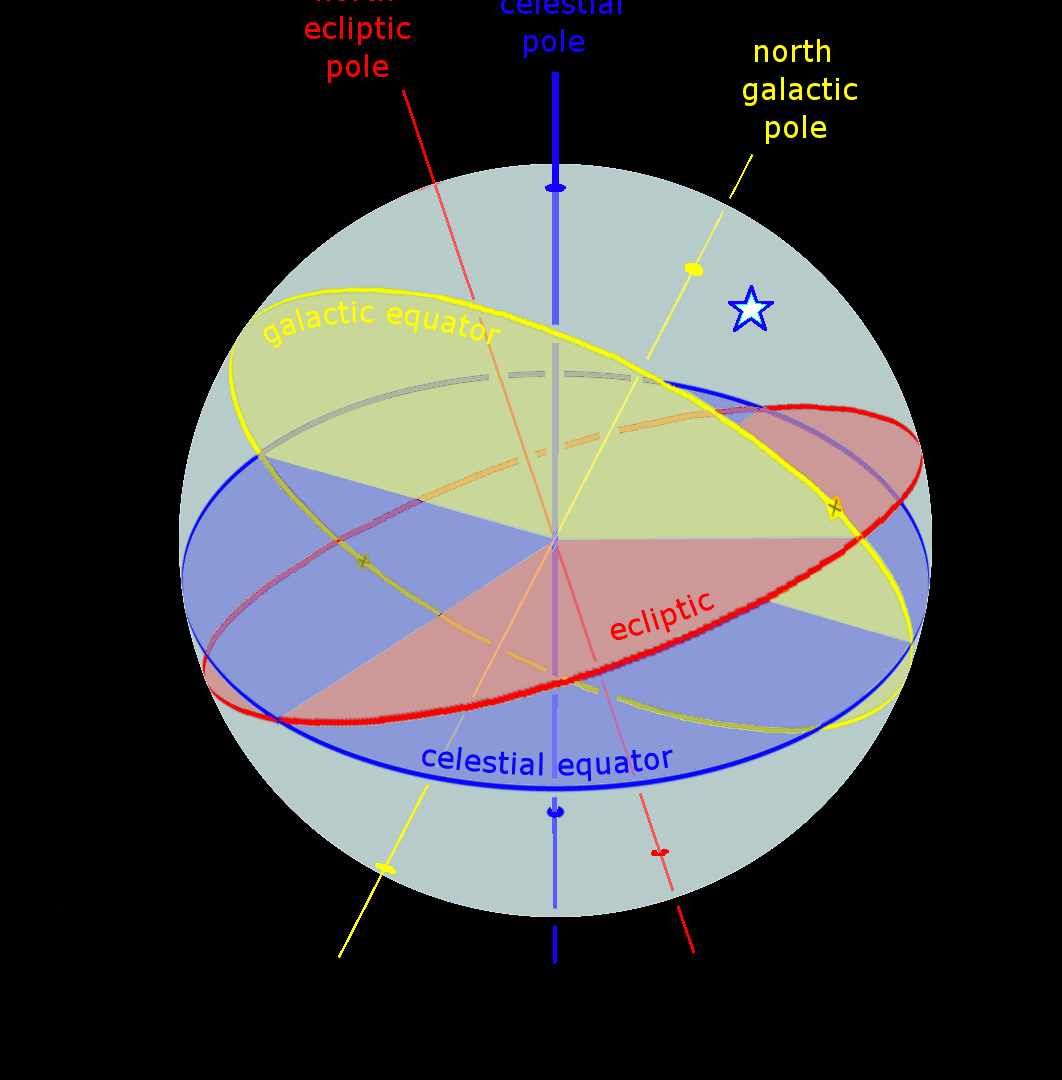
What are the different celestial coordinate systems? - Explore the Universe: Your Guide to Astronomy

A celestial coordinate system is utilized to determine the precise location of a celestial body. These systems, known as the ecliptic coordinate system or equatorial coordinate system, are constructed based on specific circles of the celestial sphere. In contrast, the geographic coordinate system is employed to determine coordinates on the Earth’s surface. Let’s explore each of these systems in detail.

Ecliptic coordinate system. Astrologers commonly utilize the ecliptic coordinate system, which is widely documented in ancient star atlases. This system is based on the plane of the ecliptic and uses two spherical coordinates – ecliptic longitude (or longitude) and ecliptic latitude – to determine the position of a celestial body.

The vernal equinox point and the poles of the ecliptic determine the plane from which the ecliptic longitude L is measured.

The Sun’s annual motion is followed in the direction of the signs of the Zodiac (Fig. 3.3). Longitude is measured from 0° to 360°.

Ecliptic latitude B is the angular distance from the ecliptic towards the poles. B has a positive value towards the north pole of the ecliptic and a negative value towards the south pole. It is measured from +90° to -90°.

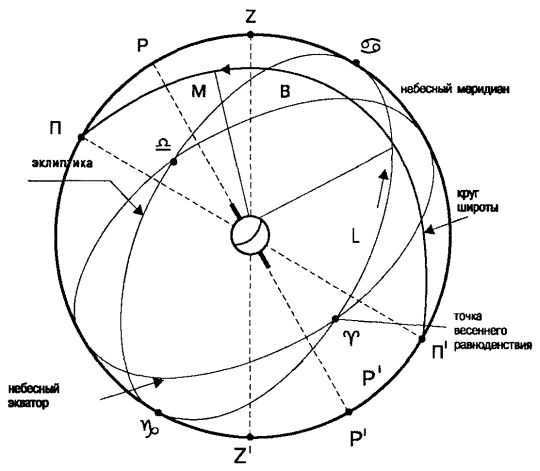
Figure 3.3: The celestial coordinates in the ecliptic system.

The equatorial coordinate system. The equatorial coordinate system is also utilized by astrologers. This system is based on the alignment of the celestial equator with the Earth’s equator (Figure 3.4). The position of a celestial body in this system is determined by two coordinates: right ascension and declination.

Right ascension is measured from the vernal equinox at 0 degrees.

The measurement of Right Ascension is used to determine the position of celestial objects and is measured against the daily rotation of the celestial sphere. It can be expressed either in degrees from 0° to 360° or in units of time, from 0 hour to 24 hours.

Declination, on the other hand, is the angle between the celestial equator and the celestial pole (similar to latitude in the ecliptic system) and is measured from -90° to +90°.

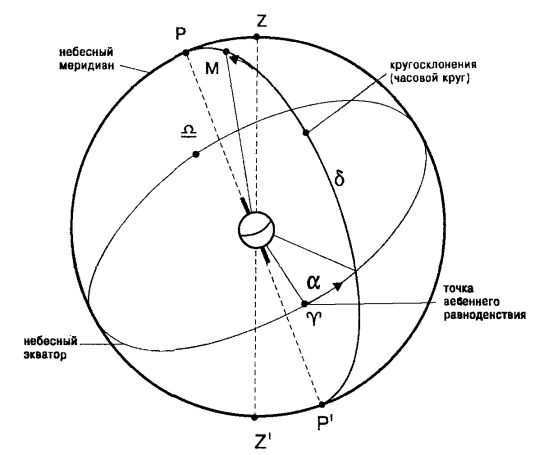
Fig.3.4 The equatorial system of celestial coordinates

Geographic coordinate system. It is determined by the longitude and latitude of a location. In astrology, it is used to indicate the birthplace coordinates.

Geographic longitude is measured from the Greenwich meridian, with a positive sign to the east and a negative sign to the west, ranging from -180° to +180° (Fig. 3.5). Sometimes, geographic longitude is measured in units of time from 0 to 24 hours, east of Greenwich.

Geographic latitude is measured along the meridians towards the geographic poles, with a positive sign to the north and a negative sign to the south of the equator. Geographic latitude ranges from -90° to +90°.

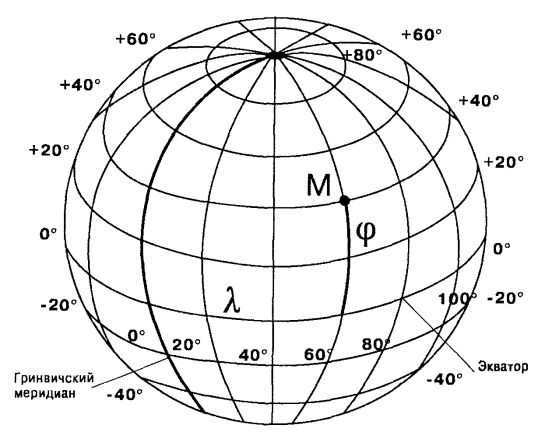
Fig.3.5 Geographic coordinates

Classification

Relative Coordinate Systems

Relative coordinate systems are based on the observer’s position. They have their reference point at the observer’s location, specifically on the Earth’s surface, and are also referred to as local coordinate systems or topocentric coordinate systems.

The coordinate system that every observer is most familiar with is the horizon system. It is positioned at its origin, with the horizon serving as the reference plane. The angle between a celestial body and the horizon is known as its altitude (h). The azimuth (a) represents the deviation of the point where the vertical line through the celestial body intersects the horizon from the south direction. In the southern hemisphere, the reference point for the horizon system is north. However, the horizon system is not well-defined at the equator and at the poles.

Astronauts utilize coordinate systems linked to their spacecraft while in space.

Coordinate systems in relation to a fixed point

Coordinate systems in relation to a fixed point are established with a neutral point of reference that is independent of the observer. This fixed point can be the center of the Earth, the Sun, another celestial body, or even the center of the Galaxy. The reference plane associated with these coordinate systems is not fixed to the observer and therefore rotates relative to their position.

The rotating equatorial coordinate system is derived from the stationary equatorial (geocentric) coordinate system mentioned earlier. It is centered around the Earth and the reference point used for measuring angles in the equatorial plane of the sky is a fixed celestial point. The angle, denoted as α, represents the direct ascent, while the declination angle, denoted as δ, remains the same as the declination angle in the stationary equatorial system.

Two astronomical coordinate systems are defined as the reference plane with the orbital plane, known as the ecliptic, in which the Earth completes one orbit around the Sun every year. The first coordinate system, geocentric, has its origin at the center of the Earth, while the second, heliocentric, has its origin at the center of the Sun. In both systems, the angles are referred to as ecliptic longitude (λ) and ecliptic latitude (β), with the vernal equinox serving as the point of reference.

In addition to the topocentric, geocentric, and heliocentric systems, barycentric and galactic coordinate systems are also utilized.

The galactic coordinate system, based on galactic coordinates (l = 0°, b = 0°), is aligned in the direction of the center of the Galaxy, with the reference plane being the disk of the Milky Way.

The barycentric coordinate system, for instance, finds its starting point in the barycenter (the shared center of gravity) of the Earth and the Moon, or in the solar system.

These systems orbit around an observer. However, in astronomy, the fixed starry sky is typically seen as stationary, hence the term “absolute”, whereas the positions related to the observer are referred to as “apparent”.

Angular characteristics are measured in hours, not degrees

When it comes to hour angle in the stationary equatorial coordinate system and direct ascent in the rotating equatorial coordinate system, it is more common to express values in hours, minutes, and seconds rather than degrees. The preference for using hours is due to the fact that a change in the hour angle of the sun directly corresponds to a change in the time of day. In fact, the original definition of an hour was based on a change of 15 degrees in the hour angle.

The reason for this tradition in direct ascent is the impact of the Earth’s rotation, which is essentially separate from the measurement. Two stars with a 15° difference in right ascent can be seen across the meridional circle in the observatory, with a one-hour discrepancy in sidereal time. An hour of sidereal time is approximately 10 seconds shorter than a regular hour. The observatory’s observation plan is based on sidereal time, which is known for each star and can be checked on the corresponding clocks. This time reads as 0 hours of sidereal time when the vernal equinox point, the reference point for equatorial celestial coordinates, crosses the meridian circle. The time of day lags behind sidereal time by one day each year, just like the sun (seemingly) moves across the starry sky once a year.

Conversions

The conversions are carried out by using the Cartesian coordinates representations of both systems. The conversion involves rotating around the y-axis and takes place between the Cartesian forms of the systems (where the y coordinates are the same in both systems). The first case involves rotation around the angle 90° – φ (where φ represents the geographic latitude), while the second case involves rotation around the angle ε (which represents the ecliptic tilt).

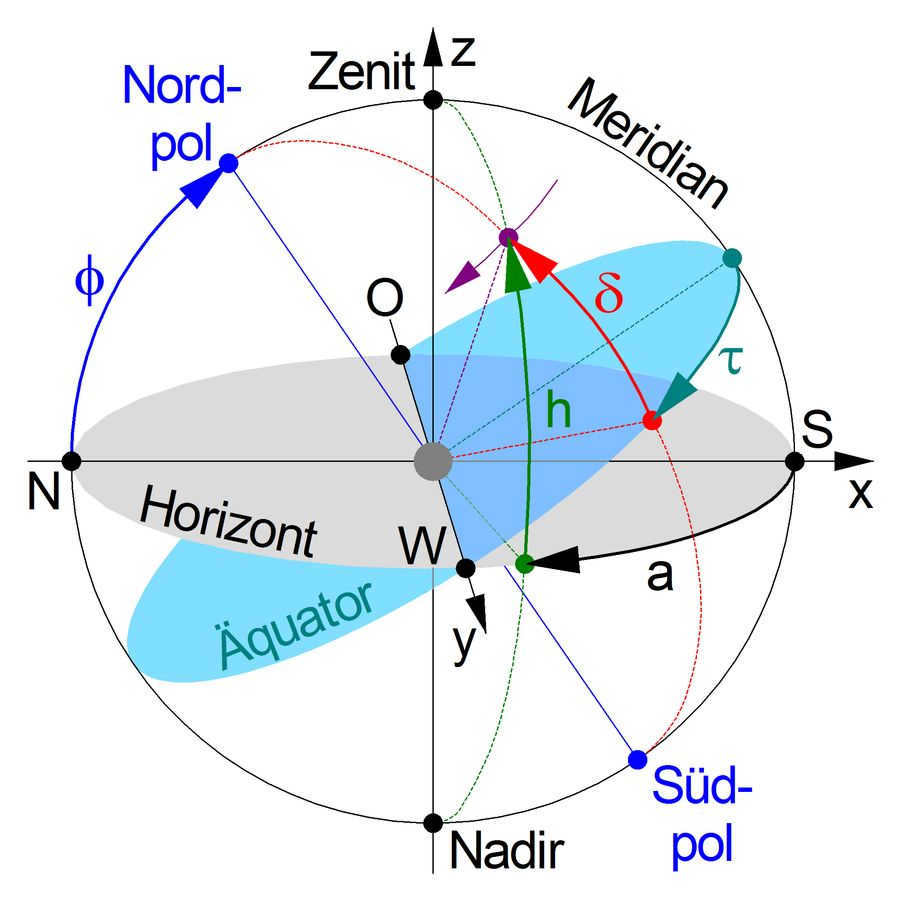
For the purpose of conversion: Horizontal system ↔ equatorial system (at rest) The zenith is directly above the observer and the nadir is directly below the observer at the center of the image. If the observer is at the North or South Pole ( ), then the horizon and equatorial plane are the same, and the zenith and nadir are located on the polar axis (blue). The ϕ sign is equal to 0

A meridian is a great circle that passes through the celestial poles, which are the North (N) and South (S) directions when viewed from the observer’s perspective.

The observer perceives the horizontal system (represented by a gray disk) in the sky, with a point (colored purple) below the azimuth a (colored black). The azimuth is measured from the meridian in the horizontal plane. Additionally, there is the place angle h (colored green) which is measured perpendicular to the horizontal plane on the great circle that passes through the observed point, between the Zenith and Nadir (both colored green). These angles can be transformed into Cartesian coordinates x, y, and z within the horizontal system.

In the equatorial system (represented by a turquoise disk), the hour angle τ (colored blue) is defined along the meridian in the equatorial plane. The declination angle δ (colored red) is measured perpendicular to the equatorial plane on a great circle that passes through the celestial poles and the observed point.

The east point (O) and west point (W) have the same characteristics in both systems, and the angle of inclination of the two planes is determined by the pole altitude φ (blue), which corresponds to the latitude where the observer is located. The observed point in the sky (purple) moves in a semicircle that runs parallel to the equatorial plane with a constant declination angle δ, and this movement occurs over half a day.

In the following lists, along with the final results of the transformations, the Cartesian coordinates are provided as intermediate results x, y, and z of the unit sphere in the target system. It’s important to note that the first two systems (horizontal and equatorial at rest) are considered as left systems, while the other two (rotating equatorial and geocentric-ecliptic) are considered as right systems.

Transformation from equatorial coordinates (δ, τ) to rotating equatorial coordinates (δ, α) and vice versa

The declination (δ) remains constant.

The sign of α is equal to θ – τ and the sign of τ is equal to θ – α

Conversion from horizontal coordinates (a, h) to Cartesian coordinates and then to stationary equatorial coordinates (τ, δ)

Converting (τ, δ) Equatorial Coordinates to Cartesian Coordinates and then to (a, h) Horizontal Coordinates

In the target system, the Cartesian coordinates ( , ) are calculated as follows:

a = CHAS * X * sign(ϕ * sin δ + sin ϕ * δ * τ)

h = CHAS * sign(δ * sin τ * z) * sign(ϕ * sin δ + ϕ * δ * τ)

In the target system, the angular coordinates are calculated as follows:

a = arcsin(sin ϕ * sin δ + ϕ * δ * τ)

h = arctan(sin τ * sin ϕ / (τ – ϕ * tan δ))

(Note: The quadrant definition is applied based on the conversion of Cartesian coordinates to polar coordinates)

Conversion of equatorial coordinates (α, δ) to Cartesian coordinates and then to horizontal coordinates (a, h)

Cartesian coordinates in the target system (a, h)

The X coordinate is equal to CHAS multiplied by the sign of a, which is equal to ϕ multiplied by the sine of δ plus the sine of ϕ multiplied by the cosine of δ multiplied by the difference between θ and α. The Y coordinate is equal to CHAS multiplied by the sine of a, which is equal to δ multiplied by the sine of the difference between θ and α. The Z coordinate is equal to CHAS multiplied by the sine of ϕ multiplied by the sine of δ plus ϕ multiplied by δ multiplied by the difference between θ and α.

Angular coordinates in the target system

The azimuth angle a is equal to the arcsine of the sine of the difference between θ and α multiplied by the sine of ϕ divided by the cosine of ϕ multiplied by the tangent of δ (here the definition of quadrant is applied according to the conversion of Cartesian coordinates to polar coordinates). The altitude angle h is equal to the arcsine of the sine of ϕ multiplied by the sine of δ plus ϕ multiplied by δ multiplied by the difference between θ and α.

Conversion from rotating equatorial (α, δ) to ecliptic (λ, β, geocentric) coordinates

The Cartesian coordinates in the target system (X, Y, Z) are calculated as follows:

X = sin(ϵ) ⋅ sin(δ) + cos(ϵ) ⋅ cos(δ) ⋅ sin(α)
Y = cos(δ) ⋅ sin(α)
Z = -sin(ϵ) ⋅ sin(δ) + cos(ϵ) ⋅ cos(δ) ⋅ sin(α)

The angular coordinates in the target system are calculated as follows:

β = arcsin(Z)
λ = arccos(Y / cos(β))

Alternatively:

λ = arcsin(X / cos(β))

Ecliptic (λ, β, geocentric) → rotating equatorial (α, δ) coordinates

The Cartesian coordinates in the target system ( , ): α δ X sign equals sin α ⋅ because δ sign equals – sin ϵ ⋅ sin β + because ϵ ⋅ because β ⋅ sin λ y sign equals because α ⋅ because δ sign equals because β ⋅ because λ z sign equals sin δ sign equals because ϵ ⋅ sin β + sin ϵ ⋅ because β ⋅ sin λ The angular coordinates in the target system are as follows: δ sign equals arcsin ( because ϵ ⋅ sin β + sin ϵ ⋅ because β ⋅ sin λ ) α sign equals arctan ( because ϵ ⋅ sin λ – sin ϵ ⋅ tan β because λ ) > \ right)>

The celestial coordinate system is utilized in astronomy to describe the positions of celestial objects in the sky or points on an imaginary celestial sphere. Two angular quantities are used to provide the coordinates of these objects or points, uniquely defining their positions on the celestial sphere. Therefore, the celestial coordinate system is a spherical coordinate system where the third coordinate, distance, is often unknown and irrelevant.

Celestial coordinate systems vary from one another based on the selection of the fundamental plane (refer to “The fundamental plane”. Fundamental plane) and the origin. Depending on the specific task, it may be more convenient to use one system over another. The most commonly employed systems are the horizon and equatorial coordinate systems. Less frequently used are the ecliptic, galactic, and others.

Topocentric Coordinate System

The topocentric coordinate system is a horizontal coordinate system where the observer’s location on the Earth’s surface is the center, and the main plane is the mathematical horizon. One of the coordinates is the altitude of a celestial object, denoted as h, or its zenith distance, denoted as z. The other coordinate is the azimuth, denoted as A. Since the observer is always on the ground or at some elevation, the term “topocentric” is often omitted.

The height h of a celestial object is the arc of a vertical circle from the mathematical horizon to the object, or the angle between the plane of the mathematical horizon and the direction towards the object. Altitudes are measured from 0° to +90° towards the zenith and from 0° to -90° towards the nadir.

The angle between the plumb line and the direction to a luminary is called the zenith distance z. It can also be defined as the arc of the vertical circle from the zenith to the luminary. Zenith distances are measured in degrees, ranging from 0° to 180° from the zenith to the nadir.

Azimuth A is defined as the angle between the noon line and the line of intersection of the plane of the mathematical horizon with the plane of the vertical circle of the luminary. It is also known as the arc of the mathematical horizon from the south point to the vertical circle of the luminary. Azimuths are measured in the direction of the daily rotation of the celestial sphere, which is west of the south point. The range of azimuths is from 0° to 360°. Sometimes, azimuths are measured from 0° to +180° in the west direction and from 0° to -180° in the east direction. In geodesy, azimuths are measured from a point north.

Changes in celestial coordinates caused by the rotation of the celestial sphere

The height h, zenith distance z, azimuth A, and hour angle t of celestial objects are constantly in flux as the celestial sphere rotates. This is because these measurements are calculated from points that are not affected by the rotation. On the other hand, the declination δ, polar distance p, and right ascension α do not change with the rotation of the celestial sphere, but they may vary due to other motions of celestial objects that are not related to the daily rotation.

The initial equatorial coordinate system

This system is based on the plane of the celestial equator. One of the coordinates in this system is known as declination δ (sometimes referred to as polar distance p). The other coordinate is called hour angle t.

Declination δ of a celestial object represents the arc of the declination circle from the celestial equator to the object, or the angle between the plane of the celestial equator and the direction to the object. Declinations are measured from 0° to +90° towards the north pole of the world, and from 0° to -90° towards the south pole of the world.

Polar displacement d of the celestial object is the distance along the declination circle from the northernmost point of the globe to the celestial object, or the angle between the axis of the globe and the direction towards the celestial object. Polar displacements are measured from 0° to 180° from the northernmost point of the globe to the southernmost point of the globe.

The next equatorial coordinate system

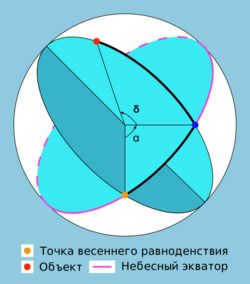
In this particular system, just like in the initial equatorial system, the primary plane is the plane of the celestial equator, and one of the coordinates is the declination δ (sometimes referred to as the polar distance p). Another coordinate is the right ascension α.

The right ascension (RA, α) of a celestial body is the arc of the celestial equator from the vernal equinox point to the celestial body’s declination circle, or the angle between the direction to the vernal equinox point and the plane of the celestial body’s declination circle. Right ascensions are measured in the opposite direction of the daily rotation of the celestial sphere, ranging from 0° to 360° (in degrees) or from 0 h to 24 h (in hours).

RA is similar to Earth’s longitude in astronomy. Both RA and longitude measure the east-west angle along the equator and both have a starting point at zero on the equator. While longitude uses the prime meridian as its zero point, RA uses the location in the sky where the Sun crosses the celestial equator at the vernal equinox.

Declination (δ) is one of the two coordinates in the equatorial coordinate system used in astronomy. It represents the angular distance on the celestial sphere from the plane of the celestial equator to the celestial object and is usually expressed in degrees, minutes, and seconds of arc. Declination is positive when north of the celestial equator and negative when south.

An object located on the celestial equator has a declination of 0°
The declination of the northern celestial pole is +90°
The declination of the southern celestial pole is -90°

The declination always has a sign, even if it is positive.

The declination of a celestial object that passes through the zenith is equal to the latitude of the observer (considering northern latitudes with a + sign and southern latitudes with a – sign). In the northern hemisphere of the Earth, for a given latitude φ, celestial objects with a declination δ > +90° – φ do not go beyond the horizon, so they are referred to as non-setting objects. However, if the declination of an object δ < -90° + φ, then the object is referred to as a non-descending object and is therefore not observable at latitude φ. [1]

Ecliptic coordinate system

The ecliptic coordinate system is based on the main plane known as the ecliptic plane. It uses two coordinates: ecliptic latitude (β) and ecliptic longitude (λ).

Ecliptic latitude (β) represents the arc of the circle of latitude from the ecliptic to the luminary, or the angle between the direction to the luminary and the ecliptic plane. It ranges from 0° to +90° towards the north pole of the ecliptic, and from 0° to -90° towards the south pole of the ecliptic.

The position λ of a celestial body is measured by the angle it makes with the vernal equinox point and the circle of latitude of the body. This angle is known as the ecliptic longitude. Ecliptic longitudes are measured in the direction of the Sun’s annual motion along the ecliptic, from the vernal equinox point to the east, and range from 0° to 360°.

In the Galactic Coordinate System, the primary plane is the plane of our Milky Way Galaxy. This system uses two coordinates: galactic latitude (b) and galactic longitude (l).

Galactic latitude (b) measures the angle between the plane of the galactic equator and the direction to a celestial object, or the arc of the circle of galactic latitude from the ecliptic to the object.

Galactic latitudes range from 0° to +90° for the north galactic pole, and from 0° to -90° for the south galactic pole.

The galactic longitude l of a celestial object is the angle measured along the galactic equator from the reference point C to the circle representing the object’s galactic latitude. It can also be defined as the angle between the line connecting the reference point C and the galactic latitude circle. Galactic longitudes are measured counterclockwise when observed from the north galactic pole, ranging from 0° to 360°, with the reference point C at the easternmost position.

The origin point C is situated near the direction leading to the center of the galaxy, but it is not exactly the same, as the latter is positioned approximately 1° south of the galactic equator due to the slight elevation of the solar system above the galactic disk plane. The chosen location for the origin point C is such that the intersection point of the galactic and celestial equators, with a direct ascent of 280°, corresponds to a galactic longitude of 32.93192° (at epoch 2000).

The equatorial coordinates of the origin point C at epoch 2000 are:

Historical Background and Practical Use

The concept of celestial coordinates has been utilized since ancient times. Various systems of celestial coordinates were documented in the works of Euclid, an ancient Greek mathematician, around 300 B.C. Additionally, the positions of 1022 stars in the ecliptic system of celestial coordinates were recorded in Hipparchus’ star catalog, which was published in Ptolemy’s Almagest.

Application of various coordinate systems

Utilization of the horizontal topocentric coordinate system

The horizontal topocentric coordinate system is employed by an observer situated at a specific location on the Earth’s surface to ascertain the location of a celestial body in the sky.

The coordinates of celestial bodies in this coordinate system can be obtained using angular measuring instruments and by observing through a telescope mounted on an azimuthal rig.

Most astronomical computer programs have the capability to determine the positions of celestial bodies in a given coordinate system.

It is important to consider refraction correction when conducting observations.

Using the initial equatorial coordinate system

The initial equatorial coordinate system is employed to determine accurate timing and for observations conducted with a telescope mounted on an equatorial mount.

Using the alternate equatorial coordinate system

The alternate equatorial coordinate system is a widely used coordinate system in the field of astrometry.

In the equatorial heliobiocentric coordinate system, modern star maps are created and the positions of celestial objects in catalogs are described. This involves aligning the coordinates of celestial objects to a specific point on the celestial equator and the vernal equinox, which corresponds to a specific epoch (in astronomy, the B1950 and J2000.0 epochs are commonly used).

The equatorial geocentric coordinate system is distinguished from that of the equatorial heliobiocentric coordinate system by the inclusion of corrections for the annual parallax phenomenon in the star coordinates, as well as the adjustment of the celestial equator and vernal equinox to the present date.

Application of the ecliptic coordinate system

The geocentric ecliptic coordinate system is employed in celestial mechanics for the computation of the Moon’s orbit.

The heliocentric ecliptic coordinate system is utilized for calculating the trajectories of the planets and other celestial bodies revolving around the Sun.

Practically, it is often required to employ multiple coordinate systems. For instance, in order to determine the Moon’s location in the celestial sphere, one must initially compute the Moon’s coordinates in the ecliptic geocentric coordinate system, transform the coordinates into the equatorial geocentric coordinate system, and subsequently convert them to the horizontal topocentric coordinate system.

Discover more

Share your thoughts on the article “Celestial coordinate system”

Additional information

↑Siegel F. Yu. A Guide to Constellations and the Moon: Treasures of the Starry Sky / Edited by G. S. Kulikov. – 5th edition. – Moscow: Nauka, 1986. – pp. 57-58. – 296 pages. – 200,000 copies.

Literature

Excerpt describing the celestial coordinate system

Boris was completely unaware of the Boulogne expedition; he hadn’t read the newspapers, and it was the first time he had heard of Villeneuve.
– In Moscow, we are more preoccupied with dinners and gossip than with politics,” he said in a calm, mocking tone. – I don’t have any knowledge about it, and I don’t have any opinion about it. Moscow is more consumed by gossip than anything else,” he continued. – Now, they are talking about you and the Count.
Pierre smiled kindly, as if concerned for his conversation partner, fearing that he might say something he would regret. But Boris spoke clearly and directly, looking directly into Pierre’s eyes.
– Moscow has nothing else to occupy itself with except gossip,” he continued. – Everyone is busy speculating about who the Count will leave his fortune to, although perhaps he will outlive all of us, which I sincerely hope….
– Yes, it’s all very challenging,” said Pierre, “very challenging. – Pierre was afraid that the officer might unintentionally engage in a conversation that would be embarrassing for him.
– And it must appear to you,” said Boris, blushing slightly but maintaining his voice and posture, “it must appear to you that everyone is simply trying to get something from the wealthy man.
“Indeed it does,” thought Pierre.
– But I want to tell you, to avoid any misunderstandings, that you would be very mistaken if you considered me and my mother among those people. We are very poor, but at least speaking for myself: it is because your father is rich that I do not consider myself related to him, and neither I nor my mother will ever ask for or accept anything from him.
Pierre could not comprehend for a long time, but when he did, he jumped up from the sofa, grabbed Boris’s arm from below with his usual quickness and clumsiness, and, blushing even more than Boris, began to speak with a mix of shame and annoyance.
– What a strange thing to say! Didn’t I–and who could have thought–I know very well…?
But Boris interrupted him once again:
– I’m glad I’ve been completely honest. It may be unpleasant for you, and I apologize,” he said, soothing Pierre instead of being soothed by him, “but I hope I haven’t offended you. I have a habit of speaking my mind directly–how should I put it? Will you come to dine at the Rostovs’?
And Boris, seemingly relieved of a heavy burden and having extricated himself from an awkward situation while putting Pierre in one, became perfectly agreeable again.
– ‘No, listen,’ said Pierre, calming down. – You are an incredible man. What you just said is very admirable, very admirable. Of course, you don’t know me. It’s been so long since we’ve seen each other…we were still children… You may have made assumptions about me… I understand you, very much. I wouldn’t have done it, I wouldn’t have had the courage, but it’s beautiful. I’m very glad to have met you. It is strange,” he added, after a moment of silence, smiling, “what you presumed about me! – He laughed. – ‘Well, we will get to know each other better. Please. – He shook hands with Boris. – You know I have never been to the Count’s house. I feel sorry for him as a man. But what can I do?
– And do you think Napoleon will have enough time to transport the army?” Boris asked, smiling.
Pierre realized that Boris wanted to change the topic of conversation, and he agreed with him, starting to outline the advantages and disadvantages of the Boulogne enterprise.
The footman came to summon Boris to the Princess. The Princess was leaving. Pierre promised to come to dinner later to get to know Boris better, shook his hand firmly, and looked affectionately into his eyes through his glasses… After Boris left, Pierre walked around the room for a long time, no longer picturing himself fighting an invisible enemy with a sword, but smiling at the memory of this pleasant, intelligent, and resolute young man.
As often happens in one’s youth, and especially when one is in a lonely position, he felt an irrational tenderness towards this young man and promised himself to make sure to befriend him.
Prince Vasily saw the Princess off. The Princess held her handkerchief to her eyes, and her face was wet with tears.
– It’s terrible! Terrible! – she said, – but no matter the cost, I will do my duty. I will come tonight. He cannot be left like this. Every minute is precious. I don’t understand why the duchesses are hesitating. Perhaps God will help me find a way to prepare him!… Farewell, prince, may God support you.
– Farewell, my good lady,” Prince Vasily replied, turning away from her.
– Ah, he is in a terrible state,” said the mother to her son when they were seated in the carriage again. – ‘He hardly recognizes anyone.
– I don’t understand, mother, what is his relationship to Pierre?” the son asked.
– The will shall reveal everything, my friend; our fate depends on it….
– But what makes you think he will leave us anything?
– Oh, my friend! He is so wealthy, and we are so poor!
– Well, that’s not reason enough, mother.
– Oh, my God! Oh, my God! Oh, my God! How awful he is!” exclaimed the mother.

Before a dinner party, there comes a moment when the guests, while waiting for the call to eat, engage in short conversations but also feel the need to move around and avoid silence, in order to demonstrate that they are not eager to sit down at the table. The hosts, meanwhile, keep their eyes on the door, occasionally exchanging glances with one another. The guests, observing these glances, attempt to deduce who or what else they are waiting for: perhaps a significant late arrival or a dish that is not yet prepared.

Blog ❘ Serious Astrology ❘ Math of the Celestial Sphere ❘ Spherical Geometry

This article will provide an overview of the equatorial, elliptical, and horizontal coordinate systems, which are three different types of spherical coordinate systems.

The Celestial Sphere

The celestial sphere is a fictional dome where stars and planets are projected. It can be visualized as the gigantic dome of a planetarium, with the observer situated at its center.

You are aware that the Earth rotates on its axis. However, from the perspective of an Earth observer, it appears that this celestial sphere completes a full revolution in 24 hours while the Earth remains motionless.

The axis of rotation of the celestial sphere aligns with that of the Earth and approximately points towards Polaris. This direction is referred to as the North Pole (P). Consequently, the celestial hemisphere facing the North Pole is known as the northern hemisphere.

Describing positions in space using spherical coordinates

When it comes to locating celestial bodies on the celestial sphere, a spherical coordinate system can be used. This system involves representing the position of a planet or star using two angular arcs, or angles. Here’s how it works:

First, the celestial sphere is divided into two equal parts, namely the northern and southern hemispheres.
Next, a starting point, which is typically referred to as zero degree, is selected on the dividing circle.
Lastly, the position of a star or planet is projected onto the separation circle.

The first coordinate (latitude) represents the angular arc of the projection, also known as the vertical angle. The second coordinate (longitude) represents the angular arc from the starting point to the projection point.

Equatorial plane

Celestial equator refers to the plane that divides the celestial sphere into two equal parts, effectively separating the northern and southern hemispheres. This dividing circle is also known as the celestial equator.

Because the equator is in constant motion along with the globe, one of the equatorial degrees appears above the eastern horizon every minute. As a result, astrologers refer to any degree of the equator as right ascension, RA. This term is used to differentiate it from the so-called “oblique ascension,” which we will discuss later.

Traditionally, the north/south deviation from the equator is known as the declination, dec.

When a planet is rising, meaning it is exactly on the horizon, its RA is typically either below or above the horizon.

In astrology, we often focus on the equatorial degree that is rising at the same time as the planet. This degree is referred to as the oblique ascension, OA.

The difference between oblique ascension and oblique ascension is known as the ascension difference, AD (ascension difference).

Ecliptic plane

Throughout the year, the Earth revolves around the Sun in its orbit. This orbit is referred to as the ecliptic plane.

From the perspective of an Earth observer, it appears that the Sun completes a full revolution around the Earth against a backdrop of fixed stars in the celestial sphere. The path that the Sun follows throughout the year is called the ecliptic circle.

Celestial longitude and latitude

The planets in our Solar System all orbit around the Sun in a shared plane known as the ecliptic plane. This can be observed in Figures 1, 2, and 3, where the planets appear to align along a near-continuous line.

The ecliptic plane is also referred to as the Zodiac, which is the circle encompassing the zodiacal degrees of the ecliptic. Celestial latitude, or lat, represents the north/south deviation from the ecliptic, while celestial longitude, or lon, signifies the degree of the Zodiac along the ecliptic.

Tilt of the ecliptic

The tilt of the Earth’s axis of rotation around the Sun differs from its axis of rotation around its own axis, causing a slight deviation between the plane of the celestial equator and the plane of the ecliptic. This deviation is known as the ecliptic tilt, which measures approximately 23-24° depending on the epoch.

Astronomers have unanimously agreed to designate the intersection of the ecliptic and the equator as the reference point for both equatorial and ecliptic coordinates.

When the Sun occupies this point, day and night are of equal length. Let’s explore the reasoning behind this phenomenon.

During the day, all the planets and stars rotate in parallel to the celestial equator. This means that when the Sun is at 0° Aries, it is also located on the celestial equator. As a result, the Sun follows the equatorial circle on this day, which is divided into two equal parts by the horizon.

It is evident that any point on the equator spends exactly 12 hours above the horizon and 12 hours below it as the celestial sphere moves. The same principle applies to the Sun at 0° Aries (and at 0° Libra). Hence, these points of the Zodiac are traditionally referred to as the equinox points, when day and night are of equal length.

Astrologers have unanimously decided to refer to the horizontal longitude, also known as the angle of deviation from the North, as the azimuth, while the deviation up or down from the horizon is referred to as the altitude.

The azimuth degrees progress clockwise from North to East, just like a compass, and the altitude of a celestial object above the horizon is considered positive, while below the horizon it is considered negative.

Below is a lovely image that illustrates all three types of coordinates for the same point.

Related Posts:

Further Reading

The celestial bodies that control the entrance to the heavens

Water energized by celestial entities

09. Mechanism of gravitational pull between objects in celestial environments

Four Celestial Creatures

THE UPRISING OF THE DIVINE DEITIES

Heliocentric coordinate system

Part Two 72 Celestial Envoys

Calculating the position of celestial bodies through careful observation

The dominant impact of massive celestial entities and the subordinate impact of colossal celestial entities.

The potency of heavenly angels

Regarding the wisdom possessed by celestial beings

Mind-altering perspective

Table of Contents