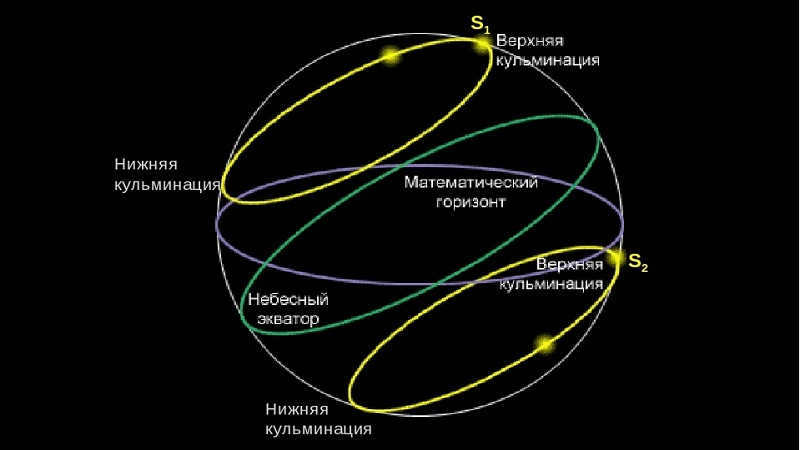
Every celestial body passes over the celestial meridian twice within a 24-hour period as it moves across the sky. When the center of a celestial body crosses the celestial meridian, it is said to reach its culmination. Culmination, derived from the Latin word for “top,” refers to the highest point of the celestial body’s path. There is a distinction between the highest and lowest points of a celestial body’s path, known as the upper and lower culmination respectively.
Fig. 1.23. Culmination of celestial bodies: a – south of the zenith; b – north of the zenith.
In the upper culmination, the luminary reaches its highest point, while in the lower culmination, it reaches its lowest point. When it comes to non-ascending luminaries, both culminations take place above the horizon. As for ascending and descending luminaries, the upper culmination happens above the horizon, while the lower culmination occurs below the horizon. In the case of non-ascending luminaries, both culminations occur below the horizon, making them impossible to observe.
The highest point of a celestial object’s path can occur between the point directly overhead and the southern point on the meridian, or between the point directly overhead and the northern point on the meridian. Figure 1.23 illustrates the celestial sphere. The primary circles are represented by diameters and chords. The figure demonstrates that luminaries with a declination less than the latitude of the location culminate to the south of the point directly overhead, while luminaries with a declination greater than the latitude of the location culminate to the north of the point directly overhead.
At the moment of the celestial object’s highest point, the hour angle is 0, and at the moment of its lowest point, the hour angle is 180 degrees. The azimuth of the celestial object at its highest point is 0 degrees if it is north of the point directly overhead, and 180 degrees if it is south of the point directly overhead.
When the luminary reaches its highest point in the sky to the south of the point directly overhead, you can calculate the altitudes at the time of both the upper and lower culminations using the following formulas:
When the luminary reaches its highest point in the sky to the north of the point directly overhead, you can calculate the altitudes at the time of both the upper and lower culminations using the following formulas:
By generalizing the formulas for calculating the luminary’s altitude at the moment of the upper culmination, we can derive the formula . The plus sign before the bracket is used when the luminary culminates to the south of the zenith, and the minus sign, – , is used when it culminates to the north.
The altitude at the moment of the lower culmination for all luminaries is determined using the same formula.
The formula for determining the altitude of a celestial body during its highest point in the sky, known as its upper culmination, is of great practical importance. By calculating the altitude of the celestial body at the time of its upper culmination and comparing it with the measured altitude at that same moment, one can determine the correction needed for the sextant. Additionally, if the declination of the celestial body is known, the altitude measured at the time of culmination can be used to determine the latitude of the observer’s location. Formulas for calculating the altitudes of celestial bodies at both their upper and lower culminations establish a relationship between the observer’s latitude, the Sun’s declination, and its altitude.
The formulas we have considered reveal that when the Sun’s declination reaches its extreme values, which are equivalent to its height at the moment of upper culmination, the Sun will be directly overhead at geographic latitudes of 90°. This means that the Sun will culminate in the zenith. On a specific geographic parallel, with a northern latitude of [insert northern latitude value], the Sun will culminate in the zenith during the summer solstice. Conversely, on another geographic parallel, with a southern latitude of [insert southern latitude value], the Sun will culminate in the zenith during the winter solstice. The geographic parallel with a northern latitude of [insert northern latitude value] is known as the northern tropic, or the tropic of Cancer. Similarly, the geographic parallel with a southern latitude of [insert southern latitude value] is known as the southern tropic, or the tropic of Capricorn. It is important to note that these constellations were once considered to be the solstice points several centuries ago.
It can be observed from formulas that when the Sun’s declination is at its maximum, its height at the moments of culmination on different latitudes is zero. On a specific geographical parallel, the Sun’s height is zero at the time of the lower culmination on the day of the summer solstice and at the time of the upper culmination on the day of the winter solstice. Consequently, on this parallel, the Sun neither sets nor rises during these days. This particular parallel is known as the Arctic Circle.
Similarly, on another geographical parallel, the Sun is a non-setting luminary on the day of the winter solstice and a non-rising luminary at the time of the summer solstice. This parallel is referred to as the South Polar Circle.
Example 1. Find the elevation of star Deneb during the upper and lower culminations, based on the star’s declination and the latitude of the observer’s location.
Solution 1. Calculate the star’s position relative to the zenith during the upper culmination, considering that the star culminates north of the zenith.
2. Determine the star’s elevation during the upper culmination:
3. Calculate the star’s altitude during the lower culmination: . Since the star Deneb rises and sets at this latitude, its elevation during the upper and lower culminations will have different signs.
Example 2. Given the date of June 22, the Sun’s declination, and the latitude of Leningrad, calculate the height of the Sun during the upper and lower culminations.
Solution 1. Determine the Sun’s position in relation to the zenith during the upper culmination. In this case, the Sun reaches its highest point south of the zenith.
2. Calculate the Sun’s elevation during the upper culmination.
3. Calculate the Sun’s elevation during the lower culmination.
Based on the given example, we can observe that at the latitude of Leningrad on the summer solstice, the Sun does not dip below the horizon lower than the Sun’s altitude minus 6 degrees. This means that during summer in Leningrad, the twilight lasts almost the entire night, resulting in the phenomenon of white nights.
Example 3. Consider the star Vega, with a declination that corresponds to the latitude of the observer’s location. Calculate the star’s elevation during the upper and lower culminations.
New Solution. Firstly, we need to determine the star’s position relative to the zenith at the time of its upper culmination. Given that the star’s declination is lower than the observer’s latitude, it culminates south of the zenith.
Secondly, we need to calculate the star’s height at the moment of its upper culmination.
Thirdly, we need to determine the star’s altitude at the time of its lower culmination.
It’s worth noting that at this latitude, the star Vega does not set as its altitude is positive during both upper and lower culminations.
ACADEMIC DISCIPLINE: ASTRONOMY
Please familiarize yourself with the lecture material on this topic.
Now, let’s answer the following test questions:
1. When does a luminary cross the celestial meridian?
2. How many times do luminaries cross the celestial meridian during their daily motion?
3. When a luminary reaches its highest point south of the horizon, what is the measure of the MOS angle?
4. To determine the geographic latitude of an observing site, what information do you need?
- The luminary’s culmination
- The declination and altitude of the luminary at its culmination
- The declination of the luminary
5. If we are in northern latitudes, what will be the elevation of the pole of the world above the horizon?
During their daily rotation around the axis of the world, the luminaries pass the celestial meridian twice. This occurrence of a luminary crossing the celestial meridian is known as culmination.
There is a difference between the upper and lower culmination. In the upper culmination, the celestial body is at its highest point above the horizon, closest to the zenith. The lower culmination, on the other hand, occurs when the celestial body is further away from the zenith than during the upper culmination, and it happens half a day after the upper culmination.
The point where the diurnal path of the celestial body intersects with the eastern part of the true horizon is known as the sunrise point, while the point where it intersects with the western part of the true horizon is called the sunset point.
Stars that do not rise are observable at the highest points (M2M2, M3M3) and lowest points (M′2M2′, M′3M3′). When stars rise and set, the lowest point (M′1M1′) passes below the horizon. In stars that do not rise, both highest points M4M4 and M′4M4′ are not visible, meaning they occur below the horizon.
Now, let’s discover the connection between geographic and celestial coordinates.
When the luminaries reach their highest point in the sky, they are located at the intersection of the celestial meridian, which is the same plane as the celestial meridian. The paths that stars follow throughout the day are represented by segments that are parallel to the celestial equator QQ′QQQ′. If we consider a star that rises and sets at its highest point of M1M1, the altitude of the celestial pole is equal to the geographic latitude φφ. The angle ∠ QOS ∠ QOS is 90°-φ90°-φ and represents the inclination of the celestial equator in relation to the horizon. The arc M1SM1S (or ∠ M1OS ∠ M1OS) represents the height of the star above the horizon. This arc is composed of two smaller arcs: M1S=SQ+QM1M1M1S=SQ+QM1. Since the arc SQSQ, which rests on ∠ QOS ∠ QOS, is equal to 90°-φ90°-φ, and the arc QM1QM1 represents the angular distance of the star from the celestial equator and is determined by the declination δδ, we can derive a formula to calculate the height of the star at its highest point:
To measure the lower culmination M2′M2′ of a non-setting star, we can use the arc M2′NM2′N or the corresponding central angle (∠ M2′ON). This angle is equal to the difference (∠ M2′OQ′ ∠ NOQ′), where ∠ M2′OQ=δ is the angular distance of the star from the celestial equator, and ∠ NOQ′=90°-φ is the inclination of the celestial equator to the horizon plane. Therefore, the altitude of the star at the lower culmination can be calculated as follows:
If both culminations of a non-setting star, such as M3M3 and M3′M3′, are on the same side of the zenith, the upper culmination can be determined using the equation: h B =180°-[(90°-φ)+δ], or simplified as:
The relationships hB = (90° – φ) + δ, hH = δ – (90° – φ), and hB = 90° + φ – δ relate geographic latitude to the altitude and declination of the stars at the time of their culmination. Note that the azimuths of the stars in the upper culmination of M1 and M2 are 0°, and the azimuths of the stars in the lower culmination of M1′ and M2′ are 180°. The azimuths of the star M3 in the upper and lower culminations are equal to 180°.
As it turns out, not everyone is familiar with the concept of star culmination. By definition, culmination refers to the highest point or peak of something. In astronomy, it specifically refers to the highest point of motion of a celestial object.
Therefore, the culmination of a star is the moment when it passes through the celestial meridian during its daily motion.
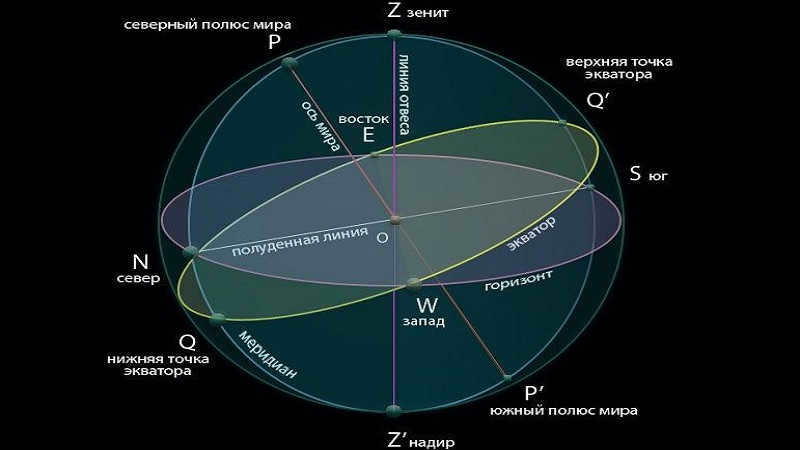
It is important to note that the celestial meridian is a circle on the celestial sphere that passes through the zenith, the celestial north pole, the celestial south pole, and the nadir.
The celestial north pole can be thought of as the starting point. It is located on the celestial sphere, and around it, there is a visible daily movement of stars. These stars move in a circle that is parallel to the celestial equator.
Both on Earth and in space, there is always something to observe. For instance, there are Netflix shows that are sure to captivate your attention.
The Meaning of Stellar Culmination
Every celestial body passes through the meridian of the sky twice a day, which is known as stellar culmination. This event occurs when a luminary reaches its highest point in the sky.
The time elapsed between these two crossings is exactly half a day, or 12 hours.
Since stellar culmination happens twice daily, it can be classified into two types:
- Upper culmination, which takes place when a celestial body reaches its maximum altitude;
- Lower culmination, on the other hand, occurs when a star’s altitude is at its minimum.
Calculation of Stellar Culmination
Calculating the culmination of stars involves determining the moment when a stellar body intersects the celestial meridian. This can be done by considering the height of the world pole above the horizon, which is equal to the geographic latitude of the area.
To calculate the upper and lower culmination of a star, the following formula is used:

Formulas for calculating culminations
Given that h represents the altitude, f represents the geographic latitude, and δ represents the declination.
It appears that once the declination and altitude of the star during culmination are known, it is possible to compute the geographic latitude of the location where the observations are conducted.
Interestingly, a star that does not set for a specific geographic latitude can be observed during both upper and lower culmination. However, if the celestial body is positioned further away from the celestial equator towards the south, its intersection with the meridian may not be easily noticeable.

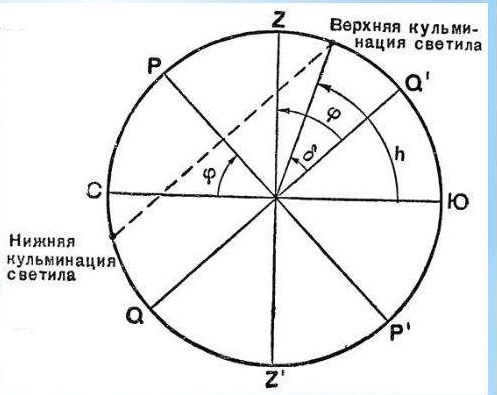
To gain insight into the phenomenon of stars culminating, we can turn our attention to our primary celestial body. The Sun serves as a simple example in this regard. Like other stars, it reaches its highest point in the sky, known as the celestial meridian, twice a day. These moments are undoubtedly familiar to us all. Firstly, we have the upper culmination of the Sun which occurs at noon. Secondly, after a span of twelve hours, we experience the lower culmination, also known as midnight.
It is evident that humans have been observing the movements of celestial objects for a considerable amount of time. Through careful observation, they have identified distinct patterns and learned to interpret them in various aspects of their lives. In general, the act of observing the mysterious and radiant points of light in the night sky, along with the celestial sphere and the vast cosmos, is an incredibly captivating and awe-inspiring experience.
Let’s proceed with discussing the culminations of the luminaries. The fundamental principles can be located in the initial article on culminations.
Southward Upper Culmination of the Zenith
As we are aware, the elevation of the pole of the globe above the horizon is equivalent to the latitude of the observation location. NS represents the plane of the mathematical horizon, PP’ is the axis of the globe, and P is the north pole of the globe. Consequently,
where φ represents the latitude of the observation location. Then
∠NOQ’ = β = 90° – φ = ∠SOQ (as vertical).
Since QQ’ denotes the celestial equator and KK’ represents the diurnal parallel of the luminary, hence
Our objective is to determine the relationship between the luminary’s altitude above the horizon at the moment of its upper culmination south of the zenith, based on the latitude of the observation location and the declination of the luminary. Thus, we are concerned with
The luminary’s height above the horizon during its upper culmination south of the zenith is equal to 90° minus the latitude plus the declination.
h = 90° – φ + δ
Upper culmination north of the zenith
After evaluating the findings from our previous analysis, we have come to the understanding that
∠NOK equals h, which is equivalent to ∠POK plus ∠NOP, or 90 degrees minus δ plus φ
The measurement of the luminary’s height above the horizon during the upper culmination north of the zenith is given by the equation h = 90 degrees minus δ plus φ
When the luminary reaches its lowest point north of the nadir
The height of the celestial body above the horizon during its lowest point south of the nadir is given by the formula: h = φ + δ – 90°
When the celestial body is at its lowest point south of the nadir
It is crucial to understand that the luminary’s declination is negative and the altitude should be negative as well.
However, since the declination is negative and the altitude should be negative, ∠K’OP’ = -90° – δ
But since the altitude should be negative, then ∠K’OS = -90° – δ – φ.
The altitude of the luminary above the horizon at the time of the lower culmination south of the nadir is given by h = -φ – δ – 90°.
Lesson Objective: To demonstrate that the height of the pole of the world hP above the horizon is always equal to the geographic latitude of the observation location, to understand the concept of the luminary’s culmination, and to derive a formula connecting values from different coordinate systems.
Educational: The purpose of this activity is to review key concepts from the geography course, such as geographical latitude, longitude, the Earth’s rotation axis, the Earth’s north and south poles, and the Earth’s equator.
Developing: This activity aims to draw an analogy between the elements of the Earth globe and the celestial sphere, develop attention and speech skills, and improve the ability to work independently. It also aims to instill the ability to apply formulas in solving calculation problems with construction.
Educational: The goal of this activity is to form a holistic view of the world, including nature, society, and self. It also aims to highlight the role and place of astronomy in the system of sciences.
Equipment: For this activity, you will need a globe, a demonstration map of the starry sky, a model of the celestial sphere, movable starry sky maps (handouts), a teacher’s computer, a multimedia projector, and the “Astronomy” disk.
Progress of the lesson
1. Organizational moment
2. Capturing the attention of students
The topic of our lesson is “Visible motion of stars at different geographical latitudes”.
Today we will be studying how the height of the North Pole above the horizon, denoted as hP, and the geographic latitude of the observation location can be linked using a formula that connects values from different coordinate systems.
3. Knowledge Base Update
What are the terms for measuring the north-south and east-west positions on Earth?
How can you determine the exact location of a point on Earth’s surface using a globe?
Draw a comparison between the equatorial coordinates of stars and the geographic coordinates of a point on Earth (geographic latitude corresponds to declination, longitude to right ascension).
Exploration of New Material
1. Relationship between the height of the North Pole and the geographic latitude of the observation location
The apparent motion of the sky is caused by the Earth’s rotation on its axis, which is in the opposite direction of the daily rotation of the celestial sphere. This means that no matter where an observer is on the Earth’s surface, they will always see the celestial sphere rotating around the world axis, which is parallel to the Earth’s axis of rotation.
When an observer moves on the Earth’s surface, the direction of the plumb line changes, resulting in different angles with the axis of rotation. The arrangement of circles and points on the celestial sphere that are connected to the world axis and the plumb line depend on the direction of the plumb line, which is determined by the observer’s position on the Earth’s surface.
This relationship can be stated as follows: “The height of the world pole hP above the horizon is always equal to the geographic latitude cf of the place of observation”.
The proof of this theorem can be seen directly from the diagram (Fig. 6), where Ð PON = hP and Ð OTq = j — are angles with sides that are perpendicular to each other. As a result of this theorem, the astronomical latitude of the observation site j is also equal to (Fig. 7):
1) zenith declination d Z = j ;
2) polar distance of the north point рN = j ;
3) zenith distance of the upper equatorial point zQ = j .
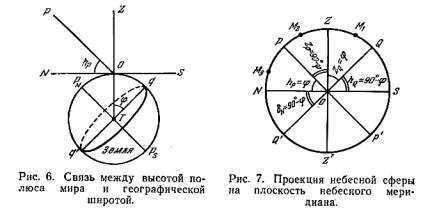
According to equation (1.1), the zenith distance of the world pole zP is equal to 90° – hP = 90° – j .
Therefore, the value of (90° – j ) can also be expressed as:
1) polar zenith distance pZ = 90° – j ;
2) declination of the north point hQ = 90° – j ;
3) height of the upper point of the equator hQ = 90° – j .
Height of the luminary at the culmination
Because of the daily rotation of the celestial sphere, all celestial objects move in circles that are parallel to the plane of the celestial equator. This means that they move along the same paths in the sky. In most cases, the part of their path that is below the horizon is not visible to observers.
The point where the diurnal parallel of the luminary intersects with the eastern part of the horizon is referred to as the luminary’s sunrise point, while the point where it intersects with the western part of the horizon is known as the luminary’s sunset point. The diurnal parallel intersects the celestial meridian at two points. The phenomenon of a luminary crossing the celestial meridian is called the luminary’s culmination. This culmination can be classified as upper if the luminary crosses the upper part of the meridian PZQSP’, where the zenith point Z is located, and lower if the luminary crosses the celestial meridian in its lower part PNQ’Z’P’, which contains the nadir point Z’. If the lower culmination occurs above the horizon (h > 0), the luminary is referred to as a non-setting luminary, and if even during the upper culmination the luminosity is below the horizon (h < 0), it is called a non-ascending luminary. Therefore, all luminaries on the celestial sphere can be categorized into three main groups – non-ascending, non-descending, and luminaries that rise and set (Fig. 8). The classification of a luminary into one of these groups is determined by its declination and the latitude of the observation location.
Fig. 8. The arrangement of luminaries that are not on the horizon and those that are on the horizon in a projection on the celestial meridian plane.
Transformation of luminary coordinates during daily movement
Horizontal coordinates
Highest point (refer to Fig. 9): A=0 o,

Culmination of celestial bodies and determination of latitude [ edit correct code ]
Culmination of celestial bodies [ edit correct code ]
The culmination of a celestial body refers to the event when a celestial body passes the celestial meridian. As celestial bodies rotate around the Earth’s axis, they cross the celestial meridian twice a day.
The difference between the upper and lower culminations lies in the fact that during the upper culmination, the celestial body reaches its highest point above the horizon, closest to the zenith. On the other hand, during the lower culmination, the celestial body is further away from the zenith compared to the upper culmination point, and the lower culmination occurs half a day after the upper culmination. [1]
Height Formulas for Luminaries’ Upper and Lower Culminations [ edit edit code ]
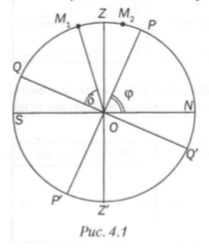
- Figure 4.1 shows the formulas for calculating the heights at the upper and lower culminations of luminaries in different scenarios:
a) When the star M 1 culminates between the zenith and the point south, the formula for the upper culmination height is h = (90° – φ) + δ – ϕ.
b) When the star M 2 culminates between the zenith and the pole of the world, the formula for the upper culmination height is 90° – δ + φ – ϕ.
| Upper | h = ( 90 ∘ – φ ) + δ -\varphi ight)+\delta > | 90 ∘ – δ + φ -\delta +\varphi > |
| Lower | δ – ( 90 ∘ – φ ) – \varphi ight)> | δ + φ – 90 ∘ > |
Star observation conditions at 55 degrees north latitude [ edit edit code ]
The 55th parallel of northern latitude is an imaginary line that extends across the Earth’s northern hemisphere. During the summer solstice at this latitude, there are 17 hours and 22 minutes of daylight, while during the winter solstice, there are only 7 hours and 10 minutes [2]. This means that the winter sky can be observed for a significant amount of time, considering the shortness of the day. Additionally, it is important to note that being at 55 degrees north latitude brings us closer to the North Pole, making the northern part of the sky more visible.
Supplementary Questions [ edit edit code ]
- Create a dynamic star chart for the specific day and time of your class in your area, and identify several constellations that will be at their highest and lowest points. Record the information in the provided table
Location: Moscow, Russia
Highest Point: Magus, Hercules, Big Dipper, Dragon, Swan.
Lowest Point: Aquila, Lyra, Sagittarius, Scorpio, Zme.
- Calculate the geographic latitude of your observation location based on the following scenarios: a) When the star Vega is directly above you; b) When the star Sirius is at an altitude of h=64°13′ below the zenith; c) When the star Deneb is at an altitude of h=83°47′ above the zenith; d) When the star Altair is directly above you.
a) When a star passes directly overhead (through the zenith), the latitude of the location is equivalent to its declination δ = +38°47′.
b) Sirius has a declination of δ = -16°43′. To determine the latitude of the area, subtract the declination from 90°: 90° – 64°13′ – 16°43′ = +9°4′.
c) The declination of Deneb is δ = +45°17′. To find the latitude of the location, subtract 90° from 83°47′ and add the declination: 83°47′ – 90° + 45°17′ = 39°4′.
- Complete Figure 4.2 with the necessary diagrams and labels illustrating the daily motion of stars at different latitudes
This is an empty page with the solution to the problem. Please help me input the answers!

It is common knowledge that Polaris, which is situated near the North Pole of the Earth, maintains a relatively consistent elevation above the horizon at a given latitude. However, as an observer starts to travel from north to south, where the geographic latitude is lower, Polaris will gradually lower towards the horizon. It can be inferred, therefore, that there is a correlation between the elevation of the North Pole and the geographic latitude of the observation location. In this lesson, we will explore and establish this relationship. Additionally, we will discover the concept of a luminary’s culmination, as well as the rising and setting points of luminaries. Lastly, we will learn how to determine the geographic latitude of a region through astronomical observations.
Unfortunately, it is currently not possible to view or distribute the instructional video with students.
In order to access this and other video lessons included in the package, you will need to add it to your personal account.
Unlock amazing functionalities

Lesson Outline: The Observable Movement of Stars at Various Geographic Latitudes
During previous lessons, we were introduced to a star chart, which represents the projection of the celestial sphere onto a flat surface with celestial objects plotted using a specific coordinate system.
Typically, star charts are constructed using the celestial equator as the main circle of the celestial sphere. This system is known as the equatorial coordinate system, with coordinates referred to as declination and right ascension.
Furthermore, we have acquired knowledge that the starry sky undergoes a daily rotation, and it has been observed that Polaris, situated near the North Pole of the Earth, maintains a relatively constant altitude above the horizon at a specific latitude. However, should an observer commence their journey from the northern region towards the southern region, where the geographic latitude is lower, Polaris will gradually descend towards the horizon.
Consequently, it is reasonable to presume that there exists a correlation between the height of the Earth’s pole and the geographic latitude of the observation location. In order to ascertain this correlation, let us examine a portion of the celestial sphere and the globe projected onto a plane of a celestial meridian.
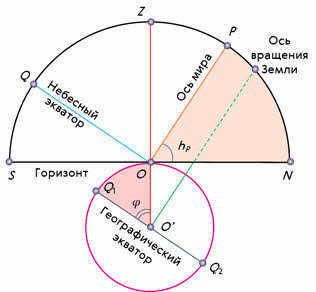
The position of the horizon on the celestial sphere can be determined by considering the world axis, the celestial equator, and the plumb line. The world axis, represented by the line OR, is parallel to the Earth’s axis of rotation. The projection of the celestial equator, represented by the line OQ, is parallel to the Earth’s equator. The plumb line, represented by the line OZ, is used as a reference point. An observer located at point O will see the pole of the world at an altitude equal to the angle NOP.
The angle formed by the plumb line and the geographic equator at the center of the Earth corresponds to the geographic latitude of the observer’s location.
Since the radius of the Earth at the observation point is perpendicular to the plane of the true horizon, and the world axis is perpendicular to the plane of the geographic equator, these two angles are equal to each other as angles with mutually perpendicular sides.
Therefore, it can be concluded that the angular height of a pole above the horizon is equal to the geographical latitude of the observation location.

To put it differently, by measuring the distance between the world pole and the horizon, we can easily determine the geographic latitude of the observation location.
Now, let’s consider the angle QOZ. From the diagram, it becomes evident that this angle represents the zenith’s declination, which is equivalent to the geographic latitude of the observation location and, consequently, the height of the world pole above the horizon.
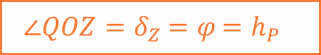
The equation obtained expresses the connection between the geographical latitude of the observer’s location and the corresponding horizontal and equatorial coordinates of the celestial body.
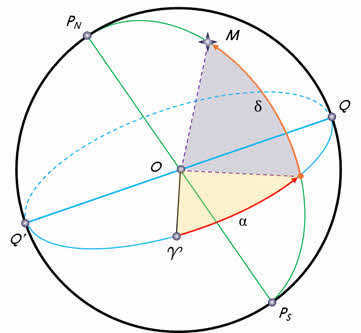
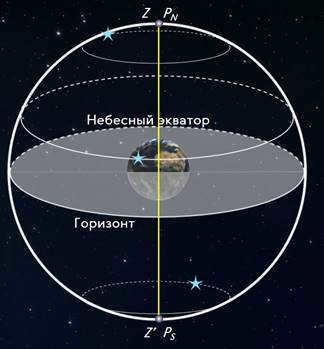
As mentioned in the previous lesson, the stars’ daily paths on the celestial sphere form circles with planes that are parallel to the celestial equator. The nature of the stars’ daily motion and the appearance of the night sky, however, differ depending on the observer’s location.
To grasp the concept of what occurs and how it unfolds at the Earth’s poles is most easily achieved. The pole serves as the point on the globe where the axis of the planet aligns with the plumb line, and the celestial equator aligns with the horizon. For an observer situated at the North Pole of the Earth, Polaris will be situated at the zenith, while the stars will traverse in circular patterns parallel to the mathematical horizon, which coincides with the celestial equator. As a result, all stars with positive declination will be visible above the horizon (conversely, at the South Pole, all stars with negative declination will be visible), and their altitude will remain constant throughout the day.
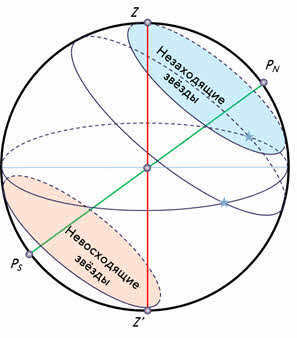
Now, let’s shift our attention to the middle latitudes, which are familiar to us. In this region, the Earth’s axis and the celestial equator are inclined towards the horizon. As a result, the paths of stars in the sky also appear inclined to the horizon. This means that observers at middle latitudes have the opportunity to witness the rising and setting of stars.
Rising is when the celestial body moves from the eastern part of the true horizon to the western part of the horizon.
In addition, certain stars found in the constellations that encircle the North Pole will never go below the horizon. These stars are commonly known as non-setting stars.
Similarly, stars situated near the South Pole from the perspective of an observer at mid-latitudes will be referred to as non-descending stars.
Let’s continue our journey to the equator, where the geographical latitude is zero. Here, the world axis aligns with the meridian (which is in the plane of the horizon), and the celestial equator passes directly overhead. The daily paths of all stars, without exception, are perpendicular to the horizon. As a result, an observer standing on the equator will have the opportunity to witness the rising and setting of all the stars throughout the day.
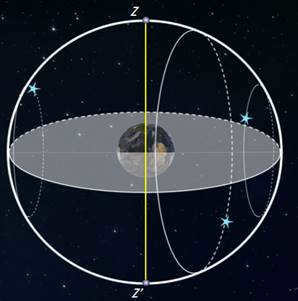
As a general rule, in order for a celestial body to rise and set, its declination must be less than a certain value.
If the declination is equal to this value, then in the Northern Hemisphere it will not rise (in the Southern Hemisphere it will not set).
Therefore, it is clear that celestial bodies with a declination of this value will not rise in the Northern Hemisphere (or will not set in the Southern Hemisphere).
For example, let’s determine the position of the star Delta Sagittarius for an observer located at latitude 55 degrees 15 minutes in terms of rising and setting.

During the daily rotation, all stars pass the celestial meridian twice. This occurrence is referred to in the field of astronomy as the luminous climax, also known as a luminous culmination.
It is customary to differentiate between the upper and lower culminations. At the moment of the upper culmination, the luminary reaches its highest point above the horizon, closest to the zenith. The lower culmination takes place twelve hours after the upper culmination.
Now, let’s derive a formula that can be used to calculate the altitude of the luminary during its upper and lower culminations. To accomplish this, we will utilize the celestial sphere and some of its principal lines.
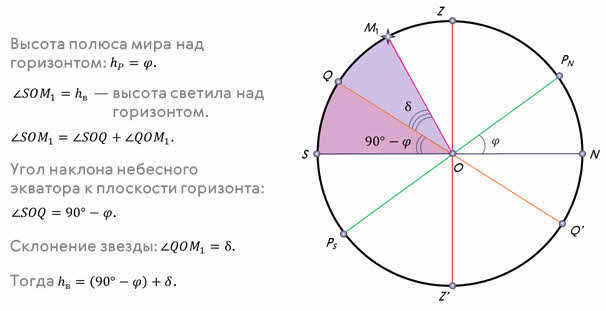
Using the same logic, we can derive an equation that calculates the altitude of the celestial body when it reaches its highest point north of the observer’s point:

By examining the two equations, one can easily deduce the universal equation for the altitude of a celestial body during its highest point in the sky:

It’s important to keep in mind that the sign “plus” before the brackets is used when the celestial body reaches its highest point to the south of the point directly overhead (known as the zenith), meaning its declination is lower than the latitude of the observer’s location. Conversely, the sign “minus” is used when the celestial body reaches its highest point to the north of the zenith.
We invite you to explore the formula for determining the altitude of the celestial body at the time of its lowest point.
It’s worth noting that by measuring the declination of the celestial body and its height at the moment of culmination, you can easily determine the geographical latitude of the observer’s location.
To reinforce the material, let’s solve this problem.
Let’s proceed with discussing the culmination of the luminaries. The fundamental ideas can be found in the initial article on culminations.
The upper culmination is situated south of the zenith
As we are already aware, the elevation of the celestial pole above the horizon is equal to the latitude of the observation location. NS represents the plane of the mathematical horizon, PP’ denotes the axis of the world, and P is the north pole of the world. Consequently, it can be inferred that
where φ signifies the latitude of the observation location. Thus,
∠NOQ’ = β = 90° – φ = ∠SOQ (as vertical).
Since QQ’ represents the celestial equator, and KK’ symbolizes the diurnal parallel of the luminary, then
Our goal is to determine the correlation between the height of the celestial body above the horizon during its highest point south of the zenith, considering both the latitude of the observation location and the declination of the celestial body. Therefore, we are interested in the angle ∠SOK = h = β + δ = 90° – φ + δ.
Here, h represents the height of the celestial body above the horizon at the time of its highest point south of the zenith. Using the formula h = 90° – φ + δ, we can calculate this value.
North Zenith Upper Culmination
Using the knowledge gained from the previous analysis, we come to understand that
∠NOK = h = ∠POK + ∠NOP = 90° – δ + φ
represents the height of the celestial body above the horizon during the occurrence of the north zenith upper culmination.
h = 90° – δ + φ
Lower culmination to the north of the nadir
The angle NOP is equal to the sum of the angles NOK’ and K’OP, which is h + K’OP = φ
The angle K’OQ’ is equal to the sum of the angles NOK’ and NOQ’, which is h + NOQ’ = δ
represents the height of the luminary above the horizon when it reaches its lowest point to the north of the nadir
h = φ + δ – 90°
Lower culmination south of the nadir
It is worth noting that the luminary’s declination is negative and the altitude should also be negative.
However, given that the declination is negative and the altitude must be negative, we can say that ∠K’OP’ = -90° – δ.
Furthermore, we can calculate ∠K’OS = ∠K’OP’ + ∠P’OS = -90° – δ + φ.
Considering that the altitude should be negative, we can conclude that ∠K’OS = -90° – δ – φ.
Therefore, the altitude of the luminary above the horizon at the time of the lower culmination south of the nadir can be expressed as h = -φ – δ – 90°.
What is the stellar culmination?
Not everyone is familiar with the concept of stellar culmination. Essentially, culmination refers to the highest point or moment of something. In the field of astronomy, it specifically pertains to the highest point of motion of a celestial object.
Therefore, the stellar culmination is the moment when a star passes through the celestial meridian during its daily movement across the sky.
It is important to note that the celestial meridian is a circular path in the sky that passes through the zenith, the North Pole, the South Pole, and the nadir.
The North Pole can be considered as the reference point, situated on the celestial sphere, around which stars undergo a visible daily rotation. They move in a circular pattern parallel to the equator.
On Earth, just like in space, there is always something fascinating to observe. Take, for instance, the captivating shows on Netflix that are bound to leave a lasting impression.
What constitutes the culmination of celestial bodies?
Every celestial body passes through the meridian of the sky twice a day, which is known as its culmination. In simpler terms, this refers to the moment when a celestial object reaches its highest point in the sky.
The time interval between these two crossings of celestial bodies is approximately 12 hours, signifying half a day.
Given that the culmination of stars occurs twice daily, it can be classified into two types:
Calculation of Stellar Culmination
Calculating the culmination of stars involves determining the moment when a star reaches its highest point in the sky. This can be done by considering the height of the pole of the world above the horizon, which is equal to the geographic latitude of the area.
To calculate the upper and lower culmination of a star, a formula is used:


Methods for determining culminations
where h – height, ф – geographic latitude, and δ – declination.
It appears that if we have knowledge of the declination and altitude of the star during the time of culmination, we can compute the geographic latitude of the location from which the observations are conducted.
Interestingly, a star that does not set for a specific geographic latitude can be observed during both the upper and lower culmination. However, if the celestial body is situated far from the celestial equator towards the south, its intersection with the meridian may go unnoticed.


Stars in space
In order to comprehend the occurrence of star culmination and its timing, one can refer to our primary celestial body. Indeed, the most straightforward example would be the Sun. Similar to other stars, it passes the celestial meridian twice a day. These instances are well-known to us all. Firstly, the upper solar culmination transpires at noon. Secondly, after a period of twelve hours, midnight or the lower culmination takes place.
As is evident, humans have been observing the motion of celestial entities for a considerable amount of time. They have distinguished specific characteristics and have learned to apply them in their daily lives. In general, the mere act of observing the enigmatic and luminous starry dots, the celestial sphere, and the cosmos is an incredibly captivating and stunning spectacle.
§ 4: Determination of geographical latitude
1. What is the culmination of a celestial body?
The culmination refers to the moment when a celestial body passes the celestial meridian.
2. What are the points known as the rising and setting points of a celestial body?
The rising point of a celestial body is the point where its diurnal parallel intersects with the eastern part of the true horizon.
The setting point of a celestial body is the point where its diurnal parallel intersects with the western part of the true horizon.
3. What causes changes in the altitude, direct ascension, and declination of a luminary during its daily motion?
Throughout the course of the day, the altitude of a luminary undergoes continuous change, initially increasing from sunrise until reaching its highest point, and then decreasing. However, the direct ascension and declination of the luminary remain constant during this diurnal motion.
4. How can you estimate the geographical latitude of a location by observing Polaris?
You can estimate the geographical latitude of a location by determining the altitude of Polaris above the horizon.
5. Determine the declination range of stars that will never rise, never set, or can rise and set at a given latitude.
Stars will rise and set at a given latitude if
Stars will not rise or set if
6. Find the latitude of the observation point when the star Vega passes directly overhead.
Answer: φ = 38° 4 7 ′ φ=38°47′ φ = 38°4 7 ′N.
7. Calculate the latitude of the observation site, the declination of the Sun, and the date of the observation based on the altitude of the Sun during its upper and lower culminations (37° and 10° respectively).
Let’s utilize the formula for determining the geographical latitude of the location:
Then, for the upper culmination:
Add both equations together and express the declination:
Consequently, the geographical latitude:
The date of observation can be determined from the calendar by the dates of the equinox and solstice and using the calculated declination. In our situation, the observation of the Sun took place: in the northern hemisphere, where the declination is +23.50 – June 22, and in the southern hemisphere – December 22.
1. Complete the sentences.
The culmination of the luminary is the phenomenon of the luminary passing through the celestial meridian during its daily movement.
The distinction between the upper and lower culminations lies in the fact that during the upper culmination, the celestial body reaches its highest point above the horizon, while during the lower culmination, it reaches its lowest point.
2. Using Figure 4.1, fill in the table with the formulas for the heights at the upper and lower culminations of the celestial bodies if:
(a) star M1 culminates between the zenith and the south point;
b) star M2 culminates between the zenith and the pole of the world.
3. Explain the visibility conditions of stars at a latitude of 55° north.
4. Create a mobile star chart for the date and time of the class in your location, and indicate several constellations that will reach their upper and lower culminations. Record the data in a table.
| Date, time, location | Constellations at the highest point | Constellations at the lowest point |
| October 15, 8 PM | Capricorn, Aquarius, Pegasus, Swan, Cepheus. | Little Leo, Big Dipper |
5. Find the latitude of the observation site if:
a) the star Vega is directly above us;
b) the star Sirius is h = 64°13′ below the highest point;
c) the star Deneb is h = 83°47′ above the highest point;
d) the star Altair is directly above us.
6. Complete Figure 4.2 with the necessary constructions and notations to explain the daily movement of stars at different latitudes:
Culmination in Astronomy
From Wikipedia, the encyclopedia that is free to use.
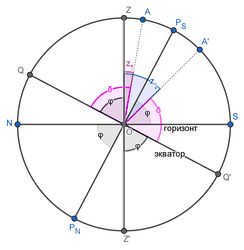
Culmination (astronomy) – The moment when the center of a celestial body passes through the celestial meridian during its daily motion. In other words, it is when the center of the celestial body crosses the point where the daily parallel of the celestial body intersects with the celestial meridian.
The upper culmination refers to when the celestial body reaches its highest point to the north or south of the zenith. If the celestial body culminates to the south of the zenith, its astronomical azimuth at the moment of culmination is 0°, while if it culminates to the north of the zenith, its azimuth at the moment of culmination is 180°.
z ↓ = ( φ + δ ) – 2 φ e P =(\varphi +\delta )-2\varphi _ >
Just like with northern geographic latitude and northern declination being positive values, and southern latitude and declination being negative values, we can also assign a sign to the zenith distance. It is convenient to follow this rule: if the observer’s shadow (real or imaginary) from the luminary falls on the northern – positive – side, then the zenith distance of the luminary is positive; if it falls on the southern side, then the zenith distance is negative. The same rule can be derived from the consideration of the astronomical azimuth of the luminary: when the luminary is at its highest point south of the zenith, the astronomical azimuth is 0 degrees, and cos (0 degrees) = +1; when the luminary is at its highest point north of the zenith, the azimuth is 180 degrees, cos (180 degrees) = -1. Algebraically, the sign of the zenith distances can be determined by calculations that follow the conventions of the signs of latitude and declination.





