The position of luminaries in the sky or points on an imaginary celestial sphere is described using celestial coordinate systems in astronomy. The horizontal coordinates, also known as azimuth and altitude, are the angular quantities that define the position of objects on the celestial sphere. These spherical coordinate systems do not consider distance and vary in their principal plane and origin.
Depending on the specific task, one coordinate system may be more convenient than another. The most commonly used systems are the horizontal and equatorial coordinate systems. The ecliptic, galactic, and other systems are used less frequently.
Coordinate System in the Horizontal Plane
The primary plane in this particular system is the height plane.
The arc zenithal distance, denoted as h, refers to the height of a luminary.
Zenithal distance, represented as z, is the arc of the vertical circle extending from the zenith to the luminary. It can also be defined as the angle between azimuth.
In this coordinate system, the celestial equator plane serves as the principal plane. The declination coordinate, denoted as δ (or alternatively, polar distance p), is one of the coordinates. The other coordinate is the hour angle t.
Declination
The declination δ represents the distance from the arc to the North Pole of the Earth and ranges from 0° to -90° towards the South Pole.
Polar distance
The polar distance p of a celestial body is the arc of the declination circle from the North Pole of the Earth to the celestial body, or the angle between the hour angle of the celestial body and the South Pole of the Earth.
The hour angle t of a celestial body is the arc of the celestial equator from the zenith point of the celestial equator (i.e., the point where the celestial equator intersects the Second Equatorial Coordinate System).
Utilizing the equatorial coordinate system.
In this system, similar to the first equatorial system, the primary plane is the plane of the celestial equator, and one coordinate is declination β (occasionally referred to as polar distance p). The other coordinate is the direct ascension α.
Direct Ascension
The direct ascension α of a celestial body is the arc from the vernal equinox to the celestial body’s declination circle, or the angle between the direction to the vernal equinox and the plane of the celestial body’s declination circle.
Direct ascensions are measured in the opposite direction of the daily rotation of the celestial sphere, ranging from 0° to 360° (in degrees) or from 0 h to 24 h (in hours).
The system of coordinates based on the ecliptic
In this particular system, the primary plane is the plane of the ecliptic. There are two coordinates utilized in this system – the ecliptic latitude, denoted as β, and the ecliptic longitude, denoted as λ.
Ecliptic latitude
The ecliptic latitude, also known as the angle to the north pole of the ecliptic, ranges from 0° to -90° towards the south pole of the ecliptic.
Ecliptic longitude
The ecliptic longitude λ represents the distance along the ecliptic from the vernal equinox point to the circle of latitude of a celestial body, or the angle between the direction to the vernal equinox point and the plane of the circle of latitude of the celestial body.
Ecliptic longitudes are measured in the direction of the apparent annual motion of the Sun along the ecliptic, specifically to the east of the vernal equinox point within the range of 0° to 360°.
Galactic coordinate system
The galactic coordinate system is based on the main plane of our Galaxy. It uses two coordinates, the galactic latitude b and the galactic longitude l.
Galactic latitude
The galactic latitude b is the arc of the circle of galactic latitude from the ecliptic to a celestial object, or the angle between the plane to the north galactic pole and from 0° to -90° to the south galactic pole.
Galactic longitude
The galactic longitude, denoted as l, is the measurement of the angle between the point of origin C and the plane of the circle of galactic latitude of a celestial object. It represents the arc of the galactic equator that extends from the point of origin C to the circle of galactic latitude of the celestial object.
When observed from the north galactic pole, galactic longitudes are measured counterclockwise, ranging from 0° to 360°. This means that they are oriented eastward from the point of origin C.
The point of origin C is located in close proximity to the direction of the galactic center, but it does not align exactly with it. This is because the galactic center is positioned approximately 1° south of the galactic equator, due to the slight elevation of the solar system above the plane of the galactic disk. The specific location of origin C is chosen so that the intersection point of the galactic and celestial equators, with a direct ascent of 280°, has a galactic longitude of 32.93192°. This calculation takes into account changes in coordinates that occur during the rotation of the celestial sphere.
The height h, zenith distance z, azimuth A, and hour angle t of the celestial bodies are in constant flux as a result of the rotation of the celestial sphere. This is because these measurements are taken from points that are not affected by this rotation. However, the declination δ, polar distance p, and direct ascent α of the celestial bodies remain unchanged by the rotation of the celestial sphere. Nonetheless, these measurements may still be subject to changes caused by the motions of the celestial bodies that are not connected to the daily rotation.
History and uses
The study of changes in celestial coordinates has been instrumental in making significant breakthroughs in the field of astronomy, providing invaluable insights into the vastness of the universe. These observations have yielded valuable information about precession and the geographic coordinates of different locations on Earth’s surface. Celestial coordinates play a crucial role in the creation of numerous star catalogs, the analysis of the actual movements of celestial bodies (both natural and man-made) in celestial mechanics and astrodynamics, and the examination of the spatial distribution of stars in the realm of stellar astronomy.
Utilization of Various Coordinate Systems
When it comes to calculating the paths of heavenly bodies, the ecliptic coordinate system is commonly employed in theoretical astronomy.
Additional Information
For further knowledge on this subject, you may refer to the following: bs:Nebeski koordinatni sistem de:Astronomische Koordinatensysteme es:Coordenadas celestes he:מערכת קואורדינטות שמימית nl:Hemelcoördinaat uk:Celestial coordinate systems
HORIZONTAL COORDINATES in astronomy, coordinates that define the position of a celestial object on the celestial sphere using the horizontal system of celestial coordinates: zenith distance $z$ and azimuth $A$. The zenith distance $z$ ranges from 0° (object at the zenith) to 180° (object at the nadir). Instead of $z$, the height $h$ above the horizon is often used, so that $z+h=90°$. If $z>90°$ (or $h$), the object is considered to be below the horizon. The azimuth $A$ is typically measured from a point south in a westward (clockwise) direction and ranges from 0° to 360°.
Through their exploration of space and the sky, scientists have observed that everything around them is in constant motion.
The history of the development of the coordinate system can be traced back to ancient times.
To begin with, the establishment of the coordinate system is linked to the necessity for navigating through the land and comprehending the composition of the celestial sphere.

To determine the position and motion of celestial objects, humanity has developed a comprehensive system of methods and techniques. Additionally, unique numerical and symbolic designations have been devised.
In reality, there exist multiple systems that establish the coordinates of objects. They primarily differ in the selection of the principal plane and the reference point.
Given that we perceive the sky as a sphere when observing from Earth, astronomical coordinates are also spherical. Furthermore, they represent certain arcs of circles on the sphere. It is important to note that they are calculated in degrees, and sometimes in hours.
System of Horizontal Coordinates
The primary plane in this coordinate system is the mathematical horizon, while the zenith and nadir represent the poles.
The system of horizontal coordinates is employed for observations conducted from the Earth, whether it be with the unaided eye or through the use of a telescope. Its purpose is to study the stars and track the motion of celestial objects in the sky, primarily within our solar system.
Horizontal coordinate system
Observation and measurement are always ongoing because celestial bodies are constantly in motion.
Definitions of the coordinate system
The plumb line is a straight line that passes through the center of the sky and coincides with the observer’s line of sight from their position on Earth. This line intersects the center of the planet and the observer’s location vertically.
Zenith and nadir are two opposite points. The plumb line intersects the sky above the observer’s head, which is known as the zenith. The nadir, on the other hand, is the point on the celestial sphere that is directly opposite the zenith.
The mathematical horizon is a vast circle on the celestial sphere. It is perpendicular to the vertical line and bisects the entire sky. These halves are known as the visible and invisible to the observer. The visible half reaches its highest point at the zenith, while the invisible half reaches its lowest point at the nadir.
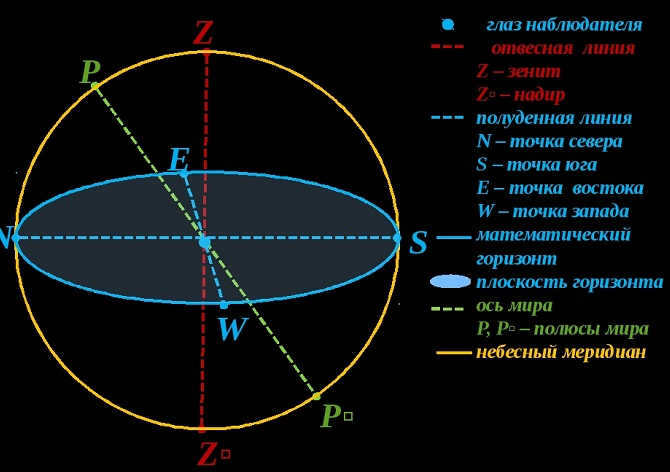
The mathematical horizon, zenith, and nadir, as well as the plumb line, are all important concepts in the field of astronomy. However, it is important to note that the mathematical horizon does not always align with the visible horizon. This is due to the uneven surface of the Earth and the curvature of rays in the atmosphere. These factors can cause the highest point of observation to differ from the mathematical horizon. Nonetheless, understanding these concepts is crucial for accurately determining the equatorial coordinates of stars.
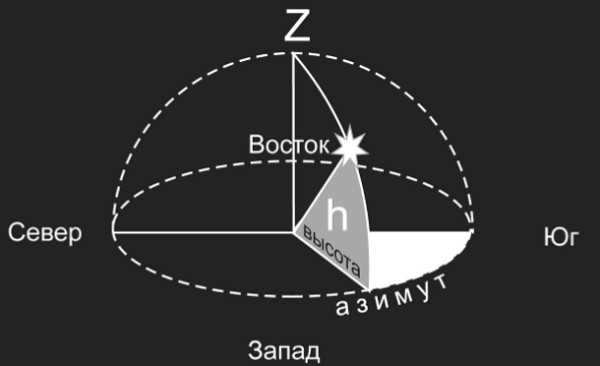
In astronomy, the horizontal coordinates of a celestial object are determined by its altitude, zenith distance, and azimuth.
The altitude of a celestial object is the angle between its vertical position and the observer’s mathematical horizon. It ranges from 0° to +90° when measured from the horizon towards the zenith, and from 0° to -90° when measured towards the nadir.
The zenith distance is the angle between the observer’s zenith and the celestial object. It is measured within the range of 0° to 180°.
Azimuth, on the other hand, is the angle between the observer’s southern point and the vertical plane that passes through the celestial object. It is measured within the range of 0° to 360°, with 0° corresponding to the direction of the daily rotation of the celestial sphere.
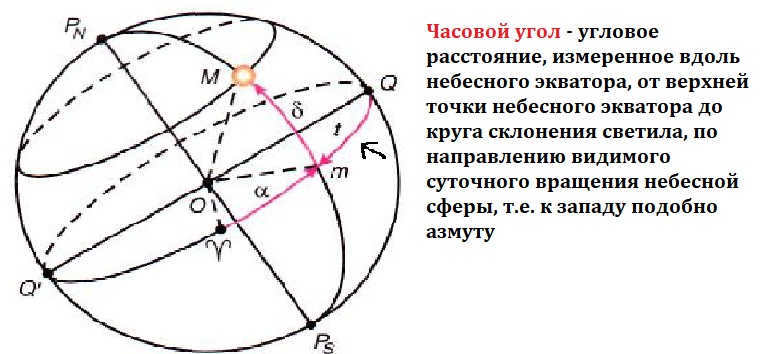
The initial equatorial coordinate system
In this coordinate system, the flat region is taken as the surface of the sky’s equator, with point Q as the reference point. The coordinates represent declination and hour angle.
You can learn about declination here.
The hour angle is the arc that lies between the celestial meridian and the circle of declination. Its measurement ranges from 0 ° to 360 °.
It is worth noting that the initial equatorial coordinate system is employed due to the continuous movement of our planet throughout the day. Hence, the starting point is set at the vernal equinox, which remains constant in relation to the stars.
The alternative equatorial coordinate system
Interestingly, the main plane and the reference point remain the same as in the previous system. However, the coordinates in this system are called declination and right ascension.
Right ascension is the arc on the celestial equator that extends from the vernal equinox to the circle of the luminary. It is measured in hours, but in a counterclockwise direction.
On the other hand, the alternative coordinate system is known for its fixed star coordinates. Unlike the first system, they are not affected by the Earth’s movement throughout the day. This system is used to track the motion of celestial bodies over the course of a year.
The alternative equatorial coordinate system
It is crucial to understand that the coordinates can vary at all times. Consequently, numerous issues arise. The resolution of these problems can be achieved by utilizing an application that is tailored to the specific situation and system. In general, alternative systems are frequently employed to address problems and determine coordinates.
The establishment of coordinate systems enabled scientists to chart the vast expanse of the night sky. Furthermore, a specific framework for the celestial system was delineated. This has played a significant role in the advancement of astronomy and astrology. Additionally, equatorial coordinate systems find utility in various scientific fields.

Undoubtedly, the advancement and implementation of specific systems serves as the foundation for space exploration. We strive to grasp its essence as closely as possible. Undoubtedly, numerous techniques, calculations, and methods that have already been applied contribute to the expansion of our knowledge.
While delving into space and observing the celestial sphere, scientists have made a fascinating discovery – everything around us is in constant motion. The history of the establishment of coordinates and their system dates back to ancient times. Evidently, the development of coordinate systems is intertwined with the necessity for orientation on Earth and comprehending the structure of the celestial surface.
Humanity has devised an entire system of methods and techniques to determine the location and movement of objects. Furthermore, they have created unique numerical and symbolic designations.
In reality, there are multiple systems that define the positional points of objects. They primarily vary in terms of their chosen main plane and point of reference.
As we observe the sky from Earth, it appears as a sphere, thus astronomical coordinates are also spherical. They represent specific arcs of circles on the sphere. It is important to mention that they are measured in degrees, and occasionally in hours.
Horizontal Coordinate System
The primary plane in the horizontal coordinate system is defined by the mathematical horizon. The zenith and nadir are represented by the poles.
Observations from Earth, whether with the naked eye or a telescope, are conducted using the horizontal coordinate system. This allows for the study of stars and the tracking of celestial objects in the sky, including those within the solar system.
Continuous observation and measurement are essential due to the constant motion of celestial bodies.
Definitions in the Coordinate System
The plumb line is a straight line that runs through the center of the sky. It also aligns with the path of the plumb line from the observer’s point of view. From the observer’s perspective, this line vertically intersects both the center of the planet and the observation site.
Zenith and nadir are two opposite points. As we know, the plumb line intersects with the sky directly above the observer’s head, which is called the zenith. On the other hand, the nadir is the point directly opposite the zenith on the celestial sphere.
The mathematical horizon is a large circle on the surface of the celestial sphere. It is perpendicular to the plumb line and divides the entire sky into two halves. These halves are known as the visible and invisible portions to the observer. The visible portion has its highest point at the zenith, while the invisible portion has its highest point at the nadir.
Simultaneously, the mathematical horizon does not align with the observable horizon. This is due to two factors. Firstly, the Earth’s surface is uneven, resulting in different points of observation. Secondly, the curvature of light rays in our planet’s atmosphere also plays a role.
In astronomy, the horizontal coordinates refer to the altitude of the celestial body and its zenith distance. Another important factor is the azimuth.
The altitude of a celestial body is the angle between its vertical position and the mathematical horizon. It ranges from 0° to +90° towards the zenith, and from 0° to -90° towards the nadir.
On the other hand, the zenith distance is the angle between the zenith and the celestial body. It is measured within a range of 0° to 180°.
As for the azimuth, it represents the angle between the southern point and the vertical of the celestial body. It is measured from 0° to 360° towards the west, following the daily rotation of the celestial sphere.
The original equatorial coordinate system
The initial equatorial coordinate system is based on the assumption that the sky’s equator is a flat surface, with point Q as the reference point. This system uses coordinates to represent declination and hour angle.
For more information on declination, click here.
Hour angle is the arc that lies between the celestial meridian and the declination circle. It is measured from 0° to 360°.
It is important to note that the original equatorial coordinate system was developed to account for the Earth’s constant movement throughout the day. As a result, the vernal equinox point was established as the starting point, as it remains fixed relative to the stars.
The second equatorial coordinate system
What is intriguing about the second equatorial coordinate system is that its main plane and reference point are similar to the previous system. However, this system utilizes declination and right ascension as its coordinates.
Right ascension can be defined as the arc on the celestial equator that extends from the vernal equinox point to the circle of the luminary. Additionally, it is measured in units of time, specifically in hours. Moreover, the measurements are taken in a counterclockwise direction.
On the other hand, the second coordinate system is distinguished by the constant coordinates of stars. Unlike the first system, the Earth’s movement throughout the day does not affect these coordinates. This system is employed to determine the movement of celestial bodies over the course of a year.
Horizonal Coordinate System [1] :40, also known as the Horizon Coordinate System [2] :30, is a celestial coordinate system that uses the mathematical horizon as its principal plane, with the zenith and nadir as its poles. This system is commonly used for observing stars and tracking the movement of celestial bodies within the solar system from the Earth’s surface, whether with the naked eye, binoculars, or telescopes equipped with azimuth settings [1]:85. The horizontal coordinates of not only the planets and the Sun, but also the stars, change continuously throughout the day as a result of the diurnal rotation of the celestial sphere.
Description
Lines and planes
The topocentric coordinate system is always utilized in the horizontal plane. The observer is constantly stationed at a fixed position on the Earth’s surface (indicated by the letter O in the diagram). We will presume that the observer is situated in the Northern Hemisphere of the Earth at latitude φ. The plumb line is employed to ascertain the direction towards the zenith (Z) as the uppermost point to which the plumb line points, and the nadir (Z’) as the lowermost point (beneath the Earth) [1]:38. Consequently, the line (ZZ’) that connects the zenith and nadir is also referred to as the plumb line [3]:12.
The plane that is perpendicular to the plumb line at point O is known as the plane of mathematical horizon. This particular plane is responsible for determining the direction towards the south (geographic, not magnetic!) and north, for example, by observing the direction of the shortest shadow produced by the gnomon during the day. The shortest shadow occurs at true noon, and the line connecting the south and north points is referred to as the noon line [1]:39. The east (E) and west (W) points are located 90 degrees from the south point, counterclockwise and clockwise, respectively, when viewed from the zenith. Therefore, NESW represents the plane of the mathematical horizon.
The celestial meridian plane, which is formed by the noon and plumb line (ZNZ’S), is referred to as the plane that passes through. On the other hand, the vertical plane of a celestial body is defined as the plane that passes through the celestial body itself. The intersection of this plane with the celestial sphere forms a great circle known as the vertical of the celestial body [1]:40.
Coordinates
In the horizontal coordinate system, one of the coordinates represents the altitude of the luminary, denoted as h, while the other coordinate represents the zenith distance, denoted as z. Additionally, there is the azimuth coordinate, denoted as A.
The altitude h of a luminary is measured as the angle between the vertical plane passing through the luminary and the plane of the mathematical horizon. Altitudes range from 0° to +90° towards the zenith, and from 0° to -90° towards the nadir [1]:40.
The zenith distance z of a luminary is measured as the angle between the vertical plane passing through the luminary and the zenith. Zenith distances range from 0° to 180° from the zenith to the nadir.
Azimuth A is the angle between the vertical plane containing a celestial body and the plane of the observer’s horizon. It is measured clockwise from the north direction. Azimuths can be counted from 0° to 360°, or from 0° to +180° to the west and from 0° to -180° to the east. In geodesy, azimuths are counted from a point north.
Unique Features of Celestial Body Coordinate Transformation
Within a 24-hour period, a star (and also, roughly speaking, a celestial body within the solar system) traces a circular path perpendicular to the Earth’s axis (PP’). This circular path is inclined to the mathematical horizon at a latitude φ, with an angle equal to φ. Hence, at a latitude of 90 degrees (i.e. the North Pole), the star will move in parallel to the mathematical horizon. Consequently, all stars visible at the North Pole will never set (including the Sun for half a year, as indicated by the longitude of the day), and their altitude h will remain constant. At other latitudes, the stars visible at any given time of the year can be categorized as:
- Setting and rising [3]:16 (h passes through 0 during the day)
- Non-ascending [3]:16 (h is always greater than 0)
- Non-ascending [3]:16 (h is always less than 0)
The star’s maximum height, h, is observed once a day during its two passages across the celestial meridian. The first passage, known as the upper culmination, represents the highest point of the star’s height. The second passage, referred to as the lower culmination, represents the lowest point of the star’s height. The star’s height, h, increases from the lower to the upper culmination and decreases from the upper to the lower culmination.
Transition to the initial equatorial
In addition to the NESW horizon plane, the ZZ’ plumb line, and the PP’ world axis, we depict the celestial equator that intersects PP’ at point O. We represent t as the hour angle of the luminary, δ as its declination, R as the luminary itself, and z as its zenith distance. The horizontal and initial equatorial coordinate systems are linked by the spherical triangle PZR, also known as the first astronomical triangle [1]:68, or the parallactic triangle [2]:36. The formulas for the transition from the horizontal coordinate system to the initial equatorial coordinate system are as follows [5]:18:
To obtain unique formulas for the spherical triangle PZR, we follow the same sequence as when deriving similar formulas for the ecliptic coordinate system. This sequence includes the application of the cosine theorem, the sine theorem, and the five elements formula [2]:37. Applying the cosine theorem, we get:
We have derived the initial equation. Next, we can utilize the sine theorem on the identical spherical triangle:

The second equation is derived. Next, we apply the five-element formula to our spherical triangle:

The third equation is derived. Thus, all three equations are derived by considering a single spherical triangle.
Transition from the initial equatorial coordinate system
The derivation of formulas for transitioning from the initial equatorial coordinate system to the horizontal coordinate system involves considering the same spherical triangle and applying the same formulas of spherical trigonometry as for the inverse transition [2]:37. These formulas can be expressed as follows [5]:17:


Related articles
Newton’s laws – Law of universal gravitation – Kepler’s laws – Two-body problem – Three-body problem – N-body gravitational problem – Bertrand’s problem – Kepler’s equation |
| Celestial coordinate systemGalactic – horizontal – first equatorial – second equatorial – ecliptic – International Celestial Coordinate System – Spherical Coordinate System – World Axis – Celestial Equator – Direct Ascension – Declination – Ecliptic – Equinox – Solstice – Fundamental Plane |
| Keplerian orbital elements: Eccentricity – Major semi-axis – Mean anomaly – Longitude of ascending node – Pericenter argument – Apocenter and pericenter – Orbital velocity – Orbital node – Epoch |
Motion of the Sun and planets on the celestial sphere – Ephemerides |
|
Space velocity: first (circular) – second (parabolic) – third – fourth Tsiolkovsky’s formula – Gravity maneuver – Goman trajectory – Osculating element method – Tidal acceleration – Change of orbital inclination – Docking – Lagrange points – Pioneer effect |
Geostationary orbit – Heliocentric orbit – Geosynchronous orbit – Geocentric orbit – Geo-transition orbit – Low reference orbit – Polar orbit – Tundra orbit – Sun-synchronous orbit – Lightning orbit – Oscillating orbit |
- Observational Astronomy
- Astrometry
- Celestial mechanics
- Coordinate systems
Wikimedia Foundation . 2010 .
The celestial coordinate system is utilized in the field of astronomy to describe the location of celestial bodies in the sky or points on an imaginary celestial sphere. The positions of these bodies or points are determined by two angular quantities (or arcs) that uniquely define their position on the celestial sphere. The celestial coordinate system, therefore, functions as a spherical coordinate system in which the third coordinate, distance, is often unknown and has no influence.
Celestial coordinate systems vary from one another in terms of the selection of the fundamental plane (cf. Fundamental plane) and the point of origin. Depending on the specific task, it may be more advantageous to utilize one particular system over another. The two most frequently employed systems are the horizontal and equatorial coordinate systems. The ecliptic, galactic, and other systems are less commonly used.
Topocentric Coordinate System in the Horizontal Plane
The horizontal topocentric coordinate system is defined with the observer’s location on the Earth’s surface as the center and the mathematical horizon as the main plane. One of the coordinates is the altitude (h) or zenith distance (z) of the celestial body. The other coordinate is the azimuth (A). Since this coordinate system is always topocentric, meaning the observer is situated on the Earth’s surface or at some elevation, the term “topocentric” is often omitted.
The height (h) of the celestial body represents the arc of the vertical circle from the mathematical horizon to the celestial body, or the angle between the plane of the mathematical horizon and the direction to the celestial body. Altitudes are measured from 0° to +90° towards the zenith and from 0° to -90° towards the nadir.
The angle between the plumb line and the direction to the luminary, known as the zenith distance z, can be measured by the arc of the vertical circle from the zenith to the luminary. Zenith distances are measured in degrees, ranging from 0° to 180° from zenith to nadir.
The azimuth A of a celestial object is the angular distance along the horizon, measured from the southern point to the vertical circle of the object. It can also be defined as the angle between the line of intersection of the mathematical horizon plane and the plane of the object’s vertical circle, and the line connecting the observer’s position to the object at noon. Azimuths are measured in the direction of the daily rotation of the celestial sphere, which means they are counted in a westward direction from the southern point, ranging from 0° to 360°. In some cases, azimuths are measured from 0° to +180° to the west and from 0° to -180° to the east. (In geodesy, azimuths are measured from a point north.)
Modifications in coordinates as the celestial sphere undergoes rotation
The values of height h, zenith distance z, azimuth A, and hour angle t for celestial bodies are in constant flux due to the rotation of the celestial sphere, as these measurements are based on points not directly affected by this rotation. However, declination δ, polar distance p, and right ascension α remain unchanged during the rotation, although they may vary due to movements of the celestial bodies unrelated to the daily rotation.
The original equatorial coordinate system
In this particular system, the fundamental plane is represented by the celestial equator. A single coordinate within this system is referred to as the declination δ (occasionally known as the polar distance p). Another crucial coordinate is the hour angle t.
Declination δ of a specific celestial body is the arc that spans from the celestial equator to the said body, or it can be described as the angle between the plane of the celestial equator and the direction towards the celestial body. Declinations are measured from 0° to +90° towards the north pole of the world, and from 0° to -90° towards the south pole of the world.
The polar distance p of the celestial body is the arc of the declination circle from the north pole of the Earth to the celestial body, or the angle between the Earth’s axis and the direction to the celestial body. Polar distances are measured from 0° to 180° from the north pole of the Earth to the south pole of the Earth.
The hour angle t is the measurement of the arc of the celestial equator starting from the upper point of the celestial equator (where it intersects with the celestial meridian) to the circle of declination of the celestial body, or the angle between the planes of the celestial meridian and the circle of declination. Hour angles are calculated in relation to the daily rotation of the celestial sphere, meaning they are measured west of the upper point of the celestial equator, ranging from 0° to 360° (in degrees) or from 0 h to 24 h (in hours). In some cases, hour angles can be measured from 0° to +180° (0 h to +12 h) to the west and from 0° to -180° (0 h to -12 h) to the east.
The other equatorial coordinate system
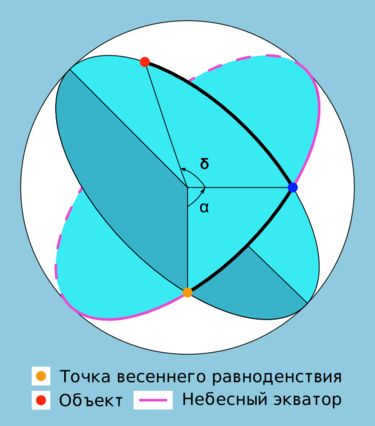
In this particular system, similar to the initial equatorial system, the primary plane is known as the celestial equator, and one of the coordinates is called the declination δ (occasionally referred to as the polar distance p). Another coordinate is referred to as the right ascension α.
The right ascension (RA, α) represents the arc of the celestial equator from the vernal equinox point to the luminary’s declination circle, or the angle between the direction to the vernal equinox point and the plane of the luminary’s declination circle. Right ascensions are measured in the opposite direction of the diurnal rotation of the celestial sphere, ranging from 0° to 360° (in degrees) or from 0 h to 24 h (in hours).
RA is the astronomical equivalent of longitude on Earth. Both RA and longitude measure the angle along the equator that goes from east to west; both measurements start from a zero point on the equator. In the case of longitude, the zero point is the prime meridian; for RA, the zero point is the location in the sky where the Sun crosses the celestial equator during the vernal equinox.
Declination (δ) is one of the two coordinates in the equatorial coordinate system used in astronomy. It represents the angular distance on the celestial sphere from the plane of the celestial equator to the celestial object, and it is usually expressed in degrees, minutes, and seconds of arc. Declination is positive when measured north of the celestial equator and negative when measured south.
- An object located on the celestial equator has a declination of 0°.
- The north pole of the celestial sphere has a declination of +90°
- The south pole of the celestial sphere has a declination of -90°
Declination always has a sign, even when positive.
The declination of a celestial object that passes directly overhead (zenith) is equal to the latitude of the observer. In the northern hemisphere, if the latitude is considered positive and the declination is greater than +90° – latitude, the object will not go below the horizon and is known as a non-setting celestial object. However, if the declination is less than -90° + latitude, the object is considered a non-descending object and is not observable at that latitude. [1]
Ecliptic coordinate system
The ecliptic coordinate system is based on the ecliptic plane as the main plane. It uses two coordinates: ecliptic latitude (β) and ecliptic longitude (λ).
Ecliptic latitude (β) represents the arc of the circle of latitude from the ecliptic to the luminary, or the angle between the ecliptic plane and the direction to the luminary. Ecliptic latitudes are measured from 0° to +90° towards the north pole of the ecliptic, and from 0° to -90° towards the south pole of the ecliptic.
The angular distance Λ between the vernal equinox point and the luminary’s circle of latitude on the ecliptic is known as the ecliptic longitude. It can also be defined as the angle formed by the line connecting the vernal equinox point and the plane of the luminary’s circle of latitude. Ecliptic longitudes are measured in the direction of the Sun’s apparent annual motion along the ecliptic, which means they range from 0° to 360° and are measured eastward from the vernal equinox point.
Galactic coordinate system
In this system, the primary plane is the plane of our Galaxy. The Galactic coordinate system consists of two coordinates: galactic latitude (b) and galactic longitude (l).
Galactic latitude (b) is the angle between the plane of the galactic equator and the direction to a celestial object, measured along the arc of the circle of galactic latitude from the ecliptic to the object.
Galactic latitudes are measured from 0° to +90° to the north galactic pole and from 0° to -90° to the south galactic pole.
Galactic longitude l refers to the distance along the galactic equator from the starting point C to the circle that represents the galactic latitude of a luminary. It can also be thought of as the angle between the direction to the starting point C and the plane of the circle that represents the galactic latitude of the luminary. When viewed from the north galactic pole, galactic longitudes are measured counterclockwise, meaning they start at the east of the starting point C and go all the way around to 360 degrees.
The point of origin C is located near the direction of the galactic center, but not exactly at it, as the solar system is slightly elevated above the galactic disk, causing it to be about 1° south of the galactic equator. The coordinates of the origin point C at epoch 2000 in the equatorial coordinate system are chosen so that the intersection of the galactic and celestial equators at a direct ascent of 280° has a galactic longitude of 32.93192°.
Coordinates of the origin point C at epoch 2000 in the equatorial coordinate system are:


Currently, 58,742 educational institutions have access to additional cumulative discounts ranging from 2% to 25%. To discover the specific discount available to all staff members at your educational institution, simply login to your personal Infoworks account.


Enroll in our professional retraining course today!
Learn the theory and methodology of teaching informatics in elementary school.
Take advantage of our special offer by adding your educational institution’s discount to our already discounted price. The amount of your discount will depend on how many of your colleagues have already completed Infowork courses.
Currently, 58,742 educational institutions are eligible for additional discounts ranging from 2% to 25%. To find out the specific discount available to all employees of your institution, simply log in to your personal Infoworks account.


Enrich your professional skills
Building and enhancing the essential skills of students for the sustainable development of the region
We can apply a special discount for your educational institution (the amount depends on the number of your colleagues who have completed Infoworks courses)
Currently, 58,742 educational institutions are benefiting from additional discounts ranging from 2% to 25%. To find out the discount available for all staff members of your educational institution, please log in to your personal Infoworks account.


Getting ready for the literature USE exam. The Silver Age of Russian poetry
An overview of the presentation by individual slides:

2 slide Main lines and points.
1. plumb line
2. Z – zenith (the point of intersection
plumb line and the celestial
sphere above the observer's head)
3. Z, – nadir
4. Mathematical horizon – the line of intersection of the celestial sphere and the plane of the horizon
7. Celestial meridian –
the great circle of the celestial sphere,
passing through the zenith and
poles of the world
5. Axis of the world is an axis parallel
to the axis of apparent rotation
of the celestial sphere
6. R, the north pole of the world
R, – south pole of the world
8. The point of the north N and the point of the south S –
points of intersection of the mathematical horizon and the celestial meridian
9. The points where the western point W and the eastern point E intersect with the horizon and the celestial equator.
10. The vertical or altitude circle.
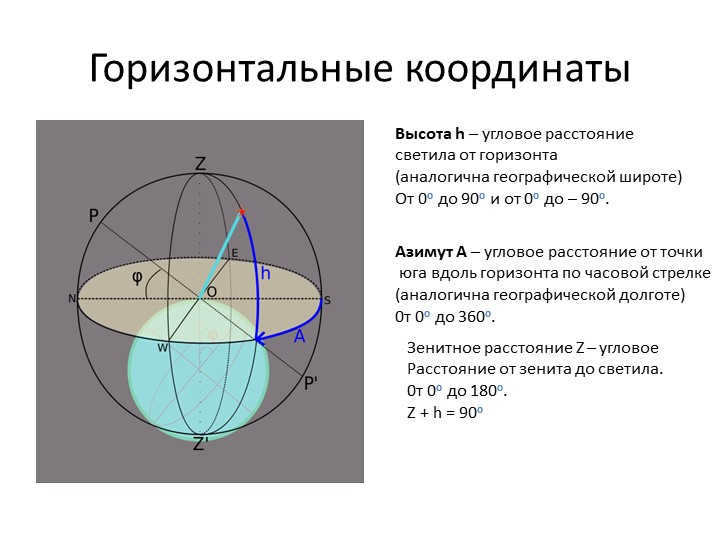
On the third slide, we will discuss the horizontal coordinates of a luminary. Altitude, denoted as h, represents the angular distance between the luminary and the horizon, similar to geographic latitude. The range of values for altitude is from 0o to 90o and from 0o to -90o.
Azimuth, denoted as A, represents the angular distance from a reference point south along the horizon in a clockwise direction, similar to geographic longitude. The range of values for azimuth is from 0o to 360o.
Zenith, denoted as Z, represents the angular distance from the zenith to the luminary. The range of values for zenith is from 0o to 180o.
It is important to note that Z + h always equals 90o.
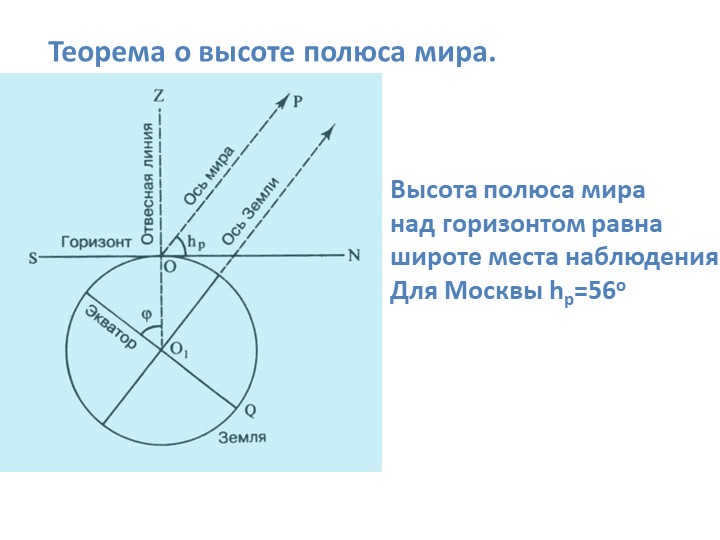
The 4 Slide Theorem states that the height of the world pole above the horizon is equivalent to the latitude of the place of observation. In the case of Moscow, the height of the pole is 56 degrees.
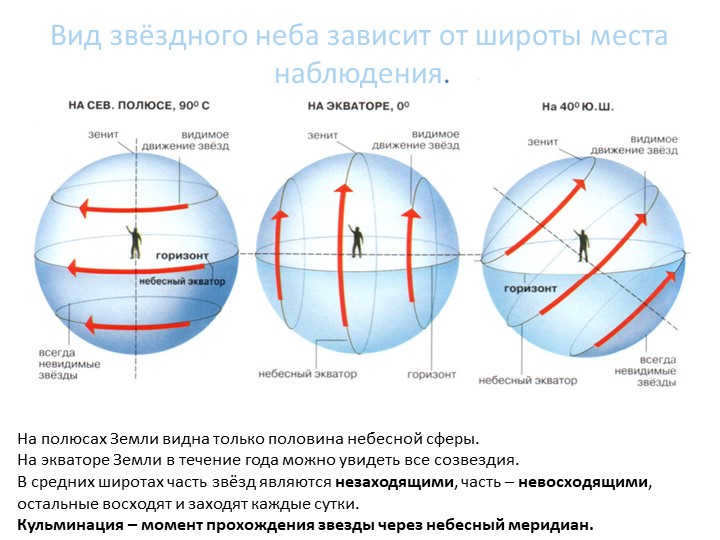

Slide 5 The appearance of the starry sky is determined by the latitude of the observation site.
At the poles of the Earth, only half of the celestial sphere is visible.
At the equator of the Earth, all constellations can be observed throughout the year.
At intermediate latitudes, some stars do not rise, some rise and set, and others rise and set every 24 hours.
The culmination is the moment when a star crosses the celestial meridian.
Horizon coordinate system [2] :30, also known as the horizontal coordinate system [1] :40, is a celestial coordinate system that uses the mathematical horizon as the main plane and the zenith and nadir as the poles. This system is commonly used for observing stars and the movement of celestial bodies in the solar system from the ground using the naked eye, binoculars, or telescopes with an azimuth setting [1] :85. Throughout the day, the horizontal coordinates of not only the planets and the Sun, but also the stars, continuously change due to the diurnal rotation of the celestial sphere.
Description [ edit ]
Lines and planes [ edit ]
The topocentric coordinate system is always used for horizontal measurements. The observer is fixed at a specific location on the Earth’s surface (designated as point O in the diagram). It is assumed that the observer is situated in the Northern Hemisphere at latitude φ. The plumb line is employed to determine the direction towards the zenith (Z) as the highest point where the plumb line is directed, and the nadir (Z’) as the lowest point (beneath the Earth) [1]:38. Accordingly, the line (ZZ’) that connects the zenith and nadir is also referred to as the plumb line [3]:12.
The plane that is perpendicular to the plumb line at point O is known as the plane of mathematical horizon. This plane determines the direction to the south (geographic, not magnetic!) and north, for example, by observing the direction of the day’s shortest shadow from the gnomon. The shortest shadow occurs at true noon, and the line connecting the south and north points is referred to as the noon line [1]:39. The east and west points are located 90 degrees away from the south point, in counterclockwise and clockwise directions when viewed from the zenith. Therefore, the plane of the mathematical horizon can be represented by NESW.
The plane that intersects the noon and plumb line (ZNZ’S) is known as the celestial meridian plane, while the plane that intersects a celestial body is referred to as the vertical plane of that particular celestial body. The celestial sphere is intersected by the great circle formed by the vertical of the celestial body [1]:40.
Coordinates [ edit ]
In the horizontal coordinate system, one of the coordinates is the altitude of the luminary, denoted as h, while the other coordinate is the zenith distance, denoted as z. The third coordinate is the azimuth, denoted as A.
The altitude h of the luminary represents the angle between the vertical plane of the mathematical horizon and the direction to the luminary. Altitudes range from 0° to +90° towards the zenith and from 0° to -90° towards the nadir [1] :40 .
The zenith distance z of a luminary is the angle between the vertical plane passing through the zenith and the direction to the luminary. Zenith distances range from 0° to 180° from the zenith to the nadir.
Azimuth A is the measurement of the angle between the south point and the vertical of a celestial body. Azimuths are calculated in relation to the rotation of the celestial sphere, specifically in the westward direction from the south point, ranging from 0° to 360° [1] :41. Occasionally, azimuths are measured from 0° to +180° in the west and from 0° to -180° in the east. (In geodesy, azimuths are measured from the north point [4].)
Distinctive features of the alteration of coordinates of celestial objects [ edit ] .
Within a 24-hour period, a star (and likewise, to a preliminary approximation, a celestial body within the solar system) traces a circular path perpendicular to the axis of the world (PP’), which, at a given latitude φ, is inclined at an angle φ to the mathematical horizon. Consequently, it will exclusively move parallel to the mathematical horizon when φ is equivalent to 90 degrees, specifically at the North Pole. Thus, all stars visible in that location will be non-setting (including the Sun for a six-month period, as indicated by the longitude of the day), and their altitude h will remain constant. At different latitudes, the stars accessible for observation during this time of the year are classified into:
- setting and rising [3] :16 (h reaches 0 at some point during the day)
- non-ascending [3] :16 (h is consistently greater than 0)
- non-descending [3] :16 (h is consistently less than 0)
Every day, a star reaches its maximum height, h, when it passes through the celestial meridian at its upper culmination. Similarly, it reaches its minimum height at its lower culmination. As the star moves from its lower culmination to its upper culmination, its height, h, increases. Conversely, as it moves from its upper culmination to its lower culmination, its height, h, decreases.
Transition to the initial equatorial [ edit ]
In addition to the NESW horizon plane, the ZZ’ plumb line, and the PP’ world axis, we can construct the celestial equator perpendicular to PP’ at point O. Let t represent the hour angle of the luminary, δ be its declination, R be the luminary itself, and z be its zenith distance. The horizontal and initial equatorial coordinate systems can be connected by the spherical triangle PZR, also known as the first astronomical triangle [1]:68, or the parallactic triangle [2]:36. The formulas for transitioning from the horizontal coordinate system to the initial equatorial coordinate system are as follows [5]:18:
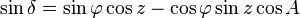
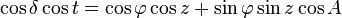
When solving the spherical triangle PZR, we use the same sequence of formulas as in the derivation of similar formulas for the ecliptic coordinate system. These include the cosine theorem, the sine theorem, and the five elements formula [2] :37. The cosine theorem is applied as follows:
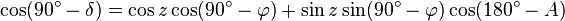
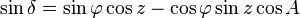
The initial equation is derived. Next, we can utilize the sine theorem on the identical spherical triangle:
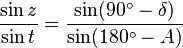
The second equation is derived. Now we can apply the five-element formula to our spherical triangle:
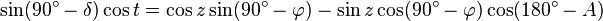
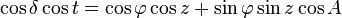
There are three formulas that have been derived. These formulas are obtained by considering a single spherical triangle.
Conversion from the initial equatorial [ edit ]
The equations for converting from the initial equatorial coordinate system to the horizontal coordinate system are obtained by analyzing the identical spherical triangle and utilizing the same spherical trigonometry equations as for the inverse conversion [2] :37 . They take the following shape [5] :17 :
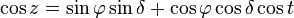
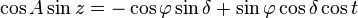
- ↑ 1,01,11,21,31,41,51,61,7Ciesiewicz V.P.. A Guide to Observing the Sky. – 6th edition. – Moscow: Nauka, 1984. – 304 pages.
- ↑ 2,02,12,22,3Belova N. A. Spherical Astronomy Course. – Moscow: Nedra, 1971. – 183 pages.
- ↑ 3,03,13,23,3Vorontsov-Vel’yaminov B.A.. Astronomy: Textbook for 10th grade of secondary school. – 17th edition. – Moscow: Prosveshchenie, 1987. – 159 pages.
- ↑ N. Alexandrovich “The Horizontal Coordinate System”.
- ↑ 5,05,1Balk M. B., Demin V. G. G., Kunitsyn A. L. Collection of Problems on Celestial Mechanics and Cosmodynamics. – Moscow: Nauka, 1972. – 336 pages.