Currently, there are additional accumulative discounts (ranging from 2% to 25%) offered to 58,753 educational establishments. To determine the applicable discount for all staff members of your educational institution, please access your personal Infoworks account.


Are you interested in a professional retraining course?
Learn about the pedagogy of additional education (arts and crafts)
We have an exciting offer for you! We can apply a discount to our courses based on the number of your colleagues who have already enrolled in Infoworks courses.
Currently, 58,753 educational institutions are benefiting from additional discounts ranging from 2% to 25%. To find out the discount that applies to all employees of your educational institution, simply log in to your personal Infoworks account.


Course for professional advancement
Characteristics of managing general education institutions
We can apply a discount for your educational institution to this offer (the amount of the discount depends on how many of your colleagues have completed Infoworks courses)
At present, 58,753 educational institutions are eligible for additional discounts (ranging from 2% to 25%). To find out what discount is available for all staff members of your educational institution, please log in to your personal Infoworks account.


Getting ready for the USE in literature. Unique creativity of the comedy “Nedorosl” by D. I. Fonvizin
Description of the presentation in separate slides:

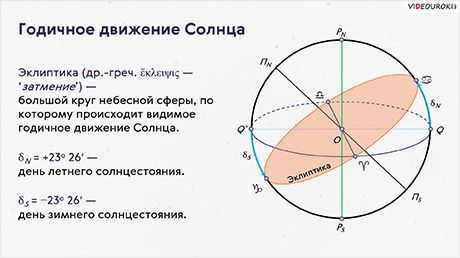
Visible movement of the Sun along the Ecliptic.
Created by Deyanova E.S., a physics teacher at MBOU “Karpogorskaya School № 118”.


Slide 3: Organizational and Motivational Stage
Epigraph for the Lesson
“Heavenly vault, ablaze with celestial splendor,
Mysteriously gazing from the depths,
And we sail on a fiery abyss.
Surrounded on all sides.
– F. Tyutchev
We, as observers on Earth, perceive different positions of the stars and the Sun relative to the horizon depending on the time of day and calendar date. However, we may not always realize that the apparent daily movement of the Sun in the sky is an illusion.


Slide 4 II. Actualization of knowledge.
In the previous lessons, we delved into the topic of the celestial sphere and explored how the position of celestial bodies changes at different geographical latitudes.
Let’s refresh our memory on the formulas that connect horizontal, equatorial, and geographic coordinates.
What is the right ascension of a celestial body when it crosses the celestial meridian?
Which point in the sky has equatorial coordinates: ?
How many times does a celestial body cross the celestial meridian in a day?


Slide 5 III. Problem statement and formulation of the purpose of the activity.
Therefore, stars possess coordinates (declination and right ascension) that enable us to mark their positions on a star chart.
The Sun, being the closest star to us, also has coordinates.
Attempt to locate its coordinates on a star chart.
Why do you think you were unable to do so?
The subject of today’s lesson is “Visible motion of the Sun. Ecliptic.”
Lesson objectives: analyze the Sun’s movement throughout the year in relation to the background of stars and during the day for an observer on Earth.
Discuss the peculiarities of daylight and nighttime durations.

Slide 7: The Sun’s movement across the zodiacal constellations
Take note of the zodiacal constellations on a star chart and record them.
What is the reasoning behind having 12 of them, and which constellation is not considered zodiacal?
Can we observe the constellation where the Sun is currently positioned (or rather where it appears from Earth)? Which constellation is visible throughout the entire night and reaches its highest point at midnight?
In a certain book, the following words can be found: “Winter had arrived; the Sun had departed from the Sagittarius constellation and was approaching Capricorn. Identify the astronomical error made by the author in these lines.
What is the origin of the name “zodiacal” for these constellations?

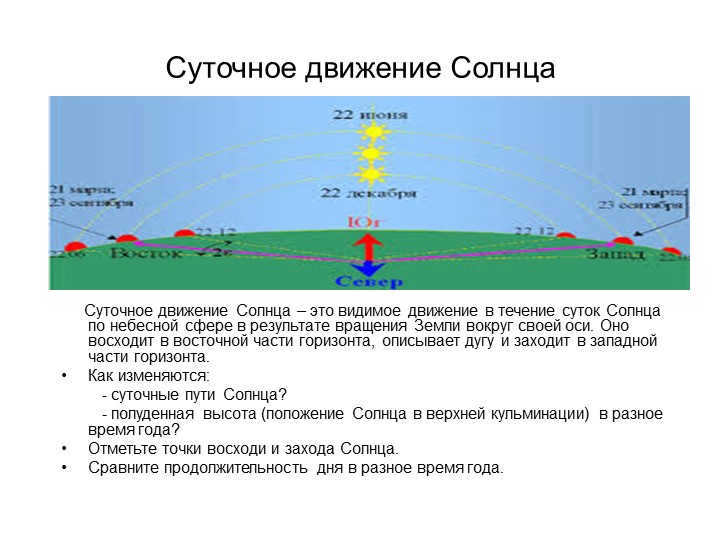
Slide 9: The Sun’s Daily Motion
The daily motion of the Sun refers to its observable movement throughout the day as a result of the Earth rotating on its axis. At sunrise, the Sun appears on the eastern horizon and then follows an arc across the sky, finally setting on the western horizon. This path is known as the Sun’s diurnal path.
What are the variations in the Sun’s diurnal path at different times of the year? How does the Sun’s position at midday (its highest point in the sky) change throughout the year?
Make note of the exact points where the Sun rises and sets.
Also, compare the length of the day at different times of the year.
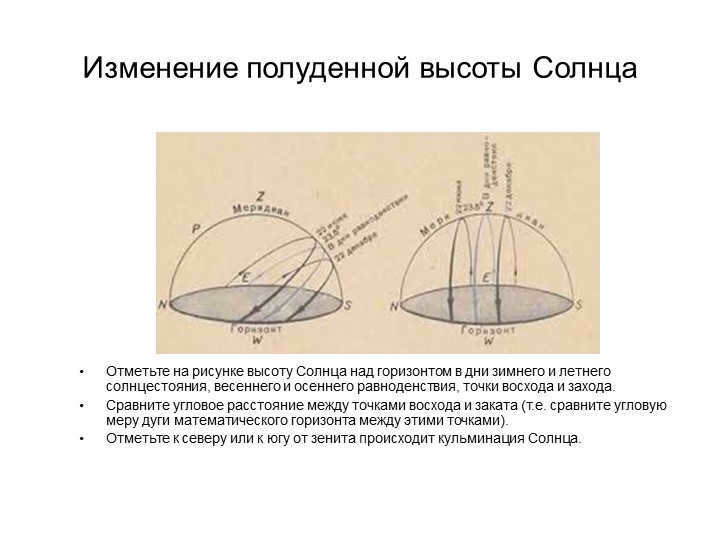
On Slide 10, we will observe the change in the Sun’s noon altitude. Your task is to mark on the figure the height of the Sun above the horizon on the days of the winter and summer solstice, spring and fall equinoxes, as well as the sunrise and sunset points. Additionally, compare the angular distance between the sunrise and sunset points by measuring the arc of the mathematical horizon between these points. Finally, take note of whether the Sun culminates to the north or south of the zenith.

Slide 11 The Sun’s declination undergoes change throughout the year. What are the boundaries within which this change occurs? Explore the chart and star map to compare the Sun’s declination on different dates. Can you identify any patterns in the Sun’s declination over the course of the year?

Slide V. Introducing fresh information into the system. Establishing the midday elevation of the Sun based on the known latitude of the observation location and declination.
Goals: 1. Determine the Sun’s elevation above the horizon in Arkhangelsk
( )
On the summer solstice
On the winter solstice
On the spring and autumn equinoxes
How does the Sun’s altitude differ on these days?
What is the difference in angular distance between the sunrise and sunset points?
The Sun reaches its highest point to the south of the zenith.
Answers:
Instructions: calculate the Sun’s declination using a star chart.
2. What is the method to determine the latitude of an observation site based on the Sun’s altitude during upper culmination and its declination?

13 Slide The duration of daylight varies at different latitudes.
Daylight duration is defined as the period between sunrise and sunset.
Civil twilight, which is the time when no bright stars are visible, continues until the Sun goes below the horizon at the
During white nights
At the boundary of the dark nights.
Which latitude experiences a consistent length of day and night throughout the year, with sunrise at 6 o’clock and sunset at 18 o’clock?

Slide 14 of the lesson VI. Reflexion “Syncwein”.
Create a synquain based on the lesson’s topic.
Write
Line 1 – one keyword that defines the content of the synquain.
Line 2 – 2 descriptive words characterizing the given concept.
Line 3 – 3 action verbs denoting activities related to the topic.
Line 4 – a brief sentence revealing the essence of the topic or expressing an attitude towards it.
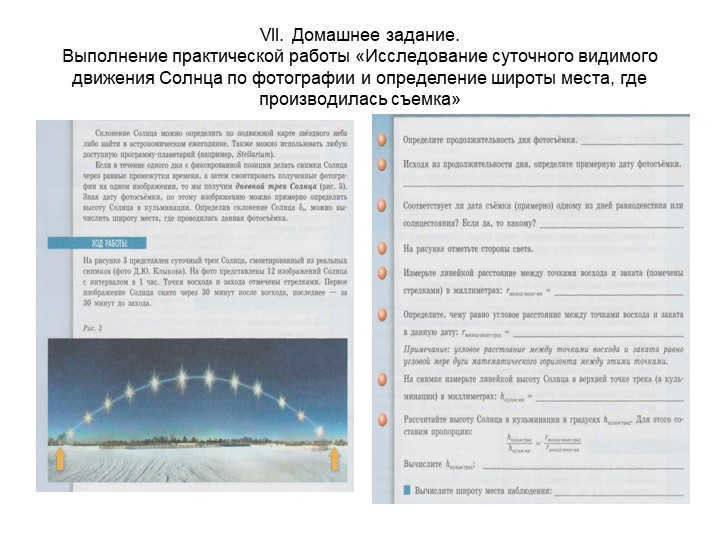
For the task of the seventh slide, you are required to complete the practical work that involves studying the daily apparent motion of the Sun. This can be achieved by capturing photographs of the Sun and determining the latitude of the location where the photographs were taken.


Following this instructional video, you will acquire a comprehensive understanding of the term “ecliptic”. Additionally, we will explore the distinct characteristics of the Sun’s daily movement at various latitudes.
Currently, it is not possible to view or share the video lesson with students.
In order to access this and other video lessons included in the package, you will need to add it to your personal account.
Enjoy amazing features

Outline of the lesson on “The Sun’s annual motion across the sky. Ecliptic.”
The path of the Sun across the celestial sphere is similar to that of other stars. In regions with moderate latitudes, we can witness its emergence from the eastern horizon every morning. Gradually, it ascends above the horizon and eventually reaches its highest point at noon. Subsequently, the Sun descends, approaching the horizon, and sets in the western part of the sky.
Even in ancient times, individuals who observed the Sun’s movement in the sky noticed that its midday height varies throughout the year, corresponding to changes in the view of the starry sky.
If we were to mark the position of the Sun on the celestial sphere at the time of its culmination every day throughout the year, we would create a large circle that represents the visible path of the center of the solar disk over the course of the year. The ancient Greeks referred to this circle as the ecliptic, which can be translated as ‘eclipse‘.
It is important to note that the apparent movement of the Sun against the background of stars is caused by the Earth’s rotation around the Sun. In other words, the Earth’s orbit is located in the ecliptic plane.
In a previous discussion, we mentioned that the celestial equator is intersected by the ecliptic at two specific locations: the vernal equinox point (also known as the point of Aries) and the autumnal equinox point (also known as the point of Libra).
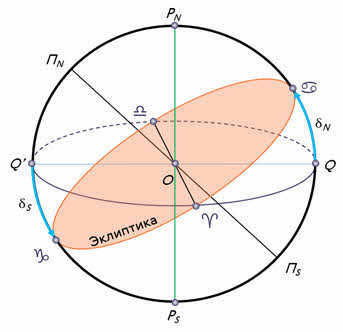
In addition to the equinox points, there are two additional points along the ecliptic where the Sun’s declination is at its highest and lowest. These points are known as the solstice points, or solstices. At the point of the summer solstice (also called the point of Cancer), the Sun reaches its maximum declination of +23 degrees 26 minutes. At the point of the winter solstice (the point of Capricorn), the Sun’s declination is at its minimum, measuring -23 degrees 26 minutes.
The constellations that the ecliptic passes through are referred to as the ecliptic.
Ancient Mesopotamians observed that the Sun, in its yearly journey, travels through 12 constellations, including Aries, Taurus, Gemini, Cancer, Leo, Virgo, Libra, Scorpio, Sagittarius, Capricorn, Aquarius, and Pisces.
The Zodiac Belt was later given this name by the ancient Greeks. It literally means “circle of animals.” If you look at the names of the zodiacal constellations, you can see that half of them in the classical Greek zodiac are represented by animals (in addition to mythological creatures).
Initially, the signs of the zodiac coincided with the zodiacal constellations, as there was no clear division yet. The counting of zodiac signs began from the point of the vernal equinox, and the zodiacal constellations divided the ecliptic into 12 equal parts.
Currently, the positioning of zodiacal and ecliptic constellations is not identical: there exist 12 zodiacal constellations, while 13 ecliptic constellations are present (the inclusion of the Serpentine constellation, in which the Sun resides from November 30 to December 17, accounts for this difference). Furthermore, due to the precession of the Earth’s axis, the locations of the spring and fall equinoxes are continuously shifting.
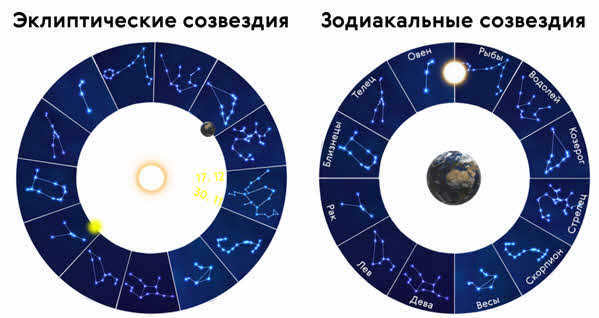
Precession, also known as the precession of the equinoxes, is a phenomenon that occurs due to the gradual wobbling of the Earth’s rotational axis. This results in a reverse movement of the constellations compared to the usual annual cycle. As a result, the point of the vernal equinox shifts to a different zodiac sign clockwise approximately every 2150 years. For instance, from 4300 to 2150 B.C., this point was in the constellation of Taurus (the Taurus era), from 2150 B.C. to 1 A.D. – in the constellation of Aries. Currently, the point of the vernal equinox is in Pisces.
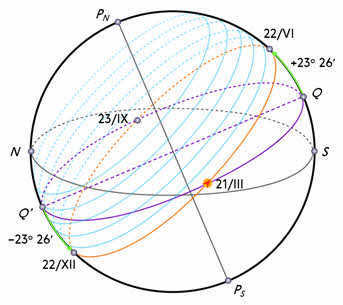
Following the solstice, there is a gradual decrease in the Sun’s declination and the long day begins to shorten until day and night are equalized (around September 23).
After the fall equinox, the Sun’s declination shifts southward. In the Northern Hemisphere, the day continues to shorten, while in the Southern Hemisphere, it lengthens. This trend will continue until the Sun reaches the winter solstice (around December 22). During this time, the Sun’s declination remains relatively stable for about 4 days. In the Northern Hemisphere, this results in the shortest days and longest nights, while the Southern Hemisphere experiences the longest day as it is in the midst of summer.
After four days, an observer in the Northern Hemisphere will notice a gradual increase in the Sun’s declination. Approximately three months later, the Sun will once again reach the vernal equinox.
Now, let’s shift our attention to the North Pole. Here, the Sun’s daily movement is nearly parallel to the horizon. As a result, for half of the year, the Sun remains above the horizon, creating circular paths – a phenomenon known as the polar day.
After six months, the Sun’s declination will change to a negative value, signaling the start of the polar night at the North Pole. This period of darkness will also persist for approximately six months.
Why don’t we relocate to the equator? At this geographical location, the Sun, along with other celestial bodies, ascends and descends at a right angle to the true horizon. Consequently, at the equator, the duration of daylight and darkness remains consistently balanced.
Let’s now focus on the star map and do some work with it. So, we already understand that the star map is a representation of the celestial sphere projected onto a plane, with celestial objects plotted on it using the equatorial coordinate system. It’s important to remember that the North Pole of the world is located at the center of the map, with Polaris right next to it. The equatorial coordinate grid on the map is depicted by rays radiating outwards and concentric circles. On the outer edges of the map, near each ray, you can find numbers indicating the hours of direct ascent (ranging from zero to twenty-three).
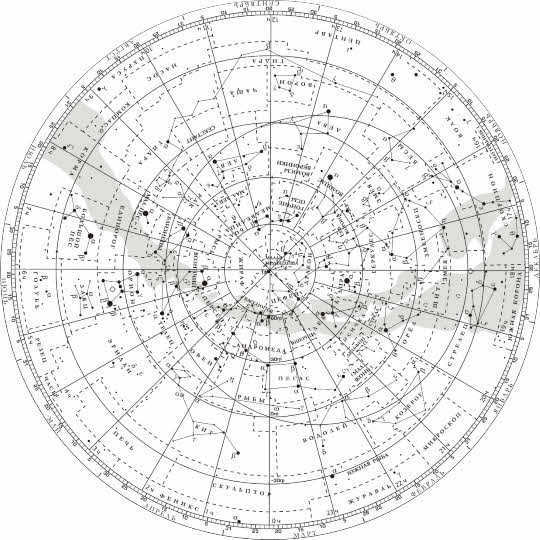
The inclination of the sun changes within certain limits, and this change is measured along the rays originating from the celestial equator, which is marked as zero degrees.
To determine the view of the sky at any given time on a specific date, a sky map with an overlay circle is used. The circle contains digitized intersecting ovals, and the outer edge of the circle has a scale with divisions corresponding to the hours of the day.

In the overlapping circle, a incision is created along the oval that is closest to the latitude of the observation location. The resulting shape of the cutout will represent the horizon with its primary directions: north, south, west, and east.
To determine the celestial view at a specific moment in time on the desired date, it is necessary to align the overlay circle and the map so that the time stroke coincides with the stroke of the date. Then, in a hole of the overlapping circle, you will be able to see the starry sky for the desired day and hour.
On the outline of the cutout, between its points Y, B, and C, you will find the stars that are ascending at that moment, and between points Y, 3, and C, the stars that are descending. Any stars covered by the overlapping circle will not be visible.
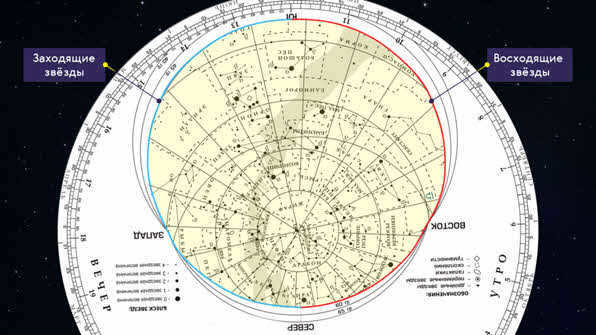
However, the use of a dynamic chart enables individuals to not only identify the specific times at which stars rise and set, but also various other celestial bodies, such as the Sun.
As previously mentioned, the observable annual path of the Sun among the stars is known as the ecliptic. On the chart, this path is depicted as an oval shape that is slightly offset from the North Pole of the globe. The points at which the ecliptic intersects with the celestial equator are referred to as the vernal and autumnal equinoxes (symbolized by the ram and scales). The remaining two points, the summer and winter solstices, are represented on our chart by a circle and a rhombus, respectively.
To determine the sunrise and sunset times for the Sun or planets, it is necessary to plot their positions on a map in advance. For the Sun, this is relatively easy: simply place a ruler on the North Pole of the world and mark the stroke for a given date. The point where the ruler intersects with the ecliptic will indicate the position of the Sun on that date.
Now, let’s utilize the mobile star map to determine the equatorial coordinates of the Sun, specifically for October 18. Additionally, we can approximate the time of its sunrise and sunset on this date.

The Sun’s position in the sky changes depending on the time and location of observations on Earth. As the Earth orbits the Sun over the course of a year, the Sun appears to move in relation to the fixed stars along a circular path known as the ecliptic.
The rotation of the Earth on its axis causes the Sun to appear to move across the sky along its path, which is determined by the latitude of the observer. The time at which the Sun passes through the observer’s meridian depends on the longitude.
Therefore, to determine the position of the Sun at a specific location and time, we can follow these three steps:
- Find the Sun’s position in the ecliptic coordinate system.
- Transform it into the equatorial coordinate system.
- Convert it into a horizontal coordinate system based on the local time and observer’s location. This system is commonly employed to determine the Sun’s position using the solar zenith angle and solar azimuth angle, both of which can represent the Sun’s trajectory.
Ecliptic Coordinates
These equations are taken from the Astronomical Almanac and can be utilized to compute the apparent coordinates of the Sun, mean equinox, and ecliptic dates with an accuracy of around 0° 0.01 (36 inches) for dates ranging from 1950 to 2050. They have been coded into a Fortran 90 subroutine in Ref. and are employed to calculate the Sun’s zenith angle and solar azimuth as observed from the Earth’s surface.
To begin, calculate the value of n – the number of days (positive or negative, including fractional days) from noon GMT to Earth time on January 1, 2000 (J2000.0). If the Julian date of the desired time is known, the value of n can be determined using the following formula:
n = J D – 2451545.0 – 2451545.0>
The mean longitude of the Sun, corrected for aberrations of light, is given by the equation:
L = 280.460° + 0.9856474°n + 0.9856474n>
The average anomaly of the Sun (or rather, the Earth in its orbit around the Sun, although it is more convenient to think of it as the Sun orbiting the Earth) is:
The formula is as follows: mean anomaly equals 357,528° + 0.9856003°n + 0.9856003^n>
Keep the value within the range of 0° to 360° by adding or subtracting multiples of 360° as necessary. This is denoted as L gram.
The value of λ sign is calculated as L + 1.915°sin gram + 0.020°sin 2 gram \ sin g + 0.020^^sin 2g>
Since the ecliptic latitude of the Sun never exceeds 0.00033°,
and the distance from the Sun to the Earth is given in astronomical units:
p sign equals 1.00014 – 0.01671 because gram – 0.00014 because 2 grams.
Tilt of the ecliptic
If the angle of inclination of the ecliptic is not given, it can be estimated:
Equatorial coordinates
The α symbol is equal to arctan (ϵ tan λ), where ϵ and λ are in the same quadrant as α.
To obtain the right ascension (RA) in the correct quadrant in computer programs, use the Arctan2 function with two arguments, such as ATAN2(y, x).
The α symbol is equal to arctan2(ϵ sin λ, λ).
Rectangular equatorial coordinates
The rectangular equatorial coordinates in the right-handed system can be represented in astronomical units as follows:
X sign equals p due to λ
Y sign equals p due to ϵ sin λ
Z sign equals p sin ϵ sin λ
Where X, Y, and Z represent the axes pointing towards the March equinox, June solstice, and the north pole of the world, respectively.
Coordinates in the Horizontal Plane
The Angle of the Sun’s Declination as Observed from Earth
The trajectory of the Sun across the celestial sphere during daylight hours for an observer located at a latitude of 56° N. The Sun’s trajectory changes throughout the year in accordance with its declination. The points where the curves intersect the horizontal axis indicate the azimuths in degrees from the north at which the Sun rises and sets.
Summary
During the spring season in the northern hemisphere, the Sun appears to move towards the north, crossing the celestial equator at the March equinox. At the June solstice, the Sun reaches its highest point with a declination equal to the angle of tilt of the Earth’s axis (23.44°). As the year progresses, the Sun’s declination decreases and reaches a minimum (-23.44°) at the December solstice. This variation in declination is responsible for the changing seasons. The graph of the Sun’s declination throughout the year follows a sinusoidal pattern, with an amplitude of 23.44°. However, there are slight differences in the length of each lobe of the wave.
If the axial slope of 90 degrees decreases, the absolute values of the maximum and minimum slopes will also decrease to match the axial slope. Moreover, the shapes of the peaks and valleys on the graph will become less pronounced, curving to resemble the peaks and valleys of a sine wave. Nevertheless, even when the axial tilt is the same as that of the actual Earth, the peaks and valleys still maintain a sharper appearance compared to those of a sine wave.
Indeed, the Earth’s path around the Sun is not a perfect circle, but rather an ellipse. During January, when the Earth is closer to the Sun (known as perihelion), it moves faster than in July, when it is farther away from the Sun (known as aphelion). This means that certain processes, such as changes in solar declination, happen more quickly in January compared to July. When represented on a graph, this results in sharper low points and less pronounced high points. Additionally, because perihelion and aphelion do not align exactly with the solstice dates, the highs and lows of solar declination are slightly asymmetrical. The rates at which these changes occur before and after perihelion/aphelion are also not exactly equal.
As a result, a graph representing the Sun’s apparent declination differs from a simple sine wave in several ways. The accurate calculation of this declination is therefore subject to certain difficulties and challenges, as illustrated below.
Calculations
The angle between the Sun’s rays and the Earth’s equator is known as the Sun’s inclination, δ☉. Astronomers refer to the tilt of the Earth’s axis as the tilt of the ecliptic, which is the angle between the Earth’s axis and a line perpendicular to its orbit. Over thousands of years, the tilt of the Earth’s axis slowly changes, but its current value of approximately ε = 23° 26′ remains relatively constant. As a result, the change in solar declination from one year to the next is almost identical.
During the solstices, the angle between the Sun’s rays and the Earth’s equator reaches its maximum value of 23° 26′. This means that on the northern summer solstice, δ☉ = +23°26′, while on the southern summer solstice, δ☉ = -23°26′.
During each equinox, the center of the Sun appears to cross the celestial equator, resulting in a declination of 0°.
To calculate the Sun’s declination at any given moment, the following formula is used:
δ ⊙ sign equals arcsine [sine (-23.44°) multiplied by sine (EL)] = \ arcsin \ left [\ sin \ left (-23.44 ^ \ right) \ cdot \ sin \ left (EL \ right) \ right]>
where EL is the ecliptic longitude (essentially the position of the Earth in its orbit). Due to the small eccentricity of the Earth’s orbit, we can approximate it as a circle, which introduces an error of up to 1°. This circle approximation causes EL to be 90° ahead of the solstices in Earth’s orbit (at the equinoxes), so we can express sin (EL) as sin (90 + NDS) = cos (NDS), where NDS represents the number of days after the December solstice. Additionally, by approximating arcsin [sin (d) – cos (NDS)] as approximately equal to d – cos (NDS), we obtain the following frequently used formula:
δ ⊙ sign equals – 23.44 ∘ ⋅ because [ 360 ∘ 365 ⋅ ( N + 10 ) ] = – 23.44 ^ ^ \ cdot \ cos \ left [<\ frac <360 ^ > > > \ cdot \ left (N + 10 \ right )\ Right]>
The calculation of the declination can be improved by avoiding two approximations and using the Earth’s orbital parameters to obtain a more accurate estimation of EL:
The sign of δ ⊙ can be determined by applying the formula Arcsin [ sin ( – 23.44 ∘ ) ⋅ cos ( 360 ∘ 365.24 ( N + 10 ) + 360 ∘ π ⋅ 0.0167 sin ( 360 ∘ 365.24 ( N – 2 ) ) ) ) ], which simplifies to: \arcsin \left [\sin \left (-23.44 ^
ight) \cdot \cos \left (\frac{360 ^}{365.24} (N + 10) + \frac{360 ^}{\pi} \cdot 0.0167 \sin \left (\frac{360 ^}{365.24} (N-2)
ight)
ight]
Furthermore, this equation can be further simplified by substituting the constant values:
The value of the δ ⊙ sign is calculated as – Arcsin[0.39779 + (0.98565 ∘ (N + 10) + 1.914 ∘ sin(0.98565 ∘ (N – 2)))] which can be written as – \ arcsin \ left [0.39779 \ cos \ left (0.98565 ^ \ left (N + 10 \ right) +1.914 ^ \ sin \ left ( 0.98565 ^ \ left (N – 2 \ right) \ right) \ right) \ right]>
N represents the number of days starting from midnight UT on January 1st, which can include decimal fractions to account for local time adjustments later or earlier in the day. The value 2 in (N-2) denotes the approximate number of days until Earth’s perihelion after January 1st. The value 0.0167 corresponds to the current eccentricity of Earth’s orbit. Although eccentricity changes slowly over time, it can be considered constant for dates close to the present. The equation has a maximum error of less than ±0.2°, but for a specific year, the error is less than ±0.03° if the number 10 is adjusted up or down based on how far the previous year’s December solstice occurred before or after noon on December 22nd. These accuracies are compared to NOAA’s advanced calculations, which use Jean Meeus’ 1999 algorithm and are accurate within 0.01°.
(The formula mentioned above pertains to a relatively straightforward and precise calculation of the equation of time, which is expounded upon in this article.)
More advanced algorithms account for variations in ecliptic longitude by incorporating additional terms to correct for the eccentricity of the orbit. These algorithms also adjust for the Earth’s tilt of 23.44°, which changes slightly over time. Additionally, corrections are made to account for the Moon’s influence on the Earth’s position offset from the center of the Sun-Earth orbit. Once the declination relative to the Earth’s center is determined, a parallax correction is applied based on the observer’s distance from the Earth’s center. This correction is typically less than 0.0025°. The margin of error in calculating the position of the Sun’s center can be as little as 0.00015°. To put this into perspective, the Sun’s width spans approximately 0.5°.
Refraction in the Earth’s atmosphere
The above calculations for declination do not take into account the phenomenon of light refraction in the Earth’s atmosphere. This phenomenon causes the apparent angle of elevation of the Sun, as observed by an observer, to be higher than the actual angle of elevation, particularly when the Sun is at low elevations. For instance, when the Sun is at an elevation of 10°, it appears to be at an angle of 10.1°. By considering the Sun’s inclination and its direct ascent, we can calculate both its azimuth and its true elevation, which can then be adjusted for refraction to determine its apparent position.
Equation of Time
The equation of time states that the sundial will appear to run faster than a clock displaying the average local time when it is positioned above the axis, and slower when positioned below the axis.
The phenomenon that primarily affects time is referred to as the equation of time, utilizing the term “equation” in an antiquated manner to denote a “correction”. This variation is quantified in temporal units, minutes and seconds, which indicates the discrepancy between the sundial and the clock. The equation of time may be either positive or negative.
Analemma
The analemma is a figure-eight-shaped curve that represents the apparent motion of the Sun in the sky over the course of a year. It is created by plotting the position of the Sun at the same time each day, usually at noon, and then connecting those points. The shape of the analemma is affected by several factors, including the tilt of the Earth’s axis and the elliptical shape of its orbit around the Sun. The analemma is often used to determine the exact time of solar noon, as well as to study the Earth’s rotation and revolution.

The analemma is an illustration that displays the yearly variations in the position of the Sun on the celestial sphere, in relation to its average position as observed from a fixed spot on Earth. (The term analemma is occasionally used in other contexts, although rarely). It can be visualized as a representation of the apparent movement of the Sun throughout the year, which resembles a figure of eight. The analemma can be presented by overlaying photographs taken at the same time of day but a few days apart over the span of a year.
The analemma can be visualized as a graph displaying the Sun’s declination vertically and the equation of time horizontally. The scale is typically chosen so that equal distances on the chart correspond to equal angles on the celestial sphere. For example, 4 minutes (or 3 minutes and 56 seconds) in the equation of time is represented by the same distance as 1° in declination. This is because the Earth rotates at an average rate of 1° every 4 minutes in relation to the Sun.
The analemma is depicted as if the observer is gazing up at the sky, with north positioned at the top and west indicated on the right. This convention is followed even when the analemma is marked on a geographic globe, which typically depicts the continents and other features from west to left.
Additional Resources
Recommended Reading
Useful Links
- The Sun Position Algorithm can be found on the Renewable Resources Data Center website of the National Renewable Energy Laboratory.
- Visit pveducation.org for a Sun position calculator that provides an interactive display of the Sun’s path in the sky.
- The NOAA Solar Calculator is available on the website of the NOAA Earth System Research Laboratory Global Monitoring Division.
- Utilize the NOAA Sun declination and position calculator to determine the position of the Sun.
- For highly accurate positions of solar system objects based on JPL DE series ephemerides, check out HORIZONS on the JPL website.
- IMCCE website offers general ephemerides of solar system bodies based on INPOP series ephemerides.
- Find the position of the Sun in the R package “Insol”.
Changes in the Sun’s daily path above the horizon at different latitudes
The Sun’s daily path above the horizon varies as we move between different latitudes throughout the year. This can be observed in the visible movement of the Sun along the ecliptic from spring to summer and then to winter.
To understand the specific changes in the Sun’s daily path at different latitudes, refer to Figure 43. At point Q, the Sun reaches its highest point at noon during the equinoxes, as it is positioned on the celestial equator on these days. On the summer solstice, it reaches a point 23°27′ above the horizon, while on the winter solstice, it reaches a point 23°27′ below the horizon (complete the drawing with the diurnal parallels of the Sun on the solstices). Figure 45, on the left, illustrates the daily paths of the Sun above the horizon at mid-latitudes.
Now let’s find out the latitude at which the Sun can reach its highest point directly overhead, also known as the zenith. Looking at Figure 43, we can see that this is possible at latitudes ranging from +23°, 5 to -23°,5. This occurs on days when the Sun’s declination is equal to the latitude of the location, which is the angular distance between the point Q on the celestial equator and the zenith. After thoroughly analyzing this information, we can conclude the following.
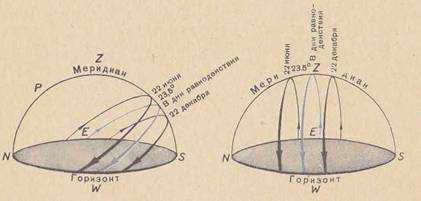
Figure 45 – The Sun’s movement above the horizon at different times of the year for an observer at mid-latitudes (left) and at the Earth’s equator (right).
There are certain points on Earth where the Sun reaches its highest point in the sky at noon only once annually. This occurs on June 22nd at a latitude of +23°27′, known as the Tropic of Cancer. On December 22nd, at locations on the southern parallel of -23°27′, the Sun is at its zenith, known as the Tropic of Capricorn.
These geographical parallels were named in ancient times because the Sun reached its highest point in the sky at the tropics when it passed through the constellations of Cancer and Capricorn. These constellations marked the summer and winter solstices. Over the thousands of years that have passed, these solstice points have shifted to the neighboring constellations of Gemini and Sagittarius. The Greek word “tropic” means “rotation” and refers to the Sun’s turning motion in relation to the celestial equator.
At the poles of the Earth, the Sun, when it is above the horizon, which aligns with the celestial equator, traces nearly horizontal circles on a daily basis. As we are aware, this phenomenon occurs at the North Pole for a duration of six months, starting from March 21 and ending on September 23. During the period from March 21 to June 22, the Sun consistently rises above the celestial equator, transitioning from the southern hemisphere of the sky to the northern hemisphere. Thus, we can draw the following inference.
At the Arctic region of our planet, the Sun appears on the horizon once a year – typically around March 21st – and remains visible for six months, continuously circling above the horizon. During this time, the Sun gradually ascends higher in the sky until reaching its peak on June 22nd. Essentially, the Sun traces a gentle spiral path in the sky. From June 22nd to September 23rd, the Sun gradually descends along the same spiral until it disappears below the horizon. For the following six months, the Sun remains hidden from view. Thus, half of the year is characterized by continuous darkness, while the other half experiences perpetual daylight.
It is evident that there exist locations on our planet where the Sun does not set except on one day of the year, specifically June 22, when it merely grazes the horizon (in the northern direction) during its lowest point (at midnight). On December 22, and exclusively on this date, the Sun does not rise in these places, and at noon it barely touches the southernmost point before remaining below the horizon. These particular locations can be found on Earth along the 66°33′ parallel, commonly referred to as the Arctic Circle.
The same phenomena occur at the South Pole as they do at the North Pole: there, the polar day extends from September 23 to March 21, while the polar night lasts from March 21 to September 23. The southern polar circle (at 66°33′ south latitude) experiences a day without sunrise on June 22, and a day without sunset on December 22.
In regions slightly south of the Arctic Circle, like Leningrad, around June 22nd, the Sun sets below the horizon at night, but not for a long time and not very deeply. As a result, its rays from below the horizon brightly illuminate the sky (“white nights“).
From all of this, it becomes evident (and it should be firmly noted) that the timing of sunrise and sunset is not only influenced by the date, but also by the geographical latitude where the observer is situated. Therefore, the timing of sunrise and sunset as indicated in regular calendars can only be accurate for one latitude, and not for the entire territory of the USSR.
Modification in the Sun’s equatorial coordinates
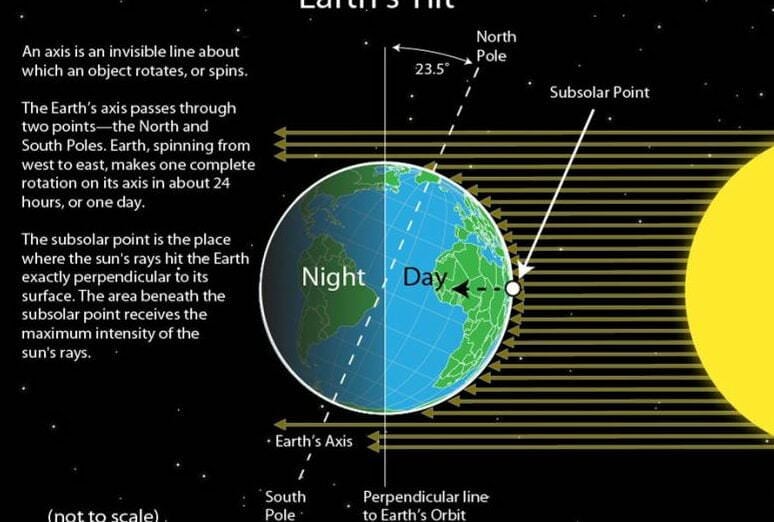
The Sun’s equatorial coordinates change as it moves along the ecliptic. When the Sun is at the vernal equinox, its declination and direct ascent are both zero. As the Sun continues to move, its direct ascent and declination increase each day. When the Sun reaches the summer solstice, its direct ascent becomes 90 degrees or 12 hours, and its declination reaches its maximum value of +23 degrees 27 minutes. After the summer solstice, the Sun’s declination starts to decrease while its direct ascent continues to increase. At the fall equinox, the direct ascent is 180 degrees or 12 hours, and the declination is 0 degrees. From there, the direct ascent of the Sun continues to increase and reaches 270 degrees or 18 hours at the winter solstice, while the declination reaches its minimum value of 23 degrees 27 minutes. The Sun’s declination then starts to increase again, and when it reaches the vernal equinox, the declination becomes zero once more, and the direct ascent, having reached 360 degrees or 24 hours, returns to zero. These changes in the Sun’s equatorial coordinates throughout the year are not uniform. The declination changes most rapidly near the equinoxes and most slowly near the solstices. On the other hand, the direct ascent changes slower near the equinoxes and faster near the solstices. Additionally, the rate of change in the direct ascent near the summer solstice is less than near the winter solstice. The visible motion of the Sun along the ecliptic is a result of the Earth’s actual motion – its revolution around the Sun. The Earth’s revolution around the Sun occurs in the same direction as its rotation around its axis, but not uniformly. The Earth’s axis of rotation is always inclined at an angle of 66 degrees 33 minutes to the plane of its orbit. As a result, it appears to us that the Sun moves irregularly across the sky among the stars from west to east, but on a circular path (ecliptic) inclined at an angle of 23 degrees 27 minutes to the celestial (and Earth’s) equator. When the Sun is at the vernal equinox, it rises in the east and sets in the west at all latitudes on Earth’s surface. Half of its daily path is above the horizon, and half is below. Therefore, on this day, except at the poles, the length of the day is equal to the length of the night. This day is known as the vernal equinox (around March 21) and marks the beginning of spring in the northern hemisphere (and the beginning of autumn in the southern hemisphere). The noon height of the Sun on the day of the vernal equinox at a given northern latitude j can be calculated using the formula (1.7) hS = 90 degrees – j. When the Sun is at the summer solstice, it rises in the northeast and sets in the northwest at a given northern latitude j. Most of its daily path is above the horizon. In the northern hemisphere, the day is longest and the night is shortest, while in the southern hemisphere, it is the opposite. This day is known as the summer solstice (around June 22) and marks the beginning of summer in the northern hemisphere (and the beginning of winter in the southern hemisphere). On the day of the summer solstice, the noon height of the Sun at a given northern latitude j reaches its maximum value hmax = 90 degrees – j + 23 degrees 27 minutes. When the Sun is at the autumnal equinox, it again rises in the east and sets in the west at all latitudes except the poles, resulting in equal day and night durations. This day is known as the autumnal equinox (around September 23) and marks the beginning of autumn in the northern hemisphere (and the beginning of spring in the southern hemisphere). The Sun’s altitude at noon on the day of the autumnal equinox at a given latitude j is again 90 degrees – j. Finally, when the Sun is at the winter solstice, it rises in the southeast and sets in the southwest. Most of its daily path is below the horizon. At a given northern latitude j, the day is shortest and the night is longest (while in southern latitudes, it is the opposite). This day is known as the winter solstice (around December 22) and marks the beginning of winter in the northern hemisphere (and the beginning of summer in the southern hemisphere). The Sun’s altitude on the day of the winter solstice at a given northern latitude j reaches its minimum value of hmin = 90 degrees – j – 23 degrees 27 minutes. On all other days of the year, the Sun’s altitude at noon falls between the values of hmax and hmin.
Presentation on “Stars and Constellations” for 11th Grade Astronomy Class

Pay attention! If the stars are shining. it is a sign that someone needs them, right? It means they are necessary so that every night above the rooftops every night above the rooftops?
The presentation was created by:
V.M.Dolgova and the 11th grade students

1. What are the characteristics of astronomy?
2. What are the horizontal coordinates called for luminaries?
3. Explain the changes in the coordinates of the Sun as it moves above the horizon throughout the day.
4. Despite the Sun’s diameter being about 400 times larger than the Moon’s diameter, why are their angular diameters almost equal?
5. What is the purpose of a telescope?
6. What is considered the primary feature of a telescope?
7. Why do the luminaries disappear from view when observing through a telescope?

1. What knowledge did you gain about astronomy during your studies of natural history, physics, and history?
2. How does astronomy differ from other natural sciences in terms of its objects and research methods?
3. Can you name different types of celestial bodies?
4. What is the significance of observations in astronomy? What instruments are used for conducting observations?
5. What role does space exploration play in our understanding of the Universe?
6. How do refractor and reflector optical systems differ from each other?

1. Celestial mechanics addresses various problems and challenges in the field of astronomy.
2. Can you name any national or international space observatories that are dedicated to observing celestial bodies?
3. The field of modern astronomy encompasses the study of all types of electromagnetic waves.
4. When observing the Moon, why is it necessary to use a telescope?
5. Are you familiar with any myths or legends that are associated with the names of stars, constellations, or planets?
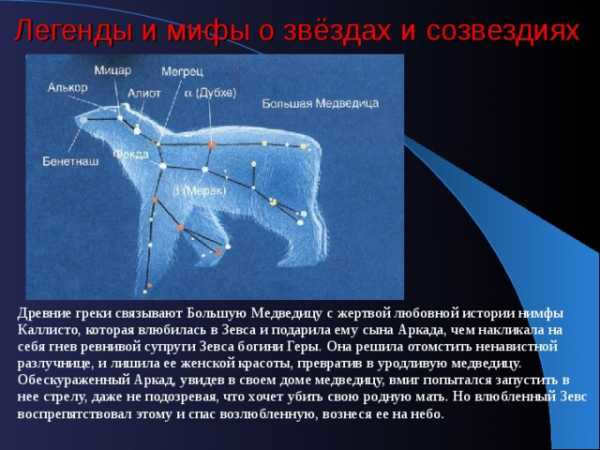
Stories and legends surrounding stars and constellations
Ancient Greeks connected the Big Dipper with the tragic love affair of the nymph Callisto, who fell in love with Zeus and bore him a son named Arcades. This enraged Zeus’s jealous wife, the goddess Hera. Seeking revenge on Callisto, Hera stripped her of her beauty and transformed her into an ugly bear. When Arcades unknowingly encountered the bear in his home, he attempted to shoot an arrow at it, not realizing that he was aiming at his own mother. However, Zeus, still in love with Callisto, intervened and saved her, taking her up to the heavens.
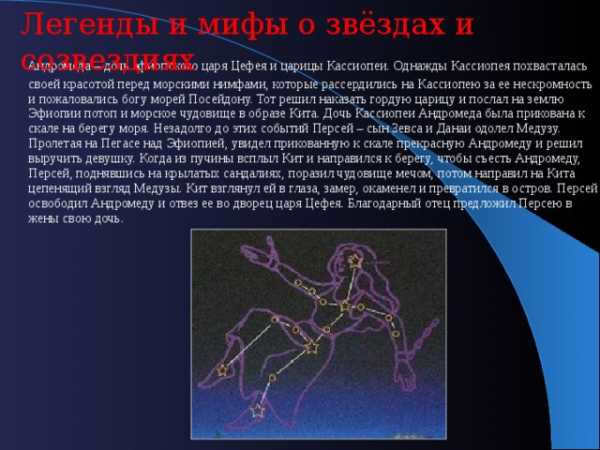
Stories and folklore surrounding stars and constellations
Andromeda is the daughter of Cepheus, the king of Ethiopia, and his wife Cassiopeia. One day, Cassiopeia bragged about her beauty to the sea nymphs, which angered them. They complained to Poseidon, the god of the seas, who decided to punish Cassiopeia for her immodesty. Poseidon sent a flood and a sea monster in the form of a whale to Ethiopia. As a result, Andromeda, Cassiopeia’s daughter, was chained to a rock by the seashore. Just before these events, Perseus, the son of Zeus and Danae, had defeated Medusa. While flying on the winged horse Pegasus over Ethiopia, Perseus noticed the beautiful Andromeda chained to the rock and decided to save her. When the sea monster rose from the depths and approached the shore to devour Andromeda, Perseus used his winged sandals to rise above the creature and struck it with his sword. Then, he used the gaze of Medusa, which turned creatures into stone, on the monster. The monster looked into Medusa’s eyes, became frozen, and transformed into an island. Perseus freed Andromeda and brought her to the palace of King Cepheus. In gratitude, Cepheus offered Andromeda’s hand in marriage to Perseus.

Astronomy assignment – virtual presentation
QUERIES
1. What are the attributes of astronomy?
2. What do we call the horizontal coordinates of celestial bodies?
3. Explain the variations in the coordinates of the Sun as it traverses the sky throughout the day.
4. In terms of size, how does the diameter of the Sun compare to that of the Moon?
Why are the angular diameters of the objects almost the same 400 times?
5. What is the purpose of using a telescope?
6. What is considered the main feature of a telescope?
7. Why do celestial bodies move out of sight when observed through a telescope?
EXERCISE:
1. What is the magnification of a telescope if a lens with an optical power of 0.4 dptr is used as its objective,
and a lens with an optical power of 10 dptr is used as an eyepiece?
2. How much more light does the largest Russian reflector telescope (mirror diameter 6 m) collect than a refractor telescope (lens diameter 60 mm)?
QUESTIONS.
1. At what points does the celestial equator intersect with the horizon line?
2. Where is the world axis located in relation to the Earth’s axis of rotation and the plane of the celestial meridian?
the plane of the celestial meridian?
3. Which circle of the celestial sphere do all celestial bodies cross twice a day?
4. How are the daily paths of the stars positioned relative to the celestial equator?
5. How can you determine an observer’s location at the North Pole of the Earth from the appearance of the sky and its rotation?
at the North Pole of the Earth?
6. At what point on the globe are no stars visible in the northern celestial
hemisphere?
QUESTIONS.
1. Why does the noon altitude of the Sun change throughout the year?
2. In what direction does the Sun appear to move annually relative to the stars?
3. What is the range of the Moon’s angular distance from the Sun?
4. How can the Moon’s phase be used to estimate its approximate angular distance from the Sun?
from the Sun?
5. By approximately how much does the Moon’s direct ascent change in a week?
in a week?
6. What observations need to be made to observe the Moon’s motion
around the Earth?
7. What observations demonstrate that there is a change of day and night on the moon
Online Presentation for Astronomy Homework
QUESTIONS.
1. What are the characteristics of astronomy?
2. What are the horizontal coordinates of the luminaries called?
3. Explain how the coordinates of the Sun change as it moves above the horizon throughout the day.
4. Despite the Sun’s larger linear size, why are its angular diameter and the Moon’s nearly equal?
5. What is the purpose of a telescope?
6. What is the primary characteristic of a telescope?
7. Why do luminaries become out of view when observed through a telescope?
EXERCISE:
1. If a lens with an optical power of 0.4 dptr is used as the objective and a lens with an optical power of 10 dptr is used as the eyepiece, what is the magnification of the telescope?
2. How much more light does Russia’s largest reflector telescope (with a mirror diameter of 6 m) gather compared to a refractor telescope with a lens diameter of 60 mm?
QUESTIONS.
1. Where does the celestial equator intersect with the horizon line?
2. How is the world axis positioned in relation to the Earth’s rotation axis and the plane of the celestial meridian?
3. Which circle of the celestial sphere do all luminaries cross twice a day?
4. How are the daily paths of stars positioned relative to the celestial equator?
5. What can be deduced from the appearance and rotation of the sky to identify an observer at the North Pole of the Earth?
6. At what location on the globe can no stars in the northern celestial hemisphere be seen?
QUESTIONS.
1. Why does the noon altitude of the Sun vary throughout the year?
2. In which direction does the Sun’s apparent annual motion occur relative to the stars?
3. Within what range does the Moon’s angular distance from the Sun vary?
4. How can the phase of the Moon be used to estimate its approximate angular distance from the Sun?
5. By approximately how much does the Moon’s direct ascent change in a week?
6. What observations need to be made to study the motion of the Moon around the Earth?
7. What are the n
What are the characteristics of the Sun’s daily movement at various latitudes?
Let’s consider the daily movement of the Sun at various latitudes. In regions with middle latitudes, the Sun consistently rises in the eastern portion of the sky, gradually ascending above the horizon. At noon, it reaches its highest point in the sky, and then begins to descend towards the horizon, eventually setting in the western part of the sky. In the Northern Hemisphere, this movement appears from left to right, while in the Southern Hemisphere, it seems to move from right to left. An observer in the Northern Hemisphere will see the Sun in the southern direction, whereas an observer in the Southern Hemisphere will see it in the northern direction. The Sun’s daily path in the sky is symmetrical with respect to the north-south direction. Beyond the Arctic Circle on Earth, where the latitude is greater than 66.5°, the Sun’s daily path becomes almost parallel to the horizon. During this time, the Sun does not set for half a year, creating circular paths above the horizon. This is known as the polar day. Then, for the following half year, the Sun sets and the polar night arrives. At the equator, the Sun, along with other celestial bodies, rises and sets perpendicular to the plane of the true horizon and remains visible for half a day. The apparent motion of celestial bodies (including the Sun), which occurs due to the Earth’s rotation on its axis, is referred to as diurnal motion. OR Throughout the course of a year, the Sun traverses the ecliptic. The ecliptic intersects with the 12 zodiacal constellations. On a daily basis, the Sun moves parallel to the celestial equator, similar to a regular star (-23°27′ ≤ δ ≤ +23°27′). This change in declination is a result of the Earth’s axial tilt in relation to its orbit. March 21st marks the vernal equinox (δ = 0). June 22nd signifies the summer solstice (δ = 23°27′). September 21st represents the autumnal equinox. December 22nd denotes the winter solstice. At the latitudes of the tropics of Cancer (Southern) and Capricorn (Northern), the Sun reaches its zenith during the summer and winter solstices. At the North Pole, the Sun and stars do not set between March 21st and September 22nd. On September 22nd, the polar night commences.
Wouldn’t it be simpler for you to evaluate books on the topic?)
Question #23(2014)
Question #23. Daily and yearly motion. Sun. Kepler’s Laws. Characteristics of the sun’s movement in tropical and polar regions.
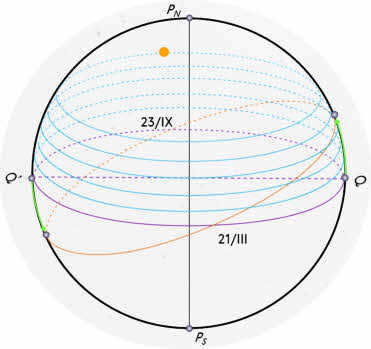
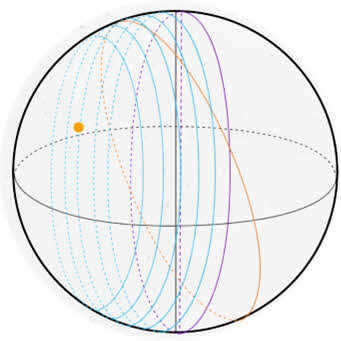
It is common knowledge that the celestial sphere, containing all the celestial bodies, revolves around the axis of the Earth. This movement is referred to as the apparent daily motion of the celestial sphere. When observing the sphere from the North Pole PN, the direction of the daily motion is clockwise. As a result of this diurnal motion, all celestial bodies, which rotate with the sphere, move in parallel to the celestial equator, also known as the celestial parallels. During this motion, they intersect the observer’s meridian, with some of them intersecting the First Vertical and the horizon. The intersection of the observer’s meridian by the celestial body during its diurnal motion at noon is referred to as the upper culmination, while the intersection at midnight is referred to as the lower culmination. From the lower illustration, it becomes apparent that for a constant latitude and a celestial body with a constant declination, the celestial body reaches its maximum height at the moment of the upper culmination, and its minimum height at the moment of the lower culmination. The intersection of the plane of the true horizon by the celestial body during its diurnal motion is known as the points of rising and setting.
The Sun’s Apparent Annual Motion
Due to the Earth’s orbit, it appears to an observer on Earth that the Sun is constantly moving across the sky in relation to the fixed stars. While we cannot directly observe the Sun’s movement relative to the stars during the day, there are several compelling pieces of evidence that support this motion:
- At different times of the year, different stars are visible at midnight.
- The Sun’s altitude at noon changes throughout the year.
- The azimuths of sunrise and sunset, as well as the length of day and night, also change.
The Earth, as it moves along its orbit, maintains a fixed position for its axis of rotation in space. The Earth’s axis of rotation is inclined at an angle of 66°33′ with respect to the plane of its orbit. This results in an angle of 23°27′ between the plane of the Earth’s orbit and the plane of its equator.