The celestial coordinate system is utilized in the field of astronomy to describe the position of celestial bodies in the sky or points on an imaginary celestial sphere. The position of these bodies or points is determined by two angular measurements (or arcs) that uniquely define their location on the celestial sphere. The celestial coordinate system is essentially a spherical coordinate system in which the third coordinate, distance, is often unknown and irrelevant.
Celestial coordinate systems vary in terms of the principal plane and origin chosen. Depending on the specific task at hand, one system may be more convenient to use than another. The most commonly employed systems include the horizontal and equatorial coordinate systems. Less commonly used systems include the ecliptic, galactic, and others.
Coordinate System in the Horizontal Plane
In this particular system, the primary plane is the plane of the mathematical horizon. One of the coordinates is the altitude of luminosity, denoted as h, or its zenith distance, denoted as z. The other coordinate is the azimuth, represented by A.
The height, h, of the luminary can be defined as the arc of the vertical circle that extends from the mathematical horizon to the luminary. It can also be described as the angle between the plane of the mathematical horizon and the direction towards the luminary. Altitudes can range from 0° to +90° towards the zenith, and from 0° to -90° towards the nadir.
The zenith distance, z, of a luminary can be defined as the arc of the vertical circle that extends from the zenith to the luminary. It can also be described as the angle between the plumb line and the direction towards the luminary. Zenith distances are measured from 0° to 180°, ranging from the zenith to the nadir.
The original equatorial coordinate system
Within this particular system, the primary plane is known as the celestial equator. One of the coordinates utilized in this system is called declination δ (occasionally referred to as polar distance p). Another coordinate employed is the hour angle t.
Declination δ of a celestial body refers to the arc between the declination circle and the celestial equator, or the angle formed by the direction towards the celestial body and the plane of the celestial equator. Declinations are measured from 0° to +90° towards the north pole of the world and from 0° to -90° towards the south pole of the world.
The polar distance p of the celestial body is the arc of the declination circle that extends from the North Pole of the Earth to the celestial body. It can also be defined as the angle between the Earth’s axis and the direction to the celestial body. Polar distances are measured from 0° to 180°, ranging from the North Pole to the South Pole of the Earth.
The hour angle t of the celestial body refers to the arc on the celestial equator that extends from the upper point of the celestial equator (where it intersects with the celestial meridian) to the circle of declination of the celestial body. It can also be described as the angle between the planes of the celestial meridian and the circle of declination of the celestial body. Hour angles are measured in the direction of the diurnal rotation of the celestial sphere, which is westward from the upper point of the celestial equator. They range from 0° to 360° in degree measure or from 0 h to 24 h in hour measure. Alternatively, hour angles can be measured from 0° to +180° (0 h to +12 h) to the west and from 0° to -180° (0 h to -12 h) to the east.
The alternative equatorial coordinate system
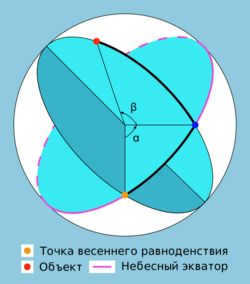
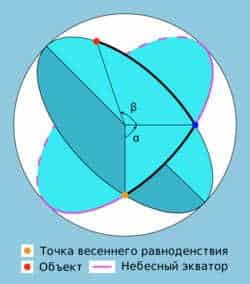
Within this system, similar to the first equatorial system, the primary plane is the plane of the celestial equator, and one of the coordinates is referred to as the declination β (less commonly known as the polar distance p). The other coordinate is the right ascension α.
The right ascension (RA,α) of a celestial body is the arc of the celestial equator between the vernal equinox and the celestial body’s declination circle, or the angle between the direction towards the vernal equinox and the plane of the celestial body’s declination circle. Right ascensions are measured in the opposite direction of the daily rotation of the celestial sphere, ranging from 0° to 360° (in degrees) or from 0 h to 24 h (in hours).
Declination (δ) is one of the two coordinates of the equatorial coordinate system used in astronomy. It represents the angular distance on the celestial sphere from the plane of the celestial equator to the luminary, and is typically expressed in degrees, minutes, and seconds of arc. The declination is considered positive when located north of the celestial equator and negative when located south.
- An object located on the celestial equator has a declination of 0°
- The declination of the north pole of the celestial sphere is +90°
- The declination of the south pole of the celestial sphere is -90°
The declination always has a sign, regardless of whether it is positive or negative.
When a celestial object passes directly overhead (the zenith), its declination is equal to the latitude of the observer. In the northern hemisphere, if the latitude is considered positive for northern latitudes and negative for southern latitudes, celestial objects with a declination greater than 90° minus the latitude do not go below the horizon. These objects are known as non-sunsetting. On the other hand, if the declination is less than -90° plus the latitude, the object is called a non-descending and cannot be observed at that latitude. [1]
Ecliptic coordinate system
The ecliptic coordinate system is based on the ecliptic plane as its main reference plane. In this system, there are two coordinates used to determine the position of an object: the ecliptic latitude (β) and the ecliptic longitude (λ).
The ecliptic latitude (β) of a celestial body is the angle between the direction to the body and the ecliptic plane. It is measured as the arc of the circle of latitude from the ecliptic to the body. Ecliptic latitudes can range from 0° to +90° to the north pole of the ecliptic, and from 0° to -90° to the south pole of the ecliptic.
The position in the sky λ of a celestial object is determined by measuring the angle along the ecliptic from the vernal equinox point to the circle of latitude of the object. This angle represents the direction from the vernal equinox point to the plane in which the object is located. Ecliptic longitudes are measured in the direction of the Sun’s apparent motion along the ecliptic, which is from west to east, within the range of 0° to 360°.
The Galactic Coordinate System
In this system, the primary plane is the plane of our Galaxy. There are two coordinates in this system: the galactic latitude (b) and the galactic longitude (l).
The galactic latitude (b) of a celestial object is the arc of the circle of galactic latitude from the ecliptic to the object, or the angle between the plane of the galactic equator and the direction to the object.
Galactic latitudes are measured from 0° to +90° towards the north galactic pole and from 0° to -90° towards the south galactic pole.
The origin C is situated near the direction leading to the galactic center, but it is not exactly aligned with it. This is because the galactic center is slightly south of the galactic equator, due to the solar system being slightly above the plane of the galactic disk. The chosen origin point C is selected in such a way that the intersection point of the galactic and celestial equators, with a direct ascent of 280°, has a galactic longitude of 32.93192° at epoch 2000.
The coordinates of the origin point C at epoch 2000 in the equatorial coordinate system are as follows:
Changes in celestial coordinates during the rotation of the celestial sphere
Elevation h, zenith distance z, azimuth A, and hour angle t of celestial objects undergo constant changes as the celestial sphere rotates. These coordinates are measured from points that are not influenced by this rotation. Declination δ, polar distance p, and right ascension α of celestial objects do not change with the rotation of the celestial sphere, but they can vary due to the movements of celestial objects unrelated to the diurnal rotation.
Origin and Usage
Ancient civilizations have long utilized celestial coordinates. The works of Euclid, an ancient Greek geometer from around 300 B.C., mention a few systems. The Almagest, a publication by Ptolemy, includes the positions of 1022 stars in the ecliptic system of celestial coordinates as cataloged by Hipparchus.
Discoveries in astronomy have been greatly influenced by observations of changes in celestial coordinates, which play a crucial role in expanding our knowledge of the universe. These coordinates encompass various phenomena such as precession, nutation, aberration, parallax, and the proper motions of stars, among others. The significance of celestial coordinates extends beyond astronomy, as they also aid in measuring time and determining the geographical coordinates of different locations on Earth’s surface. Furthermore, celestial coordinates are integral to the compilation of star catalogs, the study of celestial body motions (both natural and artificial) in celestial mechanics and astrodynamics, and the examination of star distribution in stellar astronomy problems.
The horizontal coordinate system is utilized for determining the orientation towards the celestial body using angular instruments and when observing through a telescope mounted on an azimuthal rig.
The initial equatorial coordinate system is employed for determining the precise time and for observations through a telescope mounted on an equatorial mount.
The secondary equatorial coordinate system serves as a widely used coordinate system in astrometry. This system is used for creating star maps and describing the positions of celestial bodies in catalogs.
Ecliptic coordinate system is applied in theoretical astronomy for ascertaining the orbits of celestial bodies.
Notes
- ↑Siegel F. Yu. Treasury of the celestial vault – an instruction manual for star groups and the lunar orb / Edited by G. S. Kulikov. – 5th edition. – Moscow: Nauka, 1986. – Pages 57-58. – 296 pages. – 200,000 copies.
Currently, 58,757 educational institutions have the opportunity to benefit from additional cumulative discounts ranging from 2% to 25%. To determine the specific discount available to all staff members of your educational institution, please access your personal Infoworks account.


Course for professional growth
Characteristics of the implementation and execution of the updated FSES LLC
We can combine your educational institution’s discount with this offer (depending on how many of your colleagues have completed Infowrok courses).
Currently, there are additional cumulative discounts (ranging from 2% to 25%) available for 58,757 educational institutions. To determine the discount applicable to all staff members of your educational institution, please log in to your personal Infoworks account.


Advanced Training Program
Tackling Bullying: Addressing Challenges and Finding Solutions in Childcare and Education
We can apply an exclusive discount for your educational establishment (the amount will depend on the number of your colleagues who have enrolled in Infowork courses).
At present, 58,757 educational institutions are benefiting from additional reductions (ranging from 2% to 25%). To discover the discount applicable to all staff members of your educational institution, please access your personal Infoworks account.


The Significance of the Moral Tales by I. A. Krylov
Breakdown of the Slideshow Content:

Slide 1: The Sun’s Yearly Movement on the Ecliptic
Grade 10-11
Curriculum by B.A.Vorontsov-Vel’yaminoff
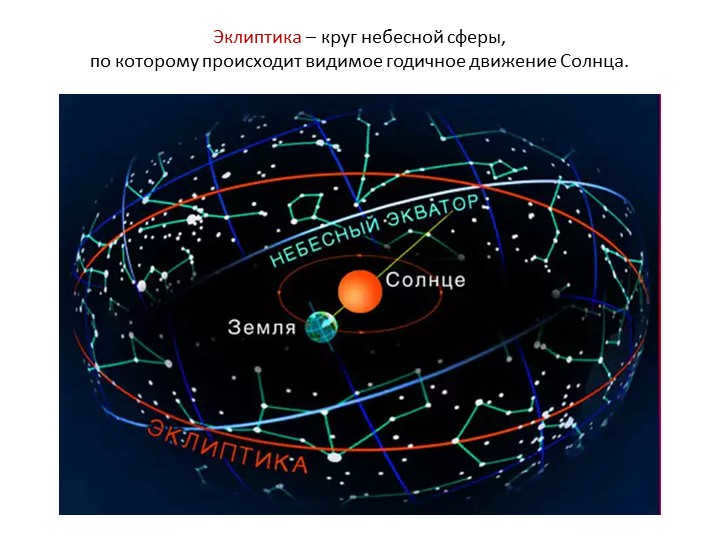
There are 3 slide Zodiacal constellations, which are the constellations that the ecliptic passes through
(derived from the Greek word “zoon” – animal).
Each zodiacal constellation is crossed by the Sun in approximately
a month.
Traditionally, there are 12 zodiacal constellations.
However, in reality, the ecliptic also passes through the constellation of Serpentor (situated between Scorpio and Sagittarius).
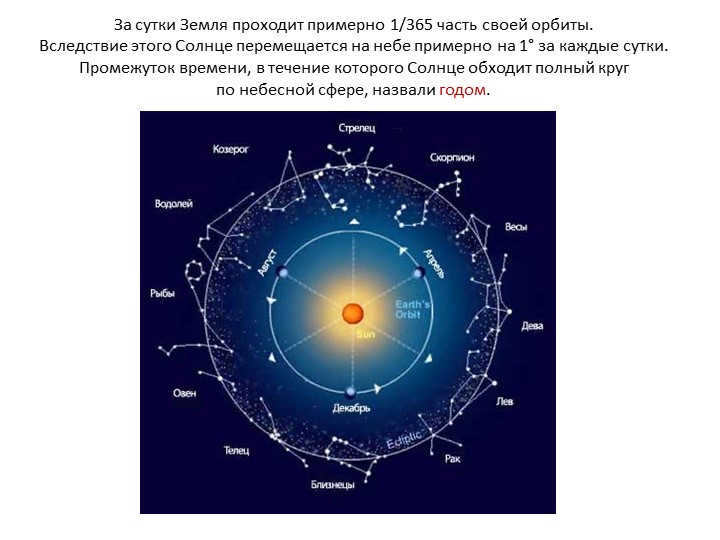
On Slide 4, it can be observed that the Earth completes approximately 1/365th of its orbit in a single day. This movement of the Earth results in the Sun shifting about 1 degree in the sky every 24 hours. The duration of time required for the Sun to complete a full rotation around the celestial sphere is referred to as a year.
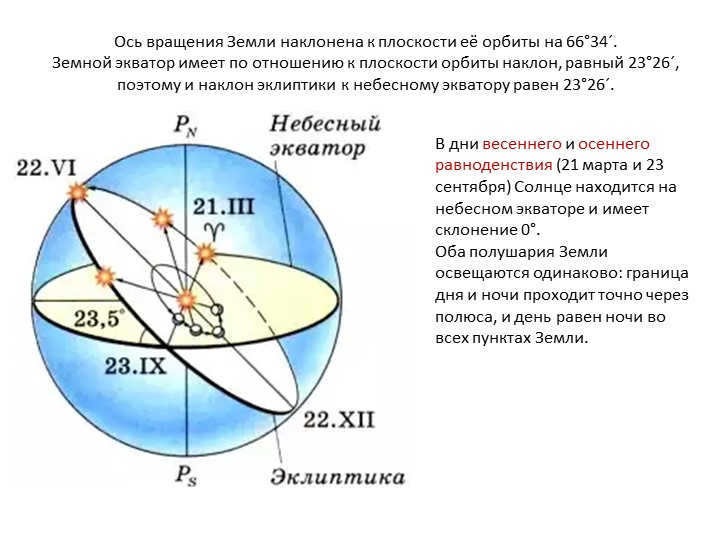

Slide 5: The Earth’s axis of rotation is tilted at an angle of 66°34′ to the plane of its orbit.
The Earth’s equator is inclined at an angle of 23°26′ to the plane of its orbit, resulting in the ecliptic being inclined at an angle of 23°26′ to the celestial equator.
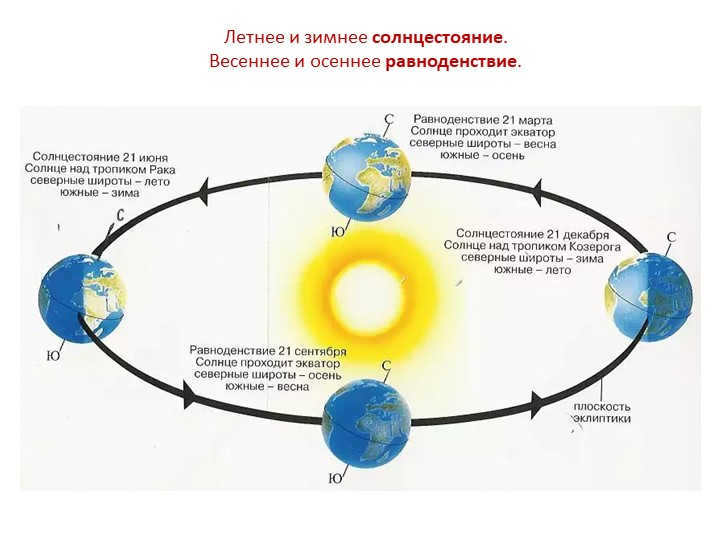
On the days of the vernal and autumnal equinoxes (March 21 and September 23), the Sun is positioned on the celestial equator and has a declination of 0°.
Both hemispheres of the Earth receive equal illumination, with the boundary between day and night passing precisely through the poles and day and night being of equal length at all points on the Earth.
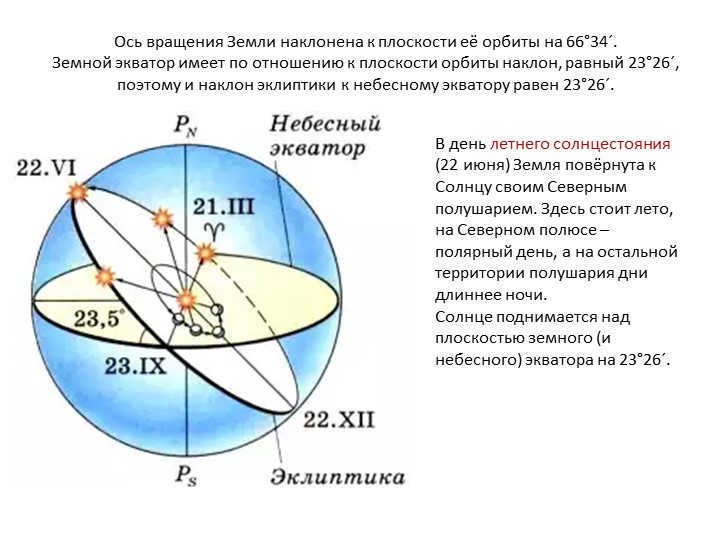

Slide 6 The Earth’s axis of rotation is tilted at an angle of 66°34′ to the plane of its orbit.
The Earth’s equator has a 23°26′ inclination with respect to the plane of its orbit, resulting in a 23°26′ inclination of the ecliptic to the celestial equator.
During the summer solstice (June 22), the Northern Hemisphere of the Earth is inclined towards the Sun. This is the season of summer, with continuous daylight at the North Pole and longer days than nights in the rest of the hemisphere.
The Sun rises above the plane of the Earth’s (and celestial) equator at 23°26′.
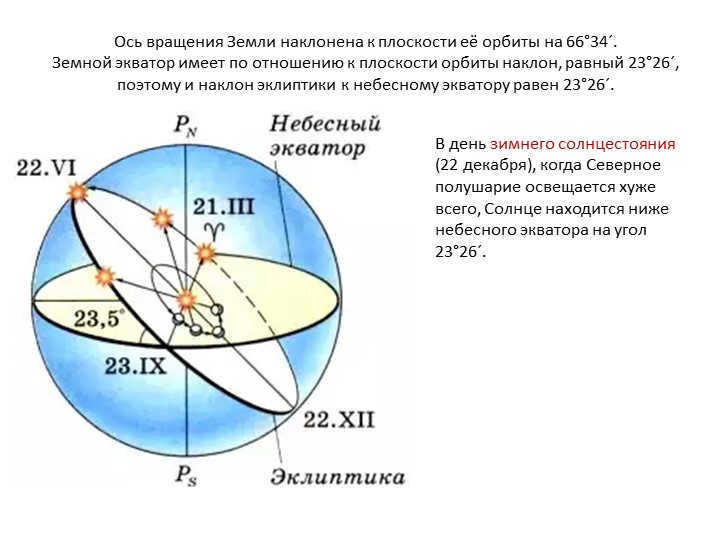

Slide 7: The Earth’s axis of rotation is inclined to the plane of its orbit by 66°34′.
The Earth’s equator has a tilt of 23°26′ with respect to the plane of its orbit, resulting in a 23°26′ angle between the ecliptic and the celestial equator.
On the day of the winter solstice (December 22), when the Northern Hemisphere receives the least sunlight, the Sun is positioned below the celestial equator at an angle of 23°26′.
Slide 9: The height of the Sun above the horizon at noon, also known as the moment of upper culmination, varies depending on its position on the ecliptic. By measuring the noon height of the Sun and knowing its declination on a particular day, we can determine the geographic latitude of our observation location.
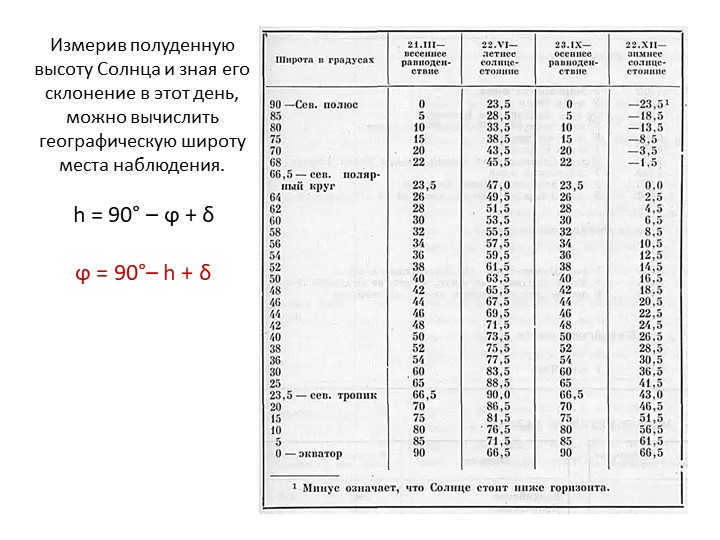
By measuring the noon height of the Sun and having knowledge of its declination on that specific day, we are able to determine the geographic latitude of the observation site. The formula to calculate this is: h = 90° – ϕ + δ
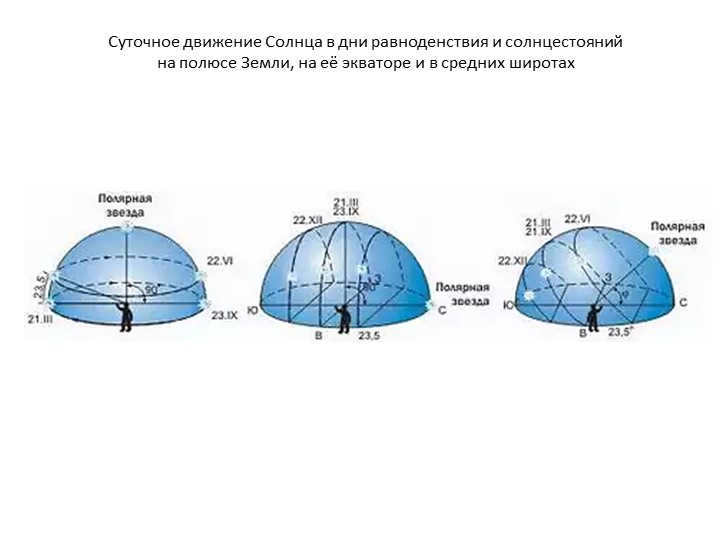

Slide 11: The Sun’s daily movement during the equinoxes and solstices differs depending on the location – the Earth’s pole, equator, and middle latitudes.

Exercise 5 (p. 33) Slide 12
№3. If the Sun’s altitude at a geographic latitude of 49° was 17°30′, on what day of the year were the observations made?
h = 90° – ϕ + δ
δ = h – 90° + ϕ
δ = 17°30′ – 90° + 49° = 23.5°
δ = 23.5° on the day of the solstice.
Since the Sun’s altitude at a geographic latitude of 49° was only 17°30′, this corresponds to the winter solstice – December 21.

13 slide Homework
1) § 6.
2) Exercise 5 (p. 33):
№5. Find out the midday height of the Sun in Arkhangelsk (geographical latitude 65 °) and Ashgabat (geographical latitude 38 °) during the summer and winter solstice.
What are the disparities in the Sun’s elevation:
a) on the same day in these cities;
b) in each of the cities on the solstices?
What conclusions can be inferred from the obtained results?
Brief overview of the document:
This presentation provides an introduction to the Ecliptic, the year, and explores the summer and fall solstices, as well as the days of equinoxes. The presentation features vibrant images and discusses the significance of geographic latitude. It can be a valuable resource for astronomy lessons and extracurricular activities focused on astronomy.
Students who embark on their astronomy journey in the 9th grade will encounter numerous new terms, many of which may be unfamiliar. One essential concept in astronomy is the ecliptic, which encompasses the Earth and other celestial bodies as they orbit the Sun. Additionally, the Earth’s axis is tilted in relation to the ecliptic, giving rise to the changing seasons.
Definition and significance
The ecliptic refers to the projection of the Earth’s orbit onto the celestial sphere. It also represents the apparent path that the Sun follows throughout the year as it passes through the twelve constellations of the zodiac. The ecliptic coincides with the plane of the Earth’s orbit and the orbits of other planets around the Sun.
Since ancient times, people have observed the changing seasons and the corresponding weather conditions. They noticed that agricultural civilizations often emerged near rivers:

Every year, the water level in these rivers undergoes significant seasonal fluctuations, so people used knowledge of the Sun’s movement to predict the weather and the timing of floods. It has long been observed that the Sun follows different paths, which repeat approximately every 365 Earth days, forming an annual cycle.
In ancient cosmology, the Sun’s movement was described by two lines. One of these lines moved from east to west on a daily basis, while the other (retrograde) created a projection on the celestial sphere known as the ecliptic.
The Greek astronomer Eratosthenes measured the Earth’s inclination in the third century BC, finding it to be 23º 51’19”. Throughout its orbit around the Sun, the Earth consistently maintains this tilt in one direction, resulting in the occurrence of seasonal variations in climate due to the varying positions of the sun’s rays.
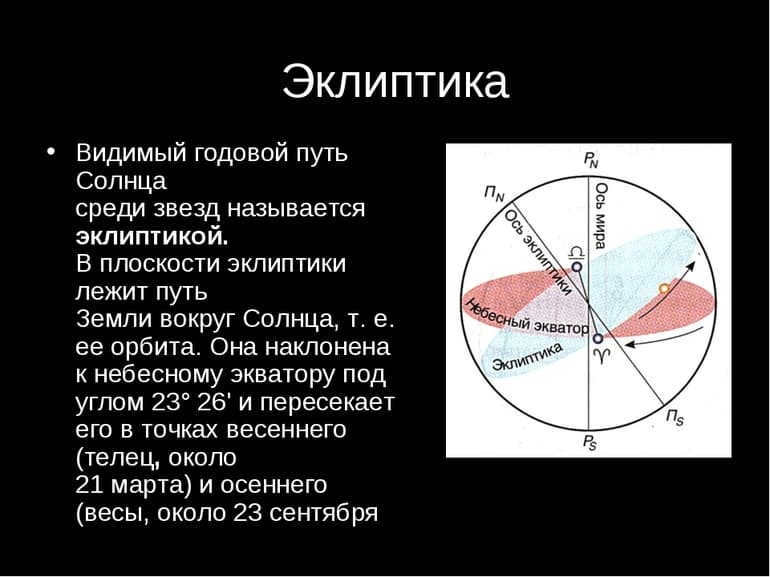
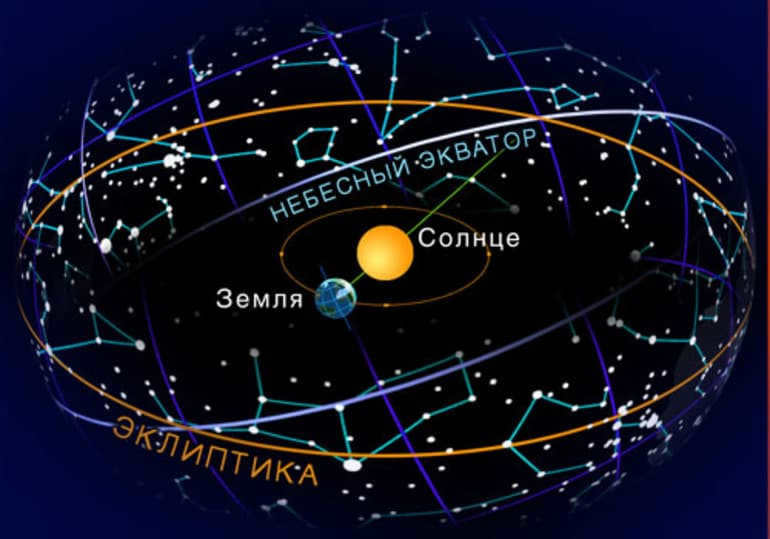
The coordinate system in astronomy utilizes the ecliptic as its fundamental circle. The measurement of celestial latitude is performed from the east to west, spanning from the north to south poles of the ecliptic (the point on the celestial sphere where it intersects with the perpendicular to the plane is referred to as the pole of the ecliptic).

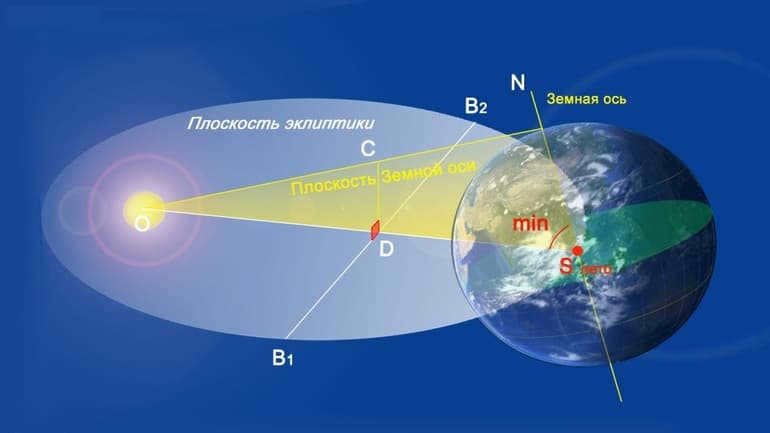
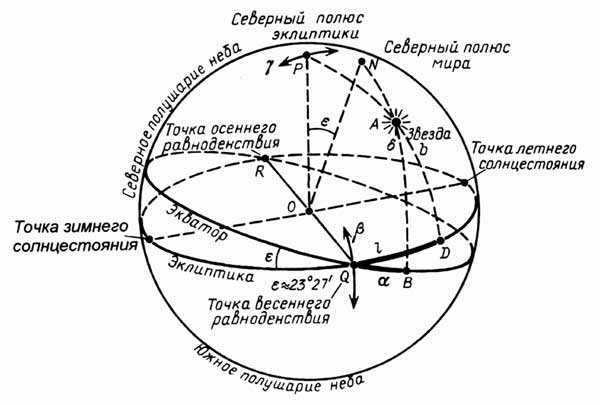
The ecliptic intersects the celestial equator at two points known as equinoxes or nodes. The summer and winter solstices are located in the middle of the path between these points.
The celestial equator or equinox line is a plane that is perpendicular to the Earth’s axis of rotation and passes through its center. Geostationary satellites are precisely positioned in this plane. On star maps, the celestial equator is represented by a line that runs precisely from east to west and follows the daily rotation of the stars.
The term “equator” is derived from the phrase “line of equality.” It is called so because the stars in this region spend an equal amount of time above and below the horizon. The same phenomenon occurs twice a year during the equinoxes for the Sun.
The celestial equator coincides with the ecliptic plane, forming an angle of 23º 27′, which is known as the ecliptic tilt. This angle has remained constant for millions of years. Currently, it is decreasing by 48 seconds per century. This trend will continue for thousands of years until it reaches a minimum of 22º 54′.
Solstice and equinox
The almost perpendicular angle of the sun’s rays covers approximately 47 degrees (precisely 46 degrees 54 minutes) of the Earth’s surface. When these rays reach 23 degrees 27 minutes north latitude, they intersect with the Tropic of Cancer (June 21). Similarly, when the rays illuminate 23 degrees 27 minutes south latitude, it is referred to as the Tropic of Capricorn (December 22). The highest and lowest points that the Sun reaches along an imaginary path across the sky are known as solstices (derived from the Latin word Solstitium, meaning “highest Sun”).
The tropics are named after two constellations: Cancer in the northern hemisphere and Capricorn in the southern hemisphere. The two points of intersection between the celestial equator and the ecliptic are:
The Vernal Point serves as the reference for the Greenwich meridian when it comes to celestial coordinates.
At these specific points, sunlight rays fall directly onto the Earth’s equator, providing equal illumination to the entire planet. These points are known as the equinoxes, derived from the Latin term Aequus Nox, which means “equal length of nights.” The Earth reaches these points on March 21 and September 21 every year as it completes its annual journey.
The movement of the equatorial plane in relation to the ecliptic causes the equinoxes to shift over time. This movement, known as precession, has a duration of approximately 25,868 years. To accurately determine the position of a star at any given moment, it is necessary to account for precession on celestial maps.
Origins of the orbital plane
The alignment of the sun and the planets on a similar plane is not a mere coincidence. The explanation for this phenomenon can be traced back to the early stages of the formation of the solar system.
The sun originated from interstellar material, which had previously given rise to generations of stars, undergoing red giant and supernova phases. This matter possesses momentum, resulting in its rotation. As a result, centrifugal forces come into play, causing the matter to deviate from its axis and form a disk-like structure.

The accumulation of matter at the center of the protoplanetary disk is caused by magnetohydrodynamic processes, resulting in rotational instability. Once this mass reaches a critical limit, fusion processes and gravitational collapse initiate.
Simultaneously, the Sun emits radiation that propagates from the photosphere into outer space. However, photons possess momentum and exert radiation pressure. Additionally, the Sun releases solar wind, which also impacts the surrounding environment.
The remaining matter from which the Sun originated is blown away by radiation pressure and solar wind. However, not all of it is lost. Within the cluster’s disk, these substances come together under the gravitational force and condense to create:
The process of the formation of the Sun and the planets from the primary disk was witnessed by the ecliptic, and even to this day, they remain in the same plane.
The Sun’s path based on the zodiac signs
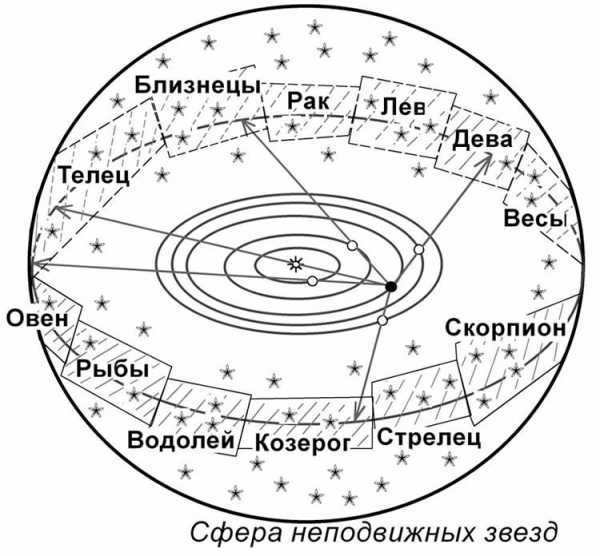
It is common knowledge that celestial bodies move within the celestial sphere, but their movement is not random; it is confined to a narrow band that divides space in half. This band passes through 12 constellations of the zodiac.
Table of constellations that intersect the Sun’s ecliptic
You can also determine the position of the Sun in the zodiac, just like the ancient astronomers did. To accomplish this, you must observe which constellations intersect the ecliptic path of the celestial luminary, completing a full revolution each year. Additionally, note which of the final constellations of the zodiac emerges prior to or following the Sun. As a result, each month within the year corresponds to a distinct zodiac sign.
Astrologers have a belief that the stars have a mysterious influence on life, depending on the zodiac sign under which a person is born. However, it is important to understand that the sign assigned to each month in the horoscope does not correspond to the constellation in which the Sun is located during that month, but to where it was located in ancient times. This difference is caused by the phenomenon known as the precession of the equinoxes.
Cosmic Objects and the Lunar Satellite
The celestial bodies that can be observed in the expanse of the heavens are consistently in proximity to the ecliptic. This signifies that their paths of revolution around the sun are never distant from the specified plane. In essence, the majority of entities within the solar system traverse their courses within a similar plane.
The Moon’s orbit intersects the ecliptic at a slight angle of approximately 5 degrees, causing it to traverse the celestial sphere and the zodiac. For half of its orbit, the Moon is situated above the ecliptic, while for the other half, it is located below. In the event that its shadow falls on Earth, a solar eclipse occurs as the Sun is obscured by the shadowed region. Conversely, a lunar eclipse transpires when the Earth obstructs the Moon. Both of these phenomena can only transpire when the Sun, Earth, and Moon are aligned.
While traversing, the Sun has the potential to be positioned at any point along the ecliptic, although typically not directly on the Earth-Moon axis. Nonetheless, there are instances when it does align with it. During such occurrences, the Moon outshines the Sun as it is situated between the Sun and the Earth. Conversely, when the Moon is in the opposite position, the Earth’s shadow is cast upon it.
The Path of the Sun, Moon, and Planets in the Sky
Understanding how to roughly trace the ecliptic is important. The ecliptic is the path that the Sun, Moon, and planets appear to follow in the sky when observed from Earth. This imaginary line is most easily seen on clear nights, especially during the days leading up to a full moon, when bright stars are visible in the sky.
It is advisable to venture into the open air immediately following sunset. The sky must be clear. The dazzling planet Venus will be visible in the western region, directly above the descending Sun. The Moon is positioned low in the eastern region, just above the horizon. Further up, Mars can be observed, offering a third reference point. Approximately 2 hours later, Saturn will emerge in the east, establishing yet another reference point. By drawing an imaginary line connecting these celestial bodies, the ecliptic can be determined.
Please take note that the Moon and the planets do not align exactly with the ecliptic line. While their orbits are nearly in the same plane as Earth, they deviate slightly. This variation is the reason why there isn’t an eclipse every month.
As a result of the slight difference in the planes of the Moon and Earth, the Moon generally passes either above or below the Sun or our planet’s shadow. The only exception is when the two orbits intersect.
This is an Astronomy Report on the constellation Aquarius ♒, including its history of origin, description, symbol and meaning, coordinates, interesting facts, legends, and a list of stars, including the brightest ones.

This image, captured during the “Clementine” mission, displays five stars that are approximately aligned with the plane of the ecliptic. Moving from right to left, you can see the Moon illuminated by the Earth’s light, the solar corona peeking out from behind the Moon, and the planets Saturn, Mars, and Mercury (three points to the left).
The plane of the ecliptic refers to the geometric plane that encompasses the Earth’s orbit around the Sun.
From a geocentric perspective, the ecliptic (a feminine noun until the 17th century) is a large circle that represents the apparent annual path of the Sun on the Earth, projected onto the celestial sphere.
From a heliocentric standpoint, it is the point at which the celestial sphere intersects with the ecliptic plane.
The plane of the ecliptic, which is also known as the ecliptic plane as mentioned earlier, serves as the frame of reference for the celestial coordinate system known as the ecliptic coordinate system.
Overview
The position and movement of stars in relation to the ecliptic
The orbits of the planets in our solar system are slightly inclined in relation to the plane of the ecliptic. The zodiac signs are also situated along (on either side of) the ecliptic plane.
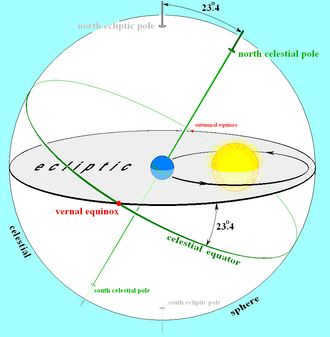
The angle known as the ecliptic tilt determines the tilt of the ecliptic plane in relation to the celestial equator. This angle is approximately 23° 26’13” and represents the inclination of the Earth’s axis of rotation with respect to the plane of its orbit. Similarly, the Moon’s orbit is inclined at different angles ranging from 5° 01’1″ to 5° 17’35” relative to the ecliptic, with an average of 5° 08’48”.
Considering that there are approximately 365.24 days in a tropical year and a circular motion of 360 degrees, it can be observed that the Sun moves along the ecliptic at a rate of 59,138.8 ft/day or almost 1°/day. This west-to-east motion contradicts the apparent east-to-west motion of the celestial sphere.
Distinct locations on the ecliptic
The intersection of the celestial equator and the ecliptic occurs at two diametrically opposed points, which are referred to as nodes.
Moments of equal day and night and extreme climatic conditions
Plan of the ecliptic
The plan of the ecliptic is the plane that encompasses the center of gravity of the Sun and the center of gravity of the Earth. Both the Sun and the Earth revolve around the Sun within this plane. The plan of the ecliptic extends infinitely and is utilized as a coordinate system for locating stars. It is called the plan of the ecliptic because it is within this plane that eclipses are observed. Additionally, the plan of the ecliptic is frequently referred to as the ecliptic plane.
The points where a star’s orbit in the solar system intersects the plane of the ecliptic are known as the nodes. The Moon, as it moves around the Earth, which in turn revolves around the Sun, also passes through the ecliptic plane at two nodes. If a new or full moon happens to occur at one of these nodes, an eclipse takes place because in this scenario, the Moon, Earth, and Sun are perfectly aligned on the ecliptic plane.
Notes and References
- ↑ (in) Plane of the ecliptic, according to NASA on July 18, 2017.
- ↑Lexicographic and etymological definitions of “Ecliptic” from the computerized treasure trove of the French language on the website of the National Center for Text and Lexical Resources
The ecliptic was originally the circular trajectory that indicates the route of the Sun in the sky of the Earth.
The ancient understanding of the Ecliptic
Since ancient times, humanity has had a deep fascination with the sky. The knowledge of early civilizations was limited, leading primitive people to develop a strong belief in supernatural forces controlling the natural world and celestial bodies. Rock drawings from the Stone and Bronze Ages often depict celestial bodies such as the Sun, the Moon, and bright stars, hinting at the primitive people’s understanding of the skies. The Sun is commonly represented as a disk, sometimes with a dot, divergent rays, or a cross enclosed in a circle.
The understanding of celestial objects also aided ancient people in navigating their surroundings. As human civilization shifted from hunting and gathering to agriculture and herding, the need for calendars arose. Knowing when to perform various agricultural tasks, such as sowing and reaping, became crucial. Ancient people observed cyclical changes in weather, such as the transition from winter to summer, and utilized this knowledge to create calendars.
It’s worth mentioning that the earliest agricultural civilizations emerged in the valleys of major rivers, such as the Nile, Euphrates, Tigris, Indus, Ganges, Huang He, and Yangtze. These civilizations relied on irrigation canals to water their fields, and the water levels in the rivers fluctuated cyclically. Understanding the movement of the Sun helped predict weather conditions and the timing of river flooding.
It was observed that the Sun’s movement across the sky repeats itself approximately every 365 Earth days, which led to the creation of the solar calendar. The first evidence of such a calendar dates back to the 5th millennium B.C. in Ancient Egypt. The introduction of the annual calendar marked the establishment of a chronological system.
One remarkable example of early civilization’s understanding of the Sun is the Stonehenge in modern-day Britain. Built in the third millennium B.C., this structure was designed to meticulously track the Sun during the summer solstice, which occurs around June 22. The summer solstice is the day with the longest daylight hours and the shortest period of darkness. The arrangement of the stones at Stonehenge allows for optimal observation of the sunrise and sunset during the winter solstice, which is the time of the year with the longest duration of darkness and the shortest duration of daylight.

However, it is observed that the alignments of the holes in the stones at Stonehenge were deliberately arranged to observe the sunsets of the Moon when it is at its furthest point from the Sun’s path (ecliptic). These occurrences are referred to as the “upper Moon” and the “lower Moon”. During these times, the Moon deviates from the ecliptic by approximately 5 degrees. This phenomenon is a result of the Moon’s orbits being inclined at a 5.1 degree angle from each other.
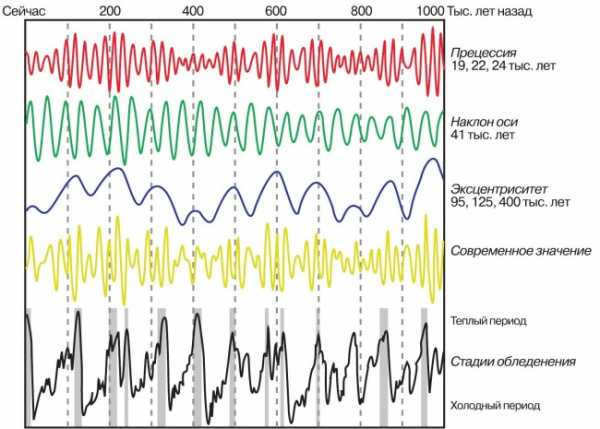
A representation of the impacts of Milankovitch’s cycles over time
The Earth’s axial tilt of approximately 24 degrees in relation to the ecliptic results in a continuous variation of seasons from the equator to the poles. Conversely, the Earth’s axis of rotation is not fixed in space and undergoes various periodic oscillations due to gravitational disturbances from other celestial bodies in the Solar System. These oscillations occur over long periods of tens of thousands of years (known as precession with a 26,000-year period) as well as shorter periods of a few tens of years (referred to as nutation with a 19-year period). The ancient Greek astronomer Hipparchus first discovered the precession, while the English astronomer James Bradley identified nutation in 1728. These oscillations cause a slight displacement of the Sun’s position relative to the ecliptic as observed from Earth. In the early 1930s, Serbian astrophysicist Milutin Milankovic (1879-1958) initiated research into longer cycles, which are now referred to as Milankovitch cycles.
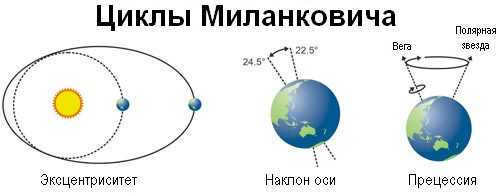
Scientists propose that the periodic ice ages that have occurred on Earth in the past million years may be caused by the 100,000-year Milankovitch cycles. These cycles involve slight variations in the amount of sunlight received by the northern and southern hemispheres over the course of several millennia. During periods when the northern hemisphere receives less sunlight, it goes through a process of accumulating polar ice due to an energy deficit. This is due to the northern hemisphere having more landmass compared to the southern hemisphere.
Astrological Signs
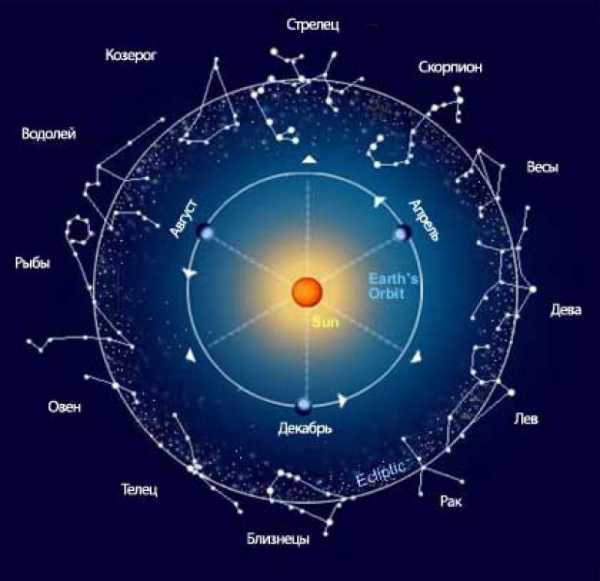
For a considerable period of time, astrologers relied heavily on zodiacal constellations to make predictions about the destiny of individuals or even entire nations (taking into account the position of the Sun in a specific constellation at the time of birth or other significant events). However, in a somewhat ironic twist, professional astronomers in 1930 decided to further subdivide the sky into constellations and introduced a 13th zodiacal constellation known as Serpentine (through which the Sun passes roughly between November 30 and December 17).
In addition to the solstice points in winter and summer, there are equinox points in spring and fall. These points indicate the moments when the duration of daylight matches the duration of darkness – around March 20-21 and September 22-23. Furthermore, these points signify the instances when the Sun crosses the celestial equator. Due to the phenomenon of precession, these points undergo a continuous movement along the ecliptic (over the past two thousand years, they have shifted by 20 degrees). Therefore, during the beginning of our era, the vernal equinox point was situated in the zodiacal constellation Aries, but currently, it has transitioned to the constellation of Pisces. Likewise, the autumnal equinox point has shifted from the constellation Libra to the constellation Virgo.
Arrangements of Orbital Paths in the Solar System
Based on contemporary theoretical frameworks, the Solar System originated from a gas-dust cloud known as a protoplanetary disk. As a result, the majority of celestial bodies within the Solar System initially followed orbits confined to a single plane. The only exceptions to this pattern were comets located within the Oort Cloud, a region where most comets were either formed within the protostellar nebula or gravitationally captured by the Sun within interstellar space. Interestingly, comets originating from the interstellar medium, often referred to as “alien” comets, are frequently identified with retrograde orbits. These unique paths, known as reverse or retrograde orbits, possess inclinations ranging from 90 to 180 degrees.
Following the creation of the Solar System as a result of ongoing gravitational disturbances among the entities within it, along with the nearby encounters with stars, a consistent alteration in the paths of the Solar System’s objects (such as planets and asteroids) occurred. Specifically, the orbits became more elliptical (less circular) and their inclinations deviated from the initial plane of the protoplanetary disk. The largest disparity in inclination between the planets of the Solar System and Earth’s orbit is observed in the case of Mercury (7 degrees), while Uranus exhibits the smallest disparity (less than one degree).


The Solar System’s largest dwarf planet, Erida, has an orbital inclination of 44 degrees, making it unique in its own right.
Typically, the orbits of celestial bodies in the Solar System are concentrated around the ecliptic. As a result, the chances of finding near-Earth asteroids and comets that could potentially collide with our planet are extremely low near the ecliptic poles.
There is a belief that the interaction between objects in the Solar System and neighboring stars has caused not only changes in the orbits of Solar System objects, but also alterations in the angles at which planets rotate in relation to the ecliptic plane. We know that the Earth’s rotation axis is inclined at an angle of 24 degrees to the ecliptic. Among the planets in our Solar System, Mercury has the smallest inclination (0.01 degrees), while Venus (177 degrees) and Uranus (98 degrees) have the largest inclinations. It is worth noting that the Sun’s rotation axis is not perfectly perpendicular to the ecliptic, with an inclination of about 6 degrees. In recent years, theorists have attributed this inclination to the gravitational influence of a yet undiscovered ninth planet, which is estimated to be 5-10 times the mass of Earth and has a orbital period of 10-20 thousand years.

Aside from planets, asteroids and comets, the Solar System is also home to a fascinating phenomenon known as the zodiacal light. These are clusters of dust particles that are primarily found in the plane of the ecliptic. Interestingly, this ethereal glow can even be observed without the aid of any nighttime illumination. Scientists believe that the main source of this dust is the result of collisions between asteroids. However, due to the constant exposure to sunlight, it is expected that this dust will eventually be blown away from the Solar System.
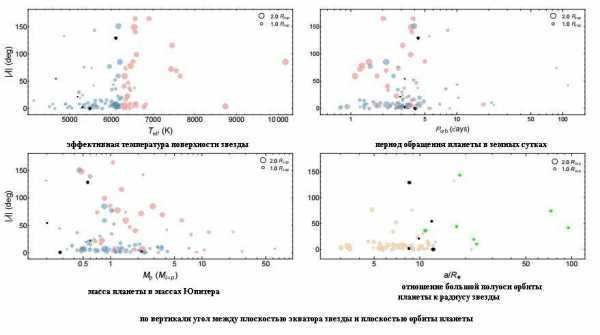
Orbital inclinations of exoplanets
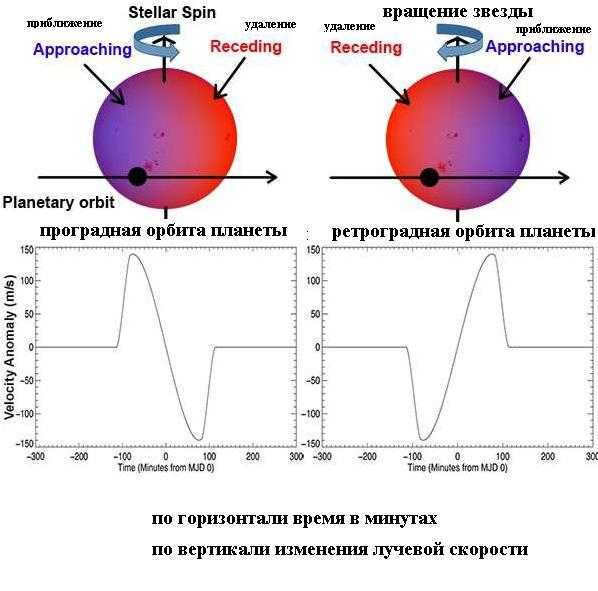
Prograde and retrograde planetary orbits
Meanwhile, by measuring the radial velocities of stars that have known transiting planets, we can calculate the angle between the star’s equator and the orbital plane of the transiting planet. This phenomenon is referred to as the Rossiter-McLaughlin (RM) effect. So far, scientists have observed this effect in 134 transiting planets.