Let’s continue our journey into the world of algebra and explore the celestial bodies. In the scale used to measure the brightness of stars, we can also include other luminaries such as the planets, the Sun, and the Moon, in addition to the fixed stars. We will focus on discussing the brightness of the planets, but first, let’s mention the stellar magnitudes of the Sun and the Moon. The stellar magnitude of the Sun is represented by the number -26.8, while the full moon has a magnitude of -12.6. The reason both numbers are negative should be clear to the reader, considering what has been explained earlier. However, one might wonder why there is not a larger difference between the stellar magnitudes of the Sun and the Moon, as the former is only “twice as large as the latter.” It is important to remember that the designation of stellar magnitude is actually a logarithm with a base of 2.5. Therefore, comparing the numbers directly or dividing one by another does not make sense. To understand the true comparison, let’s do the following calculation. If the stellar magnitude of the Sun is -26.8, it means that the Sun is 2.5 raised to the power of 27.8 times brighter than a first magnitude star. On the other hand, the Moon is 2.5 raised to the power of 13.6 times brighter than a first magnitude star. Thus, the Sun’s brightness is greater than the brightness of the full Moon by a factor of 2.5 raised to the power of (27.8 – 13.6). By calculating this value using logarithm tables, we get 447,000. Therefore, the correct ratio of the brightnesses of the Sun and the Moon is that the Sun illuminates the Earth in clear daylight 447,000 times more strongly than the full Moon on a cloudless night. Assuming that the amount of heat emitted by the Moon is proportional to the amount of light it scatters (which is likely to be true), we must acknowledge that the Moon provides us with 447,000 times less heat than the Sun. It is known that each square centimeter on the Earth’s atmosphere receives approximately 2 small calories of heat per minute from the Sun. Therefore, the Moon only provides 1/225,000th of a small calorie (which means it can heat 1 gram of water by 1/225,000th of a degree) to every square centimeter of the Earth’s surface per minute. From this, we can see how unreasonable it is to attribute any influence on the Earth’s weather to moonlight. 1) During the first and last quarters, the stellar magnitude of the Moon is -9. 2) The question of whether the Moon can affect the weather through its gravitational pull will be addressed at the end of the book (refer to “The Moon and the Weather”).
It is a widespread misconception that clouds frequently dissolve when exposed to the full Moon’s rays. However, this belief can be attributed to the fact that the disappearance of clouds at night, caused by other factors, only becomes noticeable under the illumination of the Moon. Now, let us shift our focus away from the Moon and determine the Sun’s brightness compared to the brightest star in the sky, Sirius. By employing the same reasoning as before, we can calculate the ratio of their luminosity:
i.e. The Sun is 10 billion times more luminous than Sirius. An intriguing calculation to consider is how much brighter the full Moon is compared to the combined illumination of all the stars visible to the naked eye on one hemisphere of the sky. We have previously determined that stars ranging from the first to the sixth magnitude emit the same amount of light as a hundred first magnitude stars. Therefore, the task at hand is to determine how many times brighter the Moon is compared to a hundred first magnitude stars. The ratio is 2.5:13.6:100:2700. Hence, on a clear night without the presence of the Moon, we only receive 1/2700th of the light that the full Moon emits. This means that the light we receive from the starry sky is 1200 million times less than the light the Sun provides on a cloudless day. Additionally, it is worth mentioning that a standard international “candle” has a stellar magnitude of minus 14.2 when observed from a distance of 1 meter. Therefore, at this distance, the candle illuminates four times brighter than the full Moon (2.5:14.2-12.6). An interesting fact to note is that a searchlight on an aviation beacon with a power of 2 billion candlepower would be visible from the distance of the Moon by a star of 4.5th magnitude, i.e. it could be seen with the naked eye.
The genuine brilliance of stars and the Sun
All the previous assessments of brightness have only referred to the apparent brightness of the stars. The given numbers represent the brightness of the stars at their actual distances from us. However, we are aware that the stars are not equally distant from us. Therefore, the apparent brightness of the stars does not provide us with their true brightness or their distance from us, unless we separate these two factors. In the meantime, it is important to determine the comparative brightness, or “luminosity,” of the stars if they were at the same distance from us. Astronomers use the concept of “absolute” stellar magnitude to address this question. The absolute stellar magnitude of a star is the magnitude it would have if it were 10 “parsecs” away from us.
Despite being 25 times less bright than Sirius, the Sun still shines 50 times brighter than the average of the surrounding stars.
The most luminous star known
There is a star in the Goldfish constellation, with a magnitude of eight, that possesses the greatest luminosity. This star is not visible to the naked eye. The calculation to determine its luminosity can be done using the following formula, which will be explained to the reader later on when they become more familiar with “parsec” and “parallax”:
Here, the absolute magnitude of a star, denoted as M, can be calculated using the following formula:
2.5 M = 2.5 m – 100 π^2
Alternatively, the equation can be rewritten as:
M lg 2.5 = m lg 2.5 + 2 + 2 lg π
Another form of the equation is:
0.4 M = 0.4 m + 2 + 2 lg π
From this equation, we can solve for M:
M = m + 5 + 5 lg π
For example, let’s calculate the absolute magnitude of Sirius. Given that m = -1.6 and π = 0.38, we can substitute these values into the equation:
M = -1.6 + 5 + 5 lg 0.38 = 1.3
Located in the southern hemisphere of the sky, the Goldfish constellation is invisible in the temperate regions of our hemisphere. This particular star is part of the neighboring star system called the Small Magellanic Cloud, which is estimated to be about 12,000 times farther away from us than Sirius. Due to its immense distance, a star must possess extraordinary luminosity to even appear as an eighth magnitude star. If Sirius were located at the same distance, it would only shine as a seventeenth magnitude star, making it barely visible even with the most powerful telescope. So, what is the luminosity of this extraordinary star? The calculation reveals a result of minus one-eighth magnitude. Essentially, our star is approximately 400,000 times brighter than the Sun! With such remarkable brightness, if this star were placed at the distance of Sirius, it would appear nine magnitudes brighter, similar to the brightness of a quarter moon. A star capable of illuminating the Earth with such a brilliant light from the distance of Sirius undoubtedly deserves the title of the brightest star known to us.
The brightness of the planets in the Earth’s and alien skies
Now, let’s take a moment to imagine ourselves on other planets (as we did in the section “Alien Skies”) and determine the exact brightness of the stars shining there. To start off, let’s discuss the stellar magnitudes of the planets when they are at their brightest in the Earth’s sky. Take a look at the table below:
When we examine it, we can see that Venus is more luminous than Jupiter by approximately two stellar magnitudes, that is, by a factor of 2.5^2 = 6.25, and brighter than Sirius by a factor of 2.5^-2.7 = 13 (Sirius has a luminosity of 1.6 magnitude). From the same table, we observe that the faint planet Saturn is still more luminous than all the fixed stars except Sirius and Canopus. This provides an explanation for the phenomenon of planets like Venus and Jupiter being visible to the naked eye during the daytime, while the stars are completely invisible in daylight. Additionally, we present tables showing the brightness of luminaries in the skies of Venus, Mars, and Jupiter without introducing new explanations, as they simply quantify what was already discussed in the section “Alien Heavens.” The sky of Mars:
Definition [ edit ]
In the 2nd century BC, Hipparchus, an ancient Greek astronomer, classified all stars into six magnitudes. He referred to the brightest stars as first magnitude stars, the dimmest stars as sixth magnitude stars, and evenly distributed the rest among the intermediate magnitudes.
It was later discovered that this scale has a logarithmic relationship to real physical quantities, as the change in brightness is perceived by the eye as a proportional change (Weber-Fechner’s law). Therefore, in 1856, Norman Pogson proposed the following formalization of the scale of stellar magnitudes, which became widely accepted:
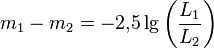5\, \mathrm \left( \frac
ight).
Given that m represents the stellar magnitudes of the objects and L represents the luminosities of the objects, this definition relates to the decrease in light flux by a factor of 100 when the stellar magnitude increases by 5 units.
This equation allows us to determine the difference in stellar magnitudes rather than the magnitudes themselves. To establish an absolute scale, a reference point must be set – the luminosity that corresponds to a stellar magnitude of zero (0 m). Initially, the luminosity of Vega was designated as 0 m. Although the zero point has since been redefined, Vega still serves as a reference for zero apparent stellar magnitude in visual observations. According to the modern system, in the V band of the UBV system, Vega’s luminosity is +0.03 m, which is practically indistinguishable from zero to the naked eye.
Based on current measurements, a star with zero apparent magnitude outside Earth’s atmosphere produces an illuminance of 2.54-10 -6 lux. The brightness from such a star is approximately 10 3 quanta/(cm²-s-Å) in green light (band V of the UBV system) or 10 6 quanta/(cm²-s) across the entire visible light spectrum.
The following characteristics make it practical to use visible stellar magnitudes:
- A 100-fold increase in luminous flux corresponds to a 5-unit decrease in apparent stellar magnitude.
- A one-unit decrease in stellar magnitude implies a 2.512-fold increase in luminous flux.
In modern times, the notion of stellar magnitude has expanded beyond just stars and now encompasses other celestial objects like the Moon, Sun, and planets. The stellar magnitude scale assigns negative values to the brightest objects. For instance, the Moon can reach a brilliance of -12.7 m during a full phase, while the Sun can have a brilliance of -26.7 m.
Apparent and absolute stellar magnitude [ edit ]
The concept of stellar magnitude can be divided into two categories: absolute magnitude (M) and apparent magnitude (m). Absolute magnitude refers to the magnitude of a star if it were located at a distance of 10 parsecs from the observer. It is a measure of a star’s intrinsic brightness and allows for comparisons of luminosity between different stars, as it is independent of distance.
On the other hand, apparent magnitude refers to the magnitude of a star as observed from Earth. This name is used to differentiate it from absolute magnitude and can be applied to magnitudes measured in various ranges, such as ultraviolet, infrared, or other. When the magnitude is measured in the visible range, it is specifically referred to as visual magnitude. For example, the apparent magnitude of the Sun is -26.7 m, while its absolute bolometric magnitude is +4.8 m.
The magnitude of a star is determined by the sensitivity of the radiation receiver, such as the eye, photoelectric detector, or photographic plate.
- The bolometric stellar magnitude represents the total radiative power of a star across all wavelengths. It is measured using a special device called a bolometer. This magnitude is particularly relevant for stars that emit primarily in the non-visible spectrum, such as very hot or very cold stars.
However, most stellar magnitudes are measured within specific wavelength intervals. Photometric systems have been developed for this purpose, each consisting of bands that cover different ranges of wavelengths. Within each band, the sensitivity is highest at a specific wavelength and decreases smoothly as the distance from it increases.
The UBV system is the most commonly used photometric system, encompassing three bands that cover different wavelength intervals. This system allows for the measurement of three stellar magnitudes for each object:
- Visual stellar magnitude (V) represents the magnitude of a star in the V filter, which has a transmission maximum close to the peak sensitivity of the human eye (555 nm).
- “Blue” stellar magnitude (B) indicates the brightness of an object in the blue region of the spectrum, with maximum sensitivity at a wavelength of approximately 445 nm.
- Ultraviolet stellar magnitude (U) has its peak in the ultraviolet region at around 350 nm.
The color of an object can be determined by the differences in stellar magnitudes in different bands, such as U-B and B-V in the UBV system. A larger difference indicates a redder object. In the UBV photometric system, stars of spectral class A0V have color indices equal to zero.
There are various photometric systems, each with its own set of stellar magnitudes.
- The photographic stellar magnitude is determined using unsensitized photographic emulsion with maximum sensitivity at a wavelength of 425 nm. It is defined to be the same as the visual stellar magnitude for A0V stars and has a brightness of (6.0±0.5) m. This magnitude, along with the photovisual stellar magnitude, was used in the outdated photographic system of stellar magnitudes.
Stellar magnitudes of various entities [ edit ]
| Sun | -26.7 (400,000 times brighter than the full Moon) |
| Moon at full moon | −12.74 |
| Iridium flash (maximum) | −9.5 |
| Supernova in 1054 (maximum) | −6.0 |
| Venus (maximum) | −4.67 |
| International Space Station (maximum) | −4 |
| Earth (viewed from the Sun) | −3.84 |
| Jupiter (maximum) | −2.94 |
| Mars (maximum) | −2.91 |
| Mercury (maximum) | −2.45 |
| Saturn (with rings; maximum) | −0.24 |
| Stars of the Big Dipper | +2 |
| Andromeda Galaxy | +3.44 |
| Jupiter’s satellites | +5-6 |
| Uranus | +5.5 |
| The faintest stars observable naked eye | +6 to +7.72 |
| Neptune | +7.8 |
| Proxima Centauri | +11.1 |
| Brightest quasar | +12.6 |
| The faintest object imaged with an 8-meter ground-based telescope. | +27 |
| The faintest object imaged with the Hubble Space Telescope. | +31.5 |
Related Articles [ edit ]
Important Points [ edit ]
- ↑ Stars / Surdin V. G. . Г. . – Moscow: Fizmatlit, 2009. – С. 63.
- ↑ 2,02,1Surdin V. G. Г. .Stellar magnitude (Russian) . Glossary Astronet.ru. Verified September 16, 2012.Archived from the original source on November 28, 2010.
- ↑ Calculated assuming that the stellar magnitude at a distance of 1 a. e. is -26.7, which corresponds to the Sun's absolute stellar magnitude of +4.87.
References [ edit ]
- Mironov A. В.Precision photometry. “Astronet. Checked August 28, 2012.Archived from the original source on October 17, 2012.
- Determining stellar magnitude in an image. “Astrotourist”. Checked November 20, 2009.Archived from the original source on May 11, 2012.
Stellar brightness (also known as “stellar magnitude”) is a non-dimensional numerical measure of an object in the celestial sphere, typically a star, indicating the amount of light it emits as observed from a specific point. The value of stellar brightness is influenced not only by the object’s intrinsic luminosity but also by its distance from the observer. Stellar brightness serves as a unit of measurement for the intensity of a star, with higher intensity corresponding to lower magnitude, and vice versa.
Definition
The concept of apparent stellar magnitude was initially introduced by the ancient Greek astronomer Hipparchus in the 2nd century B.C. Hipparchus classified all stars into six magnitudes, with the brightest stars being assigned first magnitude and the dimmest stars being assigned sixth magnitude. He evenly distributed the intermediate magnitudes among the remaining stars.
In 1856, N. Pogson proposed a formalization of the scale of stellar magnitudes. The apparent stellar magnitude is calculated using the formula:
where I represents the luminous flux from the object and C is a constant.
Due to the fact that this scale is relative, its zero point (0 m) is defined as the brightness of a star that emits a luminous flux of 10³ quanta /(cm²-s-Å) in green light (UBV scale) or 10 6 quanta /(cm²-s-Å) in the entire visible light range. A star with a magnitude of 0 m outside the Earth’s atmosphere produces an illuminance of 2.54-10 -6 lux.
The scale of stellar magnitudes is logarithmic because a change in brightness of the same magnitude is perceived as the same (according to the Weber-Fechner law). Furthermore, since Hipparchus determined that the magnitude of the star is smaller, the brighter it is, there is a minus sign in the formula.
There are two properties that enable us to utilize apparent stellar magnitudes in practical applications:
Spectral Sensitivity and Magnitude
The magnitude of a star is influenced by the spectral sensitivity of the radiation detector, such as the human eye, a photoelectric detector, or a photographic plate.
The variations in stellar magnitudes observed in different bands, such as U-B and B-V, are comprehensive indicators of the object’s color. The greater the differences in these values, the redder the object appears.
What is stellar magnitude?
On a clear night far away from the city, when the sky is dark, you can see thousands of stars. The first thing that catches your attention is that they all have different levels of brightness, or as astronomers say, brilliance.. Astronomers have long ago discovered how to accurately determine the brightness of stars and other celestial objects. This brightness is measured in stellar magnitudes. Obviously, the term “magnitude” does not refer to the size of the stars! However, this raises the question: what exactly is stellar magnitude and how is it used?
Stellar magnitude is one of the oldest measurement standards that we use.
The concept was initially introduced by the renowned ancient astronomer Hipparchus (130 BC). Hipparchus made a decision to categorize all the stars in the celestial sphere based on their luminosity into six distinct groups or “magnitudes.” He designated the highest luminosity stars as 1st magnitude, signifying their exceptional brilliance and distinction among all others. Stars with slightly lower luminosity were classified as 2nd magnitude, while those with even dimmer luminosity were assigned a 3rd magnitude. Ultimately, Hipparchus allocated the 6th magnitude to the faintest stars that are visible to the naked eye.
Based on this classification, stars such as Vega, Aldebaran, or Sirius were categorized as first magnitude stars, while stars in the handle of the Big Dipper were classified as second magnitude stars. In today’s context, it may seem peculiar that stars with greater brilliance have a lower magnitude. Nowadays, we would do the opposite: if a star is brighter, it has a higher brilliance. However, Hipparchus’ reasoning is generally understandable.
The system of stellar magnitudes was highly convenient, albeit subjective. The scale heavily relied on the observer’s perception. For instance, if one astronomer perceived a star as having a second magnitude, another astronomer might perceive it as having a first magnitude. What is the true brilliance of the star? A definitive definition of stellar magnitude was needed to transition to objective evaluations.
The Magnitude Scale of Stars
Some may find this point peculiar. The subjective perception suggests that stars of the 6th magnitude are only 6-10 times dimmer than stars of the 1st magnitude. Hipparchus was guided by this perception and developed a scale of stellar magnitudes.
Pogson introduced a logarithmic scale of magnitudes – a difference of 5 units on the stellar magnitude scale corresponds exactly to a 100-fold difference in light intensity. In other words, a star of the 1st magnitude is exactly 100 times brighter than a star of the 6th magnitude, and 100 × 100 = 10,000 times brighter than a star of the 11th magnitude. This rule remains consistent.
Why do we use stellar magnitudes?
Although there is an equivalent in physics known as lux, astronomers continue to rely on the stellar magnitude scale for one simple reason: convenience.
Let’s examine the table provided below for further illustration.
| Sirius | -1.44 | 1.0E-5 |
| Venus | -4.67 | 0.00018 |
| Moonless starry sky | -5.2 | 0.0003 |
| Supernova in 1054 | -6 | 0.00063 |
| Moon in first quarter phase | -9 | 0.01 |
| Iridium Flash (maximum) | -9.5 | 0.016 |
| Full Moon | -12.74 | 0.31 |
| In the sea at a depth of 50 meters | -17.25 | 20 |
| Cloudy day | -21.5 | 1000 |
| Sunny day in the shade | -25 | 25000 |
| Under the sun in the tropics at noon | -26.7 | 130000 |
We observe that the brightness generated by celestial bodies like the Sun, Moon, planets, and stars, varies by millions of times when measured in lux units. These are enormous values that can be quite challenging to work with.
On the other hand, stellar magnitudes provide a much more convenient scale. The Sun is only 25 magnitudes brighter than Sirius. Additionally, Sirius itself is approximately as bright as the dimmest stars that can be captured by the Hubble telescope. The Hubble telescope captures stars with a luminosity of about 30 m. Therefore, the entire range of celestial object brightness can be encompassed within a range of 60 star magnitudes. This is highly convenient!
Stellar Magnitude (from Wikipedia)
The concept of apparent stellar magnitude in modern times is based on the magnitudes assigned to stars by the ancient Greek astronomer Hipparchus in the 2nd century BC. Hipparchus classified all stars into six magnitudes. The brightest stars were called first magnitude stars, while the dimmest stars were called sixth magnitude stars. The intermediate magnitudes were evenly distributed among the remaining stars.
The visible stellar magnitude depends not only on the amount of light emitted by an object but also on its distance from the observer. The visible stellar magnitude is considered a unit of measurement for the brilliance of a star, where a higher brilliance corresponds to a smaller magnitude, and vice versa.
In 1856, N. Pogson proposed a formalization of the stellar magnitude scale. The visible stellar magnitude is determined by the following formula:
where I represents the light flux from the object, and C is a constant.
Since this scale is relative, its zero point (0 m) is defined as the brightness of a star whose luminous flux is 10³ quanta/(cm²-s-Å) in green light (UBV scale) or 10 6 quanta/(cm²-s-Å) in the entire visible light range. A star with a magnitude of 0 m outside Earth’s atmosphere creates an illuminance of 2.54-10 -6 lux.
The scale of stellar magnitudes is logarithmic because a change in brightness of the same number of times is perceived as the same (Weber-Fechner law). Additionally, since Hipparchus determined that the smaller the value, the brighter the star, there is a minus sign in the formula.
The following two properties provide practical applications for using apparent stellar magnitudes:
In modern times, apparent stellar magnitude is not only used for stars, but also for other celestial objects such as the Moon, Sun, and planets. These objects can have a negative apparent stellar magnitude if they are brighter than the brightest star.
The value of apparent stellar magnitude is influenced by the spectral sensitivity of the receiver that detects the radiation, which can be an eye, photoelectric detector, photographic plate, etc.
Differences in stellar magnitudes across different bands, such as U-B and B-V, are integral indices of an object’s color. The larger the differences, the redder the object appears.
The concept of absolute stellar magnitude (M) is defined as the apparent stellar magnitude that an object would have if it were positioned at a distance of 10 parsecs from the observer. The absolute bolometric stellar magnitude of the Sun is +4.7. If both the apparent stellar magnitude and the distance to the object are known, the absolute stellar magnitude can be calculated using the following formula:
Conversely, if we have knowledge of both the apparent and absolute stellar magnitudes, we can determine the distance using this formula:
The absolute stellar magnitude is connected to luminosity through the following relationship, where L and M☉ represent the luminosity and absolute stellar magnitude of the Sun, respectively.
Stellar magnitudes of a few objects
| Subject | m |
| Sun | -26.7 |
| Moon during full moon | -12.7 |
| Iridium flash at its maximum | -9.5 |
| Supernova 1054 at its maximum | -6.0 |
| Venus at its maximum | -4.4 |
| Earth (viewed from the Sun) | -3.84 |
| Mars at its maximum | -3.0 |
| Jupiter at its maximum | -2.8 |
| International Space Station at its maximum | -2 |
| Mercury at its maximum | -1.9 |
| Andromeda Galaxy | +3.4 |
| Proxima Centauri | +11.1 |
| Brightest quasar | +12.6 |
| Faintest stars visible to the naked eye | +6 to +7 |
| Faintest object captured by an 8-meter ground-based telescope | +27 |
| Faintest object captured by the Hubble Space Telescope | +30 |
| Thing | Constellation | m |
| Sirius | Canis Major | −1.47 |
| Canopus | Carina | −0.72 |
| Alpha Centauri | Centaurus | −0.27 |
| Arcturus | Bootes | −0.04 |
| Vega | Lyra | 0.03 |
| Capella | Auriga | +0.08 |
| Rigel | Orion | +0.12 |
| Procyon | Canis Minor | +0.38 |
| Ahernar | Eridanus | +0.46 |
| Betelgeuse | Orion | +0.50 |
| Altair | Aquila | +0.75 |
| Aldebaran | Taurus | +0.85 |
| Antares | Scorpius | +1.09 |
| Pollux | Gemini | +1.15 |
| Fomalhaut | Piscis Austrinus | +1.16 |
| Deneb | Cygnus | +1.25 |
| Regulus | Leo | +1.35 |
Varying Distances of the Sun
Measuring the Brightness of Stars
“A person who is known to everyone, famous, and bright is often referred to as a first magnitude star.” However, in the world of astronomy, first magnitude stars are not the brightest ones. There are numerous stars in the night sky that shine brighter than them. So, what exactly are these stars? They are classified as zero and negative one magnitude stars.
Question 2. What is the ratio of brightness between Sirius (-1.5 m ) and Betelgeuse (0.5 m ) in the Orion constellation?
Question 3. (the most challenging). How many times brighter is Betelgeuse (0.5 m ) compared to Antares (1 m ) in the Scorpius constellation?
Why does the eye possess such a peculiar quality that makes objects that are twice as bright or twice as faint appear to be “equally distant” in terms of brightness? It is commonly understood, for instance, that the number 2 is closer to 1 than it is to 4. However, this is not the case with brightness. In the diagram, the brightness of stars with different magnitudes is symbolically represented by segments of corresponding lengths. Adjacent to these segments are the ones representing stellar magnitudes, which reflect how we perceive these different levels of brightness (or rather, the difference between them). It is as if the ruler’s next division after 1 centimeter was 1 meter instead of 2 centimeters, and we would describe all segments larger than 10 centimeters as “about a meter!”. Subsequently, the following division – after a meter – would be 100 meters. It’s certainly a peculiar type of ruler.
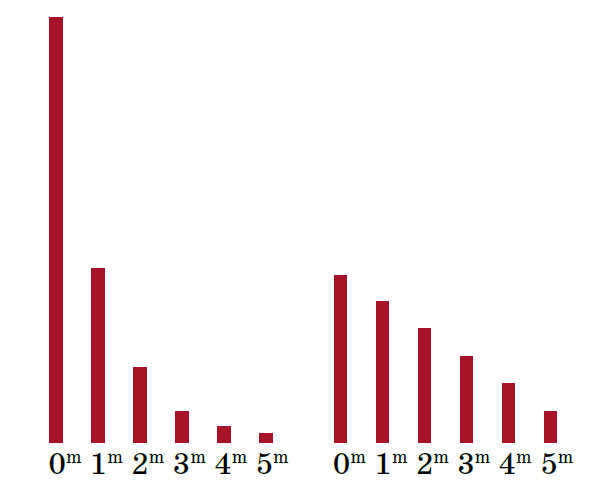
The luminosities of the celestial bodieson the leftand their visual perception.on the right)
Problem 6. What is the difference in decibels between the loudnesses of sounds with energies that differ by a factor of a thousand? And by a factor of a million?
Task 7. The threshold of hearing, which is the quietest sound the average person can discern, is exactly 0 decibels. If it is possible to view objects that are 5 times brighter than the full moon without causing harm to the eye, let’s compare the range of brightnesses that can be perceived by the human eye with the range of loudnesses that can be perceived by the ear. How many times brighter is the brightest light that is comfortable for us compared to the dimmest light? And how many times do the energies of the loudest and quietest sounds differ? Which sense organ is more versatile – the eye or the ear?
Can we determine if a star is bright or close just by looking at it? The answer is no. However, there are “clues” we can use. One clue is the color of the star. If the star appears white or blue, it is definitely bright. However, it is difficult to determine if it is just bright or extremely bright with the naked eye. On the other hand, if the star is yellow, it is likely not very bright and similar to our Sun. Red stars are more challenging to categorize as they can be either dim or incredibly bright. But that discussion is for another time. For now, let’s focus on two rather complex tasks.
Problem 9. Stars A and B have the same luminosity, but A is twice as far away. How much fainter is it in the sky? What is the difference in their stellar magnitudes? How much farther away would a star have to be to appear 10 times fainter in the sky? m times fainter than another star of the same magnitude?
1. It is 6.25 times fainter; the stellar magnitudes differ by 2.5 – 2.5 = 6.25 times.
2. 0.5 m – (-1.5 m) = 2 m; the difference is again 6.25 times.
4. The difference is -12.7 m – (-26.7 m) = 14 m; 14 = 5 + 5 + 5 – 1. So the difference is 400,000 times.
6. The difference between 1000 and 10 is that the loudness differs by 30 dB. A million is equal to six multiplied by ten, and each multiplication by 10 corresponds to a 10 dB change in loudness. Therefore, the difference between a million and 10 is 60 dB. This is equivalent to the difference in loudness between a quiet whisper and the sound of a truck driving by.
7. In terms of light, the difference between 5 m and -12.7 m is 17.7 m. This is the distance from the faintest star to the moon. The difference in brightness between the brightest and faintest is approximately 100 million times, calculated by dividing 100 by 2.5 – 2.5.
In terms of sound, a difference of 120 dB is equivalent to a difference of 1 million million million times, calculated by raising 10 to the power of 12. Therefore, the ear has a greater range than the eye when considering the night landscape.
The difference of 10 m is equal to 100 to 100, which is 10^4 times. This means that the star is 100 times farther away.
Counting the energy and the quantity of photons isn’t precisely identical, as photons of different wavelengths convey distinct quantities of energy. However, we won’t delve into these particulars in this discussion.
In regards to the sound intensity scale, you can find more information in the article “What is a decibel” written by A. Shchetnikov in the publication “Quantica” issue number 3 for the year 2016.
The Brightness of Stars
Each star possesses a unique magnitude that enables its visibility.
Stellar magnitude represents a dimensionless numerical value that characterizes the luminosity of a star or any other celestial object in relation to the visible area. In simpler terms, it denotes the amount of electromagnetic waves emitted by an object and detected by an observer. Consequently, this value is influenced by the properties of the observed entity and the distance between it and the observer. The term solely encompasses the visible, infrared, and ultraviolet spectrums of electromagnetic radiation.
For point light sources, the term “brilliance” is also utilized, while “brightness” is employed for extended light sources.
Hipparchus of Nicaea, an ancient Greek scientist who resided in Turkey during the 2nd century BC, is widely regarded as one of the most influential astronomers from the ancient world. He meticulously assembled an extensive catalogue of stars, marking the inception of its kind in Europe, which documented the precise positions of over a thousand celestial luminaries. Furthermore, Hipparchus revolutionized the field of astronomy by introducing the concept of stellar magnitude. By observing the stars with the unaided eye, the remarkable astronomer devised a system to classify their brightness into six distinct magnitudes, with the first magnitude representing the brightest object and the sixth magnitude indicating the faintest.
In the 1800s, the British astronomer Norman Pogson made significant advancements to the scale used to measure stellar magnitude. He expanded the range of values and introduced a logarithmic relationship. This means that as the stellar magnitude increases by one, the brightness of the object decreases by a factor of 2.512. For example, a star with a magnitude of 1 (1 m) is one hundred times brighter than a star with a magnitude of 6 (6 m).
Vega serves as the benchmark for stellar magnitude.
The standard for celestial bodies with a stellar magnitude of zero is initially based on the brightness of Vega, the brightest star in the constellation Lyra. A more precise definition of an object with a stellar magnitude of zero was later established – its illuminance should be equal to 2.54-10 -6 lux, and the light flux in the visible range should be 10 6 quanta/(cm²-s).
Visible stellar magnitude
Absolute stellar magnitude and luminosity
In order to compare the true brightness of celestial objects, a characteristic called absolute stellar magnitude was devised. It calculates the apparent stellar magnitude of an object as if it were situated 10 parsecs (32.62 light years) away from Earth. This eliminates the dependence on the observer’s distance when comparing different stars.
For objects in our solar system, the absolute stellar magnitude uses a different distance from the object to the observer – specifically, 1 astronomical unit, with the observer theoretically positioned at the center of the Sun.
Measurement of the Cosmos
Luminosity is a more contemporary and valuable measurement in the field of astronomy. This property is responsible for determining the overall energy emitted by a celestial object during a specific timeframe. The absolute stellar magnitude is employed in the calculation of luminosity.
The variation in spectral dependence
As mentioned previously, the measurement of stellar magnitude varies depending on the type of electromagnetic radiation being observed. This means that different values are assigned to each range of the spectrum. In order to capture an accurate representation of a cosmic object, astronomers often utilize photographic plates that are specifically designed to be more sensitive to the high-frequency portion of visible light. As a result, stars will appear blue in these images. This particular measurement of stellar magnitude is referred to as the “photographic magnitude,” denoted as mPv. To obtain a value that is more aligned with visual perception, a photographic plate is coated with a specialized orthochromatic emulsion and a yellow light filter is employed. This combination allows for the measurement of a magnitude known as “photovisual,” represented as mP.
A photograph of the Sun captured using a specialized dark light filter
Scientists have developed a photometric system of bands that allows them to gather important information about celestial bodies, including surface temperature, light reflection (excluding stars), and light absorption in interstellar space. This is achieved by taking photographs of the celestial object in various electromagnetic radiation spectra and then analyzing the results. The most commonly used filters for these photographs are ultraviolet, blue (used for measuring stellar magnitude), and yellow (similar to the photovisual range).
The measurement of the energy from various electromagnetic waves in a photograph is used to determine the bolometric stellar magnitude (mb). By considering the distance and the level of interstellar absorption, astronomers are able to calculate the luminosity of celestial bodies.
Stellar magnitudes of certain entities
The track of the International Space Station can be seen against the backdrop of the Big Dipper constellation.
In the Russian language, there are two types of noun suffixes.
Analysis of the pronunciation of the word “highway”
We will analyze the pronunciation of the word “highway” phonetically.
Let’s conduct a phonetic analysis of the word “highway”, which means we will perform a comprehensive analysis of the sounds and letters in this word.
Table: Hard and Soft Sounds in the Russian Language
When analyzing the phonetics of Russian words, it’s important for children to understand the distinction between hard and soft sounds. Although it may seem simple, this knowledge can be challenging for children to grasp. Many students become confused and overwhelmed when first learning about this concept.
Phonetic analysis of words is a crucial subject in the first year of any secondary school. It will only get more challenging to study from the second year onwards. That’s why it’s essential for the child to have a solid understanding and mastery of this analysis from the very beginning. Otherwise, any gaps in this knowledge will have an impact on their future. Make sure to encourage your child to be diligent in mastering phonetic analysis.
- You are currently on this page:
- Home
- Russian language
© 2023 QPOTOK.RU – A place for students and parents
Read for 7 minutes
Share
- Natal Astrology
- Relationship Astrology
- Self-development and psychology
- Predictive Astrology
- Horoscopes and forecasts
- Talismans
- Soul Formula
- Numerology
- Astrological Tarot
- World Astrology
- For beginners
- For professionals
- Development of an Astrologer
Read in 7 minutes
What is it. Aquarius is one of the twelve zodiac signs that we are familiar with. However, its history predates the other signs, as it was included in Ptolemy’s catalog in the 2nd century. The word “Aquarius” translates from Latin to “Wine-drinker” or “Water-bearer”.
What is its significance? What interests us more is the impact that this constellation has on the lives of those fortunate enough to be born under its stars. Despite its association with “water”, Aquarius actually belongs to the Air element. What other blessings does this celestial guardian bestow?
The location of the Aquarius constellation in the celestial sphere
The Aquarius constellation can be found nestled between Pisces and Capricorn.
Wondering how to spot the Aquarius constellation? Which hemisphere does it belong to? Zodiacally, it lies between Pisces and Capricorn. Situated in the southern hemisphere of the celestial sphere, this sign is surrounded by water-dwelling constellations such as Dolphin, Whale, Eridanus, and others.
Due to this characteristic, this region is sometimes referred to as the sea. As one of the oldest and largest constellations, it was named Aquarius by the ancient Greeks. Its presence in the celestial sphere spans an area of 980 square degrees, granting the Aquarius constellation a significant position in the field of astronomy.
When is the best time to observe the Aquarius constellation? It can be seen in Aquarius from February 16 to March 11, but it is most visible in August and September. The conditions for observation are particularly favorable in the central and southern regions of Russia.
Legends and myths have surrounded this part of the night sky since ancient times.
Aquarius became a constellation in ancient Greek culture, but even before the Greeks, the Sumerians believed that the god Ea, who governed the underground waters, was associated with it. So why did different cultures associate the same region of the sky with water? Where did the image of a young man pouring water from a jug come from?
Did you know these fascinating facts about the Aquarius constellation?
- Throughout history, the Aquarius constellation has been referred to as Aquarius (Latin Aquarius). This name can be found in Ptolemy’s “Almagest,” the oldest detailed atlas of the starry sky.
- The region of the sky where Aquarius is located is known as the Celestial Sea. Alongside Aquarius, it is also home to other constellations such as the Whale, Hydra, Dolphin, and Australian Fish.
- The astrological symbol for the Aquarius constellation is represented by two wavy lines, symbolizing both living and dead water.
- According to legends, the majority of ancient civilizations believed that the constellation Aquarius represented a young man holding a vessel of water, although the Arabs depicted him as a mule carrying barrels of water.
The Stars in the Aquarius Constellation
How many stars are there in the constellation of Aquarius? On a clear night without the moon, you can easily see around 90 stars. However, only seven of these stars have a magnitude greater than four. These seven stars form an arc, with the five brightest stars located in the center.
Together, these stars create the image of a jug with water flowing out of it. While it may not be immediately recognizable, the ancient star atlases depicted Aquarius in this way.
The most explored and brightest stars in the constellation Aquarius are Alpha, Beta, and Delta:
Beta Aquarius – Sadalsuud
Sadalsuud is the brightest star in the constellation Aquarius.
Sadalsuud, which means “Happy among the happiest” in Arabic, is the brightest star in the constellation Aquarius. The name was chosen for its philosophical significance: the Sun’s entry into the sign of Aquarius typically marks the start of spring and the season of spring rains.
Beta Aquarius has an apparent stellar magnitude of 2.91m, which classifies it as a third magnitude star. It is an exceptionally rare hot supergiant with a surface temperature of approximately 5,600 K, similar to that of the Sun, and belongs to the spectral class G0. Located 600 light-years away from Earth, Sadalsuud possesses a luminosity 2,200 times greater than that of the Sun. It has a mass six times larger than the Sun and a diameter 50 times greater.
In the telescope image capturing this section of the Aquarius constellation, Beta is revealed to be a triple star, featuring two additional optical components alongside its main star.
The main star in the Beta Aquarius system has a visible brightness of 11.0m and is approximately 35 angular seconds away from the other star. The second star, known as Beta Aquarius C, is located 57.2 arc seconds from the main star and has a visible brightness of 11.6m. Regrettably, there is currently no evidence of a gravitational link between these three stars – there is a possibility that they simply appear to form a triple system from our perspective.
Alpha Aquarius – Sadalmelik
The second brightest star in the constellation Aquarius, after Beta, is known as Sadalmelik. It earned the nickname “Lucky Star of the King” from the Arabs due to its slightly lower brightness. Sadalmelik is located on the right shoulder of Aquarius. It has a spectral class of G2 Ib and a stellar magnitude of 2.96m.
Alpha Aquarius stands out for its unique characteristics. One notable feature is its surface temperature, which is similar to that of the sun at around 6,000 K. This places the star in the category of yellow supergiants, an uncommon classification. Most other large stars in astronomy have different temperatures and colors, with hotter stars appearing blue and cooler stars appearing red.
The star is situated 750 light years away from Earth, indicating that its luminosity is 3,000 times greater than that of the Sun, while its diameter is just 60 times larger. The classification of supergiant not only places this star in the same league as giants that could be as big as Jupiter’s orbit, but also provides insight into its age. Based on theories of stellar evolution, it is likely to meet its demise in the near future.
Delta Aquarius – HD 216627 (Scud).
What is the method to locate the third most luminous star in the Aquarius constellation, Delta Aquarius? This celestial body is also known as Scat, a name derived from Arabic meaning “thigh”. Its positioning on the leg of Aquarius is responsible for its designation. Delta Aquarius is situated at a distance of 160 light years from Earth, and it belongs to the A3V spectral class. Additionally, its apparent magnitude is measured at 3.27m.
Scutus is a star that shines with a blue-white light. It belongs to the main sequence of stars in its spectral class. Moreover, its brightness and spectrum are very similar to Beta, which is a star in the Leo constellation. These similarities, combined with its distance from the central star system, lead us to speculate that Scutus may be part of the group of stars in the Big Dipper constellation.
When comparing Scutus to the Sun, it is important to note that Scutus is twice as massive as the Sun and has a diameter that is 2.5 times larger. The surface temperature of Scutus is 9,000 K. Scientists believe that Scutus may have a companion star. If this is indeed the case, the orbit of the companion star may take approximately 490 days.
How does a typical individual from the Aquarius constellation appear? In contemporary society, the Aquarius 11th house is connected with abrupt alterations in plans, occurrences that completely disrupt everything, unexpected surprises – both enjoyable and unpleasant, collaborating in a team, engaging in freelance work, and embracing a boundary-less and scientific approach.
In order to understand the essence of Aquarius as a constellation, one must closely observe those individuals who fall under this zodiac sign. They possess a deep sense of freedom and refuse to be confined by any boundaries, whether it be in relationships or ways of thinking. Aquarians always hold their own unique perspective on every matter, and their unconventional approach to situations is bound to attract opposition. It is important to note that constellations do not dictate a person’s future. For a more accurate understanding of what lies ahead, Autoprognosis is much more reliable.
Always immersed in dreams of the future, they frequently have the ability to anticipate various life changes – favoring novelty and experimentation in everything, they are the pioneers in embracing trendy fads. The professions of those born with a strong Uranus influence are often related to politics, technology, and scientific advancements. And if you desire to learn more about your immediate future in love, career, and relationships, make sure to subscribe to CHRONOS astrological forecast on Telegram.
When is the best time to observe individuals born under the Aquarius constellation? The zodiac sign Aquarius is in full force from January 21 to February 18. According to astrologers, this sign is known for “pouring” its unique personality onto the world around it.
