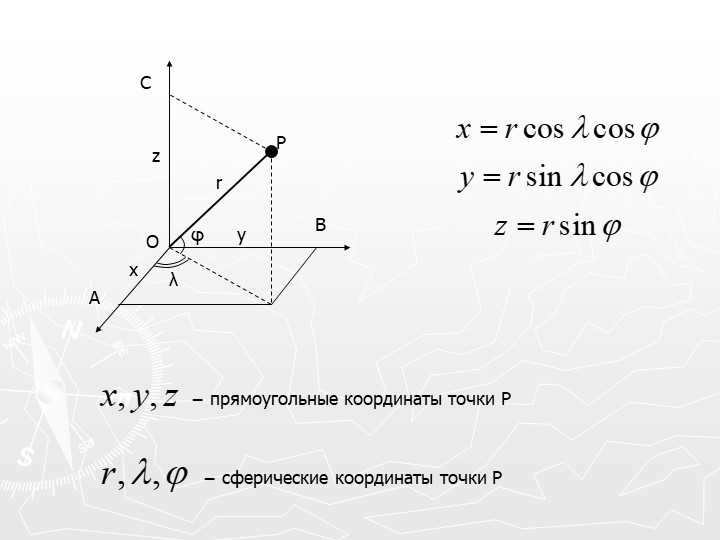
Celestial systems of coordinates are systems of coordinates that are used to describe the location of a celestial object on the celestial sphere. Typically, spherical coordinate systems are used, which describe the position on a given sphere using two angular quantities. In the case where the distances to the celestial objects are known, Cartesian coordinate systems can also be used. However, it is more common to specify the parallax of the celestial object instead of the distance. In high-precision measurements, the effects of general relativity must be taken into account. In these cases, the position of the celestial object is described relative to reference frames, which are a set of coordinate axes and a time scale (with time being considered as the fourth coordinate of the celestial object).
There are different systems of celestial coordinates depending on the chosen origin: topocentric (when the observer is on the surface of the Earth), geocentric (when the observer is at the center of mass of the Earth), barycentric (when the observer is at the center of mass of the solar system), and objectocentric (when the observer is at the center of mass of a planet, satellite, etc.). Each of these systems has its own defined time scales or time coordinates. Spherical astronomy deals with the mathematical definition of celestial coordinate systems, their relationships, as well as the definition of time scales and their interrelations. Astrometry, on the other hand, is responsible for implementing these coordinate systems by attaching them to specific celestial bodies.
To establish a coordinate system, it is important to specify its point of origin (typically the position of the observer) as well as the orientation of the axes. Subsequently, the primary plane of the system is selected, which passes through the point of origin. Within this primary plane, one of the spherical coordinates (ranging from -90° to +90°) is determined. The second coordinate is calculated within the primary plane, originating from an arbitrary point (ranging from 0° to 360° or from 0 hours to 24 hours).
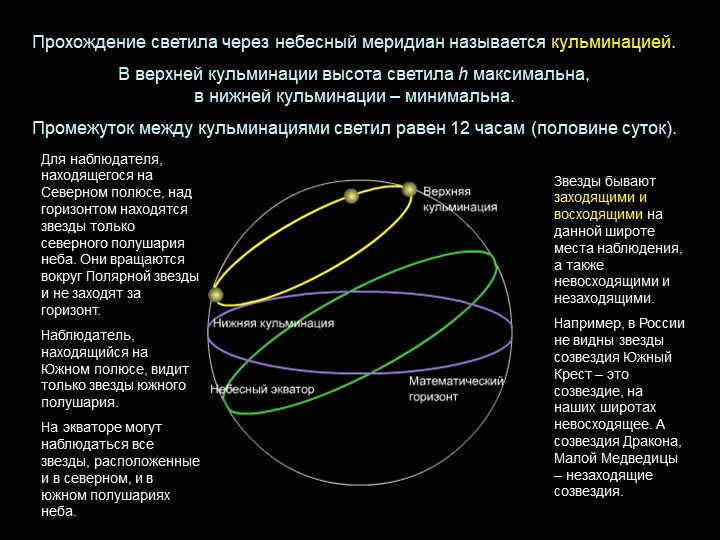
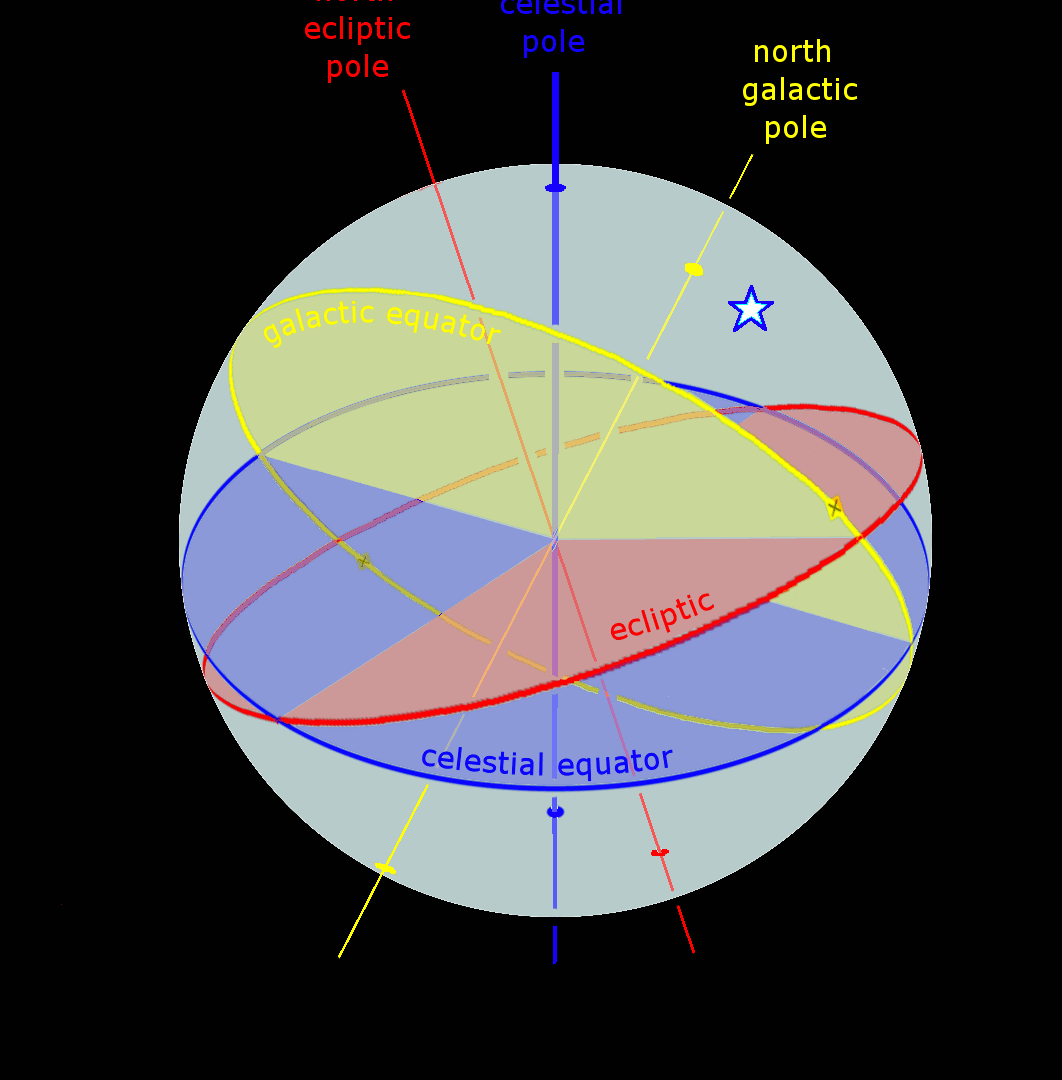
The coordinate systems utilized in astronomy are denoted by the primary plane they are associated with: horizontal, equatorial, ecliptic, and galactic (see figure).
Celestial coordinate systems: a – horizontal, b – equatorial, c – ecliptic, d – galactic. BRE. Vol. 22. Systems of celestial coordinates: a – horizontal, b – equatorial, c – ecliptic, d – galactic. BRE. Vol. 22.
System of Horizontal Coordinates
The selected orientation in this system is determined by the direction of the vertical line, while the primary plane of the system is the plane of the mathematical horizon, which is perpendicular to the vertical line. Celestial coordinates of the celestial body in this system are known as horizontal coordinates: zenith distance z z z z and azimuth A A A A (Fig, a).
If the celestial body is above the horizon, its zenith distance ranges from 0° (the body in the zenith) to 90° (the body in the plane of the horizon). If z > 90°, then the celestial body is considered to be below the horizon; in this case, it is typically not visible to the observer. Instead of the zenith distance, the altitude of the celestial body above the horizon h, which is related to the zenith distance by the equation z + h = 90°.
Azimuth is measured from a point south of S in a westward (clockwise) direction or from a point north of N to the east of E in the range of 0° to 360°; azimuth can also be measured in the range of -180° to 180°.
The plane of the celestial equator, which is perpendicular to the Earth’s axis of rotation, serves as the primary plane in this system. In this system, the celestial coordinates of the celestial body are referred to as equatorial coordinates: declination δ \delta δ and right ascension α \alpha α (Fig, б).
The declination δ \delta δ is measured from the plane of the celestial equator; it is positive if the celestial body is located in the northern hemisphere of the celestial sphere, and negative if it is in the southern hemisphere.
The choice of the reference point for the right ascension is arbitrary, as there is no fixed direction in the plane of the celestial equator. Right ascension is measured counterclockwise from the vernal equinox ♈ when viewed from the North Pole, and can range from 0 h to 24 h or from 0° to 360°.
The determination of celestial coordinates of the luminary in 1998 was based on the catalog of extragalactic radio sources by the International Astronomical Union. To establish the origin of the direct ascension, the point near the dynamical equinox at epoch J2000.0 was chosen (by comparing the direct ascension of quasar 3C 273B to the value in the fundamental catalog FK5). This new definition decouples the point of the vernal equinox from the position of the ecliptic, and its stability in space is attributed to the lack of proper motion in quasars (due to their great distance).
Ecliptic coordinate system
The primary circles within the ecliptic coordinate system (Figure a) include the ecliptic and the circle of latitude (the great circle of the celestial sphere that passes through the northern PN and southern PS poles of the ecliptic and the luminary). In this system, the celestial coordinates of the luminary are known as the ecliptic coordinates: ecliptic latitude β (measured in the range -90° ≤ β ≤ 90°) and ecliptic longitude λ (measured within 0° ≤ λ ≤ 360°).
This coordinate system is commonly employed when studying the movement of Solar System bodies, as the orbital planes of most Solar System bodies are inclined to the ecliptic plane at small angles.
The Galactic Coordinate System
Coordinate systems centered around objects
The arrangement of stars and other celestial bodies in the sky can be precisely identified using two sets of spherical coordinates. These coordinates, expressed in degrees or hours, represent the arcs along the great circles of the celestial sphere. A familiar example of such spherical coordinates can be seen in the latitude and longitude measurements used to pinpoint a location on Earth. There are numerous astronomical coordinate systems, each distinguished by its selected main plane and origin.
3.1 The Coordinate System in the Horizontal Plane
The primary plane is the true horizon plane, and the reference point is located to the south of point S. The coordinates used in this system are altitude and azimuth (see Figure 5).
The altitude, denoted by h, represents the angular distance of a celestial body above the horizon, measured along a vertical line extending from the body (similar to latitude). The altitude of a celestial body can range from -90 degrees to 90 degrees. A negative altitude indicates that the body is below the horizon. For instance, the zenith altitude is 90 degrees. Instead of using the altitude, the zenith distance, denoted by z, is often used as the first horizontal coordinate. The zenith distance represents the angular distance between the body and the zenith, measured along a vertical line extending from the body. There is a simple relationship between the zenith distance and the altitude of the celestial body: z + h = 90 degrees.
3.2 Introduction to the initial equatorial coordinate system
In the initial equatorial coordinate system, the fundamental plane is represented by the celestial equator, with the Q point serving as the origin. The coordinates in this system are given by the declination and hour angle (see Fig. 6).
Fig. 6. Representation of the initial equatorial coordinate system The declination of a celestial object refers to its angular distance from the celestial equator, measured along the declination circle. The range of declination values is from -90 o to 90 o , and
3.3 The Second Equatorial Coordinate System
The Second Equatorial Coordinate System is an alternative method of representing celestial coordinates. It is based on the same principles as the First Equatorial Coordinate System, but with a different orientation. Instead of using the celestial equator as the reference plane, the Second Equatorial Coordinate System uses the plane perpendicular to the line connecting the Earth and the Sun at a specific time.
This system is useful for describing the positions of celestial objects in relation to the Earth-Sun line. It is particularly helpful for studying the motion of planets and other objects in the solar system.
In the Second Equatorial Coordinate System, the celestial sphere is divided into two halves, known as the northern and southern hemispheres. The celestial poles are defined as the points where the Earth-Sun line intersects the celestial sphere. The celestial equator is the great circle that lies halfway between the celestial poles.
To specify the position of an object in this coordinate system, astronomers use two angles: the hour angle and the declination. The hour angle is measured along the celestial equator from the vernal equinox to the object, while the declination is the angle between the object and the celestial equator.
The Second Equatorial Coordinate System is a useful tool for astronomers, as it provides a way to locate and track objects in the sky. By understanding the motion and position of celestial objects, astronomers can gain valuable insights into the workings of the universe.
3 hours 22 minutes 8 seconds 51 degrees 7 hours 25 minutes 8 seconds 24 degrees
5. CHANGES IN COORDINATES DUE TO THE ROTATION OF THE CELESTIAL SPHERE……8
6. LUNAR-SOLAR PRECESSION……………………………………………9
7. UTILIZATION OF VARIOUS COORDINATE SYSTEMS…………………….9
REFERENCE LIST…………………………………………………..11
Hipparchus, also known as Hipparchos, was an ancient Greek scientist who lived from about 180-190 BC in Nicea and died in 125 BC in Rhodes. He was one of the pioneers in the field of astronomy and is credited with making the first systematic observations and studies of the sky. Hipparchus developed a theory and created tables to track the motion of the Sun and Moon, including predicting solar eclipses. He also described the motion of the Moon during the full and new moons and made a fairly accurate estimation of the distance between the Moon and Earth.
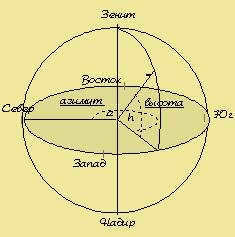
In the horizontal coordinate system, the equivalent of geographic longitude is known as azimuth. Azimuth is defined as the dihedral angle between the plane passing through the zenith and the point in question, and the plane of the celestial meridian.
Both of these planes are perpendicular to the mathematical horizon, so the dihedral angle can be measured as the corresponding angle between their traces in the horizontal plane (alpha). In geodesy, azimuths are typically measured in a clockwise direction from a point north (passing through points east, south, and west), ranging from 0 to 360 degrees. In astronomy, azimuths are also measured in the same direction, but often starting from a point south. Therefore, astronomical and geodetic azimuths differ by 180 degrees. When solving problems on the celestial sphere, it is important to identify which type of azimuth is being used.
2. The celestial coordinate system known as the equatorial system is used to locate objects in the sky.
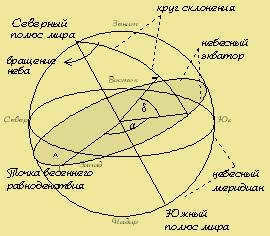
In the equatorial system of celestial coordinates, the celestial equator serves as the point of reference. Similar to the way geographic latitude is used on Earth, the coordinate in this system is known as declination, which measures the angle between the direction to the celestial object and the plane of the celestial equator. The declination is measured along the hour circle from the celestial equator, with a positive sign in the northern hemisphere of the celestial sphere and a negative sign in the southern hemisphere. It can range from +90 to -90 degrees. The diurnal parallel represents the geometric location of points with equal declinations.
Another coordinate is introduced in two different ways within the equatorial system.
In the second scenario, the original plane refers to the plane that intersects with the world axis and the point of the vernal equinox. This plane rotates alongside the entire celestial sphere. The coordinate, similar to Earth’s longitude, is known as the right ascension (alpha) in this case. It is measured in hours and goes in the opposite direction of the starry sky’s rotation. For various celestial bodies, the right ascension ranges from 0 to 24 hours. However, unlike the hour angles, the value of the right ascension for a particular celestial body remains constant regardless of the daily rotation of the sky or the observer’s location on Earth’s surface. The combination of declination and right ascension is known as the second equatorial system of celestial coordinates. This system is commonly used in star catalogs and star charts.
3. The Ecliptic System of Celestial Coordinates
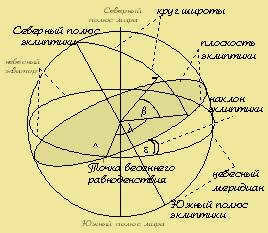
The ecliptic system was historically established prior to the second equatorial system. It gained popularity due to its convenience for ancient angular measuring instruments, such as the armillary sphere, which were specifically designed to measure the ecliptic coordinates of celestial bodies like the Sun, planets, and stars. As a result, the ecliptic system serves as the foundation for all ancient star catalogs and star atlases.
4. GALACTIC SYSTEM OF CELESTIAL COORDINATES
There are different systems of celestial coordinates that are categorized based on the position of their center in space. For instance, the topocentric system is a celestial coordinate system where the center is located at a specific point on the Earth’s surface. When a coordinate system is centered at the Earth’s center, it is referred to as a geocentric system of celestial coordinates. Similarly, a system that is centered at the Moon’s center is called selenocentric, while a system centered at one of the planets is known as planetocentric. For example, for Mars, it is called areo-centric, and for Venus, it is referred to as afro-centric. Lastly, the system of celestial coordinates that is centered at the Sun’s center is called heliocentric.
5. MODIFICATIONS IN COORDINATES DURING THE ROTATION OF THE CELESTIAL SPHERE
The elevation h, zenith distance z, azimuth A, and hour angle t of the celestial bodies are in constant flux as a result of the rotation of the celestial sphere, as they are calculated from points unaffected by this rotation.
The declination δ, polar distance p, and right ascension α of the celestial bodies remain unchanged due to the rotation of the celestial sphere, but they may be subject to modifications caused by the movements of the celestial bodies unrelated to the daily rotation.
6. LUNAR-SOLAR PROGRESSION
Due to the Earth’s axial movement, the equatorial plane perpendicular to it also undergoes rotation, resulting in the displacement of the vernal equinox point. This phenomenon, known as lunar-solar procession, occurs. The procession (or advance of equinoxes) is characterized by the vernal equinox point not remaining fixed but moving in accordance with the Sun’s apparent annual movement. As a result of this procession, the poles of the Earth also shift among the stars. Taking into consideration the gravitational effects of the planets on Earth, the vernal equinox point shifts by 50.3″ per year, or 1 degree in 71.6 years, completing a full revolution in 25,770 years.
The angle measuring instruments and azimuthal mount are used in the horizontal coordinate system to determine the direction to the luminary when observing through a telescope.
When observing with a telescope mounted on an equatorial mount, the first equatorial coordinate system is utilized to determine the precise time.
In astrometry, the second equatorial coordinate system is a widely used coordinate system that involves creating star maps and describing the positions of luminaries in catalogs.
Theoretical astronomy utilizes the ecliptic coordinate system to determine the orbits of celestial bodies.
It appears that all of this can be attributed to the field of astronomy. Astronomy is the study of stars and planets, the galaxy and interplanetary space, comets and meteorites, cosmic explosions and stellar nebulae – essentially, it encompasses the entire vast universe that surrounds our planet and Earth itself, with all its enigmatic and mysterious aspects.
Our planet, Earth, is just one among countless celestial bodies, and even the origin of Earth itself remains a subject of ongoing scientific inquiry. The events that take place in the sky – the cycle of day and night, the changing seasons, full moons and solar eclipses – have a direct impact on life here on Earth.
List of References
- Podobed V.V. Fundamental Astrometry. Establishment of the fundamental system of celestial coordinates. – Moscow: Nauka, 1968.
- The CD version of the Big Soviet Encyclopedia

Currently, 58,741 educational institutions are eligible for additional cumulative discounts ranging from 2% to 25%. To determine the discount applicable to all staff members of your educational institution, please log in to your personal Infoworks account.


Course for professional development
Enhancing teachers’ professional skills in the context of implementing FSES SOO.
We can apply a discount from your educational institution to this offer (the amount will depend on the number of your colleagues who have already taken Infoworks courses).
Currently, there are 58,741 eligible educational institutions that can receive additional cumulative discounts ranging from 2% to 25%. To find out the specific discount applicable to all employees of your institution, please log in to your personal Infoworks account.


Course on professional retraining
Teaching violin playing and organizing activities for additional education teachers
We can apply a discount to your educational institution in addition to the discount mentioned above (the amount depends on the number of colleagues from your institution who have completed Infoworks courses).
Currently, there are 58,741 educational institutions eligible for additional discounts ranging from 2% to 25%. To find out the specific discount applicable to all employees of your institution, please log in to your personal Infoworks account.


Homeschooling: Tips and Tricks for Parents
A Breakdown of the Presentation by Individual Slides:


Slide 2: Astrometry, also known as the study of celestial coordinate systems and the calculation of the positions and velocities of celestial bodies within these systems, is the ancient cornerstone of astronomy.

Slide 4 Horizontal coordinate system
When establishing any celestial coordinate system on the celestial sphere, a major circle (the primary circle of the coordinate system) and two points on the axis perpendicular to the plane of this circle (the coordinate system’s poles) are selected.
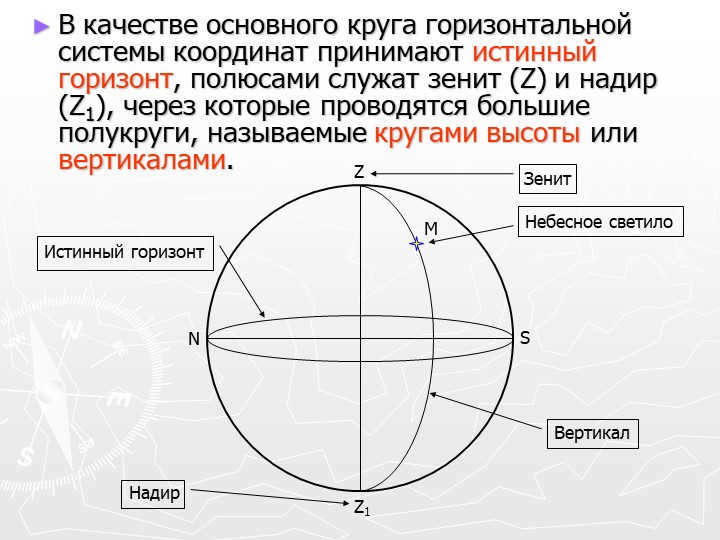
Slide 5: The primary circle of the horizontal coordinate system is known as the true horizon, with the zenith (Z) and nadir (Z1) serving as the poles. This circle is used to draw large semicircles known as circles of altitude or verticals.
Vertical
Zenith
Nadir
N
S
Z
Z1
M
Celestial luminary
True horizon
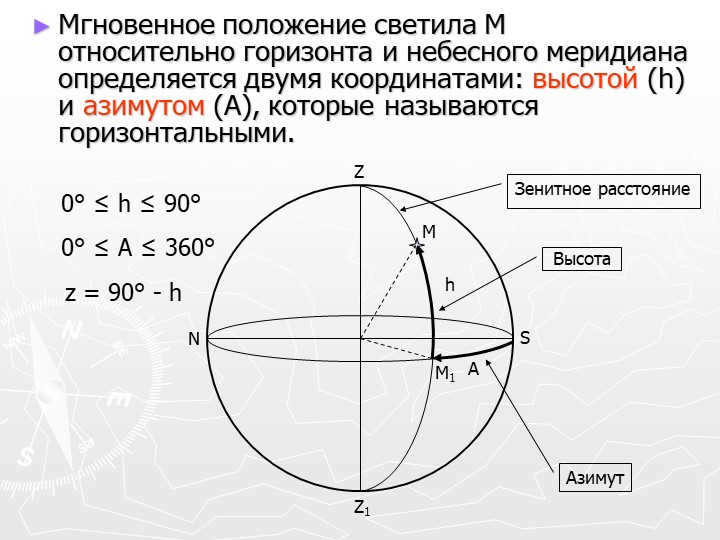
6 slide M
The luminary M’s position in relation to the horizon and celestial meridian is determined by two horizontal coordinates: altitude (h) and azimuth (A).
Azimuth
A
h
Altitude
N
S
Z
Z1
M1
0° ≤ h ≤ 90°
0° ≤ A ≤ 360°
z = 90° – h
Zenith distance
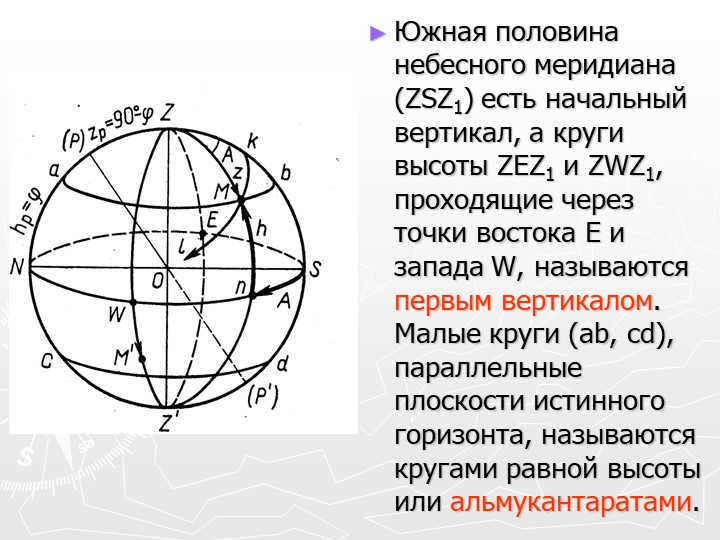
Slide number 7 describes the southern part of the celestial meridian (ZSZ1) as the starting point for the vertical axis. The first vertical includes the circles of altitude ZEZ1 and ZWZ1, which pass through the east E and west W points. In addition, there are small circles (ab, cd) that run parallel to the true horizon plane, known as circles of equal height or almucantarates.

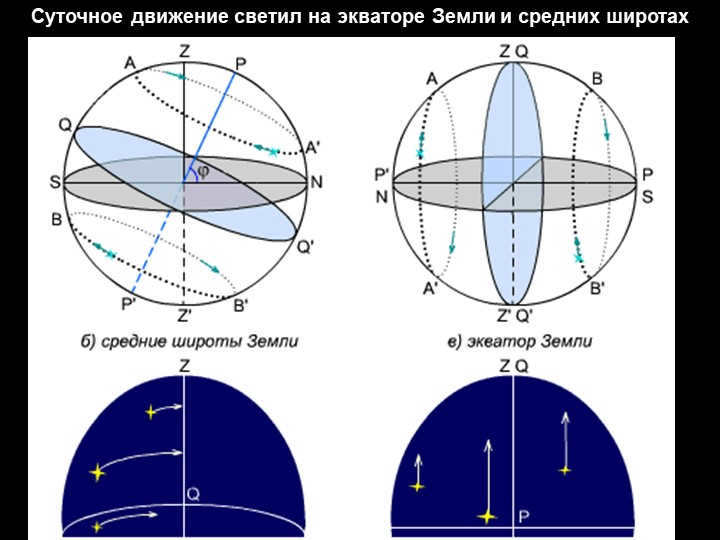
During the course of a day, the position of the stars and other celestial bodies constantly changes due to the rotation of the Earth. This makes the horizontal coordinate system impractical for creating star maps and catalogs. Instead, we need a coordinate system that remains unaffected by the Earth’s rotation, allowing us to accurately record the coordinates of the luminaries.

Slide 9 Equatorial Coordinate System
In order to maintain the spherical coordinates, the coordinate grid must rotate along with the celestial sphere. The equatorial coordinate system meets this requirement.
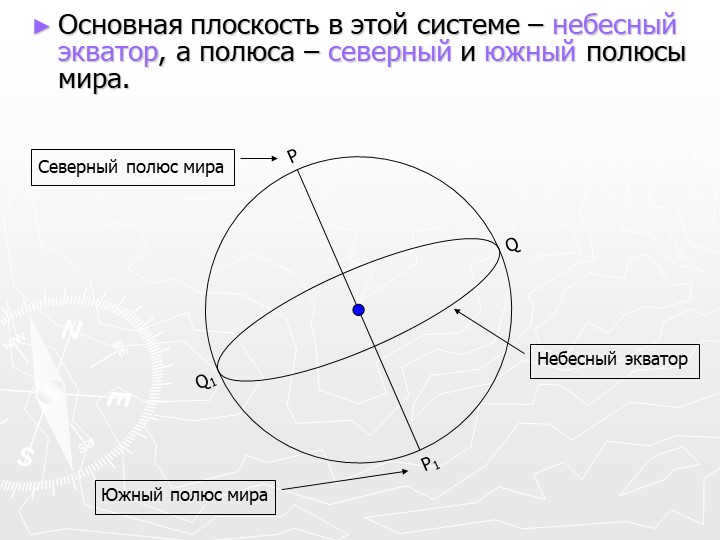
Slide 10: The primary plane within this system is known as the celestial equator, while the poles correspond to the north and south poles of the Earth.
Question
Question 1
Point
Point 1
Celestial equator
North Pole of the Earth
South Pole of the Earth
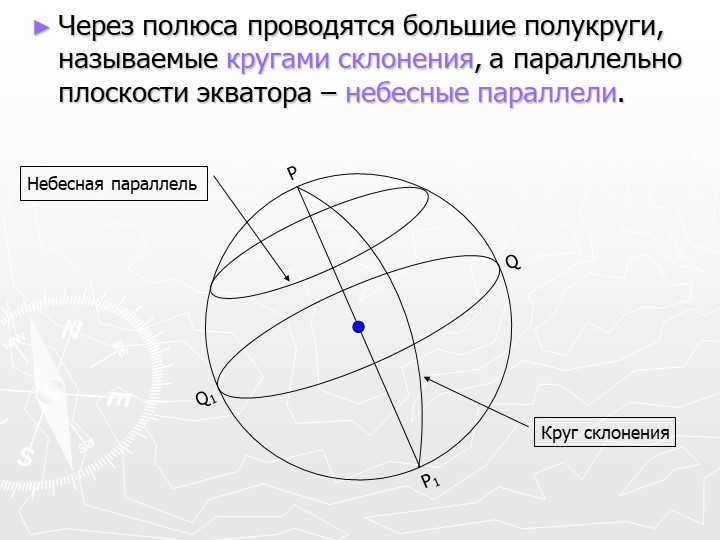
There are 11 large semicircles known as circles of declination that are drawn through the poles. Additionally, the celestial parallels are drawn to be parallel to the equator’s plane.
Q
Q1
P
P1
Circle of declination
Celestial parallel
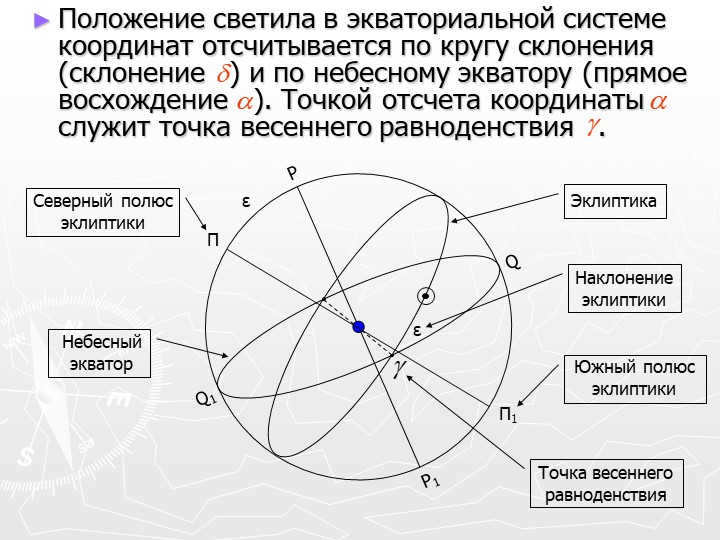
12 slide The luminary’s position in the equatorial coordinate system is determined by its declination (measured along the circle of declination) and its right ascension (measured along the celestial equator). The starting point for these coordinates is the vernal equinox point.
Q
Q1
P
P1
Π
Π1
North Pole
ecliptic
South pole
ecliptic
ε
Ecliptic
celestial
equator
ε
inclination
ecliptic
Vernal point
equinox
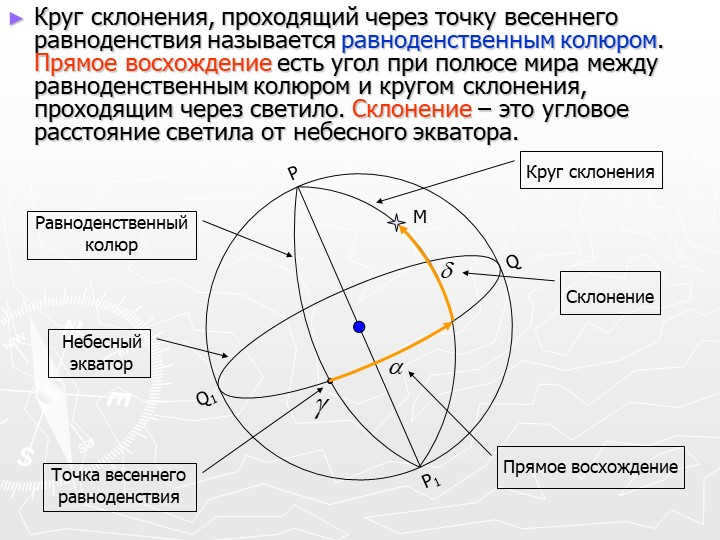
Slide 13: The equinox colure is the circle of declination that passes through the point of the vernal equinox. The angle at the celestial pole between the equinox colure and the circle of declination that passes through the luminary is called direct ascension. Declination refers to the angular distance of the luminary from the celestial equator.
The celestial
equator
The point of the vernal
equinoxes
Q
Q1
P
P1
Declination circle
Equinox
colure
M
Direct Ascension
Declination

Equatorial coordinates of stars are incredibly useful in various practical applications. They are utilized for creating star maps and catalogs, as well as determining the geographic coordinates of specific locations on Earth. Additionally, these coordinates help with orientation in outer space, checking time, and studying the rotation of our planet. The versatility of equatorial coordinates makes them invaluable tools in numerous fields.

At present, there are a total of 58,741 educational establishments that qualify for extra combined reductions (ranging from 2% to 25%). To ascertain the applicable discount for all staff members at your educational institution, kindly access your personal Infoworks account.


Advanced training program
Enhancing teacher’s expertise in the context of implementing FSES SOO.
We can apply an additional discount from your educational institution to this offer (the amount depends on the number of your colleagues who have completed Infowork courses).
At the moment, 58,741 educational institutions are eligible for extra discounts (ranging from 2% to 25%). To discover the exact discount available for all staff members at your educational institution, please log in to your personal Infoworks account.


Professional retraining course
Organizing the work of a violin teacher in additional education
In addition to this discount, you can also receive a discount from your educational institution (the amount depends on the number of your colleagues who have completed Infoworks courses).
Currently, 58,741 educational institutions are eligible for additional discounts ranging from 2% to 25%. To find out the specific discount applicable to all employees of your educational institution, please log in to your personal Infoworks account.


Homeschooling: Tips and Tricks for Parents
Breakdown of the Presentation by Slide:

Slide 1 – Celestial Coordinates
Celestial Coordinates Explained
Created by E.V. Trofimova
Astronomy and Geography Teacher
State Educational Institution “Secondary School No. 4 of Orsha”

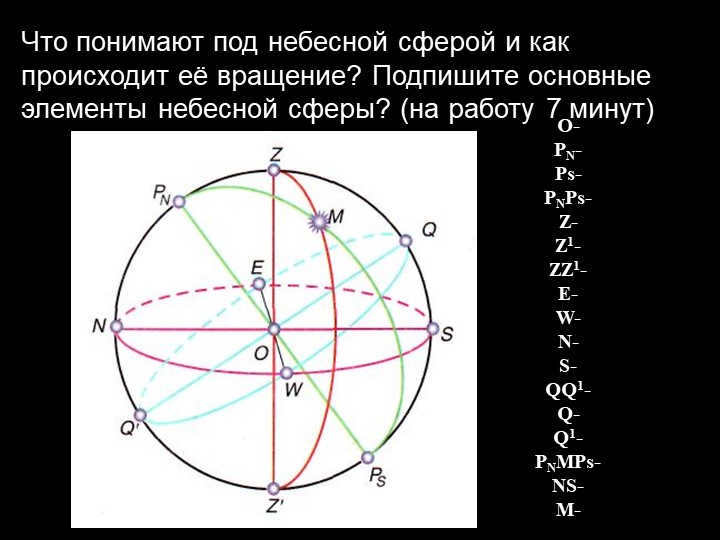
What is the definition of the celestial sphere and how does it undergo rotation? Identify the key components of the celestial sphere. (Allow 7 minutes for completion)

4-slide Plan
1. Coordinate system. Star charts. An adjustable starry sky map.
A) Horizontal
B) Equatorial
2. Lunar-solar precession
3. The elevation of the celestial pole above the horizon.

Slide 6 The positions of the celestial bodies in relation to the celestial sphere are determined using celestial coordinates, which are the central angles or arcs of the great circles. The horizontal coordinate system uses the true horizon as the main circle, with coordinates of altitude (h) and azimuth (A).
When creating star maps and compiling star catalogs, it is convenient to use the celestial equator as the main circle of the celestial sphere. The equatorial coordinate system, with coordinates of declination (δ) and right ascension (α), is used in this system.

Slide 7 is focused on Celestial coordinates. These coordinates can be classified into two main categories: horizontal coordinates and equatorial coordinates. The horizontal coordinates indicate the position of the luminaries with respect to the horizon. On the other hand, the equatorial coordinates are determined based on their relation to the celestial equator.
These celestial coordinates find their applications in various fields such as topographic surveying and navigation.
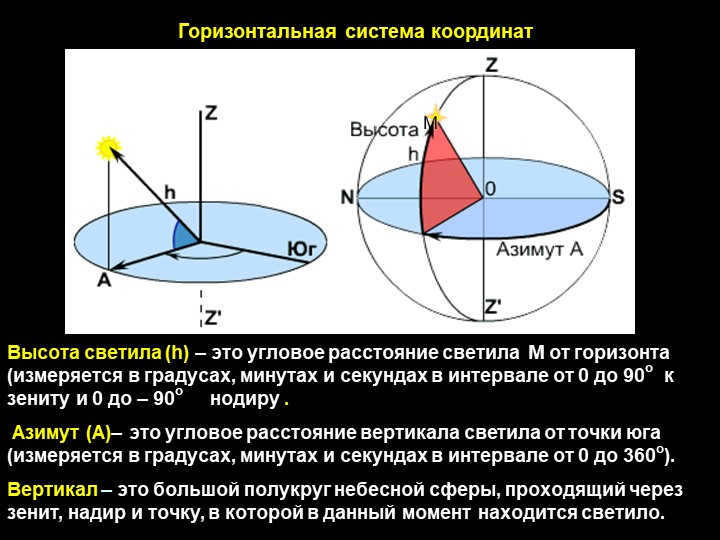
Slide 8 in the horizontal coordinate system
The luminary’s altitude (h) is the angular measurement of its distance from the horizon, ranging from 0 to 90 degrees to the zenith and 0 to -90 degrees to the nadir.
Azimuth (A) is the angular measurement of the luminary’s vertical distance from the southern point, ranging from 0 to 360 degrees.
The vertical refers to the large semicircle of the celestial sphere that passes through the zenith, nadir, and the current location of the luminary.
M
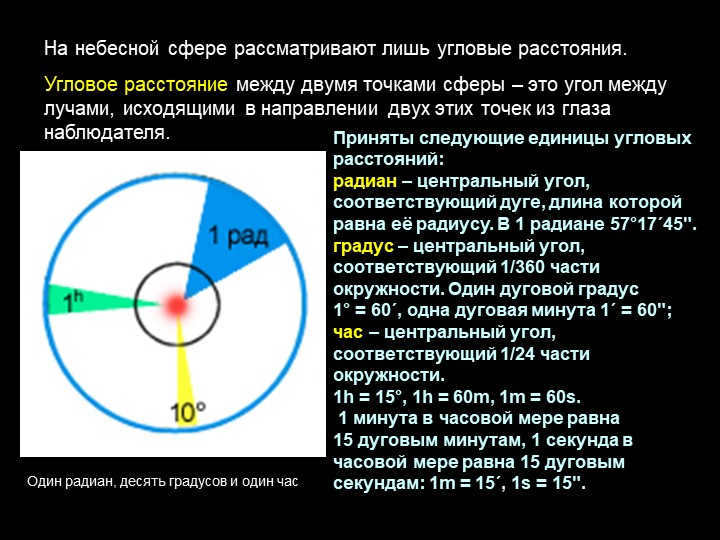
Only angular distances are taken into consideration on the celestial sphere.
The angular distance between two points on the sphere is the angle between the rays emanating towards these two points from the observer’s eye.
The following units of angular distances are used:
radian – the central angle that corresponds to an arc whose length is equal to its radius. There are 57°17’45” in 1 radian.
degree – the central angle that corresponds to 1/360th of a circle. One arc degree 1° = 60′, one arc minute 1′ = 60″;
hour is the central angle that corresponds to 1/24th of a circle.
1h = 15°, 1h = 60m, 1m = 60s.
1 minute in hour measure is equal to 15 arc minutes, 1 second in hour measure is equal to 15 arc seconds: 1m = 15′, 1s = 15″.
One radian, ten degrees, and one hour
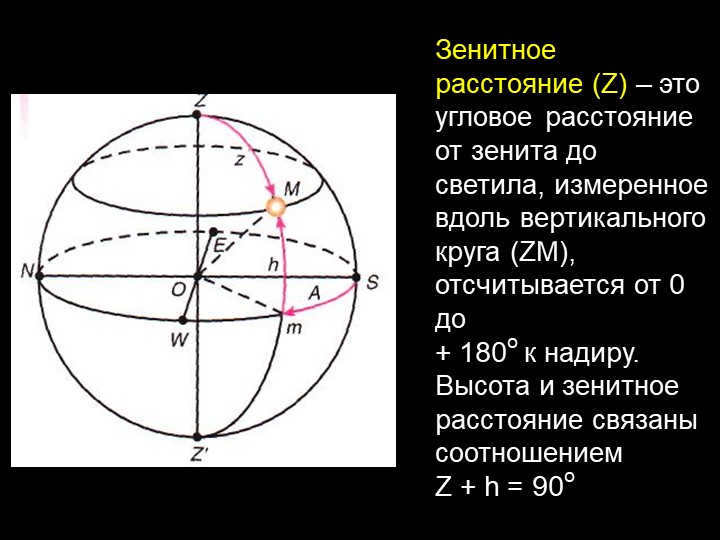
Slide 10: The zenith distance (Z) is the angular distance from the zenith to the celestial body, measured along a vertical circle (ZM), ranging from 0 to +180o towards the nadir.
The altitude and zenith distance are connected by the equation
Z + h = 90o

Before the compass was invented, the stars served as the primary landmarks for ancient travelers and sailors to find their way. Astronavigation, or navigating by the stars, remains crucial even in our modern age of space exploration and atomic energy. This skill is essential for navigators, astronauts, captains, and pilots.
There are 25 navigational stars, which are the brightest stars used to locate a ship.

15 slide The Earth revolves around the Sun for a period of 365 days.
The Earth’s axis is inclined at an angle of 66.56˚ to the plane of its orbit
and maintains a consistent orientation in space.
Due to these factors, there are cyclic variations in the lighting
and heating conditions of the Earth’s hemispheres, resulting in the changing seasons throughout the year.
Vertical sun rays provide greater intensity of light and heat compared to angled rays.
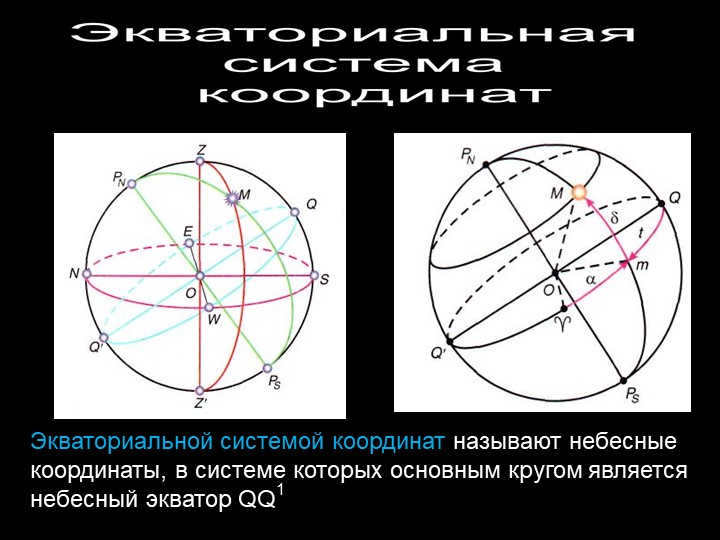
The celestial coordinate system known as the Equatorial coordinate system consists of a main circle called the celestial equator QQ1, which is utilized to determine the positions of celestial objects.
Slide 17: Equatorial Coordinate System
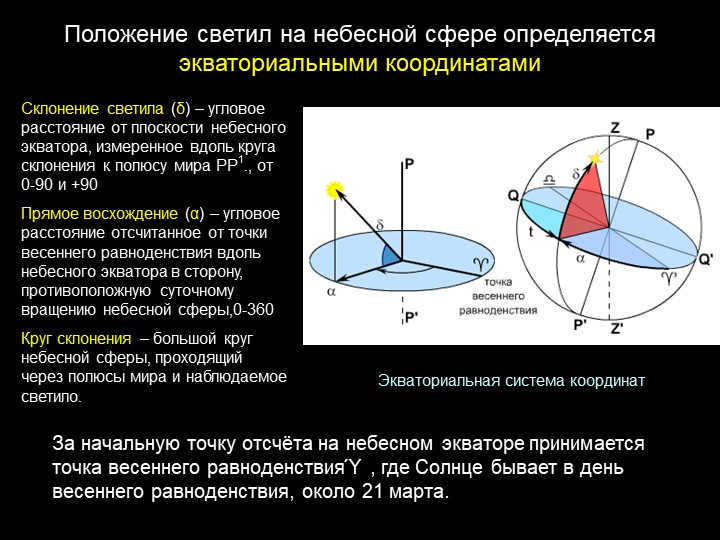
The declination (δ) of a celestial body is the angular distance from the plane of the celestial equator, measured along the declination circle to the celestial pole PP1. It can range from 0 to 90 degrees and from -90 to 0 degrees.
The right ascension (α) is the angular distance measured from the vernal equinox point along the celestial equator in the opposite direction to the daily rotation of the celestial sphere. It can range from 0 to 360 degrees.
The circle of declination is a large circle on the celestial sphere that passes through the celestial poles and the observed celestial body.
The positions of celestial bodies on the celestial sphere are determined using equatorial coordinates.
The point of the vernal equinox, denoted as Y, is the location of the Sun on the day of the vernal equinox, which usually falls on March 21st. It is used as the reference point on the celestial equator.
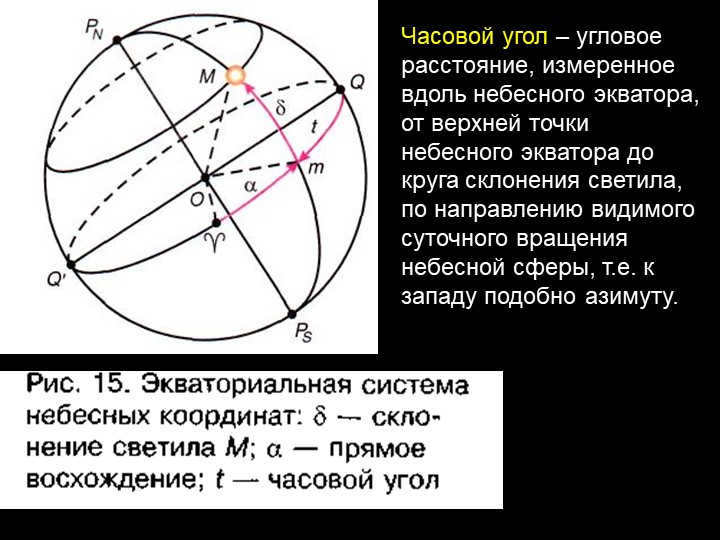
Hour angle of the 18th slide refers to the angular distance that is measured along the celestial equator, starting from the highest point of the celestial equator and extending to the declination circle of the celestial object. This measurement is made in the direction of the visible daily rotation of the celestial sphere, which is towards the west, similar to azimuth.
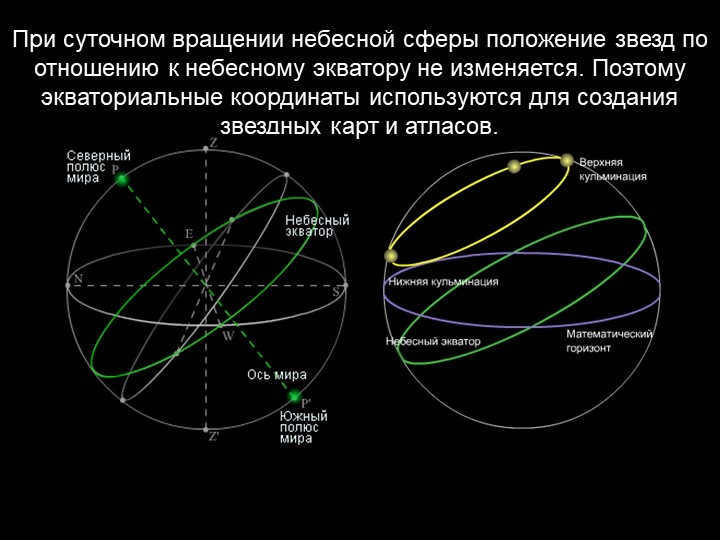
Slide 19: The stars maintain a fixed position in relation to the celestial equator during the daily rotation of the celestial sphere. This is why equatorial coordinates are utilized in the creation of star charts and atlases.
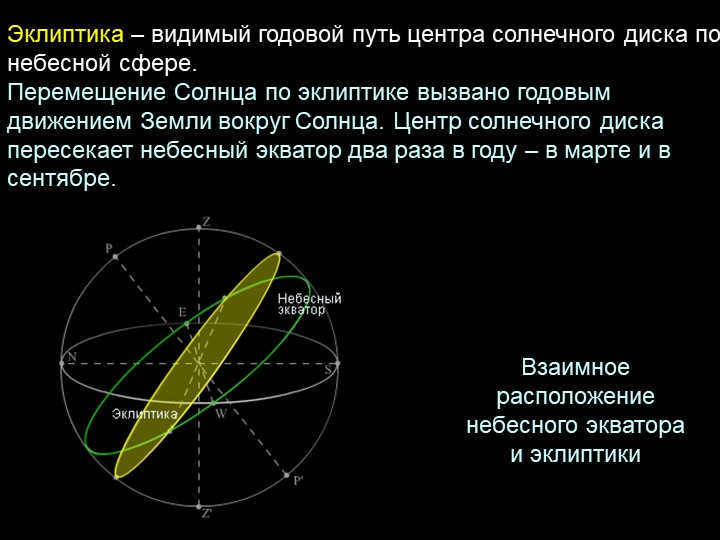
20 slide The ecliptic represents the annual path of the solar disk’s center as observed on the celestial sphere.
The Sun’s movement along the ecliptic is a result of the Earth’s yearly orbit around it. The solar disk’s center intersects the celestial equator twice a year – in March and September.
The relative position of the celestial equator and the ecliptic
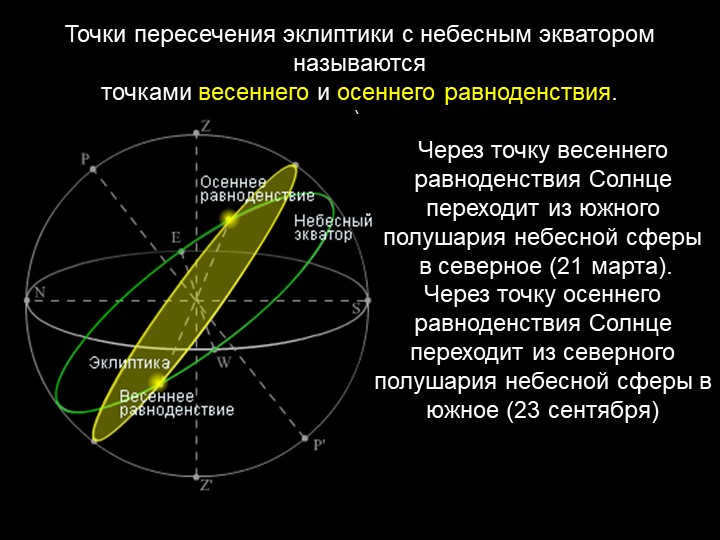
21 slide The points where the ecliptic intersects the celestial equator are referred to as the points of the vernal and autumnal equinoxes.
).
At the vernal equinox, which occurs on March 21, the Sun transitions from the southern hemisphere of the celestial sphere to the northern hemisphere.
Similarly, at the autumnal equinox on September 23, the Sun moves from the northern hemisphere of the celestial sphere to the southern hemisphere.
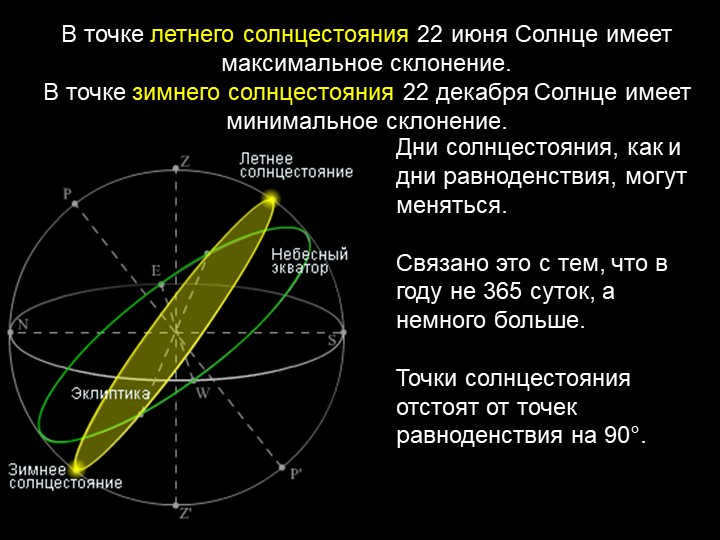
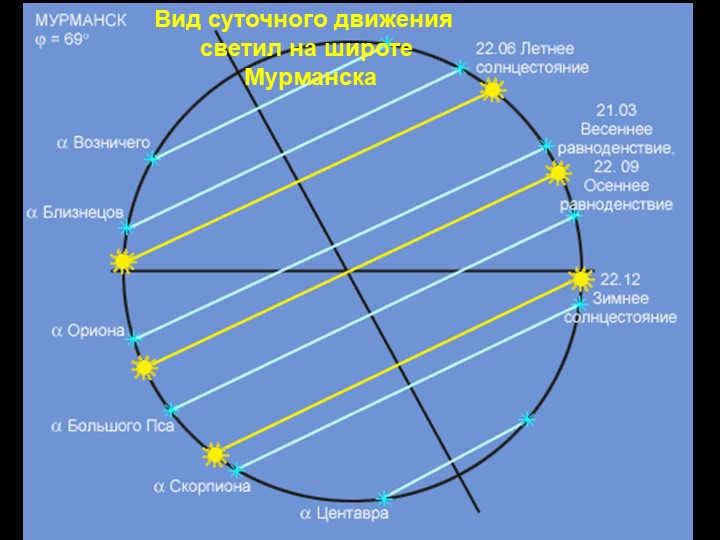
Slide 22 During the summer solstice, which occurs on June 22, the Sun reaches its highest declination in the sky.
On the winter solstice, which falls on December 22, the Sun has its lowest declination.
Both solstice days, like equinox days, can vary in duration.
This variability is a result of the fact that the length of a year is not exactly 365 days, but slightly longer.
The solstice points are positioned 90 degrees away from the equinox points.
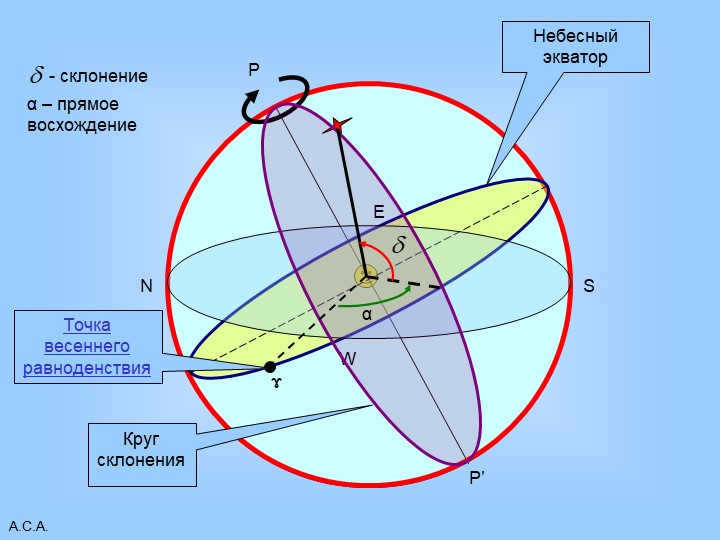
Slide 23 A.S.A.
P
P'
The equator of the sky
W
E
N
S
Circle of declination
ɤ
Point of the Vernal Equinox
– declination
α
α – straight ascent
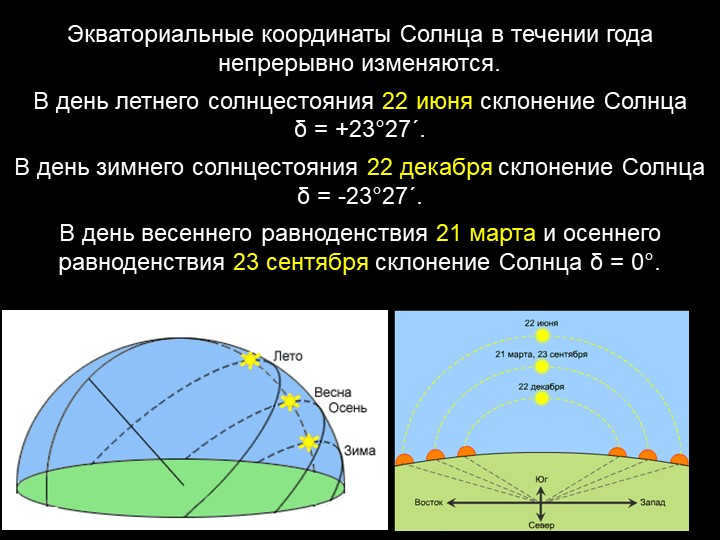
Throughout the year, the Sun’s equatorial coordinates are in a constant state of change.
During the summer solstice on June 22, the Sun’s declination is at a positive angle of +23°27′.
Conversely, on the winter solstice on December 22, the Sun’s declination is at a negative angle of -23°27′.
During the vernal equinox on March 21 and the autumnal equinox on September 23, the Sun’s declination is at a neutral angle of 0°.

There were 25 slide Star catalogs compiled to classify and account for stars. These catalogs were created by various astronomers including Ulugbek, Ptolemy, Tycho Brahe, Jan Hevelius, Edmond Halley, Lacaille, Francie Bailey, and even included a fragment of a Chinese ancient constellation map and a depiction of constellations in ancient Egypt.

Slide 26 of Ptolemy
Ptolemy was the creator of various astronomical instruments, such as the astrolabe, which was used for measuring longitudes and latitudes on the celestial sphere, and the triquetrum, which was used for measuring angular distances. He also completed the star catalog of Hipparchus, adding information on 1022 stars. Additionally, Ptolemy discovered the phenomenon of ejection, which refers to the moon’s motion deviating from a uniform circular motion.
Astrolabe
Ulugbek
In 1428, Ulugbek initiated the construction of an observatory in Samarkand. Over the course of thirty years, he made meticulous observations and compiled a highly accurate star catalog containing the positions of 1018 stars. This catalog, known as the “New Guragan Tables,” was published in 1437.
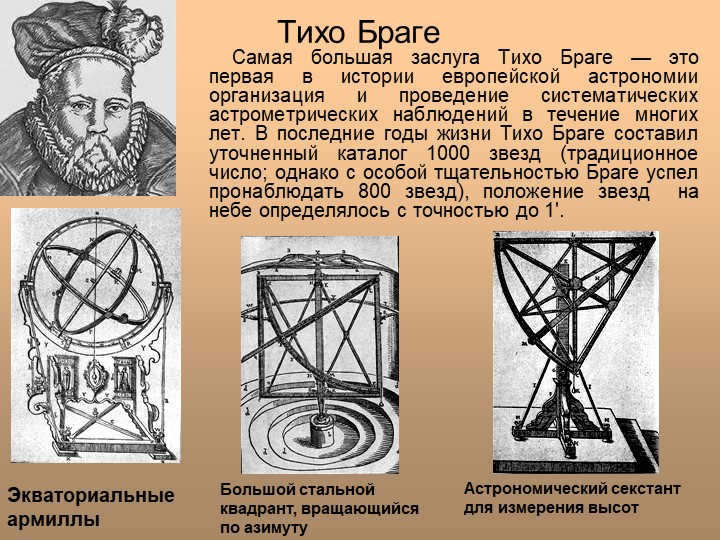
On slide 27, we learn about the significant contributions of Tycho Brahe in the field of European astronomy. He is recognized as the first person in history to organize and carry out systematic astrometric observations spanning over many years. Towards the end of his life, Tycho Brahe meticulously compiled a catalog of 1000 stars (although he managed to observe 800 stars with exceptional care) with an impressive accuracy of 1 minute. Another instrument mentioned is the astronomical sextant, which is used for measuring altitudes. This device consists of a large steel quadrant that can rotate in azimuth. Lastly, we are introduced to equatorial armillas, which are also utilized in the field of astronomy.



Francie Bailey was an English astronomer who was a member of the Royal Society of London in 1821. Despite receiving only an elementary education, Bailey went on to study at a trading firm for three years and traveled extensively. After returning to England in 1798, he became involved in stock exchange activities. However, at the age of 50, he decided to devote himself to science.
One of Bailey’s main areas of scientific research was positional astronomy. He developed methods for determining latitude and time using stars. To do this, he calculated the average positions of 2881 stars for the epoch of January 1, 1830, based on various catalogs. Bailey also reviewed and republished catalogs from other astronomers, including T.I. Mayer, N.L. Lacaille, E. Halley, J. Hevelius, T. Brahe, Ptolemy, and Ulugbek. In 1845, he published the catalog of the British Association for the Advancement of Science, which included 10,000 stars.

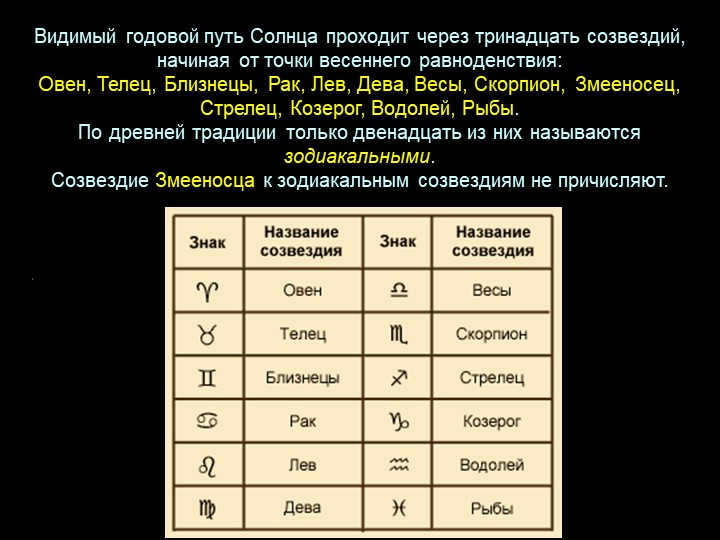
Slide 32: The annual path that is visible of the Sun passes through thirteen constellations, starting at the vernal equinox:
Aries, Taurus, Gemini, Cancer, Leo, Virgo, Libra, Scorpio, Serpentor, Sagittarius, Capricorn, Aquarius, and Pisces.
According to ancient tradition, only twelve of these are known as zodiacal constellations.
The constellation of the Serpentine is not included in the count of the zodiacal constellations.
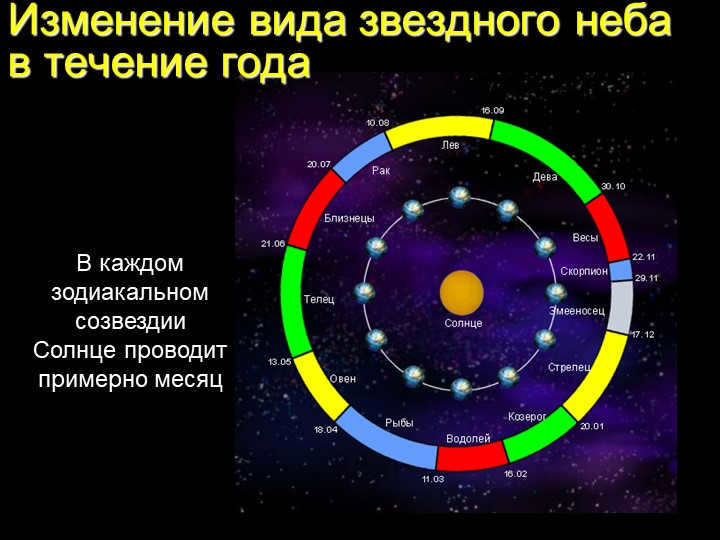
Throughout the year, the starry sky undergoes a transformation in its appearance. This is due to the movement of the Sun, which spends approximately one month in each zodiacal constellation.
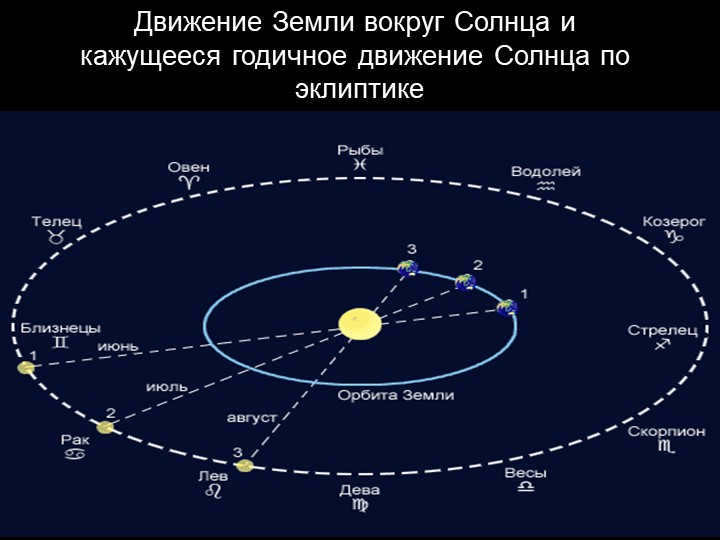

The zodiac is a band that is approximately 9 degrees wide on both sides of the ecliptic, consisting of 13 constellations and divided into 12 zodiac signs. It is the path followed by the Sun, stars, and most planets.

36 Slide About 2,000 years ago, the zodiac signs aligned with the corresponding zodiac constellations. During that time, the vernal equinox fell within the constellation of Aries, hence it was represented by the sign of Aries. Similarly, the summer solstice was in the constellation of Cancer, marked by its sign. The autumnal equinox fell within the constellation of Libra, and the winter solstice was in the constellation of Capricorn. However, over time, these points gradually shifted westward and have remained there for a significant period. Currently, the vernal equinox is located within the constellation of Pisces, while the fall equinox point is in the constellation of Virgo. Since 1988, the summer solstice has been in the constellation of Taurus.

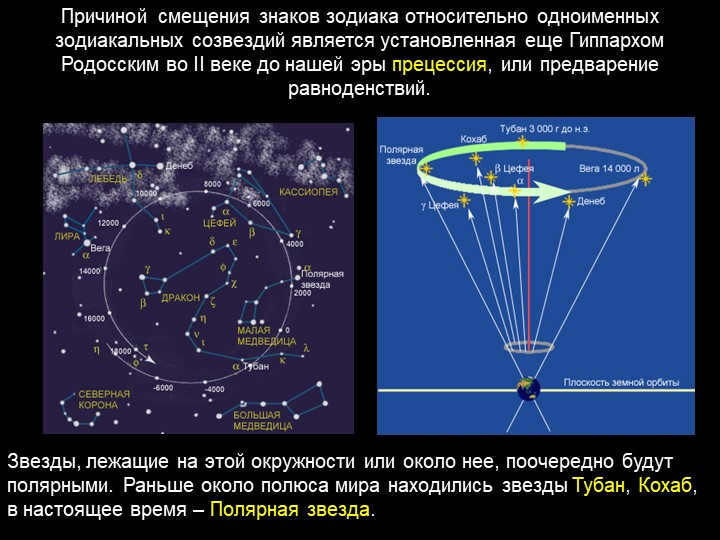
39 slide The displacement of the zodiac signs in relation to the zodiacal constellations of the same name is caused by precession, or the precession of the equinoxes, which was discovered by Hipparchus of Rhodes in the 2nd century BC.
The stars that lie on or near this circle will eventually become the pole star. In the past, the stars Tuban and Cohab were near the pole of the world; currently, Polaris is the pole star.