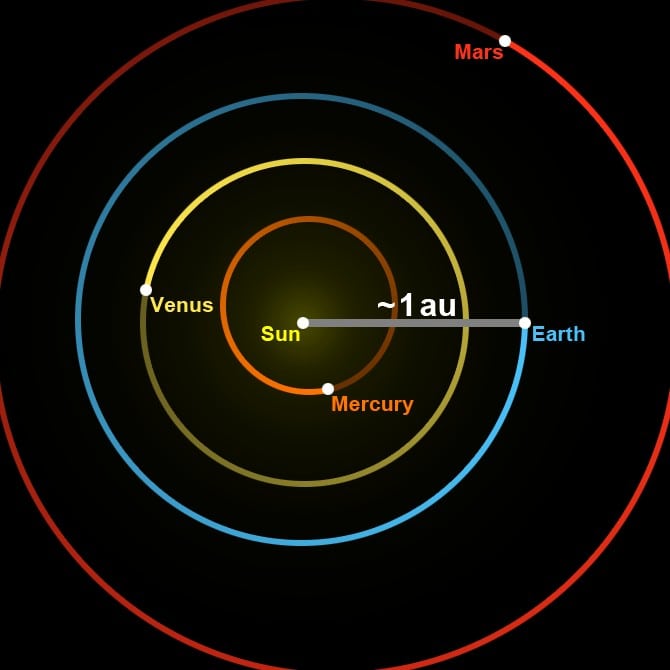
An astronomical unit, often abbreviated as AU, is a unit of length that represents the average distance between the Earth and the Sun. It is approximately 150 million kilometers (93 million miles) long. The actual distance varies throughout the year as the Earth orbits around the Sun, reaching its maximum distance (aphelion) and minimum distance (perihelion). In 2012, the AU was officially defined as exactly 149,597,870,700 meters.
The astronomical unit is primarily used for measuring distances within the solar system and to other stars. It is also an important component in defining another unit of astronomical length called the parsec.
- 1 Origins of the AU symbol
- 2 Evolution of the unit’s definition
- 3 Applications and significance
- 4 History
- 5 Developments
- 6 Examples
- 7 See Also
- 8 References
- 9 Additional literature
- 10 External links
History of symbol usage
A plethora of unit symbols and abbreviations have been utilized to represent the astronomical unit. In a resolution passed in 1976, the International Astronomical Union (IAU) employed the symbol A to signify a length equal to one astronomical unit. The AU symbol has been prevalent in astronomical literature and is still widely used today. In 2006, the International Bureau of Weights and Measures (BIPM) recommended ua as the unit symbol. In non-normative Annex C of ISO 80000-3:2006, the symbol for the astronomical unit is “ua”.
In 2012, the International Astronomical Union (IAU) acknowledged the existence of multiple symbols used to represent the astronomical unit and recommended the use of the symbol “au”. The American Astronomical Society (AAS) also adopted this symbol in their guidelines for manuscript preparation for major journals. The Bureau International des Poids et Mesures (BIPM) included the symbol “au” in the 2014 and 2019 revisions of the SI Brochure. However, ISO 80000-3:2019, which supersedes ISO 80000-3:2006, does not specifically mention the astronomical unit.
Expansion of the unit’s meaning
The Earth’s path around the Sun is not a perfect circle, but rather an elliptical shape. The distance from the nearest point to the Sun, known as perihelion, to the farthest point, known as aphelion, is called the major semi-axis. It’s important to note that the center of the Sun is not exactly in the middle of this line. By accurately measuring the extreme points of the ellipse, scientists were able to determine the exact mathematical shape of the Earth’s orbit. This knowledge allowed for precise calculations and predictions of the entire orbit, as well as observations of parallax in nearby stars. Parallax refers to the apparent shift in position of a star when viewed from different locations on Earth. By measuring this shift and knowing the displacement of the Earth, scientists could calculate the distance to the star. However, all measurements are subject to some degree of error or uncertainty, and the accuracy of astronomical units affects the accuracy of stellar distances. Improving accuracy has always been a priority in the field of astronomy. In the twentieth century, measurements became more precise and relied heavily on observations described by Einstein’s theory of relativity and mathematical tools.
In 1976, the International Astronomical Union (IAU) officially adopted a new definition in order to establish a more precise measurement for the astronomical unit (AU). This definition was based on the most accurate observational measurements available at the time, as well as the calculations derived from celestial mechanics and planetary ephemerides. According to this definition, the length of one AU is determined by Gauss’s gravitational constant (k) taking on the value 0.01720209895 when expressed in astronomical units of length, mass, and time.
Alternatively, this definition states that one AU is equivalent to the radius of an undisturbed circular Newtonian orbit around the Sun, with a particle of infinitesimal mass moving at an angular frequency of 0.01720209895 radians per day. In other words, it is the length used to describe the positions of objects in the solar system when the heliocentric gravitational constant (the product of G and M☉) is equal to (0.01720209895) AU/day.
Following space probe investigations of our solar system, accurate measurements of the relative positions of the inner planets and other celestial bodies have been obtained using radar and telemetry. Similar to all radar measurements, this method relies on determining the time it takes for photons to reflect off an object. Since photons travel at the speed of light in a vacuum, which is a constant in the universe, the distance between the object and the probe can be calculated by multiplying the speed of light by the measured time. However, precise calculations necessitate adjustments for various factors, such as the movements of the probe and the object as the photons pass by. Additionally, the time measurement itself must be converted to a standard scale that accounts for relativistic time dilation. By comparing ephemeris positions with time measurements expressed in barycentric dynamical time (TDB), the speed of light in astronomical units per day (86400 s) can be determined. In 2009, the International Astronomical Union (IAU) updated its standard measures to incorporate the advancements and calculated the speed of light at 173.1446326847 (69) a.u./day (TDB).
In 1983, the International System of Units (SI) was modified by CIPM to redefine the meter. The new definition stated that the meter is now the distance traveled by light in a vacuum in 1/299792458 of a second. This replaced the previous definition, which was in effect from 1960 to 1983, and stated that the meter was equal to a certain number of wavelengths of a specific emission line of krypton-86. The reason for this change was the development of a more accurate method for measuring the speed of light. With the new definition, the speed of light can be precisely expressed as c 0 = 299792458 m/s, which is also adopted as a standard by the IERS.
Based on this new definition and the 2009 IAU standard, the time it takes for light to travel through an astronomical unit is τ A = 499.0047838061 ± 0.00000001 s, which is a little over 8 minutes and 19 seconds. By multiplying this time with the speed of light, the best IAU estimate for 2009 was A = c 0τA = 149597870700 ± 3 m. This estimate was determined through a comparison of the Jet Propulsion Laboratory and IAA-RAS ephemerides.
In 2006, the Bureau International des Poids et Mesures (BIPM) reported the value of the astronomical unit as 1.49597870691 (6) × 10 m. However, in the 2014 version of the SI Brochure, BIPM acknowledged the redefinition of the astronomical unit by the International Astronomical Union (IAU) in 2012, setting it at 14959787070700 m.
It is important to note that this estimate, although based on observations and measurements, is still subject to error. The methods used to determine this value do not account for all relativistic effects and therefore may not be constant for all observers.
In 2012, the IAU decided to redefine the astronomical unit in a simpler way, as the relativity equation alone would have made the definition overly complicated. They chose to directly tie the astronomical unit to the meter, setting it exactly at 149597870700 m. This new definition also acknowledges that the astronomical unit will now have a smaller role, limited to its convenience in certain applications.
This definition establishes that the velocity of light, which is precisely 299792458 m/s, is equivalent to approximately 173.144632674240 a.u./day, or 299792458 × 86400 ÷ 149597870700, which is roughly 60 parts per trillion less than the estimate from 2009.
Applications and Significance
In definitions utilized prior to 2012, the astronomical unit relied on the heliocentric gravitational constant, which is the combination of the gravitational constant, G, and the mass of the Sun, M ☉. While G and M ☉ cannot be individually measured with high precision, their product is known with great accuracy through observations of the relative positions of the planets (Kepler’s Third Law expressed in terms of Newtonian gravity). Ephemerides, which are used to calculate the positions of planets, only require a product, making astronomical units more suitable than SI units.
The calculation of ephemerides also necessitates taking into account the impacts of the general theory of relativity. Specifically, time intervals measured on the Earth’s surface (Terrestrial Time, TT) are subject to change in comparison to the movements of the planets: an Earth second (TT) seems to be longer around January and shorter around July when compared to a “planetary second” (typically measured in TDB). This is due to the fact that the distance between the Earth and the Sun is not constant (it ranges from 0.9832898912 to 1.0167103335 a.u.), and when the Earth is closer to the Sun (perihelion), the Sun’s gravitational field is stronger and the Earth moves more swiftly along its orbital path. Given that the meter is defined in terms of seconds and the speed of light remains constant for all observers, the length of the Earth meter appears to vary periodically in comparison to the “planetary meter”.
The meter is a unit of length, but its definition in the SI system does not include the metric tensor. The International Committee of Weights and Measures (CIPM) states that the definition of a meter is only valid for small spatial dimensions where the effects of gravitational field inhomogeneity can be ignored. Therefore, the meter is not suitable for measuring distances in the Solar System. In 1976, the definition of the astronomical unit was incomplete as it did not specify the frame of reference for measuring time. However, it was still useful for calculating ephemerides. A more comprehensive definition consistent with the general theory of relativity was proposed, and a lively debate ensued until August 2012, when the IAU adopted the current definition that 1 astronomical unit equals 149597870700 meters.
The astronomical unit is frequently utilized for measuring distances on a stellar system scale, such as the dimensions of a protostellar disk or the distance from the Sun to an asteroid. Other units are employed for different distances in the field of astronomy. However, the astronomical unit is not suitable for interstellar distances, where the parsec and light-year are commonly employed. A parsec (abbreviated as pc) is defined in terms of astronomical units and represents the distance to an object with a parallax of 1 arcsecond. While the light-year is often mentioned in popular literature, it is not an officially recognized unit outside of the International System of Units (SI) and is rarely used by professional astronomers.
When running a numerical simulation of the solar system, using the astronomical unit as a scale helps to minimize errors related to overflow, loss of significance, and truncation in floating-point calculations.
Historical Background
In the book “On the Sizes and Distances of the Sun and Moon,” often attributed to Aristarchus, it is mentioned that he made a calculation stating that the distance from the Earth to the Sun is approximately 18 to 20 times greater than the distance from the Earth to the Moon. However, the actual ratio is significantly larger, measuring around 389,174. Aristarchus based his estimation on the angle between the crescent moon and the Sun, which he approximated to be 87° (the true value being close to 89,853°). Depending on the distance that Van Helden suggests Aristarchus used to determine the distance to the Moon, his approximation of the distance to the Sun would range from 380 to 1520 Earth radii.
As stated by Eusebius of Caesarea in Praeparatio Evangelica (Book XV, Chapter 53), Eratosthenes determined that the distance to the Sun was “σταδιων μυριαδας τετρακοσιας και οκτωκισμυριας” (equivalent to “55 million years”)>400 and 80000″). However, it should be noted that in the Greek text, the grammatical agreement is between myriads (not stages) on one side and 400 and 80000 on the other side, unlike in English where all three (or all four if stages are included) words are declinable. This has been translated as 40800000000 stadia (according to Edwin Hamilton Gifford’s 1903 translation) or 80400000000 stadia (according to the 1974-1991 revision). Taking into account the Greek stadium’s measurement of 185 to 190 meters, the former translation would be 754800 kilometers by 775200 kilometers, which is too small, while the latter translation would be 148.7 to 152.8 million kilometers (with an accuracy of 2%). Hipparchus also provided an estimate of the Earth’s distance from the Sun, as quoted by Papp, which equals 490 Earth radii. According to Noel Swerdlow and G. J. Toomer’s hypothetical reconstructions, this value was derived from his assumption of a “least noticeable” solar parallax of 7′.
The Zhubi Xuanjing, a Chinese mathematical treatise from the 1st century B.C., provides a method for geometrically calculating the distance to the Sun. This method involves observing the varying lengths of noon shadows at three locations that are 1000 li apart, under the assumption that the Earth is flat.
| Aristarchus (3rd century B.C.). (in On dimensions and distances ) | – | 380–1 520 | 0,016–0,065 |
| Archimedes (3rd century B.C.). (in The Sand Reckoner ) | 40 ″ | 10,000 | 0,426 |
| Hipparchus (2nd century BC). | 7 ′ | 490 | 0,021 |
| Posidonius (1st century B.C.). (quoted by his peer Cleomedes) | – | 10,000 | 0,426 |
| Ptolemy (2nd century). | 2 ’50 ″ | 1.210 | 0,052 |
| Godefroy Wendelin (1635) | 15 ″ | 14,000 | 0,597 |
| Jeremiah Horrocks (1639) | 15 ″ | 14,000 | 0,597 |
| Christiaan Huygens (1659) | 8.2 ″ | 25,086 | 1,068 |
| Cassini Richer (1672) | 9.5 ″ | 21,700 | 0,925 |
| Jerome Lalande (1771) | 8.6 ″ | 24,000 | 1,023 |
| Simon Newcomb (1895) | 8.80 ″ | 23,440 | 0,9994 |
| Arthur Hincks (1909) | 8.807 ″ | 23,420 | 0,9985 |
| H. Spencer Jones (1941) | 8.790 ″ | 23,466 | 1.0005 |
| modern astronomy | 8.794143 ″ | 23,455 | 1,0000 |
In the 2nd century CE, Ptolemy made an estimation that the average distance from the Earth to the Sun is 1,210 times the radius of the Earth. To arrive at this value, Ptolemy first measured the parallax of the Moon and found that the Moon’s horizontal parallax was 1° 26′, which was deemed too large. He then determined a maximum distance to the Moon which was equal to 64 plus 1/6 of the Earth’s radius. Despite potential errors in his parallax measurement, his theory of the Moon’s orbit, and other factors, this value was approximately accurate. Additionally, Ptolemy measured the apparent sizes of the Sun and the Moon and concluded that the apparent diameter of the Sun is equal to the apparent diameter of the Moon when it is furthest from the Earth. Based on records of lunar eclipses, he estimated the apparent diameter of the Sun as well as the apparent diameter of the shadow cone of the Earth that the Moon passes through during a lunar eclipse. With these data, the distance from the Sun to the Earth can be calculated trigonometrically and is found to be 1210 Earth radii. This results in a ratio of solar distance to lunar distance of approximately 19, which aligns with Aristarchus’ figure. While Ptolemy’s method is theoretically viable, it is highly sensitive to slight changes in the data, to the extent that a small alteration in the measurement can render the solar distance infinite.
In the medieval Islamic world, astronomers made some modifications to Ptolemy’s cosmological model, but they did not significantly change his estimate of the distance between the Earth and the Sun. For instance, al-Ferghani, in his introduction to Ptolemy’s astronomy, stated that the average distance to the Sun is 1170 Earth radii, while al-Battani, in his zij, used 1108 Earth radii as the average distance to the Sun. Other astronomers such as al-Biruni also utilized similar values. Later, in Europe, Copernicus and Tycho Brahe employed comparable figures (1142 and 1150 Earth radii), thus Ptolemy’s approximate distance from the Earth to the Sun persisted until the 16th century.
Johannes Kepler was the first to recognize that Ptolemy’s estimation had to be significantly underestimated (according to Kepler, at least three times) in his Rudolphin Tables (1627). Kepler’s planetary motion laws enabled astronomers to calculate the relative distances of the planets from the Sun and reignited interest in determining the absolute value for the Earth (which could then be applied to other planets). The invention of the telescope allowed for much more precise angle measurements than what was possible with the naked eye. Flemish astronomer Godefroy Wendelin repeated Aristarchus’ measurements in 1635 and discovered that Ptolemy’s value was at least eleven times too low.
A more precise approximation can be acquired by observing the passage of Venus. By measuring the passage at two distinct locations, the parallax of Venus and, based on the relative proximity of Earth and Venus to the Sun, the solar parallax α (which is not directly measurable due to the intensity of the Sun) can be accurately computed. Jeremiah Horrocks made an attempt to estimate based on his observations of the passage in 1639 (published in 1662), resulting in a solar parallax of 15″, similar to the Wendelin Figure. The solar parallax is linked to the Earth-Sun distance, measured in Earth radii, as the
The smaller the solar parallax, the larger the distance between the Sun and the Earth: the solar parallax is 15″ Equivalent to the distance between the Earth and the Sun of 13750 Earth radii.
Christiaan Huygens had a different perspective on the distance: when he compared the apparent sizes of Venus and Mars, he arrived at an estimation of approximately 24000 Earth radii, which is equivalent to a solar parallax of 8.6″. Although Huygens’ calculation is remarkably similar to modern estimates, it is often overlooked by astronomy historians due to the numerous unverified (and incorrect) assumptions he had to rely on for his method to work. The accuracy of his estimation appears to be more a result of luck than precise measurement, as his various errors offset each other.


For a long time, transits of Venus across the Sun’s surface have been the most effective way to determine the astronomical unit, despite the challenges involved (such as the “black drop effect”) and the infrequency of these observations.
In 1672, Jean Richer and Giovanni Domenico Cassini conducted a groundbreaking experiment to measure the parallax of Mars. They conducted their measurements from both Paris and Cayenne in French Guiana when Mars was at its closest point to Earth. The results of their experiment yielded a solar parallax of 9.5″, which can be translated into an Earth-Sun distance of approximately 22,000 Earth radii. This was a significant achievement, as it provided scientists with valuable information about the scale of our solar system.
Additionally, Richer and Cassini were fortunate to have access to accurate data regarding the Earth’s radius. Their colleague, Jean Picard, had previously measured the Earth’s radius in 1669 and determined it to be 3269,000 tuaz. This information played a crucial role in the calculations conducted by Richer and Cassini.
Furthermore, another colleague of theirs, Ole Rømer, made a groundbreaking discovery in 1676. He determined that light has a finite speed, and not an instantaneous one as previously believed. This discovery was so significant that it led to the concept of “light time per unit distance,” which refers to the time it takes for light to travel from the Sun to the Earth. This convention is still followed by astronomers today.
James Gregory invented the most effective method for observing the passage of Venus, which he published in his work (1663). This method was later applied by Edmond Halley during the transits of Venus in 1761 and 1769, and again in 1874 and 1882. Transits of Venus occur in pairs, but less than one pair occurs in a century. The observation of the transits in 1761 and 1769 was an unprecedented international scientific endeavor, involving the participation of astronomers such as James Cook and Charles Green, who observed from Tahiti. Despite the challenges posed by the Seven Years’ War, numerous astronomers were dispatched to observation sites around the globe, at great expense and personal risk; some even lost their lives during the mission. Jérôme Lalande compared the various observations and derived a solar parallax value of 8.6 inches.
| 1895 | aberration | 149.25 | 0.12 |
| 1941 | parallax | 149.674 | 0.016 |
| 1964 | radar | 149.5981 | 0.001 |
| 1976 | telemetry | 149.597870 | 0.000001 |
| 2009 | telemetry | 149.597870700 | 0.000000003 |
Another approach was employed to determine the constant of aberration. Simon Newcomb placed significant importance on this approach when he acquired his widely accepted solar parallax value of 8.80″ (close to the modern value of 8.794143″), although Newcomb also utilized data on Venus transits. Newcomb also collaborated with A. A. Michelson to measure the speed of light using equipment based on the ground; in combination with the aberration constant (which is linked to the time it takes for light to travel a unit distance), this provided the initial direct measurement of the Earth-Sun distance in kilometers. The Newcomb value for solar parallax (as well as for the aberration constant and the Gaussian gravitational constant) was included in the first international system of astronomical constants in 1896, which was employed to calculate ephemerides until 1964. The term “astronomical unit” was seemingly first utilized in 1903.
The identification of the asteroid 433 Eros, which orbits close to Earth, and its close approach to our planet in 1900-1901 provided a valuable opportunity for enhanced parallax measurement. In a separate international initiative, the parallax of 433 Eros was measured more accurately during the years 1930-1931.
The advent of direct radar measurements of the distances to Venus and Mars in the early 1960s marked a significant advancement. These measurements, along with more precise determinations of the speed of light, revealed a discrepancy between Newcomb’s values for solar parallax and constant aberration.
Progress
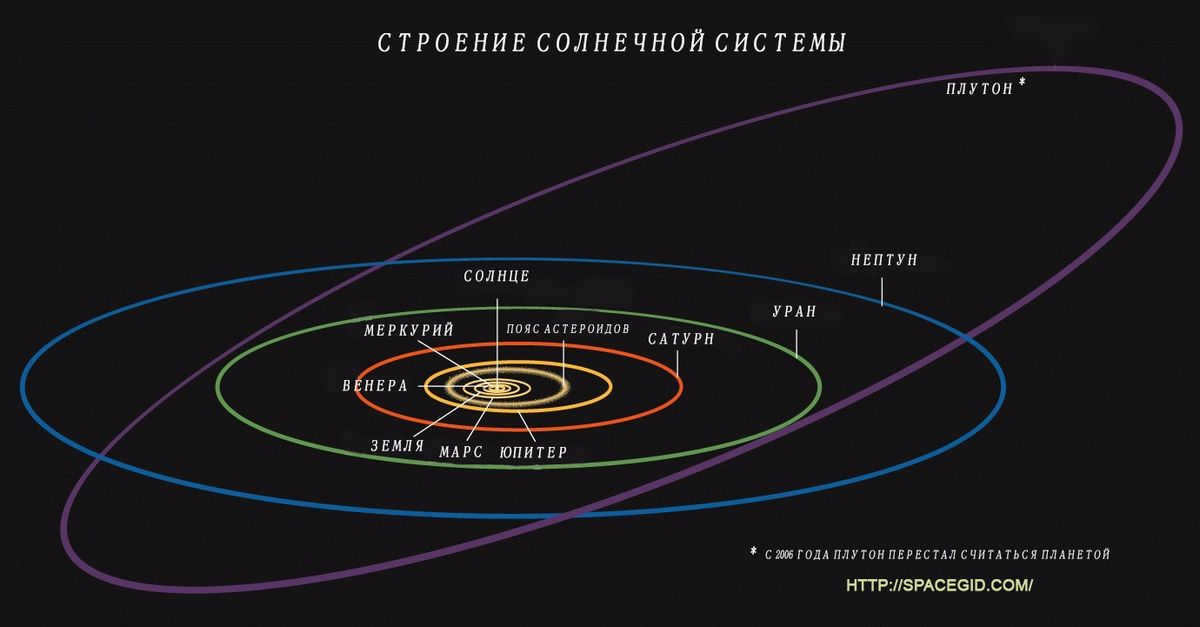
Development has taken place in the field of astronomy, where the astronomical unit has been utilized as a baseline for measuring stellar parallaxes. It is important to note that the distances in the image provided are not to scale.
Another way to express the value of the astronomical unit is through various other astronomical constants:
Here, G represents Newton’s gravitational constant, M ☉ stands for the mass of the Sun, k is the numerical value of the Gaussian gravitational constant, and D refers to the time period of one day. Over time, the Sun has been losing mass due to the emission of energy, causing the planets’ orbits to gradually move away from the Sun. As a result, there have been suggestions to discontinue the use of the astronomical unit as a unit of measurement.
Due to the fact that the speed of light has a precisely defined value in SI units, and the Gaussian gravitational constant k is fixed in the astronomical system of units, the measurement of light time per unit distance is exactly the same as measuring the product G M ☉ in SI units. As a result, it is now possible to create ephemerides entirely in SI units, which is becoming more and more common.
An examination of radiometric measurements in the inner solar system in 2004 revealed that the secular increase in the distance unit was significantly larger than what could be explained by solar radiation, with a deviation of + 15 ± 4 meters per century.
However, these measurements of the secular variations of the astronomical unit have not been confirmed by other authors and are highly inconsistent. Furthermore, the estimation of the astronomical unit by planetary ephemerides has not been done since 2010.
Illustrations
Here is a compilation of various distances presented in astronomical units. The compilation comprises a variety of instances with distances that are typically not expressed in astronomical units due to their brevity or enormity. Distances tend to fluctuate over time. The illustrations are arranged in ascending order according to their distance.
| Light-second | 0.002 | – | the distance traveled by light in one second | – |
| Distance to the Moon | 0.0026 | – | Average distance from Earth (which took the Apollo mission about 3 days) | – |
| Sun’s radius | 0.005 | – | The radius of the Sun (695500 kilometers, 432450 miles, one hundred times the radius of Earth or ten times the average radius of Jupiter) | – |
| Light-minute | 0.12 | – | the distance traveled by light in one minute | – |
| Mercury | 0.39 | – | average distance from the Sun | – |
| Venus | 0.72 | – | average distance from the Sun | – |
| Earth | 1.00 | – | average distance of the Earth’s orbit from the Sun (sunlight takes 8 minutes and 19 seconds to reach the Earth) | – |
| Mars | 1.52 | – | average distance from the Sun | – |
| Light-hour | 7.2 | – | The distance that light travels in one hour | – |
| Kuiper Belt | 30 | – | Inner edge begins at about 30 a.u. | |
| Eris | 67.8 | – | average distance from the Sun | – |
| Voyager 2 | 122 | – | distance from the Sun in 2019 | |
| Voyager 1 | 149 | – | distance from the Sun in 2020 | |
| Light-day | 173 | – | The distance that light travels in one day | – |
| Light-year | 63241 | – | The distance that light travels in one Julian year (365.25 days). | – |
| Oort cloud | 75000 | ± 25000 | distance from the outer edge of the Oort cloud from the Sun (estimated, corresponds to 1.2 light-years) | – |
| Parsec | 206265 | – | one parsec. Parsec is defined in astronomical units, used to measure distances outside the solar system, and is about 3.26 light-years: 1 pc = 1 au / tan (1 “) | |
| Proxima Centauri | 268000 | ± 126 | The distance to the nearest star to the solar system | – |
| Galactic center | 1700000000 | – | The distance from the Sun to the center of the Milky Way | – |
Related Articles
Recommended Resources
Additional Sources
Useful Links
Estimated Reading Time: 7 minutes
Share this article

- Natal astrology
- Relationship Astrology
- Self-development and psychology
- Predictive Astrology
- Horoscopes and forecasts
- Talismans
- Soul Formula
- Numerology
- Astrological Tarot
- World Astrology
- For beginners
- For professionals
- Development of an Astrologer
Read 7 min
What is the origin of the astronomical unit? The concept of the astronomical unit was developed in response to humanity’s curiosity about the distance between the Sun and Earth. This universal parameter was introduced to measure the distance from Earth to the Sun, and it only gained widespread recognition about a decade ago.
What is the significance of this term? The astronomical unit serves as a measurement tool to determine the distances between various celestial objects within the solar system, including components of binary star systems and exoplanetary systems. Thanks to advancements in technology, we now have the ability to visually comprehend the vastness of space that encompasses our planet.
The Origin of the Astronomical Unit
The concept of the astronomical unit was first introduced by scientists in 2012.
In Russian astronomical sources, this term is commonly referred to as “a.e.”. In international sources, it is denoted as “a.u.”, “AU”, or “ua” according to ISO standards.
The astronomical unit serves as the fundamental measurement for studying the solar system and should be considered as the starting point for space exploration.
Defined as the average distance between the Earth and the Sun, or the major semi-axis of an elliptical orbit, the astronomical unit takes into account the elliptical shape of our planet.

The concept of the astronomical unit provides a clearer visualization of the distance in light years to a specific object. For instance, Alpha Centauri is approximately 4.36 light years away, a measurement that is incredibly vast and difficult to comprehend. However, when expressed in astronomical units, this distance would be approximately 270, which is much more comprehensible.
What is the equivalent distance in kilometers for one astronomical unit?
As per the decision made during the tenth IAU General Assembly in 1976, the astronomical unit is defined as the radius of the circular orbit of a specified celestial body in the isotopic coordinate system.
Based on this information, it was determined that the angular velocity of the circular orbit, assuming the exclusion of all other celestial bodies in the Solar System except for the Sun, is equal to 0.017,202,098,95 radians per ephemeris day. In the IERS 2003 system, the astronomical unit in kilometers is 149,597,870,691.
The Origin of the Astronomical Unit
The establishment of the astronomical unit became necessary due to the discovery that the Earth orbits around the Sun and the ability to calculate the distances between the Earth, the Sun, and other planets within our solar system. From the 17th to the 20th century, advancements in space exploration allowed scientists to gather the most precise measurements. The horizontal parallax methods utilized during that time are still employed in modern astronomy and geometry.
The average distance from the Earth to the Sun, known as the astronomical unit, is determined by astronomers through the use of radar signals. In the International SI system, this distance is established at 149,597,870.7 kilometers.


It is challenging to determine the exact measurement of an astronomical unit since it is not a constant. Researchers have observed that the length of one astronomical unit increases by a meter every 7 years. Consequently, the Earth moves 15 meters farther away from the Sun every 100 years. The prevailing theory explaining this phenomenon suggests that the Sun loses mass due to the solar wind.
Widely recognized astronomical unit as a measuring unit
Giovanni Cassini, a scientist, was the pioneer in measuring the precise distance between the Earth and the Sun, which is commonly accepted as 140,000,000 km. Over time, advancements in technology have led to increasingly accurate calculations of this value.

Using the astronomical unit as a unit of measurement has its own drawbacks. The distance from the Sun to the Earth actually increases by 15 meters every 100 years, causing the astronomical unit to change accordingly. While this change may be insignificant in the grand scheme of the Universe, it is quite noticeable and significant for precise scientific calculations.
Utilization of the astronomical unit
Given its inclusion in the International System of SI, the astronomical unit finds application in astronomy for gauging the distance to any celestial object. However, it lacks practicality beyond the confines of our solar system due to the excessively large values involved. Instead, beyond our planetary system, the customary units of measurement are the light year or parsec.
It is important to distinguish between astrological terms and astronomical terms. A thorough examination of any nativity will provide more information regarding the natal chart.
Furthermore, it is worth noting that the astronomical unit is not utilized with prefixes such as nano-, mini-, mega-, etc. Additionally, there is no specific astronomical unit assigned to the Sun, as it serves as the primary object of calculations.
When considering distances in star systems with exoplanets, it is convenient to use astronomical units. This unit of measurement is also useful for determining distances between multiple stars.
One astronomical unit is equivalent to \(1.58125 × 10^\) light-years.
Examples of distances in astronomical units
- The average distance from the Sun to Mercury is 0.387 astronomical units or 58 million kilometers. The distance between Mercury and Earth varies between 82 and 217 million kilometers. Mercury orbits the Sun in an elongated elliptical path with a plane inclination of 7°.
- Venus is located at a distance of 0.72 astronomical units (108.2 million km) from the Sun. The planet has an average density of 5.24 g/cm 3 and a mass of (4.9 × 10) 24 , which is 0.82 times the mass of Earth. The radius of Venus is 6,051 km.
- The distance between the Earth and the Sun is equal to one astronomical unit. The planet has a radius of 6,371.160 kilometers and a mass of (6 × 10) to the power of 24 kilograms.

- The distance between the Sun and Mars is 1.5 astronomical units (a. e.) and the distance between Mars and Earth is 55.75 million kilometers.
- Jupiter is located 5.2 astronomical units away from the Sun. It has an equatorial radius of 71.4 thousand kilometers and a polar radius of 67 thousand kilometers. The mass of Jupiter is (1.9 × 10) 27 kilograms. This giant planet orbits around the Sun with a speed of 13.06 kilometers per second.
- Saturn is situated at a distance of 9.54 astronomical units from the Sun, which is approximately 1.427 billion kilometers. It has an equatorial radius of 60.3 thousand kilometers and a polar radius of 54 thousand kilometers. The mass of Saturn is (5.68 × 10) 26 kilograms, equivalent to 95.1 times the mass of Earth. It takes Saturn 29 Earth years to complete one orbit around the Sun, and it rotates around its axis every 10 hours and 39 minutes.


- The Sun-Uranus distance measures 19.18 astronomical units or 2,871 million kilometers. Uranus has a radius of 25,560 km and a mass of 14.54 times that of Earth.
- Neptune was first observed by Johann Galle on September 23, 1846. It is located 30.1 astronomical units away from the Sun. The radius of Neptune is 25,000 km, and its mass is (1.02 × 10) 26 kg.
- Pluto continues to be a subject of debate in the classification of planets. Due to its small size, many scientists initially believed its mass was comparable to that of Earth. However, recent findings indicate that its mass measures (1.2 × 10) 22 kg, which is 500 times less than Earth’s mass. Pluto is situated at a distance of 39.44 astronomical units from the Sun.
Equally significant units in the field of astronomy include
Light-year
A light-year is a unit of measurement used to represent the distance that light travels in one year.
A light year is a unit of measurement used to represent the distance that light travels in one year. The International Astronomical Union (IAU) provides a more precise definition: a light year is the distance that light travels in a vacuum (without being affected by gravity) in one Julian year (365.25 Earth days). This wording is commonly used in scientific literature as it simplifies the explanation of vast distances. However, even larger distances are often measured in parsecs.
Before 1984, the measurement known as a light-year was determined based on the distance that light traveled in a tropical year, specifically referencing the epoch 1900.0. However, the current definition of a light-year deviates from the previous one by approximately 0.002%. It’s worth noting that this unit is not employed for high-precision measurements, meaning that there are no significant disparities between the two.


One light year is equivalent to:
- 9,460,730,472,580,800 meters or approximately 9.46 pentameters (Pm);
- 63,241,077 astronomical units (a. e.);
- 0.306,601 parsecs (pk).
This unit of measurement is extremely useful in astronomy as it allows for the accurate calculation of distances. The speed of light is the fastest known speed of information transmission, and light years provide a clear representation of both the distance between celestial objects and the speed at which they can influence each other.
Allow me to provide an illustration. The celestial body known as Betelgeuse, situated in the Orion constellation, is anticipated to undergo a cataclysmic explosion within the coming centuries. Its location is approximately 495-649 light years away from our planet. Should this explosion occur at this very moment, we would only witness its magnificent display in the span of 500-600 years.
To put it differently, if we were to observe any luminous burst in the present, it would signify that the celestial entity had actually detonated during the reign of Ivan the Terrible.
Hence, a light year encompasses both spatial and temporal dimensions.

Parsec
Another fascinating, enigmatic, and practical unit of measurement in the field of astronomy is the parsec. This length measurement is more than triple the length of a light-year: 1 parsec is equivalent to 3.2616 light-years.
Parsec is derived from the combination of two words: parallax and second.
This unit of measurement is defined by the distance to an object whose annual parallax is equal to one arcsecond. To fully grasp the definition, let’s delve deeper into what this length measurement entails.
As we are aware, the position of a particular object can shift in relation to the distant background when observed from different vantage points. This displacement is referred to as parallax.
It can be noticed that the object’s relative position changes slower as it gets farther from the observer, suggesting a decrease in parallax.
If we have knowledge of the distance between the observation points, the offset angle, and trigonometry, we can easily calculate the distance to the observed object.
As the Earth orbits the Sun throughout the year, the observation point also shifts, resulting in an annual parallax of the stars. The measurement of one astronomical unit is equivalent to the angle at which the major semi-axis of Earth’s orbit is observed from the star. And as mentioned before, the major semi-axis is equal to 1 astronomical unit.
What is the astronomical unit parsec? Assuming we are positioned one parsec away from the Sun, the Earth’s angular distance to it would be one second. In terms of conversion, this is equivalent to 1/3,600, implying that 1 parsec is incredibly distant.
Astronomical unit (a.u.) refers to a historically established unit utilized in astronomy to measure distances, specifically equal to 149´ 597´ 870,610 km.
The astronomical unit is approximately equivalent to the average distance between the centers of mass of the Earth and the Sun (i.e., the average radius of the Earth’s orbit; the distance from the Earth to the Sun).
Exactly the astronomical unit is equivalent to the radius of a circular orbit that would have the same orbital period as the Earth, assuming that all other bodies in the solar system except the Sun are neglected. The major semi-major axis of the Earth’s orbit is equal to 1.000000000036406 a. e.
Its primary use is for measuring distances between objects within the solar system, beyond solar systems, and between components of binary stars.
Background
Ever since the heliocentric system was introduced, specifically Keplerian celestial mechanics, scientists have been able to determine the relative distances within the solar system with a high degree of accuracy. However, when it comes to measuring the magnitude of these distances, particularly in comparison to Earth’s scale, there have been challenges. The Sun is situated too far away for parallax measurements to be reliable, and although the distance to the Moon is known, it was not possible to estimate the ratio of distances between the Sun and the Moon based on the limited data available in the 17th century. The observations of the Moon did not provide the necessary level of precision, and the ratio of the Earth’s and the Sun’s masses was also unknown at that time.
In 1672, Giovanni Cassini and Jean Richet conducted measurements to determine the parallax of Mars. This enabled them to accurately calculate the astronomical unit, which is now known to be approximately 146 million kilometers.
Further refinements in determining the astronomical unit were made through observations of Venus passing in front of the sun. In 1901, the approach of the asteroid Eros to Earth provided an opportunity for even more precise measurements of its parallax, resulting in improved estimates of the astronomical unit.
By utilizing radar to locate planets, scientists were able to determine the value of the Astronomical Unit. In 1961, the position of Venus helped establish that the Astronomical Unit is approximately 149´599´300 km. The margin of error for this measurement was within ±2000 km. Further radar measurements of Venus in 1962 reduced the uncertainty and provided a more precise value for the Astronomical Unit: 149´598´100±750 km. Prior to the 1961 discovery, the accuracy of the Astronomical Unit was known to be within 0.1%.
When comparing the sizes of planets in our Solar System, scientists commonly use the concept of the astronomical unit. This unit represents the average distance from the Earth to the Sun and is approximately equal to 149.6 million kilometers.
Origin of the astronomical unit
Through the tireless work of scientists, particularly those studying Keplerian celestial mechanics, we have gained knowledge of the planets’ orbits around the Sun. Additionally, we have come to understand that the stars, which appear as twinkling lights in the night sky, are located at distances that are beyond our comprehension. As our understanding of the universe continues to expand, its scale has become so vast that its true size remains a mystery. The field of astronomy, constantly evolving, has emerged as one of the most cutting-edge scientific disciplines.
The idea behind the astronomical unit
300 years ago, scientists reached the conclusion that the Earth does not hold the central position in the universe. Through countless observations and meticulous verifications, astronomers began to unveil the actual magnitude of our cosmic abode – the solar system. Consequently, they discovered that its dimensions were so vast that the Earth’s conventional units of measurement became clearly inadequate. The distances to the nearest planets were denoted by numbers entailing numerous zeros, leaving virtually everyone, except for the scientists themselves, uncertain about what to name these figures. Hence, astronomers introduced a distinctive unit of measurement, known as the astronomical unit, to gauge the distances between the planets within the Solar System and from the Sun to the planets. This unit corresponds to the average distance from the Earth to the Sun, which is roughly 150 million kilometers (to be more precise, 149,597,870,691 km). In standard astronomical calculations, a rounded figure of 149,600,000 kilometers is commonly employed.
It’s not such a small distance to consider when you take into account that the Earth’s equator is the longest path that can be laid out on our planet – approximately 40,000 kilometers in length. Furthermore, the Moon, which is the Earth’s satellite and closest celestial object, orbits the Earth at a distance of over 380,000 kilometers.
Why is the distance from the Earth to the Sun used as a standard measure? Well, this is because the Sun serves as the central body of the entire solar system, while the Earth acts as the observer’s location and orbits the Sun in an almost circular (elliptical) trajectory. Hence, the radius of this orbit was established as the unit of measurement.
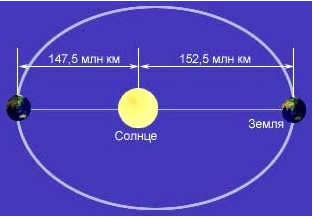
What is shown in the image is explained in the following diagram:
Therefore, the astronomical unit – is a unit of measurement used to determine distances to celestial objects. It is defined as the length of the major semi-axis of the Earth’s elliptical orbit and, based on the properties of the ellipse, represents the average distance between the Earth and the Sun. This definition is widely accepted by both amateur astronomers and professionals in the field.
Examples of astronomical unit distances
Hence, the astronomical unit is nearly 400 times larger than the distance between the Earth and the Moon. It is also highly convenient for measuring the distances between planets. For instance, the average distance from Earth to Mars is 0.3 astronomical units. Mars is located farther from the Sun than Earth, so it can be easily calculated that the distance from the Sun to Mars is 1.52 astronomical units. Even the distant Jupiter is only a little over 5 astronomical units away from the Sun. The distance from Earth to Uranus is approximately 20 astronomical units. The orbital radius of Neptune, one of the most remote objects in the solar system, is 30 astronomical units. Sirius is a binary star system, with Sirius A and Sirius B orbiting each other at a distance of 20 astronomical units.
It takes approximately 500 seconds (or 8 minutes and 20 seconds) for light to travel from Earth to the Sun. What is fascinating is that this distance appears to be gradually getting longer, increasing by about 15 meters per 100 years. One possible explanation for this phenomenon is the loss of solar mass caused by the solar wind. However, the rate at which the astronomical unit is expanding is so minuscule that it can be safely ignored, as it exceeds the calculated values by a factor of ten.
Scientists have been using the astronomical unit for several generations with great success. This unit of measurement was particularly useful for distances within the solar system, as they were relatively small and easy to work with. Additionally, the astronomical unit was universally understood, even by schoolchildren. For example, anyone could see that Venus is closer to the Sun than the Earth by looking at the distances in astronomical units. Furthermore, it was evident that Jupiter is approximately halfway between the Sun and Saturn.
However, the joy was short-lived. Once scientists were able to determine the distances to the nearest stars, it became apparent that the astronomical unit is too small in the stellar world. Therefore, it is unsuitable for measuring such vast distances.
Astronomers employ special units of measurement in their calculations, which may not always be easily comprehensible to the general public. This is understandable, as if cosmic distances were measured in kilometers, the sheer number of zeros would be overwhelming. Hence, to gauge cosmic distances, it is customary to utilize significantly larger magnitudes: astronomical unit, light year, and parsec.
Commonly, distances within our home solar system are often indicated. If we express it in kilometers (384,000 km), the nearest distance to Pluto is approximately 4,250 million km, which may be quite hard to comprehend. For such vast distances, it is more appropriate to use an astronomical unit (a.u.), which represents the average distance from the Earth’s surface to the Sun. In simpler terms, 1 a.u. corresponds to the length of the long semi-major axis of our Earth’s orbit (150 million kilometers). Thus, if we state that the shortest distance to Pluto is 28 a.u., and the longest journey could be 50 a.u., it becomes much easier to visualize.
The second largest unit of measurement is known as a light year. Despite the inclusion of the word “year,” it does not refer to a period of time. Instead, a light year is equivalent to 63,240 astronomical units (a.u.). In other words, it represents the distance that a beam of light travels within the span of one year. Remarkably, astronomers have determined that it takes over 10 billion years for light to travel from the farthest corners of the universe to reach us. To grasp the enormity of this distance, let’s express it in kilometers: 95,000,000,000,000,000,000,000,000,000,000,000. This equates to an astonishing 95 billion trillion familiar kilometers.

The awareness that light does not propagate instantaneously, but rather at a specific velocity, was first hypothesized by scientists in 1676. This revelation came about when Ole Remer, a Danish astronomer, observed that the eclipses of one of Jupiter’s satellites were starting to occur later than expected. This phenomenon coincided with the Earth’s movement in its orbit to the opposite side of the Sun, the exact opposite direction of Jupiter. After some time, the Earth started to move back, and the eclipses gradually aligned with their original schedule once again.
Therefore, a discrepancy of approximately 17 minutes in time was noted. Based on this finding, it can be inferred that it takes 17 minutes for light to traverse the entire diameter of the Earth’s orbit. Given that the diameter of the orbit is roughly 186 million miles (now equivalent to 939,120,000 kilometers), it can be deduced that light travels at a rate of approximately 186 thousand miles per second.


In our modern era, Professor Albert Michelson endeavored to determine the precise measurement of a light year using an alternate methodology. Through his efforts, the final calculation was achieved: 186,284 miles per second (approximately 300 km/s). By multiplying this value by the number of seconds in a year, we find that a light year spans a staggering distance of 5,880,000,000,000,000,000 miles, equivalent to 9,460,730,472,580.8 kilometers.
For practical purposes, astronomers often utilize the parsec as a unit of distance. This unit is defined as the displacement of a star against the backdrop of other celestial bodies, when the observer is shifted by 1 arcsecond and positioned at a distance of 1 radius.
The JCMT, situated on Mount Mauna Kea in Hawaii, is home to the James Clark Maxwell Telescope. At that specific moment, the comet was positioned 1.07 AU (AU being an astronomical unit equivalent to the average radius of Earth’s orbit) away from the Sun. Based on the calculations of scientists, the comet emits roughly 1.5 x 10^25 molecules of hydrocyanic acid. In their calculations, it is estimated that Comet Elenin will come within a minimum distance of 34.9 million kilometers (0.23 AU) from Earth on October 16, 2011.
Scientists have identified a compact gas cloud located approximately 23,000 light years away from our planet. This cloud, which spans a diameter of less than 50,000 astronomical units (where one astronomical unit represents the average distance between the Earth and the Sun), has a massive weight equivalent to 120 times that of our Sun. Interestingly, the temperature inside the cloud measures around 18 Kelvin. While this cluster is not currently undergoing any thermonuclear reactions, it still presents a fascinating subject for scientific study.
The existence of dark matter, as well as the satisfaction of several intricate conditions, is apparent. Some of these conditions contradict current understandings regarding the nature of dark matter. The gradual elongation of the astronomical unit (a.u.) serves as one of the units utilized for measuring cosmic distances. The a.u. represents the average distance between the Earth and the Sun, roughly equivalent to the major semi-axis of the Earth’s orbit.
The Earth completes one rotation every 0.000017 seconds, causing it to move approximately four centimeters away from our planet. An important astronomical parameter known as the astronomical unit represents the average distance between the Earth and the Sun. According to recent data, this astronomical unit is equivalent to 149597870.696 kilometers. In 2004, Russian astronomers Grigory Krasinski and Viktor Brumberg determined this parameter.
HD209458b, a planet located in close proximity to a Sun-like yellow dwarf, is about 0.05 kilometers away from the star. This distance is measured in astronomical units (equivalent to one astronomical unit). As a result, the surface temperature on the side of the planet that faces the sun reaches temperatures in the thousands of degrees Celsius. Due to the planet’s constant orientation towards the star, it is always exposed to its intense heat.
There is a piece of evidence that suggests that massive stars are formed in the same manner as their smaller counterparts. “The images reveal a stretched object measuring approximately 13 by 19 astronomical units (one astronomical unit is equal to the distance between the Earth and the Sun, approximately 149.6 million kilometers), which indicates the presence of a disk that can be observed at a 45-degree angle of inclination,” stated the authors of the publication.
The five “credible” planets vary in mass from 13 to 25 times that of Earth (for comparison, Neptune’s mass is 17.2 times that of Earth). They are located at distances ranging from 0.06 to 1.4 astronomical units (one astronomical unit is the distance from Earth to the Sun) from HD 10180. Depending on their distance from the star, these planets complete one orbit around it in a period of 6 to 600 days. As for the two “questionable” planets, they were observed using the LORRI camera on Neptune and its moon Triton. The photos were taken in June 2010, but were only recently published. The spacecraft was approximately 23.2 astronomical units away from Neptune (one astronomical unit is equal to the average distance from Earth to the Sun, which is 149,597,870 kilometers). In this case, the spacecraft’s angle relative to Neptune and the Sun was taken into account.
The current Earth system for measuring cosmic distances is not well-suited for mathematical representation of even our own solar system, much less our galaxy and the Universe as a whole. In order to accurately describe distances in space, we would need to work with numbers such as million, billion, and trillion (equivalent to 1,000,000, 1,000,000,000, and 1,000,000,000,000, respectively) and beyond. This can be quite cumbersome and inconvenient. As a result, scientists have devised a system of astronomical quantities. Let’s take a closer look at them.
Definition of Light Year
A light-year (abbreviated as “ly”) is a measurement of distance that represents the amount of space traveled by light in the span of one Earth year. It is an immense unit of length that is equivalent to approximately 9,460,730,472,580 kilometers, or roughly 63,200 astronomical units, or 0.31 parsecs.

What is an Astronomical Unit?
Definition of Astronomical Unit The astronomical unit (AU), also known as a.u., is the conventional unit of measurement used in astronomy to quantify distances. It is primarily used to measure the distances between celestial objects within the solar system, exoplanetary systems, and the components of binary stars.
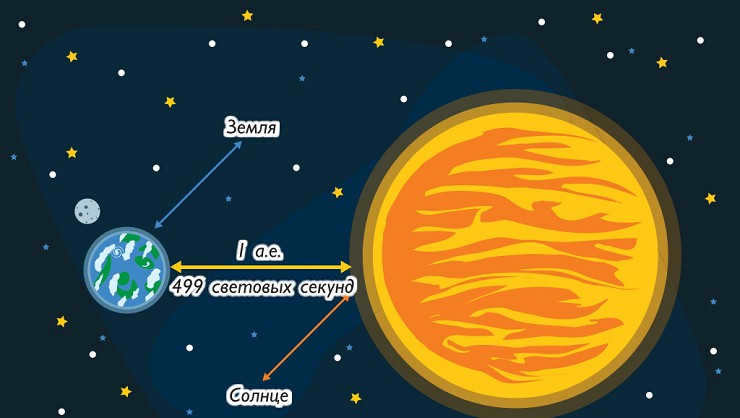
The distance that light travels in approximately 500 seconds (8 minutes 20 seconds) is equivalent to 1 astronomical unit. In other terms, 1 light-year is approximately equal to 63,241 astronomical units, and 1 parsec is approximately equal to 206,265 astronomical units. For reference, the distance to our nearest star, Proxima, in the Alpha Centauri system, is approximately 270,000 astronomical units.
An astronomical unit is defined as the average distance between the centers of the Earth and the Sun, which is equivalent to the major semi-axis of the Earth’s orbit.
Expressed in kilometers, 1 astronomical unit is equal to 149,597,870 ± 2 km, or approximately 499 light seconds.
Parallax
The parsec (pc) is the largest unit of cosmic distance. It is equal to 3.0856776-10 16 meters, 206,265 astronomical units, or 3.26 light years.
Motion in the Universe
The center of our galaxy is in motion, and so is the solar system within it. The solar system moves at a speed of approximately 40 astronomical units per year, or 200 kilometers per second. Our galaxy, the Milky Way, is not stationary either. It is actually moving towards the Andromeda galaxy at a speed of 20 astronomical units, or 100-150 kilometers per second. Additionally, the Milky Way, along with other galaxies in our local group, is also moving towards the Virgo cluster, which is the closest group of galaxies to us. This motion is occurring at a speed of 80 astronomical units, or 400 kilometers per second.
How many kilometers are there in 1.36 astronomical units? And what is the value of one astronomical unit?
Our task is to determine the number of kilometers equivalent to one astronomical unit.
Overview
An astronomical unit is a distance equivalent to the average path that sunlight travels to reach Earth. Another way to express this is as the major semi-axis of Earth’s elliptical orbit around the Sun. Both of these definitions are correct. There are several methods available for calculating the number of kilometers in an astronomical unit. The Earth and the Sun can be thought of as points A and B in a straight line, as in geometry. There are both classical and modern methods for measuring this distance. The most precise value for one astronomical unit is 149597870 + 2 kilometers. In standard calculations, a value of 149,600,000 kilometers is commonly used. This value was determined relatively recently. Now, let’s examine the classical methods of measurement, followed by an exploration of the new techniques for obtaining this information.
Traditional Approaches to Measurement

The most recent techniques for measurement

Final Thoughts

Now that we have knowledge that the distance from the Earth to the Sun is considered one astronomical unit, it is important to note that humans face challenges when it comes to covering such relatively short distances (although this does not hinder our mechanical automated companions). It is worth mentioning that there are other units of measurement used in this context. Apart from the astronomical unit, the light-year and the parsec are also widely utilized. The concept of a light-year is frequently employed, so we won’t go into too much detail about it. The parsec, on the other hand, represents a slightly larger measurement than 206 thousand astronomical units. As an alternative, it can also be expressed as 3.26 light-years. These units are often used in increments. For instance, the center of our galaxy is approximately 8 kiloparsecs away. However, us humans still need to be able to explore distances as short as one astronomical unit in space.
When it comes to estimating the relative sizes of the planets in our solar system, we commonly use a term known as the astronomical unit. This unit represents the average distance from the Earth to the Sun and is used as a reference point for measuring distances in our solar system.
The Origin of the Astronomical Unit
Over the course of many centuries, scientists, including the renowned astronomer Kepler, have made significant contributions to our understanding of celestial mechanics. Through their work, we have come to understand that each planet in our solar system orbits around the Sun in its own unique path. Furthermore, we have also come to realize that the stars we observe in the night sky are situated at such vast distances from us that it is nearly impossible to comprehend.
As our knowledge of the universe continues to expand through ongoing scientific discoveries, it becomes increasingly clear that the universe is truly immense in size. Astronomy, as a rapidly advancing field, has emerged as one of the most cutting-edge disciplines of science.
The idea behind the astronomical unit
Approximately 300 years ago, scientists reached the conclusion that the Earth does not occupy, and never has occupied, a central position in the Universe. Through extensive observations and countless repeated experiments, astronomers began to unveil the true scale of our cosmic abode – the Solar System. To their astonishment, it became evident that its dimensions were so immense that conventional units of measurement were inadequate. The distances to the neighboring planets were expressed in numbers with an abundance of zeros, leaving everyone, except the scientists themselves, at a loss for how to articulate these figures. Consequently, astronomers introduced a specialized unit for quantifying the distances between the Sun and the planets, as well as the interplanetary distances within the Solar System. This unit is known as the astronomical unit, representing the average span from the Earth to the Sun. It is approximately 150 million kilometers (to be more precise, 149,597,870,691 km). For practical purposes in ordinary astronomical calculations, a rounded value of 149,600,000 km is commonly employed.
Not so small when you take into account that the Earth’s equator is the longest path that can be traveled on our planet – approximately 40,000 kilometers in length. Moreover, the Moon, which is the Earth’s satellite and closest celestial object, revolves around the Earth at a distance exceeding 380,000 kilometers.
Why is the distance from the Earth to the Sun considered a standard? Well, the Sun serves as the central body of our solar system, while the Earth serves as the observer’s location and orbits the Sun in an almost circular (elliptical) path. That’s why the radius of this orbit has been adopted as the unit of measurement.
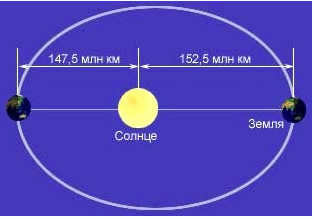
The illustration above depicts the schematic drawing that demonstrates the concept.
Hence, the astronomical unit is a unit of measurement used to quantify the distances between celestial objects. It is defined as the major semi-axis of the Earth’s elliptical orbit and, based on the properties of the ellipse, represents the average distance between the Earth and the Sun. This definition is widely accepted by both amateur and professional astronomers.
Illustrative instances of astronomical distances
Consequently, the astronomical unit surpasses the distance between the Earth and the Moon by almost 400 times. Additionally, it is highly suitable for gauging interplanetary distances. To illustrate, the average distance from Earth to Mars is 0.3 astronomical units. As Mars is situated further away from the Sun compared to Earth, it is simple to deduce that the distance from the Sun to Mars amounts to 1.52 astronomical units. Even the remote Jupiter is slightly over 5 astronomical units away from the Sun. The distance from Earth to Uranus measures around 20 astronomical units. The orbital radius of Neptune, which is one of the most remote celestial objects within the solar system, is 30 astronomical units. Sirius constitutes a binary star system, with Sirius A and Sirius B orbiting each other at a distance of 20 astronomical units.
It takes approximately 500 seconds (or 8 minutes and 20 seconds) for light to travel from the Earth to the Sun. Interestingly, this distance has been slowly increasing at a rate of about 15 meters per 100 years. This phenomenon may be attributed to the solar wind causing a loss of solar mass. However, the effect of this increase in the astronomical unit is so gradual that it can be disregarded, as it is significantly smaller than the calculated values.
Throughout multiple generations, scientists have successfully utilized the astronomical unit. It was particularly useful for measuring distances within the solar system, as they were relatively small and easy to work with. Moreover, this unit of measurement was easily understood by people of all backgrounds. Even a schoolchild could grasp the concept that Venus is closer to the Sun than the Earth, and that Jupiter lies halfway between the Sun and Saturn.
However, their joy was premature as it was soon realized that the astronomical unit was too small when it came to measuring the distance to the nearest stars in the vast stellar world.
The astronomical unit serves as a measurement that allows us to visualize the distance to various objects within the solar system.
The astronomical unit provides a value that enables us to visualize the distance between our planet and a celestial object.
The explanation behind this is quite straightforward. In reality, the astronomical unit represents the average radius length of the Earth’s orbit or the distance between the Earth and the Sun. It can be challenging to comprehend the distance between the Earth and a star system when expressed as 1.3 astronomical units. However, if we were to say that the distance is equivalent to 270,000 kilometers, it becomes much more relatable. This comparison allows us to mentally magnify the distance between the Sun and the Earth 270,000 times, enabling us to vividly imagine and grasp the immense length of this distance.
Despite its clarity, the astronomical unit is rarely used as a measurement value in professional astronomy. The reason is that it is only convenient for calculating distances to nearby objects in the Universe, such as the planets in our Solar System. If we attempt to use astronomical units to determine the distances to extremely distant objects, the numbers would be so large that they would be impractical for mathematical calculations. Instead, astronomers use another unit of measurement, called the parsec, and its derived units, to determine distances to faraway cosmic objects in the observable Universe.
Discovery Timeline
The discovery of the astronomical unit was made possible by the realization that the Earth orbits the Sun and the application of Keplerian celestial mechanics. These advancements allowed astronomers to accurately measure the distance between Earth and various planets in our solar system, including the Sun. Over the centuries, further research and advancements in technology have led to more precise calculations. One important method used in determining distances is horizontal parallax, which is still widely used in astronomy and geometry today.
In 1962, astronomers used radar signals to determine the precise distance from Earth to the Sun. The average measurement, which is 149597870.7 km, became the standard known as the astronomical unit in the International System of Units SI.
Recent studies have revealed that the astronomical unit is not a constant value. Each year, it slightly increases in length. Scientists have observed that every 7 years, the astronomical unit expands by one meter. This means that over the course of 100 years, the Earth moves 15 meters farther from the Sun. Multiple theories have been proposed to explain this phenomenon, with the most popular one suggesting that the Sun is losing mass due to the solar wind.
Astronomical unit
The Astronomical unit (AU) is a unit of length used to measure distances to celestial objects. It is defined as the average distance between the Earth and the Sun, which is equal to the major semi-axis of the Earth’s elliptical orbit around the Sun.
To determine the astronomical unit (a.e.), classical methods required measuring the radius of the Earth (RZ). However, modern methods no longer rely on this intermediate step. Instead, a set of geodetic methods is used to calculate RZ. These methods involve measuring the length of a base segment between triangulation points on the Earth’s surface with high accuracy. In the past, this measurement was done using rulers and tapes, but now it is done using optical (laser) location methods. The measuring instruments are compared to a meter, which is defined as the distance traveled by a light beam in vacuum during 1/299792458 sec.
Using trigonometric relations, the distance to a chosen point M can be determined based on the measurements of the base side and the angles between the base and the directions to the point (parallax method or serif). Numerous measurements of meridian arcs using this method have revealed that the Earth is an ellipsoid flattened at the poles, with a non-perfectly circular cross-section along the equator. The equatorial radius of the Earth (RZ) is 6378.160 km.
The simplest method for determining the astronomical unit is similar to the serif method but requires highly accurate measurements of small angles due to the relatively small base value. The distance A from the Earth to the Sun, which is equal to 1 a.e., can be found using the triangle ZNS. The largest angle, at which the base RZ is visible, is known, but from the Earth, only another angle SNP (equatorial horizontal parallax of the Sun) can be measured. SNP is determined by the largest perspective displacement of the Sun when the observation point is moved from the center of the Earth to a point H where it is observed on the horizon. The maximum displacement is then calculated using formulas.
Observations of the Sun are difficult and inaccurate since the parallax of the Sun is only a few meters. Therefore, the dark disk of the planet is projected onto a screen (Fig. 3) to facilitate observations. Venus, with its atmosphere, hinders accurate measurements. However, during the planet’s passage across the Sun’s disk, the perspective displacement of Venus can be measured from different places on Earth, representing the difference between the parallaxes of Venus and the Sun. The presence of Venus’ atmosphere was discovered by M. V. Lomonosov during one of these passages in 1761. Observations of the asteroid Eros provide greater accuracy, as its parallax can reach almost an angular minute when it passes close to the Earth. By measuring this parallax, the distance from Eros to the Earth at the time of observation can be determined.
To calculate the value of a.e. A from the distance between Eros and the Earth (EZ), the sides of the triangle ZES (Fig. 4) must be determined. By analyzing existing and new observations of Eros and calculating the improved elements of its orbit, including the period of revolution and the mean distance, using Kepler’s 3rd law, the value of a.e. can be determined. Observations of Eros in 1930-31 yielded a value of the Sun’s parallax as (8.790 + 0.001)” compared to the previously accepted value of (8.803 + 0.001)”. This difference in parallax corresponds to a difference in the distance to the Sun of over 170,000 km.
There are innovative techniques available for measuring astronomical units. One such method involves using radar to measure the distance to planets. For example, when studying Venus, a radar signal is transmitted towards the planet. This signal then reflects off the surface of Venus and returns to the receiver. By determining the speed of radio wave propagation (299,792.458 km/s), calculating the time difference between sending and receiving the signal, and considering the change in distance between the planets during the signal’s travel, scientists can accurately calculate the distance to Venus. This process is similar to how the distance to Eros is determined, allowing for the calculation of astronomical units as well.
When Venus is at its greatest elongation (the furthest visible distance from the Sun), its orbital motion, as observed from Earth, aligns with the line of sight. This alignment causes a shift in the frequency of the returning radar signal due to the Doppler effect. The extent of this frequency shift is directly proportional to Venus’ orbital velocity. By dividing the measured orbital velocity by the orbital velocity calculated using orbital elements, scientists can also obtain the value of astronomical units in kilometers.
The distance from the Earth to the Sun is approximately 150,000,000 kilometers when measured in terrestrial units of length. However, this measurement is not particularly convenient for determining large astronomical distances, as it would require expressing the distances between other planets and objects in the solar system as multi-digit numbers.
Throughout history, astronomers have developed the astronomical unit as a standardized unit of distance measurement in the field of astronomy, which is the study of the Universe. The astronomical unit is primarily used to measure the distance between various objects within our solar system, but its value is also applied in the study of extrasolar systems. In the 17th century, astronomers had the ingenious idea to define the astronomical unit as the distance between the Sun and the Earth. Since then, it has been universally accepted that 1 astronomical unit is equivalent to 149.6 million kilometers.
During the process of developing our understanding of the world, scientists were able to accurately determine the distances within the Solar System. The Sun is the central body of our system, and because the Earth orbits it in a circular path, the distance between the two remains relatively constant. This distance, known as the astronomical unit, is equivalent to the radius of the Earth’s orbit around the Sun. However, during this time period, there was no reliable method for accurately measuring this distance on Earth’s scale. In the 17th century, scientists only had limited knowledge of this data, which was not enough to determine the distance to the Sun, as the ratio between the two was still unknown.

In 1672, Giovanni Cassini, an Italian astronomer, and Jean Richet, a French astronomer, successfully measured the parallax of Mars. As a result, they were able to determine the distance from the Earth to the Sun with great precision, establishing that one astronomical unit equaled 146 million kilometers. Subsequent studies involved even more accurate measurements through the observation of Venus’s orbit. Furthermore, in 1901, the approach of the asteroid Eros to Earth allowed for an even more precise determination of the astronomical unit.

During the past century, refinements were accomplished through the utilization of radar. In the year 1961, the precise location of Venus led to the establishment of a fresh value for the astronomical unit, albeit with an error margin of 2000 kilometers. Subsequent repeat radiolocation of Venus helped to narrow down this inaccuracy to 1000 kilometers. Through years of meticulous measurements, scientists have uncovered that the astronomical unit is gradually increasing at a rate of up to 15 centimeters annually. This remarkable revelation significantly enhances the precision of contemporary astronomical distance measurements. One plausible explanation for this phenomenon could be the reduction in solar mass caused by the solar wind.