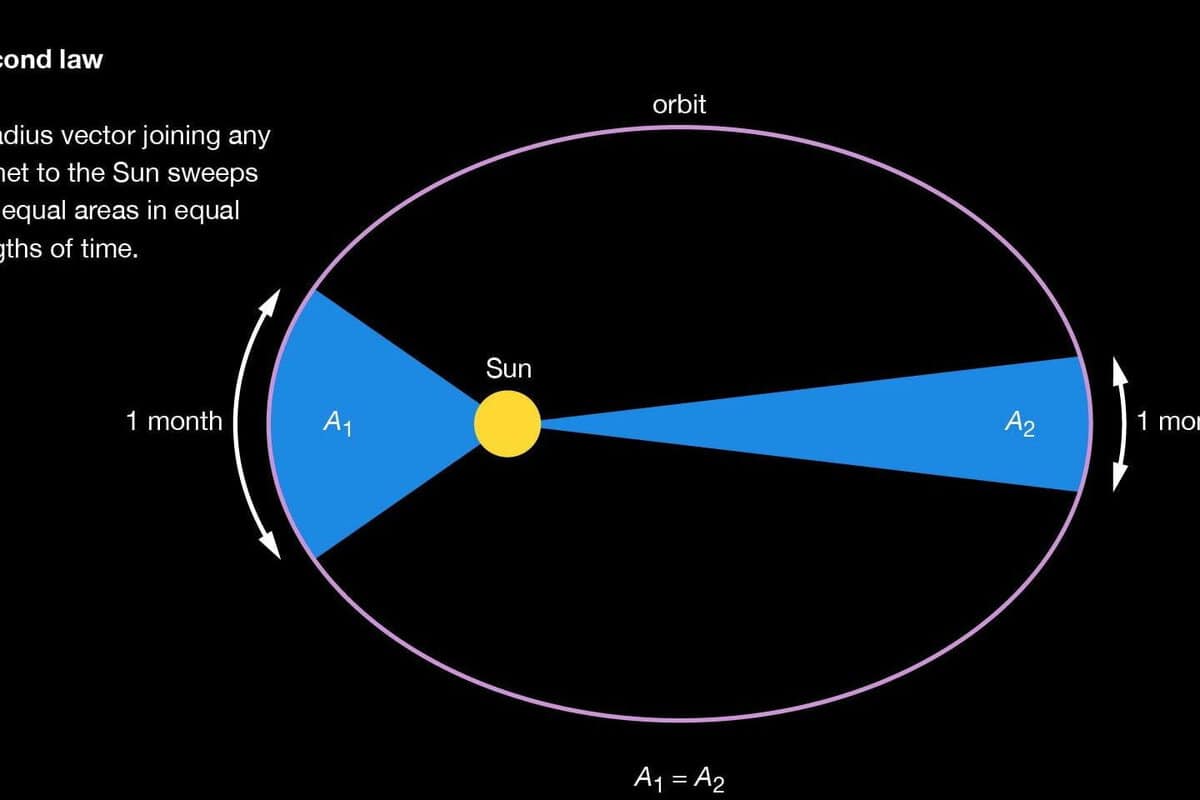
Kepler’s second law, also known as the law of areas, was formulated by Johannes Kepler to explain the peculiar orbit of Mars. According to this law, a celestial body that orbits another body in a stationary system will sweep out equal areas in equal time intervals.
An important consequence of this law is the variation in orbital velocity. When a planet is at its closest point to the Sun, known as perihelion, it will have a higher velocity. Conversely, when it is at its farthest point, aphelion, it will have a lower velocity.
Further reading: Three common errors in the study of universal gravitation
An overview of Kepler’s second principle
- The physicist Johannes Kepler conducted extensive research and made significant observations that led to the formulation of three Kepler’s laws.
- Kepler’s laws were derived from Johannes Kepler’s groundbreaking findings regarding the orbit of Mars.
- Objects revolving around the Sun follow elliptical paths, with the Sun located at one of the foci of the ellipse.
- Kepler’s Second Law states that objects orbiting a stationary body cover equal areas in equal time intervals.
Keep reading! More content awaits after the advertisement 😉
What is the meaning of Kepler’s second law?
Kepler’s second law, also known as the law of areas, was developed by Johannes Kepler (1571-1630) based on observations and data about the eccentric orbit of Mars, which follows an elliptical path and has varying orbital velocities as it approaches and departs from the sun.
The exact wording of Kepler’s second law is as follows:
“The radius-vector connecting a planet to the Sun describes equal areas in equal intervals of time.”
Applying this law to the given figure, we can conclude that if two regions have the same area, such as area 1 and area 2, their transit times will be equal, regardless of their apparent size.
Consequently, variations occur in the orbital velocity, with the velocity being greater when the body is closer to the Sun (perihelion) and lesser when it is farther away (aphelion).
It is important to mention that Kepler’s laws are not limited to the orbits of planets around the Sun; they apply to any two bodies in gravitational interaction where one body is stationary.
For example, natural satellites like the moon orbit around the Earth and Saturn’s moons orbit around Saturn, following these laws. In these cases, the Earth and Saturn serve as the stationary reference points, respectively.
Check out: What would happen if the Earth stopped rotating?
Formula for Kepler’s Second Law
The formula that describes Kepler’s second law is as follows:
- K_1 and A_2 represent the areas covered by the motion, measured in [unit of measurement].
- Δt_1 and Δt_2 represent the changes in time that occur during the displacement, measured in seconds.
When it comes to the displacements of celestial bodies that have equal areas and occur at equal time intervals, Kepler’s second law comes into play.
This law is applicable in various scenarios, such as studying the movement of planets around the sun or other stars, as well as the motion of natural and artificial satellites around planets.
Kepler’s Laws Video Lesson
Exercises Solved on Kepler’s Second Law
(Unesp) Analyze the movement of a celestial body at different points along its orbit around the Sun, as depicted in Figure A. When considering the areas between points A and B and between points C and D, the following can be concluded:
(A) The area covered by the line connecting the celestial body to the Sun is greater between points A and B compared to that between points C and D.
(B) If the shaded areas are equal, the celestial body is moving at a higher velocity between points A and B.
(C) If the shaded areas are equal, the celestial body moves at a faster speed between points C and D.
(D) If the shaded areas are equal, the celestial body is moving at the same velocity in both sections.
(E) If the shaded areas are equal, the time taken by the celestial body to travel from point A to B is greater than that between points C and D.
Option B. According to Kepler’s second law, if the shaded areas are equal, the planet will move faster when it is closer to the Sun at perihelion, and slower when it is farther at aphelion. Therefore, the velocity will be faster at segment AB.
(Unesp) The planet’s orbit is elliptical, with the Sun occupying one of its foci, as shown in the figure (not to scale). The areas bounded by the OPS and MNS curves have an equal area A.
If \(t_{OP}\) and \(t_{MN}\) represent the time intervals during which the planet passes the OP and MN sections, respectively, with average velocities \(v_{OP}\) and \(v_{MN}\), we can conclude that:
B) \(t_{OP} = t_{MN}\) and \(v_{OP} > v_{MN}\)
C) \(t_{OP} = t_{MN}\) and \(v_{OP}\) is less than \(v_{MN}\)
D) \(t_{OP} > t_{MN}\) and \(v_{OP} > v_{MN}\)
Option B. According to Kepler’s second law, the areas enclosed by the boundaries OPS and MNS intersect at equal intervals of time, therefore \(t_OP=t_MN\). Additionally, the velocity at perihelion will exceed that at aphelion, thus \(v_OP>v_MN\).
Pamella Rafaella Melo
Physics instructor
Paraguay River: geographical location, characteristics, and significance
About the Paraguay River: It is one of the most significant rivers in South America, originating in the state of Mato Grosso.
What is the current state of Venezuela-Colombia relations?
The relationship between Venezuela and Colombia has been restored in 2022, marking a significant milestone after a three-year period of strained ties.
Understanding Chalcogenes: their nature and properties
Chalcogenes refer to a group of chemical elements that can be found in group 16 of the Periodic Table. They possess similar characteristics and properties.
An interesting phenomenon related to planetary motion is that a line connecting a planet to the Sun will sweep equal areas in equal time intervals.
Objective of Learning
Main Ideas
- During a short time period, a triangle is formed by the planet with a base and a height. The area is dA = 1/2 – r – rdθ, and the constant area is dA/dt = 1/2 – r² – dθ/dt
- The period P is calculated as Ï€ab = P – 1/2r²Î¸. It can be observed that r 2 must remain constant. When a planet is farther away from the Sun, it moves at a slower pace and vice versa.
- The planet reaches its maximum speed at perihelion and its minimum speed at aphelion.
- Mean motion – the angle formed by 2Ï€ (radians) divided by the orbital period.
- Angular velocity – a vector quantity that describes an object’s motion in a circular path. Its magnitude is equal to the particle’s velocity, and its direction is perpendicular to the plane.
Kepler’s Second Law
Let’s examine the expression of Kepler’s second law for planetary motion. The line connecting the planet and the star sweeps out equal areas in equal time intervals.
Within a short span of time, the planet creates a small triangle with a base and a height. The area is determined as:
Thus, the constant area is equal to:
The planet moves along an ellipse, so its distance from the star varies in different parts of the orbit. The closer the distance to the Sun, the faster the rate of travel.
The total area, as determined by Kepler’s second law, is equal to the sum of the areas enclosed by the elliptical orbit.
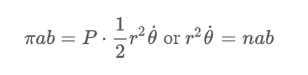
The second law of Kepler is determined by the angular velocity, θ˙ = dθ/dt, and the average motion of the planet around the Sun, n = 2π/P.
An illustration is provided below to demonstrate this phenomenon. The planet covers the same distance between points A and B, C and D, E and F in an equal amount of time. As the planet gets closer to the Sun, its velocity increases, resulting in a larger base of the triangle and a smaller height. The image below depicts Kepler’s second law.
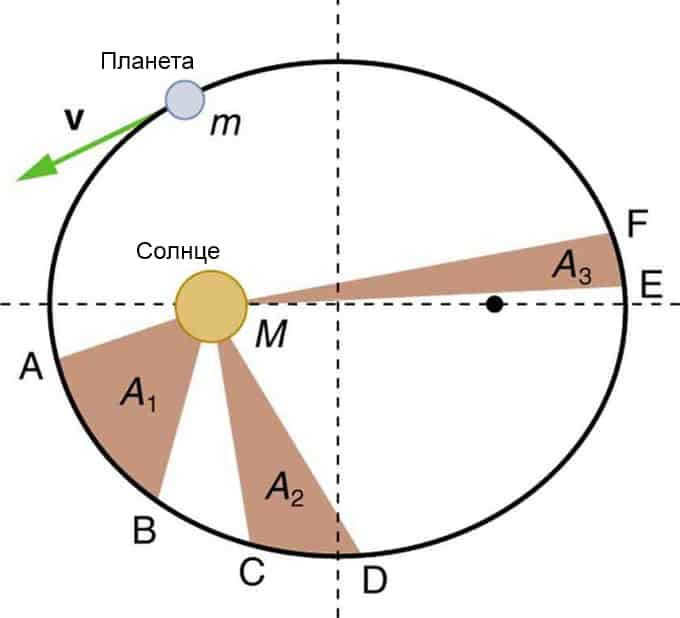
The regions that are shaded have equal areas. For any mass, it will take an equal amount of time to move from point A to point B, from point C to point D, and from point E to point F. The mass moves the fastest when it comes closest to its origin, which is in accordance with Kepler’s Second Law.
A graphical summary of Kepler’s three laws:
1. There are two elliptical orbits with the Sun at focus F1. F2 and a1 represent the other focal point or major semi-axis for Planet 1, while F3 and a2 represent the other focal point or major semi-axis for Planet 2.
2. The two gray sectors A1 and A2, which have the same area, are covered at the same time.
3. The squares of the orbital times for Planet 1 and Planet 2 behave according to the ratio of a13 : a23.
There are three Kepler’s laws which serve as the fundamental principles governing the movement of planets around the Sun. These laws were discovered by Johannes Kepler in the early 17th century as he sought to reconcile Copernicus’ heliocentric model with the precise astronomical observations made by Tycho Brahe. Later, in the late 17th century, Isaac Newton was able to mathematically derive Kepler’s laws using classical mechanics. Newton’s work provided an exact solution to the two-body problem, where two bodies are attracted to each other with a force that diminishes in proportion to the square of the distance between them. Thus, Kepler’s laws are as follows:
Kepler’s First Law states that the planets orbit the Sun in elliptical paths, with the Sun located at one of the focal points of each orbit.
Kepler’s Second Law explains that as a planet moves along its orbit, the line connecting it to the Sun sweeps out equal areas in equal time intervals.
Kepler’s Third Law states that the ratio of the squares of the orbital periods of two planets is equal to the ratio of the cubes of their semi-major axes.
These laws, formulated by Johannes Kepler, are a good approximation for the motion of planets in the solar system. However, there are slight deviations in their positions in the sky, known as orbital irregularities, which are caused by the gravitational interactions between the planets. Additionally, the general theory of relativity provides even smaller corrections to their motion.
Kepler’s laws marked a significant milestone in the shift from medieval to contemporary science and continue to hold immense significance in the field of astronomy to this very day.
Contents
Background
Kepler’s Initial Assumptions
To conduct a more precise investigation, it was initially essential to ascertain the precise paths of the planets. To accomplish this, Kepler had access to the data gathered by Tycho during years of observing the sky. This data was not only much more accurate than any obtained since ancient times (with a maximum uncertainty of about two angular minutes), but it also covered extensive portions of the planetary orbits. In analyzing this data, Kepler was the first to consistently adhere to the guiding principle that the cause behind the planets’ motion resided in the Sun, rather than the imaginary point known as the “mean sun” (introduced by Ptolemy and positioned in the empty space at the center of the Copernican circle assigned to the Earth). Kepler believed that the Sun acted on the planets like a magnet and he meticulously fleshed out this concept.
Kepler’s work was groundbreaking in several ways. Unlike his predecessors, he did not adhere to the conventional belief in uniform circular motion as prescribed by philosophers like Plato and Aristotle. Instead, he took a different approach in analyzing orbits. Kepler aimed to reconstruct the actual paths of planets and their varying speeds directly from sky observations, rather than relying on the epicyclic theory that involved adding additional uniform circular motions to match the observed positions of the planets.
Furthermore, Kepler revolutionized the way his findings were presented, distinguishing himself from other astronomers of his time. Instead of simply presenting a fully developed worldview, Kepler meticulously detailed the step-by-step progress of his years of research, even acknowledging the setbacks and failures he encountered along the way. In 1609, he published the first installment of his groundbreaking work, Astronomia Nova, which bore the subtitle “A new astronomy based on causality, or the physics of the sky, […] according to the observations of the nobleman Tycho Brahe.” This publication not only introduced Kepler’s first two laws, which applied to a single planetary orbit, but also emphasized his reliance on observational evidence from Tycho Brahe. Kepler’s comprehensive explanation of the entire celestial system and the interrelationships between planetary orbits was later published in 1619 as Harmonices mundi (Harmonies of the World). This work included Kepler’s third law, which has since become famous.
Kepler’s initial finding was that both Ptolemy’s and Copernicus’ systems were unable to accurately predict the positions of the planets, even after making certain adjustments, such as modifying eccentricity. Despite this, he continued to utilize these models as an approximation and used Tycho’s observations to determine the most suitable data for a more precise characterization of the orbits. As a result, he discovered that the eccentric orbits of Mars and Earth, in relation to the fixed stars, remained consistent and passed through the plane in which the Sun is located. Additionally, he determined that these two planes were slightly inclined towards each other.
Therefore, Kepler was able to hypothesize that Mars, even though the precise path it followed was still unknown, would occupy the same position in space after each revolution around the Sun. However, when viewed from Earth, Mars would appear in different celestial positions due to the Earth’s varying position in its own orbit. Kepler used this information to initially determine the Earth’s orbit with a high level of accuracy. Based on this, he analyzed other observations of Mars, which showed more pronounced deviations from a circular trajectory compared to Earth. After numerous failed attempts, Kepler discovered that he could not reduce the maximum error in Mars’ position in the sky to less than eight angular minutes (approximately 1/4 the diameter of the full Moon). In a stroke of luck, he stumbled upon the realization that Mars’ orbit could be best represented by an ellipse with the Sun located at one of its focal points. This finding was also consistent with the Earth’s orbit and the observations of other planets made by Tycho. Although Kepler understood that an elliptical trajectory could be composed of two circular motions, he disregarded this possibility. To accurately depict the motion, these circular motions would have to revolve around their respective center points at varying speeds, which lacked an obvious physical explanation:
“Kepler rejected the use of the epicyclic generation of the ellipse because it contradicts the natural causes that generate the ellipse [. ].”
In his subsequent quest to uncover the laws governing the entire solar system, which spanned approximately ten years, Kepler focused on the concept of harmony that underlies the divine plan of creation. Similar to the harmony found in music, he believed that this harmony could be found in simple numerical ratios. In 1619, he published his findings in “Harmonice mundi” (“Harmonies of the world”). However, it is only a brief section in Book 5 of the work that holds lasting significance for future astronomy. In this section, Kepler reveals that the squares of the orbital periods of all the planets are in proportion to the third powers of a large number, which can be understood as the semi-axes of their elliptical orbits.”
Kepler also attempted to find a physical explanation for how the Sun’s influence could cause the observed movements of the planets. However, his hypothesis about magnetic forces acting at a distance, or the the matrix of anima, that exists within the planets, was inconclusive. Later on, Isaac Newton was able to demonstrate that Kepler’s three laws accurately predict the motion of a body under the influence of Newton’s law of gravitation. This discovery is seen as a major advancement in the field of classical mechanics and modern science as a whole.
Heliocentric and fundamental formulation of the laws
Kepler initially established the laws regarding the planets known to him. However, it’s important to note that these laws have a wider applicability, as they hold true everywhere in the universe.
Although the heliocentric model of the solar system is the most significant, the laws are often specifically formulated for planets in literature. Nevertheless, they are equally applicable to moons, the asteroid belt, the Oort cloud, the rings of Jupiter and Saturn, star clusters, and objects orbiting the center of the galaxy, as well as any other celestial objects. These laws also serve as the foundation for space exploration and the orbits of satellites.
Conclusion and contemporary understanding
Kepler endeavored to explain the celestial movements using his laws. Based on the data he collected, particularly regarding the orbit of Mars, he recognized that it could not be a perfect circle. Consequently, unlike Newton’s later theoretical deductions, Kepler’s laws are derived from empirical observations. However, from a modern perspective, we can begin with Newton’s understanding of gravity and therefore validate the validity of Kepler’s laws.
Kepler’s laws can be elegantly derived directly from Newton’s theory of motion.
The first law can be deduced from the Clero equation, which elucidates the comprehensive solution of rotational motion in symmetrical force fields.
The second law is a geometric interpretation of the conservation of angular momentum.
By combining the Kepler equation and the Gauss constant, the third law can be derived either from the second law or, using the hodograph, directly from Newton’s laws. Furthermore, in accordance with the principle of mechanical similarity, it can be directly inferred from the inverse-square relationship between gravity and distance.
Kepler’s first law (ellipse theorem)
This law can be derived from Newton’s law of universal gravitation, assuming that the mass of the central body is much greater than the mass of the satellite and that the influence of the satellite on the central body can be disregarded.
The energy of a satellite with mass in the Newtonian gravitational field of the Sun with mass M is given in cylindrical coordinates by E = E_kin + E_not, where E_kin = 1/2 m (p_dot^2 + p^2 * phi_dot^2) – G * M * m / r.
By using angular momentum, L = m * p^2 * d_phi/dt, we can rewrite the energy equation as:
E = m * (p_dot^2 + p^2 * phi_dot^2) – G * M * m / r.
( d p d Ï• ) 2 sign is equal to 2 m p 4th L. 2 [ E. + gram M. m p – L. 2 2 m p 2 ] > \ right) ^ = 2m > > \ left [E + > – <\ frac <2mr ^ >> \ right]>
to alter the shape. This differential equation is utilized with a representation in polar coordinates
of the conic section. This is accomplished by utilizing the derivative
and all expressions that contain are created by substituting Ï•
The changed trajectory equation is eliminated:
When comparing the coefficients at powers of p, the solution is dependent solely on the specific energy and specific orbital angular momentum. The parameter and numerical eccentricity are important elements in the path design. In this particular case, the following equation holds true: E. / m L. / m p ε 0
The conic section described by r(Ï•) is an ellipse. > r(\ phi) >>. This is known as Kepler’s first law
| Description of the ellipse | a sign is equal to p 1 – ε 2 >>> |
| Minor semi-major axis | b sign equals n 1 – ε 2 <\ sqrt >>>> |
| Tricks | Ф. 1 sign equals ( 0 , 0 ) = (0,0)> Ф. 2 sign equals ( – 2 ε n 1 – ε 2 , 0 ) = \ left (- >>, 0 \ right)>. |
| Pericenter | P. equals sign ( p m i p equals sign n 1 + ε , 0 ) > = >, 0 \ right)> |
| Apocenter | A. sign equals ( – p m a X sign equals – n 1 – ε , 0 ) > = – >, 0 \ right)> |
Two bodies rotate around their common center of gravity –
here the idealized circular trajectories represent a special form of ellipse.
If we consider a gravity field that acts alternatively, rather than a centrally symmetric force field like Kepler’s, elliptical orbits can still be formed. Both bodies are in motion, but the center of the orbits is the common center of gravity of the “central body” and Trabant, with the total mass of the system being treated as a fictitious central mass. However, in the case of the solar system, the common center of gravity of the planets and the Sun (the barycenter of the solar system) is still located within the Sun itself. The Sun is not stationary with respect to it, but instead experiences slight wobbling due to the planets revolving around it (the length of the sun ≠0). On the other hand, in the Earth-Moon system, there are significant variations in orbital geometry, and the center of gravity remains within the Earth. The satellites even respond to fluctuations in the irregular force field caused by the Earth’s shape.
While Kepler’s laws were originally derived for the gravitational force, the aforementioned solution can also be applied to the Coulomb force. In the case of charges that repel each other, the effective potential is always positive, resulting in hyperbolic orbits.
For forces, there is also a conserved quantity that determines the orientation of the elliptical orbit, known as the Runge-Lenz vector, which aligns with the principal axis. Minor variations in the force field (often caused by the influences of other planets) allow this vector to gradually change its orientation. This phenomenon can be elucidated by the perihelion of Mercury’s orbit, 1 / r^2.
Kepler’s Second Law (The Area Theorem)
The line connecting the center of gravity in a celestial body, such as a planet or moon, to the center of gravity, for example, of the sun or planet around which it orbits, is known as the far light.
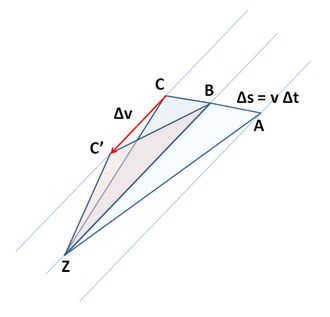
The area of the sweep is calculated for extremely small time steps.
Let F(t, t + dt) be equal to 1/2 p(t) × p'(t) dt, where p'(t) is the derivative of p(t).
Since the angular momentum is caused by the central force,
The derivative of L is m (p’ × p’ + p × p”) = m p × p” = m p × p” = m p × g(p) p = 0.
Therefore, the line integral of the area is constant.
Therefore, the identical coverage area results in identical time differences, where t – t 0 > .
The second law of Kepler defines both the geometric foundation of an astrometric orbit (as a path in the plane) and its orbital dynamics (behavior over time). Kepler originally formulated this law for the orbit of planets around the Sun, but it is also applicable to unclosed orbits. Unlike the other two laws, Kepler’s second law is not restricted to gravitational force (in fact, Kepler also considered force in his matrix of anima), but applies generally to all central forces and motions with constant angular momentum. Although Kepler’s primary focus was on describing planetary orbits, the second law can be seen as the initial formulation of the law now known as the conservation of angular momentum. Additionally, Kepler’s second law can be viewed as a specific formulation of the angular momentum theorem, as well as the law of the twisted surface theorem. 1 / p 2 > 1 / p
Kepler’s second law has two important consequences for the motion of objects in multi-body systems, such as solar systems and space travel. First, the constancy of the orbital normal vector implies that celestial mechanics can be treated as a flat problem. However, this assumption is not entirely accurate due to the presence of celestial bodies with non-zero volumes. As a result, the mass of these bodies lies outside the plane of the orbit and causes the orbit precession planes to shift in space. Consequently, not all planetary orbits are confined to the same plane as the ideal plane of the solar system, known as the ecliptic. These orbits also exhibit inclinations, rotations of the perihelion, and variations in the ecliptic latitude of the Sun. On the other hand, it is relatively straightforward to maneuver a spacecraft within the plane of the solar system. However, it becomes extremely challenging to position a probe over the north pole of the Sun.
Kepler’s third law
The relationship between the squares of orbital times and the cubes of the major semiaxes for two satellites orbiting a common center is expressed by the equation: (T1/T2)2 = (a1/a2)3 >>> \ right) ^ = \ left (> > \ right) ^ > . This is known as Kepler’s third law
Kepler’s third law is applicable to the average distances from the Sun for half of the orbital axes, which refers to the average perihelion distance and aphelion distance. a1, a2 >
S. sign is equivalent to T 2 a 3 > > >>> . The mathematical expression derived from Kepler’s third law, which is a formulation that is independent of mass and includes Kepler’s constant of central mass (known as the Gaussian gravitational constant of the solar system)
In combination with the law of universal gravitation, Kepler established a third law governing the motion of two masses, represented as M and m.
T 2 sign can be expressed as 4th Ï€ 2 grams ( M. + m ) â‹… a 3, which is approximately equal to 4th Ï€ 2 grams M. â‹… a 3 = > > > > \ cdot a ^ \ approximately > > > \ cdot a ^ > . This is Kepler’s third law in the context of a two-mass system.
This approximation is applicable when the mass is significantly smaller than the other mass involved (for example, in the solar system). By using this formulation, the total mass of double star systems can be determined by measuring the orbital period and distance between the two masses, denoted as m and M.
To make Kepler’s third law more accurate, we can use the formula (T1/T2)^2 = (a1/a2)^3 * (M + m2)/(M + m1). This formulation takes into account the different masses of the two celestial bodies. Kepler’s third law, in its three-mass formulation, is represented by the equation.
It is worth noting that the deviation becomes more significant when the masses of the two satellites differ greatly, and the central object has a mass that is similar to one of the satellites. M.
Kepler’s third law is applicable to all forces that decrease quadratically with distance, which can be easily deduced from scale considerations. In the equation.
It appears to the third power and as a square. Therefore, the scaling transformation yields the same equation, if applicable. However, it is easily recognizable that there is now an analog of Kepler’s third law for closed paths in a force field. The equation is as follows: p’ sign equals alpha p, t’ sign equals beta t, alpha cubed sign equals beta squared, and (1/pk) is greater than k times (a1/a2)k+1, which is equal to (T1/T2) squared divided by a_.
Additional Resources
- Hohmann-Transfer: The connection line between two Kepler railroads in space travel.
- Specific angular momentum: A relatively simple derivation of Kepler’s laws based on the conservation of angular momentum.
Recommended Literature
- Johannes Kepler: Astronomia nova aitiologetos seu Physica coelestis. In: Max Caspar (Ed.): Collected Works. Volume 3. C. H. Beck, Munich, 1938.
- Johannes Kepler: Harmonices Mundi Libri V. In: Max Caspar (Ed.): Collected Works. Volume 6. K. H. Beck, Munich 1990, ISBN 3-406-01648-0.
- Andreas Gutmann: Introduction to celestial mechanics and the calculus of ephemerides. BI-Wiss.-Verlag, Mannheim 1994, ISBN 3-411-17051-4.
Web links
- Walter Fendt: 1. Kepler’s Laws , 2. Kepler’s Laws (HTML5 appendices).
- Kepler’s Laws ( LEIFI ).
- Joachim Hoffmüller: 2. Kepler’s law (area theorem): understand the proof with dynamic worksheets. Geometric-descriptive proof by Newton, without higher math ( Java applet ).
- Video: Kepler’s laws of planetary motion . Institute for Scientific Film (IWF) 1978, from available in Library Technical Information ( IRT ), DOI : 10.3203 / FMO / C-1286 .
Unique evidence
- ↑ Thomas S. Kuhn: The Revolution of Copernicus. Vieweg, Brunswick 1980, ISBN 3-528-08433-2 .
- ↑ Karl B. Boyer: A remark on epicycles and the oval from Copernicus to Lahir . In: Isis . Tape 38 , 1947, pp. 54-56 . Kepler's italicized sentence here is provided as a direct translation.
- ↑ Arthur Koestler: The Sleepwalkers: The History of our World Knowledge . Zurkamp, 1980.
- ↑ Bruce Stevenson: Kepler's physical astronomy . Springer Science & Business Media, issue 13, 2012.
- ↑ Martin Holder: Kepler's oval . Universi, Siegen 2015 ( online [PDF; as of November 1, 2017]).
- ↑ Curtis Wilson: How did Kepler discover his first two laws? In: Scientific American . Tape 226 , no. 3 , 1972, pp. 92-107 , JSTOR : 24927297 .
- ↑ Gutmann, § II.1. The problem of one body and two bodies. Introduction, pp. 64 and e. 30. Clero’s equation. C. 71 sl.
- ↑ Gutmann, § II.1.26. The collection of areas. C. 66 f.
- ↑ Gutmann, § II.5. Orbital dynamics of Kepler’s problem. C. 108 ff.
- ↑ David L. Goodstein, Judith R. Goodstein: The lost Feynman lecture: The motion of the planets around the Sun. Piper Verlag GmbH, Munich 1998.
- ^ L. D. Landau and E. M. Lifshitz: Mechanics. 3rd Edition. Butterworth-Heinemann, Oxford, 1976, ISBN 978-0-7506-2896-9, pp. 22-24 (English).
- ↑ J. Wess: Theoretical mechanics. Sweater. Chapter on the problem of two bodies.
Kepler’s Laws are three empirical relationships that were intuitively selected by Johannes Kepler based on his analysis of astronomical observations made by Tycho Brahe. These laws describe the idealized heliocentric orbit of a planet. In the context of classical mechanics, they are derived from solving the two-body problem through the limit transition → 0, where and represent the masses of the planet and the Sun, respectively.
Kepler’s first law (the law of ellipses) [ edit ]
Each planet in the solar system follows a path that is shaped like an ellipse, with the Sun located at one of its foci. The shape of the ellipse and how closely it resembles a circle can be determined by the ratio , where – the distance from the center of the ellipse to its focus (half of the interfocal distance), – the major semi-axis. The value is known as the eccentricity of the ellipse. When , the ellipse becomes a circle.
Newton’s Law of Universal Gravitation states that “every object in the universe attracts every other object along a line that connects the centers of mass of the objects. The strength of this attraction is directly proportional to the mass of each object and inversely proportional to the square of the distance between them.” This means that the acceleration a can be expressed as
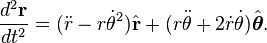
The second law of Kepler is determined by the formula:
The second equation can be rewritten as
After integrating, we get
for a certain constant value , which represents the unique angular momentum ().
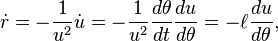
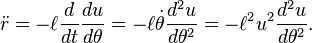
is equivalent to
This equation represents a conical section with eccentricity e and the coordinate system’s origin at one of the foci. Hence, Kepler’s first law can be derived directly from Newton’s law of universal gravitation and Newton’s second law.
Kepler’s second law (also known as the law of areas) [ edit ]
Each celestial body orbits in a plane that passes through the center of its parent star, and over equal periods of time, the line connecting the star and the celestial body sweeps out equal areas.
In our solar system, there are two terms related to this law: perihelion – which is the point in the orbit closest to the star, and aphelion – which is the point furthest from the star. Therefore, it can be deduced from Kepler’s second law that a celestial body moves at different speeds throughout its orbit, with a faster linear velocity at perihelion compared to aphelion.
In early January each year, the Earth moves faster as it passes through perihelion, causing the Sun to appear to move faster along the ecliptic to the east compared to the average speed throughout the year. Conversely, in early July, the Earth moves slower as it passes through aphelion, resulting in a slower movement of the Sun along the ecliptic. The law of areas states that the force governing the orbital motion of planets is directed towards the Sun.
The angular momentum of a point particle with mass and velocity is defined as:
.
,
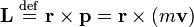where is the angle between the directions and .
.
Let's differentiate both parts of the equation by time
![\frac<d\mathbf<L></p>
<p>> = (\mathbf \times \mathbf) + \left( \frac<d\mathbf> \times m\frac<d\mathbf>[ZEBR_TAG_/p></p><p>ight) = ( \mathbf \times \mathbf ) + ( \mathbf \times \mathbf <p>) = 0 “></p><p>Since the cross product of parallel vectors is zero. It should be noted that <b>F</b> is always parallel to <b>r</b> because the force is radial, and <b>p</b> is always parallel to <b>v</b> by definition. Therefore, it can be stated that, and as a result, its proportional velocity of area sweep remains constant.</p><h2>Kepler’s third law (harmonic law) [ edit ]</h2><p><b>The squares of the periods of revolution of the planets around the Sun are proportional to the cubes of the major semi-axes of the planets’ orbits.</b></p><p>,</p><p>where and represent the periods of revolution of two planets around the Sun, and and represent the lengths of the major semi-axes of their orbits. This statement also holds true for satellites.</p><p>Newton discovered that the gravitational pull of a planet with a specific mass is solely determined by the distance to it, and not by other properties such as composition or temperature. Additionally, he proved that Kepler’s third law is not entirely precise – in fact, it takes into account the mass of the planet:</p><p><img decoding=](/wp-content/uploads/images/what-determines-the-second-law-of-kepler_47.jpg)
,
where is the mass of the Sun, and and are the masses of the planets.
Since the relationship between motion and mass has been established, this combination of Kepler’s harmonic law and Newton’s law of gravitation is utilized to determine the masses of planets and satellites if their orbits and orbital periods are known.
According to Kepler’s second law, the orbiting body’s radius-vector sweeps equal areas in equal time intervals. If we consider very small time intervals at the points A and B (perihelion and aphelion), we can estimate the area using triangles. These triangles have heights equal to the distance between the planet and the Sun, and a base equal to the product of the planet’s velocity and time.
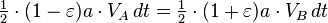
By utilizing the principle of conservation of energy for the total energy of the planet at points A and B, we can express this as
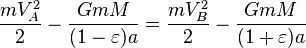
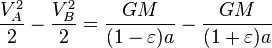
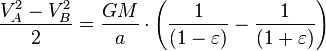
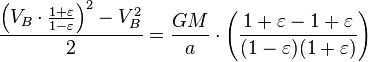
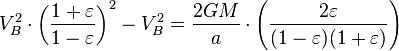
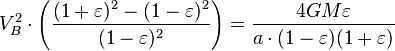
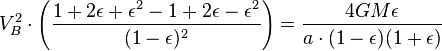
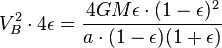
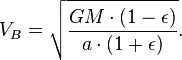
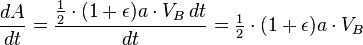
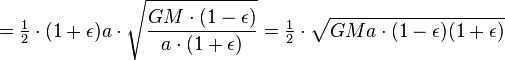
Nevertheless, the overall size of the ellipse is the same as (which is equivalent to , because ). Consequently, the total time for one complete revolution is equal to
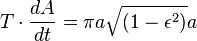
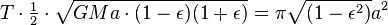
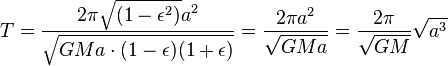
Please note that if the mass m is not negligibly small compared to M, then the planet will orbit the Sun with the same speed and along the same orbit as a material point orbiting a mass (see reduced mass). In this case, the mass M in the last formula should be replaced by:
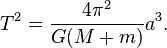
Consider a planet as a point of mass m orbiting in an elliptical orbit, in two positions:
- perihelion with radius vector , velocity ;
- aphelion with radius vector , velocity .
Now, we will proceed to write the laws of conservation of momentum and energy. Let’s represent the law of conservation of momentum by the equation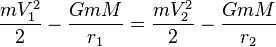 
, where M represents the mass of the Sun. By solving the system, we can easily derive the velocity ratio for the planet at the “perihelion” point as 
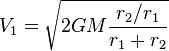. Next, let’s express the sector velocity (which remains constant according to Kepler’s second law) as 
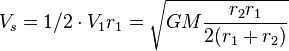. Now, we can calculate the area of the ellipse along which the planet moves. On one hand, we have the length of the major semi-axis (a) and the length of the minor semi-axis (b) of the orbit. On the other hand, we can utilize the fact that we can multiply the sector velocity by the revolution period to calculate the sector area as 
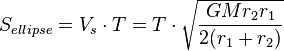. Thus, we get the equation . For further transformations, let’s use the geometrical properties of the ellipse. We have the following relations: Substituting these relations into the formula for the area of the ellipse, we get 
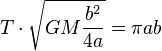. Hence, we finally obtain the equation: or in the traditional form.
Literature [ edit ]
- Kepler’s Laws // Encyclopedic Dictionary of Young Astronomer / compiled by N. P. Yerpylev. N. P. Erpylev . – 2nd ed. – M.: Pedagogy, 1986. – P. 121-122. – 336 p.
- Smorodinsky Ya. A.Planets follow elliptical paths // Quantum. – 1979. -. -.
| The laws of Newton – Law of Universal Gravitation – The Laws of Kepler – The problem of two bodies – The problem of three bodies – The problem of N-body gravitational – The problem of Bertrand – Kepler’s equation |
| The system of celestial coordinates Galactic – Horizontal – First Equatorial – Second Equatorial – Ecliptic – International Celestial Coordinate System – Spherical Coordinate System – World Axis – Celestial Equator – Right Ascension – Declination – Ecliptic – Equinox – Solstice – Fundamental Plane |
| Keplerian orbital elements: Eccentricity – Major semi-axis – Mean anomaly – Longitude of ascending node – Argument of pericenter – Apocenter and pericenter – Orbital velocity – Orbital node – Epoch |
| Motion of the Sun and planets on the celestial sphere – Ephemerides Planetary configurations: opposition – conjunction – square – elongation – parade of planets Eclipse: solar eclipse – lunar eclipse – saros – Metonic cycle – Coverage – Passage Culmination – Sidereal period – Synodic period – Rotation period – Orbital resonance – Precession of equinoxes – Convergence – Libration – Sphere of gravity – Kozai effect – Yarkovsky effect – Janibekov effect |
| Space velocity: first (circular) – second (parabolic) – third – fourth Tsiolkovsky’s formula – Gravitational maneuver – Goman trajectory – Osculating element method – Tidal acceleration – Change of orbital inclination – Interplanetary transportation network – Docking – Lagrange points – Pioneer effect |
| Geostationary orbit – Heliocentric orbit – Geosynchronous orbit – Geocentric orbit – Geo-transition orbit – Low Earth orbit – Polar orbit – Tundra orbit – Sun-synchronous orbit – Lightning orbit – Oscillating orbit |
As you are aware, Nicolaus Copernicus’s groundbreaking concept of a heliocentric world order provided a tremendous impetus to the advancement of astronomy. However, it is worth noting that Copernicus did not completely discard Aristotle’s notions regarding the “perfection” of planetary orbits. It was only in the early 17th century that Austrian astronomer Johannes Kepler unraveled the kinematic principles governing the motion of planets. In this lesson, we will delve into the formulations of Kepler’s three laws, as well as explore their significance in the subsequent progress of astronomy.
Unfortunately, you are currently unable to watch or distribute the instructional video with your students
In order to gain access to this and other video lessons within the package, you will need to incorporate it into your personal account.
Obtain astounding prospects
Outline for the Lesson on “The Laws Governing the Motion of Planets in the Solar System”
As we are aware, Nicolaus Copernicus introduced a groundbreaking concept of a heliocentric system which greatly advanced the field of astronomy. Nonetheless, it is important to note that Copernicus did not entirely discard Aristotle’s notion of the planets’ orbits being “perfect.” Consequently, his theory incorporated the use of epicycles and deferents to account for various phenomena, including the retrograde motion of planets.
Meanwhile, numerous scientists held the belief that celestial bodies should move uniformly and along the most perfect curve, namely, the circle. Consequently, they struggled to accurately predict the relative positions of planets for several years in advance until the late 16th century. This theory resulted in significant discrepancies when compared to observational data.
It wasn’t until the early 17th century that Austrian astronomer Johannes Kepler discovered the kinematic laws governing planetary motion. In his quest, he drew inspiration from the notion that numbers govern the world, a concept first expressed by Pythagoras. Kepler endeavored to establish connections between the motion of planets and the regularities found in musical scales, the lengths of polygons inscribed and circumscribed within planetary orbits, and so forth.
Unfortunately, every time Kepler compared his model with the observed paths of the planets, he had to acknowledge that their actual behavior did not fit within the elegant framework he had outlined. As the contemporary British biologist John Haldane aptly pointed out, “the concept of the universe as a geometrically flawless masterpiece turned out to be another beautiful hypothesis, shattered by unsightly facts.”
It wasn’t until he relocated to Prague and became a pupil of the Danish astronomer Tycho Brahe that Kepler encountered the concepts that would truly immortalize his name in the history of science.
Imagine the challenge that Kepler encountered in the following way. We find ourselves on a planet that, firstly, rotates on its axis, and secondly, revolves around the Sun in an unknown orbit. When we look up into the sky, we observe other planets also moving in orbits that are unknown to us. The question arises: how can we determine the orbit and velocity of these other planets based on observations made on a single ball rotating around an axis and around the Sun?
Even with the aid of modern computers, this question appears to be quite complex. However, Kepler, who had no such technology at his disposal, was able to find the solution!
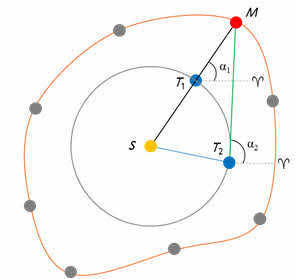
T1 – represents the Earth’s location during the opposition with Mars.
For Mars to return to the same position in its orbit, 687 days need to elapse (this is Mars’ sidereal period). The Earth has a sidereal period of 365 days. Consequently, it won’t have enough time to reach point T1 and will be at point T2 in its orbit at that moment. As a result, the direct ascent of Mars will appear different to the observer. By studying various oppositions of Mars, Kepler obtained a sequence of points. By connecting them with a smooth curve, he constructed the orbit of this planet, which turned out to be non-circular.
Kepler was confronted with a decision between two potential solutions: either to consider that the orbit of Mars is circular and that the calculated coordinates of the planet diverge from observations in certain parts of the orbit, or to believe that all observations were accurate and that the planet’s orbit is not actually a circle. Confident in the precision of his own observations as well as those of Tycho Brahe, Kepler opted for the latter solution and discovered that the optimal positions of Mars in its orbit align with a curve known as an ellipse. In this scenario, the Sun is not positioned at the center of the ellipse. As a result, he formulated a law that would later be referred to as Kepler’s first law: all planets revolve around the Sun on ellipses with the Sun situated at one of their focal points.
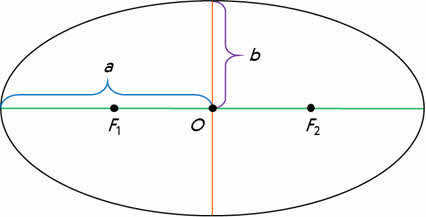
In the given diagram, point O represents the center of the ellipse, and F1 and F2 are the focal points of the ellipse.
The line passing through the focal points of the ellipse, with its endpoints lying on the ellipse, is known as the major axis of the ellipse.
Similarly, the line passing through the center of the ellipse and perpendicular to the major axis is referred to as the minor axis of the ellipse.
The segments drawn from the center of the ellipse to the vertices on the major and minor axes are respectively known as the major semi-major axis and minor semi-axis of the ellipse. These segments are denoted by the lowercase letters a and b.
The distinction between an ellipse and a circle is determined by the extent of its eccentricity. This value is equivalent to one-half of the quotient of the focal distance of the ellipse and its major semi-axis:
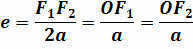
It should be noted that in the event that the eccentricity of the ellipse is zero, the focal points and the center of the ellipse combine into one point – transforming the ellipse into a circle.
Now let’s consider a scenario where the Sun is situated at the focus of the ellipse, F1. In this case, the closest point of the planet’s orbit to the Sun is referred to as the perihelion. Conversely, the point farthest from the Sun is known as the aphelion.
For instance, the Earth’s orbit has an eccentricity of 0.017, which means that the orbit is nearly circular. The perihelion of our planet occurs at the beginning of January, with a distance to the Sun of approximately 147 million kilometers. On the other hand, the aphelion of the Earth takes place in early July, and the aphelion distance measures just over 152 million kilometers.
Returning to Kepler and his calculation of Mars’ path, he observed that the speed at which Mars orbits changes. Simultaneously, the line connecting the Sun’s center to the planet’s center (known as the radius vector) traces out equal areas at consistent time intervals.
Later referred to as Kepler’s second law (also known as the law of areas).
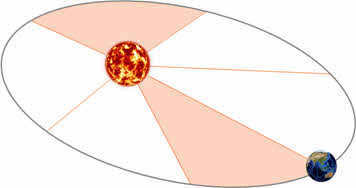
In order to grasp its physical significance, let’s recall your childhood memories. Without a doubt, you must have had the opportunity to twirl around a pole on the playground, gripping it with your hands. In truth, the planets revolve around the Sun in a comparable manner. The planet’s motion is slower the further it is from the Sun, tracing an elliptical orbit, while it moves faster the closer it gets to the Sun.
The law of conservation of energy can provide an explanation for this legislation. As you may know from physics, the overall mechanical energy of a closed system consisting of bodies that experience gravitational forces remains constant regardless of the movements of the bodies within the system. Therefore, the total sum of the planet’s kinetic and potential energies, as it orbits around the Sun, remains constant at every point along its orbit. As the planet approaches the Sun, its potential energy decreases due to the decreasing distance. Consequently, its kinetic energy must increase, which can only occur by increasing its velocity.
Consequently, the speed of the planet’s orbit fluctuates, reaching its maximum value at perihelion and its minimum at aphelion.
Kepler did not formulate his third law until 1618. The law states that the squares of the sideric orbital periods of two planets are proportional to the cubes of the major semi-axes of their orbits:
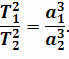
Kepler himself expressed his thoughts on this matter, stating: “The very thing I set out to find 16 years ago has finally been discovered, and this revelation has exceeded all of my wildest expectations.”
Undoubtedly, the third law is deserving of the utmost praise. It enables us to determine the relative distances between the planets and the Sun, utilizing their already known orbital periods. In doing so, there is no need to individually calculate the distance from the Sun to each planet; it suffices to measure this distance for just one of them, such as the Earth. Additionally, for the sake of simplicity in calculations, the major semi-axis of the Earth’s orbit was assigned a value of one astronomical unit (1 a. e.). This unit then served as the foundation for calculating all other distances within the Solar System.
Once more, we would like to emphasize that Kepler derived his laws solely from his personal observations and those of Tycho Brahe. In the event that you were to inquire about the cause of the elliptical shape of the orbits or the equal areas of the sectors, he would be unable to provide an answer. These conclusions were simply the result of his analysis. Furthermore, if you were to inquire about the orbital motion of planets in other stellar systems, he would be equally without a response.
